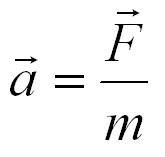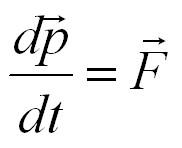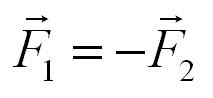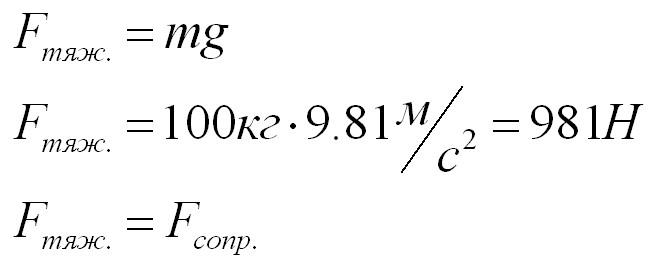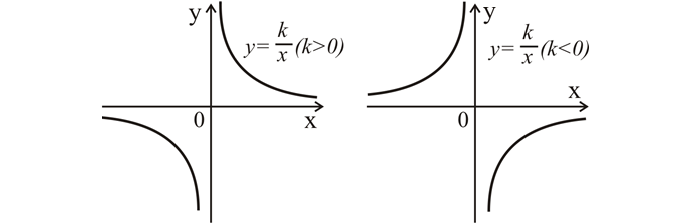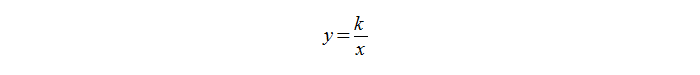Математическая концепция двух различных величин, связанных константой 

В математике две различные величины, как говорят, находятся в отношении пропорциональности, если они мультипликативно связаны с константой ; то есть, когда их соотношение или их произведение дает константу. Значение этой константы называется коэффициентом пропорциональности или константой пропорциональности .
- Если отношение (y / x) двух переменных (x и y) равно константе (k = y / x), то переменная в числителе отношения (y) является произведением другой переменной и константы (y = k⋅x). В этом случае говорят, что y прямо пропорционален x с константой пропорциональности k. Эквивалентно можно написать x = 1 / k⋅y; то есть x прямо пропорционален y с константой пропорциональности 1 / k (= x / y). Если термин пропорциональный связан с двумя переменными без дальнейших уточнений, обычно можно предположить прямую пропорциональность.
- Если произведение двух переменных (x⋅y) равно константе (k = x⋅y), тогда говорят, что эти два обратно пропорциональны друг другу с константой пропорциональности k. Эквивалентно, обе переменные прямо пропорциональны обратной величине соответствующей другой с константой пропорциональности k (x = k⋅1 / y и y = k⋅1 / x).
Если несколько пар переменных имеют одну и ту же константу прямой пропорциональности, уравнение , выражающее равенство этих соотношений, называется пропорцией, например, a / b = x / y =… = k (подробнее см. Соотношение ).
Содержание
- 1 Прямая пропорциональность
- 1.1 Примеры
- 2 Обратная пропорциональность
- 3 Гиперболические координаты
- 4 См. Также
- 4.1 Рост
- 5 Примечания
- 6 Ссылки
Прямая пропорциональность
Для двух переменных x и y, y прямо пропорционален x, если существует ненулевая константа k такая, что
- y = kx. { displaystyle y = kx.}
См. Также: Знак равенства |
Отношение часто обозначается с помощью символов «∝» (не путать с греческой буквой альфа ) или «~»:
- y ∝ x, { displaystyle y propto x,}
или y ∼ x. { displaystyle y sim x.}
для x ≠ 0 { displaystyle x neq 0}
- k = yx. { Displaystyle k = { frac {y} {x}}.}
Его также называют постоянной вариации или константой пропорциональности .
Прямая пропорциональность также может рассматриваться как линейное уравнение в двух переменных с пересечением по оси y, равным 0, и наклоном, равным k. Это соответствует линейному росту.
Примеры
- Если объект перемещается в постоянной скорости, то пройденное расстояние прямо пропорционально времени, затраченному на поездку, при этом скорость является константой пропорциональности.
- длина окружности круга прямо пропорциональна его диаметру, с константой пропорциональности, равной π.
- . На карте достаточно малая географическая область, нарисованная на расстоянии масштаба, расстояние между любыми двумя точками на карте прямо пропорционально прямому расстоянию между двумя местоположениями, представленными этими точками; константа пропорциональности — это масштаб карты.
- Сила , действующая на небольшой объект с малой массой ближайшей большой протяженной массой из-за гравитация, прямо пропорциональна массе объекта; константа пропорциональности между силой и массой известна как ускорение свободного падения.
- Чистая сила, действующая на объект, пропорциональна ускорению этого объекта по отношению к инерциальной системе отсчета. Константа пропорциональности в этом, втором законе Ньютона, является классической массой объекта.
Обратная пропорциональность

Концепция обратную пропорциональность можно противопоставить прямой пропорциональности. Рассмотрим две переменные, которые считаются «обратно пропорциональными» друг другу. Если все другие переменные остаются постоянными, величина или абсолютное значение одной обратно пропорциональной переменной уменьшается, если другая переменная увеличивается, в то время как их произведение (константа пропорциональности k) всегда одинаково. Например, время, затрачиваемое на поездку, обратно пропорционально скорости движения.
Формально две переменные обратно пропорциональны (также называемые, изменяющиеся обратно, в обратном изменении, в обратной пропорции, в обратной пропорции ), если каждая из переменных прямо пропорциональна мультипликативной обратной (обратной) другой, или эквивалентно, если их произведение является константой. Отсюда следует, что переменная y обратно пропорциональна переменной x, если существует ненулевая константа k такая, что
- y = kx, { displaystyle y = { frac {k} {x}},}
или, что эквивалентно, xy = k. { displaystyle xy = k.}
График двух переменных, изменяющихся обратно пропорционально на плоскости декартовых координат, представляет собой прямоугольную гиперболу . Произведение значений x и y каждой точки кривой равно коэффициенту пропорциональности (k). Поскольку ни x, ни y не могут равняться нулю (поскольку k не равно нулю), график никогда не пересекает ни одну ось.
Гиперболические координаты
Понятия прямой и обратной пропорции приводят к расположению точек на декартовой плоскости по гиперболическим координатам ; две координаты соответствуют константе прямой пропорциональности, которая определяет точку как находящуюся на определенном луче , и константе обратной пропорциональности, которая определяет точку как находящуюся на определенной гиперболе.
См. Также
- Линейная карта
- Корреляция
- Евдокс Книдский
- Золотое сечение
- Закон обратных квадратов
- Пропорциональный шрифт
- Соотношение
- Правило трех (математика)
- Размер выборки
- Сходство
- Основная теорема пропорциональности
Рост
- Линейный рост
- Гиперболический рост
Примечания
Литература
- Я. Б. Зельдович, И. М. Яглом : Высшая математика для начинающих, с. 34–35.
- Брайан Бурелл: Руководство Мерриам-Вебстера по повседневной математике: Справочник по дому и бизнесу. Merriam-Webster, 1998, ISBN 9780877796213 , стр. 85–101.
- Lanius, Cynthia S.; Уильямс Сьюзан Э.: ПРОПОРЦИОНАЛЬНОСТЬ: объединяющая тема для средних классов. Преподавание математики в средней школе 8.8 (2003), стр. 392–396.
- Сили, Кэти; Шилак Джейн Ф.: Взгляд на развитие соотношений, ставок и пропорциональности. Преподавание математики в средней школе, 13.3, 2007 г., стр. 140–142.
- Ван Дурен, Вим; Де Бок Дирк; Эверс Марлен; Вершаффель Ливен: Чрезмерное использование учениками принципа пропорциональности при решении проблем с пропущенными значениями: как числа могут изменить решения. Журнал исследований в области математического образования, 40.2, 2009 г., стр. 187–211.
Содержание
- Законы Ньютона
- Что такое сила
- Смысл законов Ньютона
- Первый закон Ньютона
- Второй закон Ньютона
- Формула второго закона Ньютона с пояснениями
- Третий закон Ньютона
- Прямая и обратная пропорциональность
- Основные определения
- Прямо пропорциональные величины
- Обратно пропорциональные величины
- Потренируемся
- Законы Ньютона для «чайников»: объяснение 1, 2, 3 закона, пример с формулами
- Первый закон Ньютона
- Второй закон Ньютона
- Третий закон Ньютона
- Пример задачи на законы Ньютона
- Исаак Ньютон: мифы и факты из жизни
Законы Ньютона
Ньютон первым обратил внимание на силу, как причину, по которой тела приходят в движение и меняют свою скорость.
Раздел механики, изучающий силы, называется динамикой. По-гречески «динамис», значит «сила».
Что такое сила
Тела действуют друг на друга с помощью сил.
Сила – это мера взаимодействия тел. Измеряя силу, мы измеряем величину взаимного действия тел. В обыденной жизни мы говорим: «как сильно» одно тело действует на другое тело.
Смысл законов Ньютона
Ньютон, в своих законах динамики, хотел сказать следующее:
- В I законе: Если сила не действует, скорость не меняется. Импульс тела тоже не меняется.
- Во II законе: Если сила действует, скорость меняется. Импульс тела, также, меняется, появляется ускорение.
- В III законе: Взаимодействуют два тела — возникают две силы. Они по модулю равны, а по направлению противоположны.
Примечание:
Выражение «векторы равны по модулю», понимаем так: «длины векторов одинаковые».
Перед изучением законов Ньютона рекомендую вспомнить, что такое инерциальные системы отсчета (откроется в новой вкладке).
Первый закон Ньютона
Словесная формулировка первого закона Ньютона:
В инерциальной системе отсчета тело свою скорость не меняет, если на него не действуют другие тела (или действие других тел скомпенсировано).
Формула:
( F = 0 ) – сила на тело не действует (Может быть и так: на тело действуют несколько сил, но их действие компенсируется);
( a = 0 ) – ускорение отсутствует;
( v = const ) – скорость тела не изменяется (остается одной и той же);
( p = const ) – импульс тела не изменяется (остается одним и тем же);
Важно! По первому закону Ньютона, «двигаться с одной и той же скоростью по прямой» и «покоиться» — это равнозначные виды движения.
Значит, если на тело не действуют другие тела (силы), то
- тело будет двигаться с одной и той же скоростью по прямой, если оно так двигалось до этого,
- или будет продолжать покоиться, если покоилось в прошлом.
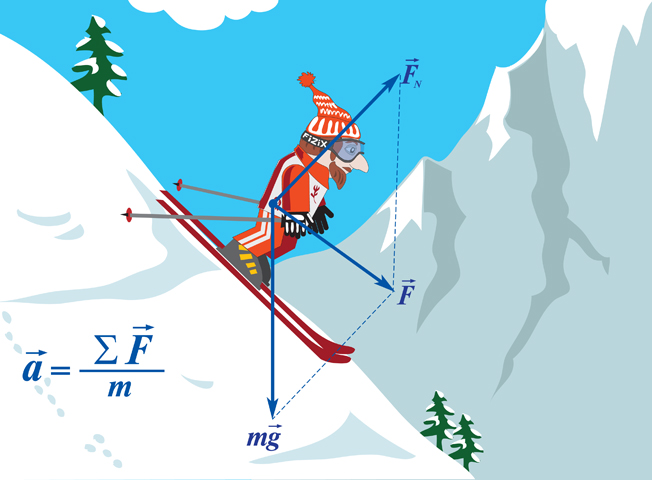
Второй закон Ньютона
Сформулируем словами второй закон Ньютона:
Ускорение, приобретаемое телом,
прямо пропорционально
приложенной силе
и обратно пропорционально
массе этого тела.
Формула второго закона Ньютона с пояснениями
( a left( frac<text<м>>> right) ) – ускорение тела
( m left( text <кг>right) ) – масса тела
( F left( H right) ) – сила, которую приложили к телу
Примечание: Ускорение отвечает на вопрос: «Как быстро меняется скорость тела?». Значит, если изменяется хотя бы одна из характеристик вектора скорости, ускорение есть. А если скорость не изменяется, ускорения нет ( vec < a >= 0 )
Ускорение прямо пропорционально силе:
Чем больше сила, тем больше ускорение тела, тем быстрее тело меняет скорость.
Ускорение обратно пропорционально массе:
Чем больше месса тела, тем труднее изменить его скорость.
Формулу второго закона часто записывают в векторном виде:
Мы можем заменить местами правую и левую части, в таком случае получим:
Расшифруем эту запись: Возьмем вектор «F», умножим его на скаляр (1/m) и получим новый вектор «a».
Дробь ( displaystyle frac<1> ) – это скалярная величина.
Примечания:
- Вместо слов «направлены в одну и ту же сторону» физики пользуются термином «сонаправлены». Лично мне удобнее пользоваться первой формулировкой.
- Часто применяют еще один вид записи, его называют так: «Второй закон Ньютона в импульсной форме».
Третий закон Ньютона
Пусть одно тело действует на второе тело. Тогда это второе тело будет в ответ действовать на первое.
Словами третий закона Ньютона можно сформулировать так:
Силы взаимного действия по модулю равны, а направлены противоположно. Они лежат на прямой, которая соединяет центры тел, действующих друг на друга.
( F_ <12>left( H right) ) – сила, с которой первое тело действует на второе тело.
( F_ <21>left( H right) ) – сила, с которой второе тело отвечает первому.
Пояснить формулу можно с помощью такого рисунка:
Обратите внимание, что длины красного и черного векторов равны.
Не важно, перед каким из векторов находится знак «минус». Этот знак показывает, что векторы направлены в противоположные стороны. Поэтому, формулу третьего закона Ньютона можно записать и так:
Примечания:
- Если перед каким-либо вектором записан знак «минус», то этот вектор развернут в противоположную от выбранной нами сторону.
- Между векторами находится знак равенства. Это значит, что длины векторов одинаковые (векторы по модулю равны).
Советую прочитать еще две статьи. Так как для решения задач кроме знания трех законов Ньютона нужно дополнительно уметь:
- находить проекции вектора на оси и
- составлять векторные силовые уравнения (ссылки открываются в новых вкладках).
Источник
Прямая и обратная пропорциональность
О чем эта статья:
Основные определения
Математическая зависимость — это соответствие между элементами двух множеств, при котором каждому элементу одного множества ставится в соответствие элемент из другого множества.
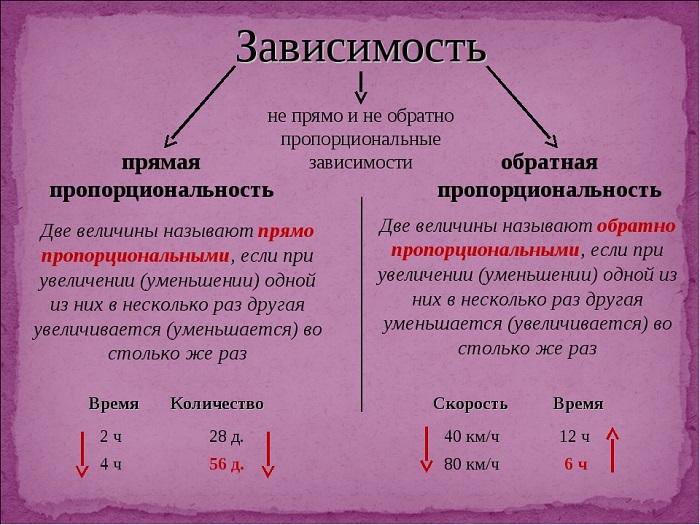
- Прямая зависимость. Чем больше одна величина, тем больше вторая. Чем меньше одна величина, тем меньше вторая величина.
- Обратная зависимость. Чем больше одна величина, тем меньше вторая. Чем меньше одна величина, тем больше вторая.
Пропорция в математике — это равенство между отношениями двух или нескольких пар чисел или величин. Пропорциональными называются две взаимно-зависимые величины, если отношение их значений остается неизменным.
Пропорциональность — это взаимосвязь между двумя величинами, при которой изменение одной из них влечет за собой изменение другой во столько же раз. Проще говоря — это зависимость одного числа от другого.
Есть две разновидности пропорциональностей:
- Прямая пропорциональность. Это зависимость, при которой увеличение одного числа ведет к увеличению другого во столько же раз. А уменьшение одного числа ведет к уменьшению другого во столько же раз.
- Обратная пропорциональность. Это зависимость, при которой уменьшение одного числа ведет к увеличению другого во столько же раз. А увеличение числа наоборот ведет к уменьшению другого во столько же раз.
Коэффициент пропорциональности — это неизменное отношение пропорциональных величин. Он показывает, сколько единиц одной величины приходится на единицу другой. Коэффициент пропорциональности обозначается латинской буквой k.
Прямо пропорциональные величины
Две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая увеличивается (или уменьшается) во столько же раз.
Прямая пропорциональность в виде схемы: «больше — больше» или «меньше — меньше».
a и d называются крайними членами, b и c — средними.
Свойство прямо пропорциональной зависимости:
Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.
Примеры прямо пропорциональной зависимости:
- при постоянной скорости пройденный маршрут прямо-пропорционально зависит от времени;
- периметр квадрата и его сторона — прямо-пропорциональные величины;
- стоимость конфет, купленных по одной цене, прямо-пропорционально зависит от их количества.
Если говорить метафорами, то прямую пропорциональную зависимость можно отличить от обратной по пословице: «Чем дальше в лес, тем больше дров». Что значит, чем дольше ты идешь по лесу, тем больше дров можно собрать.
Формула прямой пропорциональности
y = kx,
где y и x — переменные величины, k — постоянная величина, которую называют коэффициентом прямой пропорциональности.
Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных y и x, равное одному и тому же числу.
Формула коэффициента прямой пропорциональности:
Пример 1.
В одно и то же путешествие поехали два автомобиля. Один двигался со скоростью 70 км/ч и за 2 часа проделал тот же путь, что другой за 7 часов. Найти скорость второго автомобиля.
- Вспомним формулу для определения пути через скорость и время: S = V * t.
- Так как оба автомобиля проделали одинаковый путь, можно составить пропорцию из двух выражений: 70 * 2 = V * 7
- Найдем скорость второго автомобиля: V = 70 * 2/7 = 20
Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Пример 2.
Блогер за 8 дней может написать 14 постов. Сколько помощников ему понадобится, чтобы написать 420 постов за 12 дней?
Количество человек (блогер и помощники) увеличивается с увеличением объема работы, если ее нужно сделать за то же количество времени.
Если разделить 420 на 14, узнаем, что объем увеличивается в 30 раз.
Но так как по условию задачи на работу дается больше времени, то количество помощников увеличивается не в 30 раз. Таким образом:
- х = 1 (блогер) * 30 (раз) : 12/8 (дней).
- х = 1 * 30 : 12/8
- х = 20
Ответ: 20 человек напишут 420 постов за 12 дней.
Обратно пропорциональные величины
Две величины называют обратно пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая уменьшается (или увеличивается) во столько же раз.
Объясним, что значит обратно пропорционально в виде схемы: «больше — меньше» или «меньше — больше».
Свойство обратной пропорциональности величин:
Если две величины находятся в обратно пропорциональной зависимости, то отношение двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.
Примеры обратно пропорциональной зависимости:
- время на маршрут и скорость, с которой путь был пройден — обратно пропорциональные величины;
- при одинаковой продуктивности количество школьников, решающих конкретную задачу, обратно пропорционально времени выполнения этой задачи;
- количество конфет, купленных на определенную сумму денег, обратно пропорционально их цене.
Формула обратной пропорциональности
где y и x — это переменные величины,
k — постоянная величина, которую называют коэффициентом обратной пропорциональности.
Коэффициент обратной пропорциональности — это произведение любых соответствующих значений обратно пропорциональных переменных y и x, равное одному и тому же числу.
Формула коэффициента обратной пропорциональности:
Потренируемся
Пример 1. 24 человека за 5 дней раскрутили канальчик в ютубе. За сколько дней выполнят ту же работу 30 человек, если будут работать с той же эффективностью?
- В заполненном столбце стрелку ставим в направлении от большего числа к меньшему.
- Чем больше людей, тем меньше времени нужно для выполнения определенной работы (раскрутки канала). Значит, это обратно пропорциональная зависимость.
- Поэтому направим вторую стрелку в противоположную сторону. Обратная пропорция выглядит так:
- Пусть за х дней могут раскрутить канал 30 человек. Составляем пропорцию: 30 : 24 = 5 : х
- Чтобы найти неизвестный член пропорции, нужно произведение средних членов разделить на известный крайний член: х = 24 * 5 : 30; х = 4
- Значит, 30 человек раскрутят канал за 4 дня.
Пример 2. Автомобиль проезжает от одного города до другого за 13 часов со скоростью 75 км/ч. Сколько времени ему понадобится, если он будет ехать со скоростью 52 км/ч?
Скорость и время связаны обратно пропорциональной зависимостью: чем больше скорость, тем меньше времени понадобится.
- Составим пропорцию: v1/v2 = t2/t1.
Соотношения равны, но перевернуты относительно друг друга.
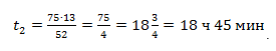
Источник
Законы Ньютона для «чайников»: объяснение 1, 2, 3 закона, пример с формулами
- 22 февраля 2021 г.
- 13 минут
- 783 302
Мы уже говорили об основах классической механики. Настала пора поговорить о них подробнее и затронуть в обсуждении чуть больше, чем просто основу. В этой статье мы подробно разберем основные законы классической механики. Как вы уже догадались, речь пойдет о законах Ньютона.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Основные законы классической механики Исаак Ньютон (1642-1727) собрал и опубликовал в 1687 году. Три знаменитых закона были включены в труд, который назывался «Математические начала натуральной философии».
Был долго этот мир глубокой тьмой окутан
Да будет свет, и тут явился Ньютон.
(Эпиграмма 18-го века)
Но сатана недолго ждал реванша —
Пришел Эйнштейн, и стало все как раньше.
(Эпиграмма 20-го века)
Что стало, когда пришел Эйнштейн, читайте в отдельном материале про релятивистскую динамику. А мы пока приведем формулировки и примеры решения задач на каждый закон Ньютона.
Первый закон Ньютона
Первый закон Ньютона гласит:
Существуют такие системы отсчета, называемые инерциальными, в которых тела движутся равномерно и прямолинейно, если на них не действуют никакие силы или действие других сил скомпенсировано.
Проще говоря, суть первого закона Ньютона можно сформулировать так: если мы на абсолютно ровной дороге толкнем тележку и представим, что можно пренебречь силами трения колес и сопротивления воздуха, то она будет катиться с одинаковой скоростью бесконечно долго.
Инерция – это способность тела сохранять скорость как по направлению, так и по величине, при отсутствии воздействий на тело. Первый закон Ньютона еще называют законом инерции.
До Ньютона закон инерции был сформулирован в менее четкой форме Галилео Галилеем. Инерцию ученый называл «неистребимо запечатленным движением». Закон инерции Галилея гласит: при отсутствии внешних сил тело либо покоится, либо движется равномерно. Огромная заслуга Ньютона в том, что он сумел объединить принцип относительности Галилея, собственные труды и работы других ученых в своих «Математических началах натуральной философии».
Понятно, что таких систем, где тележку толкнули, а она покатилась без действия внешних сил, на самом деле не бывает. На тела всегда действуют силы, причем скомпенсировать действие этих сил полностью практически невозможно.
Например, все на Земле находится в постоянном поле силы тяжести. Когда мы передвигаемся (не важно, ходим пешком, ездим на машине или велосипеде), нам нужно преодолевать множество сил: силу трения качения и силу трения скольжения, силу тяжести, силу Кориолиса.
Второй закон Ньютона
Помните пример про тележку? В этот момент мы приложили к ней силу! Интуитивно понятно, что тележка покатится и вскоре остановится. Это значит, ее скорость изменится.
В реальном мире скорость тела чаще всего изменяется, а не остается постоянной. Другими словами, тело движется с ускорением. Если скорость нарастает или убывает равномерно, то говорят, что движение равноускоренное.
Если рояль падает с крыши дома вниз, то он движется равноускоренно под действием постоянного ускорения свободного падения g. Причем любой дугой предмет, выброшенный из окна на нашей планете, будет двигаться с тем же ускорением свободного падения.
Второй закон Ньютона устанавливает связь между массой, ускорением и силой, действующей на тело. Приведем формулировку второго закона Ньютона:
Ускорение тела (материальной точки) в инерциальной системе отсчета прямо пропорционально приложенной к нему силе и обратно пропорционально массе.
Если на тело действует сразу несколько сил, то в данную формулу подставляется равнодействующая всех сил, то есть их векторная сумма.
В такой формулировке второй закон Ньютона применим только для движения со скоростью, много меньшей, чем скорость света .
Существует более универсальная формулировка данного закона, так называемый дифференциальный вид.
В любой бесконечно малый промежуток времени dt сила, действующая на тело, равна производной импульса тела по времени.
Третий закон Ньютона
В чем состоит третий закон Ньютона? Этот закон описывает взаимодействие тел.
3 закон Ньютона говорит нам о том, что на любое действие найдется противодействие. Причем, в прямом смысле:
Два тела воздействуют друг на друга с силами, противоположными по направлению, но равными по модулю.
Формула, выражающая третий закон Ньютона:
Другими словами, третий закон Ньютона — это закон действия и противодействия.
Пример задачи на законы Ньютона
Вот типичная задачка на применение законов Ньютона. В ее решении используются первый и второй законы Ньютона.
Десантник раскрыл парашют и опускается вниз с постоянной скоростью. Какова сила сопротивления воздуха? Масса десантника – 100 килограмм.
Решение:
Движение парашютиста – равномерное и прямолинейное, поэтому, по первому закону Ньютона, действие сил на него скомпенсировано.
На десантника действуют сила тяжести и сила сопротивления воздуха. Силы направлены в противоположные стороны.
По второму закону Ньютона, сила тяжести равна ускорению свободного падения, умноженному на массу десантника.
Ответ: Сила сопротивления воздуха равна силе тяжести по модулю и противоположна направлена.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
А вот еще одна физическая задачка на понимание действия третьего закона Ньютона.
Комар ударяется о лобовое стекло автомобиля. Сравните силы, действующие на автомобиль и комара.
Решение:
По третьему закону Ньютона, силы, с которыми тела действуют друг на друга, равны по модулю и противоположны по направлению. Сила, с которой комар действует на автомобиль, равна силе, с которой автомобиль действует на комара.
Другое дело, что действие этих сил на тела сильно отличаются вследствие различия масс и ускорений.
Исаак Ньютон: мифы и факты из жизни
На момент публикации своего основного труда Ньютону было 45 лет. За свою долгую жизнь ученый внес огромный вклад в науку, заложив фундамент современной физики и определив ее развитие на годы вперед.
Он занимался не только механикой, но и оптикой, химией и другими науками, неплохо рисовал и писал стихи. Неудивительно, что личность Ньютона окружена множеством легенд.
Ниже приведены некоторые факты и мифы из жизни И. Ньютона. Сразу уточним, что миф – это не достоверная информация. Однако мы допускаем, что мифы и легенды не появляются сами по себе и что-то из перечисленного вполне может оказаться правдой.
- Факт. Исаак Ньютон был очень скромным и застенчивым человеком. Он увековечил себя благодаря своим открытиям, однако сам никогда не стремился к славе и даже пытался ее избежать.
- Миф. Существует легенда, согласно которой Ньютона осенило, когда на наго в саду упало яблоко. Это было время чумной эпидемии (1665-1667), и ученый был вынужден покинуть Кембридж, где постоянно трудился. Точно неизвестно, действительно ли падение яблока было таким роковым для науки событием, так как первые упоминания об этом появляются только в биографиях ученого уже после его смерти, а данные разных биографов расходятся.
- Факт. Ньютон учился, а потом много работал в Кембридже. По долгу службы ему нужно было несколько часов в неделю вести занятия у студентов. Несмотря на признанные заслуги ученого, занятия Ньютона посещались плохо. Бывало, что на его лекции вообще никто не приходил. Скорее всего, это связано с тем, что ученый был полностью поглощен своими собственными исследованиями.
- Миф. В 1689 году Ньютон был избран членом Кембриджского парламента. Согласно легенде, более чем за год заседания в парламенте вечно поглощенный своими мыслями ученый взял слово для выступления всего один раз. Он попросил закрыть окно, так как был сквозняк.
- Факт. Неизвестно, как бы сложилась судьба ученого и всей современной науки, если бы он послушался матери и начал заниматься хозяйством на семейной ферме. Только благодаря уговорам учителей и своего дяди юный Исаак отправился учиться дальше вместо того, чтобы сажать свеклу, разбрасывать по полям навоз и по вечерам выпивать в местных пабах.
Дорогие друзья, помните — любую задачу можно решить! Если у вас возникли проблемы с решением задачи по физике, посмотрите на основные физические формулы. Возможно, ответ перед глазами, и его нужно просто рассмотреть. Ну а если времени на самостоятельные занятия совершенно нет, специализированный студенческий сервис всегда к вашим услугам!
В самом конце предлагаем посмотреть видеоурок на тему «Законы Ньютона».
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Источник
Adblock
detector
Одно из основных понятий курса математики в 6 классе – это прямая и обратная пропорциональность. Если некоторая величина (время, масса, цена) изменяется, и одновременно другая величина (расстояние, объем, затраты) тоже меняется, то величины находятся в зависимости между собой, то есть пропорциональны друг другу.
Взаимосвязь между величинами не всегда означает наличие пропорциональности. Так, высота дерева растет с его возрастом, но не во столько же раз. Составление пропорций помогает решить многие задачи как в математике, так и на практике.
Прямая пропорциональность
Если при изменении одного параметра другой изменяется таким же образом, то эти величины прямо пропорциональны друг другу. В этой пропорции увеличение расстояния вдвое означает увеличение времени также двукратно.
Например, при движении автомобиля с постоянной скоростью, время, затраченное на преодоление расстояния, будет прямо пропорционально этому расстоянию. То есть, если 50 км автомобиль проедет за 1 час, то 100 км с той же скоростью он преодолеет за 2 часа.
Функция прямой пропорциональности и ее график
Эта зависимость описывается следующей формулой:
y = k * x.
Здесь k и называется коэффициентом пропорциональности.
Графически функция изображается прямой, которая пройдет через начальную точку координат. Строят график следующим образом: находят одну точку, затем чертят прямую через эту точку и начало координат.
Пример построения
Нужно построить график у = 3х. Подставляем вместо х единицу, вычисляем y = 3, то есть находим координаты (1; 3). Отмечаем эту точку на координатной плоскости, проводим прямую линию через нее и точку (0; 0).
Вот так будет выглядеть график y = k * x при k > 0 (слева) и при k < 0 (справа).
Свойства функции прямой пропорциональности
Основные свойства следующие:
-
область определения, значений составляют все действительные числа;
-
является нечетной;
-
возрастает при всех значениях x, если k > 0;
-
если коэффициент со знаком «-», т. е. если k < 0, то убывает;
-
если k > 0, то прямая располагается в 1 — 3 координатных четвертях и образует острый угол с осью Х, если k < 0, то прямая находится во 2 — 4 четвертях и образует тупой угол с осью Х.
Обратная пропорциональность
Рост одного параметра ведет к уменьшению другого в такое же количество раз, и наоборот, при уменьшении одной величины другая увеличивается во столько же. Это значит, что они обратно пропорциональны друг другу.
Пример: трое рабочих выполнят порученную им работу за 2 часа, а 6 человек такое же задание осилят за 1 час. То есть двукратное увеличение числа работников привело к уменьшению затраченного времени вдвое. Конечно, если прочие факторы неизменны (производительность труда, условия работы).
Функция обратной пропорциональности и ее график
Функция задается формулой:
где k – любое действительное число, кроме 0.
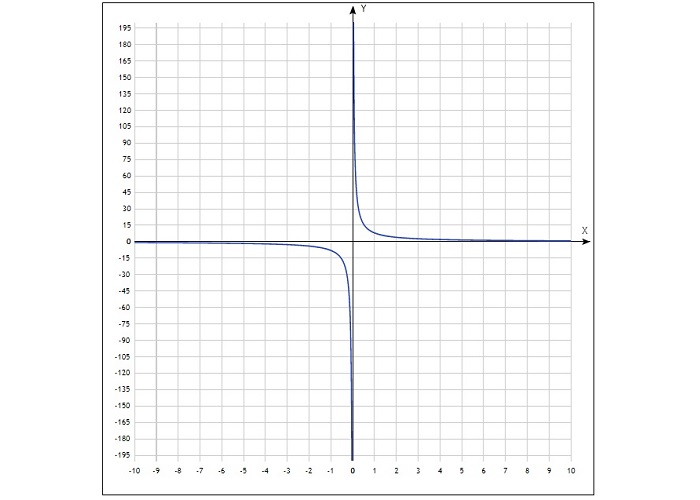
График данной зависимости — это гипербола, ее ветви находятся в 1 и 3 четвертях системы координат при k > 0, или во 2 и 4, если коэффициент меньше 0. Ветви гиперболы симметричны относительно точки (0; 0).
Строят график так: нужно задать значения х, затем вычислить значения у, результаты оформить в виде таблицы. Верхняя строка таблицы заполняется значениями х, нижняя — y.
Пример построения
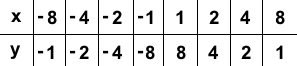
Нужно построить график функции y = 8/x.
Вот так выглядит таблица для данной функции:
Полученные точки отмечают на координатной плоскости, затем соединяют плавной линией. График будет выглядеть так:
Свойства функции обратной пропорциональности
Основные следующие:
-
области определения, значений функции D(y) – это все действительные числа, кроме 0, т. е. D(y):= x ≠ 0;
-
если коэффициент больше 0, функция является убывающей для всех x; если меньше 0, то y увеличивается для любых значений x;
-
оси координат 0х и 0у — это асимптоты по отношению к ветвям гиперболы, которые приближаются к ним, но не достигают их.
К составлению математических пропорций во многих случаях сводится решение самых разнообразных задач. Например, покупая 1 булочку по определенной цене, подсчитывают затраты на 4 булочки – получается в 4 раза больше.
Ускоряют шаг при ходьбе в 2 раза – достигнут цели вдвое быстрее. Вводят второго кассира в магазине – убывает очередь вдвое. Во всех этих случаях и им подобным применима теория о прямой и обратной пропорциональности.
Прямая и обратная пропорциональность
- Прямая пропорциональность
- Формула прямой пропорциональности
- Обратная пропорциональность
- Формула обратной пропорциональности
Пропорциональность — это зависимость одной величины от другой, при которой изменение одной величины приводит к изменению другой во столько же раз.
Пропорциональность величин может быть прямой и обратной.
Прямая пропорциональность
Прямая пропорциональность — это зависимость двух величин, при которой одна величина зависит от второй величины так, что их отношение остаётся неизменным. Такие величины называются прямо пропорциональными или просто пропорциональными.
Рассмотрим пример прямой пропорциональности на формуле пути:
s = vt,
где s — это путь, v — скорость, а t — время.
При равномерном движении путь пропорционален времени движения. Если взять скорость v равной 5 км/ч, то пройденный путь s будет зависеть только от времени движения t:
| Скорость v = 5 км/ч | |||||
|---|---|---|---|---|---|
| Время t (ч) | 1 | 2 | 4 | 8 | 16 |
| Путь s (км) | 5 | 10 | 20 | 40 | 80 |
Из примера видно, что во сколько раз увеличивается время движения t, во столько же раз увеличивается пройденное расстояние s. В примере мы увеличивали время каждый раз в 2 раза, так как скорость не менялась, то и расстояние увеличивалось тоже в два раза.
В данном случае скорость (v = 5 км/ч) является коэффициентом прямой пропорциональности, то есть отношением пути ко времени, которое остаётся неизменным:
следовательно,
| 5 | = | 10 | = | 20 | = | 40 | = | 80 | = 5. |
| 1 | 2 | 4 | 8 | 16 |
Если время движения остаётся неизменным, то при равномерном движении расстояние будет пропорционально скорости:
| Время t = 2 ч | ||||
|---|---|---|---|---|
| Скорость v (км/ч) | 5 | 15 | 45 | 90 |
| Расстояние s (км) | 10 | 30 | 90 | 180 |
В этом примере коэффициентом прямой пропорциональности, то есть, отношением пути к скорости, которое остаётся неизменным, является время (t = 2 ч):
следовательно,
| 10 | = | 30 | = | 90 | = | 180 | = 2. |
| 5 | 15 | 45 | 90 |
Из данных примеров следует, что две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз другая увеличивается (или уменьшается) во столько же раз.
Формула прямой пропорциональности
Формула прямой пропорциональности:
y = kx,
где y и x — это переменные величины, а k — это постоянная величина, называемая коэффициентом прямой пропорциональности.
Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных y и x равное одному и тому же числу.
Формула коэффициента прямой пропорциональности:
Обратная пропорциональность
Обратная пропорциональность — это зависимость двух величин, при которой увеличение одной величины приводит к пропорциональному уменьшению другой. Такие величины называются обратно пропорциональными.
Рассмотрим пример обратной пропорциональности на формуле пути:
s = vt,
где s — это путь, v — скорость, а t — время.
При прохождении одного и того же пути с разной скоростью движения время будет обратно пропорционально скорости. Если взять путь s равным 120 км, то потраченное на преодоление этого пути время t будет зависеть только от скорости движения v:
| Путь s = 120 км | ||||
|---|---|---|---|---|
| Скорость v (км/ч) | 10 | 20 | 40 | 80 |
| Время t (ч) | 12 | 6 | 3 | 1,5 |
Из примера видно, что во сколько раз увеличивается скорость движения v, во столько же раз уменьшается время t. В примере мы увеличивали скорость движения каждый раз в 2 раза, а так как расстояние, которое нужно преодолеть, не менялось, то количество времени на преодоление данного расстояния сокращалось тоже в два раза.
В данном случае путь (s = 120 км) является коэффициентом обратной пропорциональности, то есть произведением скорости на время:
s = vt,
следовательно,
10 · 12 = 20 · 6 = 40 · 3 = 80 · 1,5 = 120.
Из данного примера следует, что две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.
Формула обратной пропорциональности
Формула обратной пропорциональности:
где y и x — это переменные величины, а k — это постоянная величина, называемая коэффициентом обратной пропорциональности.
Коэффициент обратной пропорциональности — это произведение любых соответствующих значений обратно пропорциональных переменных y и x, равное одному и тому же числу.
Формула коэффициента обратной пропорциональности:
xy = k.
Как понять какая пропорциональность?
Две величины называются прямо пропорциональными, если при увеличении одной из них в несколько раз другая увеличивается во столько же раз. Обратная пропорциональность. Две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.
Какой формулой задается обратная пропорциональность?
Обратной пропорциональностью называется функция, которую можно задать формулой вида: y = k x , где — независимая переменная, — не равное нулю число.
Какое название получил коэффициент пропорциональности?
Коэффициент пропорциональности получил название постоянной Планка, и она равна: h = 6,63 ∙ 10-34 Дж∙с. После открытия Планка начала развиваться самая современная и глубокая физическая теория – квантовая физика.
Что такое прямо пропорциональные величины?
Две величины называются прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз, другая увеличивается (уменьшается) во столько же раз. Пример: такие величины, как скорость объекта и пройденное им расстояние являются прямо пропорциональными.
Какие величины называют прямо пропорциональными?
Вспомним, какие величины называют прямо пропорциональными. Две переменные величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз.
Как определить коэффициент пропорциональности k?
y = kx, где y и x — переменные величины, k — постоянная величина, которую называют коэффициентом прямой пропорциональности. Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных y и x, равное одному и тому же числу.
Как составить график прямой пропорциональности?
Алгоритм построения графика прямой пропорциональности
- Выбрать произвольное значение аргумента
- Вычислить соответствующее значение функции
- Отметить на координатной плоскости точку
- Провести прямую через начало координат (0;0) и точку
Как найти коэффициент пропорциональности химия?
Запишите отношение. Если размер меньшей фигуры увеличивается до размера большей фигуры, используйте отношение: коэффициент пропорциональности = (сторона большей фигуры)/(сторона меньшей фигуры).
Как найти коэффициент?
Числовой множитель в произведении, где есть хотя бы одна буква, называется коэффициентом. Если чисел несколько, нужно их перемножить, упростить выражение и таким образом будет получен коэффициент.
Как найти прямо пропорциональные величины?
y = kx, где y и x — переменные величины, k — постоянная величина, которую называют коэффициентом прямой пропорциональности. Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных y и x, равное одному и тому же числу.
Как найти прямо пропорциональную величину?
Прямую пропорциональность можно задать формулой. Формулу y=kx, где y и x — переменные величины, а k — коэффициент, является постоянной величиной, называют формулой прямой пропорциональности.
Что называют коэффициентом обратной пропорциональности?
График обратно пропорциональной зависимости Одно из них, как правило, у, называется функцией и зависит от х, то есть аргумента. к – постоянная величина, которая называется коэффициентом обратной пропорциональности.
Чему равен коэффициент пропорциональности G?
Коэффициент пропорциональности G в этом уравнении называется гравитационной постоянной. Численно она равна модулю силы тяготения, действующей на точечное тело единичной массы со стороны другого такого же тела, находящегося от него на единичном расстоянии.
Как правильно построить график функции?
Итак, алгоритм по шагам:
- Представьте, как выглядит ваш график.
- Составьте таблицу точек, принадлежащих графику:
- Постройте координатную плоскость и отметьте на ней точки из таблицы.
- Если нужно, найдите еще несколько точек и нанесите их на координатную плоскость.
- Постройте график
Что представляет собой график обратной пропорциональности?
Графиком обратной пропорциональности y=kx y = k x является кривая, состоящая из двух ветвей, симметричных относительно начала координат. Этот график называется гиперболой. Гипербола не имеет общих точек с осями координат, а лишь сколь угодно близко к ним приближается, т.
Чему равен коэффициент пропорции?
Коэффициент пропорциональности (линейный коэффициент пропорциональности) равен отношению двух соответствующих сторон подобных фигур. Подобные фигуры – это фигуры одинаковой формы, но разных размеров. Коэффициент пропорциональности используется для решения основных геометрических задач.
Как определить числовой коэффициент?
Если буквенное выражение является произведением одной или нескольких букв и одного числа, то это число называется числовым коэффициентом выражения. Числовой коэффициент зачастую называют просто коэффициентом.


 или y ∼ x. { displaystyle y sim x.}
или y ∼ x. { displaystyle y sim x.}