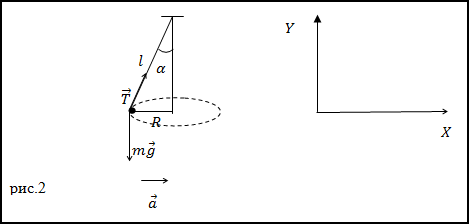Прежде чем приступить к расчету натяжения струны, давайте обсудим, что подразумевается под натяжением?
Натяжение — это контактная сила, которая передается с помощью веревки, кабеля или аналогичных предметов. Напряжение всегда действует от тела вдоль струны.
В этой статье мы собираемся рассчитать натяжение, действующее на струну.
Как рассчитать натяжение струны:
Случай (i): рассмотрим два объекта масс m1 И м2, натянутый той же струной. Масса второго объекта больше, чем масса первого объекта.
Поскольку масса объекта 2 больше, чем масса объекта1. м2 ускоряется вниз под действием силы тяжести, и m1 ускоряется вверх как m2 тянет м1.
Уравнение можно записать как
Для объекта, ускоряющегося вверх, есть
Т — м1г = м1a
Для объекта, ускоряющегося вниз
m2г — Т = м2a
Где; м1 г и м2 g — чистая сила, действующая на объекты соответственно.
При сложении двух приведенных выше уравнений мы получаем ускорение как
m2г — м1г = м1а + м2a
Переставляя термины, получаем
(m2— M1) г = а (м1+m2)
Поскольку масса объекта 2 больше, чем масса объекта1. м2 ускоряется вниз под действием силы тяжести, и m1 ускоряется вверх как m2 тянет м1.
Уравнение можно записать как
Для объекта, ускоряющегося вверх, есть
Т — м1г = м1a
Для объекта, ускоряющегося вниз
m2г -Т = м2a
Где; м1г и м2g — чистая сила, действующая на объекты соответственно.
При сложении двух приведенных выше уравнений мы получаем ускорение как
m2г — м1г = м1а + м2a
Переставляя термины, получаем
(m2-m1) g = a (m1+m2)
Это дает ускорение натяжения, действующего на струну.
Чтобы вычислить натяжение, подставив ускорение в уравнения и получим,
Приравнивая два приведенных выше уравнения, мы получаем,
Переставляя термины,
m2Т — м1m2г = м1m2г — м1T
m2Т + м1Т = м1m2г + м1m2g
Т (м1+m2) = 2 м1m2g
Это дает уравнение силы натяжения, действующей на струну, когда две массы ускоряются в противоположном направлении.
Случай (ii). Пусть две массы m1 И м2 прикреплены к веревке, как показано на рисунке. Масса m1 прикреплен к струне в горизонтальном направлении, а масса m2 висит вертикально. Поскольку масса m2 больше массы m1, масса m2 тянет массу m1 так что масса m1 ускоряется в направлении силы натяжения, а результирующая сила, действующая на массу, равна силе натяжения, поскольку сила тяжести не влияет на ускорение массы m1И м2 ускорение в нисходящем направлении.
Уравнение силы натяжения, действующей на струну, имеет вид;
Т = м1a
m2г -Т = м2a
Уравнение ускорения можно записать, добавив полученное выше уравнение;
m2г = м1а + м2a
m2г = а (м1+m2)
Подставляя указанные выше значения a, получаем,
Поскольку два приведенных выше уравнения равны ускорению, мы можем приравнять два приведенных выше уравнения
Tm2 = м1m2г-тм1
Tm1 + Тм2= м1m2g
Т (м1+m2) = м1m2g
Это дает силу натяжения, действующую на струну, когда на одну массу не действует сила тяжести.
Случай (iii): рассмотрим две массы m1 И м2, которые прикреплены к одной и той же струне вертикально в том же направлении, что и на рисунке.
Две массы ускоряются в направлении вниз под действием силы тяжести. В этом случае мы можем рассчитать натяжение, как показано ниже.
m1г — Т = м1a
m2г — Т = м2a
Ускорение двух объектов можно задать, добавив приведенные выше уравнения
m1г + м2г = м1а + м2a
(m1 + м2) g = a (m1 + м2)
Ускорение, действующее на объекты, равно ускорению свободного падения. Напряжение будет
m1г -Т = м1g
Т = м1г — м1g
T = 0
Аналогично m2г -Т = м2g
T = 0
Натяжение, действующее на струну, будет нулевым для обеих масс, ускоряющихся в одном направлении.
Решенные задачи по натяжению струны.
Два блока массой 15 кг и 23 кг подвешены на не имеющей трения струне, расположенной напротив друг друга. Масса м1 ускоряется вверх, а m2 ускоряется в нисходящем направлении. Рассчитайте ускорение и натяжение, действующие на струну.
Решение:
Дано: масса m1 = 15 кг
Масса м2 = 23 кг
Ускорение свободного падения = 9.8 мс-2
Формула для расчета ускорения имеет вид
a = 2.06 мс-2
Рассчитать натяжение
Т = 177.94 Н
Рассчитайте натяжение, действующее на струну при массе m1 когда гиря 8 кг наклонена под углом 25 °, а гиря 12 кг подвешена вертикально на тетиве. Коэффициент силы трения (µ) равен 0.35. Следовательно, узнайте и ускорение. (Примите ускорение свободного падения как 10 м / с.2).
решение:
Дано: масса m1 = 8 кг
Масса м2 = 12 кг
Угол подвеса = 25 °
Чистая сила, действующая на m1 это F1 = м1gsin θ = 8 × 10 (sin θ) = 80 (sin 25 °) = 33.80 Н
Чистая сила, действующая на m2 это F2 = м2g = 12 × 10 = 120 Н
Полная сила, действующая на струну, определяется как
Ф = Ф2 — Ж1 — Ff
Где Ff — сила трения, действующая на струну.
Ff = µ м1gcos θ
Ff = (0.35) 80 cos (25)
Ff = (0.35) 80 (0.906)
Ff = 25.3 Н
F2— F1 -FN = м1a
120 — 33.80 -25.3 = 8а
60.9 = 8а
a = 7.61 м / с2
Чтобы найти напряжение
Мы знаем, что
TF1-Ff = ма
Т- 33.80 — 25.3 = 8 × 7.61
Т = (8 × 7.61) + 33.80 + 25.3
Т = 60.88 + 33.80 + 25.3
Т = 119.98 Н.
Два блока массой по 6 кг каждый прикреплены к нити без трения. Один ускоряется вниз, а другой ускоряется в направлении общей силы. Рассчитать действующее в струне натяжение?
Решение:
Учитывая, что масса обоих блоков = 6 кг.
Уравнения можно записать в виде
T = ma …… (1)
мг — Т = ма ……. (2)
Вычитая (1) и (2), получаем
Т — (мг -Т) = ма -ма
2T-мг = 0
2T = мг
Т = 29.4 Н
Три блока A, B и C массой 4 кг, 6 кг и 8 кг соответственно нависают над шкивом, как показано на рис. Тогда Как рассчитать натяжение струны между блоками A и B.
Решение:
Учитывая, что масса блока A равна (m1) 4 кг
Масса блока В (м2) 6 кг
Масса блока C (м3) 8 кг
Можно записать уравнение движения для каждого блока как
Для блока А:
m1г — т1 = м1a
T1 = м1а + м1g
Для блока B:
m2г + т1 — Т = м1a
Для блока C:
Т — м3г = м3a
Т = м3г — м3a
Положим значение T1 и T во втором уравнении движения.
m2г + (м1г — м1являюсь3а + м3г) = м2a
m2г + м1грамм1я3я3г = м2a
г (м2 + м1 — M3) = a (m1 + м2 + м3)
a = 1.08 м / с2
Чтобы рассчитать напряжение между A и B.
T1=m1грамм1a
T1 = м1 (га)
T1 = 4 (9.8–1.088)
Т1 = 4 (8.712)
Т1 = 34.84Н.
Струна, проходящая через шкив, соединяет 2 блока массой m.1 И м2 соответственно, которые подвешены вертикально. Если ускорение системы составляет 7 м / с2. найти соотношение обеих масс.
Учитывая g = 10 м / с2 И м2 > м1 .
Решение:
Уравнение движения задается формулой
Уравнение движения задается формулой
Т- м1г = м1a
m2г -Т = м2g
Т- м1г = м1× 7
m2gT = m2× 7
Добавление приведенных выше уравнений
10m2-10m1 = 7 м1+ 7 млн2
10m2-7m2 = 10 м1+ 7 млн1
m1 : м2 = 3: 17
Часто задаваемые вопросы о натяжении тетивы.
Какую работу выполняет натяжение струны?
Работа, выполняемая натяжением струны, всегда равна нулю.
Напряжение может передавать энергию от одного объекта к другому только через гибкую среду, но оно не может работать само по себе.
Какие факторы влияют на увеличение натяжения струны?
Факторы, увеличивающие напряжение:
- Жесткость струны.
- Скручивание и настройка на конце струны.
Что произойдет, если натяжение не повлияет на струну?
Если натяжение не повлияет на струну, значит, жесткости не будет.
Натяжение действует по всей длине струны, что делает струну однородной. Если натяжение отсутствует, то в струне не будет жесткости, которая может изменить направление силы, действующей на струну.
Может ли струна иметь разное натяжение?
Да, иногда одна и та же струна может иметь разное натяжение.
Когда струна нежесткая или эластичная, можно почувствовать разное натяжение.
Может ли напряжение быть отрицательным?
Напряжение может быть как отрицательным, так и положительным.
Знак зависит от координатных осей, по которым размещен объект.
|
Перевод В.А.Клопова
Формулы для расчета фортепианных струн
Введение. Целью этой статьи является предоставление фортепианным мастерам простых и очень точных формул для расчета свойств как необвитых, так и обвитых струн. Имея любые три из четырех параметров струны — диаметр, частоту, длину и силу натяжения, по этим формулам можно вычислить четвертый. Значение константы K определяется относительной плотностью струны, и в статье дается таблица этих значений для всего возможного диапазона плотностей. Эти формулы не только легко запомнить, но они еще и лучше всего подходят для использования в электронных таблицах, сценариях и т. д. Формулу для натяжения можно использовать даже на самых простых карманных калькуляторах, а другие три — на любом калькуляторе с кнопкой «√» (квадратный корень). Никакого специального научного калькулятора не потребуется. В дополнение к четырем вышеприведенным формулам, которые будут объяснены ниже, также будут даны формулы, показывающие, как они выводятся из основной формулы Мерсенна-Тейлора, а также формулы для расчета относительной плотности и, следовательно, константы K для обвитых струн. Французский монах и математик Марен Мерсенн (1588-1648) открыл следующие соотношения:
Данные величины • Ускорение свободного падения на 45° широты = 980,6199203 см/сек2. • 1 фунт = 453,59237 грамма. • 1 фунт-сила (lbf)= 444822,16152605 дин. • 1 килограмм-сила (кгс) = 980664,999999998 дин.
Для практических целей и для того, чтобы можно было производить расчеты с помощью обычного электронного калькулятора, мы будем использовать систему единиц СГС (сантиметр, грамм, секунда). В представленном виде формула не имеет практического применения; это просто утверждение отношения между четырьмя величинами. Теперь мы приступим к получению из этой формулы набора производных практических формул для фортепианного мастера, связывающих длину струны, ее диаметр и частоту ее основного тона. В дальнейшем символ ϱ (греческая буква «ро») символизирует относительную плотность струны, рассматриваемой как цилиндр, состоящий из стального сердечника и, в случае струн с обвивкой, воздуха и материала обвивки. Относительная плотность фортепианных струн колеблется от около 6,9 для самых толстых струн с двойной обвивкой до около 7,4 для самой тонкой струны с одинарной обвивкой, а для необвитых струн из простой стали — 7,85. Данные для обвитых струн могли бы показаться преуменьшенными ввиду большей плотности меди по сравнению со сталью, однако подумайте о том, сколько воздуха содержится в измеряемом вами цилиндре.
Натяжение. В нашей основной формуле Т — это сила натяжения, она выражается в динах. Дина является единицей силы в системе единиц СГС, которую мы решили использовать. Одна дина — это сила, необходимая для ускорения массы в 1 грамм на один сантиметр в секунду за секунду, и она эквивалентна силе примерно 0,0010197 грамм-силы. Мы привыкли выражать натяжение в фунтах силы или килограммах силы, поэтому нам нужно преобразовать это также в привычные единицы, и мы вычисляем, что один фунт силы равен примерно 444822 дин, 1 килограмм-сила равен 980665 дин (см. выше). Преобразовав количества в исходной формуле в удобные для наших целей единицы, мы теперь можем создавать полезные и запоминающиеся формулы, которые можно использовать для выполнения вычислений с помощью карманного калькулятора или для использования в электронных таблицах. Практические формулы 1. Расчет натяжения по заданной длине, диаметру и частоте
В электронной таблице с ячейками с именами f, l, d и K в ячейку, которая вычисляет натяжение, будет введено следующее:
А на карманном калькуляторе результат дадут следующие шаги:
Значение K определяется путем деления нашего коэффициента преобразования (килограмм-силы в дины, 980 619,9203) на Значения K для реального диапазона ϱ Таблица
2. Расчет диаметра по заданной длине, частоте и силе натяжения
что дает 0,0799 см. Таким образом, ближайшая к нашей цели струнная сталь — это № 13½ диаметром 0,0800 см. Окончательное натяжение, используя нашу формулу натяжения выше, будет
давая нам фактическое напряжение 68,39 кгс. Вот другой пример: рабочая длина струны двухструнного хора с одинарной обвивкой на ноте E20 составляет 90 см, частота 82,41 Гц, и нам нужна пара струн с натяжением около 88 кгс каждая. Примем значение ϱ равным 7,1, и тогда K = 43871.
и получаем результат 2,65 мм. Предположим, что керн будет № 18, нам необходимо компенсировать диаметр, используя медную канитель 0,85 мм (с учетом коэффициента уменьшения из-за растяжения и овализации эффективного диаметра медной проволоки). На практике значение 44 000 для K в расчетах для обвитых струн вполне адекватно в качестве среднего числа, и его очень легко запомнить. Хотя формулы были выведены с использованием очень точных данных, нет смысла использовать слишком большую точность в окончательных расчетах, так как нет бесконечного числа размеров проволоки. В приведенном выше расчете можно было бы использовать K= 44000, и диаметр струны все равно будет 2,65 мм, а разница возникнет только в тысячных долях миллиметра – микронах. В обоих расчетах потребуется одна и та же медная обвивка, и два производителя струн, изготовляющих одну и ту же струну, вряд ли достигнут одинакового диаметра. 3, 4. Расчет длины или частоты
Некоторые наблюдения над струнами с обвивкой Можно было бы рассчитать точное теоретическое значение ϱ и, следовательно, K по диаметру сердечника и обвивки (-ок), но это довольно бесполезное занятие. Выше было показано, как мало меняет результат значительное изменение значения К, и что 44000 — хорошее рабочее значение. На самом деле относительная плотность обвитых струн колеблется от примерно 6,9 для самой толстой струны с двойной обвивкой до примерно 7,4 для самой тонкой струны с однослойной обвивкой. Если вы выберете из таблицы цифру от 6,9 до 7,4, эквивалентную положению струны в басовом участке, вы добьетесь точности, превосходящей служебный долг и хорошее мастерство. Имейте в виду, что любой теоретически рассчитанный показатель относительной плотности обвитых струн будет неточным по нескольким причинам. Неточность будет возникать: а) если не принимать во внимание длины необвитых участков у аграфа и штега; б) если и сталь, и медь не гарантированно будут вытянуты точно до заявленного диаметра; в) когда медь наматывается на сталь, она теряет свою округлость и ее сечение принимает форму яйца с плоской стороной у керна; наконец, г) если вы не вполне точно взвесили образцы обоих материалов в лабораторных условиях для определения их относительной плотности, вы не можете быть уверены, что значения, которые вы используете, являются истинными. Джон Делакур © Октябрь 2006 г. Примечание переводчика В оригинале статьи все примеры расчетов сделаны с использованием привычных для автора единиц силы натяжения струн – фунтов. Ради большей внятности для русскоязычного читателя данного перевода, я пересчитал примеры в привычные для нас килограммы, с использованием соответствующих значений константы К. Приношу мои заочные извинения автору статьи за допущенную вольность. Владимир Клопов, 2022 |
Формула Мерсенна-Тейлора названа в честь английского математика Брука Тейлора (1685-1731). Ее можно найти в большинстве учебников по физике для расчета частоты колебаний струны. Формула приведена справа и может быть словесно выражена следующим образом: «Частота колебаний струны равна единице, деленной на удвоенную длину и умноженной на корень квадратный из натяжения, деленного на погонную массу струны». В этой формуле 
Чтобы рассчитать силу натяжения данной струны, мы используем формулу, показанную слева. Константа 
При известной длине рабочего отрезка и частоте колебаний эта формула используется для расчета диаметра проволоки, необходимого для получения данной силы натяжения. В качестве примера возьмем струну верхней ноты фортепиано C88, имеющую частоту (при A49 = 440 Гц) 4187 Гц. и длиной 51 мм, и предположим, что целевое натяжение составляет 68 кгс. Приняв 7,8 в качестве значения ϱ, мы получим 42669 в качестве нашей постоянной 
Оставшиеся две формулы в этом наборе, те, которые выводят соответственно длину и частоту, даны здесь без комментариев, поскольку к настоящему времени они должны быть очевидны.Сегодня музыка пестрит поражающим воображение разнообразием видов, стилей и подстилей, а также техник игры на инструментах. В XXI веке однозначно нельзя выработать какие-то четкие формулы и точные решения для музыкальных жанров с точки зрения стремления получить идеальное звучание . И причины тому достаточно просты: каждый музыкант имеет свой особый стиль игры на гитаре – а в рамках данной статьи мы будет говорить именно о гитаристах – свои собственные предпочтения в области формирования звучания инструмента и группы в целом.
Когда мы говорим о вкусах гитаристов, наибольшие споры обычно вызывает выбор определенной толщины струн. От чего же он зависит?
Предпочтения музыкантов по выбору калибра струн во многом формируются из трех факторов:
- Строй, в котором играет гитарист;
- Особенности инструмента, в частности, величина его мензуры;
- Сила пальцев музыканта, от которой зависит комфорт при игре на комплектах разной толщины (сравните пальцы Джимми Пэйджа, который был фанатом «восьмерок» и SRV, который играл на комплектах .013-.056/.058).
И если сила пальцев – параметр сугубо индивидуальный, то составить определенные рекомендации и выявить зависимость между силой натяжения струны, ее строем и мензурой инструмента вполне возможно. Именно об этом мы сегодня и поговорим.
Натяжение струн в истории гитаростроения
Как ни странно, но жестких стандартов толщины/силы натяжения струн не было почти до середины прошлого века! Лишь в конце 30-х годов 20 века Джон Д’Аддарио (John D’Addario) ввел на своем производстве стандартизацию калибров струн и их разделение, выпустив на рынок три типа комплектов для акустической гитары: с легким, нормальным и сильным натяжением.
Почти до самого конца 20 века – если быть точнее, то где-то до середины 80-х годов – подобных стандартизированных комплектов было достаточно для удовлетворения потребностей всех музыкантов. Периодически по специальным заказам крупные производители выпускали и новые наборы: чаще всего они представляли собой гибриды из существующих струн, которые использовали для открытых строев и строев с понижением. В конце концов, к 90-м годам такие предложения стали очень многочисленными – музыканты все чаще применяли нестандартные музыкальные решения, выходили за рамки музыкальных трендов и старались по-максимуму использовать все возможности гитары в популярных музыкальных стилях. Все это привело к резко возросшей популярности открытых настроек гитары (open tuning), более частому применению вариаций пониженного строя, когда шестая струна настраивается на тон ниже традиционной ноты (drop tuning), разработке гитар-баритонов, а также нетрадиционных инструментов с 7-ю и 5-ю струнами. Такой скачок в музыкальной индустрии способствовал тому, что на рынке стали все чаще появляться необычные наборы струн, музыканты стали искать свой любимый «калибр» и свой звук – и такие крупные производители, как D’Addario, дали гитаристам возможность это сделать.
Теоретические аспекты натяжения струн
Ежегодно службы по работе с клиентами крупнейших музыкальных брендов получают тысячи писем с просьбой решить их проблемы с выбором наиболее подходящего набора струн.
В качестве ремарки: далее мы будем рассказывать про максимально точный подбор струн под свои предпочтения на примере товаров компании D’Addario. Если вы не уверены, что хотите заниматься столь кропотливыми и тщательными расчетами натяжения струн либо вы не имеете большого опыта в выборе струн или играли всего на 1-2 различных калибрах, обратитесь к нашей обзорной статье «Какие струны лучше подойдут под определенный строй?». В ней обобщенно описаны рекомендации крупнейших производителей струн по выбору оптимального комплекта для стандартного и пониженных строев гитары.
Для помощи в выборе струн компания ДиАддарио создала великолепный Онлайн-помощник по натяжению струн – в нем собраны все необходимые данные для выбора отдельных струн под желаемый строй. Далее мы расскажем, как не запутаться во всех приведенных в руководстве таблицах, а пока немного полезной информации, которая поможет лучше понять особенности расчета натяжения.
В формулах из руководства используются 3 показателя: вес струны, величина мензуры и частота (Weight, Scale Length и Frequency, соответственно. Рассчитывается натяжение по следующей формуле, которую мы приведем в русском и английском вариантах:
Натяжение = (Вес струны * (2 * Величина мензуры * Частота)^2)/386.4
Tension = (Weight * (2 * Scale * Frequency) ^2)/386.4
Как натяжение влияет на ощущения музыканта?
Как ни странно, но непосредственно толщина струны не оказывает влияние на натяжение: значение имеет в первую очередь ее масса, а также длина мензуры и величина частота, на которую данная струна настроена. Изготовители применяют самые неожиданные технологии технологии и материалы (никель, фосфор, нейлон и др.) для того, чтобы добиваться разного натяжения даже при равном диаметре керна и обмотки – и даже, порой, при использовании одинаковых материалов.
Немного о мензуре. Она представляет собой расстояние от верхнего порожка, расположенного в районе головы грифа, до места перегиба струны на бридже. Чем она длиннее – тем выше будет натяжение при прочих равных условиях. В качестве примера: первая струна с толщиной .009 на Stratocaster (мензура 25.5 дюймов) будет казаться более натянутой и жесткой, чем на Gibson Les Paul (мензура 24.75 дюймов) при условии, что обе настроены в Ми или любую другую одинаковую по высоте ноту. Поэтому в общем случае на гитару с меньшей мензурой рекомендуют струны потолще.
Приведем самые распространенные длины мензур для современных инструментов:
Большинство гитар – 24.75”, 25.5”
7- и 8-струнные электрогитары – 26.5”, 27”, 29”
Бас – 30”, 32”, 34” или 36”
Мандолина и Мандола – 13 7/8” и 15 7/8”, соответственно
Банджо – 26 ¼”
ВНИМАНИЕ! Перед тем, как начинать расчет натяжения и толщины струн, убедитесь, что ваша гитара правильно отстроена. Проверьте правильность настройки расстояния от струн до грифа, далее – мензуры, в самом конце – отстройте струны по высоте звучания.
Как измерить натяжение струны
Натяжение струн выражается в фунтах: натяжение по таблице в 12.2 фунта означает, что она тянет c силой, равной воздействию гравитации на тело массой 12.2 фунта. Если вы на данный момент ощущаете комфортное натяжение струн и планируете изменить строй всех струн – просто изучите руководство, ссылку на которое мы давали выше, и приобретите набор с таким калибром, который обеспечит идентичное натяжение в измененном строе.
Настало время привести конкретный пример!
Итак, допустим, на вашей гитаре установлен набор струн D’Addario EXL140 (10-13-17-30-42-52). Ниже приведена таблица с детализацией модели каждой струны в наборе, ее диаметра и натяжения для стандартного строя. Предположим, что вы хотите сохранить то же натяжение, но начать играть в Drop D строе (ebgDAD) – теперь по таблице необходимо лишь определить требуемый калибр шестой струны.
.jpg)
1. Находим в руководстве на странице 6 свой тип струн: XL Nickelplated Steel (серия XL, сталь с никелированной обмоткой), находим струну с калибром .052 и ноту E (Ми), получаем силу натяжения ~22 фунта (обозначены красным цветом).
2. Ищем в таблице ноту D (Ре) и схожее натяжение (обозначены зеленым цветом) – получаем, что наиболее похожими по натяжению будут струны с калибром .056 (20.9 фунтов, натяжение будет незначительно слабее) или .059 (23.3 фунта – натяжение будет немного сильнее).
.jpg)
Таким образом, для Drop D в данном случае оптимальным будет набор 10-13-17-30-42-56/59.
Используя подобную методику, вы сможете заменять любую струну в наборе на ту, с которой вам будет комфортнее играть. Купить струны поштучно вы можете в наших разделах одиночных струн:
- Для электрогитары
- Для бас-гитары
- Для акустической гитары
Обратите внимание, что приведенная информация актуальна только для продукции от D’Addario. На всякий случай дублируем ссылку на Онлайн руководство по натяжению струн.
Содержание:
- Определение и формула силы натяжения нити
- Единицы измерения силы натяжения нити
- Примеры решения задач
Определение и формула силы натяжения нити
Определение
Силу натяжения определяют как равнодействующую сил $(bar{R})$, приложенных к нити, равную ей по модулю,
но противоположно направленную. Устоявшегося символа (буквы), обозначающего силу натяжения нет. Ее
обозначают и просто $bar{F}$ и
$bar{T}$, и
$bar{N}$ . Математически определение для силы натяжения нити можно записать как:
$$bar{T}=-bar{R}(1)$$
где $bar{R}$ = векторная сумма всех сил, которые действуют на нить. Сила натяжения нити всегда направлена по нити (или подвесу).
Чаще всего в задачах и примерах рассматривают нить, массой которой можно пренебречь. Ее называют невесомой.
Еще одним важной характеристикой нити при расчете силы натяжения является ее растяжимость. Если исследуется невесомая и нерастяжимая
нить, то такая нить считается просто проводящей через себя силу. В том случае, когда необходимо учитывать растяжение нити, применяют
закон Гука, при этом:
$$T=F_{u p r}=k Delta l(2)$$
где k – коэффициент жесткости нити, $Delta l$ – удлинение нити при растяжении.
Единицы измерения силы натяжения нити
Основной единицей измерения силы натяжения нити (как и любой силы) в системе СИ является: [T]=Н
В СГС: [T]=дин
Примеры решения задач
Пример
Задание. Невесомая, нерастяжимая нить выдерживает силу натяжения T=4400Н. С каким максимальным ускорением
можно поднимать груз массой m=400 кг, который подвешивают на эту нить, чтобы она не разорвалась?
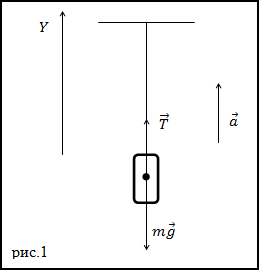
Решение. Изобразим на рис.1 все силы, действующие на груз, и запишем второй закон Ньютона.
Тело будем считать материальной точкой, все силы приложенными к центру масс тела.
$$bar{T}+m bar{g}=m bar{a}(1.1)$$
где $bar{T}$ – сила натяжения нити. Запишем проекцию уравнения (1.1) на ось Y:
$$T-m g=m a(1.2)$$
Из выражения (1.2) получим ускорение:
$$a=frac{T-m g}{m}$$
Все данные в задаче представлены в единицах системы СИ, проведем вычисления:
$$a=frac{4400-400 cdot 9,8}{400}=1,2 mathrm{~m} / mathrm{c}^{2}$$
Ответ. a=1,2м/с2
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Шарик, имеющий массу m=0,1 кг прикрепленный к нити (рис.2) движется по окружности,
расположенной в горизонтальной плоскости. Найдите модуль силы натяжения нити, если длина нити l=5 м, радиус окружности R=3м.
Решение. Запишем второй закон Ньютона для сил, приложенных к шарику, который вращается по окружности с
центростремительным ускорением:
$$bar{T}+m bar{g}=m bar{a}(2.1)$$
Найдем проекции данного уравнения на обозначенные на рис.2 оси X и Y:
$$
begin{array}{c}
X: quad T sin alpha=m a=m omega^{2} R(2.2) \
Y: quad-m g+T cos alpha=0
end{array}
$$
Из уравнения (2.3) получим формулу для модуля силы натяжения нити:
$$T=frac{m g}{cos alpha}(2.4)$$
Из рис.2 видно, что:
$$sin alpha=frac{R}{l} rightarrow cos alpha=sqrt{1-left(frac{R}{l}right)^{2}}$$
Подставим (2.5) вместо $cos alpha$ в выражение (2.4), получим:
$$T=frac{m g}{sqrt{1-left(frac{R}{l}right)^{2}}}=frac{m g l}{sqrt{l^{2}-R^{2}}}$$
Так как все данные в условиях задачи приведены в единицах системы СИ, проведем вычисления:
$$T=frac{0,1 cdot 9,8 cdot 5}{sqrt{5^{2}-3^{2}}}=1,225(H)$$
Ответ. T=1,225 Н
Читать дальше: Формула силы тяги.
Сила натяжения нити — формулировка
Определение
Силой натяжения называют силу, приложенную к концам объекта и создающую внутри него упругую деформацию.
Длина тела, к которому приложена сила, обычно многократно больше, чем его толщина. Примерами таких объектов являются веревка, канат, трос, леска, проволока. Сила натяжения визуально проявляется в следующих примерах:
- создание строительного отвеса;
- установка растяжек для фиксации радиоантенн;
- поведение арматуры внутри напряженного бетона;
- устройство корабельного такелажа.
Как определить силу, формулы
Натяжение проявляется по-разному. Поэтому сила натяжения может рассчитываться определенным образом, в зависимости от окружающих условий.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
С неподвижно закрепленным верхним концом
Простейшим примером проявления силы натяжения является нить с закрепленным на ней грузом. Верхний конец такого подвеса фиксируется неподвижно. В этом случае сила натяжения будет соответствовать силе тяжести, которая действует на тело. Формула для расчета:
(F=F_{тяж}=m*g)
где m – это масса тела, а g представляет собой ускорение свободного падения.
Если нить под углом
В случае, когда груз расположен под определенным углом, характер силы натяжения несколько изменяется. Примером такой системы выступает маятник.
(F_n=m*g*cos(a))
где а равен углу отклонения.
Формула с учетом ускорения и массы
В ситуации, при которой на груз оказывается сила натяжения, приводящая его в движение вверх, следует использовать такую формулу для ее расчета:
(F=F_{тяж}+m*a)
Сила натяжения во вращающейся системе
Описание
Такое явление можно наблюдать, когда система из нити и тела вращается во время раскручивания подвеса вокруг своей оси с закрепленным на одном его конце объектом: центрифуга, маятник, качели. Сила натяжения, возникающая внутри подвеса, характеризуется центробежной силой и в условиях вращения в вертикальной плоскости циклически претерпевает изменения. То есть можно наблюдать зависимость силы от угла отклонения от вертикали:
- приближение к земле приводит к увеличению силы;
- во время удаления от земли сила слабеет.
Формула расчета
Рассчитать силу натяжения в условиях вращающейся системы можно так:
(F=frac{mtimes nu ^{2}}{r})
Обозначение, единица измерения
Существуют определенные стандарты для написания формулы силы натяжения. Как и другие физические силы, натяжение обозначается F. В качестве единицы измерения используют Ньютон (H)
(H=frac{kgtimes m}{c^{2}})
Примеры решения задач
Задание 1
На невесомую нерастяжимую нить действует сила натяжения Т=4400Н. Необходимо определить максимальное ускорение подъема груза, масса которого равна m=400 кг, подвешенного на этой нити. При этом нить должна сохранить целостность.
Решение
Представив все силы, оказывающие действие на тело, необходимо составить формулу второго закона Ньютона. Тело является материальной точкой, а силы приложены к центру его массы.
(bar{T}+mbar{g}=mbar{a})
(bar{T}) является силой натяжения нити.
Проекция уравнения будет иметь следующий вид:
(T – mg = ma)
Данное выражение позволяет рассчитать ускорение:
(a=frac{T-mg}{m})
Так как все величины, изложенные в задании, соответствуют единицам СИ, можно провести корректные вычисления
(a=frac{4400-4*9,8}{400})
Ответ: a = 1.2 (м/с^2)
Задание 2
На иллюстрации изображен шар, который обладает массой m=0.1 кг. Будучи зафиксирован на нити, шарик совершает движение по окружности в горизонтальной плоскости. Длина подвеса составляет l=5 м, а радиус окружности – R=3 м. Требуется вычислить модуль силы натяжения нити.
Решение
Необходимо воспользоваться вторым законом Ньютона и записать его для сил, которые действуют на шар. Центростремительное ускорение при его вращении по окружности будет записано следующим образом:
(bar{T}+mbar{g}=mbar{a})
Проекции данной формулы по осям определяются следующим образом:
X: (T sin α = ma = mω2R)
Y: (-mg + T cos α = 0)
Таким образом, из уравнения Y получаем расчет модуля силы натяжения нити:
(T=frac{mg}{cos alpha })
Анализ рисунка позволяет вывести следующее уравнение:
(sin alpha = frac{R}{l}rightarrow cos alpha = sqrt{1-left(frac{R}{l} right)^{2}})
Если cos α заменить уравнением для расчета модуля силы натяжения нити, то получим следующую формулу:
(T=frac{mg}{sqrt{1-left(frac{R}{l} right)^{2}}}= frac{mgl}{sqrt{l^{2}-R^{2}}})
Значения основных величин, выраженные в СИ, можно подставить в конечную формулу для расчета силы натяжения нити:
(T=frac{0,1*9,8*5}{sqrt{5^{2}-3^{2}}}=1,225left(H right))
Ответ: Т=1,225 H