Пользуйтесь нашим приложением
Мы используем файлы cookie. Пользуясь сайтом, вы принимаете условия нашего соглашения. Принять Детальнее
Ответ: T≈454 Н.
Объяснение:
Пусть F1 — сила тяжести, F2 — центробежная сила и T — силя натяжения верёвок. В положении равновесия, т.е. в нижней точке, T=F1+F2. Пусть m=38 кг — масса девочки. Тогда, если пренебречь массой верёвок, F1=m*g и F2=m*v²/R, где v — линейная скорость движения, R — радиус окружности, по которой движется девочка. Но так как в нижней точке линейная скорость v максимальна, то v=2,5 м/с. И так как радиус окружности равен длине верёвок, то R=3,2 м. Отсюда T=m*g+m*v²/R=38*10+38*(2,5)²/3,2≈454 Н.
Условие задачи:
Мальчик массой 50 кг качается на качелях с длиной подвеса 4 м. С какой силой он давит на сиденье при прохождении положения равновесия со скоростью 6 м/с?
Задача №2.4.1 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(m=50) кг, (l=4) м, (upsilon=6) м/с, (P-?)
Решение задачи:
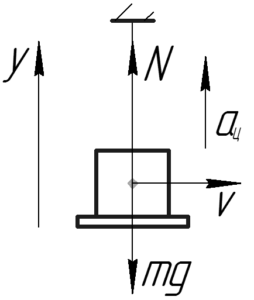
[P = N;;;;(1)]
В момент прохождения положения равновесия запишем второй закон Ньютона в проекции на ось (y):
[N – mg = m{a_ц};;;;(2)]
Центростремительное ускорение мальчика найдем по следующей формуле, учитывая, что радиус кривизны траектории равен длине подвеса качелей.
[{a_ц} = frac{{{upsilon ^2}}}{l};;;;(3)]
Подставим выражения (1) и (3) в равенство (2), тогда:
[P – mg = mfrac{{{upsilon ^2}}}{l}]
В итоге сила давления мальчика на качели (P) равна:
[P = mleft( {g + frac{{{upsilon ^2}}}{l}} right)]
Посчитаем ответ:
[P = 50 cdot left( {10 + frac{{{6^2}}}{4}} right) = 950; Н = 0,95; кН]
Ответ: 0,95 кН.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.3.22 На горизонтальной доске лежит брусок. Коэффициент трения скольжения между бруском
2.4.2 Автомобиль едет по выпуклому мосту, имеющему радиус кривизны 60 м. При какой
2.4.3 Автомобиль массой 5 т движется с постоянной по модулю скоростью 10 м/с
Какой простой машиной является качели?
рычаг
Качели — это рычаг?
Качели особый тип рычага; он состоит из длинной балки, прикрепленной к стержню, называемому точкой опоры. Как только вы переносите вес на один конец, сидя на одной стороне балки, она падает на землю.
К какому классу относятся рычажные качели?
рычаг первого класса. Примечание. Здесь следует отметить, что качели — это случай рычаг первого класса. Точка опоры может быть размещена где угодно между усилием и сопротивлением в рычаге первого класса. Ломы, ножницы и плоскогубцы также являются хорошим примером этого класса рычагов.
К какому типу движения относятся качели?
Движение ребенка в морской пиле колебательное движение. Это потому, что ребенок движется вверх и вниз с постоянной скоростью в определенный момент времени.
Качели толкают или тянут?
Работа, сила, приложенная к рычагу, совершается человеком, сидящим на другом конце качелей. Сила, которую прикладывает толкая вниз /нажатие на один конец качелей может заменить массу на другом конце. Чем длиннее рычаг, тем меньшее усилие нужно, чтобы поднять тяжелый предмет.
См. также, как предсказать заряд иона.
Являются ли качели рычагом 3 класса?
Рычаг — это тип простой машины, в которой жесткий рычаг расположен вокруг фиксированной точки или точки опоры. Входная сила, которую вы вкладываете, направляется в выходную силу. Классический пример рычага — качели.
Почему качели — это рычаг первого класса?
Рычаг первого класса. … В рычаге первого класса, точка опоры находится между усилием и сопротивлением. Как упоминалось ранее, качели — хороший пример рычага, и это рычаг первого класса. Величина веса и расстояние от точки опоры могут варьироваться в соответствии с потребностями.
Является ли колесо простой машиной?
простая машина, любое из нескольких устройств с небольшим количеством движущихся частей или без них, которые используются для изменения движения и величины силы для выполнения работы. … Простые машины — это наклонная плоскость, рычаг, клин, рулевое колесо и ось, шкив и винт.
Что такое маятниковое движение?
Движение маятника в основном изображает движение массы, подвешенной на нити, которая движется вперед и назад. Переменными в движении маятника являются масса, длина струны и положение, которое измеряется углом. Силами, действующими на массу при маятниковом движении, являются силы натяжения и силы тяжести.
Какой вид движения присутствует в движении ребенка на качелях?
Колебательное движение (iv) Движение ребенка на качелях – Колебательное движение
. Поскольку качели постоянно поднимаются и опускаются. Следовательно, это колебательное движение.
Что такое виды движения?
В мире механики есть четыре основных типа движения. Эти четыре вращательные, колебательные, линейные и возвратно-поступательные. Каждый из них движется немного по-своему, и каждый тип достигается с использованием различных механических средств, которые помогают нам понять линейное движение и управление движением.
Качели — это клин?
Примером клина является топор; Пример рычаг качели; Примером винта является винт в кресле, на котором вы сидите; Примером колеса и оси является велосипед с колесами и цепью; Примером шкива является флагшток; Примером наклонной плоскости является пандус для инвалидных колясок.
Качели — это одно слово или два?
Несмотря на то что качели (определ.2) является наиболее широко используемым термином в США, качели также широко используются в Северном, Северном Мидленде и Западном регионах.
Как качели дают механическое преимущество?
В приведенном выше примере качели умножили силу веса Джонни в 15 кг в четыре раза. … рычаг умножает вашу силу на соотношение расстояний и это соотношение является механическим преимуществом.
Что такое пример рычага класса 2?
Рычаги второго класса
Если груз ближе к усилию, чем к точке опоры, то для перемещения груза потребуется большее усилие. Тачка, открывалка для бутылок и весло являются примерами рычагов второго рода.
Смотрите также, где находятся кавказские горы на карте мира.
Что такое пример рычага класса 1?
Другими примерами рычагов первого класса являются плоскогубцы, ножницы, лом, молоток, качели и весы. Таким образом, в рычаге первого класса усилие (сила) перемещается на большое расстояние, чтобы переместить груз на меньшее расстояние, а точка опоры находится между усилием (силой) и грузом.
Что является примером простой машины с колесом и осью?
Некоторые примеры колеса и оси включают дверная ручка, отвертка, взбиватель яиц, водяное колесо, руль автомобиля и рукоятка, используемая для подъема ведра с водой из колодца. Когда колесо в колесно-осевой машине крутится, крутится и ось, и наоборот.
Как найти маму качелей?
Чтобы рассчитать MA качелей, вам нужно умножьте Силу Усилия и Силу Сопротивления или в случае качелей или любой рычаг Расстояние усилия и Расстояние сопротивления.
Является ли машина со встроенным рычагом первого класса?
Рычаг первого рода – это простая машина, которая поднимает груз через точку опоры, называемую точкой опоры. … Качели — отличный пример первоклассного рычага, потому что он демонстрирует, как работает рычаг, и является культовым изображением из детства.
Является ли маятник простым механизмом?
Обзор блока: в этом блоке вы узнаете о шести типах простых машин, седьмая машина под названием маятник и все научные концепции и термины, связанные с этими машинами. Простые механизмы являются основой всех механических систем, какими бы сложными они ни были.
Является ли колесо сложным механизмом?
Сложные машины также называются составные машины. Две или более простые машины работают вместе, образуя сложную машину. Составные машины могут выполнять более сложную работу, чем простые машины. Примерами сложных машин являются велосипед, тачка, кран, домкрат, газонокосилка и т. д.
Какой тип рычага представляет собой колесо и ось?
Колесо и ось по существу модифицированный рычаг, но он может перемещать груз дальше, чем рычаг. Центр оси служит точкой опоры. Идеальное механическое преимущество (IMA) колеса и оси — это отношение радиусов.
Какое движение представляет собой движение простого маятника?
колебательное движение
Простой маятник — еще одна механическая система, совершающая колебательные движения. Он состоит из точечной массы «m», подвешенной с помощью легкой нерастяжимой нити длиной L к неподвижной опоре, как показано на рис. 2.8. Движение происходит в вертикальной плоскости и обусловлено силой тяжести.
Какой тип движения совершает простой маятник?
периодическое движение Тип движения, связанный с маятником, называется периодическое движение
или мы можем сказать это как колебание. Груз маятника движется вперед и назад и создает колебательное движение.
Посмотрите также, почему такая большая разница в плотности между этими планетами?
Почему простой маятник называется простым?
Простой маятник (см. википедию или гиперфизику) приводит к простое дифференциальное уравнение с использованием второго закона Ньютона: ¨θ+glsin(θ)=0. Этот маятник дает самый простой способ взглянуть на гармоническое движение. Приведенный выше случай называется простым маятником.
Какой вид движения вызывает педаль велосипеда?
круговое движение — движение ног, которое используется для педалирования, оказывает круговое движение. Это движение также связано с периодическим движением. -Движение всадника на велосипеде совершается многократно и беспорядочно. Следовательно, мы можем сказать, что движение педали велосипеда будет круговым.
Какое движение совершают колеса движущегося велосипеда?
Полный ответ:
При вращении колес вокруг своей оси они совершают вращательное движение. Благодаря этому вращению с контактом с землей велосипед преодолевает определенное продольное расстояние. Таким образом, колеса также совершают поступательное движение относительно земли.
К какому типу движений относится движение рук во время бега?
Колебательное движение Решение: (i) Движение ваших рук во время бега – Колебательное движение.
Что такое машинное движение?
Значение движения
Это также обычная практика перемещения различных компонентов механической системы относительно друг друга. Примеры: игла швейной машины за работой, шина движущегося автомобиля и т. д.
Что такое тип движения?
К основным типам движения в физике относятся: Вращательное движение. Колебательное движение. Равномерное движение. Периодическое движение.
Какие 3 типа движения?
Движение можно разделить на три основных типа — поступательные, вращательные и колебательные.
Качели — это механическое устройство?
Механически качели рычаг который состоит из балки и точки опоры.
Что за простая машина велосипед?
На велосипеде есть три простых механизма: рычаг, шкив и колесо с осью. Колесо и ось — самый очевидный. Велосипед содержит колеса и оси в передних и задних колесах. Колесо и ось — это просто колесо, которое вращается на оси, как показано ниже.
Что за простая машина — продуктовая тележка?
Колесо и ось позволяют нам катить вещи, а не нести их. Подумайте о продуктовой тележке с колесами и осями. Мешок с продуктами легче переместить в тележке, чем нести. А шкив это простая машина.
Простые машины: качели
Простые машинные проекты
Могучая математика рычага — Энди Петерсон и Зак Паттерсон
Как сделать качели | Простые машины | Пример рычага | Легкий
Черноуцан А.И. Качели //Квант. — 1994. — № 3. — С. 34,36.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Наверное, правильно предположить, что человек никогда не изобретал качелей — уж слишком проста их «конструкция». Здесь не требуется никакой high technology. Достаточно взять веревку, привязать один ее конец на высоте нескольких метров, взяться за другой, разбежаться, поджать ноги — и вот вы уже раскачиваетесь на самодельных качелях.
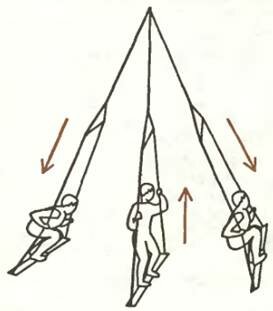
Рис. 1
Но так ли все просто? Если мы, оторвавшись от земли, не будем ничего предпринимать, то амплитуда колебаний будет постепенно уменьшаться, пока качели совсем не остановятся. Это и понятно — действие сил трения в точке подвеса качелей и сил сопротивления воздуха приводят к тому, что высота, на которую поднимается центр тяжести качелей (вместе с человеком) в крайних положениях, с каждым разом становится все меньше и меньше. Иными словами, уменьшается механическая энергия системы. Как же избежать этого? Что нужно сделать, чтобы, не касаясь земли, вновь раскачать качели и продолжать качаться столько, сколько нам хочется? Разумеется, ответ вам известен — нужно в крайних положениях чуть-чуть опускать центр тяжести своего тела относительно качелей, а в среднем — поднимать (рис. 1). Если вы стоите на качелях, то можно просто вовремя приседать и подниматься, а если вы качаетесь сидя, надо периодически сгибать и разгибать колени. В результате оказывается, что за счет работы мышц происходит увеличение механической энергии всей системы.
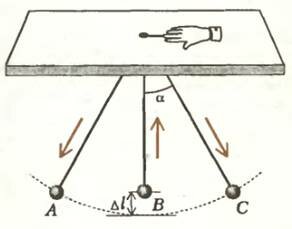
Рис. 2
Чтобы понять, почему это так, рассмотрим предельно упрощенную модель человека на качелях — обычный маятник, т.е. небольшой грузик на легкой и длинной нити. Чтобы имитировать поднимание и опускание центра тяжести, пропустим верхний конец нити через маленькое вертикальное отверстие и будем немного вытягивать нить вверх, когда маятник проходит среднее положение, и настолько же опускать нить вниз, когда маятник проходит крайние положения (рис. 2). Втягивая нить, мы совершаем положительную работу, т.е. увеличиваем энергию маятника, а отпуская нить, мы совершаем отрицательную работу, т.е. отбираем энергию у маятника. Но легко понять, что в среднем положении нить натянута сильнее, чем в крайнем, — в первом случае сила натяжения нити не только уравновешивает силу тяжести, но и сообщает маятнику центростремительное ускорение, а во втором лишь уравновешивает составляющую силы тяжести вдоль нити. Поэтому положительная работа будет больше отрицательной.
Аналогичное явление возникает и при раскачивании человека: в среднем положении его «прижимает» к качелям (можно сказать, что на него действует центробежная сила инерции — если вы знакомы с неинерциальными системами отсчета, то поймете, о чем идет речь), мышцы ног напряжены сильнее, и работа по разгибанию ног оказывается больше, чем по сгибанию.
Вернемся, однако, к нашей упрощенной модели и проделаем несложные расчеты, которые помогут нам понять, как и при каких условиях может происходить раскачивание. Натяжение нити в нижнем положении (B) равно
(~F_1 = mg + frac{m upsilon^2}{l}) ,
а в крайнем (A и C) —
(~F_2 = mg cos alpha) .
Здесь m — масса грузика, υ — его скорость в среднем положении, l — длина нити, α — угол отклонения в крайнем положении. Совершенная нами за один период работа равна
(~A = Delta E = 2(F_1 Delta l — F_2 Delta l) = 2 frac{Delta l}{l} left( mgl (1 — cos alpha) + 2frac{m upsilon^2}{2}right)) ,
где Δl — изменение длины маятника (мы считаем, что (~frac{Delta l}{l} << 1)). Выражение в скобках есть не что иное, как утроенная энергия колебаний Е. Поэтому получаем
(~frac{Delta E}{E} = 6 frac{Delta l}{l}) .
Обратите внимание: относительное увеличение энергии за период не зависит от того, слабо раскачивается маятник или сильно. Это очень важно, и вот почему. Если маятник не «подкачивать» , то за каждый период он будет терять за счет трения определенную часть своей энергии и колебания будут затухать. А чтобы размах колебаний увеличивался, необходимо, чтобы приобретаемая энергия превышала потерянную. И это условие, оказывается, одно и то же — как при маленькой амплитуде движения, так и при большой. Так, если за один период энергия свободных колебаний уменьшается на 6%,то для раскачивания маятника длиной 1 м достаточно в среднем положении уменьшать его длину на 1 см, а в крайнем — настолько же увеличивать.
Возвращаясь к качелям: если вы начали раскачиваться, то нет необходимости приседать все глубже и глубже — приседайте все время одинаково, и будете взлетать все выше и выше! Более того: если даже качели стоят на месте, а вы начали достаточно глубоко приседать с периодом, вдвое меньшим периода качелей, то колебания обязательно возникнут (правда, во-первых, надо угадать период, а во-вторых — должен помочь случай). Говоря языком техники, мы можем не только усиливать уже возникшие колебания, но и генерировать (т.е. создавать) их.
На примере детской игрушки — качелей — вы познакомились с важным физическим явлением — параметрическим резонансом. Почему такое название? Да потому, что для раскачивания колебаний периодически изменяют какой-нибудь из параметров, характеризующих свойства колебательной системы, например — период колебаний. Не обязательно менять параметр два раза за период — можно делать это один раз или даже один раз за несколько периодов. (Кстати, дети на качелях обычно приседают только тогда, когда движутся лицом вперед, т.е. один раз за период — так им, наверное, удобнее.) Какой мы при этом изменяем параметр, неважно. Например, для математического маятника период колебаний зависит от длины- нити и от ускорения свободного падения — (~T = 2 pi sqrt{frac lg}), т.е. можно изменять не только l, но и g. (Для этого не надо пытаться изменять притяжение к Земле — достаточно держаться за точку подвеса и придавать ей необходимое ускорение в вертикальном направлении. Ускорение вверх приводит к увеличению д в неинерциальной системе отсчета, связанной с точкой подвеса, ускорение вниз — кегоуменышнию.) Длягрузана пружинке период определяется массой груза и жесткостью пружинки — (~T = 2 pi sqrt{frac mk}), т.е. можно изменять либо жесткость пружинки k , либо массу груза m (придумайте сами, как это сделать). Во всех случаях надо так изменять параметр, чтобы полная работа была положительной и энергия маятника увеличивалась.