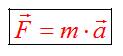Сила, второй закон Ньютона
Сила является мерой взаимодействия (взаимного действия). Если действие велико (мало), то говорят о большой (малой) силе. Сила обозначается буквой $$F$$ (первая буква слова force).
При взаимодействии чем больше сила, тем больше ускорение тела, на которое эта сила действует. Следовательно, ускорение прямо пропорционально действующей силе: a∼Fasim F.
Но уже говорилось о том, что ускорение зависит от массы тела: a∼1ma sim frac 1m
Обощая эти зависимости получим:
[a = frac{F}{m}, quad mathrm{или}quad F = ma.]
Теперь рассмотрим свойства силы, устанавливаемые опытным путём:
1) Результат действия (проявления) силы зависит от направления действующей силы, следовательно, сила – величина векторная.
2) Результат действия (проявления) силы зависит от величины приложенной силы .
3) Результат действия (проявления) силы зависит от точки приложения силы.
4) За единицу силы принято значение такой силы, которая вызывает ускорение 1 м/с21 mathrm{м}/mathrm{с}^2 у тела массой 1 кг1 mathrm{кг}. Единицу силы назвали в честь Исаака Ньютона 1 нью’тон. (Произносить фамилию считается правильным таким образом, как произносится фамилия в том государстве, где проживал или проживает учёный.)
[F→]=1 Н=1 кг·мс2 (ньютон).[overset{rightarrow}{F}] = 1 mathrm{Н} = 1 mathrm{кг}cdotfrac{mathrm{м}}{mathrm{с}^2}quad mathrm{(ньютон)}.
5) Если на тело одновременно действуют несколько сил, то каждая сила действует независимо от других. (Принцип суперпозиции сил). Тогда все силы необходимо сложить векторно и получить результирующую силу (рис. 4).
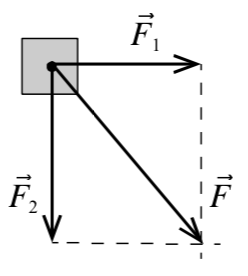 |
| Рис. 4 |
Из приведённых свойств силы следует, как обобщение опытных фактов, второй закон Ньютона:
Второй закон Ньютона: Сумма всех сил, действующих на тело, равна произведению массы тела на ускорение, сообщаемое этой суммой сил:
∑F→=ma→.boxed{sum vec{F} = mvec{a}}.
Данное выражение можно представить и в другой форме: так как a→=v→к-v→0tvec a = frac{vec v_mathrm{к} — vec v_0}{t}, то второй закон Ньютона примет вид: ∑F→=mv→к-v→0tsum vec F = mfrac{vec v_mathrm{к} — vec v_0}{t}.
Произведение массы тела и его скорости называют импульсом тела:
p→=mv→vec p = mvec v,
тогда получим новое выражение для второго закона Ньютона:
∑F→=mv→к-mv→0t=p→к-p→0t=Δp→tboxed{sum vec F = frac{mvec v_mathrm{к} — mvec v_0}{t}} = frac{vec p_mathrm{к} — vec p_0}{t} = frac{Delta vec p}{t}.
∑F→=p→к-p→0tboxed{sum vec F = frac{vec p_mathrm{к} — vec p_0}{t}} — второй закон Ньютона в импульсной форме для среднего значения силы. Здесь p→к-p→0=Δp→vec p_mathrm{к} — vec p_0 = Delta vec p — изменение импульса тела, t -t — время изменения импульса тела.
∑F→=dp→dt -boxed{sum vec F = frac{dvec p}{dt}} — второй закон Ньютона в импульсной форме для мгновенного значения силы.
Из второго закона в частности следует, что ускорение тела, подвергающегося действию нескольких сил, равно сумме ускорений, сообщаемых каждой силой:
a→=∑a→i=a→1+a→2+…+a→i=∑F→m=F→1+F→2+…+F→im=F→1m+F→2m+…+F→imboxed{vec a = sum vec a_i = vec a_1 + vec a_2 + dots + vec a_i = frac{sum vec F}{m} = frac{vec F_1 + vec F_2 + dots + vec F_i}{m} = frac{vec F_1}{m} + frac{vec F_2}{m} + dots + frac{vec F_i}{m}}.
Первая форма записи второго закона (∑F→=ma→)(sum vec F = mvec a) справедлива только при малых скоростях по сравнению со скоростью света. И, разумеется, выполняется второй закон Ньютона только в инерциальных системах отсчёта. Так же следует отметить, что второй закон Ньютона справедлив для тел неизменной массы, конечных размеров и движущихся поступательно.
Второе (импульсное) выражение имеет более общий характер и справедливо при любых скоростях.
Как правило, в школьном курсе физики сила со временем не меняется. Однако последняя импульсная форма записи позволяет учесть зависимость силы от времени, и тогда изменение импульса тела будет найдено с помощью определённого интеграла на исследуемом интервале времени. В более простых случаях (сила изменяется со временем по линейному закону) можно брать среднее значение силы.
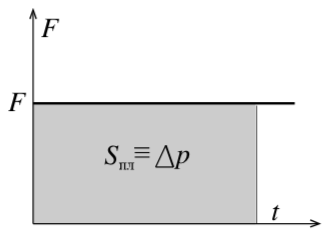 |
| Рис. 5 |
Иногда очень полезно знать, что произведение F→·tvec F cdot t называют импульсом силы, и его значение F→·t=Δp→vec F cdot t = Delta vec p равно изменению импульса тела.
Для постоянной силы на графике зависимости силы от времени можем получить, что площадь фигуры под графиком равна изменению импульса (рис. 5).
Но даже если сила будет изменяться со временем, то и в этом случае, разбивая время на малые интервалы ΔtDelta t такие, что величина силы на этом интервале остаётся неизменной (рис. 6), а потом, суммируя полученные «столбики», получим:
Площадь фигуры под графиком F(t)F(t) численно равна изменению импульса.
В наблюдаемых природных явлениях сила, как правило, меняется со временем. Мы же часто, применяя простые модели процессов, считаем силы постоянными. Сама же возможность использования простых моделей появляется из возможности подсчёта средней силы, т. е. такой постоянной силы, у которой площадь под графиком от времени будет равна площади под графиком реальной силы.
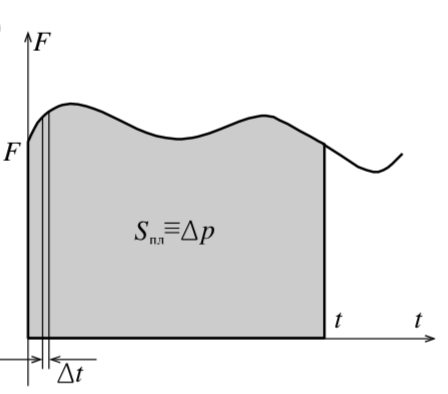 |
| Рис. 6 |
Следует добавить ещё одно очень важное следствие второго закона Ньютона, связанное с равенством инертной и гравитационной масс.
Неразличимость гравитационной и инертной масс означает, что и ускорения, вызванные гравитационным взаимодействием (законом всемирного тяготения) и любым другим тоже неразличимы.
Пример 2. Мяч массой 0,5 кг0,5 mathrm{кг} после удара, длящегося 0,02 с0,02 mathrm{с}, приобретает скорость 10 м/с10 mathrm{м}/mathrm{с}. Найти среднюю силу удара.
Решение. В данном случае рациональнее выбрать второй закон Ньютона в импульсной форме, т. к. известны начальная и конечная скорости, а не ускорение, и известно время действия силы. Также следует отметить, что сила, действующая на мяч, не остаётся постоянной. По какому закону меняется сила со временем, неизвестно. Для простоты мы будем пользоваться предположением, что сила постоянная, и её мы будем называть средней.
Тогда ∑F→=Δp→tsum vec F = frac{Delta vec p}{t}, т. е. F→ср·t=Δp→vec F_mathrm{ср}cdot t = Delta vec p. В проекции на ось, направленной вдоль линии действия силы, получим: Fср·t=pк-p0=mvкF_mathrm{ср}cdot t = p_mathrm{к}-p_0 = mv_mathrm{к}. Окончательно для искомой силы получим:
[F_mathrm{ср} = frac{mv_mathrm{к}}{t}.]
Количественно ответ будет таким: Fср=0,5 кг·10 мс0,02 с=250 НF_mathrm{ср} = frac{0,5 mathrm{кг}cdot 10 frac{mathrm{м}}{mathrm{с}}}{0,02 mathrm{с}} = 250 mathrm{Н}.
В
этом случае дифференциальное уравнение
движения имеет вид:
.
(12)
Так
как
,
то получаем дифференциальное уравнение
первого порядка:
,
или
.
Интегрируя
это уравнение в соответствующих пределах,
имеем:
,
откуда:
.
(13)
Интегрируя
это уравнение первого порядка, получим
x
как функцию от t,
т.е. найдем искомый закон движения точки.
2.3.3. Сила зависит от положения точки
Задачи,
в которых равнодействующая всех сил,
приложенных к данной материальной
точке, есть функция координаты этой
точки. В этом случае дифференциальное
уравнение движения точки имеет вид:
,
(14)
или:
.
Используя
преобразование (10), получим:
,
или:
.
(15)
Интегрируя
это уравнение в соответствующих пределах,
имеем:

(16)
Из
этого равенства определяется скорость
V
как функция от расстояния х, т.е.
,
или, разделяя переменныеи проинтегрировав это уравнение первого
порядка, найдем зависимость междуx
и t.
Если
является линейной функцией отх,
то уравнение (3) будет линейным
дифференциальным уравнением второго
порядка с постоянными коэффициентами.
Поэтому для решения этого уравнения
можно воспользоваться теорией
интегрирования таких дифференциальных
уравнений, т.е. составить соответствующее
характеристическое уравнение, найти
его корни и затем – общее решение данного
дифференциального уравнения. Две
произвольные постоянные в общем решении
находятся по начальным условиям движения
точки.
2.3.4. Сила зависит от скорости точки
Такой
вид задач будет иметь место при движении
точки в сопротивляющейся среде.
В
этом случае дифференциальное уравнение
движения имеет вид:
,
(17)
или,
разделяя переменные:
.
Отсюда:

(18)
Выполняя
здесь интегрирование и разрешая
полученное уравнение относительно V,
находим скорость точки как функцию
времени, т.е.
.
Следовательно,
,
и:
.
(19)
Это
уравнение выражает искомый закон
движения точки. Если в задаче требуется
найти скорость V
как функцию расстояния х,
то левую часть уравнения (1) преобразуем:
.
Тогда
уравнение (17) принимает вид:
,
или,
разделяя переменные:
,
откуда:

(20)
3. Примеры решения задач
3.1. Примеры решения первой задачи динамики точки
Задача
1. Материальная
точка массой m
= 0,4 кг
совершает гармонические колебания по
горизонтальной оси Ох
по закону x
= 0,2 Sin
(/2t)
(x
выражено в метрах, t
– в секундах). Найти силу, действующую
на точку в функции оси x.
Решение.
Находим проекцию ускорения точки на
ось Ох:
(м/с2).
Далее
находим проекцию на ось действующей
силы:
(Н).
Но
по условию задачи
,
следовательно:(Н).
Рис.
1.
Так как проекция силы на
осьОх и
координата х движущейся точки
противоположны по знаку, то искомая
сила направлена вдоль оси Ох
к началу координат О
и пропорциональна расстоянию от
движущейся точки до начала координат.
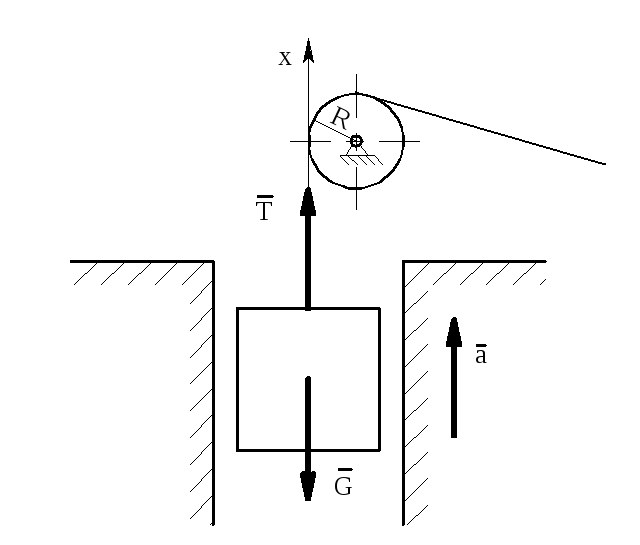
Задача
2. Лифт
весом G
поднимается с помощью каната. Канат
навернут на барабан радиуса R,
вращающийся вокруг неподвижной
горизонтальной оси по закону
.
Определить натяжение каната как функцию
высоты подъемаh.
Решение.
Так как лифт совершает поступательное
движение, при решении задачи будем
рассматривать его как материальную
точку. При повороте барабана на угол
лифт поднимается на высоту h
= R.
На него действует две силы: натяжение
каната Т
и вес лифта G.
Причем T
> G,
т.к. ускорение лифта направленно вверх.
Составим
дифференциальное уравнение движения
лифта в проекции на ось х:
,
или:
,
откуда:
Рис.
2.
.
Ускорение
лифта найдем из соотношения:
,
или:
.
Следовательно:
.
Задача
3. Материальная
точка массой m
= 0,5 кг
совершает движение согласно уравнениям:

Координаты
точки выражены в метрах, время – в
секундах. Определить величину и
направление силы, действующей на точку,
в момент времени t
= 1c.
Решение.
Находим
проекции ускорения точки на оси координат:

На
основании системы (2)
находим проекции равнодействующей на
оси координат:

По
системе уравнений (6) находим модуль и
направляющие косинусы равнодействующей
сил:

Задача
4. Материальная
точка массой m
= 2 кг описывает
криволинейную траекторию по закону
(S
выражено в метрах, время – в секундах).
В данный момент она занимает положение
М
и имеет скорость V
= 3 м/с,
радиус кривизны траектории в точке М
равен 6
м. Найти в
этот момент времени силу, действующую
на материальную точку.
Решение.
Находим скорость точки и проекции ее
ускорения на касательную и главную
нормаль траектории:

Согласно
условию задачи в данный момент времени
V
= 3 м/с.
Определяем время t:
.
Следовательно,
в этот момент:

Определяем
проекции равнодействующей на касательную
и главную нормали:
.
Модуль
равнодействующей:
Рис.
3.
.
Соседние файлы в папке Методички
- #
- #
- #
- #
I. Механика
Тестирование онлайн
Определение
Это векторная сумма всех сил, действующих на тело.
Велосипедист наклоняется в сторону поворота. Сила тяжести и сила реакции опоры со стороны земли дают равнодействующую силу, сообщающую центростремительное ускорение, необходимое для движения по окружности
Взаимосвязь со вторым законом Ньютона
Вспомним закон Ньютона:
Равнодействующая сила может быть равна нулю в том случае, когда одна сила компенсируется другой, такой же силой, но противоположной по направлению. В этом случае тело находится в покое или движется равномерно.

Сила Архимеда уравновешивается силой тяжести, тело равномерно перемещается в жидкости вниз. |

Сила тяжести уравновешивается силой упругости. Книга покоится |
Если равнодействующая сила НЕ равна нулю, то тело движется равноускоренно. Собственно именно эта сила является причиной неравномерного движения. Направление равнодействующей силы всегда совпадает по направлению с вектором ускорения.
Когда требуется изобразить силы, действующие на тело, при этом тело движется равноускоренно, значит в направлении ускорения действующая сила длиннее противоположной. Если тело движется равномерно или покоится длина векторов сил одинаковая.

Сила реакции опоры (сила, направленная вверх) длиннее силы тяжести, так как шарик движется по окружности, центростремительное ускорение направлено вверх |

Сила реакции опоры (сила, направленная вверх) короче силы тяжести, так как шарик движется по окружности, центростремительное ускорение направлено вниз. Вектор силы тяжести, направленный вниз, длиннее. |
Нахождение равнодействующей силы
Для того, чтобы найти равнодействующую силу, необходимо: во-первых, верно обозначить все силы, действующие на тело; затем изобразить координатные оси, выбрать их направления; на третьем шаге необходимо определить проекции векторов на оси; записать уравнения.
Кратко: 1) обозначить силы; 2) выбрать оси, их направления; 3) найти проекции сил на оси; 4) записать уравнения.
Как записать уравнения? Если в некотором направлении тело двигается равномерно или покоится, то алгебраическая сумма (с учетом знаков) проекций сил равна нулю. Если в некотором направлении тело движется равноускоренно, то алгебраическая сумма проекций сил равна произведению массы на ускорение, согласно второму закону Ньютона.
Примеры
На движущееся равномерно по горизонтальной поверхности тело, действуют сила тяжести, сила реакции опоры, сила трения и сила, под действием которой тело движется.
Обозначим силы, выберем координатные оси
Найдем проекции
Записываем уравнения
Тело, которое прижимают к вертикальной стенке, равноускоренно движется вниз. На тело действуют сила тяжести, сила трения, реакция опоры и сила, с которой прижимают тело. Вектор ускорения направлен вертикально вниз. Равнодействующая сила направлена вертикально вниз.
Тело равноускоренно движется по клину, наклон которого альфа. На тело действуют сила тяжести, сила реакции опоры, сила трения.
Главное запомнить
1) Если тело покоится или движется равномерно, то равнодействующая сила равна нулю и ускорение равно нулю;
2) Если тело движется равноускоренно, значит равнодействующая сила не нулевая;
3) Направление вектора равнодействующей силы всегда совпадает с направлением ускорения;
4) Уметь записывать уравнения проекций действующих на тело сил
Системы и блоки*
В задачах динамики учитывают силы, действующие на тело. Векторы сил могут действовать в различных направлениях. Большинство школьных задач можно решить, располагая векторы сил в одной плоскости. Поэтому, в статье будем рассматривать векторы, лежащие в одной плоскости — компланарные векторы.
Что такое равнодействующая
Равнодействующий вектор – это вектор, который мы получаем, когда складываем несколько векторов сил.
Результат сложения может дать:
- вектор, имеющий длину,
- или вектор, не имеющий длины.
Примечание: Когда у вектора отсутствует длина, говорят, что вектор равен нулю. На рисунке нулевой вектор можно изобразить одной точкой. Длины у точки нет – т. е. длина нулевая, а направление может быть любым.
Длина вектора содержит сумму квадратов всех его проекций на оси.
В частности, для вектора ускорения (vec{a}), лежащего на плоскости xOy, длина вычисляется так
[ large left| vec{a} right| = sqrt{ a_{x}^{2} + a_{y}^{2}} ]
Где ( a_{x} ) и ( a_{y} ) — это проекции вектора (ссылка) ( vec{a} ) на оси Ox и Oy.
Когда вектор равен нулю, равна нулю каждая его проекция на осях.
Длина вектора отлична от нуля, когда хотя бы одна его проекция ненулевая.
Прочитайте подробнее о параметрах векторов.
Левая часть силового уравнения
В левой части силового уравнения записываем силы, действующие на тело.
Когда векторы сил направлены вдоль параллельных прямых, проводим на рисунке одну ось. Если векторы сил не параллельные, проводим две оси на плоскости. Раскладываем векторы на проекции по осям. Для каждой оси составляем отдельное уравнение. Количество уравнений совпадает с количеством осей.
Если сила сонаправлена с осью, то она войдет в левую часть уравнения со знаком «+», а если она направлена против оси — то со знаком «минус».
Правая часть силового уравнения
В правой части уравнения записываем равнодействующую. В задаче может присутствовать несколько осей, вдоль каждой оси направляем отдельную проекцию равнодействующей.
Примечание: Тело может вдоль одной оси двигаться с ускорением, а вдоль другой оси двигаться без ускорения, или, вообще, покоиться. Например, тело может двигаться по вертикали под действием силы тяжести, а по горизонтали при этом не смещаться.
Когда проекция равнодействующей вдоль какой-либо оси не равна нулю, тело по оси будет двигаться с ускорением. Это следует из второго закона Ньютона.
Тогда в правой части уравнения запишем:
- (ma), если ускорение направлено туда же, куда направлена ось;
- (- ma), если ускорение направлено противоположно оси;
А когда проекция равнодействующей на ось нулевая, ускорение вдоль оси отсутствует. Тогда вдоль этой оси тело движется с неизменной скоростью, или же, вдоль этой оси движение отсутствует. Это следует из первого закона Ньютона.
В правой части уравнения запишем ноль (0 = ускорения нет).
Векторы сил параллельны
В случае, когда векторы направлены вдоль одной прямой, достаточно выбрать и провести единственную ось.
Выясним, как выглядит силовое уравнение для задачи, в которой векторы сил направлены вдоль единственной оси. Например, парашютист спускается вертикально вниз (рис. 1) на парашюте под действием силы тяжести.
Рис. 1. Парашютист спускается на парашюте, векторы сил направлены вдоль единственной оси
Проведем на рисунке ось, направим ее вверх.
Примечание: Мы можем направить ось вниз, если захотим. При таком направлении оси знаки проекций векторов изменятся на противоположные, но на конечный ответ это никак не повлияет.
Составим левую часть уравнения. В левой части мы запишем силы, действующие на парашютиста:
[large F_{text{сопр}} — m cdot g ]
Сила ( F_{text{сопр}}) направлена по оси, поэтому войдет в уравнение со знаком «+». А сила ( m cdot g ) вошла в уравнение со знаком «минус», так как направлена против оси.
В правую часть уравнения поместим равнодействующую.
Размеры парашюта рассчитаны так, что парашютист опускается вниз с постоянной (неизменной, т. е. одной и той же) скоростью. Значит, скорость есть, она не меняется, ускорения нет.
Математики запишут, что ускорение есть, но оно – нулевое (vec{a}=0).
То есть, вдоль вертикальной оси тело движется без ускорения, значит, силы компенсировались. По первому закону Ньютона, равнодействующая равна нулю и, в правой части уравнения запишем ноль.
Примечания:
- На рисунке 1 скорость обозначена красным вектором, направленным вниз и обозначенным, как (vec{v_{0}}). Обычно математики дописывают нижний индекс к величине, которая не должна меняться. Так как у вектора скорости этот индекс есть, скорость считаем неизменной.
- На рисунке векторы скоростей и ускорений нужно рисовать отдельно от векторов сил! Решая задачу, мы будем складывать векторы (ссылка), имеющие одинаковую размерность. Силы измеряют в Ньютонах, поэтому их можно складывать. А ускорения и скорости измеряют в других единицах, с Ньютонами их сложить не получится. Именно поэтому, чтобы не запутаться, ускорения и скорости рисуем на небольшом расстоянии от тела, отдельно от векторов сил.
Итоговое силовое уравнение имеет вид:
[large F_{text{сопр}} — m cdot g = 0 ]
Зная массу парашютиста, можно вычислить силу сопротивления воздуха. А зная эту силу, можно рассчитать и размеры парашюта.
Векторы сил не параллельны
Когда векторы направлены вдоль разных прямых, будем проводить две взаимно перпендикулярные оси на плоскости.
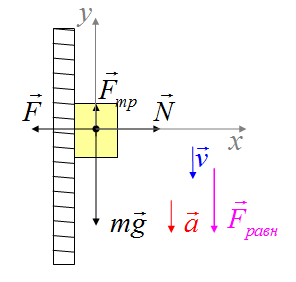
Разберем задачу равнозамедленного движения тела по горизонтальной шероховатой поверхности (рис. 2).
Рис. 2. Равнозамедленное движения тела по горизонтальной шероховатой поверхности
Поверхность шероховатая, это намек на то, что есть сила трения. А если в условии напишут, что поверхность гладкая, значит, силы трения нет.
Движение равнозамедленное (ссылка), значит, скорость тела уменьшается и есть вектор ускорения, который направлен против вектора скорости.
Нарисуем взаимно перпендикулярные оси. Ось Ox проведем горизонтально, а ось Oy – вертикально. Рассмотрим оси и проекции векторов на них по очереди.
Горизонтальная ось. Пусть движение тела происходит в положительном направлении оси Ox. Сила трения всегда направлена против движения, поэтому направим ее влево. Скорость тела направлена вправо и будет уменьшаться, значит, ускорение, так же, направим влево. Вектор ускорения рисуем отдельно от векторов сил.
Наличие ускорения говорит о том, что вдоль оси Ox равнодействующая имеет не нулевую проекцию. Ускорение направлено против оси, запишем (- ma) в правой части уравнения.
Так выглядит уравнение для горизонтальной оси
[large -F_{text{трен}} = -m cdot a_{x} ]
Вертикальная ось. Вниз направлена сила тяжести, а вверх – сила реакции опоры. Так как поверхность горизонтальная и тело не движется ни вверх, ни вниз, то движения вдоль оси Oy нет. Значит, сила тяжести и реакция опоры компенсировались и нет ускорения вдоль оси Oy. В правой части уравнения для вертикальной оси запишем ноль.
Для вертикальной оси уравнение выглядит так:
[large N — m cdot g = 0 ]
Система, пригодная для решения задачи, состоит из двух уравнений
[ large boxed{ begin{cases} -F_{text{трен}} = -m cdot a_{x} \ N — m cdot g = 0 end{cases} } ]
Куда направить оси
Разберем равнозамедленное движение тела вверх по наклонной шероховатой плоскости (рис. 3).
Силы, действующие на тело в этой задаче, не параллельные, направлены вдоль разных прямых. Поэтому для составления уравнений нужно использовать две взаимно перпендикулярные оси. Попробуем для начала провести ось Oy вертикально, а ось Ox горизонтально.
Рис. 3. Большая часть векторов не лежит на осях, такие векторы придется раскладывать на проекции, чтобы составить силовые уравнения
Из рисунка 3 видно, вдоль оси направлен только один вектор (mg). Остальные векторы сил не параллельны ни одной из осей. Такие векторы придется раскладывать на проекции, это усложнит конечную систему уравнений.
Если выберем оси так, как показано на рисунке 3, на проекции нужно будет разложить три вектора.
Попробуем теперь провести оси так, чтобы как можно большее количество векторов оказались параллельными осям (рис. 4). Из рисунка видно, что только один вектор (mg) окажется ненаправленным вдоль какой-либо оси. Остальные векторы сил параллельны осям.
Рис. 4. Большая часть векторов лежит на осях, раскладывать на проекции нужно только один вектор, силовые уравнения будут иметь простой вид
При таком выборе осей раскладывать на проекции придется только один вектор. Это позволит быстрее решить задачу и решать более простые уравнения.
Примечание: Если мы выбререм оси так, как это представлено на рисунке 3, получим более сложные уравнения. Но решив их, мы получим точно такой же ответ, как и в случае выбора осей на рисунке 4.
Выводы:
- Выбор осей на конечный результат не влияет! А влияет только на сложность полученных уравнений.
- Оси проводим так, чтобы как можно больше векторов оказались направленными вдоль осей.
Движение по наклонной плоскости
Составим систему уравнений для решения такой задачи:
Велосипедист подъезжает с начальной скоростью к подъему, посыпанному песком и, едет в гору на велосипеде по инерции, не крутя педали. Масса велосипедиста с велосипедом, начальная скорость его, коэффициент сопротивления поверхности и угол наклона известны.
Нужно составить систему силовых уравнений, чтобы найти ускорение велосипедиста. А после, зная начальную скорость и ускорение, найти путь, который велосипедист сможет проехать по инерции в горку.
Выражение для ускорения
Составим рисунок, на котором изобразим силы, действующие на велосипедиста (рис. 5)
Рис. 5. Велосипедист едет в гору по инерции, отмечены силы, действующие на велосипедиста, видно, что при таком выборе осей необходимо разложить вектор mg на проекции
Мы провели оси так, чтобы пришлось разложить на проекции только один вектор и система силовых уравнений оказалась достаточно простой.
Пользуясь осями координат, составляем теперь уравнения в проекциях.
Уравнение для проекций векторов на ось Ox:
[ large — F_{text{трен}} – m cdot g_{x} = — m cdot a ]
Уравнение для проекций векторов на ось Oy:
[ large N – m cdot g_{y} = 0 ]
Разложим теперь силу тяжести — вектор (mg) на проекции. Чтобы проделать это разложение, нужно отметить угол (alpha ) межу вектором (mg) и одной из осей. В нашем случае, это угол между вектором (mg) и осью Oy.
[ large begin{cases} m cdot g_{y} = mg cdot cos left(alpha right) \ m cdot g_{x} = mg cdot sin left(alpha right) end{cases} ]
Подставив разложение вектора (mg) в уравнения для осей, получим такую систему уравнений
[ large begin{cases} — F_{text{трен}} – mg cdot sin left(alpha right) = — m cdot a \ N – mg cdot cos left(alpha right) = 0 end{cases} ]
Дополним эту систему выражением для силы трения.
[ large F_{text{трен}} = mu cdot N ]
Запишем эти уравнения в систему и выразим из нее уравнение для ускорения.
[ large begin{cases} N = mg cdot cos left(alpha right) \ F_{text{трен}} = mu cdot mg cdot cos left(alpha right) \ mu cdot mg cdot cos left(alpha right) + mg cdot sin left(alpha right) = m cdot a end{cases} ]
Поделим нижнее уравнение системы на массу велосипедиста и запишем окончательно уравнение для ускорения:
[ large mu cdot g cdot cos left(alpha right) + g cdot sin left(alpha right) = a ]
Выражение для пройденного пути
Запишем выражения для связи скоростей и пройденного пути. Велосипедист движется по инерции в гору и его скорость уменьшается из-за силы тяжести и силы сопротивления поверхности, посыпанной песком. Когда скорость велосипедиста обратится в ноль, он, проехав часть пути в гору, остановится. Используем систему двух уравнений, она описывает путь при учете уменьшения скорости до нуля:
[ large begin{cases} 0 = v_{0} — a cdot t \ S = v_{0} cdot t — a cdot frac{t^2}{2} end{cases} ]
Получим теперь уравнение для пути, в котором будут присутствовать только начальная скорость и ускорение и, будет отсутствовать время.
[ large begin{cases} t = frac{v_{0}}{a} \ S = v_{0} cdot frac{v_{0}}{a} — a cdot frac{1}{2} cdot frac{v_{0}}{a} cdot frac{v_{0}}{a} end{cases} ]
Упрощенная система для решения задачи теперь включает всего два уравнения
[ large begin{cases} mu cdot g cdot cos left(alpha right) + g cdot sin left(alpha right) = a \ S = v_{0} cdot frac{v_{0}}{a} — frac{v_{0}}{2} cdot frac{v_{0}}{a} end{cases} ]
Подставив в эту систему известные значения начальной (v_{0}) скорости велосипедиста, коэффициент (mu) сопротивления поверхности и угол (alpha) наклона плоскости, сможем посчитать путь, пройденный велосипедистом до его полной остановки.
В статье обсуждаются различные методы нахождения чистой силы и решенные проблемы с некоторыми фактами.
Чистая сила — это полная сила, действующая на систему, которая определяется путем сложения всех сил, действующих на систему. Мы используем этот термин, когда на систему действуют разные типы сил. Чистая сила имеет точные характеристики как единая сила, которая ускоряет или замедляет любой объект с массой.
Предположим, что N сил действует на объект во всех возможных направлениях. Каким будет его ускорение и в каком направлении он будет двигаться?
Мы просуммировали все N сил, действующих на стол, что дает результирующую силу как общее количество сил, действующих на объект.
Компания основная чистая сила формула является,
Fсеть = Ф1 + F2 + F3 + F4 +…. + FN
Как единая сила, Ньютон (N) — единица чистой силы в системе СИ.
Узнайте больше о Net Force.
Во время перетягивания каната на канат работали шесть неизвестных сил: 5N, 2N, 1N, 7N, 4N, 2N. Выясните чистую силу, действующую на веревку, и в каком направлении она будет двигаться.
Данный:
F1 = 5 Н
F2 = 2 Н
F3 = 1 Н
F4 = 7 Н
F5 = 4 Н
F6 = 2 Н
Найти: Fсеть =?
Формула:
Fсеть = Ф1 + F2 + F3 + F4 +…. + FN
Решения:
Чистая сила, действующая на канат во время перетягивания каната, рассчитывается как
Fсеть = Ф1 + F2 + F3 + F4 + F5 + F6
Подставляя все значения,
Fсеть = 5 + 2 + 1 + 7 + 4 + 2
Fсеть = 22 Н
Чистая сила, действующая на веревку, составляет 22 Н, и, поскольку она имеет положительное значение, она ускоряет веревку в прямом направлении.
Узнайте больше о примерах Net Force.
Как найти чистую силу с массой?
Чистая сила с массой определяется с помощью второго закона движения Ньютона.
Если на систему не действует сила, результирующая сила также равна нулю. Следовательно, система, имеющая массу, не будет двигаться или ускоряться. Но на практике этот случай немыслим, поскольку на любой объект во Вселенной всегда действует хотя бы одна сила. то есть сила тяжести.
Сопротивление или трение, препятствующие движению объекта, незначительны во время свободное падение. Следовательно, объект с определенной массой падает на землю.
Сила тяжести всегда действует на нас и постоянно ускоряет вниз. Формула силы тяжести «mg» подчиняется второму закону движения Ньютона F = ma.
(Кредит: Shutterstock)
г является постоянное ускорение значение для всех объектов. Следовательно, чем больше масса объекта, тем больше сила гравитации и тем быстрее он будет падать.
Следовательно формула чистой силы для объекта свободного падения эквивалентно силе тяжести. т.е. Fсеть = Фg = мг
Узнайте больше о Gravity Force.
Какова чистая сила, действующая на яблоко массой 2 кг, свободно падающее на землю (g = 9.8 м / с2)?
Данный:
m = 2 кг
g = 9.8 м / с2
Найти: Fсеть =?
Формула:
Fg = мг
Решения:
Поскольку яблоко свободно падает, на него действует единственная сила тяжести.
Следовательно, результирующая сила, действующая на свободно падающее яблоко, рассчитывается с использованием формула силы тяжести,
Fсеть = мг
Подставляя все значения,
Fсеть = 2 x 9.8
Fсеть = 19.6 Н
Суммарное усилие на свободно падающее яблоко массой составляет 19.6 Н.
Узнайте больше о том, как найти гравитацию?
Как вам Net Force с двумя силами?
Суммарная сила с двумя силами определяется с помощью третьего закона движения Ньютона:
Когда объект находится в состоянии покоя, поверхность земли применяет направленную вверх нормальную силу на неподвижный объект в качестве силы реакции на силу тяжести. Следовательно, результирующая сила, действующая на неподвижный объект, включает две силы, такие как сила тяжести и нормальная сила.
Поверхность грунта использует нормальная сила противодействовать силе тяжести. Это означает, что нормальная сила равна силе тяжести и противоположна по величине. Следовательно, FN = мг
Следовательно, существует пара вертикальных сил, которые действуют на объект, когда он остается в покое на поверхности земли, создавая результирующую силу с двумя силами:
Fсеть = ФN + Fg
Поскольку сила тяжести направлена вниз, мы считаем ее значения отрицательными. т.е. -Fg.
Следовательно формула чистой силы с двумя силами является,
Fсеть = ФN + (-Фg)
Узнать больше о Типах сил.
Предположим, что на человека, стоящего на дороге, действует сила тяжести 10 Н и нормальная сила 10 Н. Какая чистая сила будет действовать на стоящего человека?
Данный:
Fg = -10 Н
FN = 10 Н
Найти: Fсеть =?
Формула:
Fсеть = Ф1 + F2 + F3 + F4 +…. + FN
Решения:
Чистая сила, действующая на стоящего человека, рассчитывается как
Fсеть = ФN + Fg
Fсеть = 10 + (-10)
Fсеть = 0
Чистая сила, действующая на стоящего человека, равна нулю. Вот почему он остается в состоянии покоя без действующей чистой силы.
Узнать больше об относительном движении.
Как рассчитать чистую силу в противоположных направлениях?
Суммарная сила в противоположном направлении определяется с помощью третьего закона движения Ньютона.
Когда мы прикладываем силу вверх к неподвижному объекту, воздух оказывает равную и противоположную силу, называемую сопротивлением воздуха. сила. Следовательно, результирующая сила действует в противоположном направлении, которое противодействует ускорению, вызванному приложенной силой.
Раньше мы понимали, что если пара сил имеет точную величину, они уравновешивают друг друга. Следовательно, объект не будет двигаться или ускоряться, поскольку его чистая сила равна нулю. Вот почему одна из сил должна иметь большую величину, чем другая, чтобы расчетная чистая сила могла ускорять или замедлять объект..
Когда мы подбрасываем мяч вверх, он быстрее возвращается к земле, преодолев определенную высоту. Это происходит потому, что сила сопротивления воздуха меняет направление движения мяча на противоположное, и сила тяжести быстро ускоряет мяч вниз.
Поскольку величина противоположных сил становится больше, чем приложенная сила, результирующая сила действует в направлении, противоположном приложенной силе..
Rузнать больше о Unbalanced Force.
Когда мы прикладываем к мячу силу 10 Н при броске, на мяч действует сила сопротивления воздуха 6 Н и сила тяжести 6 Н. Рассчитайте чистую силу, действующую на мяч.
Данный:
Fприложение = 10 Н
Fвоздух = -6 Н
Fg = -6 Н
Найти: Fсеть =?
Формула:
Fсеть = Ф1 + F2 + F3 + F4 +…. + FN
Решения:
Чистая сила, действующая на мяч, рассчитывается как
Fсеть = Фприложение + Fвоздух + Fg
Подставляя все значения,
Fсеть = 10 + (-6) + (-6)
Fсеть = -2 Н
Чистая сила, действующая на мяч, составляет -2 Н, действующая в противоположном направлении.
Как определить чистую силу угла?
Чистая сила угла определяется с помощью наклонной плоскости.
Когда объект находится под углом к горизонтальной поверхности или наклонной плоскости, сила тяжести разделяется на две составляющие. Нормальная сила уравновешивает параллельный компонент. Следовательно, чистая сила наклонного угла включает параллельную составляющую силы тяжести.
В отсутствие приложенной силы параллельная составляющая силы тяжести mgsinθ является единственной силой, которая ускоряет объект вниз под наклоном. Вот почему любой предмет быстро скользит по наклонной плоскости. Поскольку нет приложенной силы, нет сила трения, действующая на наклонный самолет.
Следовательно формула чистой силы наклонного угла является,
Fсеть = mgsinθ
Узнать больше о наклонной плоскости.
Какая чистая сила действует на кресло-коляску массой 5 кг, которое скользит вниз по наклонной рампе под углом 30 °? (g = 9.8 м / с2)
Данный:
m = 5 кг
g = 9.8 м / с2
θ = 30 °
Найти: Fсеть =?
Формула:
Fсеть = mgsinθ
Решения:
Чистая сила, действующая на кресло-коляску, рассчитывается как
Fсеть = mgsinθ
Подставляя все значения,
Fсеть = 5 x 9.8 x sin 30 °
Fсеть = 49 / 2
Fсеть = 24.5 Н
Чистая сила, действующая на кресло-коляску под углом 30 °, составляет 24.5 Н..
Подробнее о трении в наклонной плоскости.
Как вам Net Force с компонентами?
Чистая сила с компонентами определяется, когда вертикальные силы уравновешивают друг друга.
Когда мы прикладывали силу под определенным углом к горизонтальной поверхности, она распадалась на две составляющие. Перпендикулярная составляющая вместе с нормальной силой уравновешивает силу тяжести. Следовательно, результирующая сила включает параллельные компоненты приложенной силы и противоположную силу трения.
Горизонтальная или параллельная составляющая приложенной силы оценивается с помощью тригонометрическая функция в виде,
Fx = Фприложение. Sinθ
Узнайте больше о том, как разрешить силу в компонентах.
Предположим, мы прикладываем силу толчка 80 Н под углом 60 °, чтобы переместить коробку. Поверхность земли прикладывает к коробке силу трения 50 Н. Рассчитайте чистую силу, действующую на коробку.
Данный:
Fприложение = 80 Н
FФрич = -50 Н
θ = 60 °
Найти: Fсеть=?
Формула:
Fсеть = Ф1 + F2 + F3 + F4 +…. + FN
И, Fx = Фприложение. Sinθ
Решения:
Прежде чем определить чистую силу на коробке, мы должны найти параллельные составляющие приложенной силы.
Fx = Фприложение. Sinθ
Fx = 80 x sin 60 °
Fx = 80 x 0.86
Fx = 68.8 Н
Компания формула чистой силы с параллельной составляющей на коробке рассчитывается как,
Fсеть = Фx + FФрич
Fсеть = 68.8 + (-50)
Fсеть = 18.8 Н
Чистая сила, действующая на коробку из-за параллельной составляющей, составляет 18.8 Н.
Как найти Net Force на зарядке?
Чистая сила, действующая на заряд, определяется с использованием Закон Кулона.
Электростатическая сила или кулоновская сила между двумя покоящимися зарядами может быть получена с помощью закона Кулона. Поскольку атом состоит из множества заряженных частиц, суммарная сила, действующая на все заряды, складывает каждую электростатическую силу между парами зарядов.
Электростатическая сила Fа, б между зарядом a и b определяется выражением,
Fа, б=(kqaqb)/р2
Где k — постоянная кулона.
qa и дb взимается a и b соответственно.
А r — расстояние между зарядами.
Найдите чистые силы на трех зарядах 5μС 10μC и 5μC, которые одинаково разделены расстоянием 2 см. (Кулоновская постоянная k = 8.99 x 109)
Данный:
q1 = 5μС = 5 х 10-6C
q2 = 10μC = 10-5C
q3 = 5μС = 5 х 10-6C
г = 2 см = 2 х 10-2m
к = 8.99 х 109
Найти: Fсеть =?
Формула:
Fсеть = Ф1 + F2 + F3 + F4 +…. + FN
И Fа, б=(kqaqb)/р2
Решения:
Чтобы найти суммарную силу, действующую на все три заряда, нам нужно найти электростатические силы между ними.
Электростатические силы между зарядами 1 и 2 составляют,
F1,2=(kq1q2)/р2
F1,2=(44.95*10-2)/(2*10-2)
F1,2 = 22.47 Н
Электростатические силы между зарядами 2 и 3 составляют,
F2,3=(kq2q3)/р2
F2,3 = 22.47 Н
Компания электростатические силы между зарядом 1 и 3 есть,
F1,3=(kq1q3)/р2
F1,3 =(224.5*10-3)/(2*10-2)
F1,3 = 11.23 Н
Формула чистой силы для всех трех зарядов рассчитывается как,
Fсеть = Ф1,2 + F2,3 + F1,3
Fсеть = 22.47 + 22.47 + 11.23N
Fсеть = 56.17 Н
Чистая сила, действующая на заряды, составляет 56.17 Н.
Как найти чистую силу на графике зависимости скорости от времени?
Чистая сила из графика зависимости скорости от времени определяется с использованием второго закона Ньютона.
Когда на объект действуют различные силы, его скорость время от времени изменяется. Если мы построим график его скорости в зависимости от времени, мы оценим его значение ускорения при действии чистой силы. Следовательно, мы можем рассчитать чистую силу по скорости, используя формулу второго закона движения Ньютона.
Формула второго закона Ньютона в терминах чистой силы:
Fсеть = ма
Fсеть = м*(Δv/Δt)
Fсеть ==м*[(вв0)/(тт0)]
Узнать больше о скорости.
Из приведенного ниже графика зависимости скорости от времени вычислите чистую силу, действующую на автомобиль массой 20 кг.
Данный:
m = 20 кг
Найти:
а =?
Fсеть =?
Формула:
Fсеть = ма
Решения,
Прежде чем рассчитать чистую силу, нам нужно найти ускорение автомобиля по график зависимости скорости от времени.
а=(Δv/Δt)
а=(вв0)/(тт0)
Из графика зависимости скорости от времени
Машина изначально стояла в покое. Это означает, что v0 = 0 и t0 = 0
Конечная скорость автомобиля составляет 80 км / час при конечном времени 10 мин. Это означает, что v = 80 км / ч и t = 10 мин.
Компания формула чистой силы является,
Fсеть =m*(об/т)
Подставляя все значения,
Fсеть ==20*(80/10)
Fсеть = 120 Н
Чистая сила, действующая на автомобиль в зависимости от его скорости в зависимости от времени, составляет 120 Н.
Как найти чистую силу с массой и скоростью?
Компания результирующая сила с массой и скоростью определяется по формуле Работа-Энергия.
Когда чистая сила ускоряет покоящийся объект, она преобразует потенциальную энергию в кинетическую. Таким образом, объект перемещается на определенное расстояние, это когда мы говорили, что работа выполняется объектом, что позволяет нам найти результирующую силу с его массой и скоростью.
В соответствии с Формула работы-энергии,
KE = W
Но работа, выполняемая объектом, произведение чистой силы Fсеть действие и расстояние d, которое он прошел.
(1/2)мв2=Fсетьd
Узнайте больше о выполненной работе.
Когда футболист бьет ногой по футбольному мячу массой 5 кг, он движется со скоростью 10 км / ч на расстояние 8 м. Какая чистая сила действует на футбол?
Данный:
m = 5 кг
v = 10 км / ч = 10 x 1000/36000 м / сек
d = 8м
Найти: Fсеть =?
Формула:
(1/2)мв2=Fсетьd
Решения:
Чистая сила на футбольном мяче рассчитывается с использованием Формула работы-энергии в виде,
(1/2)мв2=Fсетьd
Компания результирующая сила с массой и скоростью является,
mv2/2д=Фсеть
Подставляя все значения,
Fсеть= 5000 / 368
Fсеть = 13.5 Н
Чистая сила, действующая на футбольный мяч, имеющий массу и скорость, составляет 13.5 Н.
Подробнее о преобразовании потенциала в кинетическую энергию.