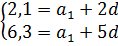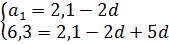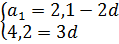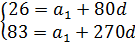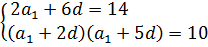Как найти шестой член арифметической прогрессии

Для того чтобы понимать, каким образом упорядочены числа арифметической прогрессии, рассмотрим следующий ряд:
a₁
a₂=a₁+d
a₃=a₂+d=a₁+d+d=a₁+2d
a₄=a₃+d=a₁+2d+d=a₁+3d

…

Очевидно прослеживается закономерность формирования каждого следующего члена прогрессии, который можно выразить через предыдущий: a_n=a_(n-1)+d или через первый член арифметической прогресии a₁. Чтобы найти член арифметической прогрессии через первый член, к нему прибавляется количество шагов прогрессии, равное n-1, где n — это порядковый номер члена прогрессии, который нужно найти по заданным условиям.
a_n=a₁+(n-1)d

Наоборот, зная какой-либо определенный n член арифметической прогрессии, можно найти первый член. Для этого выводится специальная формула из предыдущей:
a₁=a_n-(n-1)d

Если по заданию нужно найти первые члены арифметической прогрессии, то в любом случае первым действием должно быть вычисление первого члена прогрессии, и затем путем прибавления разности прогрессии к каждому предыдущему числу можно будет найти необходимое количество первых членов, например, до пятого или до десятого члена.

Общее число членов арифметической прогрессии по умолчанию неограниченно, так как прибавление разности прогрессии является действием, возможным для бесконечного повторения. Предел такой последовательности будет стремиться в сторону плюс или минус бесконечности в зависимости от знака разности прогрессии. Так как последовательность будет бесконечно расти, для арифметической прогрессии можно найти сумму первых членов или сумму членов, определенных условием задания.

Соответственно, зная сумму арифметической прогрессии, найти первый член не составляет труда, если правильно перевернуть формулу. Сумма арифметической прогрессии — это среднее арифметическое (откуда и название) первого и последнего членов прогрессии, умноженное на общее количество членов прогрессии.

Первый член прогрессии в таком случае будет равен удвоенному отношению суммы к общему количеству членов за вычетом последнего члена в сумме.

        Суперполезная формула! Позволяет легко и просто (и главное — быстро!) искать любой член арифметической прогрессии! Да-да, любой! Какой хотите.) А заодно и массу других самых разных задач по прогрессии решать. Имеет смысл освоить и разобраться, правда?

        Вот поэтому осваиваем и разбираемся. В этом уроке.)

Вывод и смысл формулы n-го члена

        Итак, прошу любить и жаловать:

a_n = a₁ + (n-1)·d

        Это и есть формула n-го члена арифметической прогрессии, собственной персоной.) Какие-то индексы, буковки непонятные. Ничего страшного! Сейчас всё расшифрую.

        В формуле:

        a₁ — первый член арифметической прогрессии;

        d — разность арифметической прогрессии;

        n — номер члена;

        a_n — энный (n-й) член арифметической прогрессии.

        Как вы видите, большая часть входящих в формулу буковок (первый член, разность прогрессии, номер члена) уже должна быть вам хорошо знакома из прошлого урока. Если не читали, настоятельно рекомендую заглянуть. Там всё просто и доступно. Осталось лишь разобраться, что же такое n-й член.

        Мы с вами знаем (надеюсь), что любую арифметическую прогрессию в общем виде всегда можно записать в виде последовательности чисел:

        a₁, a₂, a₃, a₄, a₅, …

        Символ a₁ означает первый член прогрессии, a₂ — второй член, a₅ — пятый и так далее. Если нас интересует, скажем, десятый член прогрессии, то работаем с a₁₀. Если сто тридцатый, то, соответственно, с a₁₃₀. Элементарно, Ватсон!)

        А как можно обозначить в общем виде любой член арифметической прогрессии прогрессии с любым номером? Тоже элементарно! Вот так:

        a_n

        Это и есть n-й член арифметической прогрессии. Под буковкой n здесь скрываются сразу все номера членов: и 1, и 23 и 101 — все без исключения!

        И что нам даёт такая запись? Казалось бы, всего лишь вместо цифры буковка появилась — и что из этого? А вот что.

        Запись эта представляет собой очень мощный инструмент для работы с арифметической прогрессией. Сомневаетесь? Не надо.) Используя обозначение a_n, мы можем легко и просто искать любой член любой арифметической прогрессии! Как? Читаем дальше.)

        Возвращаемся снова к нашей формуле:

a_n = a₁ + (n-1)·d

        Со всеми обозначениями мы успешно разобрались, а теперь разбираемся, в чём же её суть.

        Эта формула позволяет нам найти любой член арифметической прогрессии по его номеру «n«.

        Заманчиво, правда? Знаем номер члена — сразу же можем найти и сам этот член! Естественно, для этого нам надо знать ещё первый член a₁ и разность прогрессии d. Ну так без этих двух ключевых параметров конкретную прогрессию и не задашь вовсе.

        Формула эта связывает четыре главных параметра любой арифметической прогрессии — а_n, a₁, d и n. Именно вокруг этих четырёх параметров и крутятся все-все задачки по прогрессии!

        Откуда же берётся эта формула и как её запомнить? А то уж больно часто сомнения грызут — то ли n там, то ли n-1, то ли n+1… Особенно на контрольных и экзаменах.

        Спокойствие! Сейчас мы с вами эту формулку выведем! Не очень строго, правда, но зато с полным пониманием всего происходящего. Что, как и откуда. И у вас сразу же отпадут все сомнения!

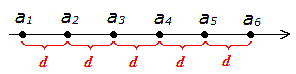
        Итак, рисуем числовую ось и последовательно отмечаем на ней члены нашей прогрессии:

        А теперь смотрим на рисунок и соображаем. Чему равен второй член прогрессии?

        Второй член равен первому члену плюс одно d:

        a₂ = a₁ + 1·d

        А третий член чему равен?

        Не вопрос! Третий член равен первому члену плюс два d:

        a₃ = a₁ + 2·d

        Ну как, улавливаете закономерность? Я же не просто так некоторые слова и цифры выделяю жирным шрифтом! Нет? Что ж, ладно. Ещё один шаг.)

        Чему равен четвёртый член?

        Четвёртый член равен первому члену плюс три d:

        a₄ = a₁ + 3·d

        Пора бы уже догадаться, что количество интервалов (т.е. d) всегда на единичку меньше, чем номер нужного нам члена n. Поэтому до номера n количество интервалов всегда будет n-1.

        Стало быть, наша формула, уже безо всяких сомнений, будет вот такой:

a_n = a₁ + (n-1)·d

        Вот и весь секрет.)

        Совсем строгое доказательство данной формулы проводится так называемым методом математической индукции. Но метод этот — для особых гурманов.) Не каждый с ходу разберётся и поймёт, что к чему. А вот по картинке всё просто и наглядно! Да и вообще, картинка — очень мощный инструмент решения многих математических задач! И не только по прогрессиям. Так что не пренебрегаем ими. Скажем, в сложной боевой обстановке ЕГЭ вы переволновались и подзабыли случайно эту формулу. Ну, вот не помните, с кем не бывает! Ничего страшного. Есть пара-тройка минуток времени — рисуем картинку, отмечаем члены прогрессии и промежутки между членами — и всё сразу становится как на ладони!

        Разумеется, всё от конкретной задачи зависит. Бывают и такие задачи, рисовать картинку к которым весьма затруднительно, а то и вовсе невозможно. Тогда — только формула, да…) Ибо формула — это тяжёлая артиллерия, позволяющая подключить к решению задачи весь мощный арсенал математики — уравнения, неравенства, системы и т.д. Картинку ведь в уравнение не вставишь!

        Ну что, коли уж мы заговорили о задачках, то пора бы уже и порешать!

Решение задач с помощью формулы n-го члена арифметической прогрессии.

        Прямое применение формулы.

        Начнём с прямого применения формулы. В самом конце прошлого урока была вот такая задачка:

        В арифметической прогрессии известно, что a₁ = 4 и d = 0,4. Найдите a₁₄₁.

        Конечно, эту задачку можно и безо всяких формул решить. Исходя из смысла арифметической прогрессии. Прибавлять себе по 0,4 да считать. Часок-другой…)

        Зато по формуле решение осуществляется в одну строчку и занимает меньше минуты! Можете засекать время.)

        Итак, у нас имеются все данные для применения формулы.

        Известен первый член: a₁ = 4.

        Известна также разность прогрессии: d = 0,4.

        Остаётся только сообразить, чему равен номер члена n. Не вопрос! Нам надо найти a₁₄₁. Так прямо и пишем:

        a₁₄₁ =

        А вот здесь сосредотачиваемся! Вместо индекса n у нас появилось конкретное число 141. Что вполне естественно. Ибо нас интересует член прогрессии номер сто сорок один. Вот именно это и будет наше n! Именно это значение n = 141 мы и подставим в формулу n-го члена в скобки.

        Подставляем все наши данные в формулу и считаем:

        a₁₄₁ = 4 + (141-1)·0,4 = 4+56 = 60

        Вот и всё, никаких фокусов. Так же быстро можно найти и четыреста третий член, и тысяча первый — любой! Какой хотим, такой и отыщем. Просто подставляем нужный номер в формулу вместо индекса n и в скобки. И считаем.)

        Рассмотрим теперь задачку похитрее.

        В арифметической прогрессии с разностью 3 пятнадцатый член равен 50. Найдите первый член этой прогрессии.

        Ну и как вам? Знаете, с чего начинать? Если знаете — вперёд и с песнями. Не знаете? Что ж, тогда подскажу.

        Пишем формулу n-го члена арифметической прогрессии!

        Да-да! Прямо на черновике или в тетрадке.)

        a_n = a₁ + (n-1)·d

        А теперь глядим внимательно на нашу формулу и соображаем, какие данные у нас уже есть, а чего не хватает.

        Во-первых, нам известна разность прогрессии d:

        d = 3

        Во-вторых, нам известен пятнадцатый член прогрессии. Так и пишем:

        a₁₅ = 50

        Всё? Не-а! У нас есть ещё номер n! Дело в том, что в условии a₁₅ = 50 скрыты сразу два параметра прогрессии. Это, во-первых, значение самого пятнадцатого члена (50) и, во-вторых, его номер (15). То есть, n=15.

        Вот теперь уже можно подставить все известные нам данные в формулу:

        50 = a₁ + 3·(15-1)

        Решаем это простенькое линейное уравнение и получаем ответ:

        a₁ = 8

        Вот и все дела.)

        Ещё одна популярная задачка:

        Найдите разность арифметической прогрессии (a_n), если

        a₁ = 6; a₂₁ = -14.

        Первый шаг тот же самый: пишем формулу n-го члена арифметической прогрессии!

        a_n = a₁ + (n-1)·d

        А теперь снова соображаем, что нам дано по условию задачи:

        a₁ = 6

        a₂₁ = -14

        n = 21

        Вот и всё. Всю ценную информацию из условия скачали. Подставляем наши известные величины в формулу и считаем банальную арифметику:

        -14 = 6 + (21-1)·d

        -14 = 6 + 20d

        -20 = 20d

        d = -1

        Всё. Это правильный ответ.)

        Так, задачки на поиск a_n, a₁ и d порешали. Осталось научиться ещё номер члена находить.)

        Известно, что число 43 является членом арифметической прогрессии (a_n) c первым членом, равным 3 и разностью 0,4. Найдите номер этого члена.

        Вы удивитесь, но первый шаг снова точно такой же.

        Пишем формулу!

        a_n = a₁ + (n-1)·d

        На первый взгляд кажется, что здесь две неизвестные величины — a_n и n. Но a_n — это какой-то член арифметической прогрессии под номером n. И этот член нам известен! Это 43. Нам неизвестен номер n этого члена. Так этот самый номер, как раз, и требуется отыскать!

        Подставляем член прогрессии 43 в формулу n-го члена вместе с остальными известными нам параметрами:

        43 = 3 + (n-1)·0,4

        Считаем простецкую арифметику и выражаем номер n:

        (n-1)·0,4 = 40

        n-1 = 100

        n = 101

        Готово дело.)

        Как вы видите, запись формулы в общем виде и подстановка в неё известных величин — весьма популярный приём в решении очень многих задач на прогрессии! Если вы, конечно, умеете выражать переменную из формулы. Ну так без этого умения математику можно и вовсе не изучать. Как, впрочем, и остальные точные науки тоже, да…

        А теперь ещё одна задачка на эту тему, но более творческая.

        Определите, будет ли число 74 членом арифметической прогрессии

        (a_n): -5,6; -4; -2,4; …

        Снова (да-да!) пишем формулу:

        a_n = a₁ + (n-1)·d

        Начинаем подставлять известные нам данные. Гм… не подставляется что-то…

        Что, не видите никаких данных? Серьёзно? Ну, тогда срочно к окулисту. Без обид.) Что же всё-таки можно увидеть из предложенной нам последовательности? Первый член видим? Видим! Это -5,6. А разность d? Пока не видим, но… её можно посчитать, да.) Если, конечно, вы в курсе, что такое разность арифметической прогрессии:

        d = -4 — (-5,6) = 1,6

        Ну вот, уже кое-что. Осталось лишь разобраться с неизвестным нам номером n и загадочным числом 74. В предыдущей задачке нам прямым текстом было указано, что дан именно член прогрессии. А здесь про число 74 ничего непонятно — член оно, не член… Что делать?

        Что-что… Включим смекалку! Мы предположим, что число 74 — это всё-таки член нашей прогрессии! С неизвестным номером n. И снова попробуем отыскать, найти этот номер! Смело подставляем в формулу все наши числа:

        74 = -5,6 + (n-1)·1,6

        И выражаем n:

        (n-1)·1,6 = 79,6

        n — 1 = 49,75

        n = 50,75

        Во как! Номер получился дробный! А дробных номеров в прогрессиях не бывает. Уравнению ведь без разницы, с какими числами работать — целыми, дробными, отрицательными. Уравнение со всякими работает.) Вот оно нам честно и ответило: «В этой арифметической прогрессии число 74 имеет номер 50,75!»

        И какой же вывод можно сделать из полученного результата? Да! Число 74 не является членом нашей прогрессии! Оно находится где-то между пятидесятым и пятьдесят первым членами. Вот, если бы наш номер получился натуральным, то тогда — да, число 74 было бы членом нашей прогрессии. С найденным номером n.

        А так, ответ задачи: нет.

        Более сложные задачи.

        Рассмотрим теперь более хитрые задачки на применение формулы n-го члена. Например, такую:

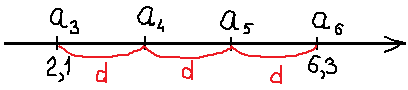
        Известно, что в арифметической прогрессии a₃ = 2,1 и a₆ = 6,3. Найдите a₄.

        Эту задачку мы с вами уже решали в прошлом уроке. Для её успешного решения мы рисовали с вами вот такую незамысловатую картинку:

        Из этой картинки мы легко определили разность прогрессии d и затем так же легко, прямо по смыслу арифметической прогрессии, посчитали нужный нам четвёртый член.

        Получили ответ: a₄ = 3,5.

        Вспомнили? Отлично!

        То был графический способ. А сейчас мы с вами решим эту же задачку, но другим способом! Аналитическим.) С помощью формулы n-го члена, да. Нам ведь с формулой размяться нужно, правда?) Вот и разминаемся.

        Итак, что нам дано в условии задачи? Нам даны два члена некоторой арифметической прогрессии. А именно — третий и шестой её члены.

        Вот и расписываем их по формуле n-го члена!

        Именно так! Просто берём формулу n-го члена арифметической прогрессии и поочерёдно подставляем в неё известные нам данные для каждого члена.

        Для третьего члена a₃ = 2,1 получим:

        2,1 = a₁ + (3-1)·d

        2,1 = a₁ + 2d

        Так, отлично. Одно уравнение составилось.

        То же самое проделываем и для шестого члена a₆ = 6,3.

        Получим:

        6,3 = a₁ + (6-1)·d

        6,3 = a₁ + 5d

        Итак, мы получили два уравнения. Эти два уравнения относятся к одной и той же прогрессии. Стало быть, они должны выполняться одновременно. И, следовательно, они должны быть записаны в виде системы уравнений.

        Вот так:

        Всё. Мы перевели задание по арифметической прогрессии в чистую алгебру. И дальше можно уже временно вообще забыть про прогрессию и просто решить эту систему уравнений.

        Системка не самая трудная. Решаем самым простым способом — подстановкой. Из первого уравнения выражаем a₁ и подставляем во второе:

        Приводим подобные во втором уравнении и получаем:

        Из второго уравнения легко находится d:

        d = 1,4

        Подставляем d = 1,4 в первое уравнение и получаем первый член:

        a₁ = 2,1-2·1,4

        a₁ = 2,1-2,8

        a₁ = -0,7

        Вот и отлично. Знаем первый член a₁, знаем разность d. И теперь мы без проблем можем найти любой интересующий нас член прогрессии. В том числе и четвёртый, да.)

        Пишем формулу n-го члена для n = 4:

        a₄ = a₁ + (4-1)·d = a₁ + 3d

        Подставляем найденные числа и считаем:

        a₄ = a₁ + 3d = -0,7+3·1,4 = -0,7+4,2 = 3,5

        Вот и всё. Как и следовало ожидать, ответ получился тем же самым.)

        Ну как, хлопотно? Да, я согласен. Но зато аналитическому способу (алгебре) любые задачи по плечу! Если её знать, конечно.) А вот картинка годится лишь для маленьких кусочков прогрессии.

        Например, такая задачка:

        Известно, что в арифметической прогрессии a₈₁ = 26 и a₂₇₁ = 83. Найдите a₁₁.

        Что, неохота картинку рисовать да безошибочно пальчиком считать промежутки? И правильно! Не надо.) Зато второму способу, алгебре, совершенно безразлично, какие числа стоят в задании! Большие числа или маленькие… Алгебра — это тяжёлая артиллерия. С любыми числами справляется.)

        Снова, как и в предыдущей задаче, расписываем каждый член прогрессии по формуле n-го члена:

        26 = a₁ + 80d

        83 = a₁ + 270d

        Объединяем эти уравнения в систему:

        А дальше решаем точно так же, как и в предыдущей задаче. Один в один. Дорешайте, чего уж там!

        Должно получиться:

        a₁₁ = 5

        Рассмотрим ещё более хитрую задачку. С подвохом. Если невнимательно читать задание…

        Сумма первого и седьмого членов возрастающей арифметической прогрессии равна 14, а произведение третьего и шестого членов равно 10. Найдите двадцатый член прогрессии.

        Что, внушает? Решение по картинке и «на пальцах» не катит, да… Попробуем перевести всё задание в чистую алгебру? А та — всё сможет.)

        Ничего не боимся и используем главное правило всей математики: «Не знаешь, что нужно, делай что можно.»

        Вот и прикидываем, что в этой эпичной задачке можно сделать. Можно хотя бы расписать все данные нам члены (1-й, 7-й, 3-й, 6-й) в виде формул n-го члена, подставляя те числа, которые даны в условии.

        Вот и расписываем каждый член! Прямо по формуле!

        Ну, с первым членом всё и так ясно. Его вообще расписывать не надо.) Идём дальше.

        Для седьмого члена мы можем записать:

        a₇ = a₁ + (7-1)·d = a₁ + 6d

        Третий член:

        a₃ = a₁ + (3-1)·d = a₁ + 2d

        Шестой член:

        a₆ = a₁ + (6-1)·d = a₁ + 5d

        А дальше снова читаем задачку и скачиваем всю остальную полезную информацию. А именно — связь между членами.

        Сумма первого и седьмого членов равна 14:

        a₁ + a₁ + 6d = 14

        2a₁ + 6d = 14

        Так, одно уравнение готово. Читаем дальше.)

        Произведение третьего и шестого членов равно 10:

        (a₁ + 2d)(a₁ + 5d) = 10

        Получили два уравнения. Раз они относятся к одной и той же прогрессии, то должны выполняться одновременно. Объединяем наши полученные уравнения в систему:

        Вот и всё. Всю ценную информацию по прогрессии мы скачали и записали в виде системы уравнений. А дальше дело за алгеброй. Решение систем —  уже её работа. И наша с вами, к сожалению, тоже, да…

        Начнём с первого уравнения. Оно попроще будет. Выражаем из него a₁. Для этого переносим 6d вправо и делим всё на двойку. Обычные тождественные преобразования, да.)

        2a₁ = 14 — 6d

        a₁ = 7 — 3d

        Теперь, ясное дело, подставляем это выражение во второе уравнение:

        (7 — 3d + 2d)(7 — 3d + 5d) = 10

        Приводим подобные в скобках:

        (7 — d)(7 + 2d) = 10

        Раскрываем скобки, приводим подобные и собираем всё слева:

        49 + 14d — 7d — 2d² — 10 = 0

        -2d² + 7d + 39 = 0

        Решаем это квадратное уравнение (помножив обе части на минус 1) и получаем корни:

        d₁ = -3

        d₂ = 6,5

        А вот и обещанный подводный камень! Что дальше? Получилось два значения разности d! Какое из них выбрать? Тупик?

        Вовсе нет! Просто ещё раз внимательно читаем условие задачи в поисках дополнительной информации! Там зачем-то употребляется слово «возрастающей». А составители задач излишним словоблудием обычно не занимаются, да.) Вспоминаем из первого урока, что у возрастающей арифметической прогрессии разность всегда положительна.

        Стало быть, из двух вариантов выбираем d = 6,5.

        Так, отлично. Разность прогрессии найдена. По первому уравнению системы считаем первый член:

        a₁ = 7 — 3d = 7 — 3·6,5 = -3,5

        Вот, практически, и всё. Что там от нас в задаче требуют? Двадцатый член? Да, пожалуйста!

        a₂₀ = a₁ + (20 — 1)·d = -3,5 + 19·6,5 = 120

        Ответ: 120

        А теперь мы рассмотрим с вами ещё несколько коротких и простых задачек. Они, по своей сути, и вправду очень простые, но многих учеников ставят в тупик своей непривычностью и нестандартной подачей условия. Вот и пугается народ. И спотыкается на ровном месте, теряя драгоценные баллы на экзамене…

        Работаем с видоизменённой формулой!

        Первым делом, давайте с вами вспомним, как мы обычно задаём любую арифметическую прогрессию? Варианта два:

        1) Отдельными параметрами прогрессии (скажем, a₁ и d или a₁ и a_n и т.п.);

        2) В виде последовательности чисел.

        Например:

        (a_n): 1, 5, 9, 13, 17, …

        К этим двум вариантам задания прогрессии мы уже попривыкли.) Но оказывается, есть ещё и третий вариант задания арифметической прогрессии! А именно — в виде формулы n-го члена. Да-да! Любую арифметическую прогрессию в общем виде можно задать формулой её n-го члена. Для каждой прогрессии — своей.)

        Смотрите сами.

        Пусть, например, в арифметической прогрессии a₁ = 3 и d = 5. Запишем для неё формулу n-го члена:

        a_n = 3 + 5·(n-1)

        Раскрываем скобки и упрощаем:

        a_n = -2 + 5n

        Это выражение — тоже формула n-го члена! Только не общая, а уже для конкретной прогрессии. Задачки с такой видоизменённой формулой очень часто попадаются на экзамене. И частенько народ, не подумав, тут же радостно ответ пишет и… приехали.) Чем же эта формула так коварна? Здесь есть подводный камень: некоторые, глядя на формулу, сразу думают, что первый член — минус два. Хотя реально первый член — тройка…

        Например, такая задачка на основе реального варианта ОГЭ:

        Арифметическая прогрессия задана условием a_n = 5 — 1,5n. Найдите сумму первого и девятого её членов.

        Здесь прогрессия задана не совсем привычно. Формула какая-то… Ничего страшного. Бывает.) Эта формула — тоже формула n-го члена арифметической прогрессии. Она тоже позволяет найти любой член прогрессии по его номеру!

        Вот и ищем наши члены. Начинаем с первого члена. Тот, кто думает, что первый член — пятёрка, фатально ошибается! Потому что формула в задаче — видоизменённая. И первый член прогрессии в ней спрятан. Не беда, сейчас мы его отыщем.)

        Просто берём и подставляем n=1 в формулу:

        a₁ = 5 — 1,5·1 = 3,5

        Вот так! Первый член — три с половиной! А вовсе не пятёрка…

        Подставляем теперь n=9 и считаем девятый член:

        a₉ = 5 — 1,5·9 = -8,5

        Ну и считаем требуемую сумму:

        a₁ + a₉ = 3,5 + (-8,5) = -5

        Ответ: -5

        Вот и все дела. Теперь, надеюсь, видоизменённая формула n-го члена арифметической прогрессии не поставит вас навечно в тупик.)

        Работаем с рекуррентной формулой!

        Рассмотрим теперь ещё один сюрприз. Частенько в задачах на арифметическую прогрессию встречается ещё одно обозначение — a_n+1. Это, как вы уже, наверное, догадались, «эн плюс первый» член прогрессии. Всё очень просто. Это член прогрессии, номер которого больше номера n на единичку. И всё.) Например, если в какой-нибудь задаче мы берём за a_n третий член, то a_n+1 будет четвёртым членом. И тому подобное.

        Чаще всего обозначение a_n+1 встречается в так называемых рекуррентных формулах. Не пугаемся этого страшного слова!) Рекуррентная формула — это всего лишь способ задания любого члена арифметической прогрессии через предыдущий член. И всё.) Это ещё один, четвёртый способ задания арифметической прогрессии. Поработаем и с ним.

        Допустим, арифметическая прогрессия нам задана рекуррентной формулой:

        a_n+1 = a_n+4

        a₁ = 3

        Можно посчитать второй член этой прогрессии? Легко! Если за a_n принять первый член прогрессии a₁, то второй член будет, как раз, a₁₊₁ = a₂. Первый член нам уже дан отдельно. Это тройка. Вот и считаем по формуле:

        a₂ = a₁ + 4 = 3+4 = 7

        Третий член можно посчитать через второй:

        a₃ = a₂ + 4 = 7+4 = 11

        Четвёртый можно посчитать через третий, пятый – через четвёртый, и так далее. Продолжая эту цепочку, можно таким способом добраться до любого интересующего нас члена. А как можно посчитать сразу, скажем, 25-й член a₂₅? К сожалению, никак… Пока предыдущий, 24-й член, не узнаем, 25-й не посчитаем. В этом и состоит принципиальное отличие рекуррентной формулы от формулы n-го члена. Рекуррентная формула работает по принципу домино, только через предыдущий член, в то время как формула n-го члена — через первый и позволяет сразу находить любой член прогрессии по его номеру. Не просчитывая всю последовательность по порядочку.)

        Кстати, а как вы думаете, почему в рекуррентной формуле

        a_n+1 = a_n+4

        a₁ = 3

        первый член a₁ нам задан отдельно? Ответ прост: для последовательного подсчёта членов рекуррентным способом, нам всегда необходима некая точка отсчёта. А именно — некоторый стартовый член, с которого следует начинать. Это, кстати, не обязательно может быть именно первый член. Можно начать счёт со второго члена, с третьего — с любого! С того члена, который дополнительно указан в условии в качестве стартового.

        Подведём итог. Как вы видите, если число последовательно просчитываемых членов не очень большое (скажем, три или пять), то рекуррентные формулы вовсе не так уж и плохи на практике. А вот если считать предстоит много, то уже начинаются неудобства, да…

        К счастью, в арифметической прогрессии рекуррентную формулу очень легко превратить в обычную. Как? Просто посчитать пару последовательных членов, вычислить разность d, найти первый член (если надо), записать формулу n-го члена в привычном виде, да и работать с ней.

        В ОГЭ подобные задания частенько встречаются. Например, такая задачка:

        Арифметическая прогрессия задана условиями:

        a_n+1 = a_n+2,8

        a₂ = 3

        Найдите 112-й член этой прогрессии.

        Здесь прогрессия задана рекуррентным способом. Ну и ничего страшного. Любой член прогрессии можно посчитать через предыдущий. Второй член нам уже известен. Это тройка. Через него можно посчитать третий член, через третий — четвёртый и так далее вплоть до нужного нам 112-го члена. Мрачноватая перспектива, вообще-то.) А времени на экзамене немного, да…

        Но! У нас же есть такой мощный инструмент, как формула n-го члена! Которая сразу выдаст нам любой член с любым номером! Вот и запустим её в дело. Для начала просто запишем в тетрадке:

        a_n = a₁ + (n-1)·d

        А теперь смотрим на формулу и соображаем, какие данные у нас уже есть, а что нужно дополнительно посчитать.

        Пока у нас есть только номер члена n = 112. А вот первого члена a₁ и разности d — пока не хватает. Не беда, сейчас отыщем!

        Читаем ещё раз задачку и видим, что:

        a_n+1 = a_n+2,8    и    a₂ = 3

        Можно посчитать третий член по известному второму? Можно!

        Считаем:

        a₃ = a₂+2,8 = 3+2,8 = 5,8

        Ну вот. Теперь нам стали известны два последовательных члена прогрессии — второй и третий. Считаем разность прогрессии:

        d = a₃ — a₂ = 5,8 — 3 = 2,8

        Внимание! Ещё раз напоминаю, что разность прогрессии d — это не просто разница между двумя соседними членами! Это именно разность между членом и предыдущим членом! Стало быть, для определения разности, надо всегда от члена с большим номером отнять член с меньшим номером.

        Кстати сказать, а можно ли было сразу найти разность прогрессии, не вычисляя третий член? Можно! Давайте ещё разок посмотрим на нашу рекуррентную формулу:

        a_n+1 = a_n+2,8

        Переводим формулу на человеческий язык: каждый член (a_n+1) больше предыдущего члена (a_n) на 2,8. Прямо по смыслу и определению арифметической прогрессии, величина 2,8 и есть разность d! Вот и всё.)

        Так, разность прогрессии найдена. Осталось отыскать первый член. Не вопрос! Второй член нам уже дан по условию, а разность мы нашли только что. Вот и отнимаем разность прогрессии от второго члена:

        a₁ = a₂ — d = 3 — 2,8 = 0,2

        Вот и финишная прямая. Подставляем все чиселки в формулу n-го члена и считаем 112-й член:

        a₁₁₂ = a₁ + (112-1)·d = 0,2 + 111·2,8 = 311

        Ответ: 311

        Ну как, прониклись? Мощная штука формула n-го члена, правда? Тогда решаем самостоятельно.

        Для разминки:

        1. Записаны первые три члена арифметической прогрессии:

        20; 17; 14; …

        Какое число стоит в этой арифметической прогрессии на 91-м месте?

        2. В третьем ряду киноконцертного зала 34 места, а в пятнадцатом — 58 мест. Сколько мест в одиннадцатом ряду, если считать число мест в каждом ряду арифметической прогрессией?

        Эта чуть покруче будет:

        3. Дана арифметическая прогрессия:

        32; 31,6; 31,2; …

        Найдите номер первого отрицательного члена этой прогрессии.

        Картинку рисовать муторно, да. Слишком уж медленно наша прогрессия к отрицательным числам приближается… Но вы же формулу n-го члена знаете! Вперёд! Ну, и элемент творчества небольшой надо проявить, да.)

        А вот это уже не разминка:

        3. Известно, что в арифметической прогрессии a₆ = 6 и a₂₅₁ = -190. Найдите a₁₀₁.

        4. Третий член арифметической прогрессии в три раза меньше шестого, а сумма второго и пятого членов равна 16. Найдите пятнадцатый член этой прогрессии.

        5. Сумма восьмого и четырнадцатого членов убывающей арифметической прогрессии равна нулю, а произведение третьего и двенадцатого членов равно -32. Найдите девятнадцатый член прогрессии.

        Задачки попроще, для отдыха:

        6. Арифметическая прогрессия задана условием: a_n = -0,6+8,6n. Найдите произведение первого и шестнадцатого её членов.

        7. Арифметическая прогрессия задана условиями:

        a_n+1 = a_n — 0,3

        a₁ = 10

        Найдите 51-й член прогрессии.

        Ответы (в беспорядке): 54; -5; 82; -70; -250; 1096; -16; 50;

        Ну вот и второй этап знакомства с арифметической прогрессией успешно пройден! Осталось ещё научиться быстро складывать её члены. Такие задачки тоже часто встречаются! Об этом — в следующем уроке.

На этой странице вы узнаете

• Как правильно расставить шары для бильярда в начале игры? 
• Как Карл Гаусс удивил своего учителя по математике?

Считаем ли мы овец перед сном, добавляем по монетке в копилку или достаем сухарик из упаковки — каждый раз мы интуитивно применяем законы математики, которые рассмотрим в этой статье.

Понятие арифметической прогрессии 

Арифметическая прогрессия является видом «Числовых последовательностей». 

У арифметической прогрессии есть особенность: каждый следующий член отличается от предыдущего на одно и то же число. В последовательности 1, 2, 3, 4 и так далее — члены отличаются друг от друга на единицу. 

Арифметическая прогрессия — последовательность чисел, в которой каждый член, начиная со второго, равен сумме предыдущего члена и разности прогрессии. 

Разность прогрессии — то число, на которое отличаются члены прогрессии друг от друга. Разность прогрессии обозначается буквой d. 

Арифметическую прогрессию можно задать формулой. 

a_n+1 = a_n + d

Например, если мы хотим найти третий член арифметической прогрессии, то нужно воспользоваться формулой: a₃ = a₂ + d

Однако бывает, что известны только первый член прогрессии и ее разность. Как быть в этом случае?

Разберемся на примере. Допустим, мы читаем книгу. Количество прочитанных страниц может быть задано с помощью арифметической прогрессии, в которой разность прогрессии и первый ее член равны 1. 

Мы прочитали 10 страниц. Десятая страница будет десятым членом прогрессии. Это 1 + 1 + 1 + 1 +1 + 1 + 1 + 1 + 1 + 1 страниц, если считать их по отдельности. 

Выделим первую страницу отдельно: 1 + (1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1) = 1 + 9 = 1 + 1 * 9 

Теперь заменим десятый член прогрессии, первый член прогрессии и ее разность на буквенные обозначения: a₁₀ = a₁ + 9 * d.

Заметим, что множитель перед d на один меньше, чем порядковый номер искомого члена прогрессии. Тогда получаем: a₁₀ = a₁ + (10 — 1) * d

Мы можем вывести формулу для n-го члена прогрессии. А выглядит она так. 

a_n = a₁ + d(n — 1)

Допустим, мы хотим купить джинсы. В магазине представлены три ценовых категорий, которые отличаются друг от друга на одинаковую сумму. Мы знаем, что самые дешевые джинсы стоят 1000 рублей, а самые дорогие 3000 рублей. Как найти, сколько стоят джинсы во второй ценовой категории?

Попробуем найти разность арифметической прогрессии. 

Джинсы во второй категории будут стоить 1000 + d, а чтобы найти стоимость третьей категории, нужно прибавить разность прогрессии ко второй категории. Получаем 1000 + d + d = 1000 + 2d.

Мы знаем, что самые дорогие джинсы стоят 3000 рублей. Получаем уравнение 1000 + 2d = 3000, откуда можем выразить разность прогрессии:

(d = frac{3000 — 1000}{2} = 1000)

Тогда джинсы во второй ценовой категории будут стоить 1000 + 1000 = 2000 рублей. 

Можно ли как-то найти это значение, не прибегая к таким большим рассуждениям? Для этого достаточно найти среднее арифметическое двух соседних членов. 

(a_n = frac{a_{n-1} + a_{n+1}}{2})

Докажем это. Если рассмотреть член а_n, то член до него будет равен a_{n — 1} = a_n — d, а член после него a_{n + 1} = a_n + d. Тогда их среднее арифметическое равно (frac{a_{n — 1} + a_{n+1}}{2} = frac{a_n — d + a_n + d}{2} = frac{2a_n}{2} = a_n). 

Проверим на нашей задаче. 

(a_2 = frac{a_1 + a_3}{2} = frac{1000 + 3000}{2} = frac{4000}{2} = 2000). Все верно. 

Чтобы найти разность прогрессии, достаточно вычесть из любого члена прогрессии предыдущий к нему. 

d = a_n+1 — a_n

Найдем сумму всех членов арифметической прогрессии. Разумеется, их можно сложить: a₁ + a₂ + a₃ + … + a_n. Но тогда нужно вычислять все члены прогрессии, а их может быть очень много. 

В этом случае используется формула суммы арифметической прогрессии. Ее удобство в том, что используются только первый и последний член прогрессии. 

(S_n = frac{a_1 + a_n}{2} * n)

Немного преобразуем формулу: 

(S_n = frac{a_1 + a_n}{2} * n = frac{a_1 + a_1 + d(n — 1)}{2} * n = frac{2a_1 + d(n — 1)}{2} * n) — это формула суммы членов арифметической прогрессии через первый член и ее разность. 

Решим небольшую задачу. Марина решила сделать картину из страз. По схеме у нее есть 15 рядов, в каждом из которых страз на три больше, чем в предыдущем. В первом ряду 6 страз. Сколько всего страз понадобится, чтобы выложить эти ряды?

Воспользуемся формулой арифметической прогрессии. Но прежде найдем, сколько страз в последнем, пятнадцатом ряду:

a₁₅ = 6 + 3 * (15 + 1) = 6 + 3 * 14 = 6 + 42 = 48

Тогда по формуле суммы арифметической прогрессии всего Марине понадобится: 

(S_{15} = frac{6 + 48}{2} * 15 = frac{54}{2} * 15 = 27 * 15 = 405) страз. 

Виды арифметических прогрессий

Существует всего три вида арифметической прогрессии. 

1. Возрастающая арифметическая прогрессия. 

Разность прогрессии — положительное число, то есть d > 0, а каждый следующий член прогрессии больше предыдущего. 

Прогрессия 2, 4, 6, 8 является возрастающей. 

2. Убывающая арифметическая прогрессия. 

Разность прогрессии — отрицательное число, то есть d < 0, а каждый следующий член прогрессии меньше предыдущего. 

Примером убывающей арифметической прогрессии может служить 100, 95, 90, 85 и так далее.  

3. Стационарная арифметическая прогрессия. 

В этой арифметической прогрессии разность будет равна 0, то есть d = 0. Следовательно, члены прогрессии не будут отличаться друг от друга. 

Например, прогрессия 3, 3, 3, 3, 3 будет являться стационарной. 

Фактчек

• Арифметическая прогрессия — последовательность чисел, в которой каждый член, начиная со второго, равен сумме предыдущего члена и разности прогрессии. 
• Разность арифметической прогрессии — это число, на которое отличаются члены прогрессии. 
• Чтобы найти n-ый член прогрессии, необходимо воспользоваться одной из трех формул: a_n+1 = a_n + d, a_n = a₁ + d(n — 1) или (a_n = frac{a_{n-1} + a_{n+1}}{2}). 
• Чтобы найти разность прогрессии, достаточно из любого члена прогрессии вычесть предыдущий ему член прогрессии. 
• По формуле (S_n = frac{a_1 + a_n}{2} * n) можно найти сумму n членов прогрессии. 
• Арифметическая прогрессия может быть убывающей, возрастающей или стационарной. 

Проверь себя

Задание 1. 
Какая прогрессия является арифметической?

1. 3, 7, 11, 15
2. 1, 1, 2, 3, 5
3. 2, 4, 8, 16
4. 1, 4, 16, 25

Задание 2. 
Первый член арифметической прогрессии равен 10, а ее разность равна -5. Найдите семнадцатый член арифметической прогрессии. 

1. Семнадцатого члена такой арифметической прогрессии не существует
2. 0
3. −70
4. −75 

Задание 3. 
Пятый член арифметической прогрессии равен 16, а седьмой член равен 20. Найдите шестой член арифметической прогрессии. 

1. 2
2. 18
3. 17,5
4. Невозможно найти шестой член арифметической прогрессии. 

Задание 4. 
Каждый день Миша катается на велосипеде, причем с каждым разом увеличивает расстояние на 2 км. В первый день он проехал 3 км. Сколько всего км проедет Миша за пять дней?

1. 14
2. 17
3. 11
4. 35

Ответы: 1. — 1 2. — 3 3. — 2 4. — 4