Избранные теоремы геометрии тетраэдра
Выпускная квалификационная
работа
Избранные теоремы геометрии
тетраэдра
Специальность / направление
подготовки Математика
Специализация / профиль Математика
— информатика
Содержание
Введение
Глава I.
Виды тетраэдров и теоремы о тетраэдрах
1.1 Теоремы о тетраэдрах
§1. Теорема Менелая
§2. Теорема Чевы
§3. Свойства медиан и бимедиан
тетраэдра
1.2 Различные виды тетраэдров.
§1. Пифагоровы тетраэдры
§2. Ортоцентрические тетраэдры
§3. Каркасные тетраэдры
§4. Равногранные тетраэдры
§5. Инцентрические тетраэдры
§6. Соразмерные тетраэдры
§7. Правильные тетраэдры
Глава II.
Тетраэдр в курсе математики средней
школы
§1. Сравнительная характеристика
изложения темы «тетраэдр» в школьных
учебниках
§2. Тестирование уровня развития
пространственного мышления у учеников
средней школы
Введение
Интерес к изучению
тетраэдра возник у человечества с
древних времен и не угасает до сих пор.
Это связано не только с его красотой,
но и с большой практической ценностью.
Тетраэдр является
одним из основных фигур стереометрии,
однако его изучение в курсе средней
школы недостаточно подробно. В некоторых
учебниках авторы избегают самой
терминологии, предпочитая называть
фигуру «треугольной пирамидой» (и
рассматривают её именно в таком ключе),
а об изучении различных видов тетраэдров
зачастую и говорить не приходится.
Роль задач о тетраэдрах
в математическом развитии школьников
трудно переоценить. Они стимулируют
накопление конкретных геометрических
представлений, способствуют развитию
пространственного мышления, что особенно
важно в процессе изучения стереометрии.
Изучению тетраэдра как школе,
так и в вузах посвящено лишь небольшое
количество занятий, поэтому целью
дипломной работы является изучение
различных видов тетраэдров, а также
теорем, связанных с геометрией тетраэдра.
В соответствии с целью сформулированы
следующие задачи:
Собрать сведения о тетраэдре
из различных источников и привести их
в систему; разобрать доказательства
теорем, связанных с тетраэдром;
Проанализировать
методику изложения материала в различных
школьных учебниках;
Разработать курс занятий о
тетраэдре для средней школы.
В первой главе моей
дипломной работы речь пойдёт о различных
видах тетраэдра и некоторых теоремах,
касающихся этой фигуры. Вторая глава
посвящена анализу учебного материала
для средней школы по заданной теме и
разработке курса занятий.
Глава I.
Виды тетраэдров и теоремы о тетраэдрах
1.1 Теоремы
о тетраэдрах
§1. Теорема Менелая
Теорема Менелая для треугольника.
Пусть точки А>1>>
>и С>1>
лежат на сторонах ВC
и АC
треугольника АВС,
точка В>1>>
>на продолжении стороны
АС этого
треугольника. Для того чтобы точки А>1>,
В>1>,
С>1>
лежали на одной прямой необходимо и
достаточно, чтобы выполнялось равенство
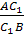
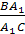
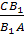
Доказательство.
Сначала докажем необходимость.
Пусть точки А>1>,В>1>,С>1>
лежат на прямой l
и AA>0>=h>1>,
CC>0>=h>3>>
>- перпендикуляры, опущенные
соответственно из точек А,
В, С на прямую l.
Из подобия треугольников АА>0>С>1>>
>и ВВ>0>С>1>>
>получаем
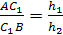
Аналогично, рассматривая другие пары
подобных треугольников, получаем
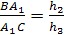
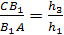
Перемножая полученные пропорции,
приходим к требуемому равенству.
Теперь докажем достаточность.
Пусть точки А>1>,
В>1>, С>1>,
лежащие на прямых ВС, АС, АВ таковы, что
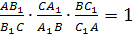
Докажем, что точки А>1>,
В>1>,
С>1>
лежат на одной прямой.
Проведем прямую А>1>В>1>>
>и докажем, что точка С>1>
ей принадлежит. Предположим, что это не
так. Сначала заметим, прямая А>1>В>1>>
>не параллельна прямой
АВ. Пусть Т
— точка пересечения А>1>В>1>>
>и АВ,
тогда
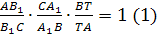
Из условия и равенства (1) следует, что
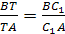
Так как точки Т
и С>1>>
>лежат вне отрезка АВ,
их совпадение вытекает из следующей
леммы.
Лемма 1.
Пусть А и В две различные точки,
тогда для любого k>0, k≠1 на прямой АВ
существуют две точки U и V такие, что
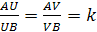
причем одна из этих точек принадлежит
отрезку АВ, а другая лежит вне отрезка.
Доказательство.
Введем на прямой АВ
координаты, приняв точку А
за начало координат. Пусть для
определенности k>1,
тогда координата искомой точки U,
лежащей внутри отрезка АВ,
удовлетворяет уравнению
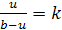
откуда
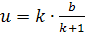
Точка V
находится вне отрезка AB,
из уравнения
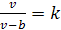
откуда
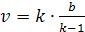
Случай 0<k<1
отличается от рассмотренного лишь тем,
что точку V
следует искать левее точки А.
Теорема Менелая допускает
интересное стереометрическое обобщение.
Теорема Менелая для тетраэдра.
Если плоскость μ
пересекает ребра АВ, ВС, CD
и DA тетраэдра
АВСD в точках
А>1>,
В>1>,
С>1>,
D>1>, то
(2).
Обратно, если для четырех точек
А>1>,
В>1>,
С>1>,
D>1>,
лежащих соответственно
на ребрах АВ, ВС, СD, DA
тетраэдра, выполнено равенство (2), то
эти четыре точки лежат в одной плоскости.
Доказательство.
Пусть h>1>,
h>2>,
h>3, >h>4>>
>- расстояния от точек
А, В, С, D соответственно до
плоскости μ,
тогда
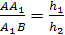
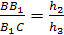
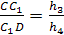
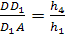
Осталось перемножить полученные
отношения.
Для доказательства обратной
теоремы построим плоскость А>1>,
В>1>, С>1>.
Пусть эта плоскость пересекает ребро
DA в точке Т.
По доказанному
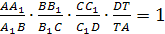
а по условию
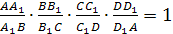
поэтому (и по лемме) точки Т
и D>1>>
>совпадают.>
>Утверждение доказано.
§2. Теорема Чевы
Теорема Чевы для треугольника.
Пусть точки А>1>,
В>1>,С>1>>
>лежат соответственно на
сторонах ВС, АС
и ВА треугольника
АВС (см. рис).
Для того чтобы отрезки АА>1>,
ВВ>1>,
СС>1>
пересекались в одной точке, необходимо
и достаточно, чтобы выполнялось
соотношение:
(3) (отрезки АА>1>,
ВВ>1>,
СС>1>>
>иногда называют чевианами).
Доказательство.
Необходимость. Пусть отрезки
АА>1>,
ВВ>1>,
СС>1>>
>пересекаются в точке М
внутри треугольника АВС.
Обозначим через S>1>,
S>2>,
S>3>>
>площади треугольников
АМС, СМВ, АМВ,
а через h>1>,
h>2> —
расстояния от точек А
и В до прямой
МС. Тогда
аналогично
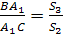
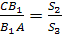
Перемножив полученные пропорции,
убеждаемся в справедливости теоремы.
Достаточность. Пусть точки А>1>,
В>1>,
С>1>>
>лежат на сторонах ВС,
СА, АС треугольника, и
выполнено соотношение (3), М
— точка пересечения отрезков АА>1>и
ВВ>1>,
а отрезок СМ
пересекает сторону АВ
в точке Q.
Тогда, по уже доказанному
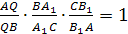
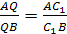
Из леммы снова следует совпадение точек
Q=C>1>.
Достаточность доказана.
Перейдем теперь к пространственному
обобщению теоремы Чевы.
Теорема Чевы для тетраэдра.
Пусть М
— точка внутри тетраэдра АВСD,
а А>1>,
В>1>,
С>1>
и D>1> —
точки пересечения плоскостей СМD,
AMD, АМВ и СМВ
с ребрами АВ, ВC,
СD и DA
соответственно. Тогда
(4). Обратно: если для точек
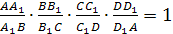
то плоскости АВС,
ВСD>1>
и DAB>1>>
>проходят через одну точку.
Доказательство.
Необходимость легко получить,
если заметить, что точки А>1>,
В>1>,>
>С>1>,
D>1>
лежат в одной плоскости (эта плоскость
проходит через прямые А>1>С>1>
и В>1>D>1>,
пересекающиеся в точке М),
и применить теорему Менелая. Обратная
теорема доказывается так же, так и
обратная теореме Менелая в пространстве:
нужно провести плоскость через точки
А>1>,
В>1>,
С>1> и
доказать с помощью леммы, что эта
плоскость пересечет ребро DA
в точке D>1>.
§3. Свойства медиан и бимедиан
тетраэдра
Медианой тетраэдра называется
отрезок, соединяющий вершину тетраэдра
с центром тяжести противоположной грани
(точкой пересечения медиан).
Теорема (Применение теоремы
Менелая).
Медианы тетраэдра пересекаются
в одной точке. Эта точка делит каждую
медиану в отношении 3:1, считая от вершины.
Доказательство.
Проведем две медианы: DD>1>
и CC>1>
тетраэдра ABCD.
Эти медианы пересекутся в точке F.
CL
– медиана грани ABC,
DL
– медиана грани ABD,
а D>1>,
C>1>
– центры тяжести грани ABC
и ABD.
По теореме Менелая:
и
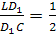
Запишем теорему для треугольника DLD>1>:
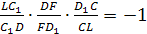
=>
Доказательство производится аналогично
для любой другой пары медиан.
Теорема (Применение теоремы
Чевы).
Для начала дадим определения
некоторых элементов тетраэдра. Отрезок,
соединяющий середины скрещивающихся
ребер тетраэдра называется бимедианой.
Бивысотами (по аналогии) называют общие
перпендикуляры скрещивающихся ребер.
Теорема.
Бимедианы тетраэдра пересекаются
в той же самой точке, что и медианы
тетраэдра.
Доказательство.
В треугольнике LDC
отрезки DC
и LF
пересекутся в точке K.
По теореме Чевы для этого треугольника:
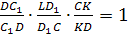
т.е.
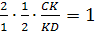
CK=KD,
LK
– бимедиана.
Замечание 1.
FL=FK.
Теорема Менелая для треугольника DLK:
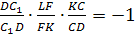
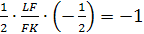
отсюда LF=FK.
Замечание 2.
Точка F
является центром тяжести тетраэдра.
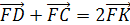
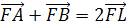
значит
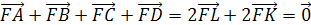
1.2 Различные
виды тетраэдров
§1. Пифагоровы
тетраэдры
Треугольник называется пифагоровым,
если у него один угол прямой, а отношение
любых сторон рационально (т.е применяя
подобие, можно из него получить
прямоугольный треугольник с целыми
длинами сторон).
По аналогии с этим, тетраэдр
называют пифагоровым, если его плоские
углы при одной из вершин прямые, а
отношение любых двух ребер рационально
(из него с помощью подобия можно получить
тетраэдр с прямыми плоскими углами при
одной из вершин и целыми длинами ребер).
Попробуем вывести «Уравнение
пифагоровых тетраэдров», т.е. такое
уравнение с тремя неизвестными ξ, η, ζ,
что любой пифагоров тетраэдр дает
рациональное решение этого уравнения,
и наоборот, любое рациональное решение
уравнения дает пифагоров тетраэдр.
Сначала дадим способ описания
всех пифагоровых треугольников.
На рисунке треугольник ОАВ
— прямоугольный, длины его катетов
обозначены через а
и b, а дина
гипотенузы — через р.
Число
(1) условимся называть параметром
прямоугольного треугольника ОАВ
(или точнее, параметром «относительно
катета а«).
Используя соотношение р2=а2+b2,
имеем:
Из этих уравнений непосредственно
получим формулы, выражающие отношения
сторон прямоугольного треугольника
через его параметр:
и
(2).
Из формул (1) и (2) непосредственно
вытекает следующее утверждение: для
того, чтобы прямоугольный треугольник
был пифагоровым, необходимо и достаточно,
чтобы число ξ было рациональным. В самом
деле, если треугольник пифагоров, то из
(1) следует, что ξ рационально. Обратно,
если ξ рационально, то согласно (2)
отношения сторон рациональны, то есть
треугольник пифагоров.
Пусть теперь ОАВС
— тетраэдр, у которого плоские углы при
вершине О
прямые. Длины ребер, исходящих из вершины
О, обозначим через a,b,с,
а длины оставшихся ребер через р,
q, r.
Рассмотрим параметры трех
прямоугольных треугольников ОАВ,
ОВС, ОСА:
(3)
Тогда по
формулам (2) можно выразить отношения
сторон этих прямоугольных треугольников
через их параметры:
(4),
(5).
Из (4) непосредственно
вытекает, что параметры ξ,
η, ζ, удовлетворяют
соотношению
(6). Это и есть общее уравнение пифагоровых
тетраэдров.
Из формул (3) — (5) непосредственно
вытекает следующее утверждение: для
того чтобы тетраэдр ОАВС
с прямыми плоскими углами при вершине
О был пифагоровым, необходимо и достаточно,
чтобы параметры ξ, η, ζ
(удовлетворяющие уравнению (6)) были
рациональными.
Продолжая аналогию пифагорова
треугольника с пифагоровым тетраэдром,
попробуем сформулировать и доказать
пространственное обобщение теоремы
Пифагора для прямоугольных тетраэдров,
которая, очевидно, будет верна и для
пифагоровых тетраэдров. В этом нам
поможет следующая лемма.
Лемма 1.
Если площадь многоугольника
равна S, то
площадь его проекции на плоскость π
равна
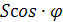
где φ — угол
между плоскостью π и плоскостью
многоугольника.
Доказательство.
Утверждение леммы очевидно для
треугольника, одна сторона которого
параллельна линии пересечения плоскости
π с плоскостью многоугольника. В самом
деле, длина этой стороны при проекции
не изменяется, а длина высоты, опущенной
на нее при проекции, изменяется в cosφ
раз.
Докажем теперь, что любой
многогранник можно разделить на
треугольники указанного вида.
Проведем для этого через все
вершины многоугольника прямые,
параллельные линии пересечения
плоскостей, многоугольник разрежется
при этом на треугольники и трапеции.
Остается разрезать каждую трапецию по
любой из ее диагоналей.
Теорема 1 (пространственная
теорема Пифагора).
В прямоугольном тетраэдре АВСD,
с плоскими углами при вершине D,
сумма квадратов площадей трех его
прямоугольных граней равна квадрату
площади грани АВС.
Доказательство.
Пусть α — угол между плоскостями
АВС и DВС,
D’ — проекция точки D
на плоскость АВС.
Тогда S>ΔDBC>=СоsαS>ΔАBC>>
>и S>ΔD’BC>=cоsαS>ΔDBC>>
>(по лемме 1), поэтому cоsα
=
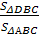
>S>Δ>>D>>‘>>BC>>
>=
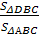
Аналогичные равенства можно
получить и для треугольников D’АВ
и D’АС. Складывая
их и учитывая, что сумма площадей
треугольников D’ВС,
D’АС и D’АВ
равна площади треугольника АВС,
получаем требуемое.
Задача.
Пусть все плоские углы при вершине
D
прямые; a,b,c
– длины ребер, выходящих из вершины D
на плоскость ABC.
Тогда
Доказательство.
По теореме Пифагора для
прямоугольного тетраэдра
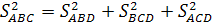
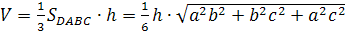
С другой
стороны
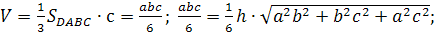
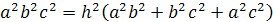
1=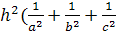
=>
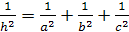
§2. Ортоцентрические
тетраэдры
В отличие от треугольника, высоты
которого всегда пересекаются в одной
точке — ортоцентре, не всякий тетраэдр
обладает аналогичным свойством. Тетраэдр,
высоты которого пересекаются в одной
точке, называется ортоцентрическим. мы
начнем изучение ортоцентрических
тетраэдров с необходимых и достаточных
условий ортоцентричности, каждое из
которых можно принять за определение
ортоцентрического тетраэдра.
(1) Высоты тетраэдра пересекаются
в одной точке.
(2) Основания высот тетраэдра
являются ортоцентрами граней.
(3) Каждые два противоположных
ребра тетраэдра перпендикулярны.
(4) Суммы квадратов противоположных
ребер тетраэдра равны.
(5) Отрезки, соединяющие середины
противоположных ребер тетраэдра, равны.
(6) Произведения косинусов
противоположных двугранных углов равны.
(7) Сумма квадратов площадей
граней вчетверо меньше суммы квадратов
произведений противоположных ребер.
Докажем некоторые из них.
Доказательство (3).
Пусть каждые два противоположных
ребра тетраэдра перпендикулярны.
Следовательно, высоты тетраэдра
попарно пересекаются. Если несколько
прямых попарно пересекаются, то они
лежат в одной плоскости или проходят
через одну точку. В одной плоскости
высоты тетраэдра лежать не могут, так
как иначе в одной плоскости лежали бы
и его вершины, поэтому они пересекаются
в одной точке.
Вообще говоря, для того чтобы
высоты тетраэдра пересекались в одной
точке, необходимо и достаточно потребовать
перпендикулярность только двух пар
противоположных ребер. Доказательство
этого предложения напрямую следует из
следующей задачи.
Задача 1.
Дан произвольный тетраэдр ABCD.
Докажите, что
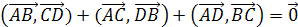
Решение.
Пусть а=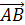
b=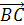
с=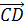
Тогда
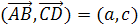
и
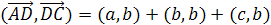
складывая эти равенства, получаем
требуемое.
Далее докажем свойство (4).
Пусть а=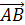
b=
и с=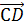
Равенство
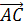
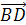
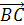
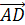
что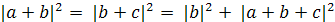
т.е. (а,с)=0.
Применяя данный алгоритм к другим парам
противоположных ребер, очевидно, получим
искомое утверждение.
Приведем оказательство свойства
(6).
Для доказательства используем
следующие теоремы:
Теорема
синусов. «Произведение длин двух
противоположных ребер тетраэдра,
деленное на произведение синусов
двугранных углов при этих ребрах, одно
и то же для всех трех пар противоположных
ребер тетраэдра».
Теорема
Бертшнейдера. «Если a
и b
– длины двух скрещивающихся ребер
тетраэдра, а
— двугранные углы при этих ребрах, то
величина
не зависит от выбора пары скрещивающихся
ребер.
Воспользовавшись теоремой
синусов для тетраэдра и теоремой
Бертшнейдера, получаем, что произведения
косинусов противоположных двугранных
углов равны тогда и только тогда, когда
равны суммы квадратов противоположных
ребер, из чего и следует справедливость
свойства (6) ортоцентрического тетраэдра.
В заключение пункта об
ортоцентрическом тетраэдре решим
несколько задач на эту тему.
Задача 2.
Докажите, что в ортоцентрическом
тетраэдре выполняется соотношение
ОН2=4R2-3d2,
где О — центр
описанной сферы, H
— точка пересечения высот, R
— радиус описанной сферы, d
— расстояние между серединами
противоположных ребер.
Решение.
Пусть К
и L — середины
ребер АВ и СD
соответственно. Точка Н
лежитт в плоскости, проходящей через
СD перепендикулярно
АВ, а точка О
— в плоскости, проходящей черех К
перпендикулярно АВ.
Эти плоскости симметричны
относительно центра масс тетраэдра —
середины отрезка KL.
Рассматривая такие плоскости для всех
ребер, получаем, что точки Н
и О симметричны
относительно М,
а значит КLМО
— параллелограмм. Квадраты его сторон
равны
и
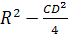
поэтому
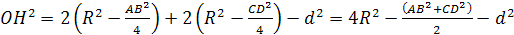
Рассматривая сечение, проходящее через
точку М
параллельно АВ
и СD, получаем
что АВ2+CD2=4d2.
Здесь можно добавить, что прямую,
на которой лежат точки О,
М и Н,
называют прямой Эйлера ортоцентрического
тетраэдра.
Замечание.
Наряду с прямой Эйлера можно
отметить существование сфер Эйлера для
ортоцентрического тераэдра, о которых
и пойдет речь в следующих задачах.
Задача 3.
Доказать, что для ортоцентрического
тетраэдра окружности 9 точек каждой
грани принадлежат одной сфере (сфере
24 точек). Для решения этой задачи
необходимо доказать условие следующей
задачи.
Задача 4.
Доказать, что середины сторон
треугольника, основания высот и середины
отрезков высот от вершин до точки их
пересечения лежат на одной окружности
— окружности 9 точек (Эйлер).
Доказательство.
Пусть АВС
— данный треугольник, Н
— точка пересечения его высот, А>1>,
В>1>,
С>1> —
середины отрезков АН, ВН,
СН; АА>2>
— высоты, А>3>
— середина ВС.
Будем считать для удобства, что АВС
— остроугольный треугольник. Поскольку
и ΔВ>1>А>2>С>1>=ΔВ>1>НС>1>,
то
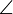
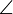
—
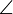
т.е. точки А>1>,
В>1>,
А>2>,
С>1>>
>лежат на одной окружности.
Также легко увидеть, что
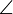
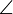
—
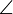
т.е. точки А>1>,
В>1>,
А>3>,
С>1>>
>тоже лежат на одной (а
значит на той же) окружности. Отсюда
следует, что все 9 точек, о которых
говорится в условии, лежат на одной
окружности. Случай тупоугольного
треугольника АВС
рассматривается аналогично.
Заметим, что окружность 9 точек
гомотетична описанной окружности с
центром в Н и коэффициентом
(именно так расположены треугольники
АВС и А>1>В>1>С>1>).
С другой стороны, окружность 9 точек
гомотетична описанной окружности с
центром в точке пересечения медиан
треугольника АВС
и коэффициентом
(именно так расположены треугольники
АВС и треугольник с вершинами в серединах
его сторон).
Теперь, после определения
окружности 9 точек, можно перейти к
доказательству условия задачи 3.
Доказательство.
Сечение ортоцентрического
тетраэдра любой плоскостью, параллельной
противоположным ребрам и проходящей
на равном расстоянии от этих ребер, есть
прямоугольник, диагонали которого равны
расстоянию между серединами противоположных
ребер тетраэдра ( все эти расстояния
равны между собой, см. необходимое и
достаточное условие ортоцентричности
(5). Отсюда следует, что середины всех
ребер ортоцентрического тетраэдра
лежат на поверхности сферы, центр которой
совпадает с центром тяжести данного
тетраэдра, а диаметр равен расстоянию
между серединами противоположных ребер
тетраэдра. Значит, все четыре окружности
9 точек лежат на поверхности этой сферы.
Задача 5.
Доказать, что для ортоцентрического
тетраэдра центры тяжести и точки
пересечения высот граней, а также точки
, делящие отрезки каждой высоты тетраэдра
от вершины до точки пересечения высот
в отношении 2:1, лежат на одной сфере (
сфере 12 точек).
Доказательство.
Пусть точки О, М
и Н — соответственно
центр описанного шара, ценетр тяжести
и ортоцентр ортоцентрического тетраэдра;
М — середина
отрезка ОН
(см. задачу 2). Центры тяжести граней
тетраэдра служат вершинами тетраэдра,
гомотетичного, с центром гомотетиии в
точке М и
коэффициентом
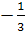
при этой гомотетии точка О
перейдет в точку О>1>,
расположенную на отрезке МН
так, что
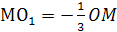
О>1>
будет центром сферы проходящей через
центры тяжестей граней.
С другой стороны, точки, делящие
отрезки высот тетраэдра от вершин до
ортоцентра в отношении 2:1, служат
вершинами тетраэдра, гомотетичного
данному с центром гомотетии в Н
и коэффициентом
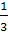
При этой гомотетии точка О,
как легко видеть, перейдет в ту же точку
О>1>.
Таким образом, восемь из двенадцати
точек лежат на поверхности сферы с
центром в О>1>
и радиусом, втрое меньшим, чем радиус
сферы, описанной около тетраэдра.
Докажем, что точки пересечения
высот каждой грани лежат на поверхности
той же сферы.
Пусть О`, Н`
и М` — центр
описанной окружности, точка пересечения
высот и центр тяжести какой-либо грани.
О` и Н`
являются проекциями точек О
и Н на плоскость
этой грани, а отрезок М`
делит отрезок О`Н`
в отношении 1:2, считая от О`(известный
планиметрический факт). Теперь легко
убедиться (см. рис), что проекция О>1>
на плоскость этой грани — точка О`>1>
совпадает с серединой отрезка М`Н`,
т.е. О>1>>
>равноудалена от М`
и Н`, что и
требовалось.
§3. Каркасные
тетраэдры
Каркасным называется тетраэдр,
для которого существует сфера, касающаяся
всех шести ребер тетраэдра. Не всякий
тетраэдр каркасный. Например, легко
понять, что нельзя построить сферу,
касающуюся всех ребер равногранного
тетраэдра, если его описанный параллелепипед
«длинный».
Перечислим свойства каркасного
тетраэдра.
(1) Существует сфера, касающаяся
всех ребер тетраэдра.
(2) Суммы длин скрещивающихся
ребер равны.
(3) Суммы двугранных углов при
противоположных ребрах равны.
(4) Окружности, вписанные в грани,
попарно касаются.
(5) Все четырехугольники,
получающиеся на развертке тетраэдра,
— описанные.
(6) Перпендикуляры, восстановленные
к граням из центров вписанных в них
окружностей, пересекаются в одной точке.
Докажем несколько свойств
каркасного тераэдра.
Доказательство (2).
Пусть О
— центр сферы, касающейся четырех ребер
во внутренних точках. заметим теперь,
что если из точки Х
провести касательные ХР
и ХQ к сфере с
центром О, то
точки Р и Q
симметричны относительно плоскости,
проходящей прямую ХО
и середину отрезка PQ,
а значит плоскости РОХ
и QОХ образуют
с плоскостью ХРQ
равные углы.
Проведем 4 плоскости, проходящие
через точку О и рассматриваемые ребра
тетраэдра. Они разбивают каждый из
рассматриваемых двугранных углов на
два двугранных угла. Выше было показано,
что полученные двугранные углы,
прилегающие к одной грани тетраэдра,
равны. Как в одну, так и в другую
рассматриваемую сумму двугранных углов
входит по одному полученному углу для
каждой грани тетраэдра. Проводя
аналогичные рассуждения для других пар
скрещивающихся ребер, получим
справедливость свойства (2).
Вспомним некоторые свойства
описанного четырехугольника:
Плоский
четырехугольник будет описанным тогда
и только тогда, когда суммы его
противоположных сторон равны;
Если
описанный четырехугольник разбить
диагональю на два треугольника, то
вписанные в треугольники окружности
касаются
Учитывая эти свойства, легко
доказать остальные свойства каркасного
тетраэдра. Свойство (3) тетраэдра напрямую
следует из свойства (b), а свойство (4) из
свойства (a)
и свойства (1) тетраэдра. Свойство (5) из
свойства (3). Действительно, ведь окружности
вписанные в грани тетраэдра, являются
пересечениями его граней со сферой,
касающейся ребер, откуда очевидно, что
перпендикуляры, восстановленные в
центрах вписанных в грани окружностей
неминуемо пересекутся в центре этой
сферы.
Задача 1.
Сфера касается ребер АВ,
ВС, СD и DA
тетраэдра АВСD
в точках L, M, N, K,
являющихся вершинами квадрата. Докажите,
что если эта сфера касается ребра АС,
то она касается и ребра BD.
Решение.
По условия КLMN
— квадрат. Проведем через точки К,
L, M, N плоскости, касающиеся
сферы. Т.к все эти плоскости одинаково
наклонены к плоскости КLMN,
то они пересекаются в одной точке S,
расположенной на прямой ОО>1>,
где — центр сферы, а О>1>>
>- центр квадрата. Эти
плоскости пересекают поверхность
квадрата KLMN
по квадрату TUVW,
серединами сторон которого являются
точки К, L, M, N.
В четырехгранном угле STUVW с вершиной S
все плоские углы равны, а точки К,
L, M, N лежат на биссектрисах
его плоских углов, причем SK=SL=SM=SN.
Следовательно,
SA=SC и SD=SB,
а значит АК=АL=CM=CN
и ВL=BM=DN=DK. По
условию АС
тоже касается шара, поэтому АC=АК+CN=2АК.
А так как SK —
биссектриса угла DSA,
то DK:КА=DS:SA=DВ:АС.
Из равенства АС=2АК
следует теперь, что DВ=2DK.
Пусть Р —
середина отрезка DВ,
тогда Р лежит
на прямой SO.
Треугольники DOK
и DOP равны,
т.к. DK=DP и
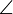
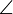
Поэтому ОР=ОК=R,
где R — радиус
сферы, а значит, DB
тоже касается сферы.
§4. Равногранные
тетраэдры
Равногранным называется тетраэдр,
все грани которого равны. Чтобы представить
себе равногранный тетраэдр, возьмем
произвольный остроугольный треугольник
из бумаги, и будем сгибать его по средним
линиям. Тогда три вершины сойдутся в
одну точку, а половинки сторон сомкнутся,
образуя боковые ребра тетраэдра.
(0) Грани конгруэнтны.
(1) Скрещивающиеся ребра попарно
равны.
(2) Трехгранные углы равны.
(3) Противолежащие двугранные
углы равны.
(4) Два плоских угла, опирающихся
на одно ребро, равны.
(5) Сумма плоских углов при каждой
вершине равна 180°.
(6) Развертка тетраэдра — треугольник
или параллелограмм.
(7) Описанный параллелепипед
прямоугольный.
(8) Тетраэдр имеет три оси симметрии.
(9) Общие перпендикуляры
скрещивающихся ребер попарно
перпендикулярны.
(10) Средние линии попарно
перпендикулярны.
(11) Периметры граней равны.
(12) Площади граней равны.
(13) Высоты тетраэдра равны.
(14) Отрезки, соединяющие вершины
с центрами тяжести противоположных
граней, равны.
(15) Радиусы описанных около граней
окружностей равны.
(16) Центр тяжести тетраэдра
совпадает с центром описанной сферы.
(17) Центр тяжести совпадает с
центром вписанной сферы.
(18) Центр описанной сферы совпадает
с центром вписанной.
(19) Вписанная сфера касается
граней в центрах описанных около этих
граней окружностей.
(20) Сумма внешних единичных
нормалей (единичных векторов,
перпендикулярных к граням), равна
нулю.
(21) Сумма всех двугранных углов
равна нулю.
Практически все свойства
равногранного тетраэдра следуют из его
определения, поэтому докажем
только некоторые из них.
Доказательство (16).
Т.к. тетраэдр ABCD
равногранный, то по свойству (1) AB=CD.
Пусть точка К
отрезка АВ, а
точка L середина
отрезка DC,
отсюда отрезок KL
бимедиана тетраэдра ABCD,
откуда по свойствам медиан тетраэдра
следует, что точка О
— середина отрезка KL,
является центром тяжести тетраэдра
ABCD.
К тому же медианы тетраэдра
пересекаются в центре тяжести, точке
О, и делятся
этой точкой в отношении 3:1, считая от
вершины. Далее, учитывая вышесказанное
и свойство (14) равногранного тетраэдра,
получаем следующее равенство отрезков
АО=ВО=СО=DО, из
которого и следует, что точка О
является центром описанной сферы (по
определению описанной около многогранника
сферы).
Обратно. Пусть К
и L — середины
ребер АВ и СD
соответственно, точка О
— центр описанной сферы тетраэдра, т.е.
середина отрезка KL.
Т.к. О — центр
описанной сферы тетраэдра, то треугольники
AOB и COD
— равнобедренные с равными боковыми
сторонами и равными медианами OK
и OL. Поэтому
ΔAOB=ΔCOD.
А значит AB=CD.
Аналогично доказывается равенство
других пар противоположных ребер, из
чего по свойству (1) равногранного
тетраэдра и будет следовать искомое.
Доказательство (17).
Рассмотрим биссектор двугранного
угла при ребре AB,
он разделит отрезок DC в отношении
площадей граней ABD
и ABC.
Т.к. тетраэдр ABCD
равногранный, то по свойству (12)
S>ΔABD>=S>ΔABD>=>DL=LС,
откуда следует, что биссектор ABL
содержит бимедиану KL.
Применяя аналогичные рассуждения для
остальных двугранных углов, и принимая
во внимание тот факт, что биссекторы
тетраэдра пересекаются в одной точке,
которая является центром вписанной
сферы, получаем, что эта точка неминуемо
будет центром тяжести данного равногранного
тетраэдра.
Обратно. Из того, что центр тяжести
и центр вписанной сферы совпадают имеем
следующее: DL=LC=>SABD=SADC.
Доказывая подобным образом равновеликость
всех граней и, применяя свойство (12)
равногранного тетраэдра, получаем
искомое.
Теперь докажем свойство (20). Для
этого сначала нужно доказать одно из
свойств произвольного тетраэдра.
тетраэдр теорема
школьный учебник
Лемма 1.
Если длины векторов перпендикулярных
к граням тетраэдра численно равны
площадям соответствующих граней, то
сумма этих векторов равна нулю.
Доказательство.
Пусть Х
— точка внутр и многогранника, h>i
>(i=1,2,3,4)
— расстояние от нее до плоскости i-ой
грани.
Разрежем многогранник на пирамиды
с вершиной Х,
основаниями которых служат его грани.
Объем тетраэдра V
равен сумме объемов этих пирамид, т.е.
3 V=∑h>i>S>i>,
где S>i>>
>площадь i-ой
грани. Пусть далее, n>i>>
>- единичный вектор внешней
нормали к i-ой грани, M>i >-
произвольная точка этой грани. Тогда
h>i >=(ХM>i>,
S>i>n>i>),
поэтому 3V=∑h>i>S>i>=∑(ХM>i>,
S>i>n>i>)=(ХО,
S>i>n>i>)+(ОM>i>,
S>i>n>i>)=(ХО,
∑S>i>n>i>)+3V,
где О — некоторая
фиксированная точка тетраэдра,
следовательно, ∑S>i>n>i>=0.
Далее очевидно, что свойство
(20) равногранного тетраэдра является
частным случаем вышеуказанной леммы,
где S>1>=>
>S>2>=>
>S>3>=>
>S>4>=>n>1>=n>2>=n>3>=n>4>,
и так как площади граней не равны нулю,
получаем верное равенство n>1>+n>2>+n>3>+n>4>=0.
В заключение рассказа о равногранном
тетраэдре приведем несколько задач на
эту тему.
Задача 1.
Прямая, проходящая через центр
масс тетраэдра и центр описанной около
него сферы, пересекает ребра AB
и CD. Докажите,
что AC=BD и AD=BC.
Решение.
Центр масс тетраэдра лежит на
прямой, соединяющей середины ребер АВ
и СD.
Следовательно, на этой прямой
лежит центр описанной сферы тетраэдра,
а значит, указанная прямая перпендикулярна
ребрам АВ и
СD. Пусть С`
и D` — проекции
точек C и D
на плоскость, проходящую через прямую
АВ параллельно
СD. Т.к. AC`BD`
— параллелограмм (по построению), то
АС=ВD и АD=ВС.
Задача 2.
Пусть h
— высота равногранного тетраэдра, h>1>>
>и h>2>>
>- отрезки, на которые одна
из высот грани делится точкой пересечения
высот этой грани. Доказать, что h2=4h>1>h>2>;
доказать также, что основание высоты
тетраэдра и точка пересечения высот
грани, на которую эта высота опущена,
симметричны относительно центра
окружности, описанной около этой грани.
Доказательство.
Пусть АВСD
— данный тетраэдр, DH
— его высота, DA>1>,
DВ>1>,
DС>1>>
>- высоты граней, опущенные
из вершины D
на стороны ВС, СА и АВ.
Разрежем поверхность тетраэдра
вдоль ребер DA, DB, DC,
и сделаем развертку. Очевидно, что Н
есть точка пересечения высот треугольника
D>1>D>2>D>3>.
Пусть F — точка
пересечения высот треугольника ABC,
АК — высота этого треугольника,
АF=h>1>,
FК=h>2>.
Тогда D>1>Н=2h>1>,
D>1>A>1>=h>1>-h>2>.
Значит, поскольку h
— высота нашего тетраэдра, h2=DН2=DA2
— НA>1>2=
(h>1+>
h>2>)2
— (h>1>—
h>2>)2=4h>1>h>2.>>
>Пусть теперь М
— центр тяжести треугольника ABC
(он же центр тяжести треугольника
D>1>D>2>D>3>),
О — центр
описанной около него окружности.
Известно, что F, М
и О лежат на
одной прямой (прямая Эйлера), причем М
— между F и О,
FM=2МО,
С другой стороны, треугольник D>1>D>2>D>3>>
>гомотетичен треугольнику
АВС с центром
в М и коэффициентом
(-2), значит МН=2FM.
Из этого следует, что ОН=FO.
Задача 3.
Доказать, что в равногранном
тетраэдре основания высот, середины
высот и точки пересечения высот граней
лежат на поверхности одной сферы (сферы
12 точек).
Доказательство.
Решая задачу 2, мы доказали, что
центр описанной около тетраэдра сферы
проецируется на каждую грань в середину
отрезка, концами которого является
основание высоты, опущенной на эту
грань, и точка пересечения высот этой
грани. А поскольку расстояние от центра
описанной около тетраэдра сферы до
грани равно
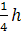
где h — высота
тетраэдра, центр описанной сферы удален
от данных точек на расстояние
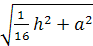
где а — расстояние
между точкой пересечения высот и центром
описанной около грани окружности.
§5. Инцентрические
тетраэдры
Отрезки, соединяющие центры
тяжести граней тетраэдра с противоположными
вершинами (медианы тетраэдра), всегда
пересекаются в одной точке, эта точка
— центр тяжести тетраэдра. Если в этом
условии заменить центры тяжести граней
на ортоцентры граней, то оно превратится
в новое определение ортоцентрического
тетраэдра. Если же заменить их на центры
вписанных в грани окружностей, называемых
иногда инцентрами, мы получим определение
нового класса тетраэдров — инцентрических.
Признаки класса инцентрических
тетраэдров тоже довольно интересны.
Отрезки,
соединяющие вершины тетраэдра с центрами
окружностей, вписанных в противоположные
грани, пересекаются в одной точке.
Биссектрисы
углов двух граней, проведенному к общему
ребру этих граней, имеют общее основание.
Произведения
длин противоположных ребер равны.
Треугольник,
образованный вторыми точками пересечения
трех ребер, выходящих из одной вершины,
с любой сферой, проходящей через три
конца этих ребер, является равносторонним.
Доказательство (2).
По свойству (1), если DF,
BE, CF, AM — биссектрисы
соответственных углов в треугольниках
АВС и FBD,
то отрезки КС
и LD будут иметь
общую точку I
(см. рис). Если же прямые DK
и СL не
пересекаются в точке F,
то, очевидно, КС
и DL не
пересекаются, чего быть не может (по
определению инцентрического тетраэдра).
Доказательство (3).
Учитывая свойство (2) и свойство
биссектрисы, получаем соотношения:
;
.
§6.
Соразмерные
тетраэдры
Соразмерными называются тетраэдры,
у которых
Бивысоты
равны.
Проекция
тетраэдра на плоскость, перпендикулярную
любой бимедиане, есть ромб.
Грани
описанного параллелепипеда равновелики.
4а2а>1>2—
(b2+b>1>2-c2-c>1>2)2=4b2b>1>2—
(c2+c>1>2-a2-a>1>2)2=4c2c>1>2—
(a2+a>1>2-b2-b>1>2)2,
где а
и а>1>,
b
и b>1>,
с
и с>1>
— длины противоположных ребер.
Для доказательства эквивалентности
определений (1) — (4) достаточно заметить,
что бивысоты тетраэдра равны высотам
параллелограмма, являющегося его
проекцией, упоминавшейся в свойстве
(2), и высотам описанного параллелепипеда,
и что квадрат площади параллелепипеда,
содержащей, скажем, ребро с,
равен
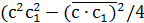
а скалярное произведение
выражается через ребра тетраэдра по
формуле (4).
Добавим сюда ещё два условия
соразмерности:
Для
каждой пары противоположных ребер
тетраэдра плоскости, проведенные через
одно из них и середину второго,
перпендикулярны.
В
описанный параллелепипед соразмерного
тетраэдра можно вписать сферу.
§7. Правильные тетраэдры
Если ребра тетраэдра равны между
собой, то равны между собой будут и
трехгранные, и двугранные, и плоские
углы. В таком случае тетраэдр называется
правильным. Заметим
также, что такой тетраэдр является и
ортоцентрическим, и каркасным, и
равногранным, и инцентрическим, и
соразмерным.
Замечание 1.
Если тетраэдр является равногранным
и принадлежит к одному из следующих
видов тетраэдров: ортоцентрический,
каркасный, инцентрический, соразмерный,
то он будет и правильным.
Замечание 2.
Тетраэдр является правильным,
если он принадлежит к двум любым видам
тетраэдров из перечисленных:
ортоцентрический, каркасный, инцентрический,
соразмерный, равногранный.
Свойства правильного тетраэдра:
Каждая его вершина является
вершиной трех треугольников. А значит,
сумма плоских углов при каждой вершине
будет равна 180º
В правильный тетраэдр можно
вписать октаэдр, притом четыре (из
восьми) грани октаэдра будут совмещены
с четырьмя гранями тетраэдра, все шесть
вершин октаэдра будут совмещены с
центрами шести рёбер тетраэдра.
Правильный тетраэдр состоит из
одного вписанного октаэдра (в центре)
и четырёх тетраэдров (по вершинам),
причем ребра этих тетраэдров и октаэдра
вдвое меньше ребер правильного тетраэдра
Правильный тетраэдр можно
вписать в куб двумя способами, притом
четыре вершины тетраэдра будут совмещены
с четырьмя вершинами куба.
Правильный тетраэдр можно
вписать в икосаэдр, притом, четыре
вершины тетраэдра будут совмещены с
четырьмя вершинами икосаэдра.
Задача 1.
Доказать, что скрещивающиеся
ребра правильного тетраэдра взаимно
перпендикулярны.
Решение:
Пусть DH – высота
правильного тетраэдра, точка H – центр
правильного ΔABC.
Тогда проекцией отрезка AD на плоскость
основания ABC будет отрезок BH.
Т.к. BHAC,
то по теореме о трех
перпендикулярах наклонная BD
AC.
Задача 2.
Дан правильный тетраэдр МАВС
с ребром 1. найдите расстояние между
прямыми AL и
МО, где
L-середина
ребра МС,
О-центр грани
АВС.
Решение:
1. Расстояние между двумя
скрещивающимися прямыми — это длина
перпендикуляра, опущенного из одной
прямой, к плоскости, параллельной этой
прямой и содержащей вторую прямую.
2. Строим проекцию AK
отрезка AL на
плоскость ABC.
Плоскость AKL
перпендикулярна плоскости ABC,
параллельна прямой MO
и содержит прямую AL.
Значит, искомая длина — это длина
перпендикуляра ON,
опущенного из точки O
к AK.
3. Найдем S>Δ>>KHA>
двумя способами.
S>Δ>=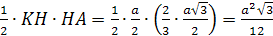
С другой стороны: S>Δ>>KHA>=
поэтому ρ
.
Найдём ON:
ρ
.
Задача 3.
Каждое ребро треугольной
пирамиды PABC равно
1; BD –
высота треугольника ABC .
Равносторонний треугольник BDE лежит
в плоскости, образующей угол ϕ с
ребром AC ,
причём точки P и E лежат
по одну сторону от плоскости ABC .
Найдите расстояние между точками P и E .
Решение. Поскольку
все рёбра пирамиды PABC равны,
это правильный тетраэдр. Пусть M
– центр
основания ABC , N
–
ортогональная проекция вершины E равностороннего
треугольника BDE на
плоскость ABC ,
K
–
середина BD ,
F
– основание
перпендикуляра, опущенного из точки E на
высоту PM тетраэдра
PABC .
Так как
EK 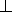
то по теореме о трёх перпендикулярах
NK 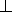
поэтому EKN –
линейный угол двугранного угла,
образованного плоскостями ABC и BDE ,
а т.к. NK
|| AC ,
то 
= ϕ .
Далее имеем:
BD
=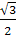
MD
= 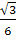
KD
= 
BD
= 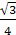
PM
= 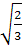
KM
= KD
— MD
= 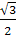
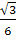
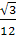
EK
= BD· 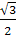

EN
= EK
sin
ϕ
= 
ϕ,
NK = EK cos
ϕ
= 
ϕ,
MN2 =
NK2 +
KM2 = 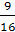
+ 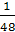
PE2 =
EF2 +
PF2 =
MN2 + (PM
— MF)2 =
MN2 + (PM
— EN)2 =
= 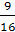
+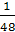
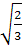

ϕ)2 = 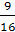
+ 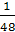
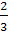
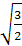
ϕ
+ 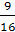
== 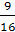
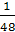

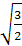
ϕ
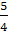
= 
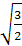
ϕ
= 
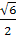
ϕ.
Следовательно,
PE =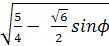
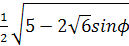
Задача 4.
Найди углы между скрещивающимися
высотами соседних граней тетраэдра.
Решение.
Случай №1.
Пусть BK
и DF – высоты
граней ABC и
BCD.
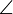
FD = α.
Обозначим длину ребра тетраэдра как a.
Проведем FL || BK,
тогда α
=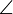
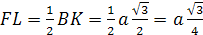
KL=LC.
Запишем теорему косинусов для
ΔDLF:
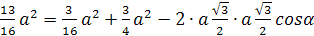
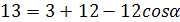
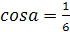
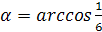
Случай
№2 (высота расположена иначе).
BK
и CN
– высоты граней ABC
и BCD. Проведем
FP || CN и FL
|| BK.
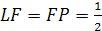
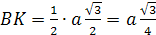
Найдем LP.
DO – высота правильного
тетраэдра, DO
=
, Q
– проекция P
на плоскость ABC,
.
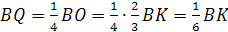
;
.
Запишем теорему косинусов для
ΔLFP:
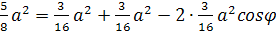
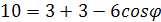
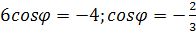
Так как угол между прямыми по
определению острый
Глава II. Тетраэдр в курсе
математики средней школы
§1. Сравнительная характеристика
изложения темы «тетраэдр» в школьных
учебниках
В школьном курсе
геометрии на изучение основ темы
«Тетраэдр» отводится достаточно много
времени. Методических проблем проведения
этой темы практически не возникает, так
как учащиеся знают, что такое пирамида
(в т.ч. и треугольная), как из пропедевтических
курсов прежних лет обучения математики,
так из жизненного опыта. Правильный
тетраэдр ассоциируется с его плоским
аналогом — правильным треугольником, а
равенство сторон с равенством ребер
или граней.
Однако проблемы в
изучении темы для учащихся существуют,
и разные учебники пытаются решить их
разными способами (порядком изложения
теоретического материала, уровнем
сложности задач и т.п.). Дадим краткую
характеристику распространенных
учебников геометрии в аспекте изучения
тетраэдра.
Изложение темы «Тетраэдр» в
учебнике «Геометрия» для 10-11 классов
Атанасяна Л. С. и др.
В базовом
учебнике «Геометрия» для 10-11 классов
средней школы Атанасяна
Л. С. и др.
информацию о тетраэдре можно найти в 7
параграфах (12, 14, 28, 29, 32, 33, 69).
Авторы учебника
определяют тетраэдр как поверхность,
составленную из четырёх треугольников.
Из теоретической базы учебника для 10
класса можно почерпнуть знания о гранях,
рёбрах и вершинах тетраэдра, о построении
сечений тетраэдра плоскостью, вычислении
площади полной поверхности тетраэдра,
в т.ч. и усечённого (глава III, §
2 «Пирамида»).
Далее рассматриваются
правильные многогранники и элементы
симметрии правильных многогранников.
Формула нахождения объёма пирамиды
приводится в заключительной главе
учебника (глава VII «Объемы тел»).
Теоретический
материал учебника изложен компактно и
стилистически единообразно. Некоторый
теоретический материал расположен в
практической части учебника (доказательства
некоторых теорем производится в задачах).
Практический материал учебника разделён
на два уровня сложности (есть т.н. «задачи
повышенной трудности», отмеченные
специальным символом «*»). Кроме того,
в конце учебника есть задачник с задачами
высокой сложности, некоторые из которых
касаются тетраэдра. Рассмотрим некоторые
задачи учебника.
Решение задач.
Задача 1 (№300).
В правильной треугольной пирамиде DABC
точки E, F
и P
— середины сторон BC,
AB
и AD.
Определите вид сечения и найдите его
площадь, если сторона основания пирамиды
равна a,
боковое ребро равно b.
Решение.
Строим сечение
плоскостью, проходящей через точки E,
F, P. Проведём
среднюю линию треугольника ABC,
EF ||
AC,
EF ||
AC, а
AC
лежит в пл.
DCA,
значит EF
|| пл.
DCA. Плоскость
сечения пересечёт грань DCA
по прямой
PK.
Т.к. плоскость сечения
проходит через прямую EF
параллельную
плоскости DCA
и пересекает
плоскость DCA,
то линия
пересечения PK
параллельна
прямой EF.
Построим в грани BDA
отрезок
FP, а
в грани BDC
— отрезок
EK.
Четырёхугольник
EFOK и
есть искомое сечение. EF
|| AC,
PK || EF
|| AC,
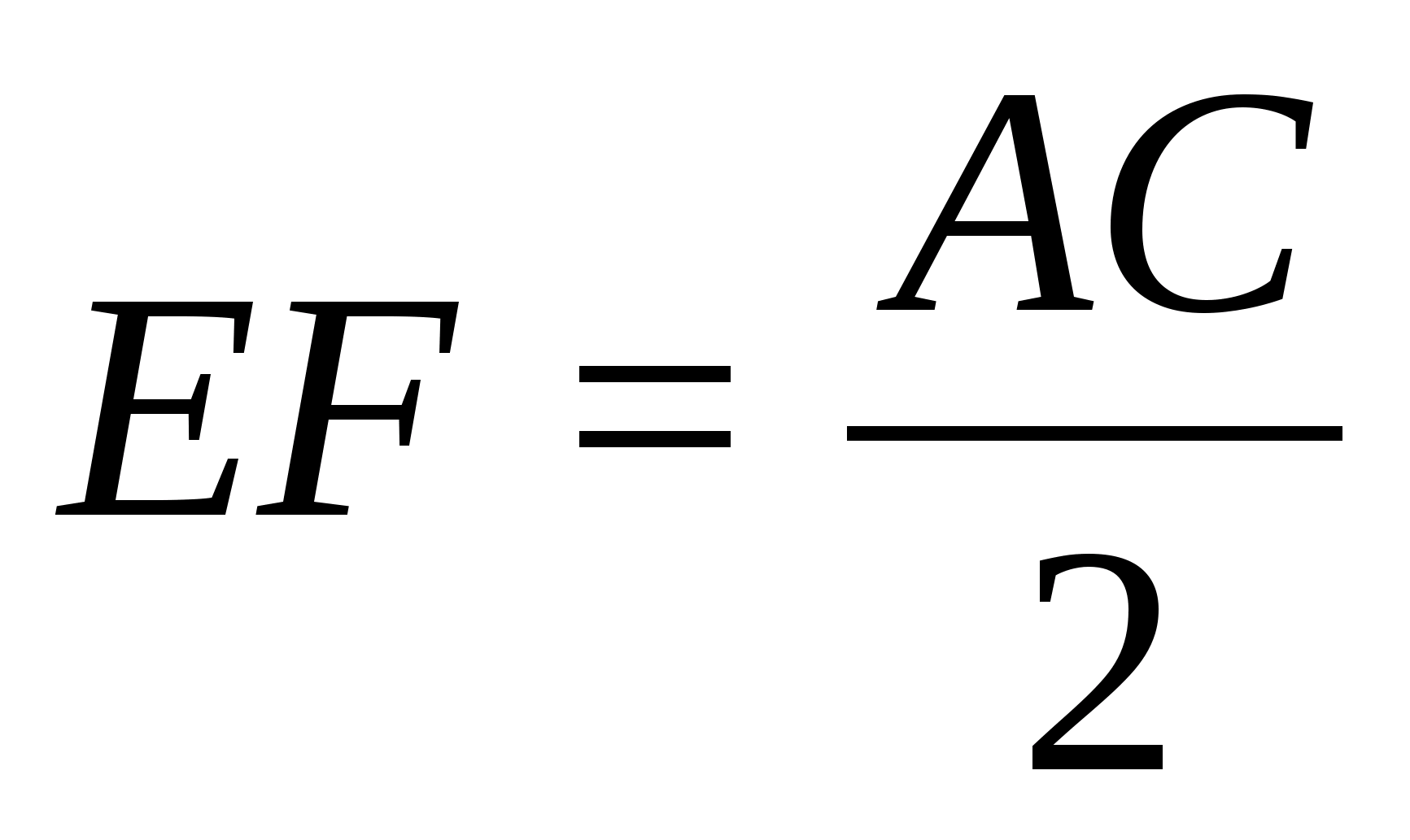
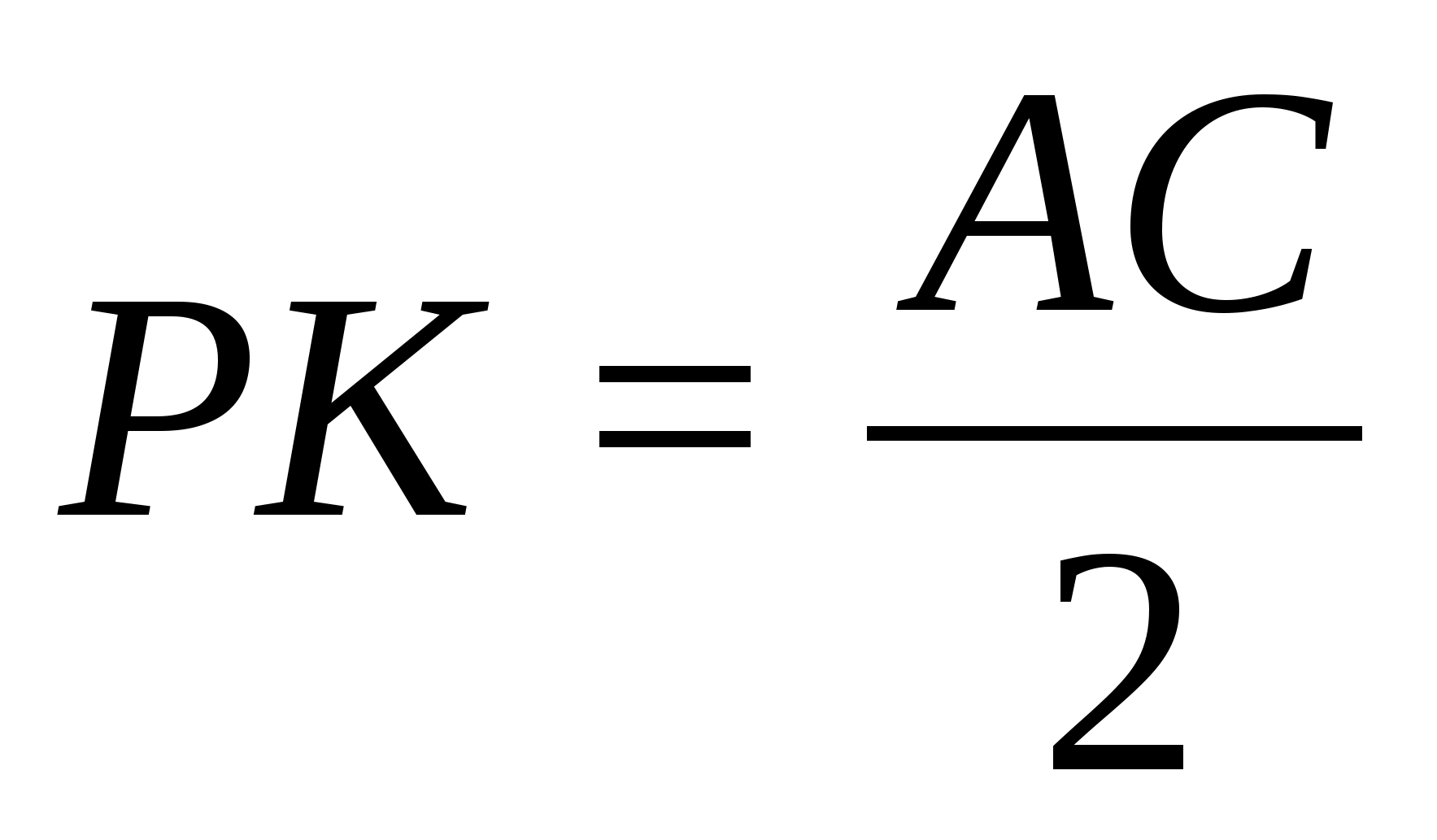
значит
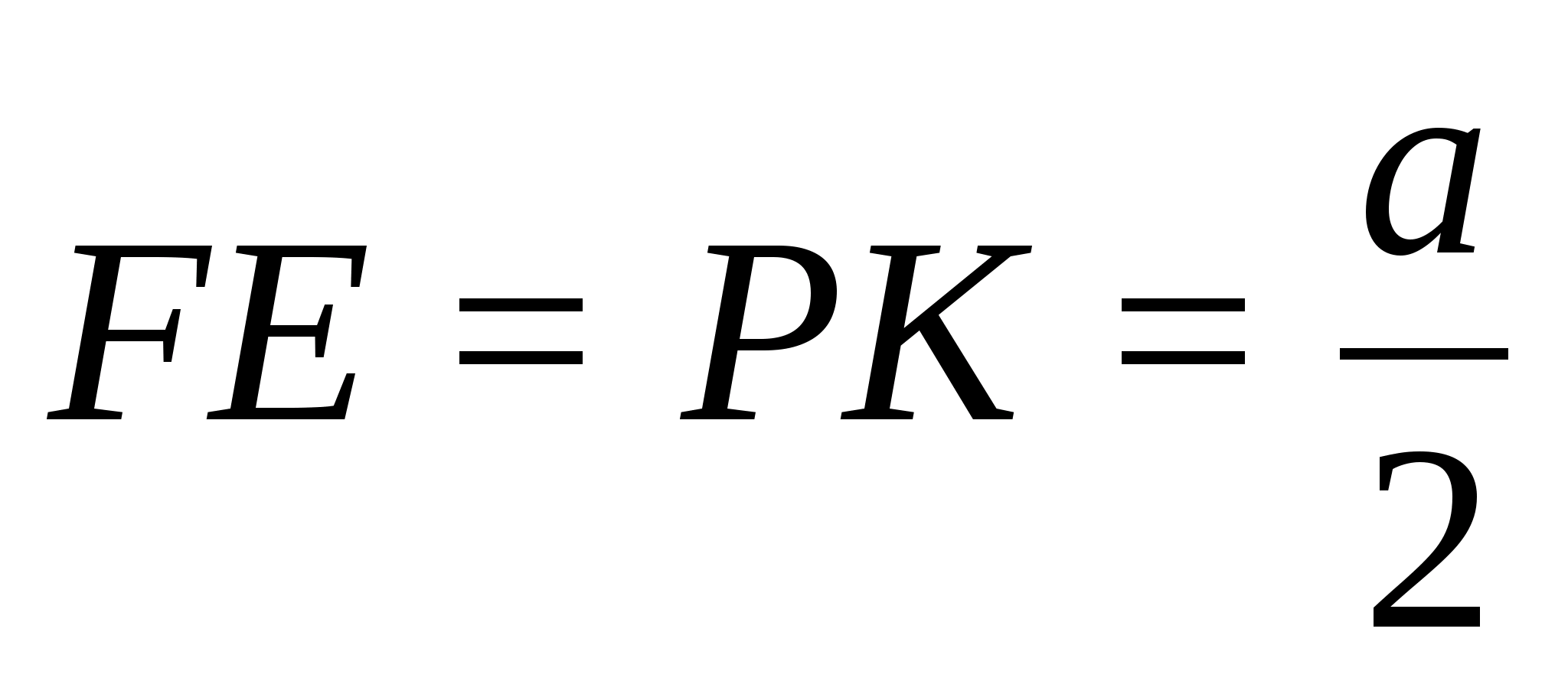
Т.к. PK
|| EF
и PK = EF,
то EFPK
— параллелограмм.
Таким образом, EK
|| EP, EP — средняя
линия треугольника BCD,
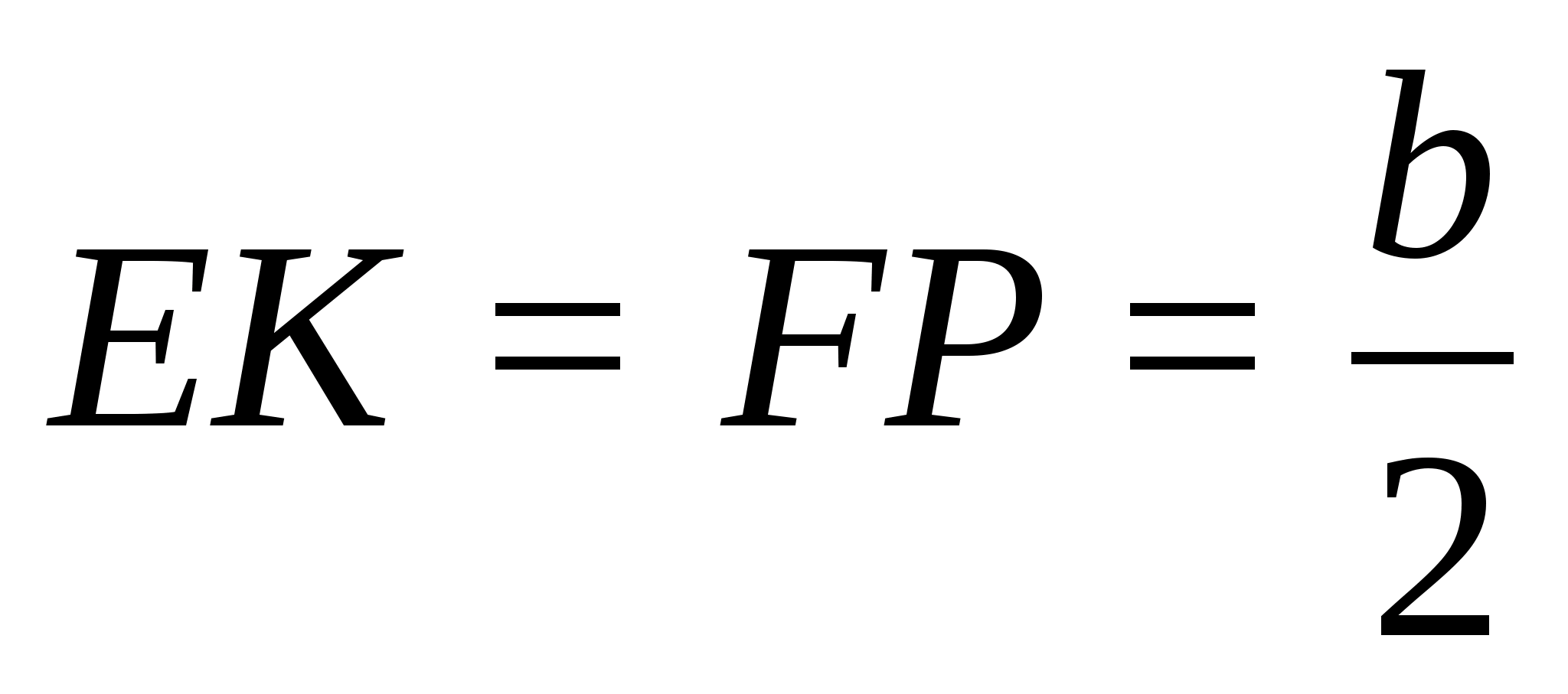
Угол между
скрещивающимися прямыми DB
и CA
равен 90°.
Докажем это. Построим высоту пирамиды
DO.
Точка O
— центр правильного треугольника ABC.
Продолжим отрезок BO
до пересечения со стороной AC
в точке M.
В правильном треугольнике ABC:
BM — высота,
медиана и биссектриса, следовательно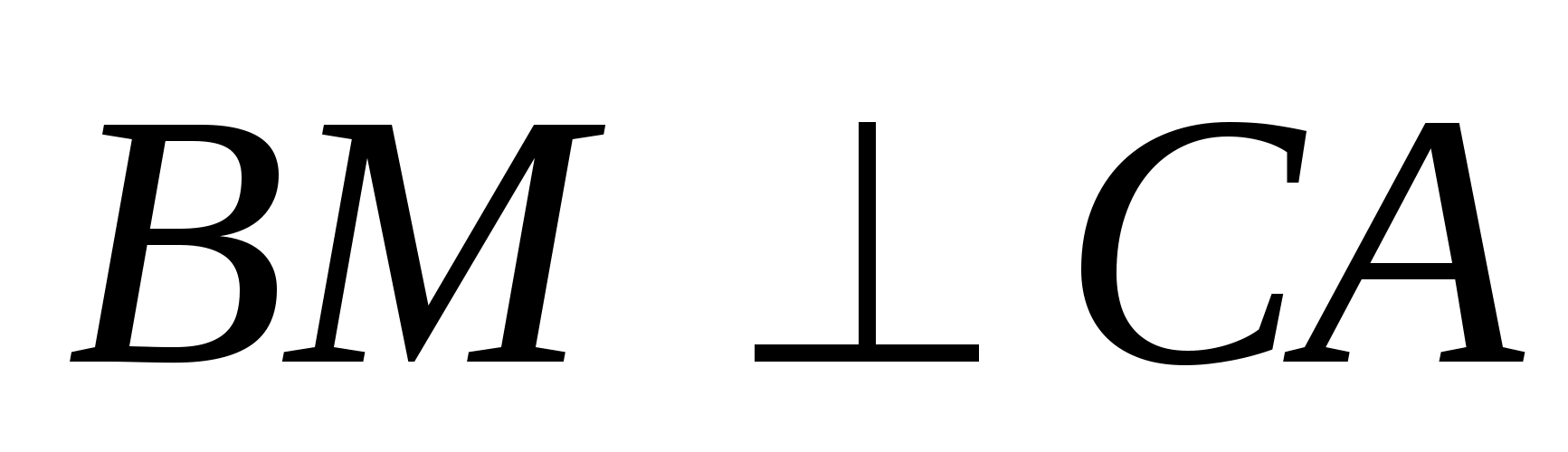
Имеем, что
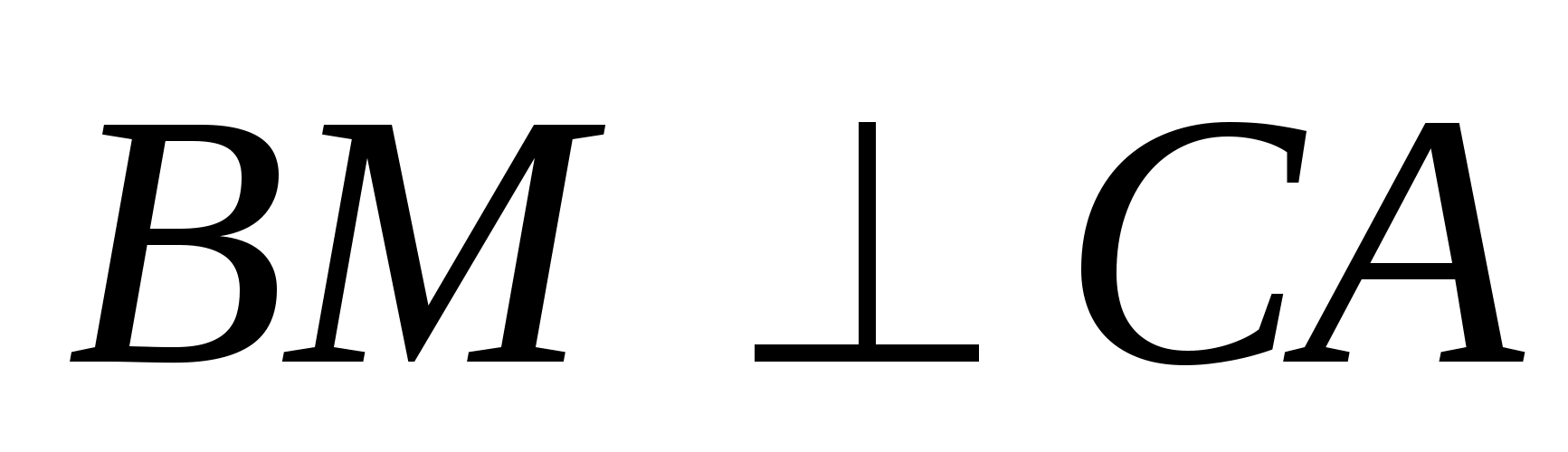
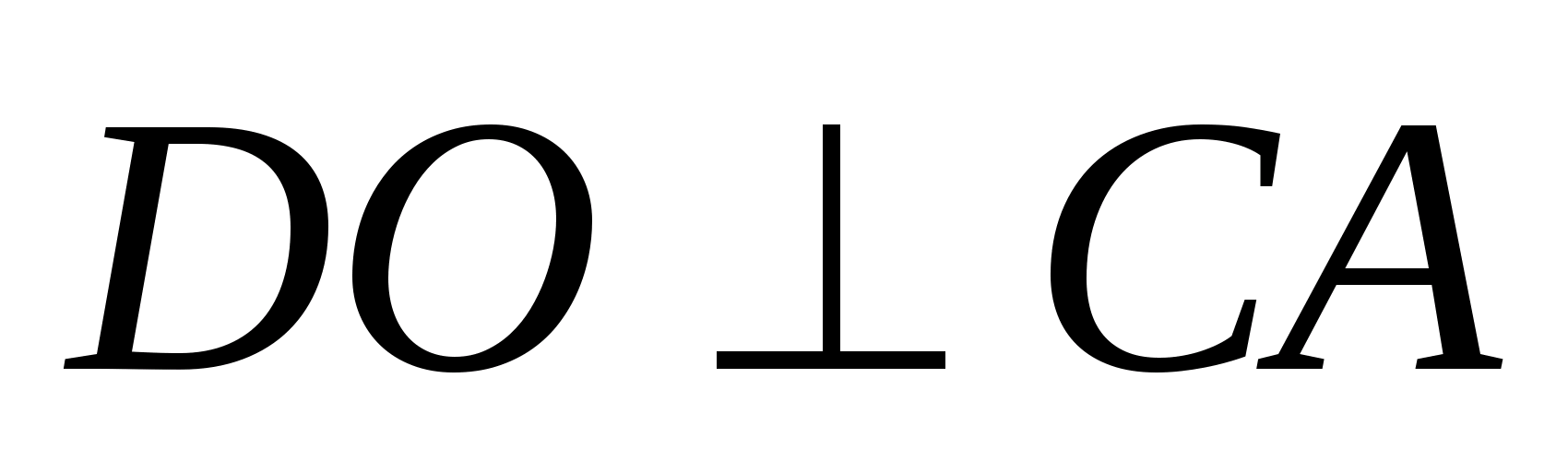
тогда по признаку перпендикулярности
прямой и плоскости
тогда
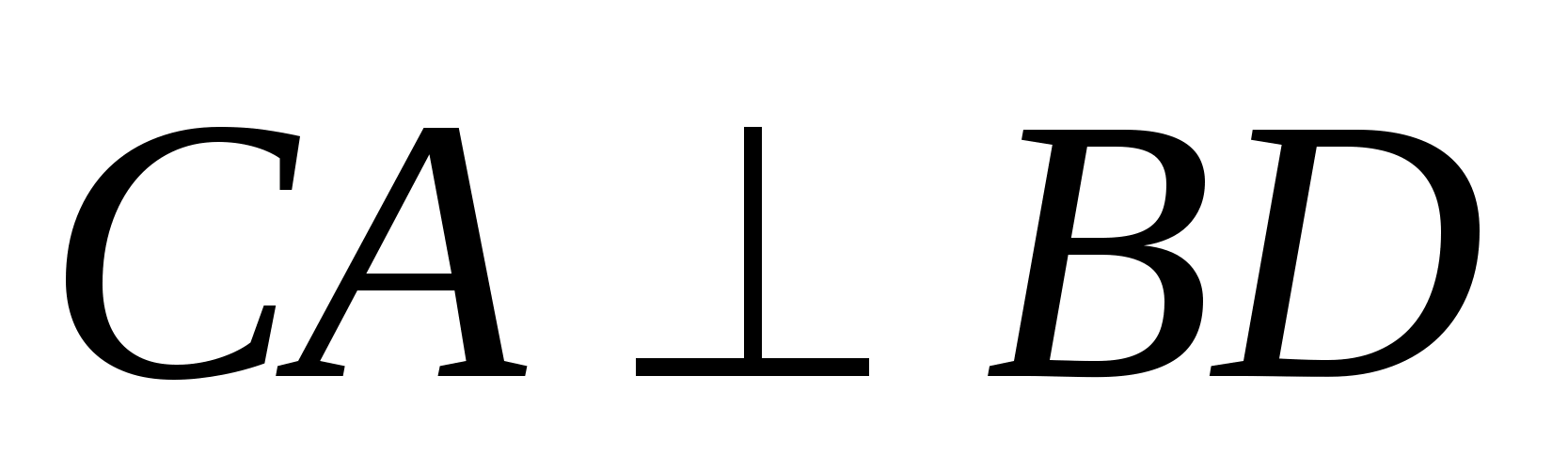
Т.к.
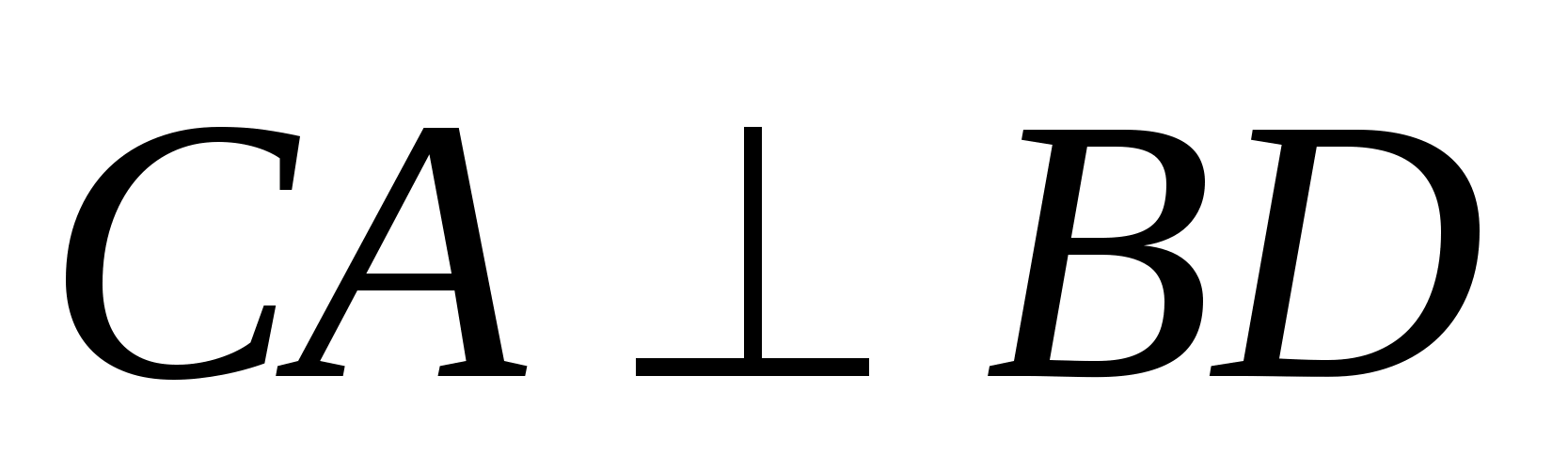
PK ||
CA
и EK
|| BD,
то
и EFPK
— прямоугольник.
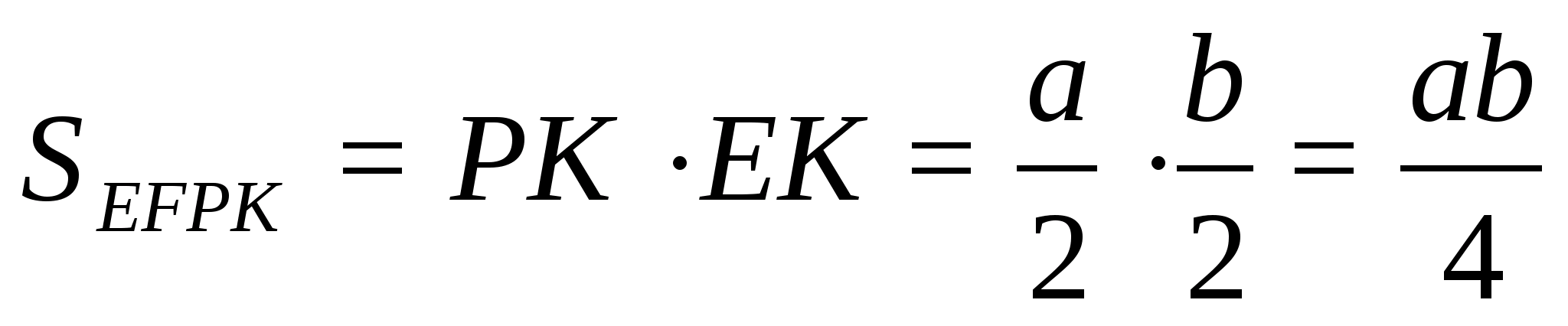
Задача 2 (№692).
Основанием пирамиды
является прямоугольный треугольник с
катетами a
и b.
Каждое её боковое ребро наклонено к
плоскости основания под углом φ.
Найдите объём пирамиды
Решение:
ABCD — пирамида,
угол ABC —
прямоугольный,
AC = b, BC = a, углы
DAO, DBO, DCO равны
. Найдем
V>DABC0>.
1) ∆DAO=∆ADC=∆DBO
по катету
и острому углу, значит
AO=OC=OB=R окружности,
описанной около
∆ABC. Т.к.
∆ABC — прямоугольный,
то
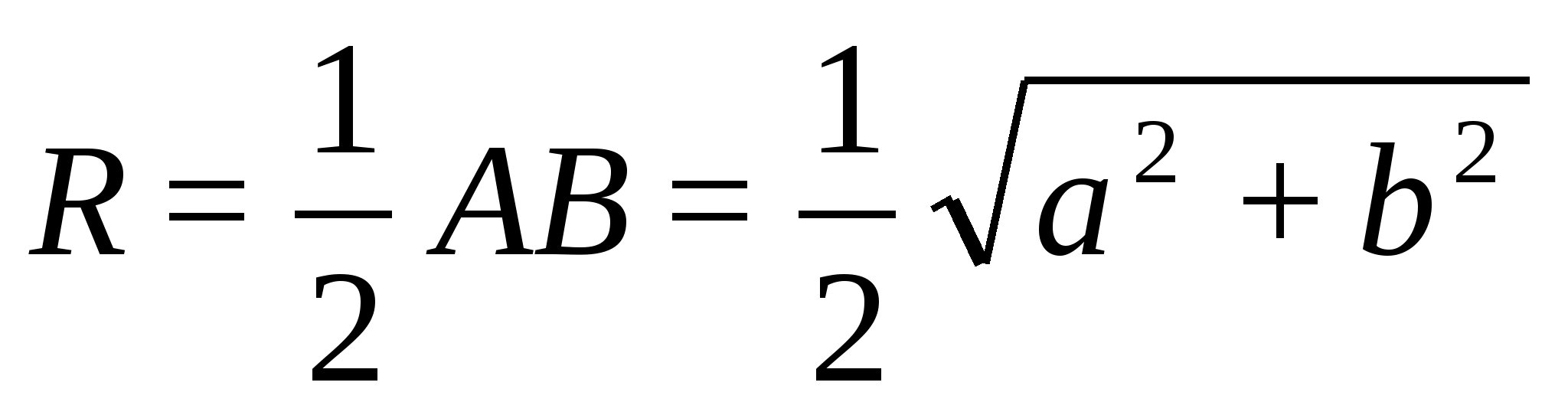
2) Из ∆DOC:
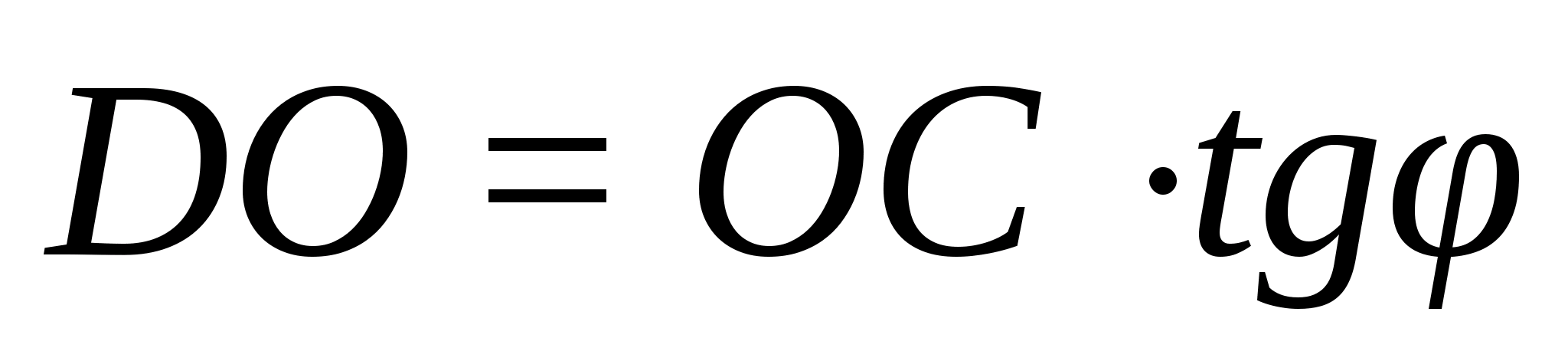
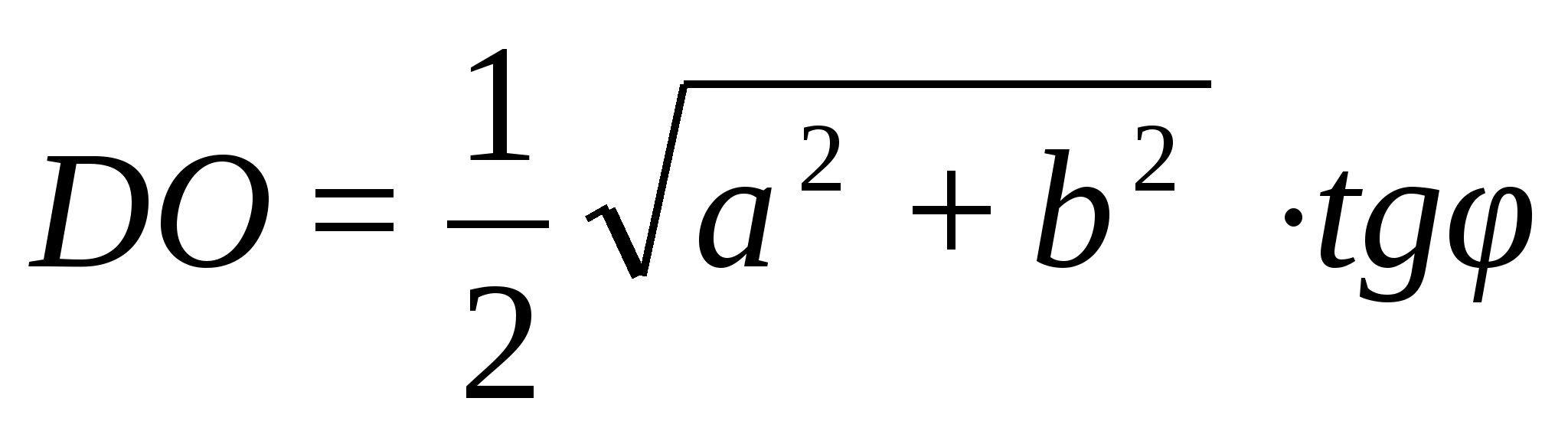
3)
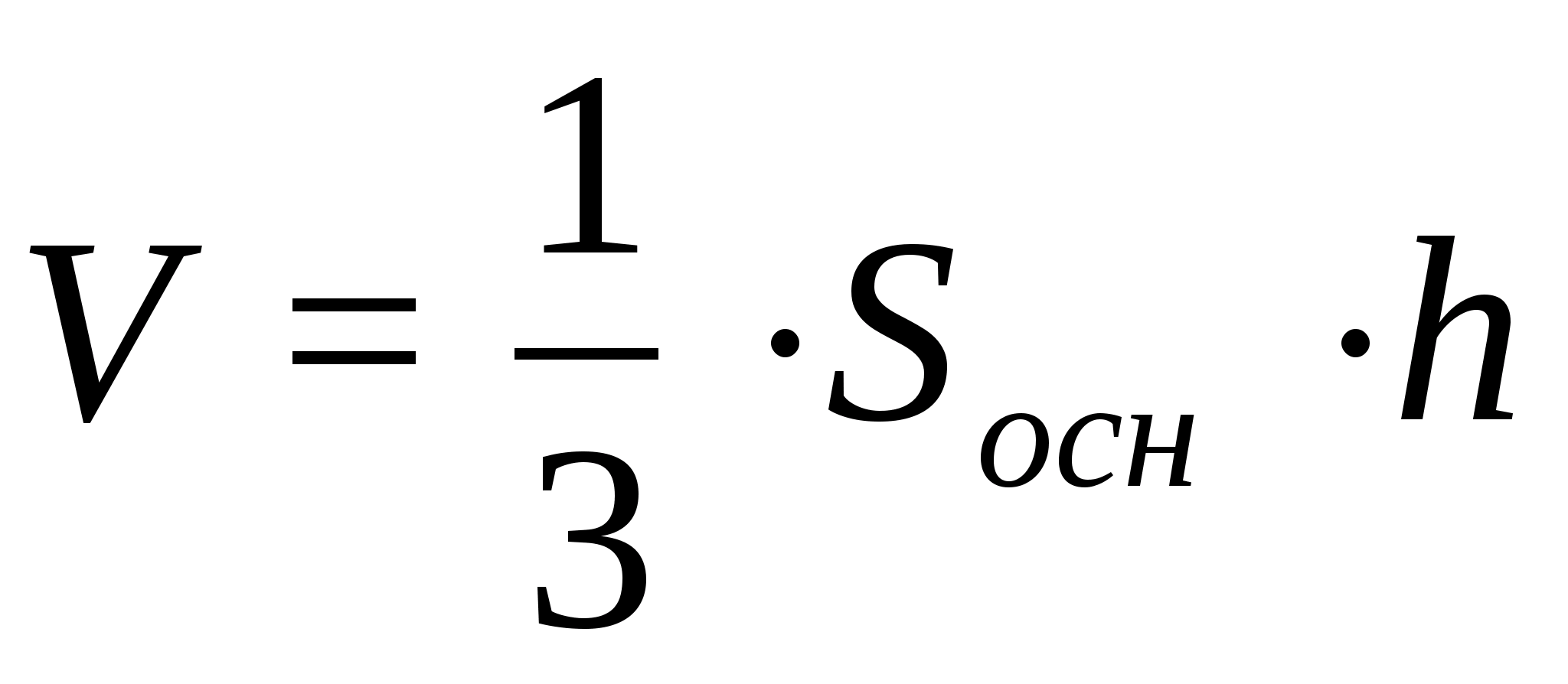
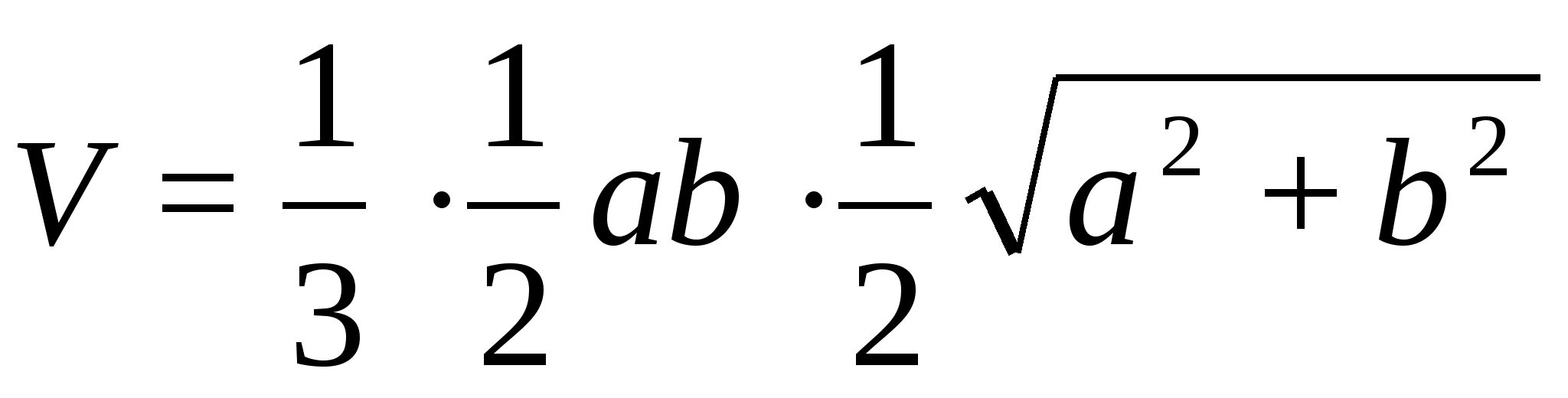
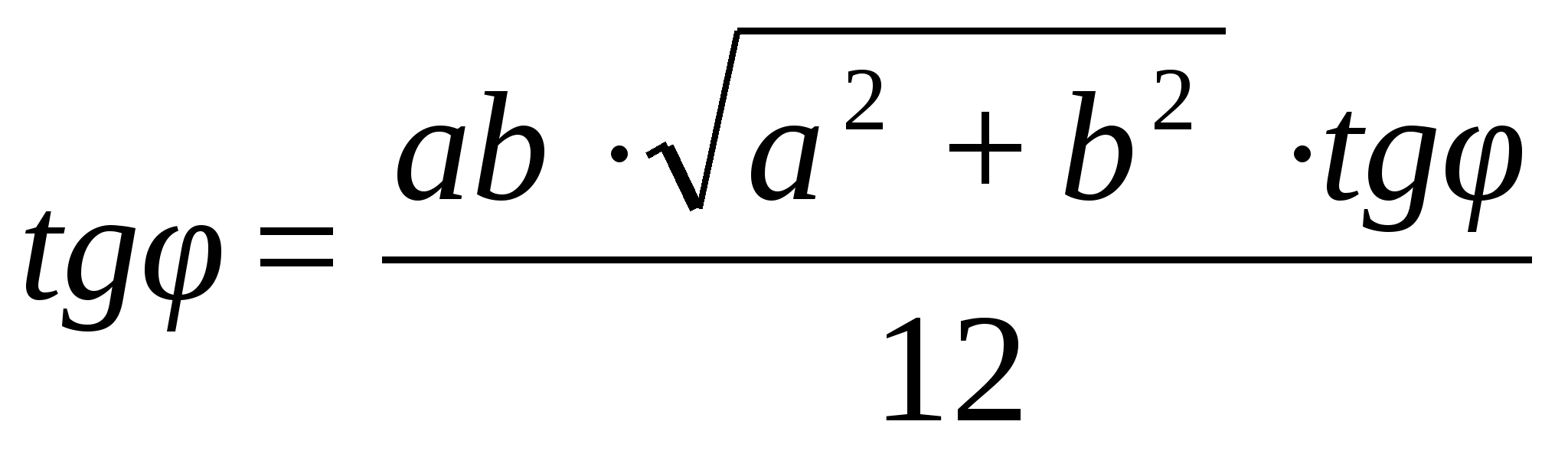
Изложение темы «Тетраэдр» в
учебнике «Геометрия» для 7-11 классов
Погорелова А.В.
В другом базовом
учебнике А.В. Погорелова и др.
теоретический
материал в той или иной степени касающийся
темы «Тетраэдр» содержится в пунктах
176-180, 186, 192, 199, 200.
В пункте 180 “Правильные
многогранники” содержится определение
понятия «правильный тетраэдр» (“Тетраэдр
представляет собой треугольную пирамиду,
у которой все рёбра равны”), доказательство
некоторых свойств и теорем о пирамиде
проиллюстрировано чертежами тетраэдра.
Однако в данном учебном пособии акцент
на изучении фигуры не ставится, и в этом
смысле его информативность (касательно
тетраэдра) можно оценить как низкую.
Практический же материал учебника
содержит удовлетворительное количество
заданий, касающихся пирамиды, в основании
которой расположен треугольник (что по
сути и есть тетраэдр). Приведём примеры
решения некоторых задач.
Решение задач.
Задача 1 (№ 41 из пункта
«Многогранники»).
Основание пирамиды
— равнобедренный треугольник, у которого
основание равно 12 см, а боковая сторона
— 10 см. Боковые грани образуют с основанием
равные двугранные углы, содержащие по
45°. Найдите высоту пирамиды.
Решение:
Проведем перпендикуляр
SO к плоскости
основания и перпендикуляры
SK, SM и
SN к сторонам
ΔABС. Тогда
по теореме о трех перпендикулярах
OK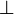
ОМ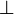
и ON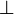
Тогда,
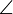
=
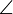
=
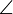
= 45° — как
линейные углы данных двугранных углов.
А следовательно, прямоугольные
треугольники SKO,
SMO и
SNO равны
по катету и острому углу.
Так что
OK=OM=ON, то
есть точка
О является
центром окружности, вписанной
в
ΔАВС.
Выразим площадь
прямоугольника
АВС:
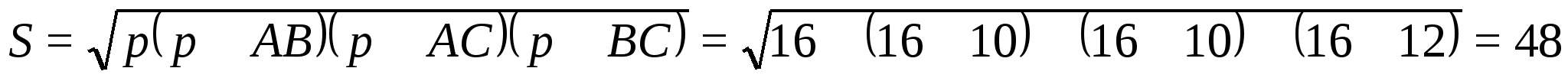
С другой стороны,
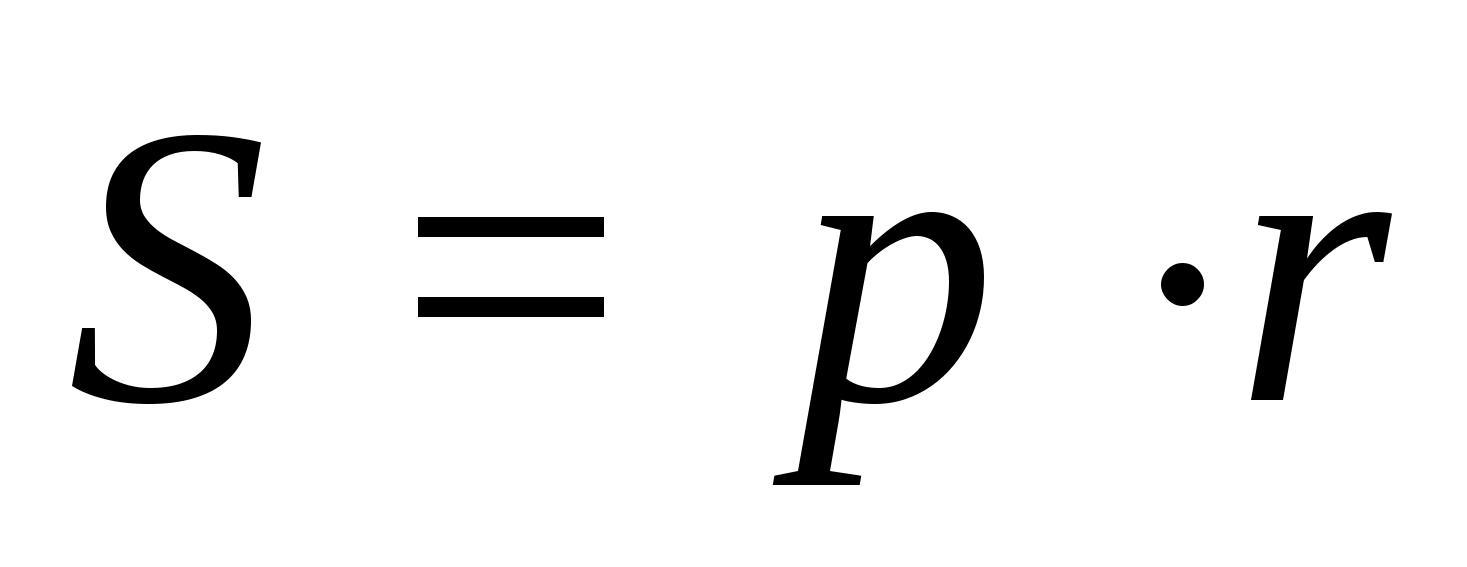
Так что
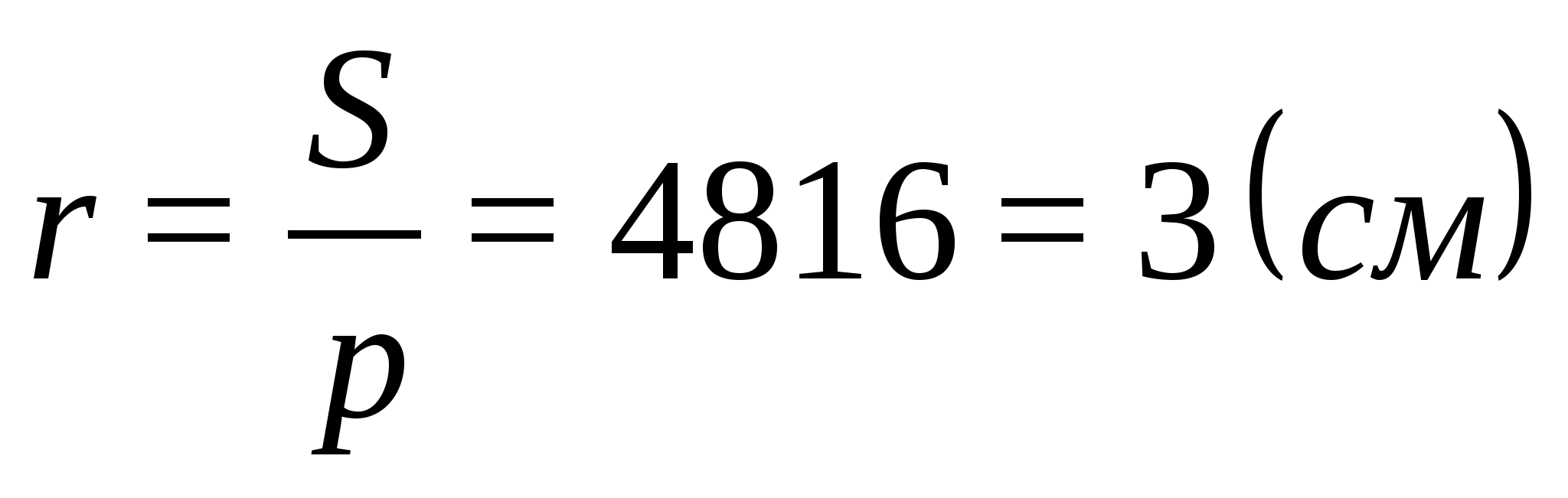
ОК=r=3 см. Так
как в прямоугольном треугольнике
SOK острый
угол равен
45°,
то
ΔSOK является
равнобедренным и
SO=OK=3(см).
Задача 2 (№ 43 из
пункта «Объёмы многогранников»).
Найдите объем
пирамиды, имеющий основанием треугольник,
два угла которого
a и β; радиус
описанного круга
R. Боковые
ребра пирамиды наклонены к плоскости
ее основания под углом
γ.
Решение.
Так как все боковые
ребра пирамиды наклонены к плоскости
основания под одним и тем же углом, то
высота пирамиды
O>1>O
проходит
через центр описанной около основания
окружности. Так что
Далее, в прямоугольном
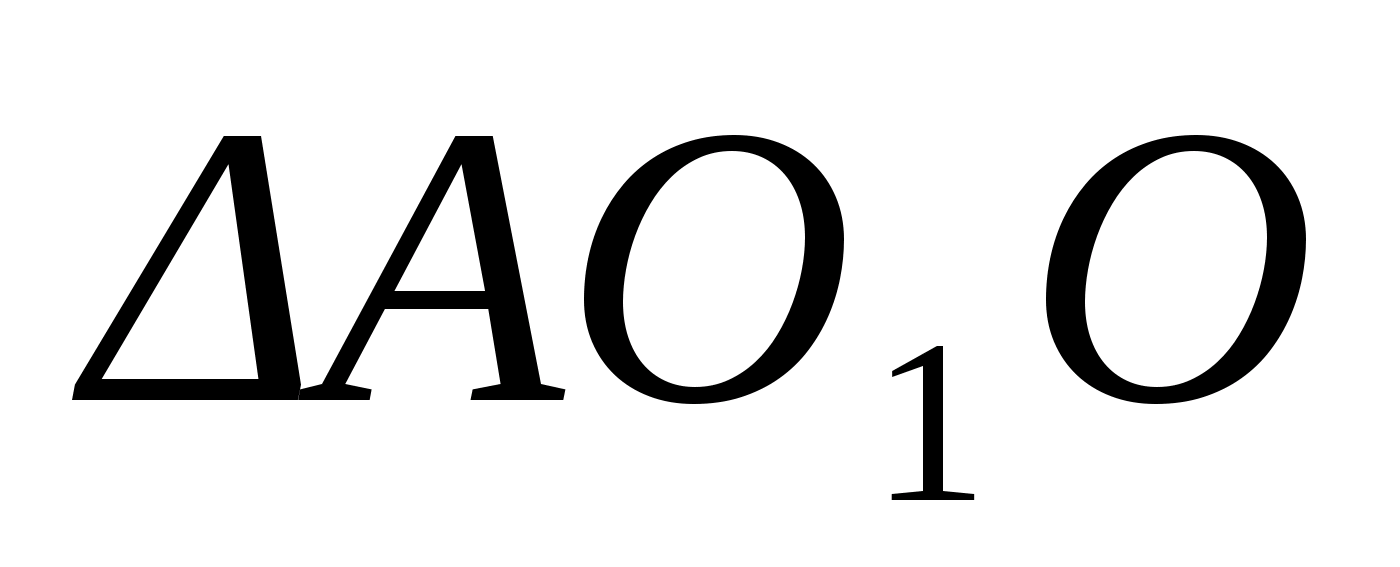
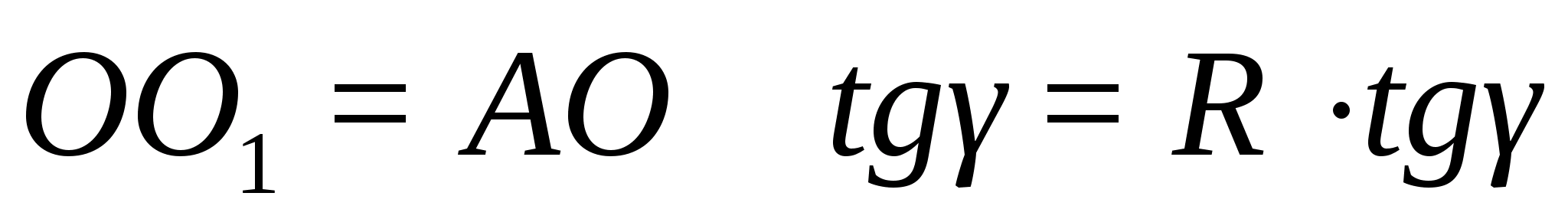
В ΔАВС
Тогда
согласно теореме синусов
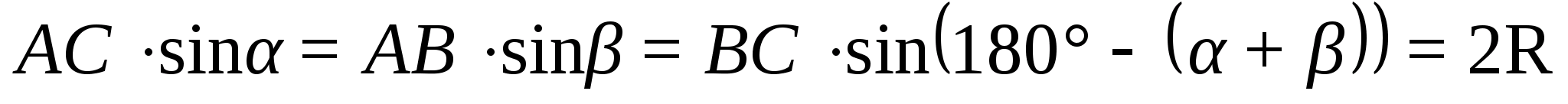
Так что
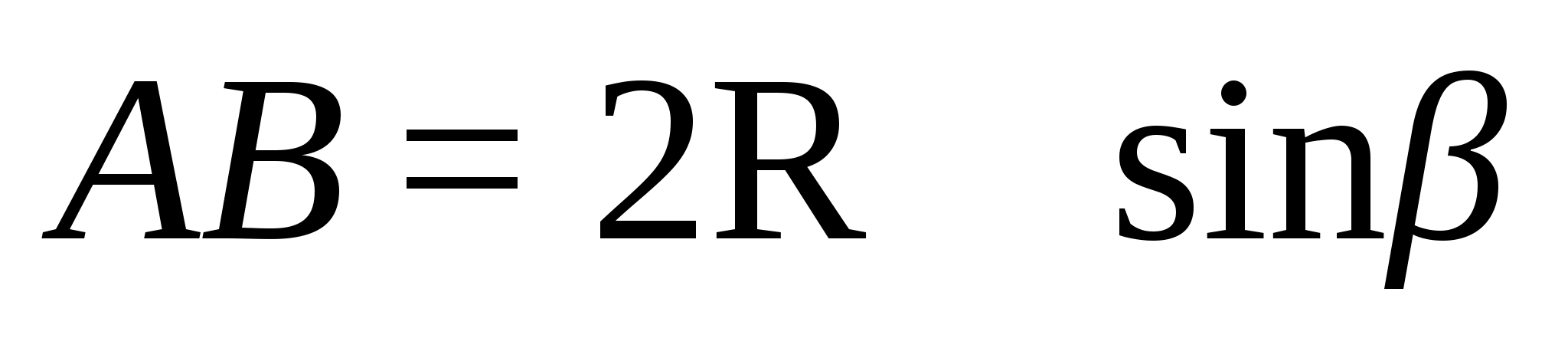
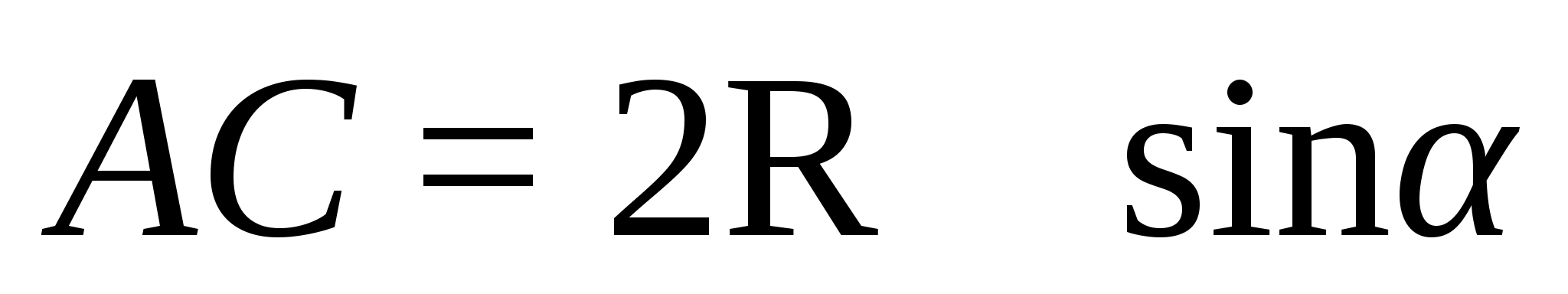
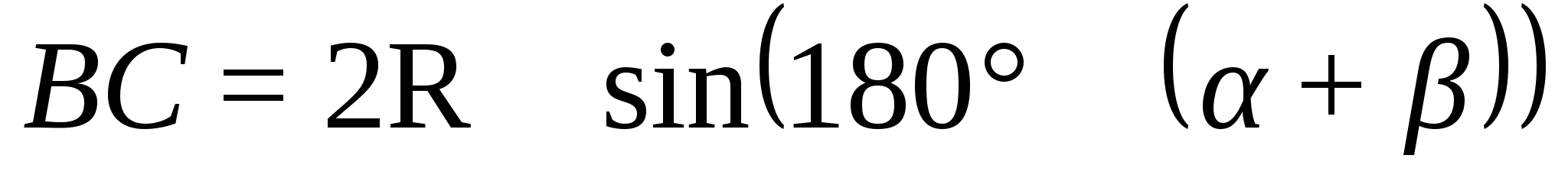
=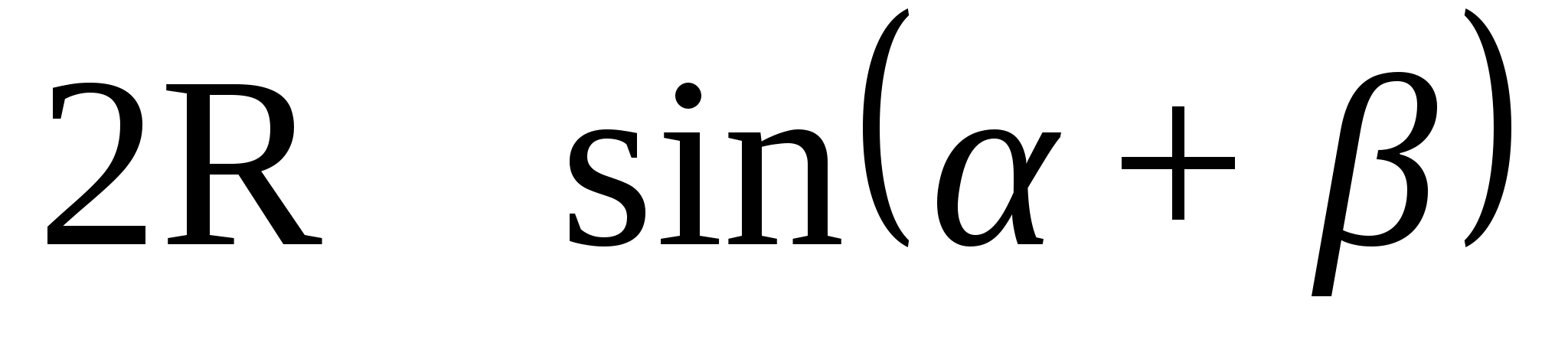
Площадь треугольника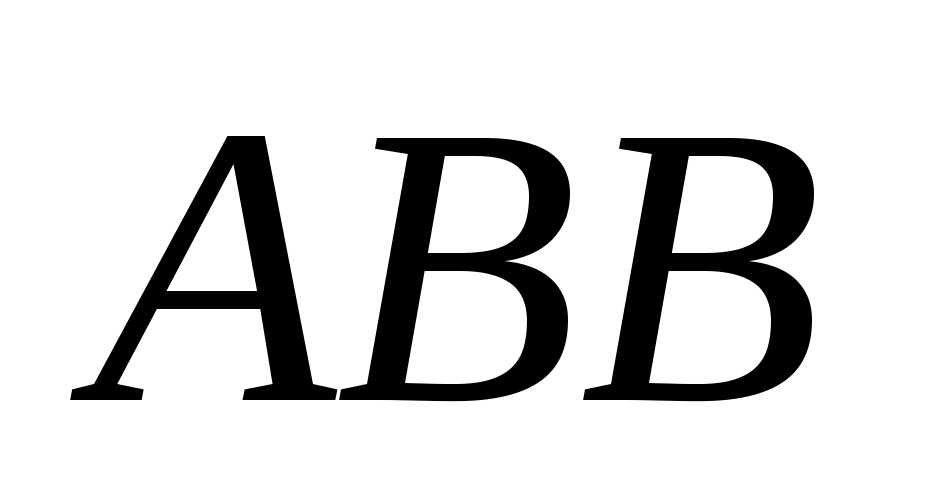
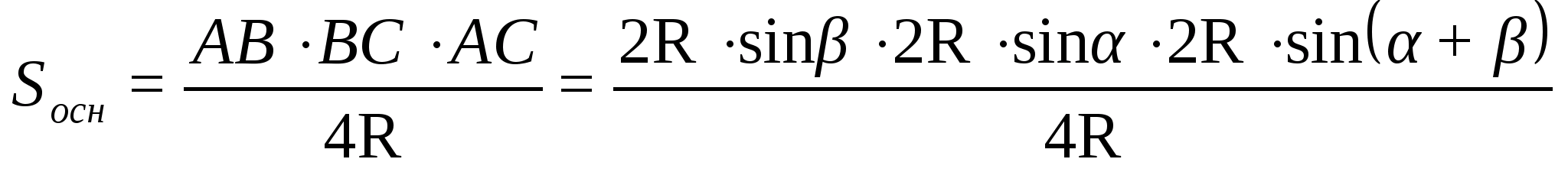
Тогда
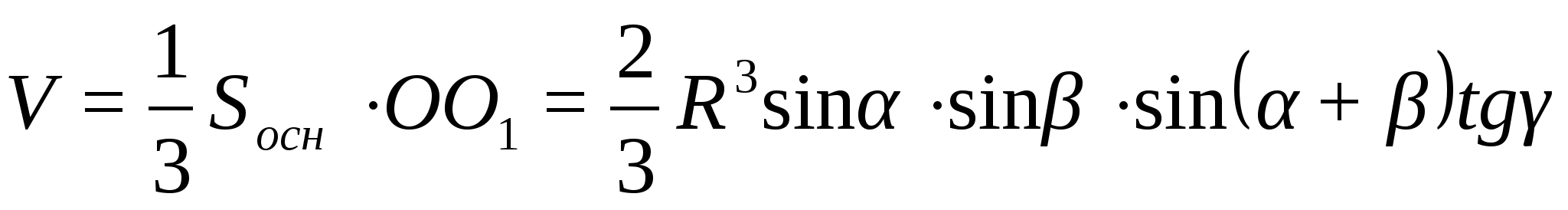
Изложение темы «Тетраэдр» в
учебнике «Геометрия» для 10-11 классов
Александрова А.Д.
Рассмотрим учебное пособие
Александрова А.Д. и др. «Геометрия:
учебник для учащихся 11 кл. с углубленным
изучением математики». Отдельных
параграфов, посвящённых тетраэдру в
этом учебнике нет, однако тема присутствует
в виде фрагментов других параграфов.
Впервые тетраэдр упоминается в
§21.3. В материале параграфа рассматривается
теорема о триангуляции многогранника,
в качестве примера выполняют триангуляцию
выпуклой пирамиды. Само понятие
«многогранник» в учебнике трактуется
двумя способами, второе определение
понятия напрямую связано с тетраэдром:
«Многогранник – это фигура, являющаяся
объединением конечного числа тетраэдров…».
Познания, касающиеся правильной пирамиды
и некоторых аспектов симметрии тетраэдра
можно обнаружить в §23.
В §26.2 описано применение теоремы
Эйлера («о правильных сетях») для
правильных многогранников (в т.ч. для
тетраэдра), а в §26.4 рассматриваются виды
симметрий, характерные для этих фигур.
Формулу для нахождения объёма
пирамиды авторы вводят в задаче №30.1(2),
а площадь боковой поверхности пирамиды
вводится в материале параграфа «Площадь
поверхности конуса и цилиндра» (§32.5).
Также, в учебнике можно найти
информацию о средней линии тетраэдра,
центре масс (§35.5) и классе равногранных
тетраэдров. Движения I
и II
рода демонстрируются в ходе решения
задач о тетраэдрах.
Отличительная особенность
учебника — высокая научность, которую
авторам удалось совместить с доступным
языком и чёткой структурой изложения.
Приведём примеры решения некоторых
задач.
Решение задач.
Задача 1.
В данную правильную
треугольную усечённую пирамиду с боковым
ребром a можно поместить сферу, касающуюся
всех граней, и сферу, касающуюся всех
рёбер. Найдите стороны оснований
пирамиды.
Решение.
Изобразим на чертеже
«полную» пирамиду. Данная пирамида
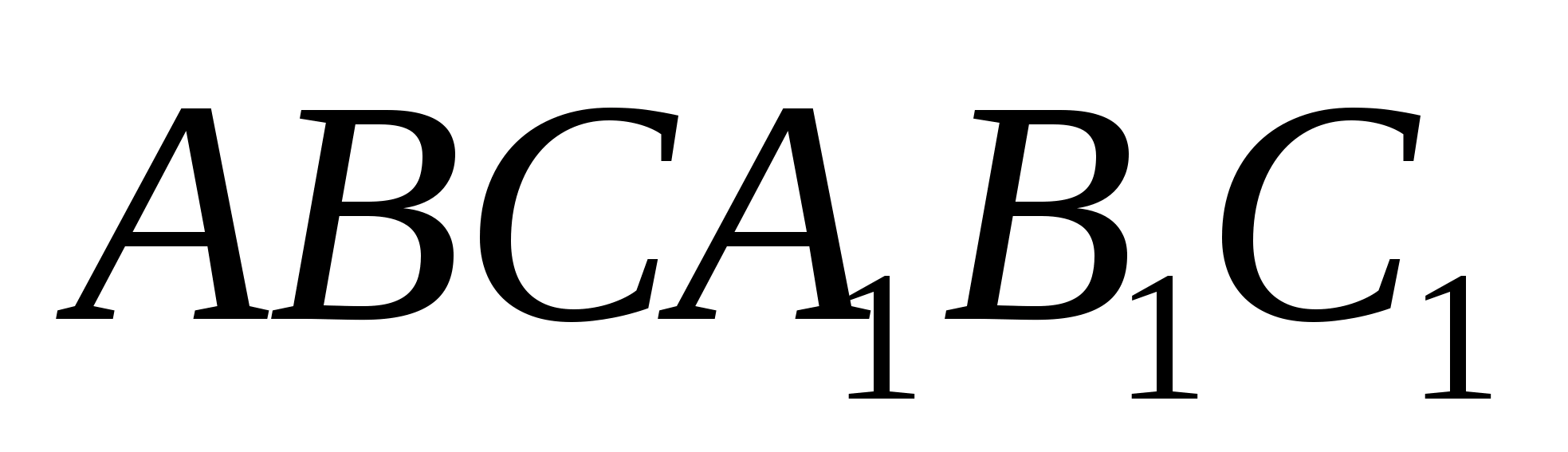
— высота «полной» пирамиды,
— ее часть до верхнего основания
усеченной. Задача сводится к
планиметрической, при этом не надо
рисовать ни одной из данных сфер. Т.к. в
усеченную пирамиду можно вписать сферу,
касающуюся всех ребер, то в её боковую
грань можно вписать окружность. Обозначим
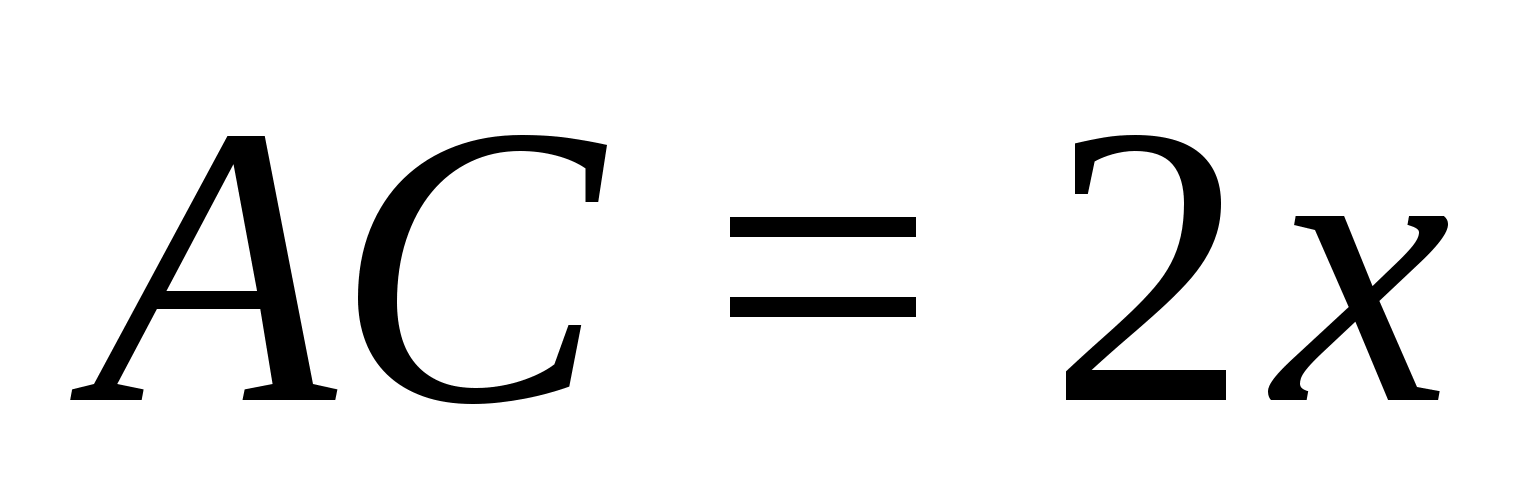
(для удобства деления пополам) и для
описанного четырехугольника
получим, что
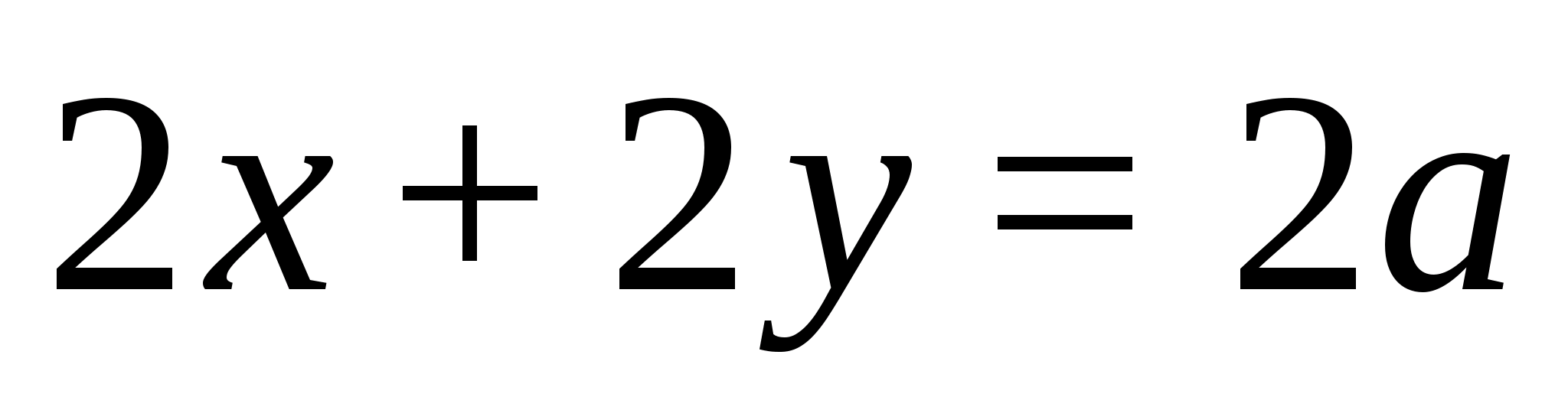
откуда
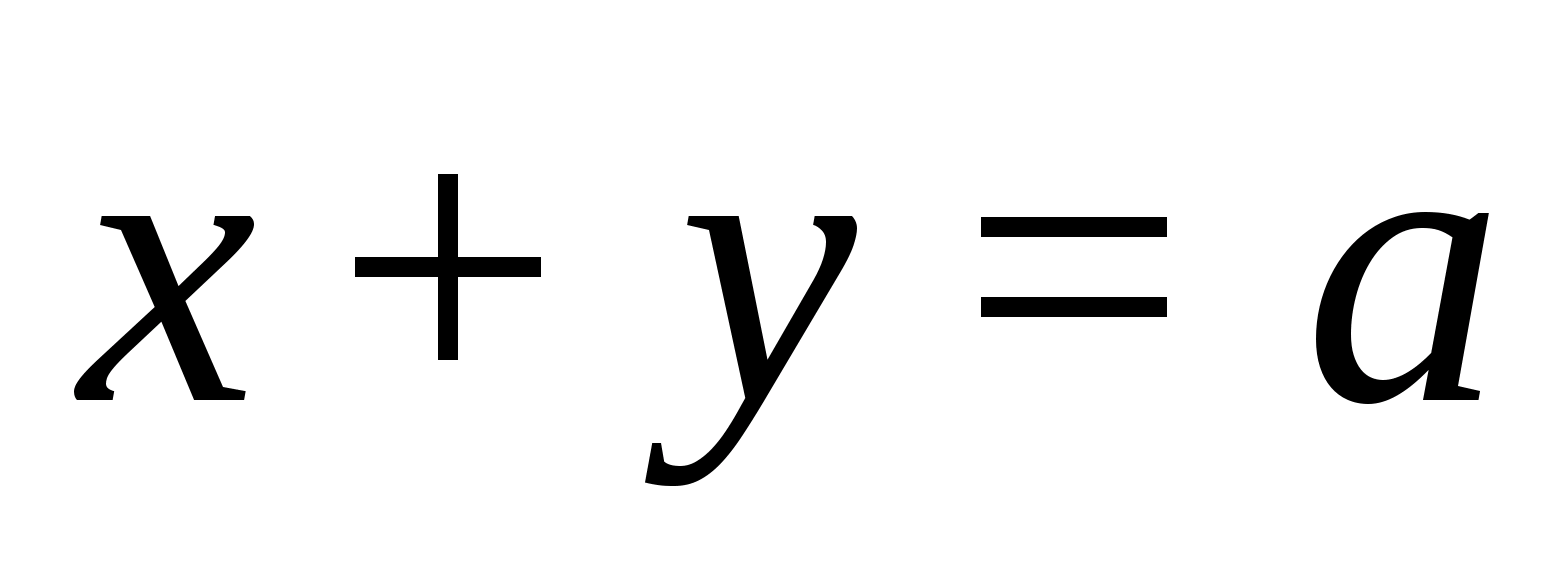
Из существования
вписанного шара следует, что существует
полуокружность, расположенная в трапеции
(
— апофема «полной» пирамиды) так, что
ее центр лежит в середине
а сама она касается остальных трёх
сторон трапеции.
— центр шара,
и
— точки касания. Тогда
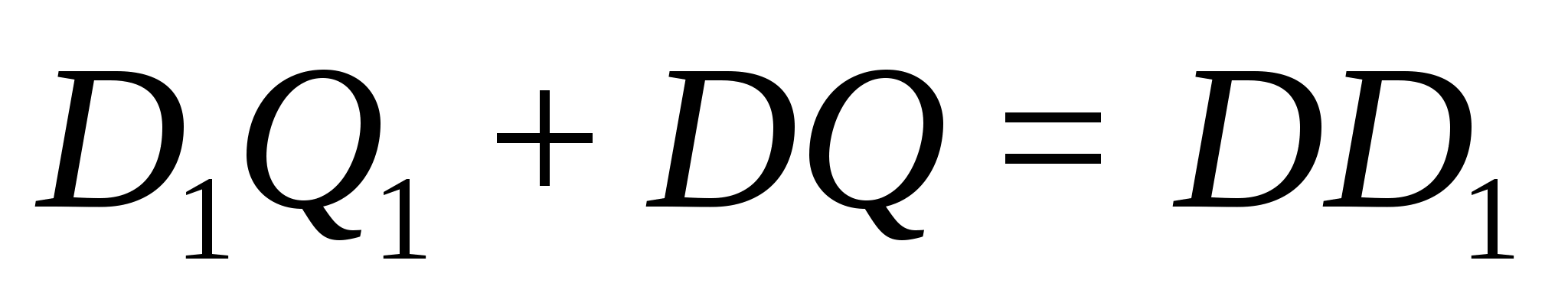
Выразим эти величину через
и
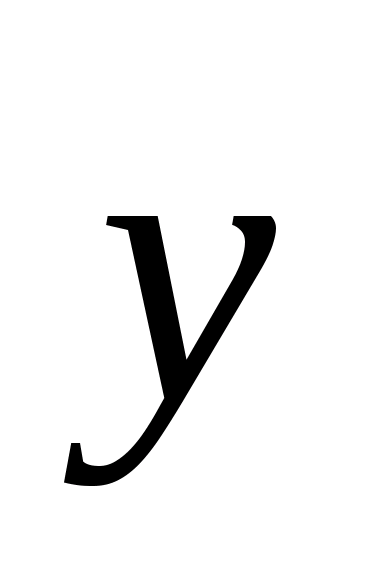
Из
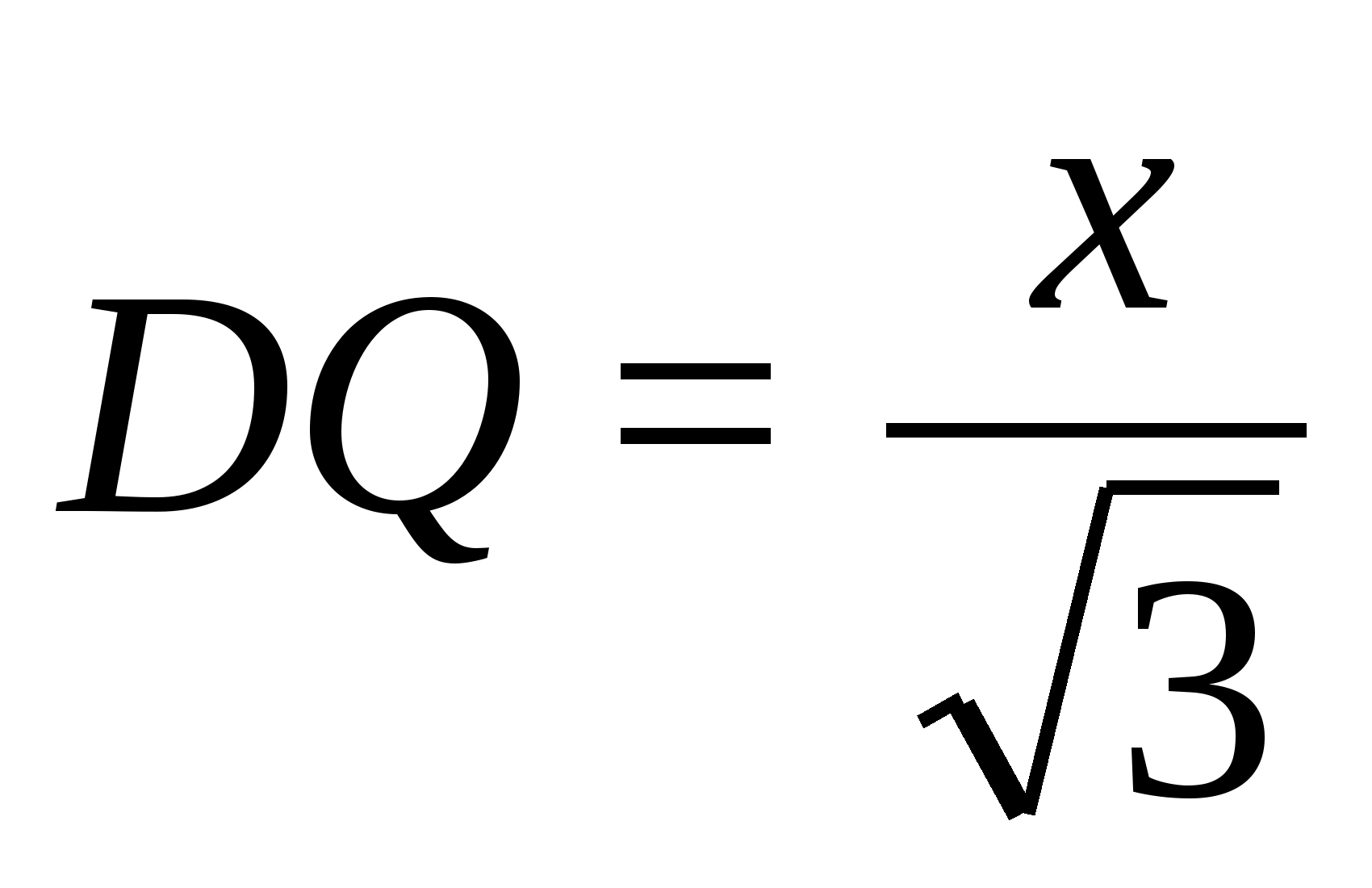
Из

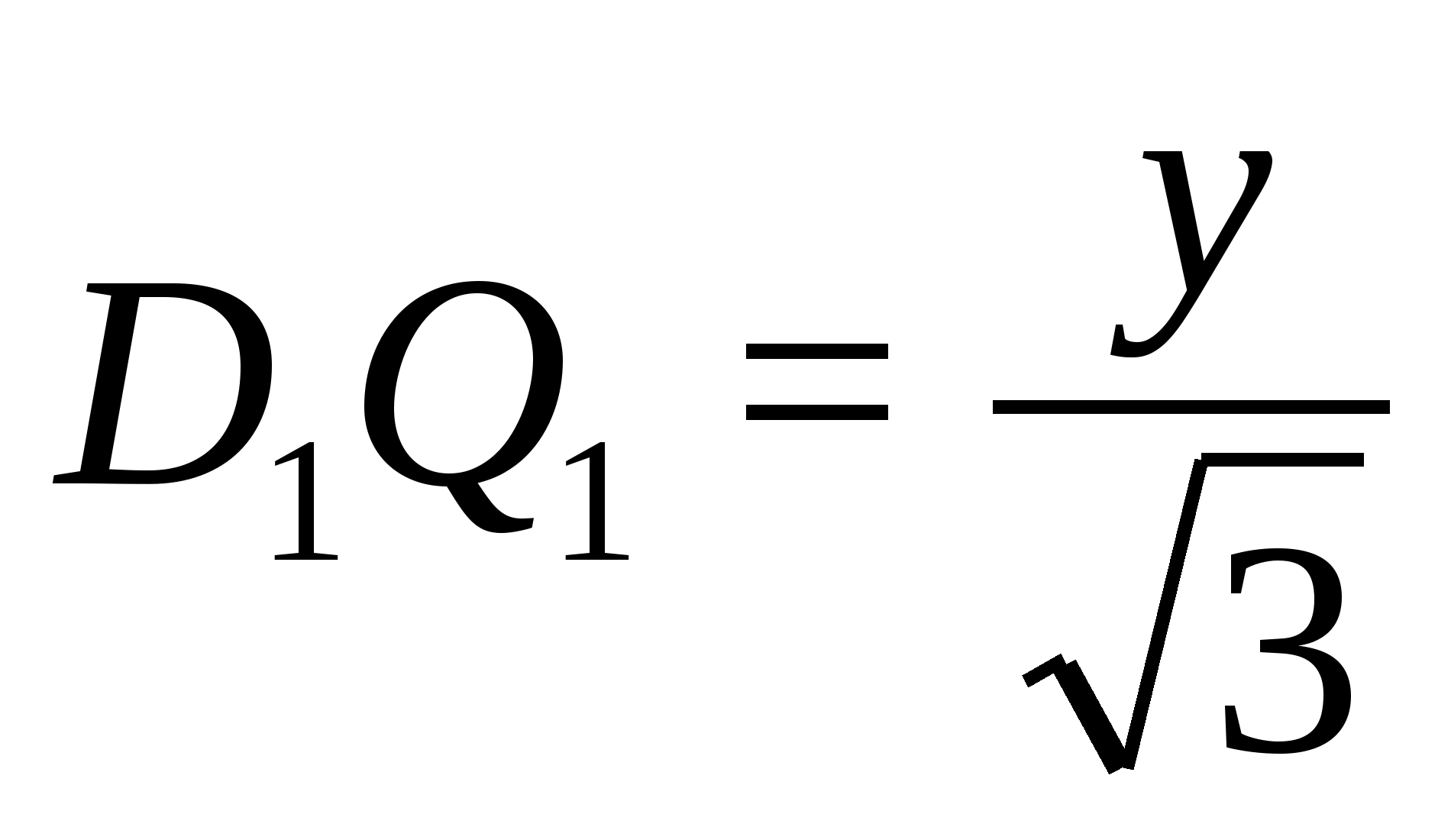
Из трапеции
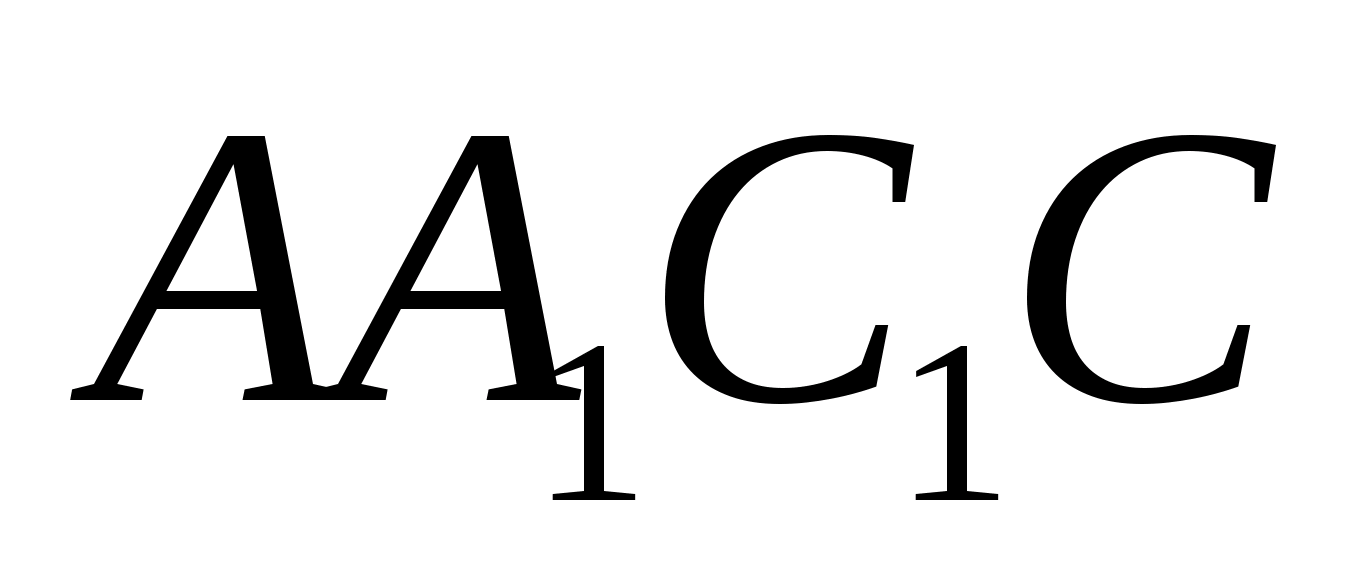
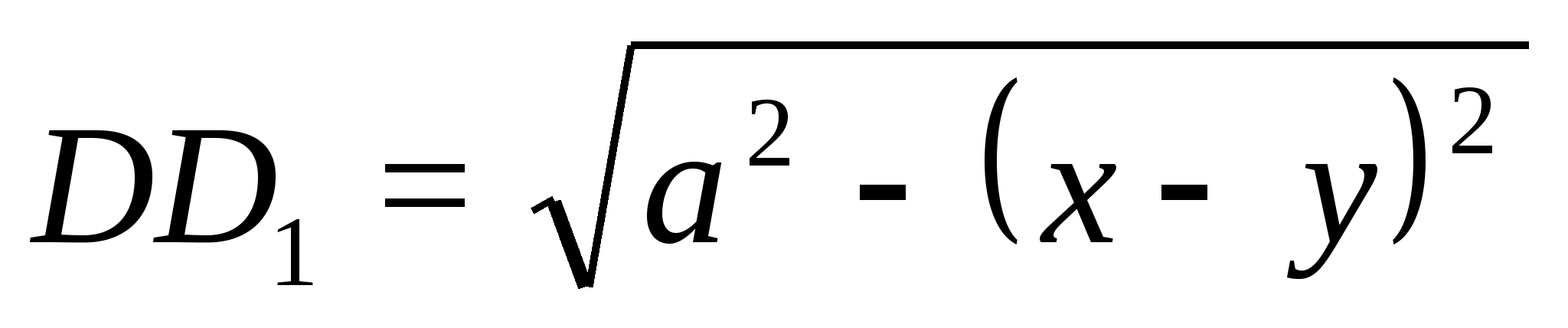
Получаем уравнение:
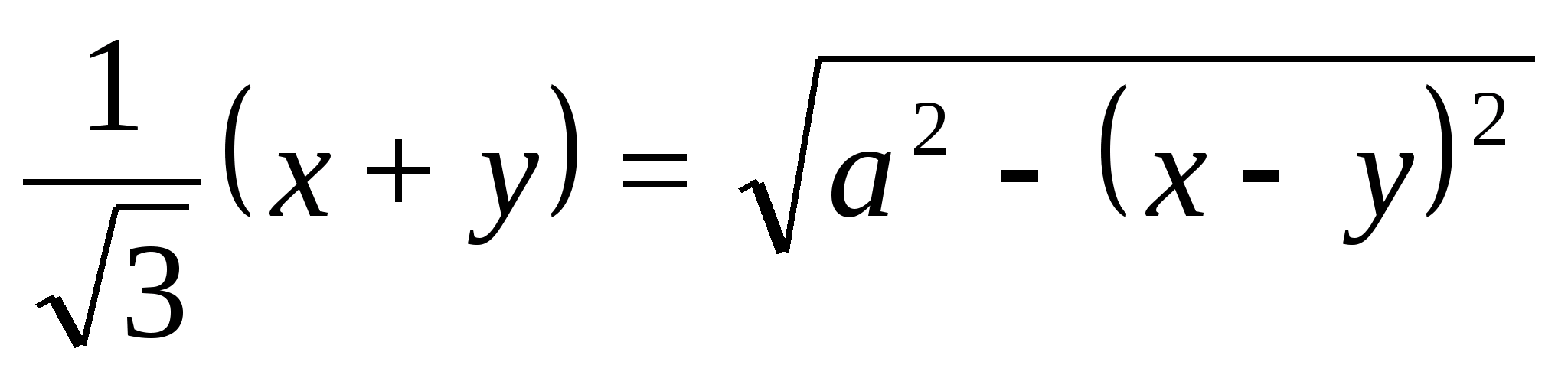
Решив систему
уравнений (1) и (2), получим, что стороны
оснований равны
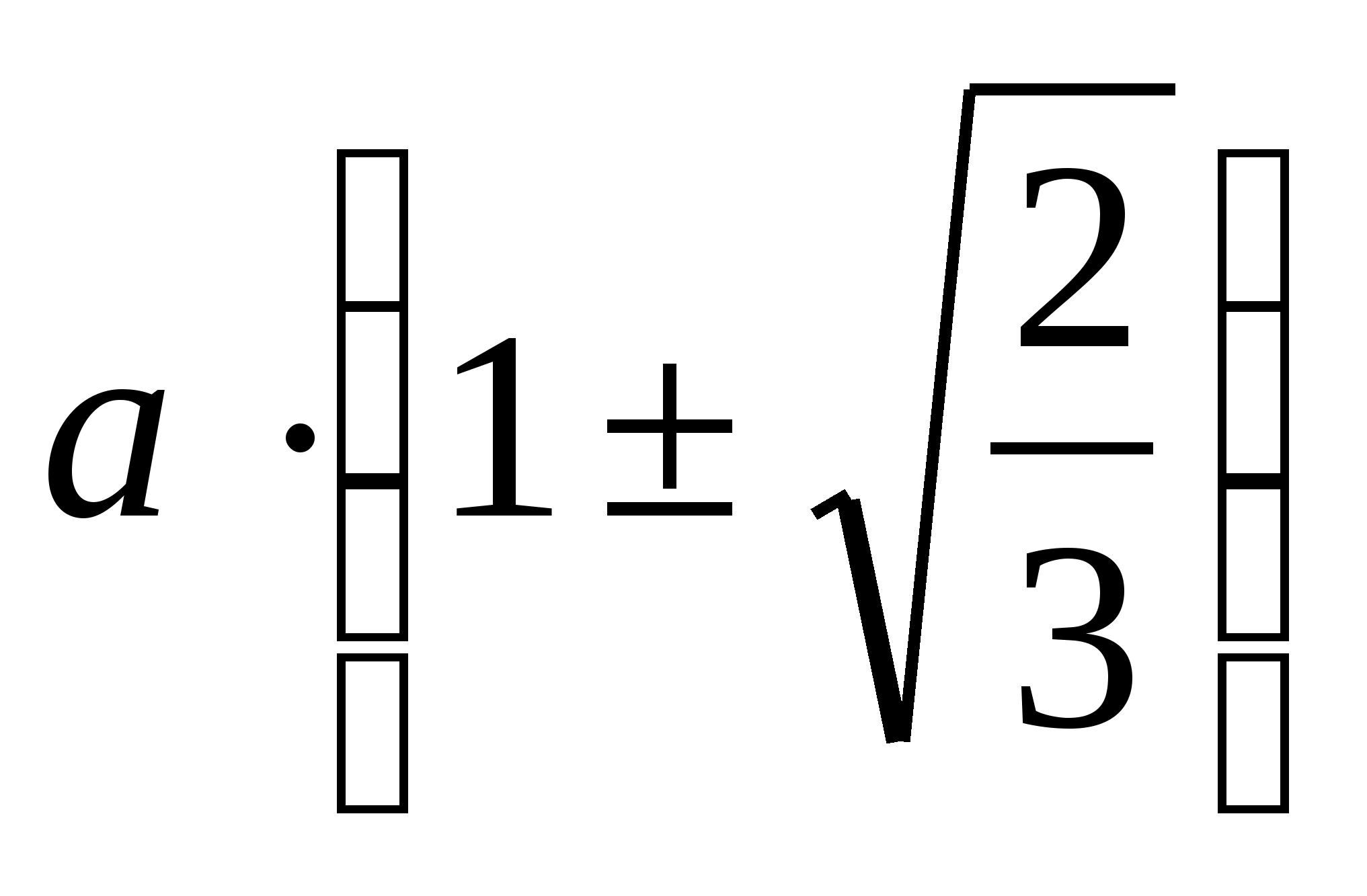
Задача 2.
Внутри правильного
тетраэдра с ребром a
расположены четыре равные сферы так,
что каждая сфера касается трех других
сфер и трех граней тетраэдра. Найти
радиус этих сфер.
Решение.
— данный тетраэдр,
— его высота,
— центры сфер,
— точка пересечения прямой
с плоскостью
Заметим, что центры равных сфер
касающихся плоскости
удалены от нее на равные расстояния,
каждое из которых равно радиусу шара
(обозначием его как x).
Значит плоскости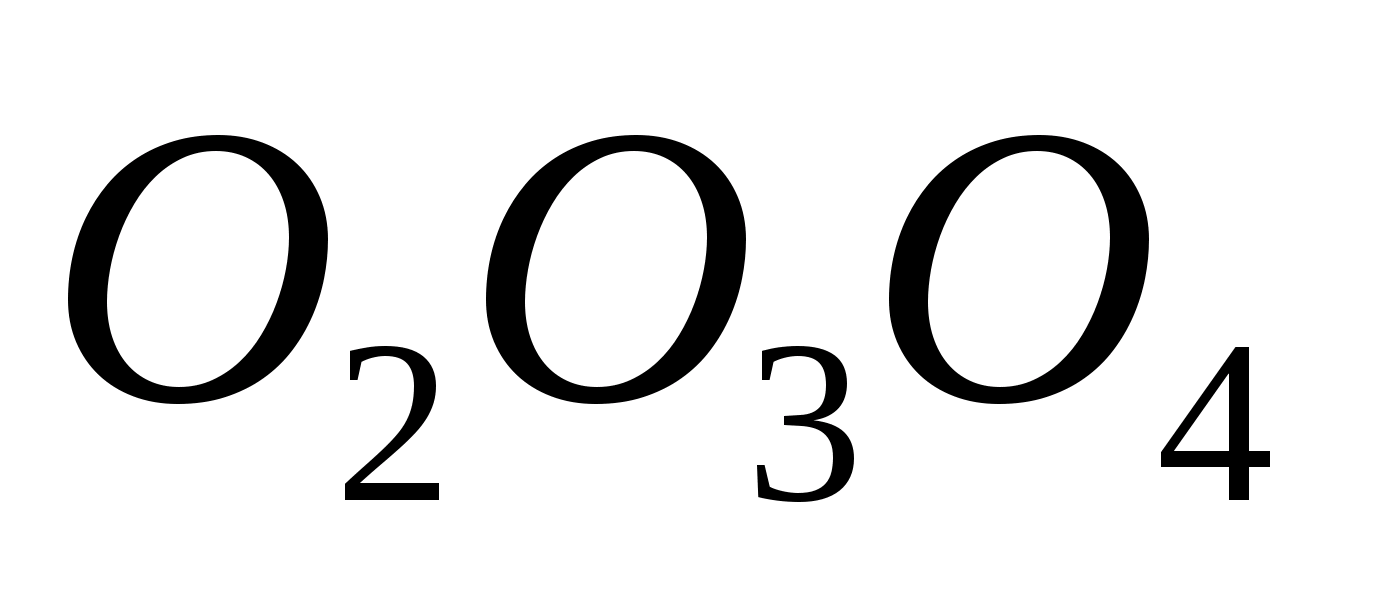
параллельны, а потому
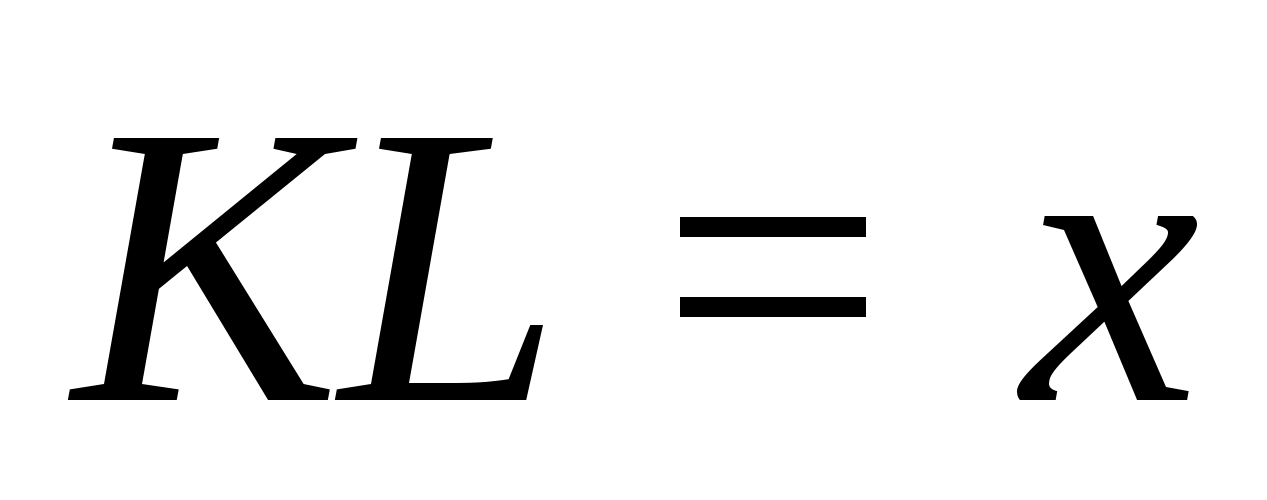
Далее, каждая пара
шаров касается между собой, а потому
расстояние между центрами равно сумме
их радиусов, то есть 2x.
Имеем:
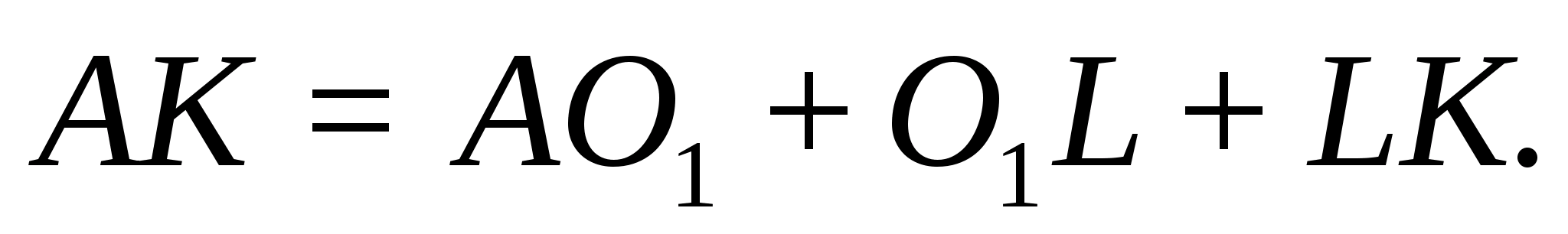
Но
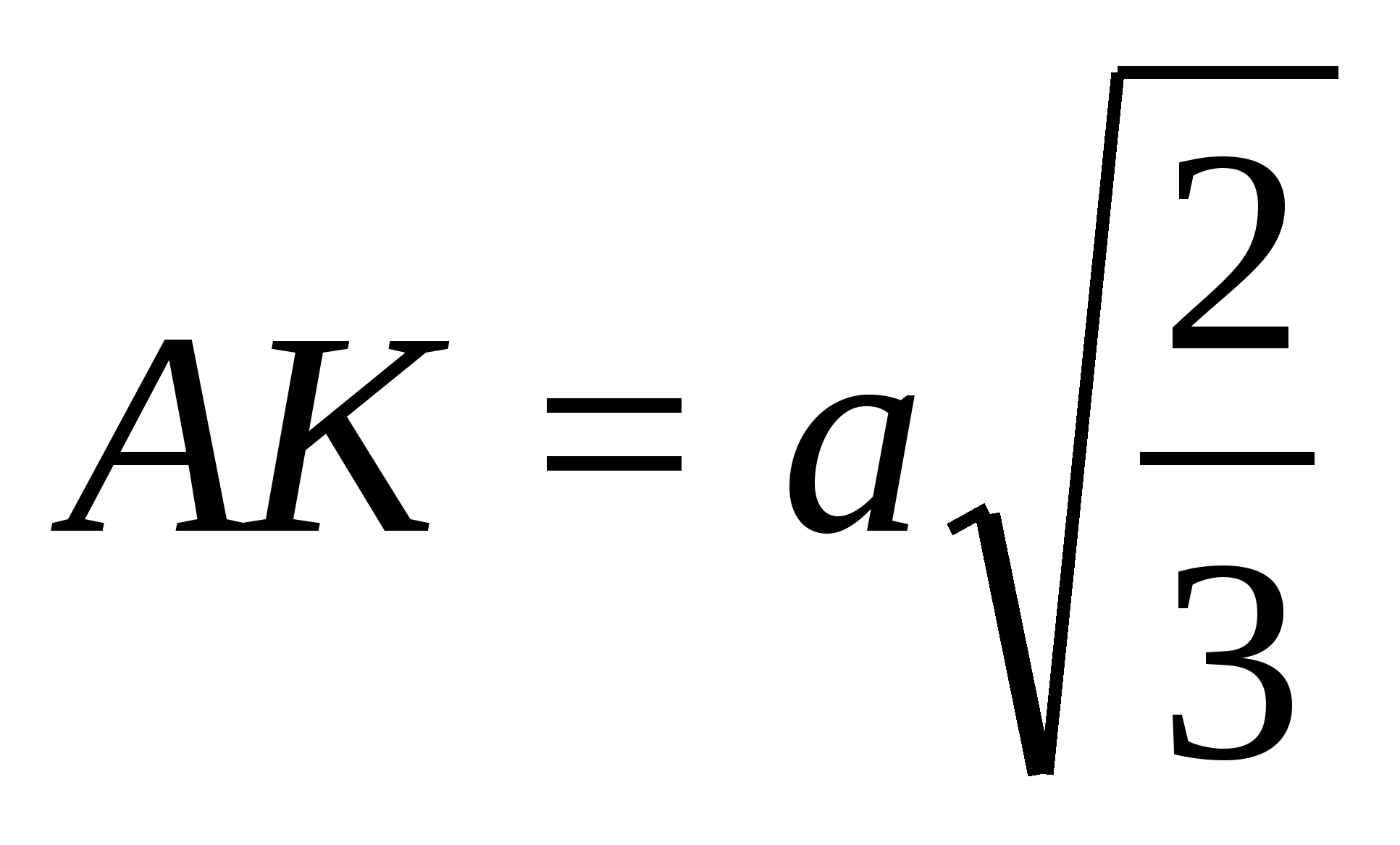
высота правильного тетраэдра с ребром
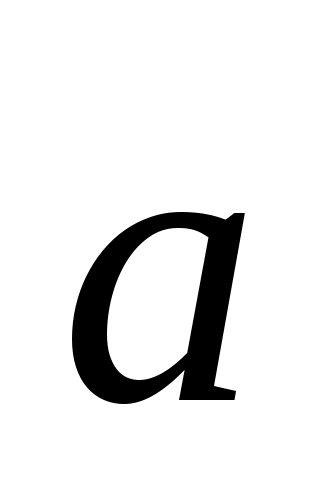
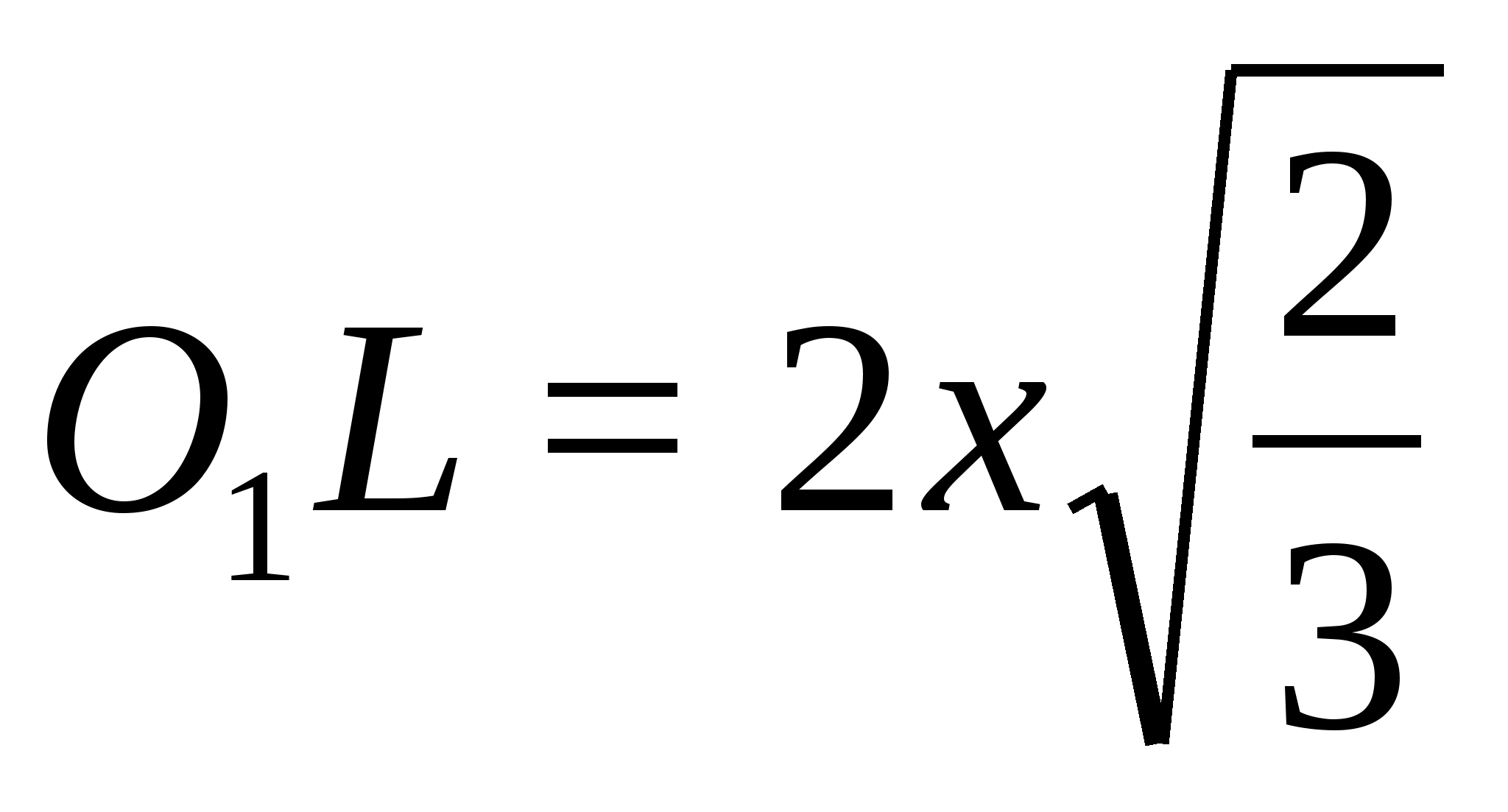
высота правильного тетраэдра с ребром
2x;
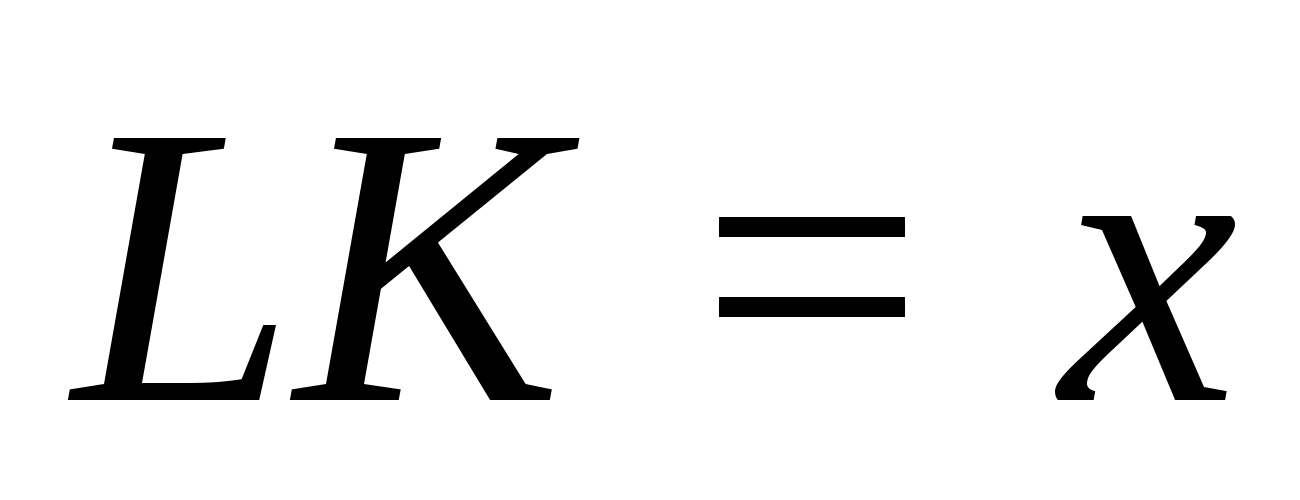
Осталось выразить
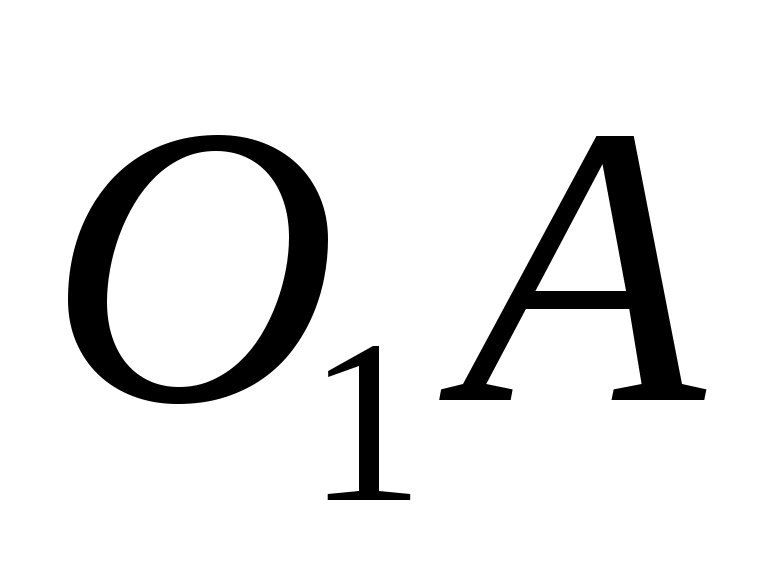
Заметим, что точка
находится внутри трехгранного угла и
удалена от его граней на расстояние
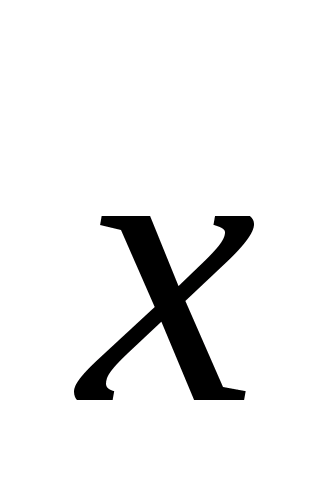
а плоские углы трехгранного угла равны

Не сложно получить то, что
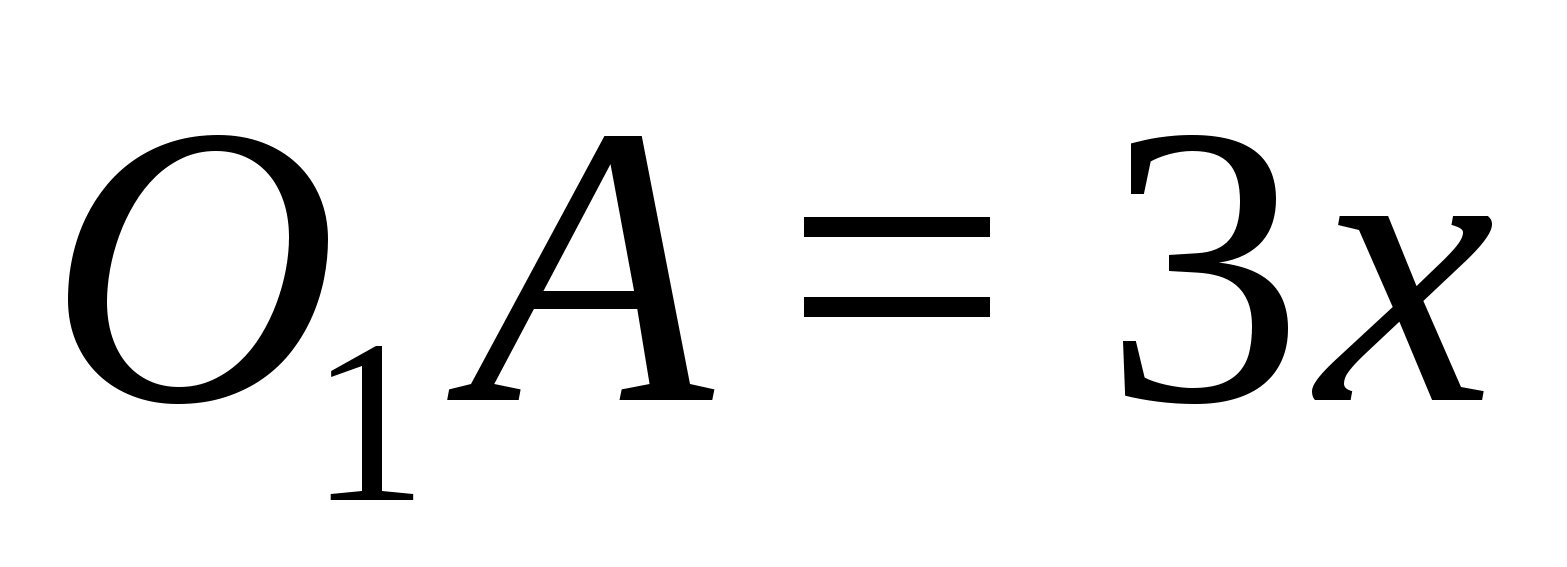
Приходим к уравнению:
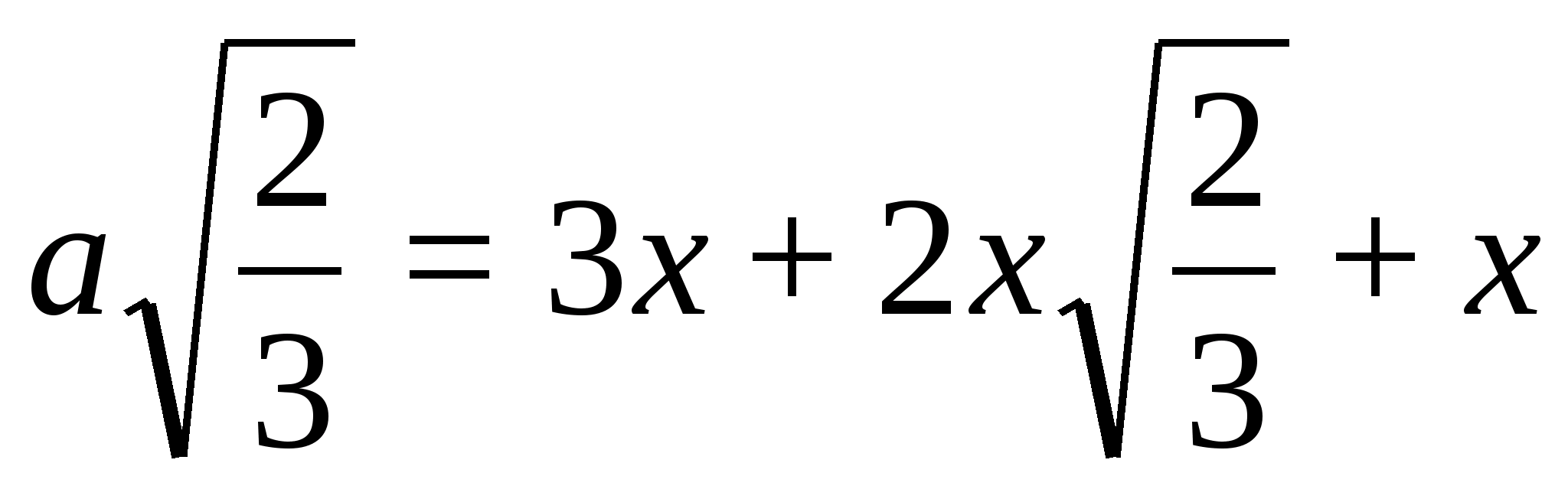
откуда после упрощений получаем
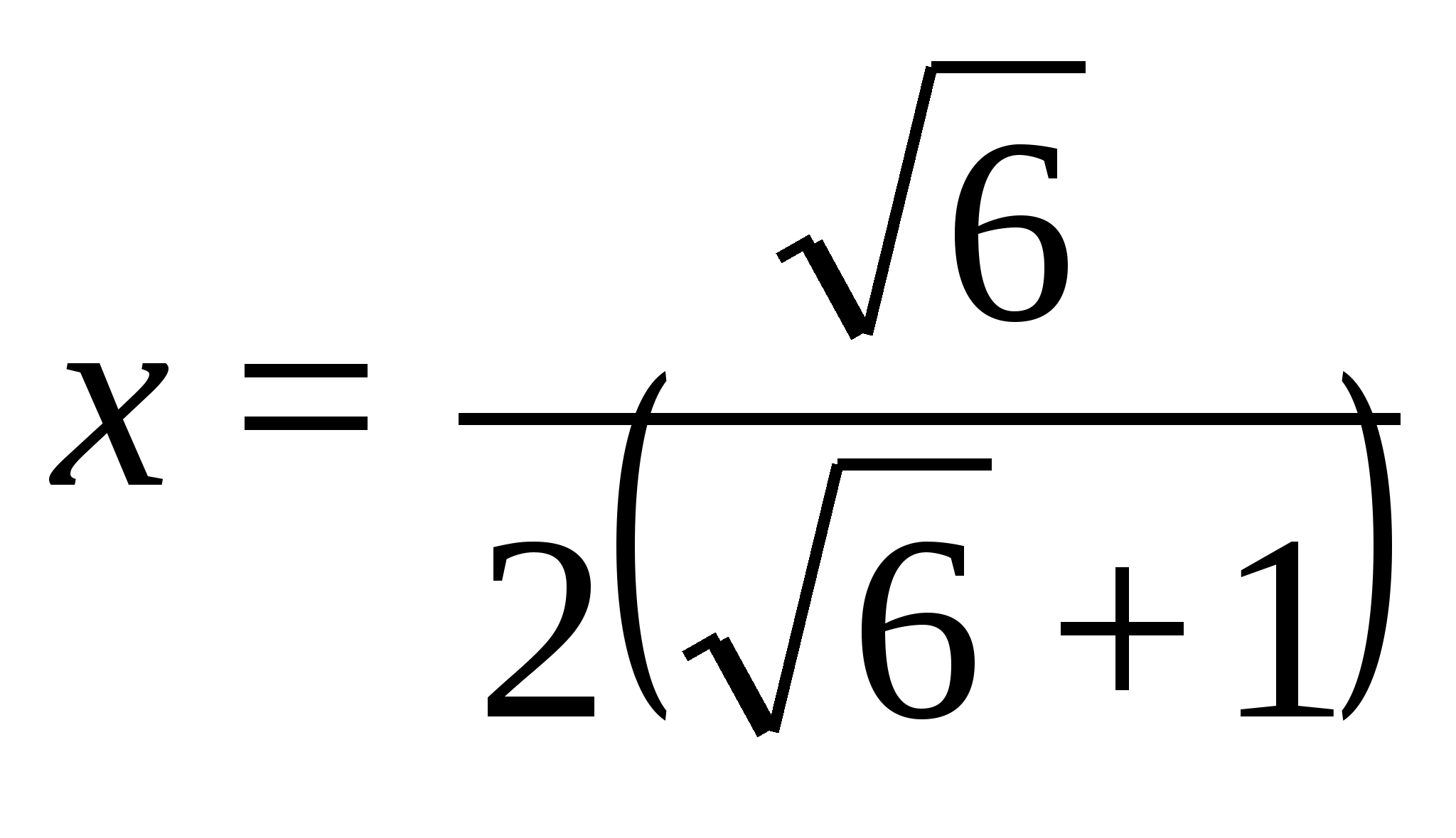
Изложение темы «Тетраэдр» в
учебнике «Геометрия» для 10-11 классов
Смирновой И.М.
Изложению темы «Тетраэдр» в
учебнике для 10-11 классов гуманитарного
профиля Смирновой И.М. посвящены
следующие занятия: 18,
19, 21, 22, 28-30, 35.
После изучения
теоремы о том, что «Всякий
выпуклый многогранник может быть
составлен из пирамид с общей вершиной,
основания которых образуют поверхность
многогранника» рассматривается теорема
Эйлера для некоторых таких многогранников,
в частности, выполнение условий теоремы
рассмотрено и для треугольной пирамиды,
которая, в сущности, и есть тетраэдр.
Учебник интересен
тем, что в нём рассматривается топология
и топологически правильные
многогранники(тетраэдр,
октаэдр, икосаэдр, куб, додекаэдр),
чье существование обосновывается при
помощи той же теоремы Эйлера.
Помимо этого в
учебнике приведено определение понятия
«правильная пирамида»; рассматриваются
теоремы о существовании вписанной и
описанной сфер тетраэдра, некоторые
свойства симметрии, касающиеся тетраэдра.
На заключительном занятии (35) приводится
формула нахождения объёма треугольной
пирамиды.
Для данного учебного
пособия характерен большой объем
иллюстративного и исторического
материала, а также небольшой объём
практического материала, обусловленный
направленностью учебника. Рассмотрим
также учебник Смирновой И.М. и др. для
10-11 классов естественно-научного профиля.
Изложение темы «Тетраэдр» в
учебнике «Геометрия» для 10-11 классов
Смирновой И.М. и др.
От предыдущего учебного пособия
данное отличается компоновкой тем и
уровнем сложности предлагаемых к решению
задач. Отличительной особенностью
изложения материала является деление
его на «семестры», которых в учебнике
четыре. Тетраэдр упоминается в самом
первом параграфе («Введение в стереометрию»)
, понятие «пирамида» определяется в §3.
Как и в предыдущем учебнике
практический материал дополнен заданиями
с развёрткой стереометрических фигур.
В материале §26 можно найти теорему о
сфере, вписанной в тетраэдр. Остальной
теоретический материал, касающийся
тетраэдра, фактически совпадает с
материалами учебника, охарактеризованного
выше.
Решение задач.
Задача 1.
Найдите кратчайший
путь по поверхности правильного тетраэдра
ABCD
соединяющий
точки E
и F,
расположенные на высотах боковых граней
в 7 см от соответствующих вершин тетраэдра.
Ребро тетраэдра равно 20 см.
Решение.
Рассмотрим развертку
трех граней тетраэдра. Кратчайшим путем
будет отрезок, соединяющий точки E
и F.
Его длина равна
20 см.
Задача 2.
В основании пирамиды
лежит прямоугольный треугольник, один
из катетов которого равен 3 см, а прилежащий
к нему острый угол равен 30 градусам. Все
боковые ребра пирамиды наклонены к
плоскости основания под углом в 60
градусов. Найдите объем пирамиды.
Решение.
Площадь треугольника
ABC равна
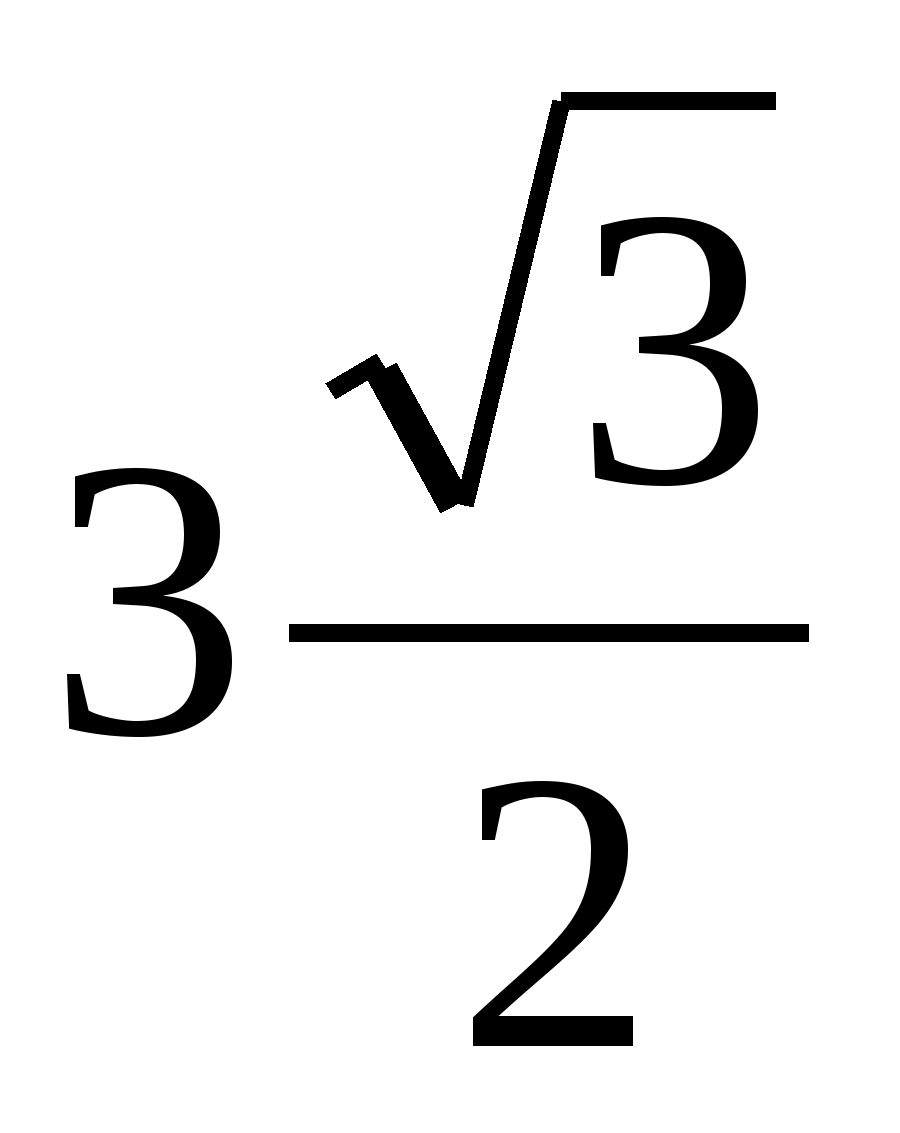
Основанием высоты
служит середина
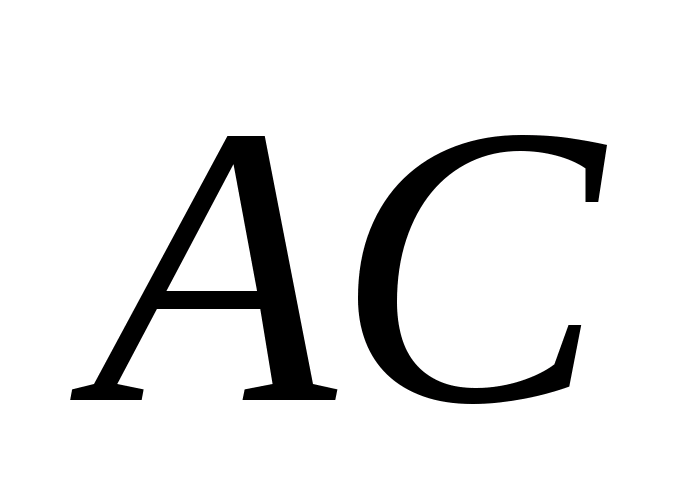
Треугольник SAC — равносторонний.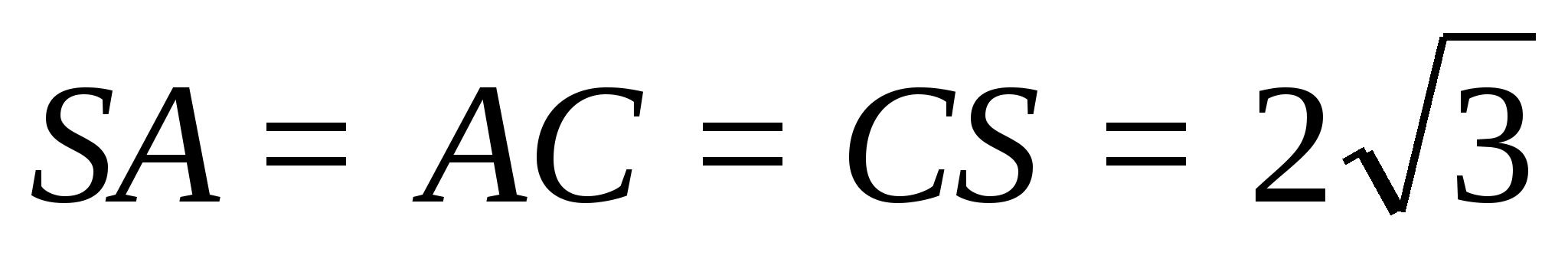
Отсюда
и, следовательно,
объем пирамиды равен
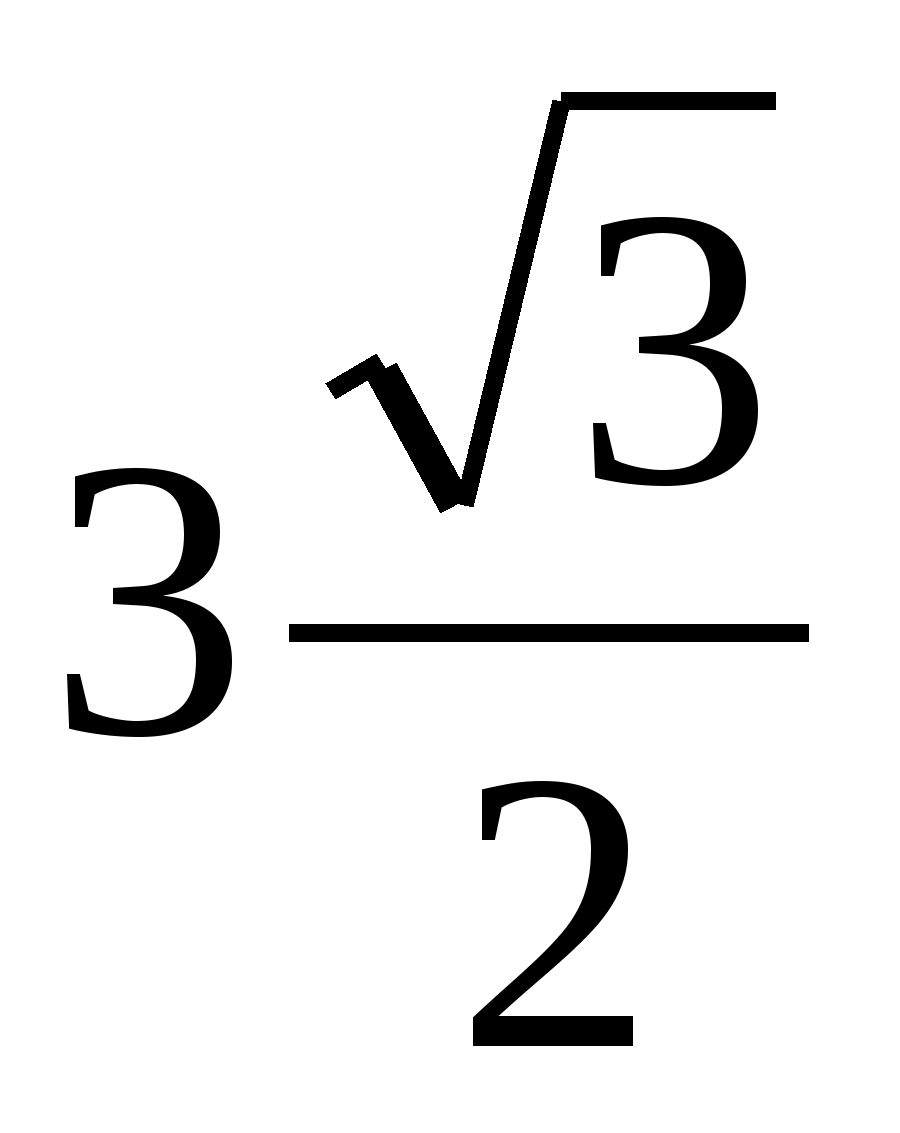
Вывод.
Отличительной
особенностью учебника Атанасяна Л.С. и
др. является то, что изучение тетраэдра
начинается достаточно рано, материал
разбросан по всему курсу и представлен
в различных уровнях сложности. В учебнике
Погорелова А.В. материал расположен
компактно, понятие «тетраэдр» как и
понятия других пространственных фигур,
вводится достаточно поздно (в конце 10
класса), практический материал,
представленный в учебнике, небольшого
объема. В учебнике Смирновой И.М. и др.
теоретический материал, как и практический
имеет небольшой объем, практический
задания низкого уровня сложности,
учебник отличается большим объём
материала из истории математики. В
учебнике Александрова А.Д. и др. уровень
сложности материала выше, сам материал
разнообразнее, множество практических
заданий содержит некоторую часть теории,
имеются экстремальные задачи и задачи
в виде вопросов, что выгодно выделяет
его на фоне остальных.
§2. Тестирование уровня развития
пространственного мышления у учеников
средней школы
Интеллект — это способность к
обучению или пониманию, которая присуща
всем людям. Одни люди обладают ею в
большей степени, другие — в меньшей,
однако у каждого человека в течение
жизни эта способность сохраняется
практически без изменений. Именно
благодаря интеллекту мы способны
правильно действовать и учиться на
своих ошибках.
В психологии интеллект определяется,
как способность воспринимать знания и
использовать их в других, принципиально
новых ситуациях. В условиях тестирования
можно определить, насколько успешно
адаптируется человек к необычным
ситуациям. Определение уровня общего
интеллектуального развития посредством
теста – довольно трудная и ёмкая по
времени работа, поэтому в тексте данной
работы будет использоваться часть
методики тестирования интеллекта,
отвечающая на вопрос об уровне развития
пространственного мышления. Пространственное
мышление – это
специфический вид мыслительной
деятельности, которая имеет место в
решении задач, требующих ориентации в
практическом и теоретическом пространстве
(как видимом, так и воображённом). В
своих наиболее развитых формах это
мышление образцами, в которых фиксируются
пространственные свойства и отношения.
Оперируя исходными образами, созданными
на различной наглядной основе, мышление
обеспечивает их видоизменение,
трансформацию и создание новых образов,
отличных от исходных.
Используемый тест («Мини-тест
уровня развития пространственного
мышления» из «Первого теста на коэффициент
развития интеллекта» Ф. Картера, К.
Рассела) универсален для всех возрастных
групп и занимает малый объём времени
(30 минут). Текст теста и его ключи можно
найти в «Приложении №1» к диплому.
| Regular tetrahedron | |
|---|---|
 (Click here for rotating model) |
|
| Type | Platonic solid |
| Elements | F = 4, E = 6 V = 4 (χ = 2) |
| Faces by sides | 4{3} |
| Conway notation | T |
| Schläfli symbols | {3,3} |
| h{4,3}, s{2,4}, sr{2,2} | |
| Face configuration | V3.3.3 |
| Wythoff symbol | 3 | 2 3 | 2 2 2 |
| Coxeter diagram | |
| Symmetry | Td, A3, [3,3], (*332) |
| Rotation group | T, [3,3]+, (332) |
| References | U01, C15, W1 |
| Properties | regular, convexdeltahedron |
| Dihedral angle | 70.528779° = arccos(1⁄3) |
 3.3.3 (Vertex figure) |
 Self-dual (dual polyhedron) |
 Net |
3D model of regular tetrahedron.
In geometry, a tetrahedron (plural: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertex corners. The tetrahedron is the simplest of all the ordinary convex polyhedra.[1]
The tetrahedron is the three-dimensional case of the more general concept of a Euclidean simplex, and may thus also be called a 3-simplex.
The tetrahedron is one kind of pyramid, which is a polyhedron with a flat polygon base and triangular faces connecting the base to a common point. In the case of a tetrahedron the base is a triangle (any of the four faces can be considered the base), so a tetrahedron is also known as a «triangular pyramid».
Like all convex polyhedra, a tetrahedron can be folded from a single sheet of paper. It has two such nets.[1]
For any tetrahedron there exists a sphere (called the circumsphere) on which all four vertices lie, and another sphere (the insphere) tangent to the tetrahedron’s faces.[2]
Regular tetrahedron[edit]
A regular tetrahedron is a tetrahedron in which all four faces are equilateral triangles. It is one of the five regular Platonic solids, which have been known since antiquity.
In a regular tetrahedron, all faces are the same size and shape (congruent) and all edges are the same length.
Five tetrahedra are laid flat on a plane, with the highest 3-dimensional points marked as 1, 2, 3, 4, and 5. These points are then attached to each other and a thin volume of empty space is left, where the five edge angles do not quite meet.
Regular tetrahedra alone do not tessellate (fill space), but if alternated with regular octahedra in the ratio of two tetrahedra to one octahedron, they form the alternated cubic honeycomb, which is a tessellation. Some tetrahedra that are not regular, including the Schläfli orthoscheme and the Hill tetrahedron, can tessellate.
The regular tetrahedron is self-dual, which means that its dual is another regular tetrahedron. The compound figure comprising two such dual tetrahedra form a stellated octahedron or stella octangula.
Coordinates for a regular tetrahedron[edit]
The following Cartesian coordinates define the four vertices of a tetrahedron with edge length 2, centered at the origin, and two level edges:
Expressed symmetrically as 4 points on the unit sphere, centroid at the origin, with lower face parallel to the 




with the edge length of 
Still another set of coordinates are based on an alternated cube or demicube with edge length 2. This form has Coxeter diagram and Schläfli symbol h{4,3}. The tetrahedron in this case has edge length 2√2. Inverting these coordinates generates the dual tetrahedron, and the pair together form the stellated octahedron, whose vertices are those of the original cube.
- Tetrahedron: (1,1,1), (1,−1,−1), (−1,1,−1), (−1,−1,1)
- Dual tetrahedron: (−1,−1,−1), (−1,1,1), (1,−1,1), (1,1,−1)
Regular tetrahedron ABCD and its circumscribed sphere
Angles and distances[edit]
For a regular tetrahedron of edge length a:
| Face area | 
|
| Surface area[3] | 
|
| Height of pyramid[4] | 
|
| Centroid to vertex distance | 
|
| Edge to opposite edge distance | 
|
| Volume[3] | 
|
| Face-vertex-edge angle |  (approx. 54.7356°) |
| Face-edge-face angle, i.e., «dihedral angle»[3] |  (approx. 70.5288°) |
| Vertex-Center-Vertex angle,[5] the angle between lines from the tetrahedron center to any two vertices. It is also the angle between Plateau borders at a vertex. In chemistry it is called the tetrahedral bond angle. This angle (in radians) is also the length of the circular arc on the unit sphere resulting from centrally projecting one edge of the tetrahedron to the sphere. |  (approx. 109.4712°) |
| Solid angle at a vertex subtended by a face |  (approx. 0.55129 steradians) (approx. 1809.8 square degrees) |
| Radius of circumsphere[3] | 
|
| Radius of insphere that is tangent to faces[3] | 
|
| Radius of midsphere that is tangent to edges[3] | 
|
| Radius of exspheres | 
|
| Distance to exsphere center from the opposite vertex | 
|
With respect to the base plane the slope of a face (2√2) is twice that of an edge (√2), corresponding to the fact that the horizontal distance covered from the base to the apex along an edge is twice that along the median of a face. In other words, if C is the centroid of the base, the distance from C to a vertex of the base is twice that from C to the midpoint of an edge of the base. This follows from the fact that the medians of a triangle intersect at its centroid, and this point divides each of them in two segments, one of which is twice as long as the other (see proof).
For a regular tetrahedron with side length a, radius R of its circumscribing sphere, and distances di from an arbitrary point in 3-space to its four vertices, we have[6]
Isometries of the regular tetrahedron[edit]
The proper rotations, (order-3 rotation on a vertex and face, and order-2 on two edges) and reflection plane (through two faces and one edge) in the symmetry group of the regular tetrahedron
The vertices of a cube can be grouped into two groups of four, each forming a regular tetrahedron (see above, and also animation, showing one of the two tetrahedra in the cube). The symmetries of a regular tetrahedron correspond to half of those of a cube: those that map the tetrahedra to themselves, and not to each other.
The tetrahedron is the only Platonic solid that is not mapped to itself by point inversion.
The regular tetrahedron has 24 isometries, forming the symmetry group Td, [3,3], (*332), isomorphic to the symmetric group, S4. They can be categorized as follows:
- T, [3,3]+, (332) is isomorphic to alternating group, A4 (the identity and 11 proper rotations) with the following conjugacy classes (in parentheses are given the permutations of the vertices, or correspondingly, the faces, and the unit quaternion representation):
- identity (identity; 1)
- rotation about an axis through a vertex, perpendicular to the opposite plane, by an angle of ±120°: 4 axes, 2 per axis, together 8 ((1 2 3), etc.; 1 ± i ± j ± k/2)
- rotation by an angle of 180° such that an edge maps to the opposite edge: 3 ((1 2)(3 4), etc.; i, j, k)
- reflections in a plane perpendicular to an edge: 6
- reflections in a plane combined with 90° rotation about an axis perpendicular to the plane: 3 axes, 2 per axis, together 6; equivalently, they are 90° rotations combined with inversion (x is mapped to −x): the rotations correspond to those of the cube about face-to-face axes
Orthogonal projections of the regular tetrahedron[edit]
The regular tetrahedron has two special orthogonal projections, one centered on a vertex or equivalently on a face, and one centered on an edge. The first corresponds to the A2 Coxeter plane.
| Centered by | Face/vertex | Edge |
|---|---|---|
| Image | 
|

|
| Projective symmetry |
[3] | [4] |
Cross section of regular tetrahedron[edit]
A central cross section of a regular tetrahedron is a square.
The two skew perpendicular opposite edges of a regular tetrahedron define a set of parallel planes. When one of these planes intersects the tetrahedron the resulting cross section is a rectangle.[7] When the intersecting plane is near one of the edges the rectangle is long and skinny. When halfway between the two edges the intersection is a square. The aspect ratio of the rectangle reverses as you pass this halfway point. For the midpoint square intersection the resulting boundary line traverses every face of the tetrahedron similarly. If the tetrahedron is bisected on this plane, both halves become wedges.
A tetragonal disphenoid viewed orthogonally to the two green edges.
This property also applies for tetragonal disphenoids when applied to the two special edge pairs.
Spherical tiling[edit]
The tetrahedron can also be represented as a spherical tiling, and projected onto the plane via a stereographic projection. This projection is conformal, preserving angles but not areas or lengths. Straight lines on the sphere are projected as circular arcs on the plane.

|

|
| Orthographic projection | Stereographic projection |
|---|
Helical stacking[edit]
Regular tetrahedra can be stacked face-to-face in a chiral aperiodic chain called the Boerdijk–Coxeter helix.
In four dimensions, all the convex regular 4-polytopes with tetrahedral cells (the 5-cell, 16-cell and 600-cell) can be constructed as tilings of the 3-sphere by these chains, which become periodic in the three-dimensional space of the 4-polytope’s boundary surface.
Irregular tetrahedra[edit]
Tetrahedra which do not have four equilateral faces are categorized and named by the symmetries they do possess.
If all three pairs of opposite edges of a tetrahedron are perpendicular, then it is called an orthocentric tetrahedron. When only one pair of opposite edges are perpendicular, it is called a semi-orthocentric tetrahedron.
An isodynamic tetrahedron is one in which the cevians that join the vertices to the incenters of the opposite faces are concurrent.
An isogonic tetrahedron has concurrent cevians that join the vertices to the points of contact of the opposite faces with the inscribed sphere of the tetrahedron.
Trirectangular tetrahedron[edit]
Kepler’s drawing of a regular tetrahedron inscribed in a cube, and one of the four trirectangular tetrahedra that surround it, filling the cube.
In a trirectangular tetrahedron the three face angles at one vertex are right angles, as at the corner of a cube.
Kepler discovered the relationship between the cube, regular tetrahedron and trirectangular tetrahedron.[8]
Disphenoid[edit]
A space-filling tetrahedral disphenoid inside a cube. Two edges have dihedral angles of 90°, and four edges have dihedral angles of 60°.
A disphenoid is a tetrahedron with four congruent triangles as faces; the triangles necessarily have all angles acute. The regular tetrahedron is a special case of a disphenoid. Other names for the same shape include bisphenoid, isosceles tetrahedron and equifacial tetrahedron.
Orthoschemes[edit]
A cube dissected into six characteristic orthoschemes.
A 3-orthoscheme is a tetrahedron where all four faces are right triangles.[a] An orthoscheme is an irregular simplex that is the convex hull of a tree in which all edges are mutually perpendicular. In a 3-dimensional orthoscheme, the tree consists of three perpendicular edges connecting all four vertices in a linear path that makes two right-angled turns. The 3-orthoscheme is a tetrahedron having two right angles at each of two vertices, so another name for it is birectangular tetrahedron. It is also called a quadrirectangular tetrahedron because it contains four right angles.[9]
Coxeter also calls quadrirectangular tetrahedra characteristic tetrahedra, because of their integral relationship to the regular polytopes and their symmetry groups.[10] For example, the special case of a 3-orthoscheme with equal-length perpendicular edges is characteristic of the cube, which means that the cube can be subdivided into instances of this orthoscheme. If its three perpendicular edges are of unit length, its remaining edges are two of length √2 and one of length √3, so all its edges are edges or diagonals of the cube. The cube can be dissected into six such 3-orthoschemes
four different ways, with all six surrounding the same √3 cube diagonal. The cube can also be dissected into 48 smaller instances of this same characteristic 3-orthoscheme (just one way, by all of its symmetry planes at once).[b] The characteristic tetrahedron of the cube is an example of a Heronian tetrahedron.
Every regular polytope, including the regular tetrahedron, has its characteristic orthoscheme.[c] There is a 3-orthoscheme which is the characteristic tetrahedron of the regular tetrahedron. The regular tetrahedron is subdivided into 24 instances of its characteristic tetrahedron
by its planes of symmetry.[d]
| Characteristics of the regular tetrahedron[13] | |||||
|---|---|---|---|---|---|
| edge | arc | dihedral | |||
| 𝒍 | 
|
109°28′16″ | 
|
70°31′44″ | 
|
| 𝟀 | 
|
70°31′44″ | 
|
60° | 
|
| 𝝓 | 
|
54°44′8″ | 
|
60° | 
|
| 𝟁 | 
|
54°44′8″ | 
|
60° | 
|

|

|
||||

|

|
||||

|

|
||||

|
35°15′52″ | 
|
If the regular tetrahedron has edge length 𝒍 = 2, its characteristic tetrahedron’s six edges have lengths 

















Space-filling tetrahedra[edit]
A space-filling tetrahedron packs with directly congruent or enantiomorphous (mirror image) copies of itself to tile space.[14] The cube can be dissected into six 3-orthoschemes, three left-handed and three right-handed (one of each at each cube face), and cubes can fill space, so the characteristic 3-orthoscheme of the cube is a space-filling tetrahedron in this sense.[e] A disphenoid can be a space-filling tetrahedron in the directly congruent sense, as in the disphenoid tetrahedral honeycomb. Regular tetrahedra, however, cannot fill space by themselves.[f]
Fundamental domains[edit]
For Euclidean 3-space, there are 3 simple and related Goursat tetrahedra. They can be seen as points on and within a cube.
An irregular tetrahedron which is the fundamental domain[15] of a symmetry group is an example of a Goursat tetrahedron. The Goursat tetrahedra generate all the regular polyhedra (and many other uniform polyhedra) by mirror reflections, a process referred to as Wythoff’s kaleidoscopic construction.
For polyhedra, Wythoff’s construction arranges three mirrors at angles to each other, as in a kaleidoscope. Unlike a cylindrical kaleidoscope, Wythoff’s mirrors are located at three faces of a Goursat tetrahedron such that all three mirrors intersect at a single point.[g]
Among the Goursat tetrahedra which generate 3-dimensional honeycombs we can recognize an orthoscheme (the characteristic tetrahedron of the cube), a double orthoscheme (the characteristic tetrahedron of the cube face-bonded to its mirror image), and the space-filling disphenoid illustrated above.[10] The disphenoid is the double orthoscheme face-bonded to its mirror image (a quadruple orthoscheme). Thus all three of these Goursat tetrahedra, and all the polyhedra they generate by reflections, can be dissected into characteristic tetrahedra of the cube.
Isometries of irregular tetrahedra[edit]
The isometries of an irregular (unmarked) tetrahedron depend on the geometry of the tetrahedron, with 7 cases possible. In each case a 3-dimensional point group is formed. Two other isometries (C3, [3]+), and (S4, [2+,4+]) can exist if the face or edge marking are included. Tetrahedral diagrams are included for each type below, with edges colored by isometric equivalence, and are gray colored for unique edges.
| Tetrahedron name | Edge equivalence diagram |
Description | |
|---|---|---|---|
| Symmetry | |||
| Schön. | Cox. | Orb. | Ord. |
| Regular tetrahedron | 
|
Four equilateral triangles It forms the symmetry group Td, isomorphic to the symmetric group, S4. A regular tetrahedron has Coxeter diagram |
|
| Td T |
[3,3] [3,3]+ |
*332 332 |
24 12 |
| Triangular pyramid | 
|
An equilateral triangle base and three equal isosceles triangle sides It gives 6 isometries, corresponding to the 6 isometries of the base. As permutations of the vertices, these 6 isometries are the identity 1, (123), (132), (12), (13) and (23), forming the symmetry group C3v, isomorphic to the symmetric group, S3. A triangular pyramid has Schläfli symbol {3}∨( ). |
|
| C3v C3 |
[3] [3]+ |
*33 33 |
6 3 |
| Mirrored sphenoid |
Two equal scalene triangles with a common base edge This has two pairs of equal edges (1,3), (1,4) and (2,3), (2,4) and otherwise no edges equal. The only two isometries are 1 and the reflection (34), giving the group Cs, also isomorphic to the cyclic group, Z2. |
||
| Cs =C1h =C1v |
[ ] | * | 2 |
| Irregular tetrahedron (No symmetry) |
Four unequal triangles Its only isometry is the identity, and the symmetry group is the trivial group. An irregular tetrahedron has Schläfli symbol ( )∨( )∨( )∨( ). |
||
| C1 | [ ]+ | 1 | 1 |
| Disphenoids (Four equal triangles) | |||
| Tetragonal disphenoid | 
|
Four equal isosceles triangles It has 8 isometries. If edges (1,2) and (3,4) are of different length to the other 4 then the 8 isometries are the identity 1, reflections (12) and (34), and 180° rotations (12)(34), (13)(24), (14)(23) and improper 90° rotations (1234) and (1432) forming the symmetry group D2d. A tetragonal disphenoid has Coxeter diagram |
|
| D2d S4 |
[2+,4] [2+,4+] |
2*2 2× |
8 4 |
| Rhombic disphenoid |
Four equal scalene triangles It has 4 isometries. The isometries are 1 and the 180° rotations (12)(34), (13)(24), (14)(23). This is the Klein four-group V4 or Z22, present as the point group D2. A rhombic disphenoid has Coxeter diagram |
||
| D2 | [2,2]+ | 222 | 4 |
| Generalized disphenoids (2 pairs of equal triangles) | |||
| Digonal disphenoid |  
|
Two pairs of equal isosceles triangles This gives two opposite edges (1,2) and (3,4) that are perpendicular but different lengths, and then the 4 isometries are 1, reflections (12) and (34) and the 180° rotation (12)(34). The symmetry group is C2v, isomorphic to the Klein four-group V4. A digonal disphenoid has Schläfli symbol { }∨{ }. |
|
| C2v C2 |
[2] [2]+ |
*22 22 |
4 2 |
| Phyllic disphenoid |
Two pairs of equal scalene or isosceles triangles This has two pairs of equal edges (1,3), (2,4) and (1,4), (2,3) but otherwise no edges equal. The only two isometries are 1 and the rotation (12)(34), giving the group C2 isomorphic to the cyclic group, Z2. |
||
| C2 | [2]+ | 22 | 2 |
General properties[edit]
Volume[edit]
The volume of a tetrahedron is given by the pyramid volume formula:
where A0 is the area of the base and h is the height from the base to the apex. This applies for each of the four choices of the base, so the distances from the apices to the opposite faces are inversely proportional to the areas of these faces.
For a tetrahedron with vertices
a = (a1, a2, a3),
b = (b1, b2, b3),
c = (c1, c2, c3), and
d = (d1, d2, d3), the volume is 1/6|det(a − d, b − d, c − d)|, or any other combination of pairs of vertices that form a simply connected graph. This can be rewritten using a dot product and a cross product, yielding
If the origin of the coordinate system is chosen to coincide with vertex d, then d = 0, so
where a, b, and c represent three edges that meet at one vertex, and a · (b × c) is a scalar triple product. Comparing this formula with that used to compute the volume of a parallelepiped, we conclude that the volume of a tetrahedron is equal to 1/6 of the volume of any parallelepiped that shares three converging edges with it.
The absolute value of the scalar triple product can be represented as the following absolute values of determinants:
or
where
are expressed as row or column vectors.
Hence
where
which gives
where α, β, γ are the plane angles occurring in vertex d. The angle α, is the angle between the two edges connecting the vertex d to the vertices b and c. The angle β, does so for the vertices a and c, while γ, is defined by the position of the vertices a and b.
If we do not require that d = 0 then
Given the distances between the vertices of a tetrahedron the volume can be computed using the Cayley–Menger determinant:
where the subscripts i, j ∈ {1, 2, 3, 4} represent the vertices {a, b, c, d} and dij is the pairwise distance between them – i.e., the length of the edge connecting the two vertices. A negative value of the determinant means that a tetrahedron cannot be constructed with the given distances. This formula, sometimes called Tartaglia’s formula, is essentially due to the painter Piero della Francesca in the 15th century, as a three dimensional analogue of the 1st century Heron’s formula for the area of a triangle.[16]
Let a, b, c be three edges that meet at a point, and x, y, z the opposite edges. Let V be the volume of the tetrahedron; then[17]
where
The above formula uses six lengths of edges, and the following formula uses three lengths of edges and three angles.
Heron-type formula for the volume of a tetrahedron[edit]
Six edge-lengths of Tetrahedron
If U, V, W, u, v, w are lengths of edges of the tetrahedron (first three form a triangle; with u opposite U, v opposite V, w opposite W), then[18]
where
Volume divider[edit]
Any plane containing a bimedian (connector of opposite edges’ midpoints) of a tetrahedron bisects the volume of the tetrahedron.[19]
Non-Euclidean volume[edit]
For tetrahedra in hyperbolic space or in three-dimensional elliptic geometry, the dihedral angles of the tetrahedron determine its shape and hence its volume. In these cases, the volume is given by the Murakami–Yano formula.[20] However, in Euclidean space, scaling a tetrahedron changes its volume but not its dihedral angles, so no such formula can exist.
Distance between the edges[edit]
Any two opposite edges of a tetrahedron lie on two skew lines, and the distance between the edges is defined as the distance between the two skew lines. Let d be the distance between the skew lines formed by opposite edges a and b − c as calculated here. Then another volume formula is given by
Properties analogous to those of a triangle[edit]
The tetrahedron has many properties analogous to those of a triangle, including an insphere, circumsphere, medial tetrahedron, and exspheres. It has respective centers such as incenter, circumcenter, excenters, Spieker center and points such as a centroid. However, there is generally no orthocenter in the sense of intersecting altitudes.[21]
Gaspard Monge found a center that exists in every tetrahedron, now known as the Monge point: the point where the six midplanes of a tetrahedron intersect. A midplane is defined as a plane that is orthogonal to an edge joining any two vertices that also contains the centroid of an opposite edge formed by joining the other two vertices. If the tetrahedron’s altitudes do intersect, then the Monge point and the orthocenter coincide to give the class of orthocentric tetrahedron.
An orthogonal line dropped from the Monge point to any face meets that face at the midpoint of the line segment between that face’s orthocenter and the foot of the altitude dropped from the opposite vertex.
A line segment joining a vertex of a tetrahedron with the centroid of the opposite face is called a median and a line segment joining the midpoints of two opposite edges is called a bimedian of the tetrahedron. Hence there are four medians and three bimedians in a tetrahedron. These seven line segments are all concurrent at a point called the centroid of the tetrahedron.[22] In addition the four medians are divided in a 3:1 ratio by the centroid (see Commandino’s theorem). The centroid of a tetrahedron is the midpoint between its Monge point and circumcenter. These points define the Euler line of the tetrahedron that is analogous to the Euler line of a triangle.
The nine-point circle of the general triangle has an analogue in the circumsphere of a tetrahedron’s medial tetrahedron. It is the twelve-point sphere and besides the centroids of the four faces of the reference tetrahedron, it passes through four substitute Euler points, one third of the way from the Monge point toward each of the four vertices. Finally it passes through the four base points of orthogonal lines dropped from each Euler point to the face not containing the vertex that generated the Euler point.[23]
The center T of the twelve-point sphere also lies on the Euler line. Unlike its triangular counterpart, this center lies one third of the way from the Monge point M towards the circumcenter. Also, an orthogonal line through T to a chosen face is coplanar with two other orthogonal lines to the same face. The first is an orthogonal line passing through the corresponding Euler point to the chosen face. The second is an orthogonal line passing through the centroid of the chosen face. This orthogonal line through the twelve-point center lies midway between the Euler point orthogonal line and the centroidal orthogonal line. Furthermore, for any face, the twelve-point center lies at the midpoint of the corresponding Euler point and the orthocenter for that face.
The radius of the twelve-point sphere is one third of the circumradius of the reference tetrahedron.
There is a relation among the angles made by the faces of a general tetrahedron given by[24]
where αij is the angle between the faces i and j.
The geometric median of the vertex position coordinates of a tetrahedron and its isogonic center are associated, under circumstances analogous to those observed for a triangle. Lorenz Lindelöf found that, corresponding to any given tetrahedron is a point now known as an isogonic center, O, at which the solid angles subtended by the faces are equal, having a common value of π sr, and at which the angles subtended by opposite edges are equal.[25] A solid angle of π sr is one quarter of that subtended by all of space. When all the solid angles at the vertices of a tetrahedron are smaller than π sr, O lies inside the tetrahedron, and because the sum of distances from O to the vertices is a minimum, O coincides with the geometric median, M, of the vertices. In the event that the solid angle at one of the vertices, v, measures exactly π sr, then O and M coincide with v. If however, a tetrahedron has a vertex, v, with solid angle greater than π sr, M still corresponds to v, but O lies outside the tetrahedron.
Geometric relations[edit]
A tetrahedron is a 3-simplex. Unlike the case of the other Platonic solids, all the vertices of a regular tetrahedron are equidistant from each other (they are the only possible arrangement of four equidistant points in 3-dimensional space).
A tetrahedron is a triangular pyramid, and the regular tetrahedron is self-dual.
A regular tetrahedron can be embedded inside a cube in two ways such that each vertex is a vertex of the cube, and each edge is a diagonal of one of the cube’s faces. For one such embedding, the Cartesian coordinates of the vertices are
- (+1, +1, +1);
- (−1, −1, +1);
- (−1, +1, −1);
- (+1, −1, −1).
This yields a tetrahedron with edge-length 2√2, centered at the origin. For the other tetrahedron (which is dual to the first), reverse all the signs. These two tetrahedra’s vertices combined are the vertices of a cube, demonstrating that the regular tetrahedron is the 3-demicube.
The volume of this tetrahedron is one-third the volume of the cube. Combining both tetrahedra gives a regular polyhedral compound called the compound of two tetrahedra or stella octangula.
The interior of the stella octangula is an octahedron, and correspondingly, a regular octahedron is the result of cutting off, from a regular tetrahedron, four regular tetrahedra of half the linear size (i.e., rectifying the tetrahedron).
The above embedding divides the cube into five tetrahedra, one of which is regular. In fact, five is the minimum number of tetrahedra required to compose a cube. To see this, starting from a base tetrahedron with 4 vertices, each added tetrahedra adds at most 1 new vertex, so at least 4 more must be added to make a cube, which has 8 vertices.
Inscribing tetrahedra inside the regular compound of five cubes gives two more regular compounds, containing five and ten tetrahedra.
Regular tetrahedra cannot tessellate space by themselves, although this result seems likely enough that Aristotle claimed it was possible. However, two regular tetrahedra can be combined with an octahedron, giving a rhombohedron that can tile space as the tetrahedral-octahedral honeycomb.
However, several irregular tetrahedra are known, of which copies can tile space, for instance the characteristic orthoscheme of the cube and the disphenoid of the disphenoid tetrahedral honeycomb. The complete list remains an open problem.[26]
If one relaxes the requirement that the tetrahedra be all the same shape, one can tile space using only tetrahedra in many different ways. For example, one can divide an octahedron into four identical tetrahedra and combine them again with two regular ones. (As a side-note: these two kinds of tetrahedron have the same volume.)
The tetrahedron is unique among the uniform polyhedra in possessing no parallel faces.
A law of sines for tetrahedra and the space of all shapes of tetrahedra[edit]

A corollary of the usual law of sines is that in a tetrahedron with vertices O, A, B, C, we have
One may view the two sides of this identity as corresponding to clockwise and counterclockwise orientations of the surface.
Putting any of the four vertices in the role of O yields four such identities, but at most three of them are independent: If the «clockwise» sides of three of them are multiplied and the product is inferred to be equal to the product of the «counterclockwise» sides of the same three identities, and then common factors are cancelled from both sides, the result is the fourth identity.
Three angles are the angles of some triangle if and only if their sum is 180° (π radians). What condition on 12 angles is necessary and sufficient for them to be the 12 angles of some tetrahedron? Clearly the sum of the angles of any side of the tetrahedron must be 180°. Since there are four such triangles, there are four such constraints on sums of angles, and the number of degrees of freedom is thereby reduced from 12 to 8. The four relations given by this sine law further reduce the number of degrees of freedom, from 8 down to not 4 but 5, since the fourth constraint is not independent of the first three. Thus the space of all shapes of tetrahedra is 5-dimensional.[27]
Law of cosines for tetrahedra[edit]
Let {P1 ,P2, P3, P4} be the points of a tetrahedron. Let Δi be the area of the face opposite vertex Pi and let θij be the dihedral angle between the two faces of the tetrahedron adjacent to the edge PiPj.
The law of cosines for this tetrahedron,[28] which relates the areas of the faces of the tetrahedron to the dihedral angles about a vertex, is given by the following relation:
Interior point[edit]
Let P be any interior point of a tetrahedron of volume V for which the vertices are A, B, C, and D, and for which the areas of the opposite faces are Fa, Fb, Fc, and Fd. Then[29]: p.62, #1609
For vertices A, B, C, and D, interior point P, and feet J, K, L, and M of the perpendiculars from P to the faces, and suppose the faces have equal areas, then[29]: p.226, #215
Inradius[edit]
Denoting the inradius of a tetrahedron as r and the inradii of its triangular faces as ri for i = 1, 2, 3, 4, we have[29]: p.81, #1990
with equality if and only if the tetrahedron is regular.
If A1, A2, A3 and A4 denote the area of each faces, the value of r is given by
.
This formula is obtained from dividing the tetrahedron into four tetrahedra whose points are the three points of one of the original faces and the incenter. Since the four subtetrahedra fill the volume, we have 
Circumradius[edit]
Denote the circumradius of a tetrahedron as R. Let a, b, c be the lengths of the three edges that meet at a vertex, and A, B, C the length of the opposite edges. Let V be the volume of the tetrahedron. Then[30][31]
Circumcenter[edit]
The circumcenter of a tetrahedron can be found as intersection of three bisector planes. A bisector plane is defined as the plane centered on, and orthogonal to an edge of the tetrahedron.
With this definition, the circumcenter C of a tetrahedron with vertices x0,x1,x2,x3 can be formulated as matrix-vector product:[32]
In contrast to the centroid, the circumcenter may not always lay on the inside of a tetrahedron.
Analogously to an obtuse triangle, the circumcenter is outside of the object for an obtuse tetrahedron.
Centroid[edit]
The tetrahedron’s center of mass computes as the arithmetic mean of its four vertices, see Centroid.
Faces[edit]
The sum of the areas of any three faces is greater than the area of the fourth face.[29]: p.225, #159
Integer tetrahedra[edit]
There exist tetrahedra having integer-valued edge lengths, face areas and volume. These are called Heronian tetrahedra. One example has one edge of 896, the opposite edge of 990 and the other four edges of 1073; two faces are isosceles triangles with areas of 436800 and the other two are isosceles with areas of 47120, while the volume is 124185600.[33]
A tetrahedron can have integer volume and consecutive integers as edges, an example being the one with edges 6, 7, 8, 9, 10, and 11 and volume 48.[34]
Related polyhedra and compounds[edit]
A regular tetrahedron can be seen as a triangular pyramid.
| Regular pyramids | ||||||||
|---|---|---|---|---|---|---|---|---|
| Digonal | Triangular | Square | Pentagonal | Hexagonal | Heptagonal | Octagonal | Enneagonal | Decagonal… |
| Improper | Regular | Equilateral | Isosceles | |||||

|

|

|

|
|||||

|

|

|

|

|

|

|

|
A regular tetrahedron can be seen as a degenerate polyhedron, a uniform digonal antiprism, where base polygons are reduced digons.
| Antiprism name | Digonal antiprism | (Trigonal) Triangular antiprism |
(Tetragonal) Square antiprism |
Pentagonal antiprism | Hexagonal antiprism | Heptagonal antiprism | Octagonal antiprism | Enneagonal antiprism | Decagonal antiprism | Hendecagonal antiprism | Dodecagonal antiprism | … | Apeirogonal antiprism |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Polyhedron image | … | ||||||||||||
| Spherical tiling image | Plane tiling image | ||||||||||||
| Vertex config. | 2.3.3.3 | 3.3.3.3 | 4.3.3.3 | 5.3.3.3 | 6.3.3.3 | 7.3.3.3 | 8.3.3.3 | 9.3.3.3 | 10.3.3.3 | 11.3.3.3 | 12.3.3.3 | … | ∞.3.3.3 |
A regular tetrahedron can be seen as a degenerate polyhedron, a uniform dual digonal trapezohedron, containing 6 vertices, in two sets of colinear edges.
| Trapezohedron name | Digonal trapezohedron (Tetrahedron) |
Trigonal trapezohedron | Tetragonal trapezohedron | Pentagonal trapezohedron | Hexagonal trapezohedron | Heptagonal trapezohedron | Octagonal trapezohedron | Decagonal trapezohedron | Dodecagonal trapezohedron | … | Apeirogonal trapezohedron |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Polyhedron image | 
|

|

|

|

|

|

|

|
… | ||
| Spherical tiling image | 
|

|

|

|

|

|

|

|
Plane tiling image | ||
| Face configuration | V2.3.3.3 | V3.3.3.3 | V4.3.3.3 | V5.3.3.3 | V6.3.3.3 | V7.3.3.3 | V8.3.3.3 | V10.3.3.3 | V12.3.3.3 | … | V∞.3.3.3 |
A truncation process applied to the tetrahedron produces a series of uniform polyhedra. Truncating edges down to points produces the octahedron as a rectified tetrahedron. The process completes as a birectification, reducing the original faces down to points, and producing the self-dual tetrahedron once again.
| Family of uniform tetrahedral polyhedra | |||||||
|---|---|---|---|---|---|---|---|
| Symmetry: [3,3], (*332) | [3,3]+, (332) | ||||||

|

|

|

|
||||
| {3,3} | t{3,3} | r{3,3} | t{3,3} | {3,3} | rr{3,3} | tr{3,3} | sr{3,3} |
| Duals to uniform polyhedra | |||||||

|

|

|

|
||||
| V3.3.3 | V3.6.6 | V3.3.3.3 | V3.6.6 | V3.3.3 | V3.4.3.4 | V4.6.6 | V3.3.3.3.3 |
This polyhedron is topologically related as a part of sequence of regular polyhedra with Schläfli symbols {3,n}, continuing into the hyperbolic plane.
*n32 symmetry mutation of regular tilings: {3,n}
|
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Spherical | Euclid. | Compact hyper. | Paraco. | Noncompact hyperbolic | |||||||

|

|

|

|

|

|

|

|

|

|

|

|
| 3.3 | 33 | 34 | 35 | 36 | 37 | 38 | 3∞ | 312i | 39i | 36i | 33i |
The tetrahedron is topologically related to a series of regular polyhedra and tilings with order-3 vertex figures.
*n32 symmetry mutation of regular tilings: {n,3}
|
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Spherical | Euclidean | Compact hyperb. | Paraco. | Noncompact hyperbolic | |||||||

|

|

|

|

|

|

|

|

|

|

|

|
| {2,3} | {3,3} | {4,3} | {5,3} | {6,3} | {7,3} | {8,3} | {∞,3} | {12i,3} | {9i,3} | {6i,3} | {3i,3} |
- Compounds of tetrahedra
-
-
-
An interesting polyhedron can be constructed from five intersecting tetrahedra. This compound of five tetrahedra has been known for hundreds of years. It comes up regularly in the world of origami. Joining the twenty vertices would form a regular dodecahedron. There are both left-handed and right-handed forms, which are mirror images of each other. Superimposing both forms gives a compound of ten tetrahedra, in which the ten tetrahedra are arranged as five pairs of stellae octangulae. A stella octangula is a compound of two tetrahedra in dual position and its eight vertices define a cube as their convex hull.
The square hosohedron is another polyhedron with four faces, but it does not have triangular faces.
The Szilassi polyhedron and the tetrahedron are the only two known polyhedra in which each face shares an edge with each other face. Furthermore, the Császár polyhedron (itself is the dual of Szilassi polyhedron) and the tetrahedron are the only two known polyhedra in which every diagonal lies on the sides.
Applications[edit]
Numerical analysis[edit]
An irregular volume in space can be approximated by an irregular triangulated surface, and irregular tetrahedral volume elements.
In numerical analysis, complicated three-dimensional shapes are commonly broken down into, or approximated by, a polygonal mesh of irregular tetrahedra in the process of setting up the equations for finite element analysis especially in the numerical solution of partial differential equations. These methods have wide applications in practical applications in computational fluid dynamics, aerodynamics, electromagnetic fields, civil engineering, chemical engineering, naval architecture and engineering, and related fields.
Structural engineering[edit]
A tetrahedron having stiff edges is inherently rigid. For this reason it is often used to stiffen frame structures such as spaceframes.
Aviation[edit]
At some airfields, a large frame in the shape of a tetrahedron with two sides covered with a thin material is mounted on a rotating pivot and always points into the wind. It is built big enough to be seen from the air and is sometimes illuminated. Its purpose is to serve as a reference to pilots indicating wind direction.[35]
Chemistry[edit]
The tetrahedron shape is seen in nature in covalently bonded molecules. All sp3-hybridized atoms are surrounded by atoms (or lone electron pairs) at the four corners of a tetrahedron. For instance in a methane molecule (CH
4) or an ammonium ion (NH+
4), four hydrogen atoms surround a central carbon or nitrogen atom with tetrahedral symmetry. For this reason, one of the leading journals in organic chemistry is called Tetrahedron. The central angle between any two vertices of a perfect tetrahedron is arccos(−1/3), or approximately 109.47°.[5]
Water, H
2O, also has a tetrahedral structure, with two hydrogen atoms and two lone pairs of electrons around the central oxygen atoms. Its tetrahedral symmetry is not perfect, however, because the lone pairs repel more than the single O–H bonds.
Quaternary phase diagrams of mixtures of chemical substances are represented graphically as tetrahedra.
However, quaternary phase diagrams in communication engineering are represented graphically on a two-dimensional plane.
Electricity and electronics[edit]
If six equal resistors are soldered together to form a tetrahedron, then the resistance measured between any two vertices is half that of one resistor.[36][37]
Since silicon is the most common semiconductor used in solid-state electronics, and silicon has a valence of four, the tetrahedral shape of the four chemical bonds in silicon is a strong influence on how crystals of silicon form and what shapes they assume.
Color space[edit]
Tetrahedra are used in color space conversion algorithms specifically for cases in which the luminance axis diagonally segments the color space (e.g. RGB, CMY).[38]
Games[edit]
The Royal Game of Ur, dating from 2600 BC, was played with a set of tetrahedral dice.
Especially in roleplaying, this solid is known as a 4-sided die, one of the more common polyhedral dice, with the number rolled appearing around the bottom or on the top vertex. Some Rubik’s Cube-like puzzles are tetrahedral, such as the Pyraminx and Pyramorphix.
Geology[edit]
The tetrahedral hypothesis, originally published by William Lowthian Green to explain the formation of the Earth,[39] was popular through the early 20th century.[40][41]
Popular culture[edit]
Stanley Kubrick originally intended the monolith in 2001: A Space Odyssey to be a tetrahedron, according to Marvin Minsky, a cognitive scientist and expert on artificial intelligence who advised Kubrick on the HAL 9000 computer and other aspects of the movie. Kubrick scrapped the idea of using the tetrahedron as a visitor who saw footage of it did not recognize what it was and he did not want anything in the movie regular people did not understand.[42]
Tetrahedral graph[edit]
| Tetrahedral graph | |
|---|---|
 |
|
| Vertices | 4 |
| Edges | 6 |
| Radius | 1 |
| Diameter | 1 |
| Girth | 3 |
| Automorphisms | 24 |
| Chromatic number | 4 |
| Properties | Hamiltonian, regular, symmetric, distance-regular, distance-transitive, 3-vertex-connected, planar graph |
| Table of graphs and parameters |
The skeleton of the tetrahedron (comprising the vertices and edges) forms a graph, with 4 vertices, and 6 edges. It is a special case of the complete graph, K4, and wheel graph, W4.[43] It is one of 5 Platonic graphs, each a skeleton of its Platonic solid.
3-fold symmetry
See also[edit]
- Boerdijk–Coxeter helix
- Möbius configuration
- Caltrop
- Demihypercube and simplex – n-dimensional analogues
- Pentachoron – 4-dimensional analogue
- Synergetics (Fuller)
- Tetrahedral kite
- Tetrahedral number
- Tetrahedron packing
- Triangular dipyramid – constructed by joining two tetrahedra along one face
- Trirectangular tetrahedron
- Orthoscheme
Notes[edit]
- ^ A 3-orthoscheme is not a disphenoid, because its opposite edges are not of equal length. It is not possible to construct a disphenoid with right triangle or obtuse triangle faces.
- ^ For a regular k-polytope, the Coxeter-Dynkin diagram of the characteristic k-orthoscheme is the k-polytope’s diagram without the generating point ring. The regular k-polytope is subdivided by its symmetry (k-1)-elements into g instances of its characteristic k-orthoscheme that surround its center, where g is the order of the k-polytope’s symmetry group.[11]
- ^ A regular polytope of dimension k has a characteristic k-orthoscheme, and also a characteristic (k-1)-orthoscheme. A regular polyhedron has a characteristic tetrahedron (3-orthoscheme) into which it is subdivided by its planes of symmetry, and also a characteristic triangle (2-orthoscheme) into which its surface is subdivided by its faces’ lines of symmetry. After subdividing its surface into characteristic right triangles surrounding each face center, its interior can be subdivided into characteristic tetrahedra by adding radii joining the vertices of the surface right triangles to the polyhedron’s center.[12] The interior triangles thus formed will also be right triangles.
- ^ The 24 characteristic tetrahedra of the regular tetrahedron occur in two mirror-image forms, 12 of each.
- ^ The characteristic orthoscheme of the cube is one of the Hill tetrahedra, a family of space-filling tetrahedra. All space-filling tetrahedra are scissors-congruent to a cube. Every convex polyhedron is scissors-congruent to an orthoscheme. Every regular convex polyhedron (Platonic solid) can be dissected into some even number of instances of its characteristic orthoscheme.
- ^ The tetrahedral-octahedral honeycomb fills space with alternating regular tetrahedron cells and regular octahedron cells in a ratio of 2:1.
- ^ The Coxeter-Dynkin diagram of the generated polyhedron contains three nodes representing the three mirrors. The dihedral angle between each pair of mirrors is encoded in the diagram, as well as the location of a single generating point which is multiplied by mirror reflections into the vertices of the polyhedron. For a regular polyhedron, the Coxeter-Dynkin diagram of the generating characteristic orthoscheme is the generated polyhedron’s diagram without the generating point marking.
References[edit]
- ^ a b Weisstein, Eric W. «Tetrahedron». MathWorld.
- ^ Ford, Walter Burton; Ammerman, Charles (1913), Plane and Solid Geometry, Macmillan, pp. 294–295
- ^ a b c d e f Coxeter, Harold Scott MacDonald; Regular Polytopes, Methuen and Co., 1948, Table I(i)
- ^ Köller, Jürgen, «Tetrahedron», Mathematische Basteleien, 2001
- ^ a b Brittin, W. E. (1945). «Valence angle of the tetrahedral carbon atom». Journal of Chemical Education. 22 (3): 145. Bibcode:1945JChEd..22..145B. doi:10.1021/ed022p145.
- ^ Park, Poo-Sung. «Regular polytope distances», Forum Geometricorum 16, 2016, 227–232. http://forumgeom.fau.edu/FG2016volume16/FG201627.pdf
- ^ «Sections of a Tetrahedron».
- ^ Kepler 1619, p. 181.
- ^ Coxeter, H.S.M. (1989). «Trisecting an Orthoscheme». Computers Math. Applic. 17 (1–3): 59–71. doi:10.1016/0898-1221(89)90148-X.
- ^ a b Coxeter 1973, pp. 71–72, §4.7 Characteristic tetrahedra.
- ^ Coxeter 1973, pp. 130–133, §7.6 The symmetry group of the general regular polytope.
- ^ Coxeter 1973, p. 130, §7.6; «simplicial subdivision».
- ^ Coxeter 1973, pp. 292–293, Table I(i); «Tetrahedron, 𝛼3«.
- ^ Coxeter 1973, pp. 33–34, §3.1 Congruent transformations.
- ^ Coxeter 1973, p. 63, §4.3 Rotation groups in two dimensions; notion of a fundamental region.
- ^ «Simplex Volumes and the Cayley-Menger Determinant», MathPages.com
- ^ Kahan, William M. (3 April 2012), What has the Volume of a Tetrahedron to do with Computer Programming Languages? (PDF), p. 11
- ^ Kahan, William M. (3 April 2012), What has the Volume of a Tetrahedron to do with Computer Programming Languages? (PDF), pp. 16–17
- ^ Bottema, O. «A Theorem of Bobillier on the Tetrahedron.» Elemente der Mathematik 24 (1969): 6-10.
- ^ Murakami, Jun; Yano, Masakazu (2005), «On the volume of a hyperbolic and spherical tetrahedron», Communications in Analysis and Geometry, 13 (2): 379–400, doi:10.4310/cag.2005.v13.n2.a5, ISSN 1019-8385, MR 2154824
- ^ Havlicek, Hans; Weiß, Gunter (2003). «Altitudes of a tetrahedron and traceless quadratic forms» (PDF). American Mathematical Monthly. 110 (8): 679–693. arXiv:1304.0179. doi:10.2307/3647851. JSTOR 3647851.
- ^ Leung, Kam-tim; and Suen, Suk-nam; «Vectors, matrices and geometry», Hong Kong University Press, 1994, pp. 53–54
- ^ Outudee, Somluck; New, Stephen. The Various Kinds of Centres of Simplices (PDF). Dept of Mathematics, Chulalongkorn University, Bangkok. Archived from the original on 27 February 2009.
{{cite book}}: CS1 maint: bot: original URL status unknown (link) - ^ Audet, Daniel (May 2011). «Déterminants sphérique et hyperbolique de Cayley-Menger» (PDF). Bulletin AMQ.
- ^ Lindelof, L. (1867). «Sur les maxima et minima d’une fonction des rayons vecteurs menés d’un point mobile à plusieurs centres fixes». Acta Societatis Scientiarum Fennicae. 8 (Part 1): 189–203.
- ^ Senechal, Marjorie (1981). «Which tetrahedra fill space?». Mathematics Magazine. Mathematical Association of America. 54 (5): 227–243. doi:10.2307/2689983. JSTOR 2689983.
- ^ Rassat, André; Fowler, Patrick W. (2004). «Is There a «Most Chiral Tetrahedron»?». Chemistry: A European Journal. 10 (24): 6575–6580. doi:10.1002/chem.200400869. PMID 15558830.
- ^ Lee, Jung Rye (June 1997). «The Law of Cosines in a Tetrahedron». J. Korea Soc. Math. Educ. Ser. B: Pure Appl. Math.
- ^ a b c d Inequalities proposed in “Crux Mathematicorum”, [1].
- ^ Crelle, A. L. (1821). «Einige Bemerkungen über die dreiseitige Pyramide». Sammlung mathematischer Aufsätze u. Bemerkungen 1 (in German). Berlin: Maurer. pp. 105–132. Retrieved 7 August 2018.
- ^ Todhunter, I. (1886), Spherical Trigonometry: For the Use of Colleges and Schools, p. 129 ( Art. 163 )
- ^ Lévy, Bruno; Liu, Yang (2010). «Lp Centroidal Voronoi Tessellation and its applications». ACM: 119.
- ^ «Problem 930» (PDF), Solutions, Crux Mathematicorum, 11 (5): 162–166, May 1985
- ^ Wacław Sierpiński, Pythagorean Triangles, Dover Publications, 2003 (orig. ed. 1962), p. 107. Note however that Sierpiński repeats an erroneous calculation of the volume of the Heronian tetrahedron example above.
- ^ Federal Aviation Administration (2009), Pilot’s Handbook of Aeronautical Knowledge, U. S. Government Printing Office, p. 13-10, ISBN 9780160876110.
- ^ Klein, Douglas J. (2002). «Resistance-Distance Sum Rules» (PDF). Croatica Chemica Acta. 75 (2): 633–649. Archived from the original (PDF) on 10 June 2007. Retrieved 15 September 2006.
- ^ Záležák, Tomáš (18 October 2007); «Resistance of a regular tetrahedron»[permanent dead link] (PDF), retrieved 25 January 2011
- ^ Vondran, Gary L. (April 1998). «Radial and Pruned Tetrahedral Interpolation Techniques» (PDF). HP Technical Report. HPL-98-95: 1–32. Archived from the original (PDF) on 7 June 2011. Retrieved 11 November 2009.
- ^ Green, William Lowthian (1875). Vestiges of the Molten Globe, as exhibited in the figure of the earth, volcanic action and physiography. Vol. Part I. London: E. Stanford. Bibcode:1875vmge.book…..G. OCLC 3571917.
- ^ Holmes, Arthur (1965). Principles of physical geology. Nelson. p. 32. ISBN 9780177612992.
- ^ Hitchcock, Charles Henry (January 1900). Winchell, Newton Horace (ed.). «William Lowthian Green and his Theory of the Evolution of the Earth’s Features». The American Geologist. Vol. XXV. Geological Publishing Company. pp. 1–10.
- ^ «Marvin Minsky: Stanley Kubrick Scraps the Tetrahedron». Web of Stories. Retrieved 20 February 2012.
- ^ Weisstein, Eric W. «Tetrahedral graph». MathWorld.
Bibliography[edit]
- Kepler, Johannes (1619). Harmonices Mundi (The Harmony of the World). Johann Planck.
- Coxeter, H.S.M. (1973). Regular Polytopes (3rd ed.). New York: Dover.
External links[edit]
- Weisstein, Eric W. «Tetrahedron». MathWorld.
- Free paper models of a tetrahedron and many other polyhedra
- An Amazing, Space Filling, Non-regular Tetrahedron that also includes a description of a «rotating ring of tetrahedra», also known as a kaleidocycle.
Fundamental convex regular and uniform polytopes in dimensions 2–10 |
|||||
|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn |
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon |
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | |
| Uniform polychoron | Pentachoron | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell |
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | ||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | |
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | |
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | |
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | ||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | ||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope |
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds |
Многогранник с 4 гранями
| Правильный тетраэдр | |
|---|---|
 . (Нажмите здесь, чтобы вращаться модель) . (Нажмите здесь, чтобы вращаться модель) |
|
| Тип | Платоновое тело |
| Элементы | F = 4, E = 6. V = 4 (χ = 2) |
| Грани по сторонам | 4 {3} |
| Обозначение Конвея | T |
| Шлефли символы | {3,3} |
| h {4,3}, s {2,4}, sr {2,2} | |
| Конфигурация лица | V3.3.3 |
| символ Wythoff | 3 | 2 3. | 2 2 2 |
| Диаграмма Кокстера | |
| Симметрия | Td, A 3, [3,3], (* 332) |
| Группа вращения | T, [3,3], (332) |
| Ссылки | U 01, C 15, W 1 |
| Свойства | правильный, выпуклый дельтаэдр |
| Двугранный угол | 70,528779 ° = arccos (⁄ 3) |
 . 3.3. 3. (Вершинная фигура ) . 3.3. 3. (Вершинная фигура ) |
 . Самодвойственный. (двойной многогранник ) . Самодвойственный. (двойной многогранник ) |
 . Сеть . Сеть |


В геометрия, тетраэдр (во множественном числе: тетраэдры или тетраэдры ), также известная как треугольная пирамида, представляет собой многогранник, состоящий из четырех треугольных граней, шести прямых ребер и четырех вершинных углов. Тетраэдр является самым простым из всех обычных выпуклых многогранников и единственным, у которого меньше пяти граней.
Тетраэдр — это трехмерный случай более общей концепции евклидова симплекса, и, таким образом, также может быть называется 3-симплексом .
Тетраэдр — это один из видов пирамиды, который представляет собой многогранник с плоским основанием многоугольника и треугольными гранями, соединяющими основание с общей точкой. В случае тетраэдра основанием является треугольник (любая из четырех граней может считаться основанием), поэтому тетраэдр также известен как «треугольная пирамида».
Как и все выпуклые многогранники, тетраэдр можно сложить из одного листа бумаги. У него две такие сети.
Для любого тетраэдра существует сфера (называемая описанной сферой ), на которой лежат все четыре вершины, и другая сфера (Insphere ) касательная к граням тетраэдра.
Содержание
- 1 Правильный тетраэдр
- 1.1 Координаты правильного тетраэдра
- 1.2 Углы и расстояния
- 1.3 Изометрии правильного тетраэдра
- 1.4 Ортогональные проекции правильного тетраэдра
- 1.5 Поперечное сечение правильного тетраэдра
- 1.6 Сферическая мозаика
- 1.7 Спиральная укладка
- 2 Другие частные случаи
- 2.1 Изометрии неправильных тетраэдров
- 3 Общие свойства
- 3.1 Объем
- 3.1.1 Формула типа Герона для объема тетраэдра
- 3.1.2 Разделитель объема
- 3.1.3 Неевклидов объем
- 3.2 Расстояние между краями
- 3.3 Свойства аналогично треугольнику
- 3.4 Геометрические соотношения
- 3.5 Закон синусов для тетраэдров и пространства всех форм тетраэдров
- 3.6 Закон синусов косинусы тетраэдров
- 3.7 Внутренняя точка
- 3.8 Inradius
- 3.9 Circumradius
- 3.10 Circumcenter
- 3.11 Centroid
- 3.12 Faces
- 3.1 Объем
- 4 Целочисленные тетраэдры
- 5 Родственные многогранники и соединения
- 6 Приложения
- 6.1 Численный анализ
- 6.2 Химия
- 6.3 Электричество и электроника
- 6.4 Игры
- 6.5 Цветовое пространство
- 6.6 Современное искусство
- 6.7 Популярная культура
- 6.8 Геология
- 6.9 Структурная инженерия
- 6.10 Авиация
- 7 Тетраэдрический граф
- 8 См. Также
- 9 Ссылки
- 10 Внешние ссылки
Правильный тетраэдр
A Правильный тетраэдр является тетраэдром в все четыре грани которого являются равносторонними треугольниками. Это одно из пяти правильных Платоновых тел, известных с древних времен.
В правильном тетраэдре все грани имеют одинаковый размер и форму (конгруэнтны), и все ребра имеют одинаковую длину.

Обычные тетраэдры сами по себе не тесселяция (заполнение пространства), но если они чередуются с правильными октаэдрами в При соотношении двух тетраэдров к одному октаэдру они образуют чередующиеся кубические соты , которые представляют собой мозаику. Некоторые тетраэдры, которые не являются правильными, включая ортосхему Шлефли и тетраэдр Хилла, могут быть мозаичными.
Правильный тетраэдр самодвойственен, что означает, что его двойственный является другим правильным тетраэдром. Составная фигура , содержащая два таких двойных тетраэдра, образует звездчатый октаэдр или октангулу стелла.
Координаты правильного тетраэдра
Следующие декартовы координаты определяют четыре вершины тетраэдра с длиной ребра 2 с центром в начале координат и двумя ребрами уровня:
- (± 1, 0, — 1 2) и (0, ± 1, 1 2) { displaystyle left ( pm 1,0, — { frac {1} { sqrt {2}}} right) quad { mbox {and}} quad left (0, pm 1, { frac {1} { sqrt {2}}} right)}
Выражается симметрично как 4 точки на единичной сфере, центр тяжести в начале координат, с уровнем нижней грани, вершины:
v 1 = (8 9, 0, — 1 3) { displaystyle v_ {1} = left ({ sqrt { frac {8} {9}}}, 0, — { frac {1} {3}} right)}
v 2 = (- 2 9, 2 3, — 1 3) { displaystyle v_ {2 } = left (- { sqrt { frac {2} {9}}}, { sqrt { frac {2} {3}}}, — { frac {1} {3}} right) }
v 3 = (- 2 9, — 2 3, — 1 3) { displaystyle v_ {3} = left (- { sqrt { frac {2} {9}}}, — { sqrt { frac {2} {3}}}, — { frac {1} {3}} right)}
v 4 = (0, 0, 1) { displaystyle v_ {4} = ( 0,0,1)}
с длиной кромки 8 3 { displaysty le { sqrt { frac {8} {3}}}}
Еще один набор координат основан на альтернативном кубе или демикубе с длиной ребра 2. Эта форма имеет диаграмму Кокстера и символ Шлефли h {4,3}. Тетраэдр в этом случае имеет длину ребра 2√2. Инвертирование этих координат генерирует двойственный тетраэдр, а пара вместе образует звездчатый октаэдр, вершины которого совпадают с вершинами исходного куба.
- Тетраэдр: (1,1,1), (1, −1, −1), (−1,1, −1), (−1, −1,1)
- Двойной тетраэдр : (−1, −1, −1), (−1,1,1), (1, −1,1), (1,1, −1)

Углы и расстояния
Для правильного тетраэдра с длиной ребра a:
| Площадь грани | A 0 = 3 4 a 2 { displaystyle A_ {0} = { frac { sqrt {3 }} {4}} a ^ {2} ,} |
| Площадь поверхности | A = 4 A 0 = 3 a 2 { displaystyle A = 4 , A_ {0} = { sqrt {3} } a ^ {2} ,} |
| Высота пирамиды | h = 6 3 a = 2 3 a { displaystyle h = { frac { sqrt {6}} {3}} a = { sqrt { frac {2} {3}}} , a ,} |
| Расстояние от центра тяжести до вершины | 3 4 h = 6 4 a = 3 8 a { displaystyle { frac {3} {4 }} , h = { frac { sqrt {6}} {4}} , a = { sqrt { frac {3} {8}}} , a ,} |
| От края до противоположного расстояние до края | l = 1 2 a { displaystyle l = { frac {1} { sqrt {2}}} , a ,} |
| Объем | V = 1 3 A 0 h = 2 12 a 3 = a 3 6 2 { displaystyle V = { frac {1} {3}} A_ {0} h = { frac { sqrt {2}} {12}} a ^ {3} = { frac {a ^ {3}} {6 { sqrt {2}}}} ,} |
| угол грань-вершина-кромка | дуга соз (1 3) знак равно arctan (2) { displaystyle arccos left ({ frac {1} { sqrt {3}}} right) = arctan left ({ sqrt {2}} right) ,} . (прибл. 54,7356 °) . (прибл. 54,7356 °) |
| угол грань-кромка-грань, т. Е. «Двугранный угол» | arccos (1 3) = arctan (2 2) { displaystyle arccos left ({ frac { 1} {3}} right) = arctan left (2 { sqrt {2}} right) ,} . (приблизительно 70,5288 °) . (приблизительно 70,5288 °) |
| Угол вершины-центра-вершины, угол между прямыми от центра тетраэдра до любых двух вершин. Это также угол между границами плато в вершине. В химии это называется тетраэдрическим валентным углом. Этот угол (в радианах) также является длиной дуги геодезического сегмента на единичной сфере, полученной в результате центрального проецирования одного края тетраэдра на сферу. | arccos (- 1 3) = 2 arctan (2) { displaystyle arccos left (- { frac {1} {3}} right) = 2 arctan left ({ sqrt { 2}} right) ,} . (приблизительно 109,4712 °) . (приблизительно 109,4712 °) |
| Телесный угол в вершине, образуемой гранью | arccos (23 27) { displaystyle arccos left ( { frac {23} {27}} right)} . (примерно 0,55129 стерадиан ). (примерно 1809,8 квадратных градусов ) . (примерно 0,55129 стерадиан ). (примерно 1809,8 квадратных градусов ) |
| Радиус описанной сферы | R = 6 4 a = 3 8 a { displaystyle R = { frac { sqrt {6}} {4}} a = { sqrt { frac {3} {8}}} , a ,} |
| Радиус Insphere, касательный к граням | r = 1 3 R = a 24 { displaystyle r = { frac {1} {3}} R = { frac {a} { sqrt {24}}} ,} |
| Радиус средней сферы, касающийся ребер | r M = r R = a 8 { displaystyle r _ { mathrm {M}} = { sqrt {rR}} = { frac {a} { sqrt {8}}} ,} |
| Радиус экзосферы | r E = 6 { displaystyle r _ { mathrm {E}} = { frac {a} { sqrt {6}}} ,} |
| Расстояние до центра экзосферы от противоположной вершины | d VE = 6 2 a = 3 2 a { displaysty le d _ { mathrm {VE}} = { frac { sqrt {6}} {2}} a = { sqrt { frac {3} {2}}} a ,} |
В отношении на базовой плоскости наклон грани (2√2) в два раза больше, чем у кромки (√2), что соответствует тому факту, что расстояние по горизонтали от основания до вершины по краю вдвое больше, чем по медиане грани. Другими словами, если C является центроидом основания, расстояние от C до вершины основания в два раза больше, чем от C до середины края основания. Это следует из того факта, что медианы треугольника пересекаются в его центроиде, и эта точка делит каждый из них на два отрезка, один из которых в два раза длиннее другого (см. доказательство ).
Для правильного тетраэдра с длиной стороны a, радиусом R описывающей его сферы и расстояниями d i от произвольной точки в 3-пространстве до его четырех вершин мы имеем
- д 1 4 + д 2 4 + д 3 4 + д 4 4 4 + 16 р 4 9 = (д 1 2 + д 2 2 + д 3 2 + д 4 2 4 + 2 р 2 3) 2; 4 (а 4 + d 1 4 + d 2 4 + d 3 4 + d 4 4) = (а 2 + d 1 2 + d 2 2 + d 3 2 + d 4 2) 2. { displaystyle { begin {align} { frac {d_ {1} ^ {4} + d_ {2} ^ {4} + d_ {3} ^ {4} + d_ {4} ^ {4}} { 4}} + { frac {16R ^ {4}} {9}} = left ({ frac {d_ {1} ^ {2} + d_ {2} ^ {2} + d_ {3} ^ {2} + d_ {4} ^ {2}} {4}} + { frac {2R ^ {2}} {3}} right) ^ {2}; \ 4 left (a ^ {4 } + d_ {1} ^ {4} + d_ {2} ^ {4} + d_ {3} ^ {4} + d_ {4} ^ {4} right) = left (a ^ {2} + d_ {1} ^ {2} + d_ {2} ^ {2} + d_ {3} ^ {2} + d_ {4} ^ {2} right) ^ {2}. end {align}} }
Изометрии правильного тетраэдра

Вершины куба можно сгруппировать в две группы по четыре, каждая из которых образует правильный тетраэдр (см. выше, а также анимацию, показывающую одну из два тетраэдра в кубе). Симметрии правильного тетраэдра соответствуют половине симметрий куба: симметрии, которые отображают тетраэдры сами по себе, а не друг в друга.
Тетраэдр — единственное платоново твердое тело, которое не отображается на себя с помощью точечной инверсии.
Правильный тетраэдр имеет 24 изометрии, формируя группу симметрии Td, [3,3 ], (* 332), изоморфна симметрической группе, S 4. Их можно разделить на следующие категории:
- T, [3,3], (332) изоморфна переменной группе, A 4 (тождество и 11 собственных вращений) с следующие классы сопряженности (в скобках даны перестановки вершин или, соответственно, граней и представление единичного кватерниона ):
- identity (identity; 1)
- поворот вокруг оси через вершину, перпендикулярную противоположной плоскости, на угол ± 120 °: 4 оси, по 2 на каждую ось, вместе 8 ((1 2 3) и т.д.; 1 ± i ± j ± k / 2)
- поворот на угол 180 °, так что край отображается на противоположный край: 3 ((1 2) (3 4) и т.д.; i, j, k)
- отражения в плоскости, перпендикулярной краю: 6
- отражений в плоскости в сочетании с поворотом на 90 ° вокруг оси, перпендикулярной плоскости: 3 оси, по 2 на каждую ось, вместе 6; эквивалентно, это повороты на 90 ° в сочетании с инверсией (x отображается в — x ): вращения соответствуют поворотам куба относительно осей лицом к лицу
Ортогонально проекции правильного тетраэдра
Правильный тетраэдр имеет две специальные ортогональные проекции, одна с центром на вершине или, что эквивалентно, на грани, и одна с центром на ребре. Первый соответствует плоскости Кокстера A 2.
| Центрированная по | Грань / вершина | Край |
|---|---|---|
| Изображение |  |
 |
| Проективная. симметрия | [3] | [4] |
Поперечное сечение правильного тетраэдра

Два скошенных перпендикуляра противоположно ребра правильного тетраэдра определяют набор параллельных плоскостей. Когда одна из этих плоскостей пересекает тетраэдр, результирующее поперечное сечение представляет собой прямоугольник . Когда пересекающаяся плоскость находится рядом с одним из краев, прямоугольник получается длинным и тонким. На полпути между двумя краями пересечение представляет собой квадрат. Соотношение сторон прямоугольника меняется на противоположное, когда вы проходите эту половину пути. Для пересечения квадрата средней точки результирующая граничная линия пересекает каждую грань тетраэдра аналогично. Если тетраэдр делится пополам на этой плоскости, обе половины становятся клиньями.

Это свойство также применяется для тетрагональных дифеноидов при применении к две специальные пары кромок.
Сферическая мозаика
Тетраэдр также может быть представлен как сферическая мозаика и спроецирован на плоскость через стереографическую проекцию . Эта проекция конформна, сохраняя углы, но не площади или длины. Прямые на сфере проектируются как дуги окружности на плоскость.
 |
 |
| Ортографическая проекция | Стереографическая проекция |
|---|
Спиральное наложение

Правильные тетраэдры могут быть уложены лицом к лицу в хиральную апериодическую цепочку, называемую спиралью Бурдейка – Кокстера. В четырехмерном все выпуклые правильные 4-многогранники с тетраэдрическими ячейками (5-ячеечная, 16-ячеечная и 600-ячейка ) могут быть построены как мозаики 3-сферы этими цепочками, которые становятся периодическими в трехмерном пространстве граничной поверхности 4-многогранника.
Другие особые случаи
равнобедренный тетраэдр, также называемый дисфеноидом, представляет собой тетраэдр, где все четыре грани — это конгруэнтные треугольники. заполняющий пространство тетраэдр упакован с конгруэнтными копиями самого себя в пространство тайла, как тетраэдрические соты дифеноида.
В треугольном тетраэдре три угла в одной вершине равны прямые углы. Если все три пары противоположных ребер тетраэдра перпендикулярны, то он называется ортоцентрическим тетраэдром. Когда перпендикулярна только одна пара противоположных ребер, это называется полуортоцентрическим тетраэдром . изодинамический тетраэдр — это тетраэдр, в котором чевианы, которые соединяют вершины с центрами противоположных граней, параллельны, а изогонический тетраэдр имеет параллельные чевианы, которые соединяют вершины с точками контакта противоположных граней с вписанной сферой тетраэдра.
Изометрии неправильных тетраэдров
Изометрии неправильных (немаркированных) тетраэдров зависят от геометрии тетраэдра, возможны 7 случаев. В каждом случае формируется 3-мерная точечная группа. Две другие изометрии (C 3, [3]) и (S 4, [2,4]) могут существовать, если включена маркировка граней или кромок. Для каждого типа ниже включены четырехгранные диаграммы с краями, окрашенными в соответствии с изометрической эквивалентностью, и серым цветом для уникальных краев.
| Название тетраэдра | Край. эквивалентность. диаграмма | Описание | |
|---|---|---|---|
| Симметрия | |||
| Шён. | Кокс. | Орб. | Порядок. |
| Правильный тетраэдр |  |
Четыре равносторонних треугольника Он образует группу симметрии T d, изоморфную симметрической группе, S 4. Правильный тетраэдр имеет диаграмму Кокстера |
|
| Td. T | [3,3 ]. [3,3 impression | * 332. 332 | 24. 12 |
| Треугольная пирамида |  |
Основание равностороннего треугольника и три равные стороны равнобедренного треугольника Это дает 6 изометрий, соответствующих 6 изометриям основания. Как перестановки вершин, эти 6 изометрий являются тождеством 1, (123), (132), (12), (13) и (23), образуя группу симметрии C 3v, изоморфную симметричная группа, S 3. Треугольная пирамида имеет символ Шлефли {3} ∨ (). | |
| C3v. C3 | [3 ]. [3pting | * 33. 33 | 6. 3 |
| Зеркальный клиновидный сустав | Два равных разностороннего треугольника с общим краем основания Имеет две пары равных ребер (1,3), (1,4) и (2,3), (2,4) и в противном случае нет равных ребер. Единственными двумя изометриями являются 1 и отражение (34), дающее группу C s, также изоморфную циклической группе, Z2. | ||
| Cs. =C1h. =C1v | [] | * | 2 |
| Неправильный тетраэдр. (Нет симметрии) | Четыре неравных треугольника
Его единственная изометрия — это тождество, а группа симметрии — тривиальная группа. Неправильный тетраэдр имеет символ Шлефли () ∨ () ∨ () ∨ (). |
||
| C1 | [] | 1 | 1 |
| Дисфеноиды (Четыре равных треугольника) | |||
| Тетрагональный дисфеноид |  |
Четыре равных равнобедренныхтреугольников
Он имеет 8 изометрий. Если ребра (1,2) и (3,4) имеют длину, отличную от длины остальных 4, то 8 изометрий являются тождественными 1, отражениями (12) и (34) и поворотами на 180 ° (12) (34), (13) (24), (14) (23) и неправильные повороты на 90 ° (1234) и (1432), образующие группу симметрии D 2d. Тетрагональный дисфеноид имеет диаграмму Кокстера |
|
| D2d. S4 | [2,4 ]. [2,4 ] | 2 * 2. 2× | 8. 4 |
| Ромбический дисфеноид | Четыре равных скалентреугольника
It имеет 4 изометрии. Изометрии равны 1 и повороты на 180 ° (12) (34), (13) (24), (14) (23). Это четырехгруппа Клейна V4или Z2, представленная как точечная группа D 2. Ромбический дисфеноид имеет диаграмму Кокстера |
||
| D2 | [2,2 ] | 222 | 4 |
| Обобщенные дисфеноиды (2 пары равных треугольников) | |||
| Дигональный дисфеноид |  . .  |
Две пары равных равнобедренных треугольников Это дает две противоположные кромки (1,2) и (3,4), которые перпендикулярны, но разной длины, а затем 4 изометрии равны 1, отражениям (12) и (34) и повороту на 180 ° (12) (34).. Группа симметрии — это C 2v, изоморфная четырехгруппе Клейна V4. Дигональный дисфеноид имеет символ Шлефли {} ∨ {}. | |
| C2v. C2 | [2 ]. [2 ] | * 22. 22 | 4. 2 |
| Филлический дисфеноид | Две пары равных разносторонних или равнобедренных треугольников
Он имеет две пары равных ребер (1,3), (2,4) и (1,4), (2,3), но в остальном нет равных ребер. Единственными двумя изометриями являются 1 и вращение (12) (34), что дает группу C 2, изоморфную циклической группе, Z2. |
||
| C2 | [2] | 22 | 2 |
Общие свойства
Объем
Объем тетраэдра определяется формулой объема пирамиды:
- V = 1 3 A 0 h { displaystyle V = { frac {1} {3}} A_ {0 } , h ,}
где A 0 — это площадь основания, а h — высота от основания до вершины. Это применимо для каждого из четырех вариантов основания, поэтому расстояния от вершин до противоположных граней обратно пропорциональны площадям этих граней.
Для тетраэдра с вершинами a = (a 1, a 2, a 3), b = (b 1, b 2, b 3), c = (c 1, c 2, c 3) и d = (d 1, d 2, d 3), объем равен 1/6 | det (a− d, b− d, c− d) |, или любая другая комбинация пар вершин, образующих односвязный граф . Это можно переписать, используя скалярное произведение и кросс-произведение, что дает
- V = | (a — d) ⋅ ((b — d) × (c — d)) | 6. { Displaystyle В = { гидроразрыва {| ( mathbf {a} — mathbf {d}) cdot (( mathbf {b} — mathbf {d}) раз ( mathbf {c} — mathbf {d})) |} {6}}.}
Если начало системы координат выбрано таким, чтобы оно совпадало с вершиной d, то d = 0, поэтому
- V = | a ⋅ (b × c) | 6, { displaystyle V = { frac {| mathbf {a} cdot ( mathbf {b} times mathbf {c}) |} {6}},}
где a, b, и c представляют три ребра, которые встречаются в одной вершине, а a · (b× c) представляет собой тройное скалярное произведение. Сравнивая эту формулу с формулой, использованной для вычисления объема параллелепипеда , мы заключаем, что объем тетраэдра равен 1/6 объема любого параллелепипеда, который имеет три сходящихся с ним ребра.
Абсолютное значение скалярного тройного произведения можно представить в виде следующих абсолютных значений определителей:
- 6 ⋅ V = ‖ abc ‖ { displaystyle 6 cdot V = { begin {Vmatrix} mathbf {a} mathbf {b} mathbf {c} end {Vmatrix}}}
или 6 ⋅ V = ‖ abc ‖ { displaystyle 6 cdot V = { begin {Vmatrix} mathbf {a} \ mathbf {b} \ mathbf {c} end {Vmatrix}}}
где a = (a 1, a 2, a 3) { displaystyle mathbf {a} = (a_ {1}, a_ {2}, a_ {3}) ,}
выражается как вектор строки или столбца и т. Д.
Следовательно
- 36 ⋅ V 2 = | a 2 a ⋅ b a ⋅ c a ⋅ b b 2 b ⋅ c a ⋅ c b ⋅ c c 2 | { Displaystyle 36 cdot V ^ {2} = { begin {vmatrix} mathbf {a ^ {2}} mathbf {a} cdot mathbf {b} mathbf {a} cdot mathbf {c} \ mathbf {a} cdot mathbf {b} mathbf {b ^ {2}} mathbf {b} cdot mathbf {c} \ mathbf {a} cdot mathbf {c} mathbf {b} cdot mathbf {c} mathbf {c ^ {2}} end {vmatrix}}}
где a ⋅ b = ab cos γ { displaystyle mathbf {a} cdot mathbf {b} = ab cos { gamma}}
и т. Д.
, что дает
- V = abc 6 1 + 2 cos α соз β соз γ — соз 2 α — соз 2 β — соз 2 γ, { displaystyle V = { frac {abc} {6}} { sqrt {1 + 2 cos { alpha} cos { beta} cos { gamma} — cos ^ {2} { alpha} — cos ^ {2} { beta} — cos ^ {2} { gamma}}}, ,}
где α, β, γ — плоские углы, входящие в вершину d . Угол α — это угол между двумя ребрами, соединяющими вершину d с вершинами b и c . Угол β имеет значение для вершин a и c, тогда как γ определяется положением вершин a и b.
Учитывая расстояния между вершинами тетраэдра объем может быть вычислен с помощью определителя Кэли – Менгера :
- 288 ⋅ V 2 = | 0 1 1 1 1 1 0 d 12 2 d 13 2 d 14 2 1 d 12 2 0 d 23 2 d 24 2 1 d 13 2 d 23 2 0 d 34 2 1 d 14 2 d 24 2 d 34 2 0 | { displaystyle 288 cdot V ^ {2} = { begin {vmatrix} 0 1 1 1 1 \ 1 0 d_ {12} ^ {2} d_ {13} ^ {2} d_ {14} ^ {2} \ 1 d_ {12 } ^ {2} 0 d_ {23} ^ {2} d_ {24} ^ {2} \ 1 d_ {13} ^ {2} d_ {23} ^ {2} 0 d_ {34} ^ {2} \ 1 d_ {14} ^ {2} d_ {24} ^ {2} d_ {34} ^ {2} 0 end {vmatrix}}}
где нижние индексы i, j ∈ {1, 2, 3, 4} представляют вершины {a, b, c, d}, а d ij — попарное расстояние между ними, то есть длина ребра, соединяющего две вершины. Отрицательное значение определителя означает, что тетраэдр не может быть построен с заданными расстояниями. Эта формула, иногда называемая формулой Тартальи, по существу создана художником Пьеро делла Франческа в 15 веке как трехмерный аналог 1 века формула Герона для площади треугольника.
Обозначим a, b, c три ребра, которые пересекаются в точке, а x, y, z — противоположные стороны. Пусть V — объем тетраэдра; тогда
- V = 4 a 2 b 2 c 2 — a 2 X 2 — b 2 Y 2 — c 2 Z 2 + XYZ 12 { displaystyle V = { frac { sqrt {4a ^ {2} b ^ {2} c ^ {2} -a ^ {2} X ^ {2} -b ^ {2} Y ^ {2} -c ^ {2} Z ^ {2} + XYZ}} {12}}}
где
- X = b 2 + c 2 — x 2 { displaystyle X = b ^ {2} + c ^ {2} -x ^ {2}}
- Y = a 2 + c 2 — y 2 { displaystyle Y = a ^ {2} + c ^ {2} -y ^ {2}}
- Z = a 2 + b 2 — z 2 { displaystyle Z = a ^ {2} + b ^ {2} -z ^ {2}}
В приведенной выше формуле используются различные выражения со следующей формулой. В приведенной выше формуле используются шесть длин ребер, а в следующей формуле используются три длины ребер и три угла.
- V = abc 6 1 + 2 cos α cos β cos γ — cos 2 α — cos 2 β — cos 2 γ { displaystyle V = { frac {abc} {6}} { sqrt {1 + 2 cos { alpha} cos { beta} cos { gamma} — cos ^ {2} { alpha} — cos ^ {2} { beta} — cos ^ {2} { gamma}}}}
Формула типа Герона для объема тетраэдра
Если U, V, W, u, v, w — длины ребер тетраэдра (первый три образуют треугольник; u напротив U и так далее), тогда
- volume = (- a + b + c + d) (a — b + c + d) (a + b — c + d) (a + b + c — d) 192 uvw { displaystyle { text {volume}} = { frac { sqrt {, (- a + b + c + d) , (a-b + c + d) , (a + b-c + d) , (a + b + cd)}} {192 , u , v , w}}}
где
- a = x YZ b = y ZX c = z XY d = xyz X = (w — U + v) (U + v + w) x = (U — v + w) (v — w + U) Y = (u — V + w) ( V + w + u) y = (V — w + u) (w — u + V) Z = (v — W + u) (W + u + v) z = (W — u + v) (u — v + W). { displaystyle { begin {align} a = { sqrt {xYZ}} \ b = { sqrt {yZX}} \ c = { sqrt {zXY}} \ d = { sqrt {xyz} } \ X = (w-U + v) , (U + v + w) \ x = (U-v + w) , (v-w + U) \ Y = (u-V + w) , (V + w + u) \ y = (V-w + u) , (w-u + V) \ Z = (v-W + u) , (W + u + v) \ z = (W-u + v) , (u-v + W). end {align}}}
Разделитель объема
Плоскость, которая разделяет два противоположных края тетраэдра в заданном соотношении также делит объем тетраэдра в таком же соотношении. Таким образом, любая плоскость, содержащая бимедиан (соединитель середин противоположных ребер) тетраэдра , делит объем тетраэдра пополам.
Неевклидов объем
Для тетраэдров в гиперболическое пространство или в трехмерной эллиптической геометрии, двугранные углы тетраэдра определяют его форму и, следовательно, его объем. В этих случаях объем определяется по формуле Мураками – Яно. Однако в евклидовом пространстве масштабирование тетраэдра изменяет его объем, но не его двугранные углы, поэтому такой формулы не может быть.
Расстояние между краями
Любые два противоположных ребра тетраэдра лежат на двух наклонных линиях, а расстояние между ребрами определяется как расстояние между двумя наклонными линиями. линий. Пусть d будет расстоянием между линиями наклона, образованными противоположными краями a и b− c, как вычислено здесь. Тогда другая формула объема задается как
- V = d | (a × (b — c)) | 6. { displaystyle V = { frac {d | ( mathbf {a} times mathbf {(bc)}) |} {6}}.}
Свойства, аналогичные свойствам треугольника
Тетраэдр имеет много свойств, аналогичных свойствам треугольника, включая внутреннюю сферу, описанную сферу, средний тетраэдр и внешние сферы. Он имеет соответствующие центры, такие как центр окружности, центр окружности, эксцентрики, центр Шпикера и такие точки, как центроид. Однако обычно нет ортоцентра в смысле пересечения высот.
Гаспар Монж обнаружил центр, который существует в каждом тетраэдре, теперь известный как точка Монжа : точка, в которой находятся шесть срединных плоскостей. тетраэдра пересекаются. Срединная плоскость определяется как плоскость, ортогональная ребру, соединяющему любые две вершины, который также содержит центроид противоположного ребра, образованного путем соединения двух других вершин. Если высоты тетраэдра пересекаются, то точка Монжа и ортоцентр совпадают, давая класс ортоцентрического тетраэдра.
. Ортогональная линия, опущенная от точки Монжа к любой грани, пересекает эту грань в середине отрезка прямой между ортоцентр лица и основание высоты упало с противоположной вершины.
Отрезок, соединяющий вершину тетраэдра с центроидом противоположной грани, называется срединной, а отрезок, соединяющий середины двух противоположных ребер, называется бимедианой тетраэдра.. Следовательно, в тетраэдре четыре медианы и три бимедианы. Все эти семь отрезков параллельны в точке, называемой центроидом тетраэдра. Кроме того, четыре медианы делятся на центроид в соотношении 3: 1 (см. теорему Коммандино ). Центроид тетраэдра — это середина между его точкой Монжа и центром описанной окружности. Эти точки определяют линию Эйлера тетраэдра, которая аналогична прямой Эйлера треугольника.
окружность из девяти точек общего треугольника имеет аналог в описанной сфере среднего тетраэдра тетраэдра. Это сфера с двенадцатью точками и, помимо центроидов четырех граней эталонного тетраэдра, она проходит через четыре замещающие точки Эйлера, по одной трети пути от точки Монжа к каждой из четырех вершин. Наконец, он проходит через четыре базовые точки ортогональных прямых, опущенных от каждой точки Эйлера к грани, не содержащей вершину, которая породила точку Эйлера.
Центр T двенадцатиточечной сферы также лежит на прямой Эйлера. В отличие от своего треугольного аналога, этот центр находится на одной трети пути от точки Монжа M к центру описанной окружности. Кроме того, ортогональная линия, проходящая через точку T к выбранной грани, копланарна с двумя другими ортогональными линиями к той же грани. Первая — это ортогональная линия, проходящая через соответствующую точку Эйлера к выбранной грани. Вторая — это ортогональная линия, проходящая через центр тяжести выбранной грани. Эта ортогональная линия, проходящая через центр из двенадцати точек, находится на полпути между ортогональной линией точки Эйлера и центроидальной ортогональной линией. Кроме того, для любой грани центр из двенадцати точек лежит в средней точке соответствующей точки Эйлера и ортоцентре этой грани.
Радиус двенадцатиточечной сферы составляет одну треть радиуса описанной окружности контрольного тетраэдра.
Существует связь между углами, образованными гранями общего тетраэдра, определяемая как
- | — 1 cos (α 12) cos (α 13) cos (α 14) cos (α 12) — 1 cos (α 23) cos (α 24) cos (α 13) cos (α 23) — 1 cos (α 34) cos (α 14) cos (α 24) cos (α 34) — 1 | Знак равно 0 { displaystyle { begin {vmatrix} -1 cos {( alpha _ {12})} cos {( alpha _ {13})} cos {( alpha _ {14}) } \ cos {( alpha _ {12})} — 1 cos {( alpha _ {23})} cos {( alpha _ {24})} \ cos {( alpha _ {13})} cos {( alpha _ {23})} — 1 cos {( alpha _ {34})} \ cos {( alpha _ {14})} cos {( alpha _ {24})} cos {( alpha _ {34})} — 1 \ end {vmatrix}} = 0 ,}
где α ij — угол между гранями i и j.
геометрическая медиана координат положения вершины тетраэдра и его изогонический центр связаны при обстоятельствах, аналогичных тем, которые наблюдаются для треугольника. Лоренц Линделёф обнаружил, что любому данному тетраэдру соответствует точка, теперь известная как изогонический центр, O, в котором телесные углы, образуемые гранями, равны, имеют общее значение π sr, и при углы между противоположными краями равны. Телесный угол π sr составляет четверть угла, охватываемого всем пространством. Когда все телесные углы в вершинах тетраэдра меньше π sr, O лежит внутри тетраэдра, а поскольку сумма расстояний от O до вершин минимальна, O совпадает с геометрической медианой , M, вершин. В том случае, если телесный угол в одной из вершин, v, составляет ровно π sr, тогда O и M совпадают с v. Однако если у тетраэдра есть вершина v с телесным углом больше π sr, M по-прежнему соответствует к v, но O лежит вне тетраэдра.
Геометрические соотношения
Тетраэдр — это 3- симплекс. В отличие от других Платоновых тел, все вершины правильного тетраэдра равноудалены друг от друга (это единственно возможное расположение четырех равноудаленных точек в трехмерном пространстве).
Тетраэдр — это треугольная пирамида, а правильный тетраэдр — самодвойственный.
. Правильный тетраэдр может быть вложен внутрь куба пополам. таких способов, что каждая вершина является вершиной куба, а каждое ребро — диагональю одной из граней куба. Для одного такого вложения декартовы координаты для вершин равны
- (+1, +1, +1);
- (−1, −1, +1);
- (−1, +1, −1);
- (+1, −1, −1).
Это дает тетраэдр с длиной ребра 2√2 с центром в начале координат. Для другого тетраэдра (который двойственен первому) поменяйте все знаки местами. Эти две вершины тетраэдра вместе являются вершинами куба, демонстрируя, что правильный тетраэдр представляет собой 3- полукуб.

Объем этого тетраэдра составляет одну треть объема куба куб. Объединение обоих тетраэдров дает правильное полиэдрическое соединение, называемое соединением двух тетраэдров или stella octangula.
Внутренняя часть stella octangula представляет собой октаэдр, и, соответственно, правильный октаэдр является результатом отсечения от правильного тетраэдра четырех правильных тетраэдров половинного линейного размера (т. е. выпрямления тетраэдра).
Приведенное выше вложение делит куб на пять тетраэдров, один из которых правильный. Фактически, пять — это минимальное количество тетраэдров, необходимое для создания куба. Чтобы убедиться в этом, начиная с базового тетраэдра с 4 вершинами, каждый добавленный тетраэдр добавляет не более 1 новой вершины, поэтому необходимо добавить еще как минимум 4, чтобы создать куб с 8 вершинами.
Включение тетраэдров внутрь правильного соединения пяти кубов дает еще два правильных соединения, содержащих пять и десять тетраэдров.
Обычные тетраэдры не могут замощить пространство сами по себе, хотя этот результат кажется достаточно вероятным, чтобы Аристотель утверждал, что это возможно. Однако два правильных тетраэдра могут быть объединены с октаэдром, давая ромбоэдр, который может занимать мозаичное пространство.
Однако известно несколько неправильных тетраэдров, копии которых могут занимать мозаичное пространство, например, тетраэдрические соты дифеноида. Полный список остается открытой проблемой.
Если ослабить требование, чтобы все тетраэдры имели одинаковую форму, можно разбить пространство, используя только тетраэдры, разными способами. Например, можно разделить октаэдр на четыре одинаковых тетраэдра и снова объединить их с двумя правильными. (В качестве примечания: эти два вида тетраэдров имеют одинаковый объем.)
Тетраэдр уникален среди однородных многогранников тем, что не имеет параллельных граней.
Закон синусов для тетраэдров и пространства всех форм тетраэдров
Следствием обычного закона синусов является то, что в тетраэдр с вершинами O, A, B, C, имеем
- sin ∠ O A B ⋅ sin ∠ O B C ⋅ sin ∠ O C A = sin ∠ O A C ⋅ sin ∠ O C B ⋅ sin ∠ O B A. { displaystyle sin angle OAB cdot sin angle OBC cdot sin angle OCA = sin angle OAC cdot sin angle OCB cdot sin angle OBA. ,}
One может рассматривать две стороны этой идентичности как соответствующие ориентации поверхности по часовой стрелке и против часовой стрелки.
Если поставить любую из четырех вершин в роли O, мы получим четыре таких тождества, но не более трех из них независимы: если стороны трех из них «по часовой стрелке» умножаются, и произведение получается равным равняется произведению сторон «против часовой стрелки» тех же трех тождеств, а затем общие множители сокращаются с обеих сторон, результатом является четвертое тождество.
Три угла являются углами некоторого треугольника тогда и только тогда, когда их сумма равна 180 ° (π радиан). Какое условие на 12 углов необходимо и достаточно, чтобы они были 12 углами какого-нибудь тетраэдра? Ясно, что сумма углов любой стороны тетраэдра должна составлять 180 °. Так как таких треугольников четыре, существует четыре таких ограничения на суммы углов, и количество степеней свободы тем самым сокращается с 12 до 8. Четыре соотношения, задаваемые этим синусоидальным законом, дополнительно уменьшают число степеней свободы: от 8 до не 4, а 5, поскольку четвертое ограничение не является независимым от первых трех. Таким образом, пространство всех форм тетраэдров является 5-мерным.
Закон косинусов для тетраэдров
Пусть {P 1,P2, P 3, P 4 } — точки тетраэдра. Пусть Δ i — площадь грани, противоположная вершине P i, и пусть θ ij — двугранный угол между двумя гранями тетраэдра, примыкающими к ребру. P iPj.
Закон косинусов для этого тетраэдра, который связывает площади граней тетраэдра с двугранными углами вокруг вершины, задается следующим соотношением:
- Δ i 2 = Δ j 2 + Δ К 2 + Δ l 2 — 2 (Δ j Δ k соз θ il + Δ j Δ l cos θ ik + Δ k Δ l cos θ ij) { displaystyle Delta _ {i} ^ {2} = Delta _ {j} ^ {2} + Delta _ {k} ^ {2} + Delta _ {l} ^ {2} -2 ( Delta _ {j} Delta _ { k} cos theta _ {il} + Delta _ {j} Delta _ {l} cos theta _ {ik} + Delta _ {k} Delta _ {l} cos theta _ { ij})}
Внутренняя точка
Пусть P — любая внутренняя точка тетраэдра объема V, вершинами которого являются A, B, C и D, а площади противоположных граней — это F a, F b, F c и F d. Тогда
- P A ⋅ F a + P B ⋅ F b + P C ⋅ F c + P D ⋅ F d ≥ 9 V. { displaystyle PA cdot F _ { mathrm {a}} + PB cdot F _ { mathrm {b}} + PC cdot F _ { mathrm {c}} + PD cdot F _ { mathrm {d}} geq 9V.}
Для вершин A, B, C и D, внутренней точки P и футов J, K, L и M перпендикуляров от P к граням, и предположим, что грани имеют равные площади, тогда
- PA + PB + PC + PD ≥ 3 (PJ + PK + PL + PM). { displaystyle PA + PB + PC + PD geq 3 (PJ + PK + PL + PM).}
Inradius
Обозначение внутреннего радиуса тетраэдра как r и inradii его треугольных граней как r i для i = 1, 2, 3, 4, мы имеем
- 1 r 1 2 + 1 r 2 2 + 1 r 3 2 + 1 r 4 2 ≤ 2 р 2, { displaystyle { frac {1} {r_ {1} ^ {2}}} + { frac {1} {r_ {2} ^ {2}}} + { frac {1} { r_ {3} ^ {2}}} + { frac {1} {r_ {4} ^ {2}}} leq { frac {2} {r ^ {2}}},}
с равенство тогда и только тогда, когда тетраэдр правильный.
Если A 1, A 2, A 3 и A 4 обозначают площадь каждой грани, значение r определяется как
- r = 3 VA 1 + A 2 + A 3 + A 4 { displaystyle r = { frac {3V} {A_ {1} + A_ {2} + A_ {3} + A_ {4}}}}
.
Эта формула получается из деления тетраэдра на четыре тетраэдра, точки которых являются тремя точками одной из исходных граней и центром. Поскольку четыре субтетраэдра заполняют объем, мы имеем V = 1 3 A 1 r + 1 3 A 2 r + 1 3 A 3 r + 1 3 A 4 r { displaystyle V = { frac {1} { 3}} A_ {1} r + { frac {1} {3}} A_ {2} r + { frac {1} {3}} A_ {3} r + { frac {1} {3}} A_ { 4} r}
Окружной радиус
Обозначим радиус описанной окружности тетраэдра как R. Пусть a, b, c — длины трех ребер, которые встречаются в вершине, а A, B, C — длина противоположных краев. Пусть V — объем тетраэдра. Тогда
- R = (a A + b B + c C) (a A + b B — c C) (a A — b B + c C) (- a A + b B + c C) 24 В. { displaystyle R = { frac { sqrt {(aA + bB + cC) (aA + bB-cC) (aA-bB + cC) (- aA + bB + cC)}} {24V}}.}
Центр описанной окружности
Центр описанной окружности тетраэдра может быть найден как пересечение трех биссектрисных плоскостей. Биссектрисная плоскость определяется как плоскость с центром и ортогональна ребру тетраэдра. С помощью этого определения центр описанной окружности C тетраэдра с вершинами x 0,x1,x2,x3может быть сформулирован как произведение матрица-вектор:
- C = A — 1 B, где A = ([x 1 — x 0] T [x 2 — x 0] T [x 3 — x 0] T) и B = 1 2 (x 1 2 — x 0 2 x 2 2 — x 0 2 x 3 2 — x 0 2) { displaystyle { begin {align} C = A ^ {- 1} B { text {where}} A = left ({ begin {matrix} left [x_ {1} -x_ {0} right] ^ {T} \ left [x_ {2} -x_ {0} right] ^ {T} \ left [x_ {3} -x_ {0} right] ^ {T} end {matrix}} right) { text {and}} B = { frac {1} {2}} left ({ begin {matrix} x_ {1} ^ {2} -x_ {0} ^ {2} x_ {2} ^ {2} -x_ {0} ^ {2} \ x_ {3} ^ {2} -x_ {0} ^ {2} end {matrix}} right) \ конец {align}}}
В отличие от центроида, центр описанной окружности не всегда может лежать внутри тетраэдра. Аналогично тупому треугольнику, у тупого тетраэдра центр описанной окружности находится вне объекта.
Центроид
Центр масс тетраэдра вычисляется как среднее арифметическое его четырех вершин, см. Центроид.
Грани
сумма площадей любых трех граней больше, чем площадь четвертой грани.
Целочисленные тетраэдры
Существуют тетраэдры, имеющие целочисленные длины ребер, площади граней и объем. Они называются тетраэдрами Герона. В одном примере один край 896, противоположный край 990 и четыре других края 1073; две грани — это равнобедренные треугольники с площадью 436800, а две другие — равнобедренные с площадью 47120, а объем равен 124185600.
Тетраэдр может иметь целочисленный объем и последовательные целые числа в качестве ребер, примером является тот, у которого есть ребра 6, 7, 8, 9, 10 и 11 и объем 48.
Родственные многогранники и соединения
Правильный тетраэдр можно рассматривать как треугольник пирамида.
| Правильные пирамиды | ||||||||
|---|---|---|---|---|---|---|---|---|
| Дигональ | Треугольник | Квадрат | Пятиугольник | Шестиугольник | Шестиугольник | Восьмиугольник | Эннеагональ | Десятиугольник… |
| Неправильный | Правильный | Равносторонний | Равнобедренный | |||||
 |
 |
 |
 |
|||||
 |
 |
 |
 |
 |
 |
 |
 |
Правильный тетраэдр можно рассматривать как вырожденный многогранник, равномерный двугранный антипризма, где базовые многоугольники редуцированы двуугольники.
Семейство однородных n-угольных антипризм [
] |
|||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Изображение многогранника | … | Апейрогональная антипризма | |||||||||||
| Сферическая мозаичное изображение | Плоское мозаичное изображение | ||||||||||||
| Vertex con конфигурация n.3.3.3 | 2.3.3.3 | 3.3.3.3 | 4.3.3.3 | 5.3.3.3 | 6.3.3.3 | 7.3.3.3 | 8.3. 3.3 | 9.3.3.3 | 10.3.3.3 | 11.3.3.3 | 12.3.3.3 | … | ∞.3.3.3 |
Правильный тетраэдр можно рассматривать как вырожденный многогранник, равномерный двойственный двояковыпуклый трапецоэдр, содержащий 6 вершин, в двух наборах коллинеарных ребер.
| Семейство n-угольных трапеций | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Изображение многогранника |  |
 |
 |
 |
 |
 |
 |
 |
… | Апейрогональный трапецоэдр | |
| Сферическое мозаичное изображение |  |
 |
 |
 |
 |
 |
 |
 |
Плоское мозаичное изображение | ||
| Конфигурация лица Vn.3.3.3 | V2.3.3.3 | V3.3.3.3 | V4.3.3.3 | V5.3.3.3 | V6.3.3.3 | V7.3.3.3 | V8.3.3.3 | V10.3.3.3 | V12.3.3.3 | … | V∞.3.3.3 |
Применен процесс усечения к тетраэдру образует серию однородных многогранников. Усечение ребер до точек дает октаэдр как выпрямленный тетраэдр. Процесс завершается двунаправленной связью, уменьшая исходные грани до точек и снова создавая самодвойственный тетраэдр.
| Семейство однородных тетраэдрических многогранников | |||||||
|---|---|---|---|---|---|---|---|
| Симметрия : [3,3], (* 332) | [3,3], (332) | ||||||
 |
 |
 |
 |
||||
| {3,3} | t {3,3} | r {3,3} | t {3,3} | {3,3} | rr {3,3} | tr {3,3} | sr {3,3} |
| Двойники к однородным многогранникам | |||||||
 |
 |
 |
 |
||||
| V3.3.3 | V3.6.6 | V3.3.3.3 | V3.6.6 | V3.3.3 | V3.4.3.4 | V4.6.6 | V3.3.3.3.3 |
Этот многогранник топологически связан как часть последовательности правильных многогранников с символами Шлефли {3, n}, продолжение в гиперболической плоскости.
* n32 мутация симметрии регулярных мозаик: {3, n} [
] |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Сферический | Евклид. | Компактный гипер. | Парако. | Некомпактный гиперболический | |||||||
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| 3.3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
Тетраэдр топологически связан с серией правильных многогранников и мозаик с фигурами вершин порядка 3 .
* n32 изменение симметрии правильных мозаик: {n, 3} [
] |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Сферическое | Евклидово | Компактное гиперболическое. | Парако. | Некомпактный гиперболический | |||||||
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| {2,3} | {3,3} | {4,3} | {5,3} | {6,3} | {7,3} | {8,3} | {∞, 3} | {12i, 3} | {9i, 3} | {6i, 3} | {3i, 3} |
- Соединения тетраэдров
Два тетраэдра в кубе
Соединение пяти тетраэдров
Соединение десяти тетраэдров
Можно построить интересный многогранник из пяти пересекающихся тетраэдров. Это соединение пяти тетраэдров было известно сотни лет. Это регулярно встречается в мире оригами. Соединение двадцати вершин даст правильный додекаэдр. Существуют как левосторонние, так и правосторонние формы, которые являются зеркальным отображением друг друга. Наложение обеих форм дает соединение десяти тетраэдров, в котором десять тетраэдров расположены как пять пар stellae octangulae. Октангула стелла представляет собой соединение двух тетраэдров в двойном положении, и его восемь вершин определяют куб как их выпуклую оболочку.
квадратный осоэдр — это еще один многогранник с четырьмя гранями, но у него нет треугольных граней.
Приложения
Численный анализ

В численном анализе сложные трехмерные формы обычно разбиваются или аппроксимируются с помощью многоугольной сетки неправильных тетраэдров в процессе создания уравнений для конечно-элементный анализ, особенно в численном решении уравнений в частных производных. Эти методы имеют широкое практическое применение в вычислительной гидродинамике, аэродинамике, электромагнитных полях, гражданском строительстве, химической инженерии., военно-морская архитектура и инженерия и смежные области.
Химия

Форма тетраэдра наблюдается в природе в ковалентно связанных молекулах. Все sp-гибридизированные атомы окружены атомами (или неподеленными электронными парами ) в четырех углах тетраэдра. Например, в молекуле метана (CH. 4) или ионе аммония (NH. 4) четыре атома водорода окружают центральный атом углерода или азота с тетраэдрической симметрией. По этой причине один из ведущих журналов по органической химии называется Tetrahedron. Центральный угол между любыми двумя вершинами идеального тетраэдра равен arccos (−1/3), или приблизительно 109,47 °.
Вода, H. 2O, также имеет тетраэдрическую структуру., с двумя атомами водорода и двумя неподеленными парами электронов вокруг центральных атомов кислорода. Однако его тетраэдрическая симметрия не идеальна, поскольку неподеленные пары отталкиваются сильнее, чем одинарные связи O – H.
Четвертичные фазовые диаграммы в химии представлены графически в виде тетраэдров.
Однако четвертичные фазовые диаграммы в технике связи представлены графически на двухмерной плоскости.
Электричество и электроника
Если шесть одинаковых резисторов спаяны вместе, чтобы образовать тетраэдр, то сопротивление, измеренное между любыми двумя вершинами, будет вдвое меньше. одного резистора.
Поскольку кремний является наиболее распространенным полупроводником, используемым в твердотельной электронике, а кремний имеет валентность из четырех, тетраэдрическая форма четырех химических связей в кремнии сильно влияет на то, как кристаллы кремния образуются и какие формы они принимают.
Игры

В Королевскую игру Ура, датируемую 2600 годом до нашей эры, играли с набором четырехгранных игральных костей.
Особенно в ролевой игре, это твердое тело известно как 4-сторонний кубик, один из наиболее распространенных многогранных кубиков с номером свернувшись, появляясь вокруг нижней или верхней вершины. Некоторые головоломки, подобные кубику Рубика, являются тетраэдрическими, например, Pyraminx и Pyramorphix.
Color space
Тетраэдры используются в алгоритмах преобразования цветового пространства. для случаев, когда ось яркости по диагонали сегментирует цветовое пространство (например, RGB, CMY).
Современное искусство
Австрийская художница Мартина Шеттина создала тетраэдр, используя люминесцентные лампы. Он был показан на биеннале светового искусства в Австрии 2010.
Он используется в качестве обложки альбома в окружении черного пламени на The End of All Things to Come от Mudvayne.
Популярная культура
Стэнли Кубрик изначально задумывал монолит в 2001: Космическая одиссея как тетраэдр, согласно Марвину Мински, когнитивному исследователю. ученый и эксперт по искусственному интеллекту, который консультировал Кубрика по поводу компьютера HAL 9000 и других аспектов фильма. Кубрик отказался от идеи использовать тетраэдр, поскольку посетитель, который видел кадры с ним, не узнал, что это было, и он не хотел, чтобы в фильме ничего не понимали обычные люди.
В сезоне 6, эпизоде 15 из Футурама, названный «Мёбиус Дик », команда «Планетного экспресса» проходит через область в космосе, известную как Бермудский тетраэдр. Многие другие корабли, проходящие через этот район, таинственным образом исчезли, в том числе и первый экипаж Planet Express.
В фильме 2013 года Oblivion большая структура на орбите над Землей имеет форму тетраэдра и называется Тет.
Геология
Тетраэдрическая гипотеза, первоначально опубликованная Уильямом Лоутианом Грином для объяснения формирования Земли, была популярна в начале 20 века..
Структурная инженерия
Тетраэдр с жесткими краями по своей природе жесткий. По этой причине его часто используют для усиления рамных конструкций, таких как космические рамки.
авиация
. На некоторых аэродромах большой каркас в форме тетраэдра с двумя закрытыми сторонами из тонкого материала устанавливается на вращающийся стержень и всегда направлен против ветра. Он достаточно большой, чтобы его можно было увидеть с воздуха, и иногда он подсвечивается. Его цель — служить ссылкой для пилотов, указывающих направление ветра.
Тетраэдрический граф
| Тетраэдрический граф | |
|---|---|
 |
|
| Вершины | 4 |
| Ребра | 6 |
| Радиус | 1 |
| Диаметр | 1 |
| Обхват | 3 |
| Автоморфизмы | 24 |
| Хроматическое число | 4 |
| Свойства | Гамильтониан, правильный, симметричный, дистанционно-регулярный, дистанционно-транзитивный, 3-вершинно-связанный, планарный граф |
| Таблица графов и параметров |
скелет тетраэдра (содержащий вершины и ребра) образует граф с 4 вершинами и 6 ребрами. Это частный случай полного графа, K 4 и колесного графа, W 4. Это один из 5 платоновых графов, каждый из которых является скелетом своего платонового тела.

См. Также
- спираль Бурдейка – Кокстера
- Конфигурация Мёбиуса
- Caltrop
- Демигиперкуб и симплекс — n-мерные аналоги
- Пентахорон — 4-мерный аналог
- Tetra Pak
- Тетраэдрический воздушный змей
- Тетраэдрическое число
- Упаковка тетраэдра
- Треугольная дипирамида — построена путем соединения двух тетраэдров вдоль одной грани
- Треугольный тетраэдр
Ссылки
Внешние ссылки
| На Викискладе есть материалы, связанные с Тетраэдр . |
- Вайсштейн, Эрик У. «Тетраэдр». MathWorld.
- Бесплатные бумажные модели тетраэдра и многих других многогранников
- Удивительный, заполняющий пространство, нерегулярный тетраэдр, который также включает описание «вращающегося кольца тетраэдров», также известного как a калейдоцикл.
Фундаментальный выпуклый правильный и равномерный многогранник в измерениях 2–10 |
||||
|---|---|---|---|---|
| An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn |
| Треугольник | Квадрат | p -угольник | Шестиугольник | Пентагон |
| Тетраэдр | Октаэдр • Куб | Демикуб | Додекаэдр • Икосаэдр | |
| 5-элементный | 16 ячеек • Tesseract | Demitesseract | 24-элементный | 120-элементный • 600-элементный |
| 5-симплексный | 5-ортоплекс • 5-куб | 5-полукуб | ||
| 6-симплекс | 6-ортоплекс • 6-куб | 6-полукуб | 122 • 221 | |
| 7-симплекс | 7-ортоплекс • 7-куб | 7-полукуб | 132 • 231 • 321 | |
| 8-симплекс | 8-ортоплекс • 8-куб | 8-полукуб | 142 • 241 • 421 | |
| 9-симплекс | 9-ортоплекс • 9-куб | 9-демикуб | ||
| 10-симплекс | 10-ортоплекс • 10-куб | 10-полукуб | ||
| n-симплекс | n-ортоплекс • n- куб | n-полукуб | 1k2 • 2k1 • k21 | n-пятиугольный многогранник |
| Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и соединений |
Материал урока.
В начале изучения
курса «Стереометрии» мы говорили, что все геометрические тела делятся на тела
вращения и многогранники. В процессе изучения геометрии в десятом классе, мы
будем подробно рассматривать с вами свойства тех или иных фигур.
Сегодня мы
познакомимся с такой фигурой как тетраэдр. Прежде чем приступить к изучению
пространственной фигуры, давайте вернемся в планиметрию и вспомним такую фигуру
как многоугольник.
Напомню, что многоугольником
называется либо замкнутая линия без самопересечений либо часть плоскости, ограниченная
этой линией, включая ее саму.
Для стереометрии
нам естественно подходит второе определение. Это определение показывает, что
каждый многоугольник представляет собой плоскую поверхность.
Напомним, что простейшим
многоугольником является треугольник. Возьмем треугольник ABC
и точку D, которая не лежит в плоскости треугольника ABC. Соединим точку D с каждой
вершиной треугольника ABC. Таким образом, мы получим
три новых треугольника DAB, DBC,
DCA. Тогда фигуру, которая состоит из четырех
треугольников ABC, DAB, DBC, DCA, называют тетраэдром и
обозначают так: DABC.
Треугольники, из
которых состоит тетраэдр, называются гранями, стороны этих треугольников
называют ребрами, вершины этих треугольников называются вершинами
тетраэдра.
Нетрудно посчитать,
что тетраэдр имеет четыре грани, 6 ребер и четыре вершины. Два ребра тетраэдра,
которые не имеют общих вершин, называются противоположными. Давайте
запишем пары противоположных ребер тетраэдра, который изображен на рисунке.
Это будут ребра AD и BC, BDи AC, CD и AB.
Иногда одну из граней тетраэдра называют основанием, а три другие – боковыми
гранями.
Слово тетраэдр
произошло от древнегреческих слов теторес – четыре и эдра –
основание или грань.
Если все грани
тетраэдра – равносторонние треугольники, то такой тетраэдр называется правильным.
Правильный тетраэдр является одним из пяти правильных многогранников. Они еще
называются телами Платона. Это — тетраэдр, гранями которого
являются четыре правильных треугольника, куб с шестью квадратными гранями, октаэдр,
имеющий восемь треугольных граней, додекаэдр, гранями которого являются
двенадцать правильных пятиугольников, и икосаэдр с двадцатью
треугольными гранями.
Последователи
Пифагорейской философской школы форму тетраэдра придавали стихии огня.
Тетраэдр, все грани
которого равные между собой треугольники, называется равногранным тетраэдром.
Если ребра
тетраэдра, которые прилегают к одной вершине, перпендикулярны между собой, то
такой тетраэдр называется прямоугольным.
Тетраэдры обычно
изображаются в виде выпуклого или невыпуклого четырехугольника с диагоналями. При
этом штриховыми линиями изображаются невидимые ребра.
На этом рисунке
невидимым является только ребро AC.
А на этом рисунке
невидимыми являются ребра ЕК, KF, KL.
Тетраэдр образует
жёсткую, статически определимую конструкцию. Тетраэдр, выполненный из стержней,
часто используется в качестве основы для пространственных несущих конструкций
пролётов зданий, перекрытий, балок, ферм, мостов.
Ярким примером
тетраэдра является разработанное для Нового Орлеана «здание-город», которое
возвышается на 360 метров, включает в себя 20000 квартир, суммарная жилая
площадь которых 2040000 квадратных метров. Здание использует экологичное
энергоснабжение — энергию ветра, воды и солнца. Кроме квартир в тетраэдре
помещаются коммерческие организации, три отеля, культурные объекты, школа,
больницы и казино. И, учитывая место, под которое создавался проект, его
немаловажная особенность — способность держаться на плаву.
Решим насколько
задач.
Задача. Назовите
все пары скрещивающихся рёбер тетраэдра . Сколько таких пар рёбер имеет тетраэдр?
Решение.
Напомним, что две
прямые называются скрещивающимися, если они не лежат в одной плоскости.
Нетрудно увидеть,
что скрещивающимися будут ребра AB и СD,
АC и BD, АD
и BC. То есть в тетраэдре есть три пары скрещивающихся
ребер.
Задача. В
тетраэдре
,
,
,
,
,
. Найти рёбра основания
данного
тетраэдра.
Решение.
Задача. Пусть
точки и
– середины рёбер
и
тетраэдра
. Доказать, что прямая
параллельна плоскости
.
Доказательство.
Что и
требовалось доказать.
Подведем итоги
урока. Сегодня на уроке мы познакомились с пространственным многогранником
– тетраэдром. Познакомились с элементами тетраэдра, решили несколько задач по
данной теме.
Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:
Скачиваний:
109
Добавлен:
16.03.2016
Размер:
1.78 Mб
Скачать

Гл а в а 6
Тетраэдр
§1. Медианы и бимедианы тетраэдра. Центроид
1.1.Бимедианы (средние линии) тетраэдра. Простейшим многогранником является тетраэдр — четырехгранник. Он обладает многими замечательными свойствами, совокупность которых принято называть геометрией тетраэдра. В этой главе излагаются ее начала.
Отрезки, каждый из которых соединяет середины противоположных (скрещивающихся) ребер тетраэдра, называются его бимедианами (средними линиями).
Теорема 1. Бимедианы тетраэдра пересекаются в одной точке, которая делит пополам каждую из них.
Д о к а з а т е л ь с т в о 1. Пусть MN, EF и P Q — бимедианы тетраэдра ABCD, соответствующие парам ребер AB и CD, AC и BD, BC и AD (рис. 74). Так как отрезки ME и F N параллельны BC и равны
B
E
M
Рис. 74
половине BC, то четырехугольник EMF N — параллелограмм. Точка G пересечения его диагоналей MN и EF делит их пополам. Из параллелограмма EP F Q следует, что середины бимедиан EF и P Q совпадают с точкой G.

Рис. 75
K
G
До к а з а т е л ь с т в о 2. Для произвольной точки O векторы OM =
=12 (OA + OB) и ON = 12 (OC + OD). Поэтому 12 (OM + ON) = 14 (OA +
+ OB + OC + OD). Следовательно, вектор OG середины G отрезка MN имеет выражение
|
= |
1 |
( |
+ |
+ |
+ |
), |
(6.1) |
||||||
|
OG |
OA |
OB |
OC |
OD |
|||||||||
|
4 |
|||||||||||||
в которое векторы вершин тетраэдра входят равноправно (симметрично). Это значит, что векторы середин отрезков EF и P Q также равны OG, т. е. середины бимедиан MN, EF и P Q совпадают. 
выражение (6.1).
1.2. Медианы тетраэдра. Отрезки, каждый из которых соединяет вершину тетраэдра с центроидом противоположной грани, называются
медианами тетраэдра.
Теорема 2. Медианы тетраэдра пересекаются в его центроиде и делятся им в отношении 3 : 1, считая от вершин.
Д о к а з а т е л ь с т в о 1. Пусть G1 и G2 — центроиды граней BCD
иACD тетраэдра ABCD (рис. 75). Они принадлежат медианам BN
иAN этих граней. По свойству цен-
троида треугольника AG2 : G2N = 2
иBG1 : G1N = 2. По обратной теореме Фалеса G1G2 k AB. На основании свойства трапеции прямые AG1, BG2
иMN пересекаются в одной точке K.
|
G2 |
D |
По теореме Менелая для треугольни- |
ка AMN и прямой BG2 имеем:
|
B |
N |
AB |
· |
MK |
· |
NG2 |
= −1, |
|
G1 |
BM |
KN |
G2A |
Cоткуда −2 MK · 12 = −1 и MK : KN =KN
= 1, т. е. точка K является серединой
бимедианы MN и потому совпадает
с центроидом G тетраэдра. Итак, две медианы AG1 и BG2 пересекаются в центроиде G. Значит, все четыре медианы имеют общую точку G. По теореме Менелая для треугольника ABG1 и прямой MN
AM · BN · G1G = −1,
MB NG1 GA
92

|
G1G |
1 |
||||||||||||||||||||||||
|
или 1 · (−3) · |
= −1, откуда G1G : GA = |
. Ясно, что это отношение |
|||||||||||||||||||||||
|
3 |
|||||||||||||||||||||||||
|
GA |
|||||||||||||||||||||||||
|
не зависит от выбора медианы. |
|||||||||||||||||||||||||
|
Д о к а з а т е л ь с т в о 2. |
Возьмем одну медиану AG1 и разделим ее |
||||||||||||||||||||||||
|
в отношении 3 : 1 некоторой точкой P : |
|||||||||||||||||||||||||
|
= |
OA + 3OG1 |
, |
где |
= |
1 |
( |
+ |
+ |
). |
||||||||||||||||
|
OP |
OG1 |
OB |
OC |
OD |
|||||||||||||||||||||
|
3 |
|||||||||||||||||||||||||
|
1 + 3 |
Тогда OP = 14 (OA + OB + OC + OD) = OG и точка P совпадает с G. Следовательно, все четыре медианы тетраэдра содержат его центроид и делятся им в отношении 3 : 1, считая от вершин.
1.3. Свойства центроида тетраэдра. Для того чтобы точка G была центроидом тетраэдра ABCD, необходимо и достаточно, чтобы
|
GA + GB + GC + GD = 0. |
(6.2) |
Д о к а з а т е л ь с т в о. Если G — центроид тетраэдра ABCD, то имеет место равенство (6.1) для произвольной точки O. Когда точка O совпадает с G, то OG = 0 и (6.1) принимает вид (6.2). Обратно,
пусть для некоторой точки G имеет место равенство (6.2), из которого GA + GB = −(GC + GD), или 12 (GA + GB) = −12 (GC + GD), или
GM = −GN, где M и N — середины ребер AB и CD. Следовательно, точка G является серединой бимедианы MN, т. е. центроидом тетраэдра. 
эдры GBCD, GCDA, GDAB, GABC равновелики.
Действительно, отношение высот AH и GH1 тетраэдров ABCD и GBCD равно отношению AG1 : GG1 = 14 (рис. 75). Эти тетраэдры име-
ют общее основание BCD. Значит, VGBCD = 14 VABCD. Объем каждого из четырех указанных тетраэдров равен четверти объема данного тетраэдра.
В силу этого свойства центроид тетраэдра называют еще центром тяжести этого тетраэдра.
Теорема 3 (Лейбница). Сумма квадратов расстояний от произвольной точки P до вершин тетраэдра A1A2A3A4 равна сумме квадратов расстояний от его центроида G до вершин, сложенной с учетверенным квадратом расстояния от точки P до центроида G:
44
XX
|
P Ai2 = |
GAi2 + 4P G2. |
(6.3) |
|
i=1 |
i=1 |
93

Действительно, P Ai = GAi − GP , откуда
P Ai2 = GAi2 − 2GAi · GP + GP 2
и поэтому
|
4 |
4 |
4 |
|||
|
X |
X |
Xi |
|||
|
P Ai2 = GAi2 − 2 |
GP |
GAi |
+ 4P G2. |
||
|
i=1 |
i=1 |
=1 |
4
P
Так как GAi = 0, то равенство (6.3) доказано.
i=1
Из теоремы Лейбница следует экстремальное свойство центроида тетраэдра: сумма квадратов расстояний от точки до вершин тетраэдра минимальна для его центроида. Оно является характеристическим
свойством центроида тетраэдра.
З а д а ч а. Выразите длину бимедианы тетраэдра через длины его ребер.
Р е ш е н и е. Обозначим DA = a, DB = b, DC = c. Тогда
NM = 12 (a + b − c), и NM2 = 14 (a2 + b2 + c2 + 2ab − 2ac − 2bc).
Пусть |AB| = c1, |AC| = b1, |BC| = a1. Так как 2ab = a2 + b2 − c21, 2ac = = a2 + c2 − b21, 2bc = b2 + c2 − a21, то проведя подстановки, получим:
|
MN2 = |
1 |
(a2 + a12 + b2 + b12 − c2 − c12). |
(6.4) |
|
4 |
Аналогично
EF 2 = 14 (a2+ a21+ c2+ c21−b2−b21), P Q2 = 14 (b2+ b21+ c2+ c21−a2−a21).
|
Отсюда следует: |
|
|
MN2 + EF 2 + P Q2 = 41 (a2 + b2 + c2 + a12 + b12 + c12). |
(6.5) |
§2. Площади граней тетраэдра
2.1.Теорема косинусов для тетраэдра. Квадрат площади любой грани тетраэдра равен сумме квадратов площадей трех остальных его граней без удвоенных произведений площадей этих граней, взятых попарно, и косинусов двугранных углов между ними.
Д о к а з а т е л ь с т в о 1. Воспользуемся формулой (3.3) ортогональной проекции трех граней на плоскость четвертой грани, применяя ее
94

для каждой грани тетраэдра ABCD:
S1 = S2 cos(CD) + S3 cos(BD) + S4 cos(BC),
S2 = S1 cos(CD) + S3 cos(AD) + S4 cos(AC),
(6.6)
S3 = S1 cos(BD) + S2 cos(AD) + S4 cos(AB), S4 = S1 cos(BC) + S2 cos(AC) + S3 cos(AB).
Умножим эти равенства соответственно на S1, S2, S3, S4 и затем найдем:
S42 − S12 − S22 − S32 = −2S1S2 cos(CD) − 2S2S3 cos(AD) − 2S1S3 cos(BD),
или
S42 = S12 + S22 + S32 − 2S1S2 cos(CD) − 2S2S3 cos(AD) − 2S1S3 cos(BD),
(6.7)
что и утверждает теорема косинусов.
В частности, если двугранные углы при ребрах AD, BD, CD прямые, то
|
S42 = S12 + S22 + S32. |
(6.8) |
Соотношение (6.8) представляет собой стереометрический аналог теоремы Пифагора. 
−n4 = n1 + n2 + n3 возведем скалярно в квадрат:
n24 = n21 + n22 + n23 + 2n1 n2 + 2n2 n3 + 2n1 n3.
Косинус угла между гранями тетраэдра отличается лишь знаком от косинуса угла между перпендикулярными к ним векторами ni, а |ni| = Si. Тогда снова приходим к зависимости (6.7).
2.2. Сумма квадратов площадей граней тетраэдра равна сумме квадратов площадей трех непараллельных граней описанного около него параллелепипеда.
Д о к а з а т е л ь с т в о 1. Определение описанного параллелепипеда дано в п. 3.2 гл. 1. Воспользуемся результатом задачи п. 1.4 гл. 3, согласно которому
2 2 − 1 · 2 2
S1 + S2 2S1S2cos(CD) = 4 AB CD sin(AB, CD) = F1 .
Правая часть этого равенства представляет собой квадрат площади F соответствующей грани описанного параллелепипеда. Аналогично
S12 + S32 − 2S1S3 cos(BD) = F22,
S12 + S42 − 2S1S4 cos (BC) = F32.
95

Складывая эти три равенства, получим:
F12 + F22 + F32 =
= S22 + S32 + S42 − 2S1(S2 cos(CD) + S3 cos(BD) + S4 cos(BC)) + 3S12 =
= S22 + S32 + S42 − 2S1S1 + 3S12 = S12 + S22 + S32 + S42.
|
Д о к а з а т е л ь с т в о 2. |
Используем |
принятые |
обозначения. По |
||||||||||||||||||||||||||||||||||||||||||||
|
определению векторного произведения |
|||||||||||||||||||||||||||||||||||||||||||||||
|
(2S1)2 = ( |
× |
)2, (2S2)2 = ( |
× |
)2, (2S3)2 = ( |
× |
)2, |
|||||||||||||||||||||||||||||||||||||||||
|
b |
b |
||||||||||||||||||||||||||||||||||||||||||||||
|
c |
c |
a |
a |
||||||||||||||||||||||||||||||||||||||||||||
|
(2S4)2 = ( |
− |
) × ( |
− |
) |
2 , (2F1)2 = |
× ( |
− |
) |
2 , |
||||||||||||||||||||||||||||||||||||||
|
b |
b |
||||||||||||||||||||||||||||||||||||||||||||||
|
a |
a |
c |
c |
a |
|||||||||||||||||||||||||||||||||||||||||||
|
(2F2)2 = |
(a |
c) |
2 , |
(2F3)2 |
= a |
( |
c) |
2 . |
|||||||||||||||||||||||||||||||||||||||
|
b |
b |
||||||||||||||||||||||||||||||||||||||||||||||
|
× |
− |
× |
− |
||||||||||||||||||||||||||||||||||||||||||||
Тогда доказываемое равенство принимает вид:
(a × b)2 + (b × c)2 + (c × a)2 + (a − b) × (a − c) 2 =
=a × (b − c) 2 + b × (a − c) 2 + c × (b − a) 2 .
Оно верно, так как обе части легко преобразуются к одному и тому же выражению
2 (a × b)2 + (b × c)2 + (c × a)2+
+ (a × b)(b × c) + (b × c)(c × a) + (c × a)(a × b) .
2.3. Зависимость между косинусами двугранных углов тетраэдра.
Запишем систему (6.6) так:
|
−S1 cos(CD) − S2 |
+ |
S3 cos(AD) + S4 cos(AC) = 0, |
||||
|
S1 |
+ S2 cos(CD) + |
S3 cos(BD) + S4 cos(BC) = 0, |
||||
|
S1 cos(BD) + S2 cos(AD) |
S3 |
+ S4 cos(AB) = 0, |
||||
|
− |
= 0. |
|||||
|
S1 cos(BC) + S2 cos(AC) + S3 cos(AB) − S4 |
||||||
Она является линейной однородной системой относительно S1, S2, S3, S4. Так как она заведомо имеет ненулевое решение, то ее определитель
необходимо равен нулю:
|
−1 |
cos(CD) |
cos(BD) cos(BC) |
|||||
|
−1 |
− |
||||||
|
cos(CD) |
cos(AD) |
cos(AC) |
= 0. |
(6.9) |
|||
|
cos(AD) |
1 |
||||||
|
cos(BD) |
cos(AB) |
||||||
|
− |
|||||||
|
cos(AC) |
cos(AB) |
1 |
|||||
|
cos(BC) |
|||||||
96

§3. Объем тетраэдра и объем клина
3.1.Первая формула Штаудта. За исходные формулы объема тетраэдра возьмем две известные формулы:
|
V = |
1 |
Sh и V = |
1 |
| |
(6.10) |
||||||
|
abc|, |
|||||||||||
|
3 |
6 |
где a, b, c — векторы трех ребер тетраэдра с общим началом в его вершине. Выведем другие формулы объема тетраэдра.
Пусть AH — высота тетраэдра ABCD, AP — высота его грани
|
ACD (рис. 76). Тогда AH = AP sin(CD) = a sin ADC sin(CD). Поэтому |
||||||||||||||
|
1 |
1 |
|||||||||||||
|
V = 3 SBCD ·AH = |
6 abc sin ADC sin BDC sin(CD). |
|||||||||||||
|
A |
||||||||||||||
|
Произведение sin ADC sin BDC sin(CD) есть си- |
||||||||||||||
|
нус Штаудта Δ(D) трехгранного угла D(ABC). |
||||||||||||||
|
a |
Итак, |
|||||||||||||
|
C |
1 |
|||||||||||||
|
B |
c |
V = |
abcΔ(D). |
(6.11) |
||||||||||
|
H |
P |
6 |
||||||||||||
|
b |
D |
Эта формула известна под именем немецкого гео- |
||||||||||||
метра Карла Штаудта (1798–1867), профессора
Рис. 76
Эрлангенского университета. Без использования обозначений ее можно высказать так: объем тетраэдра равен шестой части произведения длин трех ребер с общей вершиной и синуса Штаудта его триэдра с этой вершиной.
Формула V = 16 |abc| следует из геометрического смысла модуля смешанного произведения векторов (п. 1.3, гл. 5). Из нее сразу же получается формула (6.11), если принять во внимание выражение (5.19) синуса Штаудта через смешанное произведение единичных векторов ребер триэдра:
V = 16 |abc| = 16 abc|abcabc | = 16 abcΔ(D),
|
abc |
|||||||||||||||||||||
|
так как |
abc |
= Δ(D). |
|||||||||||||||||||
|
3.2. Формулы |
Достора. По формуле Штаудта |
||||||||||||||||||||
|
V = |
1 |
abc sin ADCsin BDCsin(CD) = |
|||||||||||||||||||
|
6 |
bc sin ADC ac sin BDC |
||||||||||||||||||||
|
1 |
sin(CD) |
1 |
sin(CD) |
||||||||||||||||||
|
= |
= |
· 2S12S2 |
. |
||||||||||||||||||
|
Итак, |
6 |
c |
6 |
CD |
|||||||||||||||||
|
V = |
2 |
S1S2 |
sin(CD) |
. |
(6.12) |
||||||||||||||||
|
3 |
CD |
97

Аналогично
|
V = |
2 |
S3S4 |
sin(AB) |
= |
2 |
S1S3 |
sin(BD) |
= . . . |
|
|
3 |
AB |
3 |
BD |
||||||
Следствие. Умножим почленно два из этих равенств:
|
V 2 = |
4 |
(S1S2)(S1S3) |
sin(CD) sin(BD) |
· |
sin BDC |
|||||||||||
|
. |
||||||||||||||||
|
9 |
CD |
· |
BD |
|||||||||||||
|
sin BDC |
||||||||||||||||
|
0 |
(D) |
|||||||||||||||
|
Произведение sin(CD) sin(BD) sin BDC есть синус второго рода |
||||||||||||||||
|
триэдра D(ABC) |
(п. 3.3, гл. 2), |
. Следова- |
||||||||||||||
|
а CD · BD sin BDC = 2S1 |
||||||||||||||||
|
тельно, |
||||||||||||||||
|
V 2 = |
2 |
S1S2S3 · 0(D). |
(6.13) |
|||||||||||||
|
9 |
3.3. Формула Сервуа. Используем параллелепипед, описанный около данного тетраэдра ABCD. Четыре тетраэдра, дополняющие данный тетраэдр до этого параллелепипеда, равновелики. Объем каждого из них равен 1/6 объема V параллелепипеда. Поэтому
|
D |
1 |
1 |
||
|
VABCD = V − 4 |
· 6 V = 3 V. |
|||
|
Объем тетраэдра составляет треть объема |
|||
|
описанного около него параллелепипеда. |
|||
|
d |
Q |
Высота параллелепипеда равна расстоя- |
|
|
A |
нию d между противоположными ребрами |
||
|
C |
тетраэдра, а площадь основания равна поло- |
||
|
P |
вине произведения длин этих ребер и синуса |
||
|
B |
|||
|
угла f между ними. Таким образом, |
|||
Рис. 77
|
VABCD = |
1 |
aa1d sin f. |
(6.14) |
|
|
6 |
||||
Приведем еще два доказательства формулы Сервуа (6.14). Дополним тетраэдр ABCD до треугольной призмы (рис. 77), объем
которой втрое больше объема данного тетраэдра и равен половине площади aa1 sin f боковой грани, умноженной на расстояние d от ребра DA до этой грани. В результате получается формула (6.14).
Векторное доказательство ее таково. Пусть P Q — общий перпендикуляр ребер BC и DA. Тогда DC = DQ+ QP + P C и поэтому получаем:
6V = DA DB DC = DA DC + CB DC = DA CB DC =
= DA CB(DQ + QP + P C) = DA CB QP = (DA × CB)QP .
98

Векторы DA × CB и QP коллинеарны, поэтому их скалярное произведение равно произведению их модулей. А поскольку |DA × CB| = aa1 ×
× sin f и |QP | = d, то 6V = aa1d sin f. Здесь учтено, что первоначальная тройка векторов правая.
Из формулы Сервуа следует теорема Штейнера: объем тетраэдра не изменяется, если его противоположные ребра перемещать без изменения длины по прямым, содержащим эти ребра.
3.4. Теоремы синусов для тетраэдра. Из приведенных формул объема тетраэдра в качестве следствий получаются соотношения, очень похожие на теоремы синусов для треугольника и триэдра.
По формуле Штаудта
6V = abcΔ(D) = a1b1cΔ(C) = a1bc1Δ(B) = ab1c1Δ(A).
Разделим эти равенства почленно на произведение abca1b1c1:
|
´(A) |
= |
´(B) |
= |
´(C) |
= |
´(D) |
= |
6V |
. |
(6.15) |
|
|
a1bc |
ab1c |
abc |
|||||||||
|
abc1 |
abca1b1c1 |
Синусы Штаудта трехгранных углов тетраэдра пропорциональны произведениям длин трех ребер граней, противолежащих этим углам
(первая теорема синусов).
Пользуясь формулой (6.13), аналогичным путем получаем:
|
´0(A) |
= |
´0(B) |
= |
´0(C) |
= |
´0(D) |
= |
9V 2 |
. |
(6.16) |
|
S1 |
S2 |
S3 |
S4 |
2S1S2S3S4 |
Синусы второго рода трехгранных углов тетраэдра пропорциональны площадям противолежащих им граней (вторая теорема синусов).
Далее, перемножим два равенства из (6.12):
|
V 2 = |
4 |
S1S2S3S4 |
sin(AB) sin(CD) |
. |
|
9 |
||||
|
AB · CD |
Из этого соотношения и двух ему аналогичных следует:
|
AB · CD |
= |
BC · AD |
= |
AC · BD |
= |
4S1S2S3S4 |
. (6.17) |
|
|
9V 2 |
||||||||
|
sin(AB) sin(CD) |
sin(BC) sin(AD) |
sin(AC) sin(BD) |
Произведения длин противоположных ребер тетраэдра пропорциональны произведениям синусов соответствующих двугранных углов
(третья теорема синусов).
3.5. Выражение объема тетраэдра через длины его ребер (формула Юнгиуса). Применим формулу (5.15) квадрата смешанного произведения:
|
2 |
. |
|||||||||||||||
|
a |
ab |
ac |
||||||||||||||
|
(6V )2 = ( |
)2 = |
2 |
||||||||||||||
|
b |
||||||||||||||||
|
abc |
||||||||||||||||
|
ab |
bc |
|||||||||||||||
|
2 |
||||||||||||||||
|
bc |
c |
|||||||||||||||
|
ac |
||||||||||||||||
99

Умножим каждую строку этого определителя на 2 и все удвоенные скалярные произведения заменим по теореме косинусов для треугольника:
|
36V 2 = 81 a2 + b2 |
c12 |
2b2− |
1 |
b2 |
+ c2 −a12 . |
||||||||||
|
2 |
a |
2 |
a2 |
+ b2 |
c2 |
a2 |
+ c2 |
b12 |
|||||||
|
a |
2 |
+ c2 − b2 |
b2 + c2 |
a2 |
2c2− |
||||||||||
|
− |
1 |
− |
1 |
||||||||||||
Представим полученный определитель в раскрытом виде. После надлежащих преобразований имеем окончательно:
144V 2 = a2a21(b2 + b21 + c2 + c21 − a2 − a21)+
+b2b21(c2 + c21 + a2 + a21 − b2 − b21) + c2c21(a2 + a21 + b2 + b21 − c2 − c21)−
−(bca1)2 − (cab1)2 − (abc1)2 − (a1b1c1)2. (6.18)
Эта формула впервые была найдена другим путем немецким ученым
И.Юнгиусом (1587–1657) и называется его именем.
3.6.Вторая формула Штаудта. Сообщим пока без доказательства еще одну формулу К. Штаудта:
где R — радиус описанной около тетраэдра сферы и
16Q2 = (aa1 + bb1 + cc1)(bb1 + cc1 − aa1)(cc1 + aa1 − bb1)(aa1 + bb1 − cc1).
Доказательство будет дано в § 4 гл. 8.
Важное значение соотношения (6.19) состоит еще и в том, что оно позволяет получить выражение диаметра описанной около тетраэдра сферы через длины его ребер, если привлечь формулу (6.18):
2 16Q2
(2R) = 144V 2 .
|
3.7. Объем клина. Клином (косоусеченной призмой) называется |
||
|
пятигранник ABCA1B1C1, три боковые грани которого — трапеции, |
||
|
а основания ABC и A1B1C1 — |
треугольники |
|
|
B |
(рис. 78). Боковые ребра AA1, BB1, |
CC1 клина по- |
|
C |
N |
парно параллельны. Обозначим их длины соответ- |
||
|
ственно a, b, c. |
||||
|
M |
S |
|||
|
A |
Клин имеет простую формулу объема: |
|||
|
C1 |
B1 |
V = 31 S (a + b + c), |
(6.20) |
|
|
A1 |
где S — площадь сечения клина плоскостью, пер- |
|||
|
Рис. 78 |
пендикулярной боковым ребрам. |
100
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #

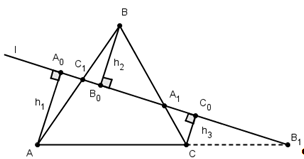
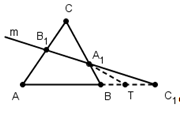

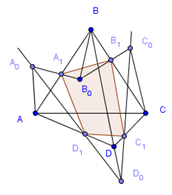
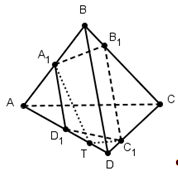
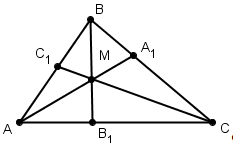
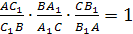
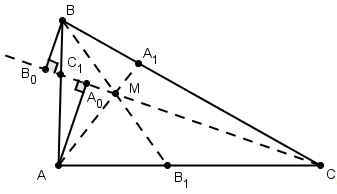
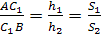
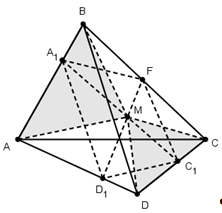
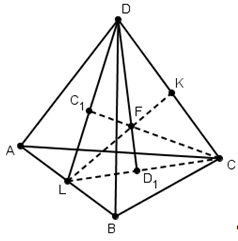
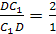
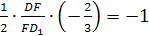
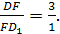
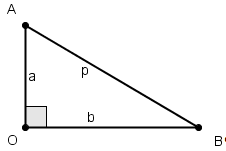
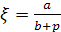
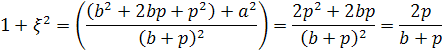
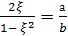
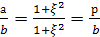
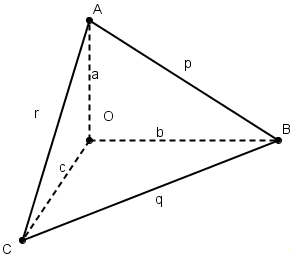
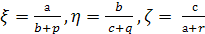
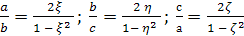
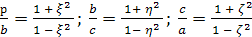
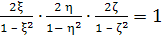
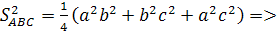
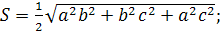
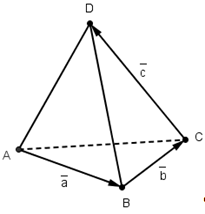
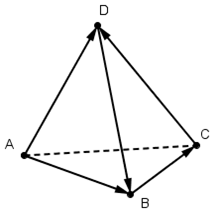
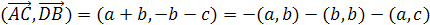
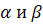
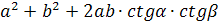
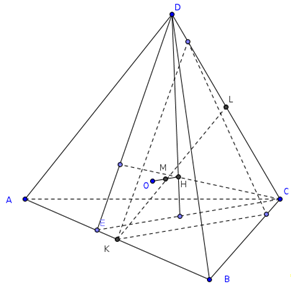
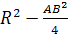
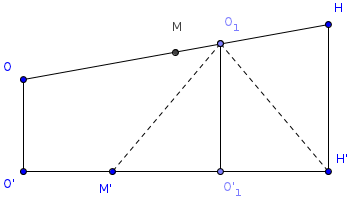
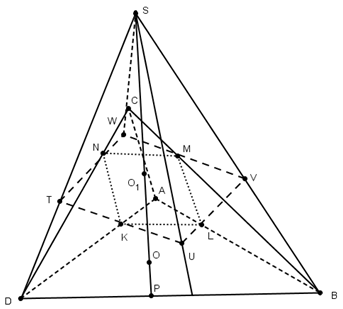
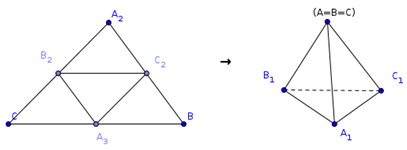
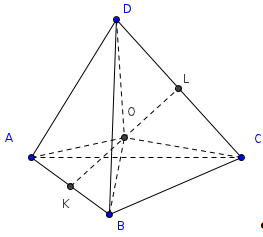
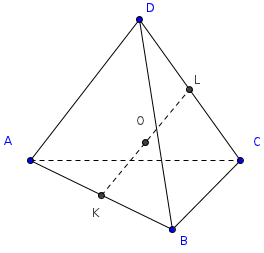
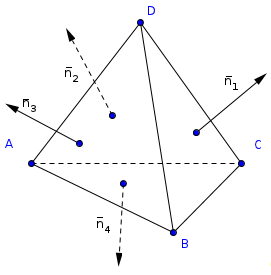
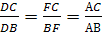
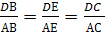
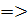
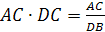
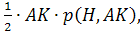
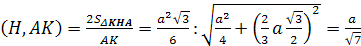
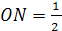
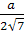
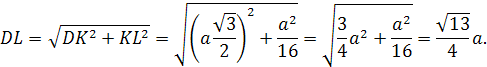
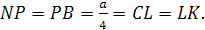
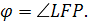
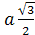
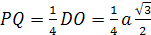
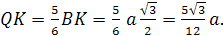
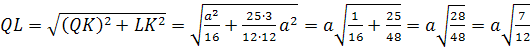
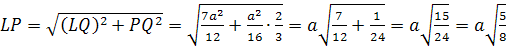
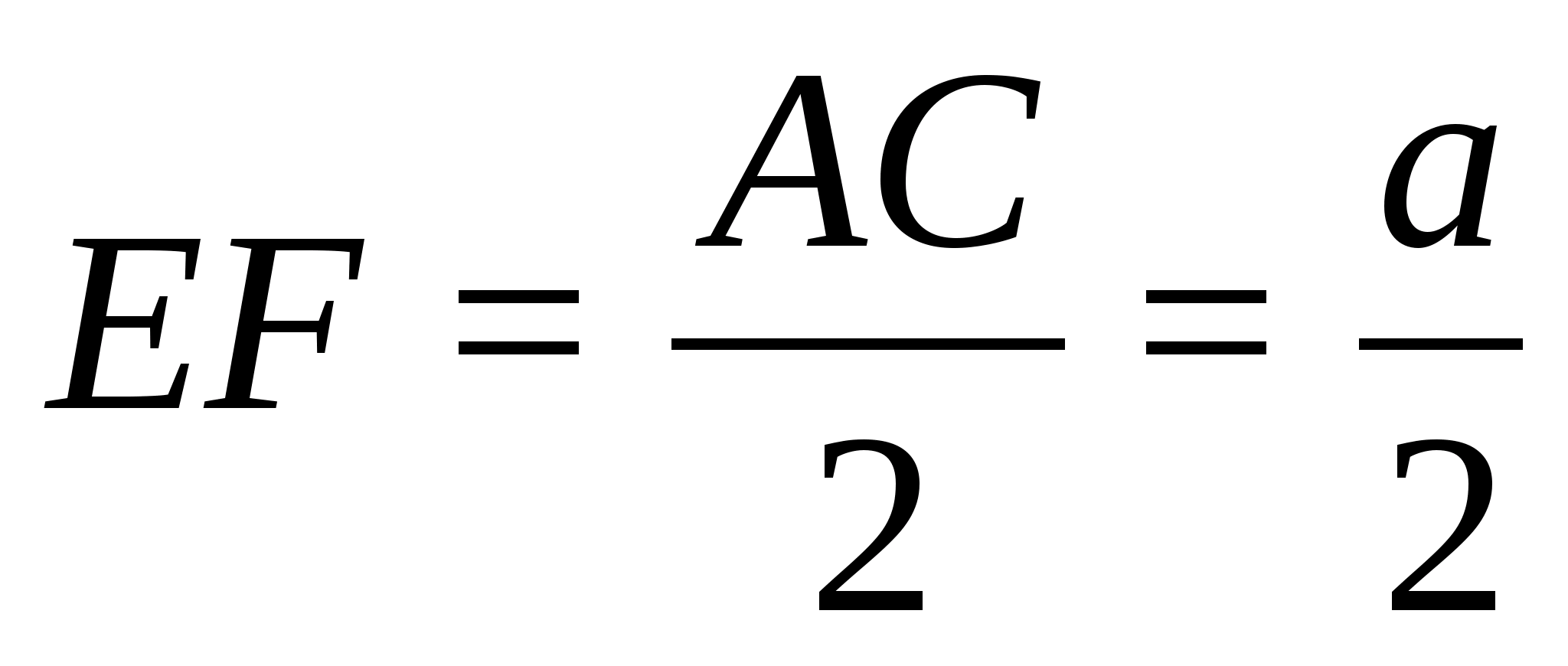
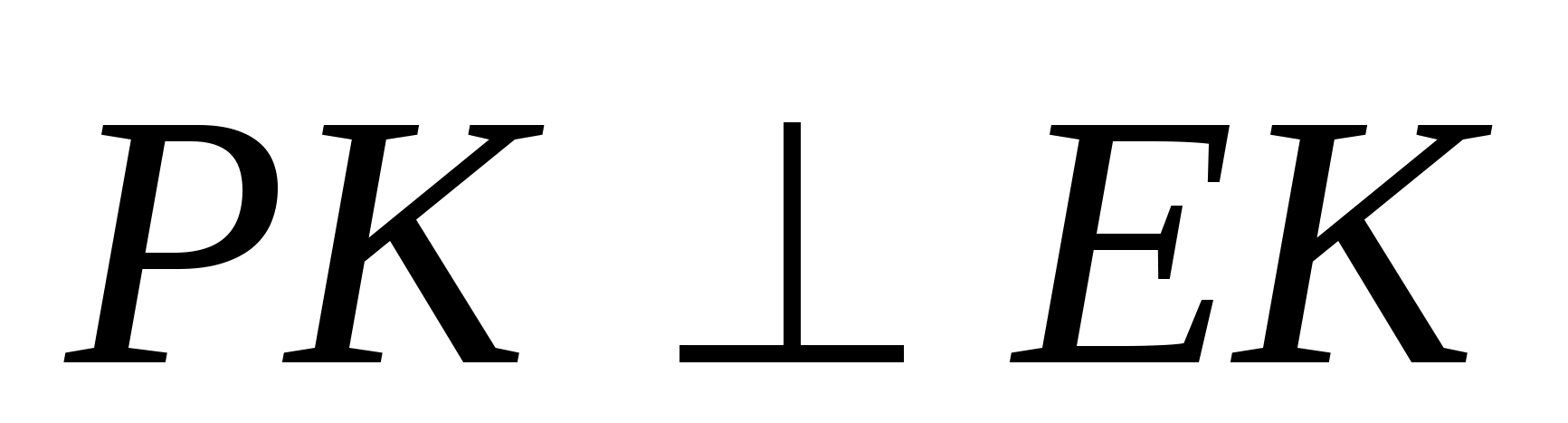
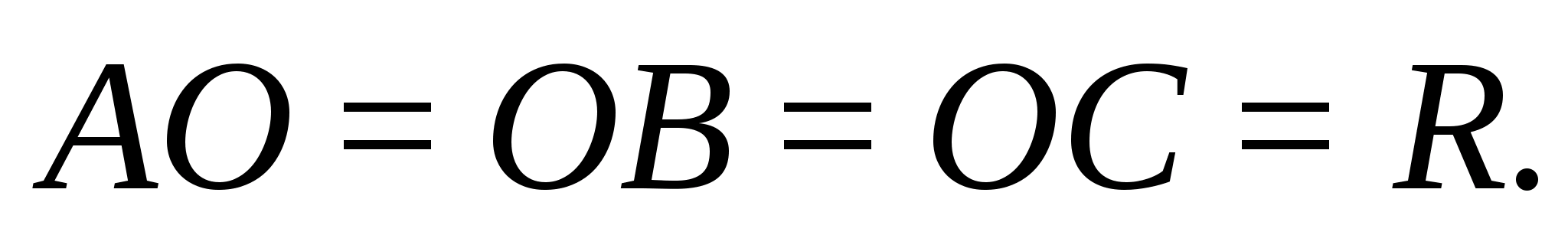
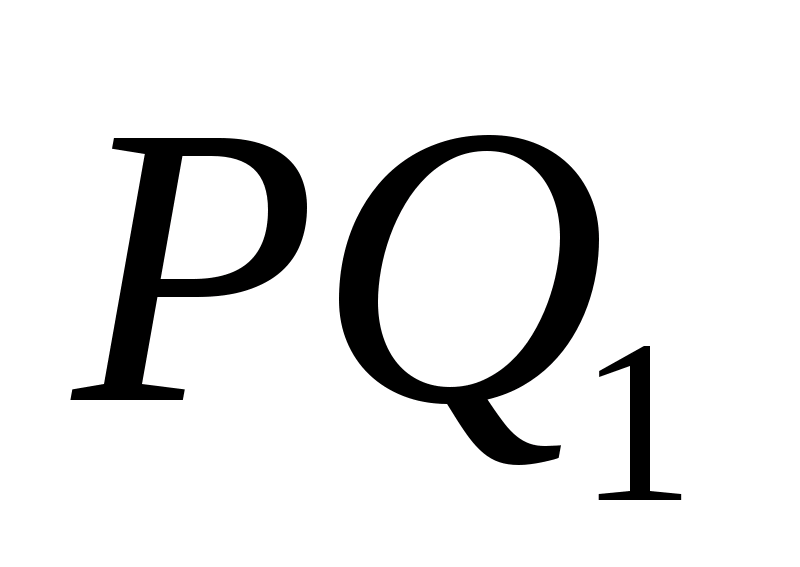
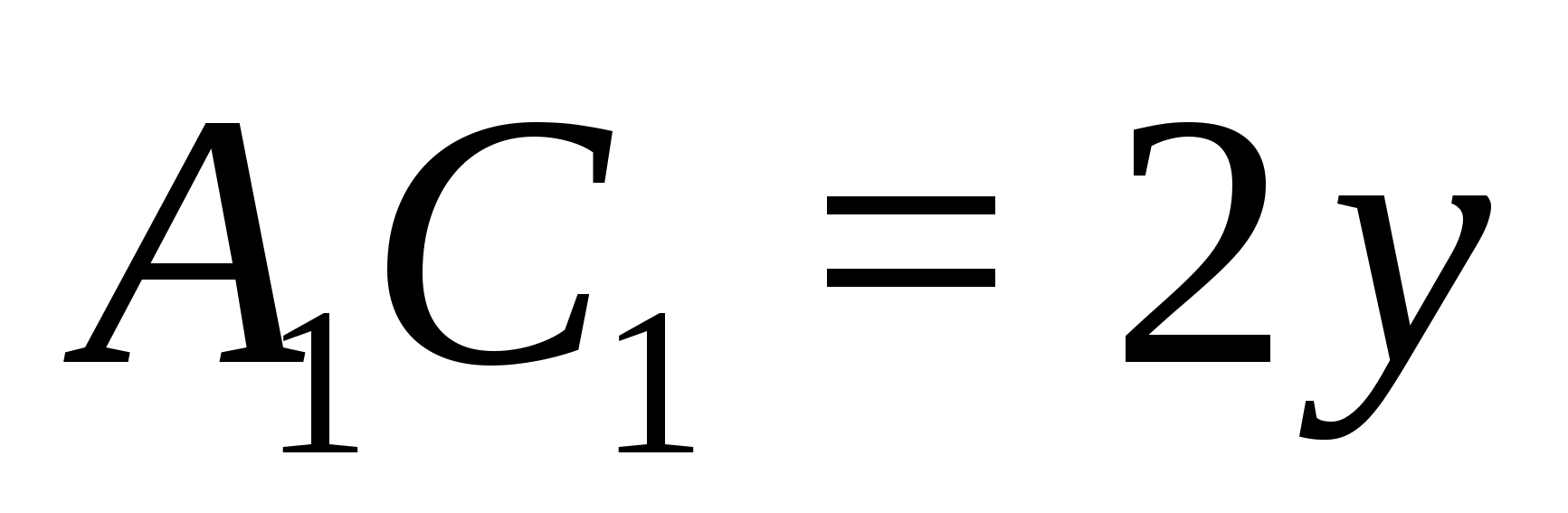
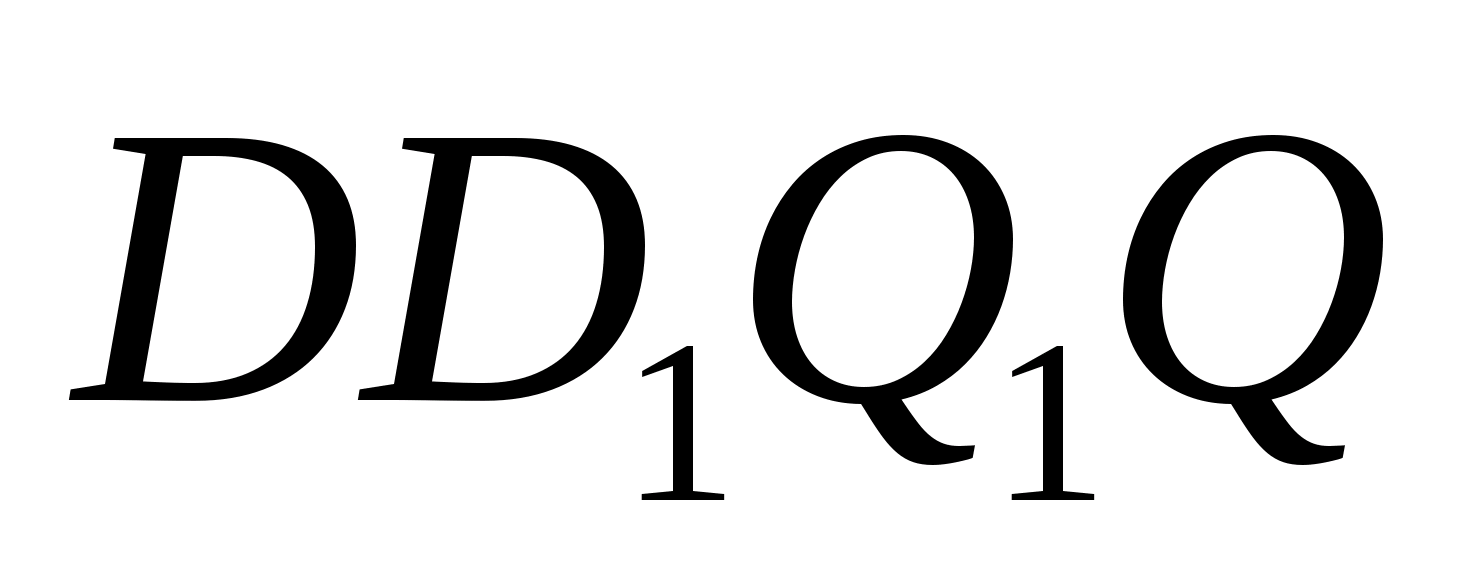

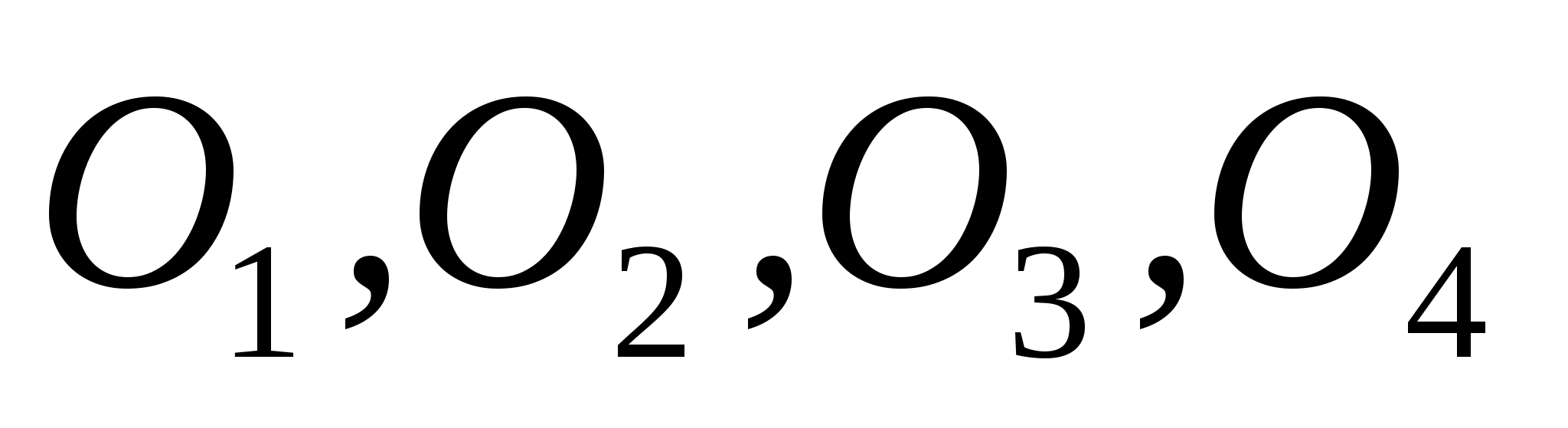
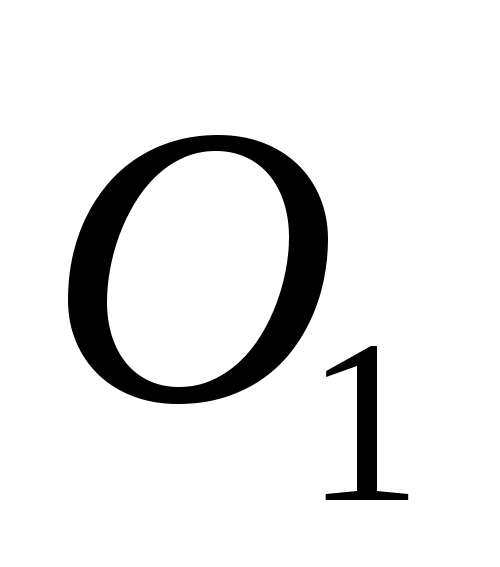





















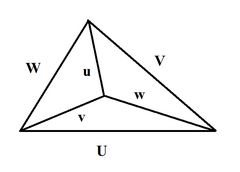












![{displaystyle {begin{aligned}C&=A^{-1}B&{text{where}}& &A=left({begin{matrix}left[x_{1}-x_{0}right]^{T}\left[x_{2}-x_{0}right]^{T}\left[x_{3}-x_{0}right]^{T}end{matrix}}right)& &{text{and}}& &B={frac {1}{2}}left({begin{matrix}|x_{1}|^{2}-|x_{0}|^{2}\|x_{2}|^{2}-|x_{0}|^{2}\|x_{3}|^{2}-|x_{0}|^{2}end{matrix}}right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3bb507beee2d2141b350ce111b961c20b502e219)




 выражается как вектор строки или столбца и т. Д.
выражается как вектор строки или столбца и т. Д. и т. Д.
и т. Д.




![{ displaystyle { begin {align} C = A ^ {- 1} B { text {where}} A = left ({ begin {matrix} left [x_ {1} -x_ {0} right] ^ {T} \ left [x_ {2} -x_ {0} right] ^ {T} \ left [x_ {3} -x_ { 0} right] ^ {T} end {matrix}} right) { text {and}} B = { frac {1} {2}} left ({ begin {matrix } x_ {1} ^ {2} -x_ {0} ^ {2} \ x_ {2} ^ {2} -x_ {0} ^ {2} \ x_ {3} ^ {2} -x_ { 0} ^ {2} end {matrix}} right) \ end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f1c9c2904efa10634ab3061ae18f348a8c851cde)









