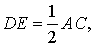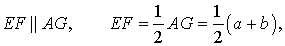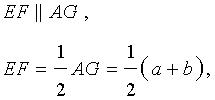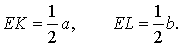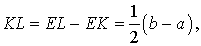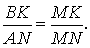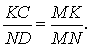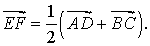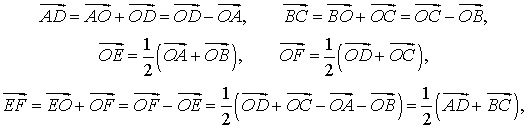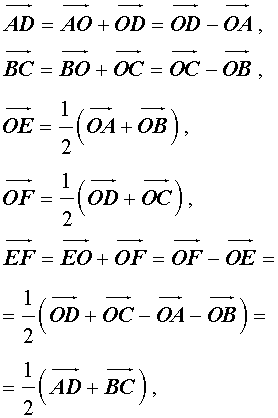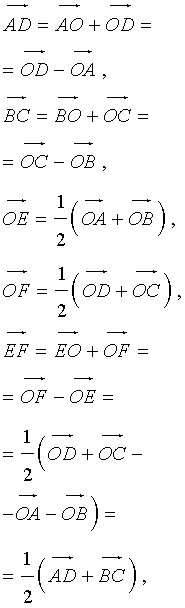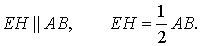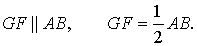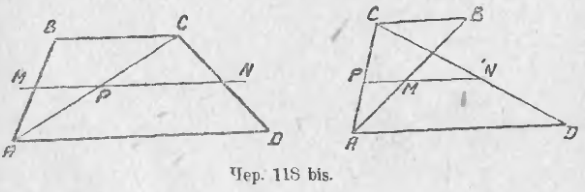Как найти середину прямой в параллелограмме - Avtoru.top

Планиметрия. Страница 4

1 2 3 4 5 6 7 8 9 10 11 12

1.Параллелограмм

Параллелограмм — это геометрическая фигура, у которой диагонали пересекаются в точке, делящей их пополам, а противолежащие стороны параллельны.

Теорема: если диагонали четырехугольника пересекаются и делятся этой точкой пересечения пополам, то такой четырехугольник называется параллелограммом.

Доказательство. Пусть АВСD данный четырехугольник. Точка О — точка пересечения его диагоналей (рис.1). Тогда треугольники Δ АОD и Δ ВOC равны по двум сторонам и углу между ними. А следовательно, угол ODA равен углу CBO и угол OAD равен углу BCO. Таким образом, эти углы являются внутренними накрест лежащими для прямых AD и BC и секущей AC. А по признаку параллельности прямых, прямые AD и BC параллельны. Аналогично можно доказать, что прямая АВ параллельна ВС. Теорема доказана.

Рис.1 Теорема. Параллелограмм.

2.Свойство диагоналей параллелограмма

Теорема. если четырехугольник является параллелограммом, то его диагонали делятся точкой пересечения пополам.

Доказательство. Пусть дан параллелограмм АВСD. (Рис. 2)

Тогда его стороны AD и BC равны и лежат на параллельных прямых а и b. Если мы проведем секущие с и d так, чтобы прямая с проходила через точку А и С, а прямая d проходила через точку B и D, то угол ОАD будет равен углу ОСВ, а угол ОDА будет равен углу ОВС, как внутренние накрест лежащие. Следовательно, треугольники АОD и ВОС равны по стороне и прилегающим к ней углам. А отсюда следует и равенство сторон этих треугольников. Т.е. АО = ОС, а ВО = ОD. Сумма этих сторон и есть диагонали параллелограмма.

Рис.2 Теорема. Свойство диагоналей параллелограмма.

3.Ромб

Ромб — это геометрическая фигура, у которой все стороны равны.

Теорема. диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов.

Доказательство. Пусть АВСD — ромб.(Рис. 3). Тогда треугольник АВС — равнобедренный. А это значит, что отрезок ВО, который является половиной диагонали, является биссектрисой медианой и высотой. Следовательно диагонали ромба АС и ВD пересекаются под прямым углом.

Рис.3 Теорема. Свойство диагоналей ромба.

Задача

В параллелограмме АВСD проведена биссектриса угла А, которая пересекает сторону ВС в точке Е. Необходимо найти отрезки ВЕ и ЕС, если АВ = 9 см, АD = 14 см (рис.4)

Решение. Так как прямая АЕ биссектриса, то это значит, что треугольники АВЕ и АЕР равны. Так как угол ВАЕ равен углу АЕР, а угол ЕАР равен углу ВЕА как внутренние накрест лежащие. Следовательно АВЕР — ромб, так как угол ВАЕ равен углу ЕАР ( по условию). Отсюда следует, что АВ = ВЕ = 9 см, а ЕС = 5 см.

4.Теорема Фалеса

Теорема: параллельные прямые, пересекающие стороны угла и отсекающие на одной его стороне равные отрезки, отсекают равные отрезки и на другой его стороне.

Доказательство. Пусть дан угол и пересекающие его параллельные прямые (рис.5). Точки А 1 А 2 А 3 А 4 и В 1 В 2 В 3 В 4 — точки пересечения. Проведем прямую ОЕ. Тогда А 1 ЕОА 3 — параллелограмм. И ОЕ = А 1 А 3 Треугольники В 1 В 2 Е и ОВ 2 В 3 равны по стороне (ОВ 2 = ЕВ 2 ) и прилегающим к ней углам. Из равенства треугольников следует, что В 1 В 2 = В 2 В 3 .

Рис.5 Теорема Фалеса.

5.Средняя линия треугольника

Теорема. средняя линия треугольника, которая соединяет середины двух данных сторон, параллельна третьей его стороне и равна ее половине.

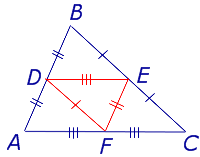
Доказательство. Пусть АВС — треугольник. Отрезок ЕР соединяет середины сторон АВ и ВС (Рис. 5). Тогда по теореме Фалеса отрезок ЕР параллелен основанию АС, так как он делит стороны АВ и ВС на равные части.
Если на стороне АС отметить точку К, которая делит ее пополам и провести отрезок РК, то он будет параллелен стороне АВ. А геометрическая фигура АЕРК будет являться параллелограммом. Отсюда следует, что средняя линия ЕР равна половине основания.
Таким образом, утверждение, что средняя линия треугольника параллельна основанию и равна его половине, верно.

Рис.5 Теорема. Средняя линия треугольника.

6.Трапеция

Трапеция — это геометрическая фигура, у которой только две противолежащие стороны параллельны.

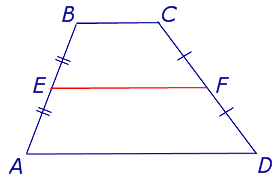
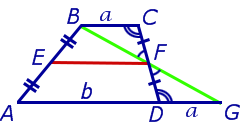
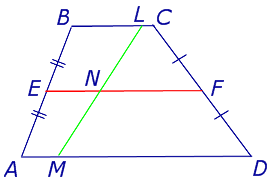
Теорема. средняя линия трапеции параллельна двум своим основаниям и равна их полусумме.

Доказательство. Пусть АВСD — трапеция.(Рис. 6). Проведем прямую от вершины В через середину стороны СD точку Н к основанию, т.е. достроим треугольник АВО. Тогда треугольники ВСН и DHO равны по сторонам СН и НD и прилегающим к ним углам. Следовательно отрезок АО равен сумме оснований АD и ВС. Рассмотрим треугольник АВО. ЕН это средняя линия треугольника, которая равна половине основания АО, т.е. полусумме оснований трапеции АD и ВС.

Рис.6 Теорема. Средняя линия трапеции.

7.Теорема о пропорциональных отрезках

Теорема. параллельные прямые, которые пересекают стороны угла, отсекают от его сторон пропорциональные отрезки.

Доказательство. Пусть дан угол и пересекающие его параллельные прямые.
Необходимо доказать, что AС 1 /AС = AВ 1 /AВ (Рис. 7).

Разобьем угол ВAС параллельными прямыми на n частей. Тогда АВ = ns, a AB1 = ms. Где s — отрезок некоторой длины. По теореме Фалеса эти прямые разбивают сторону AС также на равные части. Тогда:

Рис.7 Теорема о пропорциональных отрезках.

Отложим на луче АС отрезок АС 2 1 , который равен АС 2 = АС*АВ 1 /АВ (Рис.8). Если отрезок АС разбить на большое число частей, то между точками С 1 и С 2 будут деления. Одно из них обозначим как x и y.

Т.е. мы пришли к противоречию, так как изначально мы взяли отрезок АС 2 = АС*АВ 1 /АВ.

Рис.8 Теорема о пропорциональных отрезках.

Пример 1

Через точку пересечения диагоналей параллелограмма проведена прямая. Докажите, что ее отрезок, заключенный между параллельными сторонами, делится этой точкой пополам. (Рис.9)

Доказательство:

Пусть ABCD данный параллелограмм. EF данный отрезок, проходящий через точку О пересечения диагоналей.

Рассмотрим треугольники COF и AOE. Сторона АО треугольника АОЕ равна стороне ОС треугольника COF по свойству параллелограмма. Угол при вершине А треугольника АОЕ равен углу при вершине С треугольника COF, как внутренние накрест лежащие углы. Углы при вершине О у обоих треугольников равны как вертикальные.

Отсюда можно сделать вывод, что треугольники АОЕ и COF равны по второму признаку равенства треугольников (по стороне и прилегающим к ней углам). Следовательно, отрезки OF и ОЕ равны.

Рис.9 Задача. Через точку пересечения диагоналей.

Пример 2

Две стороны параллелограмма относятся как 3:4, а его периметр равен 2,8 м. Найдите стороны параллелограмма. (Рис.10)

Решение:

Пусть ABCD данный параллелограмм. Обозначим сторону АВ как 3х, а сторону ВС как 4х. Тогда составим следующее соотношение:

Рис.10 Задача. Две стороны параллелограмма.

Пример 3

В параллелограмме ABCD перпендикуляр, опущенный из вершины В на сторону AD, делит ее пополам. Найдите диагональ BD и стороны параллелограмма, если периметр параллелограмма равен 4 м, а периметр треугольника ABD равен 3 м. (Рис.11)

Решение:

Так как перпендикуляр BE, опущенный на сторону AD, делит ее пополам, то треугольники ABE и BED равны по первому признаку равенства треугольников (по двум сторонам и углу между ними). У них сторона АЕ равна стороне ED, сторона BE — общая, а углы при вершине Е равны 90°.Отсюда следует, что диагональ BD равна стороне АВ.

Обозначим сторону АВ как х, а сторону AD — как 2y. Тогда можно составить следующие соотношения:

P_ABCD = 2*(х + 2y) = 4, P_ABD = 2x +2y = 3

P_ABCD = 2х + 4y = 4, а 2х = 4 — 4y.

Тогда подставим 4 — 4y во второе уравнение:

4 — 4y + 2y = 3 и,следовательно, y = 0,5, а х = 1

Рис.11 Задача. В параллелограмме ABCD перпендикуляр.

Пример 4

В прямоугольный треугольник, каждый катет которого равен 8 см, вписан прямоугольник, имеющий с треугольником общий угол. Найдите периметр прямоугольника.(Рис.12)

Решение:

Пусть АВС данный треугольник. АВ = АС = 8 см. Тогда углы при вершинах В и С равны 45°. А следовательно, углы при вершине Е в треугольниках FEC и BDE также равны 45°. Если обозначить часть катета АF как х, то FC будет равно 8 — х.

Отсюда следует, что FE = AD = 8-х, а BD = х.

Теперь можно составить следующее соотношение:

Р_ADEF = 2*(х + 8 — х) = 16 см.

Периметр прямоугольника ADEF равен 16 см.

Рис.12 Задача. В прямоугольный треугольник.

Пример 5

Докажите, что если у параллелограмма диагонали перпендикулярны, то он является ромбом.(Рис.13)

Доказательство:

Пусть АВСD данный параллелограмм. По свойству параллелограмма, у него противоположные стороны параллельны и равны. Следовательно, стороны АВ и CD можно рассматривать как параллельные прямые, а диагональ BD — как секущую. Тогда в треугольниках АВО и DOC углы при вершинах B и D равны как внутренние накрест лежащие. Так же как и углы при вершинах А и С.

Отсюда следует, что эти треугольники равны по второму признаку равенства треугольников (по стороне и прилегающим к ней углам). Сторона АВ = DC и внутренние накрест лежащие углы при них равны. Следовательно, АО = ОС, а ВО = OD.

Теперь рассмотрим треугольники AOD и DOC. Они также равны, но по первому признаку равенства треугольников. Сторона АО = ОС, а сторона OD у них общая. Углы при вершине О равны 90°. Т.е. по двум сторонам и углу между ними.

Следовательно, можно сделать вывод, что сторона AD = DC = AB = BC, т.е. данный параллелограмм является ромбом.

Рис.13 Задача. Докажите, что если у параллелограмма.

Формула длины средней линии параллелограмма. Как найти среднюю линию трапеции

Понятие средней линии треугольника

Введем понятие средней линии треугольника.

Это отрезок, соединяющий середины двух сторон треугольника (Рис. 1).

Рисунок 1. Средняя линия треугольника

Теорема о средней линии треугольника

Средняя линия треугольника параллельна одной из его сторон и равна её половине.

Пусть нам дан треугольник $ABC$. $MN$ — средняя линия (как на рисунке 2).

Рисунок 2. Иллюстрация теоремы 1

Так как $frac=frac=frac<1><2>$, то треугольники $ABC$ и $MBN$ подобны по второму признаку подобия треугольников. Значит

Также, отсюда следует, что $angle A=angle BMN$, значит $MN||AC$.

Следствия из теоремы о средней линии треугольника

Следствие 1: Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении $2:1$ начиная с вершины.

Рассмотрим треугольник $ABC$, где $_1, _1, _1$ его медианы. Так как медианы делят стороны пополам. Рассмотрим среднюю линию $A_1B_1$ (Рис. 3).

Рисунок 3. Иллюстрация следствия 1

По теореме 1, $AB||A_1B_1$ и $AB=2A_1B_1$, следовательно, $angle ABB_1=angle BB_1A_1, angle BAA_1=angle AA_1B_1$. Значит треугольники $ABM$ и $A_1B_1M$ подобны по первому признаку подобия треугольников. Тогда

Аналогично доказывается, что

Следствие 2: Три средние линии треугольника делят его на 4 треугольника, подобных исходному треугольнику с коэффициентом подобия $k=frac<1><2>$.

Рассмотрим треугольник $ABC$ со средними линиями $A_1B_1, < A>_1C_1, B_1C_1$ (рис. 4)

Рисунок 4. Иллюстрация следствия 2

Рассмотрим треугольник $A_1B_1C$. Так как $A_1B_1$ — средняя линия, то

Угол $C$ — общий угол этих треугольников. Следовательно, треугольники $A_1B_1C$ и $ABC$ подобны по второму признаку подобия треугольников с коэффициентом подобия $k=frac<1><2>$.

Аналогично доказывается, что треугольники $A_1C_1B$ и $ABC$, и треугольники $C_1B_1A$ и $ABC$ подобны с коэффициентом подобия $k=frac<1><2>$.

Рассмотрим треугольник $A_1B_1C_1$. Так как $A_1B_1, < A>_1C_1, B_1C_1$ — средние линии треугольника, то

Следовательно, по третьему признаку подобия треугольников, треугольники $A_1B_1C_1$ и $ABC$ подобны с коэффициентом подобия $k=frac<1><2>$.

Примеры задачи на понятие средней линии треугольника

Дан треугольник со сторонами $16$ см, $10$ см и $14$ см. Найти периметр треугольника , вершины которого лежат в серединах сторон данного треугольника.

Так как вершины искомого треугольника лежат в серединах сторон данного треугольника, то его стороны — средние линии исходного треугольника. По следствию 2, получим, что стороны искомого треугольника равны $8$ см, $5$ см и $7$ см.

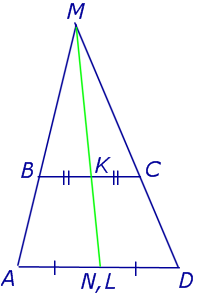
Дан треугольник $ABC$. Точки $N и M$ — середины сторон $BC$ и $AB$ соответственно (Рис. 5).

Периметр треугольника $BMN=14$ см. Найти периметр треугольника $ABC$.

Так как $N и M$ — середины сторон $BC$ и $AB$, то $MN$ — средняя линия. Значит

По теореме 1, $AC=2MN$. Получаем:

Понятие средней линии треугольника

Введем понятие средней линии треугольника.

Это отрезок, соединяющий середины двух сторон треугольника (Рис. 1).

Рисунок 1. Средняя линия треугольника

Теорема о средней линии треугольника

Средняя линия треугольника параллельна одной из его сторон и равна её половине.

Пусть нам дан треугольник $ABC$. $MN$ — средняя линия (как на рисунке 2).

Рисунок 2. Иллюстрация теоремы 1

Так как $frac=frac=frac<1><2>$, то треугольники $ABC$ и $MBN$ подобны по второму признаку подобия треугольников. Значит

Также, отсюда следует, что $angle A=angle BMN$, значит $MN||AC$.

Следствия из теоремы о средней линии треугольника

Рисунок 3. Иллюстрация следствия 1

Аналогично доказывается, что

Рассмотрим треугольник $ABC$ со средними линиями $A_1B_1, < A>_1C_1, B_1C_1$ (рис. 4)

Рисунок 4. Иллюстрация следствия 2

Рассмотрим треугольник $A_1B_1C$. Так как $A_1B_1$ — средняя линия, то

Рассмотрим треугольник $A_1B_1C_1$. Так как $A_1B_1, < A>_1C_1, B_1C_1$ — средние линии треугольника, то

Примеры задачи на понятие средней линии треугольника

Дан треугольник $ABC$. Точки $N и M$ — середины сторон $BC$ и $AB$ соответственно (Рис. 5).

Периметр треугольника $BMN=14$ см. Найти периметр треугольника $ABC$.

Так как $N и M$ — середины сторон $BC$ и $AB$, то $MN$ — средняя линия. Значит

По теореме 1, $AC=2MN$. Получаем:

Понятие средней линии треугольника

Введем понятие средней линии треугольника.

Это отрезок, соединяющий середины двух сторон треугольника (Рис. 1).

Рисунок 1. Средняя линия треугольника

Теорема о средней линии треугольника

Средняя линия треугольника параллельна одной из его сторон и равна её половине.

Пусть нам дан треугольник $ABC$. $MN$ — средняя линия (как на рисунке 2).

Рисунок 2. Иллюстрация теоремы 1

Так как $frac=frac=frac<1><2>$, то треугольники $ABC$ и $MBN$ подобны по второму признаку подобия треугольников. Значит

Также, отсюда следует, что $angle A=angle BMN$, значит $MN||AC$.

Следствия из теоремы о средней линии треугольника

Рисунок 3. Иллюстрация следствия 1

Аналогично доказывается, что

Рассмотрим треугольник $ABC$ со средними линиями $A_1B_1, < A>_1C_1, B_1C_1$ (рис. 4)

Рисунок 4. Иллюстрация следствия 2

Рассмотрим треугольник $A_1B_1C$. Так как $A_1B_1$ — средняя линия, то

Рассмотрим треугольник $A_1B_1C_1$. Так как $A_1B_1, < A>_1C_1, B_1C_1$ — средние линии треугольника, то

Примеры задачи на понятие средней линии треугольника

Дан треугольник $ABC$. Точки $N и M$ — середины сторон $BC$ и $AB$ соответственно (Рис. 5).

Периметр треугольника $BMN=14$ см. Найти периметр треугольника $ABC$.

Так как $N и M$ — середины сторон $BC$ и $AB$, то $MN$ — средняя линия. Значит

По теореме 1, $AC=2MN$. Получаем:

Перед тем как перейти к нахождению средней линии треугольника нужно вспомнить второй признак подобия треугольников и свойства параллельности прямых.

Как найти среднюю линию треугольника – второй признак подобия треугольников

На рисунке 1 показаны два треугольника. Треугольник ABC подобен треугольнику A1B1C1. И прилежащие стороны пропорциональны, то есть AB относится к A1B1 также как AC относится к A1C1. Их этих двух условий и следует подобие треугольников.

Как найти среднюю линию треугольника – признак параллельности прямых

На рисунке 2 показаны прямые a и b, секущая c. При этом образуются 8 углов. Углы 1 и 5 соответственные, если прямые параллельны, то соответственные углы равны, и наоборот.

Как найти среднюю линию треугольника

На рисунке 3, M середина AB, а N середина AC, BC основание. Отрезок MN – называется средней линии треугольника. Сама же теорема гласит – Средняя линия треугольника параллельная основанию и равна его половине.

Для того чтобы доказать, что MN – средняя линия треугольника, нам понадобится второй признак подобия треугольников и признак параллельности прямых.

Треугольник AMN подобен треугольнику ABC, по второму признаку. В подобных треугольниках соответственные углы равны, угол 1 равен углу 2, а эти углы являются соответственными при пересечении двух прямых секущей, следовательно, прямые параллельны, MN параллельно BC. Угол A общий, AM/AB = AN/AC = ½

Коэффициент подобия этих треугольников ½, из этого следует что ½ = MN/BC, MN = ½ BC

Вот мы и нашли среднюю линию треугольника, и доказали теорему о средней линии треугольника, если вам до сих пор не понятно, как найти среднюю линию, смотрите видео ниже.

Средняя линия треугольника

Свойства

средняя линия треугольника параллельна третьей стороне и равна её половине.
при проведении всех трёх средних линий образуются 4 равных треугольника, подобных (даже гомотетичных) исходному с коэффициентом 1/2.
средняя линия отсекает треугольник, который подобен данному, а его площадь равна одной четверти площади исходного треугольника.

Средняя линия четырехугольника

Средняя линия четырехугольника — отрезок, соединяющий середины противолежащих сторон четырехугольника.

Свойства

Первая линия соединяет 2 противоположные стороны. Вторая соединяет 2 другие противоположные стороны. Третья соединяет центры двух диагоналей (не во всех четырехугольниках центры пересекаются)

Если в выпуклом четырехугольнике средняя линия образует равные углы с диагоналями четырехугольника, то диагонали равны.
Длина средней линии четырехугольника меньше полусуммы двух других сторон или равна ей, если эти стороны параллельны, и только в этом случае.
Середины сторон произвольного четырёхугольника — вершины параллелограмма . Его площадь равна половине площади четырехугольника, а его центр лежит на точке пересечения средних линий. Этот параллелограмм называется параллелограммом Вариньона ;
Точка пересечения средних линий четырехугольника является их общей серединой и делит пополам отрезок, соединяющий середины диагоналей. Кроме того, она является центроидом вершин четырехугольника.
В произвольном четырёхугольнике вектор средней линии равен полусумме векторов оснований.

Средняя линия трапеции

Средняя линия трапеции — отрезок, соединяющий середины боковых сторон этой трапеции. Отрезок, соединяющий середины оснований трапеции, называют второй средней линией трапеции.

Свойства

средняя линия параллельна основаниям и равна их полусумме.

См. также

Примечания

Wikimedia Foundation . 2010 .

Смотреть что такое «Средняя линия» в других словарях:

СРЕДНЯЯ ЛИНИЯ — (1) трапеции отрезок, соединяющий середины боковых сторон трапеции. Средняя линия трапеции параллельна её основаниям и равна их полусумме; (2) треугольника отрезок, соединяющий середины двух сторон этого треугольника: третья сторона при этом… … Большая политехническая энциклопедия

Треугольника (трапеции) отрезок, соединяющий середины двух сторон треугольника (боковых сторон трапеции) … Большой Энциклопедический словарь

средняя линия — 24 средняя линия: Воображаемая линия, проходящая через профиль резьбы так, что толщина выступа равна ширине канавки. Источник … Словарь-справочник терминов нормативно-технической документации

Треугольника (трапеции), отрезок, соединяющий середины двух сторон треугольника (боковых сторон трапеции). * * * СРЕДНЯЯ ЛИНИЯ СРЕДНЯЯ ЛИНИЯ треугольника (трапеции), отрезок, соединяющий середины двух сторон треугольника (боковых сторон трапеции) … Энциклопедический словарь

средняя линия — vidurio linija statusas T sritis Kūno kultūra ir sportas apibrėžtis 3 mm linija, dalijanti teniso stalo paviršių išilgai pusiau. atitikmenys: angl. centre line; midtrack line vok. Mittellinie, f rus. средняя линия … Sporto terminų žodynas

средняя линия — vidurio linija statusas T sritis Kūno kultūra ir sportas apibrėžtis Linija, dalijanti fechtavimosi kovos takelį į dvi lygias dalis. atitikmenys: angl. centre line; midtrack line vok. Mittellinie, f rus. средняя линия … Sporto terminų žodynas

средняя линия — vidurio linija statusas T sritis Kūno kultūra ir sportas apibrėžtis Linija, dalijanti sporto aikšt(el)ę pusiau. atitikmenys: angl. centre line; midtrack line vok. Mittellinie, f rus. средняя линия … Sporto terminų žodynas

1) С. л. треугольника, отрезок, соединяющий середины двух сторон треугольника (третью сторону называют основанием). С. л. треугольника параллельна основанию и равна его половине; площади частей треугольника, на которые делит его с. л.,… … Большая советская энциклопедия

Треугольника отрезок, соединяющий середины двух сторон треугольника. Третья сторона треугольника при этом наз. основанием треугольника. С. л. треугольника параллельна основанию и равна половине его длины. Во всяком треугольнике С. л. отсекает от… … Математическая энциклопедия

Треугольника (трапеции), отрезок, соединяющий середины двух сторон треугольника (боковых сторон трапеции) … Естествознание. Энциклопедический словарь

Средние линии

Средние линии треугольника

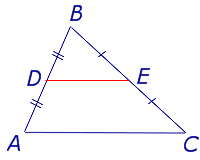
Определение . Средней линией треугольника называют отрезок, соединяющий середины двух сторон треугольника (рис. 1).

На рисунке 1 средней линией является отрезок DE .

Утверждение 1 . Средняя линия треугольника параллельна не пересекающейся с ней стороне треугольника и равна половине этой стороны.

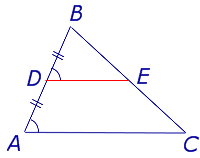
Доказательство . Рассмотрим произвольный треугольник ABC и обозначим буквой D середину стороны AB (рис. 2). Проведем через точку D до пересечения с прямой BC прямую, параллельную прямой AC . Обозначим буквой E точку пересечения прямых DE и BC .

Поскольку AD = DB , а прямые AC и DE параллельны, то выполнены все условия теоремы Фалеса, и можно заключить, что выполнено равенство: CE = EB . Отсюда вытекает, что точка E является серединой стороны CB , а отрезок DE является средней линией треугольника.

Первую часть утверждения 1 мы доказали.

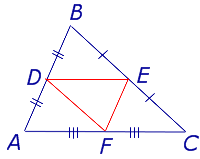
Для того, чтобы доказать вторую часть утверждения 1, заметим, что в любом треугольнике можно провести три средних линии – отрезки DE , EF и FD (рис.3).

Но поскольку AF = FC , то отсюда вытекает равенство

что и требуется доказать.

Доказательство утверждения 1 закончено.

Три средних линии делят треугольник на 4 равных треугольника ADF , DBE , ECF , DEF (рис. 4).
Каждый из четырёх треугольников ADF , DBE , ECF , DEF подобен треугольнику ABC с коэффициентом подобия 0,5 .

Средняя линия трапеции

Напомним, что трапецией трапецией называют четырёхугольник, у которого две стороны параллельны, а две другие – не параллельны.

Параллельные стороны трапеции называют основаниями , а непараллельные стороны – боковыми сторонами трапеции.

Отрезки, соединяющие противоположные вершины трапеции, называют диагоналями трапеции.

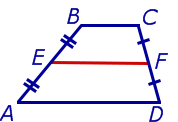
Определение . Средней линией трапеции называют отрезок, соединяющий середины боковых сторон трапеции (рис. 5).

На рисунке 5 средней линией трапеции является отрезок EF .

Утверждение 2 . Средняя линия трапеции параллельна основаниям трапеции и равна половине суммы этих оснований.

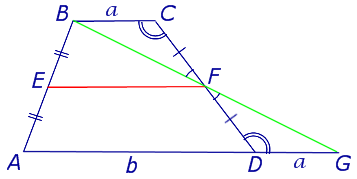
Доказательство . Проведем через вершину B и середину боковой стороны F трапеции прямую линию (рис. 6). Обозначим точку пересечения прямых BF и AD буквой G . Рассмотрим треугольники BCF и FDG . У этих треугольников стороны CF и FD равны, поскольку точка F – середина стороны CD . Углы BCF и FDG равны, поскольку они являются внутренними накрест лежащими углами, образованными при пересечении параллельных прямых BC и AD с секущей CD . Углы BFC и DFG равны, поскольку они являются вертикальными. Тем самым выполнены все условия признака равенства треугольников «По стороне и прилежащим к ней углам», и можно заключить, что треугольники BCF и FDG равны. Из равенства треугольников BCF и FDG следует равенство отрезков BF и FG , откуда вытекает, что отрезок EF является средней линией треугольника ABG . Поэтому

что и требовалось доказать.

Задача 1 . Доказать, что средняя линия трапеции делит пополам любой отрезок с концами на основаниях трапеции.

Решение . Пусть ABCD – трапеция, EF – её средняя линия, LM – указанный отрезок (рис.7). Поскольку AE = EB , то, в силу теоремы Фалеса, выполнено равенство: LN = NM , что и требовалось доказать.

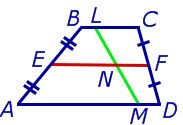
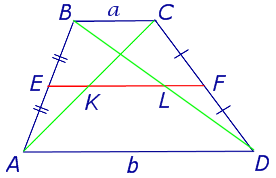
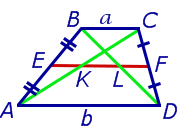
Задача 2 . Доказать, что отрезок, который диагонали трапеции высекают на средней линии трапеции, равен половине разности оснований трапеции.

Решение . Пусть ABCD – трапеция, EF – её средняя линия, KL – указанный отрезок (рис.8). В соответствии с задачей 1 можем заключить, что точка K – середина отрезка AC , а точка L – середина отрезка BD . Поэтому отрезок EK – средняя линия треугольника BAC , а отрезок EL – средняя линия треугольника ABD . В силу утверждения 1 выполнены равенства:

что и требовалось доказать.

Утверждение 3 . Прямая, проходящая через середины оснований трапеции, проходит через точку пересечения боковых сторон трапеции.

Доказательство . Пусть K и L – середины оснований BC и AD трапеции ABCD соответственно (рис.9). Обозначим буквой M точку пересечения боковых сторон AB и CD . Проведем через точки M и K прямую и обозначим точку пересечения этой прямой с основанием AD символом N . Докажем, что точки N и L совпадают. Для этого заметим, что треугольник BMK подобен треугольнику AMN . Следовательно, выполнено равенство:

Из этих соотношений получаем:

откуда вытекает, что точки N и L совпадают. Доказательство завершено.

Почти те же рассуждения позволяют доказать следующий факт, который мы предоставляем читателю в качестве упражнения.

Утверждение 4 . Прямая, проходящая через точку пересечения диагоналей и середину одного из оснований трапеции, проходит через середину другого основания трапеции.

Следствие . Точка пересечения диагоналей, середины оснований и точка пересечения боковых сторон трапеции лежат на одной прямой.

Средние линии четырехугольника. Теорема Вариньона

Определение . Средней линией четырехугольника называют отрезок, соединяющий середины непересекающихся сторон четырёхугольника.

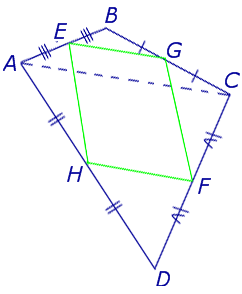
Поскольку у каждого четырехугольника имеются две пары непересекающихся сторон, то у каждого четырехугольника имеются две средних линии (рис.10).

На рисунке 10 средние линии – это отрезки EF и GH .

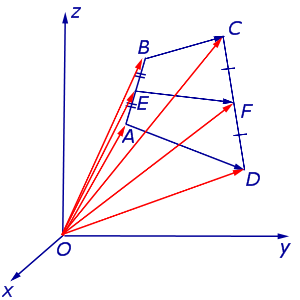
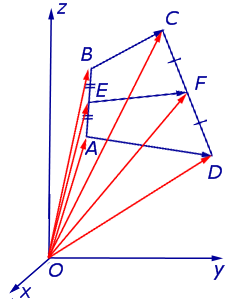
Замечание 1 . Приведенное определение средней линии относится не только к плоским четырехугольникам, но и к «пространственным четырехугольникам» (рис.11). «Пространственным четырехугольником» мы называем замкнутую ломаную линию из 4 звеньев без самопересечений, не лежащую в одной плоскости.

На рисунке 11 изображен «пространственный четырёхугольник» ABCD , средними линиями которого являются отрезки EF и GH .

Замечание 2 . Несмотря на то, что трапеция является четырехугольником, принято средней линией трапеции называть только отрезок, соединяющий середины её боковых сторон.

Замечание 3 . В данном разделе справочника не рассматриваются невыпуклые четырёхугольники и четырёхугольники с самопересечениями.

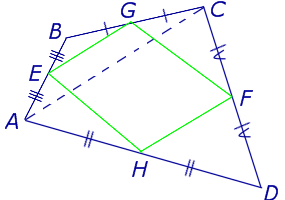
Теорема Вариньона . Середины сторон произвольного плоского или «пространственного» четырёхугольника являются вершинами параллелограмма параллелограмма .

Доказательство . Рассмотрим плоский четырёхугольник ABCD , изображенный на рисунке 12. Точки E, G, F, H – середины сторон, отрезок AC – диагональ четырёхугольника.

Поскольку отрезок EG – средняя линия треугольника ABC , то отрезок EG параллелен диагонали AC и равен её половине. Поскольку отрезок FH – средняя линия треугольника CDA , то отрезок FH параллелен диагонали AC и равен её половине. Таким образом, в четырёхугольнике EGFH противоположные стороны EG и FH равны и параллельны. В силу признака параллелограмма признака параллелограмма признака параллелограмма отсюда вытекает, что четырёхугольник EGFH – параллелограмм, что и требовалось доказать.

Замечание 4 . В случае «пространственного четырёхугольника» ABCD доказательство остаётся тем же (рис. 13).

Утверждение 5 . Средние линии произвольного четырёхугольника пересекаются и в точке пересечения делятся пополам (рис. 14).

Утверждение 6 . Рассмотрим произвольный плоский или «пространственный» четырёхугольник ABCD , у которого отрезок EF является одной из средних линий (рис. 15). Тогда будет выполнено векторное равенство:

что и требовалось доказать.

Следствие . Средняя линия четырёхугольника меньше или равна половине суммы не пересекающих её сторон четырёхугольника, причём равенство достигается лишь в том случае, когда указанные стороны четырёхугольника параллельны.

Другими словами, средняя линия четырёхугольника равна половине суммы не пересекающих её сторон четырёхугольника лишь в том случае, когда этот четырехугольник является трапецией трапецией , а не пересекающие среднюю линию стороны четырёхугольника – основания трапеции.

Средние линии тетраэдра

Тетраэдром называют произвольную треугольную пирамиду (рис.17).

У каждого тетраэдра имеется 4 вершины, 4 грани и 6 рёбер, причем все рёбра делятся на 3 пары непересекающихся рёбер . На рисунке 17 каждая пара непересекающихся рёбер выделена отдельным цветом. Каждые два непересекающихся ребра тетраэдра лежат на скрещивающихся прямых скрещивающихся прямых .

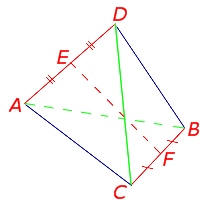
Определение . Средней линией (бимедианой) тетраэдра называют отрезок, соединяющий середины двух непересекающихся рёбер тетраэдра.

У каждого тетраэдра имеется 3 средних линии. Изображённый на рисунке 18 отрезок EF является одной из средних линий тетраэдра.

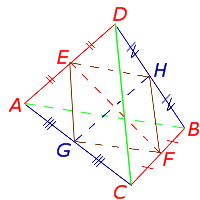
Утверждение 7 . Все средние линии тетраэдра пересекаются в одной точке и делятся этой точкой пополам.

Доказательство . Выберем какую-нибудь среднюю линию тетраэдра, например, EF и докажем, что любая другая средняя линия тетраэдра проходит через середину отрезка EF . Для этого рассмотрим, например, среднюю линию GH , соединяющую середины рёбер AC и BD , и соединим отрезками точки E, H, F, G (рис.19).

Заметим, что отрезок EH является средней линией треугольника ADB , поэтому

Определение . Точку пересечения средних линий тетраэдра называют центроидом тетраэдра .

Утверждение 8 . Рассмотрим в пространстве декартову систему координат с началом в точке O и произвольный тетраэдр ABCD . Если обозначить буквой M центроид этого тетраэдра (рис. 20), то будет выполнено векторное равенство:

источники:

http://edu02.ru/formula-dliny-srednei-linii-parallelogramma-kak-naiti-srednyuyu-liniyu-trapecii/

http://www.resolventa.ru/spr/planimetry/mline.htm

Источник

Средние линии треугольников и четырехугольников

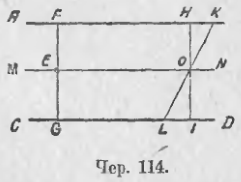
107. Мы знаем (п. 102), что геометрическим местом точек, равноотстоящих от двух данных параллельных прямых, служит средняя параллельная. Если таким образом AB и CD (чер. 114) суть две параллельные и MN для них средняя параллельная, то расстояния любой точки E этой средней параллельной от AB и CD равны между собою, т. е., построив EF ⊥ AB и EG ⊥ CD, получим, что EF = EG.

Ясно, что построенные перпендикуляры EF и EG составляют продолжение друг друга и образуют один отрезок FG, перпендикулярный к нашим параллельным AB и CD, причем этот отрезок делится среднею параллельною (в точке E) пополам. Итак, всякий отрезок, перпендикулярный к двум параллельным и заключенный между ними, делится среднею параллельною пополам.

Возникает теперь вопрос: не будет ли также делиться пополам среднею параллельною какой-нибудь отрезок KL, не перпендикулярный к AB и CD. Пусть KL пересекается с MN в точке O. Построим через точку O перпендикулярный к прямым AB и CD отрезок HI. Тогда OH = OI. Так как, кроме того, ∠HOK = ∠IOL, как вертикальные, то прямоугольные треугольники OHK и OIL равны, откуда следует, что OK = OL. Итак, оказывается, что и любой отрезок, заключенный между двумя параллельными, делится среднею параллельною пополам.

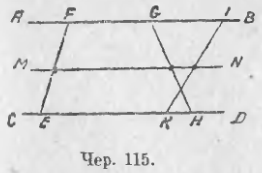
Пусть AB || CD (чер. 115). Построив между ними ряд каких-либо отрезков EF, GH, KI и т. д., мы, согласно предыдущему, найдем, что середины этих отрезков лежат на средней параллельной MN. В общем итоге мы приходим к следующему заключению:

Геометрическим местом середин всевозможных отрезков, заключенных между двумя параллельными, служит средняя параллельная.

Отсюда возникают возможности различных построений средней параллельной для двух данных параллельных прямых: 1) мы можем, построим любой отрезок EF, заключенный между двумя данными параллельными AB и CD, разделить его пополам и через его середину построить прямую MN || AB || CD — это прямая MN и должна служить среднею параллельною, и она должна делить пополам всевозможные отрезки (напр., GH, KI и т. д.), заключенные между AB и CD. 2) Мы можем построить два отрезка, напр., EH и KI, заключенные между AB и CD, разделить каждый из них пополам и через их середины построить прямую MN — она и должна служить среднею параллельною.

108. Применим свойства средней параллельной к знакомым нам фигурам и прежде всего треугольнику.

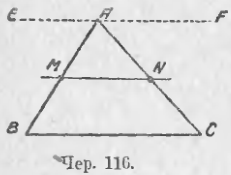
Пусть имеем ∆ABC (чер. 116). Здесь непосредственно мы не имеем двух параллельных, но мы всегда можем их получить, напр., построив через вершину A прямую EF || BC (эту прямую EF можно было бы и не рисовать на чертеже, так как она существенной роли не играет в дальнейшем и так как достаточно лишь знать, что она существует). Тогда мы имеем две параллельных BC и EF и два отрезка AB и AC, заключенных между ними. Разделив их пополам в точках M и N (AM = MB и AN = NC) и построив через M и N прямую MN, мы получим среднюю параллельную MN, т. е. MN || BC (и || EF, но это для нас не существенно). Из этого заключаем:

прямая, соединяющая середины двух сторон треугольника, параллельна его третьей стороне.

Отрезок, соединяющий середины двух сторон треугольника, называют среднею линиею треугольника. Итак, у нас отрезок MN есть средняя лини нашего треугольника.

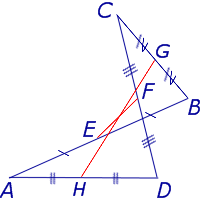
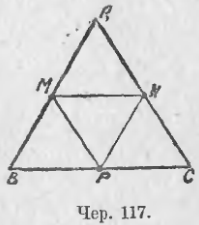
Пусть имеем ∆ABC (чер. 117). Разделим пополам каждую из его сторон: пусть M есть середина AB (сл. AM = MB), N — середина AC (AN = NC) и P — середина BC (BP = PC); соединим точки M, N и P отрезками MN, MP и PN, — каждый из этих отрезков является среднею линиею для нашего треугольника. Таким образом в треугольнике имеется три средних линии.

Согласно предыдущему, будем иметь: MN || BC, MP || AC и NP || AB. Поэтому AMPN, BMNP и PMNC суть параллелограммы. Так как в параллелограмме противоположные стороны равны, то имеем: MN = BP (из параллелограмма BMNP), но BP = BC/2 (ибо точка P есть середина BC); поэтому MN = BC/2. Также из параллелограмма AMPN получим: MP = AN = AC/2 и из параллелограмма AMPN — PN = AM = AB/2. Отсюда заключаем:

каждая средняя линия треугольника, соединяющая середины двух его сторон, параллельна третьей и равна ее половине.

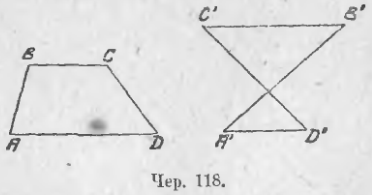
109. Перейдем теперь к четырехугольникам и остановимся сначала на таких четырехугольниках, у которых две стороны параллельны. Принято называть такие четырехугольники трапециями. На чер. 118 изображены два различных вида трапеций: 1) трапеция ABCD, где BC || AD, но AB не параллельна CD, — эта трапеция имеет площадь (см. п. 79) и 2) трапеция A’B’C’D’, где A’D’ || B’C’, — эта трапеция не имеет площади (п. 79).

Рассмотрим сначала трапецию ABCD (чер. 118 bis), имеющую площадь. Здесь BD || AD. Поэтому мы имеем две параллельных BC и AD и между ними отрезки AB и CD. Разделив эти отрезки пополам в точках M и N (AM = MB и CN = ND) и соединив их прямою MN, получим среднюю параллельную MN для BC и AD, т. е. MN || BC || AD. Отрезок MN этой прямой называется средней линиею трапеции (следует добавить: «соединяющей середины непараллельных сторон», потому что в трапеции, как и во всяком четырехугольнике, можно рассматривать 6 средних линий, что имеет место в п. 110). Итак, мы получили, что MN || BC || AD. Далее, построив диагональ AC, получим еще третий отрезок AC, заключенный между параллельными BC и AD — его середина должна лежать (п. 107) на средней параллельной, т. е. точка P, где пересекаются MN и AC, есть середина отрезка AC. Поэтому MP есть средняя линия треугольника ABC и PN — средняя линия ∆ACD. На основании предыдущего, имеем: MP = BC/2 и PN = AD/2. Отсюда получаем: MN = MP + PN = BC/2 + AD/2 или MN = (BC + AD)/2. Итак,

средняя линия, соединяющая середины непараллельных сторон трапеции, имеющей площадь, параллельна ее параллельным сторонам и равна их полусумме.

Пусть теперь имеем трапецию ABCD (чер. 118 bis), неимеющую площади. Здесь также BC || AD и поэтому середины M и N сторон AB и CD лежат на средней параллельной, т. е. здесь также имеем: MN || BC || AD. Построив диагональ AC, получим отрезок AC, заключенный между параллельными BC и AD, и его середина, точка P, должна лежать на средней параллельной. Поэтому PM есть средняя линия треугольника ABC и, следовательно PM = BC/2; также PN есть средняя линия ∆ABC и, след., PN = AD/2. Так как MN = PN – PM, то получим MN = PN – PM = AD/2 – BC/2 или MN = (AD – BC) / 2. Итак,

средняя линия, соединяющая середины непараллельных сторон трапеции, неимеющей площади, параллельна ее параллельным сторонам и равна их полуразности.

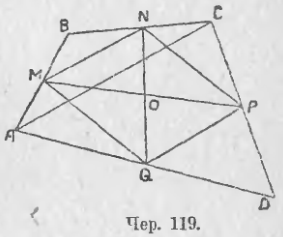
110. Пусть имеем какой-либо четырехугольник ABCD (имеющий площадь) — (чер. 119). Найдем середины M, N, P и Q его сторон и соединим их попарно. Получим 6 средних линий четырехугольника.

Вот свойства этих средних линий.

1) Средние линии, соединяющие середины последовательных сторон четырехугольника, образуют параллелограмм.

Для выяснения этого свойства построим диагональ AC. Тогда из ∆ABC имеем (п. 108) MN || AC и из ∆ACD на том же основании: PQ || AC, — следов., MN || PQ. Построив другую диагональ BD, найдем при ее помощи, что NP || MQ, следовательно, MNPQ есть параллелограмм.

2) Средние линии четырехугольника, соединяющие середины противоположных сторон, взаимно делятся пополам.

Это свойство теперь очевидно, так как MP и NQ являются диагоналями параллелограмма.
Через точку O пересечения прямых MP и NQ проходят также прямые, соединяющие середины диагоналей AC и BD (на чертеже диагональ BD не дана). Это следует из того, что AC И BD являются сторонами четырехугольника ACBD, не имеющего площади, к которому применимо все, изложенное в начале этого п.

111. Мы умели (пп. 57, 59) делить отрезок пополам и, следов., на 4, на 8 и вообще на 2n равных частей. Теперь мы можем разделить данный отрезок на 3, на 5 и вообще на сколько угодно равных частей.

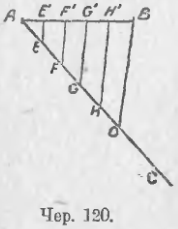
Пусть, напр., требуется отрезок AB (чер. 120) разделить на 5 равных частей. Построим через точку A произвольную прямую AC (образующую с AB угол, отличный от выпрямленного) и отложим на AC пять произвольных, но равных между собою, отрезков AE = EF = FG = GH = HO. Построим прямую OB и через точки E, F, G и Н построим прямые EE’, FF’, GG’, HH’, параллельные OB.

Рассмотрим ∆AFF’, так как AE = EF, то E есть середина стороны AF и EE’ (она || FF’) есть средняя линия этого треугольника, следовательно, AE’ = E’F’.

Рассмотрим затем трапецию EE’G’G. Так как EF = FG, FF’ || EE’, то FF’ есть средняя линия трапеции EE’GG’, — следовательно, E’F’ = F’G’. Также найдем, что GG’ есть средняя линия трапеции FF’H’H и, следов., F’G’ = G’H’ и т. д. Соединяя полученные равенства, найдем AE’ = E’F’ = F’G’ = G’H’ = H’B’, т. е. отрезок AB разделился на 5 равных частей.

Из решения этой задачи можно вывести заключение:

Если на одной стороне угла отложить равные отрезки и чрез их концы построить ряд параллельных прямых, то и на другой стороне угла получим равные между собой отрезки.

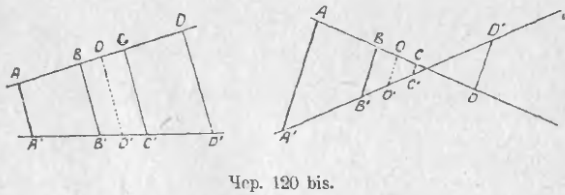
Добавление. Мы откладывали равные отрезки на одной прямой подряд, начиная от точки пересечения двух прямых (AB и AC чертежа 120), но возможно к такому же результату прийти и при ином способе отложения равных отрезков. На чертеже 120 bis дано два варианта такого построения: на прямой AD (см. чер. 120 bis слева или справа) отложим два равных отрезка AB и CD и через их концы построим параллельные AA’ || BB’ || CC’ || DD’. Затем возьмем точку O, середину отрезка BC, и построим OO’ || BB’ || CC’ || AA’ || DD’. Тогда OO’ есть средняя линия трапеции BCC’B’; поэтому B’O’ = O’C (п. 109). Так как AB = CD и BO = OC, то AO также = OD; поэтому OO’ есть также средняя линия трапеции ADD’A’ (на чертеже справа эта трапеция ADD’A’ — не имеющая площади, см. п. 109) — и также A’O’ = O’D’. Отсюда имеем A’O’ – B’O’ = O’D’ – O’C’ (ибо и уменьшаемые и вычитаемые обеих разностей равны), или A’B’ = C’D’. Возможны и иные комбинации (напр., отр. CD правой фигуры отодвинуть так, чтобы точка C оказалась правее точки пересечения прямых AD и A’D’). Общее заключение таково: если построены две прямые, на одной из них отложены как-либо два равных отрезка и через концы их построены параллельные, то эти последние выделят и на другой прямой два равных между собою отрезка.

112. Упражнения.

Через вершины данного треугольника построены прямые, параллельные его сторонам. Показать, что новый треугольник имеет стороны вдвое больше, чем стороны данного, и что вершины данного являются серединами сторон нового (сравн. упр. 7 из п. 54).
Построить треугольник, если даны середины трех его сторон.
Построить параллелограмм, если даны середины трех его сторон.
Известно (п. 110), что середины четырех сторон четырехугольника являются вершинами параллелограмма. Когда этот параллелограмм обращается в ромб, когда в прямоугольник, когда в квадрат?
Прямая, соединяющая вершину треугольника со срединою противоположной стороны (медиана) и прямая, соединяющая середины двух других сторон треугольника, взаимно делятся пополам.
Продолжим одну сторону треугольника на отрезок, равный этой стороне, и соединим конец отрезка со срединою другой стороны. Последняя соединяющая прямая отсекает от третьей стороны треугольника отрезок, равный 1/3 этой стороны. (Построить еще прямую, параллельную последней соединяющей прямой чрез вершину треугольника, противолежащую той его стороне, которая была продолжена).
Если на стороне AB параллелограмма ABCD отложить отрезок AM = (1/n)AB (напр., (1/7)AB) и соединить D с M, то DM пересечет диагональ AC в точке N так, что AN = (1/(n+1))AC (во взятом примере (1/8)AC).
Для выяснения этого надо на продолжении стороны AB отложить BM’ = AM и соединить C с M’; тогда C’M’ || DM, – приметь п. 111.

Источник

Параллелограмм. Средняя линия

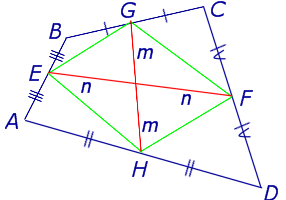
Средние линии четырехугольников и их свойства Выполнил: Матвеев Дмитрий Учитель: Рычкова Татьяна Викторовна Лицей «Дубна» 9ИМ 2007 Средние линии и Параллелограмм Вариньона Другие свойства средней линии четырехугольника Краткий перечень всех теорем и свойств

Что такое параллелограмм Вариньона? Это параллелограмм, вершины которого являются серединами сторон четырехугольника Иначе: это параллелограмм, диагоналями которого являются средние линии четырехугольника

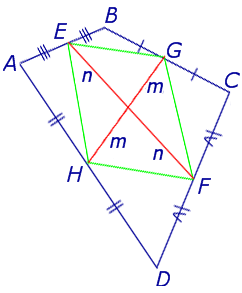
A B C D N M L K P Доказательство: Соединим точки K, L, M, N и проведем диагональ АС; В ∆ACD NM – средняя линия, значит NM  AC и NM=1/2 AC; В ∆ABC KL – средняя линия, значит KL  AC и KL=1/2 AC; NM=1/2 AC=KL, NM  AC  KL, значит четырехугольник KLMN ‑ параллелограмм. A L B M C D K P N Доказательство: Соединим точки K, L, M, N и проведем диагональ DB; В ∆CDB NM – средняя линия, значит NM  DB и NM=1/2 DB; В ∆ADC KL – средняя линия, значит KL  DB и KL=1/2 DB; NM=1/2 DB=KL, NM  DB  KL, значит четырехугольник KLMN ‑ параллелограмм. Докажем, что KLMN – параллелограмм Вариньона, при KM и NM – средних линиях ABCD.

А значит… Так как четырехугольник KLMN – параллелограмм Вариньона, то его диагонали в точке пересечения делятся пополам Средние линии любого четырехугольника делятся пополам

Следствия: 1. Если средние линии четырехугольника равны, то середины сторон четырехугольника (вершины параллелограмма Вариньона) лежат на одной окружности. Доказательство: Так как в параллелограмме Вариньона равные средние линии являются равными диагоналями, то этот параллелограмм – прямоугольник, а вокруг него всегда можно описать окружность, значит его вершины лежат на одной окружности.

Следствия: 2. Если средние линии четырехугольника перпендикулярны, то диагонали четырехугольника равны. Доказательство: Так как NL┴KM и NL с KM диагонали в параллелограмме KLMN , то KLMN – ромб. По этому KL = LM = MN = NK . Так как AC =2 KL и BD =2 NK , то AC = BD . A K B L C M D N P O A P K C D M N L B

Следствия: A K B L C M D N P O A P K C D M N L B 3. Если диагонали четырехугольника равны, то средние линии четырехугольника перпендикулярны. Доказательство: Так как AC =2 MN =2 KL , BD =2 NK =2 ML и AC = BD , то KL = LM = MN = NK . Значит KLMN – ромб, а в ромбе диагонали перпендикулярны, то есть NL┴KM.

Для примера: Решая такую задачу, пришлось бы сильно потрудится, не зная одно из свойств параллелограмма Вариньона:

Какова же площадь параллелограмма Вариньона? Доказательство для выпуклого четырехугольника: Рассмотрим ∆ABD и ∆ANK: а).

Какова же площадь параллелограмма Вариньона? Доказательство для невыпуклого четырехугольника: Рассмотрим ∆ABD и ∆ANK: а).

S KLMN =1/2 S ABCD Значит площадь параллелограмма Вариньона равна половине площади четырехугольника, чьи средние линии являются его диагоналями. Следствие: площади четырехугольников с равными средними линиями равны. Следствие: площадь четырехугольника равна произведению его средних линий на синус угла между ними.

Для примера: Теперь можно решить задачу в два шага: 1. S пар. Вариньона равна 15*18=270 см в кв. 2. S ABCD = 2*270= =540 см в кв.

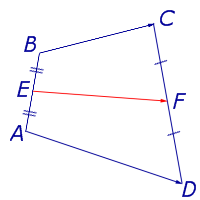
Какова длина средней линии? A D C F B G E Пусть EF – средняя линия четырехугольника ABCD (EA=ED, FB=FC , AB не параллельна DC); Тогда: NL= ND + DA + AL и NL = NC + CB + BL Сложим эти равенства и получим: 2NL = DA + CB Значит вектора 2NL, DA и CB являются сторонами треугольника При параллельном переносе векторов DC и 2EF получатся равные им вектора BG и AG , которые вместе с вектором AB образуют ∆ AGB , где по неравенству треугольника получим: AGСлайд 14

Свойство углов Проведем отрезок KD = BC и параллельный ему. Тогда BCDK – параллелограмм. Значит CD = BK и CD  BK . Отсюда Слайд 15

Краткий перечень всех теорем и свойств: Средние линии любого четырехугольника делятся пополам Если средние линии четырехугольника равны, то середины сторон четырехугольника (вершины параллелограмма Вариньона) лежат на одной окружности. Если средние линии четырехугольника перпендикулярны, то диагонали четырехугольника равны. Если диагонали четырехугольника равны, то средние линии четырехугольника перпендикулярны. Значит площадь параллелограмма Вариньона равна половине площади четырехугольника, чьи средние линии являются его диагоналями. Площади четырехугольников с равными средними линиями равны. Площадь четырехугольника равна произведению его средних линий на синус угла между ними. Длина средней линии четырехугольника не превышает полусуммы длин сторон, не соединенных ею. Если 4-хугольнике две противоположные стороны равны и не параллельны, то прямая, включающая в себя среднюю линию, не проходящую через эти стороны, образует с продолжениями этих сторон равные углы

Средние линии геометрических фигур

научная работа

1. Свойства средних линий

1. Свойства треугольника:

· при проведении всех трёх средних линий образуются 4 равных треугольника, подобных исходному с коэффициентом 1/2.

· средняя линия параллельна основанию треугольника и равна его половине;

· средняя линия отсекает треугольник, который подобен данному, а его площадь равна одной четверти его площади.

2. Свойства четырёхугольника:

· если в выпуклом четырехугольнике средняя линия образует равные углы с диагоналями четырехугольника, то диагонали равны.

· длина средней линии четырехугольника меньше полусуммы двух других сторон или равна ей, если эти стороны параллельны, и только в этом случае.

· середины сторон произвольного четырёхугольника — вершины параллелограмма. Его площадь равна половине площади четырехугольника, а его центр лежит на точке пересечения средних линий. Этот параллелограмм называется параллелограммом Вариньона;

· Точка пересечения средних линий четырехугольника является их общей серединой и делит пополам отрезок, соединяющий середины диагоналей. Кроме того, она является центроидом вершин четырехугольника.

3. Свойства трапеции:

· средняя линия параллельна основаниям трапеции и равна их полусумме;

· середины сторон равнобедренной трапеции являются вершинами ромба.

Биномиальные коэффициенты

Числа Cnk обладают рядом замечательных свойств. Эти свойства в конечном счёте выражают различные соотношения между подмножествами данного множества X. Их можно доказывать непосредственно, исходя из формулы (1)…

Биномиальные коэффициенты

1. Сумма коэффициентов разложения (a + b)n равна 2n.
Для доказательства достаточно положить a = b = 1. Тогда в правой части разложения бинома мы будем иметь сумму биномиальных коэффициентов, а слева: (1 + 1)n = 2n.
2.Коэффициенты членов…

Ввиду важности и обширности материала, связанного с понятием уравнения, его изучение в современной методике математики организовано в содержательно-методическую линию уравнений и неравенств…

Мультипликативные полугруппы неотрицательных действительных чисел

Пусть S — коммутативная мультипликативная несократимая полугруппа с 1 и без делителей единицы. Такие полугруппы называются целыми, или коническими.
Элементы и из S называются взаимно простыми, если НОД(,)=1…

Так как предметом нашего изучения будет средняя величина, скажем вначале о том, как средние определяются в литературе. Сильное определение, включающее несколько условий, состоит в следующем .
Определение…

Обобщение классических средних величин

Теперь мы готовы для квази-средних указать упомянутое выше аксиоматическое определение. Будем исходить от частных случаев — простейших средних…

Основные понятия математической статистики

При расчете средней арифметической для интервального вариационного ряда сначала определяют среднюю для каждого интервала, как полусумму верхней и нижней границ, а затем — среднюю всего ряда.
Средние…

Простейшие способы обработки опытных данных

Применение вышеназванных способов для описания реальных процессов.
При этом нельзя сделать однозначный вывод о том, какой способ наиболее точно описывает тот или иной процесс. Например…

Распределение Пуассона. Аксиомы простейшего потока событий

Теперь рассмотрим случай, когда обе совокупности подчиняются нормальному распределению, но проверка гипотез о равенстве двух генеральных дисперсий закончилась отвержением гипотезы равенства…

Регрессионный анализ корелляции субъективного ВАШ и лабораторных признаков активности реактивного артрита

Во многих случаях практики интерес представляет вопрос о том, в какой мере существенно влияние того или иного фактора на рассматриваемый признак. В данном случае фактором является вид инфекции вызвавший реактивный артрит, а признаками СОЭ, СРБ…

Случайные вектора

Ковариация случайных величин и определяется через их совместную плотность вероятности соотношением:
. (57.1)
Подынтегральная функция в (57.1) неотрицательна для таких, при которых, то есть при, или, . И наоборот, при, или…

Статистические расчеты содержания влаги

Численное интегрирование разными методами

Метод прямоугольников получается при замене подынтегральной функции на константу. В качестве константы можно взять значение функции в любой точке отрезка. Наиболее часто используются значения функции в середине отрезка и на его концах…

Численные методы

1
Чтобы уменьшить погрешность методов левых и правых прямоугольников был предложен метод средних, т.е. метод в котором высота прямоугольника вычисляется в середине отрезка h (Рис. 7). Обращаясь к рисунку легко увидеть…

Гомельская
научно-практическая конференция
школьников по математике, ее приложениям
и информационным технологиям «Поиск»

Учебно-исследовательская
работа

Средние линии
геометрических фигур

Морозовой
Елизаветы

Гомель 2010

Введение

1.Свойства
средних линий

2.
Треугольник,
четырехугольник, параллелограмм

3. Четырехугольник,
тетраэдр. Центры масс

4. Тетраэдр,
октаэдр, параллелепипед, куб

Заключение

Список
использованной литературы

Приложение

Введение

Геометрия
является неотъемлемой составляющей
общей культуры, а геометрические методы
служат инструментом познания мира,
способствуют формированию научных
представлений об окружающем пространстве,
раскрытию гармонии и совершенства
Вселенной.
Геометрия
начинается с треугольника. Вот уже два
тысячелетия треугольник является как
бы символом геометрии, но он не символ.
Треугольник – атом геометрии. Треугольник
неисчерпаем – постоянно открываются
его новые свойства. Чтобы рассказать
обо всех известных его свойствах,
необходим том сравнимый по объему с
томом Большой энциклопедии. Мы хотим
рассказать о средних линиях геометрических
фигур и их свойствах.

В нашей работе
прослеживается цепочка теорем, которая
охватывает весь курс геометрии. Она
начинается с теоремы о средних линиях
треугольника и приводит к интересным
свойствам тетраэдра и других многогранников.

Средняя
линия
фигур — отрезок, соединяющий середины
двух сторон данной фигуры.

1.
Свойства средних линий

Свойства
треугольника:

при проведении
всех трёх средних линий образуются 4
равных треугольника, подобных
исходному с коэффициентом 1/2.

средняя
линия параллельна
основанию треугольника и равна его
половине;

средняя
линия отсекает треугольник, который
подобен данному, а его площадь равна
одной четверти его площади.

Свойства
четырёхугольника:

если в
выпуклом четырехугольнике средняя
линия образует равные углы с диагоналями
четырехугольника, то диагонали равны.

длина средней
линии четырехугольника меньше полусуммы
двух других сторон или равна ей, если
эти стороны параллельны, и только в
этом случае.

середины
сторон произвольного четырёхугольника
— вершины параллелограмма.
Его площадь равна половине площади
четырехугольника, а его центр лежит на
точке пересечения средних линий. Этот
параллелограмм называется параллелограммом
Вариньона;

Точка
пересечения средних линий четырехугольника
является их общей серединой и делит
пополам отрезок, соединяющий середины
диагоналей. Кроме того, она является
центроидом
вершин четырехугольника.

Свойства
трапеции:

средняя
линия параллельна основаниям трапеции
и равна их полусумме;

середины
сторон равнобедренной трапеции являются
вершинами ромба.

2.
Треугольник, четырехугольник,
параллелограмм

К
любому треугольнику KLM
можно
пристроить три равных ему треугольника
АКМ,
BLK,
CLM,
каждый
из которых образует вместе с треугольником
KLM
параллелограмм
(рис. 1). При этом AK
= ML=KB,
и
к вершине К
примыкают
три угла, равные трем разным углам
треугольника, в сумме составляющие
180°, поэтому К
—
середина отрезка АВ;
аналогично,
L
—
середина отрезка ВС,
а
М — середина отрезка СА.

Теорема
1
.
Если
соединить в любом треугольнике середины
сторон, мы получим четыре равных
треугольника, причем средний составляет
с каждым из трех других параллелограмм.

В
этой формулировке участвуют сразу все
три средние линии треугольника.

Теорема
2
.
Отрезок,
соединяющий середины двух сторон
треугольника, параллелен третьей стороне
треугольника и равен ее половине (см.
рис. 1).

Именно
эта теорема и обратная к ней — о том,
что прямая, параллельная
основанию и проходящая через середину
одной боковой стороны треугольника,
делит пополам и другую боковую сторону,-
чаще всего нужны при решении задач.

Из
теоремы о средних линиях треугольника
вытекает свойство средней линии трапеции
(рис. 2), а также теоремы об отрезках,
соединяющих середины сторон произвольного
четырехугольника.

Теорема
3
.
Середины
сторон четырехугольника являются
вершинами параллелограмма. Стороны
этого параллелограмма параллельны
диагоналям четырехугольника, а их длины
равны половинам длин диагоналей.

В
самом деле, если К
и
L
—
середины сторон АВ
и
ВС
(рис.
3), то KL
—
средняя линия треугольника ABC,
поэтому
отрезок KL
параллелен
диагонали АС
и
равен ее половине; если М
и
N
—
середины сторон CD
и
AD,
то
отрезок MN
также
параллелен АС
и
равен АС/2.
Таким
образом, отрезки KL
и
MN
параллельны
и равны между собой, значит, четырехугольник
KLMN
—
параллелограмм.

В
качестве следствия из теоремы 3 получаем
интересный факт (т. 4).

Теорема
4
.
В
любом четырехугольнике отрезки,
соединяющие середины противоположных
сторон, делятся точкой пересечения
пополам.

В
этих отрезках можно увидеть диагонали
параллелограмма (см. рис. 3), а в
параллелограмме диагонали делятся
точкой пересечения пополам (эта точка
— центр симметрии параллелограмма).

Мы
видим, что теоремы 3 и 4 и наши рассуждения
остаются верными и для невыпуклого
четырехугольника, и для самопересекающейся
четырехугольной замкнутой ломаной
(рис. 4; в последнем случае может оказаться,
что параллелограмм KLMN
«вырожденный»
— точки К,
L,
М, N лежат
на одной прямой).

Покажем,
как из теорем 3 и 4 можно вывести основную
теорему о медианах треугольника.

Теорема
5
.
Медианы треугольника пересекаются в
одной точке и делятся ею в отношении
2:1 (считая от вершины, из которой проведена
медиана).

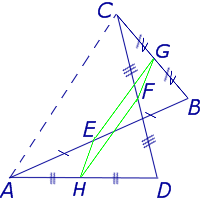
Проведем
две медианы AL
и
СК
треугольника
ABC.
Пусть
О
—
точка их пересечения. Середины сторон
невыпуклого четырехугольника АВСО
— точки
К,
L,MиN
(рис.
5) — вершины параллелограмма, причем
точкой пересечения его диагоналей КМ
и
LN
для
нашей конфигурации будет точка пересечения
медиан О.
Итак,
AN
= NO
= OL
и CM=MO
= OK,
т.
е. точка О
делит
каждую из медиан AL
и
СК
в
отношении 2:1.

Вместо
медианы СК
мы
могли бы рассмотреть медиану, проведенную
из вершины В,
и
убедиться точно так же, что и она делит
медиану AL
в
отношении 2:1, т. е. проходит через ту же
точку О.

3.Четырехугольник
и тетраэдр. Центры масс

Теоремы
3 и 4 верны и для любой пространственной
замкнутой
ломаной из четырех звеньев АВ,
ВС, CD,
DA,
четыре
вершины А,
В, С, D
которой
не лежат в одной плоскости.

Такой
пространственный четырехугольник можно
получить, вырезав из бумаги четырехугольник
ABCD
и
согнув его по диагонали под некоторым
углом (рис. 6, а).
При
этом ясно, что средние линии KL
и
MN
треугольников
ABC
и
ADC
остаются
по-прежнему их средними линиями и будут
параллельны отрезку АС
и
равны АС/2. (Здесь мы используем тот факт,
что для пространства остается верным
основное свойство параллельных прямых:
если
две прямые KL
и MN
параллельны третьей прямой АС, то KL
и MN
лежат в одной плоскости и параллельны
между собой.)

Таким
образом, точки К,
L,
М, N — вершины
параллелограмма; тем самым отрезки КМ
и
LN
пересекаются
и делятся точкой пересечения пополам.
Вместо четырехугольника здесь можно
говорить о тетраэдре — треугольной
пирамиде ABCD:
середины
К,
L,
М, N его
ребер АВ,
AC,
CD
и
DA
всегда
лежат в одной плоскости. Разрезав
тетраэдр по этой плоскости (рис. 6, б),
мы
получим параллелограмм KLMN,
две
стороны которого параллельны ребру АС
и
равны

АС/2,
а две другие — параллельны ребру BD
и
равны BD/2.

Такой
же параллелограмм — «среднее сечение»
тетраэдра — можно построить и для других
пар противоположных ребер. Каждые два
из этих трех параллелограммов имеют
общую диагональ. При этом середины
диагоналей совпадают. Итак, мы получаем
интересное следствие:

Теорема
6
.
Три
отрезка, соединяющие середины
противоположных ребер тетраэдра,
пересекаются в одной точке и делятся
ею пополам (рис. 7).

Этот
и другие обсуждавшиеся выше факты
естественно объясняются на языке
механики — с помощью понятия центра
масс. В
теореме 5 говорится об одной из
замечательных точек треугольника —
точке пересечения медиан; в теореме 6 —
о замечательной точке для четверки
вершин тетраэдра. Эти точки — центры
масс соответственно треугольника и
тетраэдра. Вернемся сначала к теореме
5 о медианах.

Поместим
в вершинах треугольника три одинаковых
груза (рис. 8).

Массу
каждого примем за единицу. Найдем центр
масс этой системы грузов.

Рассмотрим
сначала два груза, находящихся в вершинах
А
и
В:
их
центр масс расположен в середине отрезка
АВ,
так
что эти грузы можно заменить одним
грузом массой 2, помещенным в середину
К
отрезка
АВ
(рис.
8, а). Теперь нужно найти центр масс
системы из двух грузов: одного массой
1 в точке С
и
второго — массой 2 в точке К.
По
правилу рычага, центр масс такой системы
находится в точке О, делящей отрезок СК
в
отношении 2:1 (ближе к грузу в точке К
с
большей массой — рис. 8, б).

Мы
могли сначала объединить грузы в точках
В
и
С,
а
затем — полученный груз массой 2 в
середине L
отрезка
ВС
—
с грузом в точке А.
Или
сначала объединить грузы А
и С, а. затем
присоединить В.
В
любом случае мы должны получить тот же
результат. Центр масс находится, таким
образом, в точке О,
делящей
каждую из медиан в отношении 2:1, считая
от вершины. Подобными соображениями
можно было объяснить и теорему 4 — тот
факт, что отрезки, соединяющие середины
противоположных сторон четырехугольника,
делят друг друга пополам (служат
диагоналями параллелограмма): достаточно
поместить в вершинах четырехугольника
одинаковые грузы и объединить их попарно
двумя способами (рис. 9).

Конечно,
четыре единичных груза, расположенных
на плоскости или в пространстве (в
вершинах тетраэдра), можно разбить на
две пары тремя способами; центр масс
находится посередине между серединами
отрезков, соединяющих эти пары точек
(рис. 10) — объяснение теоремы 6. (Для
плоского четырехугольника полученный
результат выглядит так: два отрезка,
соединяющие середины противоположных
сторон, и отрезок, соединяющий середины
диагоналей, пересекаются в одной точке
О
и
делятся ею пополам).

Через
точку О
—
центр масс четырех одинаковых грузов
— проходят еще четыре отрезка, соединяющих
каждый из них с центром масс трех других.
Эти четыре отрезка делятся точкой О
в
отношении 3:1. Чтобы объяснить этот факт,
нужно сначала найти центр масс трех
грузов и потом присоединить четвертый.

4.
Тетраэдр, октаэдр, параллелепипед, куб

В
начале работы мы рассмотрели треугольник,
разбитый средними линиями на четыре
одинаковых треугольника (см. рис. 1).
Попробуем проделать то же построение
для произвольной треугольной пирамиды
(тетраэдра). Распилим тетраэдр на части
следующим образом: через середины трех
ребер, выходящих из каждой вершины,
проведем плоский разрез (рис. 11, а). Тогда
от тетраэдра будет отрезано четыре
одинаковых маленьких тетраэдра. По
аналогии с треугольником можно было бы
думать, что в серединке останется еще
один такой же тетраэдр. Но это не так: у
многогранника, который останется от
большого тетраэдра после удаления
четырех маленьких, будет шесть вершин
и восемь граней — он называется октаэдром
(рис.
11,6). Удобно проверить это, используя
кусок сыра в форме тетраэдра. Полученный
октаэдр имеет центр симметрии, поскольку
середины противоположных ребер тетраэдра
пересекаются в общей точке и делятся
ею пополам.

С
треугольником, разбитым средними линиями
на четыре треугольника, связана одна
интересная конструкция: этот рисунок
мы можем рассмотреть как развертку
некоторого тетраэдра.

Представим
себе остроугольный треугольник,
вырезанный из бумаги. Перегнув его по
средним линиям так, чтобы вершины сошлись
в одной точке, и склеив сходящиеся в
этой точке края бумаги, мы получим
тетраэдр, у которого все четыре грани
— равные треугольники; его противоположные
ребра равны (рис. 12). Такой тетраэдр
называется полуправильным. Каждое из
трех «средних сечений» этого тетраэдра
— параллелограммов, стороны которых
параллельны противоположным ребрам и
равны их половинам,- будет ромбом.

Поэтому
диагонали этих параллелограммов — три
отрезка, соединяющие середины
противоположных ребер — перпендикулярны
друг другу. Среди многочисленных свойств
полуправильного тетраэдра отметим
такое: сумма углов, сходящихся в каждой
его вершине, равна 180° (эти углы
соответственно равны углам исходного
треугольника). В частности, если начать
с развертки в форме равностороннего
треугольника, мы получим правильный
тетраэдр, у которог

В
начале работы мы видели, что каждый
треугольник можно рассматривать как
треугольник, образованный средними
линиями большего треугольника. Прямой
аналогии в пространстве для такого
построения нет. Но оказывается, что
любой тетраэдр можно рассматривать как
«сердцевину» параллелепипеда, у которого
все шесть ребер тетраэдра служат
диагоналями граней. Для этого нужно
проделать следующее построение в
пространстве. Через каждое ребро
тетраэдра проведем плоскость, параллельную
противоположному ребру. Плоскости,
проведенные через противоположные
ребра тетраэдра, будут параллельны друг
другу (они параллельны плоскости
«среднего сечения» — параллелограмма
с вершинами в серединах четырех других
ребер тетраэдра). Так получаются три
пары параллельных плоскостей, при
пересечении которых образуется нужный
параллелепипед (две параллельные
плоскости пересекаются третьей по
параллельным прямым).
Вершины
тетраэдра служат четырьмя несмежными
вершинами построенного параллелепипеда
(рис. 13). Наоборот, в любом параллелепипеде
можно выбрать четыре несмежные вершины
и отрезать от него плоскостями, проходящими
через каждые три из них, угловые тетраэдры.
После этого останется «сердцевина» —
тетраэдр, ребра которого являются
диагоналями граней параллелепипеда.

Если
исходный тетраэдр полуправильный, то
каждая грань построенного параллелепипеда
будет параллелограммом с равными
диагоналями, т.е. прямоугольником.

Верно
и обратное: «сердцевиной» прямоугольного
параллелепипеда служит полуправильный
тетраэдр. Три ромба — средние сечения
такого тетраэдра — лежат в трех взаимно
перпендикулярных плоскостях. Они служат
плоскостями симметрии октаэдра,
полученного из такого тетраэдра
отрезанием углов.

Для
правильного тетраэдра описанный вокруг
него параллелепипед будет кубом (рис.
14), а центры граней этого куба — середины
ребер тетраэдра — будут вершинами
правильного октаэдра, все грани которого
— правильные треугольники. (Три плоскости
симметрии октаэдра пересекают тетраэдр
по квадратам.)

Таким
образом, на рисунке 14 мы видим сразу три
из пяти платоновых тел (правильных
многогранников) — куб, тетраэдр и
октаэдр.

Заключение

Исходя из
проделанной работы можно сделать
следующие выводы:

Средние
линии имеют различные полезные свойства
в геометрических фигурах.

Одну теорему
можно доказать с помощью средней линии
фигур, а так же объяснить ее на языке
механики – с помощью понятия центра
масс.

При помощи
средних линий можно построить различные
планиметрические (параллелограмм,
ромб, квадрат) и стереометрические
фигуры (куб, октаэдр, тетраэдр и др.).

Свойства
средних линий помогают рационально
решить задачи любых уровней.

Список
использованных источников и литературы

Ежемесячный
научно-популярный физико-математический
журнал Академии наук СССР и Академии
педагогических наук литературы. “
Квант № 6 1989 г. с. 46.

С.
Аксимова. Занимательная математика. –
Санкт-Петербург, «Тригон», 1997 г. с. 526.

В.В.
Шлыков, Л.Е. Зезетко. Практические
занятия по геометрии, 10 кл.: пособие для
учителей.- Мн.: ТетраСистемс, 2004 г. с.
68,76, 78.

Приложение

Почему
средняя линия трапеции не может пройти
через точку пересечения диагоналей?

BCDA 1 B 1 C 1 D 1 —
параллелепипед.
Точки Е
и
F
точки
пересечения диагоналей граней. АА1В 1 В
и ВВ 1 С 1 С
соответственно,
а точки К
и
Т
—
середины ребер AD
и
DC
соответственно.
Верно ли, что прямые EF
и
КТ
параллельны?

В
треугольной призме АВСА 1 В 1 С 1
очки
О и
F
середины
ребер AB
и BС
соответственно. Точки Т
и К середины
отрезков AB 1
и
ВС 1
соответственно.
Как расположены прямые ТК
и OF?

АВСА 1 В 1 С 1
правильная
треугольная призма, все ребра которой
равны между собой. Точка О
— середина ребра
СС 1 ,
а точка F
лежит
на ребре ВВ ]
так,
что BF: FB X
=1:3.
Постройте точку К,
в
которой прямая l,
проходящая через точку F
параллельно
прямой АО,
пересекает плоскость
ABC.
Вычислить площадь полной поверхности
призмы, если KF
= 1
см.

фигуру

Раньше. 2. Это геометрическая
фигура
. Эта фигура
образуется замкнутой линией
. Бывают выпуклые и невыпуклые. У фигуры
есть стороны… , сектор, сфера, сегмент, синус, середина, средняя
линия
, соотношение, свойство, степень, стереометрия, секущая…

Средняя линия треугольника

Свойства

средняя линия треугольника параллельна третьей стороне и равна её половине.
при проведении всех трёх средних линий образуются 4 равных треугольника, подобных (даже гомотетичных) исходному с коэффициентом 1/2.
средняя линия отсекает треугольник, который подобен данному, а его площадь равна одной четверти площади исходного треугольника.

Средняя линия четырехугольника

Средняя линия четырехугольника
— отрезок, соединяющий середины противолежащих сторон четырехугольника.

Свойства

Если в выпуклом четырехугольнике средняя линия образует равные углы с диагоналями четырехугольника, то диагонали равны.
Длина средней линии четырехугольника меньше полусуммы двух других сторон или равна ей, если эти стороны параллельны, и только в этом случае.
Середины сторон произвольного четырёхугольника — вершины параллелограмма . Его площадь равна половине площади четырехугольника, а его центр лежит на точке пересечения средних линий. Этот параллелограмм называется параллелограммом Вариньона ;
Точка пересечения средних линий четырехугольника является их общей серединой и делит пополам отрезок, соединяющий середины диагоналей. Кроме того, она является центроидом вершин четырехугольника.
В произвольном четырёхугольнике вектор средней линии равен полусумме векторов оснований.

Средняя линия трапеции

Средняя линия трапеции
— отрезок, соединяющий середины боковых сторон этой трапеции. Отрезок, соединяющий середины оснований трапеции, называют второй средней линией трапеции.

Свойства

средняя линия параллельна основаниям и равна их полусумме.

См. также

Примечания

Wikimedia Foundation
.
2010
.

Смотреть что такое «Средняя линия» в других словарях:

СРЕДНЯЯ ЛИНИЯ
— (1) трапеции отрезок, соединяющий середины боковых сторон трапеции. Средняя линия трапеции параллельна её основаниям и равна их полусумме; (2) треугольника отрезок, соединяющий середины двух сторон этого треугольника: третья сторона при этом… … Большая политехническая энциклопедия

средняя линия
— 24 средняя линия: Воображаемая линия, проходящая через профиль резьбы так, что толщина выступа равна ширине канавки. Источник … Словарь-справочник терминов нормативно-технической документации

средняя линия
— vidurio linija statusas T sritis Kūno kultūra ir sportas apibrėžtis 3 mm linija, dalijanti teniso stalo paviršių išilgai pusiau. atitikmenys: angl. centre line; midtrack line vok. Mittellinie, f rus. средняя линия … Sporto terminų žodynas

средняя линия
— vidurio linija statusas T sritis Kūno kultūra ir sportas apibrėžtis Linija, dalijanti fechtavimosi kovos takelį į dvi lygias dalis. atitikmenys: angl. centre line; midtrack line vok. Mittellinie, f rus. средняя линия … Sporto terminų žodynas

средняя линия
— vidurio linija statusas T sritis Kūno kultūra ir sportas apibrėžtis Linija, dalijanti sporto aikšt(el)ę pusiau. atitikmenys: angl. centre line; midtrack line vok. Mittellinie, f rus. средняя линия … Sporto terminų žodynas

Многоугольник — часть плоскости, ограниченная замкнутой ломаной линией. Углы у многоугольника обозначаются точками вершин ломаной. Вершины углов многоугольника и вершины многоугольника — это совпадающие точки.

Определение. Параллелограмм — это четырехугольник, у которого противолежащие стороны параллельны.

Свойства параллелограмма

1. Противолежащие стороны равны.
На рис. 11 AB
= CD
; BC
= AD
.

2. Противолежащие углы равны (два острых и два тупых угла).
На рис. 11 ∠A
= ∠C
; ∠B
= ∠D
.

3 Диагонали (отрезки прямой, соединяющие две противолежащие вершины) пересекаются и точкой пересечения делятся пополам.

На рис. 11 отрезки AO
= OC
; BO
= OD
.

Определение. Трапеция — это четырехугольник, у которого две противолежащие стороны параллельны, а две другие — нет.

Параллельные стороны называются ее основаниями
, а две другие стороны — боковыми сторонами
.

Виды трапеций

1. Трапеция
, у которой боковые стороны не равны,
называется разносторонней
(рис. 12).

2. Трапеция, у которой боковые стороны равны, называется равнобокой
(рис. 13).

3. Трапеция, у которой одна боковая сторона составляет прямой угол с основаниями, называется прямоугольной
(рис. 14).

Отрезок, соединяющий середины боковых сторон трапеции (рис. 15), называется средней линией трапеции (MN
). Средняя линия трапеции параллельна основаниям и равна их полусумме.

Трапецию можно назвать усеченным треугольником (рис. 17), поэтому и названия трапеций сходны с названиями треугольников (треугольники бывают разносторонние, равнобедренные, прямоугольные).

Площадь параллелограмма и трапеции

Правило. Площадь параллелограмма
равна произведению его стороны на высоту, проведенную к этой стороне.

Источник

Андрей Васюнин

04.05.2021 13:36:28

Геометрия 7-9 класс

10 баллов

Доказать, что прямая, содержащая середины противоположных сторон параллелограмма, проходит через точку пересечения его диагоналей.

Ирина Каминкова

04.05.2021 14:21:23

Ответ эксперта

Все предметы

Рейтинг пользователей

Источник

Планиметрия. Страница 4

1.Параллелограмм

3.Ромб

Задача

4.Теорема Фалеса

5.Средняя линия треугольника

6.Трапеция

7.Теорема о пропорциональных отрезках

Пример 1

Пример 2

Пример 3

Пример 4

Пример 5

Формула длины средней линии параллелограмма. Как найти среднюю линию трапеции

Теорема о средней линии треугольника

Следствия из теоремы о средней линии треугольника

Примеры задачи на понятие средней линии треугольника

Теорема о средней линии треугольника

Следствия из теоремы о средней линии треугольника

Примеры задачи на понятие средней линии треугольника

Теорема о средней линии треугольника

Следствия из теоремы о средней линии треугольника

Примеры задачи на понятие средней линии треугольника

Как найти среднюю линию треугольника – второй признак подобия треугольников

Как найти среднюю линию треугольника – признак параллельности прямых

Как найти среднюю линию треугольника

Средняя линия треугольника

Свойства

Средняя линия четырехугольника

Свойства

Средняя линия трапеции

Свойства

См. также

Примечания

Смотреть что такое «Средняя линия» в других словарях:

Средние линии

Средние линии треугольника

Средняя линия трапеции

Средние линии четырехугольника. Теорема Вариньона

Средние линии тетраэдра

Средние линии треугольников и четырехугольников

Параллелограмм. Средняя линия

Средние линии геометрических фигур

1. Свойства средних линий

Средняя линия треугольника

Свойства

Средняя линия четырехугольника

Свойства

Средняя линия трапеции

Свойства

См. также

Примечания

Смотреть что такое «Средняя линия» в других словарях:

Свойства параллелограмма

Виды трапеций

Площадь параллелограмма и трапеции

Все предметы

Рейтинг пользователей

Не пропустите также: