Как найти середину прямой циркулем - Avtoru.top

Главная
Справочники
Справочник по геометрии 7-9 класс
Треугольники
Построения циркулем и линейкой
Построение середины отрезка

Пример:

Построить середину данного отрезка.

Дано: отрезок АВ.

Построить: середину АВ.

Решение:

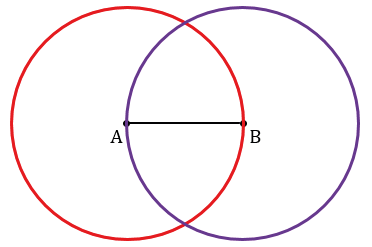
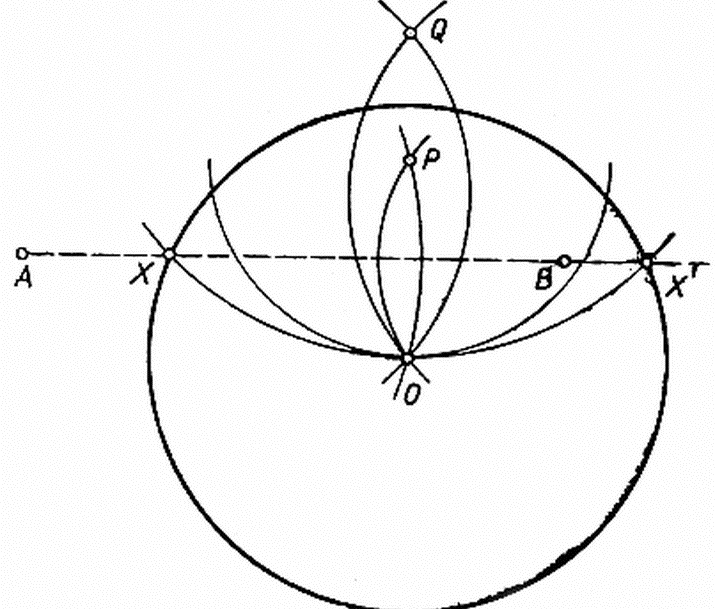
Строим с помощью линейки произвольный отрезок АВ.

Далее с помощью циркуля строим две окружности радиуса АВ с центрами в точках А и В.

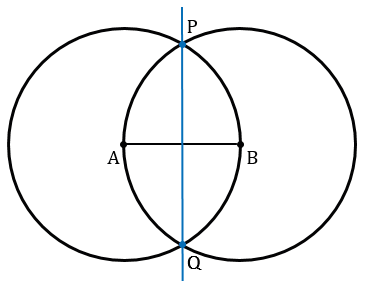
Получаем две точки пересечения данных окружностей. Обозначим их Р и Q. Проведем с помощью линейки через точки Р и Q прямую РQ.

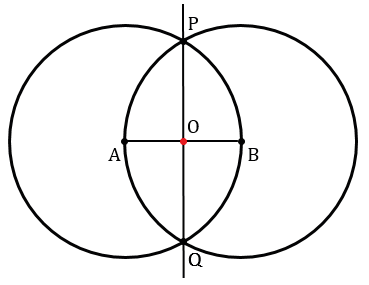
Точку пересечения прямой РQ и отрезка АВ обозначим О.

Докажем, что точка О — искомая точка, т.е. точка О — середина отрезка АВ.

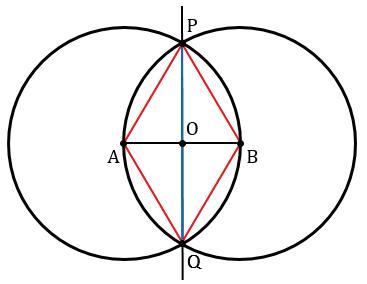
Рассмотрим треугольники РАQ и РВQ.

По построению АР = ВР, АQ = BQ (как радиусы одинаковых окружностей), PQ — общая, следовательно, РАQ =РВQ по 3 признаку равенства треугольников. Значит, по свойству равных треугольников АРО =ВРО, тогда РО — биссектриса АРВ.

В АРВ АР = ВР (как радиусы одинаковых окружностей), следовательно, АРВ — равнобедренный, тогда по свойству равнобедренного треугольника биссектриса РО АРВ и его медиана, следовательно, точка О — середина отрезка АВ. Что и требовалось доказать.

Советуем посмотреть:

Построение угла, равного данному

Построение биссектрисы угла

Построение перпендикулярных прямых

Среднее пропорциональное

Треугольник

Равенство треугольников

Первый признак равенства треугольников

Перпендикуляр к прямой

Медианы треугольника

Биссектрисы треугольника

Высоты треугольника

Равнобедренный треугольник

Свойства равнобедренного треугольника

Второй признак равенства треугольников

Третий признак равенства треугольников

Окружность

Построения циркулем и линейкой

Треугольники

Правило встречается в следующих упражнениях:

7 класс

Задание 185,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 21,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 316*,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 353,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 393,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 588,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 711,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 736,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 737,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 876,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Источник

В этой статье вы узнаете, как разделить тот или иной отрезок с помощью такого инструмента, как циркуль. Ведь не всегда есть линейка под рукой. Такие знания пригодятся на практике.

Содержание

Как определить середину отрезка с помощью одного циркуля?
Как построить середину отрезка с помощью циркуля и линейки?
Видео: Как середину отрезка только циркулем?

Геометрия – это предмет, который изучается в школе и имеет применение на практике. Благодаря знаниям этого предмета можно узнать площадь, объем той или иной фигуры, или емкости, а также с легкостью разделить отрезок пополам с помощью сподручных инструментов. Узнаем дальше, как определить середину отрезка с помощью циркуля.

Как определить середину отрезка с помощью одного циркуля?

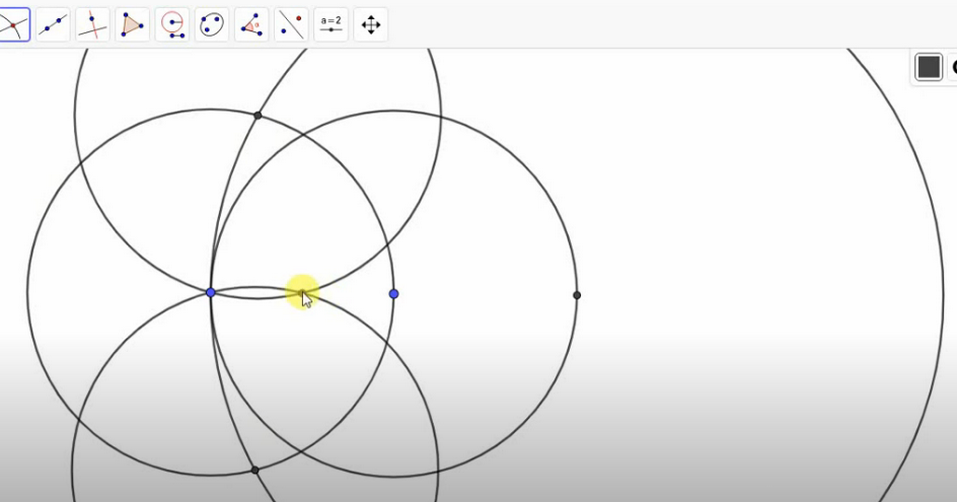
Интересно то, что определить середину отрезка с помощью циркуля можно и без линейки – это доказал еще в восемнадцатом веке итальянец Маскерони. Процесс построения сложнее, чем с помощью двух этих инструментов, но знания по этому поводу не помешают. Вначале определимся, что такое отрезок. Отрезком называют прямую, ограниченную двумя точками. И, чтобы найти середину отрезка, придется построить множество окружностей и найти множество точек их пересечения на них, пока не найдется середина отрезка.

Построение середины отрезка

Если запомнить последовательность, построения окружностей, то процесс определения середины несложный. Вначале удваивают отрезок путем построения двух окружностей радиусом равным длине заданного отрезка, фото ниже:

Окружности радиусом в длину отрезка

Следующий шаг — постройте окружность тем же радиусом вверху на точке пересечения двух окружностей, наглядно это будет смотреться так:

Три окружности

Из точки пересечения второй и третьей окружности, нарисуйте еще четвертую окружность такого же радиуса, должен получиться вот такой рисунок:

Геометрия

Эти окружности строились, чтобы получить точку (третью точку, как продолжение отрезка), она находится на пересечении четвертой и второй окружности. Теперь эту точку оставьте, а две окружности сверху сотрите, они не понадобятся вам.
Постройте окружность с радиусом в два раза больше, чем предыдущие:

Как найти середину отрезка

Отметьте две точки пересечения на первой окружности и большой. Через эти две точки проведите окружности с радиусом отрезка, а точка их пересечения и будет серединой отрезка.

Середина отрезка

ВАЖНО: Поиск середины отрезка сводится к нескольким шагам. Вначале отрезок следует удлинить ровно в два раза благодаря окружности большего диаметра, а потом рядом построений уже и найти саму точку отрезка, что делит его пополам.

Как построить середину отрезка с помощью циркуля и линейки?

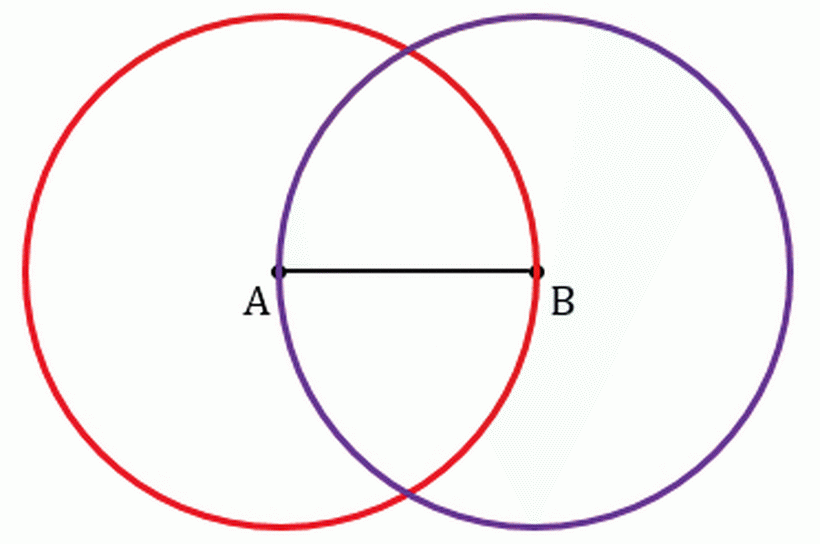
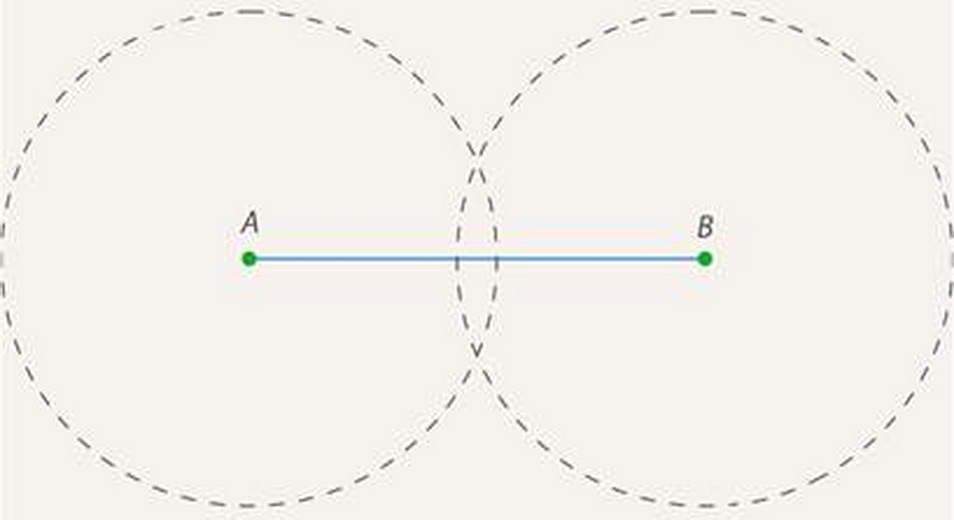
Еще можно построить середину отрезка с помощью циркуля, линейки. Сделать это намного проще, чем в предыдущем варианте. Вам не понадобится рисовать множество окружностей разного диаметра, а достаточно построить лишь две одинаковые, а после провести перпендикуляр через точки пересечения с линиями окружности. Еще этот перпендикуляр называют серединным, что означает прямую, которую проводят под углом 90 градусов к отрезку.

Далее будет представлен мастер-класс на эту тему в подробностях и наглядно:

Нарисуйте нужный отрезок на листке в клеточку, так вам удобнее будет разобраться в данной теме.
Возьмите циркуль и нарисуйте две окружности с радиусом большим, чем середина отрезка или радиусом с длину отрезка – нет особой надобности рисовать слишком большие окружности, особенно, если отрезок большой длины.

Две окружности

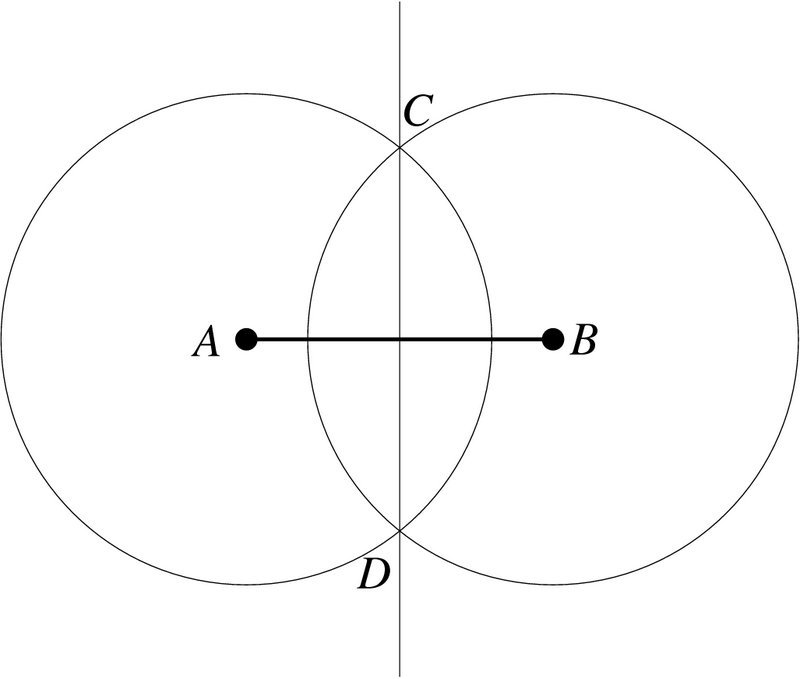
На рисунке выше видно, что окружности образуют две точки пересечения (вверху и внизу). Теперь понадобится линейка. Соедините эти две точки серединным перпендикуляром. Точка пересечения линии и отрезка и будет серединой.

Серединный перпендикуляр CD

Итак, среднюю точку отрезка нашли, теперь еще и не помешает доказать, что именно CD – срединный перпендикуляр, и он делит отрезок пополам. Это сделать просто. Ведь две окружности, что образуют линию, имеют одинаковый радиус, диаметр. А у окружностей все точки на линии одинаково удалены от ее центра. Значит точки C и D также находятся на одинаковых расстояниях от точек A и B. Прямая которая соединяет точки D и C может быть лишь одна в плоскости. И точка пересечения на отрезке находится на одном и том же расстоянии. Все это и требовалось прояснить.

Видео: Как середину отрезка только циркулем?

Источник

Как найти середину отрезка

В геометрии, найти середину отрезка можно разными способами, а также для решения такой задачи потребуется знание формул.

1

Что такое отрезок, его длина и середина?

Отрезком называется прямая линия, соединяющая две произвольные точки. Эти точки называются концами отрезка. Длина отрезка – это расстояние между двумя точками, которые изображены на прямой линии отрезка.
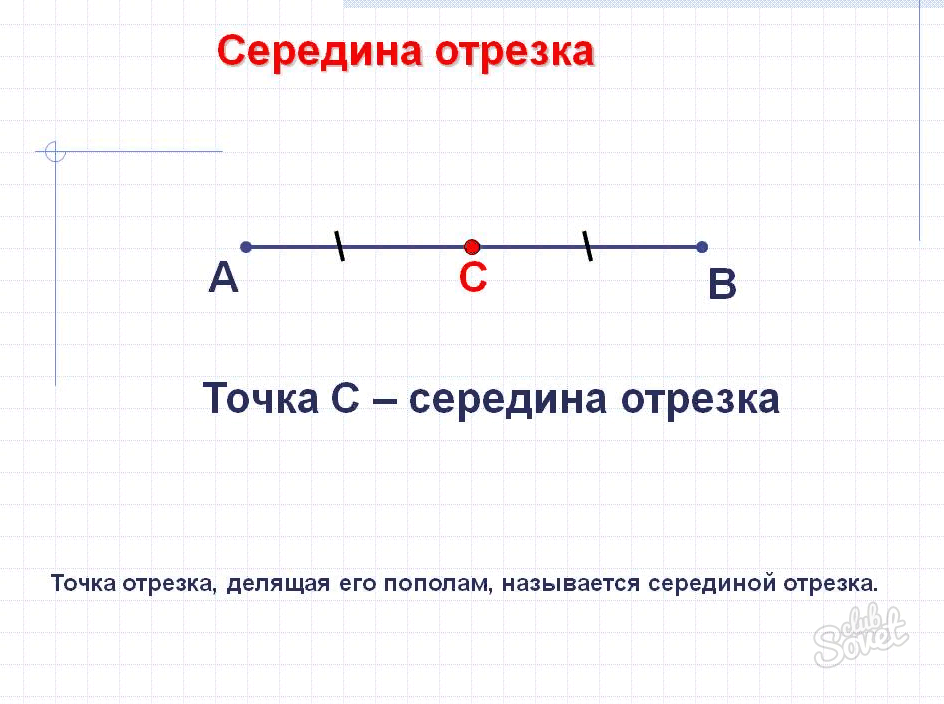
Середина отрезка – это равноудаленная точка от концов отрезка, которая лежит на середине самого отрезка.
Середину отрезка необходимо обозначать таким способом: |AB|
Например. Нужно найти середину отрезка, где АВ – отрезок, а середина равна С. Тогда будет справедливо такое равенство: A = C и B = C. Или |AC |= |CB|.

2

Как найти середину отрезка, используя циркуль?

Для нахождения середины отрезка можно использовать циркуль и линейку. А также нужно выполнить такие действия:

Изобразить отрезок нужно длины при помощи линейки.
Далее конец с иглой поставить так, чтобы расстояние между другим концом циркуля (с карандашом), равнялась большей части половины отрезка.
Прочерчиваем через отрезок полукруг.
Такие же действия проделываем с другой стороны отрезка, тем самым соединяя две части вместе.
Теперь, где пересекается окружность провести линию перпендикулярно.
Данное расстояние и будет считаться серединой отрезка.

3

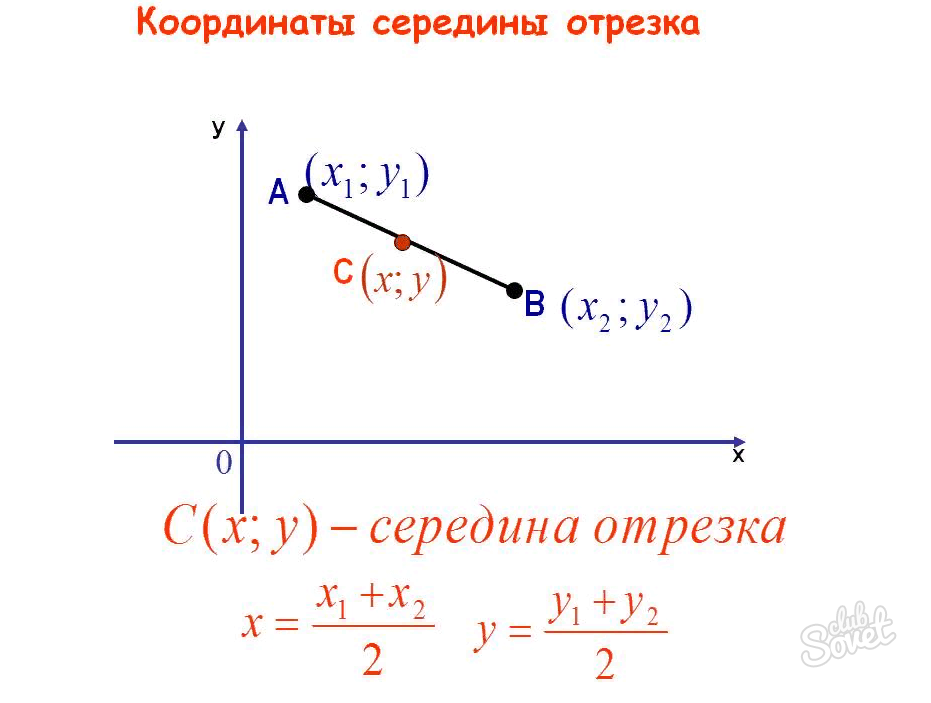
Найти середину отрезка при помощи координат?

Чтобы найти середину отрезка, нужно воспользоваться формулой: Ха + Xb / 2.

Например. Изображена координатная прямая с такими исходными данными: AB – отрезок. C – середина отрезка.
Значит можно составить равенство:
|AC| = |CB|.
Дадим этим точкам соответствующие числа: Xa, Xb.
Составим два возможных равенства: Xc − Xa = xb – x – Xa = Xb –Xc, Xc – Xa = −(Xb − Xc).
Из данного равенства можно вывести формулу: Ха + Xb / 2.
Эта формула будет основной для получения середины отрезка в пространстве или на плоскости.

Пример с использованием данной формулы:

Даны значения А (-5,3) и В (2, 4). Необходимо найти АВ.
На отрезке найдем его середину и обозначим ее, как С.
Дальше подставляем значения под формулу: Ха + Xb / 2.
– 5 + 2 / 2 = – 3/2; 3 + 4 / 2 = 7/2.
Ответ: серединой отрезка являются -3/2 и 7/2.
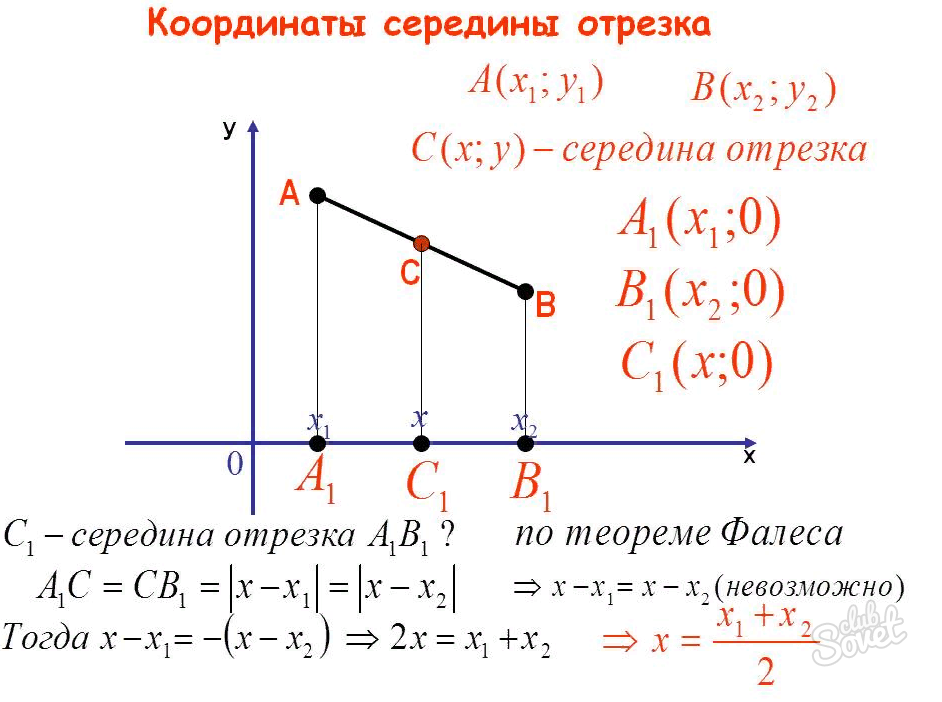
Как найти середину отрезка в пространстве

Для того, чтобы найти середину отрезка в пространстве, используется следующая формула:

Хс = Ха + Xb / 2.

При этом удобно использовать теорему Фалеса для верных равенств:

А1 А2 / В1 В2 = А2 А3 / В2 В3 = А1 / А3 / В1 В3.

На самом деле, найти середину отрезка не так уж и сложно, если правильно подставить формулу. А также решение такой задачи не займет много времени.

Источник

Вам понадобится:

Отрезок
Циркуль
Линейка без делений
Карандаш

Как найти середину отрезка с помощью циркуля?Элементарная задачка о нахождении середины отрезка при помощи циркуля была сформулирована еще в античности. Часто ее приписывают древнегреческим мудрецам, однако, скорее всего, она присутствовала и в других культурах, в которых была развита математика и геометрия (например, в древнеегипетской). В древности эта задача имела и вполне практическое применение, ведь знание того, как найти середину отрезка при помощи простейших измерительных приборов, было полезно, например, в землемерстве, землеустройстве и строительстве. Сегодня, при наличии сложной измерительной техники, такое задание скорее представляет упражнение для развития интеллектуальных способностей и пространственной фантазии школьников.

Как же на самом деле решается данная задача? Берем циркуль и открываем его таким образом, чтобы радиус предполагаемой окружности был очевидно больше половины заданного отрезка. Теперь, ставим основание (иглу) циркуля в одну из точек, ограничивающих отрезок, и рисуем окружность выбранного радиуса. В принципе, решая задачу о том, как построить середину отрезка, достаточно нарисовать и полукруг, располагающийся «внутри» отрезка. Затем устанавливаем иглу циркуля в другой конец отрезка и повторяем процедуру очерчивания полукруга.Проделав описанную процедуру, видим, что наши окружности пересекаются в двух точках. Берем линейку и соединяем эти две точки прямой линией. Получаем линию перпендикулярную исходному отрезку. Именно точка пересечения этой линии и отрезка и является серединой последнего.

Конечно, здесь важно понять саму сущность данной задачи. Почему центр отрезка получится именно там, где пересекутся линии? Знание смысла данной задачи может, например пригодиться, при поиска ответа на вопрос о том, как найти середину треугольника, а также при решении других, более сложных геометрических задач.Итак, если соединить крайние точки исходного отрезка с точками пересечения наших окружностей, то получим четырехугольник. Но какой четырехугольник? Все его стороны являются радиусами наших окружностей, а значит равными по длине (ведь мы использовали одинаковый радиус). Любой четырехугольник с равными сторонами представляет собой ромб, диагонали которого всегда пересекаются под прямым углом и, что более важно для нашей задачи, делят друг друга пополам. Именно в этом и состоит логика подобного решения задачи о построении середины отрезка при помощи циркуля.

Если же вопрос формулируется иначе, а именно о том, как найти координаты середины отрезка, то для его решения необходимо знать координаты его конечных точек. Координаты же середины будут равны полусуммам координат точек окончания отрезка. Конечно, здесь уже используется декартова система координат, в связи с чем данные задачи имеют разную сущность, хотя и решают одну проблему.

В любом случае, решение разных формулировок геометрических задач очень
полезно для развития интеллекта и образного мышления ребенка. Поэтому не
стоит пренебрегать этими инструментами личностного развития.

Источник

Загрузить PDF

Поиск середины отрезка – легкая задача когда вам известны координаты двух конечных точек. Самый распространенный способ сделать это состоит в использовании формулы для нахождения середины отрезка; но есть еще один способ найти середину отрезка, если линия вертикальная или горизонтальная. Если вы хотите знать, как найти середину отрезка в течение нескольких минут, выполните следующие действия.

1

Определение. Середина отрезка — точка, которая находится на равном расстоянии от конечных точек отрезка и лежит на нем. Таким образом, ее координаты – среднее из двух координат х и двух координат у.
2

Формула. Формула записывается в виде суммы двух координат х (конечных точек), деленной на два, и суммы двух координат у (конечных точек), деленной на два. Это даст среднее значение х и у координат. Формула:[(x₁ + x₂)/2,( y₁ + y₂)/2]
3
Найдите координаты конечных точек. Вы не можете использовать формулу, не зная х и у координаты конечных точек. Например, необходимо найти середину (точку О) отрезка, ограниченного точками М (5,4 ) и N (3, -4). Таким образом, (x₁, y₁) = (5, 4) и (x₂, y₂) = (3, -4).
- Обратите внимание, что любая пара координат может обозначаться как (x₁, y₁) или (x₂, y₂). Так как вы будете просто складывать координаты и делить результат на два, не имеет значения, какую пару координат выбрать в первую очередь.
4
Подставьте координаты в формулу. Теперь, когда вам известны координаты конечных точек, подставьте их в формулу. Вот как это делается:
- [(5 + 3)/2, (4 + -4)/2]
5
Решите. После того как вы подставили координаты в формулу, проделайте арифметические действия для вычисления середины. Вот как это делается:
- [(5 + 3)/2, (4 + -4)/2] =
- [(8/2), (0/2)] =
- (4, 0)
- Середина отрезка между точками (5,4) и (3, -4) есть точка (4,0).
Реклама

1
Рассмотрим вертикальную или горизонтальную линию.
- Линия горизонтальная, если две у- координаты конечных точек равны. Например, отрезок с концами ( -3 , 4) и (5, 4) расположен горизонтально.
- Линия расположена вертикально, если две х -координаты конечных точек равны. Например, отрезок с концами (2, 0 ) и (2 , 3) находится в вертикальном положении.
2
Найдите длину отрезка. Вот как это сделать:
- Длина горизонтального отрезка с конечными точками (-3 , 4) и ( 5, 4) равна 8. Вы можете найти это сложением абсолютных величин координат х: | -3| + |5| = 8.
- Длина вертикального отрезка с конечными точками (2 ,0) и (2,3) равна 3. Вы можете найти это сложением абсолютных величин координат у: |0| + |3| = 3.
3
Разделите длину отрезка на два. Теперь, когда вы нашли длину отрезка, нужно разделить его на два.
- 8/2 = 4
- 3/2 = 1,5
4
Вычислите координаты середины. Вот как это делается:
- Чтобы найти середину отрезка, ограниченного точками (-3,4) и (5,4), прибавьте или вычтите 4 из х-координаты первой или второй конечной точки соответственно. Для точки (-3 , 4) это будет -3+4=1 и координаты середины: (1, 4) (Вам не нужно менять у- координаты, так как линия горизонтальная и у-координаты постоянны). Итак, середина отрезка (-3,4) и (5,4) есть точка (1,4).
- Чтобы найти середину отрезка, ограниченного точками (2, 0) и (2,3), прибавьте или вычтите 1,5 из у-координаты первой или второй конечной точки соответственно. Для точки (2 ,0) это будет -0+1,5=1,5 и координаты середины: (2,1,5) (Вам не нужно менять х-координаты, так как линия вертикальная и х-координаты постоянны). Итак, середина отрезка (2, 0 ) и (2,3) есть точка (2,1,5).
Реклама