Как найти середину интервала в теории вероятности - Avtoru.top

Как найти середину интервала

При статистической обработке результатов исследований самого разного рода полученные значения часто группируются в последовательность интервалов. Для расчета обобщающих характеристик таких последовательностей иногда приходится вычислять середину интервала — «центральную варианту». Методы ее расчета достаточно просты, но имеют некоторые особенности, вытекающие как из используемой для измерения шкалы, так и из характера группировки (открытые или закрытые интервалы).

Инструкция

Если интервал является участком непрерывной числовой последовательности, то для нахождения ее середины используйте обычные математические методы вычисления среднеарифметического значения. Минимальное значение интервала (его начало) сложите с максимальным (окончанием) и разделите результат пополам — это один из способов вычисления среднеарифметического значения. Например, это правило применимо, когда речь идет о возрастных интервалах. Скажем, серединой возрастного интервала в диапазоне от 21 года до 33 лет будет отметка в 27 лет, так как (21+33)/2=27.

Иногда бывает удобнее использовать другой метод вычисления среднеарифметического значения между верхней и нижней границами интервала. В этом варианте сначала определите ширину диапазона — отнимите от максимального значения минимальное. Затем поделите полученную величину пополам и прибавьте результат к минимальному значению диапазона. Например, если нижняя граница соответствует значению 47,15, а верхняя — 79,13, то ширина диапазона составит 79,13-47,15=31,98. Тогда серединой интервала будет 63,14, так как 47,15+(31,98/2) = 47,15+15,99 = 63,14.

Если интервал не является участком обычной числовой последовательности, то вычисляйте его середину в соответствии с цикличностью и размерностью используемой измерительной шкалы. Например, если речь идет об историческом периоде, то серединой интервала будет являться определенная календарная дата. Так для интервала с 1 января 2012 года по 31 января 2012 серединой будет дата 16 января 2012.

Кроме обычных (закрытых) интервалов статистические методы исследований могут оперировать и «открытыми». У таких диапазонов одна из границ не определена. Например, открытый интервал может быть задан формулировкой «от 50 лет и старше». Середина в этом случае определяется методом аналогий — если все остальные диапазоны рассматриваемой последовательности имеют одинаковую ширину, то предполагается, что и этот открытый интервал имеет такую же размерность. В противном случае вам надо определить динамику изменения ширины интервалов, предшествующих открытому, и вывести его условную ширину, исходя из полученной тенденции изменения.

Источники:

что такое открытый интервал

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Варианты для выполнения работы

I. Установление закономерностей, которым подчинены массовые случайные явления, основано на изучении методами теории вероятностей статистических данных — результатов наблюдений.

Почти все встречающиеся в жизни величины (урожайность сельскохозяйственных растений, продуктивности скота, производительность труда и заработная плата рабочих, объем производства продукции и т.д.) принимают неодинаковые значения у различных членов совокупности. Поэтому возникает необходимость в изучении их изменяемости. Это изучение начинается с проведения соответствующих наблюдений, обследований.

В результате наблюдений получают сведения о численной величине изучаемого признака у каждого члена данной совокупности.

Пример. Имеются данные о размере прибыли 100 коммерческих банков. Прибыль, млн. рублей.

30,2	51,9	43,1	58,9	34,1	55,2	47,9	43,7	53,2	34,9
47,8	65,7	37,8	68,6	48,4	67,5	27,3	66,1	52,0	55,6
54,1	26,9	53,6	42,5	59,3	44,8	52,8	42,3	55,9	48,1
44,5	69,8	47,3	35,6	70,1	39,5	70,3	33,7	51,8	56,1
28,4	48,7	41,9	58,1	20,4	56,3	46,5	41,8	59,5	38,1
41,4	70,4	31,4	52,5	45,2	52,3	40,2	60,4	27,6	57,4
29,3	53,8	46,3	40,1	50,3	48,9	35,8	61,7	49,2	45,8
45,3	71,5	35,1	57,8	28,1	57,6	49,6	45,5	36,2	63,2
61,9	25,1	65,1	49,7	62,1	46,1	39,9	62,4	50,1	33,1
33,3	49,8	39,8	45,9	37,3	78,0	64,9	28,8	62,5	58,7

Из данной таблицы видно, что интересующий нас признак (прибыль банков) меняется от одного члена совокупности к другому, варьирует. Варьирование есть изменяемость признака у отдельных членов совокупности.

Вариационным рядом называется последовательность вариант, записанных в возрастающем порядке и соответствующих им частот.

Число, показывающее, сколько раз повторяется в данной совокупности каждое значение признака, называется частотой.

Составим ранжированный вариационный ряд (выпишем варианты в порядке возрастания):

20,4	25,1	26,9	27,3	27,6	28,1	28,4	28,8	29,3	30,2
31,4	33,1	33,3	33,7	34,1	34,9	35,1	35,6	35,8	36,2
37,3	37,8	38,1	39,5	39,8	39,9	40,1	40,2	41,4	41,8
41,9	42,3	42,5	43,1	43,7	44,5	44,8	45,2	45,3	45,5
45,8	45,9	46,1	46,3	46,5	47,3	47,8	47,9	48,1	48,4
48,7	48,9	49,2	49,6	49,7	49,8	50,1	50,3	51,8	51,9
52,0	52,3	52,5	52,8	53,2	53,6	53,8	54,1	55,2	55,6
55,9	56,1	56,3	57,4	57,6	57,8	58,1	58,7	58,9	59,3
59,5	60,4	61,7	61,9	62,1	62,4	62,5	63,2	64,9	65,1
65,7	66,1	67,5	68,6	69,8	70,1	70,3	70,4	71,5	78,0

В нашем случае каждое значение признака (варианта вариационного ряда) повторилось только один раз, т.е. значение частоты для всех вариант равно единице. Перейдем к интервальному вариационному ряду, так как интересующий нас признак принимает дробные, практически не повторяющиеся значения.

Для этого необходимо определить число интервалов (классов) и длину интервала (классного промежутка), после чего произвести разноску, т.е. подсчитать для каждого интервала число вариант, попавших в него.

Количество классов устанавливают в зависимости от степени точности, с которой ведется обработка, и количества объектов в выборке. Считается удобным при объеме выборки (n) в пределах от 30 до 60 вариант распределять их на 6-7 классов, при n от 60 до 100 вариант — на 7-8 классов, при n от 100 и более вариант — на 9-17 классов.

Нужное количество групп также может быть ориентировочно вычислено по формуле Стерджесса:

где — число групп (классов, интервалов) ряда распределения; n — объем выборки.

Можно также использовать выражение:

При они дают примерно одинаковые результаты.

В рассматриваемом примере о размере прибыли коммерческих банков, n=100. Применяя формулу Стерджесса, получим:

Однако Таким образом, число интервалов может быть равно 8, 9, 10 и т.д.

Нахождение нужного количества групп и их размеров часто бывает взаимообусловлено. Для того, чтобы как-то определиться с числом интервалов, найдем размах вариации — разность между наибольшей и наименьшей вариантой:

$[R=x_{max}-x_{min}]$

где — размах вариации,

$x_{max}$ — наибольшее значение варьирующего признака,

$x_{min}$ — наименьшее значение варьирующего признака.

Найдем размах вариации для рассматриваемой задачи:

Для того, чтобы найти длину интервала (величину классового промежутка) необходимо разделить размах вариации на число классов и полученную величину округлить таким образом, чтобы было удобно производить сначала разноску, а затем и различные вычисления. Рекомендую округлять до единиц, до которых округлены варианты в исходной таблице, в нашем случае до десятых.

$[happrox frac{R}{k}]$

Согласно формуле получаем

$[happrox frac{57,6}{8}=7,2]$

Теперь необходимо определиться с началом первого интервала. Для этого можно использовать формулу:

$[x_1approx x_{min}-frac{h}{2}]$

$[x_1approx 20,4-frac{7,2}{2}=16,8.]$

Замечание. За начало первого интервала можно принять некоторое значение, несколько меньшее $x_{min}$ или само значение $x_{min}$ . Далее в табличном виде я покажу оба варианта.

Прибавив к началу первого интервала (нижней границе) шаг, получим верхнюю границу первого интервала и одновременно нижнюю границу второго интервала. Выполняя последовательно указанные действия, будем находить границы последующих интервалов до тех пор, пока не будет получено или перекрыто $x_{max}$ .

Таким образом, верхняя граница одного интервала одновременно является нижней границей другого интервала. Чтобы не возникало сомнений, в какой интервал отнести варианту, попавшую на границу, условимся относить ее к верхнему интервалу.

Составим теперь рабочую таблицу для построения интервального вариационного ряда и произведем подсчет частот вариант, попавших в тот или иной интервал.

Как и обещал покажу две таблицы построения ряда:

1. Отсчет ведем от $x_{min}$ , т.е. нижняя граница первого интервала совпадает с $x_{min}$ .

Группы банков по размеру прибыли (границы интервалов)	Количество банков, принадлежащих данной группе (частоты, )	Накопленные частоты,
20,4 — 27,6	4	4
27,6 — 34,8	11	15
34,8 — 42	16	31
42 — 49,2	21	52
49,2 — 56,4	21	73
56,4 — 63,6	15	88
63,6 — 70,8	10	98
70,8 — 78	2	100

2. Начало первого интервала определяем с помощью формулы: $x_1approx x_{min}-frac{h}{2}$ .

Группы банков по размеру прибыли (границы интервалов)	Количество банков, принадлежащих данной группе (частоты, )	Накопленные частоты,
16,8 — 24	1	1
24 — 31,2	9	10
31,2 — 38,4	13	23
38,4 — 45,6	17	40
45,6 — 52,8	23	63
52,8 — 60	18	81
60 — 67,2	11	92
67,2 — 74,4	7	99
74,4 — 81,6	1	100

Как мы видим в 1-м случае у нас получилось восемь интервалов, что полностью совпадает с результатом, который нам дала формула Стерджесса. Во втором случае у нас получилось девять интервалов, так как при поиске начала первого интервала пользовались специальной формулой.

Для дальнейшего исследования я буду пользоваться результатами второй таблицы, так как там ярко выражен модальный интервал (одна мода) и медиана практически точно попадает на середину вариационного ряда.

Мы получили интервальный вариационный ряд — упорядоченную совокупность интервалов варьирования значений случайной величины с соответствующими частотами попаданий в каждый из них значений величины.

II. Графическая интерпретация вариационных рядов.

№ п/п	Границы интервалов, $[x_{i}; x_{i+1})$	Середины интервалов, $x_{i}^{*}=frac{x_i+x_{i+1}}{2}$	Частоты интервалов,	Относительные частоты $W_i=frac{n_i}{n}$	Плотность относит. частоты $frac{W_i}{h}$	Плотность частоты $frac{n_i}{h}$
1	16,8 — 24	20,4	1	0,01	0,001	0,139
2	24 — 31,2	27,6	9	0,09	0,013	1,250
3	31,2 — 38,4	34,8	13	0,13	0,018	1,806
4	38,4 — 45,6	42	17	0,17	0,024	2,361
5	45,6 — 52,8	49,2	23	0,23	0,032	3,194
6	52,8 — 60	56,4	18	0,18	0,025	2,500
7	60 — 67,2	63,6	11	0,11	0,015	1,528
8	67,2 — 74,4	70,8	7	0,07	0,010	0,972
9	74,4 — 81,6	78	1	0,01	0,001	0,139

Строим графики:

Далее найдем моду вариационного ряда:

$[M_o(X)=x_{M_o}+hfrac{(n_2-n_1)}{(n_2-n_1)+(n_2-n_3)}]$

где

$x_{M_o}$ — начало модального интервала;

— длина частичного интервала (шаг);

n_1 — частота предмодального интервала;

n_2 — частота модального интервала;

— частота послемодального интервала.

Определим модальный интервал — интервал, имеющий наибольшую частоту. Из таблицы видно, что модальным является интервал (45,6 — 52,8).

$[M_o(X)=45,6+7,2frac{(23-17)}{(23-17)+(23-18)}=]$

$[=45,6+7,2cdot frac{6}{6+5}=45,6+3,93=49,5]$

Медиана

Для интервального ряда медиана находится по формуле:

$[M_e(X)=x_{M_e}+hfrac{0,5n-S_{M_{e}-1}}{n_{M_e}}]$

где

$x_{M_e}$ — начало медианного интервала;

— длина частичного интервала (шаг);

— объем совокупности;

$S_{M_{e}-1}$ — накопленная частота интервала, предшествующая медианному;

$n_{M_e}$ — частота медианного интервала.

Определим медианный интервал — интервал, в котором впервые накопленная частота превышает половину объема выборки.Так как объем выборки n=100, то n/2=50. По таблице найдем интервал, где впервые накопленные частоты превысят это значение. Таким является интервал (45,6 — 52,8).

Получаем,

$[M_e(X)=45,6+7,2frac{0,5cdot 100-40}{23}approx 48,7.]$

III. Расчет сводных характеристик выборки.

Для определения $x_B, D_{B}, sigma_{B}$ составим расчетную таблицу. Для начала определимся с ложным нулем С. В качестве ложного нуля можно принять любую варианту. Максимальная простота вычислений достигается, если выбрать в качестве ложного нуля варианту, которая расположена примерно в середине вариационного ряда (часто такая варианта имеет наибольшую частоту).

Варианте, которая принята в качестве ложного нуля, соответствует условная варианта, равная нулю. В нашем случае С=49,2.

Равноотстоящими называют варианты, которые образуют арифметическую прогрессию с разностью h.

Условными называют варианты, определяемые равенством:

$[U_i=frac{(x_i-C)}{h}]$

Произведем расчет условных вариант согласно формуле:

$[U_1=frac{20,4-49,2}{7,2}=-4]$

$[U_2=frac{27,6-49,2}{7,2}=-3]$

$[U_3=frac{34,8-49,2}{7,2}=-2]$

$[U_4=frac{42-49,2}{7,2}=-1]$

$[U_5=frac{49,2-49,2}{7,2}=0]$

$[U_6=frac{56,4-49,2}{7,2}=1]$

$[U_7=frac{63,6-49,2}{7,2}=2]$

$[U_8=frac{70,8-49,2}{7,2}=3]$

$[U_9=frac{78-49,2}{7,2}=4]$

N п/п	Середины интервалов, $x_{i}^{*}$	Частоты интервалов,	Условные варианты,	Произведения частот и условных вариант,	Произведения частот и условных вариант,	Произведения частот и условных вариант,	Произведения частот и условных вариант,	Произведения частот и условных вариант,	Произведения частот и условных вариант,
1	20,4	1	-4	-4	16	-64	256	9	81
2	27,6	9	-3	-27	81	-243	729	36	144
3	34,8	13	-2	-26	52	-104	208	13	13
4	42	17	-1	-17	17	-17	17	0	0
5	49,2	23	0	0	0	0	0	23	23
6	56,4	18	1	18	18	18	18	72	288
7	63,6	11	2	22	44	88	176	99	891
8	70,8	7	3	21	63	189	567	112	1792
9	78	1	4	4	16	64	256	25	625

Контроль:

$[sum n_i U_i^2 + 2sum n_iU_i+n=sum n_i{(U_i+1)}^2]$

$[sum n_i{(U_i+1)}^2=389]$

Контроль:

$[sum n_i U_i^4 + 4sum n_iU_i^3+6sum n_iU_i^2+4sum n_iU_i+n=sum n_i{(U_i+1)}^4]$

$[sum n_i{(U_i+1)}^4=3857]$

Равенство выполнено, следовательно вычисления произведены верно.

Вычислим условные моменты 1-го, 2-го, 3-го и 4-го порядков:

$[M_1^{*}=frac{sum n_iU_i}{n}=frac{-9}{100}=-0,09;]$

$[M_2^{*}=frac{sum n_iU_i^2}{n}=frac{307}{100}=3,07;]$

$[M_3^{*}=frac{sum n_iU_i^3}{n}=frac{-69}{100}=-0,69;]$

$[M_4^{*}=frac{sum n_iU_i^4}{n}=frac{2227}{100}=22,27.]$

Найдем выборочные среднюю, дисперсию и среднее квадратическое отклонение :

$[x_{B}=M_1^{*}cdot h+C=-0,09cdot 7,2+49,2=48,552;]$

$[D_{B}=(M_2^{*}-{(M_1^{*})}^2)h^2=(3,07-{(-0,09)}^2){7,2}^2approx 158,73.]$

$[sigma_{B}=sqrt{D_B}=sqrt{158,73}=12,6.]$

Также для оценки отклонения эмпирического распределения от нормального используют такие характеристики, как асимметрия и эксцесс.

Асимметрией теоретического распределения называют отношение центрального момента третьего порядка к кубу среднего квадратического отклонения:

$[a_s=frac{m_3}{sigma_B^3}]$

Асимметрия положительна, если «длинная часть» кривой распределения расположена справа от математического ожидания; асимметрия отрицательна, если «длинная часть» кривой расположена слева от математического ожидания. Практически определяют знак асимметрии по расположению кривой распределения относительно моды (точки максимума дифференциальной функции): если «длинная часть» кривой расположена правее моды, то асимметрия положительна, если слева — отрицательна.

Эксцесс эмпирического распределения определяется равенством:

$[e_k=frac{m_4}{sigma_B^4}-3]$

где — центральный эмпирический момент четвертого порядка.

Для нормального распределения эксцесс равен нулю. Поэтому если эксцесс некоторого распределения отличен от нуля, то кривая этого распределения отличается от нормальной кривой: если эксцесс положительный, то кривая имеет более высокую и «острую» вершину, чем нормальная кривая; если эксцесс отрицательный, то сравниваемая кривая имеет более низкую и «плоскую» вершину, чем нормальная кривая. При этом предполагается, что нормальное и теоретическое распределения имеют одинаковые математические ожидания и дисперсии.

Вычисляем центральные эмпирические моменты третьего и четвертого порядков:

$[m_3=(M_3^*-3M_1^*M_2^*+2{(M_1^*)}^3)cdot h^3=51,3;]$

$[m_4=(M_4^*-4M_3^*M_1^*+6M_2^*{(M_1^*)}^2-3{(M_1^*)}^4)cdot h^4=59580,97;]$

Найдем асимметрию и эксцесс:

$[a_s=frac{51,3}{{12,6}^3}=0,026]$

$[e_k=frac{59580,97}{{12,6}^4}-3=-0,635]$

IV. Проверка гипотезы о нормальном распределении генеральной совокупности. Критерий согласия Пирсона.

Проверим генеральную совокупность значений размера прибыли банков по критерию Пирсона

Правило. Для того, чтобы при заданном уровне значимости проверить нулевую гипотезу : генеральная совокупность распределена нормально, надо сначала вычислить теоретические частоты, а затем наблюдаемое значение критерия:

$[chi^2_{nabl}=sum frac{ {(n_i-n_i^{'})}^2}{n_i^{'}}]$

и по таблице критических точек распределения , по заданному уровню значимости и числу степеней свободы найти критическую точку $chi^2_{kp}(alpha;k)$ , где s — количество интервалов.

Если $chi^2_{nabl}<chi^2_{kp}$ — нет оснований отвергнуть нулевую гипотезу.

Если $chi^2_{nabl}>chi^2_{kp}$ — нулевую гипотезу отвергают.

Найдем теоретические частоты , для этого составим следующую таблицу.

Середины интервалов, $x_{i}^{*}$	Частоты интервалов,	Произведем расчет, $x_{i}^{*}-x_B$	Произведем расчет, $V_i=frac{(x_{i}^{*}-x_B)}{sigma_B}$	Значения функции Гаусса,	Произведем расчет, $frac{nh}{sigma_B}$	Теоретические частоты, $n_i^{'}=57 cdotvarphi(V_i)$
20,4	1	-28,152	-2,23	0,0332	57	2
27,6	9	-20,952	-1,66	0,1006	57	6
34,8	13	-13,752	-1,09	0,2203	57	13
42	17	-6,552	-0,52	0,3485	57	20
49,2	23	0,648	0,05	0,3984	57	23
56,4	18	7,848	0,62	0,3292	57	19
63,6	11	15,048	1,19	0,1965	57	11
70,8	7	22,248	1,77	0,0833	57	5
78	1	29,448	2,34	0,0258	57	1
						$sum n_i^{'}=100$

Вычислим $chi^2_{nabl}$ , для чего составим расчетную таблицу.

		$n_i^{'}$	$n_i-n_i^{'}$	${(n_i-n_i^{'})}^2$	$frac{{(n_i-n_i^{'})}^2}{n_i^'}$		$frac{n_i^2}{n_i^{'}}$
1	1	2	-1	1	0,5	1	0,5
2	9	6	3	9	1,5	81	13,5
3	13	13	0	0	0	169	13
4	17	20	-3	9	0,45	289	14,45
5	23	23	0	0	0	529	23
6	18	19	-1	1	0,05	324	17,05
7	11	11	0	0	0	121	11
8	7	5	2	4	0,8	49	9,8
9	1	1	0	0	0	1	1
	100	100			Наблюдаемое значение критерия, $chi^2_{nabl}=3,30$		103,30

Контроль:

$[sumfrac{n_i^2}{n_i^{'}}-n=sum frac{{(n_i-n_i^{'})}^2}{n_i^'}]$

$[sumfrac{n_i^2}{n_i'}-n=103,3-100=3,3]$

$[sum frac{{(n_i-n_i')}^2}{n_i'}=3,3]$

Вычисления произведены правильно.

Найдем число степеней свободы, учитывая, что число групп выборки (число различных вариант) s=9;

По таблице критических точек распределения по уровню значимости и числу степеней свободы k=6 находим $chi^2_{kp}(0,025;6)=14,4.$

Так как $chi^2_{nabl}<chi^2_{kp}$ — нет оснований отвергнуть нулевую гипотезу. Другими словами, расхождение эмпирических и теоретических частот незначительное. Следовательно, данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.

На рисунке построены нормальная (теоретическая) кривая по теоретическим частотам (зеленый график) и полигон наблюдаемых частот (коричневый график). Сравнение графиков наглядно показывает, что построенная теоретическая кривая удовлетворительно отражает данные наблюдений.

V. Интервальные оценки.

Интервальной называют оценку, которая определяется двумя числами — концами интервала, покрывающего оцениваемый параметр.

Доверительным называют интервал, который с заданной надежностью покрывает заданный параметр.

Интервальной оценкой (с надежностью ) математического ожидания (а) нормально распределенного количественного признака Х по выборочной средней при известном среднем квадратическом отклонении sigma генеральной совокупности служит доверительный интервал

$[x_B-frac{tsigma}{sqrt{n}}<a<x_B+frac{tsigma}{sqrt{n}},]$

где $frac{tsigma}{sqrt{n}}=delta$ — точность оценки, n — объем выборки, t — значение аргумента функции Лапласа (см. приложение 2), при котором $phi(t)=frac{gamma}{2}$ ;

при неизвестном среднем квадратическом отклонении sigma (и объеме выборки n<30)

$[x_B-frac{t_{gamma}cdot S}{sqrt{n}}<a<x_B+frac{t_{gamma}cdot S}{sqrt{n}},]$

$[S=sqrt{frac{n}{n-1}D_B}]$

где S — исправленное выборочное среднее квадратическое отклонение, $t_{gamma}$ находят по таблице приложения по заданным n и .

В нашем примере среднее квадратическое отклонение известно, . А также , , . Поэтому для поиска доверительного интервала используем первую формулу:

$[x_B-frac{tsigma}{sqrt{n}}<a<x_B+frac{tsigma}{sqrt{n}}]$

Все величины, кроме t, известны. Найдем t из соотношения $phi(t)=frac{0,95}{2}=0,475.$ По таблице приложения находим t=1,96. Подставив t=1,96, , , в формулу, окончательно получим искомый доверительный интервал:

$[48,55-frac{1,96cdot 12,6}{10}<a<48,55+frac{1,96cdot 12,6}{10}]$

Интервальной оценкой (с надежностью ) среднего квадратического отклонения нормально распределенного количественного признака Х по «исправленному» выборочному среднему квадратическому отклонению S служит доверительный интервал

(при q<1), (*)

(при q>1),

где q — находят по таблице приложения по заданным n и .

По данным и n=100 по таблице приложения 4 найдем q=0,143. Так как q<1, то, подставив $S=sqrt{frac{n}{n-1}D_B}=sqrt{frac{100}{99}cdot 158,73}approx 12,66, quad quad q=0,143$ в соотношение (*), получим доверительный интервал:

Источник

Расчет средней величины в интервальных вариационных рядах немного отличается от расчета в рядах дискретных. Как рассчитать среднюю арифметическую и среднюю гармоническую в дискретных рядах можно посмотреть вот ЗДЕСЬ. Такое различие вполне объяснимо – это связано с особенностью интервальных рядов, в которых изучаемый признак приведен в интервале от и до.

Итак, посмотрим особенности расчета на примере.

Пример 1. Имеются данные о дневном заработке рабочих предприятия.

Дневной заработок рабочего, руб.	Число рабочих, чел.
500-1000	15
1000-1500	30
1500-2000	80
2000-2500	60
2500-3000	25
Итого	210

Нам необходимо рассчитать среднедневную заработную плату рабочего.

Начало решения задачи будет аналогичным правилам расчета средней величины, которые можно посмотреть в этой статье.

Начинаем мы с определения варианты и частоты, поскольку ищем мы средний заработок за день, то варианта это первая колонка, а частота вторая. Данные у нас заданы явным количеством, поэтому расчет проведем по формуле средней арифметической взвешенной (так как данные приведены в табличном виде). Но на этом сходства заканчиваются и появляются новые действия.

Дневной заработок рабочего, руб. х	Число рабочих, чел. f
500-1000	15
1000-1500	30
1500-2000	80
2000-2500	60
2500-3000	25
Итого	210

Дело в том, что интервальный рад представляет осредняемую величину в виде интервала. 500-1000, 2000-2500 и так далее. Чтобы решить эту проблему необходимо провести промежуточные действия, и только потом подсчитать среднюю величину по основной формуле.

Что же требуется в данном случае сделать. Все достаточно просто, чтобы провести расчет нам нужно, чтобы варианта была представлена одним числом, а не интервалом. Для получения такого значения находят так называемое ЦЕНТРАЛЬНОЕ ЗНАЧЕНИЕ ИНТЕРВАЛА (или середину интервала). Определяется оно путем сложение верхней и нижней границ интервала и делением на два.

Проведем необходимые расчеты и подставим данные в таблицу.

И так далее по всем интервалам рассчитываем центральное значение. В итоге получаем следующие результаты.

Дневной заработок рабочего, руб. х	Число рабочих, чел. f	х’
500-1000	15	750
1000-1500	30	1250
1500-2000	80	1750
2000-2500	60	2250
2500-3000	25	2750
Итого	210	—

После того как мы рассчитали центральные значения далее проведем расчеты в таблицы и подставим итоговые данные в формулу, аналогично тому как мы уже рассматривали ранее.

Дневной заработок рабочего, руб. х	Число рабочих, чел. f	х’	x’f
500-1000	15	750	11250
1000-1500	30	1250	37500
1500-2000	80	1750	140000
2000-2500	60	2250	135000
2500-3000	25	2750	68750
Итого	∑f = 210	—	∑ x’f = 392500

В итоге получаем, что среднедневная заработная плата одного рабочего составляет 1869 рублей.

Nafanya

Это пример решения, если интервальный ряд представлен со всеми закрытыми интервалами. Но достаточно часто бывает, когда два интервала открытые, первый и последний. В таких ситуациях прямой расчет центрального значения невозможен, но есть два варианта как это сделать.

Пример 2. Имеются данные о продолжительности производственного стажа персонала предприятия. Рассчитать среднюю продолжительность стада одного сотрудника.

Длительность производственного стажа, лет	Число сотрудников, человек
до 3	19
3-6	21
6-9	15
9-12	10
12 и более	5
Итого	70

В данном случае принцип решения останется точно таким же. Единственно, что поменялось в этой задаче, так это первый и последний интервалы. До 3 лет и 12 лет и более это и есть те самые открытые интервалы. Именно тут возникнет вопрос, а как же найти центральное значение интервала для таких интервалов.

Поступить в этой ситуации можно двумя способами:

Предположить какой бы мог быть интервал, учитывая, что нам приведены интервалы равные, то это вполне возможно. Интервал до 3 мог бы выглядеть как 0-3, и тогда его центральное значение будет (0+3)/2 = 1,5 года. Интервал 12 и более мог бы выглядеть как 12-15, и тогда его центральное значение было бы (12+15)/2 = 13,5 года. Все оставшиеся центральные значения интервала рассчитываются аналогично. В результате получаем следующее.

Длительность производственного стажа, лет х	Число сотрудников, человек f	х’	x’f
до 3	19	1,5	28,5
3-6	21	4,5	94,5
6-9	15	7,5	112,5
9-12	10	10,5	105,0
12 и более	5	13,5	67,5
Итого	∑f = 70	—	∑ x’f = 408,0

Средняя продолжительность стажа 5,83 года.

Принять за центральное значение, то данное которое имеется в интервале, без дополнительных расчетов. В нашем случае в интервале до 3 это будет 3, а в интервале 12 и более это будет 12. Такой способ больше подходит для ситуаций, когда интервалы неравные и предположить какой интервал мог бы быть сложно. Рассчитаем нашу задачу по таким данным далее.

Длительность производственного стажа, лет х	Число сотрудников, человек f	х’	x’f
до 3	19	3	57,0
3-6	21	4,5	94,5
6-9	15	7,5	112,5
9-12	10	10,5	105,0
12 и более	5	12	60,0
Итого	∑f = 70	—	∑ x’f = 429,0

Средняя продолжительность стажа 6,13 года.

Домашнее задание

Рассчитать средний размер посевной площади на одно фермерское хозяйство по следующим данным.

Размер посевной площади, га	Количество фермерских хозяйств
0-20	64
20-40	58
40-60	32
60-80	21
80-100	12
Итого	187

Рассчитайте средний возраст работника предприятия по следующим данным

Возраст персонала, лет	Число сотрудников, человек
до 18	7
18-25	68
25-40	79
40-55	57
55 и старше	31
Итого	242

Теперь Вы умеете рассчитывать среднюю в интервальном вариационном ряду!

Может еще поучимся? Загляни сюда!

Источник

Совет 1: Как обнаружить середину интервала

При статистической обработке итогов изысканий самого различного рода полученные значения зачастую группируются в последовательность промежутков. Для расчета обобщающих колляций таких последовательностей изредка доводится вычислять середину интервала – «центральную варианту». Способы ее расчета довольно примитивны, но имеют некоторые особенности, вытекающие как из применяемой для измерения шкалы, так и из нрава группировки (открытые либо закрытые промежутки).

Инструкция

1. Если промежуток является участком постоянной числовой последовательности, то для нахождения ее середины используйте обыкновенные математические способы вычисления среднеарифметического значения. Минимальное значение интервала (его предисловие) сложите с максимальным (окончанием) и поделите итог напополам – это один из методов вычисления среднеарифметического значения. Скажем, это правило применимо, когда речь идет о возрастных интервала х. Скажем, серединой возрастного интервала в диапазоне от 21 года до 33 лет будет отметка в 27 лет, потому что (21+33)/2=27.

2. Изредка бывает комфортнее применять иной способ вычисления среднеарифметического значения между верхней и нижней границами интервала . В этом варианте вначале определите ширину диапазона – отнимите от максимального значения минимальное. После этого поделите полученную величину напополам и прибавьте итог к минимальному значению диапазона. Скажем, если нижняя граница соответствует значению 47,15, а верхняя – 79,13, то ширина диапазона составит 79,13-47,15=31,98. Тогда серединой интервала будет 63,14, потому что 47,15+(31,98/2) = 47,15+15,99 = 63,14.

3. Если промежуток не является участком обыкновенной числовой последовательности, то вычисляйте его середину в соответствии с повторяемостью и размерностью применяемой измерительной шкалы. Скажем, если речь идет об историческом периоде, то серединой интервала будет являться определенная календарная дата. Так для интервала с 1 января 2012 года по 31 января 2012 серединой будет дата 16 января 2012.

4. Помимо обыкновенных (закрытых) промежутков статистические способы изысканий могут оперировать и «открытыми». У таких диапазонов одна из границ не определена. Скажем, открытый промежуток может быть задан формулировкой «от 50 лет и старше». Середина в этом случае определяется способом аналогий – если все остальные диапазоны рассматриваемой последовательности имеют идентичную ширину, то предполагается, что и данный открытый промежуток имеет такую же размерность. В отвратном случае вам нужно определить динамику метаморфозы ширины промежутков, предшествующих открытому, и вывести его условную ширину, исходя из полученной склонности метаморфозы.

Совет 2: Как обнаружить середину

Изредка в повседневной деятельности может появиться надобность обнаружить середину отрезка прямой линии. Скажем, если предстоит сделать выкройку, эскиз изделия либо легко распилить на две равные части деревянный брусок. На поддержка приходит геометрия и немножко житейской смекалки.

Вам понадобится

Циркуль, линейка; булавка, карандаш, нить

Инструкция

1. Воспользуйтесь обыкновенными инструментами, предуготовленными для измерения длины. Это самый легкой метод разыскать середину отрезка. Измерьте линейкой либо рулеткой длину отрезка, поделите полученное значение напополам и отмерьте от одного из концов отрезка полученный итог. Вы получите точку, соответствующую середине отрезка.

2. Существует больше точный метод нахождения середины отрезка, вестимый из курса школьной геометрии. Для этого возьмите циркуль и линейку, причем линейку может заменить всякий предмет подходящей длины с ровной стороной.

3. Установите расстояние между ножками циркуля так, дабы оно было равным длине отрезка либо же огромным, чем половина отрезка. После этого поставьте иглу циркуля в один из концов отрезка и проведите полуокружность так, дабы она пересекала отрезок. Переставьте иглу в иной конец отрезка и, не меняя размах ножек циркуля, проведите вторую полуокружность верно таким же образом.

4. Вы получили две точки пересечения полуокружностей по обе стороны от отрезка, середину которого мы хотим обнаружить. Объедините эти две точки при помощи линейки либо ровного бруска. Соединительная линия пройдет в точности посередине отрезка.

5. Если под рукой не оказалось циркуля либо длина отрезка значительно превышает возможный размах его ножек, дозволено воспользоваться простым приспособлением из подручных средств. Изготовить его дозволено из обыкновенной булавки, нитки и карандаша. Привяжите концы нитки к булавке и карандашу, при этом длина нитки должна немножко превышать длину отрезка. Таким импровизированным заменителем циркуля остается проделать шаги, описанные выше.

Видео по теме

Полезный совет
Довольно верно обнаружить середину доски либо бруска вы можете, использовав обыкновенную нитку либо шнур. Для этого отрежьте нить так, дабы она соответствовала длине доски либо бруска. Остается сложить нить верно напополам и разрезать на две равные части. Приложите один конец полученной мерки к концу измеряемого предмета, а 2-й конец будет соответствовать его середине.

Источник

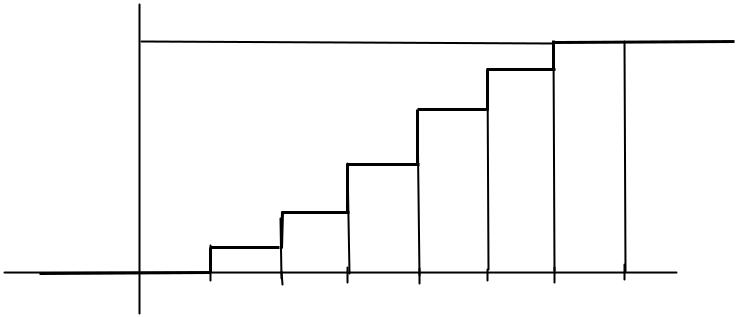
Статистическим аналогом графика функции распределения является кривая накопленных частот. Накопленной частотой mx называется число вари-

ант выборки, меньших данного числа х. Для сгруппированного статистического ряда определяется mi — число вариант, меньших правой границы i-го интервала. Относительная накопленная частота — это отношение накопленной частоты mi к объему выборки n (табл. 3.4). Графическое изображение относи-

тельных накопленных частот в виде ступенчатой (ломаной) линии называется эмпирической (кумулятивной) функцией распределения (рис. 3.3). Отметим, что эмпирическая функция распределения определена для любых действительных значений х.

Таблица 3.4

Таблица накопленных частот примера 2

Интер-	[0;3)		[3; 3.3)	[3.3; 3.6)	[3.6; 3.9)	[3.9; 4.2)	[4.2; 4.5)	[4.5; 4.8)
валы

Нако-
плен-	0		4	11	21	26	29	30
ные
часто-
ты
Отно-
ситель
ные
накоп-	0		0.133	0.367	0.7	0.867	0.967	1
лен-
ные
часто-
ты

		mi
			n

0 3 3.3 3.6 3.9 4.2 4.5 4.8 х

Рис. 3.3. Эмпирическая функция распределения для примера 2

3.3. Числовые характеристики выборки

Гистограмма и эмпирическая функция распределения дают представление об общем виде распределения, но иногда нам требуется указать «типичного» представителя выборки, т.е. указать, где находится «центр» выборочных данных. В качестве такого «центра» могут использоваться среднее арифметическое, полусумма крайних значений, медиана, мода, геометрическое среднее, гармоническое среднее (табл. 3.5).

Таблица 3.5

Средние значения для примера 2

	Название	Значение
	Полусумма крайних	3.9
	Среднее арифметическое	3.746
	Среднее геометрическое	3.725
	Среднее гармоническое	3.704
Полусумма крайних значений вычисляется по формуле	x(1) + x(n)	, где
2

x(1) — наименьшее, а x(n) — наибольшее значение выборки. Среднее арифметическое обозначается x и вычисляется по формуле

	1	n	1	k
x =	∑xi =	∑n j x j ,
	n
	n i=1	j=1

где n — объем выборки, а n j — частота варианты	x j . Если выборка сгруп-
пирована,	то неизвестно, какие именно	варианты	попали в j-й интервал
[a j ; a j+1).	Тогда частоту интервала n j	умножают на середину интервала

a j+1 + a j . Конечно, при этом получается ошибка, но при больших значениях

n она невелика: ведь в среднем половина вариант, попавших в интервал

[a j ; a j+1) будет меньше числа 1 (a j+1 + a j ), а половина — больше, поэтому
			2
ошибки компенсируют друг друга.
Геометрическое среднее есть корень n-й степени из произведения n вы-
борочных значений	n x x	2	… x	n	и рекомендуется для усреднения после-
	1

довательности дробей.

Гармоническое среднее есть величина, обратная к среднему арифметическому величин, обратных выборочным значениям. Гармоническое среднее используется для усреднения последовательности скоростей на одинаковых дистанциях.

[a j ; a j+1)

В теории вероятностей модой М дискретной случайной величины называется ее значение, которое имеет максимальную вероятность. Модой непрерывной случайной величины называется такое ее значение, при котором дос-

тигается максимум плотности распределения f (x). Закон распределения на-

зывается унимодальным, если мода единственна. В математической статисти-

ке мода M определяется по выборке, как варианта с наибольшей частотой.

Для выборки примера 1 мода M = 0.

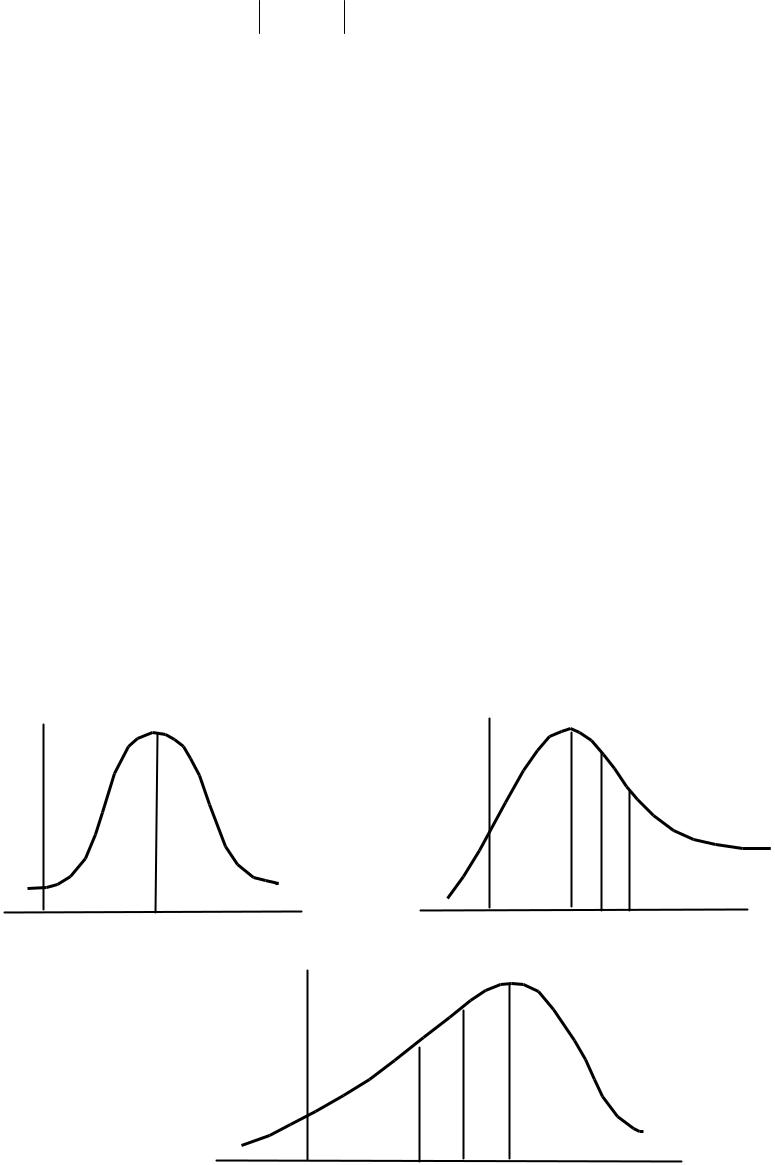
Если выборка сгруппирована, то сначала определяют модальный интервал, т.е. интервал с наибольшей частотой. В качестве моды можно взять середину модального интервала. Для выборки примера 2 середина модального интервала равна 3.75 (рис. 3.2).

В теории вероятностей медианой непрерывной случайной величины Х называется такое число x0.5, что P(x < x0.5 ) = P(x > x0.5 ) = 0.5. Соответственно, по выборке находят приближенное значение медианы — число x такое, что половина вариант выборки меньше этого числа, а половина — больше него.

Работая со сгруппированной выборкой, вначале находят медианный интервал такой, что относительная накопленная частота для a j мень-

ше 0.5, а для a j+1 — больше 0.5. В примере 2 таким интервалом является интервал [3,6; 3.9) (табл. 3.4). В качестве медианы можно взять середину этого

интервала: x0.5 = 3.75.

Медиана делит выборку на две части: половина вариант меньше медианы, половина — больше. Можно найти три числа q1, q2 , q3, которые аналогичным образом делят выборку на четыре равные части. Эти числа называются квартилями. Число q2 совпадает с медианой, q1 называется нижней, а q3 — верхней квартилью. В теории вероятностей квартилями непрерывной случайной величины Х называются значения x0.25, x0.5, x0.75, определяемые из условия (рис. 1.4):

P( X < x0.25 ) = P(x0.25 < X < x0.75 ) = P(x0.5 < X < x0.75 ) =

= P(X < x0.75 ) = 0.25

Точно так же можно найти девять чисел c1, c2 , …, c9 , которые разбива-

ют выборку на десять равных частей. Эти числа называются децентилями. Если разбить выборку на 100 равных частей, то точки деления — процентили. Общее название для всех этих точек деления — квантиль. В теории вероятно-

стей квантиль порядка р непрерывной случайной величины Х есть число xp

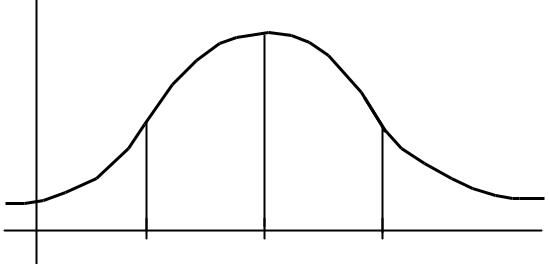
			44

такое, что	F(xp ) = P(X < xp ) = p. Выборочная квантиль	xp — это точка,
левее которой расположено 100 p % выборочных данных.
	f (x)
	25 %	25 %	25 %	25 %
		x0.25	x0.5	x0.75	x
	Рис. 3.4. Квартили непрерывной случайной величины

Простейшая мера разброса выборки — размах R = x(n) − x(1) , равный

разности максимальной и минимальной вариант. Этой характеристикой пользуются при работе с малыми выборками.

Более точно разброс оценивается с помощью выборочной дисперсии. Она вычисляется так же, как дисперсия дискретной случайной величины, только вместо вероятностей используются относительные частоты:


	1	n		k
D =	∑	(xi − x)2	= ∑	n j	(x j − x)2	,

	n i=1		j =1	n

где n — объем выборки, k — число различных вариант выборки. Если выборка сгруппирована, то формула принимает вид

		k
D =	1	∑n j (z j − x)2 ,
	n	j =1

где z j — середина j-го интервала.

Корень квадратный из выборочной дисперсии называется выборочным

средним квадратическим отклонением σ (с.к.о.).

Для выборки примера 2 выборочная дисперсия D = 0.159 , выборочное

с.к.о. σ = 0.339, т.е. в среднем вес ребенка отличается от среднего веса на

0.339 кг.

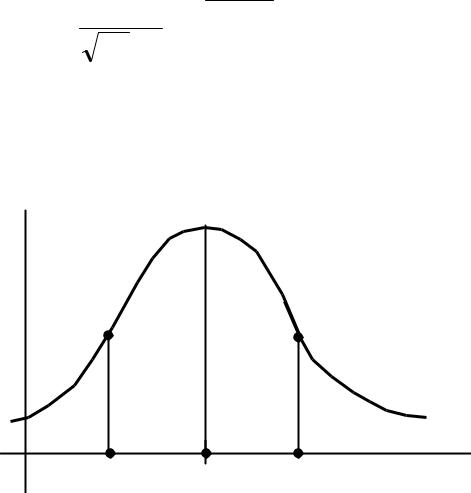
В теории вероятностей для нормального закона распределения доказывается правило «трех сигма»:

P(X −mx < 3σ)= 0.997.

Это правило приблизительно выполняется для большинства унимодальных законов распределения и для выборок из таких генеральных совокупно-


стей: более 99 % выборочных значений лежат в интервале		σ; x +3
x −3	σ .

Аналогично для «двух сигма»: более 95 % выборочных значений лежат в ин-

тервале
x −2	σ; x	+ 2 σ . Для выборки примера 2 имеем



			= (3.746 −3 0.339; 3.746 +3 0.339) = (2.549; 4.943) ,
x −3	σ; x +3σ

и 100 % выборочных значений лежат в этом интервале.

По выборке можно сделать вывод о симметричности или несимметричности закона распределения. Закон распределения непрерывной случайной величины Х называется симметричным, если график функции плотности веро-

ятности f (x) имеет ось симметрии. Для унимодального симметричного закона распределения очевидно равенство моды М, медианы x0.5 и математического ожидания mx (рис. 3.5, а). В случае положительной асимметрии

M < x0.5 < mx	(рис. 3.5, б); для распределения с отрицательной асимметрией
mx < x0.5 < M (рис. 3.5, в).
f (x)	f (x)

M = x0.5 = mx	x	M x0.5 mx	x
а	f (x)	б

mx x0.5 M x

Рис. 3.5. Плотность распределения: а) симметричного; б) с положительной асимметрией; в) с отрицательной асимметрией

Поэтому выборочную разность x − M можно использовать в качестве

меры асимметрии: чем больше она по абсолютной величине, тем больше

асимметрия. Асимметрия будет положительной, если x > M , и отрицатель-


ной, если x < M .	Для получения безразмерной меры эту разность делят на σ

и получают первый коэффициент асимметрии Пирсона:

A1 = x − M .

Для выборки примера 2 значение этого коэффициента

A = 3.746 −3.75	= −0.01
1	0.339

близко к нулю, т.е. можно принять, что наша выборка извлечена из генеральной совокупности с симметричным законом распределения.

4. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ И ВАЖНЫЕ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ

4.1. Теорема Чебышева и теорема Бернулли

Почему по выборке мы можем делать выводы о свойствах генеральной совокупности? Эти выводы опираются на закон больших чисел. Закон больших чисел — это группа теорем, которые формулируют математические закономерности, проявляющиеся при многократном наблюдении случайных явлений.

Для независимых случайных величин общий закон больших чисел выражается теоремой Чебышева (1867 г.)

Теорема Чебышева. Пусть X1, X 2 , …, X n , … последовательность неза-

висимых	случайных	величин	с	математическими	ожиданиями
m1,m2 , …,mn , …	и дисперсиями D1, D2 , …, Dn , … ,	ограниченными одной и
той же константой	(Di ≤ c, i =1,2, …). Тогда для любого ε > 0
					n	1 n
			1
					∑Xi −	∑mi	=1.
		lim P			< ε
		n→∞		n i =1	n i=1

Иначе это можно записать:

1	n	P	1	n
	∑Xi →		∑mi ,
n i=1	n→∞	n i=1

т.е. теорема Чебышева устанавливает, что при достаточно больших n с вероят-

ностью,	близкой		к единице, среднее арифметическое случайных величин
		=	1	(X1 + X 2 +… + X n ) как угодно мало колеблется около постоянного
X
	n
			1
числа	(m + m +… + m ) — среднего арифметического математических

					n	1	2	n

ожиданий этих случайных величин.

Проводя анализ выборочных данных, мы рассматриваем независимые статистические копии одной и той же случайной величины Х. Поэтому, согласно теореме Чебышева, среднее арифметическое таких статистических копий при большом числе слагаемых оказывается практически постоянной (не случайной) величиной, которая и указывает нам «центр» генеральной совокупности.

Теорема Бернулли впервые была сформулирована в XVIII веке Яковом Бернулли. Сейчас принято доказывать ее как следствие теоремы Чебышева.

Рассмотрим последовательность испытаний по схеме Бернулли, т.е. последовательность независимых испытаний, в каждом из которых вероятность интересующего нас случайного события А («успеха») одна и та же и равна р. Обозначим относительную частоту успеха (отношение числа успешных испы-

таний к общему их числу), в серии из n испытаний p . В этих условиях раз-

ность между относительной частотой p события А и вероятностью р этого

события становится сколь угодно малой, если число испытаний неограниченно возрастает.

Теорема Бернулли. В последовательности испытаний по схеме Бернулли относительная частота события сходится по вероятности к вероятности этого

события: p → p.

n→∞

Теорема Бернулли позволяет обосновывать близость гистограммы, построенной по выборке большого объема, к теоретической плотности распределения (плотности распределения генеральной совокупности). Отметим, что сама эта теорема не гарантирует устойчивости относительных частот в конкретной практической задаче, она позволяет сделать вывод, если такая устойчивость частот имеется (выполняются условия схемы испытаний Бернулли).

4.2.Нормальное распределение и центральная предельная теорема

Напомним, что случайная величина Х называется распределенной по
нормальному закону с параметрами а и σ (будем писать X ~ N (a, σ) ), если
функция ее плотности распределения имеет вид
	1	−	(x−a)2
		2σ2 , x (−∞; +∞).
f (x) =	e
2π σ
При этом математическое ожидание		M (x) = a, дисперсия	D(x) = σ2. Гра-
фик плотности распределения симметричен относительно	прямой	x = a и
имеет точки перегиба при x = a ±σ (рис. 4.1).
f (x)
a −σ	a	a +σ	x
Рис. 4.1. График плотности нормального распределения X ~ N (a, σ)

Нормальное распределение с параметрами a = 0, σ =1 называется стандартным нормальным распределением. Нормальная случайная величина X ~ N (a, σ) связана со стандартной X 0 ~ N (0,1) линейной зависимостью:

X = a +σX 0.

При вычислении вероятностей, связанных с нормальным законом распределения, мы будем пользоваться функцией Лапласа Φ(x), значения которой табулированы (приложение 1):

			x		t 2
		1	∫e−		dt.
	Φ(x) =	2
		2π	0
В курсе теории вероятностей доказываются свойства функции Лапласа:
а) Φ(0) = 0;
б) Φ(−x) = −Φ(x) (нечетность);
в) Φ(+∞) =	1 .
	2							X ~ N (a, σ)
Расчет вероятностей для случайной величины	ведется по
формуле				β−a			α −a
						(4.1)
	P(α < X < β) = Φ	σ		−Φ	σ	,

которая в частном случае (α = a −ε, β = a +ε) принимает вид:
P(a −ε < X < a +ε) = P(	X −a		ε

	< ε) = 2Φ	.	(4.2)

			σ

При ε = 3σ получим P( x −a < 3σ) = 2Φ(3) = 2 0.49865 ≈1 — пра-

вило «трех сигма».

Пример 1. На рынок поступила крупная партия говядины. Предполагается, что вес туш — случайная величина, подчиняющаяся нормальному закону распределения с математическим ожиданием a = 950 кг и средним квадрати-

ческим отклонением σ =150 кг.

Определите вероятность того, что вес случайно отобранной туши: а) окажется больше 1250 кг; б) окажется меньше 850 кг;

в) будет находиться между 800 и 1300 кг; г) отклонится от математического ожидания меньше, чем на 50 кг;

д) отклонится от математического ожидания больше, чем на 50 кг. Найдите границы, в которых отклонение веса случайно отобранной туши

от своего математического ожидания не превысит утроенного среднего квадратического отклонения (проиллюстрируйте правило «3 сигма»).

Решение. В случае а нас интересует вероятность того, что вес Х случайно отобранной туши окажется в интервале (1250;+∞).

	+∞ −950
По формуле (4.1) имеем:	P(1250 < X < +∞) = Φ	−
150

−Φ 1250 −950 = Φ(+∞) −Φ(2) = 0.5 −0.477 = 0.023 —

150

здесь мы воспользовались

таблицами функции Лапласа (приложение 1) и ее

свойством в (с. 49).

α = −∞, β = 850, a = 950,

В случае б применим формулу (2.1)

при

850 −950

−∞ −950

−2

σ =150 : P(−∞ < X < 850) = Φ

−Φ

= Φ

−

150

−Φ(−∞) = −Φ

+Φ(+∞) = 0.5 −0.249

= 0.251

— здесь мы применили

свойство нечетности функции Лапласа.

1300 −950

800

−950

В случае в:

P(800 <

X <1300) = Φ

150

−Φ

150

= Φ(2.33) −Φ(−1) = 0.49 +0.34 = 0.83 — вероятность того, что вес случай-

но отобранной туши окажется в интервале от 800 до 1300 кг, составляет 0.83. Вероятность того, что вес случайно отобранной туши отклонится от математического ожидания меньше, чем на 50 кг (случай г), определим по фор-

муле (4.2):

P(	X −950	50

	< 50) = 2Φ		= 2Φ(0.33)	= 2 0.129 = 0.258.
	150

Найдем вероятность того, что вес случайно отобранной туши отклонится от математического ожидания больше, чем на 50 кг. По свойствам вероятностей противоположных событий:

P( X −950 > 50) =1 − P( X −950 < 50) =1 −0.259 = 0.741.

Проиллюстрируем правило «3 сигма»: если случайная величина X ~ N (a, σ) , то P( X − a < 3σ) = 2Φ(3) = 0.9973 — вероятность того, что

отклонение случайной величины от своего математического ожидания по абсолютной величине превысит утроенное среднее квадратическое отклонение, очень мала и равна 0.0027. Другими словами, лишь в 27 случаях из 10000 случайная величина Х в результате испытания может оказаться вне интервала

(a −3σ; a +3σ). Такие события считаются практически невозможными. В

нашем случае (a −3σ; a +3σ) = (950 −3 150; 950 +3 150) = (500; 1400)

и можно быть практически уверенным, что вес случайно отобранной туши не выйдет за пределы от 500 до 1400 кг.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник