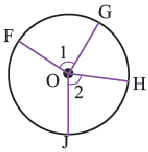
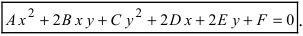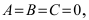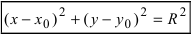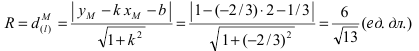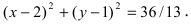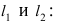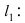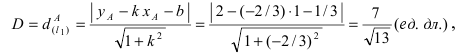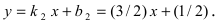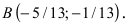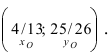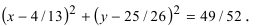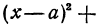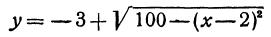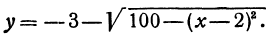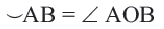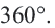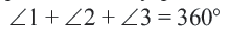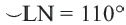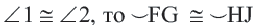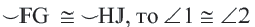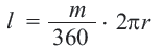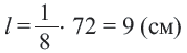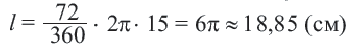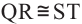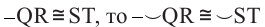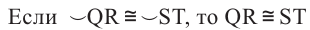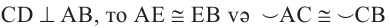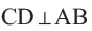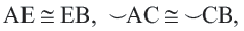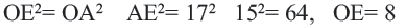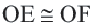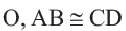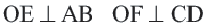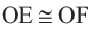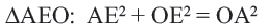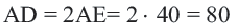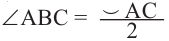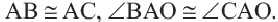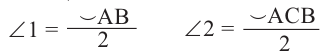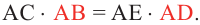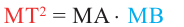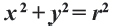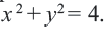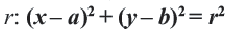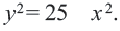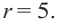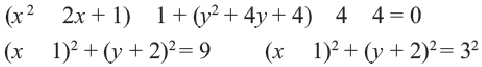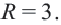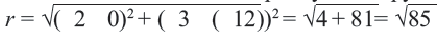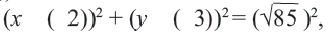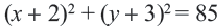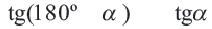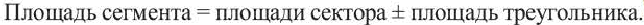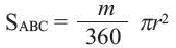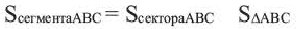Для определения центра окружности используется одно из основных свойств хорды в окружности, а именно :
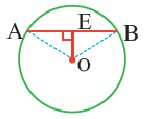
Если к середине любой хорды, проведённой произвольно в окружности, восстановить перпендикуляр, то он ( перпендикуляр) обязательно будет проходить через центр О окружности.
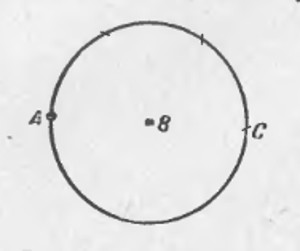
Вот используя это свойство серединного перпендикуляра и найдём центр окружности.Сначала проведём одну хорду произвольно.К середине хорды восстановим перпендикуляр.
Затем и к середине второй произвольно проведённой хорде тоже восстановим перпендикуляр.
На пересечении двух перпендикуляров и будет находиться центр окружности О.
если проведём и третью хорду и проведём те же действия, то перпендикуляр пройдёт через найденную точку О.
Планиметрия (прямая и окружность)
Планиметрия изучется в начальном курсе геометрии и зачастую сводится к решению практических задач без изучения теоретической базы.
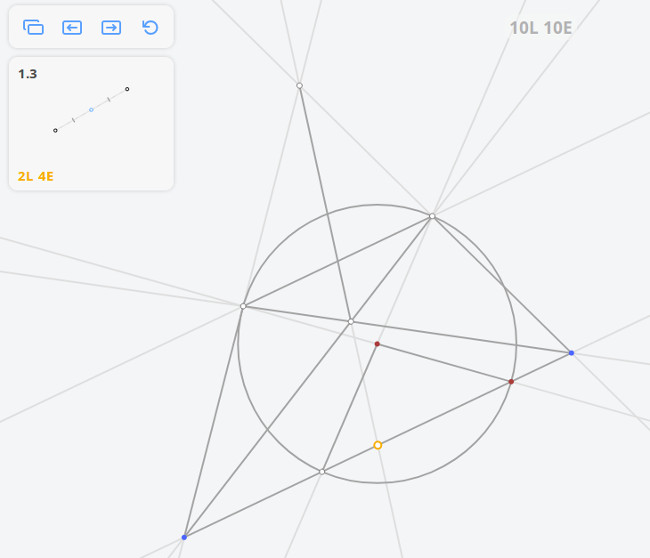
В данной статье приводятся альтернативные (подсказкам) решения задач из первого раздела (кроме 1.5) приложения Euclidea (геометрические построения с помощью циркуля и линейки).
Решения задач 1.1, 1.2 и 1.3 основаны на том, что с помощью циркуля и линейки можно построить равносторонний треугольник.
1.1 Построить угол 60° с заданой стороной
1.2 Построить серединный перпендикуляр к отрезку
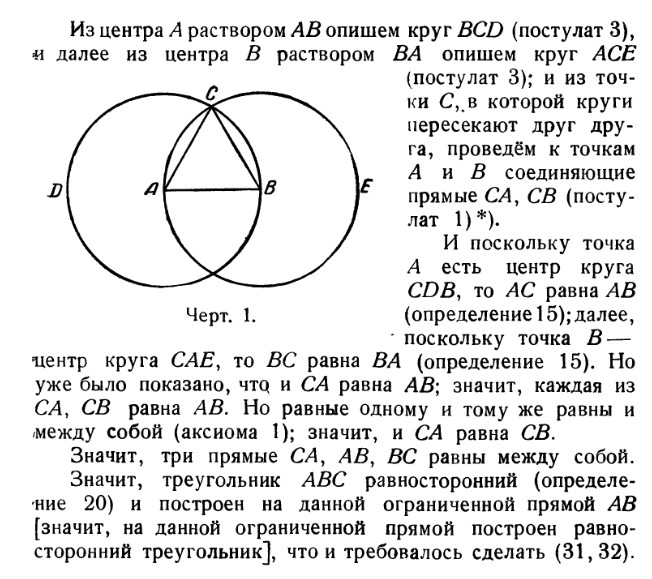
На данной ограниченной прямой построить равносторонний треугольник
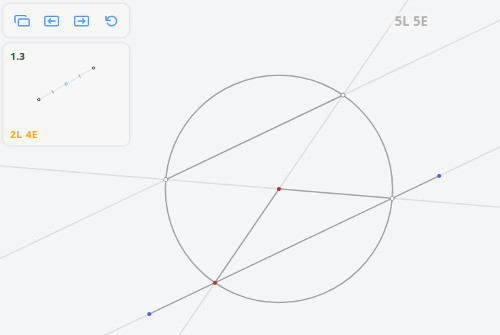
1.3 Середина отрезка
всё, что можно построить с помощью циркуля и линейки, может быть построено с помощью одного циркуля.
Из точки В радиусом АВ описываем окружность.
По этой окружности откладываем от точки А расстояние АВ три раза: получаем точку С, очевидно, диаметрально противоположную А. Расстояние АС представляет собой двойное рассрастояние АВ. Проведя окружность из С радиусом ВС, мы можем таким же образом найти точку,
диаметрально противоположную В и, следовательно, удаленную от А на
тройное расстояние АВ, и т. д.
любое построение, выполнимое на плоскости циркулем и линейкой, можно выполнить одной линейкой, если нарисована хотя бы одна окружность и отмечен её центр.
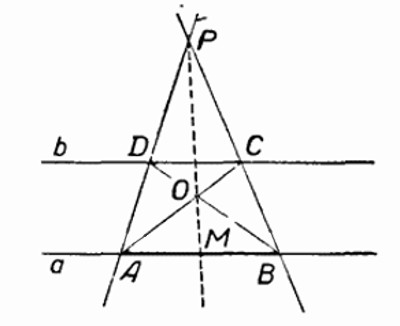
Проведем прямые PA и PB и отметим точки D и C их пересечения прямой b. Пусть О — точка пересечения прямых AC и BD. Тогда, согласно предыдущей лемме, прямая PO пересечёт отрезок AB в его середине M.
Решением задачи 1.3 по методу Штейнера-Понеселе будет:
1.4 Окружность, вписанная в квадрат
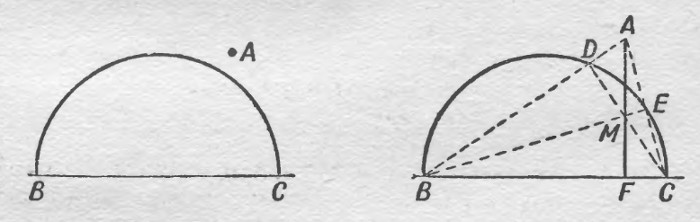
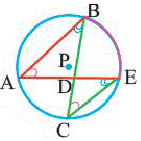
Из точки A, лежащей вне данной полуокружности, опустить на её диаметр перпендикуляр, обходясь при этом без циркуля. Положение центра полуокружности не указано.
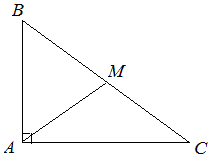
Нам пригодится здесь то свойство треугольника, что все его высоты пересекаются в одной точке. Соединим A с B и C; получим точки D и E. Прямые BE и CD, очевидно, — высоты треугольника ABC. Третья высота — искомый перпендикуляр к BC — должна проходить через пересечение двух других, т.е. через точку M. Проведя по линейке прямую через точки A и M, мы выполним требованиек задачи, не прибегая к услугам циркуля.
И опустив перпендикуляр из точки пересечения диагоналей квадрата на ребро, найдём середину ребра.
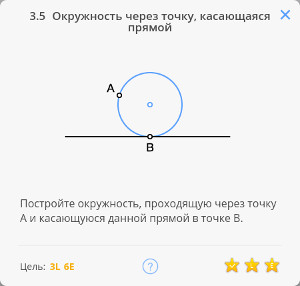
Это же построение можно использовать для решения задачи 2.9 Окружность, касающаяся прямой
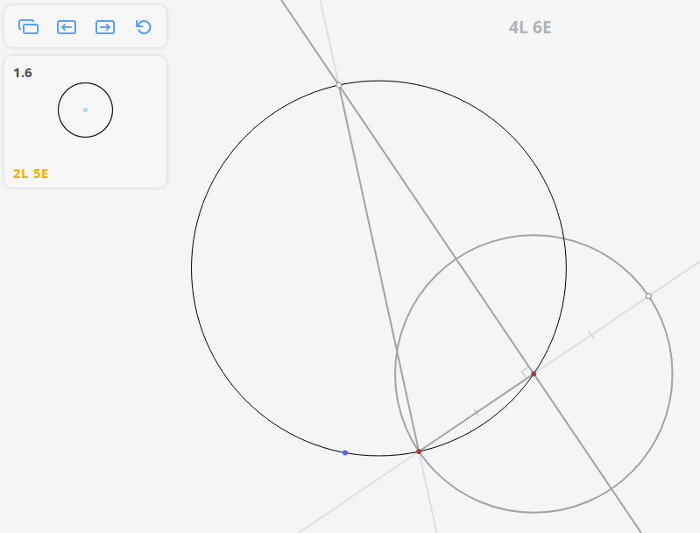
1.6 Найти центр окружности
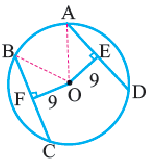
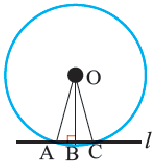
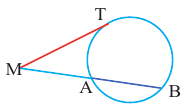
Плоский угол, опирающийся на диаметр окружности, — прямой.
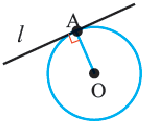
Определение: касательной к окружности называется прямая, имеющая с окружностью одну общую точку. Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.
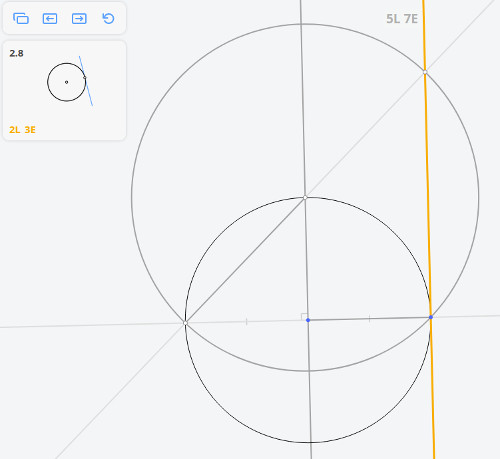
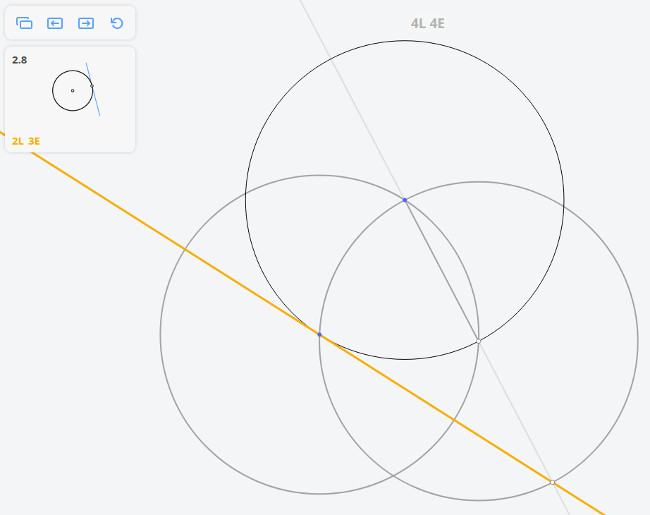
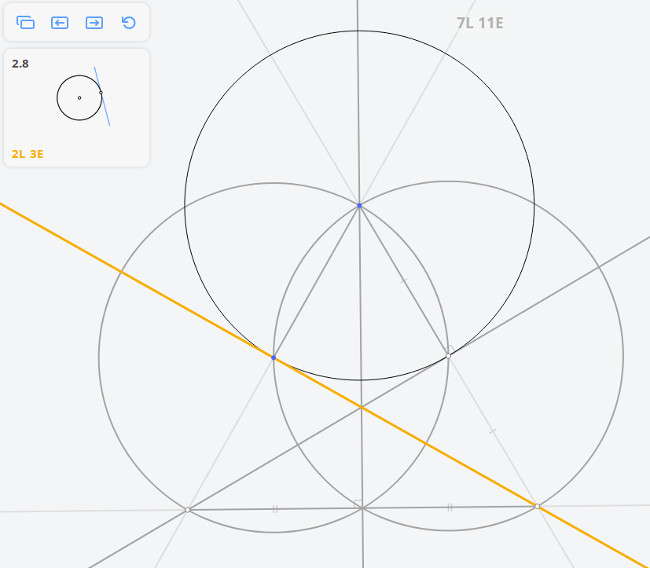
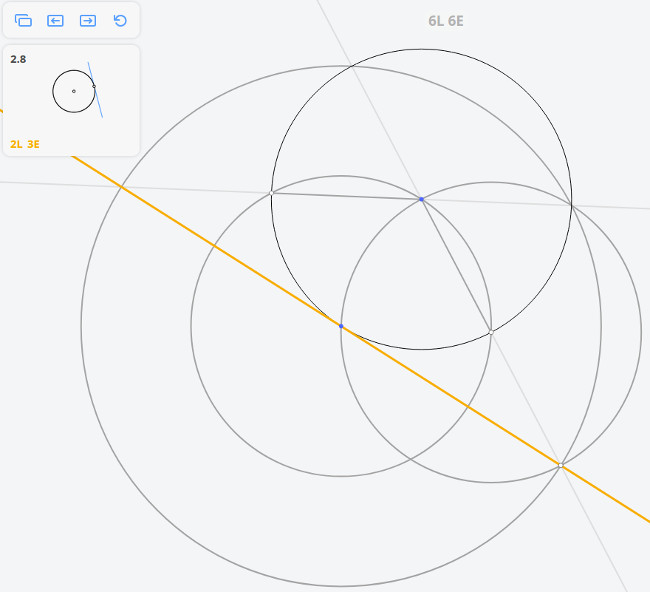
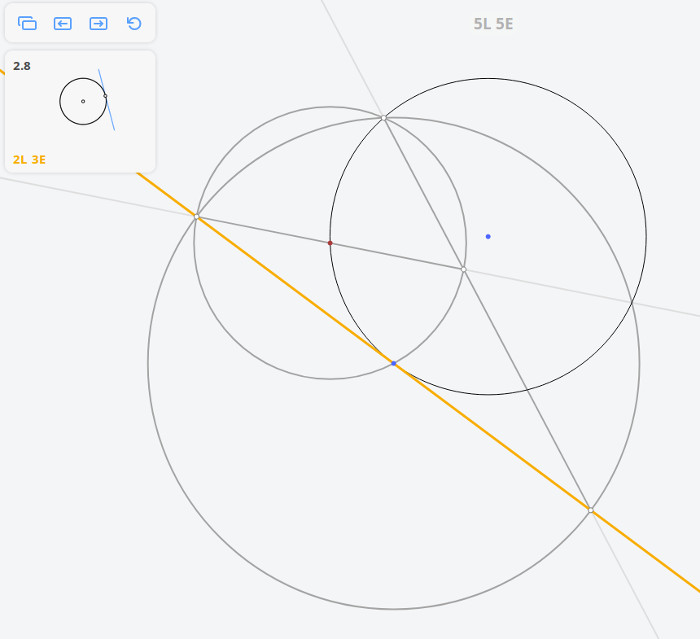
Рассмотрим задачу 2.8
2.8 Касательная к окружности в точке
Возвращаясь к предыдущей задаче, эту задачу можно решить построив угол, опирающийся на диаметр окружности по теореме Фалеса
Далее, построив перпендикуляр к касательной, найдём диаметр окружности, и, разделив его пополам, найдём центр окружности.
Ещё об одном способе построения касательной к окружности можно узнать из лекции 1.5 курса «Геометрия и группы» А. Савватеева ссылка
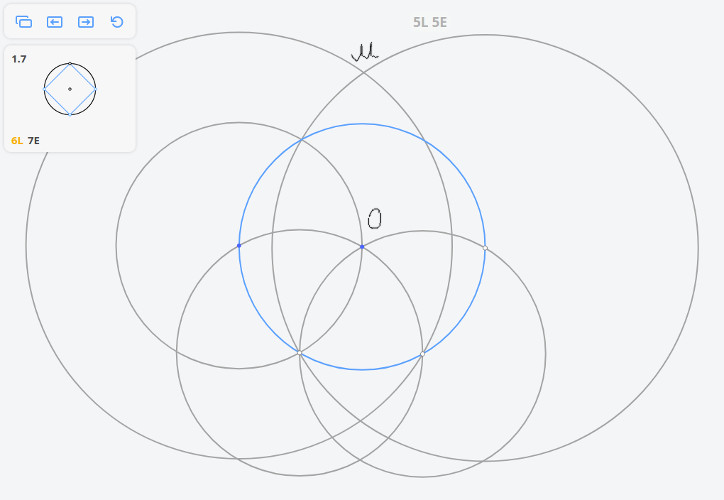
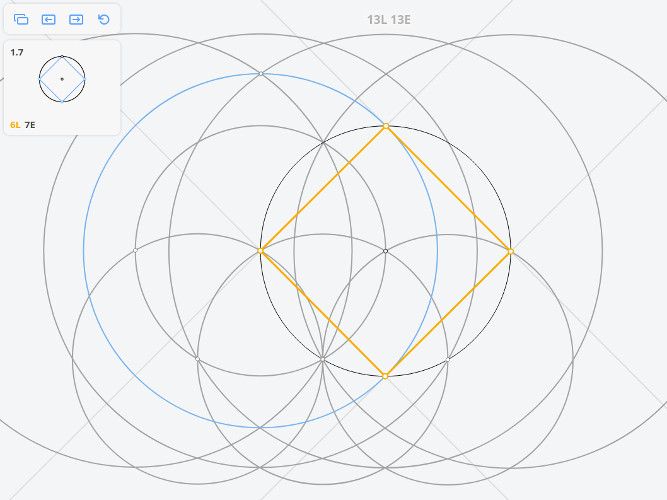
1.7 Квадрат, вписанный в окружность
Задача Наполеона
Решим задачу методом Мора-Маскерони.
Построим три окружности радиусом r и две окружности радиусом
В приложении нет такой операции, как перенос раствора циркуля (равного MO), поэтому необходимо использовать дополнительные построения.
Для того, чтобы построить касательную к исходной окружности, параллельную МО, необходимо произвести построения, которые были приведены выше (построить три окружности радиусом r и две окружности радиусом ), но вместо исходной окружности взять окружность, обозначенную на рисунке синим цветом
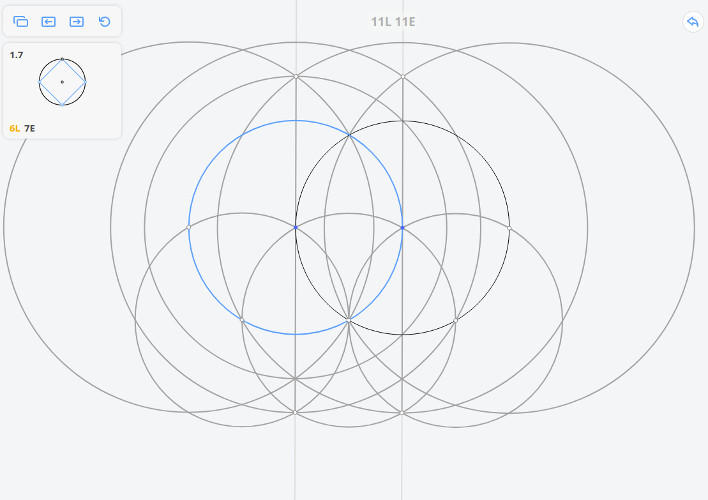
Т.о. мы перенесли раствор циркуля (равный МО) в точку А.
Далее из точки А необходимо провести окружность c радиусом МО
Быстрый способ, как найти центр окружности
В данном обзоре автор поделится с нами довольно простым способом, как быстро найти центр окружности.
Для этого нам потребуется всего два предмета: угольник и карандаш. Первым делом необходимо провести прямую линию в любом месте окружности.
Советуем также прочитать: как изготовить своими руками антенну для усиления 4G сигнала на даче или в частном доме.
После того, как начертили линию, измеряем длину, и делим это расстояние ровно пополам.
В данном случае длина линии составляет 210 мм. Разделив ее пополам, получаем 105 мм — ставим в этом месте отметку.
С помощью угольника проводим вторую линию, которая должна быть перпендикулярна первой (то есть проходить под углом 90 градусов).
Основные этапы работ
На следующем этапе проделываем те же операции с другой стороны окружности (только не параллельно, а немного в стороне).
Чертим линию, измеряем ее длину (в данном случае — 218 мм), делим пополам (109 мм) и откладываем в этом месте точку. После этого проводим перпендикулярную линию, как и в предыдущем случае.
Пересечение двух линий, которые мы чертили под углом 90 градусов, и будет являться центром круга.
Подробно об этом способе можно посмотреть на видео ниже. Статья подготовлена на основе видео с YouTube канала « ПОГРАНЕЦ 13 ».
Как найти Как найти центр окружности?
Как найти центр отверстия?
Через точки пересечения дуг проводят две прямые по направлению к центру до их пересечения в точке О. Точка пересечения этих прямых, и будет искомым центром отверстия.
Как найти центр окружности из уравнения?
Уравнение окружности ω (A; R) имеет вид (x – a) 2 + (y – b) 2 = R 2 , где a и b – координаты центра A окружности ω (A; R) .
Чем размечают отверстия?
Размечать центровые отверстия в деталях диаметром до 40 мм лучше при помощи специального приспособления, называемого колоколом. Оно состоит из корпуса, конического раструба и кернера, перемещаемого в корпусе.
Как найти центр окружности на плоской заготовки?
Есть и совсем простой способ нахождения центра плоской заготовки круглой формы. Всего-то нужно обвести её по периметру, положив на лист бумаги, затем вырезать по начерченной линии круг, согнуть его вчетверо и центр будет найден. Он находится точно на линии пересечения сгибов.
Как правильно разметить отверстия?
Разметка отверстий для сверления.
- Определить расположение отверстия по рабочему чертежу. Аккуратно отмерить расстояние отверстия от обоих краев доски. .
- Наколите центр отверстия шилом. .
- Если должны совпасть отверстия, просверленные в двух досках, зажмите обе доски в тисках.
http://sdelairukami.ru/bystryj-sposob-kak-najti-czentr-okruzhnosti/
http://dmcagency.ru/kak-naiti-kak-naiti-tsentr-okruzhnosti
Все категории
- Фотография и видеосъемка
- Знания
- Другое
- Гороскопы, магия, гадания
- Общество и политика
- Образование
- Путешествия и туризм
- Искусство и культура
- Города и страны
- Строительство и ремонт
- Работа и карьера
- Спорт
- Стиль и красота
- Юридическая консультация
- Компьютеры и интернет
- Товары и услуги
- Темы для взрослых
- Семья и дом
- Животные и растения
- Еда и кулинария
- Здоровье и медицина
- Авто и мото
- Бизнес и финансы
- Философия, непознанное
- Досуг и развлечения
- Знакомства, любовь, отношения
- Наука и техника
1
Как точно построить диаметр окружности не зная расположения её центра?
6 ответов:
2
0
Не понятен сам вопрос.
Во-первых, диаметр окружности невозможно ПОСТРОИТЬ. Его можно измерить или вычислить.
Построить можно только отрезок, который будет равен диаметру, либо саму окружность. С помощью циркуля.
Во-вторых, изначально нужно определиться с центром окружности.
Нет центра — нет окружности. Логика простая и ясная.
Если же вы имеете в виду, как НАЙТИ центр окружности, то вот вам ссылка — подробно разобраны несколько методов.
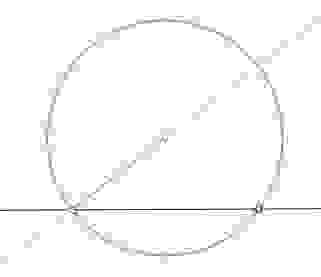
А ниже картинка — один из методов.
2
0
Рисуем окружность. Ставим на окружности две точки. Затем их соединяем и делим полученный отрезок пополам. В полученной точке проводим перпендикуляр к отрезку. Он и будет диаметром данной окружности. Методы построения не рассматриваются.
1
0
Проводим любую хорду АВ (чем длиннее хорда, тем точнее будет построение). Затем, поочерёдно ставя ножку циркуля в точки А и В проводим дуги одинакового радиуса до их пересечения в двух точках С и D. Желательно выбрать такой радиус, чтобы обе точки пересечения дуг были за пределами исходного круга. Через точки С и D проводим отрезок CD. Точки пересечения этого отрезка с исходной окружностью и дадут нам диаметр окружности.
1
0
Для определения центра окружности используется одно из основных свойств хорды в окружности, а именно :
<h2>Если к середине любой хорды, проведённой произвольно в окружности, восстановить перпендикуляр, то он ( перпендикуляр) обязательно будет проходить через центр О окружности.</h2>
Вот используя это свойство серединного перпендикуляра и найдём центр окружности.Сначала проведём одну хорду произвольно.К середине хорды восстановим перпендикуляр.
Затем и к середине второй произвольно проведённой хорде тоже восстановим перпендикуляр.
На пересечении двух перпендикуляров и будет находиться центр окружности О.
если проведём и третью хорду и проведём те же действия, то перпендикуляр пройдёт через найденную точку О.
0
0
В принципе, очень точно это сделать нельзя, но можно попробовать измерять хорды окружности линейкой до такого момента, пока измерения не покажут самую большую ширину, это и будет диаметр. Для проверки можно провести перпендикуляр, к найденному диаметру, если он будет равен, то всё хорошо получилось
0
0
Смотря , какие измерительные приборы у нас есть. Если есть возможность сделать прямой угол, то- чертим по линейке квадрат в окружности, находим пересечение биссектрис , эта точка- центр окружности. Чертим диаметр.
Читайте также
Такая поверхность получила название «тор», геометрия не очень его изучает, а аналитическая геометрия подробно ее описывает с формулой и прочими подробностями.
Большая диагональ «D» правильного N-угольника выражается через его апофему «a» очень простой формулой: D=√(2+2a). Например, апофема правильного пятиугольника равна Cos36°, тогда D5= √(2+2Cos36°)=1,902110… .
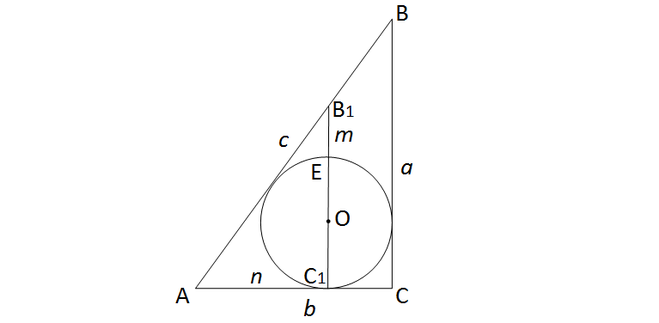
Строим произвольный треугольник АВС с катетами а и b, гипотенузой с. Впишем в него окружность диаметром D с центром в точке О. Через точку О проведем В₁С₁||ВС .Тогда расстояние от северных ворот до дерева В₁Е = m, от южных ворот на запад — С₁А = n. Диаметр окружности D, вписанный в прямоугольный треугольник, определяется формулой
D = а + b – c (1).
Тогда согласно рисунку
b = n + D/2 (2),
с = √(а² + b²) (3),
C₁B₁ = m + D.
На сновании подобия треугольников АВС и АВ₁С₁
a/(n +D/2) = (m +D)/n, откуда
a = (n +D/2)*(m +D)/n (4).
После подстановки в формулу (1) выражений (2), (3), (4) и преобразований относительно D, получаем кубическое уравнение в общем виде
D³ +m D² — 4n²m = 0 (5).
Пусть m = 1 (единичному отрезку), тогда n = 3, согласно условию.
В результате после подстановки значений имеем
D³ + D² — 36 = 0.
Решение уравнения очевидно в данном представлении
D³ + D² = 3³ +3²,
D = 3.
Искомый диаметр города 300*3 = 900 (шагов), а треугольники АВС и АВ₁С₁египетские.
Данное кубическое уравнение не может быть решено с помощью циркуля и линейки, как и знаменитые задачи древности, трисекции угла и удвоение куба. Указанными инструментами решаются уравнения первой и второй степени.
Длины параллелей в северном полушарии уменьшаются к северу и увеличиваются к югу,
пути между линиями долготы, будут короче севернее, а расстояния точек P и C от параллели одинаковые,поэтому путь, через точку P, расположенную севернее точки С ,будет короче.
Ответ:путь АРВ короче пути АСВ
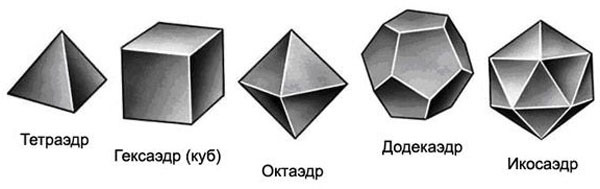
В геометрии существует всего пять правильных многогранников: тетраэдр, куб, октаэдр, додекаэдр и икосаэдр. Многогранник считается правильным, только если все его грани являются правильными, все многоугольники одинаковые и равные, и все двугранные углы равны. Кроме того такие свойства у правильных многогранников: все ребра одинаковой длины, все плоские углы тоже равны, все многогранные углы имеют одно и тоже число граней и в каждой вершине сходятся одинаковое число ребер.
Это тетраэдр, гексаэдр (то есть куб), октаэдр, додекаэдр и икосаэдр.
Сюда не входят, например, параллелепипед, пирамида, призма.
Окружность, описанная около треугольника.
Треугольник, вписанный в окружность. Теорема синусов
Определение 1 . Серединным перпендикуляром к отрезку называют, прямую, перпендикулярную к этому отрезку и проходящую через его середину (рис. 1).
Теорема 1 . Каждая точка серединного перпендикуляра к отрезку находится на одном и том же расстоянии от концов этого отрезка.
Доказательство . Рассмотрим произвольную точку D , лежащую на серединном перпендикуляре к отрезку AB (рис.2), и докажем, что треугольники ADC и BDC равны.
Действительно, эти треугольники являются прямоугольными треугольниками, у которых катеты AC и BC равны, а катет DC является общим. Из равенства треугольников ADC и BDC вытекает равенство отрезков AD и DB . Теорема 1 доказана.
Теорема 2 (Обратная к теореме 1) . Если точка находится на одном и том же расстоянии от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.
Доказательство . Докажем теорему 2 методом «от противного». С этой целью предположим, что некоторая точка E находится на одном и том же расстоянии от концов отрезка, но не лежит на серединном перпендикуляре к этому отрезку. Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точки E и A лежат по разные стороны от серединного перпендикуляра (рис.3). В этом случае отрезок EA пересекает серединный перпендикуляр в некоторой точке, которую мы обозначим буквой D .
Докажем, что отрезок AE длиннее отрезка EB . Действительно,
Таким образом, в случае, когда точки E и A лежат по разные стороны от серединного перпендикуляра, мы получили противоречие.
Теперь рассмотрим случай, когда точки E и A лежат по одну сторону от серединного перпендикуляра (рис.4). Докажем, что отрезок EB длиннее отрезка AE . Действительно,
Полученное противоречие и завершает доказательство теоремы 2
Окружность, описанная около треугольника
Определение 2 . Окружностью, описанной около треугольника , называют окружность, проходящую через все три вершины треугольника (рис.5). В этом случае треугольник называют треугольником, вписанным в окружность, или вписанным треугольником .
Свойства описанной около треугольника окружности. Теорема синусов
Для любого треугольника справедливы равенства (теорема синусов):
где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности.
Для любого треугольника справедливо равенство:
где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности.
Для любого треугольника справедливо равенство:
где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности.
| Серединные перпендикуляры к сторонам треугольника |
 |
Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.
Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.
Центр описанной около остроугольного треугольника окружности лежит внутри треугольника.
Центром описанной около прямоугольного треугольника окружности является середина гипотенузы.
Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.
Для любого треугольника справедливы равенства (теорема синусов):
где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности.
Для любого треугольника справедливо равенство:
где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности.
Для любого треугольника справедливо равенство:
где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности.
Доказательства теорем о свойствах описанной около треугольника окружности
Теорема 3 . Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.
Доказательство . Рассмотрим два серединных перпендикуляра, проведённых к сторонам AC и AB треугольника ABC , и обозначим точку их пересечения буквой O (рис. 6).
Поскольку точка O лежит на серединном перпендикуляре к отрезку AC , то в силу теоремы 1 справедливо равенство:
Поскольку точка O лежит на серединном перпендикуляре к отрезку AB , то в силу теоремы 1 справедливо равенство:
Следовательно, справедливо равенство:
откуда с помощью теоремы 2 заключаем, что точка O лежит на серединном перпендикуляре к отрезку BC. Таким образом, все три серединных перпендикуляра проходят через одну и ту же точку, что и требовалось доказать.
Следствие . Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.
Доказательство . Рассмотрим точку O , в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника ABC (рис. 6).
При доказательстве теоремы 3 было получено равенство:
из которого вытекает, что окружность с центром в точке O и радиусами OA , OB , OC проходит через все три вершины треугольника ABC , что и требовалось доказать.
Теорема 4 (теорема синусов) . Для любого треугольника (рис. 7)
Доказательство . Докажем сначала, что длина хорды окружности радиуса R хорды окружности радиуса R , на которую опирается вписанный угол величины φ , вычисляется по формуле:
Рассмотрим сначала случай, когда одна из сторон вписанного угла является диаметром окружности (рис.8).
Поскольку все вписанные углы, опирающиеся на одну и ту же дугу, равны, то для произвольного вписанного угла всегда найдется равный ему вписанный угол, у которого одна из сторон является диаметром окружности.
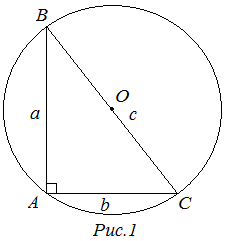
Окружность, описанная около прямоугольного треугольника
Определение и формулы описанной окружности прямоугольного треугольника
Центр описанной окружности лежит на пересечении серединных перпендикуляров, проведенных к сторонам треугольника.
Рассмотрим прямоугольный треугольник . Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы, а радиус описанной окружности равен половине гипотенузы
Для прямоугольного треугольника справедлива теорема синусов:
где – радиус описанной около прямоугольного треугольника окружности,
– катеты этого треугольника,
– его гипотенуза,
– острые углы треугольника.
Примеры решения задач
Решая квадратное уравнение , получаем
, т.е.
, а
см. Площадь прямоугольного треугольника равна половине произведения катетов, т.е.
Пусть , тогда из условия задачи следует, что
и
Отсюда получаем, что .
Поскольку , то
– равнобедренный, а значит
и
А это означает, что – равносторонний, т.е.
. Тогда по теореме Пифагора
Нахождение диаметра описанной окружности
Боковая сторона равнобедренного треугольника . Угол при вершине, противолежащий основанию, равен . Найдите диаметр окружности, описанной около этого треугольника.
Решение задачи
В данном уроке рассматривается решение геометрической задачи на определение диаметра описанной около треугольника окружности. Условие задачи для наглядности изображается схематически на рисунке. Для решения задачи проводятся дополнительные построения: из каждой вершины треугольника проводится отрезок к центру описанной около треугольника окружности. Далее в ходе решения доказывается, что треугольник — равносторонний. Следовательно, верно равенство: . Чтобы найти диаметр описанной около треугольника окружности, применяется формула нахождения диаметра: .
В случае использования данного решения в качестве примера для решения задач ОГЭ 10 подготовка к ОГЭ станет более успешной и результативной.
Содержание:
Окружность:
Определение: Кривой второго порядка называется линия, описываемая уравнением
Замечание: Если коэффициенты
При определенных значениях параметров, входящих в это уравнение, оно дает канонические у равнения окружности, эллипса (не путать с овалом), гиперболы и параболы. Рассмотрим эти кривые второго порядка в указанной последовательности.
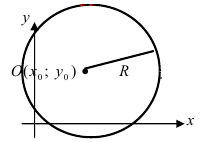
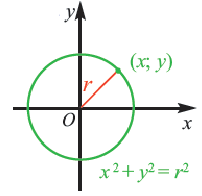
Определение: Окружностью называется геометрическое место точек равноудаленных от выделенной точки 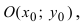
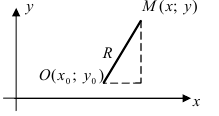
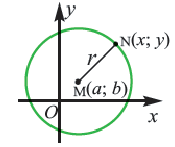
Получим уравнение окружности (Рис. 27). Пусть точка М(х;у) лежит на окружности:
Рис. 27. Вывод уравнения окружности.
Из рисунка видно, что по теореме Пифагора 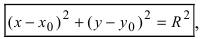
Рис. 28. Окружность.
Если 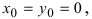
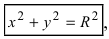
Пример:
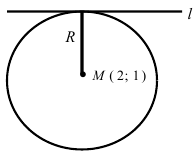
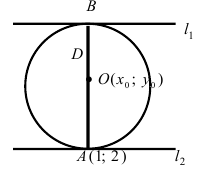
Составить уравнение окружности, центр которой совпадает с точкой М (2; 1), прямая линия 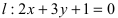
Решение:
Радиус окружности равен расстоянию от центра окружности точки М (2; 1) до прямой l, т.е.
В уравнении окружности 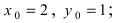
Пример:
Составить уравнение окружности, касающейся двух параллельных прямых 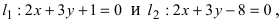
Решение:
Прежде всего определим, на какой из прямых 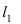
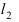
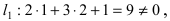
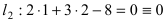
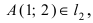
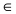
а радиус окружности 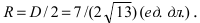
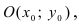
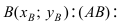
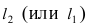
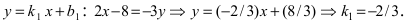
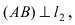
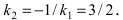
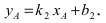
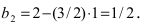
Найдем координаты точки B, которая является пересечением прямых 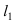
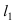
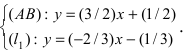
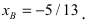
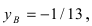
Для вычисления координат точки О применим формулы деления отрезка пополам (О): 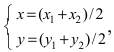
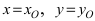
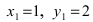
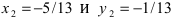
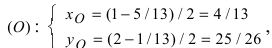
Таким образом, уравнение искомой окружности имеет вид:
Окружность в высшей математике
Рассмотрим уравнение
которое получается из уравнения (I), если положить 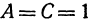
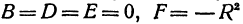
Если в формулу, выражающую расстояние между двумя точками, подставить 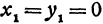
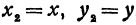
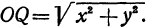
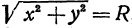
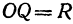
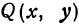
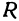

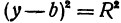

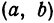
Пример:
Найдем уравнение окружности с центром в точке 
Решение:
Полагая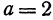
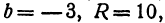
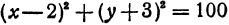
Разрешим это уравнение относительно 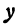
и
Первое из этих уравнений есть уравнение верхней половины окружности, второе—нижней.
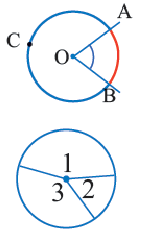
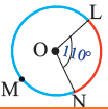
Центральный угол. Градусная мера дуги
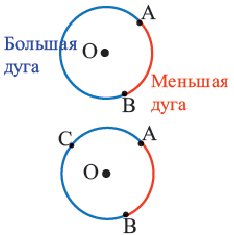
Дуга окружности. Если отметить на окружности точки 

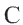
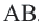
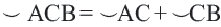


Центральный угол. Угол, вершина которого находится в центре окружности, называется центральным углом. Дугу окружности можно измерять в градусах. Градусная мера дуги равна градусной мере соответствующего центрального угла:
Сумма всех центральных углов окружности, не имеющих общую внутреннюю точку, равна
Дуги окружности и их величины
Пример: 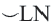
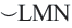
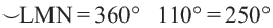
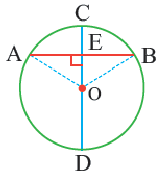
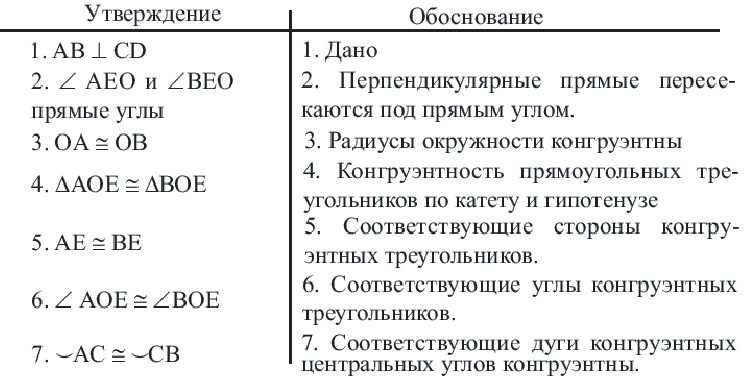
Конгруэнтные дуги
В окружности конгруэнтным центральным углам соответствуют конгруэнтные дуги и наоборот.
Если
Если
Длина дуги
Какую часть составляет центральный угол от всей окружности, такую же часть длина дуги составляет от длины всей окружности.
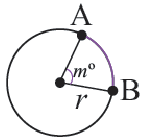
Длина дуги в 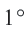
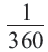
Длина дуги, соответствующей центральному углу с градусной мерой 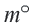
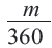
Длина дуги выражается единицами измерения длины (мм, см, м, и т.д.)
Пример №1
Длина окружности равна 72 см. Найдите длину дуги, соответствующей центральному углу 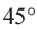
Решение:
Так как центральный угол 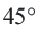
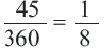
Пример №2
Найдите длину дуги, соответствующей центральному углу 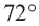
Решение: подставляя значения 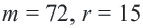
Окружность и хорда
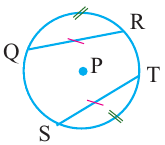
Теорема о конгруэнтных хордах
Теорема 1. Хорды, стягивающие конгруэнтные дуги окружности, конгруэнтны.
Обратная теорема 1. Дуги, стягиваемые конгруэнтными хордами окружности, конгруэнтны.
1)Если 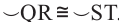
2)Если
Доказательство теоремы 1:
Теорема о серединном перпендикуляре хорд
Теорема 2.
Диаметр, перпендикулярный хорде, делит хорду и соответствующую дугу пополам.
Если
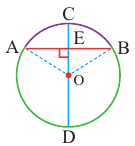
Доказательство теоремы 2.
Дано: 
Докажите:
Начертите радиусы 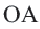
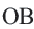
Следствие 1. Прямая, проходящая через центр окружности и перпендикулярная хорде, делит хорду и ее дугу пополам.
Следствие 2. Центр окружности расположен на серединном перпендикуляре хорды. Серединный перпендикуляр хорды проходит через центр окружности.
Пример: Найдите расстояние от центра до хорды длиной 30 единиц в окружности радиусом 17 единиц. Если 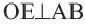
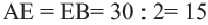
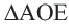
Теорема о хордах, находящихся на одинаковом расстоянии от центра окружности
Теорема 3.
Конгруэнтные хорды окружности находятся на одинаковом расстоянии от центра окружности.
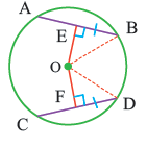
Если 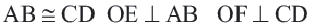
Обратная теорема 3. Хорды, находящиеся на одинаковом расстоянии от центра окружности, конгруэнтны.
Доказательство теоремы 3
Дано: Окружность с центром
Докажите:
Доказательство (текстовое): Прямая, проходящая через центр окружности и перпендикулярная хорде, делит хорду и стягивающую ее дугу пополам. 

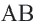
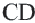

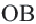
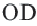
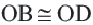
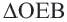
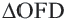


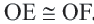
Задача. Хорды 

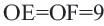
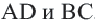
Решение: Так как хорды 

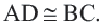
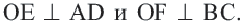
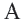
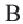
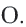
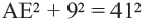
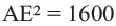
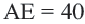
Так как
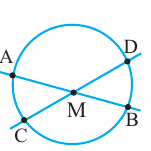
Угол, вписанный в окружность
Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется углом вписанным в окружность. Дуга, соответствующая углу, вписанному в окружность, называется дугой, на которую опирается этот угол.
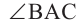
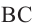
Угол, вписанный в окружность:
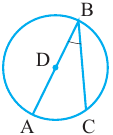
Теорема 1. Градусная мера угла, вписанного в окружность, равна половине градусной меры дуги, на которую он опирается.
Доказательство (текстовое): 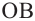
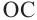
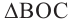
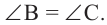
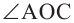
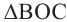
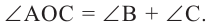
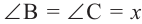
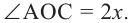
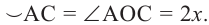
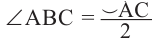
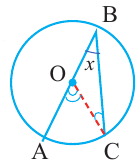
Следствие 1. Угол, вписанный в окружность, равен половине соответствующего центрального угла.
Следствие 2. Угол, вписанный в окружность и опирающийся на диаметр (полуокружность), является прямым углом.
Конгруэнтные углы, вписанные в окружность
Следствие 3. Вписанные углы, опирающиеся на одну и ту же дугу, конгруэнтны. 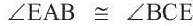
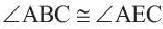
Следствие 4. Вписанные углы, опирающиеся на конгруэнтные дуги, конгруэнтны. Если 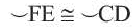
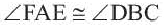
Касательная к окружности
Касательная. Признак касательной
Прямая, имеющая одну общую точку с окружностью, называется касательной. Теорема 1. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
Прямая 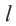
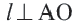
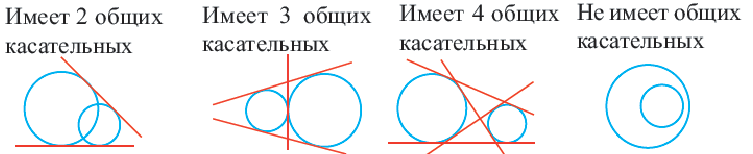
Прямая, касающаяся обеих окружностей, называется общей касательной этих окружностей. Окружности, касаясь друг друга изнутри или извне, могут иметь общую касательную в одной точке. Также окружности могут касаться одной касательной в разных точках.
Две окружности могут иметь несколько общих касательных или вообще не иметь общих касательных.
Доказательство теоремы 1. Если прямая 

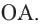
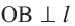

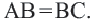
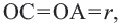
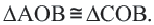

Свойства касательных, проведенных к окружности из одной точки
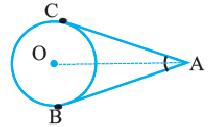
Теорема 2. Отрезки касательных к окружности, проведенных из одной точки, конгруэнтны, и центр окружности находится на биссектрисе угла, образованного касательными.
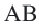
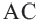
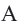
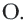
Углы, образованные секущими и касательными
Прямая, имеющая две общие точки с окружностью, называется секущей окружности.
Углы между двумя секущими
Вершина угла находится внутри окружности
Теорема. Если вершина угла, образованного двумя секущими, находится внутри окружности, то градусная мера угла равна полусумме величин дуг на которые опирается этот угол и угол вертикальный данному.
Углы между касательной и секущей
Вершина угла находится на окружности
Теорема. Если вершина угла, образованного касательной и секущей, находится на окружности, то градусная мера угла равна половине градусной меры дуги, на которую он опирается.
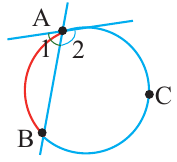
Углы, образованные касательной и секущей
Вершина угла находится вне окружности
Теорема 1.
Градусная мера угла, образованного секущей и касательной, двумя касательными, двумя секущими окружности (если вершина угла находится вне окружности), равна половине разности градусных мер дуг, находящихся между сторонами угла.
Отрезки секущих и касательных
Длина отрезков, секущих окружность
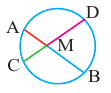
Теорема 1. При пересечении двух хорд, произведение отрезков одной хорды, полученных точкой пересечения, равно произведению отрезков второй хорды.
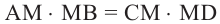
Теорема 2. Если из точки 

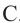
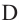
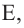
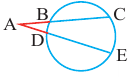
Теорема 3. Если из точки 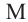


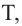
Уравнение окружности
Используя формулу расстояния между двумя точками, можно написать уравнение окружности с радиусом 
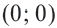
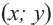

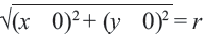
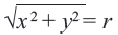
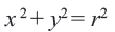
Уравнение окружности с центром в начале координат и радиусом 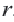
Например, уравнение окружности с центром в начале координат 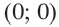
По формуле расстояния между центром окружности 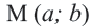
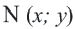
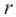
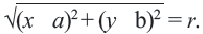
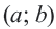
Например, уравнение окружности с центром в точке 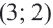
Пример №3
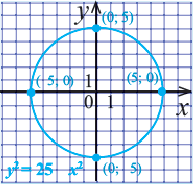
Постройте на координатной плоскости окружность, заданную уравнением
Решение: Напишем уравнение в виде 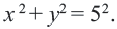
Отметим 4 точки, находящиеся на расстоянии 5 единиц от начала координат. Например, 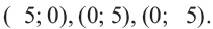
Пример №4
Точка 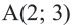
Решение: Записав координаты точки 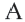
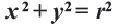
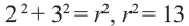
Пример №5
Найдем центр и радиус окружности, заданной уравнением
Решение:
Центр окружности точка 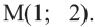
Пример №6
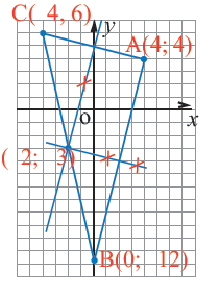
Мобильные телефоны работают с помощью передачи сигналов посредством спутников из одной передающей станции в другую. Компания мобильного оператора старается расположить передающую станцию так, чтобы обслуживать больше пользователей. Представим, что три больших города находятся в точках 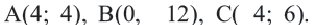
Решение: Сначала соединим эти точки и найдем точку пересечения серединных перпендикуляров сторон полученного треугольника. Эта точка 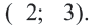
Уравнение окружности:
Заметка. Определив линейные уравнения, соответствующие серединным перпендикулярам, можно найти координаты центра окружности решением системы уравнений.
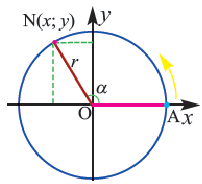
Координаты точек, находящихся на окружности, и тригонометрические отношения
Если точка 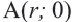
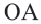
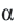
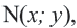
Для координат точки 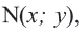

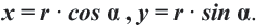

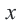
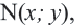
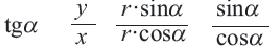
Синусы смежных углов равны, а косинусы взаимно противоположны.
Из этих формул при 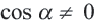
С помощью формул, приведенных выше, вычисление синуса, косинуса, тангенса для тупого угла можно свести к вычислению синуса, косинуса, тангенса острого угла, соответственно.
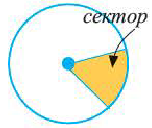
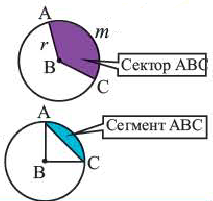
Сектор и сегмент
Сектор часть круга, ограниченная центральным углом, образованным двумя радиусами и соответствующей этому углу дугой. Площадь сектора, соответствующего центральному углу, составляет ту часть площади круга, которую составляет центральный угол от полного угла.
Например, часть круга, соответствующая центральному углу 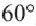
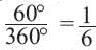
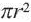

Площадь сектора
Площадь сектора:
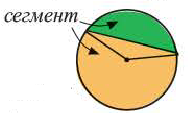
Площадь сегмента:
Указание: При нахождении площади сегмента, соответствующего большей дуге, к площади соответствующего сектора прибавляется площадь
- Эллипс
- Гипербола
- Парабола
- Многогранник
- Сфера в геометрии
- Шар в геометрии
- Правильные многогранники в геометрии
- Многогранники