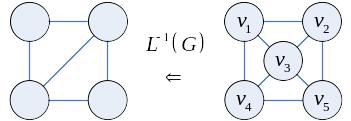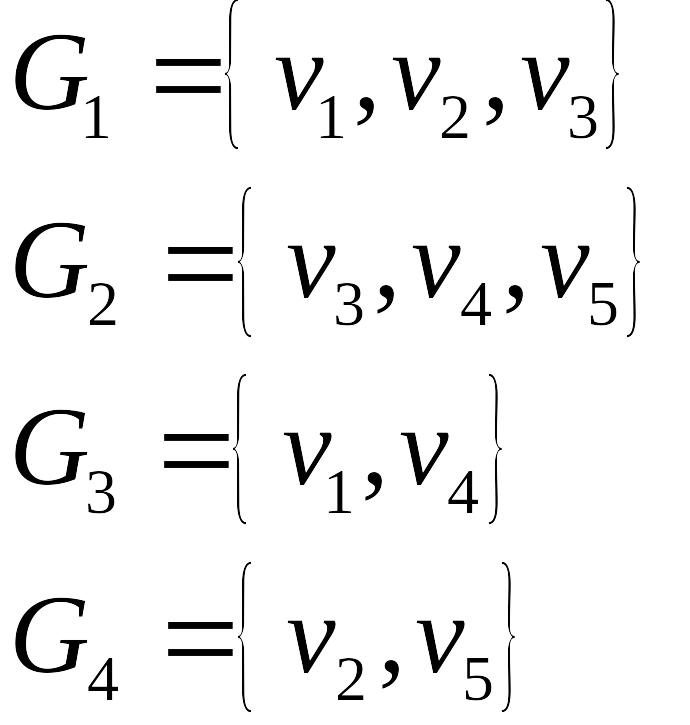При проектировании транспортных сетей встаёт задача об укладке графа на плоскости, но не каждый граф планарен. Если сеть представляет из себя непланарный граф, то придётся делать перекрёстки или строить мосты. Постройка мостов обойдётся дороже постройки обычной дороги, а перекрёстки увеличивают время поездки. Поэтому перед началом работы будет полезно вычислить род, толщину, крупность и число срещиваний графа.
Содержание
- 1 Род
- 2 Толщина
- 3 Крупность
- 4 Число скрещиваний
- 5 Укладка графа на торе
- 6 См. также
- 7 Источники информации
Род
| Определение: |
| Родом (англ. genus) графа называется наименьшее число ручек, которые нужно добавить к сфере, чтобы уложить на этой сфере. |
Обобщённая формула Эйлера, доказанная Курантом и Роббинсоном: . С её помощью можно доказать следующие утверждения.
| Утверждение: |
|
Род полного графа . |
|
Из обобщённой формулы Эйлера следует, что если граф связен, то его род , где — количество рёбер, — количество вершин. Тогда . Доказательство того, что правая часть является также верхней оценкой для рода графа, можно осуществить, произведя укладку этого графа на сфере с указанным числом ручек. |
| Утверждение: |
|
Род полного двудольного графа . |
|
Аналогично предыдущему утверждению, . Доказательство верхней оценки следует из укладки графа на сферу с ручками. |
Род планарного графа равен .
Если граф состоит из блоков , то .
Толщина
| Определение: |
| Толщиной (англ. thickness) графа называется наименьшее число планарных графов, объединение которых есть . |
По определению, если существует набор планарных графов, имеющих одинаковый набор вершин, объединение которых даёт граф , то толщина графа не больше . Таким образом, планарный граф имеет толщину . Графы с толщиной называются двупланарными графами. Концепция толщины возникла в гипотезе Фрэнка Харари: любой граф с вершинами либо сам, либо его дополнение, является непланарным. Эта гипотеза верна, так как полный граф не является бипланарным.
Толщина полного графа , но толщина графов и равна .
Крупность
| Определение: |
| Крупностью (англ. coarseness) графа называется наибольшее число непланарных графов в , не пересекающихся по рёбрам. |
Формулы для вычисления крупности полного графа не такие простые, как для других топологических инвариантов.
Крупность планарного графа равна , так как планарный граф не может содержать непланарный подграф.
Крупность и , так как и содеражат только один непланарный подграф.
Число скрещиваний
| Определение: |
| Числом скрещиваний (англ. crossing number) графа называется наименьшее число пересечений рёбер, которое будет при укладке на плоскости. |
Точное значения числа скрещиваний не известно, установлена только верхняя оценка.
Число скрещиваний полного графа .
Число скрещиваний полного двудольного графа .
Укладу планарного графа можно сделать с помощью гамма-алгоритма, где число скрещиваний будет равно .
Укладка графа на торе
| Определение: |
| Если граф можно уложить на торе, то он тороидальный. |
Тороидальный граф имеет род .
| Утверждение: |
|
и являются тороидальными. |
|
Укладки графа на торе представлены на рисунках с помощью прямоугольника, в котором отождествлены обе пары противоположных сторон. Укладка на торе. Вершины с номерами одного цвета принадлежат одной доле. |
См. также
- Укладка графа на плоскости
- Непланарность и
- Формула Эйлера
Источники информации
- Харари Фрэнк Теория графов стр. 141-148 — М.: Едиториал УРСС, 2003. — 296 с. — ISBN 5-354-00301-6
- Википедия — Толщина графа
- Wikipedia — Crossing number
Дискретная
математика: теория графов
Пример
Данный курс был прочитан для студентов
второго курса факультета «К» групп
К2-221, 222, 224, 281, 331 и 361 в весеннем семестре
2005/2006 учебного курса доц. каф. Кибернетики
Порешиным П.П.
Появление этого
конспекта на сайте кафедры для студентов
стало возможным благодаря инициативе
студента группы К2-331 Шутяева Александра,
который тщательно их записал с последующей
обработкой текста в текстовом, графическом
и формульном редакторах.
В этом файле
содержится вторяя конспекта
|
|
|
Выделяем пустые подграфы:
|
|
|
Реберные графы. Графы со свойством реберности
Пусть
— некоторый граф. Назовем граф
реберным графом
,
если носитель графа
совпадает с множеством ребер графа
,
и две вершины в
смежны, если соответствующие ребра
смежны в
.
Пример
|
(это |
Граф
обладает свойством реберности, если
существует некоторый граф, реберный
для которого является изоморфным для
.
Пример
|
|
Теорема
Граф
обладает свойством реберности, если
существует разложение ребер графа на
полные подграфы такое, что каждая вершина
графа принадлежит не более чем двум
полным подграфам.
Замечание
1. Не для любого графа
существует такое разложение ребер.
2.
В разложении ребер каждое ребро
принадлежит ровно одному подграфу.
Пример
|
|
|
Пример
|
|
|
|
не являются реберными |
Если граф обладает свойством реберности,
то как найти его образ (т.е. граф, для
которого данный является реберным)?
|
|
|
|
|
|
|
|
|
|
|
Пример
:

:
Пример
|
|
|
|
Укладки графа. Планарность
Исследуются топологические свойства
графа. Гомеоморфизм графов – еще
одно отношение эквивалентности на
графах. Два графа
и
гомеоморфны, если они изоморфны с
точностью до цепей степени 2.
Пример
|
:
|
:
|
|
Гомеоморфны. Говорят, что они имеют |
Пусть
— некоторая поверхность. Род поверхности
— это максимальное число простых замкнутых
кривых, не разделяющих эту поверхность.
|
Род плоскости: 0 |
|
|
Род сферы: 0 |
|
|
Род тора: 1 |
|
Поверхности, которые имеют род 4:

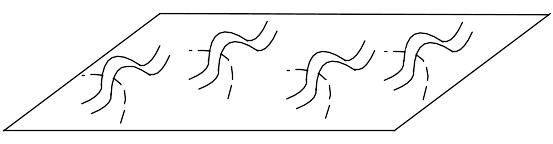
Род графа
—
— минимальный род поверхности, на которой
можно «уложить» граф
без взаимных пересечений ребер (ребра
пересекаются только в вершинах).
Пример


Граф
называется планарным (плоским),
если
.
-
печатные платы – планарные графы;
-
микросхемы (на уровне технологии их
изготовления) – планарные графы.
Критерий планарности графа (критерий
Понтрягина-Куратовского)
Граф планарен тогда и только тогда,
когда в нем отсутствуют подграфы,
гомеоморфные
или
.
|
|
|
Алгоритм приведения графа к планарному
1) Найти все подграф, гомеоморфные
и
.
2)
Построить таблицу покрытия найденных
в п.1 подграфов ребрами, которые их
образуют.
3) Найти минимальное покрытие
подграфов ребрами (удалив ребра,
образующие покрытие, получим планарный
граф).
Раскраска графов
Пусть
— некоторый граф и
— разбиение
на
внутренне устойчивых множеств (разбиение
означает, что
и
,
если
).
В этом случае говорят, что вершины
графа допускают раскраску в
цветов (цвета по номерам
).
Хроматическое число
— минимальное значение
,
которое допускает раскраску графа.
Хроматическое число пустого графа равно
1.
Хроматическое число
.
Хроматическое
число
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
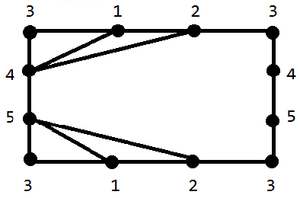
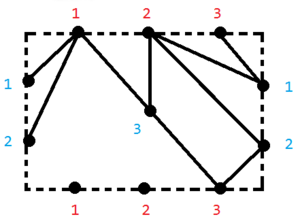
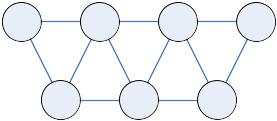
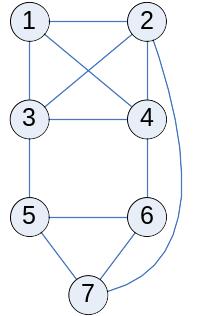
Вот пример укладки на торе без одного ребра.
Рассматриваем квадрат, в углу которого находится 4. На верхней стороне, слева направо, идут 1, 2, 6, 3. Их копии идут также на нижней стороне. На левой стороне, сверху вниз: 8, 9. Их копии есть справа. Все соединения по контуру — это рёбра.
Проводим соединения 8-1, 8-2 слева сверху, потом 4-6, 4-2 справа сверху. Справа внизу проводим линии 9-3 и 9-6.
Внутри квадрат рисуем треугольник 5-7-10 с тремя сторонами, где 10 смотрит вверх, 5 находится левее, а 7 правее. Соединяем 7 с нижними 1, 2, 6 и с 8 на правой стороне. Соединяем 5 с 4 и 9 на левой стороне. Наконец, 10 соединим с 2 наверху и 9 слева.
Здесь будут все соединения кроме 3-10. Из этого следует, что род графа не больше двух. Равен ли он 1 или 2, я не знаю. Пример строился чисто методом проб и ошибок.
Род — граф
Cтраница 1
Род графа определен корректно и не превосходит числа скрещиваний.
[1]
Необходимо проверить, что род графа определен корректно.
[2]
Получите нижнюю оценку для рода графа, обхват которого равен г. Выведите отсюда, что род К.
[3]
Представляет интерес нахождение такого рода минимальных связных частичных графов в произвольных графах.
[4]
Цель данной заметки — найти род графов из одного семейства, а именно установить род / г-мерного Куба.
[5]
Подставляя это неравенство в теорему 14В и используя то, что род графа — целое число, мы и получим нужный результат.
[6]
Баттл, Харари, Кодама и Янгс ( 1 ] показали, что род графа равен сумме родов его блоков.
[7]
Как указывается в работе Байнеке и Харари [2], с помощью этих двух соотношений легко проверить, что род графа имеет следующие нижние оценки.
[8]
Вводятся также несколько топологических инвариантов графа. Для полных графов и полных двудольных графов определяется род графа, для большинства из этих графов — толщина, и только для некоторых графов — число скрещиваний.
[9]
Тому, кто интересуется в основном чистой теорией графов, советуем посмотреть книгу Харари [1], которая представляет собой целый кладезь всевозможных сведений и является превосходным справочником. Стоит также прочитать работы Муна [7] о деревьях, Оре [5] о планарности и проблемах раскрашивания и Рингеля [16] о задачах, связанных с родом графа. Последняя книга обязательна для всех, кто хочет серьезно заняться теорией потоков в сетях.
[10]
Страницы:
1

В математике, род (множественное число род ) имеет несколько разных, но тесно связанных значений. Наиболее распространенное понятие, род (ориентируемой ) поверхности, — это количество «дырок», которые у нее есть, так что сфера сфера имеет род 0 и тор имеет род 1. Это уточняется ниже.
Содержание
- 1 Топология
- 1.1 Ориентируемые поверхности
- 1.2 Неориентируемые поверхности
- 1.3 Узел
- 1.4 Ручка
- 1.5 Теория графов
- 2 Алгебраическая геометрия
- 3 Биология
- 4 См. Также
- 5 Ссылки
Топология
Ориентируемые поверхности

Род связанной ориентируемой поверхности — это целое число, представляющее максимальное количество вырезов вдоль непересекающихся замкнутых простых кривых без отображения результирующего коллектора отключен. Он равен количеству дескрипторов на нем. В качестве альтернативы его можно определить в терминах эйлеровой характеристики χ через соотношение χ = 2 — 2g для замкнутых поверхностей, где g — род. Для поверхностей с компонентами границы b уравнение имеет вид χ = 2 — 2g — b. С точки зрения непрофессионала, это количество «дырок» в объекте («дырки» интерпретируются как дырочки от бублика; в этом смысле полая сфера будет считаться не имеющей дыр). Пончик или тор имеет 1 такое отверстие, а сфера — 0. На зеленой поверхности, изображенной выше, есть 2 отверстия соответствующего типа.
Например:
- сфера Sи диск имеют род ноль.
- A тор имеет род один, как и поверхность кофейная кружка с ручкой. Отсюда шутка «топологи — это люди, которые не могут отличить пончик от кофейной кружки».
Явное построение поверхностей рода g дается в статье о фундаментальном многоугольнике.
- Род ориентируемых поверхностей
род 0
род 1
род 2
род 3
Проще говоря, значение рода ориентируемой поверхности равно количеству «дырок» в ней.
Неориентируемые поверхности
неориентируемые род, demigenus или род Эйлера соединенной неориентируемой замкнутой поверхности — положительное целое число, представляющее количество заглушек, прикрепленных к сфере. В качестве альтернативы его можно определить для замкнутой поверхности в терминах эйлеровой характеристики χ с помощью соотношения χ = 2 — k, где k — неориентируемый род.
Например:
- A реальная проективная плоскость имеет неориентируемый род один.
- A бутылка Клейна имеет неориентируемый род два.
Узел
род узла K определяется как минимальный род всех поверхностей Зейферта для K. Поверхность Зейферта узла — это однако многообразие с границей, причем эта граница является узлом, т.е. гомеоморфна единичной окружности. Род такой поверхности определяется как род двумерного многообразия, которое получается склейкой единичного круга по границе.
Ручка
Тип трехмерного ручки представляет собой целое число, представляющее максимальное количество вырезов вдоль встроенных дисков без отключения образовавшегося коллектора. Он равен количеству ручек на нем.
Например:
- A шар имеет род ноль.
- Полностью тор D × S имеет род один.
Теория графов
род графа — это минимальное целое число n такое, что граф можно нарисовать, не пересекая себя на сфере с n ручками (т.е. ориентированной поверхности рода n). Таким образом, планарный граф имеет род 0, потому что его можно нарисовать на сфере без самопересечения.
неориентируемый род графа — это минимальное целое число n такое, что граф можно нарисовать, не пересекая себя на сфере с n перекрестными заглавными буквами ( т.е. неориентируемая поверхность (неориентируемой) рода n). (Это число также называется demigenus .)
Род Эйлера — это минимальное целое число n такое, что граф можно нарисовать, не пересекая себя на сфере с n перекрестных заглавных букв или на сфере с n / 2 ручками.
В теории топологических графов есть несколько определений рода группы. Артур Т. Уайт ввел следующую концепцию. Род группы G — это минимальный род (связного, неориентированного) графа Кэли для G.
проблема рода графов является NP- полная.
Алгебраическая геометрия
Есть два связанных определения рода любой проективной алгебраической схемы X: арифметический род и геометрический род. Когда X является алгебраической кривой с полем определения комплексными числами, и если X не имеет особых точек, то эти определения согласуются и совпадают с топологическим определением, примененным к римановой поверхности пространства X (его многообразию комплексных точек). Например, определение эллиптической кривой из алгебраической геометрии связано неособой проективной кривой рода 1 с данной рациональной точкой на ней.
По теореме Римана-Роха неприводимая плоская кривая степени d { displaystyle d}

- g = (d — 1) (d — 2) 2 — s, { displaystyle g = { frac {(d-1) ( d-2)} {2}} — s,}
где s — количество особенностей при правильном подсчете.
Биология
Род можно также рассчитать по графику, охватываемому сетью химических взаимодействий в нуклеиновых кислотах или белках. В частности, можно изучать рост рода по цепи. Такая функция (называемая следом рода) показывает топологическую сложность и доменную структуру биомолекул.
См. Также
- Группа (математика)
- Арифметический род
- Геометрический род
- Род мультипликативная последовательность
- Род квадратичной формы
- Род Spinor