Пусть
на заряд Q
действуют несколько сил со стороны
других зарядов. Для того чтобы определить
результирующую силу
,
действующую на этот заряд, нужно узнать
еёнаправление
и модуль.
Направление
результирующей силы
определяетсяпо
принципу суперпозиции
сил (векторной суммы), а модуль – из
геометрических построений.
Рекомендуемая
последовательность решения задач:
-
сделать
рисунок, на котором, в соответствии с
условием задачи, указать расположение
всех зарядов; -
построить
силы, действующие со стороны каждого
заряда на заряд Q
с учётом знаков всех зарядов (см. рис.
2). Все силы должны быть приложены к
точке, в которой расположен заряд Q
(то есть начинаться в этой точке) и
направлены по линии, соединяющей заряды; -
построить
векторную сумму всех сил (по правилу
треугольника или параллелограмма, если
силы по результатам построений не
лежат на одной прямой). Таким образом,
мы определим направление
вектора результирующей силы; -
модуль
равнодействующей силы вычисляется в
зависимости от расположения и величины
составляющих её сил, каждая из которых
рассчитывается по закону Кулона.
Например,
для системы, состоящей из трех зарядов,
.
П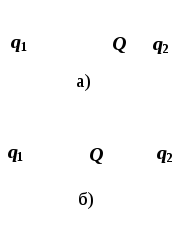
расчете модуля результирующей силы по
результатам построения возможны четыре
варианта (рис. 2, а, б, в, г):
-
векторы
составляющих сил направлены в одну
сторону. Модуль определяется как
алгебраическая сумма сил:
;
-
векторы
составляющих сил направлены в разные
стороны. Модуль определяется как
алгебраическая разность сил:
;
-
векторы
составляющих сил образуют между собой
угол α.
Модуль определяется по теореме косинусов:
;
-
векторы
составляющих сил перпендикулярны друг
другу. Модуль определяется по теореме
Пифагора (частный случай теоремы
косинусов):
.
1. Как ведет себя
положительный заряд + q1,
помещенный в поле неподвижного
отрицательного заряда– q2:
а) движется с
постоянной скоростью к q2;
б) движется
равноускоренно к заряду q2;
в) движется
равнозамедленно к заряду q2;
г) остается в покое.
2. Если отрицательный
точечный заряд, находящийся посередине
между точечными зарядами qи2q, заменить
на противоположный по знаку заряд, как
изменится модуль и направление
результирующей силы?
а) модуль силы не
меняется, направление меняется на
противоположное;
б) модуль силы
уменьшается в 2 раза, направление меняется
на противоположное;
в) модуль силы
равен нулю;
г) модуль силы
увеличится в 2 раза, направление не
меняется;
д) модуль силы
увеличится в 3 раза, направление не
меняется.
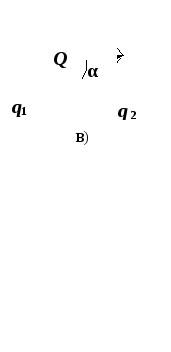
3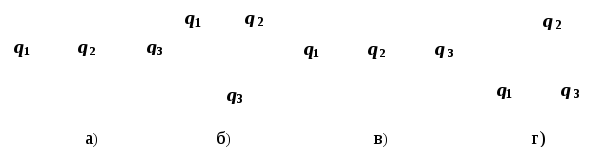
Как направлена равнодействующая сила
на зарядq3
со стороны зарядовq1иq2(|q1|=|q2|расстояния между зарядами одинаковые):
4. Как направлена
сила, действующая на положительный
точечный заряд, расположенный в центре
квадрата?
Задача
1.1. В
вершинах равностороннего треугольника
со стороной а
расположены два положительных и один
отрицательный заряды, одинаковых по
величине и равных q.
Найти силу, действующую на заряд Q0 < 0,
расположенный на пересечении медиан.
Р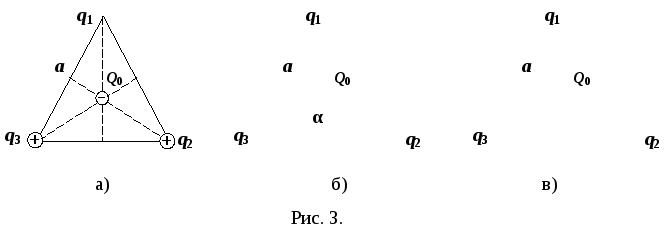
рисунок, произвольно расположив заряды
в вершинах треугольника. Расставим
силы, действующие на заряд Q0
со стороны зарядов q1,
q2,
и
q3,
и обозначим их соответственно
(рис. 3, а).
Направление
результирующей силы по определяем по
принципу суперпозиции:
.
Для
этого необходимо сложить три вектора.
Так как величина зарядов q1,
q2
и
q3
одинакова и они равноудалены от заряда
Q0,
то силы
будут одинаковы по модулю.
Из
рисунка видно, что сначала удобно сложить
векторы
по правилу параллелограмма (рис. 3 б).
.
Модуль
вектора
определим по теореме косинусов
,
где
α
– угол между векторами
.
С
учётом того, что
,α
= 120º; cos
α
= – 0,5, получим:
.
Теперь
нужно сложить векторы
.
(рис. 3 в). Из рисунка видно, что эти векторы
направлены в одну сторону, значит, их
векторная сумма равна их алгебраической
сумме. С учётом того, что,
модуль результирующей силы
.
По закону Кулона
.
Обратите
внимание,
что в законе Кулона все заряды пишутся
со знаком «+», так как знак заряда
учитывался при геометрических построениях.
Расстояние
r
выразим из рисунка через сторону
треугольника а:
.
Окончательно
получим:
.
Задача
1.2. В
вершинах правильного шестиугольника
со стороной а
расположены точечные заряды q,
2q,
3q,
4q,
5q,
6q.
Найти силу, действующую на заряд Q0
> 0, расположенный на пересечении
диагоналей.
Решение.
Сделаем
рисунок, произвольным образом расположив
заряды в вершинах шестиугольника. Если
все заряды одноимённые, то между зарядом
Q0
и остальными зарядами действует сила
отталкивания. Расставим силы, действующие
на заряд Q0
со стороны каждого заряда, и обозначим
их соответствующими индексами (рис. 4,
а).
П
закону Кулона
;
;
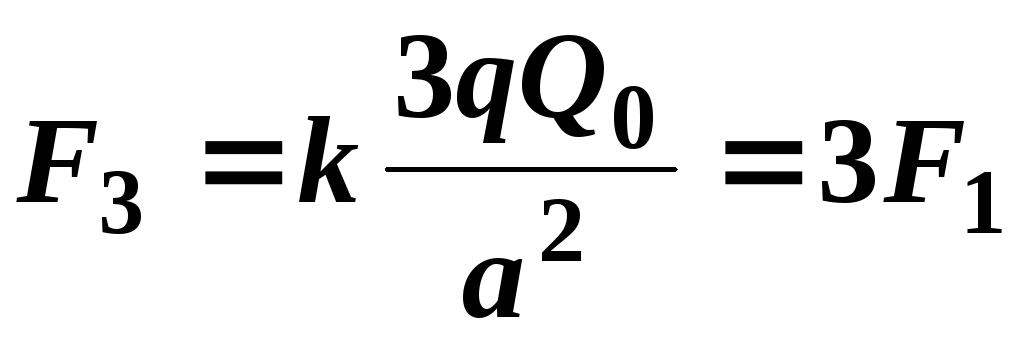
;
;
.
По принципу
суперпозиции
.
Сначала
сложим попарно силы, лежащие на одной
прямой (рис. 4 б). Так как эти силы направлены
в разные стороны, то модули равнодействующих
сил равны алгебраической разности этих
сил.
Равнодействующая
сил
равна
и направлена в сторону большей силы, то
есть в сторону.
Равнодействующая силравна
и направлена в сторону
.
Наконец, равнодействующая силравна
и направлена в сторону
.
Мы видим, что
векторы равнодействующих сил одинаковы.
Теперь
сложим векторы
(см. задачу 1.1):
.
По
теореме косинусов
.
С
учётом того, что
,α
= 120º; cos
α
= – 0,5, получим:
Теперь
осталось сложить векторы
(рис. 4 в). Так как векторы сонаправлены
и одинаковы по модулю, то окончательно
получим:
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
в первой задаче результирующая сила зависит только от зарядов -q и +q, находящихся на одной диагонали, ибо на второй диагонали заряды +q и +q друг друга компенсируют
расстояние от зарядов +q и -q до центра квадрата равно половине диагонали: x = (a √2)/2
так как сила отталкивания, создаваемая зарядом +q, и сила притяжения, создаваемая зарядом -q, сонаправлены, то достаточно провести ось и спроецировать на нее эти силы. тогда результирующая равна просто сумме этих сил (причем они равны ввиду равенства модулей зарядов и расстояний):
F = 2 F’ = 2 (k q²)/x² = 4 (k q²)/a²
во второй задаче просто спроецировать на одну ось силы не получится. необходимо нарисовать вектора сил в указанной точке, сложить их по правилу параллелограмма и воспользоваться теоремой косинусов:
F = √[F1² + F2² — 2 F1 F2 cos60°], где
F1 = (2 k q²)/a²; F2 = (k q²)/a²
F = [(k q²)/a²] * √[4 + 1 — 2] = [(k q²)/a²] √3
estil847
Вопрос по физике:
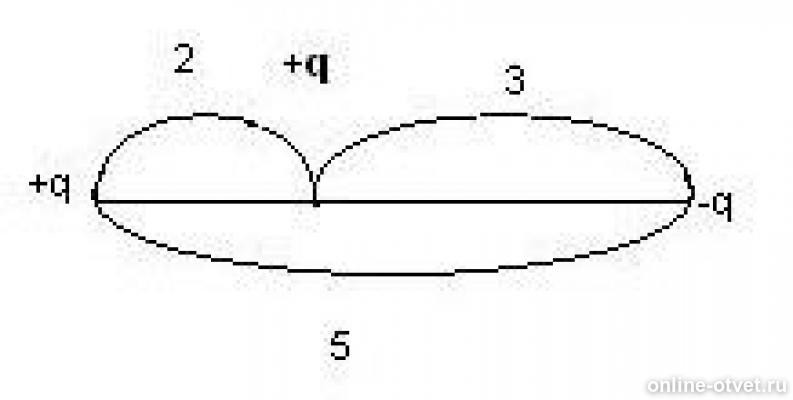
Помогите пожалуйста!Определить результирующую силу, действующую на выделенный заряд.
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 1
exthalonowan902
Если предположить, что 5, 3 и 2 это метры
тогда на заряд в +q будет действовать сила отталкивания от +q в право и сила притяжения от -q тоже в право
результирующая сила направлена в право Ответ
Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат — это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Физика.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи —
смело задавайте вопросы!
Физика — область естествознания: естественная наука о простейших и вместе с тем наиболее общих законах природы, о материи, её структуре и движении.
Закон Кулона
Между электрическими зарядами действует сила. Как она зависит от величины зарядов и других факторов?
Этот вопрос исследовал в 1780-е годы французский физик Шарль Кулон (1736-1806). Он воспользовался крутильными весами, очень похожими на те, которые применял Кавендиш для определения гравитационной постоянной.
Если к шарику на конце стержня, подвешенного на нити, подности заряд, стержень слегка отклоняется, нить закручивается, и угол поворота нити будет пропорционален действующей между зарядами силе (крутильные весы). С помощью этого прибора Кулон определил зависимость силы от величины зарядов и расстояния между ними.
В те времена еще не было приборов для точного определения величины заряда, но Кулон сумел приготовить небольшие шарики с известным соотношением зарядов. Если заряженный проводящий шарик, рассуждал он, привести в соприкосновение с точно таким же незаряженным шариком, то имевшийся на первом заряд в силу симметрии распределится поровну между двумя шариками.
Это дало ему возможность получать заряды, составлявшие 1/2, 1/4 и т.д. от первоначального.
Несмотря на некоторые трудности, связанные с индуцированием зарядов, Кулону удалось доказать, что сила, с которой одно заряженное тело действует на другое малое заряженное тело, прямо пропорциональна электрическому заряду каждого из них.
Другими словами, если заряд любого из этих тел удвоить, то удвоится и сила; если же удвоить одновременно заряды обоих тел, то сила станет вчетверо больше. Это справедливо при условии, что расстояние между телами остается постоянным.
Изменяя расстояние между телами, Кулон обнаружил, что действующая между ними сила обратно пропорциональна квадрату расстояния: если расстояние, скажем, удваивается, сила становится вчетверо меньше.
Итак, заключил Кулон, сила, с которой одно малое заряженное тело (в идеальном случае -точечный заряд, т.е. тело, подобно материальной точке не имеющее пространственных размеров) действует на другое заряженное тело, пропорциональна произведению их зарядов Q1 и Q2 и обратно пропорциональна квадрату расстояния между ними:
Здесь k -коэффициент пропорциональности.
Это соотношение известно как закон Кулона; его справедливость подтверждена тщательными экспериментами, гораздо более точными, чем первоначальные трудно воспроизводимые опыты Кулона. Показатель степени 2 установлен в настоящее время с точностью 10 -16 , т.е. он равен 2 ± 2?10 -16 .
Коль скоро мы теперь имеем дело с новой величиной — электрическим зарядом, мы можем подобрать такую единицу измерения, чтобы постоянная к в формуле равнялась единице. И действительно, такая система единиц еще недавно широко использовалась в физике.
Речь идет о системе СГС (сантиметр-грамм-секунда), в которой используется электростатическая единица заряда СГСЭ. По определению два малых тела, каждое с зарядом 1 СГСЭ, расположенные на расстоянии 1 см друг от друга, взаимодействуют с силой 1 дина.
Теперь, однако, заряд чаще всего выражают в системе СИ, где его единицей является кулон (Кл).
Точное определение кулона через электрический ток и магнитное поле мы приведем позднее.
В системе СИ постоянная k имеет величину k = 8,988?10 9 Нм 2 /Кл 2 .
Заряды, возникающие при электризации трением обычных предметов (расчески, пластмассовой линейки и т.п.), по порядку величины составляют микрокулон и меньше (1 мкКл = 10 -6 Кл).
Заряд электрона (отрицательный) приблизительно равен 1,602?10 -19 Кл. Это наименьший известный заряд; он имеет фундаментальное значение и обозначается символом е, его часто называют элементарным зарядом.
е = (1,6021892 ± 0,0000046)?10 -19 Кл, или е ? 1,602?10 -19 Кл.
Поскольку тело не может приобрести или потерять долю электрона, суммарный заряд тела должен быть целым кратным элементарного заряда. Говорят, что заряд квантуется (т.е. может принимать лишь дискретные значения). Однако, поскольку заряд электрона е очень мал, мы обычно не замечаем дискретности макроскопических зарядов (заряду 1 мкКл соответствуют примерно 10 13 электронов) и считаем заряд непрерывным.
Формула Кулона характеризует силу, с которой один заряд действует на другой. Эта сила направлена вдоль линии, соединяющей заряды. Если знаки зарядов одинаковы, то силы, действующие на заряды, направлены в противоположные стороны. Если же знаки зарядов различны, то действующие на заряды силы направлены навстречу друг другу.
Заметим, что в соответствии с третьим законом Ньютона сила, с которой один заряд действует на другой, равна по величине и противоположна по направлению силе, с которой второй заряд действует на первый.
Закон Кулона можно записать в векторной форме подобно закону всемирного тяготения Ньютона:
где F12 — вектор силы, действующей на заряд Q1 со стороны заряда Q2, 

Следует иметь в виду, что формула применима лишь к телам, расстояние между которыми значительно больше их собственных размеров. В идеальном случае это точечные заряды. Для тел конечного размера не всегда ясно, как отсчитывать расстояние r между ними, тем более что распределение заряда может быть и неоднородным. Если оба тела — сферы с равномерным распределением заряда, то r означает расстояние между центрами сфер. Важно также понимать, что формула определяет силу, действующую на данный заряд со стороны единственного заряда. Если система включает несколько (или много) заряженных тел, то результирующая сила, действующая на данный заряд, будет равнодействующей (векторной суммой) сил, действующих со стороны остальных зарядов. Постоянная к в формуле Закона Кулона обычно выражается через другую константу, ?0, так называемую электрическую постоянную, которая связана с k соотношением k = 1/(4??0). С учетом этого закон Кулона можно переписать в следующем виде:
где с наивысшей на сегодня точностью
Запись большинства других уравнений электромагнитной теории упрощается при использовании ?0, поскольку 4? в окончательном результате часто сокращается. Поэтому мы будем обычно использовать Закон Кулона, считая, что:
Закон Кулона описывает силу, действующую между двумя покоящимися зарядами. Когда заряды движутся, между ними возникают дополнительные силы, и их мы обсудим в последующих главах. Здесь же рассматриваются только покоящиеся заряды; этот раздел учения об электричестве называется электростатикой.
Продолжение следует. Коротко о следующей публикации:
Электрическое поле — один из двух компонентов электромагнитного поля, представляющий собой векторное поле, существующее вокруг тел или частиц, обладающих электрическим зарядом, либо возникающий при изменении магнитного поля.
Закон Кулона.
Закон Кулона — это один из основных законов электростатики. Он определяет величину и направление силы взаимодействия между двумя неподвижными точечными зарядами.
Под точечным зарядом понимают заряженное тело, размер которого много меньше расстояния его возможного воздействия на другие тела. В таком случае ни форма, ни размеры заряженных тел не влияют практически на взаимодействие между ними.
Закон Кулона экспериментально впервые был доказан приблизительно в 1773 г. Кавендишем, который использовал для этого сферический конденсатор. Он показал, что внутри заряженной сферы электрическое поле отсутствует. Это означало, что сила электростатического взаимодействия меняется обратно пропорционально квадрату расстояния, однако результаты Кавендиша не были опубликованы.
В 1785 г. закон был установлен Ш. О. Кулоном с помощью специальных крутильных весов. Опыты Кулона позволили установить закон, поразительно напоминающий закон всемирного тяготения.
Сила взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональна произведению модулей заряда и обратно пропорциональна квадрату расстояния между ними.
В аналитическом виде закон Кулона имеет вид:
.
где |q1| и |q2| — модули зарядов; r — расстояние между ними; k — коэффициент пропорциональности, зависящий от выбора системы единиц. Сила взаимодействия направлена по прямой, соединяющей заряды, причем одноименные заряды отталкиваются, а разноименные — притягиваются.
Сила взаимодействия между зарядами зависит также от среды между заряженными телами.
В воздухе сила взаимодействия почти не отличается от таковой в вакууме. Закон Кулона выражает взаимодействие зарядов в вакууме.
Кулон — единица электрического заряда. Кулон (Кл) — единица СИ количества электричества (электрического заряда). Она является производной единицей и определяется через единицу силы тока — 1 ампер (А), которая входит в число основных единиц СИ.
За единицу электрического заряда принимают заряд, проходящий через поперечное сечение проводника при силе тока 1 А за 1 с.
Заряд в 1 Кл очень велик. Сила взаимодействия двух точечных зарядов по 1 Кл каждый, расположенных на расстоянии 1 км друг от друга, чуть меньше силы, с которой земной шар притягивает груз массой 1 т. Сообщить такой заряд небольшому телу невозможно (отталкиваясь друг от друга, заряженные частицы не могут удержаться в теле). А вот в проводнике (который в целом электронейтрален) привести в движение такой заряд просто (ток в 1 А — вполне обычный ток, протекающий по проводам в наших квартирах).
Коэффициент k в законе Кулона при его записи в СИ выражается в Н · м 2 /Кл 2 . Его численное значение, определенное экспериментально по силе взаимодействия двух известных зарядов, находящихся на заданном расстоянии, составляет:
Часто его записывают в виде , где ɛ0 =8,85 · 10 — 12 Kл 2 /H·м 2 — электрическая постоянная. В среде с диэлектрической проницаемостью ɛ закон Кулона имеет вид:
.
Закон Кулона простым языком
Взаимодействия электрических зарядов исследовали ещё до Шарля Кулона. В частности, английский физик Кавендиш в своих исследованиях пришёл к выводу, что неподвижные заряды при взаимодействии подчиняются определённому закону. Однако он не обнародовал своих выводов. Повторно закон Кулона был открыт французским физиком, именем которого был назван этот фундаментальный закон.
Рисунок 1. Закон Кулона
История открытия
Эксперименты с заряженными частицами проводили много физиков:
- Г. В. Рихман;
- профессор физики Ф. Эпинус;
- Д. Бернулли;
- Пристли;
- Джон Робисон и многие другие.
Все эти учёные очень близко подошли к открытию закона, но никому из них не удалось математически обосновать свои догадки. Несомненно, они наблюдали взаимодействие заряженных шариков, но установить закономерность в этом процессе было непросто.
Кулон проводил тщательные измерения сил взаимодействия. Для этого он даже сконструировал уникальный прибор – крутильные весы (см. Рис. 2).
Рис. 2. Крутильные весы
У придуманных Кулоном весов была чрезвычайно высокая чувствительность. Прибор реагировал на силы порядка 10 -9 Н. Коромысло весов, под действием этой крошечной силы, поворачивалось на 1 º . Экспериментатор мог измерять угол поворота, а значит и приложенную силу, пользуясь точной шкалой.
Благодаря гениальной догадке учёного, идея которой состояла в том, что при соприкосновении заряженного и незаряженного шариков, электрический заряд делился между ними поровну. На это сразу реагировали крутильные весы, коромысло которых поворачивалось на определённый угол. Заземляя неподвижный шарик, Кулон мог нейтрализовать на нём полученный заряд.
Таким образом, учёный смог уменьшать первоначальный заряд подвижного шарика кратное число раз. Измеряя угол отклонения после каждого деления заряда, Кулон увидел закономерность в действии отталкивающей силы, что помогло ему сформулировать свой знаменитый закон.
Формулировка
Кулон исследовал взаимодействие между шариками, ничтожно малых размеров, по сравнению с расстояниями между ними. В физике такие заряженные тела называются точечными. Другими словами, под определение точечных зарядов подпадают такие заряженные тела, если их размерами, в условиях конкретного эксперимента, можно пренебречь.
Для точечных зарядов справедливо утверждение: Силы взаимодействия между ними направлены вдоль линии, проходящей через центры заряженных тел. Абсолютная величина каждой силы прямо пропорциональна произведению зарядов и обратно пропорциональна квадрату расстояния между ними (см. рис. 3). Данную зависимость можно выразить формулой: |F1|=|F2|=(ke*q1*q2) / r 2
Рис. 3. Взаимодействие точечных зарядов
Остаётся добавить, что векторы сил направлены друг к другу для разноименных зарядов, и противоположно, в случае с одноимёнными зарядами. То есть между разноимёнными зарядами действует электрическое притяжение, а между одноимёнными – отталкивание.
Таким образом, закон Кулона описывает взаимодействие между двумя электрическими зарядами, которое лежит в основе всех электромагнитных взаимодействий.
Для того чтобы действовал сформулированный выше закон, необходимо выполнение следующий условий:
- соблюдение точечности зарядов;
- неподвижность заряженных тел;
- закон выражает зависимости между зарядами в вакууме.
Границы применения
Описанная выше закономерность при определённых условиях применима для описания процессов квантовой механики. Правда, закон Кулона формулируется без понятия силы. Вместо силы используется понятие потенциальной энергии кулоновского взаимодействия. Закономерность получена путём обобщения экспериментальных данных.
Следует отметить, что на сверхмалых расстояниях (при взаимодействиях элементарных частиц) порядка 10 – 18 м проявляются электрослабые эффекты. В этих случаях закон Кулона, строго говоря, уже не соблюдается. Формулу можно применять с учётом поправок.
Нарушение закона Кулона наблюдается и в сильных электромагнитных полях (порядка 10 18 В/м), например поблизости магнитаров (тип электронных звёзд). В такой среде кулоновский потенциал уменьшается не обратно пропорционально, а экспоненциально.
Кулоновские силы подпадают под действие третьего закона Ньютона: F1 = – F2. Они используются для описания законов всемирного тяготения. В этом случае формула приобретает вид: F = ( m1* m2 ) / r 2 , где m1 и m2 – массы взаимодействующих тел, а r – расстояние между ними.
Закон Кулона стал первым открытым количественным фундаментальным законом, обоснованным математически. Его значение в исследованиях электромагнитных явлений трудно переоценить. С момента открытия и обнародования закона Кулона началась эра изучения электромагнетизма, имеющего огромное значение в современной жизни.
Коэффициент k
Формула содержит коэффициент пропорциональности k, который для согласования соразмерностей в международной системе СИ. В этой системе единицей измерения заряда принято называть кулоном (Кл) – заряд, проходящий за 1 секунду сквозь проводник, где силы тока составляет 1 А.
Коэффициент k в СИ выражается следующим образом: k = 1/4πε0, где ε0 – электрическая постоянная: ε0 = 8,85 ∙10 -12 Кл 2 /Н∙м 2 . Выполнив несложные вычисления, мы находим: k = 9×10 9 H*м 2 / Кл 2 . В метрической системе СГС k =1.
На основании экспериментов было установлено, что кулоновские силы, как и принцип суперпозиции электрических полей, в законах электростатики описывают уравнения Максвелла.
Если между собой взаимодействуют несколько заряженных тел, то в замкнутой системе результирующая сила этого взаимодействия равняется векторной сумме всех заряженных тел. В такой системе электрические заряды не исчезают – они передаются от тела к телу.
Закон Кулона в диэлектриках
Выше было упомянуто, что формула, определяющая зависимость силы от величины точечных зарядов и расстояния между ними, справедлива для вакуума. В среде сила взаимодействия уменьшается благодаря явлению поляризации. В однородной изотопной среде уменьшение силы пропорционально определённой величине, характерной для данной среды. Эту величину называют диэлектрической постоянной. Другое название – диэлектрическая проницаемость. Обозначают её символом ε. В этом случае k = 1/4πεε0.
Диэлектрическая постоянная воздуха очень близка к 1. Поэтому закон Кулона в воздушном пространстве проявляется так же как в вакууме.
Интересен тот факт, что диэлектрики могут накапливать электрические заряды, которые образуют электрическое поле. Проводники лишены такого свойства, так как заряды, попадающие на проводник, практически сразу нейтрализуются. Для поддержания электрического поля в проводнике необходимо непрерывно подавать на него заряженные частицы, образуя замкнутую цепь.
Применение на практике
Вся современная электротехника построена на принципах взаимодействия кулоновских сил. Благодаря открытию Клоном этого фундаментального закона развилась целая наука, изучающая электромагнитные взаимодействия. Понятие термина электрического поля также базируется на знаниях кулоновских сил. Доказано, что электрическое поле неразрывно связано с зарядами элементарных частиц.
Грозовые облака не что иное как скопление электрических зарядов. Они притягивают к себе индуцированные заряды земли, в результате чего появляется молния. Это открытие позволило создавать эффективные молниеотводы для защиты зданий и электротехнических сооружений.
На базе электростатики появилось много изобретений:
- конденсатор;
- различные диэлектрики;
- антистатические материалы для защиты чувствительных электронных деталей;
- защитная одежда для работников электронной промышленности и многое другое.
На законе Кулона базируется работа ускорителей заряженных частиц, в частности, функционирование Большого адронного коллайдера (см. Рис. 4).
Рис. 4. Большой адронный коллайдер
Ускорение заряженных частиц до околосветовых скоростей происходит под действием электромагнитного поля, создаваемого катушками, расположенными вдоль трассы. От столкновения распадаются элементарные частицы, следы которых фиксируются электронными приборами. На основании этих фотографий, применяя закон Кулона, учёные делают выводы о строении элементарных кирпичиков материи.
Печатать книгу
| Сайт: | Профильное обучение |
| Курс: | Физика. 10 класс |
| Книга: | § 17. Взаимодействие точечных зарядов. Закон Кулона |
| Напечатано:: | Гость |
| Дата: | Четверг, 25 Май 2023, 10:10 |
Оглавление
- Взаимодействие точечных зарядов. Закон Кулона
- Закон Кулона
- Взаимодействие системы точечных зарядов
- Диэлектрическая проницаемость вещества
- Примеры решения задач
- Упражнение 13
Электрически заряженные тела (частицы) взаимодействуют друг с другом. Но как определить силу, которой одно заряженное тело притягивает или отталкивает другое?
Вы уже встречались с физическими моделями при изучении механики (материальная точка) и молекулярной физики (идеальный газ). В электростатике при изучении взаимодействия электрически заряженных тел эффективной оказывается модель «точечный заряд».
Точечный заряд — заряд такого заряженного тела, размеры которого значительно меньше расстояния от этого тела до точки наблюдения и до других тел (т. е. размерами заряженного тела в условиях данной задачи можно пренебречь).
Вспомните, закон всемирного тяготения также сформулирован для точечных тел (материальных точек).
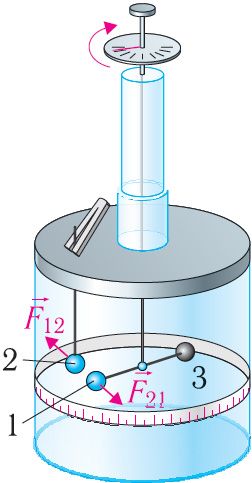
Закон Кулона. Кулон детально исследовал взаимодействие неподвижных точечных зарядов. Он на опыте изучил зависимость сил электрического взаимодействия тел от модулей зарядов этих тел и расстояния между ними.
В своих опытах Кулон использовал специальный прибор — крутильные весы (рис. 98). Крутильные весы представляют собой два стеклянных цилиндра, внутри которых на тонкой серебряной нити подвешено лёгкое непроводящее коромысло. На одном конце коромысла закреплён проводящий шар 1, а на другом — бумажный противовес 3. Шар 1 можно заряжать с помощью такого же проводящего шара 2. Он находится на изолирующем стержне, закреплённом на крышке нижнего цилиндра. При соприкосновении шара 1 с заряженным шаром 2 заряд распределяется между ними поровну, и шары отталкиваются.
Используя крутильные весы, Кулон получил зависимость модуля сил взаимодействия двух заряженных шаров от величин зарядов и от расстояния между ними. По углу закручивания нити, отсчитываемому по шкале прибора, можно определить силу взаимодействия заряженных шаров. Кулон установил, что модуль сил взаимодействия двух заряженных шаров обратно пропорционален квадрату расстояния между ними:
.
Для измерения зависимости модуля сил взаимодействия шаров от их зарядов учёный нашёл простой способ. Разряжая шар 2 прикосновением руки, а затем касаясь им уже заряженного шара 1, Кулон смог получить на нём заряды, модуль которых в 2, 4, 8 и т. д. раз меньше первоначального. Он выяснил, что при неизменном расстоянии модуль сил взаимодействия двух неподвижных небольших заряженных тел прямо пропорционален произведению модулей электрических зарядов каждого из них: .
Обобщив экспериментальные данные, Кулон сформулировал закон, получивший его имя.
Закон Кулона: модули сил взаимодействия двух неподвижных точечных заряженных тел в вакууме прямо пропорциональны произведению модулей зарядов этих тел, обратно пропорциональны квадрату расстояния между ними, а сами силы направлены вдоль прямой, соединяющей эти тела:
(17.1)
где k — коэффициент пропорциональности, зависящий от выбора единиц физических величин; |q1| и |q2| — модули точечных зарядов; r — расстояние между ними.
В СИ коэффициент пропорциональности
где — электрическая постоянная.
От теории к практике
Два маленьких положительно заряженных шарика закреплены на расстоянии r друг от друга. Как изменится модуль сил электростатического взаимодействия шариков, если: 1) уменьшить заряд каждого шарика в четыре раза; 2) увеличить расстояние между шариками в четыре раза; 3) увеличить заряд каждого шарика и расстояние между ними в два раза?
Как изменились бы силы электростатического взаимодействия шариков, если бы: 1) шарики были заряжены отрицательно; 2) один из шариков зарядить отрицательно, а другой положительно?
Интересно знать
Экспериментальные факты свидетельствуют о том, что воздействие неподвижного в данной инерциальной системе отсчёта точечного заряда на движущийся точечный заряд может быть описано законом Кулона с приемлемой точностью. Так, описание рассеяния α-частиц на ядрах атомов золота в опытах Резерфорда с помощью модели точечного заряда, на который действует кулоновская сила со стороны неподвижного ядра, согласуется с экспериментальными данными в пределах точности последних.
Два и более движущихся в данной инерциальной системе заряда не могут характеризоваться только кулоновским взаимодействием, так как каждый из них создаёт в окружающем пространстве магнитное поле, которое действует магнитной силой на остальные заряды, движущиеся в нём.
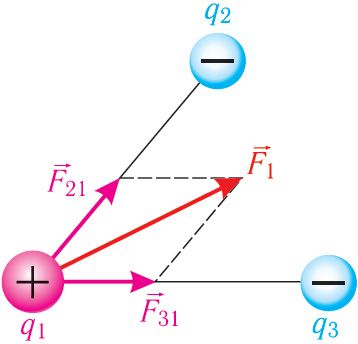
Взаимодействие системы точечных зарядов. Экспериментально установили, что силы взаимодействия двух точечных зарядов не изменяются при появлении третьего точечного заряда или любого числа точечных зарядов. В этом случае силы воздействия ,
, …,
каждого из зарядов q2, q3, …, qn на заряд q1 определяют по закону Кулона. Результирующая сила является векторной суммой сил, которыми каждый из этих зарядов в отдельности воздействует на заряд q1 (принцип суперпозиции).
Используя принцип суперпозиции и закон Кулона, можно описать электростатическое взаимодействие любой системы точечных зарядов. На рисунке 100 представлены три взаимодействующих между собой точечных электрических заряда: q1 > 0, q2 < 0, q3 < 0. Результирующей сил, действующих на заряд q1 со стороны зарядов q2 и q3, является сила , которая равна векторной сумме сил
и
:
. Силы
и
воздействия зарядов q2 и q3 на заряд q1 определяют по закону Кулона.
От теории к практике
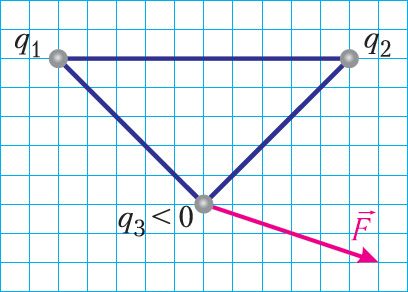
Точечные заряды q1, q2 и q3 закреплены в вершинах треугольника. Направление результирующей электростатической силы, действующей на отрицательный заряд q3 со стороны зарядов q1 и q2, представлено на рисунке 101. Каковы знаки зарядов q1 и q2? Во сколько раз отличаются модули зарядов q1 и q2?
Интересно знать
Понятие электрического заряда в некоторой степени сходно с понятием гравитационной массы. Электрический заряд определяет интенсивность электромагнитных взаимодействий, а масса — гравитационных. Закон Кулона, описывающий электростатическое взаимодействие, формально похож на закон всемирного тяготения Ньютона, определяющий силы гравитационного взаимодействия:
В обоих случаях модуль сил взаимодействия:
– обратно пропорционален квадрату расстояния между материальными точками;
– прямо пропорционален величинам, характеризующим те свойства тел (материальных точек), которые определяют взаимодействия, — массам в одном случае и электрическим зарядам — в другом.
Для измерения сил электрического отталкивания (Ш. Кулон, 1785 г.) и гравитационной постоянной (Г. Кавендиш, 1788 г.) учёные использовали похожие по устройству экспериментальные установки.
Однако между силами гравитационного и электростатического взаимодействий существует и важное различие. Ньютоновские силы тяготения — это всегда силы притяжения. кулоновские же силы взаимодействия зарядов могут быть как силами притяжения (между разноимёнными зарядами), так и силами отталкивания (между одноимёнными зарядами).
От теории к практике
Известно, что масса электрона mе = 9,1· 10–31 кг. Во сколько раз модуль сил электрического отталкивания между двумя электронами больше модуля сил их гравитационного притяжения?
Диэлектрическая проницаемость вещества. Из опытов следует, что взаимодействие электрически заряженных тел в воздухе практически не отличается от их взаимодействия в вакууме. Если заряженные тела находятся в воде, керосине, масле или какой-нибудь другой непроводящей среде, то модуль сил их взаимодействия оказывается меньше, чем в вакууме. Чтобы учесть влияние среды, ввели её специальную характеристику, называемую диэлектрической проницаемостью.
Диэлектрическая проницаемость вещества — физическая величина, показывающая, во сколько раз модуль сил электростатического взаимодействия зарядов в данной однородной среде меньше модуля сил взаимодействия этих же зарядов в вакууме:
(17.2)
где F0 и F — модули сил электростатического взаимодействия зарядов в вакууме и в однородной среде соответственно.
С учётом соотношения (17.2) закон Кулона можно записать следующим образом:
Диэлектрическая проницаемость вакуума равна 1. За 1 принимают и диэлектрическую проницаемость воздуха, поскольку её значение (при нормальном атмосферном давлении) 1,0006. Диэлектрические проницаемости других однородных сред всегда больше единицы. Например, у воды диэлектрическая проницаемость 81, у глицерина — 56, а у керосина — 2.
От теории к практике
Как и во сколько раз отличаются модули сил электростатического взаимодействия двух точечных зарядов, находящихся на одинаковом расстоянии друг от друга в воде, керосине и глицерине?
Интересно знать
Диэлектрическая проницаемость дистиллированной воды при температуре 25 °C равна 78,54, а при температуре 0 °C — 88. Обычно без указания температуры диэлектрическую проницаемость воды полагают равной 81.
1. К какому виду взаимодействий относят взаимодействие неподвижных электрических зарядов (заряженных тел)?
2. Заряды каких заряженных тел можно считать точечными?
3. Опишите эксперименты Кулона по исследованию взаимодействия электрических зарядов.
4. Сформулируйте закон Кулона. Каковы условия применимости закона Кулона?
5. Чему равен в СИ коэффициент k? Выразите наименование коэффициента пропорциональности k в законе Кулона в основных единицах СИ.
6. В чём суть принципа суперпозиции для электрического взаимодействия точечных зарядов?
7. Что называют диэлектрической проницаемостью среды?
Примеры решения задач
Пример 1. Два точечных заряда находятся в керосине на расстоянии r1 = 42 см. Определите, на каком расстоянии должны находиться эти заряды в глицерине, чтобы модуль сил их электростатического взаимодействия остался прежним. Диэлектрические проницаемости керосина ε1 = 2,0, глицерина ε2 = 56,2.
Дано:
r1 = 42 см
Fк1 = Fк2
ε1 = 2,0
ε2 = 56,2
r2 — ?
Решение: Поскольку Fк1 = Fк2, то, воспользовавшись законом Кулона, можно записать: .
Следовательно, .
Ответ: r2 = 7,9 см.
Пример 2. Точечные заряды q1 = 3,4 нКл и q2 = –5,6 нКл находятся в вакууме на расстоянии r = 36 см. Определите модуль и направление результирующей силы, действующей на заряд q3 = 3,2 нКл, помещённый в точку пространства, находящуюся на середине отрезка, соединяющего эти заряды.
Дано:
q1 = 3,4 нКл = 3,4 · 10–9 Кл
q2 = –5,6 нКл = –5,6 · 10–9 Кл
r = 36 см = 0,36 м
q3 = 3,2 нКл = 3,2 · 10–9 Кл
— ?
Решение: Изобразим на рисунке силы и
, действующие на точечный заряд q3 со стороны точечных зарядов q1 и q2 соответственно. Построив векторную сумму сил
и
, определим, что результирующая
этих сил направлена к заряду q2 (рис. 102).
Поскольку силы и
направлены одинаково, то модуль результирующей силы
.
Таким образом,
Ответ: Fp = 8,0 мкН; сила направлена к заряду q2.
Пример 3. Две бусинки, электрические заряды которых q1 = 40 нКл и q2 = 90 нКл, закреплены на непроводящем стержне на расстоянии r = 40 см друг от друга. Определите: а) где надо поместить третью бусинку, имеющую заряд q3, чтобы она оказалась в равновесии; б) каким должен быть заряд q3 третьей бусинки, чтобы результирующая сила электростатического взаимодействия каждой из трёх бусинок с остальными двумя равнялась нулю.
Дано:
q1 = 40 нКл = 4,0·10–8 Кл
q2 = 90 нКл = 9,0·10-8 Кл
r = 40 см = 0,40 м
х — ?
q3 — ?
Решение: а) Третья бусинка, имеющая заряд q3, будет находиться в равновесии, если её поместить в некоторую точку А между зарядами q1 и q2 на прямой, соединяющей эти заряды (рис. 102.1). Пусть заряд q3 < 0. Тогда со стороны зарядов q1 и q2 на заряд q3 будут действовать противоположно направленные кулоновские силы притяжения и
. Согласно второму закону Ньютона, эта бусинка будет покоиться, если модули сил F13 и F23 равны. Тогда, приняв расстояние от заряда q1 до точки А равным х, запишем:
. Так как k и q3 не равны нулю, то это выражение можно сократить:
. Извлечём из обеих частей равенства квадратный корень
. Отсюда:
Такое же значение х мы получим, если примем заряд q3 бусинки положительным (проверьте это самостоятельно).
б) Результирующая сила электростатического взаимодействия каждой из трёх бусинок с остальными двумя равна нулю, если, например, третья бусинка притягивает вторую силой, модуль которой равен модулю силы
, какой её отталкивает первая бусинка (рис. 102.2). При этом заряд третьей бусинки должен быть отрицательным, т. е. q3 < 0. Тогда
. Отсюда
.
Ответ: х = 16 см, расстояние до бусинки с зарядом q3 не зависит от значения и знака её заряда; если заряд бусинки q3 = ‒14 нКл, то результирующая сила электростатического взаимодействия каждой из трёх бусинок с остальными двумя равна нулю.
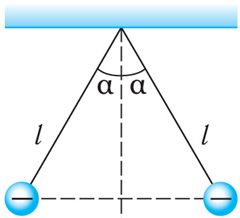
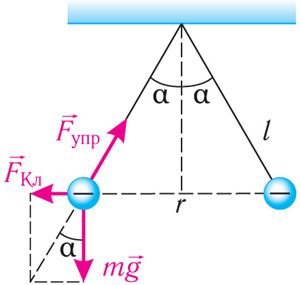
Пример 4. Два одинаковых маленьких проводящих шарика массой m = 20 мг каждый подвешены в воздухе на лёгких нерастяжимых нитях длиной l = 0,20 м, закреплённых в одной точке подвеса. Один из шариков отвели в сторону, сообщили ему заряд q < 0 и отпустили. После столкновения шарики разошлись так, что угол между нитями составил 2α = 60° (рис. 102.3). Определите заряд, который был сообщён первому шарику, а также количество избыточных электронов на каждом из шариков после их столкновения.
Дано:
m = 20 мг = 2,0·10–5 кг
l = 0,20 м
2α = 60°
q – ?
N – ?
Решение: Воспользуемся законом сохранения электрического заряда. При столкновении двух одинаковых проводящих шариков сообщённый одному из них заряд разделился поровну и на каждом шарике оказался избыточный отрицательный заряд . На каждый шарик действуют сила тяжести
сила электростатического взаимодействия
и сила упругости нити
(рис. 102.4). После столкновения шарики разошлись, и установилось равновесие. Векторная сумма сил, действующих на каждый шарик, стала равной нулю:
. Модуль силы электростатического взаимодействия
. Поскольку шарики разошлись симметрично относительно вертикали, проходящей через точку подвеса нитей, то
(рис. 102.4). Следовательно,
. Так как
, то
, откуда
. Примем
.
Количество избыточных электронов на каждом шарике .
Ответ: q = ‒45 нКл, N = 1,4 · 1011.
Упражнение 13
1. Определите модуль сил взаимодействия двух одинаковых неподвижных точечных зарядов q1 = q2 = 9,0 нКл, находящихся на расстоянии r = 0,30 м в вакууме. Во сколько раз уменьшится или увеличится модуль сил взаимодействия этих зарядов при помещении их в керосин, диэлектрическая проницаемость которого ε = 2,0?
2. Определите, во сколько раз следует увеличить расстояние между двумя неподвижными точечными зарядами, чтобы модуль сил взаимодействия остался прежним при увеличении численного значения одного из зарядов в α = 4 раза.
3. Два одинаковых маленьких проводящих шарика, заряды которых отличаются в два раза, находятся на расстоянии r = 50 см. Определите расстояние, на которое необходимо развести шарики после соприкосновения, чтобы модуль сил их взаимодействия остался прежним.
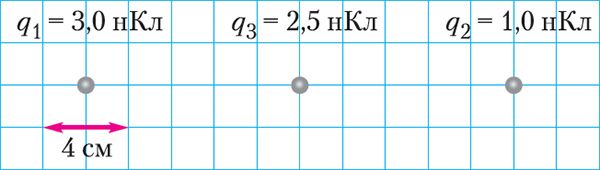
4. Точечные заряды q1 и q2 закреплены в вакууме (рис. 103). Определите модуль и направление результирующей силы, действующей на заряд q3, помещённый в точку, находящуюся на середине отрезка, соединяющего эти заряды.
5. Заряды двух одинаковых маленьких шариков массой m = 40 г каждый одинаковые. Расстояние между шариками существенно превышает их размеры. Определите модуль зарядов шариков, если кулоновская сила их отталкивания уравновешивает силу гравитационного притяжения этих шариков.
6. Небольшой шарик, заряд которого q1 = 20 нКл и масса m = 60 мг, подвешен в воздухе на шёлковой нити. После того как на вертикали, проходящей через центр шарика, на расстоянии r = 15 см ниже его поместили другой маленький шарик, заряженный отрицательно, модуль силы упругости нити увеличился в два раза. Определите заряд второго шарика.
7. Три первоначально закреплённых одинаковых точечных заряда q1 = q2 = q3 = q0 = 1,0 мкКл расположены в вершинах равностороннего треугольника. Определите, какой точечный заряд нужно поместить в центр треугольника, чтобы вся система находилась в равновесии после освобождения первоначально закреплённых зарядов.