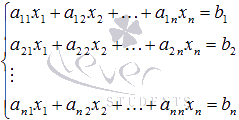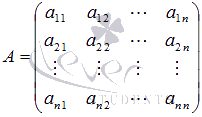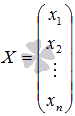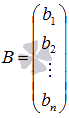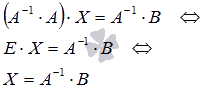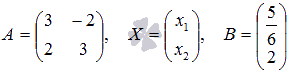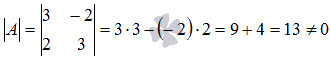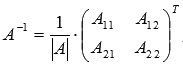Как найти решение системы матричным методом

Матричный метод решения систем линейных уравнений.

В
этой статье поговорим о матричном методе
решения систем линейных алгебраических
уравнений вида

,
которые в матричной форме записываются
как

,
где

—
основная матрица системы,

—
матрица-столбец неизвестных переменных,

—
матрица свободных членов.

Сначала
опишем суть матричного метода, остановимся
на условии применимости этого метода,
далее подробно разберем решения
нескольких примеров.

Сразу
оговоримся, что решение систем линейных
алгебраических уравнений матричным
методом и решение СЛАУ с помощью обратной
матрицы есть одно и то же. Поэтому
рекомендуем освежить в памяти теорию
раздела обратная
матрица: определение, свойства, методы
нахождения.

Приступим.

Пусть
для матрицы А
порядка n
на n
существует обратная матрица

.
Умножим обе части матричного уравнения

слева
на

(порядки
матриц A
⋅
X
и В
позволяют произвести такую операцию,
смотрите статью операции
над матрицами, свойства операций).
Имеем

.
Так как для операции умножения матриц
подходящих порядков характерно свойство
ассоциативности, то последнее равенство
можно переписать как

,
а по определению обратной матрицы

(E
– единичная матрица порядка n
на n),
поэтому

Таким
образом, решение
системы линейных алгебраических
уравнений по матричному методу
определяется равенством

.
Другими словами, решение СЛАУ находится
с помощью обратной матрицы

.

Мы
знаем, что квадратная матрица А
порядка n
на n
имеет обратную матрицу

только
тогда, когда ее определитель не равен
нулю. Следовательно, СИСТЕМУ n
ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ С n
НЕИЗВЕСТНЫМИ МОЖНО РЕШАТЬ МАТРИЧНЫМ
МЕТОДОМ ТОЛЬКО ТОГДА, КОГДА ОПРЕДЕЛИТЕЛЬ
ОСНОВНОЙ МАТРИЦЫ СИСТЕМЫ ОТЛИЧЕН ОТ
НУЛЯ.

Рассмотрим матричный
метод на примерах. В некоторых примерах
мы не будем подробно описывать процесс
вычисления определителей матриц, при
необходимости обращайтесь к статье
вычисление
определителя матрицы.

Пример.

С
помощью обратной матрицы найдите решение
системы линейных уравнений

.

Решение.

В
матричной форме исходная система
запишется как

,
где

.
Вычислим определитель основной матрицы
и убедимся, что он отличен от нуля. В
противном случае мы не сможем решить
систему матричным методом. Имеем

,
следовательно, для матрицы А
может быть найдена обратная матрица

.
Таким образом, если мы отыщем обратную
матрицу, то искомое решение СЛАУ определим
как

.
Итак, задача свелась к построению
обратной матрицы

.
Найдем ее.

Мы знаем, что для матрицы

обратная
матрица может быть найдена как

,
где

—
алгебраические дополнения элементов

.

В
нашем случае

Тогда

Выполним
проверку полученного решения

,
подставив его в матричную форму исходной
системы уравнений

.
Это равенство должно обратиться в
тождество, в противном случае где-то
была допущена ошибка.

Следовательно,
решение найдено верно.

Ответ:

или
в другой записи

.

Системы линейных уравнений: основные понятия

24 Июня 2011

Определение.
Система линейных уравнений — это
объединение из n линейных уравнений,
каждое из которых содержит k переменных.
Записывается это так:

Многие,
впервые сталкиваясь с высшей алгеброй,
ошибочно полагают, что число уравнений
обязательно должно совпадать с числом
переменных. В школьной алгебре так
обычно и бывает, однако для высшей
алгебры это, вообще говоря, неверно.

Определение.
Решение системы уравнений — это
последовательность чисел (k₁,
k₂, …, k_n),
которая является решением каждого
уравнения системы, т.е. при подстановке
в это уравнение вместо переменных x₁,
x₂, …, x_n
дает верное числовое равенство.

Соответственно,
решить систему уравнений — значит найти
множество всех ее решений или доказать,
что это множество пусто. Поскольку число
уравнений и число неизвестных может не
совпадать, возможны три случая:

1. Система
   несовместна, т.е. множество всех решений
   пусто. Достаточно редкий случай, который
   легко обнаруживается независимо от
   того, каким методом решать систему.

2. Система
   совместна и определена, т.е. имеет ровно
   одно решение. Классический вариант,
   хорошо известный еще со школьной скамьи.

3. Система
   совместна и не определена, т.е. имеет
   бесконечно много решений. Это самый
   жесткий вариант. Недостаточно указать,
   что «система имеет бесконечное множество
   решений» — надо описать, как устроено
   это множество.

Определение.
Переменная x_i
называется разрешенной, если она
входит только в одно уравнение системы,
причем с коэффициентом 1. Другими словами,
в остальных уравнениях коэффициент при
переменной x_i
должен быть равен нулю.

Если
в каждом уравнении выбрать по одной
разрешенной переменной, получим набор
разрешенных переменных для всей системы
уравнений. Сама система, записанная в
таком виде, тоже будет называться
разрешенной. Вообще говоря, одну и ту
же исходную систему можно свести к
разным разрешенным, однако сейчас нас
это не волнует. Вот примеры разрешенных
систем:

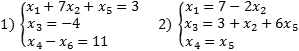
Обе
системы являются разрешенными относительно
переменных x₁,
x₃ и x₄.
Впрочем, с тем же успехом можно утверждать,
что вторая система — разрешенная
относительно x₁,
x₃ и x₅.
Достаточно переписать самое последнее
уравнение в виде x₅
= x₄.

Теперь
рассмотрим более общий случай. Пусть
всего у нас k переменных, из которых r
являются разрешенными. Тогда возможны
два случая:

1. Число
   разрешенных переменных r равно общему
   числу переменных k: r = k. Получаем систему
   из k уравнений, в которых r = k разрешенных
   переменных. Такая система является
   совместной и определенной, т.к. x₁
   = b₁, x₂
   = b₂, …,
   x_k = b_k;

2. Число
   разрешенных переменных r меньше общего
   числа переменных k: r < k. Остальные (k −
   r) переменных называются свободными —
   они могут принимать любые значения, из
   которых легко вычисляются разрешенные
   переменные.

Так,
в приведенных выше системах переменные
x₂, x₅,
x₆ (для
первой системы) и x₂,
x₅ (для
второй) являются свободными. Случай,
когда есть свободные переменные, лучше
сформулировать в виде теоремы:

Теорема.
Если в системе из n уравнений переменные
x₁, x₂,
…, x_r —
разрешенные, а x<sub>r
+ 1</sub>, x<sub>r
+ 2</sub>, …, x_k
— свободные, то:

1. Если
   задать значения свободным переменным
   (x<sub>r
   + 1</sub> = t<sub>r
   + 1</sub>, x<sub>r
   + 2</sub> = t<sub>r
   + 2</sub>, …, x_k
   = t_k), а
   затем найти значения x₁,
   x₂, …, x_r,
   получим одно из решений.

2. Если
   в двух решениях значения свободных
   переменных совпадают, то значения
   разрешенных переменных тоже совпадают,
   т.е. решения равны.

В
чем смысл этой теоремы? Чтобы получить
все решения разрешенной системы
уравнений, достаточно выделить свободные
переменные. Затем, присваивая свободным
переменным разные значения, будем
получать готовые решения. Вот и все —
таким образом можно получить все решения
системы. Других решений не существует.

Вывод:
разрешенная система уравнений всегда
совместна. Если число уравнений в
разрешенной системе равно числу
переменных, система будет определенной,
если меньше — неопределенной.

И
все бы хорошо, но возникает вопрос: как
из исходной системы уравнений получить
разрешенную? Для этого существует метод
Гаусса.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Уравнения вообще, линейные алгебраические уравнения и их системы, а также методы их решения занимают в математике, как теоретической, так и прикладной, особое место.

Это связано с тем обстоятельством, что подавляющее большинство физических, экономических, технических и даже педагогических задач могут быть описаны и решены с помощью разнообразных уравнений и их систем. В последнее время особую популярность среди исследователей, ученых и практиков приобрело математическое моделирование практически во всех предметных областях, что объясняется очевидными его преимуществами перед другими известными и апробированными методами исследования объектов различной природы, в частности, так называемых, сложных систем. Существует великое многообразие различных определений математической модели, данных учеными в разные времена, но на наш взгляд, самое удачное, это следующее утверждение. Математическая модель – это идея, выраженная уравнением. Таким образом, умение составлять и решать уравнения и их системы – неотъемлемая характеристика современного специалиста.

Для решения систем линейных алгебраических уравнений наиболее часто используются методы: Крамера, Жордана-Гаусса и матричный метод.   

Матричный метод решения — метод решения с помощью обратной матрицы систем линейных алгебраических уравнений с ненулевым определителем.

Если выписать коэффициенты при неизвестных величинах xi в матрицу A, неизвестные величины собрать в вектор столбец X, а свободные члены в вектор столбец B, то систему линейных алгебраических уравнений можно записать в виде следующего матричного уравнения A · X = B, которое имеет единственное решение только тогда, когда определитель матрицы A не будет равен нулю. При этом решение системы уравнений можно найти следующим способом X = A^-1 · B, где A^-1 — обратная матрица.

Матричный метод решения состоит в следующем.

Пусть дана система линейных уравнений с nнеизвестными:

Её можно переписать в матричной форме: AX = B, где A — основная матрица системы, B и X — столбцы свободных членов и решений системы соответственно:

Умножим это матричное уравнение слева на A^-1 — матрицу, обратную к матрице A:  A^-1 (AX) = A^-1 B

Так как A^-1A = E, получаем X = A^-1B. Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A. Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A: detA≠ 0.

Для однородной системы линейных уравнений, то есть когда вектор B = 0, действительно обратное правило: система AX = 0 имеет нетривиальное (то есть не нулевое) решение только если detA = 0. Такая связь между решениями однородных и неоднородных систем линейных уравнений носит название альтернативы Фредгольма.

Пример решения неоднородной системы линейных алгебраических уравнений.

Убедимся в том, что определитель матрицы, составленный из коэффициентов при неизвестных системы линейных алгебраических уравнений не равен нулю.

Следующим шагом будет вычисление алгебраических дополнений для элементов матрицы, состоящей из коэффициентов при неизвестных. Они  понадобятся для нахождения обратной матрицы.

Теперь найдём союзную матрицу и транспонируем  её, потом подставим в формулу для нахождения обратной матрицы.

Подставляя переменные в формулу, получаем:

Найдем неизвестные. Для этого перемножим обратную матрицу  и столбец свободных членов.

Итак, x=2; y=1; z=4.

Если у Вас есть вопросы или Вам нужна помощь в решении линейных уравнений или систем, записывайтесь на мои занятия. Буду рад Вам помочь.  

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Остались вопросы?

Задайте свой вопрос и получите ответ от профессионального преподавателя.

Матричный способ решения систем линейных уравнений

Рассмотрим систему линейных уравнений следующего вида:

$left{begin{array}{c} {a_{11} x_{1} +a_{12} x_{2} +…+a_{1n} x_{n} =b_{1} } \ {a_{21} x_{1} +a_{22} x_{2} +…+a_{2n} x_{n} =b_{2} } \ {…} \ {a_{n1} x_{1} +a_{n2} x_{2} +…+a_{nn} x_{n} =b_{n} } end{array}right. .$

Числа $a_{ij} (i=1..n,j=1..n)$ — коэффициенты системы, числа $b_{i} (i=1..n)$ — свободные члены.

Каждой СЛАУ можно поставить в соответствие несколько матриц и записать систему в так называемом матричном виде.

Столбец свободных членов образует вектор-столбец, который, как правило, обозначается буквой $B$ и называется матрицей свободных членов.

Неизвестные переменные образуют вектор-столбец, который, как правило, обозначается буквой $X$ и называется матрицей неизвестных.

Описанные выше матрицы имеют вид:

$A=left(begin{array}{cccc} {a_{11} } & {a_{12} } & {…} & {a_{1n} } \ {a_{21} } & {a_{22} } & {…} & {a_{2n} } \ {…} & {…} & {…} & {…} \ {a_{n1} } & {a_{n2} } & {…} & {a_{nn} } end{array}right),B=left(begin{array}{c} {b_{1} } \ {b_{2} } \ {…} \ {b_{n} } end{array}right),X=left(begin{array}{c} {x_{1} } \ {x_{2} } \ {…} \ {x_{n} } end{array}right).$

Используя матрицы, СЛАУ можно переписать в виде $Acdot X=B$. Такую запись часто называют матричным уравнением.

Вообще говоря, в матричном виде записать можно любую СЛАУ.

Примеры решения системы с помощью обратной матрицы

Если матрица системы имеет определитель, не равный нулю, то данная система имеет единственное решение, которое можно найти матричным способом.

Если матрица системы имеет определитель, равный нулю, то данную систему нельзя решить матричным способом.

Решение систем линейных алгебраических уравнений с помощью обратной матрицы.

Решение систем линейных алгебраических уравнений (СЛАУ) с помощью обратной матрицы (иногда этот способ именуют ещё матричным методом или методом обратной матрицы) требует предварительного ознакомления с таким понятием как матричная форма записи СЛАУ. Метод обратной матрицы предназначен для решения тех систем линейных алгебраических уравнений, у которых определитель матрицы системы отличен от нуля. Естественно, при этом подразумевается, что матрица системы квадратна (понятие определителя существует только для квадратных матриц). Суть метода обратной матрицы можно выразить в трёх пунктах:

1. Записать три матрицы: матрицу системы $A$, матрицу неизвестных $X$, матрицу свободных членов $B$.
2. Найти обратную матрицу $A^{-1}$.
3. Используя равенство $X=A^{-1}cdot B$ получить решение заданной СЛАУ.

Почему $X=A^{-1}cdot B$? показатьскрыть

Перед переходом к чтению примеров рекомендую ознакомиться с методами вычисления обратных матриц, изложенными здесь.

Пример №1

Решить СЛАУ $
left { begin{aligned}
& -5x_1+7x_2=29;\
& 9x_1+8x_2=-11.

end{aligned} right.$ с помощью обратной матрицы.

Решение

Запишем матрицу системы $A$, матрицу свободных членов $B$ и матрицу неизвестных $X$.

$$
A=left(begin{array} {cc} -5 & 7\ 9 & 8 end{array}right);;
B=left(begin{array} {c} 29\ -11 end{array}right);;
X=left(begin{array} {c} x_1\ x_2 end{array}right).
$$

Найдём обратную матрицу к матрице системы, т.е. вычислим $A^{-1}$. В примере №2 на странице, посвящённой нахождению обратных матриц, обратная матрица была уже найдена. Воспользуемся готовым результатом и запишем $A^{-1}$:

$$
A^{-1}=-frac{1}{103}cdotleft(begin{array}{cc} 8 & -7\ -9 & -5end{array}right).
$$

Теперь подставим все три матрицы ($X$, $A^{-1}$, $B$) в равенство $X=A^{-1}cdot B$. Затем выполним умножение матриц в правой части данного равенства.

$$
left(begin{array} {c} x_1\ x_2 end{array}right)=
-frac{1}{103}cdotleft(begin{array}{cc} 8 & -7\ -9 & -5end{array}right)cdot
left(begin{array} {c} 29\ -11 end{array}right)=\
=-frac{1}{103}cdot left(begin{array} {c} 8cdot 29+(-7)cdot (-11)\ -9cdot 29+(-5)cdot (-11) end{array}right)=
-frac{1}{103}cdot left(begin{array} {c} 309\ -206 end{array}right)=left(begin{array} {c} -3\ 2end{array}right).
$$

Итак, мы получили равенство $left(begin{array} {c} x_1\ x_2 end{array}right)=left(begin{array} {c} -3\ 2end{array}right)$. Из этого равенства имеем: $x_1=-3$, $x_2=2$.

Ответ: $x_1=-3$, $x_2=2$.

Пример №2

Решить СЛАУ $
left{begin{aligned}
& x_1+7x_2+3x_3=-1;\
& -4x_1+9x_2+4x_3=0;\
& 3x_2+2x_3=6.
end{aligned}right.$ методом обратной матрицы.

Решение

Запишем матрицу системы $A$, матрицу свободных членов $B$ и матрицу неизвестных $X$.

$$
A=left(begin{array} {ccc} 1 & 7 & 3\ -4 & 9 & 4 \0 & 3 & 2end{array}right);;
B=left(begin{array} {c} -1\0\6end{array}right);;
X=left(begin{array} {c} x_1\ x_2 \ x_3 end{array}right).
$$

Теперь настал черёд найти обратную матрицу к матрице системы, т.е. найти $A^{-1}$. В примере №3 на странице, посвящённой нахождению обратных матриц, обратная матрица была уже найдена. Воспользуемся готовым результатом и запишем $A^{-1}$:

$$
A^{-1}=frac{1}{26}cdot left( begin{array} {ccc} 6 & -5 & 1 \ 8 & 2 & -16 \ -12 & -3 & 37end{array} right).
$$

Теперь подставим все три матрицы ($X$, $A^{-1}$, $B$) в равенство $X=A^{-1}cdot B$, после чего выполним умножение матриц в правой части данного равенства.

$$
left(begin{array} {c} x_1\ x_2 \ x_3 end{array}right)=
frac{1}{26}cdot left( begin{array} {ccc} 6 & -5 & 1 \ 8 & 2 & -16 \ -12 & -3 & 37end{array} right)cdot
left(begin{array} {c} -1\0\6end{array}right)=\
=frac{1}{26}cdot left(begin{array} {c} 6cdot(-1)+(-5)cdot 0+1cdot 6 \ 8cdot (-1)+2cdot 0+(-16)cdot 6 \ -12cdot (-1)+(-3)cdot 0+37cdot 6 end{array}right)=frac{1}{26}cdot left(begin{array} {c} 0\-104\234end{array}right)=left(begin{array} {c} 0\-4\9end{array}right)
$$

Итак, мы получили равенство $left(begin{array} {c} x_1\ x_2 \ x_3 end{array}right)=left(begin{array} {c} 0\-4\9end{array}right)$. Из этого равенства имеем: $x_1=0$, $x_2=-4$, $x_3=9$.

Ответ: $x_1=0$, $x_2=-4$, $x_3=9$.

Естественно, что решение систем линейных уравнений с помощью обратной матрицы без применения специальных программ вроде Mathcad возможно лишь при сравнительно небольшом количестве переменных. Если СЛАУ содержит четыре и более переменных, то гораздо удобнее в таком случае применить метод Гаусса или метод Гаусса-Жордана.