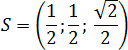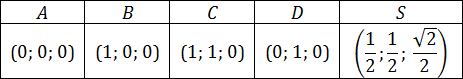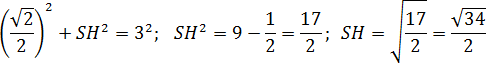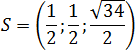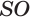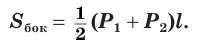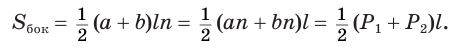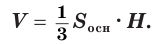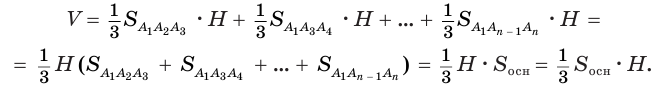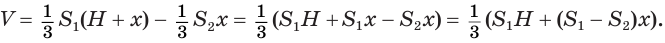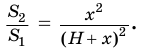9 марта 2012
Решая задачу C2 методом координат, многие ученики сталкиваются с одной и той же проблемой. Они не могут рассчитать координаты точек, входящих в формулу скалярного произведения. Наибольшие трудности вызывают пирамиды. И если точки основания считаются более-менее нормально, то вершины — настоящий ад.
Сегодня мы займемся правильной четырехугольной пирамидой. Есть еще треугольная пирамида (она же — тетраэдр). Это более сложная конструкция, поэтому ей будет посвящен отдельный урок.
Для начала вспомним определение:
Правильная пирамида — это такая пирамида, у которой:
- В основании лежит правильный многоугольник: треугольник, квадрат и т.д.;
- Высота, проведенная к основанию, проходит через его центр.
В частности, основанием четырехугольной пирамиды является квадрат. Прямо как у Хеопса, только чуть поменьше.
Ниже приведены расчеты для пирамиды, у которой все ребра равны 1. Если в вашей задаче это не так, выкладки не меняются — просто числа будут другими.
Вершины четырехугольной пирамиды
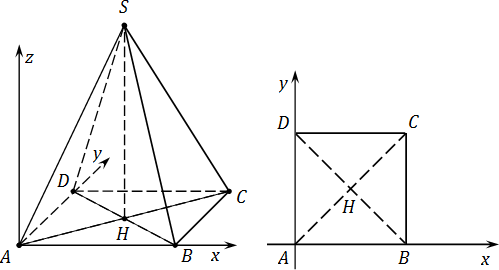
Итак, пусть дана правильная четырехугольная пирамида SABCD, где S — вершина, основание ABCD — квадрат. Все ребра равны 1. Требуется ввести систему координат и найти координаты всех точек. Имеем:
Вводим систему координат с началом в точке A:
- Ось OX направлена параллельно ребру AB;
- Ось OY — параллельно AD. Поскольку ABCD — квадрат, AB ⊥ AD;
- Наконец, ось OZ направим вверх, перпендикулярно плоскости ABCD.
Теперь считаем координаты. Дополнительное построение: SH — высота, проведенная к основанию. Для удобства вынесем основание пирамиды на отдельный рисунок. Поскольку точки A, B, C и D лежат в плоскости OXY, их координата z = 0. Имеем:
- A = (0; 0; 0) — совпадает с началом координат;
- B = (1; 0; 0) — шаг на 1 по оси OX от начала координат;
- C = (1; 1; 0) — шаг на 1 по оси OX и на 1 по оси OY;
- D = (0; 1; 0) — шаг только по оси OY.
- H = (0,5; 0,5; 0) — центр квадрата, середина отрезка AC.
Осталось найти координаты точки S. Заметим, что координаты x и y точек S и H совпадают, поскольку они лежат на прямой, параллельной оси OZ. Осталось найти координату z для точки S.
Рассмотрим треугольники ASH и ABH:
- AS = AB = 1 по условию;
- Угол AHS = AHB = 90°, поскольку SH — высота, а AH ⊥ HB как диагонали квадрата;
- Сторона AH — общая.
Следовательно, прямоугольные треугольники ASH и ABH равны по одному катету и гипотенузе. Значит, SH = BH = 0,5 · BD. Но BD — диагональ квадрата со стороной 1. Поэтому имеем:
Итого координаты точки S:
В заключение, выпишем координаты всех вершин правильной прямоугольной пирамиды:
Что делать, когда ребра разные
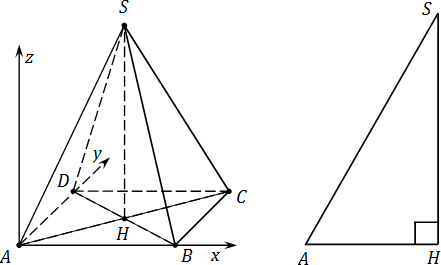
А что, если боковые ребра пирамиды не равны ребрам основания? В этом случае рассмотрим треугольник AHS:
Треугольник AHS — прямоугольный, причем гипотенуза AS — это одновременно и боковое ребро исходной пирамиды SABCD. Катет AH легко считается: AH = 0,5 · AC. Оставшийся катет SH найдем по теореме Пифагора. Это и будет координата z для точки S.
Задача. Дана правильная четырехугольная пирамида SABCD, в основании которой лежит квадрат со стороной 1. Боковое ребро BS = 3. Найдите координаты точки S.
Координаты x и y этой точки мы уже знаем: x = y = 0,5. Это следует из двух фактов:
- Проекция точки S на плоскость OXY — это точка H;
- Одновременно точка H — центр квадрата ABCD, все стороны которого равны 1.
Осталось найти координату точки S. Рассмотрим треугольник AHS. Он прямоугольный, причем гипотенуза AS = BS = 3, катет AH — половина диагонали. Для дальнейших вычислений нам потребуется его длина:
Теорема Пифагора для треугольника AHS: AH 2 + SH 2 = AS2. Имеем:
Итак, координаты точки S:
Смотрите также:
- Четырехугольная пирамида: как найти координаты вершин
- Введение системы координат
- Сложные выражения с дробями. Порядок действий
- Как решать задачи B15 без производных
- Как решать простейшие логарифмические уравнения
- Задача B4: вклад в банке и проценты
Сторона основания пирамиды является стороной правильного многоугольника, исходя из этого, можно найти все параметры пирамиды, связанные с основанием, воспользовавшись формулами для правильных многоугольников.
P=n(a+b)
S=(na^2)/(4 tan〖(180°)/n〗 )
Чтобы найти радиус окружности, вписанной в основание правильной пирамиды, нужно разделить сторону основания на два тангенса из 180 градусов, деленных на количество сторон в основании. (рис.34.1)
r=a/(2 tan〖(180°)/n〗 )
Радиус окружности, описанной вокруг основания правильной пирамиды, равен отношению стороны основания к двум синусам того же угла. (рис.34.2)
R=a/(2 sin〖(180°)/n〗 )
Угол γ между сторонами правильного многоугольника, заложенного в основание пирамиды, легко найти, умножив 180 градусов на количество сторон многоугольника без двух, и деленное на полное количество сторон. (рис.34.3)
γ=180°(n-2)/n
Зная боковое ребро в совокупности со стороной основания, можно вычислить высоту пирамиды и ее апофему из прямоугольных треугольников, которые они образуют. (рис.34.5, 35.1)
h=√(b^2-R^2 )=√(b^2-(a/(2 sin〖(180°)/n〗 ))^2 )
l=√(b^2-a^2/4)
Косинус угла между боковым ребром и основанием будет равен отношению радиуса окружности, описанной вокруг основания, к боковому ребру пирамиды, а косинус угла между апофемой и основанием – отношению радиуса вписанной в основание окружности к апофеме. (рис.34.4,34.5)
cosα=R/b=a/(2b sin〖(180°)/n〗 )
cosβ=r/l=a/(2 tan〖(180°)/n〗 √(b^2-a^2/4))
Площадь боковой поверхности пирамиды складывается из площадей треугольников, являющихся ее гранями, каждая из которых равна половине произведения апофемы на сторону основания, а площадь полной поверхности представляет собой сумму площади боковой поверхности и площади основания.
S_(б.п.)=lan/2=(√(b^2-a^2/4) an)/2
S_(п.п.)=an(l/2+a/(4 tan〖(180°)/n〗 ))=an(√(b^2-a^2/4)/2+a/(4 tan〖(180°)/n〗 ))
Чтобы найти объем пирамиды, необходимо вычислить треть от произведения ее высоты на площадь основания, последовательно подставив выражения для площади и высоты в формулу.
V=1/3 S_(осн.) h=(na^2 √(b^2-(a/(2 sin〖(180°)/n〗 ))^2 ))/(12 tan〖(180°)/n〗 )
Радиус сферы, которая может быть вписана в пирамиду, равен трем объемам, деленным на площадь полной поверхности пирамиды, а радиус сферы, описанной вокруг пирамиды – квадрату бокового ребра, деленному на две высоты. (рис.34.6,34.7)
r_1=3V/S_(п.п.) =(a√(b^2-(a/(2 sin〖(180°)/n〗 ))^2 ))/(tan〖(180°)/n〗 (2√(b^2-a^2/4)+a/tan〖(180°)/n〗 ) )
R_1=b^2/2h=b^2/(2√(b^2-(a/(2 sin〖(180°)/n〗 ))^2 ))
Вы уже знакомы с пирамидой, т. е. многогранником, одна грань которого является многоугольником, а остальные грани-треугольники имеют общую вершину.
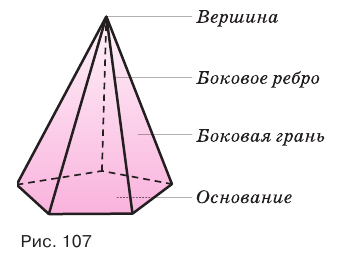
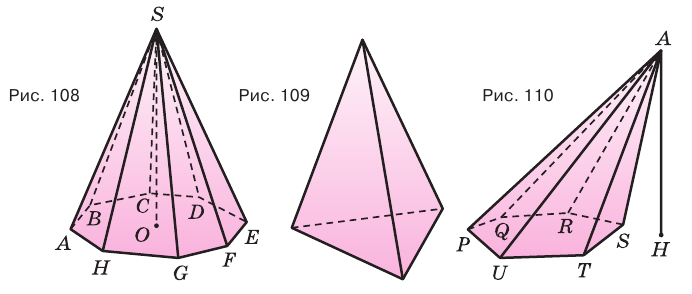
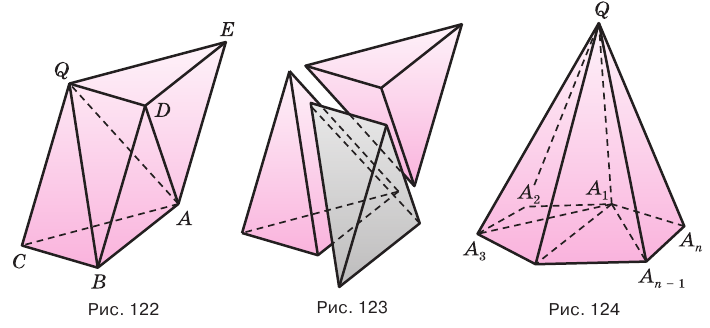
Треугольные грани пирамиды, имеющие общую вершину, называют боковыми гранями, а эту общую вершину — вершиной пирамиды. Ребра боковых граней, сходящиеся в вершине пирамиды, называют боковыми ребрами пирамиды. Многоугольник, которому не принадлежит вершина пирамиды, называют основанием пирамиды (рис. 107).
Пирамиды разделяют на треугольные, четырехугольные, пятиугольные и т. д. в зависимости от количества сторон их оснований. Пирамида, изображенная на рисунке 107, — пятиугольная, а на рисунке 108, — восьмиугольная. Треугольную пирамиду называют еще тетраэдром. У тетраэдра все грани являются треугольниками (рис. 109).
Перпендикуляр, проведенный из вершины пирамиды к плоскости ее основания, называется высотой пирамиды. На рисунке 108 показана высота
Плоскость, проходящая через два боковых ребра пирамиды, не принадлежащие одной грани, называется диагональной плоскостью, а сечение пирамиды диагональной плоскостью — диагональным сечением. На рисунке 111 показано диагональное сечение шестиугольной пирамиды.
Пирамида, основанием которой является правильный многоугольник, а основание ее высоты совпадает с центром этого многоугольника, называется правильной пирамидой (рис. 112).
Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой пирамиды.
Отметим, что в правильной пирамиде:
- боковые ребра равны;
- боковые грани равны;
- апофемы, равны;
- двугранные углы при основании равны;
- двугранные углы при боковых ребрах равны;
- каждая точка высоты равноудалена от вершин основания;
- каждая точка высоты равноудалена от ребер основания;
- каждая точка высоты равноудалена от боковых граней.
Отметим, что если в пирамиде равны все:
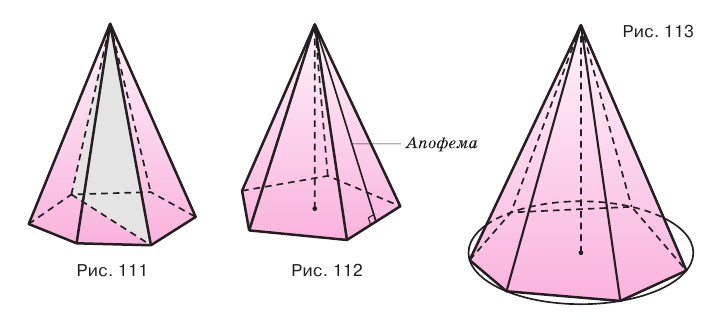
- боковые ребра, то около ее основания можно описать окружность, и центр этой окружности совпадает с основанием высоты пирамиды (рис. 113);
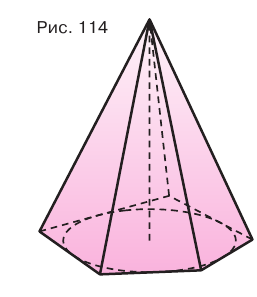
- двугранные углы при основании, то в это основание можно вписать окружность, и центр этой окружности совпадает с основанием высоты пирамиды (рис. 114).
Боковые грани составляют боковую поверхность пирамиды, а боковые грани вместе с основанием — полную поверхность пирамиды.
Вы знаете, что боковая поверхность правильной пирамиды равна произведению полупериметра ее основания и апофемы.
Теорема 1.
Если пирамиду пересечь плоскостью, параллельной основанию, то:
- а) боковые ребра и высота разделяются на пропорциональные части;
- б) в сечении получается многоугольник, подобный основанию;
- в) площади сечения и основания относятся как квадраты их расстояний от вершины пирамиды.
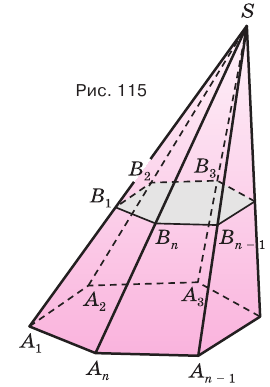
Используя рисунок 115, докажите эту теорему самостоятельно.
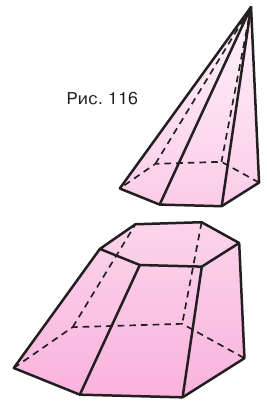
Секущая плоскость, параллельная основанию пирамиды, разделяет ее на две части (рис. 116). Одна из этих частей также является пирамидой, а другая — многогранником, который называется усеченной пирамидой.
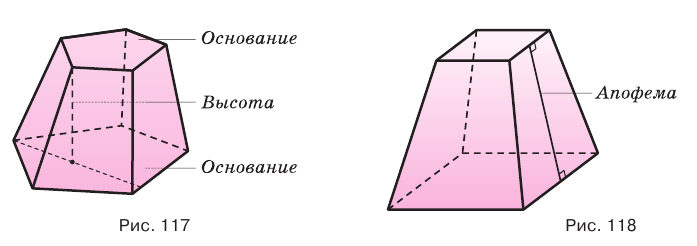
Параллельные грани усеченной пирамиды называются ее основаниями (рис. 117). Основания усеченной пирамиды — подобные многоугольники, стороны которых попарно параллельны, поэтому ее боковые грани являются трапециями.
Высотой усеченной пирамиды называется перпендикуляр, проведенный из какой-либо точки одного основания пирамиды к плоскости другого основания.
Усеченная пирамида называется правильной, если она является частью правильной пирамиды. Высота боковой грани правильной усеченной пирамиды называется апофемой усеченной пирамиды. На рисунке 118 показана четырехугольная правильная усеченная пирамида и одна из ее апофем.
Теорема 2.
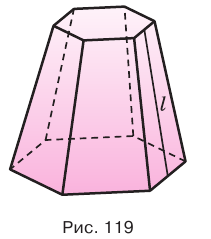
Боковая поверхность правильной усеченной пирамиды равна произведению полусуммы периметров ее оснований и апофемы:
Доказательство:
Пусть есть правильная 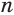
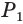
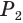
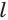
Боковая поверхность данной пирамиды состоит из 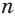
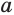
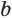
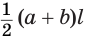
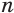
Теперь установим формулу для вычисления объема пирамиды.
Тела, имеющие равные объемы, называются равновеликими.
Теорема 3.
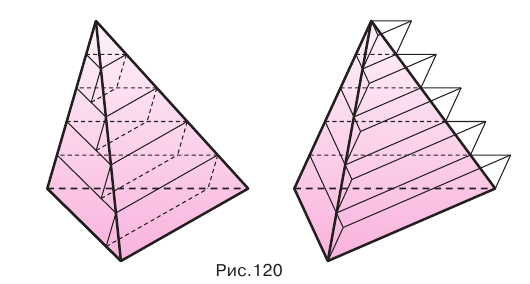
Треугольные пирамиды с равновеликими основаниями и равными высотами равновелики.
Доказательство:
Пусть есть две треугольные пирамиды с равновеликими основаниями и равными высотами (рис. 120). Разделим высоты одной и другой пирамид на 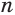
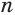
Пусть 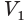
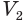


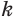
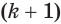


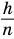
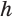
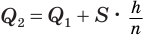
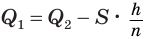
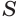
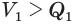
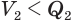
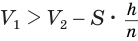
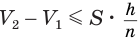
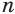
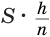
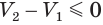
Такие же рассуждения можно провести, если первую и вторую пирамиды поменять ролями. В результате получим неравенство
Из неравенств (1) и (2) следует, что 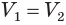
Теорема 4.
Объем пирамиды равен третьей доле произведения площади ее основания и высоты:
Доказательство:
Пусть есть треугольная пирамида 

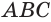
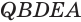
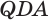


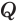
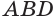
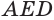




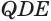

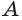
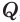





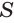

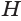



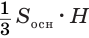
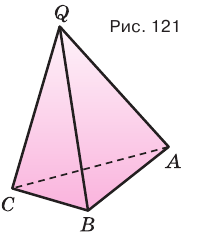
Пусть теперь есть произвольная пирамида 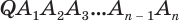
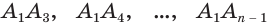
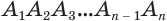
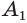
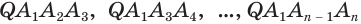

Пример:
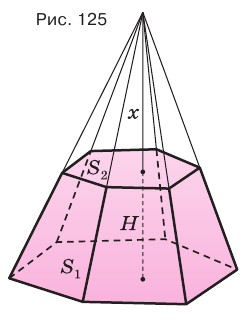
Найдем объем усеченной пирамиды, нижнее и верхнее основания которой имеют площади 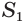
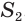

Для этого достроим данную усеченную пирамиду до полной. Пусть высота дополнительной пирамиды равна 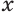
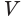
Чтобы найти высоту 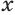
Решим это уравнение, учитывая, что 

Таким образом, объем 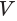
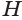


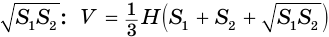
- Конус в геометрии
- Сфера в геометрии
- Шар в геометрии
- Правильные многогранники в геометрии
- Возникновение геометрии
- Призма в геометрии
- Цилиндр в геометрии
- Стереометрия — формулы, определение и вычисление
Пирамида – это объемная многогранная геометрическая фигура, состоящая из основания и треугольных
граней, собирающихся в одной точке. У нее есть: вершина, ребра (боковые и основные), боковые грани,
основание, высота и апофема – прямая, соединяющая вершину с границей вписанной в основание
окружности. Правильная пирамида –та, у которой все боковые ребра равны и находятся под одним углом к
основанию, а вершина проецируется на центр окружности, описанной вокруг основания. Тетраэдр –
частный случай правильной пирамиды, в которой боковые ребра равны основным и между собой.
Боковые ребра правильной пирамиды – выходящие из ее вершины, общие для боковых граней стороны. Длина
бокового ребра обозначается латинской буквой «b». Это одно из базовых значений, через которое можно
найти остальные элементы пирамиды. Во многих математических задачах требуется вычислить его или
подставить в формулы.
- Боковое ребро правильной треугольной пирамиды через высоту
и ребро основания - Боковое ребро правильной треугольной пирамиды через высоту
и радиус описанной окружности вокруг правильной треугольной пирамиды - Ребро основания правильной треугольной пирамиды через обьём
и высоту
Ребро основания правильной треугольной пирамиды через объём и высоту
Та часть пространства, которую занимает правильная треугольная пирамида называется ее объемом.
Является физической величиной. Его можно найти через, например, через высоту и сторону основания.
Если нам известен объем и высота правильной треугольной пирамиды, то не составит особого труда найти
ребро основания. Для этого используется формула:
a = √((V * 4 * √3) / H)
где V — объём, H — высота.
Цифр после
запятой:
Результат в:
Пример. Рассмотрим конкретную задачу. Необходимо найти ребро основания, зная что
высота H равна 56 см, a объем 268 см³, подставив все в формулу получим следующий результат: a = √((V * 4 * √3) / H) = √((268 * 4 * √3) / 56) = 5,76 см. Боковое
ребро (b) = 5,76 см.
Боковое ребро правильной треугольной пирамиды через высоту и ребро основания
Боковое ребро правильной пирамиды можно найти по теореме Пифагора, поскольку высота, опущенная в
основание пирамиды, опускается в центр вписанной и описанной окружности для данного многоугольника.
Таким образом формула для нахождения бокового ребра правильной треугольной пирамиды через высоту и
ребро основания будет следующей:
b = √(H² + (a / 2 sin (60º)²))
где H — высота, a — ребро основания.
Цифр после
запятой:
Результат в:
Пример. Рассмотрим конкретные данные. Пусть высота H равна 44 мм, a ребро основания
a равно 63 мм, подставив все в формулу получим следующий результат: b = √(H² + (a / 2 sin (60º)²)) = √(44² + (63 / 2 sin (60º)²)) = 57,09 мм.
Боковое ребро (b) = 57.08765 мм.
Боковое ребро правильной треугольной пирамиды через высоту и радиус описанной окружности вокруг
правильной треугольной пирамиды
Если пирамида вписана в окружность, то ее называют описанной вокруг пирамиды. Около пирамиды можно
описать сферу тогда и только тогда, когда около основания пирамиды можно описать
окружность. Основание перпендикуляра, опущенного из вершины такой пирамиды на плоскость ее
основания, является центром описанной около основания окружности. Если нам известна высота и радиус
этой описанной окружности, то мы сможем найти боковое ребро. Формула подходит только для правильной
треугольной пирамиды:
b = √(H² + R²)
где H — высота правильной треугольной пирамиды, R — радиус описанной вокруг
окружности.
Цифр после
запятой:
Результат в:
Пример. Рассмотрим конкретные данные. Пусть высота H равна 73 мм, a радиус описанной
вокруг окружности 114 мм, подставив все в формулу получим следующий результат: b = √(H² + R²) = √(73² + 114²) = 135 мм. Боковое
ребро (b) = 135 мм.
Почти все формулы пирамиды основываются на теореме Пифагора. Таким образом, можно вывести боковое
ребро правильной треугольной пирамиды через высоту и радиус описанной окружности, опираясь на
прямоугольный треугольник, гипотенуза которого является искомой величиной. По одному из основных
свойств правильной пирамиды, ее высота соединяет вершину с центрами окружностей, вписанных и
описанных вокруг пирамиды. Так внутри формируются 2 треугольника с углом 90°. Один состоит из
высоты, бокового ребра и соединяет их с радиусом описанной окружности, другой составляет высота и
апофема, соединённые с радиусом вписанной окружности.
Для нахожденияобъема пирамиды применим формулу: V=1/3*Sосн*Н;Найдем Sосн.=6/2*6/2=72;По условию построения, косинус угла между плоскостью( что является диагональ квадрата) и бокового ребра равен отношению 3/5;Откуда найдем диагональ квадрата( плоскость основания пирамиды);(6/2*6/2)*2=144;Извлекая корень из 144 получим длину диагонали 12;Затем найдем длину ребра пирамиды, учитывая что плоскость в которой лежит высота пирамиды является равнобедренным треугольником с основанием 12;Откуда высота делит основание на 2 равных части, т,е.12/2 =6; Найдем реброчерез косинус угла:6/х = 3/5 по условию;Откуда х=10;Найдем высоту Н равна =квадрат ребра10минус квадрат полуоснования:10^2 -6^2=100-36=64; то есть высота равна 8;Найдем объем V=1/3 Sосн.*Н=1/3*72*8 =24*8=192;ОТВЕТ : Vпир.=192
Оцени ответ