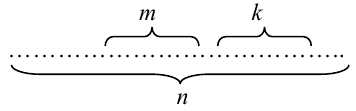
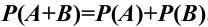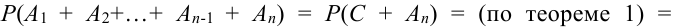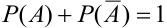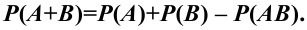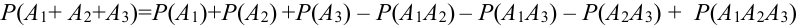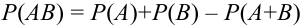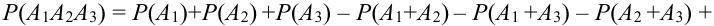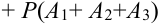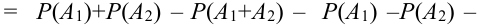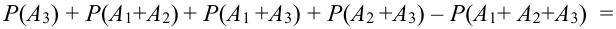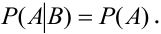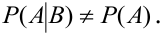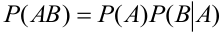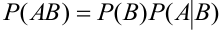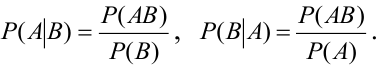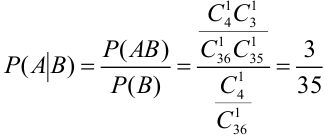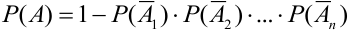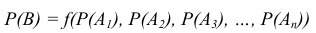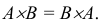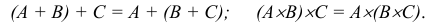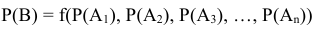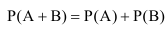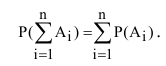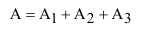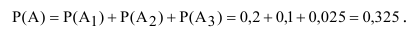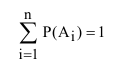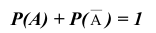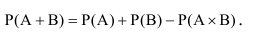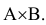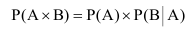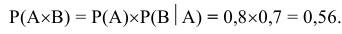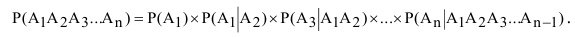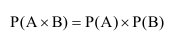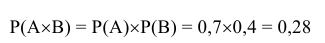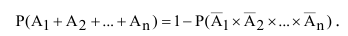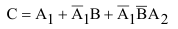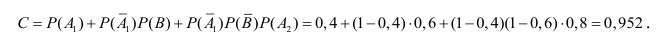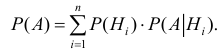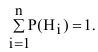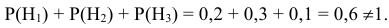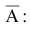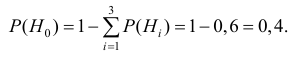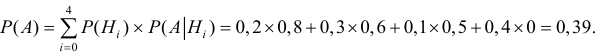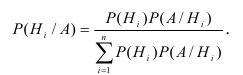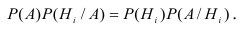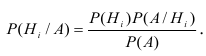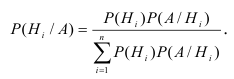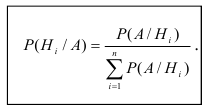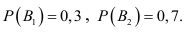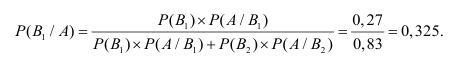Свойства вероятности
Свойство 1.Вероятность достоверного события равна
1.
Доказательство:
Так как событие достоверно, то
благоприятствующими ему будут все
элементарные события, т.е.m=nи
Р(А)
= m/n = n/m = 1.
Свойство
2. Вероятность
невозможного события равна нулю.
Доказательство:
Пусть А – невозможное событие, т.е. оно
никогда не происходит, а следовательно,
оно не происходит ни при каком элементарном
событии, т.е. m = 0. Тогда
Р(А)
= m/n = 0/n
= 0.
Свойство
3. Если А –
случайное событие, то 0
< P(A) <1.
Доказательство:
Ясно, что если А
– случайное событие, то при некоторых
элементарных событиях оно появляется,
а при остальных нет. Таким образом,
0 < m < n.
Разделим
это двойное неравенство на n
> 0.
Получаем
0/n
< m/n < n/n ,
0
< m/n < 1.
Отсюда
получаем
0
< Р(А) < 1.
Свойство
4. Если


Доказательство:
Если из n элементарных событий число
элементарных событий, благоприятствующих
событию А, равно m , то при других n – m,
элементарных событиях событие А не
появляется, т.е. появляется событие

Таким образом,
Сложение и вычитание вероятностей
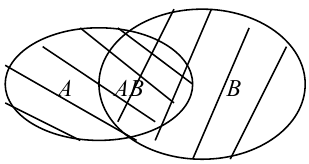
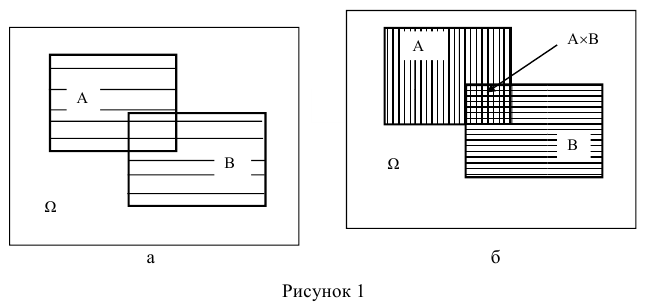
СуммойА + ВсобытийА и В в одном опыте
называется событие С, состоящее в
появления события А или события В, или
обоих событий одновременно.
ПроизведениемА х ВсобытийА и В называется
событие С, состоящее в том, что произойдут
события А и В.
Теорема сложения вероятностей
Вероятность
суммы событий А + В равна сумме вероятностей
этих событий без вероятности их
совместного появления:
Р(А + В) = Р(А) + Р(В) –
Р(А х В).
Если события
А и В несовместны, то Р(А х В) = 0 и,
следовательно, теорема сложения
вероятностей примет вид:
Р(А + В) = Р(А) + Р(В).
Вероятность
события В, вычисленная в предположениях,
что событие А уже наступало, называется
условной вероятностьюи
обозначаетсяРА(В).
Если А и В
независимы, то
РВ(А)
= Р(А),
РА(В)
= Р(В).
Если А и В
зависимы, то
РВ(А)
≠ Р(А), РА(В) ≠ Р(В).
Теорема умножения вероятностей
Вероятность
произведения двух событий равна
произведению вероятности одного из них
на условную вероятность другого, т.е.
Р(А х В) = Р(А) х РА(В)
= Р(В) х РВ(А).
Если события
А и В независимы, то условия вероятности
равны безусловным и теорема умножения
вероятностей примет вид:
Р(А х В) = Р(А) х Р(В).
Пример.
Единица продукции может содержать два
вида несоответствий: царапины и сколы.
Вероятность появления царапин равна
10%, вероятность появления сколов равна
5%. Необходимо найти вероятность того,
что единица продукции будетнесоответствующая.
Решение.
Рассмотрим события:
А – “единица
продукции содержит царапину”;
В – “единица
продукции содержит скол”;
С – “единица
продукции несоответствующая”.
С = А + В,
Так как события
А и В независимы, то по теореме сложения
и умножения вероятностей получаем:
Р(С)
= Р(А + В) = Р(А) + Р(В) – Р(АхВ) = Р(А) + Р(В) –
Р(А) х Р(В) =
= 0,1
+ 0,05 – 0,1 х 0,05 = 0,145.
Вероятность
производства несоответствующей продукции
равна 14,5%.
Формула полной вероятности
Пусть
имеется группа событий H1,
H2,…,
Hn,
обладающая следующими свойствами:
1) все
события попарно несовместны: Hi

=;
i,
j=1,2,…,n;
ij;
2) их
объединение образует пространство
элементарных исходов :
= 
В
этом случае будем говорить, что
H1, H2,…,Hn
образуют
полную группу
событий.
Такие события иногда называют гипотезами.
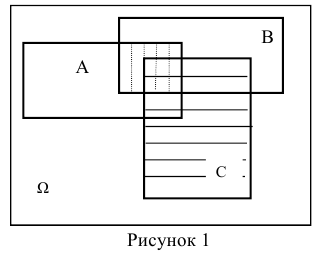
Рисунок
— Диаграмма Венна
Пусть
А –
некоторое событие: А
Тогда
имеет место формула
полной вероятности:
P(A)
= PH1(A)P(H1)
+ PH2(A)P(H2)
+ …+ PHn(A)P(Hn)
Доказательство.
Очевидно, что:
A
=

причем
все события

…, n)
попарно несовместны. Отсюда по теореме
сложения вероятностей получаем
P(A)
= P(
+P(
+…+P(
Если
учесть, что по теореме умножения
P(

где
i = 1,2,
…, n, то
из последней формулы легко получить
приведенную выше формулу полной
вероятности.
Пример.
Партия деталей формируется продукцией,
произведенной на трех станках, причем
доля первого станка — 30,
второго — 50,
третьего — 20.
Доля несоответствующих единиц продукции
каждого станка составляет соответственно
3,
2
и 1.
Какова вероятность того, что случайно
отобранная из партии единица продукции
окажется несоответствующей?
Пусть
событие H1
состоит в том, что единица продукции
произведена на первом станке, H2
на втором, H3
— на третьем заводе. Тогда
P(H1)
= 3/10,
P(H2)
= 5/10,
P(H3)
= 2/10.
Пусть
событие А
состоит в том, что единица продукции
оказалась несоответствующей; A/Hi
означает событие, состоящее в том, что
выбрана несоответствующая лампа из
ламп, произведенных на i-ом
станке. Из условия задачи следует:
P
(A/H1)
= 3/100
P(A/H2)
= 2/100
P(A/H3)
= 1/100
По
формуле полной вероятности получаем
При
изучении массовых явлений какое-либо
случайное событие или случайная величина
могут появляться несколько раз в процессе
испытаний. Например, пусть при N испытаниях
событие А фактически появилось f раз.
Число f носит название частоты
появления события
А либо статистического
веса (согласно
СТБ ГОСТ Р 50779.10 частота
– это число наступлений события данного
типа или число наблюдений, попавших в
данный класс).
Отношение частоты события А к общему
числу испытаний n
носит название частости
события или
относительной
частоты:
mA
= f/n
Согласно
СТБ ГОСТ Р 50779.10 относительная
частота — это
частота, деленная на общее число событий
или наблюдений.
Пример.
На станке обработано 100 деталей (n
= 100). При измерении деталей оказалось,
что 93 из них имеют размеры, лежащие в
пределах поля допуска (fA
= 93), а размеры остальных выходят за
пределы поля допуска (fB
= 7).
Следовательно, частость события А,
заключающегося в появлении соответствующих
деталей на 100 испытаниях, составляет
mA
= 93/100
Частость
события В, заключающегося в появлении
брака
mB
= 7/100
Следует
отметить, что если число опытов достаточно
велико, то считают, что вероятность
события приблизительно равна относительной
частоте.
В
некоторых случаях более предпочтительно
использовать накопленную
частоту N,
показывающую количество единиц
статистической совокупности, у которых
числовое значение не превышает заданного
(согласно СТБ ГОСТ Р 50779.10
накопленная
кумулятивная частота — это
число наблюдений из множества, имеющих
значения, которые меньше заданного
значения или равны ему). По мнению
авторов, само терминологическое понятие
«накопленная
кумулятивная частота» в некоторой
степени избыточно, так как слова
«накопленная» и «кумулятивная» являются
синонимами.
Соседние файлы в папке Статистика
- #
- #
- #
Содержание:
- Сумма событий
- Произведение событий
- Противоположное событие
- Следствия событий. Равные события
- Разность событий
- Некоторые тождества
- Элементы комбинаторики
- Правило произведения
- Формула включения-исключения
- Размещения
- Перестановки
- Бином Ньютона
- Некоторые примеры вычисления вероятностей
Рассмотрим опыт, состоящий в подбрасывании монеты. Ясно, что у этого опыта при каждом испытании может быть только два исхода: выпал герб или выпала цифра. Очевидно, что, во-первых, мы не можем предсказать, какая сторона монеты выпадет в очередном испытании, и, во-вторых, из соображений симметричности монеты эти два исхода можно считать равновозможными.
Следующий пример связан с подбрасыванием игральной кости — симметричного кубика с гранями, помеченными цифрами от 1 до 6. У данного опыта имеется шесть исходов: при каждом испытании может выпасть любая цифра в указанном диапазоне. Выпадение той или иной грани является случайным и равновозможным событием.
Легко усложнить любой из рассмотренных примеров. Допустим, что опыт состоит в том, что мы подбрасываем сразу три монеты. Тогда общее число исходов возрастет до восьми и мы можем все их перечислить. Обозначим для краткости выпадение герба буквой Г и цифры буквой Ц. Тогда все возможные исходы опыта можно записать в виде последовательностей из трех таких букв. Например, последовательность 
Поскольку мы считаем, что все монеты симметричные, то можно считать все эти исходы равно-возможными. Допустим, что мы хотим выяснить, насколько часто произойдет случайное событие 

Рассмотрим математическую модель таких и подобных им примеров. Итак, пространством элементарных событий назовем конечное множество 



По этой ссылке вы найдёте полный курс лекций по теории вероятности:
Будем говорить, что событие 



- В этой модели отражены существенные (и идеализированные) черты рассмотренных нами опытов. А именно, все элементарные события равноправны, что характеризует симметричность исходов, и все они различны. Такое определение вероятности называется классическим.
В опыте с подбрасыванием монеты пространство элементарных событий состоит из двух исходов 












1. Вероятность случайного события заключена в пределах от 0 до 1.
Крайние значения вероятности: 0 и 1 тоже принимаются. Введем следующие определения.
Возможно вам будут полезны данные страницы:
Событие 


2. Вероятность достоверного события равна 1.
Событие 


3. Вероятность невозможного события равна 0.
Мы видим, что в рамках этой модели подсчет вероятности состоит в установлении того, как случайное событие 
Алгебра случайных событий
При нахождении вероятностей приходится, естественно, учитывать связи между событиями. Формы таких связей весьма многообразны. Наиболее простые из них заключаются в том, что одни события являются комбинациями других. Далее мы ознакомимся с тремя основными видами комбинаций: суммой событий, произведением событий, противоположным событием.
Сумма событий
Пусть с некоторым пространством элементарных событий связаны события 




Аналогично определяется сумма трех событий, четырех и т.д. Вообще, сумма любого множества событий есть событие, состоящее из тех и только тех исходов, которые являются благоприятными хотя бы для одного из событий данного множества.
Пример 1:
Пусть пространство элементарных событий заключается в выборе наугад точки из области 
Решение:
Если 


Пример 2:
Пусть в опыте с бросанием игральной кости событие 


Произведение событий
Пусть 

Таблица, характеризующая событие 
Аналогично определяется произведение любого множества событий. Это событие, состоящее из исходов, которые благоприятны для всех событий данного множества.
Если, например, 





Противоположное событие
Противоположное событие для события 


Например, если 





Таблица, характеризующая событие 
Беря несколько событий 

Пример 3:
Покупаются три лотерейных билета; событие 


Решение:
Согласно определению операций сложения и умножения благоприятными исходами для события (1.3) являются любой из трех случаев: выигрывают 1-й и 2-й билеты, выигрывают 2-й и 3-й, выигрывают 1-й и 3-й. Другими словами, событие (1.3) означает выигрыш не менее чем по двум билетам.
Аналогичным образом, рассмотрев комбинацию
легко убедиться, что событие (1.4) означает выигрыш ровно по двум билетам.
Следствия событий. Равные события
По определению, событие 





Иными словами, все элементарные события, из которых состоит событие 
Например, пусть событие 

Другой пример. Условие: если в семье муж старше жены 


События 

Иными словами, события 
Разумеется, равные события могут иметь отличающиеся по форме словесные описания. Например, события «не все студенты данного курса успешно сдали теорию вероятностей» и «по крайней мере один из студентов данного курса не сдал теорию вероятностей» равны, хотя и выражены различными оборотами речи.
Разность событий
Событие 



Легко видеть, что выполняется равенство
И наоборот, противоположное событие можно выразить с помощью этой операции:
Надо иметь в виду, что так определенные операции сложения и вычитания событий все-таки отличаются от аналогичных действий с числами. В частности, событие 
Пример 4:
Пусть в группе из 20 студентов имеются три подгруппы, состоящие из 10 студентов, которые знают английский и французский языки, 6 — знающих французский и немецкий, 4 — английский и немецкий.
Решение:
Рассмотрим событие 




Некоторые тождества
При рассмотрении операций над событиями часто приходится пользоваться двумя важными равенствами:
Проверим справедливость первого из них; второе проверяется аналогично.
Наступление события 




Для наглядного истолкования различных соотношений между событиями удобно пользоваться так называемыми диаграммами Эйлера-Венна. В этом случае каждое событие рассматривается как попадание случайно брошенной точки в некоторую область на плоскости; иначе говоря, каждое событие задается некоторой фигурой на плоскости. При таком истолковании событие 






Элементы комбинаторики
В этом параграфе рассматриваются задачи комбинаторного характера. В каждой из них требуется подсчитать число различных вариантов, ответить на вопрос «сколько? » или «сколькими способами?». Например, интересно узнать, сколькими способами можно рассадить 


Комбинаторика имеет весьма непосредственное отношение к теории вероятностей. Близость этих разделов обусловлена, прежде всего, классическим способом подсчета вероятностей.
Формула
где 




Правило произведения
Будем рассматривать последовательности данной длины
состоящие из некоторых элементов 




Правило произведения может быть сформулировано следующим образом.
Пусть элемент 








Докажем это правило сначала для 
Обозначим через 








Пусть теперь 
можно рассматривать как строку из двух объектов: строки 




Ясно, что такое же рассуждение можно применить к строкам длины 4, затем 5 и т.д.
Пример 5:
Рассматриваются 5 различных языков. Сколько словарей нужно иметь для непосредственного перевода с любого языка на любой?
Решение:
Любой словарь задается строкой 





Пример 6:
Сколько можно составить пятизначных чисел так, чтобы любые две соседние цифры числа были различны?
Решение:
Пятизначному числу с цифрами 








Пример 7:
Сколько различных подмножеств имеет множество 

Решение:
Пусть 















по правилу произведения равно 

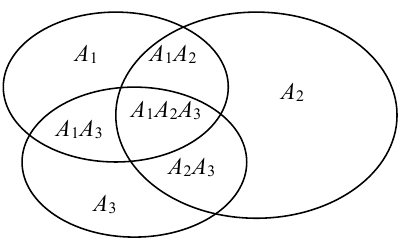
Формула включения-исключения
Для любого конечного множества 

Очевидно, что если 



Графическая иллюстрация формулы (1.9) приведена ниже (рис. 1.4). Ее вывод мы предлагаем читателю.
Пример 8:
В группе из 30 студентов 20 студентов (множество 

10 
Решение:
Имеем 
Применим формулу (1.9):

Формула (1.9) по индукции легко обобщается на случай объединения любого числа множеств и в этом случае называется формулой включения-исключения.
Размещения
Пусть 




Для множества 

Число размещений обозначается 
Для вывода этой формулы применим правило произведения. Действительно, для выбора первого элемента у нас имеется 



Пример 9:
Найти число способов распределения первых трех призовых мест для восьми участников финального забега.
Решение:
Всякий такой способ является размещением из восьми участников по три. Поэтому число способов вычисляется по формуле (1.10):
Перестановки
Пусть 


Иными словами, перестановка является размещением из 


Заметим, что произведение 


Например, 5 человек могут выстроиться в очередь (скажем, к кассе кинотеатра) 5! = 1 • 2 • 3 • 4 5 = 120 способами.
С помощью факториала формулу (1.10) можно переписать следующим образом
Для доказательства достаточно умножить и разделить правую часть формулы (1.10) на 


Сочетания. Число сочетаний. Пусть снова 






Число различных сочетаний 


Ее можно преобразовать после очевидных сокращений следующим образом:
В частности,
это вполне согласуется с тем, что в множестве 
Приведем доказательство формулы (1.13). Пусть 









откуда следует формула (1.14) или (1.13) в зависимости от того, какую формулу для числа размещений подставить: (1.10) или (1.12).
Числа 

вытекающая из (1.13) очевидным образом. Смысл формулы (1.15) состоит в том, что имеется взаимнооднозначное соответствие между множеством всех 




2) Справедлива формула
Поскольку сумма, стоящая в левой части, выражает собой число всех подмножеств множества 



3) При любом 
Это равенство нетрудно получить с помощью формулы (1.13). В самом деле,
Вывод формулы (1.17), основанный на теоретико-множественных соображениях, мы предоставляем провести читателю. Укажем, что для этого следует выделить какой-то определенный элемент 


4) Рассмотрим так называемый арифметический треугольник Паскаля.
Равенство (1.17) позволяет вычислять значения 




в 





Пример 10:
Пусть 







Решение:
Для примера приведем несколько строк с двумя буквами 
Пусть 














Бином Ньютона
Из школьного курса читателю известны формулы:
Обобщением этих формул является следующая формула, называемая обычно формулой бинома Ньютона:
В этой формуле 
где число перемножаемых скобок равно 



Из сказанного ясно, что слагаемым в выражении для 











Используя знак суммирования, формулу (1.18) можно записать короче:
Хотя формулу (1.18) называют именем Ньютона, в действительности она была открыта еще до Ньютона (например, ее знал Паскаль). Заслуга Ньютона состоит в том, что он нашел обобщение этой формулы на случай нецелых показателей.
Числа 



или
Некоторые примеры вычисления вероятностей
Мы рассмотрели классическое определение вероятности случайного события как отношение числа благоприятных исходов опыта к общему числу исходов — формулу (1.1)
В этом параграфе мы разберем ряд примеров непосредственного вычисления вероятности случайного события.
Пример 11:
В урне находятся 10 шаров: 4 белых и 6 черных. Из урны наудачу извлекают один шар. Какова вероятность того, что он окажется черным (событие
Решение:
Представим себе, что шары снабжены номерами 1, 2,…, 10, причем черные шары получили номера 1, 2,…, 6.
Обозначим через 





Пример 12:
Дважды бросается игральная кость. Какова вероятность того, что сумма очков при обоих бросаниях окажется больше 10 (событие
Решение:
Через 


можно рассматривать как элементарные исходы опыта, заключающегося в двукратном бросании игральной кости. Действительно, при каждом осуществлении опыта наступает один и только один из этих исходов, а соображения «равноправия» (между гранями игральной кости, а также между первым
и вторым бросанием) позволяют считать указанные события равновозможными. Интересующему нас событию 

Пример 13:
В лотерее разыгрывается 100 билетов. Выигрыши падают на 10 билетов. Некто
покупает три билета. Какова вероятность того, что хотя бы один из них выиграет?
Решение:
В данном случае опыт заключается в выборе наугад трех лотерейных билетов.
Перенумеруем все возможные тройки билетов. В качестве номеров будут фигурировать числа
Пусть 


Интересующее нас событие 



Полученное выражение приближенно равно:
Впрочем, выражение (1.20) нетрудно подсчитать точно. Такой подсчет дает 
Пример 14:
В условиях лотереи примера 1.10 выяснить, какое минимальное число билетов нужно купить, чтобы вероятность получения хотя бы одного выигрыша оказалась большей, чем 0,5.
Решение:
Пусть покупаются 




Следовательно, должно выполнятся неравенство
Таким образом, для наших целей достаточно, чтобы выполнялось неравенство
или 
Таким образом, искомое значение 
Многие задачи на подсчет вероятностей можно свести к так называемой схеме случайного выбора. Рассмотрим два основных варианта этой схемы: выбор с возвращением и выбор без возвращения.
1) Выбор с возвращением. Представим себе, что в некотором ящике собрано 




объема 


Описанная процедура носит название случайного выбора с возвращением. Слово «случайный» в этом названии означает нечто большее, нежели просто тот факт, что состав выборки предсказать заранее невозможно. Мы условимся вкладывать в это слово следующий смысл: все 

К схеме случайного выбора с возвращением можно свести большое число опытов. Например, бросание монеты можно представить как случайный выбор одного элемента из множества 




2) Выбор без возвращения. В этом случае выбранный предмет не кладется обратно в ящик и следующее извлечение производится из меньшего числа предметов. После 


Случайный характер выбора понимается, как и выше, в том смысле, что опыт состоит из всех равновозможных выборок данной длины.
Пример 15:
Пусть из совокупности 

Решение:
В данном случае число всех элементарных исходов опыта равно 


Остановимся на одном частном случае разобранного выше примера — так называемом парадоксе дня рождения.
Пример 16:
На лекции присутствует 
Решение:
Как уже отмечалось, выяснение дней рождения у 






откуда следует:
Найденное нами выражение для 



(все знаки после запятой, начиная с четвертого, отброшены). Из таблицы видно, что если в аудитории
находятся всего лишь 23 человека, то уже и тогда имеется более половины шансов на то, что, по крайней мере, у двух из них дни рождения совпадают!
Пример 17:
Монету бросают 10 раз. Какова вероятность того, что герб при этом выпадет ровно 3 раза (и, следовательно, цифра выпадет 7 раз)?
Решение:
Десятикратное бросание монеты можно рассматривать как составление строки длиной 10 (с повторениями) из элементов множества 




Пример 18:
Слово «карета», составленное из букв-кубиков, рассыпано на отдельные буквы, которые затем сложены в коробке. Из коробки наугад извлекают буквы одну за другой. Какова вероятность получить при таком извлечении слово «ракета»?
Решение:
Здесь нет схемы случайного выбора в прежнем понимании, так как буквы, сложенные в коробке, не все различны (три одинаковые буквы «а»). Представим себе, что одинаковые буквы (в данном случае 


Пример 19:
(задача о выборке). Партия готовых изделий содержит ровно 






Решение:
Выбор 













Лекции:
- Схема Бернулли теория вероятности
- Формула Пуассона теория вероятности
- Формула лапласа
- Статистическая вероятность
- Случайные векторы
- Элементы теории вероятности
- Найдите вероятность что случайно
- Бросили кость найти вероятность: пример решения
- Игральную кость бросают дважды найдите вероятность
- Найти вероятность что среди: пример решения
Содержание:
Основные теоремы теории вероятностей:
Теоремы сложения вероятностей
Теорема 1. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:
Доказательство.
Докажем теорему для схемы случаев. Пусть всевозможные исходы опыта сводятся к совокупности случаев, которые можно наглядно изобразить в виде
Теорема 1 (Обобщенная теорема сложения несовместных событий) Вероятность суммы 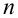
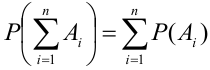
Доказательство (методом математической индукции).
Предположим, что теорема справедлива для 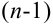
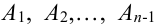
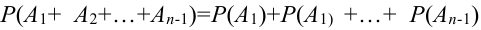
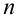
Обозначим 
Имеем 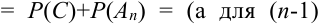
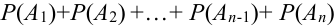
Следствие 1. Если события 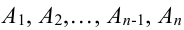
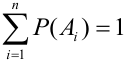
Доказательство.
Т.к. события 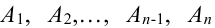
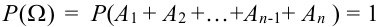
Т.к. события несовместные, то к ним применима обобщенная теорема сложения:
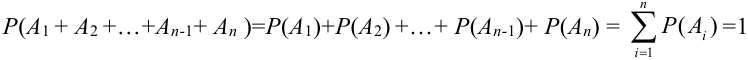
Следствие 2. Сумма вероятностей противоположных событий равна единице:
Доказательство.
События А, 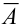
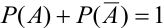
Замечание. Следствие 2 — частный случай следствия 1. На практике весьма часто оказывается легче вычислить вероятность противоположного события, чем прямого.
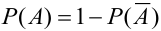
В формулировке таких задач встречаются слова «хотя бы», «не менее», «по крайней мере» и др.
Пример:
Из колоды карт (36) наудачу вынимают 3 карты. Найти вероятность того, что среди них окажется хотя бы один туз.
Решение.
1 способ (по теореме 1′).
Событие А = {из 3 карт окажется хотя бы один туз}.
Хотя бы один — это либо один, либо два, либо три, т.е. событие А может быть представлено в виде суммы трех событий: 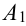
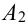
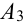
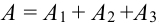
Т.к. события несовместны, то по теореме 1′: 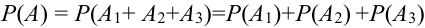
Найдем отдельно вероятности событий.
2 способ (по следствию 2).
Событие 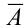
Теорема 2. Вероятность суммы двух совместных событий равна сумме вероятностей этих
событий без вероятности их произведения (совместного осуществления):
Доказательство (геометрическое)
События отождествляют с множествами. Два раза накладываем «лепесток» друг на друга, поэтому и отнимаем его. (что и треб. доказать)
Теорема 2 ( Обобщенная теорема сложения совместных событий).
Вероятность суммы 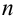
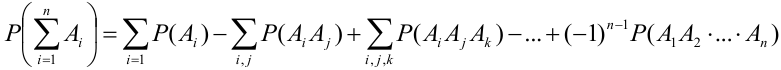
Для трех совместных событий теорема запишется в виде:
Доказательство для трех событий (геометрическое):
События отождествляют с множествами (см. рис.). (что и треб. доказать)
Замечание. Аналогичную формулу можно написать для произведения совместных событий:
Пример:
Для поражения самолета необходимо, чтобы были поражены оба двигателя (события 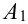
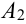
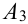
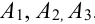
Решение.
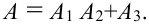
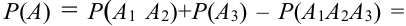
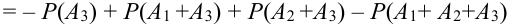
Теоремы умножения вероятностей
Определение 21. Событие А называется независимым от события В, если вероятность события А не зависит от того, произошло событие В или нет.
Определение 22. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.
Примеры:
1) А = {появление решки на первой монете}, В = {появление решки на второй монете}. А и В — независимы.
2) А = {рождение мальчика у Тани}, В = {рождение мальчика у Лены}. А и В — независимы.
3) В урне 2 белых и 1 черный шар. Двое Таня и Ваня вынимают из урны по одному шару. Зависимы или независимы события: А = {появление белого шара у Тани}, В = {появление белого шара у Вани}?
Решение.
Найдем вероятности событий. 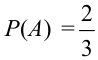
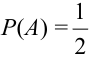
Определение 23. Два события называются независимыми, если появление одного из них не изменяет вероятности появления другого.
Определение 24. Несколько событий называются независимыми, если любое из них не зависит от любой совокупности остальных.
Определение 25. Вероятность события А, вычисленная при условии, что имело место другое событие В, называется условной вероятностью события А и обозначается 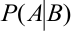
В Примере 3): 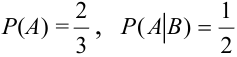
Условие независимости события А от события В:
Условие зависимости события А от события В:
Теорема 3. Вероятность произведения двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место.
Доказательство.
Докажем для схемы урн истинность тождества формулы.
Пусть всевозможные исходы опыта сводятся к 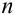
Пусть событию А благоприятствует 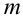
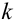
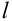
Тогда, вероятности данных событий равны: 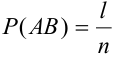
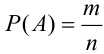
Вычислим условную вероятность 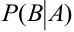
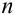
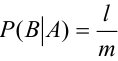
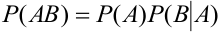
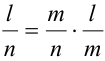
Замечание 1. При применении теоремы вполне безразлично, какое из событий А или В считать первым, а какое вторым, т.е. теорему можно записать в виде:
Замечание 2. В общем случае при 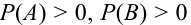
Следствие 1. Если событие А не зависит от события В, то и событие В не зависит от события А.
Замечание 3. Зависимость и независимость событий всегда взаимны.
Замечание 4. Условные вероятности обладают всеми свойствами, присущими обычным вероятностям:
1. 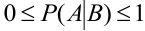
2. если наступление события В исключает возможность осуществления А, т.е. 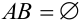
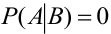
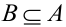
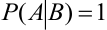
3. Если 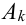
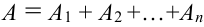
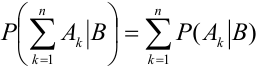
4. 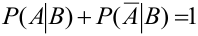
Замечание 5. Если А и В независимы, то независимы также события 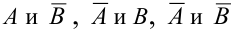
Теорема 3. ( Обобщенная теорема умножения зависимых событий).
Вероятность произведения нескольких зависимых событий равна произведению вероятностей этих событий, причем вероятность каждого следующего по порядку события вычисляется при условии, что всс предыдущие имели место:
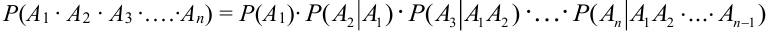
Теорема 4. {теорема умножения независимых событий).
Вероятность произведения двух независимых событий равна произведению вероятностей этих событий: 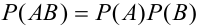
Теорема 4. ( Обобщенная теорема умножения независимых событий).
Вероятность произведения нескольких независимых событий равна произведению вероятностей этих событий:
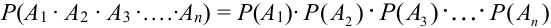
Пример:
Из колоды карт последовательно вынуты две карты. Найти: а) вероятность того, что вторая карта окажется тузом (неизвестно, какая карта была вынута вначале), б) вероятность того, что вторая карта будет тузом, если первоначально тоже был вынут туз.
Решение.
Обозначим А = {появление туза вторым}, В = {появление туза первым}.
а) 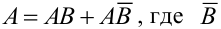
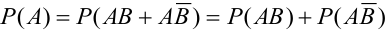
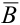
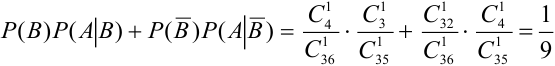
б) Если вынутая первая карта — туз , то в колоде осталось 35 карт и среди них только три туза, следовательно, 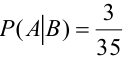
Или можно было найти эту вероятность, используя формулу условной вероятности:
Пример:
В урне 2 белых и 3 черных шара. Из урны вынимают подряд 2 шара. Найти вероятность того, что а) оба белые, б) оба белые, если после первого вынимания шар возвращают обратно в урну, и шары перемешиваются.
Решение.
Обозначим: А = {появление двух белых шаров}, В = {появление белого шара при первом вынимании}, С = {появление белого шара при втором вынимании}.
а) 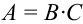
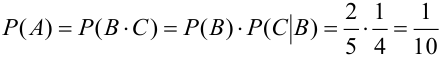
б) 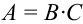
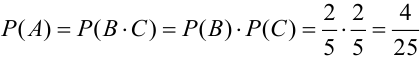
Теорема 5. Вероятность наступления события А, состоящего в появлении хотя бы одного из событий 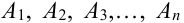
Если все 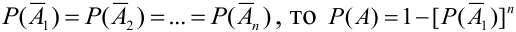
Пример:
Производится три выстрела по одной и той же мишени. Вероятности попадания при первом, втором и третьем выстрелах равны соответственно 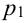
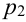
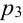
Решение.
Обозначим А = {хотя бы одно попадание в цель}.
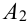
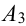
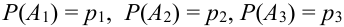
Можно расписать в алгебре событий данное событие в виде суммы произведений: 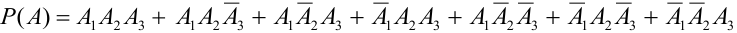
Перейдем от прямого события к противоположному: 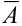
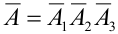
где 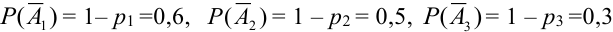
Тогда по теореме 5:
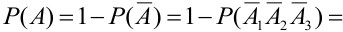
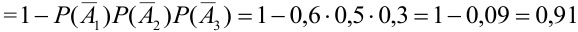
Основные формулы для вычисления вероятностей
Ограниченность классического и статистического способов определения вероятности событий, приемлемых, главным образом, для определения вероятности простых событий, приводит к тому, что в подавляющем большинстве случаев ни один из этих способов в чистом виде для решения задачи определения наступления событий применить не удаётся.
Например, требуется определить вероятность поражения движущегося танка. Определить эту вероятность по частоте наступления события на практике невозможно — необходимо провести большое число стрельб. При этом надо не только определить вероятность попадания в движущийся танк (что сделать не сложно), но и определить вероятность поражения его экипажа, если будет иметь место попадание в танк (а это выполнить на практике невозможно).
Факт сложности или невозможности определения вероятности сложных событий явился стимулом разработки аппарата теории вероятностей, с помощью которого вероятность определяется не прямым, а косвенным методом через вероятность более простых событий.
Сущность косвенного метода определения вероятности сложного события заключается в следующем: вначале анализируют условия испытания и устанавливают события 
Однако определению вероятности наступления сложного события как комбинации более простых событий должны предшествовать твёрдые знания правил применения рассмотренных в лекции теорем сложения (объединения) и умножения (пересечения) событий.
Этому вопросу и будет посвящён вопрос нашего занятия.
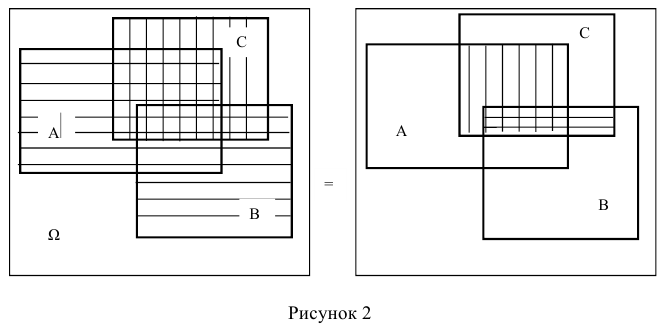
Пример:
Для того что бы вывести из строя артиллерийскую батарею необходимо поразить либо два взвода с орудиями либо центр управления огнём. Используя операции сложения (объединения) и умножения (пересечения) событий представим сложное событие D={ поражение артиллерийской батареи} как комбинацию простых событий. Результат проиллюстрируем диаграммой Эйлера-Венна.
Решение:
Обозначим через событие А = {поражение первого взвода орудий}, через событие В = {поражение второго взвода орудий}, С = {поражение центра управления огнём}. Тогда событие D = {поражение артиллерийской батареи} определится как поражение либо центра управления огнём (событие С) либо одновременно первого взвода орудий (событие А) и второго взвода орудий (событие В), т.е. будет иметь место следующая комбинация событий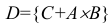
Для решения такого типа задач необходимо усвоить ряд основных свойств, которыми обладают действия над событиями.
Операции сложения (объединения) и умножения (пересечения) событий обладают рядом свойств, аналогичным свойствам сложения и умножения чисел.
1. Переместительное свойство:
А + В = В + А;
2. Сочетательное свойство:
3. Распределительное свойство:
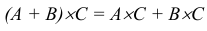
4. Операции прибавления пустого множества и умножения на пустое множество аналогичны операциям над числами, если считать пустое множество за ноль.
Ряд операций над событиями уже не обладают свойствами по аналогии с арифметическими действиями, например:
5. 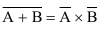
6. 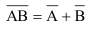
7. 
Основные теоремы теории вероятностей: сложение, умножение, формула полной вероятности
На предыдущей лекции мы говорили о том, что достаточно часто определить вероятность сложного события трудно или вообще невозможно. Для чего научились представлять события, как комбинацию других более простых событий используя понятия суммы (объединения) или произведения (пересечения) событий.
Вспомним пример, рассматриваемый нами на предыдущей лекции:
Для того что бы вывести из строя артиллерийскую батарею необходимо поразить либо два взвода с орудиями либо центр управления огнём. Используя для решения задачи правила сложения и умножения событий сложное событие — поражение артиллерийской батареи, заключающееся в поражении либо двух взводов орудий либо центра управления огнём, было представлено как следующая комбинация событий
На сегодняшнем занятии мы ответим на следующий вопрос: как определить вероятность сложного события представляющего собой функцию известных или заданных вероятностей
При определении вероятностей сложных событий пользуются теоремами сложения и умножения вероятностей. Эти теоремы теоретически могут быть доказаны только для таких событий, вероятность появления которых может быть определена классическим способом. Для других событий эти теоремы принимаются как аксиомы. Поэтому мы не будем показывать доказательство этих теорем, а ограничимся только понятием «правила», понимая при этом ряд теорем и следствий из них, с помощью которых определяется вероятность комбинации событий.
Правила сложения вероятностей
Аксиома: Вероятность суммы или наступления хотя бы одного из двух несовместных событий равна сумме вероятностей этих событий (аддитивность Р):
Данную аксиому иногда называют «теоремой сложения», так как для опытов, сводящихся к «схеме случаев», она может быть доказана.
Эта аксиома легко обращается на любое число несовместных событий: вероятность суммы несовместных событий равна сумме вероятностей этих событий:
Пример №1
Вероятность попадания в башню танка при одном выстреле- 0,2, в его корпус — 0,1, в ходовую часть — 0,025. Найти вероятность попадания в танк при одном выстреле.
Решение:
Обозначим интересующее нас событие через А = {попадание в танк}, тогда 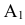
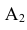
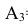
Очевидно, что попадание в танк наступит тогда, когда снаряд попадёт либо в башню, либо в корпус, либо в ходовую часть танка. Таким образом, интересующее нас событие А будет являться суммой событий
А так как события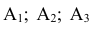
Вывод: полученный результат означает, что при проведении достаточно большого числа стрельб в аналогичных условиях в среднем в 325 случаях из 1000 будет получено попадание в танк.
Из данной аксиомы вытекают два важных следствия.
Следствие 1. Если события 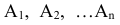
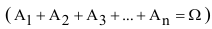
Следствие 2. Сумма вероятностей противоположных событий равна 1.
Для совместных событий аксиома примет следующий вид:
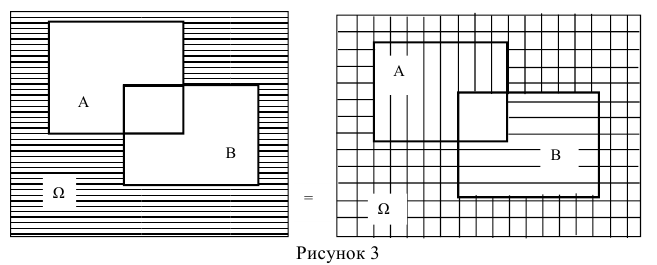
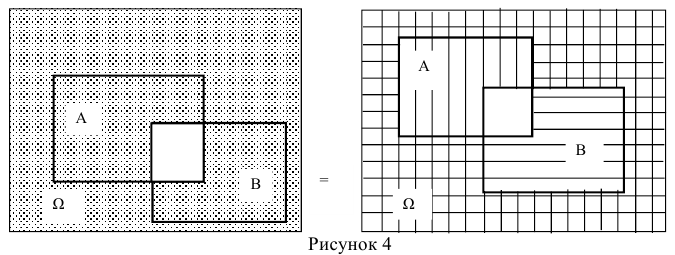
Вероятность суммы, или наступление хотя бы одного из двух совместных событий, равна сумме вероятности этих событий без вероятности произведения этих событий:
Справедливость этого тождества наглядно следует из его геометрической интерпретации (рисунок 1).
На диаграмме Эйлера-Венна вероятность наступления событий А (или
В) по существу есть площадь области, при попадании случайной точки в которую, наступает событие А (или В). Тогда вероятность комбинации А + В будет соответствовать площади заштрихованной области (рисунок 1 .а). Чтобы получить такую же по площади область, необходимо из площади областей наступления событий А и В вычесть площадь их совместного появления АхВ (рисунок 1.6).
Пример №2
Вероятность подавления батареи противника из-за потерь только в личном составе составляет 0,15; вследствие повреждения материальной части — 0,45; а из-за потерь одновременно в личном составе и материальной части — 0,25. Какова вероятность подавления артиллерийской батареи?
Решение: Пусть событие А = {подавление личного состава батареи}, а событие В= {повреждения материальной части}. Тогда одновременное подавление личного состава и повреждение материальной части будут являться совместным наступлением событий А и В или
Вероятность наступления события А по условию задачи равна 0,15 (Р(А)=0,15), вероятность наступления события В равна 0,45 (Р(В)=0,45), вероятность совместного наступления события А и В равна 0,25 (Р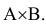
Требуется найти вероятность события С ={подавления батареи противника}, которое будет заключаться либо в подавлении личного состава батареи, либо в повреждении материальной части либо того и другого, или Р(А+В).
Применив теорему сложения вероятностей, получим:
Р(С) = Р(А + В) = Р(А) + Р(В) — Р(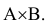
Вывод: Полученный результат означает, что при проведении достаточно большого числа стрельб в аналогичных условиях в среднем в 35 случаях из 100 батарея противника будет подавлена, т.е. поражён либо личный состав, либо повреждена техника, либо и то и другое.
Правила умножения вероятностей
Перед рассмотрением правил умножения вероятностей введём ряд новых понятий, которые необходимы для логического понимания производимых над событиями действий.
Событие А называется независимым от события В, если вероятность наступления события А не зависит от того, произошло ли событие В.
Событие А называется зависимым от события В, если вероятность наступления события А меняется в зависимости от того, произошло событие В или нет.
Факт зависимости или независимости события устанавливают из анализа условий испытания. В теории вероятностей под зависимостью случайных событий понимают не причинную зависимость, при которой два события выступают по отношению друг к другу как причина и следствие, а вероятностную или стохастическую зависимость (стохастическая зависимость [stochastic dependence] — зависимость между случайными величинами, проявляющаяся в том, что изменение закона распределения одной из них происходит под влиянием изменения закона распределения другой). Смысл вероятностной или стохастической зависимости двух событий состоит в том, что при наступлении одного из них другое наступает чаще или реже, чем наступает вообще при реализации данного комплекса условий.
В качестве примеров зависимых событий можно привести следующие:
Пример №3
Реализация комплекса условий: выстрел по танку; событие А= {попадание в танк}; реализация комплекса условий — попадание в танк; событие В = {поражение экипажа танка}.
Для появления интересующего события В = {поражение экипажа танка} при реализации комплекса условий — выстрел по танку необходимо появления события А = {попадание в танк}, в то же время при реализации комплекса условий события А = {попадание в танк} не всегда может наступить событие В = {поражение экипажа танка}.
Раз нам требуется определить вероятность совместного наступления двух зависимых событий, одно из которых может наступить только при том условии, что имело место другое из них, введём понятие условной вероятности события.
Вероятность события В, вычисленная при условии, что имело место другое событие А называется условной вероятностью события В по отношению к событию А (обозначается 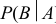
Теорема: Вероятность произведения или совместного наступления двух любых случайных событий равна произведению вероятностей одного из них на условную вероятность другого, вычисленную при условии, что первое имело место.
Пример №4
Вероятность попадания в танк при одном выстреле равна 0,8; вероятность поражения экипажа танка при попадании в танк равна 0,7. Определить вероятность поражения экипажа танка при одном выстреле.
Решение:
Пусть событие А = {попадание в танк при одном выстреле}, а событие В = {поражение экипажа танка}. Интересующее нас событие С = {поражение экипажа танка при одном выстреле} будет иметь место только в том случае, если наступит событие А, при этом наступление события С возможно только тогда, когда одновременно наступят события А и В.
Вероятность наступления события А по условию задачи равна 0,8 (Р(А)=0,8); вероятность наступления события В равна 0,7 (Р(В)=0,7).
Требуется найти вероятность поражения экипажа танка при одном выстреле, которая будет являться произведением вероятностей попадания в танк при одном выстреле и поражении экипажа танка при условии что имело место попадание в него, т.е. Р(С)=Р(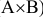
Применив теорему умножения вероятностей, получим:
Вывод: полученный результат означает, что при проведении
достаточно большого числа стрельб в аналогичных условиях по одному выстрелу в каждом в среднем в 56 случаях из 100 экипаж танка будет поражён.
Правило умножения вероятностей легко обращается на случай произвольного числа событий:
Из данной теоремы вытекает ряд важных следствий.
Следствие 1. Вероятность произведения двух независимых событий равна произведению вероятностей этих событий.
Пример №5
По цели в тире производят по одному выстрелу два студента. Вероятность попадания в цель первого студента равна 0,7, второго — 0,4. Найти вероятность того, что в цель попадут оба студента.
Решение:
Пусть событие А={попадание в цель первым студентом}, а событие В={попадание в цель вторым студентом}, тогда интересующее нас событие С={попадание в цель и первым и вторым студентом}.
Вероятность наступления события А по условию задачи равна 0,7 (Р(А)=0,7), вероятность наступления события В равна 0,4 (Р(В)=0,4).
Попадание в цель вторым студентом не зависит от того, попадёт ли в цель первый студент и наоборот, а следовательно события А и В -независимы. Применив следствие из теоремы умножения для независимых событий, получим:
Вывод: полученный результат означает, что при проведении
достаточно большого числа стрельб в аналогичных условиях в среднем в 28 случаях из 100 в цель попадут оба студента.
Зависимость и независимость событий всегда взаимны. Если событие А не зависит от события В, то и событие В не зависит от события А. Таким образом, можно уточнить данное ранее определение независимых событий. Два события называются независимыми, если появление одного из них не изменяет вероятности появления другого.
Из рассмотренных выше правил сложения и умножения вероятностей вытекает ещё одно очень важное следствие: если противоположное событие распадается на меньшее число вариантов, чем прямое событие, то имеет смысл при вычислении вероятностей переходить к противоположному событию:
Пример №6
Два орудия, начиная с первого, ведут последовательно огонь по цели до получения первого попадания. При этом первое орудие может произвести два выстрела, а второе — только один. Вероятность попадания в цель при первом выстреле первого орудия — 0,4; вторым выстрелом — 0,8; вероятность попадания в цель вторым орудием — 0,6. Чему равна вероятность поражения цели?
Решение:
Обозначим за событие 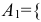
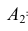
Так как события 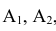
Вывод: полученный результат означает, что при проведении достаточно большого числа испытаний в аналогичных условиях в среднем в 95 случаях из 100, танк будет поражён.
Формула полной вероятности
При изложении третьего вопроса лекции преподаватель на примере поражения движущегося танка обозначает проблему определения вероятности сложного события (давая при этом понятие гипотезы).
После чего преподаватель доводит условие задачи (Пример 7), формулу для вычисления полной вероятности события (без её вывода) и условия её применения.
При постановке задачи и пояснения физической сущности вопроса преподаватель использует оверхэд-проектор и подготовленные слайды.
Решение задачи преподаватель проводит на доске, особое внимание при этом обращая на методику её решения и порядок записи. В заключении решения задачи преподаватель под запись доводит вывод, отражающий физическую сущность полученного результата.
При решении ряда практических задач вычисление вероятности некоторого сложного события можно существенно облегчить, если связать наступление этого события с наступлением единственно возможных и несовместных событий, под которыми понимаются гипотезы о всех возможных исходах испытаний.
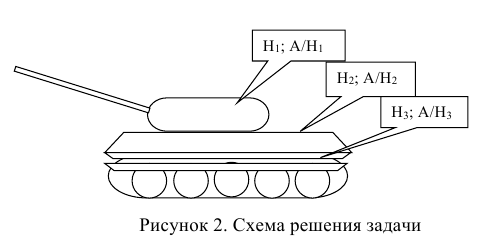
Пусть, например, производится выстрел по танку (рисунок 2).
Известно, что башня танка, его корпус или ходовая часть имеют не только различные размеры, форму и т.д., что усложняет попадание, но и различную степень уязвимости. Первое приводит к тому, что вероятность попадания в различные отсеки танка будет различной, а второе — к тому, что различной будет и вероятность поражения танка при попадании в его башню, корпус или ходовую часть, а, следовательно, и вероятность поражения танка в целом. Поэтому для облегчения вычисления вероятности поражения танка Р(А) представляется целесообразным ввести гипотезы о возможном исходе стрельбы.
Дадим определение:
Под гипотезами понимают полную группу единственно возможных несовместных событий, которые могут наступить в результате проведения испытаний.
В условиях нашей задачи гипотезы о возможном исходе стрельбы будут следующие:
Вероятности этих гипотез 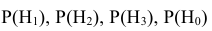
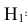
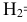
Указанные условные вероятности возможно определить опытным путём, проводя полигонные стрельбы по танку.
Пример №7
Ведётся стрельба из орудия по танку. Известно, что при попадании снаряда в башню вероятность поражения танка равна 0,8; при попадании в корпус — 0,6; при попадании в ходовую часть — 0,5.
Известны также вероятности попадания снаряда в каждый из отсеков танка. Вероятность попадания в башню танка равна 0,2. Вероятность попадания в корпус равна 0,3; вероятность попадания в ходовую часть равна 0,1.
Требуется определить вероятность поражения танка при одном выстреле.
Вычислить вероятность наступления интересующего нас события позволяет формула, получившая особое название формулы полной вероятности.
Полная вероятность события равна сумме парных произведений вероятностей каждой из гипотез на отвечающие им условные вероятности наступления этого события.
Данная формула является следствием из обеих теорем — теорем сложения и умножения вероятностей.
При определении полной вероятности необходимо следить, чтобы были учтены все гипотезы о возможном исходе испытания, при которых может наступить интересующее нас событие, т.е. гипотезы должны составлять полную группу несовместных событий. Свидетельством полного учёта всех гипотез является выполнение равенства
Если данное равенство не выполняется, то это означает, что учтены не все гипотезы о возможных исходах испытания.
Таким образом оказывается, что знания вероятностей гипотез 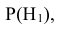
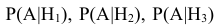
Вернёмся к решению примера.
Решение:
Таким образом, возможные гипотезы об исходах стрельбы:
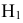
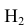
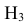
По условию задачи вероятности гипотез будут равны:
гипотеза 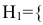
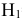
гипотеза 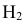
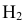
гипотеза Нз ={попадание в ходовую часть} — равна 0,1 (Р(Нз) = 0,1).
Интересующее нас событие А = {поражение танка}. По условию задачи вероятность поражения танка при реализации гипотез:
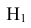
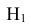
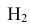
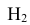
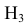
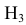
Проверим, все ли гипотезы об исходах стрельбы учтены:
Следовательно, имеющиеся гипотезы не составляют полной группы событий и не учтено событие 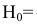
Таким образом, вероятность гипотезы 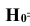
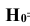
Вероятность поражения танка при реализации гипотезы 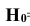
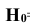
Применяя формулу полной вероятности для решения задачи получим:
Следовательно, полная вероятность поражения танка при одном выстреле равна
Р(А) = 0,39 = 39%.
Вывод: Полученный результат означает, что при проведении
достаточно большого числа стрельб в аналогичных условиях в среднем в 39 случаях из 100 танк окажется поражённым.
Формула Байеса, вероятность появления хотя бы одного события
Пусть имеется полная группа несовместных гипотез 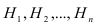
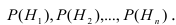
Требуется определить какие вероятности имеют гипотезы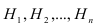
Теорема. Вероятность гипотезы после испытания равна произведению вероятности гипотезы до испытания на соответствующую ей условную вероятность события, которое произошло при испытании, делённому на полную вероятность этого события.
Эта формула называется формулой Байеса.
Доказательство.
По Теореме умножения вероятностей получаем:
Тогда если
Для нахождения вероятности Р(А) используем формулу полной вероятности.
Если до испытания все гипотезы равновероятны с вероятностью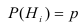
Пример №8
Известно, что 30% приборов собирает специалист высшей квалификации, 70% приборов — специалист средней квалификации. Вероятность того, что прибор, собранный специалистом высшей квалификации, надёжен, равна 0,9. Для специалиста средней квалификации эта вероятность равна 0,8. Взятый наудачу прибор оказался надёжным. Найти вероятность того, что этот прибор собран специалистом высшей квалификации.
Решение: пусть событие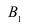
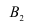
Пусть событие А означает появление надёжного прибора. По условию примера вероятность события А при условии, что появится прибор, собранный специалистом высшей квалификации,
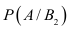
Искомая вероятность появления прибора, собранного специалистом высшей квалификации, т.е. события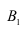
- Основные законы распределения дискретных случайных величин
- Непрерывные случайные величины
- Закон больших чисел
- Генеральная и выборочная совокупности
- Ковариация в теории вероятности
- Функциональные преобразования двухмерных случайных величин
- Правило «трех сигм» в теории вероятности
- Производящие функции
Операции над событиями. Диаграммы Эйлера – Венна
Содержание
В теории вероятностей случайными событиями являются подмножества множества элементарных исходов Ω .
Над событиями, как и над любыми множествами, можно совершать следующие операции.
Произведение (пересечение) двух событий
Операцию произведения (пересечения) двух событий A и B обозначают
, или AB, или
.
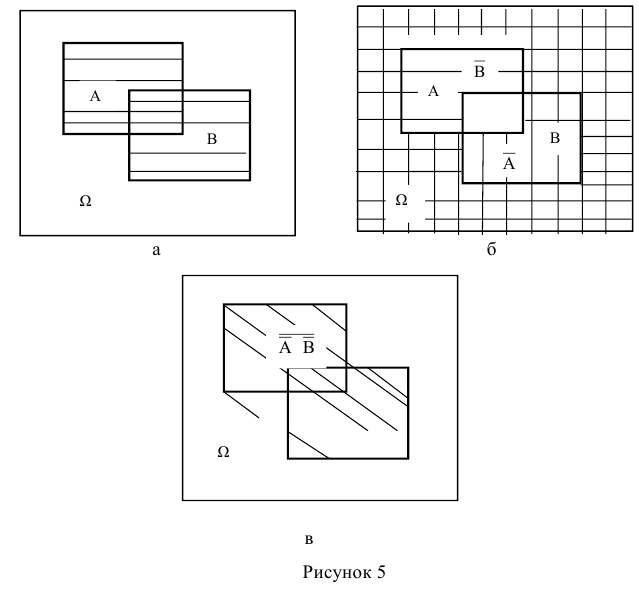
ОПРЕДЕЛЕНИЕ 1. Произведением (пересечением) двух событий A и B называют такое событие, которое состоит из всех элементов, входящих как в событие A , так и в событие B (рис. 1).
Рис.1
Сумма (объединение) двух событий
Операцию суммы (объединения) двух событий A и B обозначают
A + B или
ОПРЕДЕЛЕНИЕ 2. Суммой (объединением) двух событий A и B называют такое событие, которое состоит из элементов события A и элементов события B (рис. 2).
Рис.2
Разность двух событий
Операцию разности двух событий A и B обозначают
A B
ОПРЕДЕЛЕНИЕ 3. Разностью событий A и B называют событие, состоящее из тех элементов события A , которые не входят в событие B (рис. 3).
Рис.3
ЗАМЕЧАНИЕ 1. Разностью событий B и A является событие B A , изображенное на рисунке 4.
Рис.4
Симметрическая разность двух событий
Операцию симметрической разности двух событий A и B обозначают
ОПРЕДЕЛЕНИЕ 4 . Симметрической разностью событий A и B называют событие, состоящее из тех элементов события A , которые не входят в событие B , а также из тех элементов события B , которые не входят в событие A (рис. 5).
Рис.5
Переход к противоположному событию
Событие, противоположное к событию A , обозначают
или AC
ОПРЕДЕЛЕНИЕ 5. Противоположным событием к событию A называют событие, состоящее из тех элементов всего множества элементарных событий Ω , которые не входят в событие A (рис. 6).
Рис.6
ЗАМЕЧАНИЕ 2. Справедлива формула
ОПРЕДЕЛЕНИЕ 6. Событие Ω называют достоверным событием, пустое множество называют невозможным событием.
ЗАМЕЧАНИЕ 3. Рисунки, на которых наглядно показаны операции над множествами, называют диаграммами Эйлера-Венна. В частности, диаграммами Эйлера-Венна являются рисунки 1-6 .
Сложение и умножение вероятностей
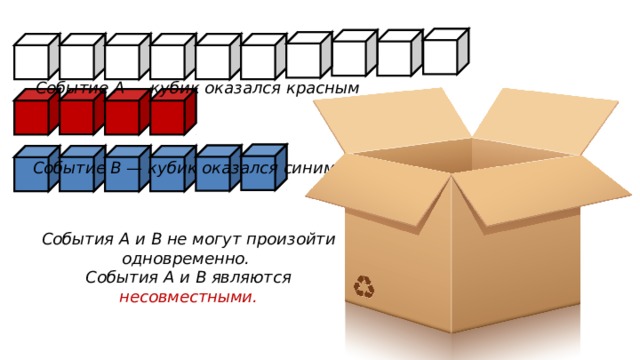
Событие А — кубик оказался красным
Событие B — кубик оказался синим
События А и B не могут произойти одновременно.
C обытия А и B являются несовместными.
Два события называют
НЕСОВМЕСТНЫМИ ,
если в одном и том же испытании они не могут произойти одновременно, то есть
наступление одного из них исключает наступление другого .
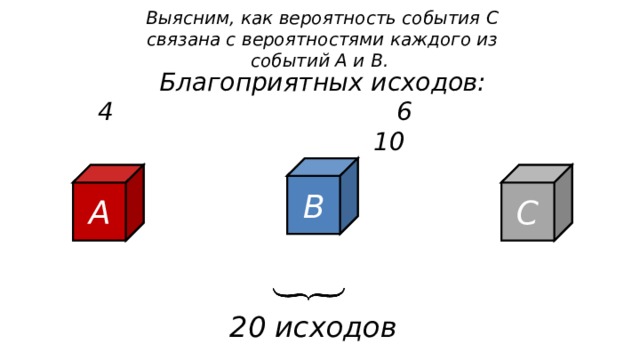
Событие А — кубик оказался красным
Событие B — кубик оказался синим
?
Событие C — кубик оказался не белым
Выясним, как вероятность события С связана с вероятностями каждого из событий А и B .
Благоприятных исходов:
4 6 10
B
A
C
20 исходов
A
B
C
E сли событие C означает, что наступает одно из двух несовместных событий А или B , то вероятность события C равна сумме вероятностей событий А и B .
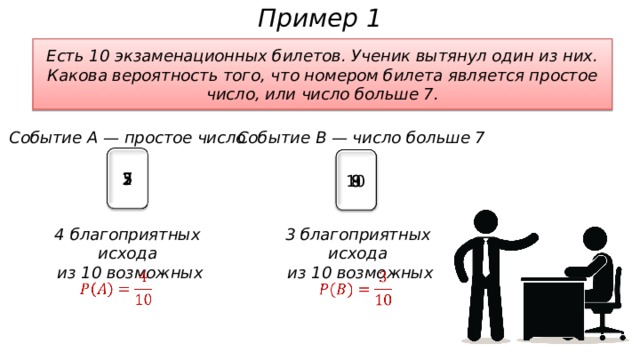
Пример 1
Есть 10 экзаменационных билетов. Ученик вытянул один из них. Какова вероятность того, что номером билета является простое число, или число больше 7.
Событие B — число больше 7
Событие А — простое число
7
5
2
3
8
9
10
3 благоприятных исхода
из 10 возможных
4 благоприятных исхода
из 10 возможных
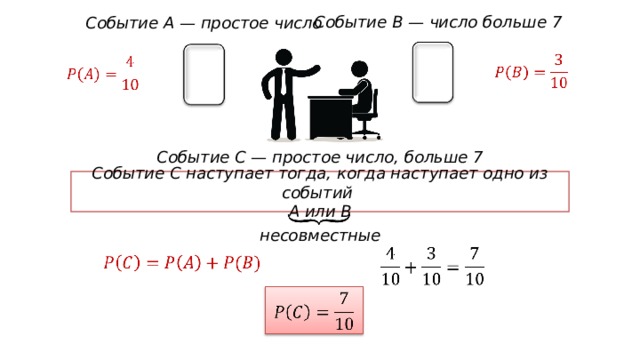
Событие B — число больше 7
Событие А — простое число
Событие C — простое число, больше 7
Событие С наступает тогда, когда наступает одно из событий
A или B
несовместные
Свойство вероятностей
противоположных событий
Пример
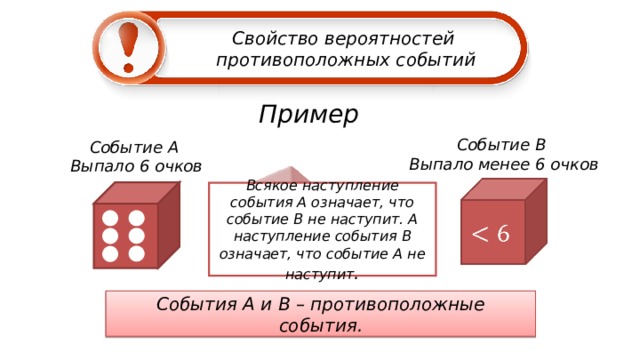
Событие B
Выпало менее 6 очков
Событие А
Выпало 6 очков
Всякое наступление события А означает, что событие B не наступит. А наступление события B означает, что событие А не наступит .
C обытия А и B – противоположные события.
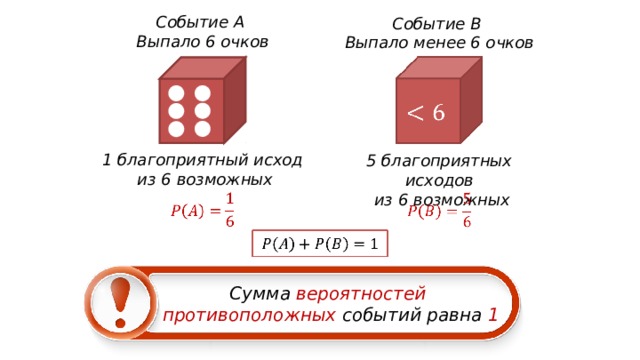
Событие А
Выпало 6 очков
Событие B
Выпало менее 6 очков
1 благоприятный исход
из 6 возможных
5 благоприятных исходов
из 6 возможных
Сумма вероятностей
противоположных событий равна 1
Пример
Какова вероятность того, что сумма очков, выпавших на двух кубиках, меньше 9?
Общее число равновозможных исходов равно 36.
4 благоприятных исхода
(3; 6), (6; 3), (4; 5), (5; 4)
Рассмотрим, как можно вычислить вероятность события, состоящего в совместном появлении двух независимых событий .
Два события называются
НЕЗАВИСИМЫМИ ,
если наступление одного из них не влияет на вероятность наступления другого события.
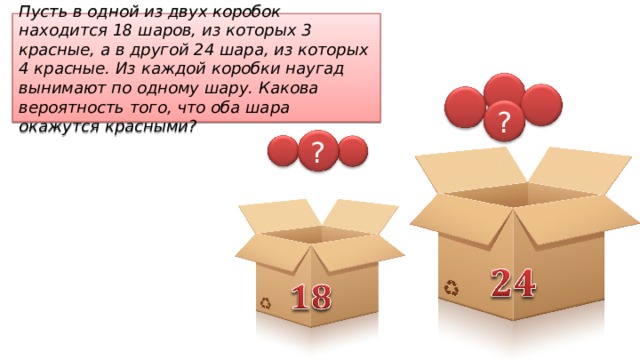
Пусть в одной из двух коробок находится 18 шаров, из которых 3 красные, а в другой 24 шара, из которых 4 красные. Из каждой коробки наугад вынимают по одному шару. Какова вероятность того, что оба шара окажутся красными?
?
?
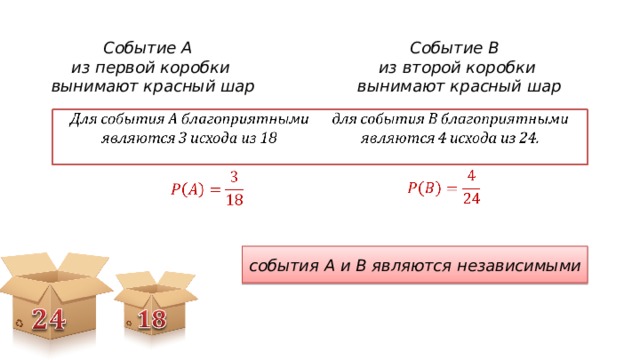
Событие А
из первой коробки
вынимают красный шар
Событие B
из второй коробки
вынимают красный шар
события A и B являются независимыми
Для события С благоприятными являются те исходы, при которых оба вытянутых шара окажутся красными.
Если событие C означает совместное наступление событий A и B , то вероятность события C равна произведению вероятностей событий А и B .
Пример. На карточках написаны числа от одного до девяти включительно. Перевернули их числами вниз и перемешали. Затем берут наугад одну карточку, записывают ее номер и кладут обратно. Карточки снова перемешивают. Затем берут еще одну карточку и записывают ее номер. Какова вероятность того, что оба раза будут вытянуты карточки, номера которых являются простыми числами.
А – событие, при котором в первый раз будет вытянута карточка с простым числом.
В – событие при котором во второй раз будет вытянута карточка с простым числом.
C – событие при котором оба раза будут вытянуты карточки с простыми числами
А и В – независимые события
Пример: В результате многократных наблюдений, было установлено, что вероятность попадания одного стрелка в мишень равна 0,7, а другого 0.6. Каждый из стрелков сделал по одному выстрелу по мишени. Какова вероятность поражения мишени?
А- первый стрелок попал в мишень
В – второй стрелок попал в мишень
С – мишень поражена
А и В независимые события