- Главная
- Справочники
- Справочник по математике для начальной школы
- Числовые и буквенные выражения
Числовые выражения
В этом разделе мы узнаем, что называют числовым выражением и значением выражения, научимся читать выражения.
Числовое выражение – это запись , состоящая из чисел и знаков действий между ними.
Например, 44 + 32
Значение выражения — это результат выполненных действий.
Например, в записи 44 + 32 = 76, значение выражения — это 76.
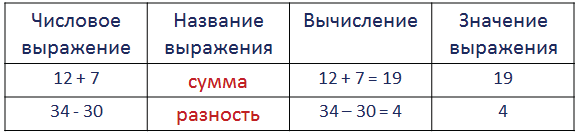
Чтение числовых выражений
12 + 9 — сумма
49 — 20 — разность
34 — (8 + 21) — из 34 вычесть сумму чисел 8 и 21
13 + (26 — 
Решение числовых выражений
45 – (30 + 2) = …
Сначала выполняем действие, записанное в скобках. К 30 прибавляем 2.
30 + 2 = 32
Теперь нужно из 45 вычесть 38.
45 – 32 = 13
45 – (30 + 2) = 13
Сравнение значений числовых выражений
Сравнить числовое выражение – найти значение каждого из выражений и их сравнить.
Давай сравним значения двух выражений: 14 — 6 и 18 — 9.
Для этого найдем значения каждого из них:
14 — 6 = 8
18 — 9 = 9
8 < 9, значит,
14 — 6 < 18 — 9
Буквенные выражения
Буквенным называется математическое выражение, в котором используются цифры, знаки действий и буквы. Например, (47 + d) – 11.
В этих выражениях буквы могут обозначать различные числа. Число, которым заменяют букву, называют значением.
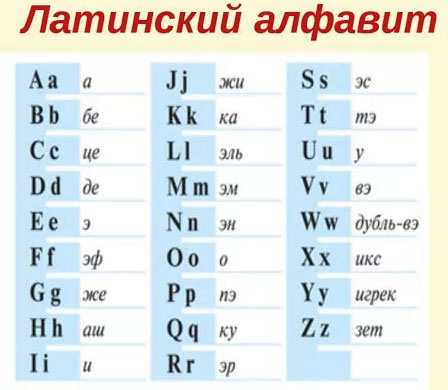
Для записи буквенных выражений необходимо знать некоторые буквы латинского алфавита. Мы приводим его полностью, чтобы ты знал, с какими буквами можешь встретиться при составлении, решении или чтении буквенных выражений.
Чаще всего используются буквы:
a, b, c, d, x, y, k, m, n
Алгоритм решения буквенного выражения
Алгоритм — значит, порядок, план выполнения команд.
1. Прочитать буквенное выражение
2. Записать буквенное выражение
3. Подставить значение неизвестного в выражении
4. Вычислить результат
Например, 28 – с
Читаем выражение: Из 28 вычесть с или Найти разность числа 28 и с
Подставим вместо неизвестного «с» число 4.
У нас получается выражение: 28 – 4
Вычисляем результат:
28 – 4 = 24
Переменные
Буквы, которые содержатся в буквенных выражениях называются переменными. Например, в выражении с + x + 2 переменными являются буквы c и x. Если вместо этих переменных подставить любые числа, то буквенное выражение с + x + 2 обратится в числовое выражение, значение которого можно будет найти.
Числа, которые подставляют вместо переменных называют значениями переменных. Например, изменим значения переменных c и x. Для изменения значений используется знак равенства
c = 2, x = 3
Мы изменили значения переменных c и x. Переменной c присвоили значение 2, переменной x присвоили значение 3, тогда выражение с + х + 2 будет выглядеть так:
2 + 3 + 2
Теперь мы можем найти значение этого выражения:
с + х + 2 = 2 + 3 + 2 = 5 + 2 = 7
Советуем посмотреть:
Уравнения
Правило встречается в следующих упражнениях:
1 класс
Страница 18. Урок 11,
Петерсон, Учебник, часть 1
Страница 8. Урок 5,
Петерсон, Учебник, часть 2
Страница 10. Урок 6,
Петерсон, Учебник, часть 2
Страница 45. Урок 23,
Петерсон, Учебник, часть 2
Страница 57. Урок 29,
Петерсон, Учебник, часть 2
Страница 15. Урок 8,
Петерсон, Учебник, часть 3
Страница 29. Урок 15,
Петерсон, Учебник, часть 3
Страница 35. Урок 18,
Петерсон, Учебник, часть 3
Страница 37. Урок 19,
Петерсон, Учебник, часть 3
Страница 44. Урок 23,
Петерсон, Учебник, часть 3
2 класс
Страница 40,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 81,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 60,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 75,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 14,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 51,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 40,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 38. Урок 15,
Петерсон, Учебник, часть 2
Страница 63. Урок 25,
Петерсон, Учебник, часть 2
Страница 69. Урок 28,
Петерсон, Учебник, часть 2
3 класс
Страница 70,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 97,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 99,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 105,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 23,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 8,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 27,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 61,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 48. Урок 18,
Петерсон, Учебник, часть 1
Страница 52. Урок 24,
Петерсон, Учебник, часть 3
4 класс
Страница 9,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 11,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 19,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 34,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 62,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 92,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 58,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 56,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 62,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 74,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
5 класс
Задание 503,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 642,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1398,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1723,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1841,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 253,
Мерзляк, Полонский, Якир, Учебник
Номер 260,
Мерзляк, Полонский, Якир, Учебник
Номер 1,
Мерзляк, Полонский, Якир, Учебник
Номер 6,
Мерзляк, Полонский, Якир, Учебник
Номер 4,
Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 126,
Мерзляк, Полонский, Якир, Учебник
Номер 315,
Мерзляк, Полонский, Якир, Учебник
Номер 1106,
Мерзляк, Полонский, Якир, Учебник
Номер 1,
Мерзляк, Полонский, Якир, Учебник
Задание 481,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 597,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1083,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1110,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1201,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1564,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 316,
Мерзляк, Полонский, Якир, Учебник
Номер 480,
Мерзляк, Полонский, Якир, Учебник
Номер 481,
Мерзляк, Полонский, Якир, Учебник
Номер 906,
Мерзляк, Полонский, Якир, Учебник
Номер 1040,
Мерзляк, Полонский, Якир, Учебник
Номер 1071,
Мерзляк, Полонский, Якир, Учебник
Номер 1139,
Мерзляк, Полонский, Якир, Учебник
Номер 1,
Мерзляк, Полонский, Якир, Учебник
Номер 2,
Мерзляк, Полонский, Якир, Учебник
Номер 4,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 2,
Мерзляк, Полонский, Якир, Учебник
Номер 3,
Мерзляк, Полонский, Якир, Учебник
Номер 4,
Мерзляк, Полонский, Якир, Учебник
Номер 46,
Мерзляк, Полонский, Якир, Учебник
Номер 47,
Мерзляк, Полонский, Якир, Учебник
Номер 229,
Мерзляк, Полонский, Якир, Учебник
Номер 391,
Мерзляк, Полонский, Якир, Учебник
Номер 392,
Мерзляк, Полонский, Якир, Учебник
Числовые выражения: что это
Числовое выражение — это запись, которая состоит из чисел и знаков арифметического действия между ними.
Именно числовые выражения окружают нас повсюду — не только на уроках математики, но и в магазине, на кухне или когда мы считаем время. Простые примеры, в которых нужно вычислить разность, сумму, получить результат умножения или деления — это все числовые выражения.
Например:
-
23 + 5
-
5 — 2
-
52 * 3
-
28 : 7
Это простые числовые выражения.
Более сложные числовые выражения состоят из нескольких чисел и знаков арифметических действий:
-
(5 * 3) — (5 * 2)
-
6 : (7 — 4)
-
(45 + 45) : 9
-
11 * (5 * 5)
Число, которое мы получаем после выполнения всех арифметических действий в числовом выражении, называют значением этого выражения.
Вспомним, какие виды арифметических действий есть.
+ — знак сложения, найти сумму.
— — знак вычитания, найти разность.
* — знак умножения, найти произведение.
: — знак деления, найти частное.
-
5 + 6 = 11
11 — значение числового выражения 5 + 6.
6 * 8 = 48
48 — значение числового выражения 6 * 8.
При вычислении сложных числовых выражений нужно строго соблюдать очередность выполнения арифметических действий:
-
Сначала выполняется действие, записанное в скобках.
-
Затем выполняются действия деления и умножения слева направо.
-
В последнюю очередь выполняются действия сложения и вычитания слева направо.
Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Пример 1. Найдите значение числового выражения: 3 * (2 + 
-
2 + 8 = 10
-
3 * 10 = 30
-
30 — 4 = 26
3 * (2 + 
Пример 2. Найдите значение числового выражения: (6 + 7) * (13 + 2)
-
6 + 7 = 13
-
13 + 2 = 15
-
13 * 15 = 195
(6 + 7) * (13 + 2) = 195
Часто бывает нужно сравнить два числовых выражения.
Сравнить числовые выражения — значит найти значения каждого выражения и сравнить их.
Пример 1. Сравните два числовых выражения: 6 + 8 и 2 * 2
-
Сначала находим значение первого выражения:
6 + 8 = 14
-
Затем находим значение второго выражения:
2 * 2 = 4
-
Сравниваем получившиеся результаты:
14 больше 4
14 > 4
6 + 8 > 2 * 2
Пример 2. Сравните следующие числовые выражения:
5 * (12 — 2) — 7 и (115 + 9) — (7 — 3)
-
Находим значение первого выражения, соблюдая порядок выполнения арифметических действий:
12 — 2 = 10
5 * 10 = 50
50 — 7 = 43
5 * (12 — 2) — 7 = 43
-
Затем находим значение:
115 + 9 = 124
7 — 3 = 4
124 — 4 = 120
-
Сравниваем полученные результаты:
43 меньше 120
43 < 120
5 * (12 — 2) — 7 < (115 + 9) — (7 — 3).
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Буквенные выражения
Кажется, с числовыми выражениями все достаточно просто. Буквенные выражения немногим сложнее.
В буквенном выражение есть цифры, знаки арифметических действия и буквы.
Получается, что буквенное выражение — это числовое выражение, в котором есть не только числа, но и буквы.
-
Например:
(5 + a) * 7
7 * (x — 2)
(6 — 2) + (3 + x)
Это буквенные выражения. Для записи буквенных выражений используют буквы латинского алфавита.
У буквенных выражений, как и у числовых, есть определенный алгоритм вычисления:
-
Сначала следует прочитать его полностью.
-
Затем оно записывается.
-
Третьим шагом идет подстановка значения неизвестного в выражение.
-
А затем производится вычисление, согласно очередности выполнения арифметических действий.
Пример 1. Найдите значение выражения при x = 4: 5 + x.
- Читаем: найдите сумму числа 5 и x.
- Подставляем вместо неизвестного x число 4.
- Вычисляем: 5 + 4 = 9.
Пример 2. Найдите значение выражения: (4 + a) * (2 + x) при а = 2 и х = 5.
-
Читаем: найдите произведение суммы числа 4 и а и суммы числа 2 и x.
-
Подставляем вместо неизвестного a число 2.
-
Вычисляем 4 + 2 = 6.
-
Подставляем вместо неизвестного x число 5.
-
Вычисляем 2 + 5 = 7.
-
Находим произведение 6 * 7 = 42.
-
Записываем результат: (4 + 2) * (2 + 5) = 42.
Выражения с переменными
Переменная — буквенное обозначение элемента, который может принимать любое числовое значение.
-
Например, в выражении x + a — 8
x — переменная
a — переменная
Если вместо переменных подставить числа, то буквенное выражение x + a — 8 станет числовым выражением. Вот так:
-
подставляем вместо переменной x число 5, а вместо переменной a — число 10, получаем 5 + 10 — 8.
Числа, которые подставляют вместо переменных — это значения переменных. В нашем примере это числа 5 и 10.
После подстановки значения переменных находим значение x + a — 8 = 5 + 10 — 8 = 7.
Часто можно встретить буквенные выражения, записанные следующим образом:
5x — 4a
Число и переменная записаны без знака арифметического действия. Так коротко записывается умножение.
-
5x — 4a = 5*x — 4*a
5x — это произведение числа 5 и переменной x.
4a — это произведение числа 4 и переменной a.
Числа 4 и 5 называют коэффициентами.
Коэффициент показывает, во сколько раз будет увеличена переменная.
Теперь вы вооружены всеми необходимыми теоретическими знаниями о числовых и буквенных выражениях. Давайте немного поупражняемся в решении задачек и примеров, чтобы научиться применять полученные знания на практике.
Задание раз.
Запишите выражения:
-
Сумма 6 и a.
-
Разность 8 и x.
-
Сумма x — 2 и 6.
-
Разность 15 и x — y.
-
Сумма 45 + 5 и 12 — 6.
Ответ:
-
6 + a.
-
8 — x.
-
(x — 2) + 6.
-
15 — (x — y).
-
(45 + 5) + (12 — 6).
Задание два.
Составьте буквенное выражение:
Сумма разности b и 345 и суммы 180 и x.
Ответ: (b — 345) + (180 + x).
Задание три.
Составьте буквенное выражение:
Разность разности 30 и y и разности a и b.
Ответ: (30 — y) — (a — b).
Задание четыре.
Составьте выражение для решения задачи и найдите его значение.
Ролл «Калифорния» стоит 480 рублей — это на 40 рублей меньше, чем ролл «Филадельфия». Сколько будут стоить оба ролла?
Как решаем:
Калифорния — 480 рублей.
Филадельфия — 480 + 40.
Калифорния + Филадельфия = ?
480 + (480 + 40).
Мы помним, что выполнение арифметических действий в числовом выражении имеет строгую последовательность. Сначала — действие в скобках:
480 + 520 = 1 000.
Ответ: роллы “Калифорния” и “Филадельфия” вместе стоят 1 000 рублей.
Задание пять.
Составьте выражение для решения задачи и найдите его значение.
Маша посмотрела за день 150 видео в ТикТок, а Лена — на 13 видео больше. Сколько всего видео было просмотрено обеими девочками?
Маша — 150 видео.
Лена — 150 + 13 видео.
Маша + Лена = ? видео.
150 + (150 + 13).
Выполняем сначала действие в скобках: 150 + 13 = 163.
150 + 163 = 313.
Ответ: Маша и Лена посмотрели всего 313 видео.
Задание шесть.
Вычислите:
(500 + 300) : a — 15,
при условии, что a = 10.
Как решаем:
Подставляем число 10 (значение переменной) вместо переменной
(500 + 300) : 10 — 15
Затем выполняем сначала арифметическое действие в скобках: 500 + 300 = 800.
Затем выполняем деление 800 : 10 = 80.
Выполняем вычитание 80 — 15 = 65.
Ответ: (500 + 300) : 10 — 15 = 65.
Задание семь.
Вычислите:
(270 — 120) * (x — 10),
при условии, что x = 45.
Как решаем: подставляем число 45 (значение переменной) вместо переменной x
(270 — 120) * (45 — 10).
Затем выполняем сначала арифметическое действие в скобках: 270 — 120 = 150.
Выполняем арифметическое действие во вторых скобках: 45 — 10 = 35.
Затем выполняем умножение 150 * 35 = 5 250.
Ответ: (270 — 120) * (45 — 10) = 5 250.
Задание восемь.
Вычислите:
(50 * x) — (3 * y)
при условии, что x = 2; y = 10
Как решаем:
Подставляем число 2 вместо переменной x
(50 * 2) — (3 * y).
Подставляем число 10 вместо переменной y
(50 * 2) — (3 * 10).
Затем выполняем сначала арифметическое действие в скобках: 50 * 2 = 100.
Выполняем арифметическое действие во вторых скобках: 3 * 10 = 30.
Затем выполняем вычитание 100 — 30 = 70
Ответ: (50 * 2) — (3 * 10) = 70.
Математическое выражение может содержать число или букву.
Пример
78,
у.
Они также могут состоять из двух и более чисел или букв, которые соединяют знаки математического действия.
Пример
х-4,
2с,
2у+х.
Математическое выражение может быть двух видов.
Определение
Числовое выражение содержит исключительно числа и не включает букв.
Пример
4,
8*7,
8-4,
47+58*2.
При выполнении действий, указанных в числовом выражении, в результате получается числовое значение выражения.
Пример
Запись 3*6+50 является числовым выражением.
После всех вычислений получится число 68 — числовое значение представленного выражения.
В любом математическом выражении числа могут заменяться строчными латинскими буквами.
Пример
7х,
ас-у,
40:5-х.
Определение
Выражение, составленное из чисел, представленных буквами либо цифрами и буквами, является буквенным.
Пример
17+a,
a+z,
7-(2+d).
Внимание!
При записи выражения не используются знаки равенства или неравенства— =, ≠, <, ≤, >, ≥.
Пример
Назвать в разности уменьшаемое и вычитаемое. Прочитать запись.
- а-(с+15)
а является уменьшаемым, а (с+15) — вычитаемое.
Читается как разность чисел а и суммы чисел с и 15.
- (с-170) – (150-k)
В представленном выражении (с-170) — является уменьшаемым, а (150-k) — вычитаемым.
Читается как разность разности чисел с и 170 и разности чисел 150 и k.
Коэффициент
В математических задачах часто встречаются выражения, в которых числа и переменные записываются вместе, без каких либо знаком математического действия. К примеру, 5с — это сокращенный вариант действия умножения числа 5 на переменную с.
Эту запись можно представить иначе — 5с=5*с.
Следовательно, выражение 5с это произведение числа 5 и переменной с.
Число 5 в данном примере выступает коэффициентом, который указывает на сколько раз требуется увеличить переменную с.
Определение
Коэффициент — число, стоящее перед переменной.
Обрати внимание!
Числовой множитель (коэффициент) всегда находится перед буквой.
При записи буквенного выражения знак действия умножения ставиться исключительно между числами, представленными цифрами. В остальных вариантах его не ставят (опускают).
Пример
- между буквенным и числовым множителем — 10*у=10у;
- между двумя и более буквенными множителями — с*х=сх;
- между множителем, представленным числом, и скобкой — 7*(а+у)=7(а+у);
- между множителем, представленным переменной, и скобкой — с*(а+х)=с(а+х).
Как прочитать буквенное выражение
Пример
5х — пять икс.
Чтения более сложного выражение, необходимо выполнять с последнего действия.
Пример
(с-а)*у
Последним действием является умножение, следовательно, запись читается как произведение разности чисел с и а на число с.
Пример
Необходимо прочитать запись 7сху.
В данном варианте число 7 является коэффициентом, который указывает, что произведение переменных сху должно быть повышено на 7 раз.
Запись можно прочитать тремя способами:
- сху семь раз,
- повысить значение переменных сху в семь раз,
- семь сху.
Определение
Буква, содержащаяся в буквенном выражении, называется переменной.
Пример
В записи с+х+9 — с и х переменные.
Если на их место поставить число, буквенное выражение с+х+9 трансформируется в числовое, которое после выполнения всех действия приобретет значение.
Определение
Число, которое становиться взамен буквы, называется значением переменной.
Пример
Необходимо изменить значение переменной в записи
с=4, а х=7
После замены буквенное выражение с+х+9 трансформируется в числовое — 4+7+9, значение которого можно вычислить. 4+7+9=20.
Пример
Необходимо вычислить значение записи 1230:у+103, если у=15.
Взамен переменной у ставим число 15.
1230:у+103=1230:15+103=82+103=185.
Свойства сложения и вычитания в буквенной записи
Сложение
Переместительное свойство — при перестановке мест слагаемых значение суммы останется неизменным.
В буквенной записи данное свойство будет иметь вид — с+х=х+с, при условии, что буквы с и х являются натуральными числами или равны нулю.
Сочетательное свойство — для сложения суммы двух чисел с третьим числом, разрешено к первому слагаемому добавить сумму второго и третьего.
В буквенной записи это свойство выглядит как — (у+с)+х=у+(с+х).
Вычитание
Чтобы вычесть сумму из числа, можно от него отнять первое слагаемое, а затем от полученного результата вычесть второе слагаемое.
а-(с+у)=(а-с)-у
или
а-(с+у)=(а-с)-у
Чтобы вычесть число из суммы двух чисел, можно отнять его от первого слагаемого, а к найденному результату добавить второе слагаемое.
(с+х)-у=(с-у)+х, при этом с >у либо с=у
или
(с+х)-у=(х-у)+с, при условии, что х>у либо х=у.
На предыдущих уроках подробно рассмотрели арифметические операции сложения и вычитания натуральных чисел.
Выяснили, какими свойствами обладают данные математические операции.
Эта информация доступна зарегистрированным пользователям
На этом занятии познакомимся с буквенной записью свойств сложения и вычитания натуральных чисел.
Определим, каким образом можно упрощать числовые и буквенные выражения, используя свойства сложения и вычитания.
Перевод математической записи из словесной формы в символьную позволяет представить математическое утверждение наглядно, кратко, однозначно.
Так, например, при передаче информации в словесной форме в предложении можно менять слова и предложения в тексте, не нарушая общего смысла, а в записи высказываний на математическом языке чаще всего это недопустимо.
Пример.
Эта информация доступна зарегистрированным пользователям
«В одной корзине 30 грибов, во второй корзине на 6 грибов больше. Всего в двух корзинах 66 грибов.»
Попробуем сказать данное утверждение по-другому.
«Всего собрали 66 грибов. В одной корзине 30 грибов, в другой на 6 грибов больше»
Математический смысл и численные значения остались прежними.
С помощью чисел и знаков данное текстовое утверждение запишем так:
30 + (30 + 6) = 66.
Осмысленная комбинация математических символов, букв и знаков, как нам уже известно, называется математическим выражением.
Математические выражения делят на числовые и буквенные.
Числовые выражения состоят только из чисел, знаков математических операций и других специальных математических символов.
Буквенные выражения помимо чисел и знаков математических операций и других специальных математических символов содержит еще и буквы.
Буквы, входящие в буквенные выражения, называют переменными.
Слово «переменная» схоже по значению со словами «меняющаяся», «измененная», «непостоянная», что говорит о том, что буква в выражении, которая является переменной, может менять свое значение, т.е. принимать множество допустимых значений.
Переменную обозначают символом (чаще всего латинской буквой), общим для любого ее значения.
Пример.
Дано буквенное выражение а + 2.
а— это переменная.
Присвоим данной переменной значение 10.
Для этого приравняем ее к десяти, т.е. запишем а = 10.
В таком случае значение переменной а можно подставить в выражение а + 2
Эта информация доступна зарегистрированным пользователям
Получим числовое выражение 10 + 2, которое можно вычислить.
10 + 2 = 12
В буквенных выражениях могут находиться одна, две, три и более переменных.
Переменные, имеющие одно и то же значение, обозначаются одной буквой.
Соответственно, разными буквами обозначают различные по значению переменные.
Значение выражения с переменными зависит от значения переменных, входящих в него.
Последовательность выполнения арифметических операций в выражениях с переменными такая же, что и для числовых выражений.
С помощью выражений с переменными удобно записывать и доказывать различные теоремы, правила, законы и т.д.
В результате получается универсальная символьная запись, которая отвлечена от конкретных количественных значений.
Рассмотрим поясняющий пример.
Тему «Сложение натуральных чисел», мы рассматривали на числовых примерах.
Например, 2 + 3 = 5
Говорили, что
число 2— это первое слагаемое
число 3— это второе слагаемое
число 5— это сумма чисел 2 и 3.
Но в таком случае мы имели конкретный пример и лишь оговаривали, что он справедлив для любых натуральных чисел.
Правило сложения натуральных чисел можно было бы сделать универсальным, заменив числовое выражение на буквенное, обозначив компоненты сложения буквами (переменными).
Например,
первое слагаемое- а
второе слагаемое- b
сумма чисел- c.
Получили бы равенство с тремя переменными a + b = c.
Эта информация доступна зарегистрированным пользователям
Пользуясь полученным равенством, с легкостью можно определить сумму, подставляя различные значения переменных a и b.
Меняя значения переменных a и b, переменная с будет соответственно меняться тоже.
Допустим дано выражение a + b.
1. Найдем значение выражения a + b, если a = 6, b = 8
Решение:
Сумму натуральных чисел найдем с помощью равенства:
a + b = c
Подставим значения переменных в равенство, получим
6 + 8 = 14.
Ответ: переменная с равна 14 при a = 6, b = 8
2. Найдем значение выражения a + b, если a = 7, b = 5
Решение:
Опять же сумму натуральных чисел найдем с помощью равенства:
a + b = c
Подставим значения переменных в равенство, получим
7 + 5 = 12
Ответ: переменная с равна 12 при a = 7, b = 5.
При изменении значений переменных a и b, менялось значение переменной с.
Эта информация доступна зарегистрированным пользователям
Чтобы тождественно преобразовать одно выражение в другое, используют различные свойства арифметических операций.
Эта информация доступна зарегистрированным пользователям
Давайте рассмотрим подробней свойства сложения и вычитания натуральных чисел и запишем их в буквенном виде.
Эта информация доступна зарегистрированным пользователям
Мы выяснили, что с помощью буквенных выражений (выражений с переменными) можно записывать различные правила, доказательства, законы, и такая запись является наиболее удобной для запоминания и эффективной при вычислениях и преобразованиях.
1. Переместительное свойство сложения натуральных чисел.
Это свойство заключается в том, что результат сложения натуральных чисел не зависит от порядка следования слагаемых.
При перестановке слагаемых сумма не меняется.
Данное свойство в буквенной форме можно записать так:
a + b = b + a
В этом равенстве переменные а и b могут принимать любые натуральные значения или 0.
Рассмотрим примеры, подтверждающий данное свойство.
Пример 1.
Дано равенство с переменными а и b.
a + b = b + a (переместительный закон сложения)
Заменим буквы в данном равенстве их значениями:
a= 16
b= 20
И найдем значение числового равенства.
Решение:
16 + 20 = 20 + 16
В правой части равенства сумма 16 и 20 равна 36
16 + 20 = 36
В левой части равенства сумма 20 и 16 равна 36
20 + 16 = 36
Значение левой и правой часть равенства равны, при перестановке слагаемых местами сумма не изменилась.
Пример 2.
Рассмотрим в качестве примера задачу.
Точка О лежит на отрезке АВ.
Дина отрезка АО равна 15 см, длина отрезка ОВ равна 24 см.
Найдите длину отрезка АВ.
Эта информация доступна зарегистрированным пользователям
Решение:
Так как точка О принадлежит отрезку АВ, то она делит этот отрезок на две части (на два отрезка АО и ОВ).
Длина отрезка АВ равна сумме длин его частей, т.е. отрезков АО и ОВ.
АВ = АО + ОВ.
Подставим в равенство значения длин отрезков АО и ОВ.
Получим:
15 + 24 = 39 (см) длина отрезка АВ
Ответ: 39 см.
Если мы в равенстве АВ = АО + ОВ поменяем местами слагаемые, то длина отрезка будет равна:
АВ = ОВ + АО
Подставим в равенство значения длин отрезков АО и ОВ.
Получим:
24 + 15 = 39 (см) длина отрезка АВ
Ответ: 39 см.
При перестановке слагаемых местами сумма не изменилась, длина отрезка в первом и во втором случае равна 39 см.
2. Сочетательное свойство сложения натуральных чисел.
Последовательность действий при суммировании чисел не важна.
Сочетательное свойство сложения звучит так:
Чтобы прибавить к числу сумму двух чисел, можно сначала к нему прибавить первое слагаемое, потом к полученной сумме второе.
Данное свойство с помощью букв записывается таким образом:
a + (b + c) = (a + b) + c
Причем переменные a, b, c— любые натуральные числа или нуль.
Приведем примеры, подтверждающий данное свойство.
Пример 1.
Дано равенство- сочетательный закон сложения
a + (b + c) = (a + b) + c
Подставим вместо букв a, b, c их значения:
a = 32
b = 8
c = 13
И найдем значение числового равенства.
Решение:
32 + (8 + 13) = (32 + 
В левой части равенства к числу 32 прибавим сумму чисел 8 и 13, соблюдая порядок выполнения арифметических операций.
Известно, что первым выполняется действие в скобках.
32 + (8 + 13) = 32 + 21 = 53.
В правой части равенства стоит выражение, в котором к сумме чисел 32 и 8 необходимо прибавить число 13.
(32 + 
Выражения левой и правой части равенства имеют одинаковые значения, следовательно, равенство 32 + (8 + 13) = (32 + 
Отметим тот факт, что значение числового выражения во втором случае найти было легче, так как в сумме 32 и 8 давали круглое число 40.
Как нам известно, выполнять действия с круглыми числами намного проще.
Такого рода упрощения математических выражений используют при решении задач.
Пример 2.
Решим в качестве примера задачу.
Дан треугольник АВС.
Эта информация доступна зарегистрированным пользователям
Сторона а = 4 см, сторона b = 6 см, сторона с = 9 см.
Найдите периметр треугольника АВС.
Решение:
Периметр треугольника равен сумме длин трех его сторон.
Найдем периметр треугольника по формуле:
РАВС = a + b + c
Сложить длины сторон треугольника можно двумя способами.
1) Сначала найти сумму длин сторон a и b, а затем прибавить длину стороны с.
РАВС = (a + b) + c
Заменим буквы их значениями, получим равенство:
РАВС = (4 + 6) + 9 = 10 + 9 = 19 (см) периметр треугольника АВС
Ответ: 19 см.
2) Можно сначала найти сумму длин сторон b и c, а затем прибавить длину стороны а.
РАВС = a + (b + c)
Заменим буквы их значениями, получим равенство:
РАВС = 4 + (6 + 9) = 4 + 15 = 19 (см) периметр треугольника АВС
Ответ: 19 см.
В первом и во втором варианте решения задачи получили периметр треугольника АВС равный 19 см, что доказывает равносильность первого и второго равенства.
Однако в первом случае найти значение выражения было проще, так как при сложении 4 и 6 получили круглое число 10.
3. Свойство сложения натурального числа с нулем.
Данное свойство говорит о том, что прибавление к любому числу нуля не изменяет это число.
Свойство сложения натурального числа с нулем звучит так:
Сумма двух слагаемых, если одно из слагаемых равно нулю, будет всегда равна ненулевому слагаемому.
Обратите внимание, как выглядит данное свойство в буквенном виде:
а = а + 0
а = 0 + а
а— любое натуральное число.
Часто говорят, что нуль- это нейтральный элемент по сложению.
Приведем примеры, подтверждающий данное свойство.
Пример 1.
Пусть даны два равенства
а + 0 = а
0 + а = а
Подставим в первое и во второе равенство вместо букв a, ее значение.
a = 48
Решение:
48 + 0 = 48
0 + 48 = 48
Прибавляя число к нулю или нуль к числу, получается в ответе само это число.
Пример 2.
Рассмотрим в качестве примера две небольшие задачи.
1. У кормушки сидели 5 птиц, к ним прилетели еще 0 птиц.
Сколько птиц всего стало у кормушки?
Эта информация доступна зарегистрированным пользователям
К 5 птицам прилетело ноль птиц,;это значит, что не прилетело ни одной, следовательно, у кормушки осталось по-прежнему 5 птиц.
5 + 0 = 5 (птиц) стало у кормушки.
Ответ: 5 птиц.
Обратная ситуация будет складываться во второй задаче.
2. У кормушки не сидело ни одной птицы, прилетели к кормушке 5 птиц.
Сколько птиц всего стало у кормушки?
Не было у кормушки ни одной птицы, значит, сидело ноль птиц, когда прилетели 5 птиц, то только эти 5 птиц и стали сидеть у кормушки.
0 + 5 = 5 (птиц) стало у кормушки.
Ответ: 5 птиц.
Прибавляя число к нулю или нуль к числу, получили в результате само это число.
Эта информация доступна зарегистрированным пользователям
Выясним, как записать свойства вычитания с помощью буквенных выражений.
1. Свойство вычитания суммы двух чисел из натурального числа.
Вспомним формулировку свойства вычитания суммы двух чисел из натурального числа.
Чтобы вычесть сумму из числа, можно сначала выполнить сложение, а затем вычесть полученную сумму из уменьшаемого числа.
Справедливо также следующее правило:
Чтобы вычесть сумму из числа, можно сначала из уменьшаемого вычесть одно из слагаемых, а затем из полученной разности вычесть другое слагаемое.
Данное свойство запишем с помощью букв.
a— (b + c) = (a— b) — c = (a— с) — b
a, b, c— натуральные числа.
Обязательно должно выполняться условие: сумма чисел, которую вычитают из числа, должна быть больше или равна вычитаемому, т.е. b + c < a или b + c = а
Рассмотрим примеры.
Пример 1.
Запишем свойства вычитания суммы двух чисел из натурального числа с помощью букв.
a— (b + c) = (a— b) — c = (a— c) — b
Подставим вместо букв a, b, c их значения:
a = 17
b = 3
c = 1
Решение:
17 — (3 + 1) = (17 — 3) — 1 = (17 —1) — 3
1) В первом выражении из числа 17 нужно вычесть сумму чисел 3 и 1.
17 — (3 + 1) = 17 — 4 = 13
2) Во втором выражении из числа 17 нужно вычесть первое слагаемое 3, затем из полученной разности вычесть число 1.
(17 — 3) — 1 = 14 — 1 = 13
3) В третьем выражении из числа 17 нужно вычесть второе слагаемое 1, затем из полученной разности вычесть число 3.
(17 — 1) — 3 = 16 — 3 = 13
Заметим, что все три выражения имеют равные значения.
Вывод: вычесть сумму из числа- это тоже самое, что вычесть из числа по отдельности каждое слагаемое этой суммы.
Пример 2.
Разберем второй пример, подтверждающий данное утверждение.
Решим задачу.
На стоянке было 9 автомобилей.
Со стоянки выехало 3 зеленых, затем 2 красных автомобиля.
Сколько автомобилей осталось на стоянке?
Эта информация доступна зарегистрированным пользователям
Решить данную задачу можно двумя способами.
1) Решение задачи первым способом:
Составим краткую запись задачи.
Было на стоянке- 9 (авт.)
Выехали:
Эта информация доступна зарегистрированным пользователям
Сколько осталось?
Разберем план решения:
Чтобы узнать сколько автомобилей осталось на стоянке, необходимо выяснить сколько всего автомобилей выехало с нее.
Затем из общего числа автомобилей вычесть общее количество уехавших.
Если зеленых выехало 3 авт., а красных 2 авт., то число всех, покинувших стоянку автомобилей, найдем суммой 3 и 2.
Получаем: 3 + 2 (авт.)- уехали со стоянки.
Из 9 вычтем сумму 3 + 2, узнаем сколько автомобилей осталось.
Составим выражение 9 — (3 + 2).
Найдем значение данного выражения.
9 — (3 + 2) = 9 — 5 = 4 (авт.) осталось на стоянке.
Ответ: 4 автомобиля.
1) Решение задачи вторым способом:
Первым делом определим сколько осталось автомобилей, когда уехали со стоянки 3 зеленых.
Для этого из общего количества, находящихся на стоянке автомобилей (9 авт.), вычтем 3 зеленых.
Получаем выражение 9 — 3.
Затем из оставшихся автомобилей необходимо отнять количество автомобилей красного цвета, покинувших автостоянку.
Таким образом, определим сколько автомобилей осталось после того, как уехали со стоянки 3 зеленых и 2 красных.
Из разности 9 — 3 вычтем число 2.
Составим числовое выражение и найдем его значение.
(9 — 3) — 2 = 6 — 2 = 4 (авт.) осталось на стоянке
Ответ: 4 автомобиля.
В первом и во втором варианте решения задачи получили ответ одинаковый- 4 автомобиля, следовательно, выражения, составленные для первой и второй задачи тождественно равны.
9 — (3 + 2) = (9 — 3) — 2.
2. Свойство вычитания натурального числа из суммы натуральных чисел.
Вспомним формулировку свойства вычитания натурального числа из суммы натуральных чисел.
Чтобы вычесть число из суммы, можно сначала определить сумму, а затем из полученного результата вычесть число.
При условии, что одно из слагаемых равно или больше числа, вычитаемого из этой суммы, возможна еще одна формулировка свойства вычитания натурального числа из суммы натуральных чисел.
Чтобы вычесть число из суммы, можно его вычесть из одного из слагаемых, затем к полученной разности прибавить второе слагаемое.
Буквенная запись данного свойства выглядит так:
(a + b) — c = (a— c) + b, где а > с или а = c
(a + b) — c = a + (b— c), где b > с или b = c
a, b, c— натуральные числа
а + b > c
Рассмотрим примеры.
Пример 1.
Запишем свойства вычитания суммы двух чисел из натурального числа с помощью букв.
(a + b) — c = (a — c) + b = a + (b — c)
Пусть a = 23, b = 12, c = 3.
Подставим вместо букв a, b, c их значения:
Решение:
(23 + 12) — 3 = (23 — 3) + 12 = (12 —3) + 23
1) В первом выражении из суммы чисел 23 и 12 вычтем число 3.
(23 + 12) — 3 = 35 — 3 = 32
2) Во втором выражении от первого слагаемого равного 23, можно отнять вычитаемое число 3 (так как 23 больше вычитаемого числа), а затем к полученной разности прибавить второе слагаемое 12.
(23 — 3) + 12 = 20 + 12 = 32
3) В третьем выражении из второго слагаемого равного 12, можно вычесть вычитаемое число 3 (так как 12 больше вычитаемого числа), а затем к полученной разности прибавить первое слагаемое 23.
(12 — 3) + 23 = 9 — 23 = 32
Во всех трех случаях получили одно и тоже значение 32, следовательно, все три числовые выражения тождественно равны.
Пример 2.
Рассмотрим задачу на вычитание числа из суммы.
С одной ветки сорвали 18 слив, а со второй- 10.
Съели 12 слив. Сколько слив осталось?
Эта информация доступна зарегистрированным пользователям
Составим краткую запись задачи.
Сорвали:
Эта информация доступна зарегистрированным пользователям
Съели- 12 слив.
Осталось- ?
Данную задачу попробуем решить разными способами.
1) Решение задачи первым способом:
Выясним план решения.
Чтобы узнать сколько осталось слив, нужно сначала определить общее количество слив, сорванных с двух веток.
Получим выражение 18 + 10.
Далее из полученной суммы необходимо вычесть сливы, которые съели, т.е. от суммы 18 + 10 нужно отнять 12.
Составим выражение и найдем его значение:
(18 + 10) — 12 = 28 — 12 = 16 (слив) осталось.
Ответ: 16 слив.
2) Решение задачи вторым способом:
Представим, что все 12 слив были съедены из числа слив, собранных с первой ветки, а затем сорвали 10 слив со второй ветки.
Тогда первым делом из 18 вычтем число 12, выясним сколько осталось слив, собранных с первого куста, получим разность 18 — 12.
К полученной разности прибавим 10 (сливы, собранные со второго куста).
Составим выражение и найдем его значение:
(18 — 12) + 10 = 6 + 10 = 16 (слив) осталось.
Ответ: 16 слив.
При решении задачи первым и вторым способом получили ответ одинаковый- 16 слив, следовательно, выражения, составленные для первой и во второй задачи тождественно равны.
(18 + 10) — 12 = (18 — 12) + 10
3. Вычитание нуля из натурального числа.
Свойства нуля при вычитании: если из числа вычесть нуль, то число не изменится.
Запишем данное свойство в буквенной форме.
а — 0 = а
Пример 1.
Пусть а = 73.
В выражение а — 0 = а вместо переменной а подставим заданное числовое значение этой переменной.
73 — 0 = 73.
Вычитая нуль из числа, получили само это число.
Рассмотрим в качестве примера такую задачу.
На клумбе расцвели 5 тюльпанов.
Ни одного тюльпана не сорвали.
Сколько тюльпанов осталось на клумбе?
Эта информация доступна зарегистрированным пользователям
Решение:
Ни одного тюльпана не сорвали, это значит, что было сорвано 0 тюльпанов.
Запишем кратко условия задачи.
Было- 5 тюльпанов.
Сорвали- 0 тюльпанов.
Осталось- ?
Составим числовое выражение и найдем его значение.
5 — 0 = 5 (тюльпанов) осталось на клумбе.
Ответ: 5 тюльпанов.
4. Вычитание из натурального числа само это число.
Данное свойство звучит так:
Разность двух одинаковых натуральных чисел равна нулю.
Можно сказать и по-другому:
Если из числа вычесть тоже самое число, то в результате получится нуль.
Буквенное представление данного свойства выглядит так:
а — а = 0
а— любое натуральное число.
Пример 1.
Допустим а = 26, то получим числовое равенство
26 — 26 = 0
Пример 2.
Данное свойство можно представить с помощью такой задачи.
В кошельке было 210 рублей.
За покупку в магазине отдали 210 рублей.
Сколько денег осталось в кошельке?
Эта информация доступна зарегистрированным пользователям
Решение:
Запишем кратко условия задачи.
Было (уменьшаемое)- 210 руб.
Отдали (вычитаемое)- 210 руб.
Осталось- ?
Чтобы найти остаток (разность), нужно из уменьшаемого вычесть вычитаемое.
Составим числовое выражение и найдем его значение.
210 — 210 = 0 (руб.) осталось в кошельке.
Ответ: 0 руб.
Эта информация доступна зарегистрированным пользователям
Читайте также
Числовые и буквенные выражения. Формула
Числовые и буквенные выражения.
Формула
Сложение, вычитание, умножение, деление — арифметические действия (или арифметические операции). Этим арифметическим действиям соответствуют знаки арифметических действий:
+ (читаем «плюс«) — знак операции сложения,
— (читаем «минус«) — знак операции вычитания,
∙ (читаем «умножить«) — знак операции умножения,
: (читаем «разделить«) — знак операции деления.
Запись, состоящая из чисел, связанных между собой знаками арифметических действий, называется числовым выражением. В числовом выражении могут присутствовать также скобки Например, запись 1290 : 2 – (3 + 20 ∙ 15) является числовым выражением.
Результат выполнения действий над числами в числовом выражении называется значением числового выражения. Выполнение этих действий называется вычислением значения числового выражения. Перед записью значения числового выражения ставят знак равенства «=». В таблице 1 приведены примеры числовых выражений и их значений.
Запись, состоящая из чисел и малых букв латинского алфавита, связанных между собой знаками арифметических действий называется буквенным выражением. В этой записи могут присутствовать скобки. Например, запись a + b – 3 ∙ c является буквенным выражением. Вместо букв в буквенное выражение можно подставлять различные числа. При этом значение букв может изменяться, поэтому буквы в буквенном выражении называют еще переменными.
Подставив в буквенное выражение числа вместо букв и вычислив значение получившегося числового выражения, находят значение буквенного выражения при данных значениях букв (при данных значениях переменных). В таблице 2 приведены примеры буквенных выражений.
Буквенное выражение может не иметь значения, если при подстановке значений букв получается числовое выражение, значение которого для натуральных чисел не может быть найдено. Такое числовое выражение называется некорректным для натуральных чисел. Говорят также, что значение такого выражения «не определено» для натуральных чисел, а само выражение «не имеет смысла». Например, буквенное выражение a – b не имеет значения при a = 10 и b = 17. Действительно, для натуральных чисел, уменьшаемое не может быть меньше вычитаемого. Например, имея всего 10 яблок (a = 10), нельзя отдать из них 17 (b = 17)!
В таблице 2 (колонка 2) приведён пример буквенного выражения. По аналогии заполните таблицу полностью.
Для натуральных чисел выражение 10 -17 некорректно (не имеет смысла), т.е. разность 10 -17 не может быть выражена натуральным числом. Другой пример: на ноль делить нельзя, поэтому для любого натурального числа b, частное b : 0 не определено.
Математические законы, свойства, некоторые правила и соотношения часто записывают в буквенном виде (т.е. в виде буквенного выражения). В этих случаях буквенное выражение называют формулой. Например, если стороны семиугольника равны a, b, c, d, e, f, g, то формула (буквенное выражение) для вычисления его периметра p имеет вид:
p = a + b + c + d + e + f + g
При a = 1, b = 2, c = 4, d = 5, e = 5, f = 7, g = 9, периметр семиугольника p = a + b + c + d + e + f + g = 1 + 2 + 4 + 5 +5 + 7 + 9 = 33.
При a = 12, b = 5, c = 20, d = 35, e = 4, f = 40, g = 18, периметр другого семиугольника p = a + b + c + d + e + f + g = 12 + 5 + 20 + 35 + 4 + 40 + 18 = 134.
Блок 1. Словарь
Составьте словарь новых терминов и определений из параграфа. Для этого в пустые клетки впишите слова из списка терминов, приведенного ниже. В таблице (в конце блока) укажите номера терминов в соответствии с номерами рамок. Рекомендуется перед заполнением клеток словаря еще раз внимательно просмотреть параграф.
- Операции: сложение, вычитание, умножение, деление.
2.Знаки «+» (плюс), «-» (минус), «∙» (умножить, «:» (разделить).
3.Запись, состоящая из чисел, которые связанны между собой знаками арифметических действий и в которой могут присутствовать также скобки.
4.Результат выполнения действий над числами в числовом выражении.
5. Знак, стоящий перед значением числового выражения.
6. Запись, состоящая из чисел и малых букв латинского алфавита, связанных между собой знаками арифметических действий (могут присутствовать также скобки).
7. Общее название букв в буквенном выражении.
8. Значение числового выражения, которое получается при подстановке переменных.в буквенное выражение.
9.Числовое выражение, значение которого для натуральных чисел не может быть найдено.
10. Числовое выражение, значение которого для натуральных чисел может быть найдено.
11. Математические законы, свойства, некоторые правила и соотношения, записанные в буквенном виде.
12. Алфавит, малые буквы которого используются для записи буквенных выражений.
Блок 2. Установите соответствие
Установите соответствие между заданием в левой колонке и решением в правой. Ответ запишите в виде: 1а, 2г, 3б…
Блок 3. Фасетный тест. Числовые и буквенные выражения
Фасетные тесты заменяют сборники задач по математике, но выгодно отличаются от них тем, что их можно решать на компьютере, проверять решения и сразу узнавать результат работы. В этом тесте содержится 70 задач. Но решать задачи можно по выбору, для этого есть оценочная таблица, где указаны простые задачи и посложнее. Ниже приведён тест.
- Дан треугольник со сторонами c, d, m, выраженными в см
- Дан четырехугольник со сторонами b, c, d, m, выраженными в м
- Скорость автомобиля в км/ч равна b, время движения в часах равно d
- Расстояние, которое преодолел турист за m часов, составляет с км
- Расстояние, которое преодолел турист, двигаясь со скоростью m км/ч, составляет b км
- Сумма двух чисел больше второго числа на 15
- Разность меньше уменьшаемого на 7
- Пассажирский лайнер имеет две палубы с одинаковым количеством пассажирских мест. В каждом из рядов палубы m мест, рядов на палубе на n больше, чем мест в ряду
- Пете m лет Маше n лет, а Кате на k лет меньше, чем Пете и Маше вместе
- m = 8, n = 10, k = 5
- m = 6, n = 8, k = 15
- t = 121, x = 1458
ТО:
- Значение данного выражения
- Буквенное выражение для периметра имеет вид
- Периметр, выраженный в сантиметрах
- Формула пути s, пройденного автомобилем
- Формула скорости v, движения туриста
- Формула времени t, движения туриста
- Путь, пройденный автомобилем в километрах
- Скорость туриста в километрах в час
- Время движения туриста в часах
- Первое число равно…
- Вычитаемое равно….
- Выражение для наибольшего количества пассажиров, которое может перевезти лайнер за k рейсов
- Наибольшее количество пассажиров, которое может перевезти лайнер за k рейсов
- Буквенное выражение для возраста Кати
- Возраст Кати
- Координата точки В, если координата точки С равна t
- Координата точки D, если координата точки С равна t
- Координата точки А, если координата точки С равна t
- Длина отрезка BD на числовом луче
- Длина отрезка CА на числовом луче
- Длина отрезка DА на числовом луче
Ответы (равно, имеет вид, не определено):
а)1; б) s=b ∙d; в) 9; г) 40; д) b + c + d + m; е) 7; ж) выражение не имеет смысла (некорректно) для натуральных чисел; з) 2 ∙ m (m + n) ∙ k; и) (m + n) – k; к) 6; л) 15; м) 3760; н) t – 3; о) фигура не может быть треугольником; п) 22; р) t – 3 ∙ 7; с) 0; т) 32; у) 59600; ф) 6019; х) 2880; ц) 10378; ч)1440; ш) на ноль делить нельзя; щ) 13; ы) 1800; э) 496; ю) 2; я) 12; аа) 14; бб) 5; вв) 35; дд) 79200; ее) 1900; жж) 118; зз) 18; ии) 12800; кк) 98; лл) 1458; мм) v = c : m; нн) 100; оо) 19900; пп) t = b : m; рр) 2520; сс) c + d + m; тт) x; уу) 1579; фф) t + 2; хх) 10206; цц) 135; чч) t + 2 ∙ 7; шш) 7 ∙ x; щщ) x – 2; ыы) 7 ∙ x – 2 ∙ 7; ээ) t + x ∙ 7; юю) 10192; яя) t + x; ааа) 123; ббб) 1456; ввв) 10327.
ПОКАЗАТЕЛИ ТЕСТА. Число задач 70, время выполнения 2 – 3 часа, сумма баллов: 1 ∙ 22 + 2 ∙ 24 + 3 ∙ 24 = 142. Для фасетного теста можно использовать следующую шкалу оценок.
Блок 4. Давайте поиграем
Блок 5. Обучающая игра «Уроки кота Леопольда»
Для учителя приводим ответы к блокам параграфа 6
Ответы к игре «Уроки Леопольда»
Западня 1 : 1/2, 1/3, 2/3, 7/8. Западня 2. 12, 2, 13 5. Западня 3. 6
Западня 4. 15. Западня 5. 396
Блок 1. Словарь
Блок 2. Установите соответствие.
Вариант 1: 1и, 2з, 3е, 4б, 5м, 6л, 7а, 8ж, 9в, 10д, 11г, 12к, 13т, 14н, 15ф, 16о, 17у, 18с, 19р, 20п
Вариант 2: 1д, 2е, 3к, 4а, 5г, 6з, 7и, 8б, 9ж, 10в
Блок 3. Фасетный тест. Числовые и буквенные выражения (ответы под заданиями)
Ответы к игре «Сокровища»
Деревянный – 10250. Оловянный – 21640. Медный – 50400. Серебряный – 191000. Золотой – 289800.