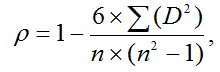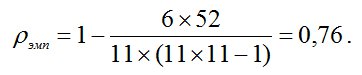Загрузить PDF
Загрузить PDF
Коэффициент корреляции ранга Спирмена позволяет определить, существует ли между двумя переменными зависимость, выражаемая монотонной функцией (то есть при росте одной переменной увеличивается и вторая, и наоборот). Приведенные в статье простые шаги позволят вам производить расчеты вручную, а также вычислять коэффициент корреляции при помощи программ Excel и R.
-
1
Составьте таблицу данных. Таким образом вы упорядочите информацию, необходимую для расчета коэффициента корреляции ранга Спирмена. При этом вам понадобится:
- 6 колонок, озаглавленных так, как показано выше на рисунке.
- Количество строк, соответствующее числу пар переменных.
-
2
Заполните первые две колонки парами переменных.
-
3
В третьей колонке запишите номера (ранги) пар переменных от 1 до n (общее число пар). Присвойте номер 1 паре с наименьшим значением в первой колонке, 2 — следующему за ним значению, и так по возрастанию величин переменной из первой колонки.
-
4
В четвертой колонке сделайте то же, что и в третьей, но на этот раз пронумеруйте пары переменных по второй колонке таблицы.
-
Если два (или более) значения переменной в одной колонке одинаковы, расположите их один за другим и найдите среднее значение их номеров, затем пронумеруйте их этим средним значением.
В приведенном справа примере два значения переменной совпадают и равны 5; в случае нормальной нумерации эти данные получили бы ранги 2 и 3. Поскольку значения одинаковы, находим среднюю величину их рангов. Среднее 2 и 3 равно 2,5, поэтому обеим величинам присваиваем ранг 2,5.
-
-
5
В колонке «d» вычислите разность между двумя рангами из предыдущих двух колонок. Например, если ранг в третьей колонке равен 1, а в четвертой – 3, то разница между ними составит 2. Знак не имеет значения, поскольку на следующем шаге эти числа будут возведены в квадрат.
-
6
Возведите каждое значение из колонки «d» в квадрат и запишите полученные величины в колонку «d2«.
-
7
Просуммируйте все значения из колонки «d2«. Вы определите сумму Σd2.
-
8
Воспользуйтесь одной из следующих формул:
-
9
Проанализируйте результат. Полученное значение находится между -1 и 1.
- Если оно близко к -1, корреляция отрицательна.
- Если близко к 0, корреляция отсутствует.
- Если близко к 1, наблюдается положительная корреляция.
- Не забудьте поделить на сумму переменных и взять корень. После этого поделите на Σd2.
Реклама
-
1
Создайте новые колонки с рангами, соответствующими колонкам данных. Например, если данные внесены в Колонку A2:A11, используйте функцию «=RANK(A2,A$2:A$11)» и занесите результаты для всех строк в новую колонку.
-
2
Найдите ранги для одинаковых величин, как описано в шагах 3 и 4 метода 1.
-
3
В новой ячейке определите корреляцию между двумя колонками рангов с помощью функции «=CORREL(C2:C11,D2:D11)». В данном случае C и D – это колонки, содержащие ранги. Таким образом, в данной ячейке вы получите коэффициент ранговой корреляции Спирмена.
Реклама
-
1
Если у вас еще нет программы R для обработки статистических данных, приобретите ее (см. http://www.r-project.org).
-
2
Сохраните данные в формате CSV, расположив их в двух колонках, корреляцию между которыми вы собираетесь исследовать. Сохранить файл в данном формате легко посредством опции «Сохранить как».
-
3
Откройте редактор R. Если вы еще не вошли в программу R, просто запустите ее. Для этого достаточно нажать иконку R на рабочем столе.
-
4
Наберите команды:
- d <- read.csv(«NAME_OF_YOUR_CSV.csv») и нажмите клавишу ввода
- cor(rank(d[,1]),rank(d[,2]))
Реклама
Советы
- Как правило, набор данных должен состоять не менее чем из 5 пар для того, чтобы можно было достоверно установить какую-либо корреляцию (3 пары было использовано в примере выше для простоты).
Реклама
Предупреждения
- Коэффициент ранговой корреляции Спирмена позволяет установить лишь то, растут ли обе переменные или уменьшаются одновременно. Если разброс данных слишком велик, этот коэффициент не даст точного значения корреляции.
- Приведенная функция даст верный результат при отсутствии одинаковых значений в массиве данных. Если такие значения существуют, как в рассмотренном нами примере, необходимо использовать следующее определение: коэффициент корреляции, основанный на рангах.
Реклама
Об этой статье
Эту страницу просматривали 69 004 раза.
Была ли эта статья полезной?
Наряду
с линейным коэффициентом корреляции r
для измерения тесноты связи между двумя
коррелируемыми признаками используются
менее точные, но более простые по расчету
непараметрические
показатели:
коэффициент Фехнера, коэффициенты
корреляции рангов
(или ранговые
коэффициенты корреляции)
Спирмэна
иКендэла
,
которые основаны на корреляции не самих
значений коррелируемых признаков, а ихрангов.
Ранг
– это порядковый номер, присваиваемый
каждому индивидуальному значению х
и у
(отдельно) в ранжированном ряду.
Ранжирование
– это процедура упорядочения объектов
изучения, которая выполняется на основе
предпочтения.
Правила
ранжирования:
-
оба
признака необходимо ранжировать
(нумеровать) в одном и том же порядке:
от меньших значений к большим (и
наоборот); -
если
встречается несколько одинаковых
значений х
(или у),
то каждому из них присваивается ранг,
равный частному от деления суммы рангов
(суммы мест), приходящихся на это
значение, на число равных значений
(например,
если за рангом 3 следуют три
равных значений признака, то им всем
присвоится ранг 5, т.к. (4 + 5 + 6) / 3 = 5); -
ранги
признаков х
и у
обозначаются символами
и
(иногда
и
).
Суждение
о связи между изменениями значений х
и у
основано на сравнении поведения рангов
по двум признакам параллельно:
-
если
у каждой пары х
и у
ранги совпадают, это характеризует
максимально
тесную прямую
связь; -
если
же наблюдается полная противоположность
рангов, т.е. в одном ряду ранги возрастают
от 1 до n,
а в другом – убывают от n
до 1, это максимально
возможная
обратная
связь.
Коэффициент
корреляции рангов Спирмэна
()
(применяется обычно на начальном этапе
выявления связи между изучаемыми
показателями иможет
быть использован для определения связи
как между количественными, так и между
качественными признаками
при условии, если их значения можно
упорядочить или проранжировать).
Коэффициент
Спирмэна рассчитывается так:
-
значения
признаков х
и у
нумеруют (отдельно) в порядке возрастания
от 1 до n,
т.е. им присваивают определенный ранг
(и
)
– порядковый номер в ранжированном
ряду; -
для
каждой пары рангов находят их разность
d
=
–
;
-
вычисляют
квадраты этих разностей
;
-
вычисляют
коэффициент корреляции рангов Спирмэна
по одной из формул
или
.
(16)
Коэффициент
корреляции рангов Спирмэна может
принимать следующие значения:
(17)
(ср.
с r).
Следует иметь в виду, что, поскольку
коэффициент Спирмэна учитывает разность
только рангов, он менее точен по сравнению
r.
Поэтому его крайние значения (1 или 0)
нельзя безоговорочно расценивать как
свидетельство функциональной связи
или полного отсутствия зависимости
между х
и у.
Пример.
Расчет коэффициента корреляции рангов
Спирмена по данным о часовой оплате
труда х
и уровне текучести кадров у
(таблица 5).
Значения
х
располагаем по возрастанию, поэтому и
значения
располагаются по порядку возраста. Если
бы значенияу
для соответствующих значений х
в первых двух строках таблицы располагались
«правильно», то они стояли бы в таком
порядке: 35, 34, …, но фактическое их
расположение – 34. 35, … Поэтому для них
не 8, 7, …, а 7, 8, и т.д. (ср. также строки 5 и
6). Для данного примера= – 0,952, что свидетельствует осильной
обратной
связи между х
и у.
Таблица
5
|
х |
у |
Ранги |
Разность d= |
|
|
|
|
|
||||
|
30 |
34 |
1 |
7 |
–6 |
36 |
|
40 |
35 |
2 |
8 |
–6 |
36 |
|
50 |
33 |
3 |
6 |
–3 |
9 |
|
60 |
28 |
4 |
5 |
–1 |
1 |
|
70 |
20 |
5 |
3 |
2 |
4 |
|
80 |
24 |
6 |
4 |
2 |
4 |
|
90 |
15 |
7 |
2 |
5 |
25 |
|
100 |
11 |
8 |
1 |
7 |
49 |
|
n |
|
Коэффициент
корреляции рангов Кендэла
()
(может быть
использован для определения связи как
между количественными, так и между
качественными признаками,
характеризующими однородные объекты,
ранжированные по одному признаку).
или
,
(18)
где
S
– сумма положительных и отрицательных
баллов.
Расчет
коэффициента
выполняется в следующей последовательности:
-
Ранги
х
(и
)
располагаются строго впорядке
возрастания. -
Значения
у
располагаются в порядке, соответствующем
значениям
х. -
Параллельно
записывают соответствующее каждому
значению
значение
(см. пример к вычислению коэффициента
).
-
Устанавливается
мера соответствия последовательности
«правильному» следованию
(напоминаем,
расположены строго по возрастанию):
а)
для каждого
последовательно определяют число
следующих за ним рангов,превышающих
его значение, т.е. определяют «правильное»
следование, и они учитываются со знаком
«+», а их сумма обозначается буквой P;
б)
для каждого
последовательно определяют число
следующих за ним рангов,меньших
по значению, т.е. определяют «неправильное»
следование, и они учитываются со знаком
«–», а их сумма обозначается буквой Q.
-
Определяется
сумма баллов по всем членам ряда, т.е.
S=P+Q. -
Вычисляется
по (18).
Пример.
По 10 хозяйствам имеются данные об
урожайности картофеля у
(ц/га) и о количестве внесенных на 1 га
удобрений х
(кг). Необходимо измерить тесноту связи
между изменениями х
и у
с помощью коэффициента корреляции
рангов Кендэла (табл. 6).
Таблица
6
-
х
у
Ранги
Подсчет
баллов«+»
«–»
1
2
3
4
5
6
138
218
1
1
9
0
175
240
2
3
7
1
190
232
3
2
7
0
196
280
4
6
4
2
200
260
5
4
5
0
235
310
6
9
1
3
250
290
7
7
2
1
260
278
8
5
2
0
275
300
9
8
1
0
290
320
10
10
–
–
n=10
P=38
Q=–7
Рассмотрим
примеры определения значений в столбцах
5
и 6.
В
первой
строке столбца 5
стоит число «9», как оно получено?
Обращаемся
к первой
строке столбца 4,
т.е. к значениям
:
там стоит число «1». Как видим, в этом
столбцевсе
последующие
значения
больше
«1», т.е. число
значений, превышающих
«1», равняется 9 = 10 – 1. Поэтому в первой
строку столбца 5
ставим число «9».
В
первой
строке столбца 6
стоит число «0».
Обращаемся
к первой
строке столбца 4,
т.е. к значениям
:
там стоит число «1». Как видим, в этом
столбцевсе
последующие
значения
больше
«1», т.е. число
значений, меньших
«1», равняется 0 = 9 – 9. Поэтому в первой
строку столбца 6
ставим число «0».
Например,
в четвертой
строке столбца 5
стоит число «4», которое получено из
следующих рассуждений.
Обращаемся
к четвертой
строке столбца 4,
т.е. к значениям
:
там стоит число «6». Как видим, в этом
столбце изпоследующих
значений
9, 7, 8, 10 (всего 4 значения)больше
«6», поэтому в четвертую
строку столбца 5
ставим число «4».
Во
второй
строке столбца 6
стоит число «2», оно получено так.
Обращаемся
ко второй
строке столбца 4,
т.е. к значениям
:
там изпоследующих
значений
числа 4 и 5 (всего 2 значения)меньше
«6». Поэтому в четвертую
строку столбца 6
ставим число «2».
Рассуждая
подобным образом, находим все значения
в столбцах для «+» и «–».
Далее
вычисляем P
= 38 и Q
= –7, т.е.
S=P+Q
= 38 – 7 = 31, и
= 0,69; полученное значение
характеризует довольно большую (выше
среднего) тесноту связи между изменениямих
и у.
Заметим,
рассчитывается аналогично и для случая
противоположной напрвленности ранговх
и у.
Преимущества
коэффициентов корреляции рангов Спирмэна
и Кендэла
:
-
они
легко вычисляются; -
могут
быть использован для определения связи
как между количественными,
так и между качественными
признаками; -
не
требуется знать форму
связи
изучаемых явлений.
Коэффициент
конкордации
(W
– множественный
коэффициент ранговой корреляции)
применяется в тех случаях, когда число
ранжируемых признаков (факторов) больше
двух и
вычисляется по следующей формуле
,
(19)
где
S
– сумма квадратов отклонений суммы m
рангов от их средней
величины;
m
– число ранжируемых признаков;
n
– число
ранжируемых единиц (число наблюдений).
Коэффициент
конкордации W
может принимать следующие значения:
;
(20)
применяется
особенно часто в экспертных оценках,
например, для того, чтобы определить
степень согласованности мнений экспертов
о важности того или иного оцениваемого
показателя или составить рейтинг
отдельных единиц по какому-либо признаку.
Соседние файлы в папке регрессия_Лекции_10-11
- #
- #
Ранговая корреляция – это метод корреляционного анализа,
отражающий отношения переменных, упорядоченных по возрастанию их значения.
Ранги — это порядковые номера единиц совокупности в
ранжированном ряду. Если проранжировать совокупность
по двум признакам, связь между которыми изучается, то полное совпадение рангов
означает максимально тесную прямую связь, а полная противоположность рангов —
максимально тесную обратную связь. Ранжировать оба признака необходимо в одном и том же
порядке: либо от меньших значений признака к большим,
либо наоборот.
Для практических целей использование ранговой корреляции
весьма полезно. Например, если установлена высокая ранговая корреляция между
двумя качественными признаками изделий, то достаточно контролировать изделия
только по одному из признаков, что удешевляет и ускоряет контроль.
Коэффициент корреляции рангов, предложенный К. Спирменом, относится к непараметрическим показателям связи
между переменными, измеренными в ранговой шкале. При расчете этого коэффициента
не требуется никаких предположений о характере распределений признаков в
генеральной совокупности. Этот коэффициент определяет степень тесноты связи
порядковых признаков, которые в этом случае представляют собой ранги
сравниваемых величин.
Величина коэффициента корреляции Спирмена
лежит в интервале +1 и -1. Он может быть положительным и отрицательным,
характеризуя направленность связи между двумя признаками, измеренными в
ранговой шкале.
Ранговый коэффициент корреляции Спирмена
подсчитывается по формуле:
— разность между рангами по двум переменным
– число
сопоставляемых пар
Первым этапом расчета коэффициента ранговой корреляции
является ранжирование рядов переменных. Процедура ранжирования начинается с
расположения переменных по возрастанию их значений. Разным значениям
присваиваются ранги, обозначаемые натуральными числами. Если встречается
несколько равных по значению переменных, им присваивается усредненный ранг.
Преимущество коэффициента корреляции
рангов Спирмена состоит в том, что ранжировать можно
и по таким признакам, которые нельзя выразить численно: можно проранжировать кандидатов на занятие определенной должности
по профессиональному уровню, по умению руководить коллективом, по личному
обаянию и т. п. При экспертных оценках можно ранжировать оценки разных
экспертов и найти их корреляции друг с другом, чтобы затем исключить из
рассмотрения оценки эксперта, слабо коррелированные
с оценками других экспертов. Коэффициент корреляции рангов Спирмена
применяется для оценки устойчивости тенденции динамики. Недостатком
коэффициента корреляции рангов является то, что одинаковым разностям рангов
могут соответствовать совершенно отличные разности
значений признаков (в случае количественных признаков). Поэтому для последних
следует считать корреляцию рангов приближенной мерой тесноты связи, обладающей
меньшей информативностью, чем коэффициент корреляции числовых значений признаков.
Задача
Опрос
случайно выбранных 10 студентов, проживающих в общежитии университета,
позволяет выявить зависимость между средним баллом по результатам предыдущей
сессии и числом часов в неделю, затраченных студентом на самостоятельную
подготовку.
| Средний балл | 4.7 | 4.4 | 3.8 | 3.7 | 4.2 | 4.3 | 3.6 | 4.0 | 3.1 | 3.9 |
| Число часов | 26 | 22 | 8 | 12 | 15 | 30 | 20 | 31 | 10 | 17 |
Определите тесноту связи при помощи коэффициента ранговой корреляции Спирмена.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Рассчитаем
коэффициент корреляции рангов.
Коэффициент ранговой
корреляции Спирмена вычисляется по формуле:
Подставляя числовые
значения, получаем:
Вывод к задаче
Связь между средним баллом по
результатам предыдущей сессии и числом часов в неделю, затраченных студентом на
самостоятельную подготовку,
умеренной тесноты.
Студента-психолога (социолога, менеджера, управленца и др.) нередко интересует, как связаны между собой две или большее количество переменных в одной или нескольких изучаемых группах.
В математике для описания связей между переменными величинами используют понятие функции F, которая ставит в соответствие каждому определенному значению независимой переменной X определенное значение зависимой переменной Y. Полученная зависимость обозначается как Y=F(X).
При этом виды корреляционных связей между измеренными признаками могут быть различны: так, корреляция бывает линейной и нелинейной, положительной и отрицательной. Она линейна — если с увеличением или уменьшением одной переменной X,вторая переменная Y в среднем либо также растет, либо убывает. Она нелинейна, если при увеличении одной величины характер изменения второй не линеен, а описывается другими законами.
Помогу с корреляцией по методу Спирмена ОНЛАЙН ЗДЕСЬ
Корреляция будет положительной, если с увеличением переменной X переменная Y в среднем также увеличивается, а если с увеличением X переменная Y имеет в среднем тенденцию к уменьшению, то говорят о наличии отрицательной корреляции. Возможна ситуация, когда между переменными невозможно установить какую-либо зависимость. В этом случае говорят об отсутствии корреляционной связи.
Задача корреляционного анализа сводится к установлению направления (положительное или отрицательное) и формы (линейная, нелинейная) связи между варьирующими признаками, измерению ее тесноты, и, наконец, к проверке уровня значимости полученных коэффициентов корреляции.
Коэффициент корреляции рангов, предложенный К. Спирменом, относится к непараметрическим показателям связи между переменными, измеренными в ранговой шкале. При расчете этого коэффициента не требуется никаких предположений о характере распределений признаков в генеральной совокупности. Этот коэффициент определяет степень тесноты связи порядковых признаков, которые в этом случае представляют собой ранги сравниваемых величин.
Помогу с корреляцией по методу Спирмена ОНЛАЙН ЗДЕСЬ
Ранговый коэффициент линейной корреляции Спирмена подсчитывается по формуле:
где n — количество ранжируемых признаков (показателей, испытуемых);
D — разность между рангами по двум переменным для каждого испытуемого;
D2 — сумма квадратов разностей рангов.
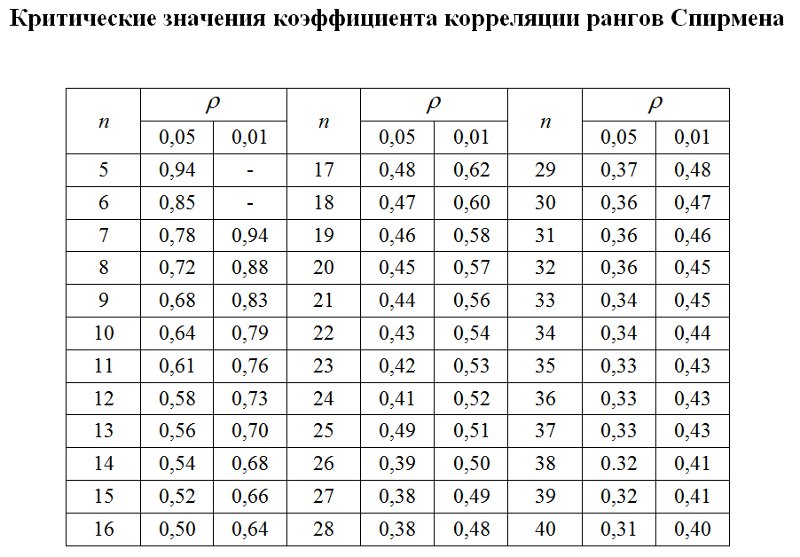
Критические значения коэффициента корреляции рангов Спирмена представлены ниже:
Величина коэффициента линейной корреляции Спирмена лежит в интервале +1 и -1. Коэффициент линейной корреляции Спирмена может быть положительным и отрицательным, характеризуя направленность связи между двумя признаками, измеренными в ранговой шкале.
Если коэффициент корреляции по модулю оказывается близким к 1, то это соответствует высокому уровню связи между переменными. Так, в частности, при корреляции переменной величины с самой собой величина коэффициента корреляции будет равна +1. Подобная связь характеризует прямо пропорциональную зависимость. Если же значения переменной X будут распложены в порядке возрастания, а те же значения (обозначенные теперь уже как переменная Y) будут располагаться в порядке убывания, то в этом случае корреляция между переменными Х и Y будет равна точно -1. Такая величина коэффициента корреляции характеризует обратно пропорциональную зависимость.
Помогу с корреляцией по методу Спирмена ОНЛАЙН ЗДЕСЬ
Знак коэффициента корреляции очень важен для интерпретации полученной связи. Если знак коэффициента линейной корреляции — плюс, то связь между коррелирующими признаками такова, что большей величине одного признака (переменной) соответствует большая величина другого признака (другой переменной). Иными словами, если один показатель (переменная) увеличивается, то соответственно увеличивается и другой показатель (переменная). Такая зависимость носит название прямо пропорциональной зависимости.
Если же получен знак минус, то большей величине одного признака соответствует меньшая величина другого. Иначе говоря, при наличии знака минус, увеличению одной переменной (признака, значения) соответствует уменьшение другой переменной. Такая зависимость носит название обратно пропорциональной зависимости. При этом выбор переменной, которой приписывается характер (тенденция) возрастания — произволен. Это может быть как переменная X, так и переменная Y. Однако если считается, что увеличивается переменная X, то переменная Y будет соответственно уменьшаться, и наоборот.
Рассмотрим пример корреляции Спирмена
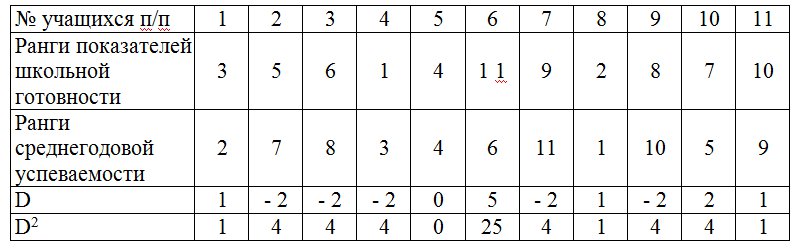
Психолог выясняет, как связаны между собой индивидуальные показатели готовности к школе, полученные до начала обучения в школе у 11 первоклассников и их средняя успеваемость в конце учебного года.
Для решения этой задачи были проранжированы, во-первых, значения показателей школьной готовности, полученные при поступлении в школу, и, во-вторых, итоговые показатели успеваемости в конце года у этих же учащихся в среднем. Результаты представим в таблице:
Помогу с корреляцией по методу Спирмена ОНЛАЙН ЗДЕСЬ
Подставляем полученные данные в вышеприведенную формулу, и производим расчет. Получаем:
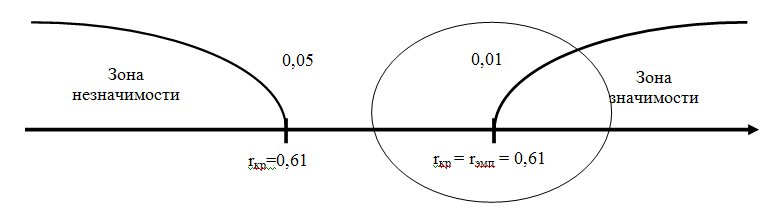
Для нахождения уровня значимости обращаемся к таблице «Критические значения коэффициента корреляции рангов Спирмена,» в которой приведены критические значения для коэффициентов ранговой корреляции.
Строим соответствующую «ось значимости»:
Полученный коэффициент корреляции совпал с критическим значением для уровня значимости в 1%. Следовательно, можно утверждать, что показатели школьной готовности и итоговые оценки первоклассников связаны положительной корреляционной зависимостью — иначе говоря, чем выше показатель школьной готовности, тем лучше учится первоклассник. В терминах статистических гипотез психолог должен отклонить нулевую (Н0) гипотезу о сходстве и принять альтернативную (Н1) о наличии различий, которая говорит о том, что связь между показателями школьной готовности и средней успеваемостью отлична от нуля.
Помогу с корреляцией по методу Спирмена ОНЛАЙН ЗДЕСЬ
3.1. Понятие выборки (применительно к исследованию в психологии)
3.2. Не любите проводить социологическое исследование? Вы просто не умеете его готовить!
3.3. Корреляционный анализ по методу Спирмена (ранги Спирмена)
3.4. Дискуссия: Объект и Предмет исследования или наоборот?
3.5. Решение задач по праву. Как решить задачу по Юриспруденции?
3.6. Как рассчитать темп роста и прироста?
3.7. Как выбрать тему дипломной работы?
3.8. Методы исследования в дипломе, пример
Коэффициент корреляции Спирмена: Определение
Коэффициент ранговой корреляции Спирмена или коэффициент корреляции Спирмена — это непараметрическая мера ранговой корреляции (статистической зависимости рангов между двумя переменными).
Названный в честь Чарльза Спирмена, он часто обозначается греческой буквой ‘?’ (rho) и используется в основном для анализа данных.
Он измеряет силу и направление связи между двумя ранжированными переменными. Но прежде чем говорить о коэффициенте корреляции Спирмена, важно сначала понять, что такое корреляция Пирсона. Корреляция Пирсона — это статистическая мера силы линейной связи между парными данными.
Для расчета и проверки значимости ранговой переменной необходимо, чтобы следующие предположения о данных были верны:
- Интервал или уровень отношения
- Линейно связанные
- Бивариантно распределенные
Если ваши данные не удовлетворяют вышеуказанным предположениям, то вам понадобится коэффициент Спирмена. Для понимания коэффициента корреляции Спирмена необходимо знать, что такое монотонная функция. Монотонная функция — это функция, которая либо никогда не уменьшается, либо никогда не увеличивается по мере увеличения независимой переменной. Монотонную функцию можно объяснить с помощью изображения ниже:
Изображение объясняет три понятия в монотонной функции:
- Монотонно возрастающая: Когда переменная ‘x’ увеличивается, а переменная ‘y’ никогда не уменьшается.
- Монотонно убывающая: Когда переменная ‘x’ увеличивается, а переменная ‘y’ никогда не увеличивается
- Не монотонно: Когда переменная ‘x’ увеличивается, а переменная ‘y’ иногда увеличивается, а иногда уменьшается.
Монотонная зависимость является менее ограничительной по сравнению с линейной зависимостью, которая используется в коэффициенте Пирсона. Хотя монотонность не является конечным требованием для коэффициента корреляции Спирмена, не имеет смысла добиваться корреляции Спирмена без фактического определения силы и направления монотонной связи, если уже было известно, что связь между переменными немонотонна.
Узнайте больше: Анализ газона с примерами
Коэффициент корреляции Спирмена: Формула и расчет на примере

n= количество точек данных двух переменных
di = разность рангов «i-го» элемента
Коэффициент Спирмена, ?может принимать значение от +1 до -1, где,
- Значение ? равное +1 означает идеальную связь рангов
- Значение ? равное 0 означает отсутствие связи рангов
- Значение ? равное -1 означает идеальную отрицательную связь между рангами.
Чем ближе значение ? к 0, тем слабее связь между двумя рангами.
Прежде чем приступить к расчету коэффициента ранговой корреляции Спирмена, мы должны уметь ранжировать данные. Важно наблюдать, если при увеличении одной переменной другая переменная следует монотонной зависимости.
На каждом уровне необходимо сравнить значения двух переменных. Вот как происходят вычисления:
Оценки 9 учеников по истории и географии приведены в таблице ниже.
Шаг 1- Создайте таблицу полученных данных.
Шаг 2- Начните с ранжирования двух наборов данных. Ранжирование данных может быть достигнуто путем присвоения рейтинга «1» самому большому числу в столбце, «2» — второму по величине числу и так далее. Наименьшее значение обычно получает самый низкий рейтинг. Это нужно сделать для обоих наборов измерений.
Шаг 3 Добавьте к набору данных третий столбец d, d здесь обозначает разницу между рангами. Например, если ранг первого студента по физике равен 3, а по математике — 5, то разница в рангах равна 3. В четвертом столбце возведите в квадрат значения d.
| История | Ранг | География | Ранг | d | d квадрат |
| 35 | 3 | 30 | 5 | 2 | 4 |
| 23 | 5 | 33 | 3 | 2 | 4 |
| 47 | 1 | 45 | 2 | 1 | 1 |
| 17 | 6 | 23 | 6 | 0 | 0 |
| 10 | 7 | 8 | 8 | 1 | 1 |
| 43 | 2 | 49 | 1 | 1 | 1 |
| 9 | 8 | 12 | 7 | 1 | 1 |
| 6 | 9 | 4 | 9 | 0 | 0 |
| 28 | 4 | 31 | 4 | 0 | 0 |
| 12 |
Шаг 4- Сложите все ваши квадратные значения d, что составляет 12 (?d квадрат)
Шаг 5- Подставьте эти значения в формулу
=1-(6*12)/(9(81-1))
=1-72/720
=1-01
=0.9
Ранговая корреляция Спирмена для этих данных равна 0,9, и, как было сказано выше, если значение ? приближается к +1, то у них идеальная ранговая связь.
Узнайте больше: Conjoint Analysis — определение, типы, пример, алгоритм и модель
Как провести коэффициент корреляции с помощью
В этом разделе вы узнаете, как можно провести коэффициент ранговой корреляции Спирмена для вашего опроса.
Шаг 1: Перейдите в раздел Мои опросы >Выберите опрос>Аналитика
Шаг 2: Нажмите на Корреляционный анализ в разделе Анализ
Шаг 3: Нажмите на кнопку Generate Spearman Coefficient, чтобы получить подробный отчет
В приведенном выше примере коэффициент корреляции Спирмена используется для выявления связи между двумя переменными — опытом работы и ежемесячным доходом. Согласно общему представлению, ежемесячный доход должен увеличиваться с ростом опыта работы, а значит, между двумя переменными должна существовать положительная связь, что подтверждается значением rs, равным 0,97
Узнайте больше: GAP-анализ — определение, метод и шаблон с примером