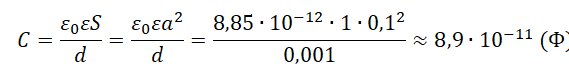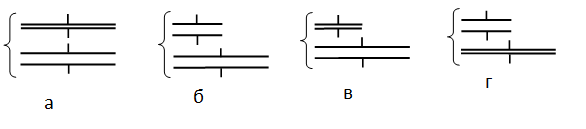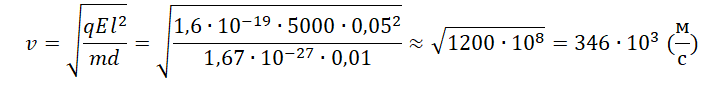Тема: разность потенциалов между пластинами конденсатора (Прочитано 13036 раз)
0 Пользователей и 3 Гостей просматривают эту тему.
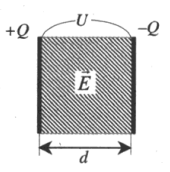
Одной из пластин плоского конденсатора емкостью С сообщили заряд Q, другой — 4Q. Найти разность потенциалов между пластинами конденсатора.
« Последнее редактирование: 27 Июля 2014, 07:32 от alsak »
Записан
Мы не можем здесь воспользоваться формулой U = C∙q, т.к. заряд пластин не одинаковый.
Разность потенциалов между обкладками конденсатора найдем следующим образом
[varphi _{1} -varphi _{2} =U=Ecdot Delta x,]
где Е — напряженность между пластинами конденсатора, Δx = d — расстояние между пластинами.
Напряженность поля между обкладками плоского конденсатора, согласно принципу суперпозиции (рис. 1), равна
[begin{array}{c} {vec{E}=vec{E}_{1} +vec{E}_{2} ,; ; ; 0X:; ; E_{x} =-E_{1} +E_{2} ,} \ {} \ {E_{1} =frac{left|sigma _{1} right|}{2varepsilon _{0} cdot varepsilon } =frac{left|q_{1} right|}{2varepsilon _{0} cdot varepsilon cdot S} ,; ; E_{2} =frac{left|q_{2} right|}{2varepsilon _{0} cdot varepsilon cdot S} ,} end{array}]
где Е1, Е2 — напряженности электростатических полей, созданных соответственно первой и второй пластинами, q1 = q, q2 = 4q. Площадь S пластин конденсатора найдем следующим образом:
[C=frac{varepsilon cdot varepsilon _{0} cdot S}{d} ,; ; S=frac{Ccdot d}{varepsilon cdot varepsilon _{0} } .]
Тогда
[begin{array}{c} {E_{x} =-frac{left|q_{1} right|}{2varepsilon _{0} cdot varepsilon cdot S} +frac{left|q_{2} right|}{2varepsilon _{0} cdot varepsilon cdot S} =-frac{left|q_{1} right|}{2Ccdot d} +frac{left|q_{2} right|}{2Ccdot d} =frac{-left|q_{1} right|+left|q_{2} right|}{2Ccdot d} =frac{-q+4q}{2Ccdot d} =frac{3q}{2Ccdot d} ,} \ {} \ {varphi _{1} -varphi _{2} , =frac{3q}{2Ccdot d} cdot d=frac{3q}{2C} .; } end{array}]
« Последнее редактирование: 27 Июля 2014, 07:32 от alsak »
Записан
2019-11-28
Плоский конденсатор имеет емкость $C$. На одну из пластин конденсатора поместили заряд $+q$, а на другую — заряд $+ 4q$. Определить разность потенциалов между пластинами конденсатора.
Решение:
Если на пластинах плоского конденсатора имеются заряды $+Q$ и $-Q$, то напряженность поля между пластинами, как известно, равна $E = frac{Q}{Cd}$. Это поле равно сумме одинаковых полей двух пластин. Поэтому напряженность поля одной пластины с равномерно распределенным зарядом равна $frac{1}{2} frac{Q}{Cd}$.
Напряженность поля пластины с зарядом $+q$ равна $frac{1}{2} frac{q}{Cd}$,а напряженность поля пластины с зарядом $+ 4q$ равна $frac{2q}{Cd}$. В отличие от случаев обычных зарядов конденсатора, когда напряженности полей пластин направлены в одну сторону и складываются, в нашем случае напряженности полей, создаваемых пластинами, направлены в разные стороны. Поэтому напряженность однородного поля между пластинами равна разности напряженностей полей каждой из пластин (рис.):
$E^{ prime} = frac{2q}{Cd} — frac{1}{2} frac{q}{Cd} = frac{3}{2} frac{q}{Cd}$.
Теперь нетрудно найти разность потенциалов пластин. Она равна работе, необходимой для перенесения единичного положительного заряда с одной пластины на другую. На такой заряд действует сила, равная $E^{ prime}$. Поэтому разность потенциалов пластин равна
$Delta phi = E^{ prime}d = frac{2}{3} frac{q^{ prime} }{C}$.
Плоский конденсатор имеет емкость С. На одну из пластин конденсатора поместили заряд +q, а на другую — заряд +4q. Определите разность потенциалов между пластинами конденсатора.
(Задача из журнала «Квант», Ф136).
Решение:

Это поле равно сумме одинаковых полей двух пластин. Поэтому напряженность поля одной пластины с равномерно распределенным зарядом равна:
Напряженность поля пластины с зарядом +q равна:
а напряженность поля пластины с зарядом +4q равна:
В отличие от случаев обычных зарядов конденсатора, когда напряженности полей, создаваемых пластинами, направлены в разные стороны. Поэтому напряженность однородного поля между пластинами равна разности напряженностей полей каждой из пластин (рис.):
| E/ = | 2q | − | 1 | • | q | = | 3 | • | q | . |
| Cd | 2 | Cd | 2 | Cd |
Теперь нетрудно найти разность потенциалов пластин. Она равна работе, необходимой для перенесения единичного положительного заряда с одной пластины на другую. На такой заряд действует сила, равная E/.Поэтому разность потенциалов пластин равна:
| Δφ = E/d = | 2 | • | q/ | . |
| 3 | C |
Далее: как уменьшится притяжение двух шариков? [тема: «нестандартные» задачи по электростатике]
Конденсатор служит для накопления электрического заряда. Он представляет собой два проводника, разделенных слоем диэлектрика.
Плоский конденсатор — система двух разноименно заряженных пластин.
Разность потенциалов U (В) между обкладками конденсатора (напряжение между пластинами), определяется произведением напряженности создаваемого ими электрического поля на расстояние между ними:
U=Ed
Электроемкость конденсатора
Определение
Электрическая емкость — характеристика проводника, мера его способности накапливать электрический заряд.
Электроемкость обозначается как C. Единица измерения электрической емкости — Фарад (Ф).
Электроемкость конденсатора определяется формулой:
C=ε0εSd
- ε0 — диэлектрическая постоянная, равная 8,85∙10–12 Кл2/(Н∙м2);
- ε — диэлектрическая проницаемость среды;
- S (м2) — площадь каждой пластины.
Внимание! У воздушного конденсатора диэлектрическая проницаемость среды равна 1.
Связь между электроемкостью конденсатора, зарядом и напряжением определяется формулами:
C=QU=qU
Важно! Электроемкость конденсатора зависит только от площади его пластин, расстояния между ними и диэлектрической проницаемости среды. От заряда и напряжения эта величина не зависит.
Энергия конденсатора
Формула энергии конденсатора
Энергия конденсатора связана с его электроемкостью и вычисляется по следующим формулам:
Wэ=q22C=CU22
Подсказки к задачам
| Конденсатор отключен от источника | q = q′ |
| Конденсатор подключен к источнику | U = U′ |
| Количество теплоты и энергия конденсатора | Q = ∆Wэ |
Пример №1. Вычислить электроемкость плоского воздушного конденсатора с квадратными пластинами со стороной 10 см, расположенными на расстоянии 1 мм друг от друга. Ответ округлить до десятых.
10 см = 0,1 м
1 мм = 0,001 м
Так как между обкладками конденсатора находится воздух, примем диэлектрическую проницаемость среды за единицу.
Площадь квадратной пластины равна квадрату ее стороны:
S = a2
Соединения конденсаторов
| Последовательное соединение | Параллельное соединение | |
| Схема | 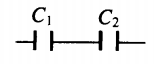 |
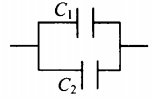 |
| Напряжение |
U=U1+U2 |
U=U1=U2 |
| Заряд |
q=q1=q2 |
q=q1+q2 |
| Электроемкость |
1C=1C1+1C2 |
C=C1+C2 |
Подсказки к задачам
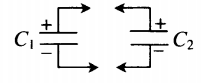
| Два конденсатора, электроемкости которых C1 и C2, заряжены до напряжения U1 и U2. Найдите разность потенциалов после соединения конденсаторов одноименными полюсами. | Схема соединения конденсаторов одноименными полюсами:
Заряд системы после соединения: q′ Электрическая емкость системы: C′ Напряжение: U′ |
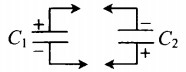
| Два конденсатора, электроемкости которых C1 и C2, заряжены до напряжения U1 и U2. Найдите разность потенциалов после соединения конденсаторов разноименными полюсами. |
Схема соединения конденсаторов разноименными полюсами: Заряд системы после соединения: q′ Электрическая емкость системы: C′ Напряжение: U′ |
Пример №2. К конденсатору, электрическая емкость которого C = 16 пФ, подключают два одинаковых конденсатора емкостью X: один параллельно, а второй — последовательно (см. рисунок). Емкость образовавшейся батареи конденсаторов равна емкости C. Какова емкость X? Ответ округлите до десятых.
Электрическая емкость параллельного соединения равна:
Cпарал=X+C
Электроемкость последовательного соединения:
1Cпослед=1Cпарал+1X=1X+C+1X
Учтем, что суммарная электроемкость равна C:
1C=1X+C+1X
Преобразуем, умножим выражение на CX(X+C):
X(X+C)=CX+C(X+C)
Раскроем скобки:
X2+XC=CX+CX+C2
X2−CX−C2=0
Решив уравнение, получим: X = 25,9 пФ.
Разбор задач на тему «Заряженная частица в поле конденсатора»
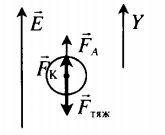
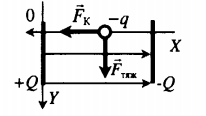
| Шарик, находящийся в масле плотностью ρ, «висит» в поле плоского конденсатора. Плотность вещества шарика ρш > ρ, его радиус r, расстояние между обкладками конденсатора d. Каков заряд шарика, если электрическое поле направлено вверх, а разность потенциалов между обкладками U? | Условие равновесия исходит из второго закона Ньютона:
−Fтяж+−FK+−FA=0 ρш > ρ, поэтому −Fтяж> −FA. В этом случае сила Кулона направлена вверх, а заряд шарика положительный. Схематически это можно отобразить так: Проекция второго закона Ньютона на ось ОУ: FK+FA=Fтяж Сила тяжести равна произведению объема на плотность шарика и на ускорение свободного падения: Fтяж=ρш43πr3g Архимедова сила равна произведению объема шарика на плотность масла и на ускорение свободного падения: FА=ρ43πr3g Сила Кулона: FK=qUd qUd+ρ43πr3g=ρш43πr3g q=(ρш43πr3g−ρ43πr3g)dU=4πr3gd(ρш−ρ)3U |
| Маленький шарик с зарядом q и массой m, подвешенный на невесомой нити с коэффициентом упругости k, находится между вертикальными пластинами воздушного конденсатора. Расстояние между обкладками конденсатора d. Какова разность потенциалов между обкладками конденсатора U, если удлинение нити ∆l? | 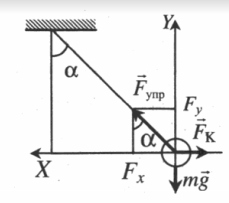
Условие равновесия исходит из второго закона Ньютона: −Fтяж+−FK+−Fупр=0 Проекции на оси ОХ и ОУ соответственно: Fупрsinα−FK=0 Fупрcosα−mg=0 Отсюда: kΔlsinα=qUd kΔlcosα=mg Чтобы избавиться от угла α, возведем уравнения в квадрат и сложим их: (kΔl)2sin2α+(kΔl)2cos2α=(qUd)2+(mg)2 (kΔl)2(sin2α+cos2α)=(qUd)2+(mg)2 sin2α+cos2α=1 (kΔl)2=(qUd)2+(mg)2 U=dq√(kΔl)2−(mg)2 |
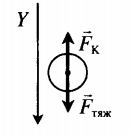
| Пластины плоского конденсатора расположены горизонтально на расстоянии d друг от друга. Напряжение на пластинах конденсатора U. В пространстве между пластинами падает капля жидкости. Масса капли m, ее заряд q. Определите расстояние между пластинами. Влиянием воздуха на движение капли пренебречь. | Второй закон Ньютона в векторной форме:
−Fтяж+−FK=0 Проекция на вертикальную ось: Fтяж−FK=0 Fтяж=mg FK=qUd mg=qUd d=qUmg |
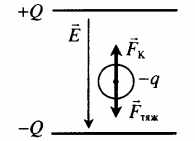
| Между двумя параллельными горизонтально расположенными диэлектрическими пластинами создано однородное электрическое поле с напряженностью −E, направленное вертикально вниз. Между пластинами помещен шарик на расстоянии d от верхней пластины и b от нижней. Заряд шарика –q, масса m. Шарик освобождают, и он начинает двигаться. Через какой промежуток времени t шарик ударится об одну из пластин, если система находится в поле силы тяжести Земли? | Второй закон Ньютона в векторной форме:
−Fтяж+−FK=m−a Согласно условию данной задачи, сила тяжести противоположно направлена силе Кулона. Построим рисунок: Если Fтяж > FK, то шарик движется с ускорением вниз. Ускорение и перемещение в этом случае равны: a=mg−qEm s=b Если Fтяж < FK, то шарик движется с ускорением верх. Ускорение и перемещение в этом случае равны: a=qE−mgm s=d Начальная скорость шарика равна нулю. Поэтому перемещение также равно: s=at22 Сделаем вычисления для случая Fтяж > FK: at22=b mg−qEmt22=b t=√2bmmg−qE Выполняя вычисления для случая Сделаем вычисления для случая Fтяж < FK, получим: t=√2bmqE−mg |
| Между двумя параллельными, вертикально расположенными диэлектрическими пластинами создано однородное электрическое поле, напряженность которого −E и направлена слева направо. Между пластинами помещен шарик на расстоянии b от левой пластины и d от правой. Заряд шарика –q, масса m. Шарик освобождают, и он начинает двигаться. Найдите смещение шарика по вертикали ∆h до удара об одну из пластин. Пластины имеют достаточно большой размер. | Второй закон Ньютона в векторной форме:
−Fтяж+−FK=m−a Если сила Кулона направлена вправо, то sx = d. Если сила Кулона направлена вправо, то sx = b. Учитывая, что заряд меньше нуля, а вектор напряженности направлен вправо, делаем вывод, что кулоновская сила направлена влево. Из проекций второго закона Ньютона выразим проекции ускорения на оси ОХ и ОУ соответственно: ax=qEm ay=g Проекции перемещений на эти же оси: sx=axt22 sx=Δh=gt22 axt22=b Или: qEmt22=b Так как время движения шарика по вертикали и горизонтали одинаково: t2=2Δhg=2mbqE Δh=mbgqE |
Задание EF17979
Введите ответ в поле ввода
Плоский конденсатор подключён к гальваническому элементу. Как изменятся при уменьшении зазора между обкладками конденсатора три величины: ёмкость конденсатора, величина заряда на его обкладках, разность потенциалов между ними?
Для каждой величины определите соответствующий характер изменения:
- увеличится
- уменьшится
- не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
1.Определить, от чего зависит емкость конденсатора, и как она изменится при уменьшении зазора между его обкладками.
2.Определить, от чего зависит величина заряда конденсатора, и как она изменится после уменьшения зазора между его обкладками.
3.Определить, от чего зависит разность потенциалов между обкладками конденсатора, и как она изменится при уменьшении зазора.
Решение
Емкость конденсатора определяется формулой:
C=ε0εSd
Следовательно, емкость имеет обратно пропорциональную зависимость от расстояния между обкладками. Если расстояние уменьшить, то емкость увеличится.
Вот как взаимосвязана электроемкость и заряд конденсатора:
C=qU
Мы выяснили, что электроемкость увеличивается. Следовательно, увеличится и заряд, так как они имеют прямо пропорциональную зависимость.
С учетом того, что плоский конденсатор подключен к гальваническому элементу, разность потенциалов никак не зависит от расстояния между обкладками. Поэтому величина U остается неизменной.
Ответ: 113
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18574
Воспользовавшись оборудованием, представленным на рис. 1, учитель собрал модель плоского конденсатора (рис. 2), зарядил нижнюю пластину положительным зарядом, а корпус электрометра заземлил. Соединённая с корпусом электрометра верхняя пластина конденсатора приобрела отрицательный заряд, равный по модулю заряду нижней пластины. После этого учитель сместил одну пластину относительно другой не изменяя расстояния между ними (рис. 3). Как изменились при этом показания электрометра (увеличились, уменьшились, остались прежними)? Ответ поясните, указав, какие явления и закономерности Вы использовали для объяснения. Показания электрометра в данном опыте прямо пропорциональны разности потенциалов между пластинами конденсатора.
Алгоритм решения
1.Проанализировать каждый этап эксперимента.
2.Установить, от чего зависит угол отклонения стрелки электрометра.
3.Выяснить, что поменяется при смещении одной пластины конденсатора относительно другой, и что при этом произойдет со стрелкой электрометра.
Решение
На первом рисунке стрелка и стержень электрометра, соединённые с нижней пластиной, но изолированные от корпуса, заряжаются положительно. Поэтому стрелка отклоняется на некоторый угол. В верхней пластине и металлическом корпусе электрометра происходит перераспределение свободных электронов таким образом, что верхняя пластина заряжается отрицательно.
На втором рисунке заряды пластин одинаковы по модулю и противоположны по знаку, пластины образуют конденсатор с ёмкостью:
C=ε0εSd
S — площадь перекрытия пластин, d — расстояние между ними, ε — диэлектрическая проницаемость диэлектрика между пластинами.
Характер изменения угла отклонения стрелки совпадает с изменением разности потенциалов между пластинами: при увеличении разности потенциалов увеличивается угол отклонения, при уменьшении разности потенциалов угол уменьшается.
На рисунке 3 площадь перекрытия пластин уменьшилась. Следовательно, уменьшилась электроемкость, которая имеет обратно пропорциональную зависимость от разности потенциалов:
C=qU
Заряд остается постоянным, поскольку система изолированная — заряду просто некуда деться. Поэтому с уменьшением электроемкость растет разность потенциалов. Поэтому показания электрометра увеличатся.
Ответ: Увеличатся
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18695
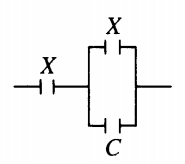
Ученик изучает свойства плоского конденсатора. Какую пару конденсаторов (см. рисунок) он должен выбрать, чтобы на опыте обнаружить зависимость ёмкости конденсатора от расстояния между его обкладками?
Алгоритм решения
- Установить, какие величины в данном эксперименте должны быть переменными, а какие — постоянными.
- Найти рисунок с парой конденсаторов, удовлетворяющий требованиям, выявленным в шаге 1.
Решение
Чтобы на опыте обнаружить зависимость ёмкости конденсатора от расстояния между его обкладками, нужно сохранить все величины постоянными, кроме самого расстояния. Поэтому площади обкладок должны быть одинаковыми, но расстояние между ними разными, как на рисунке 1.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
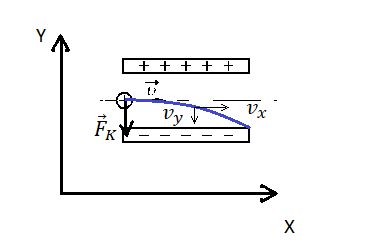
Задание EF18703
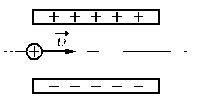
Ответ записать в км/с, округлив до десятков.
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Выполнить рисунок. Указать направление движения протона и силы, действующие на него.
3.Выяснить, при каком условии протон успеет вылететь из конденсатора.
4.Выполнить решение в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса протона: m = 1,67∙10–27 кг.
• Заряд протона: q = 1,6∙10–19 Кл.
• Расстояние между обкладками конденсатора: d = 1 см.
• Длина пластин конденсатора: l = 5 см.
• Напряженность однородного поля внутри конденсатора: E = 5000 В/м.
1 см = 0,01 м
5 см = 0,05 м
Сделаем рисунок:
Изначально протон обладает только горизонтальной скоростью v, равной vx. Влетев в однородное электростатическое поле внутри конденсатора, протон обретает вертикальную компоненту скорости, которая растет за счет ускорения, придаваемого кулоновскими силами. Положительно заряженный протон притягивается нижней отрицательно зараженной пластиной конденсатора.
Чтобы протон вылетел из конденсатора, его горизонтальная компонента скорости должна быть достаточной для того, чтобы частица не притянулась к нижней пластине раньше. Время, которое понадобится протону для преодоления длины пластин конденсатора со скоростью vx:
t=lvx=lv
Протон влетел в пространство между обкладками конденсатора на одинаковом расстоянии от них. Следовательно, прежде чем он упадет на нижнюю пластину, по оси OY он переместится на расстояние, равное 0,5d. Так как начальная компонента скорости равна нулю (мы пренебрегаем силой тяжести):
0,5d=at22
Протон вылетит из конденсатора, а не упадет на его пластину, если время горизонтального перемещения до конца пластин будет как минимум равно времени падения. Выразим время падения:
t=√da
Приравняем правые части уравнений времени и получим:
lv=√da
Отсюда скорость равна:
v=√al2d
Ускорение выразим из второго закона Ньютона:
FK=ma=qUd
a=qUmd
Но известно, что:
U=Ed
Поэтому:
a=qEdmd=qEm
Отсюда:
Минимальная скорость, с которой протон должен влететь в конденсатор, составляет 346∙103 м/с. Округлим до десятков и переведем в км/с. Получим 350 км/с.
Ответ: 350
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 6k
Электрический потенциал
Публикации по материалам Д. Джанколи. «Физика в двух томах» 1984 г. Том 2.
Электрический потенциал и потенциальная энергия
Понятие энергии исключительно полезно для решения задач механики. Прежде всего энергия сохраняется и поэтому служит важной характеристикой явлений природы. Используя представления об энергии, многие задачи удается решить, не имея детальных сведений о силах или в случае, когда применение законов Ньютона потребовало бы сложных вычислений.
Энергетическим подходом можно воспользоваться и при изучении электрических явлений, и здесь он оказывается чрезвычайно полезным: позволяет не только обобщить закон сохранения энергии, но и в новом аспекте увидеть электрические явления, а также служит средством более просто находить решения, чем путем рассмотрения сил и электрических полей.
Потенциальную энергию можно определить лишь для консервативных сил; работа такой силы по перемещению частицы между двумя точками не зависит от выбранного пути.
Легко видеть, что электростатическая сила является консервативной: сила, с которой один точечный заряд действует на другой, определяется законом Кулона: F = kQ1Q2 /r 2 ; здесь та же обратно пропорциональная зависимость от квадрата
расстояния, что и в законе всемирного тяготения: F = Gm1m2 /r 2. Такие силы консервативны. Сила, действующая на выбранный заряд со стороны любого распределения зарядов, может быть записана в виде суммы кулоновских сил; следовательно, и сила, создаваемая произвольным распределением зарядов, консервативна. А это позволяет ввести потенциальную энергию электростатического
поля.
Разность потенциальных энергий точечного заряда q в двух различных точках электрического поля можно определить как работу, совершаемую внешними силами по перемещению заряда (против действия электрической силы) из одной точки в другую. Это равносильно определению изменения потенциальной энергии заряда в поле как взятой с обратным знаком работы, совершаемой самим полем по перемещению заряда из одной точки в другую.
Рассмотрим для примера электрическое поле между двумя пластинами с равным по величине и противоположным по знаку зарядом. Пусть размеры пластин велики по сравнению с расстоянием между ними, и поэтому поле между пластинами можно считать однородным (рис. 24.1).
Поместим в точку а вблизи положительно заряженной пластины точечный положительный заряд q.
Электрическая сила, действующая на заряд, будет стремиться переместить его к отрицательной пластине (в точку b), совершая работу по переносу заряда. Под действием силы заряд приобретет ускорение и его кинетическая энергия возрастет; при этом потенциальная энергия уменьшится на величину работы, совершенной электрической силой по перемещению заряда из точки a в точку b. Согласно закону сохранения энергии, потенциальная энергия заряда в электрическом поле перейдет в кинетическую энергию, но полная энергия останется неизменной. Заметим, что положительный заряд q обладает наибольшей потенциальной энергией U вблизи положительной пластины (в этой точке его способность совершать работу над другим телом или системой максимальна). Для отрицательного заряда справедливо обратное: его потенциальная энергия будет максимальна вблизи отрицательной пластины.
Напряженность электрического поля мы определяли как силу, действующую на единичный заряд; аналогично удобно ввести электрический потенциал (или просто потенциал, если это не вызывает недоразумений) как потенциальную энергию единичного заряда.
Электрический потенциал обозначается символом V; итак, если в некоторой точке a точечный заряд q обладает
потенциальной энергией Ua, то электрический потенциал в этой точке равен Va = Ua /q.
Реально мы измеряем только изменение потенциальной энергии. Соответственно фактически можно измерить лишь разность потенциалов между
двумя точками (например, точками a и b на рис. 24.1). Если работа электрических сил по перемещению заряда от
точки a в точку b есть Wba (а разность потенциальных
энергий соответственно равна этой величине с обратным
знаком), то для разности потенциалов можно написать

Единицей электрического потенциала (и разности потенциалов) является джоуль на кулон (Дж/Кл); этой единице присвоено наименование вольт (В) в честь Алессандро Вольты (1745-1827) (он известен как изобретатель электрической батареи); 1 В = 1 Дж/Кл. Заметим, что,
согласно данному определению, положительно заряженная пластина на рис. 24.1 имеет более высокий потенциал, чем отрицательная. Таким образом, положительно заряженное тело будет стремиться перейти из точки с более высоким потенциалом в точку с более низким
потенциалом, отрицательно заряженное тело — наоборот. Разность потенциалов часто называют электрическим напряжением.
Потенциал в данной точке Va зависит от выбора «нуля» потенциала; как и в случае потенциальной энергии,
нулевой уровень может выбираться произвольно, поскольку измерить можно лишь изменение потенциальной энергии (разность потенциалов). Часто за нулевой принимают потенциал земли или проводника, соединенного с землей, и остальные значения потенциалов отсчитывают относительно «земли». (Например, говоря, что потенциал в какой-то точке равен 50 В, имеют в виду, что разность потенциалов между этой точкой и землей равна 50 В.) В иных случаях, как мы увидим, удобно считать нулевым потенциал на бесконечности.
Поскольку электрический потенциал определяется как потенциальная энергия единичного заряда, изменение потенциальной энергии заряда q при перемещении его из точки a в точку b равно
ΔU = Ub — Ua = qVba
Другими словами, когда заряд q перемещается между точками с разностью потенциалов Vba, его потенциальная
энергия изменяется на величину qVba. Если, например, разность потенциалов между пластинами на рис. 24.1 составляет 6 В, то заряд 1 Кл, перемещенный (внешней силой) из точки b в точку a, увеличит свою потенциальную энергию на (1 Кл) (6 В) = 6 Дж. (Перемещаясь же из a в b, он потеряет потенциальную энергию 6 Дж.)
Аналогично энергия заряда 2 Кл увеличится на 12 Дж и т. п. Таким образом, электрический потенциал служит мерой изменения потенциальной энергии электрического заряда в данной ситуации. А поскольку потенциальная энергия — это способность совершать работу, электрический потенциал служит мерой той работы, которую может совершить данный заряд. Количество работы зависит как от разности потенциалов, так и от величины заряда.
Чтобы лучше понять смысл электрического потенциала, проведем аналогию с гравитационным полем. Пусть камень падает с вершины скалы. Чем выше скала, тем большей потенциальной энергией обладает камень и тем больше будет его кинетическая энергия, когда он долетит до подножия скалы. Величина кинетической энергии и соответственно работа, которую может совершить камень, зависят от высоты скалы и от массы камня. Точно так же и в электрическом поле изменение потенциальной энергии (и работа, которую можно совершить) зависит от разности потенциалов (эквивалентной высоте скалы) и заряда (эквивалентного массе).
Используемые на практике источники электроэнергии — батареи, электрогенераторы — создают определенную разность потенциалов. Количество энергии, отбираемой от источника, зависит от величины переносимого заряда.
Рассмотрим, например, автомобильную фару, соединенную с аккумулятором, разность потенциалов на зажимах которого равна 12 В. Количество энергии, преобразуемой фарой в свет (и, конечно, в тепло), пропорционально заряду, протекшему через фару, что в свою очередь
зависит от того, как долго включена фара. Если за некоторое время через фару прошел заряд 5,0 Кл, то
преобразованная фарой энергия составит (5,0 Кл)*(12,0 В) = 60 Дж. Если оставить фару включенной вдвое дольше, то через нее пройдет заряд 10,0 Кл, и количество преобразованной энергии составит (10,0 Кл)*(12,0 В) = 120 Дж.
Эффекты, обусловленные тем или иным распределением зарядов, можно описать как с помощью напряженности электрического поля, так и через электрический потенциал. Между напряженностью поля и потенциалом существует тесная связь. Рассмотрим вначале эту связь для случая однородного электрического поля, например поля между пластинами на рис. 24.1 с разностью потенциалов Vba. Работа электрического поля по перемещению положительного заряда q из точки a в точку b равна
W = — qVba
Обратим внимание на то, что величина Vba = Vb — Va отрицательна (Vba < 0), так как потенциал в точке a выше, чем в точке b (и положителен по отношению к потенциалу в точке b). Поэтому совершаемая полем работа положительна.
С другой стороны, работа равна произведению силы на перемещение, а сила, действующая на заряд q,
есть F = qE, где Е — напряженность однородного электрического поля между пластинами. Таким образом,
W = Fd = qEd
где d — расстояние между точками a и b (вдоль силовой линии).
Приравняв эти выражения для работы, получим
— qVba = qEd
или
Vb — Va = Vba = — Ed (поле E однородно).
Знак минус в правой части указывает просто на то, что Va Vb , т.е. потенциал положительной пластины выше,
чем отрицательной, как мы уже говорили. Положительные заряды стремятся двигаться из области с высоким потенциалом в область с низким потенциалом. Отсюда можно найти Е:
Е = — Vba /d .
Из последнего равенства видно, что напряженность электрического поля можно измерять как в вольтах на метр (В/м), так и в ньютонах на кулон (Н/Кл). Эти единицы эквивалентны между собой: 1 Н/Кл = 1 Н·м/Кл·м = 1 Дж/Кл·м = 1 В/м.
Чтобы перейти к общему случаю неоднородного электрического поля, вспомним соотношение между силой F и потенциальной энергией U, обусловленной этой силой. Разность потенциальных энергий в двух точках пространства a и b определится формулой

где dl — бесконечно малое перемещение, а интеграл берется вдоль произвольной траектории между точками a и b. В
случае электрического поля нас больше интересует разность не потенциальных энергий, а потенциалов:
Vba = Vb — Va = (Ub — Ua )/q
Напряженность электрического поля Е в любой точке пространства определяется отношением силы к заряду: Е = F/q.
Подставляя эти два равенства в формулу, получим

Это и есть общее соотношение, связывающее напряженность электрического поля с разностью потенциалов.
Когда поле однородно, например, на рис. 24.1 вдоль траектории, параллельной силовым линиям, от точки a у положительной
пластины до точки b у отрицательной пластины (поскольку направления E и dl всюду совпадают) имеем

где d — расстояние вдоль силовой линии между точками a и b. И вновь знак минус в правой части свидетельствует
лишь о том, что на рис. 24.1 Va > Vb .
Продолжение следует. Коротко о следующей публикации:
Эквипотенциальные поверхности.
Электрический потенциал можно представить графически, изображая эквипотенциальные линии или в трех измерениях — эквипотенциальные поверхности.
Альтернативные статьи:
Электрический ток,
Закон Ома.
Замечания и предложения принимаются и приветствуются!