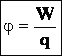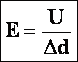Магнитное поле и его характеристики
теория по физике 🧲 магнетизм
Магнитное поле — особая форма материи, посредством которой осуществляется взаимодействие между движущимися электрическими частицами.
Основные свойства магнитного поля
- Магнитное поле порождается электрическим током (движущимися зарядами).
- Магнитное поле обнаруживается по действию на электрический ток (движущиеся заряды).
- Магнитное поле существует независимо от нас, от наших знаний о нем.
Вектор магнитной индукции
Вектор магнитной индукции — силовая характеристика магнитного поля. Она определяет, с какой силой магнитное поле действует на заряд, движущийся в поле с определенной скоростью. Обозначается как → B . Единица измерения — Тесла (Тл).
За единицу магнитной индукции можно принять магнитную индукцию однородного поля, котором на участок проводника длиной 1 м при силе тока в нем 1 А действует со стороны поля максимальная сила, равна 1 Н. 1 Н/(А∙м) = 1 Тл.
Модуль вектора магнитной индукции — физическая величина, равная отношению максимальной силы, действующей со стороны магнитного поля на отрезок проводника с током, к произведению силы тока и длины проводника:
B = F A m a x I l . .
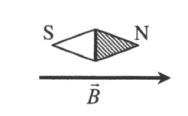
За направление вектора магнитной индукции принимается направление от южного полюса S к северному N магнитной стрелки, свободно устанавливающейся в магнитном поле.
Наглядную картину магнитного поля можно получить, если построить так называемые линии магнитной индукции. Линиями магнитной индукции называют линии, касательные к которым направлены так же, как и вектор магнитной индукции в данной точке поля.
Особенность линий магнитной индукции состоит в том, что они не имеют ни начала, ни конца. Они всегда замкнуты. Поля с замкнутыми силовыми линиями называют вихревыми. Поэтому магнитное поле — вихревое поле.
Замкнутость линий магнитной индукции представляет собой фундаментальное свойство магнитного поля. Оно заключается в том, что магнитное поле не имеет источников. Магнитных зарядов, подобным электрическим, в природе нет.
Напряженность магнитного поля
Вектор напряженности магнитного поля — характеристика магнитного поля, определяющая густоту силовых линий (линий магнитной индукции). Обозначается как → H . Единица измерения — А/м.
μ — магнитная проницаемость среды (у воздуха она равна 1), μ 0 — магнитная постоянная, равная 4 π · 10 − 7 Гн/м.
Внимание! Направление напряженности всегда совпадает с направлением вектора магнитной индукции: → H ↑↑ → B .
Направление вектора магнитной индукции и способы его определения
Чтобы определить направление вектора магнитной индукции, нужно:
- Расположить в магнитном поле компас.
- Дождаться, когда магнитная стрелка займет устойчивое положение.
- Принять за направление вектора магнитной индукции направление стрелки компаса «север».
В пространстве между полюсами постоянного магнита вектор магнитной индукции выходит из северного полюса:
При определении направления вектора магнитной индукции с помощью витка с током следует применять правило буравчика:
При вкручивании острия буравчика вдоль направления тока рукоятка будет вращаться по направлению вектора → B магнитной индукции.
Отсюда следует, что:
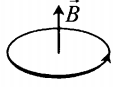
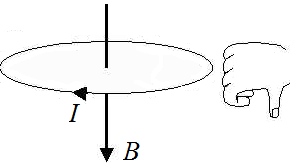
- Если по витку ток идет против часовой стрелки, то вектор магнитной индукции → B направлен вверх.
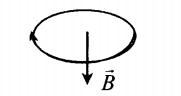
- Если по витку ток идет по часовой стрелке, то вектор магнитной индукции → B направлен вниз.
Способы обозначения направлений векторов:
| Вверх |  |
| Вниз |  |
| Влево | 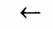 |
| Вправо | 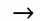 |
| На нас перпендикулярно плоскости чертежа |  |
| От нас перпендикулярно плоскости чертежа |  |
Пример №1. На рисунке изображен проводник, по которому течет электрический ток. Направление тока указано стрелкой. Как направлен (вверх, вниз, влево, вправо, от наблюдателя, к наблюдателю) вектор магнитной индукции в точке С?
Если мысленно начать вкручивать острие буравчика по направлению тока, то окажется, что вектор магнитной индукции в точке С будет направлен к нам — к наблюдателю.
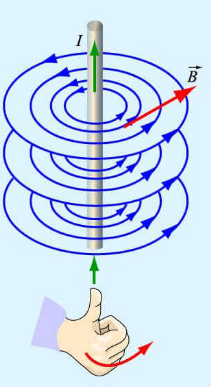
Магнитное поле прямолинейного тока
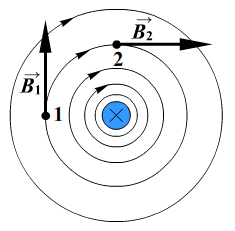
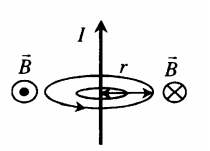
Линии магнитной индукции представляют собой концентрические окружности, лежащие в плоскости, перпендикулярной проводнику. Центр окружностей совпадает с осью проводника.
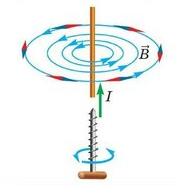
Если ток идет вверх, то силовые линии направлены против часовой стрелки. Если вниз, то они направлены по часовой стрелке. Их направление можно определить с помощью правила буравчика или правила правой руки:
Правило буравчика (правой руки)
Если большой палец правой руки, отклоненный на 90 градусов, направить в сторону тока в проводнике, то остальные 4 пальца покажут направление линий магнитной индукции.
Модуль вектора магнитной индукции на расстоянии r от оси проводника:
B = μ μ 0 I 2 π r . .
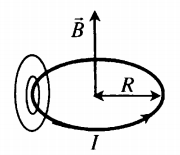
Магнитное поле кругового тока
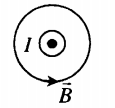
Силовые линии представляют собой окружности, опоясывающие круговой ток. Вектор магнитной индукции в центре витка направлен вверх, если ток идет против часовой стрелки, и вниз, если по часовой стрелке.
Определить направление силовых линий магнитного поля витка с током можно также с помощью правила правой руки:
Если расположить четыре пальца правой руки по направлению тока в витке, то отклоненный на 90 градусов большой палец, покажет направление вектора магнитной индукции.
Модуль вектора магнитной индукции в центре витка, радиус которого равен R:
Модуль напряженности в центре витка:
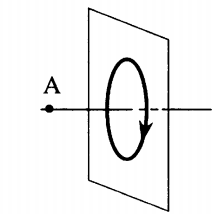
Пример №2. На рисунке изображен проволочный виток, по которому течет электрический ток в направлении, указанном стрелкой. Виток расположен в вертикальной плоскости. Точка А находится на горизонтальной прямой, проходящей через центр витка. Как направлен (вверх, вниз, влево, вправо) вектор магнитной индукции магнитного поля в точке А?
Если мысленно обхватить виток так, чтобы четыре пальца правой руки были бы направлены в сторону тока, то отклоненный на 90 градусов большой палец правой руки показал бы, что вектор магнитной индукции в точке А направлен вправо.
Магнитное поле электромагнита (соленоида)
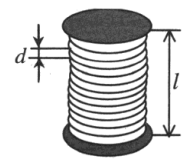
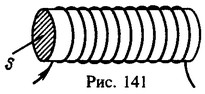
Соленоид — это катушка цилиндрической формы, витки которой намотаны вплотную, а длина значительно больше диаметра.
Число витков в соленоиде N определяется формулой:
l — длина соленоида, d — диаметр проволоки.
Линии магнитной индукции являются замкнутыми, причем внутри соленоида они располагаются параллельно друг другу. Поле внутри соленоида однородно.
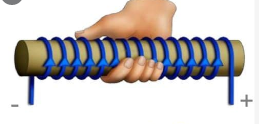
Если ток по виткам соленоида идет против часовой стрелки, то вектор магнитной индукции → B внутри соленоида направлен вверх, если по часовой стрелке, то вниз. Для определения направления линий магнитной индукции можно воспользоваться правилом правой руки для витка с током.
Модуль вектора магнитной индукции в центральной области соленоида:
B = μ μ 0 I N l . . = μ μ 0 I d . .
Модуль напряженности магнитного поля в центральной части соленоида:
H = I N l . . = I d . .
Алгоритм определения полярности электромагнита
- Определить полярность источника.
- Указать на витках электромагнита условное направление тока (от «+» источника к «–»).
- Определить направление вектора магнитной индукции.
- Определить полюса электромагнита. Там, откуда выходят линии магнитной индукции, располагается северный полюс электромагнита (N, или «–». С противоположной стороны — южный (S, или «+»).
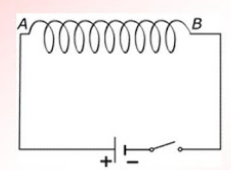
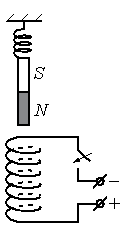
Пример №3. Через соленоид пропускают ток. Определите полюсы катушки.
Ток условно течет от положительного полюса источника тока к отрицательному. Следовательно, ток течет по виткам от точки А к точке В. Мысленно обхватив соленоид пальцами правой руки так, чтобы четыре пальца совпадали с направлением тока в витках соленоида, отставим большой палец на угол 90 градусов. Он покажет направление линий магнитной индукции внутри соленоида. Проделав это, увидим, что линии магнитной индукции направлены вправо. Следовательно, они выходят из В, который будет являться северным полюсом. Тогда А будет являться южным полюсом.
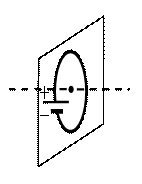
а) вертикально вверх в плоскости витка
б) вертикально вниз в плоскости витка
в) вправо перпендикулярно плоскости витка
г) влево перпендикулярно плоскости витка
Алгоритм решения
Решение
По условию задачи мы имеем дело с круглым проволочным витком. Поэтому для определения вектора → B магнитной индукции мы будем использовать правило правой руки.
Чтобы применить это правило, нам нужно знать направление течение тока в проводнике. Условно ток течет от положительного полюса источника к отрицательному. Следовательно, на рисунке ток течет по витку в направлении хода часовой стрелки.
Теперь можем применить правило правой руки. Для этого мысленно направим четыре пальца правой руки в направлении тока в проволочном витке. Теперь отставим на 90 градусов большой палец. Он показывает относительно рисунка влево. Это и есть направление вектора магнитной индукции.
pазбирался: Алиса Никитина | обсудить разбор | оценить
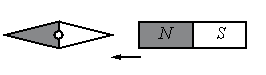
а) повернётся на 180°
б) повернётся на 90° по часовой стрелке
в) повернётся на 90° против часовой стрелки
г) останется в прежнем положении
Алгоритм решения
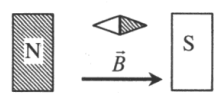
- Вспомнить, как взаимодействуют магниты.
- Определить исходное положение полюсов.
- Определить конечное положение полюсов и установить, как изменится положение магнитной стрелки.
Решение
Одноименные полюсы магнитов отталкиваются, а разноименные притягиваются. Изначально южный полюс магнитной стрелки находится справа, а северный — слева. Полосовой магнит подносят к ее южному полюсу северной стороной. Поскольку это разноименные полюса, положение магнитной стрелки не изменится.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алгоритм решения
- Определить направление тока в соленоиде.
- Определить полюса соленоида.
- Установить, как будет взаимодействовать соленоид с магнитом.
- Установить, как будет себя вести магнит после замыкания электрической цепи.
Решение
Чтобы определить направление тока в соленоиде, посмотрим на расположение полюсов источника тока. Ток условно направлен от положительного полюса к отрицательному. Следовательно, относительно рисунка ток в витках соленоида направлен по часовой стрелке.
Зная направление тока в соленоиде, можно определить его полюса. Северным будет тот полюс, из которого выходят линии магнитной индукции. Определить их направление поможет правило правой руки для соленоида. Мысленно обхватим соленоид так, чтобы направление четырех пальцев правой руки совпадало с направлением тока в витках соленоида. Теперь отставленный на 90 градусов большой палец покажет направление вектора магнитной индукции. Проделав все манипуляции, получим, что вектор магнитной индукции направлен вниз. Следовательно, внизу соленоида расположен северный полюс, а вверху — южный.
Известно, что одноименные полюса магнитов отталкиваются, а разноименные — притягиваются. Подвешенный полосовой магнит обращен к южному полюсу соленоида северным полюсом. А это значит, что при замыкании электрической цепи он будет растягивать пружину, притягиваясь к соленоиду (двигаться вниз).
pазбирался: Алиса Никитина | обсудить разбор | оценить
Разность потенциалов
Понятие потенциала в физике
Что такое потенциал в физике? Это понятие очень часто применяется для описания качеств сил и полей самой разной природы. Скалярная функция, характеризующая некоторую величину, представляющуюся вектором, – вот что это потенциал. Гравитационный потенциал описывает соответствующее поле. В термодинамике это понятие применяется для системной внутренней энергии, в механике – для той или иной приложенной к предмету силы.
Электрика, прежде всего, интересует, что такое потенциал в электричестве. Из общего определения нетрудно вывести, что характеристика электрополя – это электрический потенциал. В своей статической форме электрический потенциал показывает потенциальную энергию одиночного «плюсового» заряда, помещаемого в данное место электрополя, и является одной из разновидностей электромагнитного потенциала. Вторая его форма – векторная (в отличие от скалярной), описывает магнитное поле.
Важно! Характеристика поля, описывающая зависимость работы при передвижении исключительно от исходной точки и места назначения, – это потенциальность поля. Траектория перемещения в этом случае на работу не влияет
Поток вектора магнитной индукции
Электростатическое поле характеризуется напряженностью, которая вместе с вектором электромагнитной индукции составляет электромагнитное поле.
Если заряженная частица движется в электромагнитном поле, то полную силу, которая воздействует на частицу, определяют по закону Лоренца:
- q – величина заряда;
- v – скорость движения;
- E – величина электрического поля;
- В – вектор магнитной индукции.
Обратите внимание! В указанной формуле приведены векторные величины. Крестом обозначено векторное произведение
Силу F воздействия на частицу принято называть силой Лоренца.
Поток вектора магнитной индукции
Данная формула является наиболее общей и может использоваться для вычисления при условии точечного заряда (в том числе единичного).
Потенциал. Эквипотенциальные поверхности.
В механике взаимодействие тел характеризует силой или потенциальной энергией. Электрическое поле, которое обеспечивает взаимодействие между электрически заряженными телами, также характеризуют двумя величинами. Напряженность электрического поля — это силовая характеристика. Теперь введем энергетическую характеристику — потенциал. С помощью этой величины можно будет сравнивать между собой любые точки электрического поля. Таким образом, потенциал как характеристика поля должен зависеть от значения заряда, содержащегося в этих точках. Поделим обе части формулы A = W1 — W2 на заряд q, получим
Отношение W/q не зависит от значения заряда и принимается за энергетическую характеристику, которую называют потенциалом поля в данной точке. Обозначают потенциал буквой φ.
Потенциал электрического поля φ — скалярная энергетическая характеристика поля, которая определяется отношением потенциальной энергии W положительного заряда q в данной точке поля к величине этого заряда:
Единица потенциала — вольт:
Подобно потенциальной энергии значения потенциала в данной точке зависит от выбора нулевого уровня для отсчета потенциала. Чаще всего в электродинамике за нулевой уровень берут потенциал точки, лежащей в бесконечности, а в электротехнике — на поверхности Земли.
С введением потенциала формулу для определения работы по перемещению заряда между точками 1 и 2 можно записать в виде
Поскольку при перемещении положительного заряда в направлении вектора напряженности электрическое поле выполняет положительную работу A = q (φ1 — φ2 )> 0, то потенциал φ1 больше чем потенциал φ2 . Таким образом, напряженность электрического поля направлена в сторону уменьшения потенциала.
Если заряд перемещать с определенной точки поля в бесконечность, то работа A = q (φ — φ∞ ). Поскольку φ∞ = 0, то A = qφ. Таким образом, величина потенциала φ определенной точки поля определяется работой, которую выполняет электрическое поле, перемещая единичный положительный заряд из этой точки в бесконечность,
Если электрическое поле создается точечным зарядом q, то в точке, лежащей на расстоянии r от него, потенциал вычисляют по формуле
По этой формуле рассчитывают и потенциал поля заряженного шара. В таком случае r — это расстояние от центра шара до выбранной точки поля. С этой формулы видно, что на одинаковых расстояниях от точечного заряда, который создает поле, потенциал одинаков. Все эти точки лежат на поверхности сферы, описанной радиусом r вокруг точечного заряда. Такую сферу называют эквипотенциальной поверхностью.
Эквипотенциальные поверхности — геометрическое место точек в электрическом поле, которые имеют одинаковый потенциал, — один из методов наглядного изображения электрических полей.
Эквипотенциальные поверхности электрических полей, созданных точечными зарядами разных знаков
Силовые линии всегда перпендикулярны эквипотенциальных поверхностей. Это означает, что работа сил поля по перемещению заряда по эквипотенциальной поверхности равна нулю.
В случае наложения электрических полей, созданных несколькими зарядами, потенциал электрического поля равен алгебраической сумме потенциалов полей, созданных отдельными зарядами, φ = φ1 + φ2 + φ3 . Эквипотенциальные поверхности таких систем имеют сложную форму. Например, для системы из двух одинаковых по значению одноименных зарядов эквипотенциальные поверхности имеют вид, изображенный на рисунке. Эквипотенциальные поверхности однородного поля явлются плоскостями.
Эквипотенциальные поверхности: а — поля двух одинаковых зарядов б — однородного поля
Проводники в электростатическом поле
Размещение проводника в электростатическом поле приводит к тому, что поле начнет действовать на носители заряда внутри проводящего предмета. Носители начинают перемещаться до тех пор, пока электростатическое поле вне поверхности ни обратится в нуль.
Поскольку поле внутри вещества отсутствует, то во всех точках проводящего материала энергия будет постоянной, а поверхность эквипотенциальной. Векторы напряженности поля направлены под прямым углом в любой точке поверхности проводника.
Под действием поля заряды внутри проводника отсутствуют, поскольку они сосредоточены исключительно на поверхности. Этот факт используется при экранировке – защите тел от влияния внешних электромагнитных и электростатических полей. Для экранирования может использоваться не только сплошной проводящий материал, но и сетка, так называемая «клетка Фарадея».
Также свойство перемещения заряженных частиц (электронов) используется в электростатических генераторах для получения напряжения в несколько миллионов вольт.
Поток вектора магнитной индукции
Электростатическое поле характеризуется напряженностью, которая вместе с вектором электромагнитной индукции составляет электромагнитное поле.
Если заряженная частица движется в электромагнитном поле, то полную силу, которая воздействует на частицу, определяют по закону Лоренца:
- q – величина заряда;
- v – скорость движения;
- E – величина электрического поля;
- В – вектор магнитной индукции.
Обратите внимание! В указанной формуле приведены векторные величины. Крестом обозначено векторное произведение
Силу F воздействия на частицу принято называть силой Лоренца.
Данная формула является наиболее общей и может использоваться для вычисления при условии точечного заряда (в том числе единичного).
Падение потенциала вдоль проводника
На концах проводника, помещенного в электрическое поле, начинает наблюдаться разность потенциалов. Вследствие этого электроны начинают перемещаться в сторону увеличения разности. В проводнике возникает электрический ток. Свободные электроны продвигаются вдоль проводника до тех пор, пока разница ни будет равна нулю. На практике для поддержания заданной величины тока цепи запитываются от источников напряжения или тока. Разница заключается в следующем:
- Источник тока поддерживает в цепи постоянный ток вне зависимости от сопротивления нагрузки;
- Источник напряжения поддерживает на своих зажимах строго постоянную ЭДС, независимо от величины потребляемого тока.
Разница потенциалов (падение напряжения) пропорциональна расстоянию от концов проводника, то есть обладает линейной зависимостью.
Электроемкость уединенного проводника
Для связи величин заряда и напряжения введено понятие электрической емкости. Для уединенного проводника (такого, на который отсутствует влияние других заряженных тел) значение емкости – величина постоянная и равная отношению количества заряда к потенциалу. Другими словами, емкость показывает, какой заряд нужно сообщить проводнику, чтобы его потенциальная энергия увеличилась на единицу.
Электроемкость не зависит от степени заряженности. Роль играют только:
- форма;
- геометрические размеры;
- диэлектрические свойства среды.
Так же, как и емкость электрического конденсатора, электроемкость проводника будет обозначаться в фарадах.
Обратите внимание! На практике электроемкость проводника составляет очень малую величину. Для увеличения значения, особенно при производстве конденсаторов, как элементов с нормированным значением емкости, разработаны особые технологии
Для чего нужен потенциометр электрику
Данный прибор широко применяется в практике для модуляции напряжения. Дело в том, что у многих источников (особенно заточенных под автономное функционирование: аккумуляторные элементы, солнечные батареи и т.д.) константное напряжение, не поддающееся управлению без специальных устройств, что может вызвать проблемы. Чтобы уменьшить исходное напряжение такого элемента, используют устройства-делители, снабженные потенциометрами.
Потенциометр-реостат
Как работает потенциометр? Он представляет собой резистор, имеющий пару выводов и подвижный ползунок с еще одним выводом. Подключаться такое переменное устройство сопротивления может двумя способами:
- По типу реостата, с использованием ползункового вывода и одного из пары других. Сопротивление замеряется движением ползунка по корпусу резистора. Регуляция цепного электротока в таком случае возможна при последовательном подключении такого реостата и источника напряжения.
- Потенциометрическим методом, задействующим каждый вывод из имеющейся у прибора тройки. Два главных вывода включаются параллельно источнику, снятие сниженного напряжения реализуется с ползункового механизма и одного вывода. В этом случае через резисторное устройство течет электроток, создающий спад напряжения между ползунком и боковыми выводами. В такой модели на источник питания ложится большая нагрузка, так как для точности регуляции и отсутствия сбоев необходимо, чтобы резисторное сопротивление в несколько раз уступало нагрузочному.
Потенциометрическое подключение прибора
Таким образом, понятие потенциала используется в разных областях физики: как в механике, так и в изучении электричества. В последнем случае оно выступает в качестве характеристики поля. Непосредственно рассматриваемая величина измерению не поддается, зато можно измерить разность, тогда один заряд берется за точку отсчета.
Проводники в электростатическом поле. Электроемкость уединенного проводника.
Если поместить проводник во внешнее электростатическое поле или его зарядить, то на заряды проводника будет действовать электростатическое поле, в результате чего они начнут перемещаться. Перемещение зарядов (ток) продолжается до тех пор, пока не установится равновесное распределение зарядов, при котором электростатическое поле внутри проводника обращается в нуль. Это происходит в течение очень короткого времени. В самом деле, если бы поле не было равно нулю, то в проводнике возникло бы упорядоченное движение зарядов без затраты энергии от внешнего источника, что противоречит закону сохранения энергии. Итак, напряженность поля во всех точках внутри проводника равна нулю:
называют электроемкостью (или просто емкостью) уединенного проводника. Емкость уединенного проводника определяется зарядом, сообщение которого проводнику изменяет его потенциал на единицу.
Емкость проводника зависит от его размеров и формы, но не зависит от материала, агрегатного состояния, формы и размеров полостей внутри проводника. Это связано с тем, что избыточные заряды распределяются на внешней поверхности проводника. Емкость не зависит также ни от заряда проводника, ни от его потенциала. Сказанное не противоречит формуле, так как она лишь показывает, что емкость уединенного проводника прямо пропорциональна его заряду и обратно пропорциональна потенциалу.
Единица электроемкости — фарад (Ф): 1Ф
Поскольку электрический ток является упорядоченным движением заряженных частиц, то для определения величины тока необходимо знать, как величину энергии частиц, так и силу стороннего воздействия на них.
Теорема Гаусса для магнитного поля
Теорема Гаусса является одной из самых основных в электродинамике законов. Существуют теоремы Гаусса для электрического и магнитного полей, которые входят в состав уравнений Максвелла. При помощи данного закона устанавливается связь между напряженностью электрического поля и заряда в случае произвольной поверхности. Теорема (закон) Гаусса гласит, что в произвольной замкнутой поверхности поток вектора электрического поля пропорционален заряду, заключенному внутри поверхности. Для магнитного поля теорема Гаусса говорит о том, что поток вектора магнитной индукции через произвольную замкнутую поверхность равен нулю.
Проводники в электростатическом поле
Размещение проводника в электростатическом поле приводит к тому, что поле начнет действовать на носители заряда внутри проводящего предмета. Носители начинают перемещаться до тех пор, пока электростатическое поле вне поверхности ни обратится в нуль.
Поскольку поле внутри вещества отсутствует, то во всех точках проводящего материала энергия будет постоянной, а поверхность эквипотенциальной. Векторы напряженности поля направлены под прямым углом в любой точке поверхности проводника.
Под действием поля заряды внутри проводника отсутствуют, поскольку они сосредоточены исключительно на поверхности. Этот факт используется при экранировке – защите тел от влияния внешних электромагнитных и электростатических полей. Для экранирования может использоваться не только сплошной проводящий материал, но и сетка, так называемая «клетка Фарадея».
Также свойство перемещения заряженных частиц (электронов) используется в электростатических генераторах для получения напряжения в несколько миллионов вольт.
Движение заряда в электрическом поле
Когда носитель электрического заряда оказывается в электростатическом поле, на него неизбежно начинает действовать кулоновская сила. Это приводит к тому, что носитель заряда начинает перемещаться в пространстве, если, конечно, кулоновские силы не скомпенсированы другими, противодействующими силами. Рассмотрим случай, когда в электрическом поле оказался пробный заряд q совершенно свободный от действия других сил. Как только этот заряд окажется в зоне действия силовых линий электрического поля, то на него будет действовать сила в соответствии с Законом Кулона.
Как известно, механическая сила является векторной величиной, а значит имеет и величину, и направление. Носитель заряда в электрическом поле начнет менять свое энергетическое состояние. Как это проявляется? Одноименные заряды отталкиваются, а разноименные притягиваются. Наш заряд в зависимости от знака начнет сближаться с противоположным ему знаком заряда, которое и образует электрическое поле. Легче всего это увидеть, посмотрев на силовые линии напряженности поля. Согласно правилам они имеют направление от заряда +Q к заряду -Q, иначе говоря выходят из положительных зарядов (источника) и заходят в отрицательные заряды (источника).
Направление силы действия на пробный заряд q определить очень легко, если он положительный, то сила будет направлена по силовым линиям поля, а если отрицательный, то против силовых линий. Траектория движения будет зависеть от начальной скорости заряда, ее величины и направления. Действующая сила будет ускорять заряд, то есть его скорость по величине и направлению будет меняться в сторону действия кулоновской силы.
Движение заряда q в электрическом поле
На рисунке изображена примерная траектория движения заряда +q, имеющего некоторую начальную скорость V. Если бы заряд имел противоположный знак, то траектория движения была бы зеркально отражена от оси X, и заряд бы двигался в сторону пластины (+). По оси Y можно изобразить шкалу потенциала, которая так же будет иметь полярность.
Спрашивается. Что это за шкала и как определить где больший, а где меньший потенциал? Учитывая, что по определению и по действующим правилам силовые линии выходят из зарядов (+) и уходят в бесконечность, где потенциал равен нулю, то максимальный положительный потенциал будет в начале силовых линий от источника, а максимальный отрицательный потенциал там, где линии заходят в источник поля. Наш заряд +q, изображенный на рисунке выше будет двигаться от большего потенциала к меньшему, тем самым уменьшая потенциальную энергию поля, а точнее, преобразуя ее в кинетическую энергию. Если же в нашем случае был заряд -q, то для него потенциалы поменяли бы знак, арифметически, за счет умножения на -1, он всё также бы двигался в сторону уменьшения энергии поля.
Разность потенциалов — энергетическая характеристика
Любой заряд при своем движении в электрическом поле имеет начальную позицию, точку в пространстве поля, которая характеризуется потенциалом φначальное, и конечную точку, которая также имеет свой потенциал φконечное. Разность между двумя этими величинами потенциалов называется Δφ — разность потенциалов, а иначе еще называют электрическим напряжением поля.
Следует различать электрическое напряжение поля в электростатическом потенциальном поле, где нет вихрей, и падение электрического напряжения в электротехнических цепях, а также напряжение, которое является ЭДС (электродвижущая сила). Для того, чтобы не было путаницы, обычно для электрического поля употребляют выражение «разность потенциалов», для электрических цепей — «падение напряжения», а для источников тока — «ЭДС источника». Когда отсутствует понимание различия таких определений, становится трудно разобраться в сути сложных явлений в мире электротехники, электроники и автоматики. Что же роднит все эти три такие похожие, но всё-таки различные понятия? Прежде всего общее здесь то, что все три характеризуют энергетическое состояние. Но далее, при ответе на вопрос «Энергетическое состояние чего?», идут различия. Разность потенциалов характеризует энергетику электрического потенциального поля, падение напряжения — для участка электрической цепи, а ЭДС источника — это энергетическая характеристика устройства создающего электрический ток. Общность при ответе на вопрос: «Что это?», а различия при ответе на вопрос «Где?». Всё познается в сравнении, поэтому необходимо отлично ориентироваться во всех трёх вышеуказанных понятиях.
Имеем некоторый путь пройденный зарядом q от точки A до точки B, от начального потенциала, к конечному, а разница между ними и есть разность потенциалов. О чем это нам говорит? Если Δφ=φA-φB (разность потенциалов), тогда чтобы узнать какую работу, которую совершил заряд проделавший путь, нам надо Δφ умножить на величину заряда q, причем надо учесть знак заряда.
Полученное значение является работой, которую совершает заряд при перемещении. Иначе говоря, потенциальная энергия поля преобразуется в кинетическую энергию заряда, а так как заряд, в случае движения в сторону противоположного ему знака уменьшает напряженность поля, то потенциальная энергия поля уменьшится.
В случае, если некоторые не кулоновские силы воздействуют на заряд и тем самым переместят его в сторону поля, где знак такой же как у заряда, то работа будет совершена с противоположным знаком, точнее сказать она будет затрачена извне и общее энергетическое состояние поля увеличится. В одном случае потенциальная энергия поля уменьшается, за счет того, что часть этой энергии переходит в кинетическую, а в другом случае, если действуют на заряд внешние механические силы против кулоновских сил — потенциальная энергия возрастает из внешнего источника. В первом случае заряд движется в сторону уменьшения своего энергетического состояния, а во втором случае он движется в сторону увеличения своего энергетического состояния. Соответственно работа совершатся может либо с положительным знаком, либо с отрицательным.
Проводники в электростатическом поле
Размещение проводника в электростатическом поле приводит к тому, что поле начнет действовать на носители заряда внутри проводящего предмета. Носители начинают перемещаться до тех пор, пока электростатическое поле вне поверхности ни обратится в нуль.
Поскольку поле внутри вещества отсутствует, то во всех точках проводящего материала энергия будет постоянной, а поверхность эквипотенциальной. Векторы напряженности поля направлены под прямым углом в любой точке поверхности проводника.
Проводник в электростатическом поле
Под действием поля заряды внутри проводника отсутствуют, поскольку они сосредоточены исключительно на поверхности. Этот факт используется при экранировке – защите тел от влияния внешних электромагнитных и электростатических полей. Для экранирования может использоваться не только сплошной проводящий материал, но и сетка, так называемая «клетка Фарадея».
Клетка Фарадея
Также свойство перемещения заряженных частиц (электронов) используется в электростатических генераторах для получения напряжения в несколько миллионов вольт.
Разность потенциалов
Практическое значение имеет не сам потенциал в точке, а изменение (разница) потенциала φ1 — φ2 , которое не зависит от выбора нулевого уровня отсчета потенциала. Разность потенциалов φ1 — φ2 еще называют напряжением и обозначают латинской буквой U. Тогда формула для работы по перемещению заряда приобретает вид
Напряжение U — это физическая величина, определяемая работой электрического поля по перемещению единичного положительного заряда между двумя точками поля,
Единица разности потенциалов (напряжения), как и потенциала, — вольт,
Поскольку работа сил поля по перемещению заряда зависит только от разности потенциалов, то в случае перемещения заряда с первой эквипотенциальной поверхности на другую (потенциалы которых соответственно φ1 и φ2 ) выполненная полем работа не зависит от траектории этого движения.
Электроемкость уединенного проводника
Для связи величин заряда и напряжения введено понятие электрической емкости. Для уединенного проводника (такого, на который отсутствует влияние других заряженных тел) значение емкости – величина постоянная и равная отношению количества заряда к потенциалу. Другими словами, емкость показывает, какой заряд нужно сообщить проводнику, чтобы его потенциальная энергия увеличилась на единицу.
Электроемкость не зависит от степени заряженности. Роль играют только:
- форма;
- геометрические размеры;
- диэлектрические свойства среды.
Так же, как и емкость электрического конденсатора, электроемкость проводника будет обозначаться в фарадах.
Обратите внимание! На практике электроемкость проводника составляет очень малую величину. Для увеличения значения, особенно при производстве конденсаторов, как элементов с нормированным значением емкости, разработаны особые технологии
Разность потенциалов. Напряжение
Работа сил электростатического поля по перемещению заряда q из точки 1 в точку 2 поля
Выразим потенциальную энергию через потенциалы поля в соответствующих точках:
W_ = q_0 varphi_1 , W_ = q_0 varphi_2 .)
A_ <12>= q_0 (varphi_1 — varphi_2) .)
Таким образом, работа определяется произведением заряда на разность потенциалов начальной и конечной точек.
Из этой формулы разность потенциалов
varphi_1 — varphi_2 = frac> .)
Разность потенциалов — это скалярная физическая величина, численно равная отношению работы сил поля по перемещению заряда между данными точками поля к этому заряду.
В СИ единицей разности потенциалов является вольт (В).
1 В — разность потенциалов между двумя такими точками электростатического поля, при перемещении между которыми заряда в 1 Кл силами поля совершается работа в 1 Дж.
Разность потенциалов в отличие от потенциала не зависит от выбора нулевой точки. Разность потенциалов φ1 — φ2 часто называют электрическим напряжением между данными точками поля:
U = varphi_1 — varphi_2 .)
Напряжение между двумя точками поля определяется работой сил этого поля по перемещению заряда в 1 Кл из одной точки в другую. В электростатическом поле напряжение вдоль замкнутого контура всегда равно нулю.
Работу сил электрического поля иногда выражают не в джоулях, а в электронвольтах. 1 эВ равен работе, совершаемой силами поля при перемещении электрона (е = 1,6·10-19 Кл) между двумя точками, напряжение между которыми равно 1 В.
1 эВ = 1,6·10-19 Кл·1 В = 1,6·10-19 Дж.
1 МэВ = 106 эВ = 1,6·10-13 Дж.
Электрическое поле графически можно изобразить не только с помощью линий напряженности, но и с помощью эквипотенциальных поверхностей.
Эквипотенциальной называется воображаемая поверхность, в каждой точке которой потенциал одинаков. Разность потенциалов между двумя любыми точками эквипотенциальной поверхности равна нулю.
Следовательно, работа по перемещению заряда вдоль эквипотенциальной поверхности равна 0. Но работа рассчитывается по формуле (
A = F Delta r cos alpha = q_0E Delta r cos alpha). Здесь q ≠ 0, Е ≠ 0, Δr ≠ 0. Значит, (
cos alpha = 0 Rightarrow alpha = 90^<circ>).
Следовательно, линии напряженности перпендикулярны эквипотенциальным поверхностям. Первая эквипотенциальная поверхность металлического проводника — это поверхность самого заряженного проводника, что легко проверить электрометром. Остальные эквипотенциальные поверхности проводятся так, чтобы разность потенциалов между двумя соседними поверхностями была постоянной.
Картины эквипотенциальных поверхностей некоторых заряженных тел приведены на рис. 3.
Эквипотенциальными поверхностями однородного электростатического поля являются плоскости, перпендикулярные линиям напряженности (рис. 3, а).
Эквипотенциальные поверхности поля точечного заряда представляют собой сферы, в центре которых расположен заряд q (рис. 3, б).
Сущность понятия потенциальной разницы
Для изучения свойств заряженных частиц, помещенных в электростатическое поле, введено понятие потенциала. Оно означает отношение энергии заряда, помещенного в электростатическое поле, к его величине.
При переносе заряженной частицы в другую точку поля меняется его потенциальная энергия, а величина заряда остается неизменной. Для переноса требуется затратить некоторое количество энергии. Данная энергия по переносу единицы заряда получила название электрического напряжения. Соответственно, больший запас энергии будет ускорять перенос, то есть, чем больше напряжение, тем больше ток в цепи.
В данном случае разность потенциалов – это численное равенство напряжению между точками нахождения единичного заряда. Для общего случая здесь должна добавляться работа сторонних сил, которая называется электродвижущей силой (ЭДС). По своей сути, электричество – это работа стороннего источника (генератора) по поддержанию в электросхеме заданных уровней напряжения и тока.
Разность потенциалов (напряжение)
Напряжение является одним из важнейших терминов в электрике, оно описывается как работа, совершаемая электрополем с целью перемещения некоторого заряда из одной точки в другую. По аналогии с гравитацией, заряд при помещении в зону действия поля обладает потенциалом, который можно сравнить с соответствующим видом энергии у тела. Величина электрического потенциала прямо пропорциональна степени полевой напряженности и величине самого заряда.
Встает вопрос: потенциал в чем измеряется? Правильнее будет сказать, в чем обычно измеряется разность потенциалов, так как работники электротехники имеют дело именно с этой величиной в форме напряжения. Для самого потенциала специальной измерительной единицы не существует. В СИ принято измерять разность в вольтах (В). Она равна одному вольту в том случае, если для транспортировки заряда в один кулон из одной точки электрополя в другую потребуется совершить работу в один джоуль.
Важно! Измерить напряжение можно с помощью специального устройства – вольтметра. Стрелочная разновидность прибора, использующаяся на школьных уроках физики, оснащена градуированной шкалой, базирующейся на угле отклонения проволочной рамки, по которой проходит электроток
Помимо него, существуют и приборы с цифровым дисплеем, а также мультиметры, способные работать в нескольких режимах и измеряющие разные величины, описывающие электроцепь. Для измерения важно правильно подключить щупы.
Измерить напряжение поможет вольтметр
Сущность понятия потенциальной разницы
Для изучения свойств заряженных частиц, помещенных в электростатическое поле, введено понятие потенциала. Оно означает отношение энергии заряда, помещенного в электростатическое поле, к его величине.
При переносе заряженной частицы в другую точку поля меняется его потенциальная энергия, а величина заряда остается неизменной. Для переноса требуется затратить некоторое количество энергии. Данная энергия по переносу единицы заряда получила название электрического напряжения. Соответственно, больший запас энергии будет ускорять перенос, то есть, чем больше напряжение, тем больше ток в цепи.
Разность потенциалов
В данном случае разность потенциалов – это численное равенство напряжению между точками нахождения единичного заряда. Для общего случая здесь должна добавляться работа сторонних сил, которая называется электродвижущей силой (ЭДС). По своей сути, электричество – это работа стороннего источника (генератора) по поддержанию в электросхеме заданных уровней напряжения и тока.
Закон электромагнитной индукции Фарадея и его формулировка в дифференциальной форме
История развития и опыты Фарадея
До середины XIX века считалось, что электрическое и магнитное поле не имеют никакой связи, и природа их существования различна. Но М. Фарадей был уверен в единой природе этих полей и их свойств. Явление электромагнитной индукции, обнаруженное им, впоследствии стало фундаментом для устройства генераторов всех электростанций. Благодаря этому открытию знания человечества о электромагнетизме шагнули далеко вперед.
Фарадей проделал следующий опыт: он замыкал цепь в катушке I и вокруг нее возрастало магнитное поле. Далее линии индукции данного магнитного поля пересекали катушку II, в которой возникал индукционный ток.
Рис. 1. Схема опыта Фарадея
На самом деле, одновременно с Фарадеем, но независимо от него, другой ученый Джозеф Генри обнаружил это явление. Однако Фарадей опубликовал свои исследования раньше. Таким образом, автором закона электромагнитной индукции стал Майкл Фарадей.
Сколько бы экспериментов не проводил Фарадей, неизменным оставалось одно условие: для образования индукционного тока важным является изменение магнитного потока, пронизывающего замкнутый проводящий контур (катушку).
Закон Фарадея
Явление электромагнитной индукции определяется возникновением электрического тока в замкнутом электропроводящем контуре при изменении магнитного потока через площадь этого контура.
Основной закон Фарадея заключается в том, что электродвижущая сила (ЭДС) прямо пропорциональна скорости изменения магнитного потока.
Формула закона электромагнитной индукции Фарадея выглядит следующим образом:
Рис. 2. Формула закона электромагнитной индукции
И если сама формула, исходя из вышесказанных объяснений не порождает вопросов, то знак «-» может вызвать сомнения. Оказывается существует правило Ленца – русского ученого, который проводил свои исследования, основываясь на постулатах Фарадея. По Ленцу знак «-» указывает на направление возникающей ЭДС, т.е. индукционный ток направлен так, что магнитный поток, который он создает, через площадь, ограниченную контуром, стремится препятствовать тому изменению потока, которое вызывает данный ток.
Основные понятия и законы электростатики
Закон Кулона:
сила взаимодействия двух точечных неподвижных зарядов в вакууме прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними:
Коэффициент пропорциональности в этом законе
В СИ коэффициент k записывается в виде
где ε0 = 8, 85 · 10−12 Ф/м (электрическая постоянная).
Точечными зарядами называют такие заряды, расстояния между которыми гораздо больше их размеров.
Электрические заряды взаимодействуют между собой с помощью электрического поля. Для качественного описания электрического поля используется силовая характеристика, которая называется «напряжённостью электрического поля» (E). Напряжённость электрического поля равна отношению силы, действующей на пробный заряд, помещённый в некоторую точку поля, к величине этого заряда:
Направление вектора напряжённости совпадает с направлением силы, действующей на положительный пробный заряд. [E]=B/м. Из закона Кулона и определения напряжённости поля следует, что напряжённость поля точечного заряда
где q — заряд, создающий поле; r — расстояние от точки, где находится заряд, до точки, где создаётся поле.
Если электрическое поле создаётся не одним, а несколькими зарядами, то для нахождения напряжённости результирующего поля используется принцип суперпозиции электрических полей: напряжённость результирующего поля равна векторной сумме напряжённостей полей, созданных каждым из зарядов — источников в отдельности:
Работа электрического поля при перемещении заряда: найдём работу перемещения положительного заряда силами Кулона в однородном электрическом поле. Пусть поле перемещает заряд q из точки 1 в точку 2:
В электрическом поле работа не зависит от формы траектории, по которой перемещается заряд. Из механики известно, что если работа не зависит от формы траектории, то она равна изменению потенциальной энергии с противоположным знаком:
Отсюда следует, что
Потенциалом электрического поля называют отношение потенциальной энергии заряда в поле к этому заряду:
Запишем работу поля в виде
Здесь U = ϕ1 − ϕ2 — разность потенциалов в начальной и конечной точках траектории. Разность потенциалов называют также напряжением
Часто наряду с понятием «разность потенциалов» вводят понятие «потенциал некоторой точки поля». Под потенциалом точки подразумевают разность потенциалов между данной точкой и некоторой заранее выбранной точкой поля. Эту точку можно выбирать в бесконечности, тогда говорят о потенциале относительной бесконечности.
Потенциал поля точечного заряда подсчитывается по формуле
Проекция напряжённости электрического поля на какую-нибудь ось и потенциал связаны соотношением
Электроёмкость. Конденсаторы. Энергия электрического поля
Электроёмкостью тела называют величину отношения
Формула для подсчёта ёмкости плоского конденсатора имеет вид:
где S — площадь обкладок, d — расстояние между ними.
Конденсаторы можно соединять в батареи. При параллельном соединении ёмкость батареи C равна сумме ёмкостей конденсаторов:
Разности потенциалов между обкладками одинаковы, а заряды прямо пропорциональны ёмкостям.
При последовательном соединении величина, обратная ёмкости батареи, равна сумме обратных ёмкостей, входящих в батарею:
Заряды на конденсаторах одинаковы, а разности потенциалов обратно пропорциональны ёмкостям.
Заряженный конденсатор обладает энергией. Энергию заряженного конденсатора можно подсчитать по любой из следующих формул:
Основные понятия и законы постоянного тока
Электрический ток — направленное движение электрических зарядов. В разных веществах носителями заряда выступают элементарные частицы разного знака. За положительное направление тока принято направление движения положительных зарядов. Количественно электрический ток характеризуют его силой. Это заряд, прошедший за единицу времени через поперечное сечение проводника:
Закон Ома для участка цепи имеет вид:
Коэффициент пропорциональности R, называемый электрическим сопротивлением, является характеристикой проводника [R]=Ом. Сопротивление проводника зависит от его геометрии и свойств материала:
где l — длина проводника, ρ — удельное сопротивление, S — площадь поперечного сечения. ρ является характеристикой материала и его состояния. [ρ] = Ом·м.
Проводники можно соединять последовательно. Сопротивление такого соединения находится как сумма сопротивлений:
При параллельном соединении величина, обратная сопротивлению, равна сумме обратных сопротивлений:
Для того чтобы в цепи длительное время протекал электрический ток, в составе цепи должны содержаться источники тока. Количественно источники тока характеризуют их электродвижущей силой (ЭДС). Это отношение работы, которую совершают сторонние силы при переносе электрических зарядов по замкнутой цепи, к величине перенесённого заряда:
Если к зажимам источника тока подключить нагрузочное сопротивление R, то в получившейся замкнутой цепи потечёт ток, силу которого можно подсчитать по формуле
Это соотношение называют законом Ома для полной цепи.
Электрический ток, пробегая по проводникам, нагревает их, совершая при этом работу
где t — время, I — сила тока, U — разность потенциалов, q — прошедший заряд.
Закон Джоуля-Ленца:
Основные понятия и законы магнитостатики
Характеристикой магнитного поля является магнитная индукция ➛B. Поскольку это вектор, то следует определить и направление этого вектора, и его модуль. Направление вектора магнитной индукции связано с ориентирующим действием магнитного поля на магнитную стрелку. За направление вектора магнитной индукции принимается направление от южного полюса S к северному N магнитной стрелки, свободно устанавливающейся в магнитном поле.
Направление вектора магнитной индукции прямолинейного проводника с токам можно определить с помощью правила буравчика:
если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращения рукоятки буравчика совпадает с направлением вектора магнитной индукции.
Модулем вектора магнитной индукции назовём отношение максимальной силы, действующей со стороны магнитного поля на участок проводника с током , к произведению силы тока на длину этого участка:
Единица магнитной индукции называется тесла (1 Тл)
Магнитным потоком Φ через поверхность контура площадью S называют величину, равную произведению модуля вектора магнитной индукции на площадь этой поверхности и на косинус угла между вектором магнитной индукции ➛B и нормалью к поверхности ➛n:
Единицей магнитного потока является вебер (1 Вб).
На проводник с током, помещённый в магнитное поле, действует сила Ампера
Закон Ампера:
на отрезок проводника с током силой I и длиной l, помещённый в однородное магнитное поле с индукцией ➛B , действует сила, модуль которой равен произведению модуля вектора магнитной индукции на силу тока, на длину участка проводника, находящегося в магнитном поле, и на синус угла между направлением вектора ➛B и проводником с током:
Направление силы Ампера определяется с помощью правила левой руки:
если левую руку расположить так, чтобы перпендикулярная проводнику составляющая вектора магнитной индукции входила в ладонь, а четыре вытянутых пальца указывали бы направление тока, то отогнутый на 90° большой палец укажет направление силы Ампера.
На электрический заряд, движущийся в магнитном поле, действует сила Лоренца. Модуль силы Лоренца, действующей на положительный заряд, равен произведению модуля заряда на модуль вектора магнитной индукции и на синус угла между вектором магнитной индукции и вектором скорости движущегося заряда:
Направление силы Лоренца определяется с помощью правила левой руки: если левую руку расположить так, чтобы составляющая магнитной индукции, перпендикулярная скорости заряда, входила в ладонь, а четыре пальца были направлены по движению положительного заряда, то отогнутый на 90° большой палец покажет направление силы Лоренца, действующей на заряд. Для отрицательно заряженной частицы сила Лоренца направлена против направления большого пальца.
Основные понятия и законы электромагнитной индукции
Если замкнутый проводящий контур пронизывается меняющимся магнитным потоком, то в этом контуре возникает ЭДС и электрический ток. Эту ЭДС называют ЭДС электромагнитной индукции, а ток — индукционным. Явление их возникновения называют электромагнитной индукцией. ЭДС индукции можно подсчитать по основному закону электромагнитной индукции или по закону Фарадея:
Знак «−» связан с направлением индукционного тока. Оно определяется по правилу Ленца:
индукционный ток имеет такое направление, что его действие противодействует причине, вызвавшей появление этого тока.
Магнитный поток, пронизывающий контур, прямо пропорционален току, протекающему в этом контуре:
Коэффициент пропорциональности L зависит от геометрии контура и называется индуктивностью, или коэффициентом самоиндукции этого контура. [L] = 1 Гн
Энергию магнитного поля тока можно подсчитать по формуле
где L — индуктивность проводника, создающего поле; I — ток, текущий по этому проводнику
Электромагнитные колебания и волны
Колебательным контуром называется электрическая цепь, состоящая из последовательно соединённых конденсатора с ёмкостью C и катушки с индуктивностью L (см. рис. 7).
Для свободных незатухающих колебаний в контуре циклическая частота определяется формулой
Период свободных колебаний в контуре определяется формулой Томсона:
Если в LC-контур последовательно с L, C и R включить источник переменного напряжения, то в цепи возникнут вынужденные электрические колебания. Такие колебания принято называть переменным электрическим током
В цепь переменного тока можно включать три вида нагрузки — конденсатор, резистор и катушку индуктивности.
Конденсатор оказывает переменному току сопротивление, которое можно посчитать по формуле
Ток, текущий через конденсатор, по фазе опережает напряжение на π/2 или на четверть периода, а напряжение отстаёт от тока на такой же фазовый угол.
Катушка индуктивности оказывает переменному току сопротивление, которое можно посчитать по формуле
Ток, текущий через катушку индуктивности, по фазе отстаёт от напряжения на π/2 или на четверть периода. Напряжение опережает ток на такой же фазовый угол.
Трансформатором называется устройство, предназначенное для преобразования переменных токов. Трансформатор состоит из замкнутого стального сердечника, на который надеты две катушки. Катушка, которая подключается к источнику переменного напряжения, называется первичной обмоткой, а катушка, которая подключается к потребителю, называется вторичной обмоткой. Отношение напряжения на первичной обмотке и вторичной обмотке трансформатора равно отношению числа витков в этих обмотках:
Если K > 1, трансформатор понижающий, если K
Закон Фарадея-Максвелла
В 1873 Дж.К.Максвелл по-новому изложил теорию электромагнитного поля. Уравнения, которые он вывел, легли в основу современной радиотехники и электротехники. Они выражаются следующим образом:
- Edl = -dФ/dt – уравнение электродвижущей силы
- Hdl = -dN/dt – уравнение магнитодвижущей силы.
Где E – напряженность электрического поля на участке dl; H – напряженность магнитного поля на участке dl; N – поток электрической индукции, t – время.
Симметричный характер данных уравнений устанавливает связь электрических и магнитных явлений, а также магнитных с электрическими. физический смысл, которым определяются эти уравнения, можно выразить следующими положениями:
- если электрическое поле изменяется, то это изменение всегда сопровождается магнитным полем.
- если магнитное поле изменяется, то это изменение всегда сопровождается электрическим полем.
Рис. 3. Возникновение вихревого магнитного поля
Также Максвелл установил, что распространение электромагнитного поля равна скорости распространения света.
Что мы узнали?
Ученикам 11 класса необходимо знать, что электромагнитную индукцию впервые как явление обнаружил Майкл Фарадей. Он доказал, что электрическое и магнитное поле имеют общую природу. Самостоятельные исследования на основе опытов Фарадея также проводили такие великие деятели как Ленц и Максвелл, которые расширили наши познания в области электромагнитного поля.
Явление электромагнитной индукции
Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.
Явление электромагнитной индукции было открыто М. Фарадеем.
- На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
- Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
- Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.
Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.
Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.
Объяснения возникновения индукционного тока
Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.
Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.
Свойства вихревого электрического поля:
- источник – переменное магнитное поле;
- обнаруживается по действию на заряд;
- не является потенциальным;
- линии поля замкнутые.
Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.
Самоиндукция
Самоиндукция – это явление возникновения ЭДС индукции в проводнике в результате изменения тока в нем.
При изменении силы тока в катушке происходит изменение магнитного потока, создаваемого этим током. Изменение магнитного потока, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке.
В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи.
Это приводит к тому, что при замыкании цепи, в которой есть источник тока с постоянной ЭДС, сила тока устанавливается через некоторое время.
При отключении источника ток также не прекращается мгновенно. Возникающая при этом ЭДС самоиндукции может превышать ЭДС источника.
Явление самоиндукции можно наблюдать, собрав электрическую цепь из катушки с большой индуктивностью, резистора, двух одинаковых ламп накаливания и источника тока. Резистор должен иметь такое же электрическое сопротивление, как и провод катушки.
Опыт показывает, что при замыкании цепи электрическая лампа, включенная последовательно с катушкой, загорается несколько позже, чем лампа, включенная последовательно с резистором. Нарастанию тока в цепи катушки при замыкании препятствует ЭДС самоиндукции, возникающая при возрастании магнитного потока в катушке.
При отключении источника тока вспыхивают обе лампы. В этом случае ток в цепи поддерживается ЭДС самоиндукции, возникающей при убывании магнитного потока в катушке.
ЭДС самоиндукции ( varepsilon_ ), возникающая в катушке с индуктивностью ( L ), по закону электромагнитной индукции равна:
ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в катушке.
Индуктивность
Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный поток ( Phi ) через контур из этого проводника пропорционален модулю индукции ( vec ) магнитного поля внутри контура, а индукция магнитного поля, в свою очередь, пропорциональна силе тока в проводнике.
Следовательно, магнитный поток через контур прямо пропорционален силе тока в контуре:
Индуктивность – коэффициент пропорциональности ( L ) между силой тока ( I ) в контуре и магнитным потоком ( Phi ), создаваемым этим током:
Индуктивность зависит от размеров и формы проводника, от магнитных свойств среды, в которой находится проводник.
Единица индуктивности в СИ – генри (Гн). Индуктивность контура равна 1 генри, если при силе постоянного тока 1 ампер магнитный поток через контур равен 1 вебер:
Можно дать второе определение единицы индуктивности: элемент электрической цепи обладает индуктивностью в 1 Гн, если при равномерном изменении силы тока в цепи на 1 ампер за 1 с в нем возникает ЭДС самоиндукции 1 вольт.
Энергия магнитного поля
При отключении катушки индуктивности от источника тока лампа накаливания, включенная параллельно катушке, дает кратковременную вспышку. Ток в цепи возникает под действием ЭДС самоиндукции.
Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.
Для создания тока в контуре с индуктивностью необходимо совершить работу на преодоление ЭДС самоиндукции. Энергия магнитного поля тока вычисляется по формуле:
Основные формулы раздела «Электромагнитная индукция»
Алгоритм решения задач по теме «Электромагнитная индукция»:
1. Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.
2. Записать формулу:
- закона электромагнитной индукции;
- ЭДС индукции в движущемся проводнике, если в задаче рассматривается поступательно движущийся проводник; если в задаче рассматривается электрическая цепь, содержащая источник тока, и возникающая на одном из участков ЭДС индукции, вызванная движением проводника в магнитном поле, то сначала нужно определить величину и направление ЭДС индукции. После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.
3. Записать выражение для изменения магнитного потока и подставить в формулу закона электромагнитной индукции.
4. Записать математически все дополнительные условия (чаще всего это формулы закона Ома для полной цепи, силы Ампера или силы Лоренца, формулы кинематики и динамики).
5. Решить полученную систему уравнений относительно искомой величины.
6. Решение проверить.
Правило Ленца
Чтобы определить направление индукционного тока, нужно воспользоваться правилом Ленца.
Академически это правило звучит следующим образом: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
Давайте попробуем чуть проще: катушка в данном случае — это недовольная бабуля. Забирают у нее магнитный поток — она недовольна и создает магнитное поле, которое этот магнитный поток хочет обратно отобрать.
Дают ей магнитный поток, забирай, мол, пользуйся, а она такая — «Да зачем сдался мне ваш магнитный поток!» и создает магнитное поле, которое этот магнитный поток выгоняет.
Задачи на применение закона Фарадея
Условие: проволочный контур помещен в магнитное поле. В нулевой момент времени он пронизывает поток магнитной индукции, равный Φ1 и уменьшающийся после этого до 0. Найдите величину заряда, проходящего по цепи.
Начнем с определения мгновенного значения ЭДС. Это можно сделать с помощью формулы:
Вспомним закон Ома. Согласно ему, мгновенное значение силы тока может быть записано в следующем виде:
Полное сопротивление цепи здесь обозначено буквой R.
Для нахождения заряда, идущего по цепи, нам пригодится выражение:
Поставим эти выражения в нужную формулу и получим:
Автором этой формулы является Фарадей. Он эмпирически подтвердил прямую пропорциональность величины заряда, идущего по цепи, количеству линий магнитной индукции, пересекающей проводник, и его обратную пропорциональность величине сопротивления в цепи.
Условие: квадратная рамка со стороной a помещена в одну плоскость с проводником, сила тока которого равна l. Она движется поступательно с постоянной скоростью v в направлении, обозначенное на иллюстрации ниже. Вычислите ЭДС индукции как функцию εi от расстояния x.
Найти ответ можно с помощью закона Фарадея.
Для получения искомой функции Ei(x) нам нужно построить функцию Ф(x). Бесконечный проводник с током создает магнитное поле, которое может быть выражено так:
Расстояние до точки рассмотрения здесь обозначено буквой r.
Для решения нам нужно также выделить площадь рамки. Выразим ее такой формулой:
С учетом приведенных выше выражений, а также того факта, что B→⊥S→, мы можем найти величину элементарного магнитного потока, проходящего через элемент квадратной рамки, так:
Далее вычисляем величину полного потока, учитывая, что x≤r≤x+a:
После этого переходим к нахождению ЭДС индукции с помощью закона Фарадея и выражения для магнитного потока, выведенного ранее:
http://encom74.ru/formula-nahozdenia-potencialnoj-raznicy-mezdu-tockami-v-elektromagnitnom-pole/
Закон электромагнитной индукции Фарадея и его формулировка в дифференциальной форме
Потенциал. Разность потенциалов.
Потенциал
электростатического поля — скалярная
величина, равная отношению потенциальной
энергии заряда в поле к этому заряду:
—
энергетическая характеристика поля в
данной точке. Потенциал
не зависит от величины заряда, помещенного
в это поле.
Т.к.
потенциальная энергия зависит от выбора
системы координат, то и потенциал
определяется с точностью до постоянной.
—
следствие принципа суперпозиции
полей (потенциалы складываются
алгебраически).
Потенциал
численно равен работе поля по перемещению
единичного положительного заряда из
данной точки электрического поля в
бесконечность.
В
СИ потенциал измеряется в вольтах:
Разность
потенциалов
Напряжение
— разность значений потенциала в
начальной и конечной точках траектории.
Напряжение
численно равно работе электростатического
поля при перемещении единичного
положительного заряда вдоль силовых
линий этого поля.
Разность
потенциалов (напряжение) не зависит от
выбора
системы
координат!
Единица разности потенциалов
напряженность
равна градиенту потенциала (скорости
изменения потенциала вдоль направления
d).
Из
этого соотношения видно:
1.
Вектор напряженности направлен в сторону
уменьшения потенциала.
2.
Электрическое поле существует, если
существует разность потенциалов.
3.
Единица напряженности:
—Напряженность
поля равна
Поток вектора магнитной индукции. Теорема Гаусса для магнитного поля.
Потоком
вектора магнитной индукции (магнитным
потоком)
через площадку dS
называется
скалярная
физическая величина, равная
Поток
вектора магнитной индукции
Фв
через произвольную поверхность S
равен
Теорема
Гаусса для поля В:
поток вектора магнитной индукции
через любую замкнутую поверхность равен
нулю:
полный
магнитный поток, сцепленный со всеми
витками соленоида и называемый
потокосцеплением,
Проводники в электростатическом поле. Электроемкость уединенного проводника.
Если
поместить проводник во внешнее
электростатическое поле или его зарядить,
то на заряды проводника будет действовать
электростатическое поле, в результате
чего они начнут перемещаться. Перемещение
зарядов (ток) продолжается до тех пор,
пока не установится равновесное
распределение зарядов, при котором
электростатическое поле внутри
проводника обращается в нуль. Это
происходит в течение очень короткого
времени. В самом деле, если бы поле не
было равно нулю, то в проводнике возникло
бы упорядоченное движение зарядов без
затраты энергии от внешнего источника,
что противоречит закону сохранения
энергии. Итак, напряженность поля во
всех точках внутри проводника равна
нулю:
Е
= 0.
По
гауссу
Величину
С =
Q/ф
называют
электроемкостью
(или просто емкостью)
уединенного проводника. Емкость
уединенного проводника определяется
зарядом, сообщение которого проводнику
изменяет его потенциал на единицу.
Емкость
проводника зависит от его размеров и
формы, но не зависит от материала,
агрегатного состояния, формы и размеров
полостей внутри проводника. Это связано
с тем, что избыточные заряды распределяются
на внешней поверхности проводника.
Емкость не зависит также ни от заряда
проводника, ни от его потенциала.
Сказанное не противоречит формуле, так
как она лишь показывает, что емкость
уединенного проводника прямо
пропорциональна его заряду и обратно
пропорциональна потенциалу.
Единица
электроемкости —
фарад (Ф):
1Ф
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание
- Понятие потенциала в физике
- Поток вектора магнитной индукции
- Потенциал. Эквипотенциальные поверхности.
- Проводники в электростатическом поле
- Поток вектора магнитной индукции
- Падение потенциала вдоль проводника
- Электроемкость уединенного проводника
- Для чего нужен потенциометр электрику
- Проводники в электростатическом поле. Электроемкость уединенного проводника.
- Теорема Гаусса для магнитного поля
- Проводники в электростатическом поле
- Движение заряда в электрическом поле
- Разность потенциалов — энергетическая характеристика
- Проводники в электростатическом поле
- Разность потенциалов
- Электроемкость уединенного проводника
- Разность потенциалов. Напряжение
- Сущность понятия потенциальной разницы
- Разность потенциалов (напряжение)
- Сущность понятия потенциальной разницы
Понятие потенциала в физике
Что такое потенциал в физике? Это понятие очень часто применяется для описания качеств сил и полей самой разной природы. Скалярная функция, характеризующая некоторую величину, представляющуюся вектором, – вот что это потенциал. Гравитационный потенциал описывает соответствующее поле. В термодинамике это понятие применяется для системной внутренней энергии, в механике – для той или иной приложенной к предмету силы.
Электрика, прежде всего, интересует, что такое потенциал в электричестве. Из общего определения нетрудно вывести, что характеристика электрополя – это электрический потенциал. В своей статической форме электрический потенциал показывает потенциальную энергию одиночного «плюсового» заряда, помещаемого в данное место электрополя, и является одной из разновидностей электромагнитного потенциала. Вторая его форма – векторная (в отличие от скалярной), описывает магнитное поле.
Важно! Характеристика поля, описывающая зависимость работы при передвижении исключительно от исходной точки и места назначения, – это потенциальность поля. Траектория перемещения в этом случае на работу не влияет
Поток вектора магнитной индукции
Электростатическое поле характеризуется напряженностью, которая вместе с вектором электромагнитной индукции составляет электромагнитное поле.
Если заряженная частица движется в электромагнитном поле, то полную силу, которая воздействует на частицу, определяют по закону Лоренца:
F=q∙E+q∙vхB,
где:
- q – величина заряда;
- v – скорость движения;
- E – величина электрического поля;
- В – вектор магнитной индукции.
Обратите внимание! В указанной формуле приведены векторные величины. Крестом обозначено векторное произведение
Силу F воздействия на частицу принято называть силой Лоренца.

Данная формула является наиболее общей и может использоваться для вычисления при условии точечного заряда (в том числе единичного).
Потенциал. Эквипотенциальные поверхности.
В механике взаимодействие тел характеризует силой или потенциальной энергией. Электрическое поле, которое обеспечивает взаимодействие между электрически заряженными телами, также характеризуют двумя величинами. Напряженность электрического поля — это силовая характеристика. Теперь введем энергетическую характеристику — потенциал. С помощью этой величины можно будет сравнивать между собой любые точки электрического поля. Таким образом, потенциал как характеристика поля должен зависеть от значения заряда, содержащегося в этих точках. Поделим обе части формулы A = W1 — W2 на заряд q, получим
Отношение W/q не зависит от значения заряда и принимается за энергетическую характеристику, которую называют потенциалом поля в данной точке. Обозначают потенциал буквой φ.
Потенциал электрического поля φ — скалярная энергетическая характеристика поля, которая определяется отношением потенциальной энергии W положительного заряда q в данной точке поля к величине этого заряда:
Единица потенциала — вольт:
Подобно потенциальной энергии значения потенциала в данной точке зависит от выбора нулевого уровня для отсчета потенциала. Чаще всего в электродинамике за нулевой уровень берут потенциал точки, лежащей в бесконечности, а в электротехнике — на поверхности Земли.
С введением потенциала формулу для определения работы по перемещению заряда между точками 1 и 2 можно записать в виде
Поскольку при перемещении положительного заряда в направлении вектора напряженности электрическое поле выполняет положительную работу A = q (φ1 — φ2 )> 0, то потенциал φ1 больше чем потенциал φ2 . Таким образом, напряженность электрического поля направлена в сторону уменьшения потенциала.
Если заряд перемещать с определенной точки поля в бесконечность, то работа A = q (φ — φ∞ ). Поскольку φ∞ = 0, то A = qφ. Таким образом, величина потенциала φ определенной точки поля определяется работой, которую выполняет электрическое поле, перемещая единичный положительный заряд из этой точки в бесконечность,
Если электрическое поле создается точечным зарядом q, то в точке, лежащей на расстоянии r от него, потенциал вычисляют по формуле
По этой формуле рассчитывают и потенциал поля заряженного шара. В таком случае r — это расстояние от центра шара до выбранной точки поля. С этой формулы видно, что на одинаковых расстояниях от точечного заряда, который создает поле, потенциал одинаков. Все эти точки лежат на поверхности сферы, описанной радиусом r вокруг точечного заряда. Такую сферу называют эквипотенциальной поверхностью.
Эквипотенциальные поверхности — геометрическое место точек в электрическом поле, которые имеют одинаковый потенциал, — один из методов наглядного изображения электрических полей.
Эквипотенциальные поверхности электрических полей, созданных точечными зарядами разных знаков
Силовые линии всегда перпендикулярны эквипотенциальных поверхностей. Это означает, что работа сил поля по перемещению заряда по эквипотенциальной поверхности равна нулю.
В случае наложения электрических полей, созданных несколькими зарядами, потенциал электрического поля равен алгебраической сумме потенциалов полей, созданных отдельными зарядами, φ = φ1 + φ2 + φ3 . Эквипотенциальные поверхности таких систем имеют сложную форму. Например, для системы из двух одинаковых по значению одноименных зарядов эквипотенциальные поверхности имеют вид, изображенный на рисунке. Эквипотенциальные поверхности однородного поля явлются плоскостями.
Эквипотенциальные поверхности: а — поля двух одинаковых зарядов б — однородного поля
Проводники в электростатическом поле
Размещение проводника в электростатическом поле приводит к тому, что поле начнет действовать на носители заряда внутри проводящего предмета. Носители начинают перемещаться до тех пор, пока электростатическое поле вне поверхности ни обратится в нуль.
Поскольку поле внутри вещества отсутствует, то во всех точках проводящего материала энергия будет постоянной, а поверхность эквипотенциальной. Векторы напряженности поля направлены под прямым углом в любой точке поверхности проводника.
Под действием поля заряды внутри проводника отсутствуют, поскольку они сосредоточены исключительно на поверхности. Этот факт используется при экранировке – защите тел от влияния внешних электромагнитных и электростатических полей. Для экранирования может использоваться не только сплошной проводящий материал, но и сетка, так называемая «клетка Фарадея».
Также свойство перемещения заряженных частиц (электронов) используется в электростатических генераторах для получения напряжения в несколько миллионов вольт.
Поток вектора магнитной индукции
Электростатическое поле характеризуется напряженностью, которая вместе с вектором электромагнитной индукции составляет электромагнитное поле.
Если заряженная частица движется в электромагнитном поле, то полную силу, которая воздействует на частицу, определяют по закону Лоренца:
где:
- q – величина заряда;
- v – скорость движения;
- E – величина электрического поля;
- В – вектор магнитной индукции.
Обратите внимание! В указанной формуле приведены векторные величины. Крестом обозначено векторное произведение
Силу F воздействия на частицу принято называть силой Лоренца.
Данная формула является наиболее общей и может использоваться для вычисления при условии точечного заряда (в том числе единичного).
Падение потенциала вдоль проводника
На концах проводника, помещенного в электрическое поле, начинает наблюдаться разность потенциалов. Вследствие этого электроны начинают перемещаться в сторону увеличения разности. В проводнике возникает электрический ток. Свободные электроны продвигаются вдоль проводника до тех пор, пока разница ни будет равна нулю. На практике для поддержания заданной величины тока цепи запитываются от источников напряжения или тока. Разница заключается в следующем:
- Источник тока поддерживает в цепи постоянный ток вне зависимости от сопротивления нагрузки;
- Источник напряжения поддерживает на своих зажимах строго постоянную ЭДС, независимо от величины потребляемого тока.
Разница потенциалов (падение напряжения) пропорциональна расстоянию от концов проводника, то есть обладает линейной зависимостью.
Электроемкость уединенного проводника
Для связи величин заряда и напряжения введено понятие электрической емкости. Для уединенного проводника (такого, на который отсутствует влияние других заряженных тел) значение емкости – величина постоянная и равная отношению количества заряда к потенциалу. Другими словами, емкость показывает, какой заряд нужно сообщить проводнику, чтобы его потенциальная энергия увеличилась на единицу.
Электроемкость не зависит от степени заряженности. Роль играют только:
- форма;
- геометрические размеры;
- диэлектрические свойства среды.
Так же, как и емкость электрического конденсатора, электроемкость проводника будет обозначаться в фарадах.
Обратите внимание! На практике электроемкость проводника составляет очень малую величину. Для увеличения значения, особенно при производстве конденсаторов, как элементов с нормированным значением емкости, разработаны особые технологии
Для чего нужен потенциометр электрику
Данный прибор широко применяется в практике для модуляции напряжения. Дело в том, что у многих источников (особенно заточенных под автономное функционирование: аккумуляторные элементы, солнечные батареи и т.д.) константное напряжение, не поддающееся управлению без специальных устройств, что может вызвать проблемы. Чтобы уменьшить исходное напряжение такого элемента, используют устройства-делители, снабженные потенциометрами.

Как работает потенциометр? Он представляет собой резистор, имеющий пару выводов и подвижный ползунок с еще одним выводом. Подключаться такое переменное устройство сопротивления может двумя способами:
- По типу реостата, с использованием ползункового вывода и одного из пары других. Сопротивление замеряется движением ползунка по корпусу резистора. Регуляция цепного электротока в таком случае возможна при последовательном подключении такого реостата и источника напряжения.
- Потенциометрическим методом, задействующим каждый вывод из имеющейся у прибора тройки. Два главных вывода включаются параллельно источнику, снятие сниженного напряжения реализуется с ползункового механизма и одного вывода. В этом случае через резисторное устройство течет электроток, создающий спад напряжения между ползунком и боковыми выводами. В такой модели на источник питания ложится большая нагрузка, так как для точности регуляции и отсутствия сбоев необходимо, чтобы резисторное сопротивление в несколько раз уступало нагрузочному.
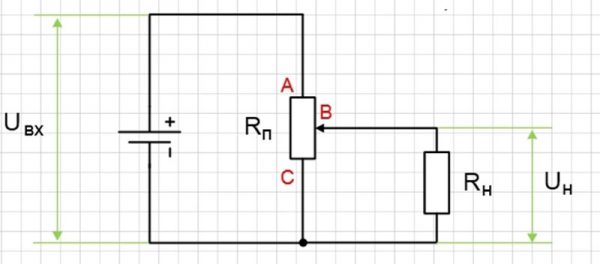
Таким образом, понятие потенциала используется в разных областях физики: как в механике, так и в изучении электричества. В последнем случае оно выступает в качестве характеристики поля. Непосредственно рассматриваемая величина измерению не поддается, зато можно измерить разность, тогда один заряд берется за точку отсчета.
Проводники в электростатическом поле. Электроемкость уединенного проводника.
Если поместить проводник во внешнее электростатическое поле или его зарядить, то на заряды проводника будет действовать электростатическое поле, в результате чего они начнут перемещаться. Перемещение зарядов (ток) продолжается до тех пор, пока не установится равновесное распределение зарядов, при котором электростатическое поле внутри проводника обращается в нуль. Это происходит в течение очень короткого времени. В самом деле, если бы поле не было равно нулю, то в проводнике возникло бы упорядоченное движение зарядов без затраты энергии от внешнего источника, что противоречит закону сохранения энергии. Итак, напряженность поля во всех точках внутри проводника равна нулю:
По гауссу
называют электроемкостью (или просто емкостью) уединенного проводника. Емкость уединенного проводника определяется зарядом, сообщение которого проводнику изменяет его потенциал на единицу.
Емкость проводника зависит от его размеров и формы, но не зависит от материала, агрегатного состояния, формы и размеров полостей внутри проводника. Это связано с тем, что избыточные заряды распределяются на внешней поверхности проводника. Емкость не зависит также ни от заряда проводника, ни от его потенциала. Сказанное не противоречит формуле, так как она лишь показывает, что емкость уединенного проводника прямо пропорциональна его заряду и обратно пропорциональна потенциалу.
Единица электроемкости — фарад (Ф): 1Ф
Поскольку электрический ток является упорядоченным движением заряженных частиц, то для определения величины тока необходимо знать, как величину энергии частиц, так и силу стороннего воздействия на них.
Теорема Гаусса для магнитного поля
Теорема Гаусса является одной из самых основных в электродинамике законов. Существуют теоремы Гаусса для электрического и магнитного полей, которые входят в состав уравнений Максвелла. При помощи данного закона устанавливается связь между напряженностью электрического поля и заряда в случае произвольной поверхности. Теорема (закон) Гаусса гласит, что в произвольной замкнутой поверхности поток вектора электрического поля пропорционален заряду, заключенному внутри поверхности. Для магнитного поля теорема Гаусса говорит о том, что поток вектора магнитной индукции через произвольную замкнутую поверхность равен нулю.
Проводники в электростатическом поле
Размещение проводника в электростатическом поле приводит к тому, что поле начнет действовать на носители заряда внутри проводящего предмета. Носители начинают перемещаться до тех пор, пока электростатическое поле вне поверхности ни обратится в нуль.
Поскольку поле внутри вещества отсутствует, то во всех точках проводящего материала энергия будет постоянной, а поверхность эквипотенциальной. Векторы напряженности поля направлены под прямым углом в любой точке поверхности проводника.
Под действием поля заряды внутри проводника отсутствуют, поскольку они сосредоточены исключительно на поверхности. Этот факт используется при экранировке – защите тел от влияния внешних электромагнитных и электростатических полей. Для экранирования может использоваться не только сплошной проводящий материал, но и сетка, так называемая «клетка Фарадея».
Также свойство перемещения заряженных частиц (электронов) используется в электростатических генераторах для получения напряжения в несколько миллионов вольт.
Движение заряда в электрическом поле
Когда носитель электрического заряда оказывается в электростатическом поле, на него неизбежно начинает действовать кулоновская сила. Это приводит к тому, что носитель заряда начинает перемещаться в пространстве, если, конечно, кулоновские силы не скомпенсированы другими, противодействующими силами. Рассмотрим случай, когда в электрическом поле оказался пробный заряд q совершенно свободный от действия других сил. Как только этот заряд окажется в зоне действия силовых линий электрического поля, то на него будет действовать сила в соответствии с Законом Кулона.
Как известно, механическая сила является векторной величиной, а значит имеет и величину, и направление. Носитель заряда в электрическом поле начнет менять свое энергетическое состояние. Как это проявляется? Одноименные заряды отталкиваются, а разноименные притягиваются. Наш заряд в зависимости от знака начнет сближаться с противоположным ему знаком заряда, которое и образует электрическое поле. Легче всего это увидеть, посмотрев на силовые линии напряженности поля. Согласно правилам они имеют направление от заряда +Q к заряду -Q, иначе говоря выходят из положительных зарядов (источника) и заходят в отрицательные заряды (источника).
Направление силы действия на пробный заряд q определить очень легко, если он положительный, то сила будет направлена по силовым линиям поля, а если отрицательный, то против силовых линий. Траектория движения будет зависеть от начальной скорости заряда, ее величины и направления. Действующая сила будет ускорять заряд, то есть его скорость по величине и направлению будет меняться в сторону действия кулоновской силы.
Движение заряда q в электрическом поле
На рисунке изображена примерная траектория движения заряда +q, имеющего некоторую начальную скорость V. Если бы заряд имел противоположный знак, то траектория движения была бы зеркально отражена от оси X, и заряд бы двигался в сторону пластины (+). По оси Y можно изобразить шкалу потенциала, которая так же будет иметь полярность.
Спрашивается. Что это за шкала и как определить где больший, а где меньший потенциал? Учитывая, что по определению и по действующим правилам силовые линии выходят из зарядов (+) и уходят в бесконечность, где потенциал равен нулю, то максимальный положительный потенциал будет в начале силовых линий от источника, а максимальный отрицательный потенциал там, где линии заходят в источник поля. Наш заряд +q, изображенный на рисунке выше будет двигаться от большего потенциала к меньшему, тем самым уменьшая потенциальную энергию поля, а точнее, преобразуя ее в кинетическую энергию. Если же в нашем случае был заряд -q, то для него потенциалы поменяли бы знак, арифметически, за счет умножения на -1, он всё также бы двигался в сторону уменьшения энергии поля.
Разность потенциалов — энергетическая характеристика
Любой заряд при своем движении в электрическом поле имеет начальную позицию, точку в пространстве поля, которая характеризуется потенциалом φначальное, и конечную точку, которая также имеет свой потенциал φконечное. Разность между двумя этими величинами потенциалов называется Δφ — разность потенциалов, а иначе еще называют электрическим напряжением поля.
Следует различать электрическое напряжение поля в электростатическом потенциальном поле, где нет вихрей, и падение электрического напряжения в электротехнических цепях, а также напряжение, которое является ЭДС (электродвижущая сила). Для того, чтобы не было путаницы, обычно для электрического поля употребляют выражение «разность потенциалов», для электрических цепей — «падение напряжения», а для источников тока — «ЭДС источника». Когда отсутствует понимание различия таких определений, становится трудно разобраться в сути сложных явлений в мире электротехники, электроники и автоматики. Что же роднит все эти три такие похожие, но всё-таки различные понятия? Прежде всего общее здесь то, что все три характеризуют энергетическое состояние. Но далее, при ответе на вопрос «Энергетическое состояние чего?», идут различия. Разность потенциалов характеризует энергетику электрического потенциального поля, падение напряжения — для участка электрической цепи, а ЭДС источника — это энергетическая характеристика устройства создающего электрический ток. Общность при ответе на вопрос: «Что это?», а различия при ответе на вопрос «Где?». Всё познается в сравнении, поэтому необходимо отлично ориентироваться во всех трёх вышеуказанных понятиях.
Имеем некоторый путь пройденный зарядом q от точки A до точки B, от начального потенциала, к конечному, а разница между ними и есть разность потенциалов. О чем это нам говорит? Если Δφ=φA-φB (разность потенциалов), тогда чтобы узнать какую работу, которую совершил заряд проделавший путь, нам надо Δφ умножить на величину заряда q, причем надо учесть знак заряда.
Полученное значение является работой, которую совершает заряд при перемещении. Иначе говоря, потенциальная энергия поля преобразуется в кинетическую энергию заряда, а так как заряд, в случае движения в сторону противоположного ему знака уменьшает напряженность поля, то потенциальная энергия поля уменьшится.
В случае, если некоторые не кулоновские силы воздействуют на заряд и тем самым переместят его в сторону поля, где знак такой же как у заряда, то работа будет совершена с противоположным знаком, точнее сказать она будет затрачена извне и общее энергетическое состояние поля увеличится. В одном случае потенциальная энергия поля уменьшается, за счет того, что часть этой энергии переходит в кинетическую, а в другом случае, если действуют на заряд внешние механические силы против кулоновских сил — потенциальная энергия возрастает из внешнего источника. В первом случае заряд движется в сторону уменьшения своего энергетического состояния, а во втором случае он движется в сторону увеличения своего энергетического состояния. Соответственно работа совершатся может либо с положительным знаком, либо с отрицательным.
Проводники в электростатическом поле
Размещение проводника в электростатическом поле приводит к тому, что поле начнет действовать на носители заряда внутри проводящего предмета. Носители начинают перемещаться до тех пор, пока электростатическое поле вне поверхности ни обратится в нуль.
Поскольку поле внутри вещества отсутствует, то во всех точках проводящего материала энергия будет постоянной, а поверхность эквипотенциальной. Векторы напряженности поля направлены под прямым углом в любой точке поверхности проводника.
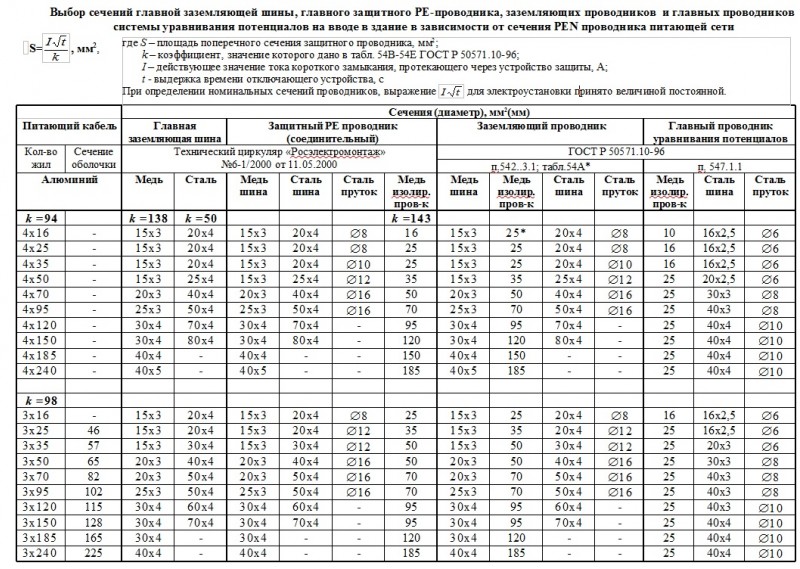
Под действием поля заряды внутри проводника отсутствуют, поскольку они сосредоточены исключительно на поверхности. Этот факт используется при экранировке – защите тел от влияния внешних электромагнитных и электростатических полей. Для экранирования может использоваться не только сплошной проводящий материал, но и сетка, так называемая «клетка Фарадея».

Также свойство перемещения заряженных частиц (электронов) используется в электростатических генераторах для получения напряжения в несколько миллионов вольт.
Разность потенциалов
Практическое значение имеет не сам потенциал в точке, а изменение (разница) потенциала φ1 — φ2 , которое не зависит от выбора нулевого уровня отсчета потенциала. Разность потенциалов φ1 — φ2 еще называют напряжением и обозначают латинской буквой U. Тогда формула для работы по перемещению заряда приобретает вид
Напряжение U — это физическая величина, определяемая работой электрического поля по перемещению единичного положительного заряда между двумя точками поля,
Единица разности потенциалов (напряжения), как и потенциала, — вольт,
Поскольку работа сил поля по перемещению заряда зависит только от разности потенциалов, то в случае перемещения заряда с первой эквипотенциальной поверхности на другую (потенциалы которых соответственно φ1 и φ2 ) выполненная полем работа не зависит от траектории этого движения.
Электроемкость уединенного проводника
Для связи величин заряда и напряжения введено понятие электрической емкости. Для уединенного проводника (такого, на который отсутствует влияние других заряженных тел) значение емкости – величина постоянная и равная отношению количества заряда к потенциалу. Другими словами, емкость показывает, какой заряд нужно сообщить проводнику, чтобы его потенциальная энергия увеличилась на единицу.
Электроемкость не зависит от степени заряженности. Роль играют только:
- форма;
- геометрические размеры;
- диэлектрические свойства среды.
Так же, как и емкость электрического конденсатора, электроемкость проводника будет обозначаться в фарадах.
Обратите внимание! На практике электроемкость проводника составляет очень малую величину. Для увеличения значения, особенно при производстве конденсаторов, как элементов с нормированным значением емкости, разработаны особые технологии
Разность потенциалов. Напряжение
Работа сил электростатического поля по перемещению заряда q из точки 1 в точку 2 поля
(~A_{12} = W_{p1} — W_{p2} .)
Выразим потенциальную энергию через потенциалы поля в соответствующих точках:
(~W_{p1} = q_0 varphi_1 , W_{p2} = q_0 varphi_2 .)
Тогда
(~A_{12} = q_0 (varphi_1 — varphi_2) .)
Таким образом, работа определяется произведением заряда на разность потенциалов начальной и конечной точек.
Из этой формулы разность потенциалов
(~varphi_1 — varphi_2 = frac{A_{12}}{q_0} .)
Разность потенциалов — это скалярная физическая величина, численно равная отношению работы сил поля по перемещению заряда между данными точками поля к этому заряду.
В СИ единицей разности потенциалов является вольт (В).
1 В — разность потенциалов между двумя такими точками электростатического поля, при перемещении между которыми заряда в 1 Кл силами поля совершается работа в 1 Дж.
Разность потенциалов в отличие от потенциала не зависит от выбора нулевой точки. Разность потенциалов φ1 — φ2 часто называют электрическим напряжением между данными точками поля:
(~U = varphi_1 — varphi_2 .)
Напряжение между двумя точками поля определяется работой сил этого поля по перемещению заряда в 1 Кл из одной точки в другую. В электростатическом поле напряжение вдоль замкнутого контура всегда равно нулю.
Работу сил электрического поля иногда выражают не в джоулях, а в электронвольтах. 1 эВ равен работе, совершаемой силами поля при перемещении электрона (е = 1,6·10-19 Кл) между двумя точками, напряжение между которыми равно 1 В.
1 эВ = 1,6·10-19 Кл·1 В = 1,6·10-19 Дж.
1 МэВ = 106 эВ = 1,6·10-13 Дж.
Электрическое поле графически можно изобразить не только с помощью линий напряженности, но и с помощью эквипотенциальных поверхностей.
Эквипотенциальной называется воображаемая поверхность, в каждой точке которой потенциал одинаков. Разность потенциалов между двумя любыми точками эквипотенциальной поверхности равна нулю.
Следовательно, работа по перемещению заряда вдоль эквипотенциальной поверхности равна 0. Но работа рассчитывается по формуле (~A = F Delta r cos alpha = q_0E Delta r cos alpha). Здесь q ≠ 0, Е ≠ 0, Δr ≠ 0. Значит, (~cos alpha = 0 Rightarrow alpha = 90^{circ}).
Следовательно, линии напряженности перпендикулярны эквипотенциальным поверхностям. Первая эквипотенциальная поверхность металлического проводника — это поверхность самого заряженного проводника, что легко проверить электрометром. Остальные эквипотенциальные поверхности проводятся так, чтобы разность потенциалов между двумя соседними поверхностями была постоянной.
Картины эквипотенциальных поверхностей некоторых заряженных тел приведены на рис. 3.
Рис. 3
Эквипотенциальными поверхностями однородного электростатического поля являются плоскости, перпендикулярные линиям напряженности (рис. 3, а).
Эквипотенциальные поверхности поля точечного заряда представляют собой сферы, в центре которых расположен заряд q (рис. 3, б).
Сущность понятия потенциальной разницы
Для изучения свойств заряженных частиц, помещенных в электростатическое поле, введено понятие потенциала. Оно означает отношение энергии заряда, помещенного в электростатическое поле, к его величине.
При переносе заряженной частицы в другую точку поля меняется его потенциальная энергия, а величина заряда остается неизменной. Для переноса требуется затратить некоторое количество энергии. Данная энергия по переносу единицы заряда получила название электрического напряжения. Соответственно, больший запас энергии будет ускорять перенос, то есть, чем больше напряжение, тем больше ток в цепи.
В данном случае разность потенциалов – это численное равенство напряжению между точками нахождения единичного заряда. Для общего случая здесь должна добавляться работа сторонних сил, которая называется электродвижущей силой (ЭДС). По своей сути, электричество – это работа стороннего источника (генератора) по поддержанию в электросхеме заданных уровней напряжения и тока.
Разность потенциалов (напряжение)
Напряжение является одним из важнейших терминов в электрике, оно описывается как работа, совершаемая электрополем с целью перемещения некоторого заряда из одной точки в другую. По аналогии с гравитацией, заряд при помещении в зону действия поля обладает потенциалом, который можно сравнить с соответствующим видом энергии у тела. Величина электрического потенциала прямо пропорциональна степени полевой напряженности и величине самого заряда.
Встает вопрос: потенциал в чем измеряется? Правильнее будет сказать, в чем обычно измеряется разность потенциалов, так как работники электротехники имеют дело именно с этой величиной в форме напряжения. Для самого потенциала специальной измерительной единицы не существует. В СИ принято измерять разность в вольтах (В). Она равна одному вольту в том случае, если для транспортировки заряда в один кулон из одной точки электрополя в другую потребуется совершить работу в один джоуль.
Важно! Измерить напряжение можно с помощью специального устройства – вольтметра. Стрелочная разновидность прибора, использующаяся на школьных уроках физики, оснащена градуированной шкалой, базирующейся на угле отклонения проволочной рамки, по которой проходит электроток
Помимо него, существуют и приборы с цифровым дисплеем, а также мультиметры, способные работать в нескольких режимах и измеряющие разные величины, описывающие электроцепь. Для измерения важно правильно подключить щупы.

Сущность понятия потенциальной разницы
Для изучения свойств заряженных частиц, помещенных в электростатическое поле, введено понятие потенциала. Оно означает отношение энергии заряда, помещенного в электростатическое поле, к его величине.
При переносе заряженной частицы в другую точку поля меняется его потенциальная энергия, а величина заряда остается неизменной. Для переноса требуется затратить некоторое количество энергии. Данная энергия по переносу единицы заряда получила название электрического напряжения. Соответственно, больший запас энергии будет ускорять перенос, то есть, чем больше напряжение, тем больше ток в цепи.

В данном случае разность потенциалов – это численное равенство напряжению между точками нахождения единичного заряда. Для общего случая здесь должна добавляться работа сторонних сил, которая называется электродвижущей силой (ЭДС). По своей сути, электричество – это работа стороннего источника (генератора) по поддержанию в электросхеме заданных уровней напряжения и тока.
Решение:
На проводник действуют: две одинаковые силы натяжения нитей Т, сила тяжести mg и сила
со стороны магнитного поля, где α — угол между направлениями тока I и магнитной индукции (в нашем случае α = 90° и sinα = 1). Подразумевается, что направления тока и магнитной индукции таковы, что сила F направлена вниз (рис. 140). В противном случае силы натяжения нитей при пропускании тока не возрастают, а уменьшаются, и нити не оборвутся.
Если проводник находится в равновесии, то
отсюда
Для разрыва одной из нитей необходимо выполнение условия
или
6 На прямой проводник длины l=0,5 м, расположенный перпендикулярно к линиям индукции магнитного поля, действует сила F=0,15 Н. Найти ток I, протекающий в проводнике, если магнитная индукция B = 20 мТл.
Решение:
Если проводник расположен перпендикулярно к направлению магнитной индукции, то F=BIl, где I-ток в проводнике; отсюда I=F/Bl=15 А.
7 Между полюсами магнита подвешен горизонтально на двух невесомых нитях прямой проводник длины l=0,2 м и массы m=10 г. Индукция однородного магнитного поля B = 49 мТл и перпендикулярна к проводнику. На какой угол α от вертикали отклонятся нити, поддерживающие проводник, если по нему пропустить ток I=2 А?
Решение: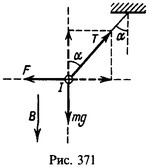
отсюда
8 Найти напряженность Н и индукцию B магнитного поля прямого тока в точке, находящейся на расстоянии r=4м от проводника, если ток I=100 А.
Решение:
9 ГОСТ 8.417—81 дает такое определение единицы силы тока — ампера: «Ампер равен силе неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожной малой площади кругового поперечного сечения, расположенным в вакууме на расстоянии 1 м один от другого, вызвал бы на каждом участке проводника длины 1 м силу взаимодействия, равную ». Исходя из этого определения, вычислить магнитную постоянную mo.
Решение:
Вокруг бесконечно длинного прямолинейного проводника, по которому течет ток I1 образуется магнитное поле, напряженность которого на расстоянии r от проводника
а индукция
При этом векторы Н и В направлены одинаково и лежат в плоскости, перпендикулярной к проводнику. На отрезок второго проводника длины l, по которому течет ток I2, магнитное поле действует с силой
где α — угол между направлениями отрезка проводника и магнитной индукции. Так как второй проводник параллелен первому, то α = 90° и sinα = 1. Таким образом,
Подставив значения
найдем
10 Индукция однородного магнитного поля B=0,5 Тл. Найти магнитный поток через площадку S=25 см2, расположенную перпендикулярно к линиям индукции. Чему будет равен магнитный поток, если площадку повернуть на угол α = 60° от первоначального положения?
Решение: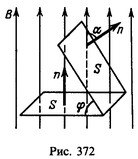
где α — угол между нормалью n к площадке и направлением магнитной индукции В. В первом случае
во втором случае α=φ (углы с взаимно перпендикулярными сторонами) и
11 Найти магнитную индукцию и магнитный поток через поперечное сечение никелевого сердечника соленоида (рис. 141), если напряженность однородного магнитного поля внутри соленоида H=25 кА/м. Площадь поперечного сечения сердечника S=20 см2, магнитная проницаемость никеля μ = 200.
Решение:
12 Магнитный поток через поперечное сечение катушки, имеющей n=1000 витков, изменился на величину ΔФ = 2 мВб в результате изменения тока в катушке от I1 = 4 А до I2 = 20А. Найти индуктивность L катушки.
Решение:
13 Виток площади S = 2 см2 расположен перпендикулярно к линиям индукции однородного магнитного поля. Найти индуцируемую в витке э.д.с, если за время Δt = 0,05 с магнитная индукция равномерно убывает от B1=0,5Тл до В2 = 0,1 Тл.
Решение:
14 Какой магнитный поток пронизывал каждый виток катушки, имеющей n =1000 витков, если при равномерном исчезновении магнитного поля в течение времени Δt = 0,1 с в катушке индуцируется э.д.с. ε = 10 В?
Решение:
15 Рамка в форме равностороннего треугольника помещена в однородное магнитное поле с напряженностью H=64кА/м. Нормаль к плоскости рамки составляет с линиями индукции магнитного поля угол α = 30°. Найти длину стороны рамки а, если в рамке при выключении поля в течение времени Δt = 0,03 с индуцируется э. д. с. ε = 10 мВ.
Решение:
Начальный магнитный поток через рамку
где
площадь рамки и B=µ0H-магнитная индукция. Конечный магнитный поток Ф2=0. Изменение магнитного потока
Э.д.с. индукции
отсюда
16 Квадратная рамка со стороной а=10см помещена в однородное магнитное поле. Нормаль к плоскости рамки составляет с линиями индукции магнитного поля угол α = 60°. Найти магнитную индукцию В этого поля, если в рамке при выключении поля в течение времени Δt = 0,01 с индуцируется э.д.с. ε = 50 мВ.
Решение:
17 Плоский виток площади S= 10 см2 помещен в однородное магнитное поле перпендикулярно к линиям индукции. Сопротивление витка R=1 Ом. Какой ток I протечет по витку, если магнитная индукция поля будет убывать со скоростью ΔB/Δt = 0,01 Тл/с?
Решение:
18 Плоский виток площади S= 10 см2 помещен в однородное магнитное поле с напряженностью H=80 кА/м, перпендикулярное к линиям индукции. Сопротивление витка R = 1 Ом. Какой заряд протечет по витку, если поле будет исчезать с постоянной скоростью?
Решение:
19 Какова индуктивность катушки с железным сердечником, если за время Δt = 0,5 с ток в цепи изменился от I1 = 10 А до I2 = 5 А, а возникшая при этом э.д.с. самоиндукции ε = 25 В?
Решение:
Э.д.с. самоиндукции
отсюда
20 Проводник длины l=2 м движется в однородном магнитном поле со скоростью v = 5 м/с, перпендикулярной к проводнику и линиям индукции поля. Какая э. д. с. индуцируется в проводнике, если магнитная индукция B=0,1 Тл?
Решение: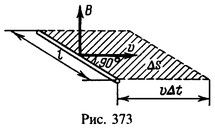
магнитный поток через площадь ΔS, «заметаемую» проводником за время Δt (рис. 373). Опуская знак минус, найдем
21 Самолет летит горизонтально со скоростью v = 900 км/ч. Найти разность потенциалов, возникающую между концами крыльев самолета, если вертикальная составляющая индукции земного магнитного поля Bo = 0,5 мкТл и размах крыльев самолета l=12 м.
Решение:
Крылья самолета за время Δt «заметают» площадь
Магнитный поток через эту площадь равен
где
вертикальная составляющая индукции земного магнитного поля (α — угол между вертикалью и направлением магнитной индукции). Разность потенциалов V между концами крыльев самолета равна э.д.с. ε, индуцируемой в металлических крыльях и корпусе самолета при его движении в магнитном поле Земли:
22 С какой скоростью должен двигаться проводник длины l=10 см перпендикулярно к линиям индукции однородного магнитного поля, чтобы между концами проводника возникла разность потенциалов V=0,01 В? Скорость проводника составляет с направлением самого проводника угол α = 30°. Линии индукции перпендикулярны к проводнику, индукция B = 0,2 Тл.
Решение: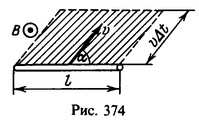
Магнитный поток через эту площадь
Разность потенциалов V между концами проводника равна э.д.с. ε, индуцируемой в этом проводнике:
23 Какой ток идет через гальванометр, присоединенный к железнодорожным рельсам, при приближении к нему поезда со скоростью v = 60 км/ч? Вертикальная составляющая индукции земного магнитного поля Bо=50 мкТл. Сопротивление гальванометра R=100 Ом. Расстояние между рельсами l=1,2 м; рельсы считать изолированными друг от друга и от земли.
Решение:
24 Квадратная рамка со стороной l=2 см помещена в однородное магнитное поле с индукцией B = 100 Тл. Плоскость рамки перпендикулярна к линиям индукции поля. Сопротивление рамки R=1 Ом. Какой ток протечет по рамке, если ее выдвигать из магнитного поля со скоростью ν = 1 см/с, перпендикулярной к линиям индукции? Поле имеет резко очерченные границы, и стороны рамки параллельны этим границам.
Решение: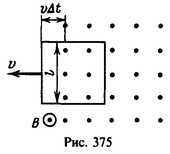
при движении рамки не изменяется. Поэтому э.д.с. индукции в рамке не возникает. После того как одна из сторон рамки вышла за границу поля (рис. 375), магнитный поток через поверхность, ограниченную рамкой, будет изменяться. За время Δt рамка перемещается на расстояние νΔt и часть площади рамки, которую пересекает магнитное поле, уменьшается на величину
Магнитный поток за это время изменяется на величину
Индуцируемая в рамке э.д.с.
и по рамке протечет ток
Когда рамка выйдет из области, где имеется магнитное поле, э.д.с. индукции снова станет равной нулю.
25 Проволочный виток площади S= 1 см2, имеющий сопротивление R = 1 мОм, пронизывается однородным магнитным полем, линии индукции которого перпендикулярны к плоскости витка. Магнитная индукция изменяется со скоростью ΔB/Δt = 0,01 Тл/с. Какое количество теплоты выделяется в витке за единицу времени?
Решение:
26 Прямоугольная рамка, подвижная сторона которой имеет длину l, помещена в однородное магнитное поле с индукцией B. Плоскость рамки перпендикулярна к линиям индукции магнитного поля. Подвижную сторону, которая вначале совпадает с противоположной ей неподвижной, начинают двигать равномерно со скоростью ν. Найти зависимость тока I в рамке от времени t. Сопротивление единицы длины проводника равно Rl.
Решение:
27 Два параллельных, замкнутых на одном конце провода, расстояние между которыми l=50 см, находятся в однородном магнитном поле с индукцией B = 5 мТл. Плоскость, в которой расположены провода, перпендикулярна к линиям индукции поля. На провода положен металлический мостик, который может скользить по проводам без трения. Мостик под действием силы F=0,1 мН движется со скоростью ν=10м/с. Найти сопротивление R мостика. Сопротивлением проводов пренебречь.
Решение:
28 Рамка из n = 1000 витков, имеющих площадь S = 5 см2, замкнута на гальванометр с сопротивлением R=10 кОм и помещена в однородное магнитное поле с индукцией B=10мТл, причем линии индукции поля перпендикулярны к ее плоскости. Какой заряд q протечет по цепи гальванометра, если направление индукции магнитного поля плавно изменить на обратное?
Решение:
При плавном изменении магнитной индукции в рамке индуцируется э.д.с.
где ΔФ-изменение магнитного потока, Δt — время, в течение которого происходило это изменение. Ток в рамке
Заряд, протекший по цепи за время Δt,
Начальный поток магнитной индукции
При изменении направления магнитного поля на обратное магнитный поток изменяет знак. Поэтому конечный магнитный поток
Изменение магнитного потока
Таким образом,
29 Замкнутая катушка диаметра D с числом витков n помещена в однородное магнитное поле с индукцией В. Плоскость катушки перпендикулярна к линиям индукции поля. Какой заряд q протечет по цепи катушки, если ее повернуть на 180? Проволока, из которой намотана катушка, имеет площадь сечения S и удельное сопротивление ρ.
Решение:
30 В цепь включены последовательно источник тока с э.д.с. ε = 1,2 В, реостат с сопротивлением R=1 Ом и катушка с индуктивностью L=1 Гн. В цепи протекал постоянный ток I0. С некоторого момента сопротивление реостата начинают менять так, чтобы ток уменьшался с постоянной скоростью ΔI/Δt = 0,2 А/с. Каково сопротивление R, цепи спустя время t = 2 с после начала изменения тока?
Решение:
Сумма э.д.с. источника тока и э.д.с, индуцируемой в цепи при равномерном изменении тока, равна
Ток изменяется
по закону
Сопротивление цепи в любой момент времени
В момент времени t= 2 с искомое сопротивление Rt= 1,75 0м.
31 Какой ток I покажет амперметр в схеме, изображенной на рис. 142, если индукция перпендикулярного к плоскости рисунка однородного магнитного поля меняется с течением времени по закону B = kt? Точки с и d лежат на концах диаметра проволочного кольца. Сопротивление единицы длины проволоки равно Rl; диаметр кольца равен D.
Формула
Разность потенциалов между концами проводника, движущегося в однородном магнитном поле
Входящие величины
(B)
—
магнитная индукция магнитного поля
((Тл))
(L)
—
длина проводника
((м))
(v)
—
скорость движения проводника
((frac{м}{с}))
(alpha)
—
угол между вектором магнитной индукции и скоростью движения проводника
((рад))
(U)
—
напряжение между концами проводника
((В))
[U = B L v sin{alpha}]
изменить / сообщить об ошибке