Как найти разность между суммой цифр

Содержание материала

Свойства разности натуральных чисел
Правила вычитания суммы из числа и числа из суммы
Как меняется разность при изменении вычитаемого или уменьшаемого
Видео
Нахождение неизвестного множителя
Вычитание в столбик многозначных чисел

Свойства разности натуральных чисел

Свойства разности натуральных чисел состоят из:

Правила вычитания суммы из числа и числа из суммы;
Зависимость разности от изменения уменьшаемого или вычитаемого.
Правило вычитания разности из числа;

Рассмотрим каждый пункт подробнее.

Правила вычитания суммы из числа и числа из суммы

Как вычесть сумму из числа

Чтобы найти разность числа и суммы чисел нужно из данного числа вычесть последовательно каждое слагаемое суммы.То есть, сначала мы находим разность между данным числом и первым слагаемым, потом от этой полученной разности отнимаем второе слагаемое, третье, и так далее до последнего слагаемого суммы.

Действительно, так как сумма – это объединение всех слагаемых, то очевидно, что, отнимая последовательно каждое слагаемое, каждое ее составляющее число, мы в конце концов отнимем всю сумму.

Рассмотрим это на примере из урока сложение чисел.

325+(12+64+5) = 325+81 = 406

Я запишу это в виде разности:

406-(12+64+5) = 325

и покажу, что результат будет равен первому слагаемому:

406—12 = 394;394-64 = 330;330-5 = 325.

Как видите, все верно.

Как вычесть число из суммы

Чтобы найти разность суммы чисел и некоторого числа, нужно отнять это число от какого-нибудь подходящего слагаемого этой суммы.То есть, мы сначала находим разность одного из слагаемых и данного числа, а потом складываем получившийся результат последовательно с остальными слагаемыми.

Действительно, вы знаете, что, если уменьшить одно из слагаемых на какое-то число, то и сумма уменьшится на это же самое число. Следовательно, если нам нужно сумму чисел уменьшить на какое-то число, то для этого достаточно уменьшить на это число одно из слагаемых суммы.

Для рассмотрения я возьму тот же пример, только сумму расчленю на слагаемые, а слагаемое в скобках заменю суммой:

325+81 = (191+65+150)

Превращаю выражение в разность:

(191+65+150)-81 = 325

и покажу, что результат также будет равен первому слагаемому:

191-81 = 110;110+65 = 175;175+150 = 325или150-81 = 69;69+191 = 260;260+65 = 325.

Я недаром написал в правиле, что нужно отнимать от подходящего слагаемого суммы, потому что, если оно будет меньше вычитаемого, то оно нам не подходит. Так, в нашем примере 65<81.

Отсюда следует, что это правило применимо не к любой сумме натуральных чисел, а только к той, в которой хотя бы одно из слагаемых больше, чем вычитаемое.

Как меняется разность при изменении вычитаемого или уменьшаемого

Изменение разности при изменении вычитаемого и уменьшаемого является следствием описанных в уроке изменений суммы чисел с изменением ее слагаемых.

Если уменьшаемое увеличить на некоторое количество единиц, то и разность увеличится на такое же количество единиц.

Если уменьшаемое уменьшить на некоторое количество единиц, то и разность уменьшится на такое же количество единиц.

Если вычитаемое увеличить на некоторое количество единиц, то разность уменьшится на такое же количество единиц.

Если вычитаемое уменьшить на некоторое количество единиц, то разность увеличится на такое же количество единиц.

Если сразу оба числа, и уменьшаемое, и вычитаемое, увеличить или уменьшить на одно и то же количество единиц, то разность не изменится.

Если нужно вычесть из числа разность других чисел, можно воспользоваться одним из двух способов:1. Прибавить к данному числу вычитаемое, и из получившейся суммы вычесть уменьшаемое;2. Вычесть из данного числа уменьшаемое, а потом результат этого действия сложить с вычитаемым.

Это свойство выводится из предыдущих, рассмотренных нами.

Рассмотрим на примере 22-(17—3).

Для начала вычислим обычным способом: сперва узнаем разность в скобках (это будет 17-3=14), а потом вычтем 14 из 22. Получится 22-14=8.

22-(17—3) = 8

Теперь вернемся к исходному примеру и отнимем от 22 не разность 17-3, то есть, не 17 без 3 единиц, а все число 17.

22—17 = 5

Но мы ведь отняли больше, чем нужно было, поэтому нам нужно вернуть лишне взятые 3 единицы обратно, а именно, прибавить их к полученному результату.

5+3 = 8

Попробуем решить другим путем: увеличим и уменьшаемое (данное число), и вычитаемое (разность в скобках) на одно и то же число 3. Получим:

22+3-(17+3-3)

Так как 22+3=25, а 3-3=0, то в итоге получается:

25-17+0 = 8

Как видите, оба способа показали верный результат.

Видео

Нахождение неизвестного множителя

Посмотрим на два уравнения: x·2=20 и 3·x=12. В обоих нам известно значение произведения и один из множителей, необходимо найти второй. Для этого нам надо воспользоваться другим правилом.

Определение 4

Для нахождения неизвестного множителя нужно выполнить деление произведения на известный множитель.

Данное правило базируется на смысле, который является обратным смыслу умножения. Между умножением и делением есть следующая связь: a·b=c при a и b, не равных , c: a=b, c: b=c и наоборот.

Пример 4

Вычислим неизвестный множитель в первом уравнении, разделив известное частное 20 на известный множитель 2. Проводим деление натуральных чисел и получаем 10. Запишем последовательность равенств:

x·2=20x=20:2x=10.

Подставляем десятку в исходное равенство и получаем, что 2·10=20. Значение неизвестного множителя было выполнено правильно.

Уточним, что в случае, если один из множителей нулевой, данное правило применять нельзя. Так, уравнение x·=11 с его помощью решить мы не можем. Эта запись не имеет смысла, поскольку для решения надо разделить 11 на , а деление на нуль не определено. Подробнее о подобных случаях мы рассказали в статье, посвященной линейным уравнениям.

Когда мы применяем это правило, мы, по сути, делим обе части уравнения на другой множитель, отличный от . Существует отдельное правило, согласно которому можно проводить такое деление, и оно не повлияет на корни уравнения, и то, о чем мы писали в этом пункте, с ним полностью согласовано.

Вычитание в столбик многозначных чисел

Так же, как и сложение, разность многозначных чисел удобно находить, используя вычитание в столбик.

Вычитание в столбик – это способ нахождения разности чисел при помощи их записи друг под другом таким образом, чтобы соответствующие разряды разных чисел находились на одной вертикали (один под другим), и последующего вычисления.

Давайте найдем разность чисел 52063-4825.

Запишем их друг под другом таким образом, чтобы совпадали соответствующие разряды обоих чисел, т.е. единицы под единицами, десятки под десятками и т.д. После этого, под вторым слагаемым проводим горизонтальную черту, а между слагаемыми ставим знак действия, т.е. минус. У нас получилась такая запись:

Вычитание в столбик выполняется подобным способом, как и при сложении, только теперь мы отнимаем единицы от единиц, десятки от десятков и так далее.

От 3 единиц в уменьшаемом мы не можем отнять 5 единиц вычитаемого, поскольку 3<5. Поэтому, мы раскладываем соседние 6 десятков на 5 десятков и 1 десяток. Этот десяток содержит 10 единиц, которые мы складываем с 3 имеющимися в уменьшаемом единицами. Теперь у нас есть 13 единиц, и мы можем отнять от них 5, получим 8 единиц. Записываем их под чертой в разряде простых единиц, а над цифрой разряда десятков в уменьшаемом ставим одну точку, чтобы не забыть, что 1 десяток единиц мы оттуда уже забрали.

Переходим к десяткам. У уменьшаемого в разряде десятков мы уже забрали 1 десяток, о чем нам напоминает поставленная точка. Поэтому, мы отнимаем 2 десятка вычитаемого не от 6, а от 5 десятков, потому что 6-1=5.

5>2, значит, действие вычитания возможно: 5-2=3. Пишем цифру 3 под чертой в разряде десятков, и переходим к сотням.

Сотен в уменьшаемом у нас нет, поэтому мы смотрим, сколько в числе содержится тысяч? Их тоже . Смотрим следующий разряд. Здесь у нас 5 десятков тысяч. Из них мы берем 1 десяток тысяч (ставим точку над цифрой 5 в уменьшаемом), что составляет 10 тысяч единиц. Из них (из взятых в десятках тысячах) мы занимаем 1 тысячу для того, чтобы закончить вычитание в разряде сотен (ставим точку над цифрой в разряде тысяч уменьшаемого).

1 тысяча единиц – это 10 сотен. Кроме этих занятых, больше в уменьшаемом сотен нет. В вычитаемом 8 сотен, поэтому находим разность сотен уменьшаемого и вычитаемого: 10-8=2. Пишем результат под чертой в разряде сотен.

В разряде тысяч уменьшаемого у нас осталось9 тысяч единиц (потому что 1 тысячу мы отдали для разряда сотен в качестве 10 сотен). Отнимаем от нее4 тысячи вычитаемого, получаем: 9-4=5, которые записываем под чертой в разряде тысяч.

Десятков тысяч в уменьшаемом осталось 5-1=4 (помните, мы для разряда сотен занимали?), в вычитаемом их нет совсем, то есть, . Поэтому мы просто сносим цифру 4 в результат под черту в разряд десятков тысяч.

• с— разница в процентах
• a — первое число
• b — второе число
Данная разница обозначает на сколько процентов второе число (b) больше (или меньше, если знак «-«) относительно первого числа (a).

Разница относительно второго числа (b) равна:
c=(a—b)/b*100, где

• с— разница в процентах
• a — первое число
• b — второе число
Данная разница обозначает на сколько процентов первое число (a) больше (или меньше, если знак «-«) относительно второго числа (b).

Источник

ERW1N

0 / 0 / 1

Регистрация: 29.10.2016

Сообщений: 71

Найти разницу между произведением и суммой цифр данного трицифрового числа

20.09.2017, 17:46. Показов 3088. Ответов 5

Метки Задачи, с (Все метки)

Здравствуйте!
Задача:Найти разницу между произведением и суммой цифр данного трицифрового числа.
Входные данные: трицифровое число
Выходные данные:Искомая розница.
Вот мой код:

C++

#include <bits/stdc++.h>
 
using namespace std;
 
int main()
{
    long long a,b,c,d;
    cin>>a;
    b=a%10;
    a/=10;
    c=a%10;
    a/=10;
    d=a%10;
    cout<<abs((c*b*d)-(c+b+d));
    return 0;
}

Но это решение проходит лишь на 85%.В чем может быть проблема???
Источник задачи https://www.e-olymp.com/ru/con… lems/74130

no swear

192 / 166 / 82

Регистрация: 01.07.2016

Сообщений: 942

20.09.2017, 18:03

По моему модуль там лишний. Сказано же найти разность а не модуль разности

Добавлено через 5 минут

C++

#include <iostream>
using std::cin;
using std::cout;
 
int main()
{
    int n;
    cin >> n;
    cout << (n % 10 * (n / 10 % 10) * (n / 100)) - (n % 10 + (n / 10 % 10) + n / 100);
    return 0;
}

0 / 0 / 1

Регистрация: 29.10.2016

Сообщений: 71

20.09.2017, 18:04

[ТС]

Без модуля вообще 28% прошло.

no swear

192 / 166 / 82

Регистрация: 01.07.2016

Сообщений: 942

20.09.2017, 18:25

Сообщение было отмечено ERW1N как решение

Решение

Так вы условия полностью не закинули!

Входные данные:
Одно трехзначное число (положительное или отрицательное). Сумма и разность сохраняет знак числа

C++

#include <iostream>
using std::cin;
using std::cout;
 
int main()
{
    int n, k = 1;
    cin >> n;
    if(n < 0) k = -1;
    cout << k * (n % 10 * (n / 10 % 10) * (n / 100)) - k * (n % 10 + (n / 10 % 10) + n / 100);
    return 0;
}

LazySlacker

93 / 77 / 31

Регистрация: 29.08.2017

Сообщений: 188

20.09.2017, 19:19

C++

#include <iostream>
 
using namespace std;
 
int main()
{
    int n;
    cin >> n;
    n = abs(n);
    int s = 0;
    int p = 1;
    do
    {
        int d = n % 10;
        s += d;
        p *= d;
    } while ((n /= 10) != 0);
    cout << p - s << endl;
    return 0;
}

no swear

192 / 166 / 82

Регистрация: 01.07.2016

Сообщений: 942

20.09.2017, 20:01

С прошлым кодом я что — то переборщил )

C++

#include <iostream>
using namespace std;
 
int main()
{
    int n, p = 1, s = 0;
    cin >> n;
    while(n)
        s += n % 10,
        p *= n % 10,
        n /= 10;
 
    cout << p - s;
    return 0;
}

Источник

Инструмент расчета онлайн процентного различия между двумя числами. Введите значения первого числа и второго числа, после чего нажмите «Рассчитать».

Первое число

Второе число

Разница в процентах

Формула:

Процентная разница = | (a — b) / [ (a + b) / 2 ] | * 100 %

где,

a = Первое число
b = Второе число

людей нашли эту статью полезной. А Вы?

Источник

Содержание

Вычисление разницы
- Способ 1: вычитание чисел
- Способ 2: денежный формат
- Способ 3: даты
- Способ 4: время
Вопросы и ответы

Вычисление разности является одним из самых популярных действий в математике. Но данное вычисление применяется не только в науке. Мы его постоянно выполняем, даже не задумываясь, и в повседневной жизни. Например, для того, чтобы посчитать сдачу от покупки в магазине также применяется расчет нахождения разницы между суммой, которую дал продавцу покупатель, и стоимостью товара. Давайте посмотрим, как высчитать разницу в Excel при использовании различных форматов данных.

Вычисление разницы

Учитывая, что Эксель работает с различными форматами данных, при вычитании одного значения из другого применяются различные варианты формул. Но в целом их все можно свести к единому типу:

X=A-B

А теперь давайте рассмотрим, как производится вычитание значений различных форматов: числового, денежного, даты и времени.

Способ 1: вычитание чисел

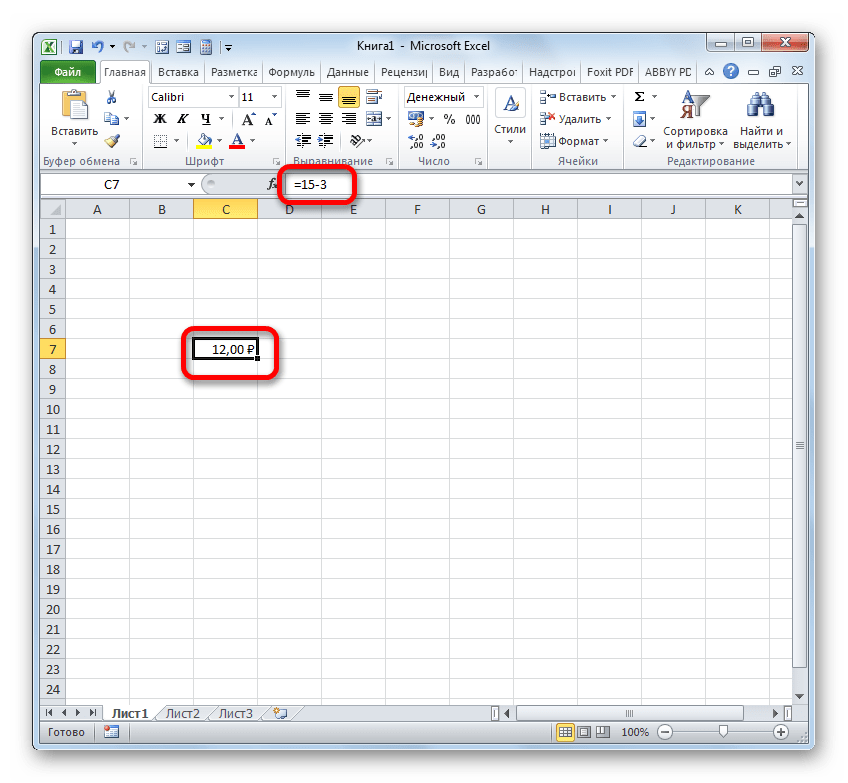
Сразу давайте рассмотрим наиболее часто применимый вариант подсчета разности, а именно вычитание числовых значений. Для этих целей в Экселе можно применить обычную математическую формулу со знаком «-».

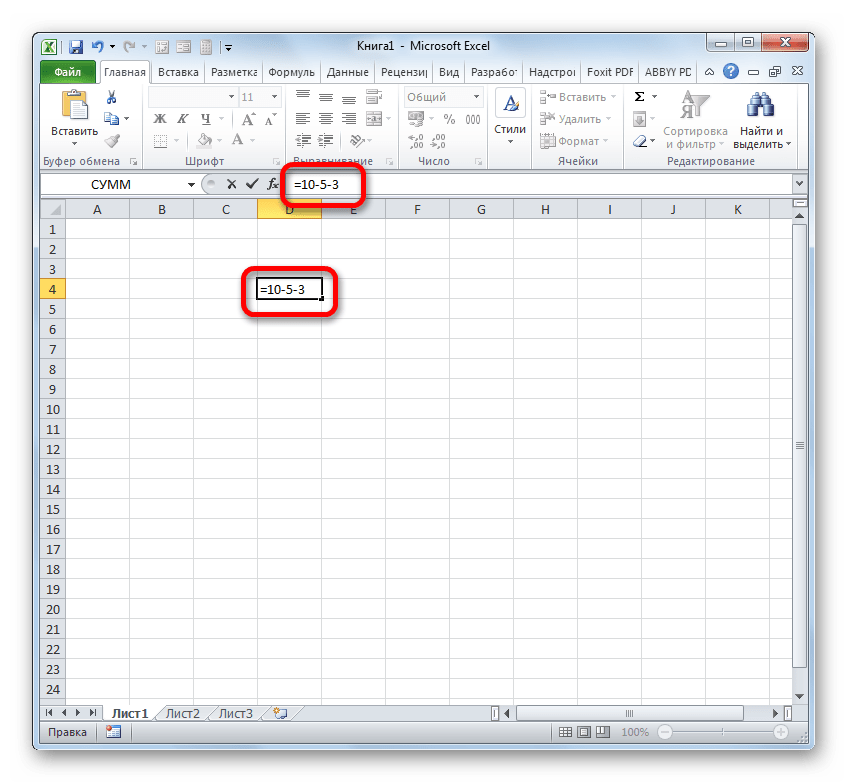
Если вам нужно произвести обычное вычитание чисел, воспользовавшись Excel, как калькулятором, то установите в ячейку символ «=». Затем сразу после этого символа следует записать уменьшаемое число с клавиатуры, поставить символ «-», а потом записать вычитаемое. Если вычитаемых несколько, то нужно опять поставить символ «-» и записать требуемое число. Процедуру чередования математического знака и чисел следует проводить до тех пор, пока не будут введены все вычитаемые. Например, чтобы из числа 10 вычесть 5 и 3, нужно в элемент листа Excel записать следующую формулу:
=10-5-3

После записи выражения, для выведения результата подсчета, следует кликнуть по клавише Enter.

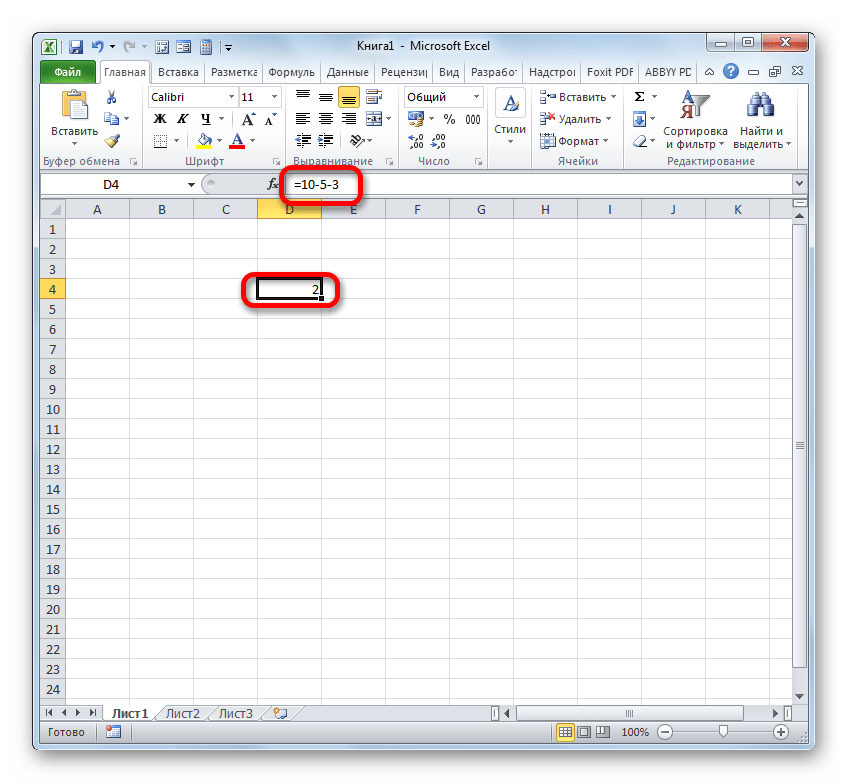
Как видим, результат отобразился. Он равен числу 2.

Но значительно чаще процесс вычитания в Экселе применяется между числами, размещенными в ячейках. При этом алгоритм самого математического действия практически не меняется, только теперь вместо конкретных числовых выражений применяются ссылки на ячейки, где они расположены. Результат же выводится в отдельный элемент листа, где установлен символ «=».

Посмотрим, как рассчитать разницу между числами 59 и 26, расположенными соответственно в элементах листа с координатами A3 и С3.

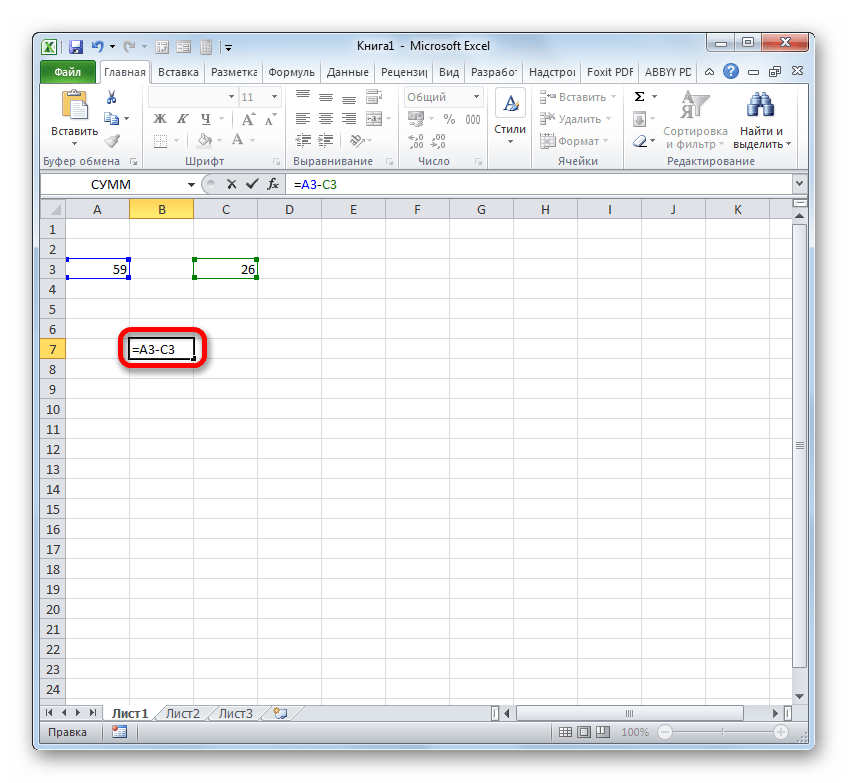
Выделяем пустой элемент книги, в который планируем выводить результат подсчета разности. Ставим в ней символ «=». После этого кликаем по ячейке A3. Ставим символ «-». Далее выполняем клик по элементу листа С3. В элементе листа для вывода результата должна появиться формула следующего вида:
=A3-C3

Как и в предыдущем случае для вывода результата на экран щелкаем по клавише Enter.

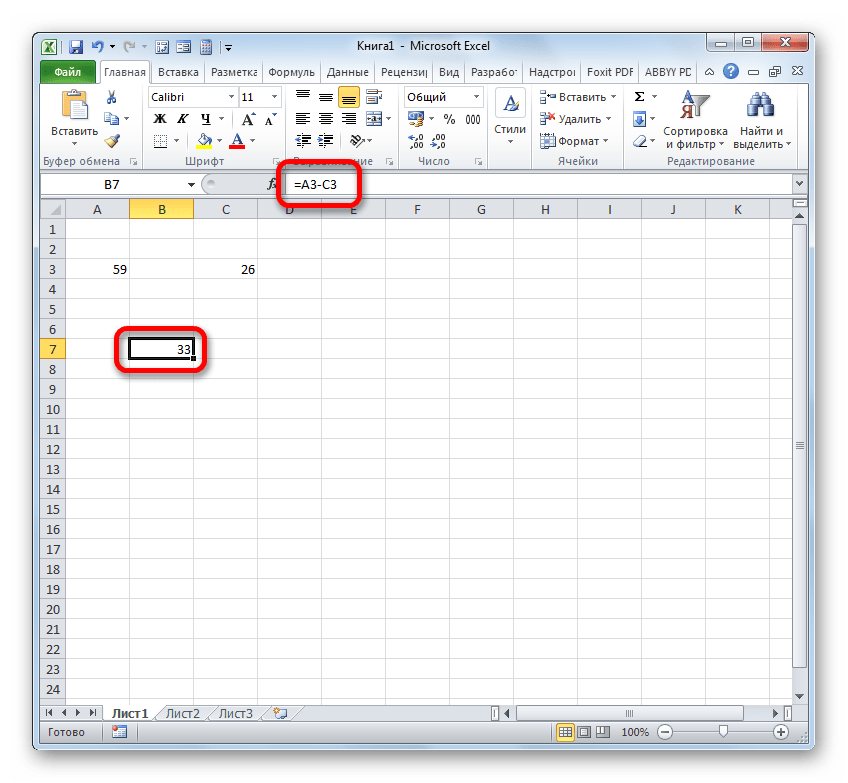
Как видим, и в этом случае расчет был произведен успешно. Результат подсчета равен числу 33.

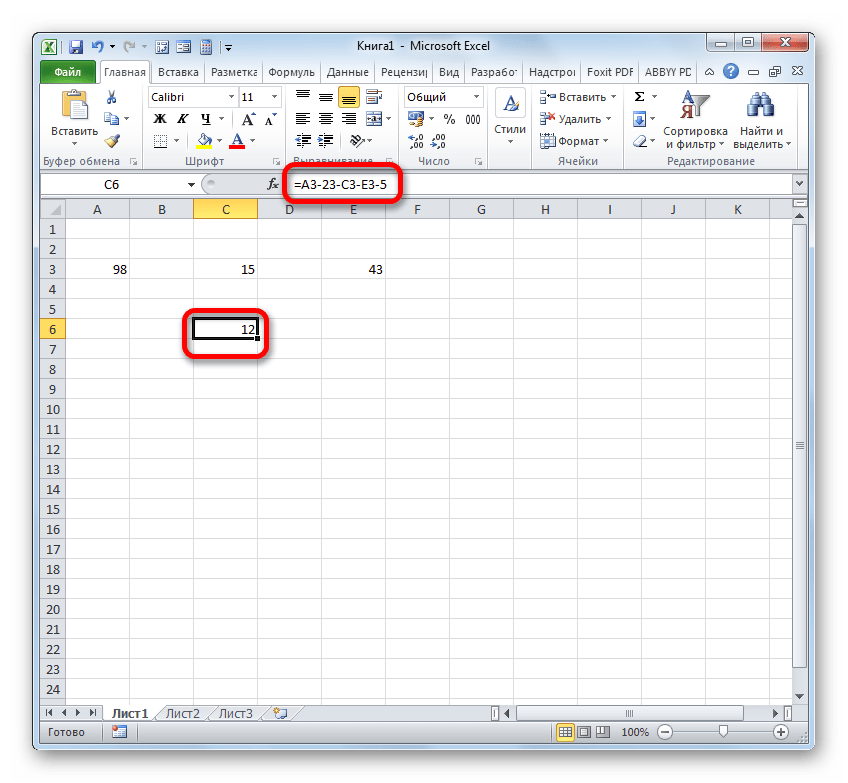
Но на самом деле в некоторых случаях требуется произвести вычитание, в котором будут принимать участие, как непосредственно числовые значения, так и ссылки на ячейки, где они расположены. Поэтому вполне вероятно встретить и выражение, например, следующего вида:

=A3-23-C3-E3-5

Урок: Как вычесть число из числа в Экселе

Способ 2: денежный формат

Вычисление величин в денежном формате практически ничем не отличается от числового. Применяются те же приёмы, так как, по большому счету, данный формат является одним из вариантов числового. Разница состоит лишь в том, что в конце величин, принимающих участие в расчетах, установлен денежный символ конкретной валюты.

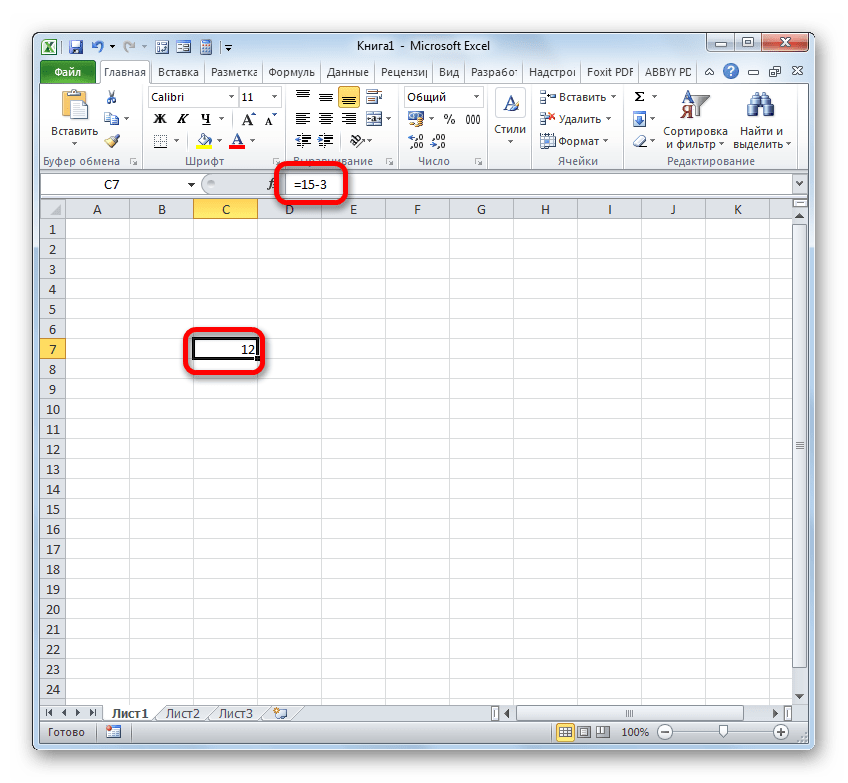
Собственно можно провести операцию, как обычное вычитание чисел, и только потом отформатировать итоговый результат под денежный формат. Итак, производим вычисление. Например, вычтем из 15 число 3.

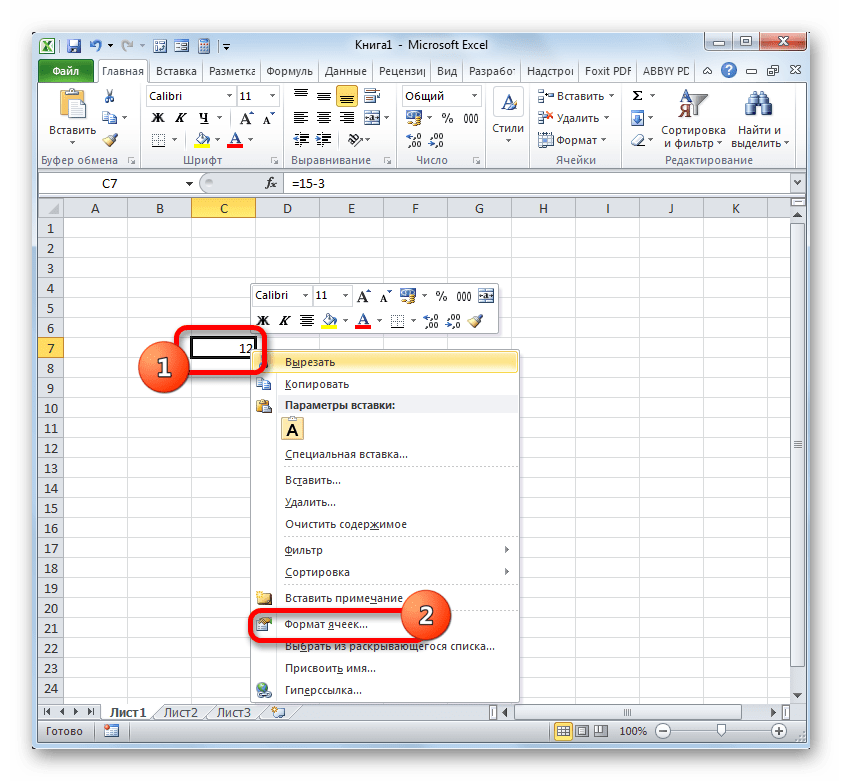
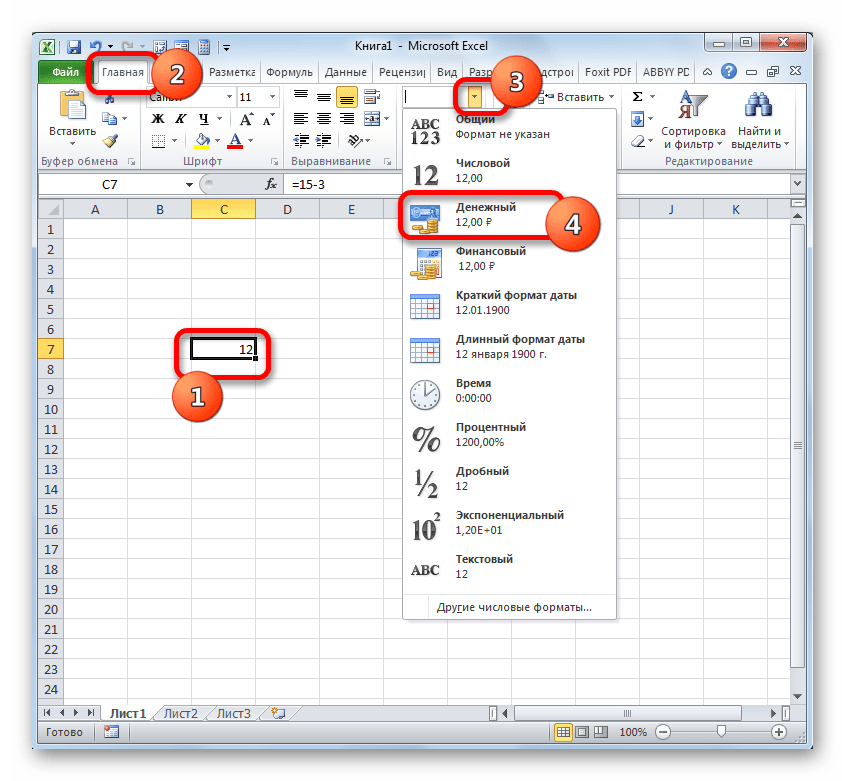
После этого кликаем по элементу листа, который содержит результат. В меню выбираем значение «Формат ячеек…». Вместо вызова контекстного меню можно применить после выделения нажатие клавиш Ctrl+1.

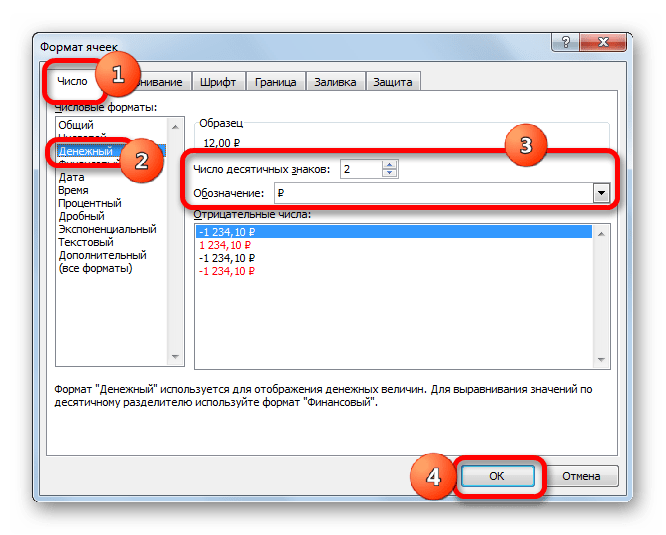
При любом из двух указанных вариантов производится запуск окна форматирования. Перемещаемся в раздел «Число». В группе «Числовые форматы» следует отметить вариант «Денежный». При этом в правой части интерфейса окна появятся специальные поля, в которых можно выбрать вид валюты и число десятичных знаков. Если у вас Windows в целом и Microsoft Office в частности локализованы под Россию, то по умолчанию должны стоять в графе «Обозначение» символ рубля, а в поле десятичных знаков число «2». В подавляющем большинстве случаев эти настройки изменять не нужно. Но, если вам все-таки нужно будет произвести расчет в долларах или без десятичных знаков, то требуется внести необходимые коррективы.
Вслед за тем, как все необходимые изменения сделаны, клацаем по «OK».

Как видим, результат вычитания в ячейке преобразился в денежный формат с установленным количеством десятичных знаков.

Существует ещё один вариант отформатировать полученный итог вычитания под денежный формат. Для этого нужно на ленте во вкладке «Главная» кликнуть по треугольнику, находящемуся справа от поля отображения действующего формата ячейки в группе инструментов «Число». Из открывшегося списка следует выбрать вариант «Денежный». Числовые значения будут преобразованы в денежные. Правда в этом случае отсутствует возможность выбора валюты и количества десятичных знаков. Будет применен вариант, который выставлен в системе по умолчанию, или настроен через окно форматирования, описанное нами выше.

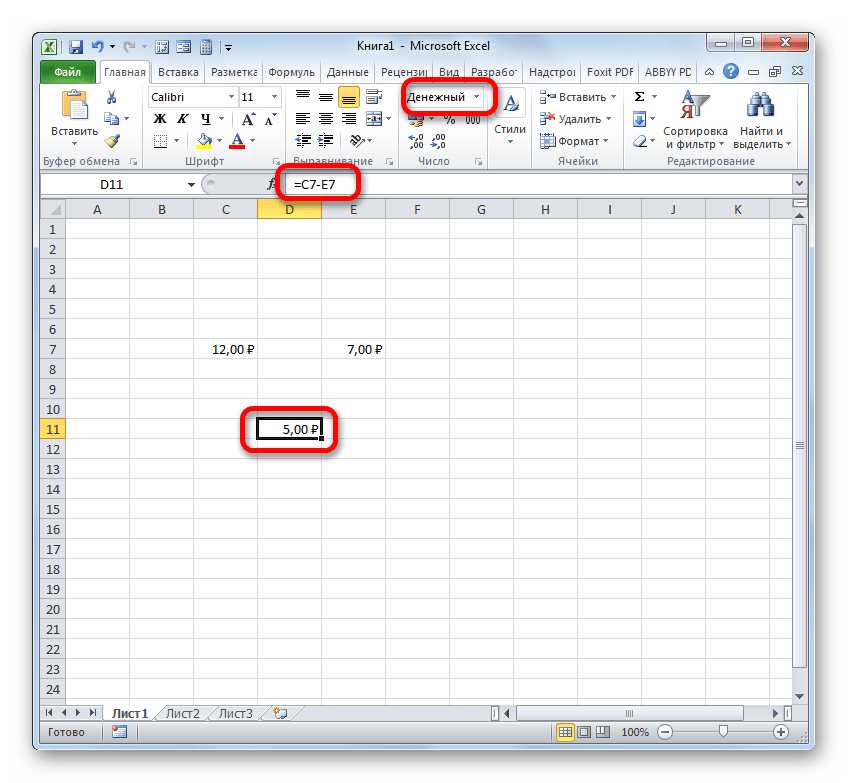
Если же вы высчитываете разность между значениями, находящимися в ячейках, которые уже отформатированы под денежный формат, то форматировать элемент листа для вывода результата даже не обязательно. Он будет автоматически отформатирован под соответствующий формат после того, как будет введена формула со ссылками на элементы, содержащие уменьшаемое и вычитаемые числа, а также произведен щелчок по клавише Enter.

Урок: Как изменить формат ячейки в Экселе

Способ 3: даты

А вот вычисление разности дат имеет существенные нюансы, отличные от предыдущих вариантов.

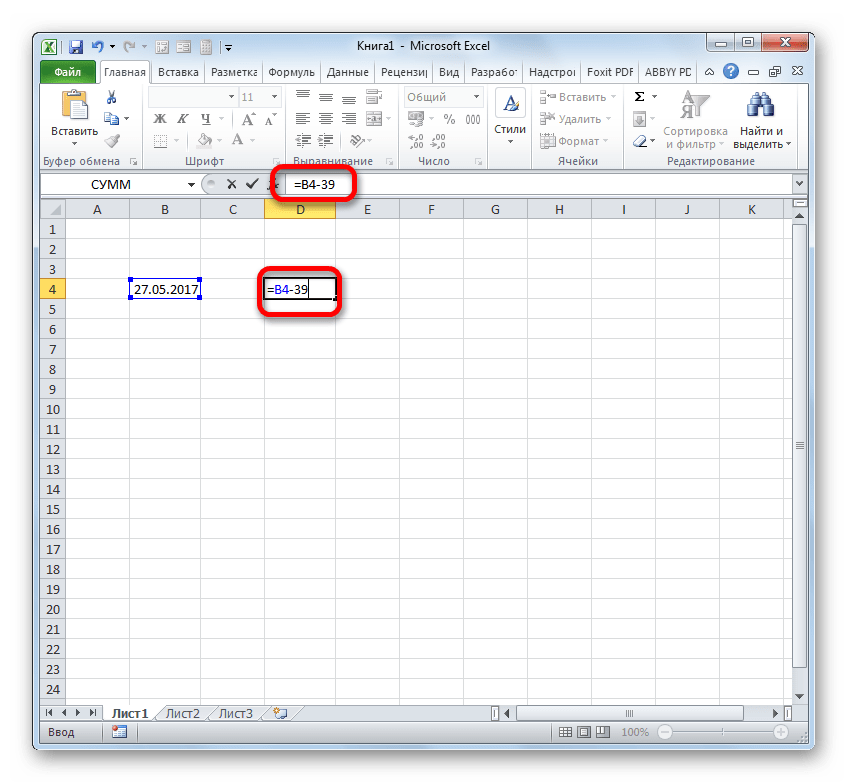
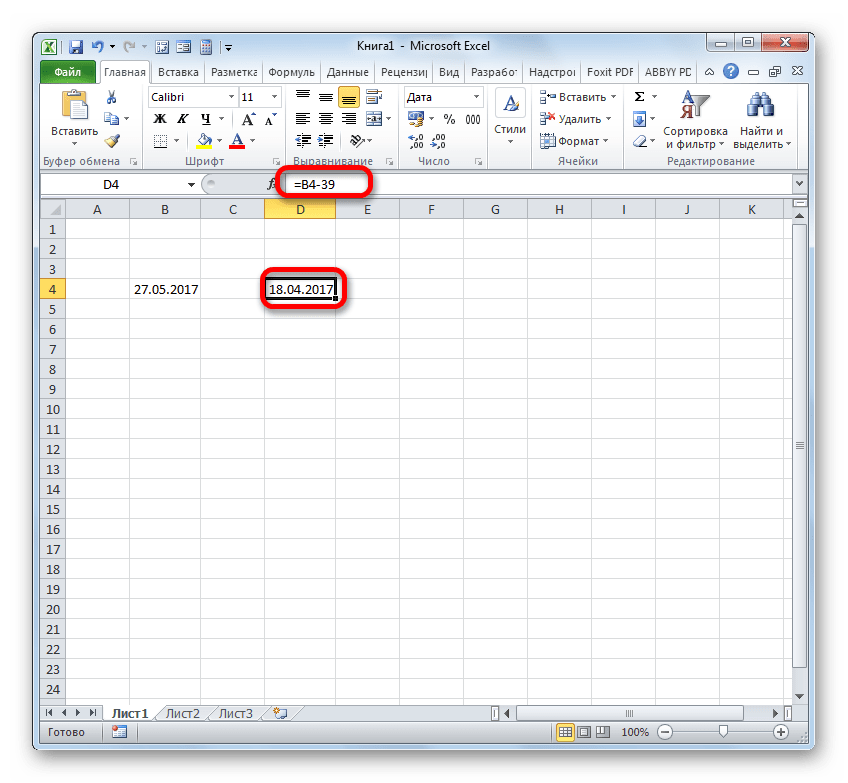
Если нам нужно вычесть определенное количество дней от даты, указанной в одном из элементов на листе, то прежде всего устанавливаем символ «=» в элемент, где будет отображен итоговый результат. После этого кликаем по элементу листа, где содержится дата. Его адрес отобразится в элементе вывода и в строке формул. Далее ставим символ «-» и вбиваем с клавиатуры численность дней, которую нужно отнять. Для того, чтобы совершить подсчет клацаем по Enter.

Результат выводится в обозначенную нами ячейку. При этом её формат автоматически преобразуется в формат даты. Таким образом, мы получаем полноценно отображаемую дату.

Существует и обратная ситуация, когда требуется из одной даты вычесть другую и определить разность между ними в днях.

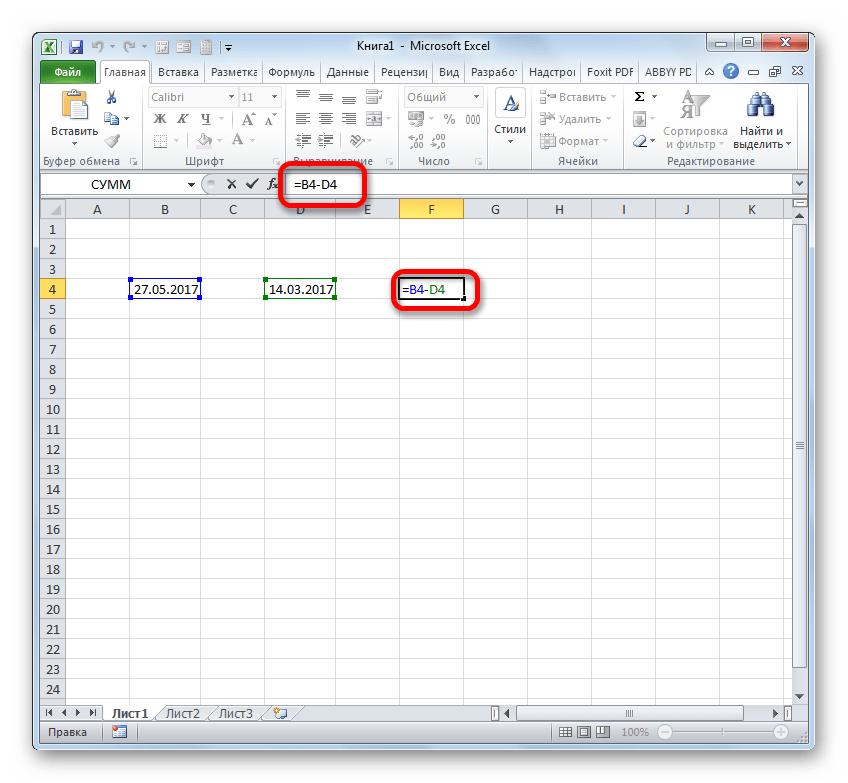
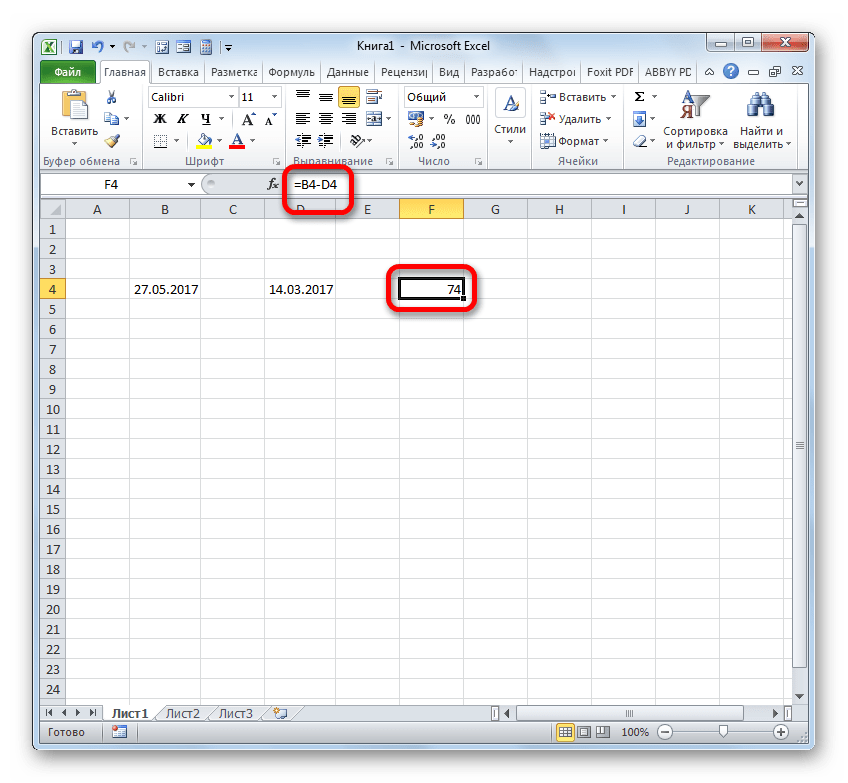
Устанавливаем символ «=» в ячейку, где будет отображен результат. После этого клацаем по элементу листа, где содержится более поздняя дата. После того, как её адрес отобразился в формуле, ставим символ «-». Клацаем по ячейке, содержащей раннюю дату. Затем клацаем по Enter.

Как видим, программа точно вычислила количество дней между указанными датами.

Также разность между датами можно вычислить при помощи функции РАЗНДАТ. Она хороша тем, что позволяет настроить с помощью дополнительного аргумента, в каких именно единицах измерения будет выводиться разница: месяцы, дни и т.д. Недостаток данного способа заключается в том, что работа с функциями все-таки сложнее, чем с обычными формулами. К тому же, оператор РАЗНДАТ отсутствует в списке Мастера функций, а поэтому его придется вводить вручную, применив следующий синтаксис:

=РАЗНДАТ(нач_дата;кон_дата;ед)

«Начальная дата» — аргумент, представляющий собой раннюю дату или ссылку на неё, расположенную в элементе на листе.

«Конечная дата» — это аргумент в виде более поздней даты или ссылки на неё.

Самый интересный аргумент «Единица». С его помощью можно выбрать вариант, как именно будет отображаться результат. Его можно регулировать при помощи следующих значений:

«d» — результат отображается в днях;
«m» — в полных месяцах;
«y» — в полных годах;
«YD» — разность в днях (без учета годов);
«MD» — разность в днях (без учета месяцев и годов);
«YM» — разница в месяцах.

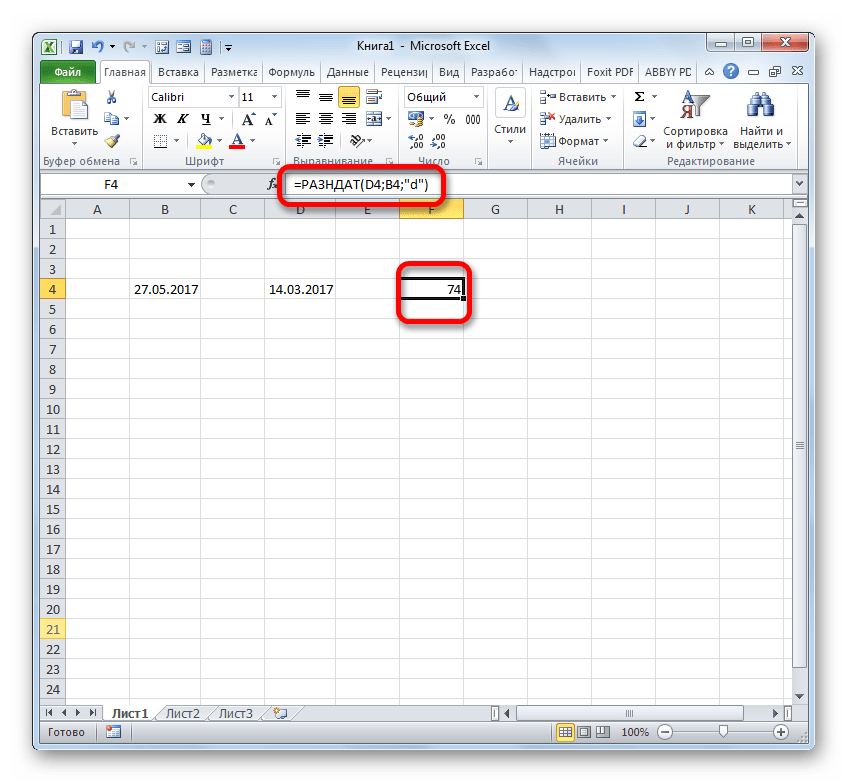
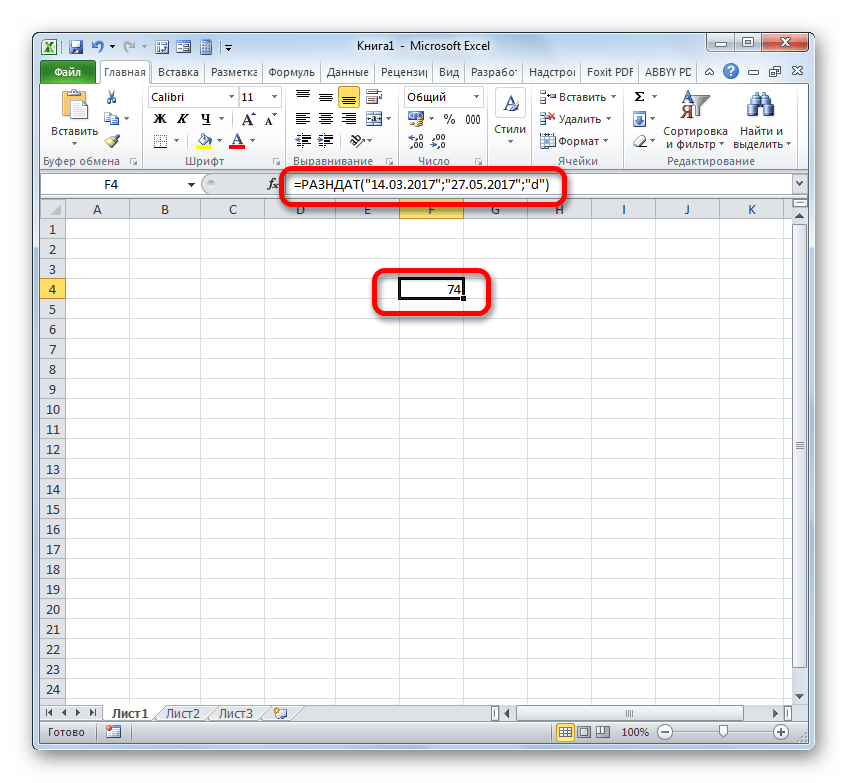
Итак, в нашем случае требуется вычислить разницу в днях между 27 мая и 14 марта 2017 года. Эти даты расположены в ячейках с координатами B4 и D4, соответственно. Устанавливаем курсор в любой пустой элемент листа, где хотим видеть итоги расчета, и записываем следующую формулу:

=РАЗНДАТ(D4;B4;"d")

Жмем на Enter и получаем итоговый результат подсчета разности 74. Действительно, между этими датами лежит 74 дня.

Если же требуется произвести вычитание этих же дат, но не вписывая их в ячейки листа, то в этом случае применяем следующую формулу:

=РАЗНДАТ("14.03.2017";"27.05.2017";"d")

Опять жмем кнопку Enter. Как видим, результат закономерно тот же, только полученный немного другим способом.

Урок: Количество дней между датами в Экселе

Способ 4: время

Теперь мы подошли к изучению алгоритма процедуры вычитания времени в Экселе. Основной принцип при этом остается тот же, что и при вычитании дат. Нужно из более позднего времени отнять раннее.

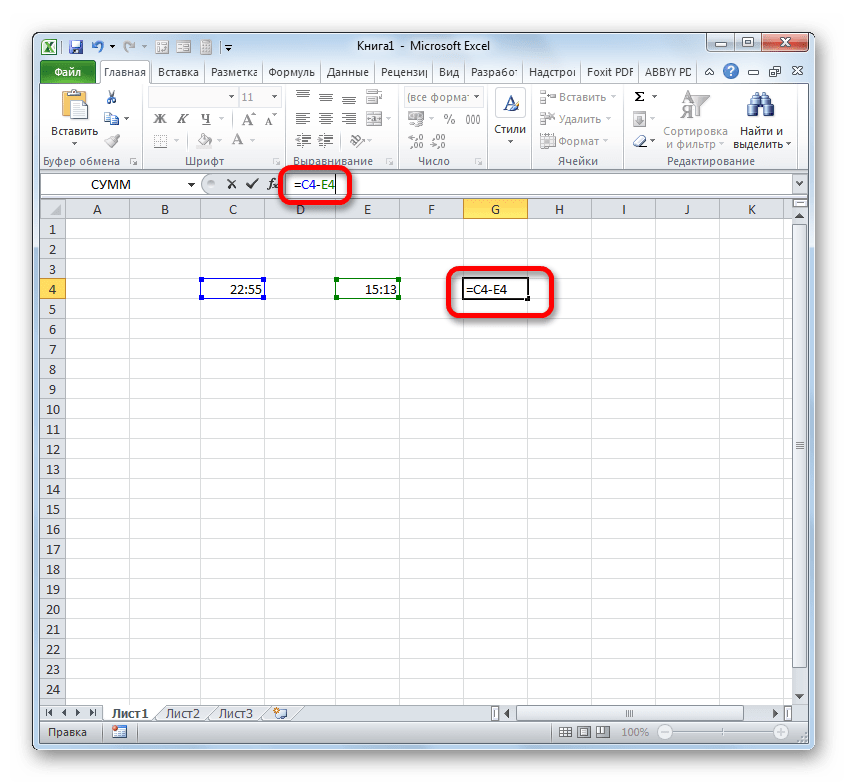
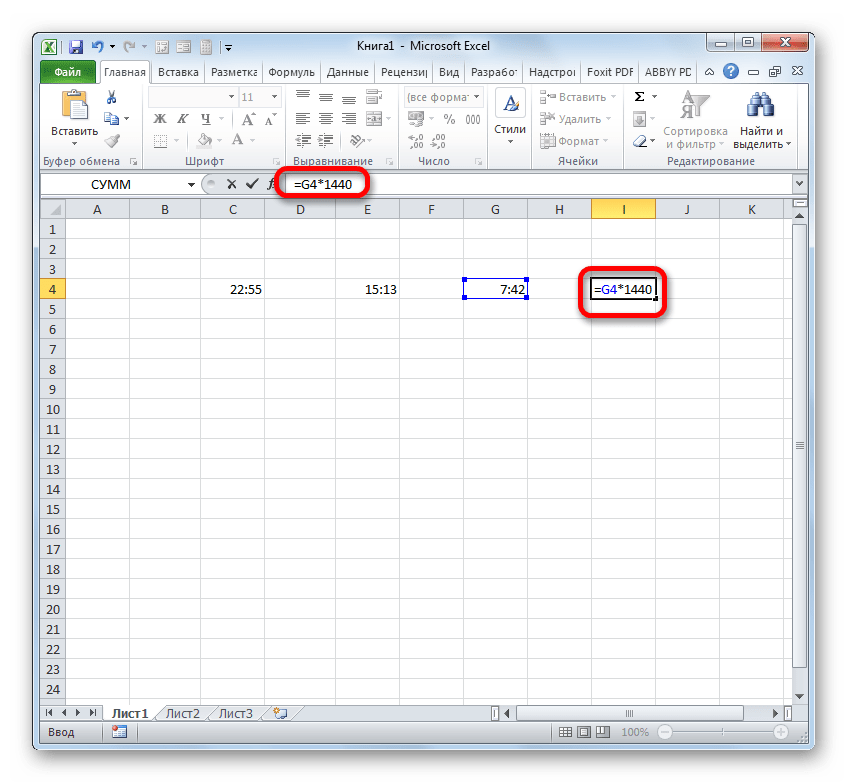
Итак, перед нами стоит задача узнать, сколько минут прошло с 15:13 по 22:55. Записываем эти значения времени в отдельные ячейки на листе. Что интересно, после ввода данных элементы листа будут автоматически отформатированы под содержимое, если они до этого не форматировались. В обратном случае их придется отформатировать под дату вручную. В ту ячейку, в которой будет выводиться итог вычитания, ставим символ «=». Затем клацаем по элементу, содержащему более позднее время (22:55). После того, как адрес отобразился в формуле, вводим символ «-». Теперь клацаем по элементу на листе, в котором расположилось более раннее время (15:13). В нашем случае получилась формула вида:
=C4-E4

Для проведения подсчета клацаем по Enter.

Но, как видим, результат отобразился немного не в том виде, в котором мы того желали. Нам нужна была разность только в минутах, а отобразилось 7 часов 42 минуты.
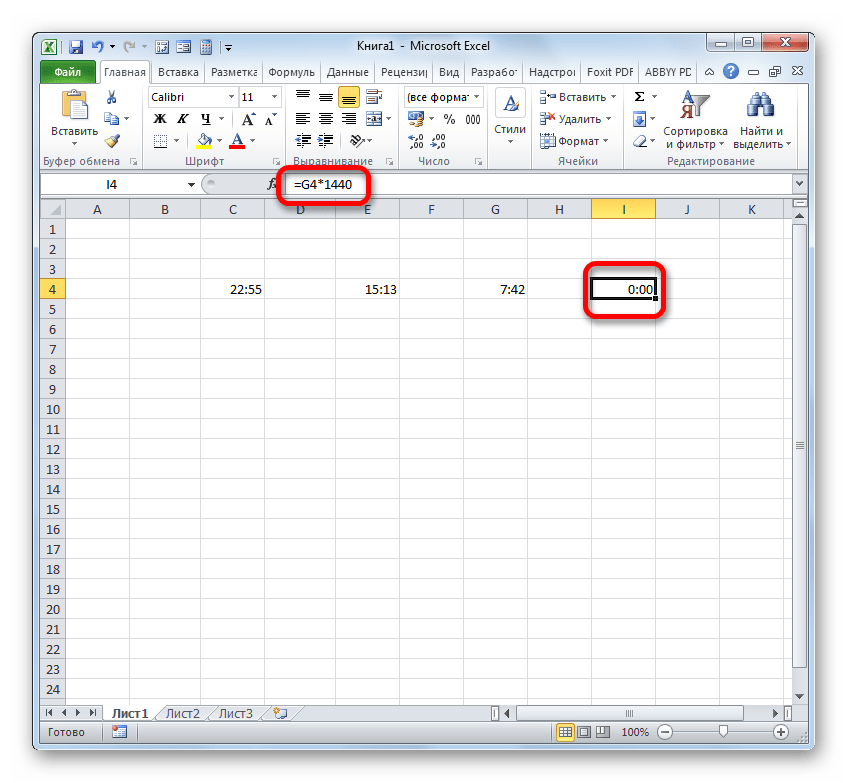
Для того, чтобы получить минуты, нам следует предыдущий результат умножить на коэффициент 1440. Этот коэффициент получается путем умножения количества минут в часе (60) и часов в сутках (24).

Итак, устанавливаем символ «=» в пустой ячейке на листе. После этого производим клик по тому элементу листа, где находится разность вычитания времени (7:42). После того, как координаты данной ячейки отобразились в формуле, жмем на символ «умножить» (*) на клавиатуре, а затем на ней же набираем число 1440. Для получения результата клацаем по Enter.

Но, как видим, опять результат отобразился некорректно (0:00). Это связано с тем, что при умножении элемент листа был автоматически переформатирован в формат времени. Для того, чтобы отобразилась разность в минутах нам требуется вернуть ему общий формат.

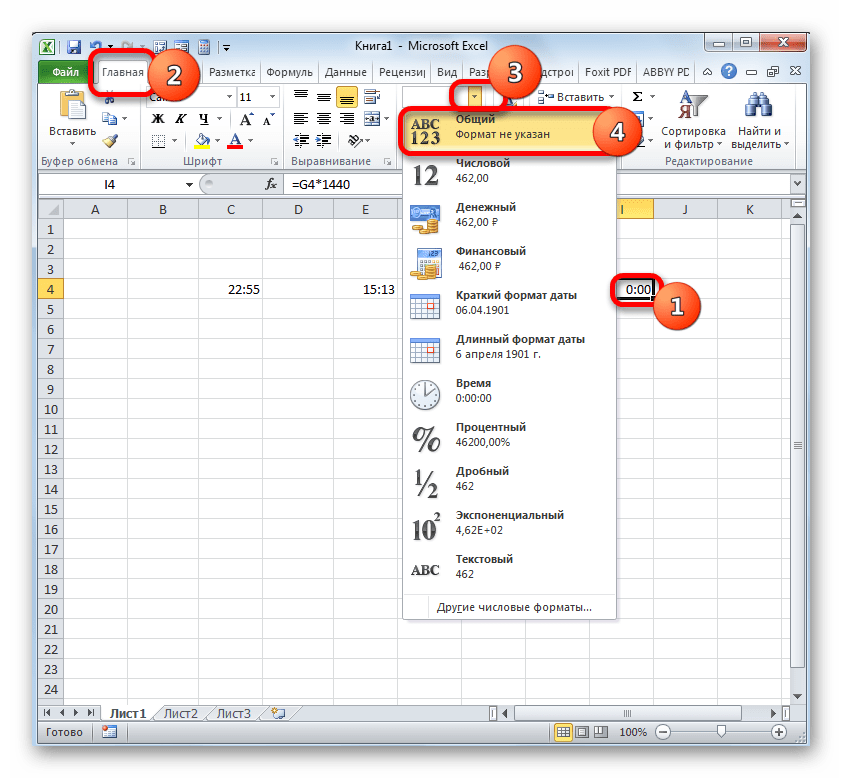
Итак, выделяем данную ячейку и во вкладке «Главная» клацаем по уже знакомому нам треугольнику справа от поля отображения форматов. В активировавшемся списке выбираем вариант «Общий».

Можно поступить и по-другому. Выделяем указанный элемент листа и производим нажатие клавиш Ctrl+1. Запускается окно форматирования, с которым мы уже имели дело ранее. Перемещаемся во вкладку «Число» и в списке числовых форматов выбираем вариант «Общий». Клацаем по «OK».

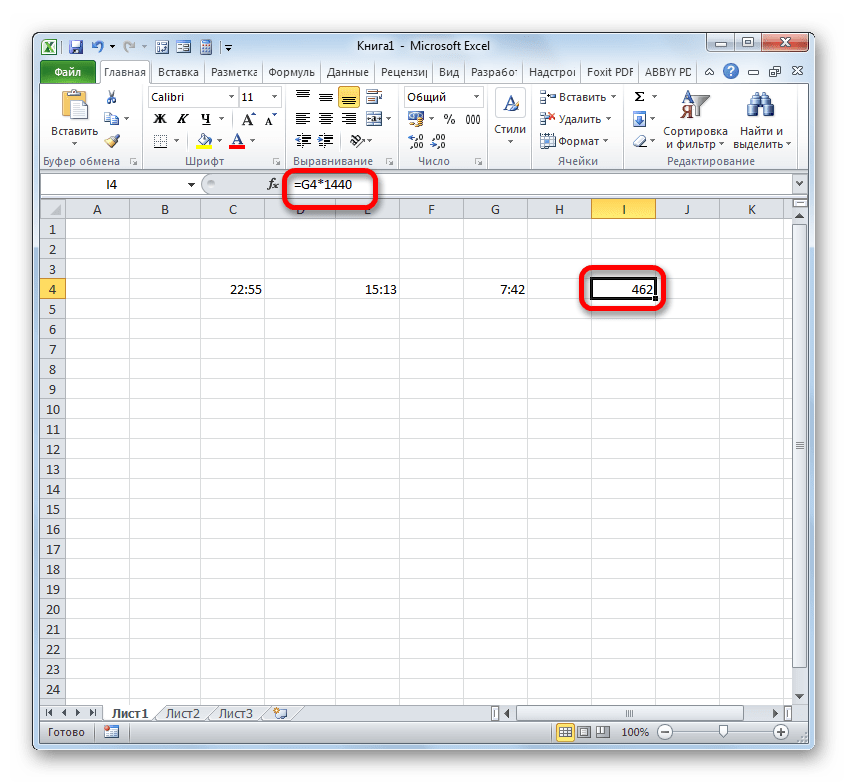
После использования любого из этих вариантов ячейка переформатируется в общий формат. В ней отобразится разность между указанным временем в минутах. Как видим, разница между 15:13 и 22:55 составляет 462 минуты.

Урок: Как перевести часы в минуты в Экселе

Как видим, нюансы подсчета разности в Excel зависят от того, с данными какого формата пользователь работает. Но, тем не менее, общий принцип подхода к данному математическому действию остается неизменным. Нужно из одного числа вычесть другое. Это удается достичь при помощи математических формул, которые применяются с учетом специального синтаксиса Excel, а также при помощи встроенных функций.

Источник

Свойства разности натуральных чисел

Правила вычитания суммы из числа и числа из суммы

Как меняется разность при изменении вычитаемого или уменьшаемого

Видео

Нахождение неизвестного множителя

Вычитание в столбик многозначных чисел

Теги

Найти разницу между произведением и суммой цифр данного трицифрового числа

Решение

Формула:

Вычисление разницы

Способ 1: вычитание чисел

Способ 2: денежный формат

Способ 3: даты

Способ 4: время

Не пропустите также: