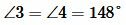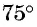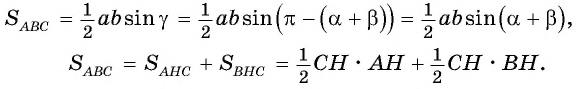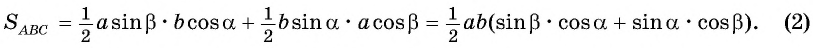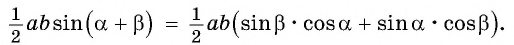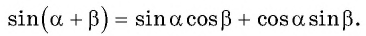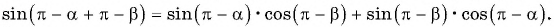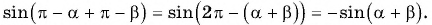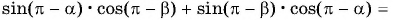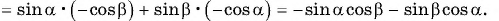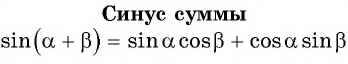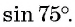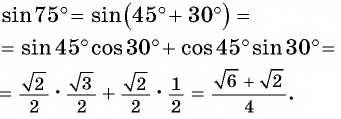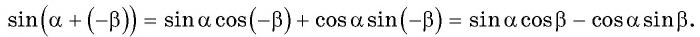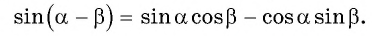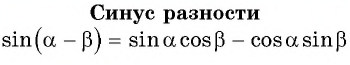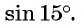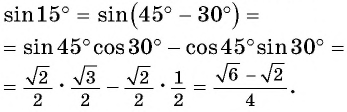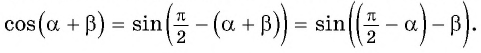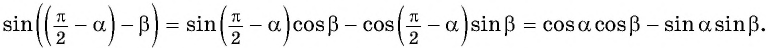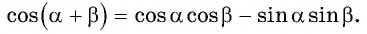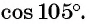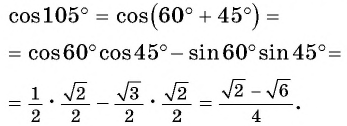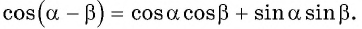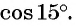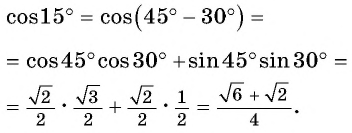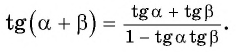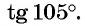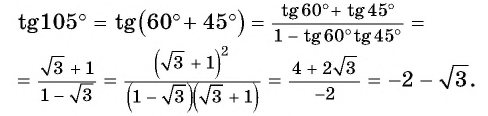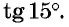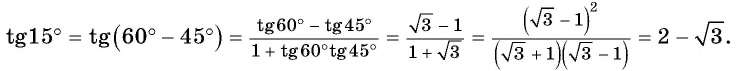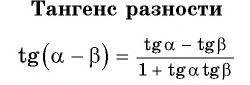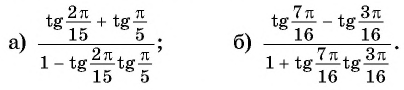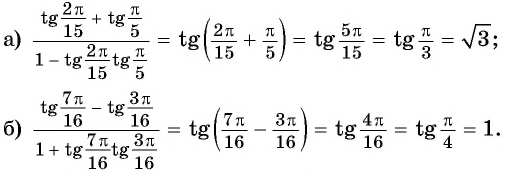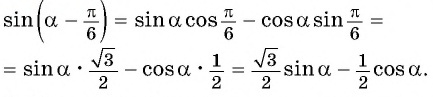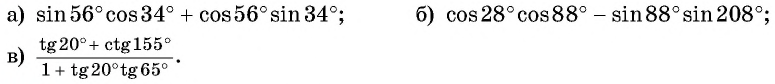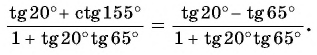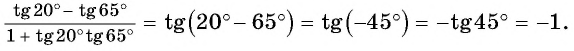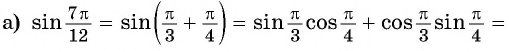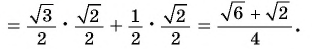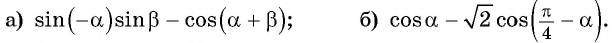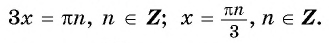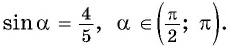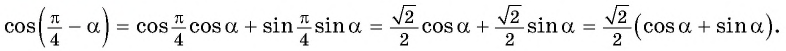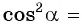Как найти разность треугольников?
Математика | 1 — 4 классы
Как найти разность треугольников.
Измерь стороны треугольников и сравни.
И найдёшь разность.
Величина одного из углов треугольника равна 12 градусов, а разность между величинами двух других углов равна 32 градусов?
Величина одного из углов треугольника равна 12 градусов, а разность между величинами двух других углов равна 32 градусов.
Найти величины всех углов треугольника.
Длины сторон треугольника относится как 4 : 3 : 5, причем разность наибольшей и наименьшей сторон равна 16 см?
Длины сторон треугольника относится как 4 : 3 : 5, причем разность наибольшей и наименьшей сторон равна 16 см.
Найти периметр треугольника.
Разность между величинами острых углов прямоугольного треугольника составляет 54 градусов?
Разность между величинами острых углов прямоугольного треугольника составляет 54 градусов.
Найти величины всех углов треугольника.
Периметр треугольника равен 24 дм, Сумма длин двух его сторон равна 160см?
Периметр треугольника равен 24 дм, Сумма длин двух его сторон равна 160см.
А их разность — 200мм, найти длины сторогн этого треугольника.
Кака найти суму и разность?
Кака найти суму и разность.
ПЕриметр треугольника равен 24дм, Сумма длин двух его сторон равна 160см, а их разность — 200мм, найти длины сторон этого треугольника?
ПЕриметр треугольника равен 24дм, Сумма длин двух его сторон равна 160см, а их разность — 200мм, найти длины сторон этого треугольника.
Периметр треугольника равен 24 дм?
Периметр треугольника равен 24 дм.
Сумма длин двух его сторон равна 160 см, а их разность — 200 мм.
Найти длины сторон этого треугольника.
Найти длины сторон этого треугольника?
Сумма гипотенузы и катета прямоугольного треугольника равна 9, а их разность равна 4?
Сумма гипотенузы и катета прямоугольного треугольника равна 9, а их разность равна 4.
Найти другой катет.
Стороны треугольника относятся как 3 : 4 : 5?
Стороны треугольника относятся как 3 : 4 : 5.
Найти периметр треугольника если разность его наибольшей и наименьшей стороны ровна 18.
Найти разность 18и 58?
Найти разность 18и 58.
На этой странице находится вопрос Как найти разность треугольников?. Здесь же – ответы на него, и похожие вопросы в категории Математика, которые можно найти с помощью простой в использовании поисковой системы. Уровень сложности вопроса соответствует уровню подготовки учащихся 1 — 4 классов. В комментариях, оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С ними можно обсудить тему вопроса в режиме on-line. Если ни один из предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой строке, расположенной вверху, и нажмите кнопку.
57. 6 см в кубе, там легко просто умножь.
(x — 7) — 5x ( — 10 — 2x) (5x — 6)(5x + 6) — 25x(x — 3) = 25x² + 30x — 30x — 36 — 25x² + 75x = 75x — 36 18a + (a — 9) = 18a + a — 9 = 19a — 9.
Сколько времени потратил Коля а все уроки? 10 + 15 = 25 минут — на чтение 15 + 10 + 25 = 50 минут потратил Коля на все уроки.
Для начала начнём с 3 ты должен 4 рубля 40 копеек слаживать вот так к примеру 4р 40 коп + 4р 40коп = 8р 80 коп потом ты ещё раз 8 р 80 коп + 4р 40коп = и так далее пока не дойдёш до 60 рублей понятно.
Представим, что X это расстояние, которое прошел второй лыжник, значит первый прошел X + 300. X + 300 потому что первый лыжник за 20 минут проходит на 300 метров больше чем второй, составляем уравнение : X + X + 300 = 6700 2X = 6700 — 300 2X = 6400 ..
1)89100 : 900 = 99. 2)31250 : 250 = 125. 3) 10780 : 110 = 98. 4)28600 : 440 = 65.
А) 99 б) 125 в) 98 г) 65 Как — то так.
A)8 — 4, 53 + 0, 355 = 3, 47 + 0, 355 = 3, 825 b)1, 029 : 0, 098 — 0, 29•24 = 10, 5 — 6, 96 = 3, 54.
8 — 4, 53 + 0 ; 355 = 3, 47. 1, 029 : 0, 098 — 0, 29 * 24 = 10493, 04.
1) 367 — 167 = 120 — 20 = 100 2) 185 — 143 = 100 — 58 = 42 3) 523 — 373 = 400 — 250 = 150.
Неравенство треугольника
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
Данный видеоурок предназначен для самостоятельного ознакомления с темой «Неравенство треугольников», которая входит в школьный курс геометрии за седьмой класс. На занятии учитель познакомит с неравенством треугольника, вытекающим из теоремы о сторонах и углах треугольника.
Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть уроки «Связь числа и геометрии. Часть 2. Треугольники. Координаты», «Основы геометрии»
Треугольник. Формулы и свойства треугольников.
Типы треугольников
По величине углов
По числу равных сторон
Вершины углы и стороны треугольника
Свойства углов и сторон треугольника
Сумма углов треугольника равна 180°:
В треугольнике против большей стороны лежит больший угол, и обратно. Против равных сторон лежат равные углы:
если α > β , тогда a > b
если α = β , тогда a = b
Сумма длин двух любых сторон треугольника больше длины оставшейся стороны:
a + b > c
b + c > a
c + a > b
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов.
| a | = | b | = | c | = 2R |
| sin α | sin β | sin γ |
Теорема косинусов
Квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 — 2 bc · cos α
b 2 = a 2 + c 2 — 2 ac · cos β
c 2 = a 2 + b 2 — 2 ab · cos γ
Теорема о проекциях
Для остроугольного треугольника:
a = b cos γ + c cos β
b = a cos γ + c cos α
c = a cos β + b cos α
Формулы для вычисления длин сторон треугольника
Медианы треугольника
Свойства медиан треугольника:
В точке пересечения медианы треугольника делятся в отношении два к одному (2:1)
Медиана треугольника делит треугольник на две равновеликие части
Треугольник делится тремя медианами на шесть равновеликих треугольников.
Формулы медиан треугольника
Формулы медиан треугольника через стороны
ma = 1 2 √ 2 b 2 +2 c 2 — a 2
mb = 1 2 √ 2 a 2 +2 c 2 — b 2
mc = 1 2 √ 2 a 2 +2 b 2 — c 2
Биссектрисы треугольника
Свойства биссектрис треугольника:
Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
Угол между биссектрисами внутреннего и внешнего углов треугольника при одной вершине равен 90°.
Формулы биссектрис треугольника
Формулы биссектрис треугольника через стороны:
la = 2√ bcp ( p — a ) b + c
lb = 2√ acp ( p — b ) a + c
lc = 2√ abp ( p — c ) a + b
где p = a + b + c 2 — полупериметр треугольника
Формулы биссектрис треугольника через две стороны и угол:
la = 2 bc cos α 2 b + c
lb = 2 ac cos β 2 a + c
lc = 2 ab cos γ 2 a + b
Высоты треугольника
Свойства высот треугольника
Формулы высот треугольника
ha = b sin γ = c sin β
hb = c sin α = a sin γ
hc = a sin β = b sin α
Окружность вписанная в треугольник
Свойства окружности вписанной в треугольник
Формулы радиуса окружности вписанной в треугольник
r = ( a + b — c )( b + c — a )( c + a — b ) 4( a + b + c )
Окружность описанная вокруг треугольника
Свойства окружности описанной вокруг треугольника
Формулы радиуса окружности описанной вокруг треугольника
R = S 2 sin α sin β sin γ
R = a 2 sin α = b 2 sin β = c 2 sin γ
Связь между вписанной и описанной окружностями треугольника
Средняя линия треугольника
Свойства средней линии треугольника
MN = 1 2 AC KN = 1 2 AB KM = 1 2 BC
MN || AC KN || AB KM || BC
Периметр треугольника
Периметр треугольника ∆ ABC равен сумме длин его сторон
Формулы площади треугольника
Формула Герона
Равенство треугольников
Признаки равенства треугольников
Первый признак равенства треугольников — по двум сторонам и углу между ними
Второй признак равенства треугольников — по стороне и двум прилежащим углам
Третий признак равенства треугольников — по трем сторонам
Подобие треугольников
∆MNK => α = α 1, β = β 1, γ = γ 1 и AB MN = BC NK = AC MK = k ,
где k — коэффициент подобия
Признаки подобия треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
http://interneturok.ru/lesson/geometry/7-klass/sootnosheniya-mezhdu-storonami-i-uglami-treugolnikov/neravenstvo-treugolnika
http://ru.onlinemschool.com/math/formula/triangle/
Содержание
- Сравнение углов. Сложение и вычитание углов
- Вертикальные углы. Свойства вертикальных углов
- Свойства вертикальных углов
- Задачи и решения
Сравнение углов. Сложение и вычитание углов
Углы различают по их величине. Большим считается не тот угол, стороны которого длиннее, а тот, стороны которого сильнее расходятся врозь. На черт. 13 уг. EDF больше, чем угол 2, потому, что у первого стороны сильней расходятся врозь. Встречаются углы, стороны которых расходятся врозь совершенно одинаково; такие углы можно наложить один на другой так, что их вершины совпадут, а стороны сольются. Углы, которые можно таким образом наложить друг на друга, считаются равными, хотя бы стороны их были неодинаковой длины.
На черт. 13 равны, например, уг. DEH и уг. DFH, уг. 2 и уг. а; вы можете убедиться в этом, есля обведете один угол на прозрачной бумаге и покроете им другой.
Если при наложении сравниваемых углов их вершины и одна сторона совпали, вторая же сторона накладываемого угла оказалась внутри или вне другого угла, то такие углы, конечно, не равны. Тот угол, который оказался внутри другого, считается меньшим.
Рассмотрите на том же черт. 13 углы, вершины которых лежат в точке D. Здесь три угла: уг. EDF, уг. EDH и уг. HDF. Вы видите, что оба меньших угла как раз заполняют собою уг. EDF, который составляется из них, как целое из своих частей. Когда углы так расположены, то говорят, что уг. EDF есть с у м м а углов EDH и HDF. С л о ж и т ь два угла значит найти их сумму, т. е. тот угол, который составится, если приложить их друг к другу, как показано на чертеже 13.
Если на черт. 13 от угла EDF отнять угол EDH, то останется уг. HDF; этот. угол называется р а з н о с т ь ю углов EDF и EDH. Вычесть один угол из другого значит найти их разность.
Повторительные вопросы
Какие углы называются равными? – Зависит ли величина угла от длины сторон? – Покажите на чертеже, что называется суммой и разностью двух углов.
Развернутый угол
Представьте себе, что мы разводим врозь стороны какого-нибудь угла, – напр. уг. 1 (черт. 14). От этого угол станет увеличиваться: он превратится сначала в уг. 2, потом в уг. 3 и, наконец, в уг. 4, стороны которого составляют одну прямую линию. Такие углы, как уг. 4, называются р а з в е р н у т ы м и углами.
Может ли один развернутый угол быть больше или меньше другого развернутого? Конечно, нет: ведь всякие прямые линии, если их наложить одну на другую, сливаются между собою; значит, должны слиться при наложении и всякие развернутые углы. Итак:
В с е р а з в е р н у т ы е у г л ы р а в н ы м е ж д у с о б о ю.
Смежные углы. Прямой угол
На черт. 15 вы видите углы 1 и 2, которые расположены так, что вершины их совпадают (в точке А) и одна сторона (AD) у них общая, т. е. принадлежит одновременно обоим углам, другие же стороны АВ и АС этой пары углов составляют одну прямую линию. Углы, которые так расположены, называются с м е ж н ы м и. На черт. 16 вы видите несколько пар смежных углов: уг. 1 и уг. 2; уг. 3 и уг. 4; уг. 5 и у г. 6; у г. а и у г. b; уг. с и у г. d, и др.
Если углы, составляющие одну пару смежных углов, равны между собою, – как уг. 7 и 8 на черт. 16, – то каждый из них называется прямым углом. Значит:
П р я м о й у г о л е с т ь о д и н и з д в у х р а в н ы х с м е ж н ы х у г л о в.
Так как оба равных смежных угла составляют вместе один развернутый угол, то прямой угол есть половина развернутого угла. Но все развернутые углы равны друг другу; поэтому равны и их половины, т. е. прямые углы. Значит:
В с е п р я м ы е у г л ы р а в н ы д р у г д р у г у.
Прямые линии, встречающиеся под прямым углом (черт. 17), называются перпендикулярными друг к другу. На черт. 17, например, уг. 1 = уг. 2, а так как эти углы смежные и притом равные, то они – прямые. Поэтому CD перпендикулярно к АВ и АВ перпендикулярно к CD.
Слово «перпендикулярный» не надо смешивать со словом «вертикальный». В е р т и к а л ь н о й, или о т в е с н о й, называют всякую прямую линию, имеющую направление свободно свешивающейся нагруженной нити.
Все те линии, которые составляют с вертикальной линией прямой угол, называются г о р и з о н т а л ь н ым и. Горизонтальны, например, все линии, проведенные по поверхности воды (черт. 18). Отвесное направление проверяют отвесом (черт. 18); горизонтальное – плотничьим ватерпасом.
На бумаге прямой угол чертят помощью линейки и чертежного треугольника (черт. 19). Проверить, правильно ли изготовлен чертежный треугольник, можно так. Проведя по линейке прямую линию и начертив с помощью треугольника другую прямую к ней, перпендикулярную, прикладывают чертежный треугольник прямым углом к смежному углу: если эти углы равны, то треугольник изготовлен правильно.
Углы, меньшие, чем прямой, называются о с т р ы м и; большие, чем прямой, – т у п ы м и.
Повторительные вопросы к §§ 6 и 7
Какой угол называется развернутым? – Какие углы называются смежными (начертите несколько таких углов)? – Какой угол называется прямым? – Как называется угол, который равен смежному с ним? – Могут ли прямые углы иметь различную величину? – Объясните значение слов: перпендикулярный, вертикальный, отвесный, горизонтальный. – Как чертить перпендикулярные прямые помощью чертежного треугольника? – Какие углы называются острыми? Тупыми? Начертите несколько острых и несколько тупых углов.
1. Уменье чертить взаимно-перпендикулярные прямые позволяет строить так наз. «графики», т. е. ломаные (или кривые) линии, наглядно показывающие ход изменения явлений. Пусть требуется построить график температуры за неделю по следующим данным:
Изобразим эти температуры рядом перпендикуляров к одной прямой, приведенных на равных расстояниях друг от друга: длина перпендикулярных отрезков будет изображать температуру дня. Верхушки перпендикуляров соединим прямыми линиями: полученная ломаная линия и есть «график температур».
2. На черт. 20 изображены графики годового хода температуры воздуха в разных местах земного шара: на о-ве Цейлон, в Ницце, в Самаре, во Владивостоке и в Верхоянске. Рассматривая эти графики, мы можем ответить себе на ряд могущих возникнуть вопросов, например:
a) Какова температура в среднем за много лет во всех на званных местах 1 мая?
О т в е т. На Цейлоне +27° в Ницце +18°, в Самаре +15°, во Владивостоке +10°, в Верхоянске 0°.
b) Какие дни в году (в среднем) самые жаркие и самые холодные в Верхоянске?
О т в е т. 1-е июля + 15°1-е января – минус 50°
c) В каких городах в апреле средняя температура ниже0°?
О т в е т. В Верхоянске, Владивостоке и Самаре.
d) Какова разница между самой высокой и самой низкой средней температурой в Ницце? В Самаре?
О т в е т ы. В Ницце средняя температура колеблется от +9° до +24°; в Самаре – от минус 10° до +21°.
Свойство смежных углов
Сумма обоих смежных углов, очевидно, равна развернутому углу. Но развернутый угол равен двум прямым углам, взятым вместе. Поэтому:
С у м м а о б о и х с м е ж н ы х у г л о в р а в н а д в у м п р я м ы м у г л а м.
Например, на черт. 21 уг. 1 +уг. 2 = двум прямым углам.
Бывает, что по одну сторону прямой расположено не два угла, как в случае смежных углов, а несколько углов, – как на черт. 22. Легко убедиться, что сумма этих углов также равна двум прямым: из них всегда можно составить одну пару смежных углов (на черт. 22 углы АОD и DOВ, или АОЕ и ЕОВ).
Подобным же образом можно найти, чему равна сумма углов,! расположенных вокруг общей вершины, как на черт. 23. Продолжив одну из сторон за общую вершину (черт. 24), получим две группы углов: группу 1 и а, сумма которых равна двум прямым (почему?), и группу углов 2, 3, Ь, сумма которых равна также двум прямым углам; значит, сумма всех углов вокруг общей вершины равна 4 прямым углам.
Повторительные вопросы
Чему равна сумма смежных углов? – Сумма нескольких углов, расположенных по одну сторону прямой линии? – Сумма всех углов, расположенных вокруг общей вершины?
Противоположные углы
Предварительные упражнения
1) На черт. 25 уг. 1 = 48°. Найти прочие углы.
2) На черт. 25 уг. b = 136 °. Найти прочие углы.
Когда две прямые линии пересекают друг друга (черт. 25), они образуют две пары углов, стороны которых составляют продолжение одни других: одна пара – уг. 1 и уг. 2; другая – уг. а и уг. b. Особенность противоположных углов та, что углы, составляющие такую пару, всегда равны между собою: у г. 1 = уг. 2, уг. а = у г. b. Действительно, если например (черт. 25) уг. 1 = 40°, то уг. b = 180° – 40° = 140°, уг. 2 = 180° – 140° = 40°, и уг. а = 180° – 40° = 140°; мы видим, что уг. 1 = уг. 2, и уг. а = уг. b. Вообще, так как уг. 1 вместе с углом а равен двум прямым (почему?), а уг. 2 вместе с тем же углом а тоже равен двум прямым, то ясно, что уг. 1 должен равняться уг. 2. Итак:
П р о т и в о п о л о ж н ы е у г л ы р а в н ы.
Повторительные вопросы.
Какие углы называются противоположными? знаете свойство противоположных углов?
Окружность
До сих пор мы говорили только о прямых линиях. Из к р и в ы х линий остановимся на о к р у ж н о с т и (черт. 26). Окружность чертят циркулем. Острие ножки раздвинутого циркуля втыкают в бумагу, другую же ножку с карандашом вращают вокруг первой; когда карандаш сделает полный оборот, он проведет на бумаге замкнутую кривую – окружность. Та точка, в которую было воткнуто острие циркуля, называется ц е н т р о м окружности. Понятно, что все точки окружности удалены от центра на одинаковое расстояние; это расстояние называется р а д и у с о м окружности. Значит:
О к р у ж н о с т ь е с т ь к р и в а я л и н и я, в с е т о ч к и к о т о р о й о д и н а к о в о у д а л е н ы о т о д н о й
т о ч к и, н а з ы в а е м о й ц е н т р о м.
Прямая, соединяющая две точки окружности через центр, называется д и а м е т р о м.
Всякая часть окружности называется ее д у г о ю (черт. 27).
Плоская фигура, ограниченная окружностью, называется к р у г о м.
Повторительные вопросы
Что такое окружность? Центр? Радиус? Дуга? – Покажите все это на чертеже. – Все ли радиусы одной окружности равны между собою? – Что больше: диаметр или радиус? Во сколько раз?
Применения
3. Гудок завода слышен на 4 км. Начертить в масштабе 1 км в 1 см границу местности, где слышен гудок этого завода.
Р е ш е н и е. Вокруг точки, обозначающей положение завода, начертить окружность радиусом 4 см.
4. Радиус круга 100 см. Некоторая точка удалена от центра на 40 см. Лежит ли она внутри круга или вне его? Каково ближайшее расстояние от этой точки до окружности?
Р е ш е н и е. Точка лежит внутри круга. Ближайшее расстояние ее от окружности надо считать вдоль диаметра, проведенного через эту точку; оно равно 60 см. Дальнейшее расстояние (вдоль того же диаметра) – 140 см.
Источник
Вертикальные углы. Свойства вертикальных углов
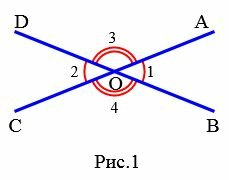
Определение 1. Вертикальными углами называются два угла, у которых стороны одного угла являются продолжениями сторон другого угла.
На Рис.1 углы AOB и COD вертикальные. Вертикальные также углы AOD и BOC.
Свойства вертикальных углов
1. Вертикальные углы равны.
2. Две пересекающие прямые образуют две пары вертикальных углов.
Доказательство пункта 1. Поскольку 1, 3 и 2, 3 смежные углы, то имеем
Следовательно 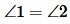
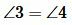
Задачи и решения
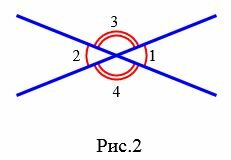
Задание 1. Угол 1 равен 32°. Найти углы 2, 3, 4 (Рис.2).
Решение. Так как углы 1 и 2 вертикальны, то 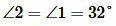
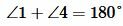
Углы 3 и 4 вертикальные. Тогда
Ответ. 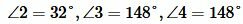
Задание 2. При пересечении двух прямых образовались четыре угла. Сумма двух углов равна 220°. Найти все углы.
Решение. Из образованных четырех углов любые две или смежные, или вертикальные. Поскольку в нашей задаче сумма двух углов равна 220°, то эти углы вертикальные (так как сумма смежных углов равна 180°). Тогда каждый из этих углов равен 220°:2=110°. Смежный по отношению угла 110° , будет угол 180°-110°=70°. Следовательно остальные два угла равны 70°. Отметим, что сумма всех четырех углов равен 360°:
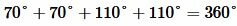
Ответ. 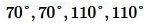
Источник
Геометрия
7 класс
Урок №5
Измерение углов
Перечень рассматриваемых вопросов:
- Измерительные инструменты.
- Градусная мера угла; биссектриса.
- Транспортир.
- Классификация углов.
Тезаурус:
Градус – угол, равный одной сто восьмидесятой части развернутого угла.
Градусная мера угла – положительное число, которое показывает, сколько раз градус и его части укладываются в данном углу.
Минута – 1/60 часть градуса.
Секунда – 1/60 часть минуты.
Луч – часть прямой, состоящий из всех точек, лежащих по одну сторону от заданной точки, которая является началом луча.
Угол – это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.
Стороны угла – лучи, из которых состоит угол.
Вершина угла – общее начало сторон угла.
Биссектриса – это луч, исходящий из вершины угла и делящий его на два равных угла.
Основная литература:
- Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.
Дополнительная литература:
- Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
- Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
- Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
- Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
- Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.
Теоретический материал для самостоятельного изучения.
Ранее вы уже познакомились с геометрической фигурой – уголи его составными элементами.
Сегодня мы продолжим изучать углы, познакомимся с их классификацией и будем измерять углы с помощью транспортира.
Измерение углов аналогично измерению отрезков – оно основано на сравнении, только отрезки сравнивались с отрезком, принятым за единицу измерения, а углы с углом, тоже принятым за единицу измерения.
Обычно за единицу измерения углов принимают градус.
Градус – угол, равный 1/180 части развёрнутого угла.
Положительное число, которое показывает, сколько раз градус и его части укладываются в данном углу, называется градусной мерой угла.
Для измерения углов используют транспортир. Вспомним, как проводить измерение углов с помощью транспортира.
Транспортир накладывают на угол так, чтобы вершина угла совпала с центром транспортира, а одна из сторон угла прошла через нулевое деление на шкале. Тогда другая сторона угла укажет величину угла в градусах на той же шкале.
Например:
∠О = 50°
Но обычно говорят кратко – угол О равен 50 градусам.
Если масштабныйугол не укладываетсяцелое число раз в измеряемом угле, тоединицу измерения делят ещё на части.
Определённые части градуса носят специальные названия.
Части градуса.
Минута – 1/60 часть градуса.
Обозначается «´».
Секунда – 1/60 часть минуты.
Обозначается «´´».
Например:
∠А = 40 ° 15´ 16 ´´
Далее, аналогично понятию равные отрезки, ведём понятие равные углы.
Дваугла считаются равными, если градус и его части укладываются в этих углах одинаковое число раз, т.е. равные углы имеют равные градусные меры.
Если один угол меньше другого, то градус в нём (или его часть) укладываются в этом углу меньшее число раз, чем в другом, т.е. меньший угол имеет меньшую градусную меру.
Когда луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов.
∠АОС =∠АОL + ∠LОС,
∠АОL = 64°,
∠LОС = 64°,
∠АОС = 64° + 64° = 128°.
Далее рассмотрим классификацию углов.
Мы уже знаем, что есть развёрнутый угол, его градусная мера сто восемьдесят градусов.
Но есть и другие углы.
Например, прямой угол, его градусная мера девяносто градусов;
острый угол, его градусная мера меньше девяноста градусов;
тупой угол, его градусная мера больше девяноста градусов, но меньше ста восьмидесяти.
Выполним практическое задание – построим биссектрису угла с помощью транспортира.
Мы знаем, что биссектриса – это луч, исходящий из вершины угла и делящий его на два равных угла.
∠АОС = 128°,
128° : 2 = 64°,
OL – биссектриса ∠АОС.
Поэтому для начала определим градусную меру ∠АОС, она составляет 128°, тогда биссектриса этого угла, исходя из определения, составит 64 °.
Итак, сегодня получили представление о том, как измерять и изображать угол с помощью транспортира. Перейдем к практическим заданиям.
Способы измерения на местности.
Измерение углов на местности проводят с помощью различных приборов. Один из таких – астролябия, она состоит из диска (лимб), разбитого на градусы и вращающейся вокруг центра диска линейки (алидады). На концах алидады есть окошечки, которые нужны, чтобы устанавливать её в определённом направлении.
Опишем, как происходит измерение углов с помощью этого прибора. При измерении углов астролябию устанавливают в его вершине, например, точке О, при этом лимб должен находится горизонтально плоскости угла, а отвес, в центе диска, совпадать с вершиной угла.
Затем устанавливаем алидаду вдоль одной из сторон угла, например, АО, отмечаем деление, напротив которого находится указатель алидады.
Далее поворачиваем алидаду по часовой стрелке, пока она не совпадёт со второй стороной угла, у нас это сторона ОВ, отмечаем деление, напротив которого оказался указатель алидады. Теперь можно найти градусную меру измеряемого угла, как разность второго и первого измерения.
Тренировочные задания.
1. Луч ВК делит развернутый ∠ОВС на два угла, разность которых равна 56°. Найдите образовавшиеся углы.
Решение: нарисуем рисунок, исходя из условия задачи.
Обозначим ∠СВК за х, тогда ∠ОВК= х + 56°, исходя из условия задачи (разность углов равна 56°). Развёрнутый угол равен 180°. Составим уравнение и решим его.
х + х +56 =180,
2х= 180 – 56,
2х= 124,
х = 124:2,
х = 62° (∠СВК).
Тогда ∠ОВК= х + 56°= 62° +56° = 118°.
Ответ: ∠СВК = 62°; ∠ОВК = 118°.
2. Чему равен ∠ЕОА, если ∠ВОА = 130° 54´, а ∠ВОЕ = 105° 76´?
Решение: Найдём ∠ЕОА = ∠ВОА – ∠ВОЕ, т.к. ОЕ – луч, проведённый из вершины ∠ВОА и делящий этот угол на 2 части. Подставим в выражение градусные меры углов и найдём градусную меру ∠ЕОА. Так как в градусе 60 минут, то 105° 76´ = 106° 16´.
∠ЕОА = 130° 54´ – 106° 16´ = 24° 38´.
Ответ: ∠ЕОА = 24° 38´.
Формулы суммы и разности углов тригонометрических функций онлайн
С помощю этого онлайн калькулятора можно получить формулы суммы и разности углов тригонометрических функций. Для получения формулы выберите нужную тригонометрическую функцию, нажав на «sin», выберите нужный аргумент, нажав на аргумент в формуле. В результате получится формула для этой функции и аргумента. Теоретическую часть и численные примеры смотрите ниже.
Формулы суммы и разности углов тригонометрических функций − теория, доказательство, примеры
Выведем формулы суммы и разности углов тригонометрических функций. Начнем с формулы
Как мы знаем, угол между векторами не может быть больше 180° (π). На рисунке Рис.1 угол между векторами 





Рассмотрим, теперь косинусы этих углов. Из формул приведения мы знаем (подпрбнее о формулах приведения смотрите на странице Формулы приведения тригонометрических функций онлайн):
Cкалярное произведение векторов 

Так как точка 





Поскольку левые части формул (2) и (3) равны, то равны и правые части этих формул. Следовательно выполнено равенство (1).
Докажем, далее, справедливость следующей формулы
Представим косинус суммы углов α и β в виде косинуса разности двух углов и воспользуемся формулой (1) и тем, что косинус четная функция а синус нечетная функция:
Перейдем к доказательству формул синусов суммы и разности углов:
Для доказательства формулы (5) воспользуемся формулами приведения тригонометрических функций и формулой (1):
Для доказательства формулы (6), представим разность углов в виде суммы и воспользуемся тем, что косинус четная функция а синус нечетная функция:
Формулы тангенса суммы и разности углов имееют следующий вид:
Докажем формулу (7):
Разделим числитель и знаменатель дроби в правой части уравнения (9) на 


Для доказательства формулы (9) представим разность углов в виде суммы, воспользуемся формулой (8) и учтем, что тангенс нечетная функция:
Формулы котангенса суммы и разности углов имееют следующий вид:
Докажем формулу (10):
Разделим числитель и знаменатель дроби в правой части уравнения (12) на 


Для доказательства формулы (11), представим разность углов α и β в виде суммы и учтем, что котангенс нечетная функция:
Умножив числитель и знаменатель в правой части уравнения (13) на −1, получим формулу (11).
Примеры использования формул суммы и разности углов тригонометрических функций
Пример 1. Найти точное значение 
Решение:
Ответ:
Пример 2. Найти косинус для угла 15°.
Решение:
Ответ:
Пример 3. Найти точное значение тангенса для угла 15° .
Решение:
Тангенсы для углов 45° и 15° известны. Подставим эти значения в (14):
Дробь в правой части уравнения (15) можно упростить, умножив числитель и знаменатель дроби на 
Ответ:
Синус, косинус, тангенс суммы и разности с примерами решения
Известные значения синуса, косинуса, тангенса углов можно использовать для вычисления значений синуса, косинуса, тангенса других углов.
Угол
Выведем формулу 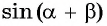
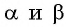
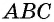
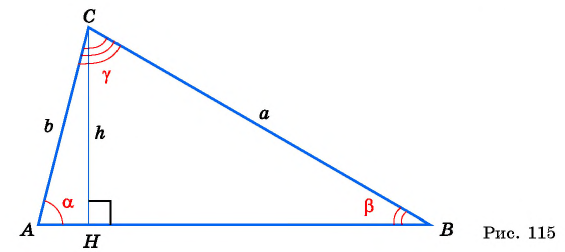
Выразим площадь треугольника 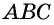
Треугольник 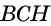
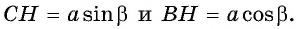
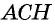
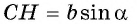
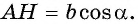
Приравняем правые части равенств (1) и (2):
Разделим обе части равенства на 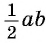
Если углы 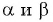
Например, если 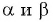
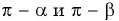
Применим к ним выведенную для острых углов формулу синуса суммы:
Воспользуемся формулами приведения в левой части равенства (3) и получим:
Применим формулы приведения к правой части равенства (3):
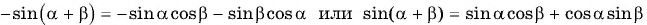
Остальные случаи принадлежности углов различным четвертям рассматриваются аналогично предыдущему.
Синус суммы
Воспользуемся полученной формулой
Выведем формулу синуса разности двух углов.
Для этого 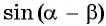
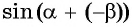
Получили формулу синуса разности двух углов:
Синус разности
Вычислим, например,
Для вывода формулы косинуса суммы двух углов воспользуемся формулами приведения и получим:
Тогда по формуле синуса разности двух углов имеем:
Получили формулу косинуса суммы двух углов:
Косинус суммы
Применим полученную формулу и вычислим, например,
Представив разность 
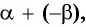
Косинус разности
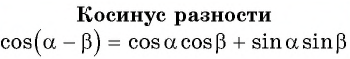
Пример №1
Решение:
Применим полученные формулы «справа налево»: 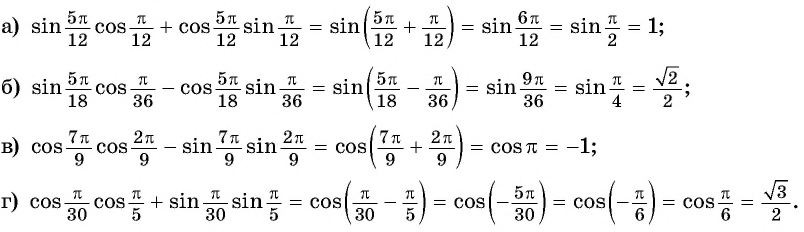
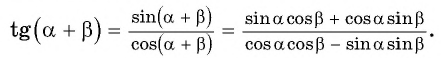
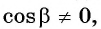
Таким образом, получили формулу тангенса суммы двух углов:
Воспользуемся формулой тангенса суммы и вычислим, например,
Тангенс суммы
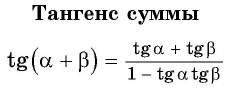
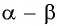
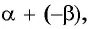
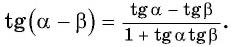
Тангенс разности
Пример №2
Решение:
Применим формулы тангенса суммы и тангенса разности «справа налево»:
Полученные формулы синуса суммы, синуса разности, косинуса суммы, косинуса разности, тангенса суммы, тангенса разности двух углов называют формулами сложения.
Примеры заданий и их решения
Пример №3
С помощью формул сложения преобразуйте выражение:
Решение:
а) По формуле синуса разности получим:
б) Применим формулу тангенса суммы:
Пример №4
Найдите значение выражения:
Решение:
а) По формуле синуса суммы получим:
б) По формулам приведения получим, что
Тогда 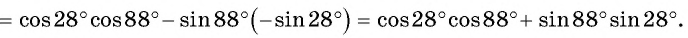
в) По формулам приведения
Тогда
По формуле тангенса разности:
Пример №5
Решение:
б) По формулам приведения:
По формуле тангенса разности получим:
Таким образом,
Пример №6
Решение:
а) Воспользуемся нечетностью синуса и формулой косинуса разности:
б) Применим формулу косинуса разности и получим:
Пример №7
Решите уравнение
Решение:
Запишем уравнение в виде 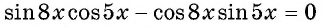
Ответ:
Пример №8
Вычислите 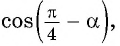
Решение:
Применим формулу косинуса разности:
Из основного тригонометрического тождества выразим 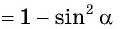
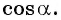
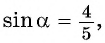
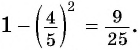
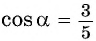
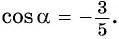
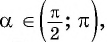
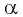
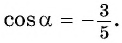
Пример №9
Докажите тождество
Решение:
Воспользуемся формулами сложения и получим:
Пример №10
Найдите значение выражения:
Решение:
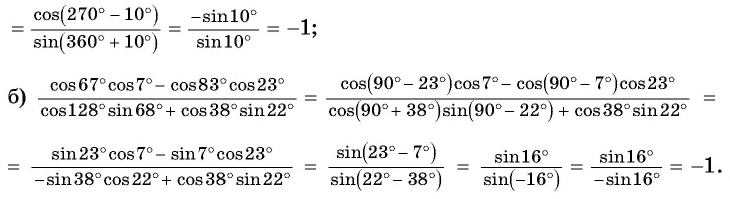
Пример №11
Найдите множество значений функции
Решение:
Применим формулу синуса разности и запишем функцию в виде
Так как 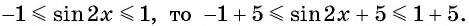
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Как найти разность углов
Разделы 
Дополнительно
Пример 1. На рис. изображены два угла с общей начальной стороной $bar $ и общей конечной стороной $bar $: один равен $+270^$, другой $-90^$.
Сумма двух углов. На координатной плоскости $Oxу$ рассмотрим окружность единичного радиуса с центром в начале координат (рис.). Пусть произвольный угол $alpha$ (на чертеже положительный) получен в результате вращения некоторото подвижного радиуса-вектора от его начального положения $bar$, совпадающего с положительным направлением оси $Ox$, до его конечного положения $bar$. Примем теперь положение радиуса-вектора $bar$ за начальное и отложим от него произвольный угол $beta$ (на чертеже положительный), который получим в результате вращения некоторого подвижного радиуса-вектора от его начального положения $bar$ до его конечного положения $bar$. В результате этих действий мы получим угол, который будем называть суммой углов $alpha$ и $beta$. (Начальное положение подвижного радиуса-вектора $bar$, конечное положение радиуса-вектора $bar $.)
Разность двух углов.
Под разностью двух углов $alpha$ и $beta$, которую обозначим $alpha — beta$, мы будем понимать такой третий угол $gamma$, который в сумме с углом $beta$ дает угол $alpha$, т. е. $gamma = alpha — beta$, если $beta + gamma = alpha$. Разность двух углов $alpha$ и $beta$ можно трактовать как сумму углов $alpha$ и $- beta$. В самом деле, $[alpha + (- beta)] + beta = alpha$ (рис.). Вообще, для любых углов их сумма измеряется алгебраической суммой действительных чисел, измеряющих эти углы.
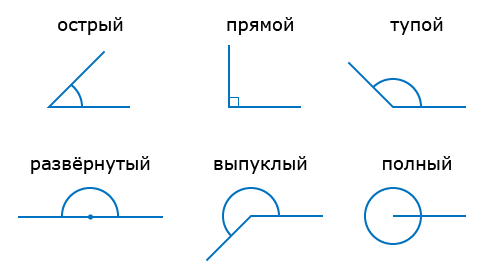
Виды углов
Каждый угол, в зависимости от его величины, имеет своё название:
- Острый угол — это угол, который меньше прямого угла (<90°).
- Прямой угол — это угол, стороны которого перпендикулярны друг другу. Прямой угол обозначается буквой d и равен 90°.
Если два смежных угла равны между собой, то каждый из них называется прямым углом. Прямой угол обычно обозначается не дугой, а уголком:
∠AOC и ∠COB — прямые углы. Общая сторона прямых углов OC называется перпендикуляром к прямой AB, а точка O — основанием перпендикуляра.
Развёрнутый угол равен сумме двух прямых углов или, короче, двум прямым углам. Следовательно, развёрнутый угол равен 180° или 2d.
Все развёрнутые углы равны между собой.
180° < выпуклый угол < 360°.
Полный угол равен сумме четырёх прямых углов, то есть 4d (360°).
Прилежащие углы
Прилежащие углы — это пара углов, имеющих общую вершину и общую сторону, другие стороны которых лежат по разные стороны от общей стороны.
∠AOB и ∠BOC — прилежащие углы, O — общая вершина, OB — общая сторона.
Если из вершины любого угла провести луч, разделяющий угол на два угла, то образованные углы будут прилежащими.
Угол, разделённый лучом, будет называться суммой полученных углов, например угол AOB является суммой углов AOC и COB:
∠AOB = ∠AOC + ∠COB.
Каждый из прилежащих углов, ∠AOC и ∠COB, называется разностью углов AOB и другого прилежащего, то есть: