Как найти разность двух отрезков

Сумма и разность отрезков

• Сумма
• Разность

Сумма

Суммой нескольких отрезков называют отрезок, составленный из длин данных отрезков.

Рассмотри два отрезка  AB  и  CD:

Для нахождения их суммы можно расположить данные отрезки друг за другом на одной прямой, длина полученного отрезка и будет являться суммой данных отрезков:

Полученный отрезок, длина которого равна  12 см,  и будет являться суммой данных отрезков, то есть:

AB + CD = 5 см + 7 см = 12 см.

Из данного примера можно сделать вывод, что для нахождения суммы отрезков надо сложить их длины.

Разность

Разностью двух отрезков называют отрезок, длина которого равна разности от вычитания длины меньшего отрезка из длины большего.

Рассмотри два отрезка  AB  и  CD:

Для нахождения их разности можно взять больший отрезок, а затем от его начальной точки отложить длину меньшего отрезка. Длина отрезка, который лежит между конечными точками двух данных отрезков и будет их разностью:

Полученный отрезок, длина которого равна  7 см,  и будет являться разностью данных отрезков, то есть:

CD — AB = 12 см — 5 см = 7 см.

Из данного примера можно сделать вывод, что для нахождения разности двух отрезков надо вычесть из длины большего отрезка длину меньшего.

Математика, 2 класс

Урок №2. Сумма и разность отрезков

Перечень вопросов, рассматриваемых в теме:

1. Что такое сумма и разность отрезков?
2. Как строить отрезок – сумму двух отрезков и отрезок-разность?

Глоссарий по теме:

Сумма – результат сложения двух или нескольких чисел.

Разность – результат вычитания.

Отрезок – это часть прямой, у которой есть начало и конец.

Основная и дополнительная литература по теме урока:

1. Волкова А. Д. Математика. Рабочая тетрадь. 2 кл. 1 часть: учебное пособие для общеобразовательных организаций. М.: Просвещение, 2017. — с.3.

2. Моро М. И., Бантова М. А., Бельтюкова Г. В.и др. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1.– 8-е изд. – М.: Просвещение, 2017. – с.6, 27.

3. Волкова А. Д. Математика. Тетрадь учебных достижений. 2 кл.: учебное пособие для общеобразовательных организаций. М.: Просвещение, 2017. – с. 19.

Теоретический материал для самостоятельного изучения

Отрезок – это часть прямой, у которой есть начало и конец.

 Длина отрезка — это расстояние между его начальной и конечной точками.

Начало и конец отрезка обозначают заглавными буквами латинского алфавита. Например: АС (а-цэ)

Начертим два отрезка длиной 6 см и 3 см.

Обозначим их точками.

Научимся складывать отрезки. Сделаем это двумя способами.

Первый способ: начертим эти отрезки так, чтобы конец первого отрезка был началом другого:

Теперь с помощью линейки измерим длину большого отрезка-сумму. Получим 9 см.

Обозначим эту длину на чертеже.

Второй способ: с помощью линейки измеряем длину каждого отрезка. Длина первого отрезка 6 см. Длина второго — 3 см.

Найдем сумму этих отрезков.

6см+3см=9см

Научимся вычитать отрезки. Сделаем это двумя способами.

Первый способ: на большем по длине отрезке отложим меньший по длине отрезок.

Теперь с помощью линейки измерим длину другого маленького отрезка разности большего и меньшего отрезков. Получим 3 см. Обозначим эту длину на чертеже.

Второй способ:

С помощью линейки измерим длину каждого отрезка. Длина первого отрезка 6 см, длина второго отрезка 3 см. Найдем разность этих длин.

6см — 3см = 3см

Выводы: Как складываются и вычитаются длины отрезков? Как обыкновенные числа.

Чтобы найти сумму длин двух отрезков, нужно сложить длины этих отрезков.

Чтобы найти разность длин двух отрезков, нужно из длины большего отрезка вычесть длину меньшего отрезка.

Тренировочные задания.

1.Вычислите сумму или разность отрезков и запишите ответ:

Правильные ответы:

10см — 7см = 3см 2см + 4см = 6см

2. Какие отрезки видите на чертеже, запишите их имена:

Правильные ответы:

АБ, БВ, АВ.

— Буду делать та-а-к, потом вот та-ак, а потом вот так.

— Привет, Плюс! Я хотел пригласить тебя погулять. Но, как
видно, ты опять чем-то занят.

— О, минус! Привет! Да вот получил очередное задание от
царицы Математики — научиться складывать отрезки, то есть находить сумму
отрезков.

— Ой, вот здорово! Мне она тоже дала похожее задание, только
находить не сумму, а разность отрезков. Давай разберемся вместе, а потом
пойдем гулять.

— Хорошо. Вместе — веселее. Ну, вот посмотри. Надо нарисовать
отрезок. Ставлю точку, кладу линейку, и от точки провожу прямую линию.

Получился луч, то есть прямая, у которой есть начало —
наша точка, но нет конца.

— Стоп-стоп, Плюс. Как это нет конца. Ты же остановился и
перестал ее рисовать.

— Да, остановился. Но, её можно тянуть бесконечно, но не
будем. Нам хватит и того, что нарисовали.

— А что дальше?

— Дальше я могу отложить на этом луче отрезок двумя
способами. Например, мне нужен отрезок длиной 6 сантиметров. Я могу приложить
линейку к лучу так, чтобы отметка ноль на линейке совпала с точкой, которую мы
поставили. Это обязательно! А сама линейка должна лежать точно под
прямой, близко-близко. И напротив нужной отметки, на прямой, ставим еще одну
точку.

Расстояние между двумя точками и будет отрезком длиной
6 сантиметров. А теперь от этой второй точки я построю еще один отрезок длиной,
например, 5 сантиметров.

— А почему от второй точки? Почему не от первой?

— Потому что, если надо найти сумму отрезков, конец первого
отрезка как раз и будет началом второго отрезка. Не перебивай меня, пожалуйста.
Итак, я продолжаю.

Опять прикладываю линейку к прямой, но теперь так, чтобы
отметка ноль оказалась строго напротив второй точки. А там, где на линейке
стоит пятерка, на прямой ставлю еще одну точку.

Вот появился и еще один отрезок. Если сложить их вместе,
получится третий, более длинный отрезок. А теперь найдем сумму первых двух
отрезков, то есть длину полученного третьего отрезка. Получаем:

— Так это и есть нахождение суммы двух отрезков?

— Да. Чтобы найти сумму двух отрезков, надо к длине
первого отрезка прибавить длину второго отрезка.

— А ты что-то там говорил про второй способ построения
отрезков.

— Да, можно построить отрезки и с помощью циркуля. Главное,
чтобы циркуль был хороший, не разболтанный.

— Что значит, циркуль разболтанный?

— Это когда ножки циркуля плохо закреплены и легко сдвигаются
и раздвигаются. Измерения таким циркулем будут неточные.

Ну так вот. Допустим, нам надо нарисовать отрезки длиной 8 и 4
сантиметра. Начинаем точно так же, как и в первый раз. Ставим точку. От точки
под линейку проводим луч.

А теперь возьмем циркуль, установим его ножки так, чтобы
иголочка циркуля встала на линейке на отметку ноль, а грифель на отметку 8

Теперь переносим циркуль на прямую так, чтобы иголочка встала
на точку начала луча, а грифель сделает на луче еще одну точку. Вот и получится
отрезок, длина которого 8 сантиметров.

Опять ставим циркуль на линейку, устанавливаем ножки так,
чтобы иголочка стояла на нулевой отметке, а грифель на отметке 4. Переносим
циркуль на луч, но теперь его иголочка стоит на второй точке, а грифель ставит новую
точку на прямой.

Получился отрезок длиной 4 сантиметра

— А теперь будешь находить сумму двух отрезков?

— Да. Складываю длины первого и второго отрезков. Получаем:

В результате сложения двух маленьких отрезков получился
третий, больший, длина которого равна сумме длин двух меньших
отрезков.

— Ну, Плюсик, ты своё задание закончил?

— Да. Теперь давай разбираться с твоим заданием. Тебе надо
найти разность двух отрезков?

— Да, разность двух отрезков… Как же мне это задание выполнить?
А, кажется, я догадался!

Я возьму два отрезка, которые ты складывал. Первый длиной 6
сантиметров, а второй — 5 сантиметров. Построю на луче отрезок в 6 сантиметров,
а потом из той же точки начала луча построю второй отрезок длиной 5 сантиметров.

А вот видна разница между длинами отрезков. Эта разница и
будет разностью длин отрезков. А найдем мы ее так:

— А теперь найди разность второй пары отрезков.

— Легко! Опять отмеряю от начала луча 8 сантиметров, потом от
той же точки начала луча отмеряю 4 сантиметра. И вот она, разность двух
отрезков.

— Ух ты! Классно! Ты так быстро справился с заданием!

— Это потому, что рядом был ты, мой друг.

— Действительно, вместе любое дело легче делать. Недаром
говорят: «Совместная работа, как песня весёлая». А ты заметил, что когда я
находил сумму двух отрезков, то первый отрезок начинал строить от начала
луча, а второй — от конца первого отрезка. И при этом выполнял действие сложение.

— Конечно, заметил. А когда я находил разность двух
отрезов, то оба отрезка строил от начала луча. И выполнял вычитание.

Ну, гулять теперь можно идти?

— Конечно можно. Сделал дело — гуляй смело!

— Ура! Гулять!

Сумма и разность отрезков

Сумма

Суммой нескольких отрезков называют отрезок, составленный из длин данных отрезков.

Рассмотри два отрезка AB и CD:

Для нахождения их суммы можно расположить данные отрезки друг за другом на одной прямой, длина полученного отрезка и будет являться суммой данных отрезков:

Полученный отрезок, длина которого равна 12 см, и будет являться суммой данных отрезков, то есть:

AB + CD = 5 см + 7 см = 12 см.

Из данного примера можно сделать вывод, что для нахождения суммы отрезков надо сложить их длины.

Разность

Разностью двух отрезков называют отрезок, длина которого равна разности от вычитания длины меньшего отрезка из длины большего.

Рассмотри два отрезка AB и CD:

Для нахождения их разности можно взять больший отрезок, а затем от его начальной точки отложить длину меньшего отрезка. Длина отрезка, который лежит между конечными точками двух данных отрезков и будет их разностью:

Полученный отрезок, длина которого равна 7 см, и будет являться разностью данных отрезков, то есть:

CD — AB = 12 см — 5 см = 7 см.

Из данного примера можно сделать вывод, что для нахождения разности двух отрезков надо вычесть из длины большего отрезка длину меньшего.

Источник

Сравнение отрезков. Действия над отрезками.

Равные и неравные отрезки

Пусть нам даны два отрезка АВ и СD (рис.). Наложим отрезок АВ на отрезок CD так, чтобы точка А совпала с точкой С, и отрезок АВ направим по отрезку CD. Если точка В совпадаете точкой D, то отрезки АВ и CD равны; АВ = CD.

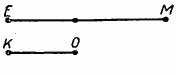
Сравним два отрезка КО и ЕМ (рис.).

Наложим отрезок КО на отрезок ЕМ так, чтобы точки К и Е совпали. Отрезок КО направим по отрезку ЕМ. Если точка О окажется где-нибудь между точками Е и М, то говорят, что отрезок ЕМ больше отрезка КО; отрезок КО меньше отрезка ЕМ.

Записывается это тaк: ЕМ > КО, КО 1 /₅ часть отрезка МN.

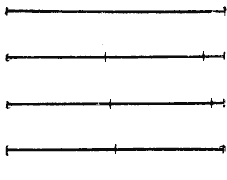
в) Чтобы разделить отрезок на равные части с помощью циркуля, поступают таким образом. Например, если нужно разделить отрезок на две равные части, то циркуль раздвигают на глаз так, чтобы раствор циркуля составлял примерно половину отрезка. Затем на данном отрезке от его конца последовательно один за другим откладывают этим раствором циркуля два отрезка. Если полученная сумма отрезков будет меньше данного отрезка, тo раствор циркуля увеличивают; если сумма окажется больше данного отрезка, то раствор циркуля уменьшают. Так, постепенно исправляя ошибку, можно отыскать довольно точнo половину отрезка (рис.).

Таким же образом выполняется приближённое деление отрезка на 3, 4, 5 и т. д. равных частей. Только в этом случае надо брать на глаз 1 /₃; 1 /₄; 1 /₅ . отрезка и откладывать взятый отрезок 3, 4, 5. раз, смотря по тому, на сколько равных частей надо разделить данный отрезок.

Свойство отрезков, отсекаемых параллельными прямыми на сторонах угла

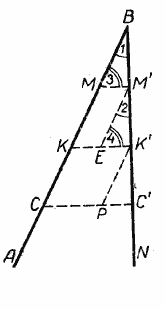
Пусть на стороне АВ угла АВN отложены равные отрезки ВМ = МК = КС (рис.) и через точки деления М, К и С проведены параллельные прямые, пересекающие сторону ВN того же угла.

На этой стороне образовались три отрезка: ВМ’, М’К’ и К’С’. Требуется доказать, что ВМ’ = М’К’ = К’С’.

Для доказательства через точки М’ и К’ проведём прямые, параллельные АВ. Мы получим треугольники ВММ’, М’ЕК’ и К’РС’. Сравним эти треугольники.

Сначала сравним треугольники МВМ’ и М’ЕК’. В этих треугольниках имеем:

∠1 = ∠2, как соответственные углы при параллельных ВА и М’Е и секущей ВN;

∠3 = ∠4, как острые углы 1 с соответственно параллельными сторонами (АВ || М’Е и ММ’ || КК’).

ВМ = МК по построению;

МК = М’Е, как противоположные стороны параллелограмма.

Углы 1-й и 4-й могут оказаться оба тупыми, но и в этом случае они останутся равными, а потому доказательство теоремы не изменится.

Следовательно, ВМ = М’Е. Таким образом, ΔВММ’ = ΔМ’ЕК’ (по стороне и двум прилежащим к ней углам). Отсюда следует, что ВМ’ = М’К’.

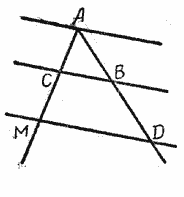
Так же можно доказать, что ВМ’ = К’С’, т. е. ВМ’ = М’К’ = К’С’. При доказательстве теоремы мы откладывание отрезков начали от вершины угла, но теорема справедлива и для того случая, когда откладывание отрезков будет начато не от вершины угла, а от любой точки его стороны.

В этом случае вершину угла на чертеже можно не отмечать (рис.).

Теорема справедлива и для случая, когда прямые КО и МР параллельны.

Пропорциональные отрезки

Из арифметики известно, что равенство двух отношений называется пропорцией. Например: 16 /₄ = 20 /₅; 2 /₃ = 4 /₆ To же самое имеем и в геометрии: если даны две пары отрезков, отношения которых равны, то можно составить пропорцию.

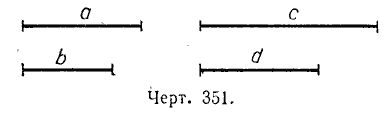
отрезки а, b, c, d называются пропорциональными.

Отношение a /_b называется, как и в арифметике, первым отношением, c /_d — вторым отношением; а и d называются крайними членами пропорции, b и с — средними членами.

В пропорции можно поменять местами отношения; можно переставить крайние члены, средние члены; можно переставить те и другие одновременно.

Поскольку в пропорции a /_b = c /_d под буквами подразумевают числа, выражающие длины отрезков, то произведение крайних членов её равно произведению средних членов. Отсюда, зная три члена пропорции, можно найти неизвестный четвёртый её член. Так, в пропорции a /_x = c /_d x = a • d /_c

Отметим ещё некоторые свойства пропорций, которыми придётся в дальнейшем пользоваться при доказательстве некоторых теорем и при решении задач.

а) Если три члена одной пропорции соответственно равны трём членам другой пропорции, то равны и четвёртые члены этих пропорций.

б) Если в пропорции равны предыдущие члены, то равны и последующие, т. е. если a /_x = a /_y , то х = у.

Чтобы убедиться в этом, переставим средние члены в этой пропорции.

А это возможно лишь в том случае, когда числитель и знаменатель дроби равны, т. е.

в) Если в пропорции равны последующие члены, то равны и предыдущие, т. е. если x /_a = y /_a , то х = у.

В справедливости этого свойства предлагается вам убедиться самостоятельно. Для этого проведите рассуждение, аналогичное предыдущему.

Построение пропорциональных отрезков

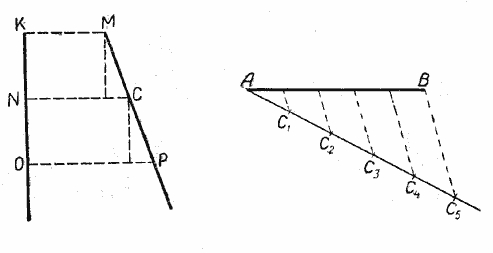
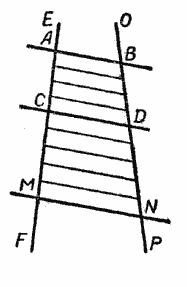
Пусть две прямые ЕF и ОР пересечены тремя параллельными прямыми АВ, СD и МN (рис.).

Требуется доказать, что отрезки АС, СМ, ВD и DN, заключённые между параллельными секущими, пропорциональны, т. е.

Пусть длина отрезка АС равна р, а длина отрезка СМ равна q.

Например, р = 4 см. и q = 5 см.

Разделим АС и СМ на отрезки, равные 1 см, и из точек деления проведём прямые, параллельные прямым АВ, СD и МN, как это показано на рисунке.

Тогда на прямой ОР отложатся равные между собой отрезки, при этом на отрезке BD их будет 4, а на отрезке DN — 5.

Отношение АС к СМ равно 4 /₅ , точно так же и отношение ВD к DN равно 4 /₅.

Значит, отрезки АС, СМ, ВD и DN пропорциональны. Пропорциональны также и отрезки АС, АМ, ВD и ВN (налегающие друг на друга), т. е. AC /_AM = BD /_BN,

Теорема будет справедлива и при любых других целых значениях р и q.

Если длины отрезков АС и СМ не выразятся в целых числах при данной единице измерения (например, сантиметре), то надо взять такую более мелкую единицу (например, миллиметр или микрон), при которой длины отрезков АС и СМ практически выразятся в целых числах.

Доказанная теорема справедлива и в том случае, когда одна из параллельных секущих проходит через точку пересечения данных прямых. Она справедлива также и в том случае, когда отрезки откладываются не непосредственно один за другим, а через некоторый промежуток.

Источник

2 класс — Математика 6. Сумма и разность длин отрезков

6. Сумма и разность длин отрезков

Прозвенел звонок и смолк –
Начинается урок.

Мы за парты тихо сели

И на доску посмотрели

2.Этап подготовки учащихся к активному сознательному усвоению знаний

Сегодня на уроке мы будем учиться складывать и вычитать длины отрезков. И узнаем что такое “сумма отрезков” и “разность отрезков”

Задание 1

Вставьте нужный знак

1см… 10мм 1cм =10мм

1дм …10см 1дм =10см

100cм… 1м 100см=1м

23мм … 32см 23мм 4дм

3м7дм …40дм 3м7дм 20мм 2см–это 20мм, значит 2см9мм>20мм

Задание 2

Назовите фигуры, изображенные на экране точка, отрезок, ломаная, треугольник, квадрат, четырёхугольник.

Что такое отрезок?

Отрезок – это часть прямой, у которой есть начало и конец.

Как обозначают начало и конец отрезка?

Начало и конец отрезка обозначают заглавными буквами латинского алфавита.

3.Этап усвоения новых знаний

Вспомните, при каком действии мы находим сумму?

Сумму находим сложением.

Какой знак при этом ставим?

Сложение обозначает знак (+)

При каком действии мы находим разность?

Разность находим при вычитании.

Какой знак при этом ставим?

Вычитание обозначает знак(-)

Начертите два отрезка длиной 3 см и 6 см.

Как найти сумму этих отрезков?

Измерить длину первого отрезка при помощи циркуля.

Отложить длину первого отрезка на луче, обозначив его начало и конец.

Измерить при помощи циркуля второй отрезок.

Отложить длину второго отрезка на луче от конца отрезка, полученный отрезок является суммой.

Запомните, конец одного отрезка является началом другого; суммой отрезков является отрезок.

Чтобы найти сумму длин двух отрезков, нужно сложить длины этих отрезков.

6 см + 3 см = 9 см

Как найти разность этих же отрезков?

Чтобы найти разность отрезков, необходимо:

Измерить длину первого отрезка при помощи циркуля

Отложить длину первого отрезка на луче, выделить его “дугой”.

Измерить длину второго отрезка при помощи циркуля.

Отложить длину второго отрезка на луче, выделить его “дугой” другого цвета.

Измерить длину оставшейся части отрезка – это будет разностью отрезков.

Запомните, что при вычитании отрезков оба отрезка нужно построить на луче от его начала.

Чтобы найти разность длин двух отрезков, нужно из длины большего отрезка вычесть длину меньшего отрезка.

6 см — 3 см = 3 см

4.Этап закрепления новых знаний

Задание 1

Сколько отрезков на этом рисунке?

Найдите длину самого большого отрезка. 4см+3см=7см

Задание 2

Начертите отрезок 9см. Отметьте на нём точку так, чтобы получился отрезок длиной 2см. Узнайте длину второго отрезка. 9cм-2cм=7cм

Задание 3

Начертите путь божьей коровки: вверх 2см, вправо 5см вниз 2 см, влево 5 см.

Какая фигура получилась?

Правильно, получился четырёхугольник. Как найти, сколько сантиметров проползла божья коровка?

Надо сложить длины всех сторон.

Задание

Нарисуйте такую же фигуру произвольных размеров. Узнайте, на сколько меньшая сторона в четырёхугольнике короче большей. Используйте при этом циркуль.

5.Этап подведения итогов

Что нового вы узнали о сумме и разности?

Мы узнали, что бывает сумма и разность длин отрезков.

Чем выражена разность отрезков?

Она выражена отрезком.

Чем выражена сумма отрезков?

Она выражена отрезком.

Чем отличается построение отрезков на луче при их сложении от построения отрезков при их вычитании?

При сложении конец первого отрезка является началом второго отрезка, а при вычитании – оба отрезка имеют общее начало.

Источник

Математика. 2 класс

Сумма и разность отрезков

Сумма и разность отрезков

Необходимо запомнить

Длины отрезков складываются и вычитаются, как обыкновенные числа.

Чтобы найти сумму длин двух отрезков, нужно сложить длины этих отрезков.

Чтобы найти разность длин двух отрезков, нужно из длины большего отрезка вычесть длину меньшего отрезка.

Интересные факты

Люди давно приметили, что число семь – непростое число, даже, можно сказать, волшебное. Прислушайтесь: именно семь дней творения мира, семь дней в неделе, семь, а не восемь, цветов радуги, семь нот на нотном стане.

В народных и авторских сказках очень часто встречается число семь. Например, в сказках «Волк и семеро козлят», «Сказка о мёртвой царевне и семи богатырях», «Белоснежка и семь гномов», «Храбрый портняжка», «Цветик – семицветик». В устном народном творчестве ни с одним числом нет столько пословиц и поговорок. Приведём примеры: «Семеро одного не ждут», «Семь раз отмерь, один отрежь», «У семи нянек дитя без глаза (без присмотра)», «Семь пядей во лбу» (талантливый), «Семь пятниц на неделе» (о человеке, который часто меняет свои решения), «До седьмого пота» (работать до утомления).

НАШИ ПАРТНЁРЫ

© Государственная образовательная платформа «Российская электронная школа»

Источник

Что значит разность длин

6. Сумма и разность длин отрезков

1. Организационный этап

Прозвенел звонок и смолк –
Начинается урок.
Мы за парты тихо сели
И на доску посмотрели

2. Этап подготовки учащихся к активному сознательному усвоению знаний

1. Целеполагание

Сегодня на уроке мы будем учиться складывать и вычитать длины отрезков. И узнаем что такое “сумма отрезков” и “разность отрезков”

2. Устный счёт

Задание 1

Вставьте нужный знак

1 см… 10 мм 1 cм =10 мм

1 дм …10 см 1 дм =10 см

100 cм… 1 м 100 см=1 м

23 мм … 32 см 23 мм 4 дм

3 м 7 дм …40 дм 3 м 7 дм 20мм 2 см – это 20 мм, значит 2 см 9 мм>20 мм

Задание 2

Назовите фигуры, изображенные на экране (точка, отрезок, ломаная, треугольник, квадрат, четырёхугольник)

Что такое отрезок?

Отрезок – это часть прямой, у которой есть начало и конец.

Как обозначают начало и конец отрезка?

Начало и конец отрезка обозначают заглавными буквами латинского алфавита.

3. Этап усвоения новых знаний

Вспомните, при каком действии мы находим сумму?

Сумму находим сложением.

Какой знак при этом ставим?

Сложение обозначает знак (+)

При каком действии мы находим разность?

Разность находим при вычитании.

Какой знак при этом ставим?

Вычитание обозначает знак (-)

Начертите два отрезка длиной 3 см и 6 см.

Как найти сумму этих отрезков?

Измерить длину первого отрезка при помощи циркуля.

Отложить длину первого отрезка на луче, обозначив его начало и конец.

Измерить при помощи циркуля второй отрезок.

Отложить длину второго отрезка на луче от конца отрезка, полученный отрезок является суммой.

Запомните, конец одного отрезка является началом другого; суммой отрезков является отрезок.

Чтобы найти сумму длин двух отрезков, нужно сложить длины этих отрезков.

Как найти разность этих же отрезков?

Чтобы найти разность отрезков, необходимо:

Измерить длину первого отрезка при помощи циркуля

Отложить длину первого отрезка на луче, выделить его “дугой”.

Измерить длину второго отрезка при помощи циркуля.

Отложить длину второго отрезка на луче, выделить его “дугой” другого цвета.

Измерить длину оставшейся части отрезка – это будет разностью отрезков.

Запомните, что при вычитании отрезков оба отрезка нужно построить на луче от его начала.

Чтобы найти разность длин двух отрезков, нужно из длины большего отрезка вычесть длину меньшего отрезка.

4. Этап закрепления новых знаний

Задание 1

Сколько отрезков на этом рисунке?

Найдите длину самого большого отрезка. 4 см+3 см=7 см

Задание 2

Начертите отрезок 9 см. Отметьте на нём точку так, чтобы получился отрезок длиной 2 см. Узнайте длину второго отрезка. 9 cм-2 cм=7 cм

Задание 3

Начертите путь божьей коровки: вверх 2 см, вправо 5 см. вниз 2 см, влево 5 см.

Какая фигура получилась?

Правильно, получился четырёхугольник. Как найти, сколько сантиметров проползла божья коровка?

Надо сложить длины всех сторон.

2 см+5 см+2 м+5 см=14 см

Логические задания

Задание

Нарисуйте такую же фигуру произвольных размеров. Узнайте, на сколько меньшая сторона в четырёхугольнике короче большей. Используйте при этом циркуль.

5. Этап подведения итогов

Что нового вы узнали о сумме и разности?

Мы узнали, что бывает сумма и разность длин отрезков.

Чем выражена разность отрезков?

Она выражена отрезком.

Чем выражена сумма отрезков?

Она выражена отрезком.

Чем отличается построение отрезков на луче при их сложении от построения отрезков при их вычитании?

При сложении конец первого отрезка является началом второго отрезка, а при вычитании – оба отрезка имеют общее начало.

Рефлексия

сегодня я узнал

Спасибо за урок!

Остались вопросы по теме? Наши репетиторы готовы помочь!

Подготовиться к ЕГЭ, ОГЭ и другим экзаменам

Подготовиться к поступлению в любой ВУЗ страны

Источник