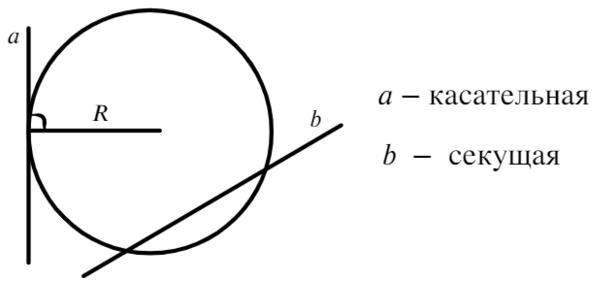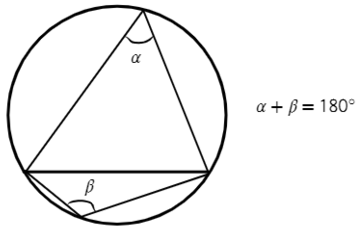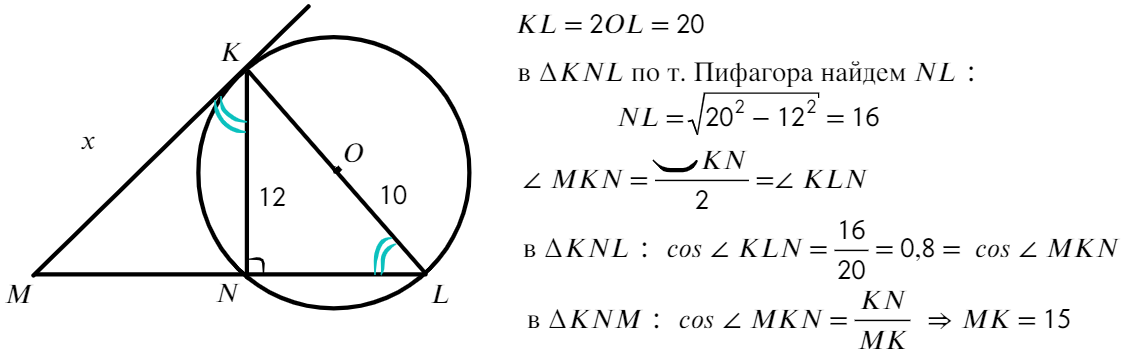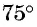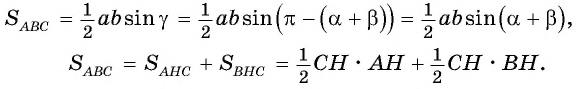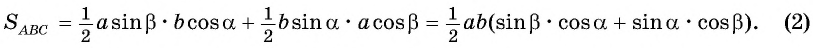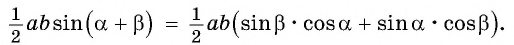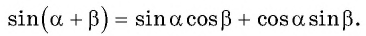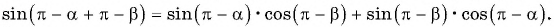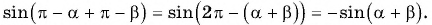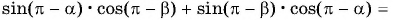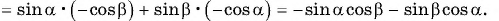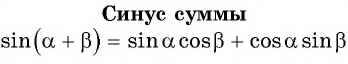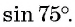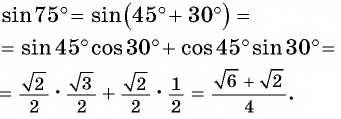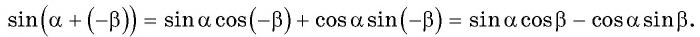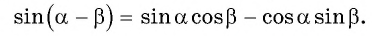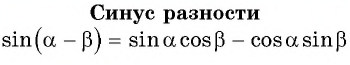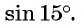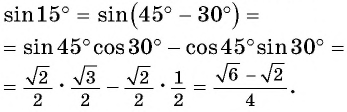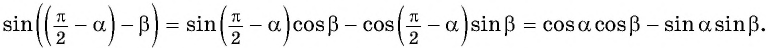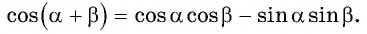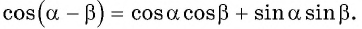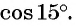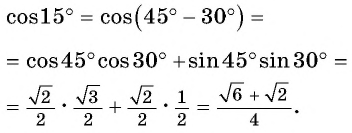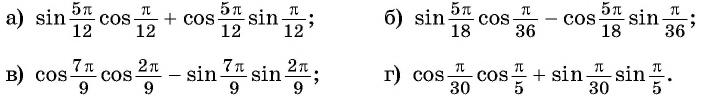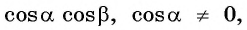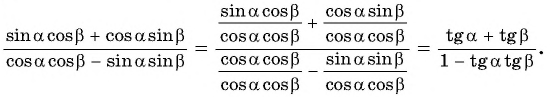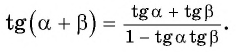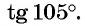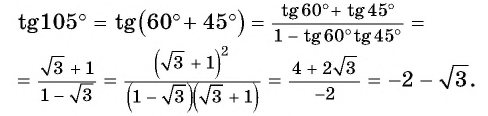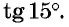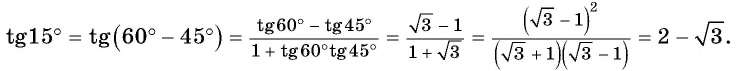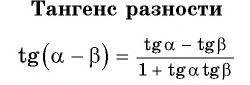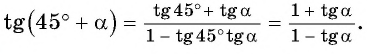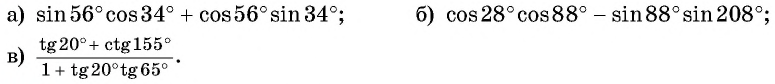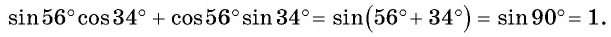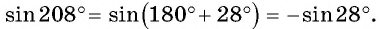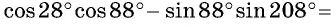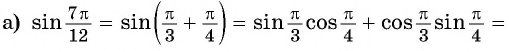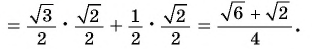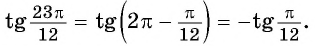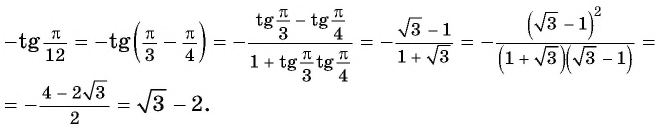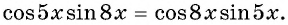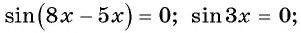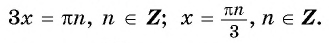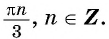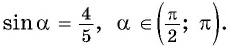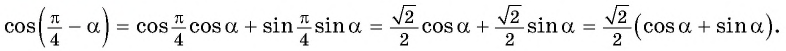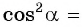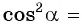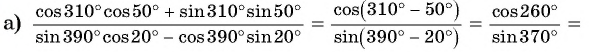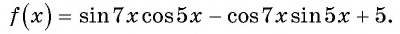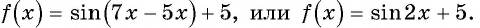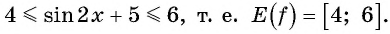I. Механика
Тестирование онлайн
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.
Угловая скорость
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.
Период и частота
Период вращения T — это время, за которое тело совершает один оборот.
Частота вращение — это количество оборотов за одну секунду.
Частота и период взаимосвязаны соотношением
Связь с угловой скоростью
Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T. Путь, который преодолевает точка — это есть длина окружности.
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.
Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
Вращение Земли
Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.
Связь со вторым законом Ньютона
Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.
Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой
Как вывести формулу центростремительного ускорения
Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна vA и vB соответственно. Ускорение — изменение скорости за единицу времени. Найдем разницу векторов.
Разница векторов есть . Так как , получим
Движение по циклоиде*
В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.
Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.
Мгновенная скорость определяется по формуле
Как найти радиус окружности
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Основные понятия
Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.
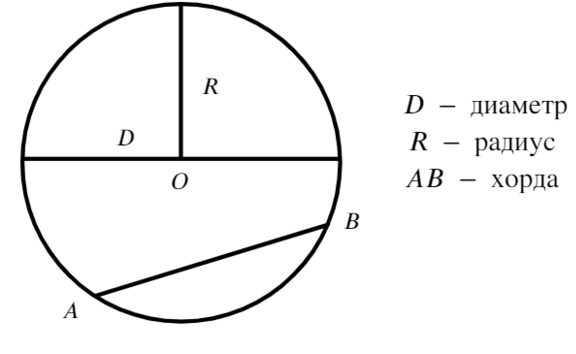
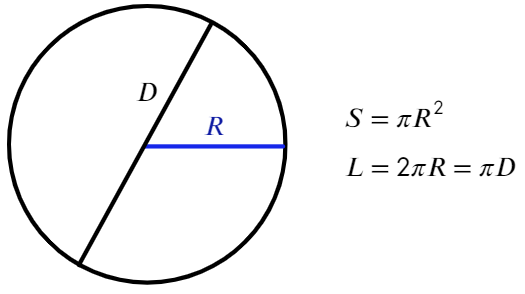
Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.
Возможно тебе интересно узнать — как найти длину окружности?
Формула радиуса окружности
Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.
Если известна площадь круга
R = √ S : π, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.
Если известна длина
R = P : 2 * π, где P — длина (периметр круга).
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).
Если известен диаметр окружности
R = D : 2, где D — диаметр.
Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.
Если известна диагональ вписанного прямоугольника
R = d : 2, где d — диагональ.
Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:
d = √ a 2 + b 2 , где a, b — стороны вписанного прямоугольника.
Если известна сторона описанного квадрата
R = a : 2, где a — сторона.
Сторона описанного квадрата равна диаметру окружности.
Если известны стороны и площадь вписанного треугольника
R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.
Если известна площадь и полупериметр описанного треугольника
R = S : p, где S — площадь треугольника, p — полупериметр треугольника.
Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.
Если известна площадь сектора и его центральный угол
R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.
Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.
Если известна сторона вписанного правильного многоугольника
R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.
В правильном многоугольнике все стороны равны.
Скачать онлайн таблицу
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.
Всё про окружность и круг
Окружность — это геометрическое место точек плоскости, равноудаленных от некоторой заданной точки (центра окружности). Расстояние между любой точкой окружности и ее центром называется радиусом окружности (радиус обозначают буквой R).
Значит, окружность — это линия на плоскости, каждая точка которой расположена на одинаковом расстоянии от центра окружности.
Кругом называется часть плоскости, ограниченная окружностью и включающая ее центр.
Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, представляет собой диаметр. Диаметр окружности равен ее удвоенному радиусу: D = 2R.
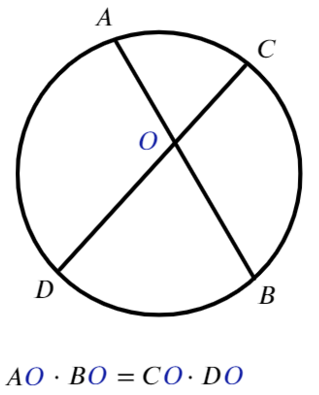
Точка пересечения двух хорд делит каждую хорду на отрезки, произведение которых одинаково: a1a2 = b1b2
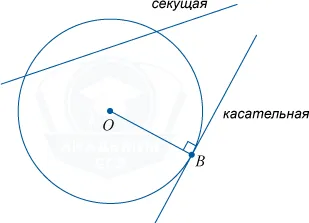
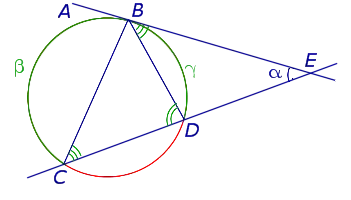
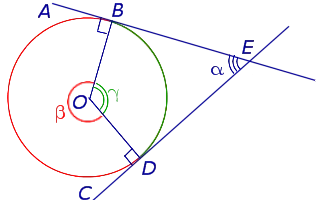
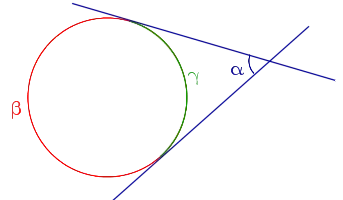
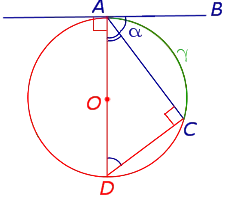
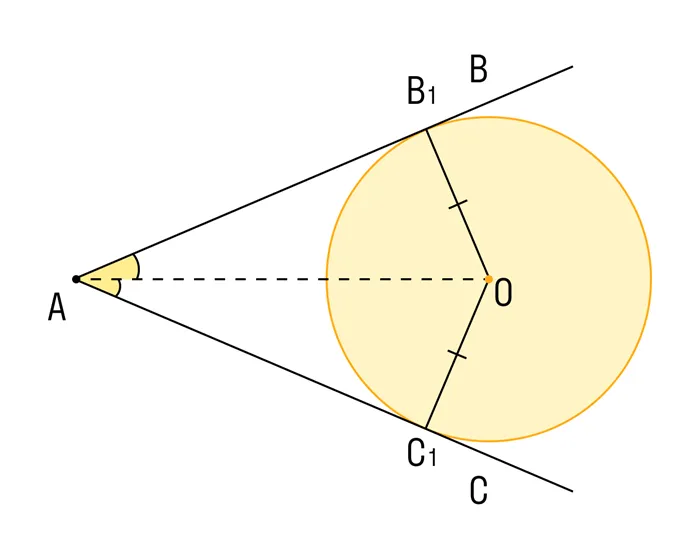
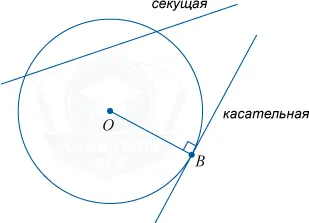
Касательная к окружности всегда перпендикулярна радиусу, проведенному в точку касания.
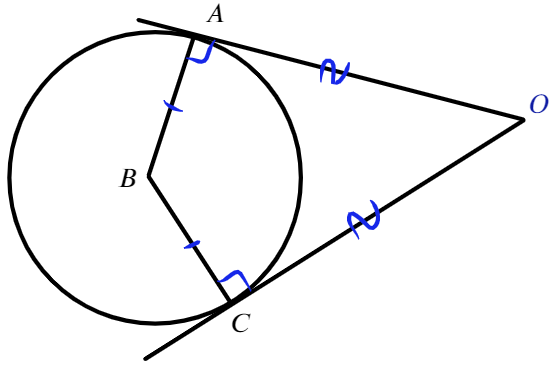
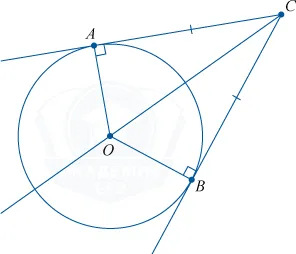
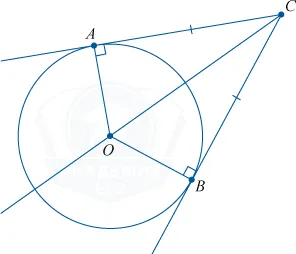
Отрезки касательных к окружности, проведенные из одной точки, равны: AB = AC, центр окружности лежит на биссектрисе угла BAC.
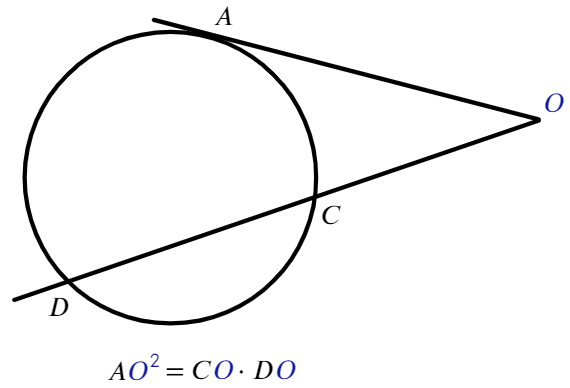
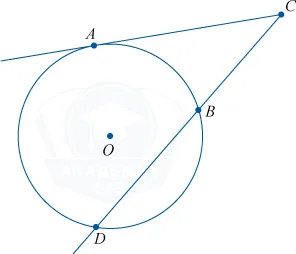
Квадрат касательной равен произведению секущей на ее внешнюю часть
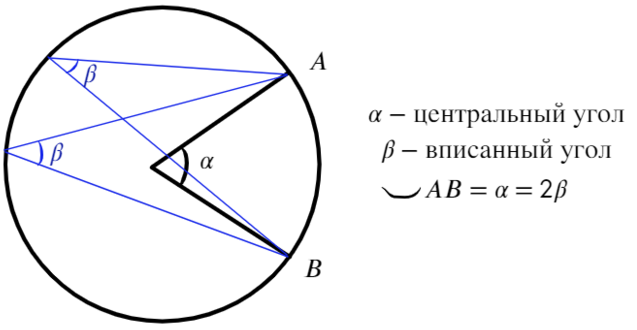
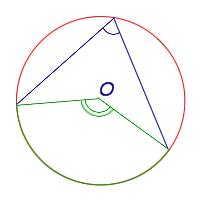
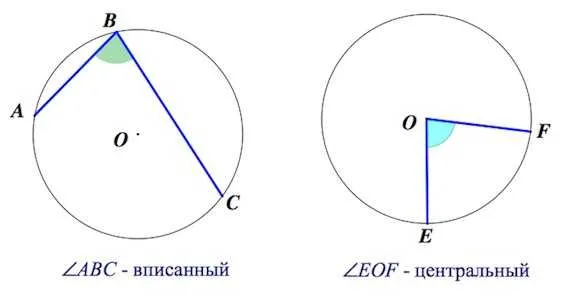
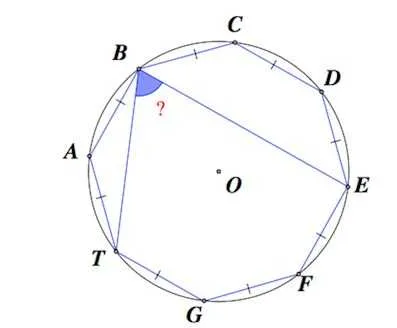
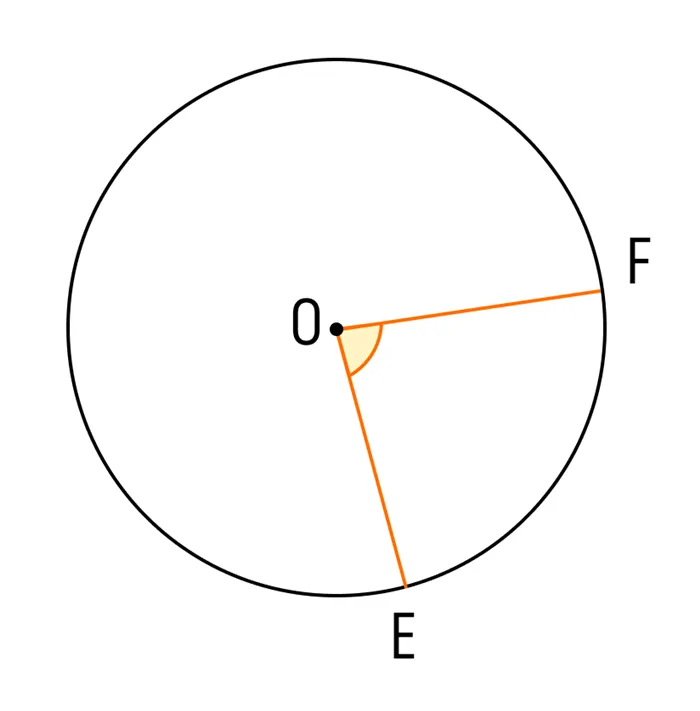
Центральный угол — это угол, вершина которого совпадает с центром окружности.
Дугой называется часть окружности, заключенная между двумя точками.
Мерой дуги (в градусах или радианах) является центральный угол, опирающийся на данную дугу.
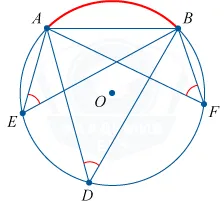
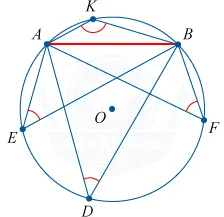
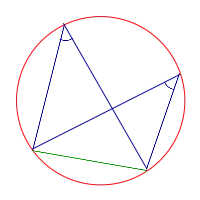
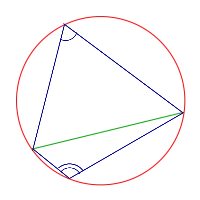
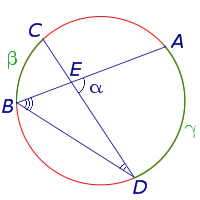
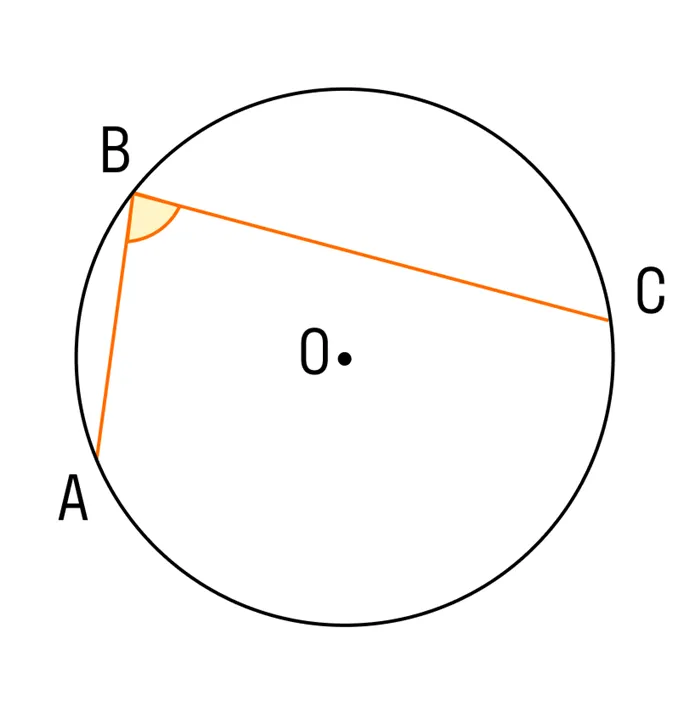
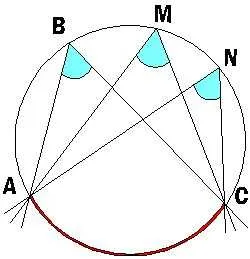
Вписанный угол это угол, вершина которого лежит на окружности, а cтороны угла пересекают ее.
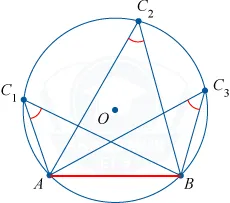
Вписанный угол равен половине центрального, если оба угла опираются на одну и ту же дугу окружности.
Внутренние углы, опирающиеся на одну и ту же дугу, равны.
Сектором круга называется геометрическая фигура, ограниченная двумя радиусами и дугой, на которую опираются данные радиусы.
Периметр сектора: P = s + 2R.
Площадь сектора: S = Rs/2 = ПR 2 а/360°.
Сегментом круга называется геометрическая фигура, ограниченная хордой и стягиваемой ею дугой.
http://skysmart.ru/articles/mathematic/radius-okruzhnosti
http://www.stranamam.ru/post/8974384/
Свойства касательных и секущих.
Свойства хорд.
Углы окружности.
Площадь, сектор, длина окружности.
Задачи на окружности.
По статистике окружности никто не любит, но при этом леденец любим, солнце любим, давай и окружность полюбим!
Окружность − геометрическое место точек плоскости, равноудаленных от одной ее точки (центра). На рисунке центр − точка О.
В окружности может быть проведено 3 типа отрезка:
Отрезок, проходящий через две точки окружности, но не через центр, называют хордой (AB).
Хорда, проходящая через центр окружности, называется диаметром (самая большая хорда в окружности − диаметр (D)).
Радиус − отрезок, соединяющий центр окружности с точкой на окружности. Диаметр в два раза больше радиуса (R).
А также две прямые снаружи от окружности:
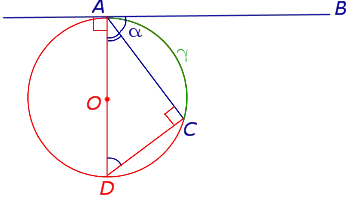
Касательная имеет одну общую точку с окружностью. Сразу стоит сказать о том, что радиус, проведенный в точку касания, будет иметь с касательной угол 90°.
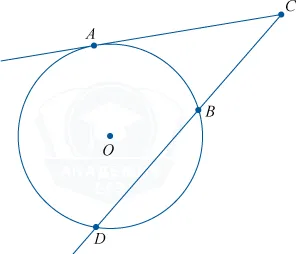
Секущая пересекает окружность в двух точках, внутри окружности получается хорда или, в частном случае, диаметр.
Теперь чуть-чуть об углах и дугах:
Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают ее. Он в два раза меньше дуги, на которую опирается.
Центральный угол — это угол, вершина которого находится в центре окружности, равен дуге на которую опирается.
Вписанные углы, опирающиеся на одну дугу, равны между собой (β=β=α/2) и равны половине дуги, на которую опираются.
Градусная мера дуги – величина в °, соответствует центральному углу. Длина дуги равна α.
А вот такой угол НЕвписанный, такой угол «никто и звать никак».
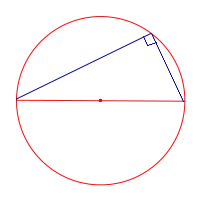
Можно сделать вывод, что вписанный угол, который опирается на половину дуги окружности, будет прямым, а также будет опираться на диаметр:
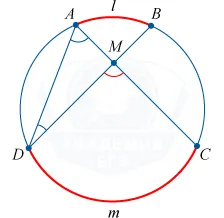
Любая пара углов, опирающихся на одну и ту же хорду, вершина которых находится по разные стороны от хорды, составляет в сумме 180°.
Запишем основные свойства углов в окружности:
Нашел что-то общее?
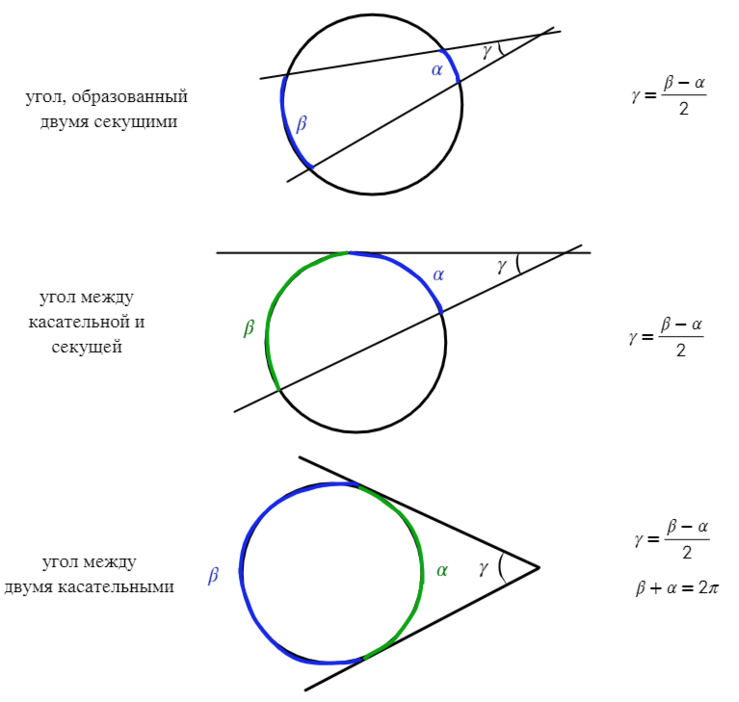
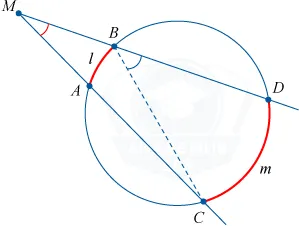
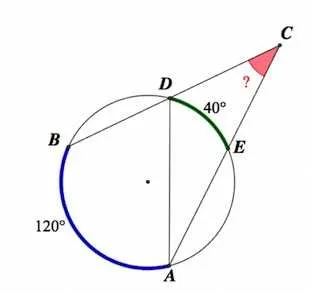
Если угол находится вне окружности, без разницы, чем он получен (касательной или секущей), то найти его можно через половину разности дуг.
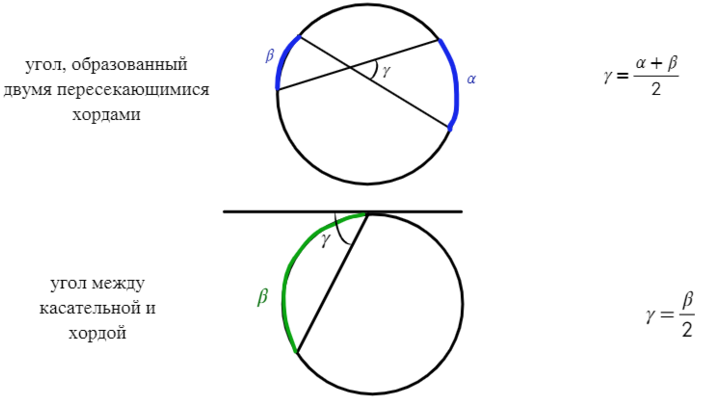
Если угол находится внутри окружности, то находим его через полусумму дуг.
Если есть одна дуга, которая находится на требуемом угле, то угол равен половине этой дуги.
Отношение отрезков:
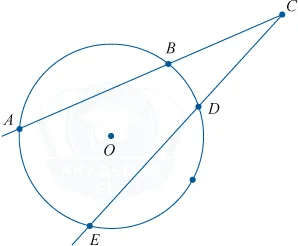
Для любых двух хорд, проходящих через некоторую точку О, выполняет равенство:
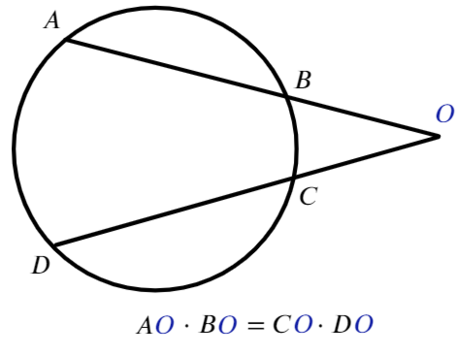
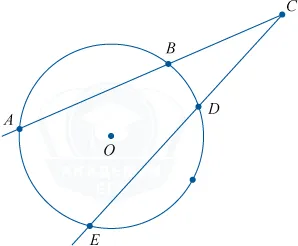
Для любых двух секущих, проходящих через некоторую точку O, выполняется равенство:
Согласен, что они похожи, особенно если не смотреть на картинки.
Как не перепутать такие равенства? В каждом отрезке должна присутствовать точка, вне окружности (О).
Если из точки, лежащей вне окружности, проведены касательная и секущая:
Аналогично в каждом отрезке присутствует точка, вне окружности (О).
Если теперь провести две касательные из точки O, то получим такие равные отрезки:
Касательные равны, как, сообственно, и радиусы!
Площадь и длина окружности находятся по формуле:
По своему определению число π показывает, во сколько раз длина окружности больше диаметра, отсюда такая формула: L = πD
Если хочешь вывести площадь круга, можешь проинтегрировать длину окружности относительно R или вывести зависимость, как сделал Архимед!
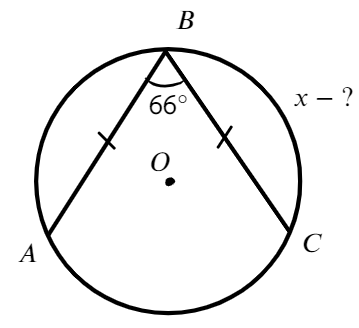
Задача №1. Дано на рисунке:
Достаточно вспомнить свойства центральных и вписанных углов.
Ответ: 39°
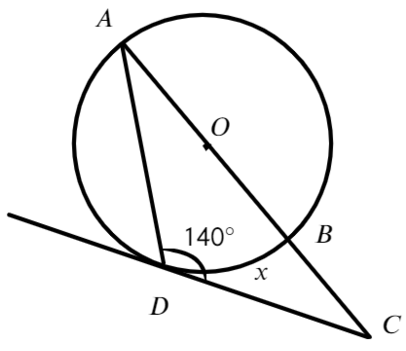
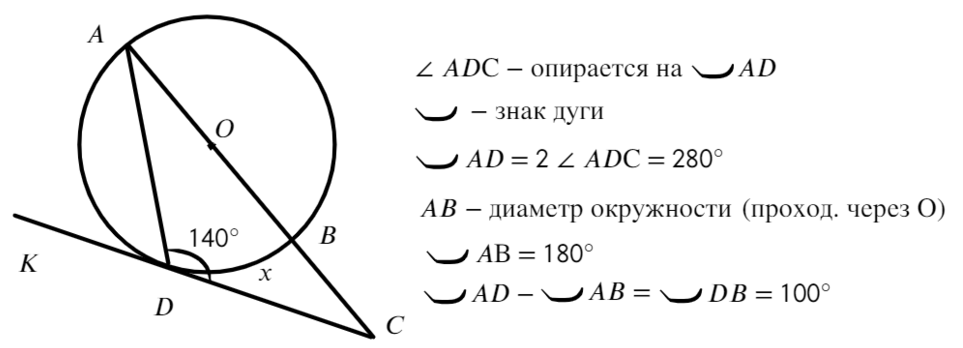
Задача №2. Дано на рисунке:
Найти нужно меньшую дугу BD
Ответ: 100°Задача №3. Дано на рисунке:
Найти меньшую дугу ВС
Ответ: 114°
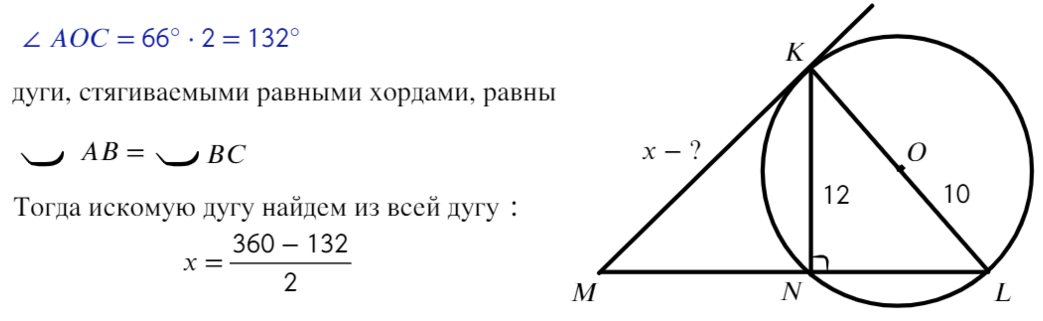
Задача №4. Дано на рисунке:
Найти отрезок МК
Ответ: МК = 15.
Задача №5. Дано на рисунке:
Попробуй найти подобные треугольники
Ответ: 6
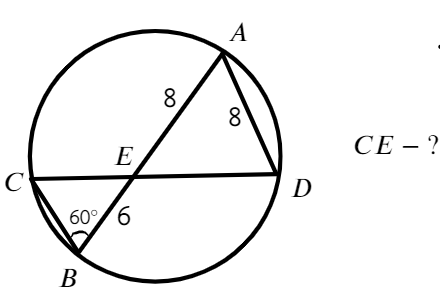
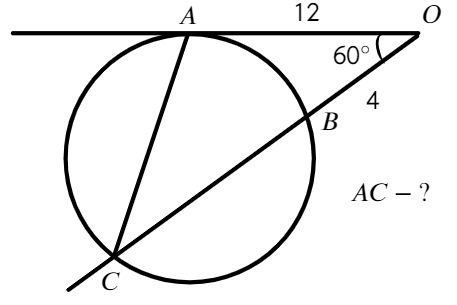
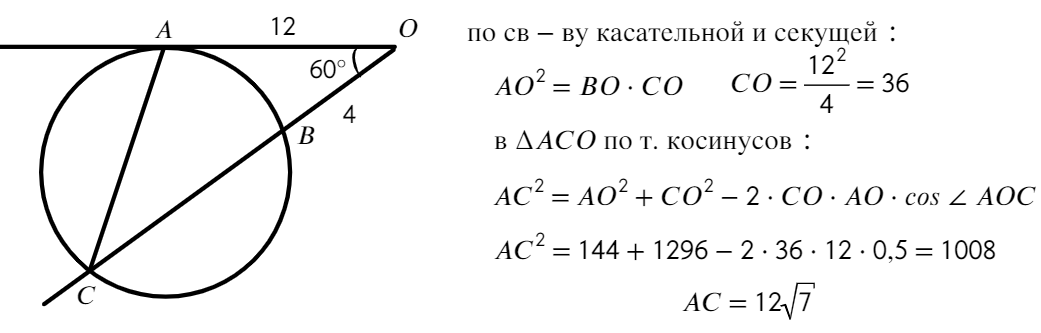
Задача №5. Дано на рисунке:
Без свойства секущей и касательной здесь будет тяжело
Ответ: 12√7.
Я могу долго тебе показывать, как решать задачи, но без твоих усилий ничего не выйдет.
Попробуй эти задачи с подсказками.
О треугольниках
О четырехуголникахp.s. Не бойся ошибаться и задавать вопросы!
Если нашел опечатку, или что-то непонятно − напиши.
Разница между 2 углами
, Надо найти очень быстро
- Подписаться на тему
- Сообщить другу
- Скачать/распечатать тему
|
|
|
|
Full Member Рейтинг (т): 5 |
Всем доброго времени суток Подскажите, существует ли способ быстро (очень быстро) определить превышает ли разница между 2 углами pi/2, или к примеру pi/6 Под разницей я понимаю минимальное расстояние (радианах) между 2 углами на тригонометрической окружности. Углы даны в радианах Заранее спасибо |
|
Yakudza |
|
|
Member Рейтинг (т): 10 |
ИМХО быстрее чем тупо посчитать угол и сравнить не получится. #define PI 3.1415 float distance(float a, float b) // считает разницу между двумя углами { float r1, r2; if (a>b) { r1 = a-b; r2 = b-a+2*PI } else { r1 = b-a; r2=a-b+2*PI; } return (r1>r2) ? r2 : r1; } Недостаточно быстро? Сообщение отредактировано: Yakudza — 30.11.12, 23:08 |
|
Daiver |
|
|
Full Member Рейтинг (т): 5 |
Цитата Yakudza @ 30.11.12, 22:54 ИМХО быстрее чем тупо посчитать угол и сравнить не получится. #define PI 3.1415 float distance(float a, float b) // считает разницу между двумя углами { float r1, r2; if (a>b) { r1 = a-b; r2 = b-a+2*PI } else { r1 = b-a; r2=a-b+2*PI; } return (r1>r2) ? r2 : r1; } Недостаточно быстро? Примерно так и считаю, хотелось бы пошустрее конечно. (речь идет о тысячах таких операций в секунду) |
|
shm |
|
|
Цитата Daiver @ 01.12.12, 02:40 хотелось бы пошустрее конечно Быстрее только таблицу готовую сделать. Можешь заинлайнить еще. Добавлено 01.12.12, 08:11 Цитата Daiver @ 01.12.12, 02:40 речь идет о тысячах таких операций в секунду Несколько тысяч вызовов этой функции отработают на порядок быстрее 1 сек. Сообщение отредактировано: shm — 01.12.12, 08:14 |
|
Daiver |
|
|
Full Member Рейтинг (т): 5 |
shm Насчет таблицы — можно поподробней? Пускай не тысячи, а десятки тысяч, плюс все пишется на питоне Добавлено 01.12.12, 10:00 |
|
shm |
|
|
Цитата Daiver @ 01.12.12, 09:59 Насчет таблицы — можно поподробней? Да все банально: создаешь двухмерный массив n*n, чем больше n, тем больше будет точность, но тем больше потребуется памяти. Пусть столбцы будут первым углом, а стоки вторым. Ну и заполняешь эту матрицу своей функцией. Потом дял получения искомого результата пользуешься уже вычисленным значением. Правда не знаю как это будет выглядеть на питоне. Сообщение отредактировано: shm — 01.12.12, 15:05 |
|
Yakudza |
|
|
Member Рейтинг (т): 10 |
Цитата shm @ 01.12.12, 15:05 Да все банально: создаешь двухмерный массив n*n, чем больше n, тем больше будет точность Я бы создавал одномерный и индексировал его по (a-b). Так и памяти меньше и индексировать проще. С другой стороны будет ли залезть в этот массив быстрее? Еще же углы нужно к индексам привести, проинтерполировать между соседними точками… Исходная функция-то дешевенькая. Хотя если сделать плотный массив, приведеие к индексу свести к приведению типа и брать первый попавшийся элемент без интерполяции, то должно помочь. Хотя, если в некоторых вычислительных пакетах пришли к тому, что интеграл быстрее лишний раз взять численно, чем из памяти его доставать… Если совсем проблема будет с ускорением, то можно на С модуль к питону (плагин? как оно называется) написать и просить эту функцию. Сообщение отредактировано: Yakudza — 02.12.12, 00:02 |
|
Daiver |
|
|
Full Member Рейтинг (т): 5 |
Yakudza Боюсь что сам вызов сишной ф-ии будет слишком дорогой |
|
Yakudza |
|
|
Member Рейтинг (т): 10 |
Если развивать идею с хешем. Если набор углов фиксирован, то ускорения можно добиться тупо массивом bool. bool hash_half_pi[720]; // fill for pi/2 for (int i = 0; i < 90; ++i) hash_half_pi[i] = false; for (int i = 90; i < 270; ++i) hash_half_pi[i] = true; for (int i = 270; i < 450; ++i) hash_half_pi[i] = false; for (int i = 450; i < 630; ++i) hash_half_pi[i] = true; for (int i = 630; i < 720; ++i) hash_half_pi[i] = false; bool is_larger(float a, float b, bool* hash) { return hash[int(a-b)+360]; } Но на границах может врать. |
|
MBo |
|
|
откуда берутся эти углы и какова более общая задача? |
|
Daiver |
|
|
Full Member Рейтинг (т): 5 |
Yakudza Хэш не совсем пойдет, т.к. углы могут быть произвольными MBo Гм, в общем-то да, углы вычисляются через arctan2. Так я ищу угол наклона градиента А задача — реализация SWT-оператора с последующей фильтрацией. Углы сравниваются на этапе отслеживания лучей |
|
MBo |
|
|
Daiver |
|
amk |
|
|
Пожалуй, самый быстрый способ найти угол между двумя углами (лучами) это: da = a1 — a2 # Ищем разность if da < -pi: da += 2*pi # и загоняем её в промежуток +-pi elif da > pi: da -= 2*pi Цитата MBo @ 02.12.12, 13:41 достаточно будет найти отношение векторного и скалярного произведений векторов Не совсем, можно нарваться на ошибку деления на ноль. Так что лучше раскрывать пропорцию. Но действительно, вычислять арктангенс, даже если предполагается сравнивать каждый угол с каждым незачем. Это дольше, чем сравнивать пропорции. |
|
#SI# |
|
|
Цитата Daiver @ 30.11.12, 20:02 Под разницей я понимаю минимальное расстояние (радианах) между 2 углами на тригонометрической окружности Так и флаг в руки Цитата const double TOLERANCE = 0.0001; А уж что на вход дельтаУгол — сам решай. Мне хватает двух точек — точки вставки (база) и точки ориентации (направление). |
0 пользователей читают эту тему (0 гостей и 0 скрытых пользователей)
0 пользователей:
- Предыдущая тема
- Алгоритмы
- Следующая тема
[ Script execution time: 0,0593 ] [ 15 queries used ] [ Generated: 27.05.23, 14:25 GMT ]
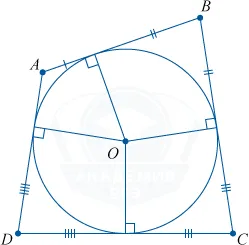
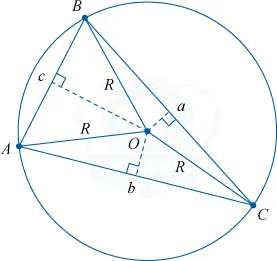
Вокруг любого треугольника можно описать окружность и описать только один цикл. Центр такого цикла находится в точке пересечения средних вертикалей треугольников.
Окружность и круг
Во-первых, поймите разницу между циклом и периметром. Чтобы определить разницу, достаточно рассмотреть, что представляют собой эти два элемента. Это бесконечное количество точек на уровне на равных расстояниях от одной центральной точки. Однако круг состоит из внутренностей, в то время как окружность не состоит из внутренностей. Установлено, что круг является одновременно и окружностью, которая его очерчивает (O-Circus), и бесконечным числом точек круга.
Цикл — это серия точек, расположенных на фиксированном расстоянии от центра, представленного одной точкой.
Для каждой точки L окружности выполняется равенство OL = r. (Длина отрезка OL равна радиусу окружности).
Отрезок, соединяющий две точки окружности, является ее струной.
Нить, проходящая непосредственно через центр круга, является диаметром круга (d). Диаметр можно рассчитать по следующему виду: d = 2R
Окружность круга вычисляется по типу c = 2 pi r
Площадь круга: s = pi r^
Дуга окружности — это часть окружности между двумя ее точками. Эти две точки определяют два лука окружности. Струна CD сжимает два смычка CMD и CLD. Одна и та же струна натягивает один и тот же лук.
Центральный угол — это угол между двумя лучами.
Длина дуги может быть найдена с помощью следующих типов
Диаметр, перпендикулярный струне, разделяет струну и узкую дугу посередине.
Если прямые AB и CD окружности имеют общую точку n, то прямые равны между собой.
Касательная к окружности
Касательная к окружности — это прямая, имеющая общую точку с окружностью.
Если прямой объект имеет две общие точки, он называется квадратичным.
Когда балка проектируется с помощью касательной линии, она перпендикулярна окружности.
Проведите две касательные из этой точки к окружности. Отрезки касательных совпадают друг с другом, а центр окружности находится в дихотомической форме угла при вершине в этой точке.
Теперь постройте касательную и вторичную из нашей точки к окружности. Находим, что квадрат длины касательного сечения равен произведению всего вторичного сечения на его внешнюю часть.
Мы можем заключить, что. Произведение внешней части первой вторичной части равно произведению целой части второй вторичной части на внешнюю часть.
Углы в окружности
Градус центрального угла и дуги, на которой он базируется, равны.
Регистрационный угол — это угол, вершина которого находится на окружности, а сторона содержит строку.
Она равна половине этого лука и поэтому может быть вычислена путем нахождения меры лука.
Угол, основанный на диаметре и угле регистрации, является прямым углом.
угол cbd = угол ced = угол cad = 90^
Углы регистрации, основанные на одном и том же смычке, идентичны.
угол adb = угол ab = угол afb
Регистрационные углы, основанные на одной и той же струне, одинаковы или в сумме равны 180^.
угол adb + угол akb = 180^.
угол adb = угол ab = угол afb
Тот же круг имеет верхнюю часть треугольника с тем же углом и определенным основанием.
Угол между верхней окружностью и двумя струнами равен половине суммы углов окружностей, окружающих данный угол и вертикальный угол.
угол dmc = угол adm + угол dam = frac слева ( чашка dmc + чашка alb справа)
Угол с внешней вершиной окружности между двумя частями равен половине разницы между значениями угла окружности, заключенной внутри угла.
Угол M = Угол CBD — Угол Acb = frac слева (ߋ cup dmc- cup alb справа)
На этой диаграмме изображена пара дуг dž (dž displaystyle ab dž) и два центральных угла. Самый большой лук соответствует самому большому углу, но больше, чем 섹 (섹 displaystyle 180<>^ ⌘ circ ) и наименьшая дуга соответствует меньшему углу.
Теоремы о вписанных и центральных углах
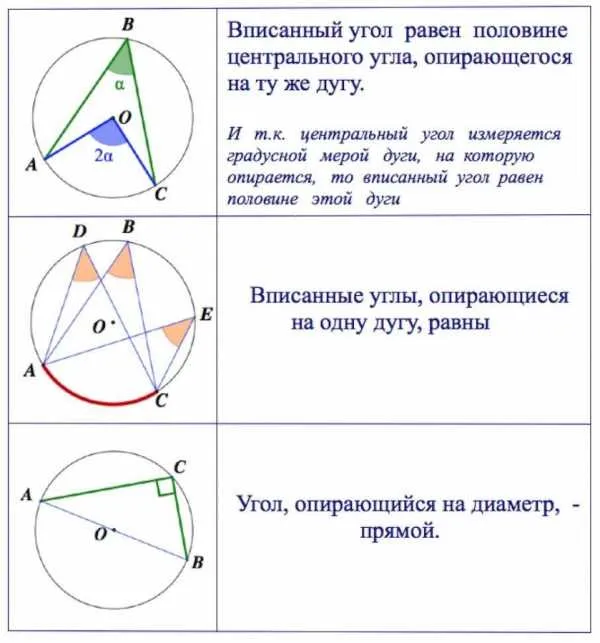
Стоимость зарегистрированного угла равна половине стоимости центрального угла на той же дуге.
Центр под прямоугольного треугольника является центром периметра периметра.
Стоимость зарегистрированного угла равна половине стоимости центрального угла на той же дуге.
Углы регистрации, основанные на одной и той же дуге, равны.
Регистрационные углы, перпендикулярные одной и той же струне, равны, если вершины находятся по одну сторону от этой струны.
Два регистрационных угла, перпендикулярных одной и той же струне, складываются в 180°, если вершины находятся на противоположных сторонах этой струны.
Регистрационные углы перпендикулярны только в том случае, если они лежат на диаметре
Центр под прямоугольного треугольника является центром периметра периметра.
Теоремы об углах, образованных хордами, касательными и секущими
Цена угла, образованного пересекающимися струнами, равна половине суммы арок, заключенных между их сторонами.
Угол, образованный пересекающимися отрезками на внешней стороне диска, равен половине суммы углов дуг, примыкающих к его сторонам.
Угол, образованный касательной и струной, проходящей через точку касания, равен половине цены дуги, заключенной между ее сторонами.
Угол, образованный касательной и вторичным углом, равен половине разности размеров дуги, заключенной между его сторонами.
Угол, образованный двумя касательными к окружности, равен половине разности размеров дуги, заключенной между сторонами.
Цена угла, образованного пересекающимися струнами, равна половине суммы арок, заключенных между их сторонами.
Угол, образованный пересекающимися отрезками на внешней стороне диска, равен половине суммы углов дуг, примыкающих к его сторонам.
Угол, образованный касательной и струной, проходящей через точку касания, равен половине цены дуги, заключенной между ее сторонами.
Угол, образованный касательной и вторичным углом, равен половине разности размеров дуги, заключенной между его сторонами.
Угол, образованный двумя касательными к окружности, равен половине разности размеров дуги, заключенной между сторонами.
Доказательства теорем об углах, связанных с окружностью
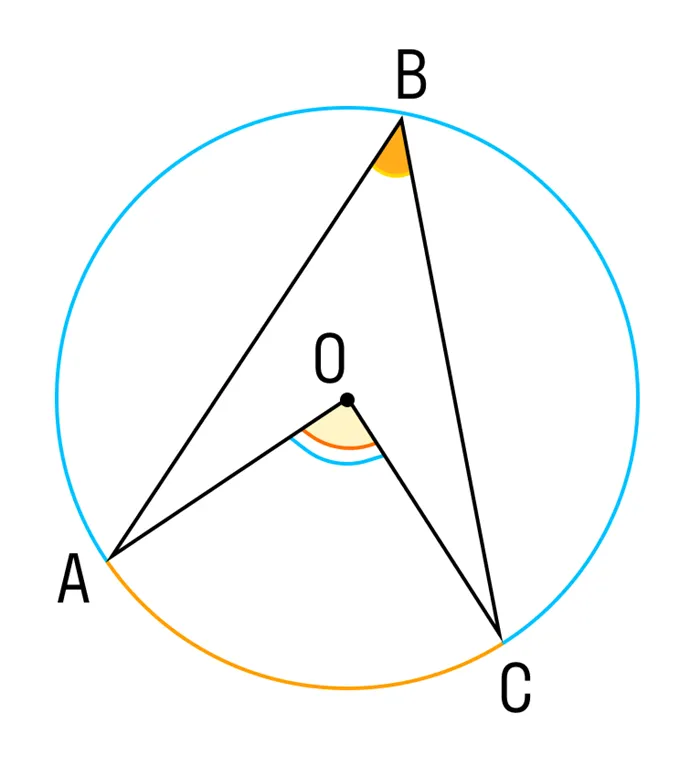
Теорема 1. Размер зарегистрированного угла равен половине размера центрального угла, расположенного на том же луке.
Доказательство Сначала рассмотрим зарегистрированный угол ABC, сторона BC которого является диаметром окружности, а центральный угол AOC (рис. 5).
Таким образом, Теорема 1 доказывается, если одна сторона в клетке проходит через центр цикла.
Теперь рассмотрим случай, когда центр окружности лежит внутри зарегистрированного угла (рис. 6).
Применяется следующее
Теорема 1 доказана.
Еще неизвестно, что центр цикла лежит вне угла регистрации (рис. 7).
Применяется следующее
Доказательство Теоремы 1 завершено.
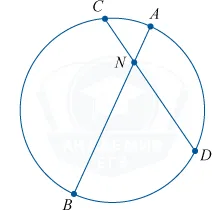
Теорема 2. Цена угла, образованного пересекающимися струнами, равна половине суммы дуг между их сторонами.
Доказательства Рассмотрим рисунок 8.
Нас интересует величина угла AED, образованного нитями AB и CD, пересекающимися в точке E. Поскольку угол AED является внешним углом треугольника BED, а углы CDB и ABD — штампованные углы, следует, что
Доказательство.
Теорема 3. Угол, образованный сторонами пересекающихся сторон вне круга, равен половине разности размеров дуги, заключенной между сторонами угла.
Доказательства. Рассмотрим рисунок 9.
Нас интересует угол BED, образованный пересечением AB и CD в точке E. Поскольку ADC — внешний угол треугольника ADE, а углы ADC, DCB и DAB — углы штампованные, получаем следующее уравнение.
Доказательство.
Теорема 4. Угол, образованный касательной, нитью касания и нитью, проходящей через точку касания, равен половине величины дуги, ограниченной его сторонами.
Доказательства. Рассмотрим рисунок 10.
Нас интересует угол BAC, образованный касательной AB и струной AC. Углы DAB и DCA являются прямыми углами, так как AD — это диаметр, проходящий через точку контакта, а угол ACD — это угол, вырезанный на основе диаметра. Поэтому применяется следующее уравнение
Дуга окружности — это часть окружности между двумя ее точками. Эти две точки определяют два лука окружности. Струна CD сжимает два смычка CMD и CLD. Одна и та же струна натягивает один и тот же лук.
Центральный угол и вписанный угол
Окружность — это замкнутая линия, все точки которой равноудалены от центра.
Установка центрального угла:.
Центральный угол — это угол, при котором вершина лежит в центре окружности. Центральный угол равен углу дуги, на которой он расположен.
Изображение: центральный угол окружности EOF и дуга, на которой находится EF.
Установите угол записи.
Выгравированный угол — это угол, под которым вершина является круговой.
Выгравированный угол равен половине дуги, на которой он расположен.
Угол ABC, выгравированный на окружности, и дуга, на которую наклонена AC
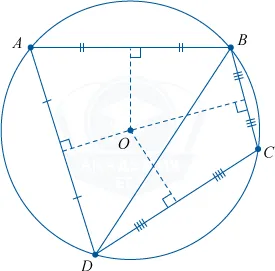
Свойства центральных и вписанных углов
Ракурсы на первый взгляд просты. Свойства центрального угла и гравированного угла помогают быстро и легко решить проблему.
AOC является центром, а ABC зарегистрирован. Поскольку оба угла опираются на AC, центральный угол равен AC, а угол ABC равен половине угла AOC.
ㄥADC=ㄥABC=. AEC, так как все три угла, вписанные в окружность, опираются на одну и ту же дугу AC.
ㄥACB основывается на диаметре и дуге AB — диаметр делит круг на две равные части. Поэтому дуга AB = 180ㄥΕ4D, ㄥCAB равна половине дуги, на которой она расположена, поэтому ㄥCAB =90ㄥΕ4D.
Если есть гравированный угол, то есть и гравированный угол. Выгравированный угол — это угол, образованный двумя касательными к окружности. Такие как:.
На диаграмме: ㄥCAB образована двумя касательными к окружности. AO — биссектриса ㄥCAB, поэтому центр окружности находится на биссектрисе окружающей окружности.
Для решения этих задач недостаточно знать, какие углы являются вписанными, а какие — очерченными. Вам необходимо знать, что такое строка и каковы ее свойства.
Нужно упорядочить свои знания перед экзаменом? Записывайтесь на занятия ЕГЭ по математике в Skysmart!
Струна — это отрезок, соединяющий две точки окружности.
AB * AC = AE*AD Докажите, что стороны угла, вписанного в окружность, — струны.
ㄥBAC=ㄥCAB, потому что он находится на строке BC.
Примеры решения задач
Как и все остальное, центрированные, гравированные и обведенные углы требуют практики для решения. Изучите примеры решения и потренируйтесь самостоятельно.
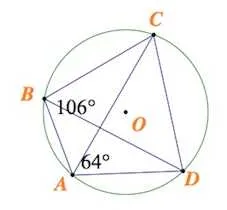
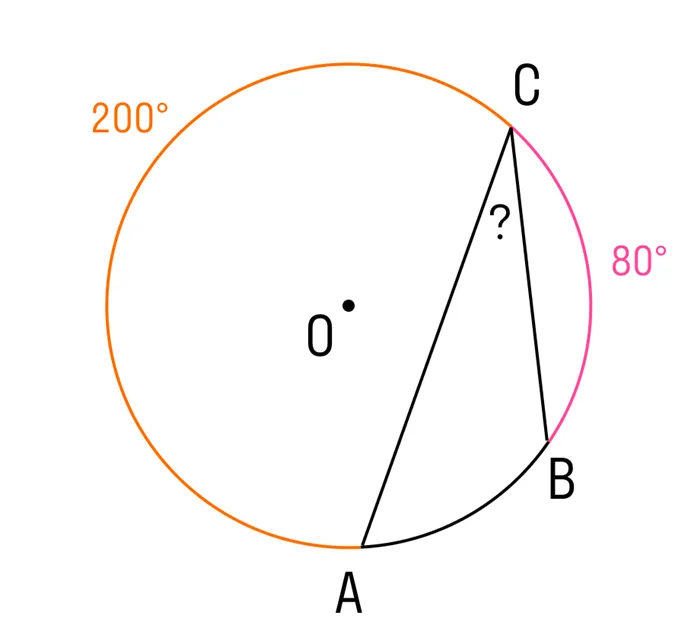
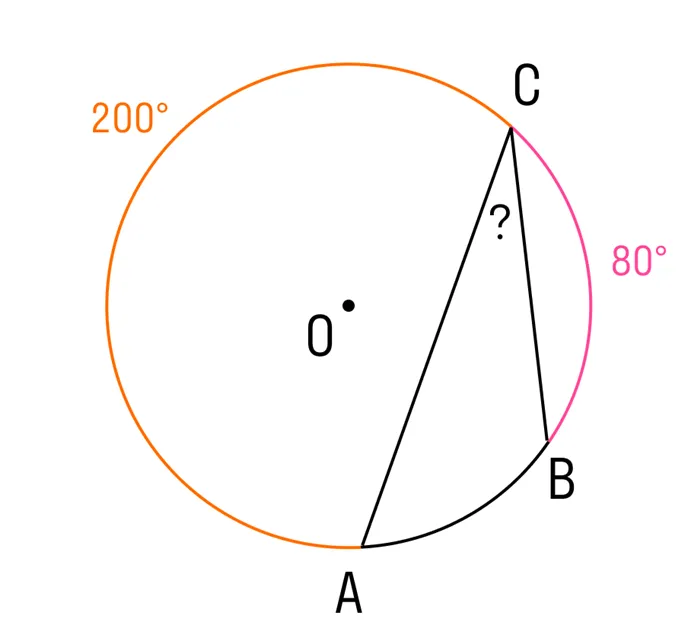
Вопрос 1. Дан цикл, ARC AC = 200°, ARC BC = 80°. Найдите угол, зарегистрированный в дуге AB. ㄥacb =?
Решение: 360°-AC -CB = 360°-200°-80°= 80°Теорема: Зарегистрированный угол равен одной дуге ½. acb =½ab= 40°.
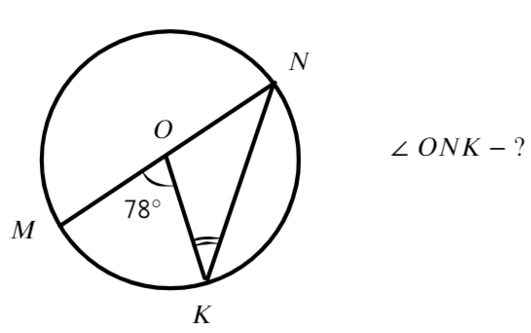
Задача 2. Учитывая цикл, AOC = 140°, найдите значение угла регистрации.
Мы уже практиковались и знаем, как найти записанный угол. На диаграмме окружности мы знаем, что для центрального угла и дуги AC = 140°, угол регистрации равен половине центрального угла.
Вопрос 3: Какой угол записан на окружности на основе лука?
CB = 360° = 72°, так как угол регистрации равен половине носового угла, cb = cb = 72° / 2 = 36° Cab =½.
Теорема 5. Угол, образованный касательной и квадратиком квадрата, равен половине разности дуг между сторонами угла.
Вписанный угол вдвое меньше центрального — доказательство
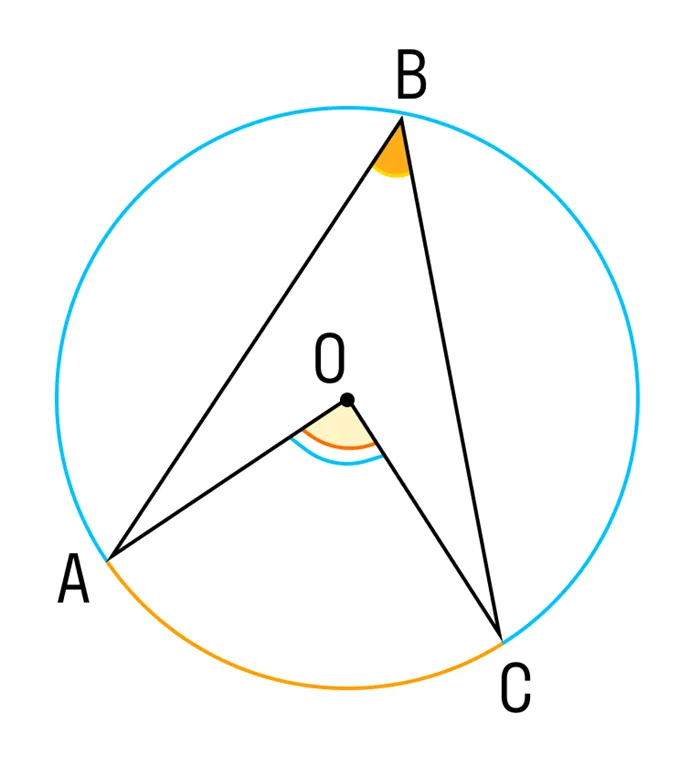
Есть великое событие:
Цена зарегистрированного угла составляет половину цены соответствующего центрального угла.
Посмотрите на рисунок, чтобы увидеть, как выглядит это утверждение. Соответствующим» центральным углом считается такой, у которого край совпадает с краем угла регистрации, а вершина находится в центре.
Соответствующий центральный угол также должен «отображать» тот же код (⌘ displaystyle ac ), что и регистрационный угол.
Почему? Почему зарегистрированные углы составляют половину от центральных углов?
Сначала рассмотрим простой случай.
Случай 1. Хорда проходит через центр окружности
Предположим, что одна из струн проходит через центр. Иногда это случается, не так ли?
Что не так? Согласитесь с (⌘ displaystyle delta aob ). Это потому, что ( displaystyle ao ) и ( displaystyle ob ) являются световыми лучами. поэтому (⌘ displaystyle угол a = угол b ) (мы называем это ⌘ displaystyle альфа ).
Теперь давайте рассмотрим 팀 (팀 displaystyle 팀 angle aoc 팀). Это внешний угол ɑ (ɑ displaystyle delta aob )!
Мы можем заключить, что. Произведение внешней части первой вторичной части равно произведению целой части второй вторичной части на внешнюю часть.
Примеры решения задач
Существуют определенные циклы, в которых дуга символизации AC равна ⌘ (⌘ DisplayStyle 200<>^\\ circ ), bc bow is ( DisplayStyle 80).<>^\\ круг ). Вычислите значение зарегистрированного угла на дуге ab.
Окружности — это ዄ (ዄ displaystyle 360.).<>^ circ ). Для того чтобы найти лук аб, вам нужно.
displaystyle 360.<>^ circ -ac -cb = 360-200-80 = 80 )
Согласно теореме о регистрационном угле, его величина равна половине лука, на который он опирается. Итак.
(ac =½ab= displaystyle 40)<>^ круг )
Ответ: ac Угол IS (⌘ DisplayStyle 40<>^ круг )
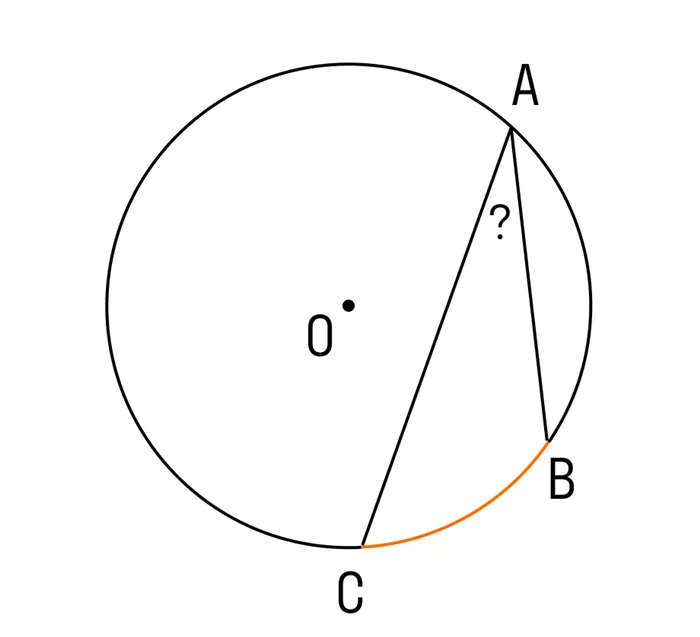
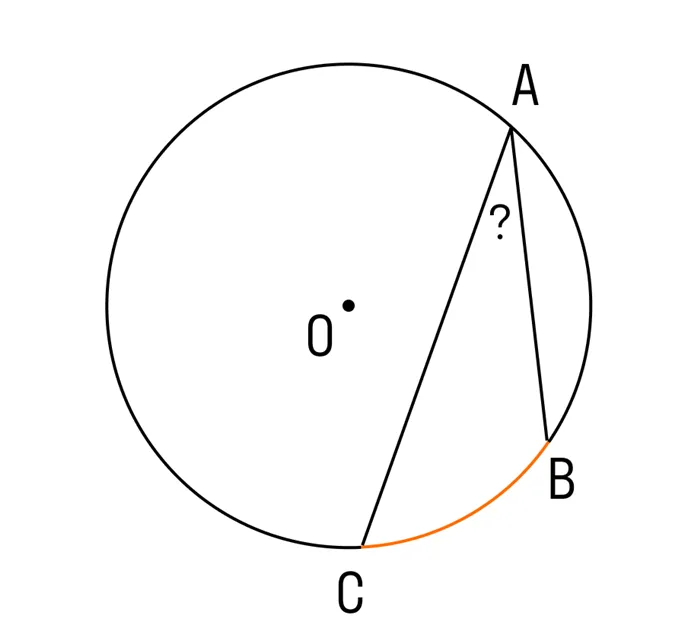
Дана окружность. Угол AC IS ⌘ (⌘ Displaystyle 140.<>^ circ ). Необходимо определить значение угла регистрации.
На этой диаграмме показано, что окружность имеет центральный угол и дугу AC. Это ⌘ (⌘ displaystyle 140).<>^ circ ). Из теоремы к зарегистрированному и центральному углам, зарегистрированный угол равен половине центрального угла. Тип может быть записан:.
(ABC =½AC= 140/2 = DisplayStyle 70)<>^ круг )
ОТВЕТ: угол ABC равен ⌘ (⌘ DisplayStyle 70.<>^ circ ).
Вам необходимо рассчитать значение угла, записанного на носовом круге. Лук составляет 1/5 цикла.
Известно, что окружность ⌘ (⌘ displaystyle 360)<>(^ circ ). Итак.
(cb =⅕ от 360 = displaystyle 72)<>^ круг )
Согласно теореме о зарегистрированном угле, он равен половине лежащей в основе дуги.
Здесь мы имеем еще одно распространенное выражение: «струна сжимает лук». Здесь, например, строка (⌘ displaystyle ab ) ограничивает смычок (⌘ displaystyle ab ).
Касательная к окружности
Касательная к окружности — это прямая, имеющая общую точку с окружностью. Если линия имеет две общие точки, она называется вторичной.
Когда балка проектируется с помощью касательной линии, она перпендикулярна окружности.
Проведите две касательные из этой точки к окружности. Отрезки касательных совпадают друг с другом, а центр окружности находится в дихотомической форме угла при вершине в этой точке.
Теперь постройте касательную и вторичную из нашей точки к окружности. Находим, что квадрат длины касательного сечения равен произведению всего вторичного сечения на его внешнюю часть.
Мы можем заключить, что. Произведение внешней части первой вторичной части равно произведению целой части второй вторичной части на внешнюю часть.
Углы в окружности
Градус центрального угла и дуги, на которой он базируется, равны.
Регистрационный угол — это угол, вершина которого находится на окружности, а сторона содержит строку.
Она равна половине этого лука и поэтому может быть вычислена путем нахождения меры лука.
Угол, основанный на диаметре и угле регистрации, является прямым углом.
Угол cbd = угол ced = угол cad = 90^.
Углы регистрации, основанные на одном и том же смычке, идентичны.
Угол ADB = Угол AEB = Угол AFB
Регистрационные углы, основанные на одной и той же струне, одинаковы или в сумме равны 180^.
Угол ADB + Угол AKB = 180^.
Угол ADB = Угол AEB = Угол AFB
Тот же круг имеет верхнюю часть треугольника с тем же углом и определенным основанием.
Угол между верхней окружностью и двумя струнами равен половине суммы углов окружностей, окружающих данный угол и вертикальный угол.
Угол dmc = угол ADM + угол dam = frac left (чашка DMC + чашка альбита)
Угол с внешней вершиной окружности между двумя частями равен половине разницы между значениями угла окружности, заключенной внутри угла.
Угол M = угол CBD — Угол ACB = FRAC LEFT (CUP DMC -CUP ALBIGHT)
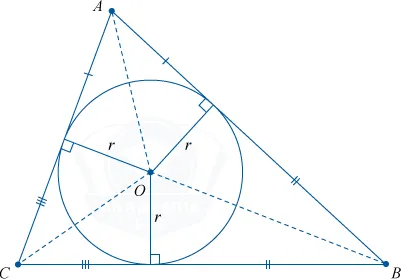
Вписанная окружность
Зарегистрированный цикл — это конкретный круг на стороне многоугольника.
Его центр находится в точке пересечения угловых дихотомий многоугольников.
Не все многоугольники могут быть зарегистрированы как круг.
Площадь многоугольника с циклом регистрации задается типом
p — половина границы многоугольника, и
R — радиус в камере.
Предполагается, что радиусы в ячейках равны.
Сумма противоположных длин такая же, как если бы окружность была зарегистрирована на выпуклом четырехугольнике. И наоборот, если сумма противоположных длин одинакова, то круг регистрируется в выпуклом четырехугольнике.
Можно зарегистрировать круг в любом из треугольников. Только один. В точке, где найден внутренний угол, находится центр в клетке.
Академические радиусы рассчитываются с использованием следующих типов.
Синус, косинус, тангенс суммы и разности с примерами решения
Известные значения синуса, косинуса, тангенса углов можно использовать для вычисления значений синуса, косинуса, тангенса других углов.
Угол
Выведем формулу 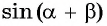
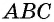
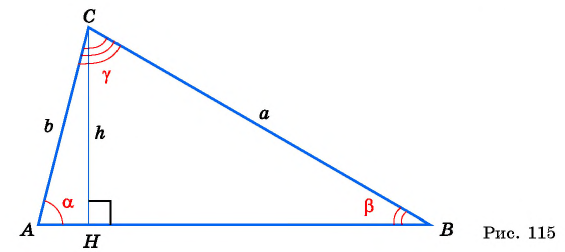
Выразим площадь треугольника 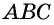
Треугольник 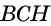
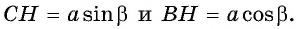
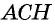
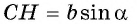
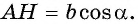
Приравняем правые части равенств (1) и (2):
Разделим обе части равенства на 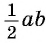
Если углы 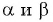
Например, если 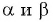
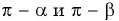
Применим к ним выведенную для острых углов формулу синуса суммы:
Воспользуемся формулами приведения в левой части равенства (3) и получим:
Применим формулы приведения к правой части равенства (3):
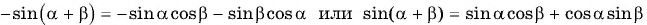
Остальные случаи принадлежности углов различным четвертям рассматриваются аналогично предыдущему.
Синус суммы
Воспользуемся полученной формулой
Выведем формулу синуса разности двух углов.
Для этого 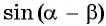
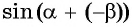
Получили формулу синуса разности двух углов:
Синус разности
Вычислим, например,
Для вывода формулы косинуса суммы двух углов воспользуемся формулами приведения и получим:
Тогда по формуле синуса разности двух углов имеем:
Получили формулу косинуса суммы двух углов:
Косинус суммы
Применим полученную формулу и вычислим, например,
Представив разность 
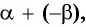
Косинус разности
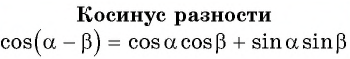
Пример №1
Решение:
Применим полученные формулы «справа налево»: 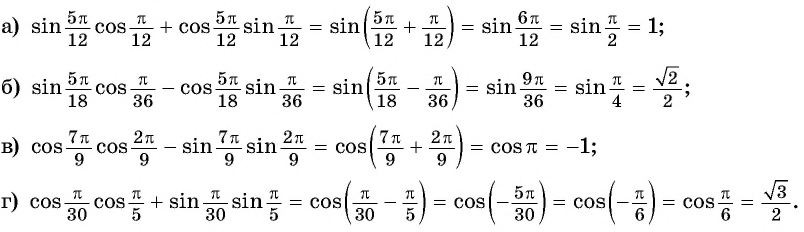
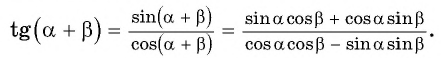
Таким образом, получили формулу тангенса суммы двух углов:
Воспользуемся формулой тангенса суммы и вычислим, например,
Тангенс суммы
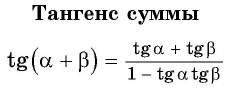
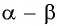
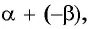
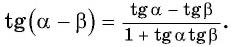
Тангенс разности
Пример №2
Решение:
Применим формулы тангенса суммы и тангенса разности «справа налево»:
Полученные формулы синуса суммы, синуса разности, косинуса суммы, косинуса разности, тангенса суммы, тангенса разности двух углов называют формулами сложения.
Примеры заданий и их решения
Пример №3
С помощью формул сложения преобразуйте выражение:
Решение:
а) По формуле синуса разности получим:
б) Применим формулу тангенса суммы:
Пример №4
Найдите значение выражения:
Решение:
а) По формуле синуса суммы получим:
б) По формулам приведения получим, что
Тогда 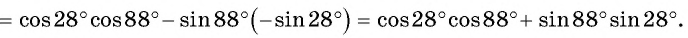
в) По формулам приведения
Тогда
По формуле тангенса разности:
Пример №5
Решение:
б) По формулам приведения:
По формуле тангенса разности получим:
Таким образом,
Пример №6
Решение:
а) Воспользуемся нечетностью синуса и формулой косинуса разности:
б) Применим формулу косинуса разности и получим:
Пример №7
Решите уравнение
Решение:
Запишем уравнение в виде 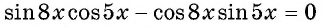
Ответ:
Пример №8
Вычислите 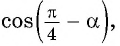
Решение:
Применим формулу косинуса разности:
Из основного тригонометрического тождества выразим 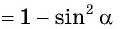
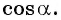
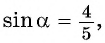
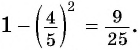
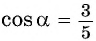
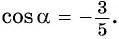
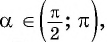
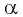
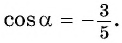
Пример №9
Докажите тождество
Решение:
Воспользуемся формулами сложения и получим:
Пример №10
Найдите значение выражения:
Решение:
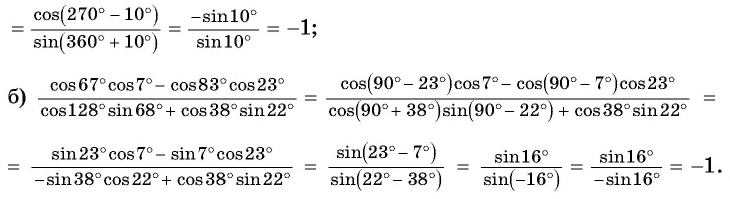
Пример №11
Найдите множество значений функции
Решение:
Применим формулу синуса разности и запишем функцию в виде
Так как 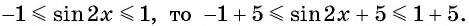
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
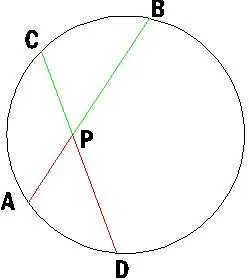
Как найти разность углов
Разделы 
Дополнительно
Пример 1. На рис. изображены два угла с общей начальной стороной $bar $ и общей конечной стороной $bar $: один равен $+270^$, другой $-90^$.
Сумма двух углов. На координатной плоскости $Oxу$ рассмотрим окружность единичного радиуса с центром в начале координат (рис.). Пусть произвольный угол $alpha$ (на чертеже положительный) получен в результате вращения некоторото подвижного радиуса-вектора от его начального положения $bar$, совпадающего с положительным направлением оси $Ox$, до его конечного положения $bar$. Примем теперь положение радиуса-вектора $bar$ за начальное и отложим от него произвольный угол $beta$ (на чертеже положительный), который получим в результате вращения некоторого подвижного радиуса-вектора от его начального положения $bar$ до его конечного положения $bar$. В результате этих действий мы получим угол, который будем называть суммой углов $alpha$ и $beta$. (Начальное положение подвижного радиуса-вектора $bar$, конечное положение радиуса-вектора $bar $.)
Разность двух углов.
Под разностью двух углов $alpha$ и $beta$, которую обозначим $alpha — beta$, мы будем понимать такой третий угол $gamma$, который в сумме с углом $beta$ дает угол $alpha$, т. е. $gamma = alpha — beta$, если $beta + gamma = alpha$. Разность двух углов $alpha$ и $beta$ можно трактовать как сумму углов $alpha$ и $- beta$. В самом деле, $[alpha + (- beta)] + beta = alpha$ (рис.). Вообще, для любых углов их сумма измеряется алгебраической суммой действительных чисел, измеряющих эти углы.
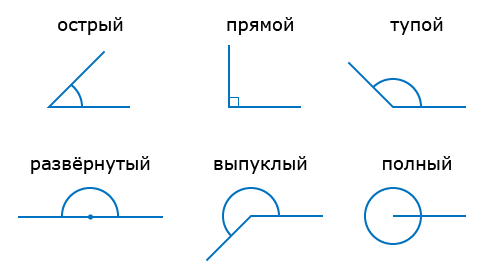
Виды углов
Каждый угол, в зависимости от его величины, имеет своё название:
- Острый угол — это угол, который меньше прямого угла (<90°).
- Прямой угол — это угол, стороны которого перпендикулярны друг другу. Прямой угол обозначается буквой d и равен 90°.
Если два смежных угла равны между собой, то каждый из них называется прямым углом. Прямой угол обычно обозначается не дугой, а уголком:
∠AOC и ∠COB — прямые углы. Общая сторона прямых углов OC называется перпендикуляром к прямой AB, а точка O — основанием перпендикуляра.
Развёрнутый угол равен сумме двух прямых углов или, короче, двум прямым углам. Следовательно, развёрнутый угол равен 180° или 2d.
Все развёрнутые углы равны между собой.
180° < выпуклый угол < 360°.
Полный угол равен сумме четырёх прямых углов, то есть 4d (360°).
Прилежащие углы
Прилежащие углы — это пара углов, имеющих общую вершину и общую сторону, другие стороны которых лежат по разные стороны от общей стороны.
∠AOB и ∠BOC — прилежащие углы, O — общая вершина, OB — общая сторона.
Если из вершины любого угла провести луч, разделяющий угол на два угла, то образованные углы будут прилежащими.
Угол, разделённый лучом, будет называться суммой полученных углов, например угол AOB является суммой углов AOC и COB:
∠AOB = ∠AOC + ∠COB.
Каждый из прилежащих углов, ∠AOC и ∠COB, называется разностью углов AOB и другого прилежащего, то есть: