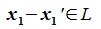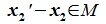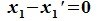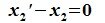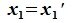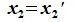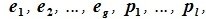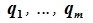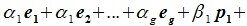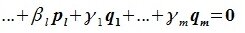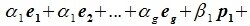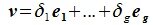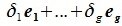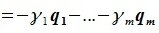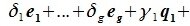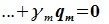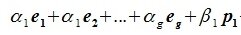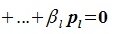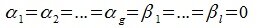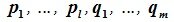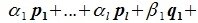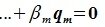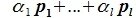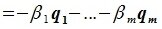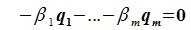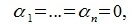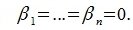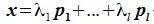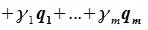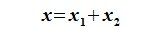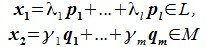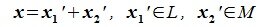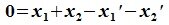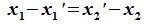Пересечение и сумма подпространств линейного пространства
Пусть и
— подпространства линейного пространства
.
Пересечением подпространств и
называется множество
векторов, каждый из которых принадлежит
и
одновременно, т.е. пересечение подпространств определяется как обычное пересечение двух множеств.
Алгебраической суммой подпространств и
называется множество векторов вида
, где
. Алгебраическая сумма (короче просто сумма) подпространств обозначается
Представление вектора в виде
, где
, называется разложением вектора
no подпространствам
и
.
Замечания 8.8
1. Пересечение подпространств является подпространством. Поэтому понятия размерности, базиса и т.п. применяются к пересечениям.
2. Сумма подпространств является подпространством. Поэтому понятия размерности, базиса и т.п. применяются к суммам.
Действительно, нужно показать замкнутость линейных операций в множестве . Пусть два вектора
и
принадлежат сумме
, т.е. каждый из них раскладывается по подпространствам:
Найдем сумму: . Так как
, а
, то
. Следовательно, множество
замкнуто по отношению к операции сложения. Найдем произведение:
. Так как
, a
, то
. Следовательно, множество
замкнуто по отношению к операции умножения на число. Таким образом,
— линейное подпространство.
3. Операция пересечения определена на множестве всех подпространств линейного пространства . Она является коммутативной и ассоциативной. Пересечение любого семейства подпространств V является линейным подпространством, причем скобки в выражении
— можно расставлять произвольно или вообще не ставить.
4. Минимальным линейным подпространством, содержащим подмножество конечномерного линейного пространства
, называется пересечение всех подпространств
, содержащих
, т.е.
. Если
, то указанное пересечение совпадает с нулевым подпространством
, поскольку оно содержится в любом из подпространств
. Если
— линейное подпространство
, то указанное пересечение совпадает с
, поскольку
содержится в каждом из пересекаемых подпространств (и является одним из них:
).
Минимальное свойство линейной оболочки: линейная оболочка любого подмножества
конечномерного линейного пространства
является минимальным линейным подпространством, содержащим
, т.е.
.
Действительно, обозначим . Надо доказать равенство двух множеств:
. Так как
(см. пункт 6 замечаний 8.7), то
. Докажем включение
. Произвольный элемент
имеет вид
, где
. Пусть
— любое подпространство, содержащее
. Оно содержит все векторы
и любую их линейную комбинацию (см. пункт 7 замечаний 8.7), в частности, вектор
. Поэтому вектор
принадлежит любому подпространству
, содержащему
. Значит,
принадлежит пересечению
таких подпространств. Таким образом,
. Из двух включений
и
следует равенство
.
5. Операция сложения подпространств определена на множестве всех подпространств линейного пространства . Она является коммутативной и ассоциативной. Поэтому в суммах
конечного числа подпространств скобки можно расставлять произвольно или вообще не ставить.
6. Можно определить объединение подпространств
и
как множество векторов, каждый из которых принадлежит пространству
или пространству
(или обоим подпространствам). Однако, объединение подпространств в общем случае не является подпространством (оно будет подпространством только при дополнительном условии
или
).
7. Сумма подпространств совпадает с линейной оболочкой их объединения
. Действительно, включение
следует из определения. Любой элемент множества
имеет вид
, т.е. представляет собой линейную комбинацию двух векторов из множества
. Докажем противоположное включение
. Любой элемент
имеет вид
, где
. Разобьем эту сумму на две, относя к первой сумме все слагаемые
, у которых
. Остальные слагаемые составят вторую сумму:
Первая сумма — это некоторый вектор , вторая сумма — это некоторый вектор
. Следовательно,
. Значит,
. Полученные два включения говорят о равенстве рассматриваемых множеств.
Теорема 8.4 о размерности суммы подпространств. Если и
подпространства конечномерного линейного пространства
, то размерность суммы подпространств равна сумме их размерностей без размерности их пересечения (формула Грассмана):
(8.13)
В самом деле, пусть — базис пересечения
. Дополним его упорядоченным набором
векторов до базиса
подпространства
и упорядоченным набором
векторов до базиса
подпространства
. Такое дополнение возможно по теореме 8.2. Из указанных трех наборов векторов составим упорядоченный набор
векторов. Покажем, что эти векторы являются образующими пространства
. Действительно, любой вектор
этого пространства представляется в виде линейной комбинации векторов из упорядоченного набора
Следовательно, . Докажем, что образующие
линейно независимы и поэтому они являются базисом пространства
. Действительно, составим линейную комбинацию этих векторов и приравняем ее нулевому вектору:
(8.14)
Первые две суммы обозначим — это некоторый вектор из
, последнюю сумму обозначим
— это некоторый вектор из
. Равенство (8.14):
означает, что вектор
принадлежит также и пространству
. Значит,
. Раскладывая этот вектор по базису
, находим
. Учитывая разложение этого вектора в (8.14), получаем
Последнее равенство можно рассматривать, как разложение нулевого вектора по базису подпространства
. Все коэффициенты такого разложения нулевые:
и
. Подставляя
в (8.14), получаем
. Это возможно только в тривиальном случае
и
, так как система векторов
линейно независима (это базис подпространства
). Таким образом, равенство (8.14) выполняется только в тривиальном случае, когда все коэффициенты равны нулю одновременно. Следовательно, совокупность векторов
линейно независима, т.е. является базисом пространства
. Подсчитаем размерность суммы подпространств:
что и требовалось доказать.
Пример 8.6. В пространстве радиус-векторов с общим началом в точке
заданы подпространства:
и
— три множества радиус-векторов, принадлежащих пересекающимся в точке
прямым
и
соответственно;
и
— два множества радиус-векторов, принадлежащих пересекающимся плоскостям
и
соответственно; прямая
, при надлежит плоскости
, прямая
принадлежит плоскости
, плоскости
и
пересекаются по прямой
(рис. 8.2). Найти суммы и пересечения каждых двух из указанных пяти подпространств.
Решение. Найдем сумму . Складывая два вектора, принадлежащих
и
соответственно, получаем вектор, принадлежащий плоскости
. На оборот, любой вектор
(см. рис.8.2), принадлежащий
, можно представить в виде
, построив проекции
и
вектора
на прямые
и
соответственно. Значит, любой радиус-вектор плоскости
раскладывается по подпространствам
и
, т.е.
. Аналогично получаем, что
, а
— множество радиус-векторов, принадлежащих плоскости, проходящей через прямые
и
.
Найдем сумму . Любой вектор
пространства
можно разложить по подпространствам
и
. В самом деле, через конец радиус-вектора
проводим прямую, параллельную прямой
(см. рис. 8.2), т.е. строим проекцию
вектора
на плоскость
. Затем на
откладываем вектор
так, чтобы
. Следовательно,
. Так как
, то
. Аналогично получаем, что
. Остальные суммы находятся просто:
. Заметим, что
.
Используя теорему 8.4, проверим, например, равенство по размерности. Подставляя
и
в формулу Грассмана, получаем
, что и следовало ожидать, так как
.
Пересечения подпространств находим по рис. 8.2, как пересечение геометрических фигур:
где — нулевой радиус-вектор
.
Прямая сумма подпространств
Алгебраическая сумма подпространств и
линейного пространства
называется прямой суммой, если пересечение подпространств состоит из одного нулевого вектора. Прямая сумма подпространств обозначается
и обладает следующим свойством: если
, то для каждого вектора
существует единственное представление в виде
, где
.
Действительно, если предположить противное, а именно существование двух разных разложений: , где
, то получим противоречие: из равенства
следует, что ненулевой вектор
принадлежит обоим подпространствам
и
одновременно, значит, принадлежит их пересечению, а по определению их пересечение состоит из одного нулевого вектора.
Признаки прямых сумм подпространств
Сумма является прямой суммой, если:
– существует вектор , который однозначно представляется в виде
, где
;
– базис пространства является объединением базисов подпространств
и
;
– справедливо равенство .
Замечания 8.9
1. Понятие прямой суммы распространяется на любое конечное число слагаемых. Сумма называется прямой суммой подпространств, если пересечение каждого из них с суммой остальных равно одному нулевому вектору:
2. Свойства и признаки, указанные для прямой суммы двух подпространств, справедливы и для любого конечного числа слагаемых. Отметим еще одно свойство: если — базис пространства
, то
.
Пример 8.7. В примере 8.6 найдены алгебраические суммы подпространств. Какие суммы являются прямыми?
Решение. Так как , то сумма
— прямая. Аналогично полу чаем, что суммы
— прямые.
Остальные суммы подпространств, найденные в примере 8.6, не являются прямыми:
поскольку их пересечение содержит не только нулевой вектор. Например, пересечение .
Алгебраические дополнения подпространств
Пусть — подпространство конечномерного линейного пространства
. Подпространство
называется алгебраическим дополнением подпространства
в пространстве
, если
. Говорят, что
дополняет (алгебраически) подпространство
до
.
Рассмотрим свойства алгебраических дополнений подпространств.
1. Для любого подпространства существует алгебраическое дополнение
.
Действительно, если , то
. Если
, то
. В остальных случаях базис
подпространства
можно дополнить по теореме 8.2 до базиса
пространства
. Тогда
. В примере 8.7 получено равенство
, т.е. подпространства
и
дополняют друг друга до всего пространства.
2. Базис любого подпространства дополняется базисом алгебраического дополнения
до базиса всего пространства.
3. Алгебраическое дополнение подпространства
, кроме случаев
или
, определяется неоднозначно.
В примере 8.7 дополнением плоскости в пространстве
служит множество радиус-векторов, принадлежащих любой прямой, пересекающей плоскость
в точке
, в частности, подпространство
.
4. Для любого подпространства .
Это равенство следует непосредственно из определения. Заметим, что равенство в силу неоднозначности определения алгебраического дополнения, вообще говоря, не справедливо.
5. Если и
— подпространства пространства
, то пересечение их алгебраических дополнений является алгебраическим дополнением суммы подпространств, и, наоборот, сумма алгебраических дополнений является алгебраическим дополнением пересечения подпространств:
(8.15)
Заметим, что равенства и
в силу неоднозначности определения алгебраического дополнения, вообще говоря, не справедливы.
Докажем последнее свойство. Как при доказательстве теоремы 8.4 по строим базис суммы подпространств из трех наборов векторов:
. Дополним теперь этот базис (по теореме 8.2) век торами
до базиса
пространства
. Так как
базис
, то по свойству 2 алгебраических дополнений заключаем, что
— базис
. Аналогично получаем, что
— базис
. Следовательно,
— базис пересечения
. Таким образом, базис всего пространства
получается объединением базиса суммы
и базиса пересечения
. Используя признак 2 прямой суммы подпространств, получаем
. Равенство
следует аналогично из структуры
базиса пространства
.
Линейная зависимость и линейная независимость векторов над подпространством
Говорят, что система векторов пространства
линейно зависима над подпространством
, если существует нетривиальная линейная комбинация этих векторов, принадлежащая подпространству
, т.е. найдутся такие числа
, неравные нулю одновременно, что
Если последнее включение возможно только в тривиальном случае, т.е при , то векторы
называют линейно независимы ми над подпространством
.
Понятие линейной зависимости или независимости над подпространством обобщает обычное, рассмотренное ранее, понятие линейной зависимости или независимости векторов, и совпадает с ним, если в качестве подпространства взять нулевое
.
Следующие свойства прямых сумм подпространств можно сформулировать при помощи понятия линейной зависимости и линейной независимости над подпространством.
1. Если пространство представлено в виде прямой суммы подпространств
, то любая линейно независимая система векторов подпространства
будет линейно независимой над подпространством
.
2. Базисом алгебраического дополнения подпространства
является максимальная совокупность векторов пространства
, линейно независимая над подпространством
(см. свойство 2 алгебраических дополнений подпространств).
Пусть имеется цепочка подпространств . Подпространство
называется алгебраическим дополнением подпространства
относительно подпространства
(или относительным дополнением
до подпространства
). Базисом относительного дополнения
служит максимальная система векторов
, линейно независимая над
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Пересечение и сумма подпространств линейного пространства
Пусть и
—
подпространства линейного пространства .
Пересечением
подпространств и
называется
множество векторов,
каждый из которых принадлежит и
одновременно,
т.е. пересечение подпространств
определяется как обычное пересечение
двух множеств.
Алгебраической
суммой подпространств и
называется
множество векторов вида ,
где .
Алгебраическая сумма (короче просто
сумма) подпространств обозначается
Представление
вектора в
виде ,
где ,
называетсяразложением
вектора no
подпространствам и
.
Замечания
8.8
1. Пересечение
подпространств является подпространством.
Поэтому понятия размерности, базиса и
т.п. применяются к пересечениям.
2. Сумма
подпространств является подпространством.
Поэтому понятия размерности, базиса и
т.п. применяются к суммам.
Действительно,
нужно показать замкнутость линейных
операций в множестве .
Пусть два вектора и
принадлежат
сумме ,
т.е. каждый из них раскладывается по
подпространствам:
Найдем
сумму: .
Так как ,
а ,
то .
Следовательно, множество замкнуто
по отношению к операции сложения. Найдем
произведение: .
Так как ,
a ,
то .
Следовательно, множество замкнуто
по отношению к операции умножения на
число. Таким образом, —
линейное подпространство.
3. Операция
пересечения определена на множестве
всех подпространств линейного
пространства .
Она является коммутативной и ассоциативной.
Пересечение любого семейства подпространств
V является линейным подпространством,
причем скобки в выражении —
можно расставлять произвольно или
вообще не ставить.
4. Минимальным
линейным подпространством,
содержащим подмножество конечномерного
линейного пространства ,
называется пересечение всех
подпространств ,
содержащих ,
т.е. .
Если ,
то указанное пересечение совпадает с
нулевым подпространством ,
поскольку оно содержится в любом из
подпространств .
Если —
линейное подпространство ,
то указанное пересечение совпадает
с ,
поскольку содержится
в каждом из пересекаемых подпространств
(и является одним из них: ).
Минимальное
свойство линейной оболочки: линейная
оболочка любого
подмножества конечномерного
линейного пространства является
минимальным линейным подпространством,
содержащим ,
т.е. .
Действительно,
обозначим .
Надо доказать равенство двух множеств: .
Так как (см.
пункт 6 замечаний 8.7), то .
Докажем включение .
Произвольный элемент имеет
вид 
где .
Пусть —
любое подпространство, содержащее .
Оно содержит все векторы и
любую их линейную комбинацию (см. пункт
7 замечаний 8.7), в частности, вектор .
Поэтому вектор принадлежит
любому подпространству ,
содержащему .
Значит, принадлежит
пересечению таких
подпространств. Таким образом, .
Из двух включений и
следует
равенство .
5. Операция
сложения подпространств определена на
множестве всех подпространств линейного
пространства .
Она является коммутативной и ассоциативной.
Поэтому в суммах конечного
числа подпространств скобки можно
расставлять произвольно или вообще не
ставить.
6. Можно
определить объединение подпространств
и
как
множество векторов, каждый из которых
принадлежит пространству или
пространству (или
обоим подпространствам). Однако,
объединение подпространств в общем
случае не является подпространством
(оно будет подпространством только при
дополнительном условии или
).
7. Сумма
подпространств совпадает
с линейной оболочкой их объединения .
Действительно, включение следует
из определения. Любой элемент
множества имеет
вид ,
т.е. представляет собой линейную
комбинацию двух векторов из множества .
Докажем противоположное включение .
Любой элемент имеет
вид 
где .
Разобьем эту сумму на две, относя к
первой сумме все слагаемые ,
у которых .
Остальные слагаемые составят вторую
сумму:
Первая
сумма — это некоторый вектор ,
вторая сумма — это некоторый вектор .
Следовательно, .
Значит, .
Полученные два включения говорят о
равенстве рассматриваемых множеств.
Теорема
8.4 о размерности суммы
подпространств. Если и
подпространства
конечномерного линейного пространства ,
то размерность суммы подпространств
равна сумме их размерностей без
размерности их пересечения (формула
Грассмана):
|
(8.13) |
В
самом деле, пусть —
базис пересечения .
Дополним его упорядоченным набором векторов
до базиса подпространства
и
упорядоченным набором векторов
до базиса подпространства
.
Такое дополнение возможно по теореме
8.2. Из указанных трех наборов векторов
составим упорядоченный набор векторов.
Покажем, что эти векторы являются
образующими пространства .
Действительно, любой вектор этого
пространства представляется в виде
линейной комбинации векторов из
упорядоченного набора
Следовательно, .
Докажем, что образующие линейно
независимы и поэтому они являются
базисом пространства .
Действительно, составим линейную
комбинацию этих векторов и приравняем
ее нулевому вектору:
|
(8.14) |
Первые
две суммы обозначим —
это некоторый вектор из ,
последнюю сумму обозначим —
это некоторый вектор из .
Равенство (8.14): означает,
что вектор принадлежит
также и пространству .
Значит, .
Раскладывая этот вектор по базису ,
находим 
Учитывая разложение этого вектора в
(8.14), получаем
Последнее
равенство можно рассматривать, как
разложение нулевого вектора по
базису подпространства
.
Все коэффициенты такого разложения
нулевые: и
.
Подставляя в
(8.14), получаем .
Это возможно только в тривиальном
случае и
,
так как система векторов линейно
независима (это базис подпространства ).
Таким образом, равенство (8.14) выполняется
только в тривиальном случае, когда все
коэффициенты равны нулю одновременно.
Следовательно, совокупность
векторов линейно
независима, т.е. является базисом
пространства .
Подсчитаем размерность суммы
подпространств:
что
и требовалось доказать.
Пример
8.6. В
пространстве радиус-векторов
с общим началом в точке заданы
подпространства: и
—
три множества радиус-векторов,
принадлежащих пересекающимся в
точке прямым
и
соответственно;
и
—
два множества радиус-векторов,
принадлежащих пересекающимся
плоскостям и
соответственно;
прямая ,
при надлежит плоскости ,
прямая принадлежит
плоскости ,
плоскости и
пересекаются
по прямой (рис.
8.2). Найти суммы и пересечения каждых
двух из указанных пяти подпространств.
Решение. Найдем
сумму .
Складывая два вектора,
принадлежащих и
соответственно,
получаем вектор, принадлежащий
плоскости .
На оборот, любой вектор (см.
рис.8.2), принадлежащий ,
можно представить в виде ,
построив проекции и
вектора
на
прямые и
соответственно.
Значит, любой радиус-вектор
плоскости раскладывается
по подпространствам и
,
т.е. .
Аналогично получаем, что ,
а —
множество радиус-векторов, принадлежащих
плоскости, проходящей через прямые и
.
Найдем
сумму .
Любой вектор пространства
можно
разложить по подпространствам и
.
В самом деле, через конец
радиус-вектора проводим
прямую, параллельную прямой (см.
рис. 8.2), т.е. строим проекцию вектора
на
плоскость .
Затем на откладываем
вектор так,
чтобы .
Следовательно, .
Так как ,
то .
Аналогично получаем, что .
Остальные суммы находятся просто: .
Заметим, что .
Используя
теорему 8.4, проверим, например,
равенство по
размерности. Подставляя и
в
формулу Грассмана, получаем ,
что и следовало ожидать, так как .
Пересечения
подпространств находим по рис. 8.2, как
пересечение геометрических фигур:
где —
нулевой радиус-вектор .
-
Пряма
сума підпросторів. Критерії прямої
суми.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5
Подпространство линейного пространства
Определение и размерность подпространства
Определение 6.1. Подпространством L n-мерного пространства R называется множество векторов, образующих линейное пространство по отношению к действиям, которые определены в R.
Другими словами, L называется подпространством пространства R, если из x, y∈L следует, что x+y∈L и если x∈L, то λx∈L, где λ— любое вещественное число.
Простейшим примером подпространства является нулевое подпространство, т.е. подмножество пространства R, состоящее из единственного нулевого элемента. Подпространством может служить и все пространство R. Эти подпространства называются тривиальными или несобственными.
Подпространство n-мерного пространства конечномерно и его размерность не превосходит n: dim L≤ dim R.
Сумма и пересечение подпространств
Пусть L и M — два подпространства пространства R.
Cуммой L+M называется множество векторов x+y, где x∈L и y∈M. Очевидно, что любая линейная комбинация векторов из L+M принадлежит L+M, следовательно L+M является подпространством пространства R (может совпадать с пространством R).
Пересечением L∩M подпространств L и M называется множество векторов, принадлежащих одновременно подпространствам L и M (может состоять только из нулевого вектора).
Теорема 6.1. Сумма размерностей произвольных подпространств L и M конечномерного линейного пространства R равна размерности суммы этих подпространств и размерности пересечения этих подпространств:
dim L+dim M=dim(L+M)+dim(L∩M).
Доказательство. Обозначим F=L+M и G=L∩M. Пусть G g-мерное подпространство. Выберем в нем базис 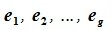
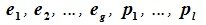
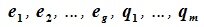
|
|
(6.1) |
составляют базис F=L+M. Для того, чтобы векторы (6.1) составляли базис пространства F они должны быть линейно независимы и любой вектор пространства F можно представить линейной комбинацией векторов (6.1).
Докажем линейную независимость векторов (6.1). Пусть нулевой вектор пространства F представляется линейной комбинацией векторов (6.1) с некоторыми коэффициентами:
|
|
(6.2) |
Тогда
|
|
(6.3) |
Левая часть (6.3) является вектором подпространства L, а правая часть является вектором подпространства M. Следовательно вектор
принадлежит подпространству G=L∩M. С другой стороны вектор v можно представить линейной комбинацией базисных векторов подпространства G:
|
|
(6.5) |
Из уравнений (6.4) и (6.5) имеем:
|
|
(6.6) |
или
|
|
(6.7) |
Но векторы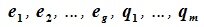
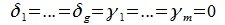
|
|
(6.8) |
В силу линейной независимости базиса подпространства L имеем:
|
|
(6.9) |
Так как все коэффициенты в уравнении (6.2) оказались нулевыми, то векторы
|
|
(6.10) |
линейно независимы. Но любой вектор z из F (по определению суммы подпространств) можно представить суммой x+y, где x∈L, y∈M. В свою очередь x представляется линейной комбинацией векторов 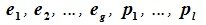
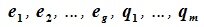
Изучая базисы подпространств L и M и базис подпространства F=L+M (6.10), имеем: dim L=g+l, dim M=g+m, dim (L+M)=g+l+m. Следовательно:
dim L+dim M−dim(L∩M)=dim(L+M). ■
Прямая сумма подпространств
Определение 6.2. Пространство F представляет собой прямую сумму подпространств L и M, если каждый вектор x пространства F может быть единственным способом представлен в виде суммы x=y+z, где y∈L и z∈M.
Прямая сумма обозначается L⊕M. Говорят, что если F=L⊕M, то F разлагается в прямую сумму своих подпространств L и M.
Теорема 6.2. Для того, чтобы n-мерное пространство R представляло собой прямую сумму подпространств L и M, достаточно, чтобы пересечение L и M содержало только нулевой элемент и чтобы размерность R была равна сумме размерностей подпространств L и M.
Доказательство. Выберем некоторый базис 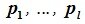
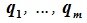
|
|
(6.11) |
является базисом пространства R. По условию теоремы размерность пространства R n равна сумме подпространств L и M (n=l+m). Достаточно доказать линейную независимость элементов (6.11). Пусть нулевой вектор пространства R представляется линейной комбинацией векторов (6.11) с некоторыми коэффициентами:
|
|
(6.12) |
или
|
|
(6.13) |
Так как левая часть (6.13) является вектором подпространства L, а правая часть — вектором подпространства M и L∩M=0, то
|
|
(6.14) |
Но векторы 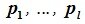
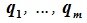
|
|
(6.15) |
Установили, что (6.12) справедливо лишь при условии (6.15), а это доказывает линейную независимость векторов (6.11). Следовательно они образуют базис в R.
Пусть x∈R. Разложим его по базису (6.11):
|
|
(6.16) |
Из (6.16) имеем:
|
|
(6.17) |
|
|
(6.18) |
Из (6.17) и (6.18) следует, что любой вектор из R можно представить суммой векторов x1∈L и x2∈M. Остается доказать что это представление является единственным. Пусть кроме представления (6.17) есть и следующее представление:
|
|
(6.19) |
Вычитая (6.19) из (6.17), получим
или
|
|
(6.20) |
Так как