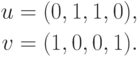Системы линейных уравнений: основные понятия
— это объединение из n линейных уравнений, каждое из которых содержит k переменных. Записывается это так:
Многие, впервые сталкиваясь с высшей алгеброй, ошибочно полагают, что число уравнений обязательно должно совпадать с числом переменных. В школьной алгебре так обычно и бывает, однако для высшей алгебры это, вообще говоря, неверно.
— это последовательность чисел ( k 1, k 2, . kn ), которая является решением каждого уравнения системы, т.е. при подстановке в это уравнение вместо переменных x 1, x 2, . xn дает верное числовое равенство.
Соответственно, решить систему уравнений — значит найти множество всех ее решений или доказать, что это множество пусто. Поскольку число уравнений и число неизвестных может не совпадать, возможны три случая:
- Система несовместна, т.е. множество всех решений пусто. Достаточно редкий случай, который легко обнаруживается независимо от того, каким методом решать систему.
- Система совместна и определена, т.е. имеет ровно одно решение. Классический вариант, хорошо известный еще со школьной скамьи.
- Система совместна и не определена, т.е. имеет бесконечно много решений. Это самый жесткий вариант. Недостаточно указать, что «система имеет бесконечное множество решений» — надо описать, как устроено это множество.
Переменная xi называется , если она входит только в одно уравнение системы, причем с коэффициентом 1. Другими словами, в остальных уравнениях коэффициент при переменной xi должен быть равен нулю.
Если в каждом уравнении выбрать по одной разрешенной переменной, получим набор разрешенных переменных для всей системы уравнений. Сама система, записанная в таком виде, тоже будет называться разрешенной. Вообще говоря, одну и ту же исходную систему можно свести к разным разрешенным, однако сейчас нас это не волнует. Вот примеры разрешенных систем:
Обе системы являются разрешенными относительно переменных x 1, x 3 и x 4. Впрочем, с тем же успехом можно утверждать, что вторая система — разрешенная относительно x 1, x 3 и x 5. Достаточно переписать самое последнее уравнение в виде x 5 = x 4.
Теперь рассмотрим более общий случай. Пусть всего у нас k переменных, из которых r являются разрешенными. Тогда возможны два случая:
- Число разрешенных переменных r равно общему числу переменных k : r = k . Получаем систему из k уравнений, в которых r = k разрешенных переменных. Такая система является совместной и определенной, т.к. x 1 = b 1, x 2 = b 2, . xk = bk ;
- Число разрешенных переменных r меньше общего числа переменных k : r k . Остальные ( k − r ) переменных называются свободными — они могут принимать любые значения, из которых легко вычисляются разрешенные переменные.
Так, в приведенных выше системах переменные x 2, x 5, x 6 (для первой системы) и x 2, x 5 (для второй) являются свободными. Случай, когда есть свободные переменные, лучше сформулировать в виде теоремы:
Обратите внимание: это очень важный момент! В зависимости от того, как вы запишете итоговую систему, одна и та же переменная может быть как разрешенной, так и свободной. Большинство репетиторов по высшей математике рекомендуют выписывать переменные в лексикографическом порядке, т.е. по возрастанию индекса. Однако вы совершенно не обязаны следовать этому совету.
Теорема. Если в системе из n уравнений переменные x 1, x 2, . xr — разрешенные, а x r + 1, x r + 2, . x k — свободные, то:
- Если задать значения свободным переменным ( x r + 1 = t r + 1, x r + 2 = t r + 2, . xk = tk ), а затем найти значения x 1, x 2, . xr , получим одно из решений.
- Если в двух решениях значения свободных переменных совпадают, то значения разрешенных переменных тоже совпадают, т.е. решения равны.
В чем смысл этой теоремы? Чтобы получить все решения разрешенной системы уравнений, достаточно выделить свободные переменные. Затем, присваивая свободным переменным разные значения, будем получать готовые решения. Вот и все — таким образом можно получить все решения системы. Других решений не существует.
Вывод: разрешенная система уравнений всегда совместна. Если число уравнений в разрешенной системе равно числу переменных, система будет определенной, если меньше — неопределенной.
И все бы хорошо, но возникает вопрос: как из исходной системы уравнений получить разрешенную? Для этого существует метод Гаусса.
Исследование СЛАУ. Общие сведения
В данной статье мы расскажем о методах, видах, условиях и определениях исследований решений систем линейных уравнений, что такое метод Кронекера-Капели, а также приведем примеры.
Общие сведения (определения, условия, методы, виды)
Системы линейных алгебраических уравнений с n неизвестными могут иметь:
- единственное решение;
- бесконечное множество решение (неопределенные СЛАУ);
- ни одного решения (несовместные СЛАУ).
Пример 1
Система x + y + z = 1 2 x + 2 y + 2 z = 3 не имеет решений, поэтому она несовместна.
Система x + y = 1 2 x + 7 y = — 3 имеет единственное решение x = 2 ; y = 1 .
Система x + y = 1 2 x + 2 y = 2 3 x + 3 y = 3 имеет бесконечное множество решений x = t y = 1 — t при — ∞ t ∞ .
Перед решением системы уравнений необходимо исследовать систему, т.е. ответить на следующие вопросы:
- Совместна ли система?
- Если система совместна, то, какое количество решений она имеет — одно или несколько?
- Как найти все решения?
Если система малоразмерна при m = n , то ответить на поставленные вопросы можно при помощи метода Крамера:
- если основной определитель системы, то система совместна и имеет единственное решение, которое вычисляется методом Крамера;
- если, и один из вспомогательных определителей, то система не является совместной, т.е. не имеет решений;
- если и все, и один из коэффициентов СЛАУ, то система не является определенной и имеет бесконечное множество решений.
Ранг матрицы и его свойства
Бывают случаи, которые выбиваются из представленных вариантов решения СЛАУ, например, линейные уравнения с большим количеством уравнений и неизвестных.
Для такого варианта решения существует ранг матрицы, который представляет собой алгоритм действий в случае решения системы матрицы, когда
В математике выделяют следующие подходы к определению ранга матрицы:
- при помощи понятия линейной зависимости/независимости строк/столбцов матрицы. Ранг равен максимальному количеству независимых строк (столбцов) матрицы
- при помощи понятия минора матрицы в качестве наивысшего порядка минора, который отличается от нуля. Минор матрицы порядка k — определитель k-го порядка, составленный из элементов, которые стоят на пересечении вычеркиваемых k-строк и k-столбцов матрицы;
- при помощи метода Гаусса. По завершении прямого хода ранг матрицы равняется количеству ненулевых строк.
Обозначение ранга матрицы: r ( A ) , r g ( A ) , r A .
Свойства ранга матрицы:
- квадратная невырожденная матрица обладает рангом, который отличается от нуля;
- если транспонировать матрицу, то ранг матрицы не изменяется;
- если поменять местами 2 параллельные строки или 2 параллельных столбца, ранг матрицы не изменяется;
- при удалении нулевого столбца или строки ранг матрицы не изменяется;
- ранг матрицы не изменяется, если удалить строку или столбец, которые являются линейной комбинацией других строк;
- при умножении все элементов строки/столбца на число k н е р а в н о н у л ю ранг матрицы не изменяется;
- ранг матрицы не больше меньшего из ее размеров: r ( А ) ≤ m i n ( m ; n ) ;
- когда все элементы матрицы равны нулю, то только тогда r ( A ) = 0 .
Пример 2
А 1 = 1 1 1 2 2 2 3 3 3 , B 1 = 1 0 0 0 0 0
r ( A 1 ) = 1 , r ( B 1 ) = 1
А 2 = 1 2 3 4 0 5 6 7 0 0 0 0 ; В 2 = 1 1 3 1 2 1 4 3 1 2 5 0 5 4 13 6
Системы линейных уравнений с примерами решений
Содержание:
Системы уравнений, как и отдельные уравнения, используют для решения сложных и необходимых задач. Системы уравнений бывают с двумя, тремя и более переменными. В этой главе вы ознакомитесь с простейшими системами двух уравнений с двумя переменными. Основные темы лекции:
- уравнения с двумя переменными;
- график линейного уравнения;
- системы уравнений;
- способ подстановки;
- способ сложения;
- решение задач составлением системы уравнений.
Уравнения с двумя переменными
До сих пор мы рассматривали уравнение с одной переменной. Однако существуют задачи, решение которых приводит к уравнениям с двумя переменными.
Пример:
На 22 руб. купили несколько книжек по 5 руб. и географических карт — по 3 руб. Сколько купили книжек и карт?
Решение:
Пусть купили х книжки у карт. За книжки заплатили 5х руб., а за карты — 3у руб. Всего заплатили 22 руб., то есть, 5х + Зу = 22.
Это уравнение с двумя переменными. Приведём и другие примеры таких уравнений с двумя переменными:
Уравнение вида ах + by = с, где а, b, с — данные числа, называется линейным уравнением с двумя переменными х и у. Если
Примеры линейных уравнений:
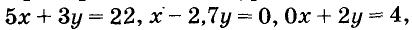
Паре чисел х = -1 и у = 9 удовлетворяет уравнение 5х + Зу -= 22, так как 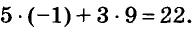
Каждая пара чисел, удовлетворяющая уравнение с двумя переменными, т. е. обращающая это уравнение в верное равенство, называется решением этого уравнения.
Обратите внимание: одно решение состоит из двух чисел, на первом месте записывают значение х, на втором — у. Корнями их не называют.
Чтобы найти решение уравнения с двумя переменными, следует подставить в уравнение произвольное значение первой неременной и, решив полученное уравнение, найти соответствующее значение второй переменной.
Для примера найдем несколько решений уравнения
Если х = 1, то 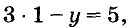
Уравнение 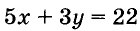
Два уравнения с двумя переменными называют равносильными, если каждое из них имеет те же решения, что и другое. Уравнения, не имеющие решений, также считаются равносильными.
Для уравнения с двумя переменными остаются справедливыми свойства, сформулированные для уравнений с одной переменной.
Обе части уравнения с двумя переменными можно умножить или разделить на одно и то же число, отличное от нуля. Любой член такого уравнения можно перенести из одной части уравнения в другую, изменив его знак на противоположный. В результате получается уравнение, равносильное данному.
Например, уравнение 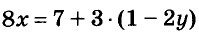
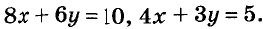
Иногда возникает потребность решить уравнение с двумя переменными во множестве целых чисел, то есть определить решения, являющиеся парами целых чисел. Способы решения таких уравнений определил древнегреческий математик Диофант (III в.), поэтому их называют диофантовыми уравнениями. Например, задача о книжках и картах сводится к уравнению 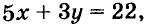
Переменную у из этого уравнения выразим через х:
Будем подставлять в равенство вместо х первые натуральные числа до тех пор, пока не получим целое значение переменной у. Это можно делать устно. Если х = 2, то у = 4. Других натуральных решений уравнение не имеет. Поэтому задача имеет единственное решение: 2 книги и 4 карты.
Пример:
Решение:
а) При любых значениях х и у значения выражения 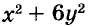
б) Значение выражения 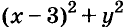
Пример:
Составьте уравнение с двумя переменными, решением которого будет пара чисел (1; -5).
Решение:
Пишем любой двучлен с переменными х и у, например 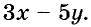
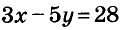
Есть много других линейных уравнений с двумя переменными, имеющих такое же решение (1; -5).
График линейного уравнения с двумя переменными
Рассмотрим уравнение 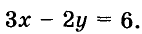
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
http://zaochnik.com/spravochnik/matematika/issledovanie-slau/slau/
http://www.evkova.org/sistemyi-linejnyih-uravnenij
Размерность пространства решений однородной системы линейных уравнений
Как мы отметили ранее, совокупность решений Xодн однородной системы линейных уравнений с матрицей 
Теорема 9.17.1. Если r=r(A)<n, то 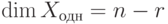
Доказательство. Для удобства записи переупорядочим неизвестные, если это необходимо, так, чтобы
Пусть 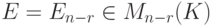

Эта система n-r строк-решений линейно независима (поскольку строки единичной матрицы, конечно, линейно независимы). Если
произвольное решение, то
Однако, конечно,
при этом 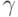
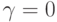
Итак, мы построили базис 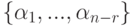
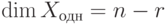
Замечание 9.17.2. Если вместо строк единичной матрицы En-r для свободных неизвестных брать строки всевозможных матриц 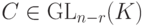

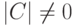
Замечание 9.17.2. Любой базис линейного пространства решений Xодн однородной системы линейных уравнений называется в ряде алгебраических текстов » фундаментальной системой решений однородной системы линейных уравнений «.
Задание любого подпространства в _K V = K^n как пространства решений однородной системы линейных уравнений
Пусть K — поле, 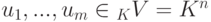
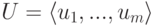
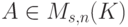
совпадает с U.
Если U — нулевое подпространство, то в качестве A мы можем взять любую матрицу 
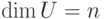




Рассмотрим матрицу 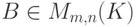

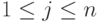
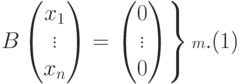 |
( 9.2) |
Ясно, что 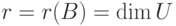
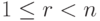
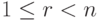
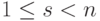
Пусть строки 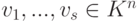
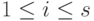
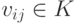
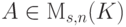
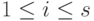
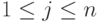
Действительно, по построению матрицы A любая строка из U (как линейная комбинация строк u1,…,um ) является решением однородной системы уравнений
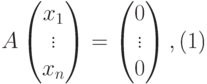 |
( 9.3) |
т. е. 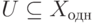
Следовательно, U=Xодн.
В заключение отметим, что матрица A определена неоднозначно. Например, другая матрица A’ может быть получена с помощью другой фундаментальной системы решений системы (9.2).
Полученное задание линейных подпространств оказывается полезным при решении ряда практических задач. Например, пусть 
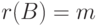
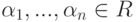
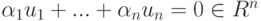
имеем 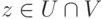
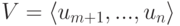
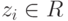

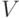
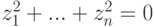
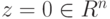
Но u1,…,um — линейно независимые строки, поэтому 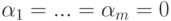
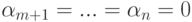
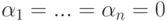
Таким образом, мы рассмотрели два способа задания линейных подпространств в K V=Kn :
- как множество решений Xодн однородной системы линейных уравнений;
- как линейную оболочку
строк
.
При этом мы научились переходить от первого задания ко второму (фундаментальная система решений) и от второго задания к первому. Первый способ задания удобен для задания пересечения 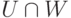
В следующем примере мы увидим комбинацию этих приемов.
Пример 9.18.1. Пусть 
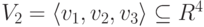

Решение Запишем строки u1, u2, u3, v1, v2, v3 по столбцам и приведем полученную матрицу к ступенчатому виду с помощью элементарных преобразований строк:
Поскольку 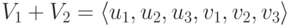

Поэтому v’_2=u’_1+u’_2+u’_3-v’_1 и, следовательно, v2=u1+u2+u3-v1. Для v’3 мы видим, что v’3+v’1=(2,0,2,0)*=2u’1+2u’3, поэтому v3=2u1+2u3-v1. Проведенные вычисления равносильны завершению приведения матрицы к главному ступенчатому виду:
Рассмотрим теперь 
Для V1:
система уже имеет ступенчатый вид, x1, x2, x3 — главные неизвестные, x4 — свободная. Фундаментальная система решений состоит из одной строки (-1,1,-1,1). Итак, подпространство V1 совпадает с пространством решений однородной системы линейных уравнений
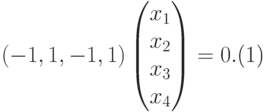 |
( 9.4) |
Для V2 :
и мы приходим к ступенчатому виду, при этом x1, x2, x3 — главные неизвестные, а x4 — свободная. Фундаментальная система решений состоит из одной строки (-1,-1,1,1). Значит, однородная система линейных уравнений
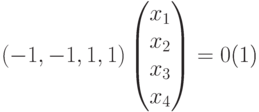 |
( 9.5) |
задает подпространство V2.
Ясно, что система
задает подпространство 
Решим эту систему:
x1, x2 — главные неизвестные, x3, x4 — свободные неизвестные. Фундаментальная система решений состоит из двух строк
Следовательно, {u,v} — базис линейного подпространства 
Определение. Система линейных
уравнений называется однородной, если
В=0.
Лемма. Однородная система имеет
ненулевые решение тогда и только тогда,
когда
rankA<n
Теорема. Совокупность решений
однородной системы линейных уравнений(ОСЛУ)
является векторным
пространством. (Обозначим U). Причем
dimU=n-r, где n —
кол-во неизвестных r =rankA
Определение. Любой базис пространства
решений ОСЛУ называется фундаментальной
системой решений(ФСР)
Система линейных алгебраических
уравнений имеет следующий вид
a11x1
+ a12x2
+ …+ a1nxn
= b1
a21x1
+ a22x2
+ …+ a2nxn
= b2
……………………………..
an1x1
+ an2x2
+ …+ annxn
= bn
Коэффициенты при неизвестных (матрица
коэффициентов)
a11
a21
… an1
A = a12 a22
… an2
… … … …
a1n
a2n
…
ann
Расширенная матрица системы
a11 a21
… an1
b1
Ā = a12 a22
… an2
b2
… … … … …
a1n
a2n
…
ann
bn
X = (x)T
B =( bi
)T столбцы
неизвестных и свободных членов
AX = B
матричная запись
Определение. Решением системы
линейных уравнений называется такой
упорядоченный
набор (λ1
… λn), что после
замены неизвестных ( xi
) на ( λi
) каждое
уравнение системы
обращается в равенство.
Система называется несовместной, если
множество решений – пустое множество.
Если система имеет решения, то она
совместна. Если система имеет единственное
решение, то она называется определенной.
Если решение не единственное —
неопределенной.
Системы называются эквивалентными,
если они обладают одними и теми же
решениями.
Определение. Рангом системы векторов
называется число векторов в любой ее
max
линейно независимой
подсистеме. Ранг матрицы — ранг ее системы
строк.
Теорема. (Критерий Кронекера-Капелли)
AX = B совместна тогда и только тогда,
когда rankA=rankĀ
Метод Гаусса
1. Составляем расширенную матрицу.
2. Элементарными преобразованиями
приводим ее к стандартному виду.
3. Записываем систему эквивалентную
1-ой.
4. Определяем совместна ли система.
Находим главные и свободные неизвестные.
5. Выражаем главные неизвестные через
свободные двигаясь снизу вверх.
Правило Крамера
d = detA
a11 a21
… b1
… an1
di
= det a12 a22
… b2
… an2
… … … … … …
a1n
a2n
…
bn …
ann
↑i-ый
столбец
Для ( xi
) – решений AX=B имеют место следующие
равенства: d * xi=
di ,
i=1,n
6. Векторные пространства. Линейная
зависимость и независимость векторов.
Базис, размерность. Координаты вектора,
их изменение при изменении базиса. Ранг
матрицы и его основные свойства.
Подпространства и операции над ними:
пересечение, сумма, прямая сумма.
Определение. V-векторное пространство
над полем P, если P: 1≠-1 и
1. (V, +) – абелева группа
2.Для любых α € P и a € V :
(α,a) → α∙a
€ V
3. Для любых α,β€P
и для любого a € V :
(α∙β)a=α∙(βa)-свойство
дистрибутивности
4. 1€P, для любого a € V
: 1∙а=а
5. Для любых α,β€P
и для любых a,b € V
α(a+b)=αa+αb
и (α+β)а= αa+βа
a € V: а – называется
вектором, α € P: α – называется скаляром
Определение. L –
подпространство V, где V-векторное
пространство, если
1. L — подгруппа в (V, +).
2. Для любого α € P и для
любого a € L: α∙a
€ L.
Пусть V-векторное пространство {Li}i€I—
подпространства
L = ∩ i€I
Li –
векторное подпространство в V
L1U L2
– векторное подпространство в V,
L1≤ L2
либо L2≤ L1.
Определение. L = L1+
L2 +…+ Ln
={ x1+ x2
+…+ xn;
xi
€ Li
}- сумма подпространств.
Сумма Li
— min векторное подпространство,
содержащее каждое Li
.
Определение. L = L1+
L2 +…+ Ln
называется прямой суммой и обозначается
L = L1L2
… Ln
если любое x € L
представляется в виде x= x1+
x2 +…+ xn
однозначно.
Теорема. L1+ L2
+…+ Ln
прямая Li
∩ (∑j≠i Lj
)={0}, для любого i=1,n
Определение. Сумма векторов — набор
а1, …,аk , аi
€ V, V-векторное
пространство.
Определение. Последовательность
а1, …,аn € V называется
линейно зависимой, если
существуют (α1, …,
αn)≠0 αi€
P: α1а1 +…+ αnаn=0.
В противном случае она
называется линейно
независимой.
Определение. Система векторов U €
V называется системой
образующих для V, если
для любого a € V
существует конечная линейная комбинация
векторов € U.
Определение. U € V
называется базисом V, если
-
U – линейна независима
-
U – система образующих для V
Теорема. Любых два базиса векторного
пространства содержат одинаковое
количество
векторов и называются
размерностью пространства: dimV
Определение. U – базис V, w
€ V, w=x1u1+…+xnun,
xi€
P , ui€U
тогда (x1,…,
xn)
называются координатами w по базису U.
[U]= (u1,…,
un) –
базис V
x1
(X)= … — координаты w
по [U], т.е. w=[U](X)
xn
[v] – новый базис, А –
матрица перехода от [U] к
[v], т.е. [v]=
[U]А, тогда (y1,…,
yi) –
координаты w по [v] находятся
из следующего соотношения А(y)=(x).
Определение. Любая max линейно
независимая подсистема системы векторов
содержит
одинаковое количество
векторов – это число называется рангом
системы
векторов
rankA=rank(a1,
…, an),
ai –
строки.
Теорема. Ранг матрицы равен max порядку
ее ненулевых миноров.
Лемма. Элементарные преобразования
не меняют ранга матрицы.
Теорема. А≠0, rankA=r =>
r –
штук единиц
|
1 |
0 |
|||||
|
1 |
||||||
|
… |
||||||
|
0 |
1 |
|||||
|
0 |
||||||
|
… |
||||||
|
0 |
A~
Свойства 1.
rank(AB)≤min{rank(A),rank(B)}
-
Anxm ;
Cmxm и
Bnxn
– невырожденные =>
rank(A∙C)=rank(B∙A)=rank(A)
-
Линейное отображение векторных
пространств, его ядро и образ. Матрица
линейного оператора. Матрица суммы и
композиции линейных операторов. Теорема
о сумме ранга и дефекта линейного
оператора. Собственные значения и
собственные векторы.
Определение. V,V’ – векторные
пространства над P.
φ: V → V’
называется линейным оператором, если
-
φ(a+b)= φ(a)+ φ(b) для любых a,b€V.
-
φ(λa)= λφ(a) для любых λ€ P, a€V.
Определение. φ€L(V;V’).
Ядром φ (Ker
φ) называется прообраз
OV’
Ker φ:=
φ-1 (OV’)={
a€V : φ(a)=
OV’}.
Определение. φ€L(V;V’).
Образом φ называется
совокупность всех векторов из V’,
Которые являются образами
пространства V при отображении φ.
Imφ= φ(V).
Теорема. φ€L(V;V’),
def φ=dim Kerφ,
rank φ=dim
Imφ
def φ+ rank φ=dimV.
Определение. φ –
линейный оператор, если φ€L(V;V)=:
L(V)
L(V)
– алгебра над P (векторное подпространство
над P и ассоциативное
кольцо с 1).
Матрица φ:
[U] базис V
φ(Ui)=
α1iu1+…+αniun
, где αji€P
α11 … α1n
M(φ)= α21
… α2n
… … …
αn1 …
αnn
Теорема. f,j€L(V);
M(f), M(g)
– их матрицы в [v]-базисе
=>
M(f)M(g)
– матрица gf
M(f)+M(g)
– матрица f+g
αM(f)
– матрица αf
Определение. φ€L(V).
Если существует u€V{0}:
φ(u)=λu
для некоторого λ € P, то
Будем говорить, что u –
собственный вектор собственного значения
λ.
Теорема. Собственные векторы
оператора, отвечающие попарно различным
собственным
значениям, линейно независимы.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #


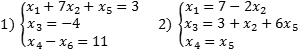
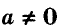
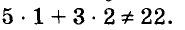
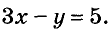
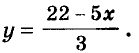
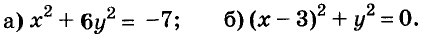
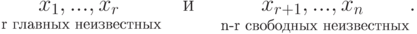
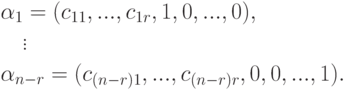
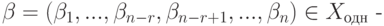
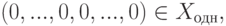
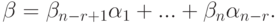
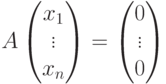
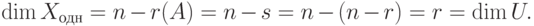
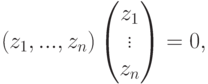

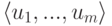 строк
строк 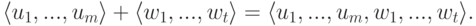
![begin{mult}
begin{gathered}
u_1 u_2 u_3,, ! v_1 v_2 v_3 kern53mm
\
left(
begin{array}{cccccc}
1 & 0 & 0 & 1 & 0 & 1\
1 & 1 & 0 & 0 & 2 & 2\
0 & 1 & 1 & 1 & 1 & 1\
0 & 0 & 1 & 0 & 1 & 2
end{array}right)to
left(
begin{array}{cccccc}
1 & 0 & 0 & phm 1 & 0 & 1\
0 & 1 & 0 & -1 & 2 & 1\
0 & 1 & 1 & phm 1 & 1 & 1\
0 & 0 & 1 & phm 0 & 1 & 2
end{array}right)to{}
end{gathered}
\[3mm]
begin{gathered}
kern55mm u'_1, u'_2, u'_3 v'_1; v'_2; v'_3
\
{}to
left(
begin{array}{cccccc}
1 & 0 & 0 & phm 1 & phm 0 & 1\
0 & 1 & 0 & -1 & phm 2 & 1\
0 & 0 & 1 & phm 2 & -1 & 0\
0 & 0 & 1 & phm 0 & phm 1 & 2
end{array}right)to
left(
begin{array}{cccccc}
multicolumn{1}{|c}{1} & 0 & 0 & phm 1 & phm 0 & phm 1\
cline{1-1}
0 & multicolumn{1}{|c}{1} & 0 & -1 & phm 2 & phm 1\
cline{2-2}
0 & 0 & multicolumn{1}{|c}{1} & phm 2 & -1 & phm 0\
cline{3-3}
0 & 0 & 0 & multicolumn{1}{|c}{phm 1} & -1 & -1\
cline{4-6}
end{array}right).
end{gathered}
end{mult}](https://intuit.ru/sites/default/files/tex_cache/dd0dbbb69869493ca81113a368c90d5a.png)
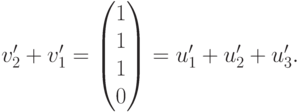

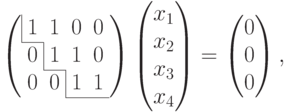
![begin{align*} & begin{pmatrix}
1 & 0 & 1 & 0\
0 & 2 & 1 & 1\
1 & 2 & 1 & 2
end{pmatrix}
begin{pmatrix}
x_1\
x_2\
x_3\
x_4
end{pmatrix} =
begin{pmatrix}
0\
0\
0
end{pmatrix} to
begin{pmatrix}
1 & 0 & 1 & 0\
0 & 2 & 1 & 1\
0 & 2 & 0 & 2
end{pmatrix}
begin{pmatrix}
x_1\
x_2\
x_3\
x_4
end{pmatrix} =
begin{pmatrix}
0\
0\
0
end{pmatrix} to{}
\[1mm] & quad {}to
begin{pmatrix}
1 & 0 & 1 & 0\
0 & 2 & 1 & 1\
0 & 1 & 0 & 1
end{pmatrix}
begin{pmatrix}
x_1\
x_2\
x_3\
x_4
end{pmatrix} !=!
begin{pmatrix}
0\
0\
0
end{pmatrix} to!
%{}
%\[3mm]
%& quad {}to
begin{pmatrix}
1 & 0 & 1 & 0\
0 & 1 & 0 & 1\
0 & 2 & 1 & 1
end{pmatrix}
begin{pmatrix}
x_1\
x_2\
x_3\
x_4
end{pmatrix} !=!
begin{pmatrix}
0\
0\
0
end{pmatrix} to{}
\[1mm] & quad {}to
left(
begin{array}{cccc}
multicolumn{1}{|c}{1} & 0 & 1 & phm 0\
cline{1-1}
0 & multicolumn{1}{|c}{1} & 0 & phm 1\
cline{2-2}
0 & 0 & multicolumn{1}{|c}{1} & -1\
cline{3-4}
end{array}right)
begin{pmatrix}
x_1\
x_2\
x_3\
x_4
end{pmatrix} =
begin{pmatrix}
0\
0\
0
end{pmatrix},
end{align*}](https://intuit.ru/sites/default/files/tex_cache/9b3e5cd07c99c5ba9b0cfe865a6061bc.png)
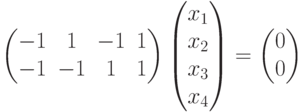
![begin{align*} & begin{pmatrix}
-1 & phm 1 & -1 & 1\
-1 & -1 & phm 1 & 1
end{pmatrix}
begin{pmatrix}
x_1\
x_2\
x_3\
x_4
end{pmatrix} =
begin{pmatrix}
0\
0
end{pmatrix} to{}
\[1mm] & quad {}to
begin{pmatrix}
phm 1 & -1 & 1 & -1\
-1 & -1 & 1 & phm 1
end{pmatrix}
begin{pmatrix}
x_1\
x_2\
x_3\
x_4
end{pmatrix} =
begin{pmatrix}
0\
0
end{pmatrix} to{}
\[1mm] & quad {}to
left(
begin{array}{cccc}
multicolumn{1}{|c}{1} & -1 & 1 & -1\
cline{1-1}
0 & multicolumn{1}{|c}{-2} & 2 & phm 0\
cline{2-4}
end{array}right)
begin{pmatrix}
x_1\
x_2\
x_3\
x_4
end{pmatrix} =
begin{pmatrix}
0\
0
end{pmatrix},
end{align*}](https://intuit.ru/sites/default/files/tex_cache/514a0838571b1cf6b55788bbade81424.png)