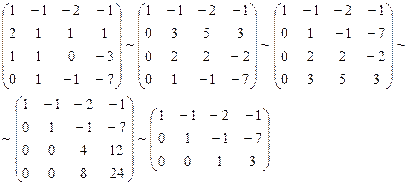-
Размерность подпространства
Все
базисы подпространства L
состоят
из одного и того же числа векторов.
Действительно,
пусть
и
– два базиса подпространства L.
Тогда каждая из этих систем векторов
является базисом системы векторов
.
Теперь из теоремы 2.15 [1] следует, что
Размерностью
подпространства
называется число векторов в любом его
базисе. Если размерность подпространства
L
равна k,
то будем писать: dim
L=k.
Примеры
1.
Из теоремы 1.5 вытекает, что
.
2.
,
так как левая и правая части равны
количеству векторов в базисе системы
(теорема 1.6).
3.
Из теоремы 1.7 следует, что размерность
подпространства решений однородной
системы уравнений
равна
где n
– число неизвестных в системе уравнений,
–
ранг матрицы А.
□ Теорема
1.8.
Дано подпространство L,
размерность которого равна k,
и система векторов
из L,
содержащая столько векторов, какова
размерность L.
Тогда следующие утверждения равносильны:
1)
базис подпространства L;
2)
каждый вектор
подпространства L
разлагается
по системе векторов
;
3)
система
векторов
линейно независимая.
Доказательство
1)
2).
Вытекает из определения базиса
подпространства.
2)
3).
Доказательство от противного.
Предположим, что система векторов
линейно зависима и
− базис этой системы. Тогда
.
Из условия 2 утверждения 5 §1
[1] следует, что каждый вектор из L
разлагается по векторам
и, значит,
− базис подпространства L.
Следовательно,
,
что противоречит условию теоремы.
3)
1).
Доказательство от противного. Если
линейно независимая система векторов
не является базисом L,
то ее можно дополнить до базиса
подпространства L
(теорема
1.3). Следовательно,
что противоречит условию теоремы. ■
Пример
Выяснить,
образуют ли векторы
,
базис подпространства
решений системы линейных уравнений
Решение.
Прежде всего
надо проверить, что векторы
и
являются решениями системы уравнений.
После подстановки координат векторов
в систему вместо неизвестных получим
верные числовые равенства. Координаты
векторов
и
не пропорциональны и, значит, они образуют
линейно независимую систему. Размерность
подпространства
равна
,
где
основная
матрица системы уравнений,
число
неизвестных в системе уравнений. Ранг
матрицы
равен двум,
,
а поэтому
.
Теперь из теоремы 1.8 следует, что векторы
будут базисом подпространства
.
Весьма часто
необходимо знать, когда два подпространства,
из которых одно содержится в другом,
совпадают.
□ Теорема
1.9. Пусть
и
подпространства пространства
и
.
Тогда справедливы следующие утверждения:
1.
.
2.
=
=
.
Доказательство
1.
Пусть
− базис подпространства
и, значит, линейно независимая система
векторов. Из условия
вытекает, что векторы
принадлежат подпространству
,
а, следовательно, линейно независимую
систему векторов
можно дополнить до базиса
.
Отсюда следует, что dim
L
≤ dim
L
.
2.
Необходимость.
Пусть dim
L
=
dim
L
=
k
и
− базис подпространства
.
Из условия
следует, что линейно независимые векторы
принадлежат
,
и система
содержит столько векторов, какова
размерность подпространства
.
Из теоремы 1.8 вытекает, что система
векторов
− базис
.
Итак,
и
обладают общим базисом и, значит,
(следствие из теоремы 1.2).
Достаточность.
Если
,
то они имеют общий базис и dim
L
dim
L
.
■
Следствие.
Если
− подпространство пространства
,
то справедливы следующие утверждения:
1.
;
2.
.
Доказательство
Заметим,
что
и n
dim
.
Теперь следствие есть частный случай
теоремы, когда
и
.
Задачи
1.
Подпространство
имеет размерность
.
Доказать, что ранг системы векторов
,
принадлежащих подпространству
,
не больше
.
2.
Доказать, что подпространство
является линейной оболочкой системы
векторов
из подпространства
тогда и только тогда, когда размерность
равна рангу системы векторов
.
3.
Подпространство
имеет размерность
и является линейной оболочкой системы
векторов
.
Доказать, что
− базис подпространства
.
4.
Подпространство
содержится в подпространстве
и
линейно независимые векторы из
подпространства
.
Доказать, что
,
если размерность
равна
.
5.
Сформулировать алгоритм, позволяющий
установить совпадение двух подпространств
и
в следующих случаях:
а)
и
− линейные оболочки системы векторов;
б)
и
− подпространства решений однородной
системы линейных уравнений;
в)
;
.
6.
Выяснить, совпадет ли пространство
с линейной оболочкой
:
а)
;
б)
.
7.
Выяснить, совпадают ли подпространства
и
пространства
,
где
задано системой уравнений
а
− линейная оболочка системы векторов
.
8.
Система векторов
эквивалентна базису
подпространства
.
Доказать, что
базис
подпространства
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Подпространство, его базис и размерность.
Пусть L – линейное пространство над полем P и A – подмножество из L. Если A само составляет линейное пространство над полем P относительно тех же операций, что и L, то A называют подпространством пространства L.
Согласно определению линейного пространства, чтобы A было подпространством надо проверить выполнимость в A операций:
1) :
;
2) :
;
и проверить, что операции в A подчинены восьми аксиомам. Однако последнее будет излишним (в силу того, что эти аксиомы выполняются в L) т.е. справедлива следующая
Теорема. Пусть L линейное пространство над полем P и . Множество A тогда и только тогда является подпространством L, когда выполняются следующие требования:
1. :
;
2. :
.
Утверждение. Если L – n-мерное линейное пространство и A его подпространство, то A также конечномерное линейное пространство и его размерность не превосходит n.
П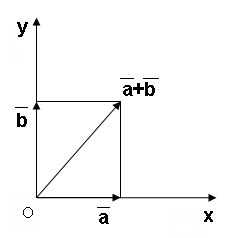
Решение: Пусть ,
и
,
. Тогда
. Следовательно, S не является подпространством
.
Пример 2. Является ли линейным подпространством линейного пространства V2 векторов-отрезков плоскости множество S всех векторов плоскости, начала и концы которых лежат на данной прямой l этой плоскости?
Решение.
Е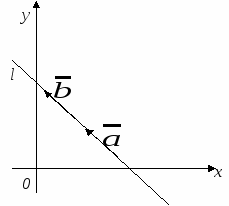
умножить на действительное число k, то получим вектор
, также принадлежащий S. Если
и
– два вектора из S, то
(по правилу сложения векторов на прямой). Следовательно, S является подпространством
.
Пример 3. Является ли линейным подпространством линейного пространства V2 множество A всех векторов плоскости, концы которых лежат на данной прямой l, (предположить, что начало любого вектора совпадает с началом координат)?
Р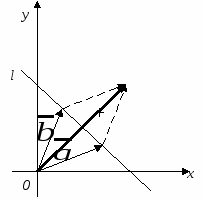
В случае, когда прямая l не проходит через начало координат множество А линейным подпространством пространства V2 не является, т.к. .
В случае, когда прямая l проходит через начало координат, множество А является линейным подпространством пространства V2, т.к. и при умножении любого вектора
на действительное число α из поля Р получим
. Таким образом, требования линейного пространства для множества А выполнены.
Пример 4. Пусть дана система векторов из линейного пространства L над полем P. Доказать, что множество всевозможных линейных комбинаций
с коэффициентами
из P является подпространством L (это подпространство A называют подпространством, порожденным системой векторов
или линейной оболочкой этой системы векторов, и обозначают так:
или
).
Решение. Действительно, так как , то для любых элементов x, y
A имеем:
,
, где
,
. Тогда
Так как , то
, поэтому
.
Проверим выполнимость второго условия теоремы. Если x – любой вектор из A и t – любое число из P, то . Поскольку
и
,
, то
,
, поэтому
. Таким образом, согласно теореме, множество A – подпространство линейного пространства L.
Для конечномерных линейных пространств справедливо и обратное утверждение.
Теорема. Всякое подпространство А линейного пространства L над полем является линейной оболочкой некоторой системы векторов.
При решении задачи нахождения базиса и размерности линейной оболочки используют следующую теорему.
Теорема. Базис линейной оболочки совпадает с базисом системы векторов
. Размерность линейной оболочки
совпадает с рангом системы векторов
.
Пример 4. Найти базис и размерность подпространства линейного пространства Р3[x], если
,
,
,
.
Решение. Известно, что векторы и их координатные строки (столбцы) обладают одинаковыми свойствами (в отношении линейной зависимости). Составляем матрицу A=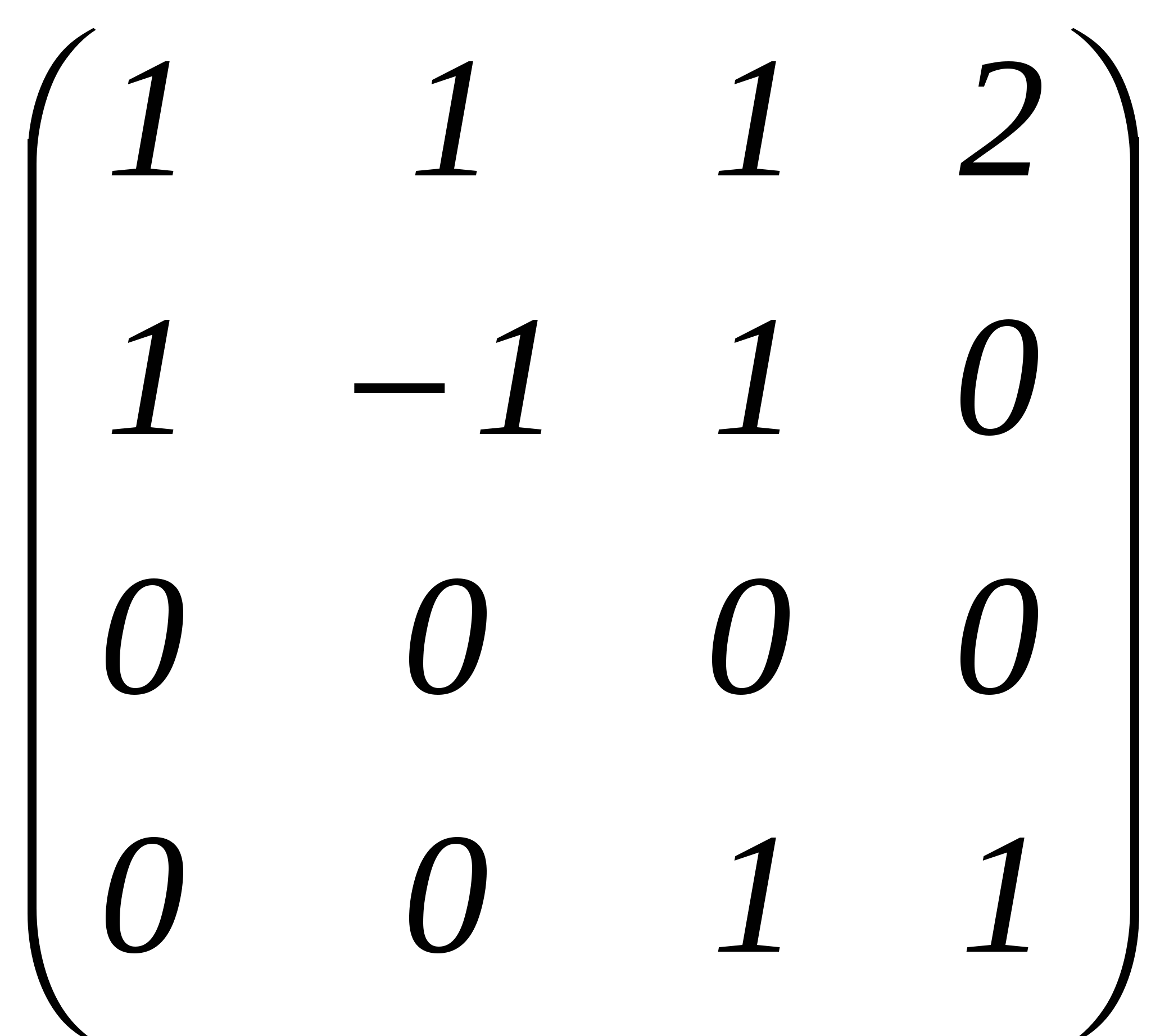
в базисе
.
Найдем ранг матрицы A.
. М3=
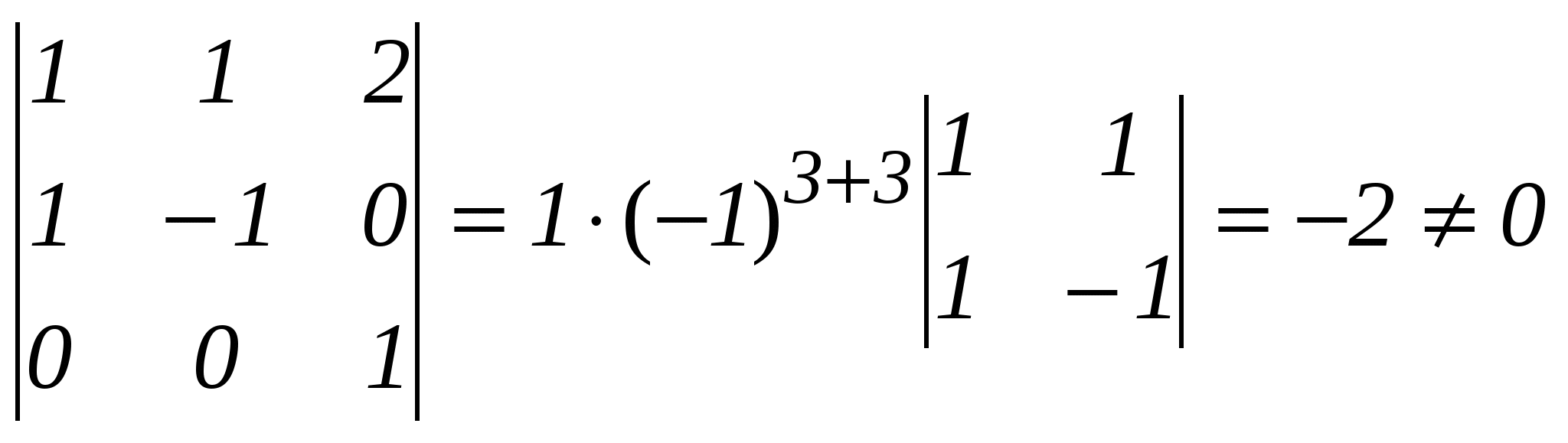
.
Следовательно, ранг r(A)=3. Итак, ранг системы векторов равен 3. Значит, размерность подпространства S равна 3, а его базис состоит из трех векторов
(т.к. в базисный минор
входят координаты только этих векторов).
Пример 5. Доказать, что множество H векторов арифметического пространства , у которых первая и последняя координаты равны 0, составляет линейное подпространство. Найти его базис и размерность.
Решение. Пусть .
Тогда ,
и
. Следовательно,
для любых
. Если
,
, то
. Таким образом, согласно теореме о линейном подпространстве, множество H является линейным подпространством пространства
. Найдем базис H. Рассмотрим следующие векторы из H:
,
,
. Эта система векторов линейно независима. Действительно, пусть
.
Тогда
и
.
Можно убедиться, что система линейно зависима при любом векторе x из H. Этим доказано, что
максимальная линейно независимая система векторов подпространства H, т.е.
– базис в H и dimH=n 2.
Достарыңызбен бөлісу:
Предположим, вы запишете векторы в строки и помощью преобразований вы выясните, что базисными строками последней матрицы будут первая и вторая. Этот факт никак не поможет вам определить, какие строки были базисными у исходной матрицы. Например, вы могли первую менять местами с десятой.
Если вы ставите векторы в столбцы, а преобразуете строки, то исходные векторы «не портятся». Несложно показать, что столбцы преобразованной матрицы представляют собой координаты тех же самых векторов в новом базисе. Поэтому линейные свойства столбцов исходной и полученной матриц совпадают. Например, пусть a1, a2, a3 — столбцы исходной матрицы, b1, b2, b3 — столбцы преобразованной. Тогда если b1 и b3 — базис столбцов преобразованной матрицы, и b2 = 2 b1 + b3, то автоматически получается, что a1 и a3 — базис столбцов исходной матрицы, и a2 = 2 a1 + a3.
В ЛА векторы естественно ставить в столбцы. Почему?
Когда вы работаете просто с наборами чисел, разницы, конечно, нет. Разница появляется, когда возникает двумерный формализм — матрицы. Здесь всё завязано, видимо, на матрицу линейного оператора. Определения таковы, что применение линейного оператора к вектору соответствует умножению матрицы на вектор-столбец справа. Столбец. Если записывать векторы в строки, обычный формализм транспонируется.
Соответственно, ковекторы (линейные функционалы) естественно записывать строками, так что применение функционала к вектору есть умножение матрицы-строки на матрицу-столбец, которое даёт число. Поэтому если, например, неизвестные СЛУ рассматривать как компоненты вектора, то коэффициенты каждого уравнения естественно задают ковектор и ставятся в строку. Получается привычный формализм: в матрице системы коэффициенты уравнений записываются в строки. Потому что это ковекторы.
В евклидовых пространствах противопоставление может терять смысл, потому что векторы и ковекторы в нём естественно отождествляются.
Линейные оболочки и подпространства
Определение. Подпространством 
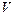
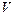

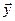
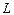
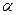
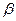
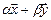
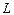
Утверждение. Подпространство само является линейным пространством.
Определение. Линейной оболочкой системы векторов 

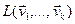
Утверждение. Линейная оболочка системы векторов является подпространством.
Определение. Пересечением двух подпространств и называется множество всех векторов, принадлежащих одновременно и ,и . Обозначается .
Определение. Суммой двух подпространств 



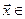

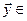

Утверждение. Сумма и пересечение подпространств 


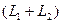

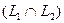




Определение. Сумма двух подпространств называется прямой суммой, если пересечение этих подпространств состоит только из нулевого вектора.
Примеры
1. Найти размерность и какой-нибудь базис суммы и пересечения подпространств, порождённых векторами 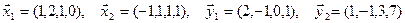
Решение. Вычислим вначале размерность подпространств. С этой целью установим, являются ли линейно независимыми векторы, порождающие данные подпространства. Для подпространства 

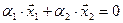
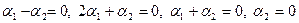
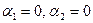

независимы и размерность подпространства 
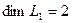

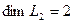
Вычислим теперь размерность пересечения подпространств 




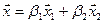

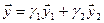
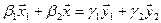
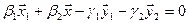

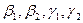
Как видно ранг системы равен 3. Значит ФСР состоит из одного линейно независимого вектора. Найдём его, решив систему уравнений, соответствующих последней матрице, получим 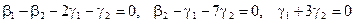
откуда 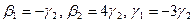
Полагая свободное неизвестное 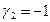
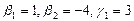
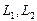
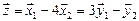
Размерность пересечения 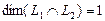
размерность суммы подпространств 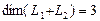

Задачи
3.39. Найти размерность и какой-нибудь базис подпространства, порожденного векторами 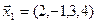
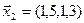

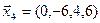
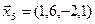
3.40. Найти размерность и какой-либо базис линейной оболочки векторов 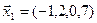
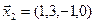
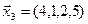
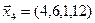
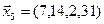
3.41. Является ли подпространством в указанном пространстве множество
а) векторов, выходящих из начала координат и заканчивающихся на фиксированной прямой, в пространстве R 2 ;
б) бесконечно малых числовых последовательностей в пространстве сходящихся последовательностей;
в) сходящихся к числу 
г) диагональных матриц в пространстве квадратных матриц того же порядка;
д) невырожденных матриц в пространстве симметричных матриц того же порядка;
е) дифференцируемых на интервале 
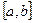
3.42. Почему не является подпространством в указанном пространстве множество
а) векторов, каждый из которых лежит на одной из координатных плоскостей, в пространстве R 3 ;
б) векторов из пространства R n , координаты которых удовлетворяют уравнению 
в) расходящихся числовых последовательностей в пространстве ограниченных последовательностей;
г) вырожденных матриц в пространстве квадратных матриц того же порядка;
д) монотонно возрастающих и ограниченных на множестве 
3.43. Найти размерность и какой-либо базис подпространства решений однородной системы:
а) 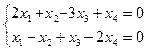
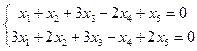
в) 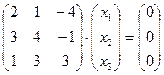
3.44. Доказать, что данное множество является подпространством в R n , найти его размерность и какой-либо базис:
а) все n-мерные векторы, координаты которых удовлетворяют уравнению 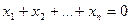
б) все n-мерные векторы, у которых первая координата равна нулю;
в) все n-мерные векторы, у которых первая и последняя координаты равны между собой;
г) все n-мерные векторы, у которых координаты с четными номерами равны нулю;
д) все n-мерные векторы, у которых координаты с нечетными номерами равны между собой.
3.45. Найти размерность суммы и пересечения подпространств, порожденных векторами 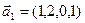
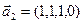
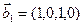
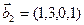
3.46. Найти размерность суммы и пересечения линейных оболочек векторов 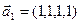
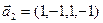
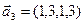

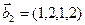
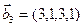
3.47. Найти базис суммы и пересечения двух подпространств, порожденных соответственно векторами 
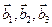
а) 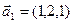
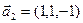
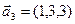
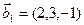
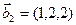
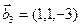
б) 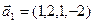
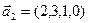
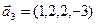
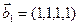
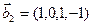
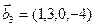
3.48. Найти базис суммы и пересечения линейных оболочек 
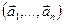

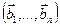
а) 
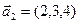
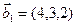
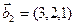
б) 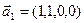
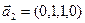
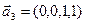
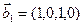
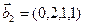
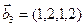
Является ли прямой сумма этих подпространств?
Векторное пространство: размерность и базис, разложение вектора по базису
В статье о n -мерных векторах мы пришли к понятию линейного пространства, порождаемого множеством n -мерных векторов. Теперь нам предстоит рассмотреть не менее важные понятия, такие как размерность и базис векторного пространства. Они напрямую связаны с понятием линейно независимой системы векторов, так что дополнительно рекомендуется напомнить себе основы и этой темы.
Введем некоторые определения.
Размерность векторного пространства – число, соответствующее максимальному количеству линейно независимых векторов в этом пространстве.
Базис векторного пространства – совокупность линейно независимых векторов, упорядоченная и в своей численности равная размерности пространства.
Рассмотрим некое пространство n -векторов. Размерность его соответственно равна n . Возьмем систему из n -единичных векторов:
e ( 1 ) = ( 1 , 0 , . . . , 0 ) e ( 2 ) = ( 0 , 1 , . . . , 0 ) e ( n ) = ( 0 , 0 , . . . , 1 )
Используем эти векторы в качестве составляющих матрицы A : она будет являться единичной с размерностью n на n . Ранг этой матрицы равен n . Следовательно, векторная система e ( 1 ) , e ( 2 ) , . . . , e ( n ) является линейно независимой. При этом к системе невозможно добавить ни одного вектора, не нарушив ее линейной независимости.
Так как число векторов в системе равно n , то размерность пространства n -мерных векторов равна n , а единичные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом указанного пространства.
Из полученного определения сделаем вывод: любая система n -мерных векторов, в которой число векторов меньше n , не является базисом пространства.
Если мы поменяем местами первый и второй вектор, получим систему векторов e ( 2 ) , e ( 1 ) , . . . , e ( n ) . Она также будет являться базисом n -мерного векторного пространства. Составим матрицу, взяв за ее строки векторы полученной системы. Матрица может быть получена из единичной матрицы перестановкой местами первых двух строк, ранг ее будет равен n . Система e ( 2 ) , e ( 1 ) , . . . , e ( n ) линейно независима и является базисом n -мерного векторного пространства.
Переставив местами в исходной системе другие векторы, получим еще один базис.
Мы можем взять линейно независимую систему неединичных векторов, и она также будет представлять собой базис n -мерного векторного пространства.
Векторное пространство с размерностью n имеет столько базисов, сколько существует линейно независимых систем из n -мерных векторов числом n.
Плоскость является двумерным пространством – ее базисом будут два любых неколлинеарных вектора. Базисом трехмерного пространства послужат три любых некомпланарных вектора.
Рассмотрим применение данной теории на конкретных примерах.
Исходные данные: векторы
a = ( 3 , — 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , — 1 , — 2 )
Необходимо определить, являются ли указанные векторы базисом трехмерного векторного пространства.
Решение
Для решения поставленной задачи исследуем заданную систему векторов на линейную зависимость. Составим матрицу, где строки – координаты векторов. Определим ранг матрицы.
A = 3 2 3 — 2 1 — 1 1 2 — 2 A = 3 — 2 1 2 1 2 3 — 1 — 2 = 3 · 1 · ( — 2 ) + ( — 2 ) · 2 · 3 + 1 · 2 · ( — 1 ) — 1 · 1 · 3 — ( — 2 ) · 2 · ( — 2 ) — 3 · 2 · ( — 1 ) = = — 25 ≠ 0 ⇒ R a n k ( A ) = 3
Следовательно, заданные условием задачи векторы линейно независимы, и их численность равна размерности векторного пространства – они являются базисом векторного пространства.
Ответ: указанные векторы являются базисом векторного пространства.
Исходные данные: векторы
a = ( 3 , — 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , — 1 , — 2 ) d = ( 0 , 1 , 2 )
Необходимо определить, может ли указанная система векторов являться базисом трехмерного пространства.
Решение
Указанная в условии задачи система векторов является линейно зависимой, т.к. максимальное число линейно независимых векторов равно 3. Таким образом, указанная система векторов не может служить базисом трехмерного векторного пространства. Но стоит отметить, что подсистема исходной системы a = ( 3 , — 2 , 1 ) , b = ( 2 , 1 , 2 ) , c = ( 3 , — 1 , — 2 ) является базисом.
Ответ: указанная система векторов не является базисом.
Исходные данные: векторы
a = ( 1 , 2 , 3 , 3 ) b = ( 2 , 5 , 6 , 8 ) c = ( 1 , 3 , 2 , 4 ) d = ( 2 , 5 , 4 , 7 )
Могут ли они являться базисом четырехмерного пространства?
Решение
Cоставим матрицу, используя в качестве строк координаты заданных векторов
A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7
По методу Гаусса определим ранг матрицы:
A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7
1 2 3 3 0 1 0 2 0 1 — 1 1 0 1 — 2 1
1 2 3 3 0 1 0 2 0 0 — 1 — 1 0 0 — 2 — 1
1 2 3 3 0 1 0 2 0 0 — 1 — 1 0 0 0 1 ⇒ ⇒ R a n k ( A ) = 4
Следовательно, система заданных векторов линейно независима и их численность равна размерности векторного пространства – они являются базисом четырехмерного векторного пространства.
Ответ: заданные векторы являются базисом четырехмерного пространства.
Исходные данные: векторы
a ( 1 ) = ( 1 , 2 , — 1 , — 2 ) a ( 2 ) = ( 0 , 2 , 1 , — 3 ) a ( 3 ) = ( 1 , 0 , 0 , 5 )
Составляют ли они базис пространства размерностью 4?
Решение
Исходная система векторов линейно независима, но численность векторов в ней недостаточна, чтобы стать базисом четырехмерного пространства.
Ответ: нет, не составляют.
Разложение вектора по базису
Примем, что произвольные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом векторного n-мерного пространства. Добавим к ним некий n -мерный вектор x → : полученная система векторов станет линейно зависимой. Свойства линейной зависимости гласят, что хотя бы один из векторов такой системы может линейно выражаться через остальные. Переформулируя это утверждение, можно говорить о том, что хотя бы один из векторов линейно зависимой системы может раскладываться по остальным векторам.
Таким образом, мы пришли к формулировке важнейшей теоремы:
Любой вектор n -мерного векторного пространства единственным образом раскладывается по базису.
Докажем эту теорему:
зададим базис n -мерного векторного пространства — e ( 1 ) , e ( 2 ) , . . . , e ( n ) . Сделаем систему линейно зависимой, добавив к ней n -мерный вектор x → . Этот вектор может быть линейно выражен через исходные векторы e :
x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) , где x 1 , x 2 , . . . , x n — некоторые числа.
Теперь докажем, что такое разложение является единственным. Предположим, что это не так и существует еще одно подобное разложение:
Отнимем от левой и правой частей этого равенства соответственно левую и правую части равенства x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) . Получим:
1 — x 1 ) · e ( 1 ) + ( x
2 — x 2 ) · e ( 2 ) + . . . ( x
Система базисных векторов e ( 1 ) , e ( 2 ) , . . . , e ( n ) линейно независима; по определению линейной независимости системы векторов равенство выше возможно только тогда, когда все коэффициенты ( x
2 — x 2 ) , . . . , ( x
n — x n ) будут равны нулю. Из чего справедливым будет: x 1 = x
n . И это доказывает единственный вариант разложения вектора по базису.
При этом коэффициенты x 1 , x 2 , . . . , x n называются координатами вектора x → в базисе e ( 1 ) , e ( 2 ) , . . . , e ( n ) .
Доказанная теория делает понятным выражение «задан n -мерный вектор x = ( x 1 , x 2 , . . . , x n ) »: рассматривается вектор x → n -мерного векторного пространства, и его координаты заданы в некотором базисе. При этом также понятно, что этот же вектор в другом базисе n -мерного пространства будет иметь другие координаты.
Рассмотрим следующий пример: допустим, что в некотором базисе n -мерного векторного пространства задана система из n линейно независимых векторов
e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )
а также задан вектор x = ( x 1 , x 2 , . . . , x n ) .
Векторы e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) в этом случае также являются базисом этого векторного пространства.
Предположим, что необходимо определить координаты вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) , обозначаемые как x
Вектор x → будет представлен следующим образом:
2 · e ( 2 ) + . . . + x
Запишем это выражение в координатной форме:
( x 1 , x 2 , . . . , x n ) = x
1 · ( e ( 1 ) 1 , e ( 1 ) 2 , . . . , e ( 1 ) n ) + x
2 · ( e ( 2 ) 1 , e ( 2 ) 2 , . . . , e ( 2 ) n ) + . . . + + x
n · ( e ( n ) 1 , e ( n ) 2 , . . . , e ( n ) n ) = = ( x
2 e 1 ( 2 ) + . . . + x
2 e 2 ( 2 ) + + . . . + x
n e 2 ( n ) , . . . , x
2 e n ( 2 ) + . . . + x
Полученное равенство равносильно системе из n линейных алгебраических выражений с n неизвестными линейными переменными x
n e 2 n ⋮ x n = x
Матрица этой системы будет иметь следующий вид:
e 1 ( 1 ) e 1 ( 2 ) ⋯ e 1 ( n ) e 2 ( 1 ) e 2 ( 2 ) ⋯ e 2 ( n ) ⋮ ⋮ ⋮ ⋮ e n ( 1 ) e n ( 2 ) ⋯ e n ( n )
Пусть это будет матрица A , и ее столбцы – векторы линейно независимой системы векторов e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) . Ранг матрицы – n , и ее определитель отличен от нуля. Это свидетельствует о том, что система уравнений имеет единственное решение, определяемое любым удобным способом: к примеру, методом Крамера или матричным методом. Таким образом мы сможем определить координаты x
n вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) .
Применим рассмотренную теорию на конкретном примере.
Исходные данные: в базисе трехмерного пространства заданы векторы
e ( 1 ) = ( 1 , — 1 , 1 ) e ( 2 ) = ( 3 , 2 , — 5 ) e ( 3 ) = ( 2 , 1 , — 3 ) x = ( 6 , 2 , — 7 )
Необходимо подтвердить факт, что система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) также служит базисом заданного пространства, а также определить координаты вектора х в заданном базисе.
Решение
Система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) будет являться базисом трехмерного пространства, если она линейно независима. Выясним эту возможность, определив ранг матрицы A , строки которой – заданные векторы e ( 1 ) , e ( 2 ) , e ( 3 ) .
Используем метод Гаусса:
A = 1 — 1 1 3 2 — 5 2 1 — 3
1 — 1 1 0 5 — 8 0 3 — 5
1 — 1 1 0 5 — 8 0 0 — 1 5
R a n k ( A ) = 3 . Таким образом, система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) линейно независима и является базисом.
Пусть в базисе вектор x → имеет координаты x
3 . Связь этих координат определяется уравнением:
3 e 1 ( 3 ) x 2 = x
3 e 2 ( 3 ) x 3 = x
Применим значения согласно условиям задачи:
Решим систему уравнений методом Крамера:
∆ = 1 3 2 — 1 2 1 1 — 5 — 3 = — 1 ∆ x
1 = 6 3 2 2 2 1 — 7 — 5 — 3 = — 1 , x
1 ∆ = — 1 — 1 = 1 ∆ x
2 = 1 6 2 — 1 2 1 1 — 7 — 3 = — 1 , x
2 ∆ = — 1 — 1 = 1 ∆ x
3 = 1 3 6 — 1 2 2 1 — 5 — 7 = — 1 , x
Так, вектор x → в базисе e ( 1 ) , e ( 2 ) , e ( 3 ) имеет координаты x
Ответ: x = ( 1 , 1 , 1 )
Связь между базисами
Предположим, что в некотором базисе n-мерного векторного пространства даны две линейно независимые системы векторов:
c ( 1 ) = ( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) c ( 2 ) = ( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) ⋮ c ( n ) = ( c 1 ( n ) , e 2 ( n ) , . . . , c n ( n ) )
e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )
Указанные системы являются также базисами заданного пространства.
n ( 1 ) — координаты вектора c ( 1 ) в базисе e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) , тогда связь координат будет задаваться системой линейных уравнений:
1 ( 1 ) e 1 ( 1 ) + c
2 ( 1 ) e 1 ( 2 ) + . . . + c
n ( 1 ) e 1 ( n ) с 2 ( 1 ) = c
1 ( 1 ) e 2 ( 1 ) + c
2 ( 1 ) e 2 ( 2 ) + . . . + c
n ( 1 ) e 2 ( n ) ⋮ с n ( 1 ) = c
1 ( 1 ) e n ( 1 ) + c
2 ( 1 ) e n ( 2 ) + . . . + c
В виде матрицы систему можно отобразить так:
( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) = ( c
n ( 1 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
Сделаем по аналогии такую же запись для вектора c ( 2 ) :
( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) = ( c
n ( 2 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
И, далее действуя по тому же принципу, получаем:
( c 1 ( n ) , c 2 ( n ) , . . . , c n ( n ) ) = ( c
n ( n ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )
Матричные равенства объединим в одно выражение:
c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n ) = c
n ( n ) · e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n )
Оно и будет определять связь векторов двух различных базисов.
Используя тот же принцип, возможно выразить все векторы базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) через базис c ( 1 ) , c ( 2 ) , . . . , c ( n ) :
e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n ) = e
n ( n ) · c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n )
Дадим следующие определения:
n ( n ) является матрицей перехода от базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 )
к базису c ( 1 ) , c ( 2 ) , . . . , c ( n ) .
n ( n ) является матрицей перехода от базиса c ( 1 ) , c ( 2 ) , . . . , c ( n )
к базису e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) .
http://zaochnik.com/spravochnik/matematika/vektory/vektornoe-prostranstvo/