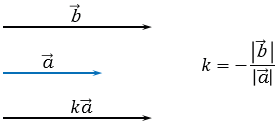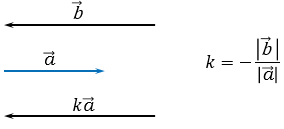Как найти разложение вектора по неколлинеарным векторам - Avtoru.top

На чтение 6 мин. Просмотров 1.4k.

Вы узнаете в этой статье что значит разложить вектор по двум неколлинеарным векторам.

Представление вектора vec{c} в виде vec{c}=x vec{a}+y vec{b}, где векторы vec{a} и vec{b} являются неколлинеарными векторами, называется разложением вектора по двум неколлинеарным векторам.

Теорема (о разложении вектора по двум неколлинеарным векторам)

Теорема. Любой вектор с можно единственным образом представить в виде vec{c}=x vec{a}+y vec{b}, где vec{a} и vec{b} — неколлинеарные векторы, х и у — числа.

Коллинеарные вектора vec{m} и vec{n} — это такие вектора, где один из векторов параллелен другому и связан с ним соотношением

vec{m}=kvec{n}

Доказательство:

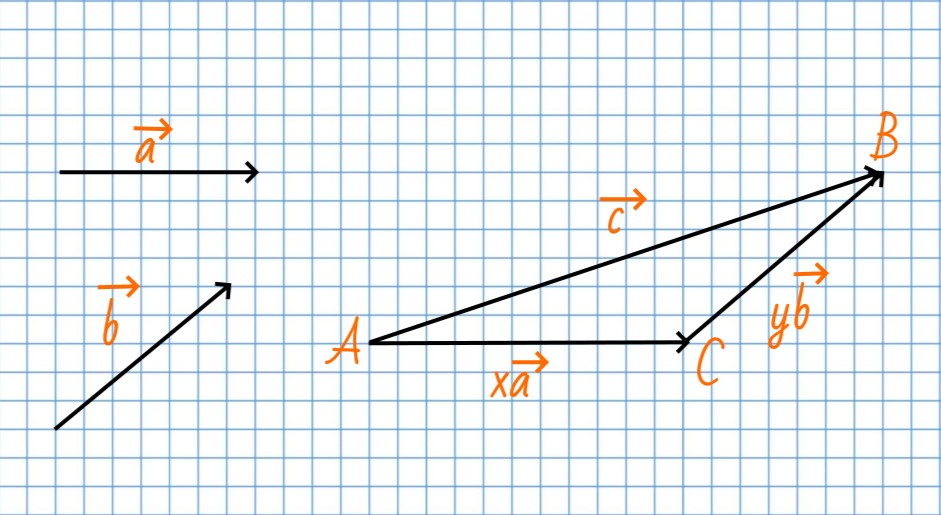
Пусть даны векторы vec{c}=overrightarrow{AB}, vec{a} и vec{b}. Проведем через точки A и B прямые, параллельные векторам vec{a} и vec{b}, и обозначим точку C их пересечения. Тогда overrightarrow{AB}=overrightarrow{AC}+overrightarrow{CB}.

К теореме о разложении вектора по двум коллинеарным векторам

Так как векторы vec{a} и overrightarrow{AC} коллинеарные, то существует такое число х, что overrightarrow{AC} =хvec{a}. Векторы vec{b} и overrightarrow{CB} тоже коллинеарные, следовательно, существует такое число у, что overrightarrow{CB} =yvec{b}.

Таким образом, vec{c}=x vec{a}+y vec{b}.

Докажем единственность такого представления вектора с способом от противного. Допустим, что имеется другое разложение вектора, например, такое:

vec{c}=n vec{a}+m vec{b}, тогда два разложения вектора vec{c} можно приравнять:
n vec{a}+m vec{b}=x vec{a}+y vec{b} (если равны левые части равенств, то равны и правые).

Перенесем все в левую часть равенства:

n vec{a}+m vec{b}-x vec{a}-y vec{b}=0
(n-x)vec{a}+(m-y) vec{b}=0
displaystyle vec{a}=frac{y-m}{n-x} vec{b}

То есть векторы vec{a} и vec{b} получаются коллинеарными. А у нас условие — векторы vec{a} и vec{b} — неколлинеарные вектора.

Таким образом, возможно только единственно возможное представление вектора vec{c} в виде vec{c}=x vec{a}+y vec{b}, где векторы vec{a} и vec{b} являются неколлинеарными векторами.

Теорема доказана.

Если вектор vec{c} коллинеарен какому-либо из векторов vec{a} и vec{b}, то либо число x, либо число y равно нулю.

Базис векторов и разложение вектора по базису

В декартовой системе координат Oxy вектор с координатами (x, y) можно разложить по единичным векторам vec{e_1}(1;0) и vec{e_2}(0;1).

Тогда, например, вектор vec{c}(3; -1) можно представить в виде разложения:

vec{c}=x vec{e_1}+y vec{e_2}=3 vec{e_1}-1 vec{e_2}

Действительно:

begin{cases} 3=3 cdot 1+(-1)cdot 0, \ — 1=3 cdot 0+(-1)cdot 1. end{cases}

Система векторов, по которым можно разложить вектор с коэффициентами разложения равными его координатам, называется базисом вектора. Вектора базиса всегда не коллинеарные. Координаты вектора будут верны только в отношении данного базиса.

Однако, это не отменяет тот факт, что вектор можно разложить и по другим векторам, то есть по новому базису. Тогда говорят о переходе к новому базису векторов.

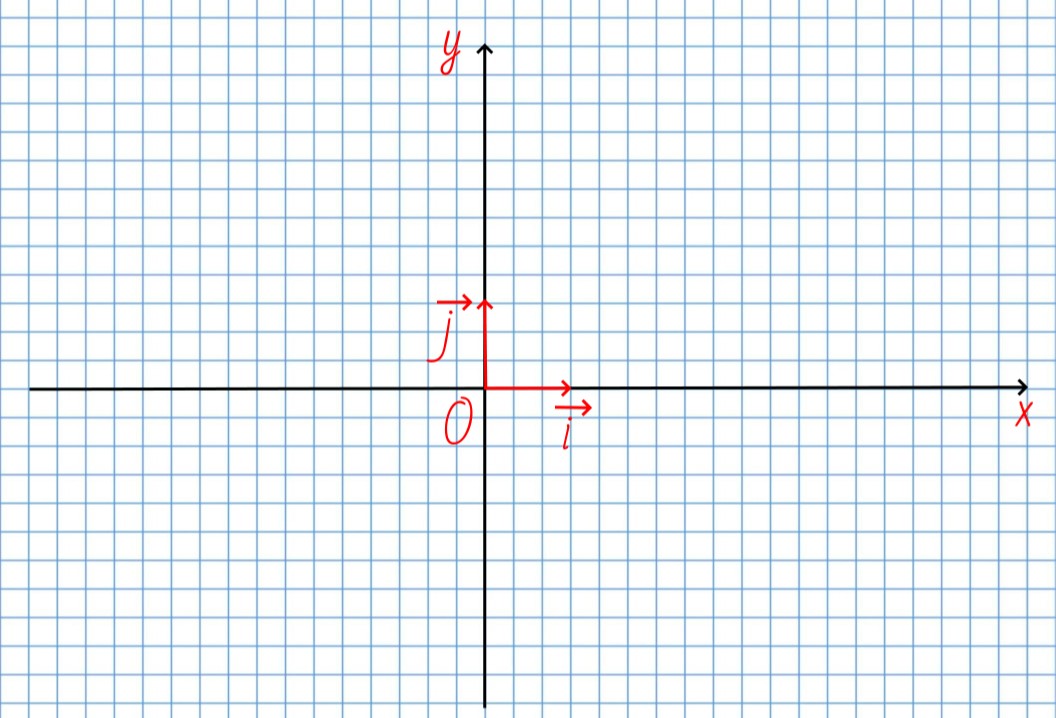
Обычно в декартовой системе координат базисные векторы на плоскости обозначают так: vec{i}(1;0) и vec{j}(0;1).

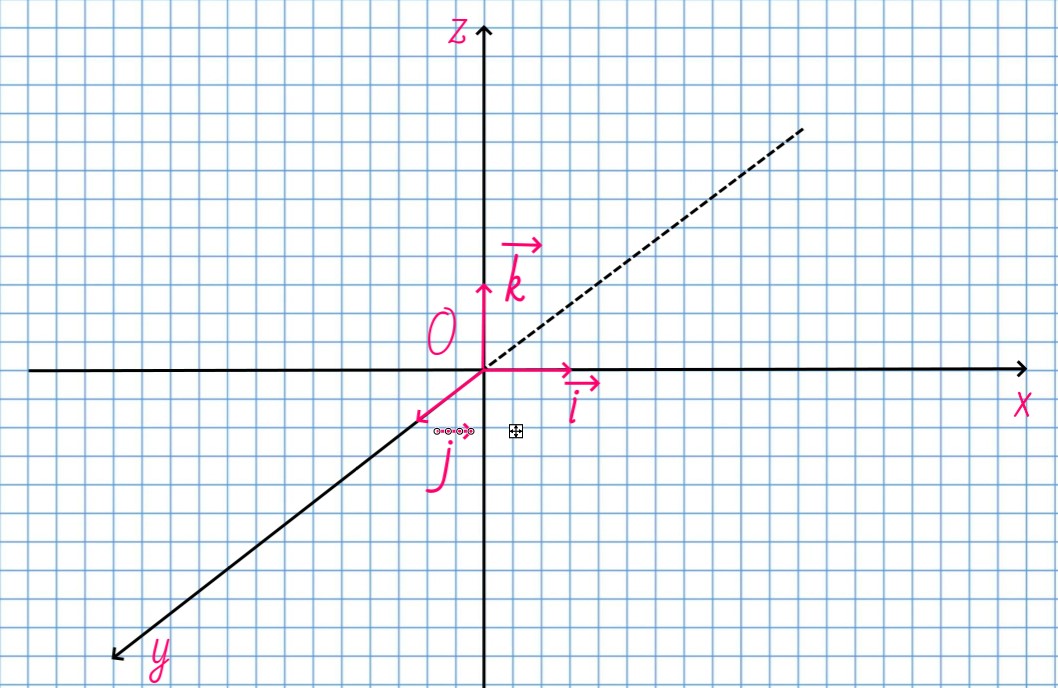
В пространственной декартовой системе координат базис векторов будет: vec{i}(1; 0; 0), vec{j}(0;1; 0), vec{k}(0;0;1)

В то же время на любых векторах можно построить свою систему отсчета, тогда данные вектора будут считаться базисом этой системы и в этой системе можно найти координаты любого вектора. То есть любой вектор можно разложить по базису, конечно, если при этом базисные вектора не являются коллинеарными.

Примеры разложения вектора

Пример 1. Разложить вектор vec{c}(0; 1) по двум векторам vec{a}(3; 6) и vec{b}(4; 9).

Решение:

Для разложения вектора vec{c} запишем:

vec{c}=x vec{a}+y vec{b}

Нам нужно найти коэффициенты разложения x и y, для этого разложим каждую координату вектора vec{c}:

Для абсциссы: 0=x cdot 3+y cdot 4
Для ординаты: 1=x cdot 6+y cdot 9

Получаем систему из двух уравнений с двумя неизвестными, которую решаем:

begin{cases} 3x+4y=0, \ 6x+9y=1. end{cases}

Решая, получаем: displaystyle x=frac{-4}{3} и y=1
И разложение вектора vec{c} будет иметь вид: displaystyle vec{c}=-frac{4}{3} vec{a}+vec{b}

Пример 2. Найти координаты вектора vec{a} в базисе, если известно разложение вектора по базису vec{e_1} и vec{e_2}:

vec{a}=7 vec{e_1}+5 vec{e_2}

Решение: Координаты вектора в базисе векторов vec{e_1} и vec{e_2} будут равны коэффициентам разложения, то есть vec{a}(7; 5)

Ответ: vec{a}(7; 5)

Пример 3. Разложить вектор vec{b}(1; 2) по базису vec{e_1}(2; 3) и vec{e_2}(2; 5).

Решение:

Запишем разложение вектора по базису:

vec{b}=b_1 vec{e_1}+b_2 vec{e_2}

Получим систему уравнений:

begin{cases} 1=2b_1+4b_2, \ 2=2b_1+5b_2. end{cases}

От второго уравнения системы отнимем первое, получим:

begin{cases} 1=b_2, \ 2=2b_1+5b_2. end{cases}

Тогда:

begin{cases} b_2=1, \ b_1=-1,5. end{cases}

И разложение вектора будет иметь вид: vec{b}=-1,5 vec{e_1}+vec{e_2}

Источник

Вам
уже хорошо знакомо понятие вектора, и вы умеете выполнять некоторые действия
над векторами. А именно: складывать, вычитать и умножать вектор на число.

На
этом уроке мы приступаем к более глубокому изучению вопроса о векторах и для
начала запишем лемму о коллинеарных векторах.

Лемма. Если
векторы и
коллинеарны
и ,
то существует такое число ,
что .

Доказательство.

Пусть,
тогда .

Что
и требовалось доказать.

Выполним
задание.

Выразить
коллинеарные векторы ,
,
,
,
и
через
коллинеарный им вектор .

Решение.

Итак,
начнём с вектора Видим,
что векторы и
сонаправлены.
Значит, k>0.

Также,
взяв длину вектора за
единицу, видим что длина вектора в
3 раза больше.

Можем
записать, что вектор равен
произведению вектора на
число 3.

Рассмотрим
следующий вектор, вектор .
Он так же сонаправлен с вектором ,
поэтому k>0. При этом длина
вектора в
6,5 раза больше длины вектора .

Тогда
вектор равен
произведению вектора на
6,5.

Далее
рассмотрим вектор .

Он противоположно
направлен с вектором .
Поэтому k<0. К тому же длина
вектора в
5,5 раза больше длины вектора .
Тогда вектор .

Далее
не сложно записать, что вектор .

Следующим рассмотрим вектор
.
Он противоположно направлен вектору и
его длина в 2 раза меньше, поэтому вектор .

Остался вектор .
Как видите, он нулевой. Нам известно, что нулевой вектор сонаправлен любому
вектору. И его длина равна нулю. Поэтому вектор .

Сейчас
вспомним правило параллелограмма сложения двух векторов.

Если векторы-слагаемые и
отложены
от одной точки, то, построив на них параллелограмм ABCD,
мы получим вектор их
суммы.

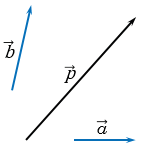
Обозначим
вектор как
вектор .
Он равен сумме .

В
свою очередь вектор всегда
можно выразить как произведение коллинеарного ему вектора на
некоторое число x, а вектор —
как произведение коллинеарного ему вектора на
некоторое число y.

Тогда
можно записать, что вектор .

В
таком случае говорят, что Вектор разложен по неколлинеарным векторам и . , коэффициенты разложения.

Теорема. На
плоскости любой вектор можно разложить по двум данным неколлинеарным векторам,
причём коэффициенты разложения определяются единственным образом.

Доказательство.

Пусть данными векторами
будут неколлинеарные векторы и
.

Докажем, что любой вектор
можно
разложить по данным векторам.

В
этом случае по лемме о двух коллинеарных векторах получаем, что вектор
.

Так
же можно записать его разложение по векторам и
.
Только коэффициент разложения при векторе будет
равен нулю .

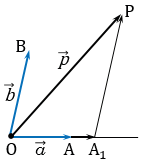
Отметим
некоторую точку О и отложим от неё векторы ,
и
,
равные векторам ,
и
соответственно.

Через
точку P проведём прямую
параллельную прямой .
Точку пересечения полученной прямой с ОА обозначим как А₁.

По
правилу треугольника вектор .
Вектор коллинеарен
вектору ,
вектор коллинеарен
вектору .
Это значит, что вектор ,
а вектор .

Отсюда
получаем, что вектор .
Тем самым мы разложили его по векторам и
.

Первая
часть теоремы доказана. Действительно, на плоскости любой вектор можно
разложить по двум данным неколлинеарным векторам.

Теперь
докажем, что коэффициенты разложения x
и y определяются единственным способом.

Допустим,
что кроме разложения возможно
другое разложение, .

Вычтем
второе равенство из первого.

Получаем,
что нулевой вектор можно разложить по векторам и
,
при этом коэффициенты разложения равны и
.

Такое
возможно только в том случае, если данные коэффициенты разложения равны нулю. А
значит, при и
.

Значит,
коэффициенты разложения определяются единственным способом.

Что
и требовалось доказать.

Рассмотрим
пример. Запишем разложение вектора по
векторам и
.

Все
они отложены от точки О. При этом векторы ,
и
равны
векторам ,
и
соответственно.

Через
точку P проведём прямую,
параллельную OB. И точку пересечения
этой прямой с ОА назовём А₁.

По
правилу треугольника вектор .
Вектор .

Аналогично,
выразим .

Тогда
разложение вектора по
векторам

Теперь
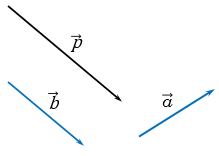
выполним задание, в котором векторы и
,
изображённые в координатной плоскости, нужно разложить по двум векторам и
.

Итак,
начнём с вектора .
Восстановим для него правило треугольника сложения двух векторов так, чтобы
вектор являлся
вектором суммы, а векторы-слагаемые и
были
коллинеарны векторам и
соответственно.

Аналогично
поступим с другими векторами.

На
примере этого задания вы увидели, как можно раскладывать векторы по двум
неколлинеарным векторам.

Подведём
итоги урока.

Сегодня
вы узнали, что любой вектор можно выразить через коллинеарный ему вектор
умножением на некоторое число k.

Также
мы рассмотрели примеры и убедились в том, что на плоскости любой вектор можно
разложить по двум данным неколлинеарным векторам, причём коэффициенты
разложения определяются единственным образом.

Источник

Главная
Справочники
Справочник по геометрии 7-9 класс
Метод координат
Разложение вектора по двум неколлинеарным векторам

Лемма

Доказательство

Дано: и коллинеарны, .

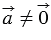
Доказать: существует такое число 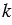, что .

Доказательство:

Возможны два случая:

1) .

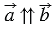
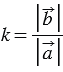
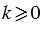
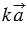
Пусть число . Так как , то векторы и сонаправлены.

При этом, их длины равны: 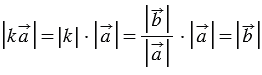. Следовательно, .

2) .

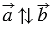
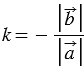
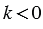
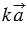
Пусть число . Так как , то векторы и сонаправлены.

При этом, их длины равны: 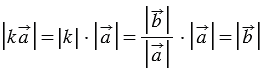. Следовательно, . Лемма доказана.

Пусть и два данных вектора. Если вектор представлен в виде , где и — некоторые числа, то говорят, что вектор разложен по векторам и . Числа и называются коэффициентами разложения.

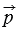
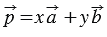
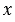
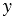
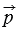
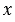
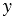
Теорема

На плоскости любой вектор можно разложить по двум данным неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом.

Доказательство

Дано: и неколлинеарные.

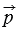
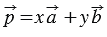
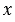
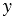
Доказать: любой вектор можно разложить по векторам и , т.е. , и определяются единственным образом.

Доказательство:

1 случай

Вектор 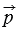коллинеарен одному из векторов и , например, вектору .

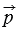
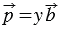
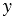
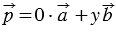
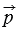
Тогда по лемме о коллинеарных векторах вектор можно представить в виде , где — некоторое число, следовательно, , т.е. вектор можно разложить по векторам и .

2 случай

Вектор 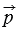не коллинеарен ни вектору , ни вектору .

Отметим какую-нибудь точку О и отложим от нее векторы 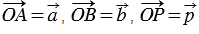. Через точку Р проведем прямую, параллельную прямой ОВ, которая пересечет прямую ОА в точке А₁.

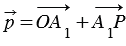
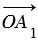
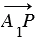
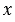
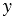
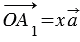
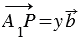
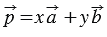
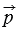
По правилу треугольника сложения двух векторов , при этом векторы и коллинеарны векторам и , следовательно, по лемме о коллинеарных векторах существуют такие числа и такие, что и . Поэтому , т.е. вектор можно разложить по векторам и .

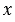
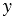
Докажем, что коэффициенты и определяются единственным образом.

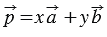
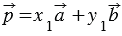
Допустим, что вместе с разложением (1) существует и другое разложение . (2)

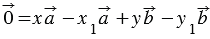
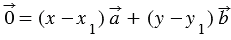
Вычтем из равенства (1) равенство (2), получим: , откуда, учитывая правила действий над векторами, . (3)

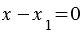
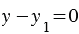
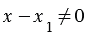
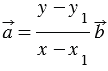
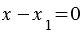
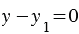
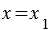
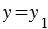
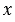
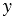
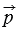
Равенство (3) выполнимо только в том случае, когда и . Действительно, если предположить, что , то из равенства (3) получим, что , значит, векторы и коллинеарны, что противоречит условию теоремы. Следовательно, и , откуда и , а это говорит о том, что коэффициенты и разложения вектора определяются единственным образом. Теорема доказана.

Советуем посмотреть:

Координаты вектора

Связь между координатами вектора его начала и конца

Простейшие задачи в координатах

Уравнение линии на плоскости

Уравнение окружности

Уравнение прямой

Взаимное расположение двух окружностей

Метод координат

Правило встречается в следующих упражнениях:

7 класс

Задание 912,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 914,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 915,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 916,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 919,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 920,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 921,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 3,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 988,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Источник

Математика

Тема 5: Метод координат

Урок 4: Координаты вектора. Разложение вектора по двум неколлинеарным векторам

Видео
Тренажер
Теория

Заметили ошибку?

Координаты вектора. Разложение вектора по двум неколлинеарным векторам.

Если векторы a⃗ и b⃗ коллинеарны и a⃗≠0⃗, то существует такое число k, что b⃗=ka⃗.

Пусть a⃗ и b⃗ – два данных вектора. Если вектор p представлен в виде p⃗=xa⃗+yb⃗, где x и y – некоторые числа, то говорят, что вектор p⃗ разложен по векторам a⃗ и b⃗. Числа x и y называются коэффициентами разложения.

Теорема

Напомню, что для задания прямоугольной системы координат нужно провести две взаимно перпендикулярные прямые, на каждой из них выбрать направление (оно обозначается стрелкой) и выбрать единицу измерения отрезков. При выбранной единице измерения отрезков длина каждого отрезка выражается положительным числом.

В дальнейшем под длиной отрезка мы будем понимать это число.

Отложим от начала координат O единичные векторы (т.е. векторы, длины которых равны единице) i⃗ и j⃗ так, чтобы направление вектора i⃗совпало с напралением оси Ox, а направление вектора j⃗ – с направлением оси Oy. Векторы i⃗ и j⃗ назовем координатными векторами.

Координатные векторы не коллинеарны, поэтому любой вектор p⃗ можно разложить по координатным векторам, т.е. представить в виде p⃗=xi⃗+yj⃗, причем коэффициенты разложения (числа x и y) определяются единственным образом. Коэффициенты разложения вектора p⃗ по координатным векторамназываются координатными векторамиp⃗ в данной системе координат. Координаты вектора будем записывать в фигурных скобках после обозначения вектора: p⃗{x;y}.

Так как нулевой вектор можно представить в виде 0⃗=0.i⃗+0^.j⃗, то его координаты равны нулю: 0⃗{0;0}. Если векторы a⃗=x1i⃗+y1j⃗ и b⃗=x₂i⃗+y₂j⃗ равны, то x₁ = x₂ и y₁ = y₃. Таким образом, координаты равных векторов соответственно равны.

Рассмотрим правила, позволяющие по координатам векторов находить координаты их суммы, разности и произведения вектора на число.

Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов.

Докажем это утверждение для двух векторов. Рассмотрим векторы a{x1;y1} и b{x2;y2}. Так как a⃗=x1i⃗+y1j⃗ и b ⃗=x2i⃗ +y2j⃗ ,то, пользуясь свойствами сложения векторов и умножения вектора на число, получим:

a⃗+b⃗=x₁i⃗+y₁j⃗+x₂i⃗+y₂j⃗=(x₁+x₂)i⃗+(y₁+y₂)j⃗ .

Следовательно, что координаты вектора a⃗+b⃗ равны {x1+x2; y1+y2}.

Аналогично доказывается следующее утверждение:
Каждая координата разности двух или более векторов равна разности соответствующих координат этих векторов.

Иными словами, если a⃗{x₁;y₁} и b⃗{x₂;y₂} – данные векторы, то вектор a⃗–b⃗ имеет координаты {x1-x2;y1-y2}.
Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.

В самом деле, пусть вектор a⃗ имеет координаты {x;y}. Найдем координаты вектора ka⃗, гдеk – произвольное число. Так как a⃗=xi⃗+yj⃗, то kxi⃗+kyj⃗. Отсюда следует, что координаты вектора ka⃗ равны {kx;ky}.

Рассмотренные правила позволяют определить координаты любого вектора, представленного в виде алгебраической суммы данных векторов с известными координатами.

Найти координаты вектора a⃗+b⃗,если a⃗{3;2},b⃗{2;5}

Чтобы найти координаты вектора суммы, надо сложить соответствующие координаты данных векторов, получим:

a⃗+b⃗ имеет координаты {3 + 2; 2 + 5}, то есть {5; 7}

Найти координаты вектора 2a⃗, если a⃗{3;2}

Значит, вектор 2a⃗ имеет координаты {2 ⋅ 3; 2 ⋅ 2}, то есть {6;4}

Итак, сегодня мы узнали, что любой вектор можно разложить по двум неколлинеарным векторам, ввели понятие координат вектора и рассмотрели правила, позволяющие находить координаты суммы, разности векторов, и произведения вектора на число. А в следующий раз мы найдем связь между координатами вектора и координатами его начала и конца.

Заметили ошибку?

Расскажите нам об ошибке, и мы ее исправим.

Источник

Разложение вектора по двум неколлинеарным векторам.

Напомним, что коллинеарными называются векторы, лежащие на одной прямой или на параллельных прямых. Соответственно, неколлинеарными будут векторы, которые не лежат на одной прямой и не параллельны.

Любой вектор можно разложить (т.е. представить в виде суммы или разности) по двум неколлинеарным векторам. Мы докажем такую теорему, но чуть позже. Сначала лемма.

ЛЕММА. Если векторы и коллинеарны и , то существует такое число , что .

Дано: ,

Доказать: .

Доказательство.

По условию, векторы и коллинеарны, значит, они либо лежат на одной прямой, либо на параллельных прямых. Доказательство для обоих случаев одинаково, поэтому рассмотрим второй из них. Коллинеарные векторы могут быть сонаправленными или противоположно направленными.

a) . Поскольку число произвольное, то и выбрать мы его можем произвольным образом, например, . Правая часть состоит из частного модулей, значит, . Учитывая, что при умножении положительного числа на вектор, этот вектор своего направления не меняет, заключаем, что , и, значит, .

Посмотрим, какое соотношение имеют длины этих векторов.

Итак, векторы и сонаправлены и равны по модулю, значит, эти векторы равны (по определению равных векторов), т.е. .

b) . По аналогии с предыдущим объяснением, выбираем . Правая часть состоит из числа, противоположного частному модулей, значит, . Учитывая, что при умножении отрицательного числа на вектор, этот вектор меняет своё направление, заключаем, что , и, значит, .

Посмотрим, какое соотношение имеют длины этих векторов.

Лемма доказана.

Определение. Вектор называется разложенным по двум неколлинеарным векторам и , если для любых чисел и выполняется равенство:

Числа и называются коэффициентами разложения.

ТЕОРЕМА. На плоскости любой вектор можно разложить по двум данным неколлинеарным векторам, причём коэффициенты разложения определяются единственным образом.

Дано: и неколлинеарны,

Доказать:

Доказательство.

Поскольку векторы и неколлинеарны, то в расположении трёх векторов возможны два случая: когда вектор коллинеарен одному из векторов и ; и когда вектор неколлинеарен ни одному из векторов и .

a) коллинеарен вектору . Тогда, по лемме о коллинеарных векторах, существует такой коэффициент , что . Это равенство можно записать в виде суммы, в которой первое слагаемое равно нулю, т.е. . Формула доказана.

b) неколлинеарен ни одному из векторов и . Тогда мы можем отложить все три вектора от некоторой точки , при этом, . От точки проведём прямую, параллельную вектору . Эта прямая пересекает прямую, содержащую вектор , в точке . По правилу треугольника вектор является суммой векторов и , т.е. . Вектор

коллинеарен вектору , значит, ; аналогично, вектор коллинеарен вектору , значит, . Поэтому,

. В этом случае формула также доказана.

Предположим теперь не единственность существования коэффициентов и , т.е. существуют такие числа и , что . Найдём разность двух равенств.

Т.к. векторы и ненулевые, то последнее равенство будет выполняться только в том случае, когда и , т.е. и . Значит, что коэффициенты и разложения единственные.

Теорема доказана.

Координаты вектора.

Введём понятие координат вектора. Для этого определим сначала понятие координатных векторов. По оси абсцисс направим единичный (т.е. с длиной, равной 1) вектор , а по оси ординат – единичный вектор . Эти векторы называются координатными. Т.к. они направлены по осям координат, то являются неколлинеарными. Поэтому любой другой вектор в координатной плоскости можно разложить по координатным векторам, т.е. представить в виде .

Приведём пример. На координатной плоскости отмечен вектор . От точки отложим вектор , а от точки отложим вектор . По правилу треугольника, вектор равен: . Значит, вектор

разложен по координатным векторам. Коэффициенты в этом разложении и есть координаты вектора: .

Перечислим и проверим некоторые свойства действий с координатами векторов.

Равные векторы имеют равные координаты.

На рисунке видно, что если векторы равны, то неважно в каком месте на координатной плоскости они располагаются. У них будет одинаковое разложение по координатным векторам, а значит, и равные координаты.

Каждая координата суммы (или разности) двух или более векторов равна сумме (или разности) соответствующих координат этих векторов.

Пусть даны два вектора и . Векторы и разложены по координатным векторам: , значит, имеет координаты . Аналогично, вектор разложен по координатным векторам: и имеет координаты . Найдём сумму (или разность) этих векторов.

Значит, вектор суммы (или разности) имеет координаты, равные сумме (или разности) соответствующих координат данных векторов, т.е. .

Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.

Пусть дан вектор . Вектор разложен по координатным векторам: , значит, имеет координаты . Найдём произведение вектора на число .

Значит, вектор имеет координаты: , т.е. при умножении вектора на число координаты данного вектора умножаются на это число.

Даны векторы и . Найдите координаты вектора .

Воспользуемся сначала правилом умножения вектора на число, а затем правилом сложения векторов.

Разложите вектор по векторам и .

Напомним, что разложить вектор по двум неколлинеарным векторам, это значит представить его в виде суммы (разности) данных векторов, или векторов, им коллинеарным, т.е. . Наша задача найти числа и .

Вектор имеет координаты , а вектор . Найдём их сумму:

. Т.к. этот вектор суммы должен равняться вектору , то соответствующие координаты у них должны быть равны. Получаем систему уравнений:

Значит, вектор раскладывается по векторам и следующим образом: .

При каком значении параметра векторы и коллинеарны?

Векторы и коллинеарны, если выполняется равенство . Тогда . Учитывая равенство, получаем систему уравнений:

Значит, при векторы и коллинеарны. И правда, , .

Отрезок разделён на шесть равных частей. Найдите значение числового множителя в каждом равенстве:

В трапеции с основаниями см и см отмечены точки – середины сторон и соответственно. Выразите вектор через вектор: а) ; б) .
В параллелограмма точки и – середины стороны и . Выразите через векторы и векторы: а) ; б) ; в) ; г) .
Векторы и неколлинеарны. Найдите числа и , удовлетворяющие равенству:

Докажите, что если векторы и неколлинеарны, то векторы и тоже неколлинеарны.
Отложите данные векторы от указанных точек.
1. Даны векторы и . Найдите координаты вектора .
2. Разложите вектор по векторам и .
3. Укажите координаты вектора .
4. Найдите значение , при котором векторы и будут коллинеарны.
5. Найдите значение , при котором векторы и будут коллинеарны.
1. Найдите координаты вектора , изображённого на рисунке.
2. Даны векторы . Найдите координаты вектора и постройте его.
3. Разложите вектор по векторам .
1. Найдите координаты вектора , изображённого на рисунке.
1. Даны векторы и . Найдите координаты вектора .
1. На рисунке даны четыре вектора и . Для каждого вектора запишите его разложение по координатным векторам и определите их координаты.
2. Найдите , если .
3. Разложите вектор по векторам и .
4. Найдите , если .
5. Даны векторы . Найдите .
6. При каком значении параметра векторы и коллинеарны?
7. Разложите вектор по векторам и .
8. На рисунке – трапеция, у которой . Найдите, если возможно такое число , что:
1. В треугольнике точка – середина стороны , а – середина отрезка . Разложите вектор по векторам и .
2. Запишите координаты векторов и .
3. На рисунке – квадрат, . Разложите вектор по координатным векторам.
1. Даны два вектора и .
1. Найдите координаты вектора .
2. Будут ли векторы и коллинеарными?
1. На рисунке – трапеция, у которой . Найдите, если это возможно, такое число , что:
1. В треугольнике точка – середина стороны , а точка – середина стороны . Разложите вектор по векторам и .
2. Запишите координаты векторов и .
3. На рисунке – квадрат, . Разложите вектор по координатным векторам.
4. Даны два вектора и .
1. Найдите координаты вектора .
2. Будут ли векторы и коллинеарными?
1. В трапеции и – основания, и пересекаются в точке , причём . Найдите, если возможно, такое число , что:
1. В параллелограмме , причём, . Разложите вектор по векторам и .
2. На рисунке . Разложите векторы и по координатным векторам.
3. Даны два вектора и .
1. Найдите координаты вектора .
2. Сонаправлены или противоположно направлены векторы и .
1. В треугольнике медианы и пересекаются в точке . Через точку проведена прямая, параллельная и пересекающая стороны и в точках и соответственно. Найдите, если возможно, такое число , что:
1. В параллелограмме , причём, . Разложите вектор по векторам и .
2. На рисунке . Разложите векторы и по координатным векторам.
3. Даны два вектора и .
1. Найдите координаты вектора .
2. Сонаправлены или противоположно направлены векторы и ?
1. В треугольнике , причём, . Разложите вектор по векторам и .
2. В треугольнике и , причём, . Используя векторы, докажите, что .
3. Даны два вектора . Постройте вектор, равный сумме векторов и . Какие координаты имеет этот вектор?
4. На рисунке треугольник равносторонний со стороной, равной . Разложите векторы и по координатным векторам и , если и – середины сторон и соответственно.
1. Даны два вектора и . При каких значениях эти векторы будут коллинеарны?
2. В треугольнике , причём, . Разложите вектор по векторам и .
3. В параллелограмме , причём, . Используя векторы, докажите, что .
4. Даны два вектора . Постройте вектор, равный разности векторов и . Какие координаты имеет этот вектор?
5. На рисунке треугольник равносторонний со стороной, равной . Разложите векторы и по координатным векторам и , если и – середины сторон и соответственно.
1. Даны два вектора и . При каких значениях эти векторы будут коллинеарны?
2. В треугольнике , причём, пересекает в точке . Найдите .
3. В трапеции , где и – основания, , причём, . Докажите, что если , то и .
4. Даны векторы и . Найдите разложение вектора по векторам и .
5. На рисунке . Разложите вектор по координатным векторам.
6. Векторы и заданы своими координатами: . Найдите координаты вектора .
7. В треугольнике и пересекаются в точке , причём, . Найдите .
8. В параллелограмме , причём, . Докажите, что точки лежат на одной прямой.
9. Даны векторы . Разложите вектор по векторам и .
10. На рисунке . Разложите вектор по координатным векторам.
11. Векторы и заданы своими координатами: . Найдите координаты вектора .
12. Даны векторы . Разложите вектор по векторам и .
13. Даны векторы . Разложите вектор по векторам и .
14. Точка – середина отрезка ; точка не принадлежит прямой . Найдите коэффициенты соответственно и в разложении вектора по векторам и .
15. Точка лежит на отрезке так, что . Точка не принадлежит прямой . Найдите коэффициенты соответственно и в разложении вектора по векторам и .
16. Векторы и неколлинеарны. Найдите все действительные значения , при которых векторы и коллинеарны.
17. Точка не принадлежит прямой . Для точек выполняется векторное равенство : . Какое утверждение является верным?
1. Точка совпадает с одной из точек и .
2. Точки и лежат в разных полуплоскостях относительно прямой .
3. Точка лежит на отрезке .
4. Точка лежит на прямой , вне отрезка .
5. Точки и лежат в одной полуплоскости относительно прямой .
1. Вектор имеет координаты . Найдите координаты вектора , если вектор имеет координаты .
2. Вектор имеет координаты , а вектор имеет координаты . Найдите координаты вектора .
3. Диагонали параллелограмма пересекаются в точке , точка – середина отрезка . Найдите, если возможно, такое число , чтобы выполнялось равенство:
1. В параллелограмме , изображённом на рисунке, и .
1. Разложите по векторам и векторы: и .
2. Разложите вектор по векторам:
1. и
2. и .
1. Векторы и неколлинеарны. Найдите числа и такие, что:
1. На рисунке изображены векторы.
1. Какой из данных векторов равен вектору ?
2. Напишите разложение вектора по координатным векторам.
3. Найдите координаты вектора .
4. Напишите, какой вектор имеет координаты .
5. Отложите от точки вектор с координатами .
1. Выпишите координаты векторов: .
2. Разложите по координатным векторам векторы:
1. Даны векторы . Найдите координаты векторов:
4. .
1. В прямоугольной системе координат постройте векторы: .
2. Найдите координаты векторов: , если .
3. Найдите координаты векторов: , если .
4. Векторы и коллинеарны. Найдите число .
5. Векторы и коллинеарны. Найдите число .
10