Формула равнодействующей всех сил в физике
Формула равнодействующей всех сил
Первый закон Ньютона говорит нам о том, что в инерциальных системах отсчета тела могут изменять скорость только, если на них оказывают воздействие другие тела. При помощи силы ($overline{F}$) выражают взаимное действие тел друг на друга. Сила способна изменить величину и направление скорости тела. $overline{F}$ — это векторная величина, то есть она обладает модулем (величиной) и направлением.
Определение и формула равнодействующей всех сил
В классической динамике основным законом, с помощью которого находят направление и модуль равнодействующей силы является второй закон Ньютона:
[overline{F}=moverline{a} left(1right),]
где $m$ — масса тела, на которое действует сила $overline{F}$; $overline{a}$ — ускорение, которое сила $overline{F}$ сообщает рассматриваемому телу. Смысл второго закона Ньютона заключается в том, что силы, которые действуют на тело, определяют изменение скорости тела, а не просто его скорость. Следует знать, что второй закон Ньютона выполняется для инерциальных систем отсчета.
На тело могут действовать не одна, а некоторая совокупность сил. Суммарное действие этих сил характеризуют, используя понятие равнодействующей силы. Пусть на тело оказывают действие в один и тот же момент времени несколько сил. Ускорение тела при этом равно сумме векторов ускорений, которые возникли бы при наличии каждой силы отдельно. Силы, которые оказывают действие на тело, следует суммировать в соответствии с правилом сложения векторов. Равнодействующей силой ($overline{F}$) называют векторную сумму всех сил, которые оказывают действие на тело в рассматриваемый момент времени:
[overline{F}={overline{F}}_1+{overline{F}}_2+dots +{overline{F}}_N=sumlimits^N_{i=1}{{overline{F}}_i} left(2right).]
Формула (2) — это формула равнодействующей всех сил, приложенных к телу. Равнодействующая сила является искусственной величиной, которую вводят для удобства проведения вычислений. Равнодействующая сила направлена как вектор ускорения тела.
Основной закон динамики поступательного движения при наличии нескольких сил
Если на тело действуют несколько сил, тогда второй закон Ньютона записывают как:
[sumlimits^N_{i=1}{{overline{F}}_i}=moverline{a}left(3right).]
$overline{F}=0$, если силы, приложенные к телу, взаимно компенсируют друг друга. Тогда в инерциальной системе отсчета скорость движения тела постоянна.
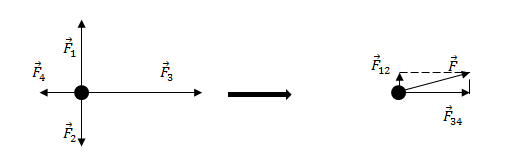
При изображении сил, действующих на тело, на рисунке, в случае равноускоренного движения, равнодействующую силу, изображают длиннее, чем сумму сил, которые противоположно ей направлены. Если тело перемещается с постоянной скоростью или покоится, длины векторов сил (равнодействующей и сумме остальных сил), одинаковы и направлены они в противоположные стороны.
Когда находят равнодействующую сил, на рисунке изображают все учитываемые в задаче силы. Суммируют эти силы в соответствии с правилами сложения векторов.
Примеры задач на равнодействующую сил
Пример 1
Задание. На материальную точку действуют две силы, направленные под углом $alpha =60{}^circ $ друг к другу. Чему равна равнодействующая этих сил, если $F_1=20 $Н; $F_2=10 $Н?
Решение. Сделаем рисунок.
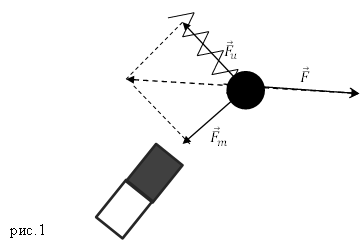
Силы на рис. 1 складываем по правилу параллелограмма. Длину равнодействующей силы $overline{F}$ можно найти, используя теорему косинусов:
[F=sqrt{F^2_1+F^2_2+2F_1F_2{cos alpha }} left(1.1right).]
Вычислим модуль равнодействующей силы:
[F=sqrt{{20}^2+{10}^2+2cdot 20cdot 10{cos (60{}^circ ) }}approx 26,5 left(Нright).]
Ответ. $F=26,5$ Н
Пример 2
Задание. На материальную точку действуют силы (рис.2). Какова равнодействующая этих сил?
Решение. Равнодействующая сил, приложенных к точке (рис.2) равна:
[overline{F}={overline{F}}_1+{overline{F}}_2+{overline{F}}_3+{overline{F}}_4left(2.1right).]
Найдем равнодействующую сил ${overline{F}}_1$ и ${overline{F}}_2$. Эти силы направлены вдоль одной прямой, но в противоположные стороны, следовательно:
[F_{12}=F_1-F_2=17-11=6 left(Hright).]
Так как $F_1>F_2$, то сила ${overline{F}}_{12}$ направлена в туже сторону, что и сила ${overline{F}}_1$.
Найдем равнодействующую сил ${overline{F}}_3$ и ${overline{F}}_4$. Данные силы направлены вдоль одной вертикальной прямой (рис.1), значит:
[F_{34}=F_3-F_4=18-10=8 left(Нright).]
Направление силы ${overline{F}}_{34}$ совпадает с направлением вектора ${overline{F}}_3$, так как ${overline{F}}_3>{overline{F}}_4$.
Равнодействующую, которая действует на материальную точку, найдем как:
[overline{F}={overline{F}}_{12}+{overline{F}}_{34}left(2.2right).]
Силы ${overline{F}}_{12}$ и ${overline{F}}_{34}$ взаимно перпендикулярны. Найдем длину вектора $overline{F}$ по теореме Пифагора:
[F=sqrt{F^2_{12}+F^2_{34}}=sqrt{6^2+8^2}=10 left(Нright).]
Ответ. $F$=10 Н
Читать дальше: формула равнодействующей силы.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Законы сложения сил в механике
При воздействии на одно тело нескольких сил одновременно тело начинает двигаться с ускорением, являющимся векторной суммой ускорений, которые бы возникли под воздействием каждой силы по отдельности. К действующим на тело силам, приложенным к одной точке, применяется правило сложения векторов.
Векторная сумма всех сил, одновременно воздействующих на тело, это сила равнодействующая, которая определяется по правилу векторного сложения сил:
R → = F 1 → + F 2 → + F 3 → + . . . + F n → = ∑ i = 1 n F i → .
Равнодействующая сила действует на тело также, как и сумма всех действующих на него сил.
Правило параллелограмма и правило многоугольника
Для сложения 2 -х сил используют правило параллелограмма (рисунок 1 ).
Рисунок 1 . Сложение 2 -х сил по правилу параллелограмма
Выведем формулу модуля равнодействующей силы с помощью теоремы косинусов:
R → = F 1 → 2 + F 2 → 2 + 2 F 1 → 2 F 2 → 2 cos α
При необходимости сложения более 2 -х сил используют правило многоугольника: от конца
1 -й силы необходимо провести вектор, равный и параллельный 2 -й силе; от конца 2 -й силы необходимо провести вектор, равный и параллельный 3 -й силе и т.д.
Рисунок 2 . Сложение сил правилом многоугольника
Конечный вектор, проведенный от точки приложения сил в конец последней силы, по величине и направлению равняется равнодействующей силе. Рисунок 2 наглядно иллюстрирует пример нахождения равнодействующей сил из 4 -х сил: F 1 → , F 2 → , F 3 → , F 4 → . Причем суммируемые векторы совсем необязательно должны быть в одной плоскости.
Результат действия силы на материальную точку будет зависеть только от ее модуля и направления. У твердого тела есть определенные размеры. Потому силы с одинаковыми модулями и направлениями вызывают разные движения твердого тела в зависимости от точки приложения.
Линией действия силы называют прямую, проходящую через вектор силы.
Рисунок 3 . Сложение сил, приложенных к различным точкам тела
Если силы приложены к различным точкам тела и действуют не параллельно по отношению друг к другу, тогда равнодействующая приложена к точке пересечения линий действия сил (рисунок 3 ). Точка будет находиться в равновесии, если векторная сумма всех сил, действующих на нее, равняется 0 : ∑ i = 1 n F i → = 0 → . В данном случае равняется 0 и сумма проекций данных сил на любую координатную ось.
Разложение вектора силы по направлениям
Разложение сил на две составляющие – это замена одной силы 2 -мя, приложенными в той же точке и производящими на тело такое же действие, как и эта одна сила. Разложение сил осуществляется, как и сложение, правилом параллелограмма.
Задача разложения одной силы (модуль и направление которой заданы) на 2 , приложенные в одной точке и действующие под углом друг к другу, имеет однозначное решение в следующих случаях, когда известны:
- направления 2 -х составляющих сил;
- модуль и направление одной из составляющих сил;
- модули 2 -х составляющих сил.
Пример 1
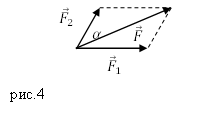
Необходимо разложить силу F на 2 составляющие, находящиеся в одной плоскости с F и направленные вдоль прямых a и b (рисунок 4 ). Тогда достаточно от конца вектора F провести 2 прямые, параллельные прямым a и b . Отрезок F A и отрезок F B изображают искомые силы.
Рисунок 4 . Разложение вектора силы по направлениям
Второй вариант данной задачи – найти одну из проекций вектора силы по заданным векторам силы и 2 -й проекции (рисунок 5 а ).
Рисунок 5 . Нахождение проекции вектора силы по заданным векторам
Во втором варианте задачи необходимо построить параллелограмм по диагонали и одной из сторон, как в планиметрии. На рисунке 5 б изображен такой параллелограмм и обозначена искомая составляющая F 2 → силы F → .
Итак, 2 -й способ решения: прибавим к силе силу, равную — F 1 → (рисунок 5 в ). В итоге получаем искомую силу F → .
Три силы F 1 → = 1 Н ; F 2 → = 2 Н ; F 3 → = 3 Н приложены к одной точке, находятся в одной плоскости (рисунок 6 а ) и составляют углы с горизонталью α = 0 ° ; β = 60 ° ; γ = 30 ° соответственно. Необходимо найти равнодействующую силу.
Решение
Рисунок 6 . Нахождение равнодействующей силы по заданным векторам
Нарисуем взаимно перпендикулярные оси О Х и O Y таким образом, чтобы ось О Х совпадала с горизонталью, вдоль которой направлена сила F 1 → . Сделаем проекцию данных сил на координатные оси (рисунок 6 б ). Проекции F 2 y и F 2 x отрицательны. Сумма проекций сил на координатную ось О Х равняется проекции на данную ось равнодействующей: F 1 + F 2 cos β — F 3 cos γ = F x = 4 — 3 3 2 ≈ — 0 , 6 Н .
Точно также для проекций на ось O Y : — F 2 sin β + F 3 sin γ = F y = 3 — 2 3 2 ≈ — 0 , 2 Н .
Модуль равнодействующей определим с помощью теоремы Пифагора:
F = F x 2 + F y 2 = 0 , 36 + 0 , 04 ≈ 0 , 64 Н .
Направление равнодействующей найдем при помощи угла между равнодействующей и осью (рисунок 6 в ):
t g φ = F y F x = 3 — 2 3 4 — 3 3 ≈ 0 , 4 .
Сила F = 1 к Н приложена в точке В кронштейна и направлена вертикально вниз (рисунок 7 а ). Необходимо найти составляющие данной силы по направлениям стержней кронштейна. Все необходимые данные отображены на рисунке.
Решение
Рисунок 7 . Нахождение составляющих силы F по направлениям стержней кронштейна
Дано:
F = 1 к Н = 1000 Н
Пускай стержни прикручены к стене в точках А и С . На рисунке 7 б изображено разложение силы F → на составляющие вдоль направлений А В и В С . Отсюда понятно, что
F 1 → = F t g β ≈ 577 Н ;
F 2 → = F cos β ≈ 1155 Н .
Ответ: F 1 → = 557 Н ; F 2 → = 1155 Н .
Как найти равнодействующую трех векторов
Скорость автомобиля массой 1000 кг, движущегося вдоль оси Ox, изменяется со временем в соответствии с графиком (см. рисунок). Систему отсчета считать инерциальной. Чему равна равнодействующая всех сил, действующих на автомобиль? (Ответ дайте в ньютонах.)
Согласно второму закону Ньютона, равнодействующая всех сил, действующих на тело, связана с ускорением и массой тела соотношением Из графика определим ускорение, которое остается постоянным на протяжении всего интервала времени:
Таким образом, равнодействующая всех сил равна
а если бы ускорение было отрицательно, то и равнодействующая была бы отрицательной?
Скорость, сила, ускорение — все это векторные величины. Правильно говорить не про их знак, а про знак проекции этих векторов на некоторую ось. Если проекция скорости уменьшается, то ускорение направлено против оси, а значит, так же направлена и равнодействующая. Следовательно, проекции этих величин отрицательны. По графику модуля скорости о знаке проекций судить нельзя. Действительно, имея только график, приведенный в условии, мы не можем сказать, ускоряется тело вдоль оси или против. Проекция ускорения может быть тут как положительной, так и отрицательной.
«Систему отсчета считать инерциальной.» Возможно ошибаюсь, ребят, но, вроде, в ИСО равнодействующая всех сил равна нулю.
ИСО — это система отсчета, в которой тело, на которое не действует никаких внешних сил, двигается равномерно и прямолинейно или покоится.
Равнодействующая сил, конечно, же может и отличаться от нуля, это, согласно второму закону Ньютона, приведет к появлению ускорения.
т.е. в инерциальной системе отсчёта нет силы трения?
и ещё: вы говорите, что тело в ИСО движется равномерно, а в условии задачи дано равноускоренное движение. так бывает?
Я не так говорю, не вырывайте слова и контекста. Я даю определение ИСО: это система отсчета, в которой тело, НА КОТОРОЕ НЕ ДЕЙСТВУЮТ ВНЕШНИЕ СИЛЫ, двигается равномерно и прямолинейно, либо покоится. А вот если СИЛЫ ДЕЙСТВУЮТ, то это приводит к появлению ускорения, о чем нам и говорит второй закон Ньютона.
Наличие силы трения определяется свойством поверхностей, а не выбором системы отсчета. И в данной задаче, она, конечно, присутствует и направлена по скорости движения автомобиля, иначе бы он просто не мог бы разгоняться. Но чему она равна, мы найти из данного графика не можем, так как есть и другие силы, например, сила сопротивления воздуха. Что мы может тут определить, так это равнодействующую всех сил. Именно ей определяется ускорение.
Пыталась найти ускорение как тангенс угла наклона касательной, то есть производную от v по t. Тут угол — 45 град, тангенс = 1, ускорение, стало быть, так же 1 м/с^2.
Подскажите пожалуйста, где в моих рассуждениях ошибка?
Ошибка в том, что тангенс надо считать, учитывая масштаб графика по осям. То есть Вы должны определить катеты прямоугольного треугольника, используя числа на осях, а потом поделить один катет на другой.
Кстати, простое доказательство, почему Ваше решение не верно. Сожмем картинку с графиком по вертикали в два раза. Угол на рисунке изменится, а ускорение, конечно, же останется прежним.
а почему считают ускорение до 8с. а не до 18, если найдем ускорение по всей длине то получается 10-0/18=1,8 и получается другой ответ!
Делить нужно на 20. Масштаб по горизонтальной оси: в одной клеточке 4 с
На тело, находящееся на горизонтальной плоскости, действуют три горизонтальные силы (см. рисунок, вид сверху). Каков модуль равнодействующей этих сил, если (Ответ дайте в ньютонах и округлите до десятых.)
На рисунке обозначена равнодействующая векторов и
Поскольку модуль вектора силы равен 1 Н, заключаем, что масштаб рисунка такой, что сторона одного квадрата сетки соответствует модулю силы 1 Н. Таким образом, модуль равнодействующей равен по теореме Пифагора
А как определили эту равнодействующую трёх сил, я понять не могу?!
Чтобы найти равнодействующую, необходимо сложить вектора всех сил (например, по правилу треугольника или параллелограмма складываем вектора по два).
Если сложить вектор и вектор , получится вектор, направленный вверх длиной в одну клеточку. Теперь осталось прибавить к нему вектор . В результате и получается то, что показано красной стрелкой.
векторы F1 и F3 никак нельзя сложить правилом треугольника! дак как эту задачц решить тут решения совсем непонятные!
Когда Вы складываете параллельные вектора, у Вас просто получается «вырожденный треугольник». Правила все те же, к концу первого вектора прикладываем начало второго. Сумма векторов — это вектор, который начинается в начале первого и заканчивается в конце второго. То есть в данном случае у Вас получится вектор, направленный вверх и длиной в одну клеточку.
Две силы 3 H и 4 H приложены к одной точке тела, угол между векторами сил равен 90°. Чему равен модуль равнодействующей сил? (Ответ дайте в ньютонах.)
Силы и их равнодействующая указаны на рисунке. По теореме Пифагора, модуль равнодействующей сил равен
Под действием одной силы F1 тело движется с ускорением 4 м/с 2 . Под действием другой силы F2, направленной противоположно силе F1, ускорение тела равно 3 м/с 2 . С каким ускорением тело будет двигаться при одновременном действии сил F1 и F2? Ответ дайте в метрах на секунду в квадрате.
Согласно второму закону Ньютона, ускорение тела пропорционально равнодействующей всех сил, действующих на него: Силы и по условию, направлены противоположно, поэтому при их одновременном действии тело будет двигаться с ускорением
Тело подвешено на двух нитях и находится в равновесии. Угол между нитями равен 90°, а силы натяжения нитей равны 3 H и 4 H. Чему равна сила тяжести, действующая на тело? (Ответ дайте в ньютонах.)
Всего на тело действует три силы: сила тяжести и силы натяжения двух нитей. Поскольку тело находится в равновесии, равнодействующая всех трех сил должна равняться нулю, а значит, модуль силы тяжести равен
в условии написано,что нужно найти вес тела.
а в решении модуль силы тяжести.
Как вес может измеряться в Ньютонах.
В условии ошибка(
Вы путаете понятия массы и веса. Весом тела называется сила (а потому вес измеряется в Ньютонах), с которой тело давит на опору или растягивает подвес. Как следует из определения, эта сила приложена даже не к телу, а к опоре. Невесомость — это состояние, когда у тела пропадает не масса, а вес, то есть тело перестает давить на другие тела.
Согласен, в решении была допущена некоторая вольность в определениях, сейчас она поправлена.
Понятие «вес тела» введен в учебную физику крайне неудачно. Если в бытовом понятии вес обозначает массу то в школьной физике, как вы правильно заметили весом тела называется сила (а потому вес измеряется в Ньютонах), с которой тело давит на опору или растягивает подвес. Заметим, что речь идет об одной опоре и об одной нити. Если опор или нитей несколько несколько, понятие веса исчезает.
Привожу пример. Пусть в жидкости на нити подвешено тело. Оно растягивает нить и давит на жидкость с силой равной минус сила Архимеда. Почему же, говоря о весе тела в жидкости, мы не складываем эти силы, как Вы делаете в своем решении?
Я зарегистрировался на Вашем сайте, но не заметил, что же изменилось в нашем общении. Прошу извинить мою тупость, но я, будучи человеком старым, недостаточно свободно ориентируюсь на сайте.
Действительно, понятие веса тела весьма расплывчато, когда тело имеет несколько опор. Обычно вес в этом случае определяют как сумму взаимодействий со всеми опорами. При этом воздействие на газообразные и жидкие среды, как правило, исключается. Это как раз подпадает под описанный Вами пример, с подвешенным в воде грузиком.
Здесь сразу вспоминается детская задачка: «Что весит больше: килограмм пуха или килограмм свинца?» Если решать эту задачу по-честному, то нужно несомненно учитывать силу Архимеда. А под весом скорее всего мы будем понимать то, что нам будут показывать весы, то есть силу, с которой пух и свинец давят, скажем, на чашку весов. То есть здесь сила взаимодействие с воздухом как бы из понятия веса исключается.
С другой стороны, если считать, что мы откачали весь воздух и кладем на весы тело, к которому привязана веревочка. То сила тяжести будет уравновешиваться суммой силы реакции опоры и силой натяжения нити. Если мы понимаем вес как силу действия на опоры, препятствующие падению, то вес тут будет равен этой сумме силы растяжения нити и силы давления на чашку весов, то есть совпадать по величине с силой тяжести. Опять возникает вопрос: чем нитка лучше или хуже силы Архимеда?
В целом тут можно договориться до того, что понятие веса имеет смысл только в пустом пространстве, где есть только одна опора и тело. Как тут быть, это вопрос терминологии, которая, к сожалению, у каждого здесь своя, поскольку не столь уж это и важный вопрос 
Если уж быть совсем честным, то разделение сил на виды весьма условно. Представим себе ящик, который тащат по горизонтальной поверхности. Обычно говорят, что на ящик действуют две силы со стороны поверхности: сила реакции опоры, направленная вертикально, и сила трения, направленная горизонтально. Но ведь это две силы, действующие между одними и теми же телами, почему же мы просто не рисуем одну силу, являющуюся их векторной суммой (так, кстати, иногда и делается). Тут, это, наверное, вопрос удобства 
Так что я немного в замешательстве, что делать с данной конкретной задачей. Проще всего, наверное, переформулировать ее и задавать вопрос про величину силы тяжести.
Не переживайте, все в порядке. При регистрации Вы должны были указать e-mail. Если теперь зайти на сайт под своим аккаунтом, то при попытке оставить комментарий в окне «Ваш e-mail» должен сразу появляться тот самый адрес. После этого система будет автоматически подписывать Ваши сообщения.
Формула модуля равнодействующей силы
На тело могут оказывать действие не одна, а некоторая совокупность сил. Суммарное действие этих сил характеризуют, используя понятие равнодействующей силы.
Формула равнодействующей всех сил
Пусть на тело воздействуют в один и тот же момент времени N сил. Ускорение тела при этом равно сумме векторов ускорений, которые возникли бы при наличии каждой силы отдельно. Сила является векторной величиной. Следовательно, силы, действующие на тело, нужно складывать в соответствии с правилом сложения векторов. Равнодействующей силой ($overline$) называют векторную сумму всех сил, которые оказывают действие на тело в рассматриваемый момент времени:
Формула (1) — это формула равнодействующей всех сил, приложенных к телу. Равнодействующая сила является искусственной величиной, которую вводят для удобства проведения вычислений. Равнодействующая сила направлена также как вектор ускорения тела.
Складывают векторы, используя правило треугольника (рис.1)
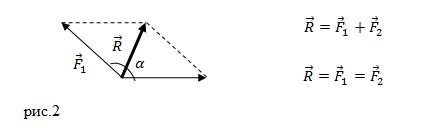
правило параллелограмма (рис.2).
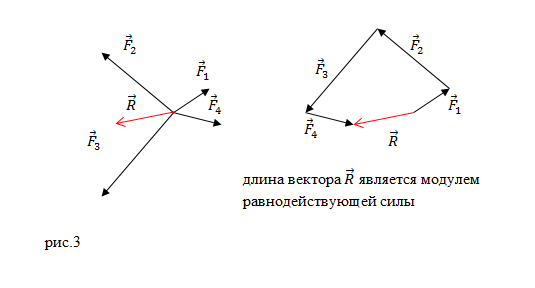
или многоугольника (рис.3):
Второй закон Ньютона и формула модуля равнодействующей
Основной закон динамики поступательного движения в механике можно считать формулой для нахождения модуля равнодействующей силы, приложенной к телу и вызывающей ускорение этого тела:
$overline=0$, если силы, приложенные к телу, взаимно компенсируют друг друга. Тогда в инерциальной системе отсчета тело скорость движения тела.
При изображении сил, действующих на тело, на рисунке, в случае равноускоренного движения, равнодействующую силу, изображают длиннее, чем сумму сил, которые противоположно ей направлены. Если тело перемещается с постоянной скоростью или покоится, длины векторов сил (равнодействующей и сумме остальных сил), одинаковы и направлены они в противоположные стороны.
Когда находят равнодействующую сил, на рисунке изображают все учитываемые в задаче силы. Суммируют эти силы в соответствии с правилами сложения векторов.
Примеры задач с решением
Задание. К материальной точке приложены силы, направленные под углом $alpha =60<>^circ $ друг к другу (рис.4). Чему равен модуль равнодействующей этих сил, если $F_1=40 $Н; $F_2=20 $Н?
Решение. Силы на рис. 1 сложим, используя правило параллелограмма. Длину равнодействующей силы $overline$ найдем, применяя теорему косинусов:
Вычислим модуль равнодействующей силы:
[F=sqrt<<40>^2+<20>^2+2cdot 40cdot 20<cos (60<>^circ ) >>approx 52,92 left(Нright).]
Ответ. $F=52,92$ Н
Задание. Как изменяется модуль равнодействующей силы со временем, если материальная точка массы $m$ перемещается в соответствии с законом: $s=A<cos (omega t)(м) >$, где $s$ — путь пройденный точкой; $A=const;; omega =const?$ Чему равна максимальная величина этой силы?
Решение. По второму закону Ньютона равнодействующая сил, действующих на материальную точку равна:
Следовательно, модуль силы можно найти как:
Ускорение точки будем искать, используя связь между ним и перемещением точки:
Первая производная от $s$ по времени равна:
Подставим полученный в (2.5) результат, в формулу модуля для равнодействующей силы (2.2) запишем как:
Так как косинус может быть меньше или равен единицы, то максимальное значение модуля силы, действующей на точку, составит:
http://phys-ege.sdamgia.ru/test?theme=206
http://www.webmath.ru/poleznoe/fizika/fizika_134_formula_modulja_ravnodejstvujushhej_sily.php
Равнодействующая сила

4.7
Средняя оценка: 4.7
Всего получено оценок: 166.
Обновлено 31 Октября, 2021
4.7
Средняя оценка: 4.7
Всего получено оценок: 166.
Обновлено 31 Октября, 2021
Законы Ньютона – математическая абстракция. В реальности причиной движения или покоя тел, а также их деформации, выступают сразу несколько сил. Поэтому важным дополнениям к законам механики будет введение понятия равнодействующей силы и его применение.
О причинах изменений
Классическая механика разделена на два раздела – кинематику, при помощи уравнений описывающую траекторию движения тел, и динамику, которая разбирается с причинами изменения положения объектов или самих объектов.
Причиной изменений выступает некоторая сила, которая есть мера действия на тело других тел или силовых полей (например, электромагнитное поле или гравитация). К примеру, сила упругости вызывает деформацию тела, сила тяжести – падение тел на Землю.
Сила – это векторная величина, то есть, ее действие – направленное. Модуль силы в общем случае пропорционален некоему коэффициенту (для деформации пружины – это ее жесткость), а также параметрам действия (масса, заряд).
Например, в случае кулоновской силы – это величина обоих зарядов, взятых по модулю, квадрат расстояние между зарядами и коэффициент k, в системе СИ определяемый выражением: $k = {1 over 4 pi epsilon}$, где $epsilon$ – диэлектрическая постоянная.
Сложение сил
В случае, когда на тело действует n сил, говорят о равнодействующей силе, а формула второго закона Ньютона принимает вид:
$mvec a = sumlimits_{i=1}^n vec F_i$
Поскольку F – векторная величина, сумма сил называется геометрической (или векторной). Такое сложение выполняется по правилу треугольника или параллелограмма, либо по компонентам. Поясним каждый метод на примере. Для этого запишем формулу равнодействующей силы в общем виде:
$F = sumlimits_{i=1}^n vec F_i$
А силу $F_i$ представим в виде:
$F = (F_{xi}, F_{yi}, F_{zi})$
Тогда суммой двух сил будет новый вектор $F_{ab} = (F_{xb} + F_{xa}, F_{yb} + F_{ya}, F_{zb} + F_{za})$.
Абсолютное значение равнодействующей можно рассчитать так:
$F = sqrt{(F_{xb} + F_{xa})^2 + (F_{yb} + F_{ya})^2 + (F_{zb} + F_{za})^2}$
Теперь дадим строгое определение: равнодействующая сила есть векторная сумма всех сил, оказывающих влияние на тело.
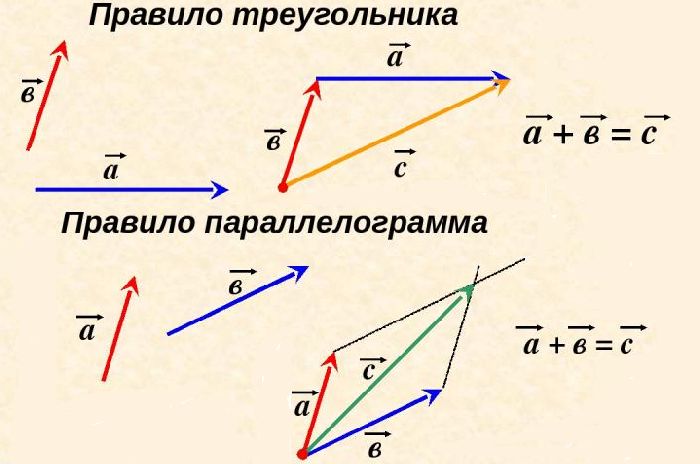
Разберем правила треугольника и параллелограмма. Графически это выглядит так:
Внешне они кажутся различными, но когда доходит до вычислений, сводятся к нахождению третьей стороны треугольника (или, что тоже самое, диагонали параллелограмма) по теореме косинусов.
Если сил больше двух, иногда удобней пользоваться правилом многоугольника. По своей сути – это всё тот же треугольник, только повторенный на одном рисунке некоторое количество раз. В случае, если по итогу контур получился замкнутым, общее действие сил равно нулю и тело покоится.
Задачи
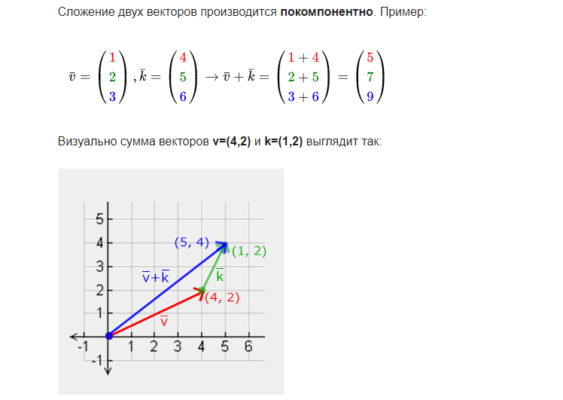
- На ящик, размещенный в центре декартовой прямоугольной системы координат, действуют две силы: $F_1 = (5, 0)$ и $F_2 = (3, 3)$. Рассчитать равнодействующую двумя методами: по правилу треугольника и при помощи покомпонентного сложения векторов.
Решение
Равнодействующей силой будет векторная сумма $F_1$ и $F_2$.
Поэтому запишем:
$vec F = vec F_1 + vec F_2 = (5+3, 0+3) = (8, 3)$
Абсолютное значение равнодействующей силы:
$F = sqrt{8^2 + 3^2} = sqrt{64 + 9} = 8,5 Н$
Теперь получим тоже значение при помощи правила треугольника. Для этого сначала найдем абсолютные значения $F_1$ и $F_2$, а также угол между ними.
$F_1 = sqrt{5^2 + 0^2} = 5 Н$
$F_2 = sqrt{3^2 + 3^2} = 4,2 Н$
Угол между ними – 45˚, так как первая сила параллельна оси Оx, а вторая делит первую координатную плоскость пополам, то есть является биссектрисой прямоугольного угла.
Теперь, разместив вектора по правилу треугольника, рассчитаем по теореме косинусов равнодействующую:
$F = sqrt{F_1^2 + F_2^2 – 2F_1F_2 cos135} = sqrt{F_1^2 + F_2^2 + 2F_1F_2 sin45} = sqrt{25 + 18 + 2 cdot 5 cdot 4,2 cdot sin45} = 8,5 Н$
- На машину действуют три силы: $F_1 = (-5, 0)$, $F_2 = (-2, 0)$, $F_1 = (7,0)$. Какова их равнодействующая?
Решение
Достаточно сложить иксовые компоненты векторов:
$F = -5 – 2 + 7 = 0$
Что мы узнали?
В ходе урока было введено понятие равнодействующей сил и рассмотрены различные методы ее расчета, а также введена запись второго закона Ньютона для общего случая, когда количество сил неограниченно.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.7
Средняя оценка: 4.7
Всего получено оценок: 166.
А какая ваша оценка?
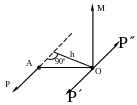
Если к телу
приложены три непараллельные взаимно
уравновешивающиеся силы, то они образуют
систему сходящихся сил (линии
действия этих сил пересекаются в одной
точке).
Д
ве
силы
и
(рис.2.5) образуют равнодействующую
,
которая при равновесии сил (что считается
известным) равна силе
по модулю, лежит на одной прямой и
направлена в противоположную сторону.
Рис.2.5
Следовательно,
три силы пересекаются в одной точке (и
лежат в одной плоскости).
Эта теорема
часто используется при поиске величины
и направления одной из реакций опор
конструкции, к которой приложены 3 силы.
Лекция 3 Произвольная система сил в пространстве и на плоскости
Система
пар сил. Сложение пар сил Условие
равновесия пар сил. Уравнения равновесия.
Система сил, произвольно расположенных
в пространстве. Приведение силы к центру
(метод Пуансо). Сложение сил
Сложение пар
сил
Е
сли
к телу приложить пары сил, то можно
использовать для их сложения векторы
– моменты пар сил. Так как момент пары
сил не изменяется при переносе пары сил
в параллельную плоскость и не изменяется
при перемещении пары сил в плоскости
ее действия, то момент пары сил считается
свободным вектором (в отличие от силы
– скользящего вектора). А это означает,
что векторы – моменты пар сил можно
приложить к одной точке тела и сложить
их по правилу сложения сходящихся
векторов – построить векторный
многоугольник, замыкающая которого
определяет момент пары сил, эквивалентной
заданной системе пар сил (см. рис.3.1).
Рис.3.1
Таким образом,
,
что означает, что в результате сложения
пар сил получается одна пара сил, момент
которой равен геометрической сумме
моментов пар сил. Эту пару сил можно
представить расположенной в плоскости,
перпендикулярной к вектору
и
стремящейся повернуть тело вокруг оси,
совпадающей с вектором
против хода часовой стрелки, если
смотреть вдоль вектора
к его основанию. При этом пару сил могут
образовывать любые две силы
и
(
)
так, чтобы произведение одной из сил
пары на плечо пары сил было равно моменту
М.
Условие
равновесия пар сил. Уравнения равновесия
Пары сил,
приложенные к твердому телу, взаимно
уравновешиваются, если векторный
многоугольник моментов пар сил замкнут,
т.е. если
.
Так как вектор
можно определить аналитическим способом,
зная моменты заданных пар сил (по аналогии
с аналитическим методом определения
равнодействующей сходящихся сил), т.е.
,
где
;
;
,
то при равновесии пар сил
моменты пар сил должна удовлетворять
трем уравнениям равновесия
;
;
(алгебраическая сумма проекций
моментов пар сил на каждую из прямоугольных
координатных осей должна равняться
нулю).
Если пары сил
лежат в одной плоскости, то следует
использовать одно уравнение равновесия
пар сил:
.
Система сил, произвольно расположенных в пространстве
Приведение
силы к центру (метод Пуансо). Сложение
сил
Для сложения
сил в самом общем случае широко
используется метод Пуансо – приведение
каждой силы к центру.
В результате
приведения силы
к центру О (рис.3.2) получаются вместо
одной три силы, из которых можно выделить
силу
,
геометрически равную заданной силе
,
приложенную к центру, и пару сил
,
момент которой
равен моменту
заданной силы
относительно центра О.
~
~
,
при этом
,
(имеется в виду, что к центру О
приложены две взаимоуравновешивающиеся
силы
и
,
параллельные и равные силе Р по
модулю, но направленные в противоположные
стороны, так что
).
Рис.3.2
Р
ассмотрим
последовательность операций при сложении
нескольких сил, линии действия которых
не пересекаются в одной точке и не лежат
в одной плоскости (самый общий случай).
Силы
;
и
(для примера достаточно трех сил) приводим
к центру (рис.3.2) и получаем три сходящиеся
силы
;
;
и три пары сил
;
и
,
моменты которых
;
и
. Рис.3.3
Складывая
сходящиеся силы построением силового
многоугольника, получаем силу
,
приложенную к центру. Складывая моменты
пар сил построением многоугольника
моментов, получаем момент
той пары сил, которая эквивалентна трем
парам сил.
Так как момент
каждой пары сил геометрически равен
моменту заданной силы относительно
центра, следует записать
,
отсюда следует, что
,
т.е. момент пары сил, эквивалентной трем
парам сил, равен геометрической сумме
моментов заданных сил
,
и
относительно центра О. Эта сумма
моментов получила название главного
момента заданных сил относительно
центра. А сила
получила название главного вектора
заданных сил (Главный вектор нельзя
назвать равнодействующей заданной
системы сил, хотя
,
так как он один не эквивалентен заданной
системе сил; эквивалентна заданной
системе сил – совокупность силы
и пары сил, момент которой
).
Итак, в результате
сложения сил, произвольно расположенных
в пространстве, методом приведения их
к центру получаются сила и пара сил.
Сила
,
приложенная к центру, называется главным
вектором; он равен геометрической
сумме заданных сил. Момент пары сил
равен геометрической сумме моментов
заданных сил относительно центра,
которая образует главный момент
заданных сил относительно центра
.
Нетрудно
сообразить, что главный вектор
не зависит от выбора центра приведения,
а главный момент
изменяет свою величину и направление
при изменении положения центра приведения.
Возможные
случаи приведения сил к центру
Сложение сил,
произвольно расположенных в пространстве,
методом приведения их к центру, дает
различные результаты при разных значениях
и
.
1
)
,
а
.
Силы приводятся к одной силе, следовательно,
заданные силы можно заменить их
равнодействующей (главный вектор
превращается в равнодействующую).
2)
,
а
.
Силы приводятся к одной паре сил, она
эквивалентна заданной системе сил. (В
этом случае вектор
не изменяет свою величину и свое
направление при изменении положения
центра приведения).
3)
и
,
но
.
Рис.3.4
В этом случае (см. рис.3.4) следует
показать пару сил, соответствующую
моменту
,
выбрав силу этой пары сил
равной величине главного вектора
и направив ее в сторону, противоположную
главному вектору (приложив эту силу к
центру приведения).
Тогда две силы
и
можно отбросить как две взаимно
уравновешивающиеся силы и останется
только одна сила
,
равная главному вектору, т.е. геометрической
сумме заданных сил. Эта сила –
равнодействующая заданных сил. Ее линия
действия отстоит от центра приведения
на расстоянии, равном плечу пары сил
,
т.е
.
4
)
и
,
но
(самый общий случай). Можно в этом случае
получить новую картину сил, если пару
сил, момент которой
,
заменить двумя парами сил, моменты
которых
и
(см. рис.3..5), причем
.
Рис.35
Покажем пару
сил, соответствующую моменту
,
выбрав силы этой пары равными главному
вектору, приложив одну из сил (
)
к центру приведения и направив ее
противоположно главному вектору.
Тогда две силы
и
можно отбросить (см. случай 3). Остаются
сила
и пара сил, соответствующая моменту
,
расположенная в плоскости, перпендикулярной
силе. Такая совокупность силы и пары
сил получила название: «силовой винт»
или «динама».
Определение
главного вектора и главного момента
системы сил относительно центра
аналитическим способом
Зная силы
,
,
…
,
приложенные к твердому телу (зная их
величину и углы между силой и осями
координат), можно определить модуль и
направление главного вектора заданных
сил по способу проекций:
,
;
;
(аналогично определению
аналитическим способом равнодействующей).
Главный момент
системы сил относительно центра (его
величину и направление) также можно
определить по способу проекций:
,
где
— алгебраическая сумма моментов сил
относительно координатной оси Ox,
определяющая проекцию вектора
на ось Ox, которая
получила название главного момента
системы сил относительно оси —
;
(главный момент системы сил относительно
оси Oy);
(главный
момент системы сил относительно оси
Oz).
Условия
равновесия сил. Уравнения равновесия
Если при сложении
сил, произвольно расположенных в
пространстве, силовой многоугольник
получается замкнутым и векторный
многоугольник моментов также получится
замкнутым, то силы взаимно уравновешиваются.
Следовательно, условие равновесия сил
получают вид:
и
.
Это позволяет записать условия равновесия
сил в аналитической форме – уравнения
равновесия:
1.
; 2.
; 3.
;
4.
; 5.
; 6.
.
Получаем 6
уравнений равновесия пространственной
системы сил.
Соседние файлы в папке Первый курс Летняя сессия
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
06.07.20214.74 Mб4Статика.docx
- #
§4. Примеры из физики
Простейшие примеры векторов в физике — скорость и сила.
1. Всякое движение можно представить как результат сложения нескольких движений, его составляющих. Скорость результирующего движения изображается по величине и направлению диагональю параллелограмма, построенного на отрезках, изображающих составляющие скорости, как на сторонах. Рассмотрим конкретный пример.
Рыбак переправляется на лодке `A` через реку, которая течёт в сторону, указанную стрелкой (рис. 18). Пусть скорость течения воды `vec(v_1)` изображается по величине и направлению отрезком `AB`, а скорость `vec(v_2)` движения лодки относительно воды под влиянием усилий гребца изображается отрезком `AC` (в стоячей воде лодка двигалась бы по направлению `AC` со скоростью `vec(v_2)`). Лодка будет двигаться относительно берега по направлению `AM` со скоростью `vec v`, изображаемой диагональю `AD` параллелограмма, построенного на векторах `vec(v_1)` и `vec(v_2)` (в данном случае параллелограмм `ABCD` является прямоугольником).
2. Сила — как векторная величина — всегда имеет определённое направление, модуль, а также точку приложения.
Часто встречаются случаи, когда на тело действуют несколько сил. Тогда бывает удобно заменить их одной силой, которая производит на тело такое же действие, как и несколько одновременно действующих сил. Такую силу (если она существует) называют равнодействующей. Нахождение равнодействующей нескольких сил осуществляется с помощью правил векторного сложения, при этом слагаемые силы называют составляющими.
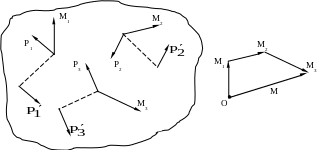
Так, несколько сил, действующих на одну и ту же точку тела, всегда можно заменить одной равнодействующей, как бы ни были направлены силы и каковы бы ни были их величины. Пусть, например, на тело действуют четыре силы `vec(F_1)`, `vec(F_2)`, `vec(F_3)` и `vec(F_4)`, приложенные к одной точке `O` и лежащие в одной плоскости (рис. 19). Тогда их равнодействующая `vec F` будет равна векторной сумме этих сил, найденной по правилу многоугольника (рис. 20).
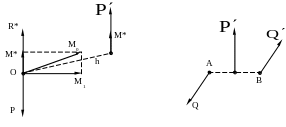
Найти равнодействующую `vec R` трёх равных по модулю сил, приложенных к телу в одной точке и расположенных в одной плоскости, если углы между всеми силами равны между собой.
`F_1 = F_2 = F_3 = F`.
См. рис. 21. Углы между парами векторов `vec(F_1)` и `vec(F_2)`, `vec(F_2)` и `vec(F_3)`, а также между векторами `vec(F_1)` и `vec(F_3)`, равны друг другу и равны `120^@`. Сложим силы `vec(F_2)` и `vec(F_3)` по правилу параллелограмма. Вследствие равенства модулей сил `vec(F_2)` и `vec(F_3)` этот параллелограмм есть ромб. Сумма сил `vec(F_2) + vec(F_3)` есть диагональ ромба, поэтому углы между парами векторов `vec(F_2)` и `vec(F_2) + vec(F_3)`, а также `vec(F_3)` и `vec(F_2) + vec(F_3)` равны по `60^@`, т. е. векторы `vec(F_1)` и `vec(F_2) + vec(F_3)` направлены вдоль одной прямой, но в противоположные стороны. Силовой параллелограмм, построенный на векторах `vec(F_2)` и `vec(F_3)`, состоит из двух равносторонних треугольников, поэтому модуль силы
`|vec(F_2) + vec(F_3)| = F_2 = F_3 = F = F_1`, т. е `vec F_1 = — (vec(F_2) + vec(F_3))`,
откуда следует `vec(F_1) + vec(F_2) + vec(F_3) = 0`.
К телу приложено `6` сил, лежащих в одной плоскости и составляющих друг с другом углы в `60^@`. Силы последовательно равны `1`, `2`, `3`, `4`, `5` и `6 Н`. Найти равнодействующую `vec R` этих шести сил.
Сложение сил по правилу многоугольника здесь нецелесообразно. Поступим иначе. Сложим сначала попарно силы, направленные вдоль одной прямой (см. рис. 22 а, б, в).
Получим
`|vec(F_2) + vec(F_4)| = 4 — 1 = 3`,
аналогично `|vec(F_2) + vec(F_5)| = 5 — 2 = 3` и `|vec(F_3) + vec(F_6)| = 6 — 3 = 3`.
Сумма сил `vec(F_2) + vec(F_5)` направлена вдоль вектора `vec(F_5)`. Туда же направлена и сумма сил `vec(F_1) + vec(F_4) + vec(F_3) + vec(F_6)`, причём модуль этой силы равен `3`. В итоге получаем, что сумма всех шести сил `vec(F_1) + vec(F_2) + vec(F_3) + vec(F_4) + vec(F_5) + vec(F_6)` направлена вдоль направления силы `vec(F_5)`, а модуль этой силы `|vec(F_1) + vec(F_2) + vec(F_3) + vec(F_4) + vec(F_5) + vec(F_6)| = 3 + 3 = 6 Н`.
Найти равнодействующую `vec R` пяти равных по модулю сил, приложенных к телу в одной точке и расположенных в одной плоскости, если углы между всеми соседними силами равны между собой (см. рис. 23). (Эти углы, разумеется, равны `360^@ //5 = 72^@`.)
В отличие от предыдущего примера здесь мы имеем нечётное число сил, поэтому невозможно образовать из них целое число пар. Поступим иначе. Возьмём какую-нибудь силу, например, `vec(F_1)`, а остальные сгруппируем в пары и попарно сложим их (см. рис. 24):
`vec(F_2) + vec(F_5)` и `vec(F_3) + vec(F_4)`.
Почему удобна именно такая группировка сил в пары? Дело в том, что обе суммы сил (и `vec(F_2) + vec(F_5)` и `vec(F_3) + vec(F_4)`) направлены вдоль линии действия силы `vec(F_1)`. Ясно, что равнодействующая всех сил будет направлена вдоль линии действия силы `vec(F_1)`. Модули сумм сил легко найти из геометрии. Например, в силовом параллелограмме, построенном на векторах `vec(F_2)` и `vec(F_5)`, который является ромбом, длина диагонали ромба (модуль силы `vec(F_2) + vec(F_5)`) равна удвоенной половинке диагонали, а та легко ищется из любого из четырёх прямоугольных треугольников, на которые ромб разбивается диагоналями. В результате
`|vec(F_2) + vec(F_5) | = 2F cos 72^@`,
где `F` — модуль любой из пяти исходных сил. Аналогично
`|vec(F_3) + vec(F_4)| = 2F cos 36^@`.
В итоге для модуля искомой силы получаем формулу
`R = F(1 + 2 cos 72^@ — 2 cos 36^@)` (*).
Для углов `72^@` и `36^@` нет таких простых формул, как для углов `30^@`, `45^@` или `60^@`. Пользуясь калькулятором, можно, однако, показать, что согласно формуле (*) `R = 0`.
Имеется и более красивое доказательство того, что результирующий вектор есть нулевой вектор. В самом деле, мы довольно произвольно взяли в качестве силы, которой не хватило пары, силу `vec(F_1)`. Если бы в качестве такой взять силу `vec(F_2)`, а в пары объединить `vec(F_1)` и `vec(F_3)` (одна пара) и `vec(F_4)` и `vec(F_5)`, то, повторив рассуждения, получим, что равнодействующая всех пяти сил `vec R` должна быть направлена вдоль линии действия силы `vec(F_2)`. Возможно ли, чтобы вектор был одновременно направлен вдоль двух несовпадающих друг с другом направлений (и `vec(F_1)`, и `vec(F_2)`; а на самом деле, как догадался читатель, ещё и вдоль направления действия сил `vec(F_3)`, `vec(F_4)` и `vec(F_5)`!)? Ненулевым вектор не может быть! Остаётся одна возможность: суммарный вектор – нулевой!
В примерах 10 и 11 мы искали по правилу параллелограмма суммы сил.
В примере 12 нас интересовала лишь проекция равнодействующей силы на направление (например, силы `vec(F_1)`).
В следующих примерах наш интерес будет также скорее не к равнодействующей силе, а только к каким-то её проекциям.
Электрический фонарь весом `Q = 16 Н` укреплён, как показано на рис. 25.
Определите отношение натяжений `T_1` и `T_2` в проволоках `BA` и `BC`, углы наклона которых даны на рисунке.
В условиях равновесия сумма всех сил, приложенных к точке `B`, равна нулю. Поэтому проекция равнодействующей всех сил на горизонтальное направление тоже равна нулю. Проекция силы со стороны проволоки, идущей к фонарю, на это направление равна нулю (эта сила вертикальна). Остаются вклады от двух натяжений со стороны проволок `BA` и `BC`. Горизонтальную ось направим слева направо. Тогда имеем: T1, гор+T2, гор=0T_{1,;mathrm{гор}}+T_{2,;mathrm{гор}}=0 (см. рис. 26), т. е.
`T_1 * cos 60^@ — T_2 cos 45^@ = 0`
(или `T_1 * sin 30^@ — T_2 sin 45^@ = 0`), откуда получаем `T_1//T_2 = sqrt2`.
Однородная массивная верёвка подвешена за два конца на разных высотах (см. рис. 27). Масса верёвки `m`. Углы, которые составляет верёвка с вертикалью в точках закрепления, равны `30^@` и `60^@`.
Определите силы натяжения верёвки вблизи её точек крепления.
Задача кажется очень трудной, т. к. не ясно, какую роль играет неизвестная нам форма верёвки, которую она примет под действием сил тяжести всех частей верёвки. (В предыдущем примере мы не интересовались провисанием проволок под действием силы тяжести, молчаливо считая провисание малым.) И всё же задача в той постановке, в какой дана, имеет простое решение. Мысленно проведём горизонтальную ось слева направо. Поскольку верёвка находится в равновесии, то сумма проекций всех сил на горизонтальное направление равна нулю. Сила тяжести верёвки имеет нулевую проекцию на это направление (эта сила направлена вертикально). Снова остаются вклады от двух натяжений (см. рис. 28):
T1, гор+T2, гор=0T_{1,;mathrm{гор}}+T_{2,;mathrm{гор}}=0, или `- T_1 * sin 30^@ + T_2 sin 60^@ = 0`.
Полагая `sin 30^@ = 1//2` и `sin 60^@ = sqrt3 //2`, находим `T_1 // T_2 = sqrt3`. Мысленно проведём ещё и вертикальную ось, направив её вниз. Сумма проекций всех сил на эту ось также равна нулю:
`mg — T_1 cos 30^@ — T_2 cos 60^@ = 0`.
Учитывая найденное ранее соотношение между `T_1` и `T_2` и значения `cos 60^@ = 1//2` и `cos 30^@ = sqrt3 //2`, получаем:
`mg — sqrt3 * T_2 * sqrt3 //2 — T_2 //2 = 0`,
откуда
`T_2 = mg//2` и `T_1 = sqrt3 mg//2`.
На гладкой наклонной плоскости с углом наклона `alpha` лежит брусок массой `m`. Какую горизонтальную силу нужно приложить к бруску, чтобы он находился в покое (рис. 29)?
Определите также модуль нормальной силы реакции на брусок со стороны наклонной плоскости.
Брусок по условию задачи покоится. Значит, сумма всех сил, приложенных к бруску, равна нулю. Равны нулю и суммы проекций сил на любые направления, в частности, на направление вдоль наклонной плоскости и перпендикулярное ему. Нормальная сила реакции `vec N` со стороны наклонной плоскости имеет равную нулю составляющую вдоль наклонной плоскости.
Проекция сила тяжести `m vec g` на ось `Ox` вдоль наклонной плоскости (рис. 30) равна `- mg sin alpha`, а проекция горизонтальной силы `F` на эту ось равна `F cos alpha`. Других сил вдоль наклонной плоскости не действует (плоскость, по условию задачи, гладкая, т. е. сила трения пренебрежимо мала). Приравнивая нулю сумму проекций на ось `Ox` всех сил, действующих на тело, получаем: `- mg sin alpha + F cos alpha = 0`, откуда находим
`F = mg (sin alpha)/(cos alpha) = mg * bbb»tg» alpha`.
Для отыскания `N` обратимся к проекциям сил на направление `Oy`. Приравняем нулю и сумму проекций на ось `Oy`:
`N — mg cos alpha — F sin alpha = 0`,
откуда `N = mg cos alpha + F sin alpha`, или с учётом найденного значения `F`:
`N = mg cos alpha + mg (sin^2 alpha)/(cos alpha) = mg (cos^2 alpha + sin^2 alpha)/(cos alpha)`,
тогда с учётом основного тригонометрического тождества, `sin^2 alpha + cos^2 alpha = 1`, получаем окончательно
`N = (mg)/(cos alpha)`.
На шероховатой поверхности доски лежит брусок массой `m`. К нему приложена сила, направленная под углом `alpha` к горизонту (см. рис. 31).
Определите модуль нормальной силы реакции со стороны поверхности.
Поскольку брусок не проваливается и не подскакивает вверх, то сумма проекций сил на вертикальную ось равна нулю:
`N + F * sin alpha — mg = 0`,
(см. рис. 32), откуда находим
`N = mg — F * sin alpha`.
Часто совершенно безосновательно приравнивают силу реакции `N` силе тяжести `mg`. Мы видим, что даже в случае горизонтальной поверхности это в общем случае не так. Для наклонной плоскости это тоже не так. В предыдущем примере нормальная сила реакции равнялась `mg//cos alpha`. Кстати, если бы удерживающая сила `F` действовала там не вдоль горизонтали, а вдоль наклонной плоскости, то для удержания бруска на наклонной плоскости потребовалась бы сила величиной `F = mg sin alpha`, а нормальная сила реакции была бы равна `N = mg cos alpha` (и снова не равнялась бы `mg`!)
Докажите это самостоятельно.
Самолёт взлетает с аэродрома со скоростью v=220 км/чv=220;mathrm{км}/mathrm ч под углом `alpha = 20^@` к горизонту. Найдите модули горизонтальной и вертикальной составляющих скорости самолёта.
(См. рис. 33). В данном примере мы имеем дело с весьма простым случаем разложения скорости на два взаимно перпендикулярных направления:
`vec v = vec(v _sf»гор») + vec(v_sf»верт»)`,
vгор=v cos α≈207 км/чv_mathrm{гор}=v;cos;alphaapprox207;mathrm{км}/mathrm ч, vверт=v sin α≈75 км/чv_mathrm{верт}=v;sin;alphaapprox75;mathrm{км}/mathrm ч.
В безветренную погоду самолёт летит на север со скоростью 180 км/ч180;mathrm{км}/mathrm ч (50 м/с50;mathrm м/mathrm с) относительно земли. С какой скоростью относительно земли будет лететь самолёт, если дует западный ветер со скоростью 10 м/с10;mathrm м/mathrm с?
(См. рис. 34). В данном случае мы имеем дело со сложением движений: `vec(v_sf»с») = vec(v_sf»св») + vec(v_sf»в»)`, где `vec(v_sf»св»)` — скорость самолёта относительно воздуха (модуль которой равен скорости самолёта относительно земли в безветренную погоду), а `vec(v_sf»в»)` — скорость воздуха. Далее по теореме Пифагора получаем:
vс=502+102=2600≈51 м/сv_mathrm с=sqrt{50^2+10^2}=sqrt{2600}approx51;mathrm м/mathrm с.
Лодка пытается пересечь реку, текущую со скоростью u=3 км/чu=3;mathrm{км}/mathrm ч. Скорость лодки в стоячей воде v=5 км/чv=5;mathrm{км}/mathrm ч. Под каким углом `alpha` к нормали к берегу надо направить лодку, чтобы она двигалась поперек реки (без сноса)? Какой будет при этом модуль скорости лодки `v` относительно берега?
Как и в примере 9, мы также имеем дело со случаем сложения движений. Но там было проще: не требовалось выбирать никакой стратегии, рыбак лишь наблюдал, как снесёт его лодку течением воды в реке. Если бы вода в реке покоилась, то, направив корпус лодки под углом `alpha` к нормали, мы заставили бы её двигаться в направлении вектора `vec V` (см. рис. 35). В действительности, вода в реке не стоячая, а имеет скорость `vec u` Поэтому сносимая течением лодка будет двигаться в направлении вектора `vec v` таком, что `vec v = vec V + vec u`. Учитывая, что оба треугольника в параллелограмме на рис. 35 прямоугольные (по условию, лодка должна двигаться перпендикулярно берегам), находим
`sin alpha = u//V = 3//5`, `alpha ~~ 37^@`,
а по теореме Пифагора v=V2-u2=4 м/сv=sqrt{V^2-u^2}=4;mathrm м/mathrm с.
Лодка пытается пересечь реку, текущую со скоростью u=5 км/чu=5;mathrm{км}/mathrm ч. Скорость лодки в стоячей воде V=3 км/чV=3;mathrm{км}/mathrm ч. Под каким углом `alpha` к нормали к берегу надо направить корпус лодки, чтобы её снесло как можно меньше? Под каким углом `beta` к нормали к берегу будет при этом плыть лодка?
В данном примере скорость лодки относительно воды меньше, чем скорость воды в реке, `V < u`, поэтому реализовать план из предыдущего примера (рис. 35) невозможно. Наша цель состоит в том, чтобы направить корпус лодки под таким углом `alpha` к нормали к берегу, чтобы сносимая течением лодка двигалась под углом `beta`, по возможности наименьшим (см. рис. 36 ф, б, в).
В данном примере складывать скорости (лодки относительно воды `vec V` и воды в реке `vec u`) удобно по правилу треугольника, а не параллелограмма: приставим начало вектора `vec V` к концу вектора `vec u`. Выбирая оптимальный план (с наименьшим углом сноса), будем мысленно поворачивать вектор `vec V`. При этом конец вектора будет описывать окружность с центром в конце вектора `vec u`. Из рисунков видно, что минимальному углу сноса лодки `beta` соответствует случай, когда вектор `vec v = vec V + vec u` направлен по касательной к этой окружности. При этом вектор `vec V _|_ vec v` т. е. треугольник скоростей на рис. 36 в прямоугольный. Отсюда получаем:
`sin alpha = V//u = 3//5`; `alpha ~~37^@`; `beta = 90^@ — alpha ~~53^@`.
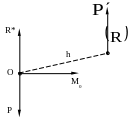
Лодку вытягивают из воды, стоя на крутом берегу и выбирая верёвку, которая привязана к носу лодки, со скоростью `v` (см. рис. 37).
Какой будет скорость лодки `u` в момент, когда верёвка будет составлять угол `alpha` с горизонтом? Верёвка нерастяжима.
Традиционная ошибка решающих эту задачу состоит в том, что пытаются разложить движение лодки на два направления – горизонтальное и вертикальное, делая (неправильное!) построение, как показано на рис. 38а и получая неверный ответ `u = v * cos alpha`. Что здесь неправильно? В отличие от самолёта из примера 17, который двигался под отличным от нуля углом к горизонту (см. рис. 33), здесь лодка движется горизонтально! Сделаем другое разложение скорости лодки `vec u` по двум направлениям – вдоль верёвки (в данный момент времени!) и перпендикулярно ей (см. рис. 38б).
Проекция вектора `vec u` на направление верёвки будет равна скорости `v`, с которой выбирают верёвку: `v = u cos alpha`, поэтому `u = v/(cos alpha)`.
Поясним ещё, почему проекция вектора `vec u` на направление верёвки будет равна скорости `v` с которой выбирают верёвку. Если мы имеем абсолютно твердое тело (АТТ), деформациями в котором можно пренебречь, или нерастяжимую нить (но уже максимально натянутую), то как бы ни двигались АТТ или нерастяжимая нить, они будут обладать следующим свойством. Возьмём две произвольные точки `A` и `B` нити или АТТ и мысленно соединим их прямой. Тогда составляющие скоростей выбранных точек вдоль этой прямой в любой момент времени будут равны друг другу: vA∥→=vB∥→overrightarrow{v_{Aparallel}}=overrightarrow{v_{Bparallel}} (см. рис. 39). В противном случае изменялось бы расстояние между точками `A` и `B`. Составляющие скорости, перпендикулярные отрезку прямой `AB`, могут быть при этом любыми.
Две лодки 1 и 2 буксируют третью лодку с помощью двух тросов (см. рис. 40). В некоторый момент времени силы натяжения тросов, идущих от лодок 1 и 2, равны друг другу по модулю и равны `F`. Угол между тросами равен `2 alpha`. Какая равнодействующая сила приложена к буксируемой лодке со стороны тянущих её лодок? Чему будет равна эта сила в случае малого угла `alpha` (когда буксирующие лодки тянут третью лодку почти в одном направлении)?
Две силы нужно сложить по правилу параллелограмма, который в данном случае будет ещё и ромбом с перпендикулярными друг другу диагоналями, разбивающими его на четыре равных прямоугольных треугольника. Из геометрии рис. 41 видно, что модуль равнодействующей силы `R` равен удвоенной длине прилежащего катета: `R = 2F cos alpha`. При стремлении угла между направлениями тросов к нулю `R -> 2F` (`cos alpha -> 1` при `alpha -> 0`).
Хитрее оказывается похожая задача, когда заданы не силы, а скорости.
Две лодки 1 и 2 буксируют третью лодку с помощью двух тросов (см. рис. 42). В некоторый момент времени модули скоростей лодок 1 и 2 равны друг другу и равны `v_1 = v_2 = v`. Найти модуль и направление скорости буксируемой лодки `u`. Тросы нерастяжимы. Чему будет равна эта скорость в случае малого угла `alpha` (когда буксирующие лодки тянут третью лодку почти в одном направлении)?
Ясно, что «решение» `u = 2v cos alpha` (как в предыдущем примере) не подходит, т. к. при `alpha -> 0` мы получили бы, что `u -> 2v`, чего не может быть. Если, например, две собаки в упряжке бегут с одинаковыми скоростями `v` в одном направлении, то и скорость упряжки будет равна этой же скорости `v` (если, конечно, упряжка не отцепилась или к ней не подключили дополнительно мотор).
Решение задачи такое же, как в примере 21. В данном примере важнейшими словами являются «Тросы нерастяжимы». Ясно, что правильное построение, учитывающее это условие, должно быть таким, как на рис. 43, откуда немедленно получаем `v = u cos alpha`, поэтому `u = v/(cos alpha)`. Тогда в предельном случае, когда `alpha -> 0`, имеем `u -> v`, как и должно быть.
Заметим, что четырёхугольник на рис. 43 весьма мало похож на параллелограмм из предыдущего примера. Еще меньше будет похож на параллелограмм этот четырёхугольник, когда модули скоростей `v_1 != v_2` (см. рис. 44).
Две лодки буксируют третью с помощью двух тросов (рис. 45). В некоторый момент времени скорость 2-ой лодки в 2 раза больше, чем скорость 1-ой, `v_2 = 2v_1 = 2v`, а угол между тросами равен `90^@`. В каком направлении и с какой скоростью движется в этот момент буксируемая лодка? Тросы нерастяжимы.
В данном случае четырёхугольник на рис. 44 будет прямоугольником — см. рис. 46 (т. е. всё же параллелограммом).
По определению тангенса угла `»tg»varphi _1 = v_2 //v_1 = 2`, откуда, пользуясь калькулятором, находим `varphi _1 ~~63^@`; `varphi _2 = 90^@ — varphi _1 ~~ 27^@`.
Модуль скорости буксируемой лодки найдём по теореме Пифагора (раз уж у нас «случайно» появились прямоугольные треугольники):
`u = sqrt(v_1^2 + v_2^2) = sqrt(v^2 + (2v)^2) = sqrt5 * v ~~ 2,2 v`.