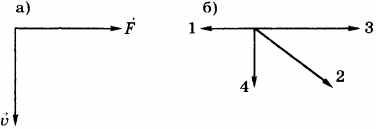Формула модуля равнодействующей силы
На тело могут оказывать действие не одна, а некоторая совокупность сил. Суммарное действие этих сил характеризуют, используя понятие равнодействующей силы.
Формула равнодействующей всех сил
Пусть на тело воздействуют в один и тот же момент времени N сил. Ускорение тела при этом равно сумме векторов ускорений, которые возникли бы при наличии каждой силы отдельно. Сила является векторной величиной. Следовательно, силы, действующие на тело, нужно складывать в соответствии с правилом сложения векторов. Равнодействующей силой ($overline$) называют векторную сумму всех сил, которые оказывают действие на тело в рассматриваемый момент времени:
Формула (1) — это формула равнодействующей всех сил, приложенных к телу. Равнодействующая сила является искусственной величиной, которую вводят для удобства проведения вычислений. Равнодействующая сила направлена также как вектор ускорения тела.
Складывают векторы, используя правило треугольника (рис.1)
правило параллелограмма (рис.2).
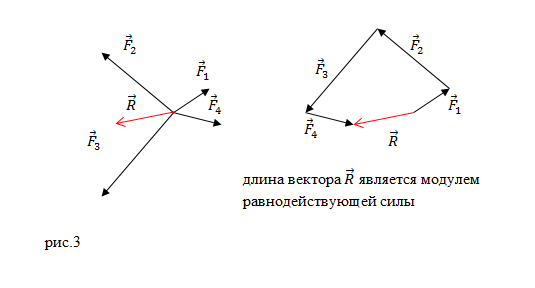
или многоугольника (рис.3):
Второй закон Ньютона и формула модуля равнодействующей
Основной закон динамики поступательного движения в механике можно считать формулой для нахождения модуля равнодействующей силы, приложенной к телу и вызывающей ускорение этого тела:
$overline=0$, если силы, приложенные к телу, взаимно компенсируют друг друга. Тогда в инерциальной системе отсчета тело скорость движения тела.
При изображении сил, действующих на тело, на рисунке, в случае равноускоренного движения, равнодействующую силу, изображают длиннее, чем сумму сил, которые противоположно ей направлены. Если тело перемещается с постоянной скоростью или покоится, длины векторов сил (равнодействующей и сумме остальных сил), одинаковы и направлены они в противоположные стороны.
Когда находят равнодействующую сил, на рисунке изображают все учитываемые в задаче силы. Суммируют эти силы в соответствии с правилами сложения векторов.
Примеры задач с решением
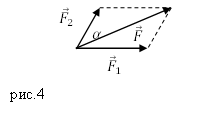
Задание. К материальной точке приложены силы, направленные под углом $alpha =60<>^circ $ друг к другу (рис.4). Чему равен модуль равнодействующей этих сил, если $F_1=40 $Н; $F_2=20 $Н?
Решение. Силы на рис. 1 сложим, используя правило параллелограмма. Длину равнодействующей силы $overline$ найдем, применяя теорему косинусов:
Вычислим модуль равнодействующей силы:
[F=sqrt<<40>^2+<20>^2+2cdot 40cdot 20<cos (60<>^circ ) >>approx 52,92 left(Нright).]
Ответ. $F=52,92$ Н
Задание. Как изменяется модуль равнодействующей силы со временем, если материальная точка массы $m$ перемещается в соответствии с законом: $s=A<cos (omega t)(м) >$, где $s$ — путь пройденный точкой; $A=const;; omega =const?$ Чему равна максимальная величина этой силы?
Решение. По второму закону Ньютона равнодействующая сил, действующих на материальную точку равна:
Следовательно, модуль силы можно найти как:
Ускорение точки будем искать, используя связь между ним и перемещением точки:
Первая производная от $s$ по времени равна:
Подставим полученный в (2.5) результат, в формулу модуля для равнодействующей силы (2.2) запишем как:
Так как косинус может быть меньше или равен единицы, то максимальное значение модуля силы, действующей на точку, составит:
Законы сложения сил в механике
При воздействии на одно тело нескольких сил одновременно тело начинает двигаться с ускорением, являющимся векторной суммой ускорений, которые бы возникли под воздействием каждой силы по отдельности. К действующим на тело силам, приложенным к одной точке, применяется правило сложения векторов.
Векторная сумма всех сил, одновременно воздействующих на тело, это сила равнодействующая, которая определяется по правилу векторного сложения сил:
R → = F 1 → + F 2 → + F 3 → + . . . + F n → = ∑ i = 1 n F i → .
Равнодействующая сила действует на тело также, как и сумма всех действующих на него сил.
Правило параллелограмма и правило многоугольника
Для сложения 2 -х сил используют правило параллелограмма (рисунок 1 ).
Рисунок 1 . Сложение 2 -х сил по правилу параллелограмма
Выведем формулу модуля равнодействующей силы с помощью теоремы косинусов:
R → = F 1 → 2 + F 2 → 2 + 2 F 1 → 2 F 2 → 2 cos α
При необходимости сложения более 2 -х сил используют правило многоугольника: от конца
1 -й силы необходимо провести вектор, равный и параллельный 2 -й силе; от конца 2 -й силы необходимо провести вектор, равный и параллельный 3 -й силе и т.д.
Рисунок 2 . Сложение сил правилом многоугольника
Конечный вектор, проведенный от точки приложения сил в конец последней силы, по величине и направлению равняется равнодействующей силе. Рисунок 2 наглядно иллюстрирует пример нахождения равнодействующей сил из 4 -х сил: F 1 → , F 2 → , F 3 → , F 4 → . Причем суммируемые векторы совсем необязательно должны быть в одной плоскости.
Результат действия силы на материальную точку будет зависеть только от ее модуля и направления. У твердого тела есть определенные размеры. Потому силы с одинаковыми модулями и направлениями вызывают разные движения твердого тела в зависимости от точки приложения.
Линией действия силы называют прямую, проходящую через вектор силы.
Рисунок 3 . Сложение сил, приложенных к различным точкам тела
Если силы приложены к различным точкам тела и действуют не параллельно по отношению друг к другу, тогда равнодействующая приложена к точке пересечения линий действия сил (рисунок 3 ). Точка будет находиться в равновесии, если векторная сумма всех сил, действующих на нее, равняется 0 : ∑ i = 1 n F i → = 0 → . В данном случае равняется 0 и сумма проекций данных сил на любую координатную ось.
Разложение вектора силы по направлениям
Разложение сил на две составляющие – это замена одной силы 2 -мя, приложенными в той же точке и производящими на тело такое же действие, как и эта одна сила. Разложение сил осуществляется, как и сложение, правилом параллелограмма.
Задача разложения одной силы (модуль и направление которой заданы) на 2 , приложенные в одной точке и действующие под углом друг к другу, имеет однозначное решение в следующих случаях, когда известны:
- направления 2 -х составляющих сил;
- модуль и направление одной из составляющих сил;
- модули 2 -х составляющих сил.
Пример 1
Необходимо разложить силу F на 2 составляющие, находящиеся в одной плоскости с F и направленные вдоль прямых a и b (рисунок 4 ). Тогда достаточно от конца вектора F провести 2 прямые, параллельные прямым a и b . Отрезок F A и отрезок F B изображают искомые силы.
Рисунок 4 . Разложение вектора силы по направлениям
Второй вариант данной задачи – найти одну из проекций вектора силы по заданным векторам силы и 2 -й проекции (рисунок 5 а ).
Рисунок 5 . Нахождение проекции вектора силы по заданным векторам
Во втором варианте задачи необходимо построить параллелограмм по диагонали и одной из сторон, как в планиметрии. На рисунке 5 б изображен такой параллелограмм и обозначена искомая составляющая F 2 → силы F → .
Итак, 2 -й способ решения: прибавим к силе силу, равную — F 1 → (рисунок 5 в ). В итоге получаем искомую силу F → .
Три силы F 1 → = 1 Н ; F 2 → = 2 Н ; F 3 → = 3 Н приложены к одной точке, находятся в одной плоскости (рисунок 6 а ) и составляют углы с горизонталью α = 0 ° ; β = 60 ° ; γ = 30 ° соответственно. Необходимо найти равнодействующую силу.
Решение
Рисунок 6 . Нахождение равнодействующей силы по заданным векторам
Нарисуем взаимно перпендикулярные оси О Х и O Y таким образом, чтобы ось О Х совпадала с горизонталью, вдоль которой направлена сила F 1 → . Сделаем проекцию данных сил на координатные оси (рисунок 6 б ). Проекции F 2 y и F 2 x отрицательны. Сумма проекций сил на координатную ось О Х равняется проекции на данную ось равнодействующей: F 1 + F 2 cos β — F 3 cos γ = F x = 4 — 3 3 2 ≈ — 0 , 6 Н .
Точно также для проекций на ось O Y : — F 2 sin β + F 3 sin γ = F y = 3 — 2 3 2 ≈ — 0 , 2 Н .
Модуль равнодействующей определим с помощью теоремы Пифагора:
F = F x 2 + F y 2 = 0 , 36 + 0 , 04 ≈ 0 , 64 Н .
Направление равнодействующей найдем при помощи угла между равнодействующей и осью (рисунок 6 в ):
t g φ = F y F x = 3 — 2 3 4 — 3 3 ≈ 0 , 4 .
Сила F = 1 к Н приложена в точке В кронштейна и направлена вертикально вниз (рисунок 7 а ). Необходимо найти составляющие данной силы по направлениям стержней кронштейна. Все необходимые данные отображены на рисунке.
Решение
Рисунок 7 . Нахождение составляющих силы F по направлениям стержней кронштейна
Дано:
F = 1 к Н = 1000 Н
Пускай стержни прикручены к стене в точках А и С . На рисунке 7 б изображено разложение силы F → на составляющие вдоль направлений А В и В С . Отсюда понятно, что
F 1 → = F t g β ≈ 577 Н ;
F 2 → = F cos β ≈ 1155 Н .
Ответ: F 1 → = 557 Н ; F 2 → = 1155 Н .
I. Механика
Тестирование онлайн
Определение
Это векторная сумма всех сил, действующих на тело.
Велосипедист наклоняется в сторону поворота. Сила тяжести и сила реакции опоры со стороны земли дают равнодействующую силу, сообщающую центростремительное ускорение, необходимое для движения по окружности
Взаимосвязь со вторым законом Ньютона
Вспомним закон Ньютона:
Равнодействующая сила может быть равна нулю в том случае, когда одна сила компенсируется другой, такой же силой, но противоположной по направлению. В этом случае тело находится в покое или движется равномерно.
|
Сила Архимеда уравновешивается силой тяжести, тело равномерно перемещается в жидкости вниз. |
Сила тяжести уравновешивается силой упругости. Книга покоится Если равнодействующая сила НЕ равна нулю, то тело движется равноускоренно. Собственно именно эта сила является причиной неравномерного движения. Направление равнодействующей силы всегда совпадает по направлению с вектором ускорения. Когда требуется изобразить силы, действующие на тело, при этом тело движется равноускоренно, значит в направлении ускорения действующая сила длиннее противоположной. Если тело движется равномерно или покоится длина векторов сил одинаковая.
|
Зильберман А. Р. Равнодействующая — как ее найти? //Квант. — 1988. — № 11. — С. 50-52.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Мы часто решаем задачи «с практическим содержанием», вовсе не отдавая себе отчета, насколько они сложны. Даже простой автомобиль содержит тысячи деталей, на каждую из которых действует множество сил. Просто перечислить их — и то трудно, а написать и решить столько уравнений… Однако мы умудряемся обойти это затруднение, вводя понятие равнодействующей силы. Поговорим об этом подробнее.
Для определения равнодействующей нужно все силы, действующие на тело, векторно сложить (не всегда это просто, но об этом чуть позже). Полученный суммарный вектор будет эквивалентен исходной системе сил.
Так уж и эквивалентен? Представьте, что лично вас тянут с силой 500 Н влево за левую руку и с такой же силой — вправо за правую руку. Сумма этих сил равна нулю, т. е. их как бы нет вовсе. Вам от этого легче?
На самом деле эквивалентность тут понимается в довольно узком смысле — при замене всех сил их равнодействующей не должно измениться движение тела, а вот о деформациях, разрывах и т. п. речи нет.
Какие же трудности могут возникнуть при сложении сил? Бели все они приложены в одной точке — то никаких. И складывать легко, и ясно, куда приложить суммарный вектор — равнодействующую. А если силы приложены в разных точках (чаще всего так и бывает)? Тогда придется силы переносить. Как это можно сделать? Тут нам понадобится специальная физическая величина — момент силы.
Рис. 1
Момент силы (~vec F) относительно точки О (рис. 1) равен
(~M = Fr sin alpha) ,
где r — расстояние от точки О до точки приложения силы А. Можно сделать иначе — разложить силу (~vec F) на две составляющие — вдоль r и перпендикулярно r. Вращающий момент создает только перпендикулярная составляющая (~vec F_2) :
(~M = F_2 r) .
Конечно, это просто предыдущая формула, переписанная немного иначе, но во многих задачах удобнее пользоваться именно ею.
Легко видеть, что при переносе силы (~vec F) вдоль линии ее действия момент силы не изменяется, поэтому такой перенос допустим. (Заметим, что деформации тела при переносе точки приложения силы изменяются. Это легко понять на простом примере. Потянем привязанную одним концом к стене резиновую ленту вначале за середину, а потом за второй конец — она растянется неодинаково.)
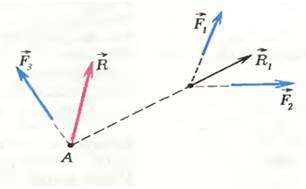
Теперь вернемся к равнодействующей. Если силы приложены в разных точках, но линии их действия пересекаются в одной,— опять все просто. Перенесем силы вдоль линий их действия в эту точку и сложим — все, как в первом случае. Бели же линии действия сил не пересекаются в одной точке, задача нахождения равнодействующей усложняется.
Рис. 2
Разберем для простоты частный случай, когда все векторы сил лежат в одной плоскости (плоская система сил). Можно попробовать решить задачу за несколько шагов — складывая силы попарно, как показано на рисунке 2. Вначале сложим силы (~vec F_1) и (~vec F_2) — получим вектор (~vec R_1), а потом сложим его с вектором (~vec F_3). Равнодействующая (~vec R) приложена в точке А.
Рис. 3
Так можно получить ответ не во всех случаях. Проблемы возникают, если векторы сил параллельны. Рассмотрим пример: нужно найти равнодействующую параллельных сил (~vec F_1) и (~vec F_2) (рис. 3). Ясно, что модуль равнодействующей равен сумме F1 и F2, а вот в какой точке должна быть приложена равнодействующая? Тут поможет простое рассуждение: какую бы точку приложения мы ни взяли, все равно момент равнодействующей относительно оси, проходящей через эту точку, равен нулю. Но при замене сил их равнодействующей моменты меняться не должны — значит, нужно взять такую точку, относительно которой суммарный момент исходной системы сил равен нулю. В нашем примере эту точку О можно найти из условия
(~F_1 cdot AO = F_2 cdot OB) .
Если (~vec F_1) и (~vec F_2) направлены в разные стороны, то точка О окажется за пределами отрезка АВ, ближе к той из сил, которая по величине больше. (Убедитесь в этом самостоятельно.)
Задачи, где нужно находить равнодействующую параллельных сил, вы наверняка решали. Так, обычно силы тяжести, приложенные к разным частям тела, считают параллельными. Центр тяжести тела — это как раз и есть точка приложения равнодействующей этих сил. Вот почему, например, тело, закрепленное на оси, которая проходит через центр тяжести тела, находится в равновесии.
Есть один важный частный случай параллельной системы сил, когда равнодействующую найти нельзя. Так будет для двух параллельных сил, которые равны по величине и противоположны по направлению. Эту систему называют парой сил. Попытка найти точку приложения пары сил приводит к делению на нуль — найти эту точку не удается. У пары сил есть одно интересное свойство: ее момент одинаков относительно любой оси вращения (проверьте это). Оказывается, таким свойством обладает любая система сил, сумма которых равна нулю (пара сил — частный случай такой системы).
Но именно такими системами сил мы и интересуемся, когда говорим об условиях равновесия тел (статика). Одно из условий — сумма сил равна нулю. Отсюда вытекает важное следствие: уравнение моментов, т. е. второе условие равновесия — сумма моментов равна нулю, можно записывать в этом случае относительно любой точки, в том числе и не лежащей внутри тела. Эту точку следует выбирать из соображений простоты получающегося уравнения (удобно ее взять, например, на пересечении линий действия нескольких сил, особенно тех, которые мы не хотим находить).
Как найти равнодействующую двух сил? Проще говоря, сложение и вычитание всех сил, присутствующих в системе, называются равнодействующими силами.
Когда считается, что изолированная система находится в движении, на систему могут действовать более двух сил. Итак, вопрос в том, как найти равнодействующую двух сил в конкретной системе. Ответ может быть простым, но нужно определить силы, присутствующие в системе, или, возможно, воздействовать на одну из них.
Также необходимо знать результирующую силу и то, как она действует на систему в движении, а иногда даже в неподвижном состоянии. Когда отдельные векторные силы складываются вместе, полученный результат считается Равнодействующая сила.
Говорят, что результирующая сила представляет собой комбинацию всех сил, присутствующих в системе. Итак, какие другие силы могут существовать? Основной и основной силой, существующей во всех системах, является гравитационная сила.
Как правило, гравитационная сила направлена вниз, и в противовес этому существует восходящая сила, которую чаще всего называют нормальной силой. В тех случаях, когда просят рассчитать результирующую силу, этих двух сил будет недостаточно.
Когда тело находится в состоянии покоя, сила, действующая на него, будет нормальной силой. Также, когда объект находится в движении, на объект действует гравитационная сила за счет ускорения. Предполагается, что гравитационная и нормальная силы одинаковы.; на самом деле это заблуждение, поскольку обе силы действуют на один и тот же объект.
Теперь, когда вкратце рассмотрены основы значительной силы, давайте посмотрим, какие другие силы влияют и обеспечивают движение любого объекта.

Что является равнодействующим двух сил?
Равнодействующая двух сил — это просто векторная сумма отдельных сил в системе.
Термин результирующая сила относится к результату только в том случае, если сложены две точные векторные величины. Также может быть результирующее смещение, результирующая скорость, если сложить две скорости, а также может быть результирующий импульс.
Теперь, когда мы имеем дело с равнодействующими силами, давайте воспользуемся примером, чтобы ясно понять, как найти Равнодействующая сила из двух сил.
На восток действует вектор силы, и другой вектор силы также направлен на восток. Величина векторов представляет собой размер силы как таковой, имеющей значения 100 Н и 120 Н соответственно.
Теперь мы возьмем две силы, действующие в двух разных направлениях, один на запад, а другой на восток с разной величиной. Поскольку направление изменяется, результирующая сила оказывается меньше исходной силы.
Следовательно, направление равнодействующей вектора силы будет направлено в сторону силы, имеющей меньшую величину, чем другая.
Рассмотрим два вектора под прямым углом друг к другу и как найти равнодействующую двух сил?

Когда говорят, что две силы перпендикулярны друг другу, мы должны провести линию гипотенузы, чтобы найти результирующую силу системы. При этом будет сформирован треугольник.
Используя теорему Пифагора, можно найти третье значение, которое также является значением равнодействующей силы.
Как рассчитать результирующую силу с углами?
Теперь, когда мы знаем, как найти результирующую силу двух сил, используя диаграмму свободного тела, давайте углубимся в область, где должна быть рассчитана результирующая сила с углом.
В предыдущем разделе мы обсуждали, как найти равнодействующую двух сил, которая в основном была величиной равнодействующей силы. Угол вектора силы с касательной дает направление этой конкретной силы.
Угол можно определить по формуле ϴ = тангенс-1 (у / х). Здесь буквы x и y обозначают направление компонентов, а также направление действия двух разных сил.
Давайте рассмотрим пример с использованием диаграммы свободного тела, чтобы лучше понять это.

Если у нас есть вектор силы, направленный на запад (50), а другая сила — на север (120), как мы выяснили в предыдущем примере с помощью теоремы Пифагора, можно оценить величину равнодействующей силы, и что составляет 130 Н.
Теперь с заданной информацией об угле направление теперь можно было определить, используя значения магнитуды. Пусть 40N будет компонентом y, а 120N будет компонентом x. Используя формулу ϴ = тангенс-1 (у / х) и применяя формулу соответствующим образом, мы получаем ответ как 67.4⁰.
Этот угол ϴ=67.4⁰ называется опорным углом. Теперь следует определить относительный угол к этому конкретному опорному углу, чтобы сформировать диаграмму свободного тела. Относительный угол равен 247.4⁰.

Следовательно, приведенные выше расчеты являются результатом направления вектора силы. Также они могут меняться в зависимости от различных случаев, когда упоминается вид сил.
Как найти равнодействующую трех сил?
В этом разделе мы будем работать с числами, чтобы найти результирующую силу трех сил.
Проблема:
Три векторные силы действуют в трех разных направлениях, образуя углы с их касательными, как показано на рисунке ниже. Теперь вычислите результирующую величину и направление силы с заданными данными.

Решение:
Все силы имеют свои компоненты x и y. Итак, сначала вычислим силы F1 и F2. Определив x-компоненты F1 и F2, получим ответ Fx= -30.84N. Далее, определяя y-компоненты F1 и F2, получаем результат Fy=-0.0794N. Так как значение компонента почти равно нулю, это не существенно.
Теперь вычисляя F’, мы получаем F’= -30.84Ni-0.794Nj, а третья сила F3=50N направлена по оси x, так как I не имеет компоненты y. Теперь F’+f3 = Fr (результирующая сила). Fr = 19.17, что является величиной, и 2.37⁰, что является направлением равнодействующей силы.
Так обычно определяют равнодействующую трех сил, и это относится ко всем остальным задачам с подобным опросником.
Для расчета полной силы или Равнодействующая сила всей системы, на которую действуют три силы, нам нужно знать, в каком направлении действует векторная сила вместе со значением угла.
Равнодействующая двух сил
Проще говоря, равнодействующую двух сил можно легко найти, добавляя или вычитая соответствующую индивидуальную силу, действовавшую на систему.
Когда считается, что система находится в движении, мы говорим, что сила ответственна за это конкретное движение. Диаграмма свободного тела необходима для определения результирующей силы, действующей на систему, находящуюся в постоянном движении.
Из нарисованной диаграммы свободного тела и значений приложенных сил становится легче теоретически определить силы, присутствующие в системе.
1 задачи:
Теперь рассмотрим систему, на которую действуют силы, действующие в двух разных направлениях. Скажем, одна векторная сила действует на восток, а другая векторная сила действует на запад. Значения силы равны 10 Н и 30 Н соответственно. Теперь найдите результирующую силу, действующую на систему.
Решение:
Результирующая сила обозначается Fr, поэтому
Фр= -10Н+30Н
Fr = 20N
Говорят, что результирующая сила действует в направлении более значительной силы, которая действует на запад.
2 задачи:
Теперь давайте рассмотрим изолированная система на них действуют две силы. Величина сил 50Н и 30Н. Обе силы имеют тенденцию действовать в одном и том же направлении, то есть на восток, поэтому значения окажутся положительными. Вычислите равнодействующую двух сил с заданными значениями.
Решение:
Фр= 50Н+30Н
Фр= 80Н
Направление силы будет только на восток, так как обе силы действуют на восток.
Как найти равнодействующую двух действующих сил?
Как найти равнодействующую двух сил, если они действуют одновременно? Смысл, как найти равнодействующую сил, если они лежат в одной плоскости.
Мы все должны знать о законе параллелограмма, который изображает и объясняет, что две или более сил, движущихся в одном направлении, проходят через общую точку.
Проблема:
Две силы называются совпадающими, если силы расходятся из общей точки. Величины для данных сил равны 100 Н и 70 Н. Найдите результирующую силу, действующую на систему.

Решение:
Согласно соглашению о знаках, силы называются положительными и должны быть сложены, чтобы найти результирующую силу.
Фр=F1+F2
Фр= 100Н + 70Н
Фр= 170Н.
Таким образом, когда мы хорошо знаем правило знаков, мы можем вычислить результирующую силу.
Как найти равнодействующую двух перпендикулярных сил?
Когда говорят, что две силы перпендикулярны друг другу, результирующие силы можно найти, используя закон параллелограмма и определяя угол между ними.
Когда два векторные силы перпендикулярны относительно друг друга, и равнодействующая этих сил может быть найдена с использованием различных математических методов.
Можно сложить все компоненты x сил, которые им параллельны, а сложив все компоненты y сил, которые им параллельны.
Метод «хвост к хвосту» — один из наименее используемых методов для нахождения результирующей силы двух сил, расположенных под прямым углом друг к другу.
Загрузить PDF
Загрузить PDF
Равнодействующая сила – это векторная сумма всех сил, которая действует на тело.[1]
Если равнодействующая сила равна нулю, то тело находится в покое. Неуравновешенная сила, или равнодействующая сила, значение которой больше или меньше нуля, приводит к ускорению тела.[2]
Суммировать все силы для поиска равнодействующей достаточно просто, но для этого сначала нужно рассчитать или измерить их величину. Как только вы изобразите простую схему действующих сил и убедитесь, что все силы имеют правильный вектор, вычисление равнодействующей силы покажется вам плевым делом.
-
1
Начертите диаграмму свободного тела. Диаграмма свободного тела – это схематичный набросок тела с обозначением векторов всех сил, которые на него действуют. Прочитайте задачу и набросайте схему рассматриваемого тела, обозначив каждую силу, действующую на это тело, стрелками.[3]
- Пример: Вычислить равнодействующую силу тела весом 20 Н, которое лежит на столе и которое толкают вправо под действием силы 5 Н, но при этом остается неподвижным из-за действующей на нее силы трения, равной 5 Н.
-
2
Обозначьте положительные и отрицательные направления сил. Как правило, вверх и вправо направлены силы с положительным значением, а вниз и влево – с отрицательным. Имейте в виду, что в одном направлении могут действовать сразу несколько сил. Силы, действующие в противоположном направлении, должны иметь отрицательные значения (одна положительная, одна отрицательная).[4]
- Если вам нужно представить несколько схем действующих сил, убедитесь, чтобы вектора сил были перенесены правильно.
- Согласно направлению векторов на схеме, пометьте силы знаком «+» или «-».
- Пример: Сила тяжести направлена вниз, делая ее отрицательной. Сила нормальной реакции направлена вверх, что делает ее положительной. Сила, с которой прижимают тело, направлена вправо, что делает ее положительной, тогда как сила трения действует в обратном направлении, то есть, влево (отрицательная).
-
3
Обозначьте все силы. Обозначьте все силы, которые действуют на тело. Если тело лежит на горизонтальной поверхности, на него действует сила тяжести (Fтяж), направленная вниз, а также равная ей сила нормальной реакции, направленная в противоположную сторону (Fн). Помимо этих двух сил отметьте также и другие силы, указанные в задаче. Величину сил запишите в ньютонах рядом с их обозначением.[5]
- Для обозначения силы обычно используется символ F и первые буквы силы в нижнем индексе. Сила трения, к примеру, обозначается так: Fтр.
- Сила тяжести: Fтяж = -20 Н
- Сила нормальной реакции: Fн = +20 Н
- Сила трения: Fтр = -5 Н
- Сила, с которой прижимают тело: Fт = +5 Н
-
4
Сложите все значения. Теперь, когда мы определили вектора и величину всех действующих сил, осталось лишь сложить их вместе. Запишите уравнение для результирующей силы (Fрез), где Fрез будет равна сумме действующих на тело сил.[6]
- Пример: Fрез = Fтяж + Fн + Fтр + Fт = -20 + 20 -5 + 5 = 0 Н. Так как равнодействующая сила равна 0, тело находится в состоянии покоя.
Реклама
-
1
Изобразите схему действующих сил. Когда действие силы на тело происходит под углом, для определения ее величины необходимо найти горизонтальную (Fx) и вертикальную (Fy) проекции этой силы. Для этого мы будем использовать тригонометрию и угол наклона (обозначается символом θ «тета»). Угол наклона θ измеряется против часовой стрелки, начиная от положительной оси х.[7]
- Нарисуйте диаграмму действующих сил, включая угол наклона.
- Укажите вектор направления действия сил, а также их величину.
- Пример: Тело с силой нормальной реакции, равной 10 Н, движется вверх и вправо с силой 25 Н под углом в 45°. Также на тело действует сила трения, равная 10 Н.
- Перечень всех сил: Fтяж = -10 Н, Fн = + 10 Н, Fт = 25 Н, Fтр = -10 Н.
-
2
Вычислите Fx и Fy, используя основные тригонометрические соотношения. Представив наклонную силу (F) в качестве гипотенузы прямоугольного треугольника, а Fx и Fy – в качестве сторон этого треугольника, можно вычислить их по отдельности.[8]
- Напоминаем, что косинус (θ) = прилежащая сторона/гипотенуза. Fx = соз θ * F = cos(45°) * 25 = 17,68 Н.
- Напоминаем, что синус (θ) = противолежащая сторона/гипотенуза. Fy = sin θ * F = sin(45°) * 25 = 17,68 Н.
- Обратите внимание, что под углом на объект одновременно может действовать несколько сил, поэтому вам придется найти проекции Fx и Fy для каждой такой силы. Суммируйте все значения Fx, чтобы получить результирующую силу в горизонтальном направлении, и все значения Fy, чтобы получить результирующую силу в вертикальном направлении.
-
3
Перерисуйте схему действующих сил. Определив все горизонтальные и вертикальные проекции силы, действующие под углом, можете нарисовать новую схему действующих сил, указав также и эти силы. Сотрите неизвестную силу, а вместо нее укажите векторы всех горизонтальных и вертикальных величин.
- К примеру, вместо одной силы, направленной под углом, на схеме теперь будут представлены одна вертикальная сила, направленная вверх, величиной 17,68 Н, и одна горизонтальная сила, вектор которой направлен вправо, а величина равна 17,68 Н.
-
4
Сложите все силы, действующие по координатам х и у. После того как нарисуете новую схему действующих сил, вычислите результирующую силу (Fрез), сложив отдельно все горизонтальные силы и все вертикальные силы. Не забудьте следить за правильным направлением векторов.
- Пример: Горизонтальные вектора всех сил вдоль оси х: Fрезx = 17,68 – 10 = 7,68 Н.
- Вертикальные вектора всех сил вдоль оси у: Fрезy = 17,68 + 10 – 10 = 17,68 Н.
-
5
Вычислите вектор равнодействующей силы. На данном этапе у вас есть две силы: одна действует вдоль оси х, другая – вдоль оси у. Величина вектора силы является гипотенузой треугольника, образованного этими двумя проекциями. Для вычисления гипотенузы достаточно лишь задействовать теорему Пифагора: Fрез = √ (Fрезx2 + Fрезy2).[9]
- Пример: Fрезx = 7,68 Н, а Fрезy = 17,68 Н
- Подставим значения в уравнение и получим: Fрез = √ (Fрезx2 + Fрезy2) = √ (7,682 + 17,682)
- Решение: Fрез = √ (7,682 + 17,682) = √(58,98 + 35,36) = √94,34 = 9,71 Н.
- Сила, действующая под углом и вправо равна 9,71 Н.
Реклама
Об этой статье
Эту страницу просматривали 124 963 раза.
Была ли эта статья полезной?
Сила. Сложение сил
1. Ускорения взаимодействующих тел обратно пропорциональны их массам: ( frac{a_1}{a_2}=frac{m_2}{m_1} ). Преобразовав это равенство, получаем: ( m_1a_1=m_2a_2 ). В правой и в левой частях равенства стоят одинаковые величины для двух взаимодействующих тел, причем значения ускорений тел не зависят от условий их взаимодействия. Следовательно, можно считать, что произведение массы тела и его ускорения характеризует взаимодействие тел и это произведение равно силе, действующей на тело со стороны другого взаимодействующего с ним тела, т.е.: ( vec{F}=mvec{a} ).
Силой называют физическую величину, характеризующую взаимодействие тел и равную произведению массы тела и его ускорения. Поскольку ускорение векторная величина, а масса скалярная, то сила — векторная величина: ( vec{F}=mvec{a} ).
2. Единица силы, в отличие от единицы массы, является производной единицей СИ. ( [,F,]=[,m,][,a,] ); ( [,F,] ) = 1кг · 1 м/с2. ( [,F,] ) = 1 Н (1 ньютон).
Один ньютон — это такая сила, которая телу массой 1 кг сообщает ускорение 1 м/с2.
3. Результат действия силы зависит от её модуля, направления и точки приложения. Например, дверную ручку прикрепляют как можно дальше от петель, на которых она висит, поскольку, чем ближе к петлям подействовать силой, тем труднее дверь открыть.
4. Прибором для измерения силы служит динамометр. В соответствии с законом Гука удлинение пружины прямо пропорционально силе упругости, поэтому по удлинению пружины можно судить о приложенной к пружине силе, которая равна силе упругости.
5. Обычно на тело действуют несколько сил. Например, на тело, падающее в воздухе, действуют сила тяжести и сила сопротивления воздуха; на груз, висящий на нити, действуют сила тяжести и сила упругости нити.
При этом действие каждой силы не зависит от действия других, т.е. каждая сила сообщает телу такое ускорение, какое она сообщила бы ему в отсутствие действия других сил. Это утверждение носит название принципа независимости действия сил. Поэтому при расчёте ускорения движения тела все действующие на него силы заменяют одной силой.
Равнодействующей силой называют силу, которая оказывает на тело такое же действие, как и все действующие на него силы вместе.
Равнодействующую силу находят по правилу сложения векторов, она равна геометрической сумме действующих на тело сил.
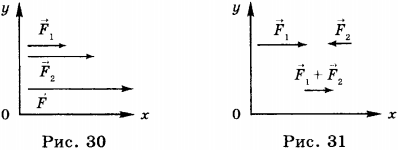
Если силы, действующие на тело, направлены по одной прямой в одну сторону, то ( vec{F}=vec{F}_1+vec{F}_2 ), а модуль равнодействующей равен сумме модулей действующих сил ( F=F_1+F_2 ) (рис. 30).
Если силы, действующие на тело, направлены в разные стороны, то ( vec{F}=vec{F}_1+vec{F}_2 ), а модуль равнодействующей равен разности модулей действующих сил: ( F=F_1-F_2 ) (рис. 31 ).
Если силы направлены под углом друг к другу, то равнодействующая равна диагонали параллелограмма, построенного на действующих на тело силах как на сторонах, или стороне треугольника, начало которой совпадает с началом вектора ( vec{F}_1 ), а конец с концом вектора ( vec{F}_2 ) (рис. 32).
Содержание
- ПРИМЕРЫ ЗАДАНИЙ
- Часть 1
- Часть 2
- Ответы
ПРИМЕРЫ ЗАДАНИЙ
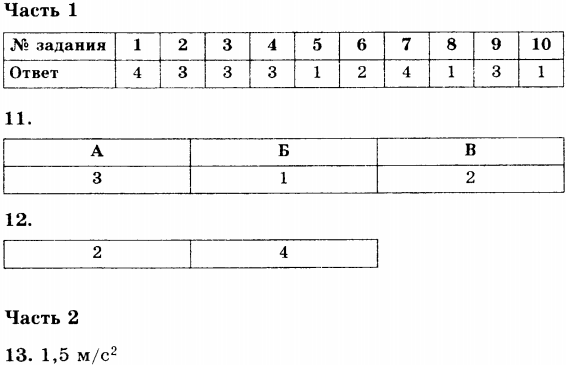
Часть 1
1. Ускорение движения парашютиста с раскрытым парашютом определяется его взаимодействием
1) только с Землёй
2) только с Землёй и с воздухом
3) только с Землёй и с парашютом
4) с Землёй, воздухом и парашютом
2. Сила — это мера
1) быстроты движения
2) инертности
3) взаимодействия
4) быстроты изменения скорости
3. Какие из приведённых ниже величин всегда совпадают по направлению?
1) сила и скорость
2) сила и перемещение
3) сила и ускорение
4) ускорение и перемещение
4. На рисунке а) показаны направления силы, действующей на тело, и его скорости. Какой из четырёх векторов, приведённых на рисунке б), указывает направление ускорения, с которым движется это тело?
1) 1
2) 2
3) 3
4) 4
5. На тело, находящееся на полу движущегося лифта, действуют сила тяжести 90 Н и сила упругости со стороны пола лифта, равная 75 Н. Чему равна равнодействующая этих сил и как она направлена?
1) 45 Н, направлена в ту же сторону, что и сила тяжести
2) 45 Н, направлена в ту же сторону, что и сила упругости
3) 125 Н, направлена в ту же сторону, что и сила тяжести
4) 125 Н, направлена в ту же сторону, что и сила упругости
6. На тело действуют две силы модули которых, — ( F_1 ) = 30 Н и ( F_2 ) = 40 Н, направленные под углом 90° друг к другу. Чему равна равнодействующая этих сил?
1) 70 Н
2) 50 Н
3) 40 Н
4) 10 Н
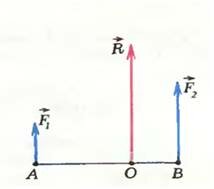
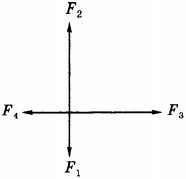
7. Чему равна равнодействующая сил, действующих на тело (рис.), если ( vec{F}_1 ) = 4 Н, ( vec{F}_2 ) = 16 Н, ( vec{F}_3 ) = 22 Н, ( vec{F}_4 ) = 6 Н?
1) 48 Н
2) 34 Н
3) 28 Н
4) 20 Н
8. Чему равна сила, под действием которой тело массой 8 кг получает ускорение 4 м/с2?
1) 32 Н
2) 8 Н
3) 2 Н
4) 0,5 Н
9. Результат действия силы зависит от
А. Её направления
Б. Точки приложения
Правильный ответ:
1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б
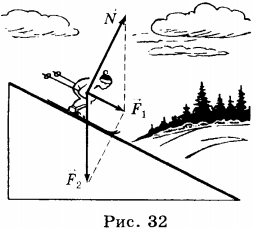
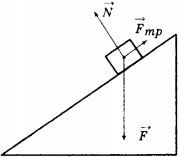
10. На наклонной плоскости покоится брусок, на который действуют сила тяжести ( vec{F} ), сила реакции опоры ( vec{N} ) и сила трения покоя ( vec{F}_{тр} ). Чему равна равнодействующая этих сил?
1) 0
2) ( F+N+F_{тр} )
3) ( F_{тр} )
4) ( F + N )
11. Установите соответствие между физическими величинами в левом столбце и их единицами в правом столбце. В таблице под номером физической величины левого
столбца запишите соответствующий номер выбранной вами единицы величины из правого столбца.
ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A) масса
Б)сила
B)ускорение
ЕДИНИЦА ВЕЛИЧИНЫ
1) Ньютон (Н)
2) метр в секунду в квадрате (м/с2)
3) килограмм (кг)
12. Из приведённых высказываний выберите два верных и запишите их номера.
1) Из двух тел разной массы при действии на них одинаковой силы большее ускорение приобретет тело большей массы.
2) Сила равна произведению массы тела и его ускорения.
3) Направление движения тела всегда совпадает с направлением силы.
4) Сила — причина ускорения тела.
Часть 2
13. На автомобиль массой 1 т действуют сила тяги 1700 Н и сила трения 200 Н. С каким ускорением движется автомобиль?
Ответы
Сила. Сложение сил
3.2 (64.12%) 34 votes