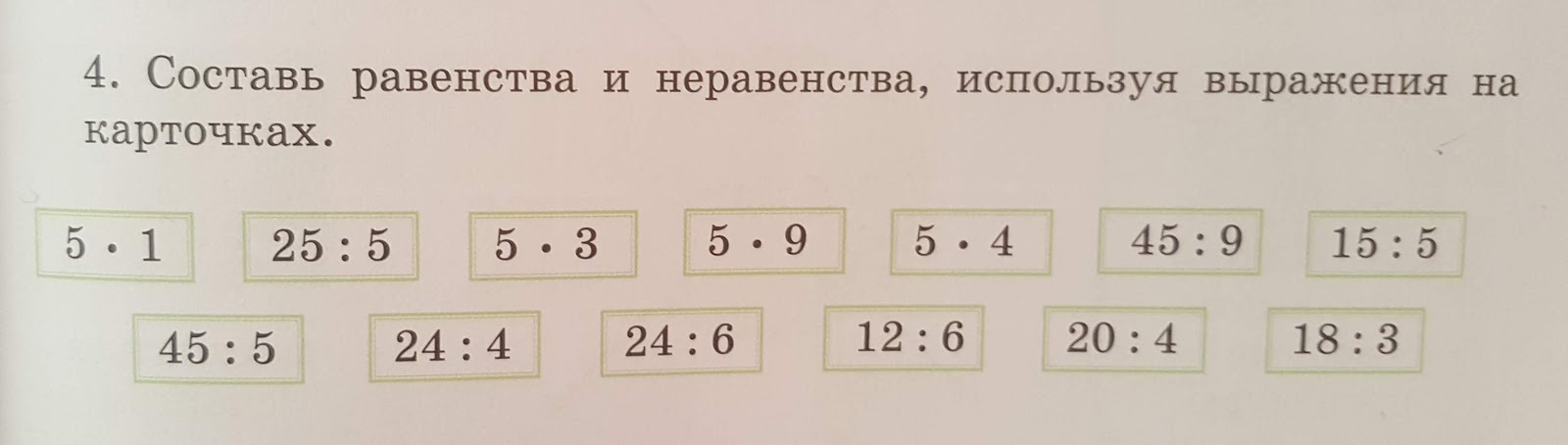
Часто приходится описывать реальную ситуацию, процесс, явление с помощью математического языка.
Математический язык- универсальный язык, с помощью него можно однозначно и кратко описать многие закономерности, процессы, задачи и т.д.
Связать реальную жизнь и математическое описание любой ситуации нам позволяет математическая модель.
Описывая реальность с помощью математического языка, люди создают математические модели, превращающие слова в формулы, неравенства, равенства, уравнения и т.п.
Математическая модель дает возможность решать огромное количество практических (природных, технических, научных, экономических, социальных и других) задач.
Эта информация доступна зарегистрированным пользователям
Математические модели делят на:
- Словесные.
- Графические (схемы, графики, чертежи, рисунки и т.д.).
- Аналитические (алгебраические: числовые равенства, неравенства, уравнения, формулы и т.д.).
На данном уроке подробно рассмотрим одну из аналитических математических моделей- уравнение.
Эта информация доступна зарегистрированным пользователям
Выясним, что такое уравнение и что называют корнем уравнения.
Рассмотрим простейшие виды уравнений.
Разберем способы и приемы решения уравнений с одним неизвестным.
Рассмотрим алгоритм и примеры решения задач с помощью уравнений.
Часто при решении задач приходится составлять равенства.
Два выражения (числовые или буквенные), соединенные знаком равно «=», образуют равенство.
В математике различают два вида равенств: тождества и уравнения.
Эта информация доступна зарегистрированным пользователям
Тождества- это числовые равенства, а также равенства, которые выполняются при всех допустимых значениях переменных, входящих в него.
Уравнение- это равенство, содержащее неизвестные числа, обозначенные буквами, значение которых можно определить.
Неизвестное число, входящее в уравнение, называют неизвестным членом уравнения (или просто «неизвестным»).
Чаще всего в математике неизвестные величины обозначают маленькими буквами латинского алфавита x, y, z.
Эта информация доступна зарегистрированным пользователям
Пример 1:
4 + х = 18 является уравнением с неизвестной х.
12у — 5 = 19 является уравнением с неизвестной у.
(2 + z) — (3 — 1) = 2 является уравнением с неизвестной z.
Все три записи являются равенствами, в каждом из них есть неизвестное число, обозначенное буквой.
Пример 2:
4х — 18 не является уравнением, так как не является равенством.
24 — 5 = 19 не является уравнением, так как не содержит неизвестную.
у + 2 > 12 не является уравнением, так как не является равенством.
Решить уравнение- это значит найти неизвестное число, при котором из уравнения получается верное равенство.
Эта информация доступна зарегистрированным пользователям
Уравнение считается решенным, если все его решения найдены или доказано, что уравнение решения не имеет.
Значение неизвестного, обращающее уравнение в верное равенство, называют корнем уравнения.
Следовательно, если в уравнение вместо неизвестной подставить ее численное значение и получится верное числовое равенство, то это значение неизвестной будет решением этого уравнения.
Рассмотрим пример.
Дано уравнение 12 — х + 3 = 10.
1) Пусть х равно 6, получаем
12 — 6 + 3 = 10
9 ≠ 10 (девять не равно десяти)
При подстановке вместо неизвестного число 6, получаем неверное числовое равенство 9 ≠ 10, т.е. число 6 не является корнем уравнения.
2) Пусть х равно 5, получаем
12 — 5 + 3 = 10
10 = 10
При подстановке вместо неизвестного число 5, получаем верное числовое равенство 10 = 10, т.е. число 5 является корнем уравнения.
Уравнение может иметь разное количество корней: существуют уравнения, имеющие один единственный корень, уравнения, имеющие два, три корня.
Встречаются уравнения, вообще не имеющие верного решения, и даже такие уравнения, решением которых являются бесконечное множество решений.
Пример.
7 — х = 4 уравнение имеет один корень, х = 3, любое другое значение х будет давать неверное равенство.
х = х — 15 уравнение не имеет решения, так как любое значение неизвестного х будет данное равенство обращать в неверное, не существует таких чисел, которые были бы меньше самого себя.
0 ⋅ y = 0 уравнение имеет бесконечное множество верных решений, так как при умножении любого числа на 0, получается 0.
Уравнение, содержащее одну неизвестную, называют уравнением с одной неизвестной.
Уравнения с большим количеством неизвестным называют соответственно уравнением с двумя, тремя и т.д. неизвестными.
Такие уравнения и их решение будете рассматривать в старших классах.
Например, 26 — 2х = 23 — х— это уравнение с одной неизвестной х.
53 — х = 19у— это уравнение с двумя неизвестными х и у.
Любое уравнение имеет левую и правую часть.
Выражение, стоящее слева от знака равно, называют левой частью уравнения, а выражение, которое стоит справа, правой частью уравнения.
Каждый компонент, из которых состоит уравнение, называют членами этого уравнения.
Эта информация доступна зарегистрированным пользователям
Обычно все члены уравнения, содержащие неизвестное, следует группировать в левой части уравнения, а известные — в правой.
Чаще всего уравнение записывают в левой части страницы, справа делают письменные вычисления (вычислительные операции).
При решении уравнения каждое новое равенство записывается с новой строки (т.е. решение оформляется в виде столбика равенств).
Таким образом, знак равенства при решении уравнения используют только один раз в каждой строке.
Эта информация доступна зарегистрированным пользователям
Уравнения позволяют записать информацию в таком виде, в котором с ней можно выполнять математические действия и известные нам преобразования.
Эта информация доступна зарегистрированным пользователям
Необходимо помнить, что при нахождении корней уравнения с правой и левой частью уравнения можно производить различные действия, однако эти действия не должны нарушать равенство между ними.
Эта информация доступна зарегистрированным пользователям
Если уравнение составное, содержит несколько арифметических операций, то прежде всего необходимо установить последнее действие и выделить в качестве неизвестного компонента арифметической операции целое выражение, а затем упрощать уравнение.
Рассмотрим некоторые способы решения уравнений.
1. Нахождение неизвестных компонентов арифметических операций.
Чтобы найти корни уравнения, необходимо знать, каким образом связаны между собой компоненты арифметических операций.
Ранее мы подробно рассмотрели такие математические операции, как сложение и вычитание.
Вспомним, как найти каждый из компонентов сложения и вычитания и попробуем разобраться, каким образом данные знания могут быть применены при решении уравнений.
Решение уравнений с неизвестным слагаемым.
В общем виде операция сложения выглядит так:
Эта информация доступна зарегистрированным пользователям
В данном случае может быть неизвестным первое или второе слагаемое.
Вспомним, как связаны между собой компоненты операции сложения.
Правило: чтобы найти неизвестное слагаемое (первое или второе), необходимо из суммы вычесть известное слагаемое.
Это правило позволит решать уравнения с неизвестным слагаемым.
Рассмотрим на примерах.
Пример 1.
Решим уравнение х + 7 = 12.
Неизвестное обозначено маленькой латинской буквой х.
В данном уравнении неизвестно первое слагаемое.
Применим правило: чтобы найти неизвестное слагаемое (х), необходимо из суммы (равной 12) вычесть известное слагаемое (равное 7).
х = 12 — 7
х = 5.
Выполним проверку найденного корня.
Для этого в исходное уравнение х + 7 = 12 вместо неизвестного (х) нужно подставить найденное значение х = 5.
5 + 7 = 12
Вычислим левую часть равенства.
12 = 12
Получили тождество, следовательно, корень уравнения найден верно.
Запишем ответ.
Ответ: х = 5.
Опуская все наши пояснения и рассуждения, решение уравнения запишем так:
х + 7 = 12
х = 12 — 7
х = 5
Проверка:
5 + 7 = 12
12 = 12
Ответ: х = 5.
Пример 2.
Решим уравнение 16 + х = 24 — 4.
Найдем значение неизвестного х, при котором данное уравнение обратится в верное равенство.
Сумма 16 и неизвестного числа х равна разности 24 и 4.
В этом уравнение значение суммы представлено не просто числом, а числовым выражением 24 — 4.
Упростим выражение, для этого найдем значение разности.
24 — 4 = 20.
Левую часть уравнения перепишем в первоначальном виде 16 + х, а справа запишем полученный результат разности 24 и 4.
16 + х = 20
Получили простое уравнение, в котором неизвестно второе слагаемое.
Нам известно, как связаны между собой компоненты сложения.
Применим правило: чтобы найти неизвестное слагаемое (х), необходимо из суммы равной 20 вычесть известное слагаемое равное 16.
х = 20 — 16
х = 4.
Выполним проверку найденного корня.
В исходное уравнение 16 + х = 24 — 4 вместо неизвестного числа (х) подставим найденный корень х = 4.
16 + 4 = 24 — 4
20 = 20
Сумма чисел 16 и 4 равна 20, разность 24 и 4 равна 20, следовательно, значение левой и правой части равенства одинаково.
Значит корень уравнения найден верно.
Запишем ответ.
Ответ: х = 4.
Опуская все наши пояснения и рассуждения, решение уравнения запишем так:
16 + х = 24 — 4
16 + х = 20
х = 20 — 16
х = 4
Проверка:
16 + 4 = 24 — 4
20 = 20
Ответ: х = 4.
Решение уравнения с неизвестным уменьшаемым или вычитаемым.
В общем виде операция вычитания выглядит так:
Эта информация доступна зарегистрированным пользователям
В таком случае неизвестным компонентом может быть уменьшаемое и вычитаемое.
Вспомним, как связаны компоненты арифметической операции вычитания.
Если неизвестно уменьшаемое число, необходимо сложить два известных компонента вычитания.
Правило: чтобы найти уменьшаемое, нужно к разности прибавить вычитаемое.
Эта информация доступна зарегистрированным пользователям
Если из исходного уменьшаемого числа вычесть один из компонентов, то в итоге получается второй компонент.
Правило: чтобы найти вычитаемое, нужно от уменьшаемого отнять разность.
Эта информация доступна зарегистрированным пользователям
Эти правила позволят решать уравнения, в которых неизвестны уменьшаемое или вычитаемое.
Рассмотрим примеры.
Пример 1.
Решим уравнение х — 28 = 34.
Найдем значение неизвестного х, при котором данное уравнение обратится в верное равенство.
В данном уравнении неизвестно уменьшаемое.
Применим правило: чтобы найти уменьшаемое (х), необходимо к разности (равной 34) прибавить вычитаемое (равное 28).
х = 34 + 28
х = 62.
Выполним проверку.
Подставим в исходное уравнение х — 28 = 34 вместо неизвестного (х) найденный корень х = 62.
62 — 28 = 34
Вычислим левую часть равенства.
34 = 34
Получили верное равенство, следовательно, корень уравнения найден верно.
Запишем ответ.
Ответ: х = 62.
Опустим все наши пояснения и рассуждения; решение уравнения будет выглядеть так:
х — 28 = 34
х = 34 + 28
х = 62
Проверка:
62 — 28 = 34
34 = 34
Ответ: х = 62.
Пример 2.
Решим уравнение 48 — х = 17 + 20.
Найдем значение неизвестного х, при котором данное уравнение обратится в верное равенство.
Разность 48 и х равна сумме чисел 17 и 20.
Упростим уравнение, для этого в правой части равенства найдем сумму 17 и 20.
17 + 20 = 37
Левую часть равенства перепишем, сохраняя исходный вид, а справа запишем полученный результат суммы чисел 17 и 20.
48 — х = 37
Получили простое уравнение, в котором неизвестно вычитаемое.
Нам известно, как связаны между собой компоненты вычитания.
Применим правило: если из уменьшаемого (равного 48) вычесть разность (равную 37), то получится вычитаемое (х).
х = 48 — 37
х = 11
Выполним проверку.
В исходное уравнение 48 — х = 17 + 20 вместо неизвестного числа (х) подставим найденный корень х = 11.
48 — 11 = 17 + 20
Разность чисел 48 и 11 равна 37, сумма чисел 17 и 20 равна 37.
37 = 37
Получили верное равенство, следовательно, корень уравнения найден верно.
Запишем ответ.
Ответ: х = 11.
Опустим все наши пояснения и рассуждения, решение уравнения будет выглядеть так:
48 — х = 17 + 20
48 — х = 37
х = 48 — 37
х = 11
Проверка:
48 — 11 = 17 + 20
37 = 37
Ответ: х = 11.
Пример 3.
Попробуем решить более сложное уравнение.
Эта информация доступна зарегистрированным пользователям
(4 + х) — 5 = 19
Сразу решить такое уравнение невозможно.
Первым делом нужно определить арифметическую операцию, которая будет выполняться в последнюю очередь.
В данном равенстве это разность суммы (4 + х) и 5.
За неизвестное принимаем целое выражение, содержащее букву (4 + х), в уравнении оно является уменьшаемым.
Нам известно, чтобы найти уменьшаемое, необходимо к разности прибавить вычитаемое.
4 + х = 19 +5
Упростим данное равенство, вычислим правую часть уравнения, найдем сумму 19 и 5.
4 + х = 24
Получили простое уравнение, в котором неизвестно второе слагаемое.
Из суммы (равной 24) вычтем известное слагаемое (равное 4).
х = 24 — 4
х = 20
Проверка:
(4 + 20) — 5 = 19
24 — 5 = 19
19 = 19
После подстановки х =20 получили верное равенство, следовательно, уравнение решено верно.
Ответ: х = 20.
2. Метод весов.
Эта информация доступна зарегистрированным пользователям
При решении уравнения с левой и правой частью уравнения приходится совершать различные преобразования, которые не должны нарушать равенство между ними.
Правило весов заключается в следующем: обе части уравнения можно поменять местами или уменьшить (увеличить) на одно и то же число, или разделить (умножить) на одно и то же число.
Данное правило позволяет упростить уравнение или избавиться от ненужных членов в уравнении, не влияя на тождественность.
Равносильные преобразования не меняют корни уравнения.
Представим уравнение в виде весов, чаши которых находятся в равновесии.
В нашей аналогии левая и правая чаши весов- это левая и правая части уравнения соответственно.
В таком случае:
- Если поменять местами грузы, т.е. переложить груз с левой чаши на правую, а с правой на левую, то равенство весов не нарушится.
Так и в уравнении, если переставить левую и правую части уравнения, равенство между ними сохранится.
- Какой массы груз положим на одну чашу весов, такой же массы груз необходимо положить на вторую чашу, чтобы равновесие весов не нарушилось.
Так и в уравнении, если обе части уравнения уменьшить или увеличить на одно и то же число, то на равенство левой и правой части уравнения это не повлияет.
Эта информация доступна зарегистрированным пользователям
В качестве примера рассмотрим уравнение уже решенное выше:
16 + х = 24 — 4.
Чтобы получить равенство, в котором в левой части будет находиться неизвестная величина, а в правой число, можно из левой и правой части уравнения вычесть число 16.
Получим равенство:
16 + х — 16 = 24 — 4 — 16
х = 20 — 16
х = 4
Уменьшая левую и правую часть равенства, мы получили уравнение, которое уже решали ранее (находили неизвестный компонент суммы).
Проверка данного корня показала, что корень уравнения х = 4 найден верно.
Ответ: х = 4.
У нас получилось верно решить одно и то же уравнение разными способами.
Эта информация доступна зарегистрированным пользователям
Часто решение практических задач сводится к составлению и решению уравнений или системы уравнений.
Уравнение зачастую упрощают процесс решения задач.
Математическая модель в виде уравнения позволяет установить связь между всеми данными задачи, выразить неизвестную величину через известные.
Различного рода задачи могут решаться с помощью похожих уравнений.
Таким образом, большое количество задач сводится к решению определенного типа уравнений.
После того как уравнения составлены, определить алгоритм и способ решения несложно.
Рассмотрим общий алгоритм решения задач с помощью уравнений.
1) Внимательно прочитать задачу
2) Проанализировать задач
-
- выделить исходные данные
- выделить искомые величины
- определить взаимосвязь между величинами
3) Составить план решения (краткую запись, рисунок-схему)
4) Ввести переменные (буквами обозначить неизвестные величины, которые требуется найти по условию задачи)
5) Составить математическую модель задачи- уравнение
6) Решить уравнение (найти корни уравнения)
7) Найти ответ на вопрос задачи (выбрать те решения, которые соответствуют условию задачи)

9) Записать ответ
Разберем несколько задач, которые можно решить с помощью уравнения.
Задача № 1.
Маша загадала число.
Если это число уменьшить на 16, то получится 7.
Какое число загадала Маша?
Эта информация доступна зарегистрированным пользователям
Решение:
Пусть Маша задумала число х.
Уменьшив это число на 16, получится разность х — 16.
Полученная разность будет равняться (по условию задачи) семи.
Составим уравнение.
х — 16 = 7
Получим простое уравнение, в котором неизвестно уменьшаемое.
Чтобы найти неизвестное уменьшаемое, необходимо вычитаемое и разность сложить, получим равенство
х = 16 + 7
х = 23— задуманное число.
Проверим результат.
В исходное уравнение х — 16 = 7 подставим найденное значение х = 23.
23 — 16 = 7
7 = 7
Получили верное равенство, значит корень найден верно.
Ответ: х = 23.
Задача № 2.
Эта информация доступна зарегистрированным пользователям
На полке было 12 книг.
Когда Дима взял с полки несколько книг, там осталось 9 книг.
Сколько книг Дима взял с полки?
Решение:
Пусть х книг Дима взял с полки.
На полке было 12 (книг).
Осталось 9 (книг).
Изобразим схематичный рисунок к задаче.
Эта информация доступна зарегистрированным пользователям
Если от общего количества книг, которые стояли на полке, отнять (вычесть) некоторое количество книг, которые взял Дима, то получим разность (остаток), а выражение 12 — х будет описывать эту разность.
По условию задачи данная разность равна 9.
Составим уравнение.
12 — х = 9
Получим простое уравнение, в котором неизвестно вычитаемое.
Найдем вычитаемое, из уменьшаемого вычтем разность.
12 — х = 9
х = 12 — 9
х = 3 (книги) Дима взял с полки.
Проверим полученный результат, подставим найденное значение х = 3 в исходное уравнение 12 — х = 9.
12 — 3 = 9
9 = 9
Получили верное равенство, значит, корень найден верно.
Ответ: х = 3
Задача № 3
После того как Миша взял из пенала несколько карандашей, в нем осталось 8 карандашей.
Сколько карандашей взял Миша, если в пенале было 12 карандашей?
Эта информация доступна зарегистрированным пользователям
Решение:
Пусть х карандашей Миша взял из пенала
Было- 12 (карандашей).
Осталось- 8 (карандашей).
Изобразим схематичный рисунок к задаче.
Эта информация доступна зарегистрированным пользователям
Карандаши, которые взял Миша, и карандаши, которые остались в пенале, определим суммой х + 8.
Данная сумма описывает общее количество карандашей, которые изначально лежали в пенале, а по условию эта сумма равна 12.
Составим уравнение.
х + 8 = 12
Получили простое уравнение, в котором неизвестно слагаемое.
Найдем неизвестное слагаемое, из суммы вычтем известное слагаемое.
х = 12 — 8
х = 4 (карандаша) Миша взял из пенала.
Проверим полученный корень уравнения, подставим найденное значение х = 4 в исходное уравнение х + 8 = 12.
4 + 8 = 12
12 = 12
Получили верное равенство, значит, корень найден верно.
Ответ: х = 4.
Задача № 4.
Попробуем решить составную задачу с помощью уравнения.
На остановке из автобуса вышли 11 пассажиров, а вошли 8, после чего в автобусе стало 32 пассажира.
Сколько пассажиров было в автобусе до остановки?
Эта информация доступна зарегистрированным пользователям
Решение:
Запишем кратко условие задачи.
Пусть х пассажиров были в автобусе до остановки.
Вышли- 11 (пассажиров).
Зашли- 8 (пассажиров).
Стало в автобусе 32 (пассажира).
Из общего количества пассажиров, которые были в автобусе вычтем пассажиров, которые вышли.
Получим выражение (х — 11)- пассажиры которые остались после того, как вышли 11 человек.
Затем 8 человек зашли, следовательно, прибавим к оставшимся (х — 11) пассажирам 8 человек.
Получим выражение (х — 11) + 8 — столько стало после того, как на остановке люди вышли и зашли.
А по условию в автобусе после остановки стало 32 пассажира, приравняем выражение (х — 11) + 8 к 32.
Составим уравнение.
(х — 11) + 8 = 32
Определим арифметическую операцию, которая будет выполнятся в последнюю очередь.
В нашем случае это сумма (х — 11) и 8.
На начальном этапе решения неизвестным в уравнении является слагаемое, целое выражение (х — 11).
Найдем слагаемое (х — 11), из суммы (равной 32) вычтем известное слагаемое (равное 8).
х — 11 = 32 — 8.
Упростим равенство, вычислим его правую часть, найдем разность 32 — 8.
х — 11 = 24
Получили уравнение, в котором неизвестным является уменьшаемое.
Подобные уравнения мы уже умеем решать.
Найдем уменьшаемое (х), сложив разность и вычитаемое.
х = 24 + 11
х = 35 (пассажиров) были в автобусе до остановки.
Проверим полученный корень уравнения, подставим найденное значение х = 35 в исходное уравнение (х — 11) + 8 = 32.
(35 — 11) + 8 = 32
24 + 8 = 32
32 = 32
Получили верное равенство, значит, корень найден верно.
Ответ: х = 35.
Эта информация доступна зарегистрированным пользователям
Читайте также
Понятие равенства, знак равенства, связанные определения
Материал статьи позволит ознакомиться с математической трактовкой понятия равенства. Порассуждаем на тему сути равенства; рассмотрим его виды и способы его записи; запишем свойства равенства и проиллюстрируем теорию примерами.
Что такое равенство
Само понятие равенства тесно переплетено с понятием сравнения, когда мы сопоставляем свойства и признаки, чтобы выявить схожие черты. Процесс сравнения требует наличия двух объектов, которые и сравниваются между собой. Данные рассуждения наводят на мысль, что понятие равенства не может иметь место, когда нет хотя бы двух объектов, чтобы было что сравнивать. При этом, конечно, может быть взято большее количество объектов: три и более, однако, в конечном, счете, мы так или иначе придем к сравнению пар, собранных из заданных объектов.
Смысл понятия «равенство» в обобщенном толковании отлично определяется словом «одинаковые». О двух одинаковых объектах можно говорить – «равные». Например, квадраты и . А вот объекты, которые хоть по какому-то признаку отличаются друг от другу, назовем неравными.
Говоря о равенстве, мы можем иметь в виду как объекты в целом, так и их отдельные свойства или признаки. Объекты являются равными в целом, когда одинаковы по всем характеристикам. Например, когда мы привели в пример равенство квадратов, имели в виду их равенство по всем присущим им свойствам: форме, размеру, цвету. Также объекты могут и не быть равными в целом, но обладать одинаковыми отдельными признаками. Например: и . Указанные объекты равны по форме (оба – круги), но различны (неравны) по цвету и размеру.
Таким образом, необходимо заранее понимать, равенство какого рода мы имеем в виду.
Запись равенств, знак равно
Чтобы произвести запись равенства, используют знак равно (или знак равенства), обозначаемый как =.Такое обозначение является общепринятым.
Составляя равенство, равные объекты размещают рядом, записывая между ними знак равно.
Определение 1
Равенство – запись, в которой использован знак равно, разделяющий два математических объекта (или числа, или выражения и т.п.).
Когда возникает необходимость письменно обозначить неравенство объектов, используют знак не равно, обозначаемый как ≠, т.е. по сути зачеркнутый знак равно.
Верные и неверные равенства
Составленные равенства могут соответствовать сути понятия равенства, а могут и противоречить ему. По этому признаку все равенства классифицируют на верные равенства и неверные равенства. Приведем примеры.
Составим равенство 7=7. Числа 7 и 7, конечно, являются равными, а потому 7=7 – верное равенство. Равенство 7=2, в свою очередь, является неверным, поскольку числа 7 и 2 не равны.
Свойства равенств
Запишем три основных свойства равенств:
Определение 2
- свойство рефлексивности, гласящее, что объект равен самому себе;
- свойство симметричности: если первый объект равен второму, то второй равен первому;
- свойство транзитивности: когда первый объект равен второму, а второй – третьему, тогда первый равен третьему.
Буквенно сформулированные свойства запишем так:
- a=a;
- если a=b, то b=a;
- если a=b и b=c, то a=c.
Отметим особенную пользу второго и третьего свойств равенств – свойств симметричности и транзитивности – они дают возможность утверждать равенство трех и более объектов через их попарное равенство.
Двойные, тройные и т.д. равенства
Совместно со стандартной записью равенства, пример которой мы приводили выше, также часто составляются так называемые двойные равенства, тройные равенства и т.д. Подобные записи представляют собой как бы цепочку равенств. К примеру, запись
2+2+2=4+2=6 — двойное равенство, а |AB|=|BC|=|CD|=|DE|=|EF| — пример четвертного равенства.
При помощи таких цепочек равенств оптимально составлять равенство трех и более объектов. Такие записи по своему смыслу являются обозначением равенства любых двух объектов, составляющих исходную цепочку равенств.
Например, записанное выше двойное равенство 2+2+2=4+2=6 обозначает равенства: 2+2+2=4+2, и 4+2=6, и 2+2+2=6, а в силу свойства симметричности равенств и 4+2=2+2+2, и 6=4+2, и 6=2+2+2.
Составляя подобные цепочки, удобно записывать последовательность решения примеров и задач: такое решение становится наглядным и отражает все промежуточные этапы вычислений.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Числовые равенства, свойства числовых равенств
После получения общих сведений о равенствах в математике переходим к более узким темам. Материал этой статьи даст представление о свойствах числовых равенств.
Что такое числовое равенство
Первый раз мы сталкиваемся с числовыми равенствами еще в начальной школе, когда происходит знакомство с числами и понятием «столько же». Т.е. самые примитивные числовые равенства это: 2=2, 5=5 и т.д. И на том уровне изучения мы называли их просто равенствами, без уточнения «числовые», и закладывали в них количественный или порядковый смысл (который несут натуральные числа).
По мере появления знаний об арифметических действиях числовые равенства становятся сложнее: 5+7=12; 6-1=5; 2·1=2; 21:7=3 и т.п. Затем начинают встречаться равенства, в записи которых участвуют числовые выражения разного рода. Например, (2+2)+5=2+(5+2); 4·(4−(1+2))+12:4−1=4·1+3−1 и т.п. Дальше мы знакомимся с прочими видами чисел, и числовые равенства приобретают все более и более интересный и разнообразный вид.
Определение 1
Числовое равенство – это равенство, обе части которого состоят из чисел и/или числовых выражений.
Свойства числовых равенств
Сложно переоценить значимость свойств числовых равенств в математике: они являются опорой многому, определяют принцип работы с числовыми равенствами, методы решений, правила работы с формулами и многое другое.Очевидно, что существует необходимость детального изучения свойств числовых равенств.
Свойства числовых равенств абсолютно согласованы с тем, как определяются действия с числами, а также с определением равных чисел через разность: число a равно числу bтолько в тех случаях, когда разность a−b есть нуль. Далее в описании каждого свойства мы проследим эту связь.
Основные свойства числовых равенств
Изучать свойства числовых равенств начнем с трех базовых свойств, которые присущи всем равенствам. Перечислим основные свойства числовых равенств:
- свойство рефлексивности: a=a;
- свойство симметричности: если a=b, то b=a;
- свойство транзитивности: если a=b и b=c, то a=c,где a, b и c – произвольные числа.
Определение 2
Свойство рефлексивности обозначает факт равенства числа самому себе: к примеру, 6=6, −3=−3, 437=437 и т.п.
Доказательство 1
Нетрудно продемонстрировать справедливость равенства
a−a=0для любого числа a: разность a−a можно записать как сумму a+(−a), а свойство сложения чисел дает нам возможность утверждать, что любому числу a соответствует единственное противоположное число −a, и сумма их есть нуль.
Определение 3
Согласно свойству симметричности числовых равенств: если число a равно числу b,
то число b равно числу a. К примеру, 43=64, тогда 64=43.
Доказательство 2
Обосновать данное свойство можно через разность чисел. Условию a=b соответствует равенство a−b=0. Докажем, что b−a=0.
Запишем разность b−aв виде −(a−b), опираясь на правило раскрытия скобок, перед которыми стоит знак минус. Новая запись выражения равна -0, а число, противоположное нулю, это нуль. Таким образом,
b−a=0, следовательно: b=a.
Определение 4
Свойство транзитивности числовых равенств гласит, что два числа равны друг другу в случае их одновременного равенства третьему числу. К примеру, если 81=9 и 9=32, то 81=32.
Свойству транзитивности также отвечает определение равных чисел через разность и свойства действий с числами. Равенствам a=b и b=c соответствуют равенства a−b=0 и b−c=0.
Доказательство 3
Докажем справедливость равенства a−c=0, из чего последует равенство чисел a и c. Посколькусложение числа с нулем не меняет само число, то a−c запишем в виде a+0−c. Вместо нуля подставим сумму противоположных чисел −b и b, тогда крайнее выражение станет таким: a+(−b+b)−c. Выполним группировку слагаемых: (a−b)+(b−c). Разности в скобках равны нулю, тогда и сумма
(a−b)+(b−c) есть нуль. Это доказывает, что, когда a−b=0 и b−c=0, верно равенство a−c=0, откуда a=c.
Прочие важные свойства числовых равенств
Основные свойства числовых равенств, рассмотренные выше, являются базисом для ряда дополнительных свойств, довольно ценных в разрезе практики. Перечислим их:
Определение 5
Прибавив к (или убавив от) обеим частям числового равенства, являющегося верным, одно и то же число, получим верное числовое равенство. Запишем буквенно: если a=b, где a и b – некоторые числа, то a+c=b+c при любом c.
Доказательство 4
В качестве обоснования запишем разность (a+c)−(b+c).
Это выражение легко преобразуется в вид (a−b)+(c−c).
Из a=b по условию следует, что a−b=0 и c−c=0, тогда (a−b)+(c−c)=0+0=0. Это доказывает, что (a+c)−(b+c)=0, следовательно,
a+c=b+c;
Определение 6
Если обе части верного числового равенства перемножить с любым числом или разделить на число, не равное нулю, тогда получим верное числовое равенство.
Запишем буквенно: когда a=b, то a·c=b·c при любом числе c. Если c≠0, тогда и a:c=b:c.
Доказательство 5
Равенство верно: a·c−b·c=(a−b)·c=0·c=0, и из него следует равенство произведений a·c и b·c. А деление на отличное от нуля число c возможно записать как умножение на обратное число 1c;
Определение 7
При a и b, отличных от нуля и равных между собой, обратные им числа также равны.
Запишем: когда a≠0, b≠0 и a=b, то 1a=1b.
Укажем еще на пару свойств, которые позволяют осуществлять сложение и умножение соответствующих частей верных числовых равенств:
Определение 8
При почленном сложении верных числовых равенств получается верное равенство. Запись этого свойства такова: если a=b и c=d, то a+c=b+d для любых чисел a, b, c и d.
Доказательство 6
Обосновать это полезное свойство возможно, опираясь на указанные ранее свойства. Мы знаем, что к обеим частям верного равенства возможно прибавить любое число.
К равенству a=bприбавим число c, а к равенству c=d — число b, итогом станут верные числовые равенства: a+c=b+c и c+b=d+b. Крайнее запишем в виде: b+c=b+d. Из равенств a+c=b+c и b+c=b+d согласно свойству транзитивности следует равенство a+c=b+d. Что и нужно было доказать.
Необходимо уточнить, что почленно можно сложить не только два верных числовых равенства, но и три, и более;
Определение 7
Наконец, опишем такое свойство: почленное перемножение двух верных числовых равенств дает верное равенство. Запишем при помощи букв: если a=b и c=d, то a·c=b·d.
Доказательство 7
Доказательство этого свойства подобно доказательству предыдущего. Умножим обе части равенства на любое число, умножим a=b на c, а c=d на b, получим верные числовые равенства a·c=b·c и c·b=d·b. Крайнее запишем как b·c=b·d. Свойство транзитивности дает возможность из равенства a·c=b·c и b·c=b·d вывести равенство a·c=b·d, которое нам необходимо было доказать.
И вновь уточним, что данное свойство применимо для двух, трех и более числовых равенств.
Так, можно записать: если a=b, то an=bn для любых чисел a и b, и любого натурального числа n.
Завершим данную статью, собрав для наглядности все рассмотренные свойства:
a=a.
Если a=b, то b=a.
Если a=bи b=c, то a=c.
Если a=b, то a+c=b+c.
Если a=b, то a·c=b·c.
Если a=bи с≠0, то a:c=b:c.
Если a=b, a=b, a≠0 и b≠0, то 1a=1b.
Если a=b и c=d, то a·c=b·d.
Если a=b, то an=bn.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
035. Равенства. Тождества. Уравнения
Равенство – это два выражения, между которыми стоит знак «=» (равно). Например, – это равенство, где – это левая часть равенства, – это правая часть равенства.
Свойства равенств:
1) ; 2) ;
3) ; 4) ;
5) .
Равенства бывают: Числовые или С переменными.
Числовое равенство может быть Верным или Неверным.
Например, 1) ; – это верные числовые равенства; ; – это неверные числовые равенства.
2) – это равенство с переменными. Переменные и в этом равенстве могут принимать различные числовые значения. Если а , то – это верное числовое равенство. Если а , то – это неверное числовое равенство.
Тождество – это равенство с переменными, которое будет верным числовым равенством при любых значениях переменных.
Например, ; ; , если ; , если – это тождества.
Уравнение – это равенство с переменными, которое будет верным числовым равенством при определенных значениях переменных.
Так, – это уравнение с одной переменной ,
Где и – это алгебраические выражения; – это переменная или неизвестная.
Например, – это уравнение с одной перемен-ной ; – это уравнение с двумя переменными и .
Корень (решение) уравнения – это такое значение переменной, при котором уравнение будет верным числовым равенством.
Решить уравнение – это значит найти все его корни или доказать, что их нет.
Пример 1.
Решение. Выполним тождественные преобразования: . Это уравнение имеет один единственный корень . Только если уравнение будет верным числовым равенством: , или .
Ответ. .
Пример 2. Найдите корни уравнения .
Решение. .
– это множество корней уравнения.
Ответ. .
Пример 3. Найдите корни уравнения .
Решение. , следовательно, это уравнение не имеет действительных корней (не имеет решений в области действительных чисел).
Ответ. Æ.
Пример 4. Найдите решение уравнения .
Решение. Уравнение имеет бесчисленное множество корней (решений). Любое неотрицательное число – это решение данного уравнения.
Ответ. .
Область определения Уравнения (или область допустимых значений уравнения (ОДЗ или )) – это множество значений переменной , при которых имеют смысл (определены) левая и правая части уравнения.
Чтобы найти ОДЗ уравнения , нужно найти пересечение множеств, на которых определены заданные алгебраические выражения и .
Пример 5. Найдите область допустимых значений уравнения .
Решение. Найдем ОДЗ левой и правой части уравнения.
ОДЗ левой части уравнения – это все действительные числа, кроме :
.
ОДЗ правой части уравнения – это все положительные числа :
.
ОДЗ уравнения – это пересечение множеств и :
Ответ. .
Два уравнения и называются Равносильными (эквивалентными), если множества их корней (решений) совпадают: ( – это знак эквивалентности (равносильности)).
Например, 1) уравнения и – эквивалент-ны, т. к. эти уравнения имеют корень: ;
2) уравнения и не равносильны, т. к. уравнение имеет только один корень: , а уравнение имеет два корня: ; .
Рассмотрим некоторые эквивалентные преобразования, которые удобно использовать при решении уравнений.
Таблица 4.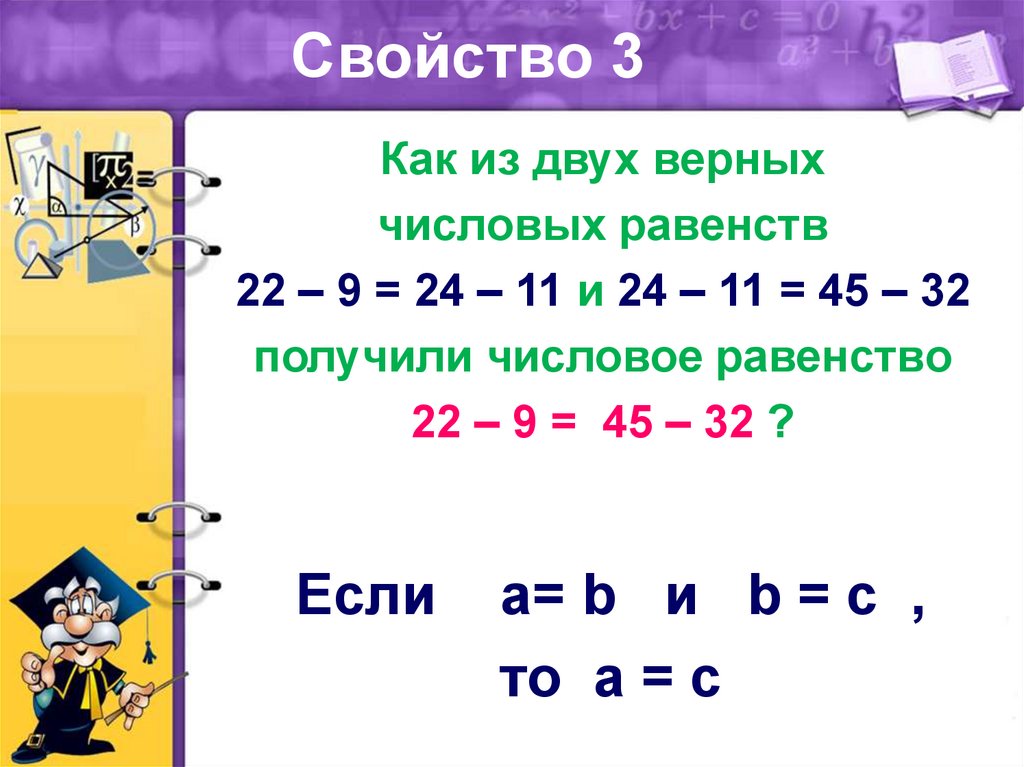
|
№ |
Действия |
Примеры |
|
1. |
Замена левой части уравнения на правую часть или правой части на левую |
|
|
2. |
Перенос слагаемых из одной части уравнения в другую с противоположным знаком |
|
|
3. |
Умножение или деление обеих частей уравнения на одно и то же число, не равное нулю |
|
|
4. |
Вычитание или прибавление одного и того же числа к обеим частям уравнения |
|
|
5. |
Вычитание или прибавление одного и того же алгебраического выражения к обеим частям уравнения. При этом области определения полученного и данного уравнения должны совпадать |
|
В процессе решения уравнений при помощи эквивалентных преобразований, необходимо:
1) найти область допустимых значений (ОДЗ) исходного уравнения;
2) проверить, принадлежат ли полученные значения ОДЗ исходного уравнения.
Пример 6. Решите уравнение .
Решение. Найдем ОДЗ уравнения: . Преобразуем уравнение, для этого перенесем все члены уравнения в левую часть. Получим уравнение . Корни этого уравнения: ; . Но корень не принадлежит области допустимых значений (ОДЗ). Поэтому – это посторонний корень, который не нужно рассматривать. Решением уравнения будет .
Ответ. .
Уравнения бывают различных видов. Приведем примеры некоторых уравнений:
ü линейные: ;
ü квадратные: ;
ü рациональные (высших степеней):
;
ü иррациональные: ;
ü с модулем: ;
ü логарифмические: ;
ü показательные: ;
ü тригонометрические: и другие.
| < Предыдущая | Следующая > |
|---|
Предварительное исчисление по алгебре
. Как решить неравенства, в которых обе стороны не равны нулю и в которых используются абсолютные значения и дроби?
Ответ Особо Лайма показывает более простой способ, который работает в вашем конкретном случае, но общий метод, который работает всегда (но в некоторых конкретных случаях, в том числе и в этом, этот метод будет дольше выполнять) — решить отдельно в интервалы, где выражения абсолютного значения могут быть записаны без использования абсолютных значений.
Обратите внимание, что $|x-2|$ равно $-(x-2)$, когда $x-2 leq 0$, и $|x-2|$ равно $(x-2)$, когда $ x-2 geq 0.$ Это просто определение абсолютного значения (т. е. $|u|$ равно $-u$, когда $u leq 0$, и $|u|$ равно $u$, когда $u geq 0$; теперь перепишем это, заменив $u$ на $x-2).$ Таким образом, немного упрощая, мы имеем $|x-2|$, равный $-x+2$, когда $x leq 2$ и равный в $x-2$, когда $x geq 2.$ То есть версия $|x-2|$ с неабсолютным значением изменяет свою форму при $x=2.$
Таким же образом не -абсолютная версия $|2x + 8|$ изменяет свою форму, где $2x + 8 = 0,$ или $x = -4.$ Для $x leq -4$ мы имеем $|2x + 8| = -2x — 8$ и для $x geq -4$ имеем $|2x + 8| = 2x + 8. $
Объединяя результаты двух последних абзацев, мы видим, что все дробное выражение, с которым вы имеете дело, имеет три различных формы выражения в трех интервалах, которые определяются точками $x = 2$ и $x = -4 ,$ места, где внутренности хотя бы одного из выражений абсолютного значения равны нулю.
Заменить $|x-2|$ на $(-x+2)$ и заменить $|2x + 8|$ на $(-2x — 8).
$$frac{(-x + 2) ) + 3}{4 — (-2x — 8)} ; geq; -5$$
$$frac{-x + 5}{2x + 12} ; geq; -5$$
Решите это обычным способом, а затем включите ТОЛЬКО те полученные значения, которые ТАКЖЕ удовлетворяют $x leq -4.$
Замените $|x-2|$ на $(-x+2)$ и замените $| 2x + 8|$ с $(2x + 8).$
$$frac{(-x + 2) +3}{4 — (2x+8)} ; geq; -5$$
$$frac{-x + 5}{-2x — 4} ; geq; -5$$
Решите это обычным способом, а затем включите ТОЛЬКО те значения, которые вы получили, которые ТАКЖЕ удовлетворяют $-4 leq x leq 2.$
Замените $|x-2|$ на $(x-2 )$ и замените $|2x + 8|$ на $(2x + 8).$
$$frac{(x — 2) + 3}{4 — (2x + 8)} ; geq; -5$$
$$frac{x + 1}{-2x — 4} ; geq; -5$$
Решите это обычным способом, а затем включите ТОЛЬКО те полученные значения, которые ТАКЖЕ удовлетворяют $x geq 2.$
три интервала.
Хотя это кажется довольно длинным, один и тот же метод работает как для уравнений, так и для неравенств, а также когда используются экспоненциальные и/или логарифмические и/или тригонометрические функции (и другие возможности).
$$-frac{1}{2} leq x leq frac{1}{2}$$
В случае A мы можем использовать только те значения, указанные выше, которые также удовлетворяют $-frac{1}{sqrt 2} < x < frac{1}{sqrt 2}.$ Поскольку $frac{1}{sqrt 2}$ составляет приблизительно 0,707$ (все, что нам нужно знать, это то, что это больше $frac{1}{2}$, чтобы сделать следующий вывод, и это можно увидеть, сравнив квадраты $frac{1}{ sqrt 2}$ и $frac{1}{2},$ или наблюдая, какой из знаменателей $2$ и $sqrt 2$ больше), это означает, что все эти значения подходят для включения в подслучай A. , Следовательно, значения $x$, которые мы получаем из подслучая A, удовлетворяют $-frac{1}{2} leq x leq frac{1}{2}.
$$x leq -frac{sqrt 3}{2} ;; text{ИЛИ} ;; x geq frac{sqrt 3}{2}$$
Поскольку мы находимся в подслучай B, мы можем использовать только те значения выше, которые также удовлетворяют $x leq -frac{1}{sqrt 2}$ ИЛИ $x geq frac{1}{sqrt 2}.$ Так как $frac{1}{sqrt 2} < frac{sqrt 3}{2}$ (это можно увидеть, возведение в квадрат каждой из этих положительных дробей), и, следовательно, $-frac{sqrt 3}{2} < -frac{1}{sqrt 2},$ следует, что все значения $x$, которые мы получили из Подслучай B подходит для включения в подслучай B. Чтобы убедиться в этом, поможет провести числовую прямую, пометив следующие точки в порядке слева направо: $-frac{sqrt 3}{2}, ;$ $-frac{1}{sqrt 2},;$ $0,;$ $frac{1}{sqrt 2},;$ $frac{sqrt 3}{2} .$
Следовательно, значения $x$, которые мы получаем при объединении подслучая A и подслучая B, равны $-frac{1}{2} leq x leq frac{1}{2}$ вместе с $x leq -frac{sqrt 3}{2}$ вместе с $x geq frac{sqrt 3}{2}.
Таким образом, значения $x$, которые мы получаем в случае 1, равны объединенные значения $x$ (только что перечисленные), которые ТАКЖЕ удовлетворяют $-1 leq x leq 1$ (исходное условие, с которого мы начали для случая 1). Это дает $-frac{1}{2}leq x leq frac{1}{2}$ вместе с $-1 leq x leq -frac{sqrt 3}{2}$ вместе с $frac{sqrt 3}{2} leq x leq 1.$ 92 — 1), право| ;; экв;; 1$$
$$слева | 1 , право| ; экв;; 1$$
Так как это верно для всех значений $x,$, мы не получаем никаких ограничений на $x$ в Случае 2, и, таким образом, значения $x$ из Случая 2 являются просто ограничением Случая 2, а именно $x leq -1$ OR $x geq 1.$
Объединение всех значений $x$, полученных в случае 1, со значениями, полученными в случае 2, дает $x leq -frac{sqrt 3}{2} $ OR $-frac{1}{2} leq x leq frac{1}{2}$ OR $x geq frac{sqrt 3}{2}.$ См. этот график для визуализации в чем дело. 92 — 1| geq frac{1}{2}$ после определения координат некоторых подходящих точек на вашем графике.
Решение уравнений и неравенств | Техасский шлюз
Давайте начнемРешение уравнений с одной переменной: часть 1Решение уравнений с одной переменной: часть 2Преобразование линейных уравненийПреобразование линейных неравенствСловарный запас Занятие в журнале
Стандарты TEKS и ожидания учащихся , с техникой и без нее, линейные уравнения и оценить обоснованность их решений. Студент должен:
А(5)(А) решать линейные уравнения с одной переменной, в том числе такие, для которых необходимо применение дистрибутивного свойства и для которых переменные включены с обеих сторон
А(5)(Б) решать линейные неравенства с одной переменной, в том числе те, для которых необходимо применение распределительного свойства и для которых переменные включены с обеих сторон
Ресурс Цель(и)
Учащийся будет использовать различные методы для решения уравнений и неравенства с переменными с обеих сторон.
Основные вопросы
Как можно использовать алгебраические плитки для решения уравнений и неравенств?
Какие шаги используются для алгебраического решения уравнений и неравенств?
Как уравнение или неравенство можно записать в стандартной форме?
Словарь
- Уравнение
- Неравенство
- Стандартная форма
- Переменная
- Нулевые пары
Чтобы решить уравнения, вы должны изолировать переменную. Нулевые пары и обратные операции могут использоваться для устранения констант в уравнении.
В приведенном ниже примере показано, как решать уравнения с использованием моделей и алгебраических шагов.
Чтобы попрактиковаться в решении двухэтапных уравнений, щелкните изображение ниже, чтобы открыть интерактивный инструмент. Следуйте указаниям «Обратная связь» под рабочим ковриком, чтобы построить модель с плитками алгебры и решить уравнение.
Некоторые уравнения могут быть более сложными, и для их решения требуется несколько шагов.
Пример 1
Решение для x в следующем уравнении: 2 x — 4 = x + 5.
Шаг 1 : Переместите все вар. уравнения путем вычитания 90 172 x 90 173 из обеих частей.
2 х — 4 = х + 5
— x — x
x — 4 = 5
Шаг 2 : Добавьте 4 к обеим частям уравнения.
x — 4 = 5
+4 +4
x = 9
Пример 2
Решай для x в следующем уравнении: 3 x + х +2).
Шаг 1 : Распределите 2 на ( x + 2) путем умножения на 2.
3 x + 15 — 9 = 2( x + 2)
3 x + 15 — 9 = 2 x + 4
.
3 x + 6 = 2 x + 4
Шаг 3 : Переместите все переменные в одну часть уравнения, вычитая 2 x из обеих сторон.
3 x + 6 = 2 x + 4
-2 x -2 x
x + 6 = 4
Шаг 4 : Вычтите 6 с обеих сторон.
x + 6 = 4
-6 -6
x = -2
Мы собираемся научиться преобразовывать уравнение или неравенство в эквивалентное уравнение или неравенство. Это включает перестановку значений неравенства или уравнения с использованием обратных операций. Давайте исследуем различные способы преобразования линейных уравнений из одного представления в другое.
Самое распространенное преобразование линейного уравнения, которое вам нужно знать, это как взять уравнение в стандартной форме (A x + B y = C) и переписать его в форме пересечения наклона ( y = m x + b), или наоборот.
В таблице ниже представлена важная информация для каждой формы.
| Форма линейного уравнения | Важная информация | Где вы увидите эту форму |
|
Форма пересечения уклонов у = м х + б |
Уклон м. Координата y точки пересечения y равна b. |
Задачи, включающие начальную точку (b) и скорость изменения. |
|
Стандартная форма А х + В у = С |
Координата x точки пересечения x — C/A. y -координата пересечения y — C/B. |
Задачи, включающие комбинацию кратных x и y. |
Для преобразования стандартной формы в форму с пересечением наклона обычно требуется два шага.
Шаг 1 . Добавьте или вычтите член размером 90 172 x 90 173 с обеих сторон.
Шаг 2 . Разделите все члены на коэффициент y .
Пример 1
Преобразуйте уравнение в форму: 2y + 3x = 12 0003
Для преобразования из формы пересечения наклона в стандартную форму обычно требуется не более четырех шагов.
Шаг 1 . Добавьте или вычтите член размером 90 172 x 90 173 с обеих сторон.
Шаг 2 . Если коэффициент x отрицательный (термин A), умножьте все члены на -1.
Шаг 3 . Если есть дробь, умножьте все члены на знаменатель, чтобы исключить дроби.
Шаг 4 . Если есть десятичная дробь, умножьте все члены на степень 10, чтобы исключить десятичные дроби.
Пример 2
Преобразуйте уравнение в стандартный вид: -y = 94(34x-y = 9)3x-4y=36
Проверьте свое понимание, выполнив следующие подсказки.
Линейные неравенства могут быть преобразованы аналогично линейным равенствам. Этот первый пример показывает, как преобразовать неравенство.
Пример 1
Как еще можно записать следующее неравенство?
3 x + 2 y ≥ 6
Чтобы записать неравенство по-другому, мы должны убедиться, что значения решений остаются прежними.
Мы можем переписать неравенство, решив для y ИЛИ мы можем переписать неравенство, решив для x . Попробуем оба.
При работе с неравенствами важно помнить, что символ неравенства должен переворачиваться (переворачиваться) при умножении или делении на отрицательное число.
Посмотрите следующее видео о решении уравнений и неравенств и отвечайте на подсказки, когда они появляются.
- Печать
- Поделиться
Решение неравенств с использованием всех 4 основных операций (видео и практика)
TranscriptPractice
Здравствуйте! Добро пожаловать в это видео о решении неравенств. В этом видео мы обсудим:
- Что такое неравенство и
- Как решать неравенства с помощью сложения, вычитания, умножения и деления
При решении уравнений у вас есть два выражения, которые равны между собой.
| Less than | |
| Less than or equal to | ≤ |
| Greater than | > |
| Greater than or equal to | ≥ |
When Решая неравенства, вы выполняете все те же шаги, что и при решении уравнения, за исключением специального правила, когда речь идет об умножении и делении. Основное отличие состоит в том, что вместо знака равенства между двумя выражениями вы будете писать один из четырех символов неравенства.
Давайте сначала рассмотрим неравенство с помощью сложения.
x + 7 больше или равно 4
x + 7 ≥ 4
Если мы находим x отдельно, мы хотим избавиться от этой 7 рядом с ним, поэтому мы вычитаем 7 из обеих частей.
x + 7 – 7 ≥ 4 – 7
Это дает нам ответ
x больше или равно отрицательному числу 3
x ≥ -3
Это так просто!
Теперь я хочу, чтобы вы сами попробовали вычитание.
х минус 3 меньше 9
х – 3 12
Чтобы получить х сам по себе, нам нужно разделить обе части на минус 4.
Помните, так как мы делим на -4, мы должны инвертировать знак неравенства! Итак, x меньше отрицательного числа 3.
x -3. Итак, давайте попробуем подставить 2, так как 2 больше отрицательного числа 3. Если мы подставим 2 вместо х, мы получим отрицательное 4, умноженное на 2 больше 12. Отрицательное число 8 больше 12.
-4(2) > 12
-8 > 12
Но мы знаем, что это неправда. Отрицательное 8 не больше 12,
Теперь вернемся к нашему правильному ответу: x меньше отрицательного числа 3. Отрицательное значение 20 меньше отрицательного значения 3, так что давайте подставим это в наше уравнение, чтобы проверить, работает ли оно.
Отрицательное 4 раза отрицательное 20 больше 12
80 больше 12
-4(-20) > 12
80 > 12
Верно! 80 больше 12. Так что просто помните, когда вы умножаете или делите на отрицательное число, вы ДОЛЖНЫ перевернуть знак. В противном случае ваше неравенство не будет верным.
Что, если бы у нас было это неравенство?
x/3 ≤ 2
x больше 3 меньше или равно 2
Для этого неравенства нам нужно умножить обе части на 3. При этом мы меняем знак? Нет, нам не нужно, так как мы умножаем на положительное число.
Итак, мы умножаем обе стороны на 3, тогда мы получаем, что x меньше или равно 6.
x ≤ 6
Я хочу, чтобы вы попробовали еще один вариант самостоятельно. Для этого мы собираемся объединить все, чему мы научились, так что это будет выглядеть немного сложнее, но вы справитесь. Просто применяйте каждый шаг, о котором мы говорили до сих пор.
2x плюс 3 больше или равно x минус 7
2x + 3 ≥ x – 7
Приостановите это видео и решите это неравенство самостоятельно, а затем посмотрите, совпадает ли ваш ответ с моим.
Думаешь, у тебя получилось? Посмотрим!
Во-первых, я собираюсь добавить 7 к обеим частям моего уравнения.
Это дает нам 2x плюс 10 больше или равно x
2x + 10 ≥ x
Теперь мне нужно вычесть 2x с обеих сторон.
10 больше или равно отрицательному значению x 10 ≥ -x
Наконец, мне нужно разделить на минус 1 и перевернуть знак.
Итак, наш окончательный ответ отрицательный. 10 меньше или равно x
-10 ≤ x
Теперь обратите внимание на это неравенство: вы могли бы вычесть x и вычесть 3 из обеих частей. Это даст вам тот же ответ, и вы сможете избежать деления на минус. Иногда есть несколько способов решить неравенство или уравнение, поэтому ищите способы немного облегчить себе жизнь.
Надеюсь, это видео о решении неравенств было полезным. Спасибо за просмотр и удачной учебы!
Знаки больше и меньше | Таблицы умножения
Вопрос №1:
Решите следующее неравенство для x :
(4+x)
}{x>frac)1{x>frac)1
(x)
(x)
(x>frac{1}{4})
Показать ответ
Ответ:
Чтобы решить это неравенство, помните, что нам нужно получить x с одной стороны, как и в случае с обычными уравнениями.
(4-4+x)
Упрощая, у нас остается:
(x)
Теперь мы переместим этот отрицательный x в левую часть, добавив его к обеим сторонам.
(x+x) (2x)
Наконец, мы разделим на 2 обе части, чтобы получить решение. Неравенство (4+x)
Скрыть ответ
Вопрос №2:
Решите следующее неравенство для x :
(frac{x}{4}geq3)
(xgeq12)
3 (xgeq4)
(xleq12)
(xleq3)
Показать ответ
Ответ:
Чтобы увидеть это, нам просто нужно обе части умножить на 4. Это уберет знаменатель слева и оставит нам x :
(4timesfrac{x}{4}geq3times4)
Упростить:
(xgeq12)
Скрыть ответ
Вопрос № 3:
Решите следующее неравенство, чтобы определить, какие значения x ему удовлетворяют (frac 9019×1 +2}{7} > 2-x)
(x>5)
(x>frac{3}{2})
(x)
(x )
Показать Ответ
Ответ:
Чтобы начать решать это неравенство, удалим знаменатель слева, умножив обе части на 7.
(7timesfrac{x+2}{7}>(2-x)times7)
Обратите внимание, что мы не изменили знак неравенства. Это потому, что мы умножили на положительное число. Приведенное выше выражение упрощается до:
(x+2>14-7x)
Отсюда мы переместим 2 вправо с вычитанием, а (7x) влево сложением.
(х+2-2>14-7х-2)
(х>12-7х)
(х+7х>12-7х+7х)
(8х>12)
Наконец, мы делим обе части на 8, чтобы получить x , и мы видим, что осталось (x>128), что упрощается до (x>32).
Скрыть ответ
Вопрос №4:
Решите следующее неравенство для x .
(-4x+2geq6)
(xleq-1)
(xgeq-1)
(xleq2)
(xgeq2 )
Показать Ответ
Ответ:
Давайте начнем работать над этой задачей, вычитая 2 из обеих сторон.
(-4x+2-2geq6-2)
(-4xgeq4)
Теперь, чтобы выделить x и найти решение, нам нужно обе части разделить на -4. Помните, что деление на минус меняет знак неравенства! Это относится и к умножению на минусы.
(frac{-4x}{-4}geqfrac{4}{-4})
(xleq-1)
Скрыть ответ
Вопрос №5:
Решите следующее неравенство для x .
(-frac{1}{4}x+3>-4)
(x)
(x)
(x>34)
(x>21)
Показать ответ
Ответ:
Сначала переместите 3 в правую часть неравенства, вычитая 3 из обеих частей.
(-frac{1}{4}x+3-3)>(-4-3)
(-frac{1}{4}x)>(-7)
Теперь мы получим x , умножив обе части на -4. Это сократит дробь в левой части. Это приведет к тому, что знак неравенства перевернется, и после упрощения мы останемся с нашим решением.
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Натуральные числа и действия над ними
- Уравнения
Уравнение — это равенство, содержащее букву, значение которой надо найти. Например: 


Корень уравнения — это число, которое при подстановке вместо буквы обращает уравнение в верное числовое равенство.
Корень уравнения — это решение уравнения. Уравнение может иметь один и более корней или не иметь их вообще. Тогда говорят, что решить уравнение — значит найти все его корни или показать, что их нет вообще.
Для решения уравнений используют правило нахождения неизвестного:
1) слагаемого: чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.
Решим уравнение 


Ответ: 
2) уменьшаемого: чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
Решим уравнение 


Ответ: 
3) вычитаемого: чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
Решим уравнение 135 — 


Ответ: 
4) множителя: чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
Решим уравнение 


Ответ: 
5) делимого: чтобы найти неизвестное делимое, надо частное умножить на делитель.
Решим уравнение 


Ответ: 
6) делителя: чтобы найти неизвестный делитель, надо делимое разделить на частное.
Решим уравнение 184 : 


Ответ: 
При решении уравнений проводится проверка решения, для этого найденный корень (или корни) подставляются в уравнение вместо переменной. Если числовое равенство получается верным, то решение найдено верно. При оформлении решения проверка записывается под чертой после решения, а затем пишется ответ, при этом каждое действие записывается на новой строке (т.е. одна строка один знак равенства).
Например, решим уравнение 


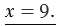
9 + 36 = 45;
45 = 45 — верно.
Ответ: 
Советуем посмотреть:
Понятие о натуральном числе
Сложение натуральных чисел
Вычитание натуральных чисел
Умножение натуральных чисел
Деление натуральных чисел
Порядок выполнения действий
Степень числа. Квадрат и куб числа
Меньше или больше
Меньше или больше на сколько? во сколько раз?
Формулы
Натуральные числа и действия над ними
Правило встречается в следующих упражнениях:
5 класс
Задание 522,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 593,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 676,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 878,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1236,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1254,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 457,
Мерзляк, Полонский, Якир, Учебник
Номер 1130,
Мерзляк, Полонский, Якир, Учебник
Номер 1212,
Мерзляк, Полонский, Якир, Учебник
Номер 1220,
Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 890,
Мерзляк, Полонский, Якир, Учебник
Номер 914,
Мерзляк, Полонский, Якир, Учебник
Номер 1038,
Мерзляк, Полонский, Якир, Учебник
Задание 205,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 828,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1155,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1224,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1299,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1411,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1514,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 80,
Мерзляк, Полонский, Якир, Учебник
Номер 95,
Мерзляк, Полонский, Якир, Учебник
Номер 110,
Мерзляк, Полонский, Якир, Учебник
Номер 199,
Мерзляк, Полонский, Якир, Учебник
Номер 319,
Мерзляк, Полонский, Якир, Учебник
Номер 350,
Мерзляк, Полонский, Якир, Учебник
Номер 662,
Мерзляк, Полонский, Якир, Учебник
Номер 794,
Мерзляк, Полонский, Якир, Учебник
Номер 870,
Мерзляк, Полонский, Якир, Учебник
Номер 1189,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 59,
Мерзляк, Полонский, Якир, Учебник
Номер 142,
Мерзляк, Полонский, Якир, Учебник
Номер 193,
Мерзляк, Полонский, Якир, Учебник
Номер 207,
Мерзляк, Полонский, Якир, Учебник
Номер 213,
Мерзляк, Полонский, Якир, Учебник
Номер 12,
Мерзляк, Полонский, Якир, Учебник
Номер 369,
Мерзляк, Полонский, Якир, Учебник
Номер 373,
Мерзляк, Полонский, Якир, Учебник
Номер 477,
Мерзляк, Полонский, Якир, Учебник
Номер 521,
Мерзляк, Полонский, Якир, Учебник
Математика, 2 класс
Урок №26. Уравнение. Решение уравнений подбором неизвестного числа
Перечень вопросов, рассматриваемых в теме:
— Что такое уравнение, корень уравнения?
— Как решить уравнение?
Глоссарий по теме:
Уравнение – равенство, содержащее неизвестное число, которое надо найти.
Корень уравнения – это значение буквы, при котором из уравнения получается верное равенство.
Решить уравнение, значит найти его корни.
Основная и дополнительная литература по теме урока
1. Моро М. И., Бантова М. А., Бельтюкова Г. В. и др. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1.– 8-е изд. – М.: Просвещение, 2017. – С. 80-81.
2. Моро М. И., Бантова М. А. Математика. Рабочая тетрадь. 2 класс. Учебное пособие для общеобразовательных организаций. В 2 ч. Ч.1. – 6-е изд., дораб. – М.: Просвещение, 2016. – С. 60.
3. Моро М. И., Волкова С. И. Для тех, кто любит математику. Пособие для учащихся общеобразовательных организаций. 9-е изд. – М.: Просвещение, 2014. – С. 60.
Теоретический материал для самостоятельного изучения
Вы умеете читать буквенные выражения. Например:
Вы уже знаете, что равенства бывают верные и неверные.
Рассмотрим верное равенство с окошком: 
Запишем вместо окошка маленькую латинскую букву 
Это число 8. Получили верное равенство: сумма чисел 8 и 4 равна 12.
х + 4 = 12
х = 8
8 + 4 = 12
Равенство с буквой 
Неизвестное число обозначается маленькими латинскими буквами, как и в буквенном выражении.
Решить уравнение – значит найти все такие значения х (если они есть), при которых равенство будет верным. Значение буквы, при котором из уравнения получается верное равенство, называется корень уравнения.
Решим уравнение 10 – d = 6 способом подбора.
Возьмём число 5. Сейчас проверим, верно ли подобрали число. Заменим d в уравнении числом 5. Получим равенство: 10 – 5 = 6. Оно неверно. Значит, число подобрали неверно.
Попробуем взять другое число. Например, 4. При подстановке его вместо d получили верное равенство: 10 – 4 = 6. Значит, число четыре – корень уравнения, его решение.
Сейчас мы с вами рассмотрим, как по схеме составить уравнение. Перед нами такая схема. Изучим, что обозначает каждое число в схеме. Число 27 обозначает «целое». Оно состоит из двух частей. Первая «часть» – это число 20, вторая «часть» – это число х.
20 х
27
Воспользуемся правилом,
ЧАСТЬ + ЧАСТЬ = ЦЕЛОЕ
Запишем равенства:
20 + x = 27
27 – x = 20
Рассмотрим другой пример. Перед вами другая схема. Изучим, где на схеме целое, а где части: х — это «целое», а 30 и 6 – это части.
30 6
х
Воспользуемся правилом,
Вывод: Уравнение – это равенство, содержащее неизвестное число, которое надо найти. Когда решение уравнения находится легко, пользуются способом подбора. Нужно подобрать такое число, чтобы получилось верное равенство.
Тренировочные задания.
- Соедините уравнение с его решением.
Правильные ответы:
2. Выберите и подчеркните среди математических записей уравнения.
15 + 6 = 21
17 – d
b + 3 = 12
3 + 5 > 6
48 – a = 8
9 + e < 39
k – 4 = 10
Правильные ответы:
15 + 6 = 21
17 – d
b + 3 = 12
3 + 5 > 6
48 – a = 8
9 + e < 39
k – 4 = 10
Равенство
- Свойства равенств
Два числовых или буквенных выражения, соединённых знаком =
(равно), составляют равенство. Выражение, стоящее слева от знака =
, называется левой или первой частью равенства, а стоящее справа от него — правой или второй частью равенства:
Части равенства можно менять местами. Например, если
10x — 7 = 15 + 3x,
то и
15 + 3x = 10x — 7.
Равенства делятся на два типа: тождества и уравнения.
Свойства равенств
Все равенства имеют два свойства, на которых основано преобразование и решение уравнений:
1) Обе части равенства можно увеличить или уменьшить на одно и то же число или алгебраическое выражение – равенство от этого не нарушится.
Пример. Если a = b, то и
a + m = b + m
и
a — m = b — m.
2) Обе части равенства можно умножить или разделить на одно и то же число или алгебраическое выражение (не равное нулю) – равенство от этого не нарушится.
Пример. Если a = b, то и
am = bm
и