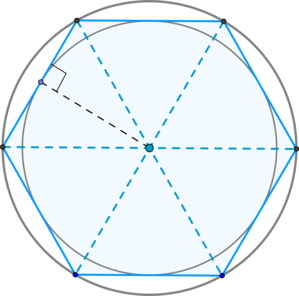
Это хорошо, что в поставленной задаче все многоугольники оснащены чётным количеством сторон. Ведь не секрет, что именно у таких фигур имеются пары параллельных сторон. Но, мало того, расстояние между такими сторонами является диаметром вписанной окружности. И тут мне сразу вспомнились картинки из предыдущего ответа, который я давал по теме «Площади 6-угольников».
То есть в шестиугольнике мы банально делим диаметр вписанной окружности на корень из трёх и всё:
- t6 = 2 * r / √3 = d / √3 = 5,7735027 см
Что же, лиха беда начало. Берём справочник и находим в нём формулу для аналогичных расчётов в тех случаях, когда число углов равно восьми. Нашлась такая и выглядит она следующим образом:
- t8 = 2 / (1 + √2) * r = d / (1 + √2) = 4,1421356 см
Однако при переходе к двенадцатиугольнику дело застопорилось. Быстро отыскать подходящую формулу мне не удалось. Но, может быть, это и к лучшему, потому что мне на глаза попалась другая — универсальная. Такая формула, которая вычисляет длину стороны многоугольника через радиус вписанной окружности. И в этом случае мы можем первым делом перепроверить уже сделанные вычисления, а потом разобраться и двенадцатью углами.
- t6 = 2 * r * Tg (π / n) = 10 * Tg (π / 6) = 5,7735027 см
- t8 = 10 * Tg (π /
= 4,1421356 см
- t12 = 10 * Tg (π / 12) = 2,6794919 см
По окончании проделанной работы я по старой привычке нашёл ещё один альтернативный способ, который может послужить нам средством для проверки. Идём в Интернет, где находим площадку, предназначенную для выполнения расчётов такого рода. Подставляем в форму одно за другим значения радиуса вписанной окружности и количества вершин многоугольника, а потом подшиваем скриншоты и показываем здесь:
На сколько я вижу, все ответы сошлись. И мы можем привести их отдельными строками:
- t6 = 5,7735026919 см
- t8 = 4,1421356237 см
- t12 = 2,6794919243 см.
Iterative solution
Solution valid for each regular polygon with $n$-sides long $L$, of center $(0,,0)$ and with a vertex lying on the positive $x$-axis, but still easily translatable and rotatable as desired.
In Wolfram Mathematica, defining:
{n, L, dx, xP, yP} = {6, 1, 0, 0, 0};
R = L / (2 Sin[Pi/n]);
poly = Table[{R Cos[2 k Pi/n] (1 + dx), R Sin[2 k Pi/n] / (1 + dx)}, {k, n}];
and executing the following simple algorithm:
{perimeter, area, flag} = {0, 0, 0};
For[k = 1, k <= n, k++,
{xA, yA} = poly[[k]];
{xB, yB} = If[k < n, poly[[k + 1]], poly[[1]]];
dAB = Sqrt[(xA - xB)^2 + (yA - yB)^2];
perimeter = perimeter + dAB;
area = area + (xA - xB) (yA + yB) / 2;
xQ = ((xA - xB)^2 xP + (yA - yB) (xA (yP - yB) - xB (yP - yA))) / dAB^2;
yQ = ((yA - yB)^2 yP + (xA - xB) ((yA - yB) xP + xA yB - xB yA)) / dAB^2;
dAQ = Sqrt[(xA - xQ)^2 + (yA - yQ)^2];
dBQ = Sqrt[(xB - xQ)^2 + (yB - yQ)^2];
If[Abs[N[dAB - dAQ - dBQ]] > 10^-10,
{xQ, yQ} = If[N[dAQ - dBQ] < 0, {xA, yA}, {xB, yB}]
];
dPQ = Sqrt[(xP - xQ)^2 + (yP - yQ)^2];
If[flag == 0,
flag = 1;
dmin = dPQ;
points = {{xQ, yQ}},
If[Abs[N[dPQ - dmin]] < 10^-10,
points = Union[points, {{xQ, yQ}}],
If[N[dPQ - dmin] < 0,
dmin = dPQ;
points = {{xQ, yQ}}
]
]
]
];
it’s soon achieved as desired:
Graphics[{Green, RegionBoundary[Polygon[poly]],
Red, PointSize[Large], Point[{xP, yP}],
Blue, PointSize[Large], Point[points]}]
Print["points = ", FullSimplify[points]]
Print["dmin = ", FullSimplify[dmin]]
Print["2p = ", FullSimplify[n L]]
Print["2p' = ", FullSimplify[perimeter]]
Print["A = ", FullSimplify[n R^2 Sin[2 Pi/n] / 2]]
Print["A' = ", FullSimplify[area]]
If then, again by way of example, we re-run the same code with:
{n, L, dx, xP, yP} = {6, 1, 0, 2, 1};
we obtain:
while, if we impose:
{n, L, dx, xP, yP} = {6, 1, 1/10, 2, 1};
we obtain:
Of course, if the numerical results are sufficient, in the output phase replace FullSimplify[] with N[]; the code will be executed more quickly.
Analytical solution
Solution valid for each regular hexagon with long sides $L$, of center $(0,,0)$ and with a vertex lying on the positive $x$-axis, but still easily translatable and rotatable as desired.
In Wolfram Mathematica, defining:
{L, dx, xP, yP} = {1, 0, 0, 0};
poly = Table[{L Cos[2 k Pi/6] (1 + dx), L Sin[2 k Pi/6] / (1 + dx)}, {k, 6}];
and executing the following simple algorithm:
f[x_, y_] := (x - xP)^2 + (y - yP)^2
g[x_, y_] := RealAbs[2 y] + RealAbs[y + Sqrt[3] x] + RealAbs[y - Sqrt[3] x] - 2 Sqrt[3] L
h[x_, y_, z_] := f[x, y] + z g[x / (1 + dx), y (1 + dx)]
grad = D[h[x, y, z], {{x, y, z}, 1}];
sol = Solve[grad == {0, 0, 0}, Reals];
flag = 0;
For[k = 1, k <= Length[sol], k++,
d = Sqrt[f[x, y] /. sol[[k]]];
point = {sol[[k, 1, 2]], sol[[k, 2, 2]]};
If[flag == 0,
flag = 1;
dmin = d;
points = {point},
If[Abs[N[d - dmin]] < 10^-10,
points = Union[points, {point}],
If[N[d - dmin] < 0,
dmin = d;
points = {point}
]
]
]
];
perimeter = Integrate[1, {x, y} ∈ ImplicitRegion[g[x/(1 + dx), y(1 + dx)] == 0, {x, y}]];
area = Integrate[1, {x, y} ∈ ImplicitRegion[g[x/(1 + dx), y(1 + dx)] <= 0, {x, y}]];
it’s soon achieved as desired:
Graphics[{Green, RegionBoundary[Polygon[poly]],
Red, PointSize[Large], Point[{xP, yP}],
Blue, PointSize[Large], Point[points]}]
Print["points = ", FullSimplify[points]]
Print["dmin = ", FullSimplify[dmin]]
Print["2p = ", FullSimplify[6 L]]
Print["2p' = ", FullSimplify[perimeter]]
Print["A = ", FullSimplify[3 Sqrt[3] L^2 / 2]]
Print["A' = ", FullSimplify[area]]
Of course, if the numerical results are sufficient, in the output phase replace FullSimplify[] with N[], while in the body of the algorithm replace Solve[] and Integrate[] respectively with NSolve[] and NIntegrate[]; the code will be executed more quickly.
6. Геометрия на плоскости (планиметрия). Часть II
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Правильный шестиугольник (страница 2)
Правильный шестиугольник — выпуклый шестиугольник, у которого все углы равны и все стороны равны.
(blacktriangleright) Каждый угол правильного шестиугольника равен (120^circ).
(blacktriangleright) Около правильного шестиугольника можно описать окружность: ее радиус равен его стороне.
(blacktriangleright) Большие диагонали правильного шестиугольника делят его на (6) равносторонних треугольников, у которых высота равна радиусу вписанной в правильный шестиугольник окружности.
(blacktriangleright) Центры вписанной и описанной около правильного шестиугольника окружностей есть точка пересечения больших диагоналей этого шестиугольника.
(blacktriangleright) Площадь правильного шестиугольника со стороной (a) равна [S=dfrac{3sqrt3}2a^2]
Задание
8
#667
Уровень задания: Равен ЕГЭ
Сторона правильного шестиугольника (ABCDEF) равна (sqrt[4]{3}). Найдите его площадь.
Пусть (O) – центр описанной около (ABCDEF) окружности
тогда треугольники (AOF), (AOB), (BOC), (COD), (DOE), (EOF) – равносторонние и все они попарно равны.
[S_{triangle{AOF}} = 0,5 AF^2 cdot sin{60^{circ}} = dfrac{AF^2sqrt{3}}{4}, qquadqquad S_{ABCDEF} = 6cdot S_{triangle{AOF}} = dfrac{3sqrt{3}AF^2}{2}.] В данной задаче (S_{ABCDEF} = 6cdot S_{triangle{AOF}} = dfrac{3sqrt{3}AF^2}{2} = 4,5).
Ответ: 4,5
Задание
9
#2428
Уровень задания: Сложнее ЕГЭ
Найдите расстояние между двумя параллельными сторонами правильного шестиугольника со стороной (sqrt{108}).
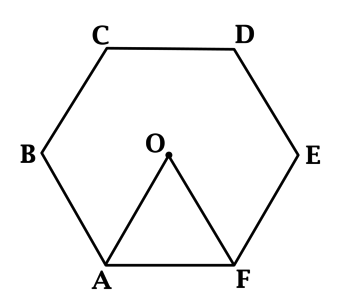
Рассмотрим правильный шестиугольник (ABCDFE) и в нем треугольник (ABC). Параллельными сторонами являются пары (AB) и (DF), (BC) и (FE), (CD) и (EA).
Помним, что угол правильного шестиугольника равен (120^circ).
(triangle ABC) равнобедренный ((AB=BC,)), следовательно, (angle
BAC=0,5cdot (180^circ-120^circ)=30^circ). Таким образом, (angle
CAE=120^circ-30^circ=90^circ).
Следовательно, (AC) – расстояние между сторонами (AE) и (CD) (по определению расстояние между двумя параллельными прямыми – отрезок, проведенный из любой точки одной прямой перпендикулярно ко второй прямой).
Найдем (AC) по теореме косинусов ((AB=BC=a=sqrt{108})):
(AC^2=a^2+a^2-2a^2cdot cos120^circ=2a^2(1-cos120^circ)=2cdot
108cdot left(1+frac12right)=3cdot 108 quad Rightarrow
)
(Rightarrow quad AC=sqrt{3cdot 108}=sqrt{3cdot 3cdot
36}=3cdot 6=18.)
Ответ: 18
Задание
10
#2431
Уровень задания: Сложнее ЕГЭ
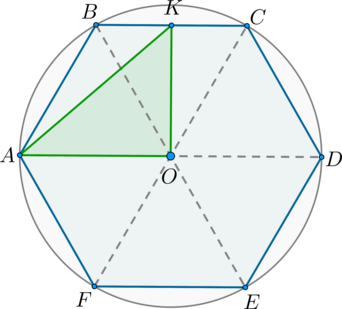
Около правильного шестиугольника (ABCDEF) описана окружность с центром в точке (O). Во сколько раз площадь этого шестиугольника больше площади треугольника (AOK), где (K) – середина стороны (BC).
По свойству правильного шестиугольника центр описанной окружности лежит на пересечении больших его диагоналей. Следовательно, (AO) – радиус описанной окружности. Также по свойству радиус описанной окружности равен стороне правильного шестиугольника, следовательно, (AB=AO=x).
Т.к. (triangle AOB) – правильный, то (angle AOB=60^circ). (triangle BOC) также правильный. Т.к. по условию (OK) – медиана в правильном (triangle BOC), то она и биссектриса, то есть (angle
BOK=frac12cdot 60^circ=30^circ). Таким образом, (angle
AOK=90^circ), то есть (triangle AOK) – прямоугольный.
Следовательно, [S_{triangle AOK}=dfrac12cdot AOcdot OK=dfrac
x2cdot OK]
Площадь правильного шестиугольника равна сумме площадей шести правильных треугольников:
[S_{ABCDEF}=6cdot dfrac12cdot BCcdot OK=6cdot dfrac x2cdot OK]
Таким образом, [dfrac{S_{ABCDEF}}{S_{triangle AOK}}=6.]
Ответ: 6
Задание
11
#2432
Уровень задания: Сложнее ЕГЭ
Около правильного шестиугольника (ABCDEF) описана окружность с центром в точке (O). Найдите большую сторону треугольника (AOK), где (K) – середина стороны (BC=sqrt7) шестиугольника (ABCDEF).
По свойству правильного шестиугольника центр описанной окружности лежит на пересечении больших его диагоналей. Следовательно, (AO) – радиус описанной окружности. Также по свойству радиус описанной окружности равен стороне правильного шестиугольника, следовательно, (AB=AO=sqrt7).
Т.к. (triangle AOB) – правильный, то (angle AOB=60^circ). (triangle BOC) также правильный. Т.к. по условию (OK) – медиана в правильном (triangle BOC), то она и биссектриса, то есть (angle
BOK=frac12cdot 60^circ=30^circ). Таким образом, (angle
AOK=90^circ), то есть (triangle AOK) – прямоугольный.
Следовательно, большая сторона в (triangle AOK) – это гипотенуза (AK). По теореме Пифагора из (triangle BOK) ((OK) также является в нем высотой):
[OK=sqrt{BO^2-BK^2}=sqrt{(sqrt7)^2-left(dfrac{sqrt7}2right)^2}=
dfrac{sqrt3}2cdot sqrt7]
Таким образом, по теореме Пифагора из (triangle AOK):
[AK=sqrt{AO^2+OK^2}=sqrt{(sqrt7)^2+left(dfrac{sqrt3}2cdot sqrt7right)^2}=
dfrac72=3,5.]
Ответ: 3,5

Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды
Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды
Вопрос:
Я работаю над созданием шестиугольной (плоской вершины) сетки для моделирования, над которым я работаю. Я попытался выработать расстояние между шестиугольниками, из заданного шестиугольника цели.
Решение, в котором я работаю большую часть времени, кроме каждого нечетного столбца от целевого шестиугольника к северу от цели, сдвинуто на 1. Я знаю, что это звучит запутанно, но я добавил изображение, чтобы объяснить, что я имею в виду:
Как вы, ребята, видите, нижняя половина сетки ниже целевого шестиугольника и каждого другого столбца над целевым шестиугольником правильна. Я не могу понять, почему: S
Вот объяснение осевых и кубических коорд.
http://www.redblobgames.com/grids/hexagons/#coordinates
Вот код, ответственный за преобразование Осевых Координатов в Cube Co-ords.
public void setQR(int theQ, int theR){
this.q = theQ;
this.r = theR;
this.x = this.q;
this.z = this.r - (this.q - (this.q&1)) /2;
this.y = -(this.x + this.z);
}
И heres код для разработки расстояния.
FYI, шестиугольники создаются из CentrePoint (CPx, CPy).
private double distance = 0;
public double workOutDistance(Hexagon hexagon, HexagonFood target){
double targetX = target.getCPX();
double targetY = target.getCPY();
double hexagonX = hexagon.getCPX();
double hexagonY = hexagon.getCPY();
double deltaX = (targetX-hexagonX)*-1;
double deltaY = (targetY-hexagonY)*-1;
double deltaXRadius = (deltaX/(SimField.hexSize)/1.5);
double deltaYApothem = (deltaY/(SimField.hexSize/1.155)/2);
hexagon.setQR((int)deltaXRadius, (int)deltaYApothem);
ArrayList<Integer> coords = new ArrayList<>();
coords.add(
Math.abs(hexagon.getX() - target.getX())
);
coords.add(
Math.abs(hexagon.getZ() - target.getZ())
);
coords.add(
Math.abs(hexagon.getY() - target.getY())
);
System.out.println(coords);
distance = Collections.max(coords);
return distance;
}
Может кто-нибудь скажет мне, почему это происходит? Было бы очень благодарно.
РЕДАКТИРОВАТЬ:
После изменения Int в Double, как было предложено Тимом, я получаю это.
**
РЕШЕНИЕ
**
после экспериментов с ответами, данная малая настройка решает эту проблему.
меняя это..
public void setQR(int theQ, int theR){
this.q = theQ;
this.r = theR;
this.x = this.q;
this.z = this.r - (this.q - (this.q&1)) /2;
this.y = -(this.x + this.z);
}
к этому..
public void setQR(int theQ, int theR){
this.q = theQ;
this.r = theR;
this.x = this.q;
if (this.r>0){
this.z = this.r - (this.q - (this.q&1))/2;
}
else {
this.z = this.r - (this.q + (this.q&1))/2;
}
this.y = -(this.x + this.z);
}
Лучший ответ:
Вы вызываете double в int при вызове setQR(); вы уверены, что делаете то, что ожидаете? В парном разряде используется математика с плавающей запятой, поэтому число, которое вы ожидаете от 2.0, может быть 1,999999989, которое затем округляется до 1 при добавлении к int.
Я также скептически отношусь к строке, которая читает this.z = this.r - (this.q - (this.q&1))/2; , Вы добавляете 1, когда число нечетное, что похоже на случай сбоя, который вы испытываете; Я бы удостоверился, что линия тоже делает то, что вы ожидаете.
Если вы не перешагиваете это с помощью отладчика и не проверяете значения, вы делаете это неправильно.
Ответ №1
Вы также можете использовать совершенно другой подход к этой проблеме. Вы знаете координаты X/Y (декартовых) двух шестиугольников, что означает, что вы можете получить каждую шестиугольную кубическую координату относительно начала вашего гексагонального пространства. Расстояние между двумя шестиугольниками – это просто сумма абсолютных значений различий между двумя координатами X, Y и Z шестиугольников. (То есть dist = |h2.X - h1.X| + |h2.Y - h1.Y| + |h2.Z - h1.Z|) Поэтому вместо того, чтобы пытаться вычислить вектор между двумя центральными точками, а затем преобразуйте это в кубические координаты, вы можете просто вычислить расстояние непосредственно в кубических координатах (точно так же, как если бы это были квадраты в декартовых координатах)…
Даже если вы примете такой подход, я настоятельно рекомендую вам отлаживать то, что происходит с вашим оригинальным подходом. Даже если вы в конечном итоге выбросите код, упражнение отладки, вероятно, научит вас ценным урокам, которые вы сможете применить в будущем.
Примечание для читателей: “кубические” координаты не являются 3-мерными декартовыми координатами, они представляют собой систему координат, специфичную для шестиугольника, для которой ссылка была предоставлена ОП.
Ответ №2
Тот факт, что вычисление (т.е. Преобразование из offset- в координаты куба и вычисление расстояния в координатах куба) кажется правильным, указывает на то, что Тим был прав с его предположением о ошибках с плавающей точкой.
Вы должны попытаться изменить строку
hexagon.setQR((int)deltaXRadius, (int)deltaYApothem);
от вашего исходного кода до чего-то вроде
hexagon.setQR((int)Math.round(deltaXRadius), (int)Math.round(deltaYApothem));
Что может решить проблему в этом случае.
Если нет… или… в любом случае, вот небольшой пример, в основном делающий то же, что и вы, но как MVCE…
import java.awt.Point;
public class HexagonsTest
{
public static void main(String[] args)
{
// Above and below
test(8,6, 8,5, 1);
test(8,6, 8,7, 1);
// Left
test(8,6, 7,5, 1);
test(8,6, 7,6, 1);
// Right
test(8,6, 9,5, 1);
test(8,6, 9,6, 1);
// The first one that was wrong:
test(8,6, 7,4, 2);
}
private static void test(int x0, int y0, int x1, int y1, int expected)
{
int distance = computeStepsDistance(x0, y0, x1, y1);
System.out.println(
"Distance of (" + x0 + "," + y0 + ") to " +
"(" + x1 + "," + y1 + ") is " + distance +
", expected " + expected);
}
private static int computeStepsDistance(int x0, int y0, int x1, int y1)
{
Point cp0 = convertOffsetToCubeCoordinates(x0, y0, null);
Point cp1 = convertOffsetToCubeCoordinates(x1, y1, null);
int cx0 = cp0.x;
int cy0 = cp0.y;
int cz0 = -cx0-cy0;
int cx1 = cp1.x;
int cy1 = cp1.y;
int cz1 = -cx1-cy1;
int dx = Math.abs(cx0 - cx1);
int dy = Math.abs(cy0 - cy1);
int dz = Math.abs(cz0 - cz1);
return Math.max(dx, Math.max(dy, dz));
}
private static Point convertOffsetToCubeCoordinates(
int ox, int oy, Point p)
{
int cx = ox;
int cz = oy - (ox - (ox&1)) / 2;
int cy = -cx-cz;
if (p == null)
{
p = new Point();
}
p.x = cx;
p.y = cy;
return p;
}
}
Правильный шестиугольник: свойства, формулы, площадь
Знаете ли вы, как выглядит правильный шестиугольник?
Этот вопрос задан не случайно. Большинство учащихся 11 класса не знают на него ответа.
Правильный шестиугольник — такой, у которого все стороны равны и все углы тоже равны.
Железная гайка. Снежинка. Ячейка сот, в которых живут пчелы. Молекула бензола. Что общего у этих объектов? — То, что все они имеют правильную шестиугольную форму.
Многие школьники теряются, видя задачи на правильный шестиугольник, и считают, что для их решения нужны какие-то особые формулы. Так ли это?
Проведем диагонали правильного шестиугольника. Мы получили шесть равносторонних треугольников.
Мы знаем, что площадь правильного треугольника: .
Тогда площадь правильного шестиугольника — в шесть раз больше.
, где — сторона правильного шестиугольника.
Обратите внимание, что в правильном шестиугольнике расстояние от его центра до любой из вершин одинаково и равно стороне правильного шестиугольник.
Значит, радиус окружности, описанной вокруг правильного шестиугольника, равен его стороне.
Радиус окружности, вписанной в правильный шестиугольник, нетрудно найти.
Он равен .
Теперь вы легко решите любые задачи ЕГЭ, в которых фигурирует правильный шестиугольник.
Ты нашел то, что искал? Поделись с друзьями!
. Найдите радиус окружности, вписанной в правильный шестиугольник со стороной .
Радиус такой окружности равен .
. Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?
Мы знаем, что сторона правильного шестиугольника равна радиусу описанной вокруг него окружности.
Как найти длину окружности описанной около правильного шестиугольника
Вопрос по геометрии:
Сторона правильного шестиугольника равна 12 см. Вычислите длину.
а) окружности, описанной около этого шестиугольника.
б) окружности, вписанной в данный шестиугольника.
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 1
Сторона правильного шестиугольника равна a=12 см.
Длина окружности вычисляется по формуле: L=2 r. Значит нам надо сначала найти радиусы вписанной и описанной окружностей.
a) Радиус окружности, описанной около правильного шестиугольника, равен R=a.
Длина описанной окружности: L=2 *12=24
б) Радиус окружности, вписанной в шестиугольник, вычисляется по формуле: r= = = .
Длина вписанной окружности: L=2 * =
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
Геометрия
План урока:
Понятие правильного многоугольника
У выпуклого многоугольника могут быть одинаковы одновременно и все стороны, и все углы. В таком случае он именуется правильным многоугольником.
Нам уже известны некоторые правильные многоуг-ки. Например, правильным является равносторонний треугольник. У него все стороны одинаковы по его определению, а все углы составляют по 60°. Поэтому иногда его так и называют – правильный треугольник. Среди четырехугольников правильной фигурой является квадрат, у которого также по определению одинаковы стороны, а углы составляют уже по 90°.
Заметим, что бывают фигуры, у которых одинаковы все стороны, а углы различны. Примером такой фигуры является ромб. Возможна и обратная ситуация – все углы у фигуры одинаковы, но стороны отличаются своей длиной. Таковым является прямоугольник. Важно понимать, такие фигуры (в частности, ромб и прямоугольник) НЕ являются правильными.
Для любого заданного числа n, начиная от n = 3, можно построить правильный n-угольник. На рисунке ниже показано несколько примеров таких n-угольников:
Существует зависимость, которая позволяет определить величину угла правильного многоугольника. Мы уже знаем, что в любом выпуклом n-угольнике сумма углов равна величине 180°(n– 2). Обозначим угол правильного многоуг-ка буквой α. Так как у n-угольника ровно n углов, и все они одинаковы, мы можем записать равенство:
Легко проверить, что эта формула верна для равностороннего треуг-ка и квадрата и позволяет правильно определить углы в этих фигурах. Для треугольника n = 3, поэтому мы получаем 60°:
Задание. Какова величина углов в правильном пятиугольнике, шестиугольнике, восьмиугольнике, пятидесятиугольнике?
Решение. Надо просто подставить в формулу число сторон правильного многоугольник. Сначала считаем для пятиугольника:
Задание. Сколько сторон должно быть у правильного многоуг-ка, чтобы каждый угол в нем был равен 179°?
Решение. В формулу
Задание. Может ли существовать правильный многоуг-к, угол которого равен 145°?
Решение. Предположим, что он существует. Тогда по аналогии с предыдущей задачей найдем количество его сторон:
Получили не целое, а дробное количество сторон. Естественно, что это невозможно, а потому такой многоуг-к существовать не может.
Описанная и вписанная окружности правильного многоугольника
Докажем важную теорему о правильном многоуг-ке.
Для доказательства обозначим вершины произвольного правильного n-угольника буквами А1, А2, А3…Аn. Далее проведем биссектрисы углов ∠А1 и ∠А2. Они пересекутся в некоторой точке О. Соединим О с другими вершинами многоуг-ка отрезками ОА3, ОА4 и т. д.
∠А1 и ∠А2 одинаковы по определению правильного многоуг-ка:
Из этого факта вытекает два равенства:
Получается, что ОА3 – это также биссектриса ∠А3. Тогда, повторив все предыдущие рассуждения, мы можем доказать равенство, аналогичное (1):
Это равенство означает, что точка О равноудалена от вершин многоуг-ка. Значит, можно построить окружность с центром в О, на которой будут лежать все вершины многоуг-ка:
Естественно, существует только одна такая описанная окружность, ведь через любые три точки, в частности, через А1, А2 и А3, можно провести только одну окружность, ч. т. д.
Продолжим рассматривать выполненное нами построение с описанной окружностью. Ясно, что ∆ОА1А2, ∆ОА2А3, ∆ОА3А4, …, равны, ведь у них одинаковы по 3 стороны. Опустим из О высоты ОН1, ОН2, ОН3… на стороны многоуг-ка.
Так как высоты проведены в равных треуг-ках, то и сами они равны:
Теперь проведем окружность, центр которой находится в О, а радиус – это отрезок ОН1. Он должен будет пройти и через точки Н2, Н3, … Нn. Причем отрезки ОН1, ОН2, ОН3 окажутся радиусами. Так как они перпендикулярны сторонам многоуг-ка, то эти самые стороны будут касательными к окружности (по признаку касательной). Стало быть, эта окружность является вписанной:
Ясно, что такая окружность будет единственной вписанной. Если бы существовала вторая вписанная окружность, то ее центр был бы равноудален от сторон многоуг-ка, а потому лежал бы в точке пересечения биссектрис углов ∠А1, ∠А2, ∠А3, то есть в точке О. Так как расстояние от О до А1А2 – это отрезок ОН1, то именно такой радиус был бы у второй окружности. Получается, что вторая окружность полностью совпала бы с первой, так как их центр находился бы в одной точке, и радиусы были одинаковы.
Примечание. Точка, которая центром и вписанной, и описанной окружности, именуется центром правильного многоуг-ка.
Ещё раз вернемся к приведенному доказательству и заметим, что высоты ОН1, ОН2, ОН3,… проведены в равнобедренных треуг-ках∆ОА1А2, ∆ОА2А3, ∆ОА3А4,… Следовательно, эти высоты являются ещё и медианами, то есть точки Н1, Н2, Н3,… – это середины сторон многоуг-ка.
Задание. Могут ли две биссектрисы, проведенные в правильном многоуг-ке, быть параллельными друг другу?
Решение. Центр правильного многоуг-ка находится в точке пересечения всех его биссектрис. То есть любые две биссектрисы будут иметь хотя бы одну общую точку. Параллельные же прямые общих точек не имеют. Получается, что биссектрисы не могут быть параллельными.
Примечание. Аналогичное утверждение можно доказать и для серединных перпендикуляров, проведенных к сторонам правильного многоуг-ка.
Формулы для правильного многоугольника
Правильный многоуг-к, как и любая другая плоская фигура, имеет площадь (она обозначается буквой S) и периметр (обозначается как Р). Длина стороны многоуг-ка традиционно обозначается буквой an, где n– число сторон у многоуг-ка. Например a4– это сторона квадрата, a6– сторона шестиугольника. Наконец, мы выяснили, что для каждого правильного многоуг-ка можно построить описанную и вписанную окружность. Радиус описанной окружности обозначается большой буквой R, а вписанной – маленькой буквой r.
Оказывается, все эти величины взаимосвязаны друг с другом. Ранее мы уже получили формулу
для многоуг-ка, в который вписана окружность. Подходит она и для правильного многоуг-ка.
Для вывода остальных формул правильного многоугольника построим n-угольники соединим две его вершины с центром:
Теперь у нас есть формула, связывающая друг с другом Rи r. Наконец, прямо из определения периметра следует ещё одна формула:
С их помощью, зная только один из параметров правильного n-угольника, легко найти и все остальные параметры (если известно и число n).
Задание. Докажите, что сторона правильного шестиугольника равна радиусу описанной около него окружности.
Решение. Запишем следующую формулу:
Это равенство как раз и надо было доказать в этом задании.
Задание. Около окружности описан квадрат. В свою очередь и около квадрата описана окружность радиусом 4. Найдите длину стороны квадрата и радиус вписанной окружности.
Решение. Запишем формулу:
Задание. Вычислите площадь правильного многоугольника с шестью углами, длина стороны которого составляет единицу.
Найдем периметр шестиугольника:
Задание. Около правильного треугольника описана окружность. В ту же окружность вписан и квадрат. Какова длина стороны этого квадрата, если периметр треугольника составляет 18 см?
Решение. Зная периметр треуг-ка, легко найдем и его сторону:
Далее вычисляется радиус описанной около треугольника окружности:
Задание. Необходимо изготовить болт с шестигранной головкой, причем размер под ключ (так называется расстояние между двумя параллельными гранями головки болта) должен составлять 17 мм. Из прутка какого диаметра может быть изготовлен такой болт, если диаметр прутков измеряется целым числом?
Решение. Здесь надо найти диаметр окружности, описанной около шестиугольника. Ранее мы уже доказывали, что у шестиугольника длина этого радиуса совпадает с длиной его стороны:
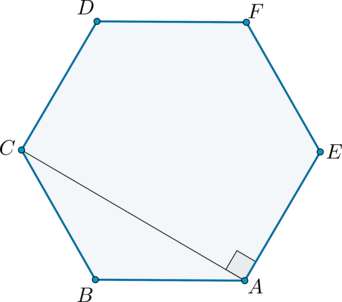
Осталось найти сторону шестиугольника. Для этого соединим две его вершины (обозначим их А и С) так, как это показано на рисунке:
Отрезок АС как раз и будет расстоянием между двумя параллельными гранями, что легко доказать. Каждый угол шестиугольника будет составлять 120°:
В частности ∠АВС = 120°. Так как АВ = ВС, то ∆АВС – равнобедренный, и углы при его основании одинаковы:
Аналогично можно показать, что и ∠ACD – прямой. Таким образом, АС перпендикулярен сторонам AF и CD, а значит является расстоянием между ними, и по условию равно 17 мм:
∆АВС – равнобедренный. Опустим в нем высоту НВ, которая одновременно будет и медианой. Тогда АН окажется вдвое короче АС:
AH = AC/2 = 17/2 = 8,5 мм
Теперь сторону АВ можно найти из ∆АВН, являющегося прямоугольным:
Здесь мы округлили ответ до ближайшего большего целого числа, так как по условию можно использовать лишь пруток с целым диаметром.
Построение правильных многоугольников
При использовании транспортира или иного прибора, позволяющего откладывать заранее заданные углы, построение правильного многоуг-ка проблем не вызывает. Например, пусть надо построить пятиугольник со стороной, равной 5 см. Сначала по известной формуле вычисляем величину его угла:
Однако напомним, что в геометрии большой интерес вызывают задачи, связанные с построением с помощью всего двух инструментов – циркуля и линейки, то есть без использования транспортира. В таком случае построение многоугольников правильной формы становится значительно более сложной задачей. Если речь идет не о таких простых фигурах, как квадрат и равносторонний треугольник, то при построении обычно приходится использовать описанную окружность.
Сначала рассмотрим построение правильного шестиугольника по заранее заданной стороне. Ранее мы уже узнали, что его сторона имеет такую же длину, как и радиус описанной окружности:
На основе этого факта предложен следующий метод построения шестиугольника. Сначала строится описанная окружность, причем в качестве ее радиуса берется заданная сторона а6. Далее на окружности отмечается произвольная точка А, которая будет первой вершиной шестиугольника. Из нее проводится ещё одна окружность радиусом а6. Точки, где она пересечет описанную окружность (В и F), будут двумя другими вершинами шестиугольника. Наконец, и из точек B и F проводим ещё две окружности, которые пересекутся с исходной окружностью в точках С и F. Наконец, из С (можно и из F)провести последнюю окружность и получить точку D. Осталось лишь соединить все точки на окружности (А, В, С, D, Еи F):
Данное построение довольно просто. Однако для пятиугольника построение несколько более сложное, а для семиугольника и девятиугольника вообще невозможно осуществить точное построение. Этот факт был доказан только в 1836 г. Пьером Ванцелем.
Если удалось возможно построить правильный n-угольник, вписанный в окружность, то несложно на его основе построить многоуг-к, у которого будет в два раза больше сторон (его можно назвать 2n-угольником) и который будет вписан в ту же окружность. Рассмотрим это построение на примере квадрата и восьмиугольника.
Изначально дан квадрат, вписанный в окружность. Надо построить восьмиугольник, вписанный в ту же окружность. Обозначим любые две вершины квадрата буквами А и В. Для начала нам надо разбить дугу ⋃АВ на две равные дуги. Для этого мы проводим из А и В окружности радиусом АВ. Они пересекутся в некоторых точках С и D. Соединяем их отрезком, который в свою очередь пересечется с исходной окружностью в точке Е.
Е – это середина дуги ⋃АВ. Точки А, В и Е как раз являются тремя первыми точками восьмиугольника. Для получения остальных точек необходимо из вершин квадрата строить окружности радиусом АЕ. Точки, где эти окружности пересекутся с исходной окружностью, и будут вершинами восьмиугольника. Также его вершинами являются вершины самого квадрата:
Аналогичным образом можно из шестиугольника получить 12-угольник, из восьмиугольника – 16-угольник, из 16-угольника – 32-угольник. То есть можно удвоить число сторон многоуг-ка.
Древние греки умели строить правильные многоуг-ки с 3, 4, 5, 6 и 15 сторонами, а также умели на их основе строить многоуг-ки с вдвое большим числом сторон. Лишь в 1796 г. Карл Гаусс смог построить 17-угольник. Также удалось найти способ построения 257-угольника и 65537-угольника, причем описание построения 65537-угольника занимает более 200 страниц.
В этом уроке мы узнали о правильных многоуг-ках и их свойствах. Особенно важно то, что для каждого такого многоуг-ка можно построить описанную и вписанную окружность, причем их центры совпадают. Это позволяет использовать правильные многоуг-ки для более глубокого исследования свойств окружности.
http://online-otvet.ru/geometria/5cea707b96f4e19a29f1f506
http://100urokov.ru/predmety/pravilnye-mnogougolniki



 = 4,1421356 см
= 4,1421356 см