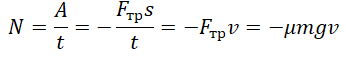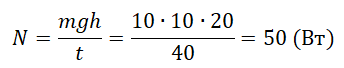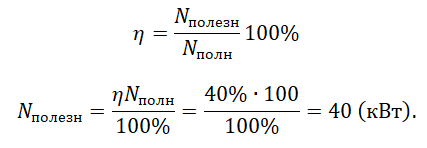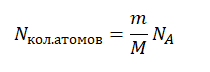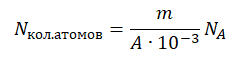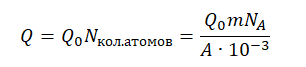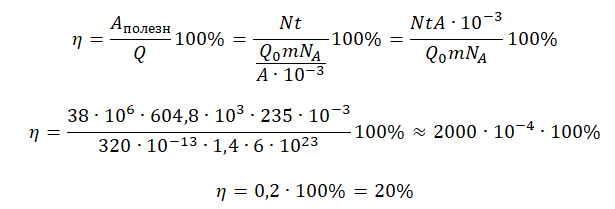ПАМЯТКА ДЛЯ РЕШЕНИЯ ЗАДАЧ ПО ФОРМУЛАМ
Формула пути
S = v• t
S – расстояние(км, дм,м)
v – скорость (км/ч, м/с, м/мин)
t – время (час, мин., сек.)
- Чтобы найти расстояние, надо скорость умножить на время.
S = v• t
- Чтобы найти скорость, надо расстояние разделить на время. v = S : t
- Чтобы найти время, надо расстояние разделить на скорость. t =S : v
Формула стоимости
С = a • n
C – стоимость (руб.)
a – цена товара (руб.)
n – количество товара (шт., кор., л, кг, м,…)
- Чтобы найти стоимость покупки, надо цену умножить на количество товара. С = a • n
- Чтобы найти цену, надо стоимость разделить на количество товара. a = С : n
- Чтобы найти количество товара, надо стоимость разделить на цену. n =С : a
Формула работы
A = v• t
A – работа (дет., стр., маш,…)
v – производительность (дет./час, маш./мес., стр./мин,…)
t – время (час, мин., сек.)
- Чтобы найти работу, надо производительность умножить на время. A = v • t
- Чтобы найти производительность, надо работу разделить на время. v = А : t
- Чтобы найти время, надо работу разделить на производительность. t =А : v
Основные цели урока:
Сформировать представление о величине «производительность», выявить зависимость между величинами: объемом выполненной работы (А), производительностью (V) и временем (t), сформировать способность к построению формулы работы А=v×t.
Формировать умение находить по формуле работы v и t и использовать формулу работы для решения задач.
Тренировать способность детей к решению задач на все изученные виды зависимости между величинами.
Закрепить алгоритм умножения многозначного числа на трехзначное.
Развивать самостоятельность, умения преодолевать трудности в учении, используя проблемные ситуации, разноуровневые задания, самостоятельные упражнения.
Развивать мыслительные операции, внимание, речь, коммуникативные способности, прививать интерес к математике.
Ход урока
I. ЭМОЦИОНАЛЬНЫЙ НАСТРОЙ НА ПРЕДСТОЯЩУЮ ДЕЯТЕЛЬНОСТЬ
I. Организационный момент.
Урок я хочу начать словами французского философа Ж.Ж. Руссо (1712-1778гг.): «Вы — талантливые дети! Когда-нибудь вы сами приятно поразитесь, какие вы умные, как много и хорошо умеете, если будете постоянно работать над собой, ставить новые цели и стремиться к их достижению…”
—Я желаю вам уже сегодня на уроке убедиться в этих словах, ведь вас ждёт открытие новых знаний при решении задач..
II. АКТУАЛИЗАЦИЯ ЗНАНИЙ УЧАЩИХСЯ
1. Устный счет
– Вот песочные часы, песок высыпается в нижнюю часть за 1 минуту.
– Сколько заданий вы выполните за 1 минуту. (1 ученик выполняет у доски)
У 640-560х0=
М 240:60х100=
Ф 3х(180-90)-70=
А (940-720)х4=
Л 1000:5х4=
Р 400:50х40=
О (320-80)х1=
Самопроверка. Самооценивание.
Критерии выставления оценок:
«5» – без ошибок
«4» – 1 ошибка
«3» – 3-4 ошибки
«2» – 5 и более ошибок
– Что интересного заметили в ответах? (Все числа трехзначные, круглые, кратные 2,4,5,8,10).
– Расположите ответы в порядке возрастания.Ф О Р М У Л А
200
240
320
400
630
800
880
– Что мы называем формулой? По словарю (Формулой мы называем равенство, которое помогает нам установить зависимость между величинами).
2. Повторение известных формул.
Работа в группах
Восстановите формулы.
Слайды
Ученики крепят под названиями таблички с восстановленными формулами.
Проверка. (Чтобы найти …, надо …)
– По какому правилу можно получить 2 последние формулы? (По правилу нахождения неизвестного множителя).
– Для чего вам нужны формулы? (Для решения задач).
– Как вы думаете, какое теперь задание я вам предложу? (Решение задач).
3. Решение задач
На листочках даны задачи трех уровней каждому ученику.
– Прочитать задания, выбрать уровень сложности, записать только решение.1 уровень
Избушка на курьих ножках за 8 часов пробежала 72 км. С какой скоростью бегает избушка?
Кощей Бессмертный проехал на Змее Горыныче 180 км. Сколько часов они были в пути, если средняя скорость Змея Горыныча 90 км/ч?
Иван-царевич шёл тропинками нехожеными 6 часов со скоростью 6 км/ч. Какова длина тех тропинок?
2 уровень
Ковер-самолет летит со скоростью 200 км/ч. Какое расстояние он пролетит за а часов?
Ступа Бабы Яги пролетела x км за y часов. Какова скорость ступы Бабы Яги?
Иван-царевич за 3 часа проехал на волшебном коне d км. За сколько времени он преодолеет расстояние t, если скорость останется прежней?
3 уровень
Водяной плывет d км за 4 часа, а Баба Яга на метле это же расстояние пролетает за 2 часа. На сколько километров в час скорость Бабы Яги больше?
Жар-птице нужно пролететь х км. Она уже пролетела а часов со скоростью b км/ч. Сколько ей осталось пролететь?
Средняя скорость полета Финиста-ясного сокола b м/с, Жар-птицы – с м/с. На сколько метров больше пролетит Финист-ясный сокол, чем Жар-птица, за 20 секунд?
Самопроверка.
Сравните свое решение с правильным (слайд 1).1 уровень
72:8=9 км/ч
180:90=2 ч
6×6=36 км 2 уровень
200:а = (км)
x:y = км/ч
t: (d:3) = км 3 уровень
d:2-d:4= (км/ч)
x-b×a= (км)
b×20-c×20= (км) или (b-c) × 20 = (км)
– Если вы решали задания 1 уровня, и все решили без ошибок, запишите себе три балла. Задания 2 уровня соответствуют 4 баллам. 5 баллов ставит себе тот, кто решил задания 3 уровня и не допустил ни одной ошибки.
– Что общего в задачах, которые вы решали? (Задачи на движение).
– Какой формулой вы воспользовались, когда решали задачи? (Формулой пути).
– Как найти путь? (S=v×t)
– Как из этой формулы можно получить ещё две? (Находим неизвестный множитель: V= s÷t; t=s÷t).
III. ПОСТАНОВКА ПРОБЛЕМЫ
– А сейчас я вам предложу «вкусную задачу». Мама одной ученицы приготовила для вас эту задачу. Видеоролик включается (слайд 2): «На масленицу я вам напекла гору вкусных блинов. Я их выпекала в несколько приемов. В начале, я выпекала 3 блина в минуту. Сколько блинов приготовила я, работая 20 минут».
– Подберите формулу к задаче.
– Чем эта задача отличается от тех, которые мы решали. (Задачи были с известными величинами: стороны и площадь; время, скорость и путь; стоимость, количество и цена. А в этой задаче не все величины знакомы, знаем только время).
– Почему возникли затруднения? (Новые величины, нет формул).
IV. ОТКРЫТИЕ ДЕТЬМИ НОВОГО ЗНАНИЯ
Как же назвать эту формулу?
– Что нужно найти в задаче? (Сколько всего блинов испекла мама, т.е. её работу).
Эта формула называется «ФОРМУЛА РАБОТЫ».
– О каких величинах ещё идет речь? (Выпекала 3 блина в минуту, т.е. скорость работы).
– Скорость работы называют «ПРОИЗВОДИТЕЛЬНОСТЬЮ». Обозначим эту величину буквой «V».
– Что еще известно в задаче? (Время работы).
– О какой величине идет речь? (О времени).
– Какой буквой обозначается эта величина? («t»).
– Что нужно узнать в задаче? (Количество всех блинов, т.е. какую работу выполнила мама)
– Как найти количество блинов, которые испекла мама за 20 минут, если известно, что за 1 минуту мама выпекает 3 блина. (Надо 3 блина умножить на 20 минут: 3×20=60 блинов испекла мама).
– Записать в тетрадь решение.
– Какую величину находим? (Работу).
– Как находили? (Производительность работы умножили на время).
– Запишите формулу зависимости этих величин.A = V×t
– Все ли формулы открыты? (Нет).
– Чтобы их открыть, нужно отдохнуть.
Физпауза
– Выведите две другие формулы.
– По какому правилу можно получить? (По правилу нахождения неизвестного множителя)
– Какую величину будете находить? (Время)t = A÷V
– Чтобы найти время нужно работу разделить на производительность труда.
– Запишите эту формулу в тетради и на доске.
– Какая величина еще неизвестна? (Производительность труда)
– А что такое производительность труда? (Это работа, выполненная за единицу времени).
– Как найти производительность? V= A÷t
– Все ли формулы открыты? (Да)
– Как можно проверить правильность ваших выводов? (Можно посмотреть в учебнике). Работа с учебником (с.43).
– Сравните выведенные вами формулы.
– Прочтите формулировки.
– Как найти работу?
– Время работы?
– Как называется работа, выполненная за единицу времени? (Производительность труда).
– А теперь мы вернемся к практической работе, которую выполняли в начале урока. Сколько заданий вы выполнили за одну минуту? Это наша производительность.
– Одинаковым ли было количество заданий у каждого из вас? (Нет, одни выполнили больше заданий, другие – меньше).
– Что можно сказать о производительности труда наших учеников? (Она разная. Это зависело от того, кто сразу начал работу, кто отвлекался, кто хорошо знает таблицу умножения,..).
А если бы вы решали 10 минут, сколько всего таких заданий вы бы выполнили? Какие задачи теперь сможете решать (Задачи на работу).
V. ПЕРВИЧНОЕ ЗАКРЕПЛЕНИЕ ВО ВНЕШНЕЙ РЕЧИ
– Откройте учебник на стр. 44, №1.
– Какое задание надо выполнить? (Объяснить смысл предложений)
а) Вася каждый час съедает 3 мороженых. А сколько мороженых Вася съест за 2 часа? (3×2=6 мороженых)
– Какую величину находили? (Работу).
б) Оля за одну минуту лепит 2 штуки пельменей. Дополните условие и поставьте вопрос к задаче.
№2. Какое задание будете выполнять? (Решать задачу).
– Прочтите задачу.
– Анализ задачи. Один из учащихся анализирует условие задачи.
– Какие величины известны? Что надо найти?
V= 8 дет/ч
A= V×t
– Найдите работу, выполненную мастером за 6 часов, 7 часов. (Учащиеся работают в парах)
– Найдите работу за 9 часов и за время t самостоятельно.
Заполненная таблица вывешивается на доску.
VI. САМОСТОЯТЕЛЬНАЯ РАБОТА С САМОПРОВЕРКОЙ ПО ЭТАЛОНУ
По данным таблицы составьте задачи и решите их.
1 вариант – с.44, №4а; 2 вариант – с.44, № 4б.
Проверьте по эталону (слайд 3)?
– Какой формулой пользовались? Как решали? Правильность оцените с помощью знаков «+» или «-». У кого все верно? Молодцы!
VII. ВКЛЮЧЕНИЕ В СИСТЕМУ ЗНАНИЙ И ПОВТОРЕНИЕ
Где сможем применить полученное знание? (При решении задач)
№5, стр. 44. Двое учащихся работают на закрытой части доски, остальные – в тетрадях. Фронтально проводится проверка правильности выполнения задания.
– Чем пользовались? (Алгоритм решения задач, формулой работы, алгоритмом умножения многозначных чисел).
– Кто допустил ошибки? Проанализируйте их. Запишите ответ задачи. Можно ли по этой записи определить число автомобилей, которые выпускает завод:
за 5 дней (1040 м)
за 6 дней (1248 м)
за 60 дней (12480 м)
за 300 дней (62400 м).
– Можно ли, не вычисляя, сказать, на сколько второе произведение больше первого? (208×365 < 208×366 на 208).
VII. РЕФЛЕКСИЯ УЧЕБНОЙ ДЕЯТЕЛЬНОСТИ НА УРОКЕ
– Какие цели ставили на уроке? (Установить, какие величины описывают процесс выполнения работы, ввести обозначения этих величин и установить взаимосвязь между ними, т.е. построить формулу работы).
– Что явилось итогом работы? (Формулы).
– Достигли вы этой цели? Докажите.
– Заполните эталон. (слайд 4)
Формула…….(работы) A = V×…10010
(Производительность) – это работа, выполненная за единицу времени.V= … : t
t=A : …
– Если затрудняетесь, где можно найти ответ? (В учебнике).
– Вы сами сделали открытие и ряд изученных формул пополнился.
Проанализируйте свою работу. (Внимательно слушал, смотрел, сделал открытие, все получилось – доволен собой/ не доволен).
Оцените свою работу на полях тетради – нарисуйте лицо человечка.
– Благодарю вас за активную работу на уроке.
Урок я хочу закончить пословицей о труде.
Всегда помните: «Всякое умение трудом дается».
VIII. ДОМАШНЕЕ ЗАДАНИЕ
Презентация (слайд 5).
На слайде представлены данные о ежегодном выпуске автомобилей на российских заводах. Почему заводы выпускают разное количество машин? От чего это зависит? (От опыта работы, возраста, модернизации, от производительности труда, оборудования). Придумайте задачи на нахождение производительности, времени, работы, используя данные из таблицы.
Найти пословицы и поговорки о работе.
Решить №6, стр. 45.
Рефлексия: Слайд № 10
дети оценивают свои знания и умения при помощи цветных сигнальных карточек.
(красная) Я могу
(желтая) Я сомневаюсь, надо ещё поработать.
(зеленая) Мне многое непонятно.
Общая самооценка.
Чтобы вы хотели пожелать себе и своим товарищам на следующий урок?
Поблагодарите друг друга за помощь, поддержку на уроке. (Выставление оценок.)
Вы были внимательны!
Вы успели сделать все!
Вы м о л о д ц ы!
В отличие от повседневной жизни, термин «механическая работа» в физике связан с перемещением тела под воздействием приложенной к нему силы. Примеры работы: малыш тащит на веревочке игрушечный автомобиль, сброшенный с высоты предмет падает на землю, грузчик переносит вещи.
Направление движения не может быть перпендикулярно действию силы. Книга, лежащая на столе, действует на него с силой, направленной перпендикулярно столешнице и равной своему весу. Но стол остается на месте, поэтому работа равна нулю.
Если предмет перемещается в направлении приложенной к нему силы, то совершается положительная работа. Ее величина равна произведению силы и расстояния, на которое переместилось тело.
A = F x D, где:
A — работа;
F — сила, действующая на тело;
D — расстояние, на которое переместилось тело под действием приложенной силы F;
Пример положительной работы: локомотив тянет за собой вагоны.
[A] = 1 Дж = 1 Н x м
Если перемещение противоположно действию силы, то совершается отрицательная работа.
В этом случае A = — F x D.
Например, при запуске летучего змея работа силы тяжести — отрицательная.
Если величина приложенной силы непостоянна или направлена под углом к направлению движения тела, работа рассчитывается по другим, более сложным формулам.
Полная работа определяется как совокупность работы всех сил, действующих на предмет. В зависимости от величины работы и времени на ее выполнение подбирают необходимую мощность машин и механизмов и расход топлива.
Математика
5 класс
Урок № 35
Задачи на движение
Перечень вопросов, рассматриваемых в теме:
- Понятия скорости, времени, расстояния.
- Формулы нахождения скорости, времени, расстояния.
- Понятия скорости сближения, скорости удаления.
Глоссарий по теме
Расстояние – это длина от одного пункта до другого.
Большие расстояния, в основном, измеряются в метрах и километрах.
Расстояние обозначается латинской буквой S.
Чтобы найти расстояние, надо скорость умножить на время движения:
S = v ∙ t
Скорость – это расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда.
Скорость обозначается латинской буквой v.
Чтобы найти скорость, нужно расстояние разделить на время движения:
v = S : t
Время – это продолжительность каких-то действий, событий.
Время движения обозначается маленькой латинской буквой t.
Чтобы найти время, нужно расстояние разделить на скорость движения:
t = S : v
Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Чтобы найти скорость сближения, нужно сложить скорости объектов.
Скорость удаления – это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
Основная литература
1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К., Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.
2. Потапов М. К., Шевкин А. В. Математика. Книга для учителя. 5 – 6 классы — М.: Просвещение, 2010
Дополнительная литература
1. Чесноков А. С., Нешков К. И. Дидактические материалы по математике 5 кл. – М.: Академика учебник, 2014
2. Бурмистрова Т. А. Математика. Сборник рабочих программ. 5–6 классы // Составитель Бурмистрова Т. А.
3. Потапов М. К. Математика: дидактические материалы. 6 кл. // Потапов М. К., Шевкин А. В. — М.: Просвещение, 2010
Теоретический материал для самостоятельного изучения
Очень часто нам встречаются задачи на нахождение скорости, времени и расстояния. Что же всё это такое? Сейчас нам предстоит в этом разобраться.
Расстояние – это длина от одного пункта до другого. (Например, расстояние от дома до школы 2 километра). В основном большие расстояния измеряются в метрах и километрах. Общепринятое обозначение расстояния – заглавная латинская буква S.
Скоростью называют расстояние, пройденное телом за единицу времени. Под единицей времени подразумевается 1 час, 1 минута или 1 секунда. Скорость обозначается маленькой латинской буквой v.
Рассмотрим задачу:
Двое школьников решили проверить, кто быстрее добежит от двора до спортплощадки. Расстояние от двора до спортплощадки 200 метров. Первый школьник добежал за 50 секунд. Второй за 100 секунд. Кто из ребят бежал быстрее?
Решение:
Быстрее бежал тот, кто за 1 секунду пробежал большее расстояние. Говорят, что у него скорость движения больше. Чтобы найти скорость, нужно расстояние разделить на время движения.
Давайте найдём скорость первого школьника. Для этого разделим 200 метров на время движения первого школьника, то есть на 50 секунд:
200 м : 50 с = 4
Если расстояние дано в километрах, а время движения в часах, скорость измеряется в километрах в час (км/ч).
У нас расстояние дано в метрах, а время в секундах. Значит, скорость измеряется в метрах в секунду:
200 м : 50 с = 4 (м/с)
Скорость движения первого школьника составляет 4 метра в секунду.
Теперь найдём скорость движения второго школьника. Для этого разделим расстояние на время движения второго школьника:
200 м : 100 c = 2 (м/с)
Скорость движения первого школьника – 4 (м/с).
Скорость движения второго школьника – 2 (м/с).
4 (м/с) > 2 (м/с)
Скорость первого школьника больше. Значит, он бежал до спортплощадки быстрее.
Иногда возникает ситуация, когда требуется узнать, за какое время тело преодолеет то или иное расстояние. Время движения обозначается маленькой латинской буквой t.
Рассмотрим задачу:
От дома до спортивной секции 1200 метров. Мы должны доехать туда на велосипеде. Наша скорость будет 600 метров в минуту. За какое время мы доедем до спортивной секции?
Решение:
Если за одну минуту мы будем проезжать 600 метров, то сколько таких минут нам понадобится для преодоления тысячи двухсот метров? Очевидно, что надо разделить 1200 метров на то расстояние, которое мы будем проезжать за одну минуту, то есть на 600 метров. Тогда мы получим время, за которое мы доедем до спортивной секции:
1200 : 600 = 2 (мин)
Ответ: мы доедем до спортивной секции за 2 минуты.
Скорость, время и расстояние связаны между собой.
Если известны скорость и время движения, то можно найти расстояние. Оно равно скорости, умноженной на время:
S = v ∙ t
Рассмотрим задачу:
Мы вышли из дома и направились в магазин. Мы дошли до магазина за 15 минут. Наша скорость была 60 метров в минуту. Какое расстояние мы прошли?
Решение:
Если за одну минуту мы прошли 60 метров, то сколько таких отрезков по шестьдесят метров мы пройдём за 15 минут? Очевидно, что умножив 60 метров на 15 минут, мы определим расстояние от дома до магазина:
v = 60 (м/мин)
t = 15 (минут)
S = v ∙ t = 60 ∙ 15 = 900 (метров)
Ответ: мы прошли 900 метров.
Если известно время и расстояние, то можно найти скорость:
v = S : t
Рассмотрим задачу:
Расстояние от дома до школы 800 метров. Школьник дошёл до этой школы за 8 минут. Какова была его скорость?
Скорость движения школьника – это расстояние, которое он проходит за одну минуту. Если за 10 минут он преодолел 800 метров, то какое расстояние он преодолевал за одну минуту?
Чтобы ответить на этот вопрос, нужно разделить расстояние на время движения школьника:
S = 800 метров
t = 8 минут
v = S : t = 800 : 8 = 100 (м/мин)
Ответ: скорость школьника была 100 м/мин.
Если известна скорость и расстояние, то можно найти время:
t = S : v
Рассмотрим задачу:
От дома до спортивной секции 600 метров. Мы должны дойти до неё пешком. Наша скорость будет 120 метров в минуту (120 м/мин). За какое время мы дойдём до спортивной секции?
Если за одну минуту мы будем проходить 120 метров, то сколько таких минут со ста двадцатью метрами будет в шестистах метрах?
Чтобы ответить на этот вопрос, нужно 600 метров разделить на расстояние, которое мы будем проходить за одну минуту, то есть на 120. Тогда мы получим время, за которое мы дойдём до спортивной секции:
S = 600 метров
v = 120 (м/мин)
t = S : v = 600 : 120 = 5 (минут).
Ответ: мы дойдём до спортивной секции за 5 минут.
Итак, все рассмотренные нами формулы мы можем представить в виде треугольника для лучшего запоминания:
Теперь рассмотрим типы задач на движение.
Задачи на сближение.
Скорость сближения – это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Например, если из двух пунктов навстречу друг другу отправятся два пешехода, причём скорость первого будет 100 метров в минуту, а второго – 105 метров в минуту, то скорость сближения будет составлять 100 плюс 105, то есть 205 метров в минуту. Значит, каждую минуту расстояние между пешеходами будет уменьшаться на 205 метров.
Чтобы найти скорость сближения, нужно сложить скорости объектов.
Задача.
Из двух пунктов навстречу друг другу выехали одновременно два велосипедиста. Скорость первого велосипедиста 13 км/ч, а скорость второго – 15 км/ч. Через 3 часа они встретились. Определите расстояние между населёнными пунктами.
Решение:
- Найдём скорость сближения велосипедистов:
13 км/ч + 15 км/ч = 28 км/ч
- Определим расстояние между населёнными пунктами. Для этого скорость сближения умножим на время движения:
28 ∙ 3 = 84 км
Ответ: расстояние между населёнными пунктами 84 км.
Задачи на скорость удаления.
Скорость удаления – это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Например, если два пешехода отправятся из одного и того же пункта в противоположных направлениях, причём скорость первого будет 4 км/ч, а скорость второго 6 км/ч, то скорость удаления будет составлять 4 плюс 6, то есть 10 км/ч. Каждый час расстояние между двумя пешеходами будет увеличиваться на 10 километров.
Чтобы найти скорость удаления, нужно сложить скорости объектов.
Рассмотрим задачу:
С причала одновременно в противоположных направлениях отправились теплоход и катер. Скорость теплохода составляла 60 км/ч, скорость катера 130 км/ч. Какое расстояние будет между ними через 2 часа?
Решение:
- Определим скорость удаления. Для этого сложим их скорости:
60 + 130 = 190 км/ч.
Получили скорость удаления равную 190 км/ч. Данная скорость показывает, что за час расстояние между теплоходом и катером будет увеличиваться на 190 километров.
- Чтобы узнать какое расстояние будет между ними через два часа, нужно 190 умножить на 2:
190 ∙ 2 = 380 км.
Ответ: через 2 часа расстояние между теплоходом и катером будет составлять 380 километров.
Задачи на движение объектов в одном направлении.
В предыдущих пунктах мы рассматривали задачи, в которых объекты (люди, машины, лодки) двигались либо навстречу друг другу, либо в противоположных направлениях. В первом случае мы находили скорость сближения – в ситуации, когда два объекта двигались навстречу друг другу. Во втором случае мы находили скорость удаления – в ситуации, когда два объекта двигались в противоположных направлениях. Но объекты также могут двигаться в одном направлении, причём с различной скоростью.
Чтобы найти скорость удаления при движении в одном направлении, нужно из большей скорости вычесть меньшую скорость.
Рассмотрим задачу:
Из города в одном и том же направлении выехали легковой автомобиль и автобус. Скорость автомобиля 130 км/ч, а скорость автобуса 90 км/ч. Какое расстояние будет между ними через 1 час? Через 3 часа?
Решение:
- Найдём скорость удаления. Для этого из большей скорости вычтем меньшую:
130 км/ч − 90 км/ч = 40 км/ч
- Каждый час легковой автомобиль отдаляется от автобуса на 40 километров. За один час расстояние между автомобилем и автобусом будет 40 км. За 3 часа в три раза больше:
40 ∙ 3 = 120 км
Ответ: через один час расстояние между автомобилем и автобусом будет 40 км, через три часа – 120 км.
Рассмотрим ситуацию, в которой объекты начали своё движение из разных пунктов, но в одном направлении.
Задача.
Пусть на одной улице имеется дом, школа и аттракцион. Дом находится на одном конце улицы, аттракцион на другом, школа между ними. От дома до школы 900 метров. Два пешехода отправились в аттракцион в одно и то же время. Причём первый пешеход отправился в аттракцион от дома со скоростью 90 метров в минуту, а второй пешеход отправился в аттракцион от школы со скоростью 85 метров в минуту. Какое расстояние будет между пешеходами через 3 минуты? Через сколько минут после начала движения первый пешеход догонит второго?
Решение:
- Определим расстояние, пройденное первым пешеходом за 3 минуты. Он двигался со скоростью 90 метров в минуту. За три минуты он пройдёт в три раза больше, то есть 270 метров:
90 ∙ 3 = 270 метров
- Определим расстояние, пройденное вторым пешеходом за 3 минуты. Он двигался со скоростью 85 метров в минуту. За три минуты он пройдёт в три раза больше, то есть 255 метров:
85 ∙ 3 = 255 метров
- Теперь найдём расстояние между пешеходами. Чтобы найти расстояние между пешеходами, можно к расстоянию от дома до школы (900м) прибавить расстояние, пройденное вторым пешеходом (255м), и из полученного результата вычесть расстояние, пройденное первым пешеходом (270м):
900 + 255 = 1155 м
1155 – 270 = 885 м
Либо из расстояния от дома до школы (900 м) вычесть расстояние, пройденное первым пешеходом (270 м), и к полученному результату прибавить расстояние, пройденное вторым пешеходом (255 м):
900 – 270 = 630 м
630 + 255 = 885 м
Таким образом, через три минуты расстояние между пешеходами будет составлять 885 метров.
- Теперь давайте ответим на вопрос: через сколько минут после начала движения первый пешеход догонит второго?
В самом начале пути между пешеходами было расстояние 900 м. Через минуту после начала движения расстояние между ними будет составлять 895 метров, поскольку первый пешеход двигается на 5 метров в минуту быстрее второго:
90 ∙ 1 = 90 м
85 ∙ 1 = 85 м
900 + 85 – 90 = 985 – 90 = 895 м
Через три минуты после начала движения расстояние уменьшится на 15 метров и будет составлять 885 метров. Это был наш ответ на первый вопрос задачи:
90 ∙ 3 = 270 м
85 ∙ 3 = 255 м
900 + 255 – 270 = 1155 – 270 = 885 м
Можно сделать вывод, что каждую минуту расстояние между пешеходами будет уменьшаться на 5 метров.
А раз изначальные 900 метров с каждой минутой уменьшаются на одинаковые 5 метров, то мы можем узнать сколько раз 900 метров содержат по 5 метров, тем самым определяя через сколько минут первый пешеход догонит второго:
900 : 5 = 180 минут.
Ответ: через три минуты расстояние между пешеходами будет составлять 885 метров, первый пешеход догонит второго через 180 минут = 3 часа.
Разбор решения заданий тренировочного модуля
№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте
Заполните таблицу:
|
S |
v |
t |
|
|
1. |
135 км |
9 км/ч |
____ ч |
|
2. |
____ м |
12 м/с |
4 с |
|
3. |
132 м |
____ м/мин |
11 мин |
Для заполнения пропусков воспользуемся формулами нахождения скорости, времени, расстояния:
- Надо найти время: t = S : v
135 : 9 = 15 часов.
- Надо найти расстояние: S = v ∙ t
12 ∙ 4 = 48 м.
- Надо найти скорость: v = S : t
132 : 11 = 12 м/мин.
Верный ответ:
|
S |
v |
t |
|
|
1. |
135 км |
9 км/ч |
15 часов |
|
2. |
48 м |
12 м/с |
4 с |
|
3. |
132 м |
12 м/мин |
11 мин |
№2. Тип задания: единичный / множественный выбор
Выберите верный ответ к задаче:
Из пунктов А и В, расстояние между которыми 300 км, отправились одновременно навстречу друг другу мотоциклист и автомобилист. Скорость автомобиля 60 км/ч, а мотоцикла 30 км/ч. Какое расстояние будет между ними через 3 часа?
Варианты ответов:
- 70
- 30
- 270
- 240
Эта задача относится к типу задач на сближение, т.е. нам надо:
- сложить скорости мотоциклиста и автомобилиста:
60 + 30 = 90 км/ч – скорость сближения;
- узнать, сколько километров они пройдут за 3 часа вместе. Для этого:
90 ∙ 3 = 270 км;
- из общего расстояния нам осталось вычесть пройденное:
300 – 270 = 30 км
Верный ответ: 2. 30 км.
Второй закон Ньютона в импульсной форме позволяет определить, как меняется скорость тела по модулю и направлению, если в течение некоторого времени на него действует определенная сила:
Работа силы
В механике также важно уметь вычислять изменение скорости по модулю, если при перемещении тела на некоторый отрезок на него действует некоторая сила. Воздействия на тела сил, приводящих к изменению модуля их скорости, характеризуется величиной, зависящей как от сил, так и от перемещений. Эту величину в механике называют работой силы.
Работа силы обозначается буквой А. Это скалярная физическая величина. Единица измерения — Джоуль (Дж).
Работа силы равна произведению модуля силы, модуля перемещения и косинусу угла между ними:
Важно!
Механическая работа совершается, если:
- На тело действует сила.
- Под действием этой силы тело перемещается.
- Угол между вектором силы и вектором перемещения не равен 90 градусам (потому что косинус прямого угла равен нулю).
Внимание! Если к телу приложена сила, но под ее действием тело не начинает движение, механическая работа равна нулю.
Пример №1. Груз массой 1 кг под действием силы 30 Н, направленной вертикально вверх, поднимается на высоту 2 м. Определить работу, совершенной этой силой.
Так как перемещение и вектор силы имеют одно направление, косинус угла между ними равен единице. Отсюда:
Работа различных сил
Любая сила, под действием которой перемещается тело, совершает работу. Рассмотрим работу основных сил в таблице.
| Работа силы тяжести |
Модуль силы тяжести: Fтяж = mg Работа силы тяжести: A = mgs cosα |
| Работа силы трения скольжения |
Модуль силы трения скольжения: Fтр = μN = μmg Работа силы трения скольжения: A = μmgs cosα |
| Работа силы упругости |
Модуль силы упругости: Fупр = kx Работа силы упругости: |
Работа силы упругости
Работа силы упругости не может быть определена стандартной формулой, так как она может применяться только для постоянной по модулю силы. Сила же упругости меняется по мере сжатия или растяжения пружины. Поэтому берется среднее значение, равное половине суммы сил упругости в начале и в конце сжатия (растяжения):
Нужно также учесть, что перемещение тела под действием силы упругости равно разности удлинения пружины в начале и конце:
s = x1 – x2
Перемещение и направление силы упругости всегда сонаправлены, поэтому угол между ними нулевой. А косинус нулевого угла равен 1. Отсюда работа силы упругости равна:
Работы силы трения покоя
Работы силы трения покоя всегда равна 0, так как под действием этой силы тело не сдвигается с места. Исключение составляет случай, когда покоящееся тело лежит на подвижном предмете, на который действует некоторая сила. Относительно системы координат, связанной с подвижным предметом, работа силы трения покоя будет нулевой. Но относительно системы отсчета, связанной с Землей, эта сила будет совершать работу, так как тело будет двигаться, оставаясь на поверхности движущегося предмета.
Пример №2. Груз массой 100 кг волоком перетащили на 10 м по плоскости, поверхность которой имеет коэффициент трения 0,4. Найти работу, совершенной силой трения скольжения.
A = μmgs cosα = 0,4∙100∙10∙10∙(–1) = –4000 (Дж) = –4 (кДж)
Знак работы силы
Знак работы силы определяется только косинусом угла между вектором силы и вектором перемещения:
- Если α = 0о, то cosα = 1.
- Если 0о < α < 90o, то cosα > 0.
- Если α = 90о, то cosα = 0.
- Если 90о < α < 180o, то cosα < 0.
- Если α = 180о, то cosα = –1.
Работа силы трения скольжения всегда отрицательна, так как сила трения скольжения направлена противоположно перемещению тела (угол равен 180о). Но в геоцентрической системе отсчета работа силы трения покоя будет отличной от нуля и выше нуля, если оно будет покоиться на движущемся предмете (см. рис. выше). В таком случае сила трения покоя будет направлена с перемещением относительно Земли в одну сторону (угол равен 0о). Это объясняется тем, что тело по инерции будет пытаться сохранить покой относительно Земли. Это значит, что направление возможного движения противоположно движению предмета, на котором лежит это тело. А сила трения покоя направлена противоположно направлению возможного движения.
Геометрический смысл работы
Графическое определение
Механическая работа численно равна площади фигуры, ограниченной графиком с осями OF и OX.
A = Sфиг
Мощность
Определение
Мощность — физическая величина, показывающая, какую работу совершает тело в единицу времени. Мощность обозначается буквой N. Единица измерения: Ватт (Вт). Численно мощность равна отношению работы A, совершенной телом за время t:
Рассмотрим частные случаи определения мощности в таблице.
Мощность при равномерном прямолинейном движении тела |
Работа при равномерном прямолинейном движении определяется формулой: A = Fтs Fт — сила тяги, s — перемещение тела под действием этой силы. Отсюда мощность равна: |
Мощность при равномерном подъеме груза |
Когда груз поднимается, совершается работа, по модулю равная работе силе тяжести. За перемещение в этом случае можно взять высоту. Поэтому: |
Мгновенная мощность при неравномерном движении |
Выше мы уже получили, что мощность при постоянной скорости равна произведению этой скорости на силу тяги. Но если скорость постоянно меняется, можно вычислить мгновенную мощность. Она равна произведению силы тяги на мгновенную скорость: |
Мощность силы трения при равномерном движении по горизонтали |
Мощность силы трения отрицательна так же, как и работа. Это связано с тем, что угол между векторами силы трения и перемещения равен 180о (косинус равен –1). Учтем, что сила трения скольжения равна произведению силы нормальной реакции опоры на коэффициент трения: |
Пример №3. Машина равномерно поднимает груз массой 10 кг на высоту 20 м за 40 с. Чему равна ее мощность?
Коэффициент полезного действия
Не вся работа, совершаемая телами, может быть полезной. В реальном мире на тела действует несколько сил, препятствующих совершению работы другой силой. К примеру, чтобы переместить груз на некоторое расстояние, нужно совершить работу гораздо большую, чем можно получить при расчете по формулам выше.
Определения:
- Работа затраченная — полная работа силы, совершенной над телом (или телом).
- Работа полезная — часть полной работы силы, которая вызывает непосредственно перемещение тела.
- Коэффициент полезного действия (КПД) — процентное отношение полезной работы к работе затраченной. КПД обозначается буквой «эта» — η. Единицы измерения эта величина не имеет. Она показывает эффективность работы механизма или другой системы, совершающей работу, в процентах.
КПД определяется формулой:
Работа может определяться как произведение мощности на время, в течение которого совершалась работа:
A = Nt
Поэтому формулу для вычисления КПД можно записать в следующем виде:
Частые случаи определения КПД рассмотрим в таблице ниже:
Устройство |
Работа полезная и полная |
КПД |
| Неподвижный блок, рычаг |
Aполезн = mgh Асоверш. |
 |
| Наклонная плоскость |
Aполезн = mgh Асоверш. = Fl l — совершенный путь (длина наклонной плоскости). |
 |
Пример №4. Определите полезную мощность двигателя, если его КПД равен 40%, а его мощность по паспорту равна 100 кВт.
В данном случае необязательно переводить единицы измерения в СИ. Но в таком случае ответ мы тоже получим в кВт. Из этой формулы выразим полезную мощность:
Задание EF17557
Какую мощность развивает сила тяги трактора, перемещая прицеп со скоростью 18 км/ч, если она составляет 16,5 кН?
Ответ:
а) 916 Вт
б) 3300 Вт
в) 82500 Вт
г) 297000 Вт
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Записать формулу для расчета мощности.
3.Выполнить общее решение задачи.
4.Подставить известные данные и выполнить вычисления.
Решение
Запишем исходные данные:
• Сила тяги, перемещающая прицеп, равна: Fт = 16,5 кН.
• Скорость перемещения прицепа под действием силы тяги: v = 18 км/ч.
Переведем единицы измерения в СИ:
16,5 кН = 16,5∙103 Н
18 км/ч = 18000/3600 м/с = 5 м/с
Мощность равна отношению работы ко времени, в течение которого эта работа совершалась:
N=At
Но работа равна произведению силы, перемещения и косинуса угла между векторами силы и перемещения. В данном случае будем считать, что угол равен нулю, следовательно косинус — единице. Тогда работа равна:
A = Fs
Тогда мощность равна:
N=Fst=Fv=16,5·103·5=82500 (Вт)
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17574
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
|
Время движения |
Ускорение |
Модуль работы силы трения |
Алгоритм решения
1.Установить наличие и характер зависимости кинематических характеристик движения от массы тела.
2.Вывести формулу для модуля работы силы трения.
3.Установить, как изменится модуль работы силы трения при уменьшении массы тела вдвое.
Решение
При скольжении с наклонной плоскости происходит равноускоренное движение. Положение тела в любой момент времени при таком движении можно определить с помощью кинематических уравнений:
x=xo+v0xt+axt22
y=yo+v0yt+ayt22
Из этих уравнений видно, что ускорение и время никак не зависят от массы тела. Следовательно, при уменьшении массы тела в 2 раза его время движения и ускорение не изменятся.
Чтобы выразить модуль работы силы трения, выберем такую систему отсчета, чтобы вектор силы трения был расположен вдоль оси Ox.Тогда сила трения будет равна:
Fтр = μmg
Известно, что работа определяется формулой:
A = Fs cosα
Тогда работа силы трения равна:
A = μmgs cosα
Вектор силы трения всегда направлен противоположно вектору перемещения. Поэтому косинус угла между ними равен –1. Но нас интересует только модуль работы. Поэтому будем считать, что он равен:
A = μmgs
Модуль работы силы трения и масса тела зависят прямо пропорционально. Следовательно, если массу тела уменьшить вдвое, то и модуль работы силы трения уменьшится вдвое.
Поэтому правильная последовательность цифр в ответе: 332.
Ответ: 332
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18646
В первой серии опытов брусок перемещают при помощи нити равномерно и прямолинейно вверх по наклонной плоскости. Во второй серии опытов на бруске закрепили груз, не меняя прочих условий.
Как изменятся при переходе от первой серии опытов ко второй сила натяжения нити и коэффициент трения между бруском и плоскостью?
Для каждой величины определите соответствующий характер её изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждого ответа. Цифры в ответе могут повторяться.
| Сила натяжения нити | Коэффициент трения |
Алгоритм решения
- Определить, какая величина изменилась во второй серии опытов.
- Определить, как зависит от этой величины сила натяжения нити.
- Определить, как зависит от этой величины коэффициент трения.
Решение
Когда к бруску подвесили груз, увеличилась масса. Когда тело на нити перемещается вверх прямолинейно и равномерно, сила натяжения нити определяется модулем силы тяжести:
T = mg
Эта формула показывает, что сила натяжения нити и масса тела зависят прямо пропорционально. Если, добавив к бруску груз, масса увеличится, то сила натяжения нити тоже увеличится.
Коэффициент трения — это величина, которая зависит только от материалов и типа поверхности. Поэтому увеличение массы тела на него никак не повлияют.
Верная последовательность цифр в ответе: 13.
Ответ: 13
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18271
Определите коэффициент полезного действия атомной электростанции, расходующей за неделю уран-235 23592U массой 1,4 кг, если её мощность равна 38 МВт. При делении одного ядра урана-235 выделяется энергия 200 МэВ.
Алгоритм решения
1.Записать исходные данные и перевести их в СИ.
2.Записать формулу для определения КПД атомной электростанции.
3.Решить задачу в общем виде.
4.Подставить известные данные и вычислить искомую величину.
5.Массовое число: A = 235.
6.Зарядовое число: Z = 92.
Решение
Запишем исходные данные:
• Энергия, выделяемая при делении одного ядра урана-235: Q0 = 200 МэВ.
• Масса урана-235: m = 1,4 кг.
• Время, в течение которого происходит деление: t = 1 неделя.
• Мощность атомной электростанции: N = 38 МВт.
Переведем все единицы измерения в СИ:
1 эВ = 1,6∙10–19 Дж
200 МэВ = 200∙106∙1,6∙10–19 Дж = 320∙10–13 Дж
1 неделя = 7∙24∙60∙60 с = 604,8∙103 с
38 МВт = 38∙106 Вт
КПД атомной электростанции есть отношение полезной работы к выделенной за это же время энергии:
η=AполезнQ100%
Полезную работу мы можем вычислить по формуле:
A=Nt
Выделенное количество теплоты мы можем рассчитать, вычислив количество атомов, содержащихся в 1,4 кг урана-235 и умножив их на энергию, выделяемую при делении одного такого атома.
Количество атомов равно произведению количество молей на постоянную Авогадро:
Nкол.атомов = νNA
Количество молей равно отношения массы вещества к его молярной массе, следовательно:
Молярная масса численно равна массовому числу в граммах на моль. Следовательно:
M = A (г/моль) = A∙10–3 (кг/моль)
Отсюда количество атомов равно:
Энергия, выделенная всеми атомами, равна:
Теперь можем вычислить КПД:
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 12k