Лучший ответ
|
|
 |
|
геометрия — Расстояние от точки до функции
|
Необходимо написать функцию, которая вычисляет минимальное расстояние от точки p до функции $$f(x) = Asin(Bx + C) + D$$ |
Здравствуйте
Математика — это совместно редактируемый форум вопросов и ответов для начинающих и опытных математиков, с особенным акцентом на компьютерные науки.
Присоединяйтесь!
отмечен:
геометрия
×3,294
задан
21 Апр ’18 19:53
показан
808 раз
обновлен
21 Апр ’18 22:57
Связанные исследования
Связанные вопросы
Отслеживать вопрос
по почте:
Зарегистрировавшись, вы сможете подписаться на любые обновления
по RSS:
Ответы
Ответы и Комментарии
Комментарии преподавателя
Задачи на расстояние от точки до кривой
1. Опорные факты
Что такое расстояние от точки


Рис. 1. Расстояние от точки до кривой.
Видим, что задача на расстояние – это задача на экстремум, на минимум, то есть без производной не обойтись.
Вспомним, что расстояние от точки до прямой – это длина перпендикуляра (см. рис.2).
Рис. 2. Расстояние от точки до прямой.
Расстояние между прямыми – это тоже длина перпендикуляра (см. рис.3).
Рис. 3. Расстояние между прямыми.
Расстояние от точки до окружности легко найти. Нужно соединить центр с точкой 


Рис. 4. Расстояние от точки до окружности.
Расстояние между двумя окружностями, которые не пересекаются. Нужно соединить центры, получим две точки 


Рис. 5. Расстояние между двумя окружностями.
Сформулируем задачу в общем виде и напомним, каким образом ее решать. Мы повторили, что такое расстояние. Вспомним формулу расстояния между двумя заданными точками. Предположим, что на координатной плоскости даны две точки 

Рис. 6. Расстояние между двумя заданными точками.
Расстояние между точками вычисляется по формуле

Таким образом, находится расстояние между точками, если известны координаты этих точек.
2. Задача 1
На параболе 

Рис. 7. График функции
Решение.
Из простейшего анализа задачи можно увидеть, что задача имеет два решения, в силу симметрии графика функции относительно оси Y (см. рис.7).
Координаты искомой точки: 



Можно сразу использовать производную для решения задачи, но пока попытаемся воспользуемся свойствами биквадратной функции. С помощью замены переменной 



Рис. 8. Абсцисса вершины параболы.
Задача практически решена. Наименьшее значение этой функции будет тогда, когда 


Рис. 9. Схематический график функции 
Без производной, с помощью свойств квадратичной функции, решили задачу. Если 









Итак, была задача: найти точки на кривой, которые бы отстояли от начала координат на наименьшее расстояние. Такие точки найдены. Первая точка — 

Напомним ход решения задачи. Точка 




Ответ: 
3. Задача 2
На графике функции 


Сделаем рисунок (см. рис.10).
Рис. 10. График функции 
Заданы координаты двух точек: 

Найдем расстояние АМ:













Ответ: 
4. Итог
Итак, мы рассмотрели задачи на расстояние от точки до кривой. Можно находить само это расстояние, можно искать точки, которые обеспечивают минимум этого расстояния. Повторили, что такое расстояние между фигурами. Расстояние от точки до кривой – это наименьшее из расстояний, которое получается, когда точка на кривой пробегает все возможные значения. Например, точка 




Типовые задачи на производную с иррациональными функциями
5. Техника дифференцирования
Важнейшие задачи на производную с иррациональными функциями – это задачи на экстремум. Прежде всего, нужно вспомнить технику дифференцирования.
Повторим ее на следующем примере.
Дана функция 

Напомним, что 




Следующее действие – найти производную в конкретной точке.


6. Исследование функции и построение графика (задача 1)
Построить график функции 
Сначала надо попытаться все сделать без производной и понять эскиз графика функции.
1. Интервалы знакопостоянства функции.



Найдем корни (нули) функции: 

Во всех точках области определения функция положительна, значит, график будет находиться над осью 
Рис. 1. Интервалы знакопостоянства функции 
2. Построить график в окрестности каждого корня.
Функция в точке 



Рис. 2. Схематический график функции в окрестности каждого корня.
Точек разрыва нет, и когда 

Рис. 3. Схематический график функции при 
Построили эскиз графика функции.
3. Проведем исследование функции 
Приравняем производную к нулю и найдем критические точки:


Оба значения 
Найдем интервалы знакопостоянства производной. Сделаем иллюстрацию (см. рис.4):
Рис. 4. Интервалы знакопостоянства производной.
Итак, 



Таким образом, можем построить график функции 
Рис. 5. График функции 
7. Решение задачи с параметром
Дано уравнение 


Решение.
Воспользуемся графиком функции 



Ответ: При 
Итак, мы рассмотрели функцию 
8. Исследование функции и построение графика (задача 2)
Построить график функции 
Решение.
Эта функция иррациональная. Методику применяем ту же самую. Сначала попытаемся построить эскиз графика функции без производной.



Найдем нули функции.



Рис. 6. Интервалы знакопостоянства функции.
Итак, знаем, что на промежутке 



Построим график функции в окрестности каждого корня (см. рис.7).
Рис. 7. Схематический график функции в окрестности каждого корня.
Если 

Рис. 8. Эскиз графика функции 
Мы предполагаем, что на промежутке 
Проведем исследование функции с помощью производной.
Приравняем производную к нулю, получим:


Рис. 9. Интервалы знакопостоянства производной.
Осталось вычислить значение функции в точке 


Рис. 10. График функции 
Если мы провели полное исследование функции и построили график, то на любые типовые вопросы, связанные с этой функцией, мы можем получить ответы.
Например, найти все значения параметра 

Ответ: если уравнение не имеет решений, значит параметр 
Рис. 10. Множество значений функции.
Ответ: уравнение 

9. Итог
Итак, мы рассмотрели типовые задачи на производную для тех функций, в которых присутствует иррациональность. Вспомнили, как дифференцируются такие функции, каким образом исследуются функции, и как строятся графики функций.
ИСТОЧНИК
http://interneturok.ru/ru/school/algebra/10-klass/proizvodnaya/zadachi-na-rasstoyanie-ot-tochki-do-krivoy
http://interneturok.ru/ru/school/algebra/10-klass/proizvodnaya/tipovye-zadachi-na-proizvodnuyu-s-irratsionalnymi-funktsiyami
http://www.youtube.com/watch?v=iOz-YH_48GU
http://www.youtube.com/watch?v=t2tyJqTSn8U
http://znanija.com/task/2437276
https://downloader.disk.yandex.ru/disk/779ef72b0b73617de61c4dc2c21838459e86176ed8f801b37481d34346768467/56a16f54/KmTYbqVG3TgKGL9iUHPR0em0RlLtpxhP_BVgRtkosSgfwonkMOj8PI__aMfad3WZY71hHToni_M3mTC7aMwq3A%3D%3D?uid=0&filename=666.PDF&disposition=attachment&hash=RaLDsjqwggBTdSmademPwU40mOjt%2BFWdduHVDt9R80E%3D&limit=0&content_type=application%2Fpdf&fsize=8352787&hid=021760e85b03ef221c6c4091fc10c607&media_type=document&tknv=v2
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте
его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву
, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения
и указать конкретные затруднения.
Обязательно просмотрите тему
Правила данного раздела, иначе Ваша тема может быть удалена
или перемещена в Карантин, а Вы так и не узнаете, почему.
|
|
Расстояние от точки до кривой.
|
|
06/01/07 |
Пусть на плоскости точка
|
|
|
|
|
Someone |
|
||
23/07/05 |
Задача эквивалентна поиску наименьшего значение функции
|
||
|
|
|||
|
Bug |
|
|
06/01/07 |
Про это я уже думал… Поэтому и написал, что надо найти только расстояние. Т.к. этим методом мы в начале находим
|
|
|
|
|
PAV |
|
||
29/07/05 |
Если и можно, то в очень частных случаях, используя очень специальные знания о кривой. На самом деле, едиснтвенный пример, который пришел в голову — это расстояние до прямой, которое можно найти скалярным произведением на единичный вектор, ортогональный этой прямой. Другого примера, чтобы расстояние было бы найти хоть чуточку проще, чем точку, даже и не придумывается.
|
||
|
|
|||
|
Someone |
|
||
23/07/05 |
Ну, может быть, ещё окружность.
|
||
|
|
|||
|
Bug |
|
|
06/01/07 |
Про расстояние до прямой я знаю… Хотелось бы что-нибудь по сложнее. А если вид функции извесетен, то какой может быть ход решения, кроме как искать точку минимума функции расстояния? Например, если рассмотреть функцию вида
|
|
|
|
|
Gordmit |
|
||
19/06/05 |
Думаю, в этом случае вряд ли можно придумать что-то проще…
|
||
|
|
|||
|
Bug |
|
|
06/01/07 |
А если необходимо узнать, проходит ли кривая вблизи данной точки. Т.е. для заданной точки и заданного радиуса окрестности
|
|
|
|
|
ГАЗ-67 |
|
|
09/06/06 |
Тогда необходимо решить систему нелинейных уравнений .
|
|
|
|
|
Hypokeimenon |
|
|
09/11/06 |
Можно еще попытаться найти точку
|
|
|
|
|
ГАЗ-67 |
|
|
09/06/06 |
Честно говоря , я не понял условие . Пожалуйста , сформулируйте более чётко .
|
|
|
|
|
Zai |
|
||
11/04/07 |
Аналитически можно решить для полинома второго порядка с помощью формул Кардано.
|
||
|
|
|||
Модераторы: Модераторы Математики, Супермодераторы
15 мая 2014
Иногда в задаче 6 из ЕГЭ по математике вместо всеми любимых графиков функции или производной дается просто уравнение расстояния от точки до начала координат. Что делать в этом случае? Как по расстоянию найти скорость или ускорение.
На самом деле все просто. Скорость — это производная от расстояния, а ускорение — это производная скорости (или, что то же самое, вторая производная от расстояния). В этом коротком видео вы убедитесь, что такие задачи решаются ничуть не сложнее «классических» заданий 6.
Сегодня мы разберем две задачи на физический смысл производных из ЕГЭ по математике. Эти задания встречаются в части Bи существенно отличаются от тех, что большинство учеников привыкло видеть на пробниках и экзаменах. Все дело в том, что они требуют понимать физический смысл производной функции. В данных задачах речь пойдет о функциях, выражающих расстояния.
Если $S=xleft( t right)$, то $v$ мы можем посчитать следующим образом:
[v={S}’={x}’left( t right)]
Точно так же мы можем посчитать и ускорение:
[a={v}’={{S}’}’={{x}’}’left( t right)]
Эти три формулы – все, что вам потребуется для решения таких примеров на физический смысл производной. Просто запомните, что $v$ — это производная от расстояния, а ускорение — это производная от скорости.
Давайте посмотрим, как это работает при решении реальных задач.
Пример № 1
Материальная точка движется по закону:
[xleft( t right)=-frac{1}{5}{{t}^{5}}+{{t}^{4}}-{{t}^{3}}+5t]
где $x$ — расстояние от точки отсчета в метрах, $t$ — время в секундах, прошедшее с начала движения. Найдите скорость точки (в м/с) в момент времени $t=2c$.
Это означает, что у нас есть функция, задающая расстояние, а нужно посчитать скорость в момент времени $t=2c$. Другими словами, нам нужно найти $v$, т.е.
[v={S}’={x}’left( 2 right)]
Вот и все, что нам нужно было выяснить из условия: во-первых, как выглядит функция, а во-вторых, что от нас требуется найти.
Давайте решать. В первую очередь, посчитаем производную:
[{x}’left( t right)=-frac{1}{5}cdot 5{{t}^{4}}+4{{t}^{3}}-3{{t}^{2}}+5]
[{x}’left( t right)=-{{t}^{4}}+4{{t}^{3}}-3{{t}^{2}}+5]
Нам требуется найти производную в точке 2. Давайте подставим:
[{x}’left( 2 right)=-{{2}^{4}}+4cdot {{2}^{3}}-3cdot {{2}^{2}}+5=]
[=-16+32-12+5=9]
Вот и все, мы нашли окончательный ответ. Итого, скорость нашей материальной точки в момент времени $t=2c$ составит 9 м/с.
Пример № 2
Материальная точка движется по закону:
[xleft( t right)=frac{1}{3}{{t}^{3}}-4{{t}^{2}}+19t-11]
где $x$ — расстояние от точки отсчета в метрах, $t$ — время в секундах, измеренное с начала движения. В какой момент времени ее скорость была равна 3 м/с?
Взгляните, в прошлый раз от нас требовалось найти $v$ в момент времени 2 с, а в этот раз от нас требуется найти тот самый момент, когда эта скорость будет равна 3 м/с. Можно сказать, что нам известно конечное значение, а по этому конечному значению нам требуется найти исходное.
В первую очередь, вновь ищем производную:
[{x}’left( t right)=frac{1}{3}cdot 3{{t}^{2}}-4cdot 2t+19]
[{x}’left( t right)={{t}^{2}}-8t+19]
От нас просят найти, в какой момент времени скорость будет равна 3 м/с. Составляем и решаем уравнение, чтобы найти физический смысл производной:
[{{t}^{2}}-8t+19=3]
[{{t}^{2}}-8t+16=0]
[{{left( t-4 right)}^{2}}=0]
[t-4=0]
[t=4]
Полученное число означает, что в момент времени 4 с $v$ материальной точки, движущейся по выше описанному закону, как раз и будет равна 3 м/с.
Ключевые моменты
В заключении давайте еще раз пробежимся по самому главному моменту сегодняшней задачи, а именно, по правилу преобразования расстояние в скорость и ускорение. Итак, если нам в задаче прямо описан закон, прямо указывающий расстояние от материальной точки до точки отсчета, то через эту формулу мы можем найти любую мгновенную скорость (это просто производная). И более того, мы можем найти еще и ускорение. Ускорение, в свою очередь, равно производной от скорости, т.е. второй производной от расстояния. Такие задачи встречаются довольно редко, поэтому сегодня мы их не разбирали. Но если вы увидите в условии слово «ускорение», пусть оно вас не пугает, достаточно просто найти еще одну производную.
Надеюсь, этот урок поможет вам подготовиться к ЕГЭ по математике.
Смотрите также:
- Не допускайте таких ошибок, когда видите график производной в задаче 6 из ЕГЭ по математике!
- ЕГЭ 2022, задание 6. Касательная и квадратичная функция с параметром
- Схема Бернулли. Примеры решения задач
- Комбинаторика в задаче B6: средний тест
- Как решать задачи про летающие камни?
- B4: счетчики на электричество



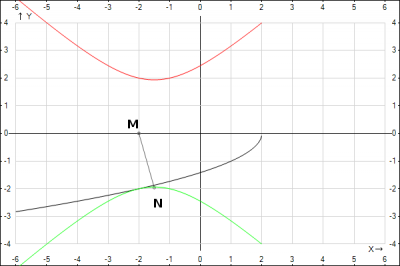






















 и кривая вида
и кривая вида .
. (или её квадрата). «Можно ли эту задачу решить аналитически для любой кривой?» Я ничего о таком не слышал.
(или её квадрата). «Можно ли эту задачу решить аналитически для любой кривой?» Я ничего о таком не слышал. , а потом расстояние
, а потом расстояние 

 , определить проходит ли кривая эту окрестность.
, определить проходит ли кривая эту окрестность. , до которой расстояние минимально, из условия
, до которой расстояние минимально, из условия