Две сосны растут на расстоянии 15 м одна от другой. Высота одной сосны — 30 м, а другой — 22 м. Чему равно расстояние между их верхушками?
Знакомая со школы теорема Пифагора поможет нам решить задачу.
Да, макушки находятся на некотором расстоянии, эту линию определить можно исходя из разницы высот сосенок, а она составляет 8 метров.
От верхушки сосны, что значительно ниже опустим перпендикуляр в направлении высокой сосны, заведомо известна его длина и это 15 метров.
Сумма квадратов этих известных величин даст : 225 + 64 = 289, извлечь корень не сложно, такие числа держим всегда в уме, заучили давненько, получается 17 метров.
Это и есть правильный ответ — расстояние между макушками — верхушками этих замечательных сосен равно 17 метрам…
система выбрала этот ответ лучшим
Валентина МД
[33.2K]
4 года назад
Мысленно можно представить прямоугольный треугольник:
расстояние между соснами один катет (а), его длина 15 метров,
разница высот у сосен — это второй катет (в), он равен 30 — 22 = 8 (м);
расстояние между вершинами сосен является гипотенузой (с) и, согласно теореме Пифагора, она равна квадратному корню из суммы квадратов катетов.
Сумма квадратов катетов = (15*15) + (8*8) = 225 + 64 = 289
Гипотенуза равна 17 метрам.
Ответ: 17 метров между верхушками сосен.
Лёля Про
[20.9K]
4 года назад
решение:
1)Если две сосны растут ровно вверх на расстоянии друг от друга, то они являются основаниями прямоугольной трапеции.
2)Расстояние между верхушками сосен, это не перпендикулярная основаниям боковая сторона прямоугольной трапеции.
Найти это расстояние, можно по теореме Пифагора:
С^2 = а^2 + в^2
С = √ (15^2 + (30-22)^2)
С = √ (225 + 64)
С = √ 289
С = 17 (м)
Ответ: 17 метров — расстояние между верхушками сосен
rodleoil2
[437K]
4 года назад
Действительно, 17 метров 
Если по действия.
расстояние по горизонтали (считая сосны прямыми) — 15 м.
Расстояние по вертикали 30 — 22 = 8 м.
Получаем прямоугольный треугольник со сторонами катетов 15 и 8 м.
Рассчитываем гипотенузу. Квадрат гипотенузы равен сумме квадратов катетов.
Гипотенуза = корень квадратный от (15^2+8^2)=корень квадратный от (225+64)=17 м
Знаете ответ?
Соединим верхушки сосен, получим трапецию, проведем от верхушки сосны высотой 18 м перпендикуляр на сосну высотой 50 м. Получили прямоугольный треугольник и прямоугольник.
Одна сторона треугольника (катет) равна 24 м, вторая (катет) 50-18=32 м
по теореме Пифагора находим гипотенузу
24^2+32^2=576+1024=1600, извлекаем корень из 1600, получаем 40.
Расстояние между верхушками составляет 40 м
Goshkawdx
+10
Решено
1 год назад
Геометрия
5 — 9 классы
Две сосны растут на расстоянии 15м друг от друга.Высота одной сосны 20м,а другой 12м.
Найдите расстояние между верхушками
Смотреть ответ

zmeura1204
20-12=8; т.Пифагора √(15²+8²)=17
Goshkawdx
Спасибо!
Ответ
4
(8 оценок)
15
ludmilaksenija2005
1 год назад
Светило науки — 9422 ответа — 0 раз оказано помощи
Ответ:
17 см
Объяснение:
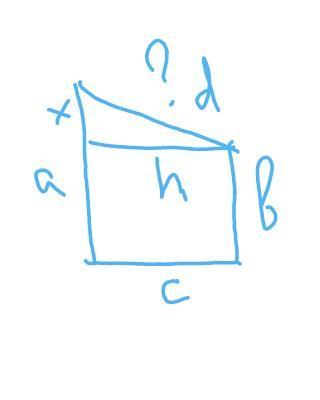
Прямоугольная трапеция
а=20 м
b=12 м
с=15 м
Найти : d
Решение :
Х=а-b=20-12=8 cм
h=c=15 cм
По теореме Пифагора :
d=корень (х^2+h^2)=
=корень (8^2+15^2)=корень 289=17 см
(8 оценок)
Остались вопросы?
Задай вопрос
Найди нужный
Новые вопросы по предмету Математика
Медіана, проведена до основи рівнобедреного трикутника дорівнює 12. Знайти бісектрису, провед до основи
Найдите длину отрезка x:
скажите пожалуйста пошагово как нужно это найти и это срочно умоляю отдаю все баллы!!!) это геометрия пожалуйста завтра сдавать надо!!!!!!!!!!! …
65, 12 37,015 48, 47 500,05
Прямая АВ -общая внешняя касательная двух окружностей с центрами О1 и 02, которые касаются внешним образом (рис. 346), точки касания прямой А и …
Найдем расстояние между верхушками двух сосен, если известно:
Растут они на расстоянии = 12 м;
Высота 1 сосны = 11 м.
Высота 2 сосны = 6 м.
1) Соединим все точки, расстояние верхушки. Получим форму в виде прямоугольной трапеции.
2) Трапеции можно разбить на прямоугольника и на прямоугольный треугольник.
3) Катет в прямоугольном треугольнике равен разнице двух сосен 11 м — 6 м = 5 м, а второй катет равен расстоянию между соснами 12 м.
4) Расстояние между верхушками равен гипотенузе прямоугольного треугольника.
5) Найдем расстояние между верхушками по теореме Пифагора.
√ (5^2 + 12^2) = √ (25 + 144) = √169 = 13 м.
Светило науки — 4 ответа — 81 помощь
расстояние между верхушками 15 метров.
рисуем трапецию: в основании расстояние между соснами 12м, одна сторона (высота 1 сосны)-15м, другая сторона (высота 2ой сосны)-6м. Теперь делим трапецию на треугольник и прямоугольник. Треугольник получился прямоугольным, а значит сумма квадратов катетов равна квадрату гипотенузы. Одна сторона треуг. = 12м, т.к она параллельна основанию трапеции. Вторая = 15м- 6м=9м.
Отсюда получаем (9 в квадрате+ 12 в Квадрате)= 81+144= 225, извлекаем кв. корень и получаем расстояние между макушками =15м
