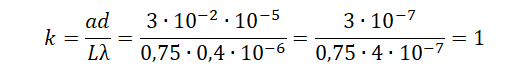google.com/+ВикторЦекунов
Репетитор по математике, физике (Минск): Виктор Иванович.
Высшая математика и физика для студентов.
Профессиональный репетитор окажет помощь в решении задач, подготовит к экзаменам. Занятия в Серебрянке, индивидуально. (90 мин)
= 20 $.
Тел: +375(29) 127 61 86.
___________________________________________________________________________________
Оказываю
платные услуги: решение задач по физике. Оплата WebMoney.
Заказы направляйте сюда: Платные услуги
___________________________________________________________________________________
5.1. Фотометрия и геометрическая оптика.
5.2. Интерференция света.
5.3. Дифракция света.
5.4. Поляризация света.
5.5. Дисперсия и поглощение света.
5.6. Оптика движущихся источников.
5.7. Тепловое излучение. Квантовая природа света.
5.1. Фотометрия и геометрическая оптика.
5.1-1. На рабочем месте для переработки с/х продуктов необходимо создать
освещенность Е=150 лк. Определить силу света лампы, подвешенной на высоте 2 м.
Решение:
E = 150 лк
R = 2 м
I – ?
Закон освещённости:
E = Icosα/R² , (1)
где α – угол между падающими
лучами и нормалью к площадке.
Если лампа висит над рабочим местом, то α = 0 и cosα = 1. Из (1) найдём силу
света I
I = ER².
I = 150·2² = 600 кд.
Ответ: I = 600 кд.
5.1-2. Как
математически записать зависимость между E и cosα, если E₀
освящёность при α=0.
Решение:
α = 0
E₀
E = f(cosα) – ?
При
освещении бесконечно малой площадки точечным источником света закон
освещённости имеет вид
E = Icosα/r², (1)
где r –
расстояние от площадки до источника света; α –
угол падения лучей на площадку (угол между падающими лучами и нормалью к
площадке, восставленной в точке падения лучей);
I –
сила света источника.
При α = 0
из (1) имеем
E₀ = Icos0/r² или (т.к. cos0 = 1)
E₀ = I/r². (2)
Разделим (1) на (2)
E/E₀ = (Icosα/r²)/(I/r²)
или E/E₀ = cosα,
отсюда E = E₀cosα.
Ответ:
E = E₀cosα.
___________________________________________________________________________________ 5.2. Интерференция света.
5.2-1.
Определить толщину воздушной прослойки между линзой и стеклянной пластинкой
там, где в отражённом свете с длиной волны λ = 600 нм видно третье тёмное
кольцо Ньютона.
Решение:
λ = 600 нм
m = 3 (тёмное кольцо)
d − ?
В отражённом монохроматическом свете с длиной волны λ радиусы r тёмных колец
Ньютона равны
(1)
где m = 0,1,2, … − номер кольца, R – радиус кривизны выпуклой поверхности
линзы, d − толщина воздушной прослойки.
Из рис. для ∆АВС по теореме Пифагора имеем:
R² = (R — d)² + r² или R² = R² — 2Rd + d² + r², отсюда
— 2Rd + d² + r² = 0.
Ввиду малости d, пренебрегаем величиной d². Тогда из последнего равенства
получим
2Rd = r².
Подставляя сюда r² из (1), получим
2Rd = mRλ, отсюда
d = ½mλ.
d = ½·3·600 = 900 нм.
Ответ: d = ½mλ = 900 нм.
5.2-2.
Найти минимальную толщину плёнки с показателем преломления 1,33, при которой
свет с длиной волны 0,64 мкм испытывает максимальное отражение, а свет с длиной
волны 0,40 мкм не отражается совсем. Угол падения света равен 30°.
Решение:
n = 1,33
λ₁ = 0,64 мкм
λ₂ = 0,4 мкм
θ = 30° (угол падения света)
dmin − ?
Условие для интерференционных максимумов отражения света с длиной волны λ₁:
(1)
(m = 0,1,2, …)
Так как в (1) величины n, θ, λ₁ постоянны, то минимальная толщина d плёнки
будет при минимальном числе m.
Условие для интерференционных минимумов отражения света с длиной волны λ₂:
(2)
(k = (1,2, …)
Так как в (2) величины n, θ, λ₂ постоянны, то минимальная толщина d плёнки
будет при минимальном числе k.
В (1) и (2) левые части уравнений равны, поэтому равны их правые части:
Подставляя сюда λ₁ = 0,64 мкм и λ₂ = 0,4 мкм, получим
(2m + 1)·0,32 = k·0,4 или
5k – 8m = 4,
отсюда выражаем k
(3)
(m = 0,1,2, …), (k = (1,2, …).
Из (3) ясно, что минимальное число k будет при минимальном числе m. Задавая m = 0,1,2, …,
по (3) вычисляем k. Результаты занесём в таблицу.
Из таблицы видно, что при минимальном числе m = 2 получили минимальное натуральное
число k = 4.
Теперь из (2) при k = 4 (или из (1) при m = 2) получаем минимальную толщину
dmin плёнки:
___________________________________________________________________________________
5.3. Дифракция света.
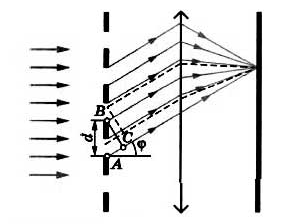
5.3-1.
Лучи
света с длиной волны λ = 600 нм падают на дифракционную решетку под углом ϕ = 30⁰ к
нормали. За решеткой последний максимум виден под углом α.
Найти sinα, если
постоянная решетки равна d = 21 мкм.
Решение:
λ = 600·10⁻⁹ м
ϕ = 30⁰
k = max
d =
21·10⁻⁶ м
sinα − ?
При наклонном падении света на дифракционную решётку условие для главных
максимумов имеет вид:
d(sinα – sinϕ) = kλ, (1)
где ϕ –
угол падения света; α – угол дифракции; k = 0,
±1, ±2, … – порядок максимума.
Из (1) выражаем
sinα = kλ/d + sinϕ. (2)
Так как -1 ≤ sinα ≤ 1,
то по (2)
-1 ≤ kλ/d + sinϕ ≤ 1,
или -1 ≤ k·600·10⁻⁹/(21·10⁻⁶)
+ sin30⁰ ≤
1, или
-1 ≤ k/35 +
0,5 ≤ 1 (вычтем 0,5). Тогда
-1,5 ≤ k/35 ≤
0,5 (умножим на 35). Тогда
-52,5 ≤ k ≤
17,5, (k −
целые).
Отсюда последний максимум достигается при k = —
52. Тогда
из (2) находим
sinα = — 52·600·10⁻⁹/(21·10⁻⁶) + 0,5 = — 0,9857.
Ответ: sinα = — 0,9857.
5.3-2.
На дифракционную решетку с периодом 14 мкм падает нормально монохроматическая
световая волна. На экране, удалённом от решетки на 2 м, расстояние между
спектрами второго и третьего порядков 8,7 см. Какова длина волны падающего
света?
Решение:
d =
14·10⁻⁶ м
L = 2 м
k₂ = 2
k₃ = 3
x =
8,7·10⁻² м
λ − ?
Условия главных фраунгоферовых максимумов для дифракционной решётки при
нормальном падении света:
dsinθ = kλ, k = 1,
2, 3, … ;
Отсюда для порядков k₂ и k₃ имеем два уравнения
dsinθ₂ = k₂λ (*)
dsinθ₃ = k₃λ. (**)
Так как углы θ₂ и θ₃
малы, то sinθ₂ ≈ tgθ₂ = x₂/L и sinθ₃ ≈ tgθ₃ = x₃/L (см.
рис.). Тогда (*) и (**) примут вид
dx₂/L = k₂λ
dx₃/L = k₃λ,
отсюда
x₂ = k₂λL/d и x₃ = k₃λL/d.
Расстояние x между
спектрами второго и третьего порядков (см. рис.):
x = x₃ — x₂ или x = k₃λL/d — k₂λL/d,
отсюда находим длину волны λ света
λ = xd/( L(k₃ — k₂) ).
λ =
8,7·10⁻²·14·10⁻⁶/( 2· (3 — 2) ) = 6,09·10⁻⁷ м.
Ответ: λ = xd/( L(k₃ — k₂) ) = 6,09·10⁻⁷ м.
___________________________________________________________________________________ 5.4. Поляризация света.5.4-1. Чему
равна степень поляризации Р света, представляющего собой смесь естественного
света с плоскополяризованным, если отношение интенсивности поляризованного
света к интенсивности естественного равна 10?Решение:
η = Iпол/Iест = 10
P − ?
Степень поляризации P света:
P = (Imax – Imin)/(Imax + Imin), (1)
где Imax, Imin –
максимальная и минимальная интенсивности света, прошедшего через анализатор.
Известно, что естественный свет, пройдя через анализатор (поляризатор),
уменьшает свою интенсивность в два раза, т.е.
I₁ = Iест/2,
(2)
где I₁ –
интенсивность естественного света, прошедшего анализатор.
Имеем
Imax = Iпол + I₁ = Iпол + Iест/2;
Imin = I₁ = Iест/2.
Подставим Imax и Imin в (1)
P = (Iпол + Iест/2
– Iест/2)/(Iпол + Iест/2
+ Iест/2)
или
P = (Iпол)/(
Iпол + Iест) =
(Числитель и знаменатель разделим на Iест) = (Iпол/Iест)/(Iпол/Iест + 1).
P =
η/(η + 1).
P = 10/(10 + 1) = 0,909.
Ответ: P = η/(η + 1) = 0,909.
_______________________________________________________________________________________________
Примеры решения задач к теме
8.3 Дифракция света Основные формулы и методические указания
1.
Радиусы зон Френеля для сферической
поверхности световой волны, испускаемой
точечным изотропным источником
,
определяется формулой:
, (8.
3. 3)
где –
радиус внешней границы‑той
зоны;
–
радиус волновой поверхности;
–
расстояние от вершины волновой поверхности
до точки наблюденияР,
для которой построены зоны Френеля.
2.
Для дифракции в параллельных лучах от
одной щели положение минимумов
освещенности на экране определяется
углом
от нормали к плоскости щели и удовлетворяющим
условие
,
где –
ширина щели;
–
длина световой волны;
–
порядок минимумов.
При
нормальном падении света на дифракционную
решетку положение главных максимумов
интенсивности света определяется углами
,
от нормали плоскости решетки и выражаются
формулой
,
, (8.
3. 4)
где –
постоянная (период) решетки, равная
расстоянию между серединой двух соседних
щелей;
—
порядок соответствующего максимума.
В
явлении дифракции света волны огибают
оптические неоднородности на пути
распределения света. Попадая на экран,
волны дают распределение интенсивности
света на нем вследствие интерференции.
В
случае дифракции в параллельных лучах
от одной щели для максимумов интенсивности
света на экране не существует столь
простого соотношения, как (8.3.2), определяющая
положение дифракционных минимумов.
Иногда пишут формулу
где –
угол соответствующий дифракционному
максимуму–ого
порядка.
Однако,
эта формула неточная: она дает завышенные
значения для угла
.
Так ошибка придля
составляет около 5%, при увеличении
ошибка убывает.
Решение задач
З а д а ч а 8. 3. 1
На непрозрачную пластину с круглым
отверстием (дифракция Френеля) радиуса
мм
падает нормально параллельный пучок
монохроматического света снм.
На пути лучей, проходящих через отверстие,
помещен экран, на котором наблюдается
дифракционная картина. При каком
минимальном расстоянии между пластиной
и экраном, превышающем 20 см, в центре
экрана будет наблюдаться темное пятно?
|
Дано:
|
Решение
Расстояние |
|
|
Рис. 8.6 |
Френеля,
укладывающихся в отверстие: если число
зон
– четное, то в центре – темное пятно.
Если в отверстие укладываетсязон Френеля (рис. 8.6), то расстояние
от центра экрана 0 до края отверстия набольше, чем расстояние между центром
экрана и центром отверстия –.
Теорема
Пифагора дает (см. рис. 8.6)
или
.
Выражение
и им можно пренебречь, поэтому
и
(1)
Так
как значение
должно быть четным,
,
то значения,
при которых в центре экрана будет темное
пятно соответственно равны
м,
м,
м,
м.
Последнее
расстояние
(при
)
меньше 20 см и поэтому не удовлетворяет
условию задачи. Прионо будет еще меньше. Следовательно,
искомым минимальным расстоянием будет
значение(при
)
м.
Ответ:
м.
З а д а ч а 8. 3. 2
Между точечным монохроматическим
источником света с
мкм
и экраном поместили диафрагму с круглым
отверстием радиусамм.
Расстояние от диафрагмы до источника
и экрана равны соответственном
им.
Как изменится интенсивность света в
точке Р, если диафрагму убрать?
|
Дано: |
Решение |
|
|
|
Рис. 8. |
В |
|
|
В
зависимости от числа зон Френеля,
укладывающихся в поверхности волнового
фронта радиуса
,
ограниченного краями отверстия, в центре
экрана (в точке Р) будет темное или
светлое пятно. Четному числу зон Френеля
соответствует темное пятно, нечетному
– светлое. Найдем это число.
Полагая
в формуле (8.3.3) величину
равной радиусу
,
получим
.
Следовательно,
в точке Р – светлое пятно.
Далее
заметим, что в силу
и
колебания светового вектора Е, приходящие
в точку Р от каждой из трех зон Френеля
имеют приблизительно одинаковые
амплитуды. При этом колебания, приходящие
от любых двух соседних зон, будучи в
противофазе, гасят друг друга и весь
эффект сводится к действию всего лишь
одной зоны, например, первой. И поскольку,
когда диафрагма отсутствует, то действие
всей волны равно половине действия
первой зоны Френеля. Следовательно,
изъятие диафрагмы приведет к уменьшению
амплитуды световых колебаний в точке
Р в два раза. Так как интенсивность света
пропорциональна квадрату амплитуды
световых колебаний, то она уменьшится
в четыре раза.
Ответ:
.
З а д а ч а 8. 3. 3
На прямоугольную щель нормально к ее
плоскости падает параллельный пучок
монохроматического света (дифракция
Фраунгофера); расположенная за щелью
линза с фокусным расстоянием
м
проецирует на экран дифракционную
картину в виде чередующихся светлых и
темных полос. Ширина центральной светлой
полосысм.
Как надо изменить ширину щели, чтобы
центральная светлая полоса заняла весь
экран (при любой ширине)?
|
Дано:
|
Решение
Рис. 8. |
|
|
Изображенная
на рис. 8.8 кривая показывает распределение
интенсивности света на экране.
Центральная
светлая полоса на экране заключена
между двумя минимумами первого порядка.
Ее ширина
зависит от угла
,
соответствующего минимуму первого
порядка. Уголсвязан с шириной
формулой (8.3.4), где
.
И так как при изменении ширины щели отдо
,
и
остаются
постоянными, то из (8.3.4) следует:
, (1)
где и
–
углы соответствующие первым дифракционным
минимумам, которые соответствуют
размерам щелии
.
Так
как угол
весьма мал (из условия задачи), то
.
Для того, чтобы центральная полоса
занимала весь экрандолжен стремиться к 90°,
так что
.
Следовательно,
с учетом сказанного, из (1) находим
.
Таким
образом, ширину щели следует уменьшить
в 80 раз.
Ответ:
.
З а д а ч а 8. 3. 4
На дифракционную решетку нормально к
ее поверхности падает свет от газоразрядной
трубки, наполненной гелием. Под углом
совпадают красная (
м)
и голубая (м)
линии. Определить максимальный порядок
красной линии ()
в спектре этой решетки, если главное
фокусное расстояние собирающей линзы,
проектирующей спектр на экранм,
а границами видимого спектра испускания
гелия являются фиолетовая см
и красная см
линии. Чему равно расстояние(в мм) между спектрами первого и второго
порядков на экране?
|
Дано:
|
Решение
Рис. 8.9 |
|
|
1)
Прежде всего необходимо найти постоянную
дифракционной решетки ,
которую можно рассчитать, зная номера
спектров красной или голубой линий,
совпадающих между собой. Условием
совпадения является равенство углов,
под которыми видны эти линии в
перекрывающихся спектрахIII
и IV
порядка, и следовательно
Þ
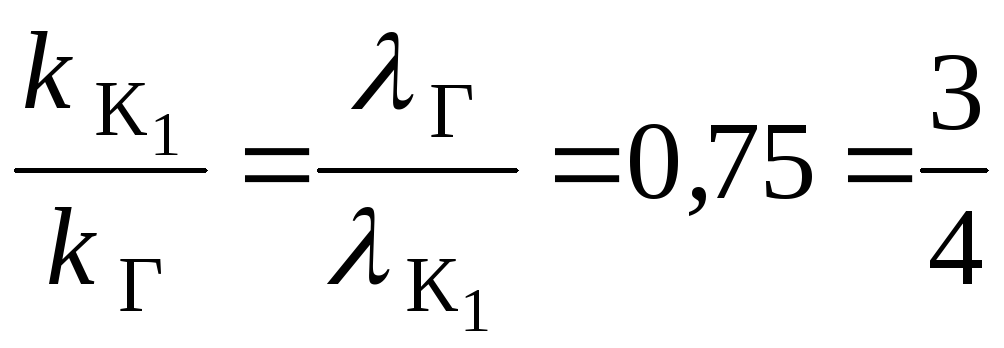
Значит
;
.
Таким
образом
м.
2)
Из основной формулы дифракционной
решетки найдем максимальный порядок
красной линии (м):
,
откуда

Так
как
–
может быть только целым числом, то,
для,
что невозможно. Следовательно, в спектре
испускания гелия с помощью данной
решетки можно наблюдать пять порядков
линий красного цвета см.
3)
Для определения расстояния между
спектрами 1-го и 2-го порядков найдем
углы
в спектре 1-го порядка и
в спектре 2-го порядка (границ спектров):
Þ
Þ
Искомое
расстояние (рис. 8.9) между спектрами
1-го и 2-го порядков равно
м
мм.
Ответ:
,
мм.
З а д а ч а 8. 3. 5
На дифракционную решетку нормально к
ее поверхности падает параллельный
пучок монохроматических лучей с
м.
Период решетким.
Определить число главных минимумов,
которое дает эта решетка, а также
максимальный уголотклонения лучей, соответствующих
последнему дифракционному максимуму.
|
Дано:
|
Решение
Из
|
|
|
Но
–
целое число, следовательнонадо округлить до целого числа. Округлить
донельзя, так как при этом окажется, что
,
чего быть не может. Поэтому округляем
до.
Таким
образом, по обе стороны от центрального
максимума, которому соответствует
,
будет наблюдаться поглавных максимумов. Так что, число
главных максимумов, которое дает эта
решетка (включая центральный) равно
.
Максимальное
значение угла
найдем из условия (8.3.5), полагая в нем
:
откуда .
Ответ:
,
.
Соседние файлы в папке Кононенко_Зеневич Методич. указания
- #
13.02.20164.13 Кб37._MU KZ (chast 3, page 23).doc
- #
13.02.20164.1 Кб31._MU KZ(chast 3, page 03_23).doc
- #
13.02.20164.1 Кб39._МУиКЗ по ФИЗИКЕ, часть1.doc
- #
- #
- #
Время на прочтение
7 мин
Количество просмотров 6.9K
В первой части мы взяли в руки молоток (спектр матрицы Грина) и опробовали его на паре гвоздей (наборе из трех точек). Пока я возился с этими спектрами, возникло предложение к производителям строительных рулеток. Надо с обратной стороны измерительной ленты добавить параболическую шкалу (сантиметры в квадрате). Поскольку квадраты расстояний здесь просто кишат, а обычные (линейные) расстояния выглядят жалким частным случаем. При строительстве дачи такой рулеткой можно будет проверять прямоугольность углов, ну и прочие инварианты для расстояний между точками в пространстве и на плоскости.
Спектры вершин правильных многоугольников и многогранников
Спектр вершин равностороннего треугольника логично обобщить на спектры вершин правильных многоугольников в целом.
Пусть вершины правильного многоугольника вписаны в окружность радиуса R. Центр собственной системы координат (центроид) будет расположен в центре окружности. Поскольку все вершины находятся на одной плоскости, то количество собственных значений спектра будет равно 2. Также очевидно, что собственные значения должны быть равны ввиду симметрии.
Согласно формуле (2.2) из первой части сумма собственных чисел спектра равна сумме квадратов расстояний от центроида до вершин, — то есть равна произведению количества вершин на квадрат радиуса окружности. В итоге получаем выражение для собственных значений правильных многоугольников:
Попутно отметим один из инвариантов — для правильного n-угольника существует простое выражение для суммы квадратов расстояний между заданной вершиной и остальными:
(Для контроля данного инварианта при проектировании n-угольной беседки и пригодилась бы параболическая рулетка).
Для вывода формулы спектра правильных многогранников, вписанных в сферу радиуса R, можно использовать рассуждения, аналогичные приведенным выше. Отличие лишь в том, что собственных чисел в пространстве три, поэтому и делить спектральную сумму надо на три:
Как известно, существует лишь 5 типов правильных многогранников с количеством вершин (4, 6, 8, 12 и 20). Но формула (4.7) сама по себе никаких ограничений на набор вершин не накладывает. Соответственно, формула применима не только к правильным многогранникам, но и к любым симметричным, вершины которых расположены на сфере. В качестве примера такого многогранника можно привести куб (8 вершин), дополненный вершинами в центре граней, вынесенными на сферу (ромб — 6 вершин). Итого получаем симметричный многогранник из 14 вершин, для которого формула (4.7) должна быть применима (автор не проверял).
5. Спектры решеток
Решетки встречаются в нашей жизни чаще, чем многогранники (к сожалению, конечно).
Выражения для спектров решеток единичной постоянной
Простейшей невырожденной решеткой является набор точек (узлов), расположенных на одинаковом расстоянии друг от друга на одной прямой. Расстояние между узлами решетки называют постоянной решетки. Для простоты вначале рассмотрим решетки с постоянной равной 1.
Спектр одномерной решетки будет содержать только одно собственное значение. Формальный вывод значения спектра оставим читателям, здесь приведем конечный ответ. Собственное значение одномерной решетки кубично зависит от количества узлов решетки:
Степенью в скобках обозначены убывающие степени:
Собственное значение одномерной 1-решетки в том или ином виде входит в многомерные спектры решеток. Поэтому дадим ему специальное обозначение g(n), название — базовый, и приведем таблицу первых значений:
Спектр квадратной решетки содержит два одинаковых собственных значения. Выражается через базовый:
Здесь n — размер решетки (количество точек) в одном направлении.
Аналогичным образом для получения спектра кубической решетки надо спектр квадратной умножить на n. Общая формула спектров 1-решеток размерности d:
Если решетка содержит разное количество узлов по различным измерениям (что возможно для двух и более мерных решеток), то собственные значения спектра в общем случае будут неравны. Для прямоугольной решетки на плоскости с размерами (k:l) собственные числа имеют вид:
Например, для спектра решетки размером (3:2) получаем:
Подобные формулы имеют место и для трехмерной (кубической) решетки размером (k:l:m):
Наблюдаем перестановки.
По формулам (5.4), (5.5) можно определить среднее значение квадрата расстояний между узлами регулярной решетки (радиус) — сумма собственных чисел спектра.
Учитываем размер ячейки решетки
Для полноты картины хорошо бы выяснить, как на спектр влияют размеры ячейки (постоянной) решетки. Из соображений размерности логично предположить, что постоянная решетки должна входить в формулу для собственных значений как квадрат. Так и есть на самом деле:
Если ячейка решетки не квадратная, а прямоугольная (разные постоянные решетки для каждого направления), то и собственные числа будут отличаться. Для каждого измерения — своя постоянная решетки. Например, для прямоугольной решетки размерами a и b собственные числа будут иметь вид:
Если и ячейка решетки, и сама решетка являются несимметричными, то для вычисления собственных значений такой решетки необходимо следить в формулах за порядком измерений и размеров решетки. Например, собственные значения двумерной решетки размером (k:l) с прямоугольной ячейкой размера a x b выражаются формулой:
Здесь порядок размеров и размерностей важен, — размер a задает длину ячейки решетки в направлении k, а размер b в направлении l. Видна связь двумерного спектра с одномерным, — спектр одной мерности умножается на количество точек другой.
Аналогично будут выглядеть и формулы для 3-мерной решетки с учетом размера ячейки abc:
Псевдорешетки
Под двумерной псевдорешеткой здесь понимается совокупность двух одномерных, расположенных перпендикулярно друг к другу и пересекающихся в центре (образуют крест). Присоединяя к данной решетке еще одну одномерную по другой координате (перпендикулярно первым двум), получаем трехмерный крест (псевдорешетку).
Собственные числа спектра псевдорешеток определяются спектром одномерной решетки. Отличие лишь в количестве (размерности). Для двумерной решетки имеем два отличных от нуля собственных числа, для трехмерной — три:
Здесь n — количество узлов по одной координате (в одном из направлений). (5.6) выражает спектр координатных осей.
6. Сложение наборов
Сложные конфигурации наборов точек удобно разбивать на несколько простых. Поэтому критическим (важным) для спектрального анализа наборов расстояний является рассмотрение вопроса о спектрах объединения — как ведут себя спектры нескольких наборов.
Прежде всего отметим, что сложение любого набора с самим собой просто удваивает значение спектра (поскольку удваивается кратность точек набора).
Обратимся к спектрам решеток. Решетки удобны тем, что имеют относительно простые выражения для значений спектра. Это позволяет рассчитывать на получение явных формул для спектров сложения решеток.
Возьмем для простоты одномерную решетку. Объединим решетку с собой и начинаем сдвигать одну относительно другой. Как поведет себя собственное значение? Выражение для спектра двух одномерных решеток, состоящих из n узлов, с постоянной a, сдвинутых относительно друг друга на расстояние d имеет вид:
Убедиться в правильности формулы (6.1) можно тут.
Во-первых, очевидно, что при сдвиге на половину постоянной (d = a/2) должны получить значение спектра одномерной решетки, постоянная которой вдвое меньше постоянных складываемых решеток. Сравнивая (6.1) и (5.5′), получаем полезный функциональный инвариант для базового спектра g(n) и убеждаемся в его справедливости:
Во-вторых, при сдвиге на (d = na) должны получить значение спектра одномерной решетки с удвоенным количеством узлов. Отсюда получаем еще один решеточный инвариант, который также справедлив:
Итак, видим, что результирующее значение спектра объединения двух наборов может быть выражено как сумма трех членов — два из них представляют собой спектры индивидуальных наборов, а третий — спектр между наборами (взаимный спектр).
Проверим данное утверждение еще на одном примере. Будем объединять одномерные спектры с разной постоянной решетки. Фактически получим набор точек на прямой, отображающих частоту биений. Некоторые точки могут совпадать (кратность 2), и для простоты примем, что два набора выровнены по одной их крайних точек (начала совпадают).
Надо сказать, что значения объединенного спектра разных частот выглядят довольно загадочно.
Например, объединяя решетки из 5 точек, получаем следующие значения (в скобках через двоеточие приведены постоянные решеток):
Поскольку спектры индивидуальных решеток известны, то можем вычленить спектр взаимодействия и найти его явное выражение:
То есть выражение для взаимного спектра (в данном контексте — спектра квадрата расстояния) между наборами, состоящими из одномерных решеток разных постоянных (но одного размера) имеет вид:
Это выражение нами просто подобрано. Можно ли его вывести каким-либо образом из начальных данных, матрицы взаимных расстояний — вопрос открытый.
Рассмотрим еще одно объединение наборов, но уже не связанных с декартовыми решетками. Будем раздвигать в пространстве два множества из трех равноудаленных точек. В итоге получим вершины некой треугольной призмы с высотой h. Ожидаем, что в спектре появится 3-е собственное число (пространство). Его значение будет определяться размером высоты (взаимного удаления вершин двух равносторонних треугольников). Первые два значения спектра просто удваиваются:
В этом примере видим, что взаимный спектр также может быть выделен, как и спектры исходных наборов. В данной конфигурации значение взаимного спектра формирует новое собственное число (измерение).
Опять передышка
Выше рассмотрены спектры декартовых (прямоугольных) решеток, — все прочие типы оставим за скобками. Спектры таких решеток имеют явные и простые выражения.
Также просты спектры правильных многоугольников и многогранников.
Для куба и квадрата пересекаются со спектрами решеток.
Куб можно рассматривать как правильный многогранник с 8 вершинами, так и как кубическую решетку размеров (2:2:2). Отсюда вытекает формула связи между постоянной куба и радиусом его описанной окружности:
Решетки существуют не только в физическом пространстве. Временные отсчеты (такты, ритмы) — пример одномерной временной решетки.
Важным является расчет взаимного спектра двух множеств. Это позволяет выражать спектры сложных конфигураций через простые.
Для проверки приведенных формул понадобятся математические библиотеки (NumPy для Питона вполне подойдет).
Продолжение
Тема: Найти угловое расстояние между линиями (Прочитано 2841 раз)
0 Пользователей и 1 Гость просматривают эту тему.
5.105. Минимальное значение угловой дисперсии некоторой дифракционной решётки D=1,266∙10-3 рад/нм. Найти угловое расстояние между линиями с l1=480 нм и l2=680 нм в спектре первого порядка. Сделать рисунок.
Записан
Угловое расстояние между линиями [Delta varphi = {varphi _2} — {varphi _1}.]
Угловая дисперсия [D = frac{m}{{d cdot cos varphi }}.]
В спектре первого порядка m = 1, следовательно минимальная угловая дисперсия [{D_{min }} = frac{1}{d},] так как максимальное значение [cos varphi = 1.]
Постоянная решетки [d = frac{1}{{{D_{min }}}}.]
Формула дифракционной решетки [d cdot sin varphi = m cdot lambda ] и для m = 1
[d cdot sin {varphi _1} = {lambda _1}] или [frac{1}{{{D_{min }}}} cdot sin {varphi _1} = {lambda _1}]
[frac{1}{{{D_{min }}}} cdot sin {varphi _2} = {lambda _2}]
[{varphi _1} = arcsin left( {{lambda _1} cdot {D_{min }}} right) = arcsin left( {480 cdot {{10}^{ — 9}} cdot 1,266 cdot {{10}^6}} right) = {37,37^0}, ]
[{varphi _2} = arcsin left( {{lambda _2} cdot {D_{min }}} right) = arcsin left( {680 cdot {{10}^{ — 9}} cdot 1,266 cdot {{10}^6}} right) = {59,41^0},]
[{varphi _2} — {varphi _1} = {22^0}.]
Ответ: 220.
« Последнее редактирование: 12 Апреля 2017, 12:45 от alsak »
Записан
Дифракция — явление, присущее всем волновым процессам подобно интерференции. Чтобы лучше понять, в чем заключается явление дифракции света, сначала рассмотрим дифракцию механических волн.
Дифракция механических волн
Иногда на пути волны встречаются препятствия разных размеров. Если препятствия небольшие, волны легко их огибают и смыкаются за ними. Поэтому морские волны свободно огибают выглядывающие из воды камни и распространяются за ними так, как если бы их не было совсем. Если размер препятствия больше длины волны, за ним образуется «тень» — область, в которую волны проникнуть не могут.
На рисунке ниже видно, что за мелкими камнями волны распространяются так же, как если бы их не было. Но за большой глыбой поверхность воды спокойная — волны в эту область не проникают.
Внимание! Малыми препятствиями будем считать те, размеры которых намного меньше длины распространяющейся волны или сравнимы с ней.
Способность волн огибать препятствия является следствием отклонения распространения волн от их прямолинейного распространения. Такой способностью обладают не только волны на поверхности воды, но и звуковые волны. Вы услышите, как сигналит автомобиль за домом, который стоит между ним и вами препятствием именно благодаря дифракции. Звуковая волна обогнет дом и продолжит распространяться за ним. По этой же причине в лесу так далеко распространяется клик «Ау!» — деревья для звуковой волны не являются серьезным препятствием, и она их легко огибает.
Дифракция — явление отклонения от прямолинейного распространения волн.
Дифракция волн проявляется особенно отчетливо в случаях, когда размеры препятствий меньше длины волны или сравнимы с ней. Это явление встречается в природе, но его также можно вызвать искусственно. К примеру, дифракцию волн на поверхности воды можно наблюдать, налив воду в ванночку и поставив на пути возбуждаемых волн искусственное препятствие.
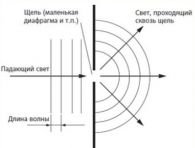
Если на пути распространения волн поставить экран с узкой щелью, размеры которой меньше длины волны, то увидим, что за ней начинает распространяться круговая волна. Такая же волна получилась, если бы в щели экрана находилось колеблющееся тело — источник волн.
Если же на пути распространения волны поставить экран с широкой щелью, за ним будет распространяться волна почти такой же формы. Волновая поверхность в этом случае искривляется только по краям щели.
Понять, почему появляется явление дифракции волн, помогает принцип Гюйгенса. Согласно ему, каждая точка волновой поверхности является источником вторичных волн. Вторичные волны, испускаемые участками среды, проникают за края препятствия, расположенного на пути распространения волны.
Дифракция световых волн
Если свет — это волна, то ему тоже должно быть присуще явление дифракции. Однако наблюдать дифракцию света сложно. Ведь дифракцию можно наблюдать тогда, когда препятствие сравнимо с длиной волны или меньше ее. А длина световой волны очень мала. Поэтому чтобы наблюдать дифракцию света, нужны очень малые препятствия.
Дифракция света на узкой щели
Наблюдать отклонение от прямолинейного распространения света можно, если пропустить пучок световых волн через узкую щель. При этом светлое пятно на экране будет больше, чем сама щель. Это возможно только в случае, если свет отклоняется от своего прямолинейного распространения.
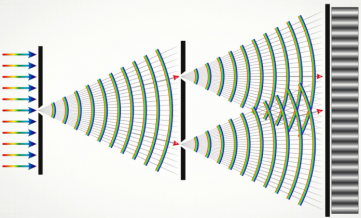
Опыт Юнга
В 1802 г. Т. Юнг, который открыл интерференцию света, поставил классический опыт по наблюдению дифракции. В непрозрачной ширме он проколол булавкой два небольших отверстия В и С на малом расстоянии друг от друга. Эти отверстия он осветил узким световым пучком, прошедшим через малое отверстие А в другой ширме. Именно эта деталь, до которой очень трудно было додуматься в то время, определила успех эксперимента. Интерферируют ведь только когерентные волны. Возникшая в соответствии с принципом Гюйгенса сферическая волна от отверстия А вызвала в отверстиях В и С образование когерентных источников световых волн. Вследствие дифракции от отверстий В и С выходили два световых конуса, которые частично перекрывались. В результате интерференции этих двух световых волн на экране появлялись картина, состоящая из чередующихся светлых и темных полос.
Закрыв одно из отверстий, Юнг обнаружил, что интерференционные полосы исчезали. Именно с помощью этого опыта впервые ученый измерил длины волн, соответствующие световым лучам разного цвета. И ему удалось сделать это с высокой точностью.
Принцип Гюйгенса — Френеля
Исследование дифракции завершил французский ученый О. Френель. Он занимался детальным исследованием различных случаев дифракции, что позволило ему разработать количественную теорию дифракции. Она помогла физику получить точные расчеты дифракционной картины, которая возникала при огибании светом различных препятствий. Френелю также удалось впервые объяснить, почему в однородной среде свет распространяется прямолинейно.
Успех Френеля объясняется тем, что он стал первым, кто решил объединить принцип Гюйгенса с идеей интерференции вторичных волн. В результате зародилась теория, которая получила название принципа Гюйгенса — Френеля:
Волновая поверхность в любой момент времени представляет собой не просто огибающую вторичных волн, а результат их интерференции.
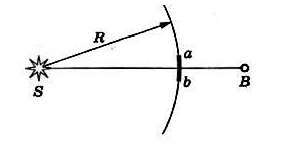
Чтобы вычислить амплитуду световой волны в любой точке пространства, необходимо мысленно окружить источник света замкнутой поверхностью. Интерференция волн от вторичных источников, расположенных на этой поверхности, определяет амплитуду колебаний в рассматриваемой точке пространства. Такие расчеты дали объяснение тому, как свет от точечного источника S, являющегося источником сферических волн, достигает любой точки В пространства.
Если рассмотреть вторичные источники на сферической волновой поверхности радиусом R, то результат сложения вторичных волн от этих источников в точке В оказывается таким, как если бы только вторичные источники на малом сферическом сегменте ab посылали свет в точку В. Вторичные волны, распространяющие от источников, расположенных на остальной части поверхности, гасят друг друга в результате сложения. Поэтому все происходит так, как если бы свет распространялся вдоль прямой SB, т. е. прямолинейно. Эта теория Френеля доказала закон прямолинейного распространения света в однородной среде и позволила рассмотреть дифракцию с количественной точки зрения.
Внимание! Закон прямолинейного распространения света и другие законы геометрической оптики выполняются достаточно точно лишь в том случае, если размеры препятствий на пути распространения света много больше длины световой волны.
Дифракционные картины от различных препятствий
Расчеты Френеля получили экспериментальное подтверждение. Из-за малой длины световой волны угол ее отклонения от прямолинейного направления распространения небольшой. Поэтому наблюдать дифракцию можно только при использовании очень маленьких препятствий. Другой вариант наблюдения этого явления — расположение экрана вдали от препятствия.
Так, чтобы наблюдать дифракцию при расстоянии между экраном и препятствием в 1 м, размеры этого препятствия должны составлять сотые доли миллиметра. Если расстояние от препятствия до экрана увеличить до нескольких сотен метров, то размеры препятствия могут быть несколько сантиметров. Если расстояние между экраном и препятствием будет составлять несколько километров, дифракцию можно будет наблюдать при размерах препятствия в несколько метров.
Дифракционная картина — картина на экране, полученная в результате интерференции вторичных световых волн.
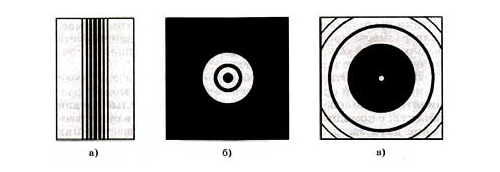
Подобную картину вы уже видели на картинке, иллюстрирующей опыт Юнга. Так, дифракционная картина от двух малых щелей — это чередующиеся темные и светлые полосы. Если использовать другие препятствия, картина будет меняться. На рисунке ниже схематично показаны дифракционные картины от различных препятствий: а — от тонкой проволочки; б — от круглого отверстия; в — от круглого экрана.
Вместо тени проволочка оставляет на экране светлые и темные полосы. В центре дифракционной картины, полученного от отверстия, появляется темное пятно, окруженное светлыми и темными кольцами. В центре тени, образованной круглым экраном, видно светлое пятнышко, а сама тень окружена темными кольцами. Если изменять диаметр отверстия, в центре дифракционной картины можно получить как светлое, так и темное пятно, окруженное либо темными, либо светлыми кольцами соответственно.
Дифракционная решетка
Дифракционная решетка — оптический прибор, принцип действия которого основан на явлении дифракции.
Дифракционная решетка представляет собой совокупность большого числа очень узких щелей, разделенных непрозрачными промежутками. Ее изготавливают путем нанесения на стекло штрихов. Их число может доходить до нескольких тысяч на 1 мм. Общее их число часто превышает 100 тысяч. Решетку также можно получить из металла, на котором чередуются участки, отражающие и рассеивающие свет.
Условные обозначения:
- a — ширина прозрачных щелей (отражающих полос);
- b — ширина непрозрачных промежутков (рассеивающих полос);
- d — период дифракционной решетки.
Период дифракционной решетки равен сумме ширины прозрачных щелей и ширины непрозрачных промежутков:
d=a+b
Внимание! Обычно изготавливают дифракционные решетки с периодом в 10 мкм.
Пусть на дифракционную решетку с периодом d падает плоская монохроматическая волна, длина волны которой составляет λ.
При этом вторичные источники, расположенные в щелях решетки, создают световые волны, распространяющиеся по всем направлениям. Найдем условие, при котором идущие от щелей волны усиливают друг друга (складываются). Для этого рассмотрим волны, распространяющиеся в направлении под углом φ к дифракционной решетке.
Разность хода между волнами от краев соседних щелей равна длине отрезка АС. Если на этом отрезке вмещается целое число длин волн, то волны от всех щелей при сложении будут усиливать друг друга. Из треугольника АВС найдем длину катета АС:
AC=ABsinφ−dsinφ
При этом максимумы будут наблюдаться под углом φ в соответствии с условием:
dsinφ=±kλ
где величина k = 0, 1, 2, … определяет порядок спектра.
Нужно учитывать, что при выполнении условия друг друга усиливают как волны, распространяющиеся от нижних краев щелей, так и волны, распространяющиеся от всех других точек щелей. Каждой точке в первой щели соответствует точка во второй щели, находящаяся на расстоянии d от первой точки. Поэтому разность хода испущенных этими точками вторичных волн равна kλ, и эти волны взаимно усиливаются.
Рассмотрим следующий случай. За решеткой поместим собирающую линзу, а за ней — экран на фокусном расстоянии от линзы. Линза фокусирует лучи, идущие параллельно, в одной точке (в фокусе). В этой точке волны складываются и взаимно усиливаются. Углы φ, удовлетворяющие условию, определяют положение так главных максимумов на экране (соответствующих 1, 2 и т.д. порядку).
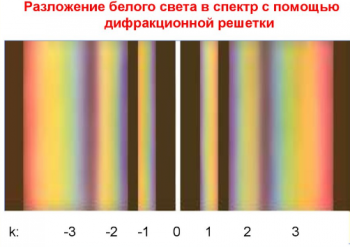
Наряду с картиной, получаемой в результате дифракции света, в случае дифракционной решетки наблюдается дифракционная картина и от отдельных щелей. Интенсивности максимумов в ней меньше интенсивности главных максимумов. Так как положение максимумов (кроме центрального, соответствующего k = 0) зависит от длины волны, то решетка разлагает белый свет в спектр. Чем больше λ, тем дальше от центрального максимума располагается тот или иной максимум, соответствующий данной длине волны.
Каждому значению k соответствует свой порядок спектра. Между максимумами расположены минимумы освещенности. Чем больше число щелей, тем более резко очерчены максимумы и тем более широкими минимумами они разделены.
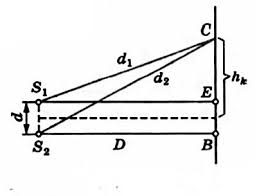
Пример №1. В опыте Юнга по дифракции расстояние между щелями равно d = 7∙10–4 м. Расстояние от двойной щели до экрана равно D = 2 м. При освещении прибора зеленым светом расстояние между соседними светлыми дифракционными полосами оказалось равным ∆h = 16∙10–2 м. Вычислите длину волны.
В некоторой точке С экрана будет наблюдаться максимум освещенности при выполнении условия:
d2−d1=kλ
где величина k = 0, 1, 2, … — целые числа.
Применим теорему Пифагора к треугольникам S1CE и SsCB:
d22=D2+(hk+d2)2
d21=D2+(hk−d2)2
Вычитая из первого равенства второе, получаем:
d22−d21=2hkd
Отсюда:
(d2+d1)(d2−d1)=2hkd
Так как расстояние между щелями много меньше расстояния между ними и экраном, то можем считать, что:
d2+d1≈2D
Тогда:
d2−d1≈hkdD
Учитывая, что d2−d1=kλ, можем считать, что:
kλ≈hkdD
Отсюда можем найти расстояние k-той светлой полосы от центра экрана:
hk≈kλDd
Расстояние между соседними полосами равно:
Δh=hk+1−hk≈λDd
Следовательно:
λ≈dΔhD≈7·10−4·16·10−22=56·10−6(м)=56 (мкм)
Задание EF17638
На плоскую непрозрачную пластину с узкими параллельными щелями падает по нормали плоская монохроматическая волна из красной части видимого спектра. За пластиной на параллельном ей экране наблюдается интерференционная картина, содержащая большое число полос. При переходе на монохроматический свет из синей части видимого спектра
Ответ:
а) расстояние между интерференционными полосами увеличится
б) расстояние между интерференционными полосами уменьшится
в) расстояние между интерференционными полосами не изменится
г) интерференционная картина станет невидимой для глаза
Алгоритм решения
- Записать, как зависит расстояние между интерференционными полосами от частоты световых лучей.
- Выбрать ответ, удовлетворяющий установленной зависимости.
Решение
Зависимость расстояния между интерференционными полосами от частоты световых лучей удалось установить экспериментально. Было выяснено, что чем выше частота, тем меньше расстояние между ними. Частота света из синего части спектра больше частоты из красной части спектра. Поэтому при переходе из красной части спектра в синюю часть расстояние между полосами интерференционной картины уменьшится.
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18119
В прозрачном сосуде, заполненном водой, находится дифракционная решётка. Решётка освещается лучом света лазерной указки, падающим перпендикулярно её поверхности через боковую стенку сосуда. Как изменятся частота световой волны, длина волны, падающей на решётку, и угол между падающим лучом и первым дифракционным максимумом при удалении воды из сосуда?
Для каждой величины определите соответствующий характер изменения:
- Увеличится
- Уменьшится
- Не изменится
Запишите в таблицу выбранные цифры для каждого ответа. Цифры в ответе могут повторяться.
Алгоритм решения
1.Объяснить, что изменится, когда вода будет извлечена из сосуда.
2.Установить, как при этом изменится частота светового луча, достигающей решетки.
3.Установить, как при этом изменится длина световой волны, достигающей решетки.
4.Установить, как при этом изменится угол между нормалью к решётке и первым дифракционным максимумом.
Решение
Когда воды в сосуде не станет, изменится оптическая плотность среды — ею будет воздух, имеющий абсолютный показатель преломления 1 (у воды он равен 1,33).
Частота световой волны — величина постоянная. Она не меняется при изменении любых величин.
Длина световой волны меняется с учетом оптической плотности среды. Она определяется формулой:
λ=vν
В оптически более плотной среде скорость распространения волны уменьшается. Но когда их сосуда была удалена вода, оптическая плотность уменьшилась, значит, скорость волны увеличилась. Так как частота волны — постоянная, а длина волны прямо пропорциональна ее скорости, то при увеличении скорости длина волны тоже увеличится.
В оптически более плотной среде волны отклоняются от прямолинейного распространения сильнее в сторону нормали. Поэтому при удалении воды, когда оптическая среда станет менее плотной, лучи отклонятся от нормали. В этом случае угол между нормалью к решётке и первым дифракционным максимумом увеличится.
Ответ: 311
pазбирался: Алиса Никитина | обсудить разбор
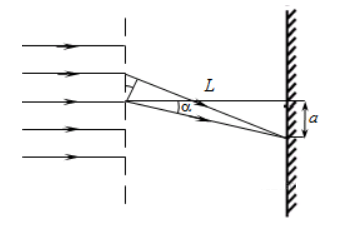
Задание EF18230
Дифракционная решётка с периодом 10–5 м расположена параллельно экрану на расстоянии 0,75 м от него. На решётку по нормали к ней падает пучок света с длиной волны 0,4 мкм. Какого порядка максимум в спектре будет наблюдаться на экране на расстоянии 3 см от центра дифракционной картины? Считать sina ≈ tga.
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Выполнить пояснительный рисунок.
3.Записать условие интерференционных максимумов дифракционной решётки.
4.Выполнить решение в общем виде.
5.Подставить неизвестные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Длина волны пучка света: λ = 0,4 мкм.
• Период дифракционной решетки: d = 10–5 м.
• Расстояние между дифракционной решеткой и экраном: L = 0,75 м.
• Расстояние от k-того максимума до центра дифракционной картины: a = 3 см.
0,4 мкм = 0,4∙10–6 м.
3 см = 3∙10–2 м
Сделаем пояснительный чертеж:
Запишем условие интерференционных максимумов дифракционной решётки:
dsinα=kλ
Из курса геометрии известно, что тангенс угла равен отношению прилежащего катета к противолежащему. Следовательно:
tanα=aL
Из условия задачи синус и тангенс этого угла равны. Следовательно:
sinα=tanα=aL
Найдём номер дифракционного максимума, который будет наблюдаться на экране на расстоянии 3 см от центра дифракционной картины:
daL=kλ
Ответ: 1
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 5.7k