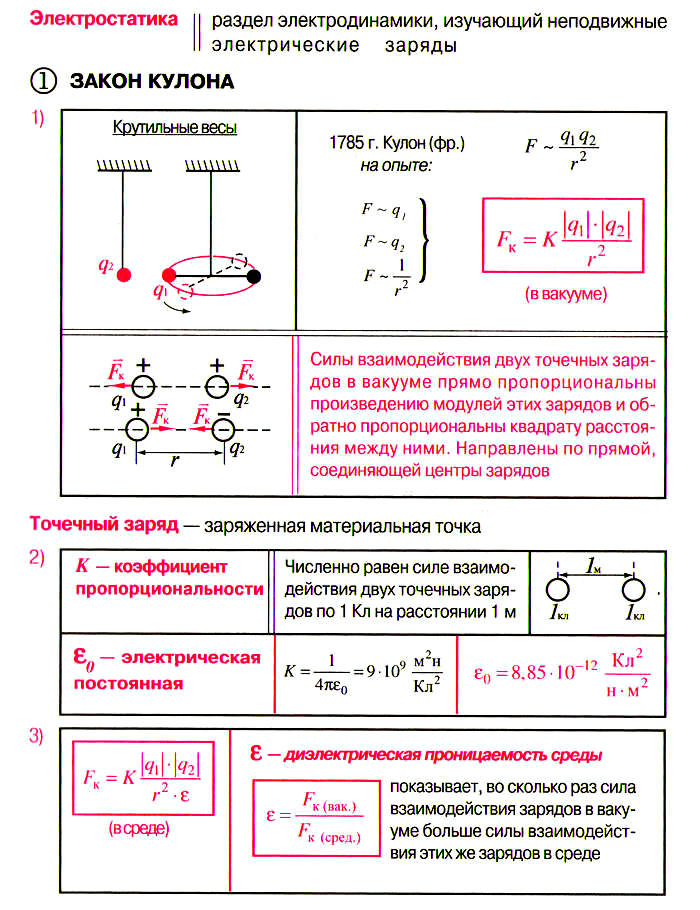
Закон Кулона. Калькулятор онлайн.
Онлайн калькулятор Закона Кулона с решением позволит вычислить силу взаимодействия двух зарядов, электрический заряд, а так же расстояние между зарядами, единицы измерения которых, могут включать любые приставки Си. Калькулятор автоматически переведет одни единицы в другие и даст подробное решение.
Калькулятор вычислит:
Силу взаимодействия двух точечных зарядов.
Точечный электрический заряд.
Расстояние между зарядами.
Сила взаимодействия двух точечных зарядов F
Сила взаимодействия двух точечных неподвижных зарядов в вакууме направлена вдоль прямой, соединяющий эти заряды, прямо пропорциональна произведению модулей этих зарядов и обратно пропорциональна квадрату расстояния между ними. Коэффициент пропорциональности k = 8.9875517873681764 × 109
Единицей измерения силы в СИ является Ньютон (Н). Международное обозначение: N
Первый заряд q1 =
Второй заряд q2 =
Расстояние r =
Единица измерения силы F
Точечный электрический заряд Q
Заряд, равный одному кулону, характеризуется как заряд, проходящий через поперечное сечение проводника, по которому идет постоянный ток силы 1 Ампер за одну секунду. Заряд 1 кулон — это заряд , который в вакууме воздействует на такой же равный ему заряд, находящийся на расстоянии 1 метр с силой 8.9875517873681764 × 109 ньютонов.
Сила F =
Второй заряд q2 =
Расстояние r =
Единица измерения заряда q1
Расстояние между зарядами R
Исходя из закона Кулона расстояние между зарядами, можно выразить как корень квадратный из частного, где числителем
выступает Коэффициент пропорциональности k = 8.9875517873681764 × 109 умноженный на произведение первого и второго зарядов, а знаменатель равен силе F взаимодействия двух зарядов.
Первый заряд q1 =
Второй заряд q2 =
Сила F =
Единица измерения расстояния r
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы (физика) |
|
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
| Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
|
Оптика |
| Калькулятор отражения и преломления света |
|
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
|
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
| Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор упрощения выражений |
| Калькулятор со скобками |
| Калькулятор уравнений |
| Калькулятор суммы |
| Калькулятор пределов функций |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Калькулятор делителей числа |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
| Длина отрезка. Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажер по математике |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
| Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Как найти расстояние между зарядами
Под точечными зарядами понимают тела, имеющие электрический заряд, линейными размерами которых можно пренебречь. Расстояние между ними можно измерить измерять непосредственно с помощью линейки, штангенциркули или микрометра. Но сделать это практически очень сложно. Поэтому можно воспользуйтесь законом Кулона.
Вам понадобится
- — чувствительный динамометр;
- — калькулятор;
- — таблица диэлектрической проницаемости веществ.
Инструкция
Присоедините известные заряды к рычагам чувствительного динамометра. Используйте крутильный динамометр, который измеряет силу в зависимости от поворота проволоки, на которой подвешено одно из тел. При размещении зарядов избегайте из прикосновения, иначе величина электрического заряда перераспределится, сила взаимодействия изменится, и измерение будет не верным.
При измерении силы взаимодействия обязательно учитывайте полярность зарядов, поскольку одноименные заряды отталкиваются, а разноименные притягиваются. Поэтому весы могут вращаться в разные стороны. При определении расстояния между разноименными зарядами, воспрепятствуйте их соприкосновению.
Измерьте силу взаимодействия зарядов в Ньютонах. Чтобы определить расстояние между двумя зарядами r, найдите произведение модулей величин этих зарядов q1 и q2, умножьте получившееся число на коэффициент 9•10^9, результат поделите на модуль силы, измеренной динамометром F. Из получившегося результата извлеките квадратный корень r=√((9•10^9•q1•q2)/F). Результат получите в метрах.
Если взаимодействие зарядов осуществляется не в вакууме или воздухе, учитывайте диэлектрическую проницаемость среды, где происходит взаимодействие. Найдите ее значение в специальной тематической таблице. Например, если заряда находятся в керосине, то учитывайте, что его диэлектрическая проницаемость ε=2. Диэлектрическая проницаемость вакуума и воздуха равна ε=2.
При расчете расстояния между зарядами, которые находятся в веществе, диэлектрическая проницаемость которого отличается от 1, перед извлечением квадратного корня поделите результат вычисления для расстояния между двумя зарядами на диэлектрическую проницаемость ε. В этом случае формула для расчета расстояния между двумя точечными зарядами примет вид r=√((9•10^9•q1•q2)/ε•F).
Видео по теме
Источники:
- как необходимо изменить расстояние между двумя зарядами
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Как найти расстояние между зарядами
Под точечными зарядами понимают тела, имеющие электрический заряд, линейными размерами которых можно пренебречь. Расстояние между ними можно измерить измерять непосредственно с помощью линейки, штангенциркули или микрометра. Но сделать это практически очень сложно. Поэтому можно воспользуйтесь законом Кулона.
Присоедините известные заряды к рычагам чувствительного динамометра. Используйте крутильный динамометр, который измеряет силу в зависимости от поворота проволоки, на которой подвешено одно из тел. При размещении зарядов избегайте из прикосновения, иначе величина электрического заряда перераспределится, сила взаимодействия изменится, и измерение будет не верным.
При измерении силы взаимодействия обязательно учитывайте полярность зарядов, поскольку одноименные заряды отталкиваются, а разноименные притягиваются. Поэтому весы могут вращаться в разные стороны. При определении расстояния между разноименными зарядами, воспрепятствуйте их соприкосновению.
Измерьте силу взаимодействия зарядов в Ньютонах. Чтобы определить расстояние между двумя зарядами r, найдите произведение модулей величин этих зарядов q1 и q2, умножьте получившееся число на коэффициент 9•10^9, результат поделите на модуль силы, измеренной динамометром F. Из получившегося результата извлеките квадратный корень r=√((9•10^9•q1•q2)/F). Результат получите в метрах.
Если взаимодействие зарядов осуществляется не в вакууме или воздухе, учитывайте диэлектрическую проницаемость среды, где происходит взаимодействие. Найдите ее значение в специальной тематической таблице. Например, если заряда находятся в керосине, то учитывайте, что его диэлектрическая проницаемость ε=2. Диэлектрическая проницаемость вакуума и воздуха равна ε=2.
При расчете расстояния между зарядами, которые находятся в веществе, диэлектрическая проницаемость которого отличается от 1, перед извлечением квадратного корня поделите результат вычисления для расстояния между двумя зарядами на диэлектрическую проницаемость ε. В этом случае формула для расчета расстояния между двумя точечными зарядами примет вид r=√((9•10^9•q1•q2)/ε•F).
Calculate the electrostatic force of attraction/repulsion, distance, or charge using Coulomb’s Law by entering known values in the calculator below.
Calculate Force
Calculate Distance
Calculate Charge
Electrostatic Force:
Learn how we calculated this below
scroll down
On this page:
-
Coulomb’s Law Calculator
-
How to Calculate Electrostatic Force
-
Coulomb’s Law Formula
-
How to Calculate the Distance Between Objects
-
How to Calculate the Charge of an Object
How to Calculate Electrostatic Force
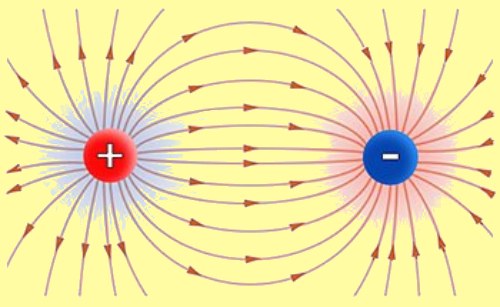
When two charges are brought together, they experience a force of attraction if they are opposite charges and a force of repulsion if they are like charges. Using Coulomb’s Law it’s possible to calculate the electrostatic force between two charges if the distance between them is known.
Coulomb’s Law Formula
Coulomb’s Law defines the following formula for this.
FE = keq1q2 / r2
Where:
FE = electrostatic force in newtons
ke = Coulomb constant, which is equal to 8,987,551,787.3681764 Nm2C−2 (8.988×109 Nm2C-2)
q1 = charge of the first object in coulombs
q2 = charge of the first object in coulombs
r = distance between the objects in meters
The electrostatic force FE between two charges is equal to the Coulomb constant ke times the charge of an object q1 times the charge of the other object q2 divided by the distance between them r squared.
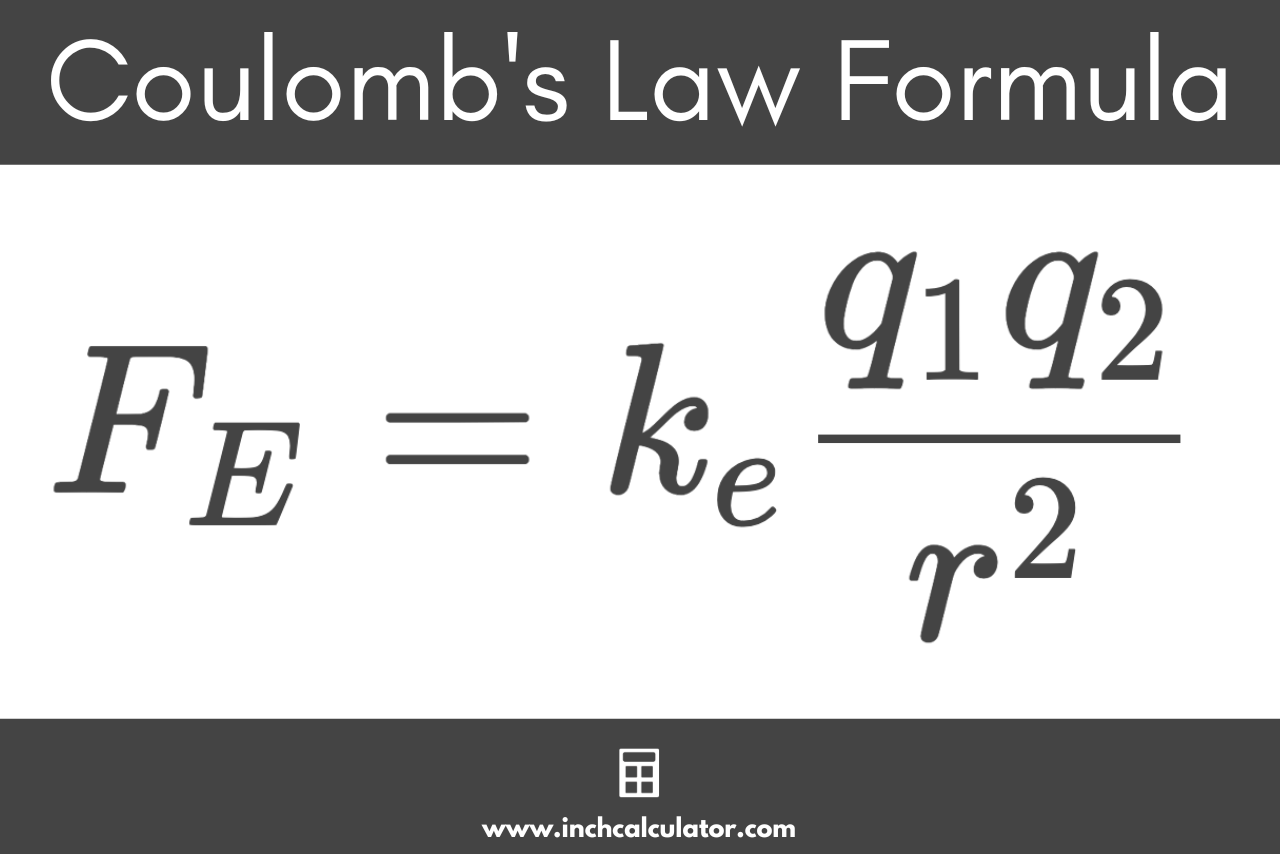
For example, let’s find the electrostatic force between two +2µC and +4µC point charges if a distance of 10 millimeters separates them.
F(N) = (8.988×109 Nm2C-2)(2×10-6 C)(4×10-6 C) / (10×10-3 m)2
F(N) = 719 N
So, the electrostatic force is equal to 719 newtons.
How to Calculate the Distance Between Objects
If the electrostatic charge and force are known, then it’s possible to use Coulomb’s Law to find the distance between the objects.
r = √ (ke × q1 × q2 ÷ FE)
So, the distance between objects r is equal to the square root of the Coulomb constant ke times the charge of an object q1 times the charge of the other object q2 divided by the electrostatic force FE.
For example, let’s find the separation between two charges, 3µC and 6µC, when a force of 2 N acts between them.
r(m) = √ ((8.988×109 Nm2C-2)(3×10-6 C)(6×10-6 C) ÷ 2 N)
r(m) = 0.288 m
Thus, the distance between the charges is 0.288 meters.
How to Calculate the Charge of an Object
If the electrostatic charge of one object, the force, and the distance are known, then the following formula can be used to solve the charge of the second object.
q2 = FE × r2 ÷ ke ÷ q1
Thus, the charge of an object q2 is equal to the electrostatic force FE times the distance between objects r squared divided by the Coulomb constant ke divided by the charge of the other object q1.
For example, let’s find the charge on an object if the other object has a charge of 8µC, a separation of 5 millimeters, and a force of 10N acts between them.
q2 (nC) = 10 N × (5×10-3 m)2 ÷ 8.988×109 Nm2C-2 ÷ 8×10-6 C
q2 (nC) = 3.5 nC
The charge of the object is equal to 3.5 nC.
ЕГЭ Закон Кулона. ЗАДАЧИ с решениями
Формулы, используемые на уроках «Задачи на взаимодействие зарядов и закон Кулона».
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Два шарика, расположенных на расстоянии г = 20 см друг от друга, имеют одинаковые по модулю заряды и взаимодействуют в воздухе с силой F = 0,3 мН. Найти число нескомпенсированных электронов N на каждом шарике.

Задача № 2.
С какой силой взаимодействовали бы в воздухе две капли воды массами по m = 1 г, расположенные на расстоянии г = 50 см друг от друга, если бы одной из них передали 10% всех электронов, содержащихся в другой капле?
Задача № 3.
Два одинаковых шарика зарядили так, что заряд одного из них оказался по модулю в п раз больше другого. Шарики привели в соприкосновение и развели на вдвое большее, чем прежде, расстояние. Во сколько раз изменилась сила их кулоновского взаимодействия, если их заряды до соприкосновения были разноименными?
Задача № 4.
Два маленьких заряженных шарика взаимодействуют в вакууме с некоторой силой, находясь на расстоянии r1 друг от друга. На каком расстоянии r2 друг от друга они будут взаимодействовать в среде с диэлектрической проницаемостью ε2, если сила их взаимодействия останется прежней?
Задача № 5.
Маленьким шариком с зарядом q коснулись внутренней поверхности очень большого незаряженного металлического шара, в результате чего на большом шаре поверхностная плотность зарядов стала равна σ. Найти объем V большого шара. Среда — воздух.
Смотреть решение и ответ

Задача № 6.
Два металлических шарика имеют массу m = 10 г каждый. Какое число электронов N надо удалить с каждого шарика, чтобы сила их кулоновского отталкивания стала равна силе их гравитационного тяготения друг к другу?
Смотреть решение и ответ

Задача № 7.
Между двумя одноименными точечными зарядами q1 = 1 • 10–8 Кл и q2 = 4 • 10–8 Кл, расстояние между которыми r = 9 см, помещают третий заряд q0 так, что все три заряда оказываются в равновесии. Чему равен этот третий заряд q0 и каков его знак? На каком расстоянии r1 от заряда q1 он располагается?
Задача № 8.
Заряды q1 = 20 нКл и q2 = –30 нКл расположены на некотором расстоянии друг от друга (рис. 1-10). Заряд q0 помещают сначала в точку 1, расположенную слева от заряда q1 на расстоянии r/2 от него, а затем в точку 2, расположенную между зарядами q1 и q2. Найти отношение силы F1, с которой заряды q1 и q2 действуют на заряд q0 в точке 1, к силе F2, с которой они действуют на него в точке 2.
Задача № 9.
В вершинах равностороннего треугольника находятся одинаковые заряды q = 2 нКл (рис. 1-11). Какой заряд q0 надо поместить в центр треугольника С, чтобы система всех этих зарядов оказалась в равновесии? Будет ли равновесие устойчивым?
Задача № 10.
В вершинах квадрата расположены заряды q (рис. 1-12). Какой заряд q0 и где надо поместить, чтобы вся система зарядов оказалась в равновесии? Будет ли равновесие устойчивым?
Задача № 11.
В трех соседних вершинах правильного шестиугольника со стороной а расположены положительные заряды q, а в трех других — равные им по модулю, но отрицательные заряды. С какой силой F эти шесть зарядов будут действовать на заряд q0, помещенный в центр шестиугольника (рис. 1-13)?
Задача № 12.
Два одинаковых маленьких шарика массами по m = 10 г каждый заряжены одинаково и подвешены на непроводящих и невесомых нитях так, как показано на рис. 1-14. Какой заряд q должен быть на каждом шарике, чтобы нити испытывали одинаковое натяжение? Среда — воздух, длина каждой нити l = 30 см.
Задача № 13.
На изолирующей нити подвешен маленький шарик массой m = 1 г, имеющий заряд q1 = 1 нКл. К нему снизу подносят на расстояние г = 2 см другой заряженный маленький шарик, и при этом сила натяжения нити уменьшается вдвое. Чему равен заряд q2 другого шарика? Среда — воздух.
Задача № 14.
Два одинаковых маленьких шарика подвешены на невесомых нитях длиной I каждая в одной точке. Когда им сообщили одинаковые заряды q, шарики разошлись на угол а (рис 1-16). Найти силу натяжения Fн каждой нити. Среда — воздух.
Задача № 15.
Два одинаково заряженных шарика, подвешенных на нитях равной длины, разошлись на некоторый угол (рис. 1-17, а). Чему равна плотность материала шариков р, если после погружения их в керосин угол между нитями не изменился (рис. 1-17, б)? Относительная диэлектрическая проницаемость воздуха ε1 = 1, относительная диэлектрическая проницаемость керосина ε2 = 2. Плотность керосина р0 = 800 кг/м3.
(с) В учебных целях использованы цитаты из учебного пособия «Новый репетитор по физике для подготовки к ЕГЭ : задачи и методы их решения / И.Л. Касаткина; под ред. Т.В. Шкиль. — Ростов н /Д : Феникс».
Это конспект по теме «ЕГЭ Закон Кулона. ЗАДАЧИ с решениями». Выберите дальнейшие действия:
- Вернуться к списку конспектов по Физике.
- Проверить свои знания по Физике.