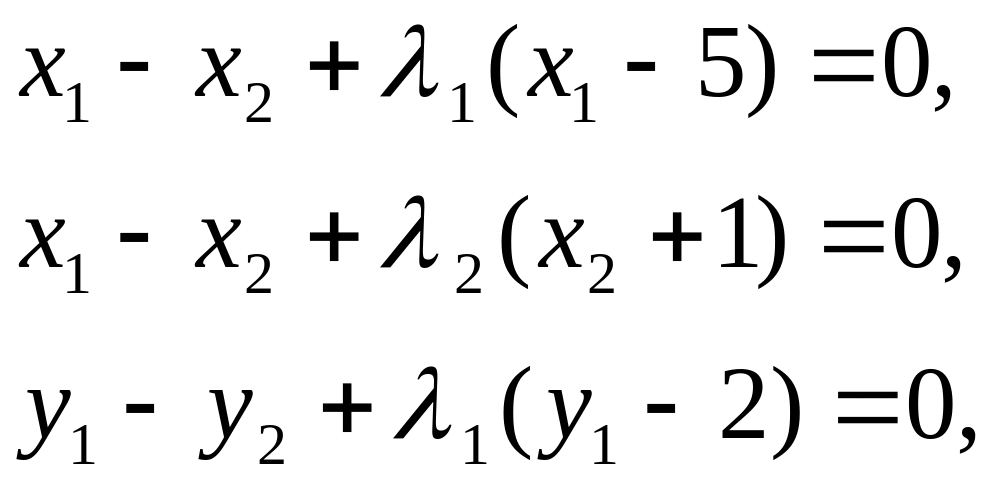Цель
работы:
найти расстояние между двумя фигурами
на плоскости, используя оптимизационный
подход и метод неопределенных множителей
Лагранжа. Для компьютерного получения
решения и его визуализации использовать
пакет MAPLE.
1. Теоретические сведения
-
Метод
множителей Лагранжа
Стандартная
условно-экстремальная задача формулируется
следующим образом:
найти
минимум функции (критерия) J
=
f(x1,
…,
xn)
при наличии ограничений
g1(x1,
…,
xn)
= 0,
…, gm(x1,
…,
xn)
= 0,
или
коротко
Основной
аналитический метод решения связан с
введением вектора множителей Лагранжа
и построением составного критерия
(функции
Лагранжа)
L
= f(X)
+
g(X)
min
или
в более подробной записи
Экстремум
этой функции ищется обычным образом
путем взятия производных и приравнивания
их нулю. Тем самым исходная
условно-экстремальная задача сводится
к задаче отыскания безусловного
экстремума.
Пример
1. Вписанный прямоугольник максимального
периметра.
Эллипс
задан своим каноническим уравнением
Требуется среди всех вписанных в него
прямоугольников (рис. 1) найти прямоугольник
с максимальным периметром.
y
b
y
x
x
a
2x
2y
Рисунок
1
Решение.
Формализуем задачу, выписав критерий
и ограничения:
J
= 4x
+ 4y
max;
,
x,
y
0.
Строим
составной критерий (функцию Лагранжа):
Приравниваем
нулю производные по
x
и
y:
откуда
x
=
2a2
/ ,
y
=
2b2
/ ,
x
/y
= a2
/ b2,
Таким
образом,
стороны прямоугольника с максимальным
периметром относятся как квадраты
полуосей эллипса. Подставляя эти значения
в уравнение эллипса, находим, что 2
= 4а2
+ 4b2.
Окончательно имеем
П
ример
2. Расстояние
между окружностью и параболой.
Пусть
требуется найти расстояние между
окружностью
и параболой
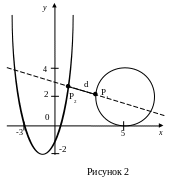
Решение.
Изобразим окружность и параболу на
плоскости (рис. 2). Задача сводится к
отысканию точки P1
с координатами (x1,
y1),
принадлежащей окружности, и точки P2
с координатами
(x2,
y2),
принадлежащей параболе, таких, чтобы
расстояние между ними
было минимальным. Для облегчения
дальнейших вычислений расстояние d
можно заменить его квадратом. Выписываем
критерий и ограничения:
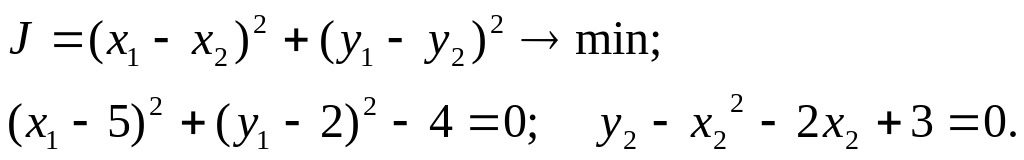
Строим
функцию Лагранжа:
Решение
задачи теперь сводится к отысканию
минимума функции от шести переменных
x1,
x2,
y1,
y2,
λ1,
λ2.
Это можно сделать, приравняв соответствующие
шесть производных нулю:
|
|
|
Заметим,
что два последних уравнения – это просто
описание исходных кривых.
Данная
ыимееи три различных решения. Геометрически
им соответствуют три прямые, показанные
на рис. 3. Все они проходят через центр
окружности и пересекают одну из ветвей
параболы под прямым углом. Заметим, что
ортогональность
кратчайшего отрезка, соединяющего две
кривые, каждой из них – общее свойство
задач о минимальном расстоянии.
Отбрасывая
лишние решения, находим, что минимальное
расстояние между кривыми равно
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
ОДНА
ЗАДАЧА ВАРИАЦИОННОГО АНАЛИЗА, связанная с нахождением кратчайшего расстояния
между кривыми
Постановка
задачи.
Указание.
Теорема.
Доказательство.
Резюме.
Авторы
Манасян Сергей Керопович,
доктор технических наук, профессор, член-корреспондент РАЕ
Красноярский
техникум социальных технологий
КГБПОУ
«КТСТ», преподаватель
Ассоциация
научных сотрудников «СибАК», рецензент
Черняева Ольга, магистрант
Санкт-Петербургский
горный университет, выпускник
Санкт-Петербургский
государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова
(Ленина), магистрант
СПбГЭТУ
«Ленинградский электротехнический институт»
Красноярск
– Санкт-Петербург
2021
ОДНА
ЗАДАЧА ВАРИАЦИОННОГО АНАЛИЗА, связанная с нахождением кратчайшего расстояния
между кривыми
Имеем две кривые .
Постановка задачи.
Пусть функции – непрерывные и непрерывно
дифференцируемые. Требуется найти кратчайшее расстояние между ними.
Указание.
Решите задачу разными способами. Для решения используйте методы оптимизации и
вариационный анализ, школьный курс алгебры, понятие производной, уравнение
касательной к графику функции, элементы аналитической геометрии, нормальный
вектор к кривой в точке, нормаль к прямой, расстояние между прямыми, длина дуги
по кривой. Задача сводится к нахождению минимального расстояния между двумя
точками, одна из которых лежит на кривой а другая – на кривой
Пример.
— ? (1)
Решение.
1 способ


(3)
(4)
Ответ:
d(f1,f2)=1,75.
Решение.
2 способ
d=min |f|
= min |-x2-1-x-1|=min
|x**2+x+2|,
(5)
(6)
(7)
Решение.
3 способ
, min J(y)=
,
(8)
где y – экстремальная кривая (точнее, это – экстремаль, и она является
стационарной кривой, – причем понятие стационарной кривой является более общим
по сравнению с понятием «экстремальная кривая»); точка принадлежит
первой кривой f1(x),
точка – второй кривой f2(x).
Пояснение. Подынтегральная
функция зависит только от производной функции, поэтому экстремальная кривая
(экстремаль функционала J(y))
имеет вид:
.
Возможные
ориентации касательных к экстремали (эта кривая является аналогом «стационарной
точки», если бы J(y)
был не целевым функционалом, т.е. функцией от функции, а целевой функцией) в точках ее пересечения с граничной кривой определяются условием
трансверсальности:
+(
—
=0.
(9)
а)
Применим условие трансверсальности для кривой в точке
:
= 0.
(10)
.
(11)
b)
Применим условие трансверсальности для кривой в точке
:
= 0.
(10)
. (11)
c)
Совместим условие трансверсальности для кривой с экстремалью в точке
:
. (12)
= 0.
(13)
d) Совместим
условие трансверсальности для кривой с экстремалью в точке
:
. (14)
= 0.
(15)
Выражение (15) принимает вид:
В результате получаем систему из 4
уравнений с 4 неизвестными:
(16)
;
(17)
.
Решение системы (16-17)
имеет вид:
(из уравнения (17)),
(18)
(подставляя (18) в (16),
) (19)
,
(20)
(
, (21)
Решение. 4 способ
Пусть искомые точки, доставляющие минимум целевой функции
«расстояние между кривыми 1 и 2, есть точки М1 и М2, соответственно на кривой 1
и на кривой 2:
Целевая
функция – евклдово расстояние между М1 и М2, равное длине отрезка М1М2:
® min.
(22)
Ограничения
– принадлежность точки М1 кривой f1 и
точки М2 кривой М2:
(23)
(24)
Составляем
функцию Лагранжа:
L(
(25)
Cоставляем систему 6 уравнений
из 6 неизвестных:
Решая данную систему, получим
ответ: D=7/4.
Другие способы решения данной
задачи Вы можете предложить сами.
Как составить функцию расстояния между кривыми?
Здравствуйте!
Нужно найти наименьшее расстояние между двумя кривыми методом градиентного спуска:
x^2+y^2−2*x+4*y+3 = 0 и x = (cosϕ)^3 − 1, y = 2 + (sinϕ)^3
Суть вопроса в том, что я не могу составить функцию расстояния между точками на этих прямых, чтобы потом её минимизировать. Подскажете, как это сделать? Заранее спасибо
-
Вопрос заданболее трёх лет назад
-
1548 просмотров
Пригласить эксперта
Есть же формула расстояния между двумя точками:sqrt((x2-x1)^2+(y2-y1)^2)
Вот в неё подставляем x и y из первого и второго уравнения, причём в первом придётся выразить y через x.
Получаем функцию расстояния между двумя произвольными точками кривых:d = f(x; ф) >= 0
p.s.
Если мы говорим про вещественные числа.
-
Показать ещё
Загружается…
25 мая 2023, в 05:30
1000 руб./за проект
25 мая 2023, в 05:14
5000 руб./за проект
25 мая 2023, в 02:38
1000 руб./за проект
Минуточку внимания
Главная » 2013 » Август » 4 » найти расстояние между кривыми
|
20:17 найти расстояние между кривыми |
|
Пример 1. Найти расстояние ρ0 между кривыми y= x и y1=x2 на отрезке [0,1]. Решение. 
Пример 2. Найти расстояние первого порядка между кривыми y(x)=x2 и y1(x)=x3 на отрезке [0,1]. Решение. Расстояние между кривыми (пояснение)
|
Категория: Вариационное исчисление | Просмотров: 10438 | Добавил: Admin | Теги: экстремум функционала, найти, непрерывность функционала, близость кривых | Рейтинг: 2.0/1 |
| Всего комментариев: 0 | |
Войдите:
Ну, да, мне нужно найти такие точки, одну на одной кривой, другую на второй, расстояния между которыми будет минимально. Я знаю формулу расстояния между двумя точками: sqrt((x2-x1)**2 — (y2-y1)**2), проблема в том, чтобы из данных уравнений кривых составить такое уравнение
– SHOUMEN
30 мар 2019 в 7:21