Как найти расстояние до плоскости oyz

Данная статья посвящена способам вычисления расстояния от точки до плоскости. Рассмотрен метод координат, который позволит находить расстояние от заданной точки трехмерного пространства. После изложения теоретических аспектов приведены решения нескольких характерных примеров и задач.

Расстояние от точки до плоскости находится посредством известного расстояния от точки до точки, где одна из них заданная, а другая – проекция на заданную плоскость.

Когда в пространстве задается точка с плоскостью φ, то через точку можно провести перпендикулярную плоскости прямую. является общей точкой их пересечения. Отсюда получаем, что отрезок – это перпендикуляр,который провели из точки к плоскости φ, где точка – основание перпендикуляра (рис. 1).

(рис.1)

Определение. Расстоянием от точки до плоскости называют расстояние от заданной точки к основанию перпендикуляра, который провели из заданной точки к заданной плоскости.

Расстояние от точки к плоскости φ определяется так: расстояние от точки до плоскости φ будет являться наименьшим от заданной точки до любой точки плоскости. Если точка располагается в плоскости φ и не равна точке , тогда получаем прямоугольный треугольник вида , который является прямоугольным, где имеется катет , – гипотенуза. Значит, отсюда следует, что . Тогда отрезок считается наклонной, которая проводится из точки до плоскости φ. Мы имеем, что перпендикуляр, проведенный из заданной точки к плоскости, меньше наклонной, которую проводят из точки к заданной плоскости. Рассмотрим этот случай на рисунке 2, приведенном ниже.

(рис.2)

Существует ряд геометрических задач, решения которых должны содержать расстояние от точки до плоскости. Способы выявления этого могут быть разными. Для разрешения применяют теорему Пифагора или подобия треугольников. Когда по условию необходимо рассчитать расстояние от точки до плоскости, заданные в прямоугольной системе координат трехмерного пространства, решают методом координат. Данный пункт рассматривает этот метод.

По условию задачи имеем, что задана точка трехмерного пространства с координатами с плоскостью φ, необходимо определить расстояние от к плоскости φ. Для решения применяется несколько способов решения.

Первый способ

Данный способ основывается на нахождении расстояния от точки до плоскости при помощи координат точки , которые являются основанием перпендикуляра из точки к плоскости φ. Далее необходимо вычислить расстояние между (рис.2).

Чтобы вычислить расстояние нужно применить формулу:

,

где — длина вектора нормали плоскости φ, а число — есть результат подстановки координат точки в левую часть общего уравнения плоскости.

Условие:

Вычислить расстояние от точки до плоскости

Решение:

Вектор нормали имеет координаты , тогда

Ответ: 3

Второй способ

По условию имеем, что является основанием перпендикуляра, который опустили из точки на плоскость φ. Тогда определяем координаты точки . Искомое расстояние от к плоскости φ находится по формуле:

где и .

Для решения необходимо узнать координаты точки .

Имеем, что является точкой пересечения плоскости φ с прямой , которая проходит через точку , расположенную перпендикулярно плоскости φ. Отсюда следует, что необходимо составление уравнения прямой, проходящей через заданную точку перпендикулярно к заданной плоскости. Именно тогда сможем определить координаты точки Необходимо произвести вычисление координат точки пересечения прямой и плоскости.

Способ нахождения расстояния от точки с координатами к плоскости x:

составить уравнение прямой , проходящей через точку и одновременно перпендикулярной к плоскости φ;

найти и вычислить координаты точки , являющимися точками пересечения прямой с плоскостью φ;

вычислить расстояние от до φ, используя формулу

Третий способ

В заданной прямоугольной системе координат имеется плоскость φ, тогда получаем нормальное уравнение плоскости вида:

+ .

Отсюда получаем, что расстояние с точкой , проведенной на плоскость φ, вычисляемое по формуле:

| |=| + |.

Эта формула справедлива, так как это установлено благодаря следующей теореме.

Теорема. Если задана точка в трехмерном пространстве, имеющая нормальное уравнение плоскости φ вида

+ ,

тогда вычисление расстояния от точки до плоскости | | производится из формулы

| |=| + |,

так как

Рассмотрим задачу, для которой применим данный способ.

Условие:

Найдите расстояние от точки до координатной плоскости Oxyz и до плоскости .

Решение:

Координатной плоскости Oyz соответствует неполное общее уравнение плоскости вида . Это же уравнение является нормальным уравнением плоскости Oyz. Подставив в левую часть записанного уравнения значение и взяв модуль, получаем искомое расстояние от точки до заданной плоскости: .

Нормальное уравнение плоскости имеет вид . Поэтому, искомое расстояние от точки до плоскости равно

Ответ: искомое расстояние от точки до координатной плоскости Oyz равно 3, а до плоскости равно .

Список использованных источников

1. Расстояние от точки до плоскости: определение и примеры нахождения [Электронный ресурс] – Режим доступа: https://www.zaochnik.com/spravochnik/matematika/prjamaja-ploskost/rasstojanie-ot-tochki-do-ploskosti/

2. Расстояниеотточкидоплоскости.Среднийуровень.[Электронный ресурс] – Режим доступа:https://youclever.org/book/rasstoyanie-ot-tochki-do-ploskosti-2

3. Вычисление расстояния от точки до плоскости. [Электронный ресурс] – Режим доступа: https://studfiles.net/preview/1970740/

А (- 2 ; 3 ; 4), В(4 ; — 1 ; 6)

а) C(x ; y ; z)

(x + (-2))/2 = 4        

x — 2 = 8

x = 10

(y + 3)/2 = — 1

y + 3 = — 2

y = — 5

(z + 4)/2 = 6

z + 4 = 12

z = 8

C(10 ; — 5 ;

б) Расстояние от точки В до плоскости Oyz — это координата х точки: 4.

Подробнее — на Znanija.com — https://znanija.com/task/2960154#readmore

Пусть в пространстве
Oxyz
плоскость задана уравнением

,. (10)

г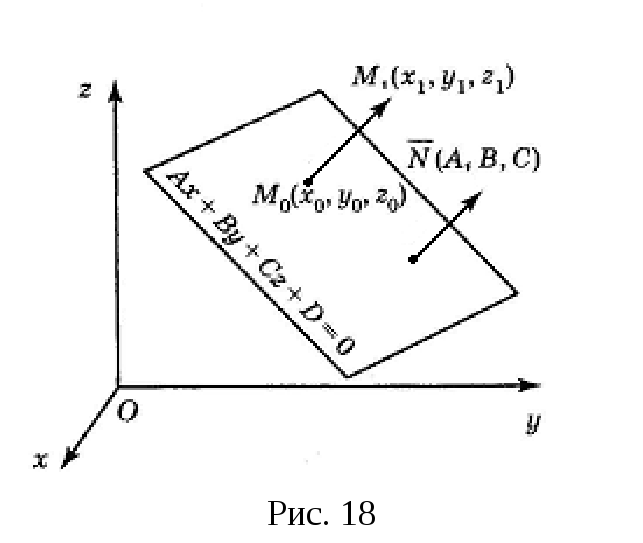де
A,
B,
C,
D
– известные числа. Дана точка
,
ее координаты

– заданные числа. Нужно найти d
– расстояние от точки

до плоскости с уравнением (10). Нормальный
вектор этой плоскости равен

Пусть

– основание
перпендикуляра, опущенного из точки

на заданную плоскость (рис. 18). Ясно,
что длина вектора

равна искомому расстоянию d.
Ясно также, что вектор

коллинеарен
.
Проекции вектора

на оси координат равны разностям
координат конца и начала:

Скалярное
произведение этого вектора и вектора

определим по формуле (17) главы 1:

.
(11)

С другой стороны,
скалярное произведение в левой части
(11) равно

.
(12)

Здесь

берётся, когда угол
,
и
,
когда этот угол равен

Выражение (12) подставим в левую часть
формулы (11), а в правой части раскроем
скобки. Получим

. (13)

Точка

лежит на плоскости с уравнением (10),
поэтому её координаты

удовлетворяют (10), т. е. имеет место
соотношение
.
Значит,

Теперь формулу (13) можно записать так:
.
Найдем теперь
,
учитывая, что
:

.
(14)

Из формулы (14)
видно, что для нахождения расстояния

от точки

до плоскости с уравнением (10) нужно в
левую часть уравнения (10) вместо

поставить координаты

заданной точки
,
а затем найденное число поделить на
.
Полученное число будет равно
,
если оно положительное, и

если это число отрицательное. Тем самым
найдём искомое расстояние
.

§5. Прямая в пространстве и ее уравнения

Общие уравнения
прямой в пространстве. Пусть
в пространстве Oxyz
две плоскости заданы уравнениями

(15)

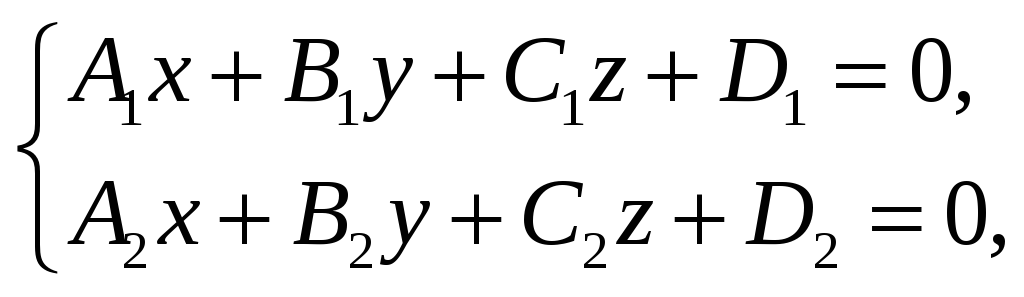
где

– известные числа. Пусть эти плоскости
не параллельны (не выполняется условие
параллельности плоскостей), тогда они
пересекаются по прямой. Уравнения в
системе (15) являются уравнениями этой
прямой. Их называют общими
уравнениями прямой в пространстве.

Векторное
уравнение прямой. Параметрические
уравнения прямой. Пусть
в системе Oxyz
прямая определена следующим образом:

Пусть

– произвольная
точка рассматриваемой прямой и
,

– радиусы-векторы точек
,
.
Из рис. 19 видно, что

. (16)

Так как вектор

коллинеарен
,
то ясно, что

можно получить умножением

на некоторый скалярный множитель
.
Тогда

.
(17)

Отсюда
,
вектор

направлен, как
,
при
,
и в противоположную сторону при
.
Запишем (16) с учётом (17) в виде

. (18)

Это соотношение
называется векторным
уравнением рассматриваемой прямой, а
скалярная величина

– параметром.
Каждому значению

согласно (18) отвечает вектор
,
конец

которого лежит на прямой. При изменении

этот вектор изменяется, его конец –
точка

– движется по прямой. Мы учли, что
,

–заданные постоянные векторы, причём
проекции вектора

на оси координат равны координатам
точки
,
так как

есть радиус-вектор этой точки, т. е.
в (18)
.
Поскольку

есть радиус-вектор точки

его проекции равны координатам точки

т. е.
.

Как известно, при
умножении вектора на число умножаются
на это число все проекции вектора на
оси координат, поэтому
.
При сложении векторов их проекции
складываются, поэтому
,
но согласно (18) этот вектор равен
,
следовательно, равны соответствующие
проекции:

(19)

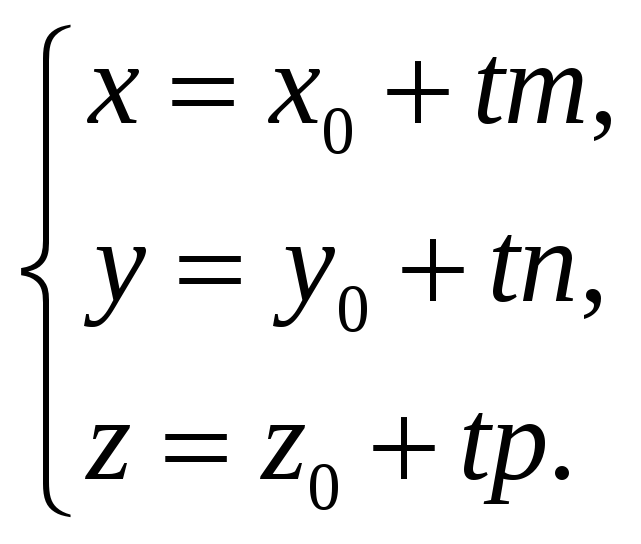
Эти соотношения
называют параметрическими
уравнениями рассматриваемой прямой.
Каждому значению параметра

на прямой отвечает определённая точка

координаты

которой вычисляются по формуле (19). При
изменении

точка

с указанными координатами движется по
прямой, и её координаты изменяются
согласно (19).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Ответ:

Расстояние от точки В до плоскости 0yz = |x| = 3 ед.

Объяснение:

Расстояние от точки до плоскости — это длина перпендикуляра, опущенного из этой точки на данную плоскость. Абсолютная величина координаты х точки b — это и есть расстояние от точки b до плоскости 0yz.  Ответ:

точка b(-3;2;-4)  находится на расстоянии 3 ед. от плоскости 0yz.