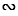МБОУ Алексинская СОШ
Дорогобужского района Смоленской области
ИТОГОВЫЙ
ИНДИВИДУАЛЬНЫЙ
ПРОЕКТ
на тему:
ОПРЕДЕЛЕНИЕ
РАССТОЯНИЯ
ДО
НЕДОСТУПНОГО ПРЕДМЕТА
(геометрия на местности)
Работу выполнил:
ученик 9 класса Мережко Андрей
Руководитель:
учитель математики Законова Т.Н.
2018 – 2019
учебный год.
«Окружающий нас мир – это мир геометрии,
чистой, истинной, безупречной в наших глазах. Все вокруг – геометрия».
(А.Д.Александров)
Актуальность темы исследования.
Мир, в котором мы живем,
наполнен геометрией домов и улиц, гор и полей, творениями природы и человека.
Геометрия зародилась в глубокой древности. Строя жилища и храмы, украшая их
орнаментами, размечая землю, измеряя расстояния и площади, человек применял свои
знания о форме, размерах и взаимном расположении предметов, полученные из
наблюдений и опытов.
Тема нашей исследовательской
работы актуальна тем, что принцип определения расстояний до
«недоступного» предмета на земле, с одной стороны, лежит в основе определения
расстояний до небесных тел, а с другой стороны, неоценим с точки зрения
приложения его в практической жизни: на стройках, при геодезических работах,
прокладке трасс, в военном деле и т. д.
Цель исследовательской работы: определить расстояние до
недоступного предмета геометрическими способами без специальных приборов.
Задачи:
1) рассмотреть различные способы
определения расстояния до выбранного недоступного предмета;
2) провести соответствующие
измерения и вычисления;
3) оформить результаты.
Объект исследования: недоступные предметы на
местности.
Предмет исследования: определение расстояния до
недоступного предмета различными способами.
Гипотеза: можно ли определить расстояние
до недоступного предмета на местности без специальных приборов.
Практическая значимость
исследования
состоит в получении знаний об измерительных работах на местности, изучении и
применении полученных знаний на уроках геометрии, в повседневной жизни.
Методы исследования: знакомство и обработка литературных материалов,
данных из Интернета, проведение экспериментальной работы, обработка
результатов.
Этапы выполнения исследовательской
работы:
·
Этап
«Сбор данных».
Включает в себя: изучение
поставленных задач, определение значимых понятий, подбор источников информации,
сбор информации.
Для выполнения задачи было предложено пять геометрических
способов (приведены их геометрические чертежи):
 |
Источниками
наших способов явились литература и сайты Интернет научно-популярного
характера.
·
Этап
«Экспериментальная работа».
Включает в себя проведение эксперимента по определению
расстояния до недоступного предмета на местности различными геометрическими
методами. Каждый эксперимент представить в виде пошагового выполнения и
измерительных расчетов.
Оборудование: фотоаппарат, рулетка, вешки,
калькулятор, блокнот, карандаш или ручка, тонкая проволока или слабо
растягивающийся шнур, колышки, молоток.
1 способ: (с помощью равнобедренного
прямоугольного треугольника)
Ход работы:

Стать напротив недоступной точки В и зафиксировать свое
положение А колышком.
С помощью шнура и двух колышков построить угол ВАС,
равный 900 (шнур и колышки используются вместо
циркуля).
Следы прямых на местности задают шнуры, натянутые между
колышками.
Аналогично правее точки А построить ещё один угол 900,
который необходимо разделить пополам с помощью того же шнура и колышков и
зафиксировать угол 450 планкой.
Осуществляя параллельный перенос планки вправо-влево, добиться
того, чтобы направление планки совпало с направлением на недоступный объект
(на точку В), в результате чего будет найдена точка С, в которой ВС и АС
образуют угол 450.
Измерить расстояние АС, которое заведомо будет равно
АВ, так как треугольник АВС – прямоугольный и равнобедренный.
Измерения:
АС = 14,3 м
АВ = АС = 14,3 м
2 способ: (с помощью подобия
треугольников)
Ход работы:
 |
1. Стать напротив недоступной
точки В и зафиксировать свое положение А колышком.
2. С помощью шнура и двух
колышков построить угол ВАС, равный 900.
3. Из произвольной точки Е,
лежащей на прямой АЕ, задать планкой направление на недоступный объект (на
точку В) под произвольным углом.
4. Правее точки А построить ещё
один угол DСЕ равный 900.
Точка D образуется на пересечении
двух планок.
5.
Треугольник
АВЕ подобен треугольнику CDE, откуда следует пропорция AB:CD = AE:CE. Из пропорции следует формула:
Произвести вычисления по формуле
Измерения:
AC = 9,5 м
CE = 1,7 м
CD = 2,2 м
3 способ: (с помощью подобия треугольников)
Ход работы:
 |
1. Стать напротив недоступной
точки В и зафиксировать свое положение А колышком.
2. С помощью шнура и двух
колышков построить угол ВАЕ, равный 900.
3. Из произвольной точки Е,
лежащей на прямой АЕ, задать планкой направление на недоступный объект (на
точку В) под произвольным углом. Из точки Е перпендикулярно ВЕ
направить планку;
4. Точка С лежит на пересечении
планок ЕС и АС.
5.
Из подобия
прямоугольных треугольников ВЕС и ЕАС получить расчётную формулу, произвести
нужные измерения и вычислить АВ по формуле:
Измерения:
AE = 5,5 м
AC = 2,2 м
EC = 6 м
4 способ: (с помощью равенства
треугольников)
Ход работы:
 |
1. Стать напротив недоступной
точки В и зафиксировать свое положение А колышком.
2. Двигаясь из точки А
перпендикулярно вправо определенное расстояние, зафиксировать положение
точкой Е.
3. Зафиксировать середину С
отрезка АЕ.
4. Из точки С планкой задать
направление на недоступный объект (точку В), впоследствии планку следует
удлинить с помощью шнура.
5. Из точки Е перпендикулярно АЕ
пройти расстояние и найти точку F,
которая лежит на прямой ВС.
6. Треугольники АВС и EFC равны по стороне и двум прилежащим к
ней углам.
7.
Произвести
измерения и вычислить AB = EF
Измерения:
AC = CE = 2,5 м
EF = 14,5 м
AB = EF = 14,5 м
5 способ: ( с помощью двойного равенства
треугольников)
Ход работы:

1. Стать напротив недоступной
точки В и зафиксировать свое положение А колышком.
2. По направлению ВА пройти
определенное расстояние АЕ и зафиксировать положение Е;
3. Двигаясь из точки А
перпендикулярно вправо определенное расстояние, зафиксировать положение
точкой D;
4. Отмерить FD = DE
и зафиксировать точку F;
5. Отмерить DQ = DA
и зафиксировать точку Q;
6. Из точки F по прямой FQ пройти расстояние и найти точку Н, из
которой через точку D видна точка В (при помощи
вешек).
7. Треугольники ABD и QHD
равны по второму признаку, а значит и отрезки AB и HQ тоже равны.
8.
Провести
измерения и вычислить HQ = AB.
Измерения:
AD = DQ = 2,5 м
AE = FQ = 2,2 м
ED = DF = 3,4 м
HQ = AB = 14,8 м
·
Этап
«Анализ данных»
Мы рассмотрели несколько геометрических методов
определения расстояния до выбранной нами недоступной точки. Все эти методы
основаны либо на определении понятия длины отрезка и измерения, либо на
свойствах равнобедренного треугольника, на свойствах равенства или подобия
треугольников.
Эксперименты проводились в неблагоприятных условиях: пасмурная
погода, холод, отсутствие опыта и сноровки.
Результаты
различных экспериментов отличались.
Размах ряда:
разница между наибольшим и наименьшим значениями
расстояний:
Среднее арифметическое:
Выводы:
Мы можем предположить, что
расстояние до выбранной нами недоступной точки около 14,5 метров. Такой
результат получен вторым способом (с помощью подобия треугольников) и четвёртым
способом (с помощью равенства треугольников), то есть будем считать их наиболее
точными.
Самым простым методом мы считаем
четвёртый способ с помощью равенства треугольников.
Вообще, используя данные методы, можно найти расстояние до любой
недоступной (видимой) точки. Так, например, с помощью второго способа легко
решается задача нахождения высоты дерева, если считать верхушку дерева
недоступной точкой. Решение опирается на тему подобия треугольников. Многие из
нас, изучая математику в школе, думали: «Зачем всё это? Как это
применяется?» Вместо ответа разберём очень интересный отрывок из повести
Эрнеста Сетона-Томпсона «Маленькие дикари»:
«— Ставлю свой скальп против твоего, что определю
высоту вон того дерева точнее, чем ты! — сказал Маленький Бобр.
— Нет, скальп я не буду ставить, а вот кто проиграет, тому
мыть посуду.
— Идёт.
— Лучше брать до той ветки. Ведь на макушку не влезешь,
чтобы проверить, — сказал Чёрный Ястреб. — Ты суди, Дятел.
— Нет, я тоже хочу попробовать! Второй будет мыть посуду в
следующую очередь.
Чёрный Ястреб внимательно осмотрел ствол и записал: тридцать
восемь футов.
— Ястреб, — сказал Сэм, — около дерева надо вбить
колышек, чтобы мерить от определенного места. Земля-то ведь неровная.
Чёрный Ястреб пошёл вбивать колышек и тем самым помог Дятлу —
теперь у Дятла было с чем сравнивать. Он знал, что Чёрный Ястреб ростом чуть
больше пяти футов. И Сэм написал: тридцать пять.
Теперь пришла очередь Яна. Ян отошёл от дерева и воткнул в землю
шест в десять футов длиной. Затем лёг на землю так, чтобы его глаз был на одной
линии с верхушкой шеста и веткой. Конец этой линии он отметил колышком.
Ян измерил расстояние от этого колышка до шеста: оно равнялось
тридцати одному футу, а от колышка до основания дерева — восьмидесяти семи;
тогда он составил уравнение: число тридцать один (расстояние от колышка до
шеста) относится к десяти, то есть высоте шеста, как восемьдесят семь
(расстояние от колышка до дерева) — к высоте дерева. Вышло: высота дерева
равнялась двадцати восьми футам.
Один из бойлеров влез на дерево и верёвкой измерил высоту.
Оказалось двадцать девять футов. Победителем стал Ян.
Индейцы присудили Маленькому Бобру «ку» за его знания. Но
Рафтен, услыхав об этом, воскликнул:
— Послушайте! Это же великолепно, что он делает! И он не
успокоился до тех пор, пока Ян не получил «гран ку».»
Ян — один из героев этого произведения — применил на практике
свойства подобных треугольников. И благодаря этому получил главный приз в их
мальчишеском соревновании. Вот как всё это можно схематично представить:
«Главная сила
математики состоит в том, что вместе с решением одной конкретной задачи она
создаёт общие приёмы и способы, применимые во многих ситуациях, которые даже не
всегда можно предвидеть».
М. Башмаков
Список использованных источников
и литературы:
1. Я. И. Перельман. Занимательная геометрия. – М.: АСТ,
2005.
2.Л. С. Атанасян и др. Геометрия: учебник для 7-9 кл. общеобразовательных
учреждений. – М.: Просвещение, 2017.
3. http://piterhunt.ru/pages/nk-os/5/15.htm сайт
«Питерский охотник»
4. http://www.scouts.ru «Центральный сайт
скаутов-разведчиков России»
5. А.В.Погорелов Геометрия: учебник для 7-9 кл.
общеобразовательных учреждений. – М.: Просвещение, 2016.
6. Математика для всех/Яндекс Дзен
7.
Эрнест Сетон-Томпсон «Маленькие дикари»- ЗАО «ЭНАС-КНИГА», 2012
Человеку, находящемуся в какой-либо местности может понадобится возможность измерения расстояний до определенных объектов, а также определение ширины и высоты этих обьектов. Такие измерения лучше и точнее можно провести с иcпользованием специальных средств (лазерных дальномеров, дальномерных шкал оптический приборов и.т.д.), но таковые не всегда могут оказаться под рукой. Поэтому в данной ситуации на выручку придет знание «дедовских», проверенных временем, способов. К таковым относятся:
- определение расстояний на глаз
- по угловой величине
- определение расстояний при помощи линейки и сподручных предметов
- по звуку
Определение расстояний на глаз
Данный способ является наиболее простым и быстрым. Определяющим здесь является умение мысленно откладывать на местности равные отрезки в 50, 100, 500 и 1000 м. Данные отрезки расстояний необходимо изучить и хорошо закрепить в зрительной памяти. При этом необходимо принимать во внимание следующие особенности:
- на ровной местности и водном пространстве расстояния кажутся меньше, чем они есть на самом деле,
- лощины и овраги уменьшают видимое расстояние,
- более крупные предметы кажутся ближе мелких, находящимися на одной с ними линией,
- все предметы кажутся ближе во время тумана, дождя, во время пасмурных дней,
- предметы с яркой окраской кажутся ближе,
- при наблюдении снизу вверх, расстояния кажутся ближе, а при наблюдении сверху вниз больше,
- ночью светящиеся предметы кажутся ближе.
Дистанции более 1 км определяются с большей погрешностью, достигающей 50%. У опытных людей, собенно на малых дистанциях погрешность составляет менее 10%. Глазомер необходимо постоянно тренировать в различных условиях видимости, на различной местности. При этом огромную положительную роль вносит занятие туризмом, альпинизмом, охотой.
Определение расстояний по угловой величине
Этот способ основывается на понятии тысячной. Тысячная — это единица измерения расстояний по горизонту, и составляет 1/6000 горизонта. Понятие тысячной принято во всех странах мира, и применяется для введения горизонтальных поправок ведения огня стрелкового оружия и артиллерийских систем, а также определение расстояний и дистанций. Тысячные записываются и читаются след. образом:
- 1 тысячная 0-01, читается как ноль, ноль один,
- 5 тысячных 0-05, читается как ноль, ноль пять,
- 10 тысячных 0-10, читается как ноль, десять,
- 150 тысячных 1-50, читается как один, пятьдесят,
- 1500 тысячных 15-00, читается как пятнадцать, ноль ноль.
Применение этого способа возможно, если известна одна из линейных величин предмета — ширина или высота. Дальность до предмета определяется по след. формуле: Д = (Bx1000) / Y , где Д — дальность до цели B — ширина или высота объекта в метрах Y — угловая величина в тысячных. Для того, чтобы определить угловую величину, необходимо знать, что отрезок в 1 мм, удаленному на 50 см от глаза соответствует углу в 2 тысячные (0-02). На основании этого существует метод определения расстояний при помощи линейки:
- линейку с миллиметровыми делениями вытянуть на расстояние 50 см,
- засечь, во сколько делений на линейке укладывается ширина или высота объекта,
- полученное кол-во миллиметров умножить на 2, и подставить в выше приведенную формулу.
Еще удобней для этих целей использовать штангенциркуль, который для компактности можно укоротить.
Пример: Высота телеграфоного столба равна 6 м при измерения на линейке займет 8 мм (16 тысячных ,т.е. 0-16),следовательно расстояние до столба будет (6×1000)/16 = 375 м
Также существует более простая формула определения дистанции при помощи линейки:
Д = (высота или ширина объекта в см / кол-во миллиметров на линейке) x 5
Пример: ростовая фигура имеет высоту 170 см и на линейке закрывает 2 мм, следовательно дистанция до нее будет:(170см / 2мм) x 5 = 425 м
Определение расстояний при помощи линейки и сподручных предметов
Линейные размеры распространенных объектов
| Объект | Высота, м | Длина, м |
| Телеграфный столб деревянный | 6 | —- |
| Телеграфный столб бетонный | 8 | —- |
| Расстояние между столбами ЛЭП 6м | —- | 50 |
| Расстояние между столбами высковольт. линий | —- | 100 |
| Товарный вагон, 4-х осный | 4 | 14-15 |
| Пассажирский вагон цельнометаллический | 4 | 24 |
| Цистерны, 2-х осные | 3 | 6,75 |
| Цистерны, 4-х осные | 3 | 9 |
| Один этаж панельного дома | 3 | —- |
| Дом сельского типа | 6-7 | —- |
| Высота железнодорожной будки | 4 | —- |
| Ростовая фигура (средн.) | 1,7 | —- |
| Голова без каски | 0,25 | 0,20 |
| Голова в каске | 0,30 | 0,30 |
| Танк | 2,5-3 | —- |
| Грузовой автомобиль | 2-2,5 | —- |
При отсутствии линейки угловые величины можно измерять помощи подручных предметов, зная их линейные размеры. Это может быть, например спичечный коробок, спичка, карандаш, монета, патроны, пальцы рук и.т.д Например, спичечный коробок имеет длину — 45 мм, ширину 30 мм, высоты 15 мм, следовательно если его вытянуть на расстояние 50 см, его длина будет соответствовать 0-90, ширина 0-60, высота 0-30.
Определение расстояний по звуку
Человек обладает способностью улавливать и различать звуки различной природы, как в горизонтальной плоскости, так и в вертикальной, что позволяет весьма успешно навскидку определять расстояния до источников звука. Слух, как и глазомер необходимо постоянно тренировать.
- Слух работает с полной отдачей только при полном спокойствии психики.
- Лежа на спине, слуховая ориентация ухудшается, а лежа на животе улучшается
- Зеленый цвет улучщает слух
- Кусочек сахара, положенный под язык, заметно улучшает ночное зрение и слух, поскольку глюкоза необходима для работы сердца, мозга, нервной системы, а следовательно и органов чувств.
- Звуки хорошо слышны на открытой местности, особенно водной, в спокойную погоду
- Слышимость ухудшается в жаркую погоду, против ветра, в лесу, в камышах, на рыхлой траве.
Средняя дальность слышимости различных источников
| Объект | Расстояние, км |
| Выстрел их охотничьего ружья | 3,5 |
| Шум поезда | 10 |
| Паровозный гудок | 7-10 |
| Сигнал автомобиля | 2-3 |
| Рокот работающего трактора | 3-4 |
| Топот лошадей | 1-1,5 |
| Крики человека | 1-1,5 |
| Лай собак | 2-3 |
| Негромкая речь, шум шагов | 0,3-0,5 |
| Всплески от весел | 0,25-0,5 |
| Кашель | 0,05 |
| Движение автомобиля (ровный шум мотора) | 1 |
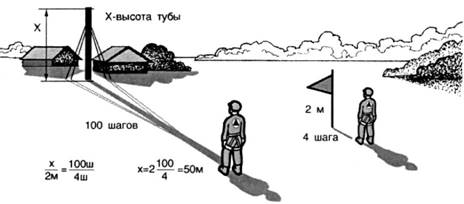
Определение
расстояния до недоступного предмета
Расстояние до недоступного
предмета можно определить по идущему человеку. Для этого необходимо закрыть
левый глаз, вытянуть руку вперед и отогнуть большой палец вверх; уловив момент,
когда палец прикроет фигуру движущегося человека, необходимо закрыть правый
глаз, а левый открыть. При этом ведется подсчет шагов до того момента, когда
палец наблюдателя снова закроет идущего человека. Полученное количество ша-гов
умножается на 10, в результате определяется расстояние до идущего человека.
Определение высоты
вертикальных предметов
Определение
высоты предмета по длине тени
Если
берег реки представляет собой ровное пространство, то для измерения ши-рины
реки может быть использован и такой способ. Наблюдатель стоит в точке А и
выбирает на противоположном берегу около воды два неподвижных предмета (
ори-ентира), затем, держа в вытянутой руке травинку (проволоку), которая
закрывает про-межуток между ориентирами, складывает ее пополам и отходит от
реки до тех пор, пока расстояние между ориентирами не уложится в сложенную
пополам травинку (В).
Расстояние между точками А и В равно ширине реки. Для
определения высоты предметов используют способ, который включает в себя
измерение длины теней самого предмета и специальной вехи, установ-ленной
вертикально, длина которой известна. После измерения длины теней предмета и
вехи определяет-ся, во сколько раз тень предмета длиннее тени вехи, результат
умножается на длину вехи. Полученное чис-
ло является искомой величиной.
При отсутствии тени высота вертикальных
пред-метов определяется следующим способом. Рядом с измеряемым предметом
необходимо установить вер-тикально палку заранее известной длины и отойти на
расстояние 25-30 шагов. В вытянутой руке держать перед глазами вертикально
карандаш или ровную па-лочку. Отметить на карандаше высоту вертикальной
палки
и измерить это расстояние. Мысленно уложить это расстояние на измеряемый
предмет. Умножив полученное количество раз на длину палки, можно получить
ис-комую величину.
Наряду с описанными способами определения
рас-стояния применяются также дальномеры. В качестве дальномера
спасатели используют бинокль. Простей-ший дальномер может быть изготовлен из
картона, ме-талла, дерева. Основание прямоугольного треугольника имеет длину 80
мм, а высота равна 17 мм. Для опреде-
ления
расстояния до предмета дальномер необходимо Дальномер
удерживать на расстоянии 50 см от глаза, передвигать
его вправо (влево) так, чтобы
фигура точно поместилась между линиями. Цифра, рас-положенная против предмета,
покажет расстояние до него.
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Подобные треугольники
- Практические приложения подобия треугольников
- Измерительные работы на местности
Свойства подобных треугольников могут быть использованы при проведении различных измерительных работ на местности.
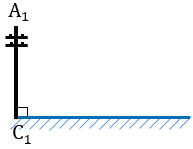
Определение высоты предмета
Пусть нам нужно определить высоту телеграфного столба А1С1.
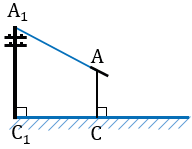
Для этого на некотором расстоянии от столба ставим шест АС с вращающейся планкой и направляем планку на верхнюю точку столба А1.
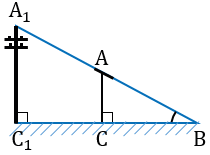
Далее отмечаем на поверхности земли точку В, в которой прямая А1А пересекается с поверхностью земли.
В 






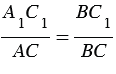
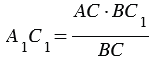
Измерив расстояния ВС1 и ВС, зная длину шеста АС, по полученной формуле вычисляем высоту А1С1 телеграфного столба. Пусть, например, ВС1 = 6,3 м, ВС = 2,1 м, АС = 1,7 м, тогда: 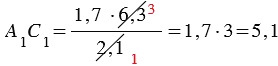
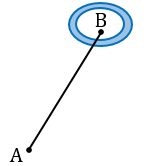
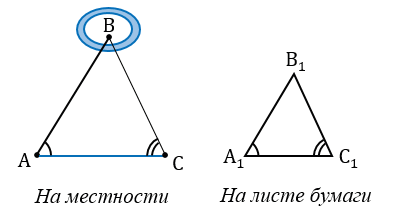
Определение расстояния до недоступной точки
Пусть, нам нужно найти расстояние от пункта А до недоступного пункта В.
Для этого на местности выбираем точку С, провешиваем отрезок АС и измеряем его.
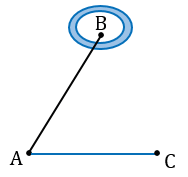
Затем с помощью астролябии измеряем углы А и С.
На листе бумаги строим какой-нибудь треугольник А1В1С1, у которого 







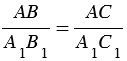
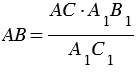
Измерив при помощи линейки длину отрезков А1В1 и А1С1, зная расстояние АС, по полученной формуле вычисляем расстояние АВ.
Чтобы сделать вычисления проще, 
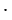
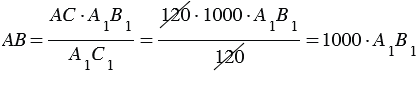
Пример:
Пусть АС = 130 м, 



Измеряем с помощью линейки отрезок А1В1. Он равен 153 мм, поэтому искомое расстояние АВ = 153 м.
Советуем посмотреть:
Задачи на построение
Пропорциональные отрезки
Определение подобных треугольников
Отношение площадей подобных треугольников
Первый признак подобия треугольников
Второй признак подобия треугольников
Третий признак подобия треугольников
Средняя линия треугольника
Пропорциональные отрезки в прямоугольном треугольнике
Практические приложения подобия треугольников
О подобии произвольных фигур
Синус, косинус и тангенс острого угла прямоугольного треугольника
Значение синуса, косинуса и тангенса для углов 30, 45 и 60
Подобные треугольники
Правило встречается в следующих упражнениях:
7 класс
Задание 579,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 580,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 581,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 582,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 583,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Тема 4.8. Топография и ориентирование на местности
Ориентироваться на местности — значит найти направление сторон горизонта и свое местонахождение относительно окружающих местных предметов и элементов рельефа. Ориентирование при передвижении по незнакомой местности состоит в определении расстояний и выдерживании нужного направления маршрута.
Способность человека оценивать на глаз расстояния до окружающих его предметов и размеры предметов называется глазомером.
Точность определения расстояния глазомером весьма различна. На дистанции в 1 км и более ошибки достигают 50 % и больше, на малых дистанциях они значительно меньше, а у людей опытных не превышают 10 %. При этом относительные расстояния (ближе, дальше, выше, ниже) глаз оценивает гораздо точнее, чем абсолютные.
Величина ошибок при определении расстояний невооруженным глазом характеризуется данными таблицы 1.
Таблица 1
|
Дитстанции в км. |
Ошибка в % |
|
Ближние (до 0,5) |
10 |
|
Средние (от 2 до 4) |
До 20 |
|
Большие (свыше 4) |
До 40-50 |
У каждого человека существуют присущие лишь ему особенности различения предметов. Их необходимо выяснить путем личных наблюдений. Умение глазомерно оценивать расстояния по показателям видимости отдельных предметов приобретается путем использования индивидуальных особенностей видимости, которые устанавливаются следующим образом.
Наблюдатель определяет на глаз различные расстояния. Степень уменьшения предметов по высоте в зависимости от расстояния показана ниже.
|
Расстояние в м |
100 |
200 |
300 |
400 |
500 |
. |
|
Степень уменьшения |
1:1 |
1:2 |
1:3 |
1:4 |
1:5 |
и т.д. |
При этом учитывается влияние перечисленных выше факторов на видимость предметов. Затем установленные глазомерно расстояния проверяются по карте или непосредственно измерением шагами и определяется величина погрешности. Такие определения расстояний и их проверка повторяются в различных условиях видимости до тех пор, пока наблюдатель не приобретет соответствующих навыков оценки всех расстояний, при которых ошибка не превышает 10 %.
Установленные особенности видимости окружающих предметов наблюдатель заносит в памятку расстояний, с которых он начинает их различать (табл. 2).
Таблица 2
|
Предметы |
Факторы, влияющие на видимость |
Предмет становится видимым с расстояния в м. |
|||||
|
цвет |
освещенность |
возвышение над горизонтом |
время суток |
наличие водного пространства |
прочие факторы |
||
|
. |
. |
. |
. |
. |
. |
. |
. |
Памятку надо постоянно проверять, корректировать и пополнять новыми данными, которые помогут точнее определить расстояния.
Полезно отмечать в графе «Прочие факторы» атмосферные явления, при которых ведется наблюдение, пользуясь приведенными условными обозначениями, принятыми в метеорологии.
Глазомер — индивидуальная способность человека, которую можно развить путем постоянных и терпеливых упражнений.
Житель равнины неплохо оценивает расстояние на ровном месте, но делает грубые ошибки в горах и на море. Горожанин часто теряется, когда ему надо определить расстояние в естественных природных условиях. Для развития глазомера надо в разных условиях местности, в разную погоду упражнять свой глаз в определении расстоянии, сравнивая результаты с показателями расстояний, измеренных каким-либо точным приемом (прибором или по карте). В развитии глазомера огромную роль играют туризм, альпинизм, охота, различные спортивные игры: футбол, хоккей, теннис, городки, баскетбол, волейбол и другие виды спорта.
Чтобы уметь правильно ориентироваться, необходимо овладеть навыками быстрого и наиболее точного выбора главного ориентира (объекта местности, выделяющегося на окружающем фоне), определения простейшими способами расстояний и размеров наблюдаемых предметов, используемых для ориентирования. Рассмотрим некоторые из этих способов.
Определение расстояний
- Измерение шагами. Многие при ходьбе делают настолько одинаковые шаги, что они могут служить единицей измерения расстояний.
Если приучить себя считать не отдельные шаги, а через два шага на третий, производя счет переменно под правую и левую ногу, то пройденное расстояние просто переводится в метры. Некоторые считают шаги не тройками, а парами. Постоянно упражняясь, можно привыкнуть считать шаги в уме почти механически.
После каждой сотни троек шагов счет начинают снова из-за сложности повторения больших трехзначных чисел. Для облегчения запоминания пройденных сотен троек шагов прибегают к последовательному загибанию пальцев, перекладыванию спичек из одного кармана в другой, отметкам на бумаге или другим средствам.
Для получения наиболее точных результатов измерения расстояний необходимо проверить длину своего шага, узнать так называемую цену шага. Проверку лучше производить на шоссейной дороге с километровыми столбами. Расстояние между ними проходят несколько раз и выводят среднюю величину шага.
Пусть, например, на 1000 м среднее количество шагов оказалось равным 450 тройкам.
| Тогда |
Каждые 9 троек шагов считаем за 20 м, т.е. в 100 тройках шагов заключается приблизительно 222 м.
Обыкновенно длина шага равна половине человеческого роста, считая до уровня глаз, т.е. в среднем 0,7‑0,8 м.
Точность измерения расстояний шагами зависит как от характера рельефа местности, так и от опытности наблюдателя. На ровной местности шаги почти одинаковы.
В среднем можно принять, что ошибка в измерении отрезка пути шагами составляет около 0,02 пройденного расстояния. При этом надо стараться делать ровные шаги, не уклоняться в сторону от намеченного направления и не топтаться на месте.
Расстояния можно измерять и временем, затраченным на ходьбу или езду. Для этого нужно заметить количество часов или минут, необходимых для прохождения или проезда известного расстояния.
Человек проходит в час столько километров, сколько делает шагов в 3 сек(при шаге длиной 0,83 м).
Шагом человек и лошадь проходят около 5-6 км/ч; рысью лошадь пробегает 12‑15 км/ч.
Проходимость местности обусловливается рельефом, почвенно-грунтовым и растительным покровом, гидрографической сетью, путями сообщения, а также временем года и состоянием погоды.
Вдоль железнодорожного полотна нередко встречаются косые дощечки с дробной надписью. Это уклоноуказатели, показывающие числителем дроби размер уклона (например, 0,003 или 0,005 указывает, что путь поднимается (если вверх) или опускается (если вниз) на 3 или на 5 мм на каждую 1000 мм),а знаменателем — протяженность уклона (150 или 200 — уклон идет на протяжении 150 или 200 м). Читая дроби, можно легко сосчитать пройденное расстояние и вычислить разность высот двух соседних точек пути. Для данных величин разность высот составляет
Следуя вдоль железнодорожного пути и учитывая знаки уклоноуказателя, можно ориентироваться не только в пройденном расстоянии, но и вычислить, на какую высоту в общей сложности пешеход поднялся или опустился на местности.
Уклон местности под ногами начинает ощущаться, когда он превышает 2,5°.
2. Измерение по видимым деталям предметов.Наблюдая человека с разных расстояний, легко заметить, что по мере его удаления отдельные подробности одежды, лица, фигуры делаются для наблюдателя неразличимыми, а затем исчезают. Видимость деталей меняется в зависимости от времени суток, состояния погоды, яркости фона и самого предмета. Так, например, в сумерки, в дождливый день в тени леса все предметы кажутся дальше и, наоборот, в ясный солнечный день на открытой местности — ближе.
Для распознавания предметов при нормальном зрении и хороших условиях видимости можно руководствоваться таблицей расстояний различимости предметов, составленной по многолетним наблюдениям (табл. 3).
Таблица 3
|
Наименование предмета |
Расстояние (в км.) |
|
|
Большие башни, церкви, элеваторы |
16-21 |
|
|
Населенные пункты |
11 |
|
|
Крупные здания |
9 |
|
|
Заводские трубы |
6 |
|
|
Отдельные дома |
5 |
|
|
Окна в домах без переплетов |
4 |
|
|
Трубы на крышах |
3 |
|
|
Отдельные деревья, столбы, люди |
2 |
|
|
Машины, повозки на земле |
1,5-1 |
|
|
Расстояние (в м.) |
||
|
Шасси самолета |
800 |
|
|
Лошади, скот — различаются ноги |
700 |
|
|
Переплеты в окнах |
500 |
|
|
Голова человека |
400 |
|
|
Цвета и части одежды |
270 |
|
|
Черепица, доски на крышах, листья деревьев |
210 |
|
|
Пуговицы, подробности одежды |
160 |
|
|
Лица людей |
115 |
|
|
Выражение лица |
100 |
|
|
Глаза человека — точками |
60 |
|
|
Белки глаз |
20 |
3. Измерение по угловым величинам предметов. Расстояние можно определять приближенно по угловой величине видимых объектов, если их линейная величина заранее известна.
Видимая, или кажущаяся, величина объекта зависит от угла зрения, или от угловой величины этого объекта, которая уменьшается по мере его удаления от глаза и увеличивается по мере его приближения к наблюдателю.
Если известны высоты или размер объекта П (таблица 4), величина подручного предмета Н и расстояние до него Л, то можно определить расстояние Д до объекта П по формуле:
| откуда |
| Если принять отношение |
за постоянную величину, равную 100, а величину П — за переменную, равную, например, 3 м, то расстояние Д будет равно
В качестве постоянного расстояния от глаза наблюдателя до предмета Н для удобства принимают длину вытянутой руки Л, равную примерно 60 см.
Тогда величина предмета Н при постоянной величине отношения
должна быть равна
т.е. примерно ширине граненого или диаметру круглого карандаша.
Пример. Мы видим велосипедиста, высота которого принимается равной 1,75 м. Ставим перед собой горизонтально карандаш на расстоянии вытянутой руки. Видим, что он по своей толщине точно покрывает велосипедиста. Тогда расстояние до него равно
Если карандаш покрывает объект с высотой, в 2 раза большей среднего роста человека, то расстояние равно примерно
Если нет предмета, в 100 раз меньшего длины вытянутой руки, можно воспользоваться случайными предметами, находящимися в другом соотношении с длиной вытянутой руки (табл.4).
Таблица 4
|
Наименование предметов |
Средний размер предмета |
|
|
Средний рост пешехода |
1,75 м |
|
|
Шаг среднего человека |
75 см |
|
|
Высота части обутой ноги от земли до колена |
50 см |
|
|
Размах руки от середины груди до основания пальцев |
71 см |
|
|
Ширина двух ладоней, сжатых в кулаки, с вытянутыми навстречу большими пальцами |
30 см |
|
|
Длина части руки от локтя до косточек пальцев сжатого кулака |
35-40 см |
|
|
Раствор между концами большого и указательного пальцев руки |
18 см |
|
|
Длина вытянутой руки |
60 см |
|
|
Длина саперной лопаты с черенком |
1,1 м |
|
|
Длина велосипеда или высота его с велосипедистом |
1,75 м |
|
|
Длина лошади |
2,13 м |
|
|
Высота всадника |
2,5 м |
|
|
Легковая машина, высота кузова и длина |
1,6 и 4,2 м |
|
|
Грузовая машина, высота кузова и длина |
2 и 5,5 м |
|
|
Высота и длина пассажирского железнодорожного вагона |
4,25 и 24,5 м |
|
|
Высота и длина товарного 4-осного железнодорожного вагона |
4 и 13,6 м |
|
|
Высота и длина 4-осной железнодорожной цистерны |
3 и 9 м |
|
|
Высота и длина 4-осной железнодорожной платформы |
1,6 и 13 м |
|
|
Высота железнодорожной будки |
4 м |
|
|
Ширина железнодорожного междупутья |
4,1 м |
|
|
Ширина железнодорожного пути |
1,52 м |
4. Пластинка Лионде. Если в формулу
подставить длину вытянутой руки Л=60 см, а рост человека П принять равным 167 см, то формула для частного случая — определения расстояния до видимого во весь рост человека — может быть упрощена
После превращения в километры и деления на 1000 формула примет вид
, т.е. расстояние в километрах до человека равно единице, деленной на число миллиметров, отсчитанных по линейке на вытянутой руке (на расстоянии 60 см).
Пример. Если человек закрывается спичкой толщиной 2 мм, то расстояние до него равно 0,5 км, или 500 м, а если тонким круглым карандашом толщиной 4 мм, то
Для упрощения измерения расстояний этим способом профессор Ф.Г. Де-Лионде предложил применять подручный прибор из алюминиевой пластинки со ступенчатыми вырезами, размеры которых соответствуют кажущейся величине человека среднего роста, находящегося на разных расстояниях от наблюдателя (рис. 1).

Например, направив на человека пластинку в вытянутой руке, устанавливаем, что фигура целиком заполняет четвертый слева вырез пластинки с надписью «125». Это значит, что расстояние от наблюдателя до объекта равно 125 м.
Измерение расстояний по угловой величине предметов с применением подручных приспособлений практически не зависит от рельефа местности, от освещения и окраски предметов. Погрешности таких измерений носят более постоянный характер и после тренировки и приобретения соответствующего навыка не должны превышать 10 %.
5. Определение расстояний при помощи «тысячных». Одним из способов измерения расстояний по угловой величине предмета является определение их при помощи «тысячных». Этот способ заключается в следующем.
Круг содержит 360°. Каждый градус делится на 60′, а минута — на 60″, т.е. окружность содержит 21600′ или 1296000″. Для получения простейшей зависимости между линейными и угловыми величинами надо разделить окружность на 6000 равных частей, называемых «тысячными». В таком случае угловые величины будут измеряться не в градусах, минутах и секундах, а в «тысячных».
Угол в одну «тысячную» в обычном градусном измерении равен
и обозначается 0-0,1. 1° обычного углового измерения равен
, округленно 17 «тысячных», или 0-17.
Угол в 30 «тысячных» обозначают 0-30, в 123 «тысячных» — 1-23 и т.д.
«Тысячная» — величина центрального угла окружности, опирающегося на хорду, длина которой равна 0,001 длины радиуса (принимая во внимание, что при малых углах и значительных радиусах круга величины хорды и дуги могут быть приравнены).
Если в формуле
заменить Л=1000, Н=У (угол зрения), то получится зависимость между угловой и истинной величинами предмета и расстоянием до него
Всегда имеется достаточное количество подручных мер, величину которых в «тысячных» можно видеть на рисунках или вычислить самим (рис. 2).

Угловая величина, или угломерная «цена» пальцев, кулака, спичечной коробки, спички, карандаша, двадцатикопеечной монеты, гильзы и других подручных предметов в «тысячных» определяется следующим способом.
Берется длина вытянутой руки наблюдателя, измеренная при самоконтроле, т.е. расстояние в миллиметрах от глаза наблюдателя до подручного предмета, что можно измерить ниткой (рис. 3).

Затем измеряется величина данного подручного предмета в миллиметрах и делится на длину вытянутой руки.
Число тысячных долей в десятичной дроби, полученной от этого деления, и дает угломерную «цену» избранного предмета в «тысячных».
Пример. Ширина обыкновенной спичечной коробки равна 37 мм. Если принять длину вытянутой руки 600 мм, то угломерная «цена» ширины спичечной коробки будет равна
, т.е. 61 «тысячная», или 0-61.
Пользоваться этими мерами надо так: взяв копейку в вытянутую руку, смотрим, закрывает ли она по ее диаметру высоту железнодорожной будки (рис. 4).

Если высота будки нам известна (4 м), то это значит, что мы видим ее под углом 0-25.
Находим величину одной «тысячной»
| ( | ). |
Следовательно, расстояние до будки будет равно .
Пример. Надо измерить расстояние до дома, длина которого известна и составляет 40 м. Определяем его угловую величину. Допустим, получилось 50 «тысячных». Тогда расстояние до дома
(рис 5).

Если угловую величину предмета в «тысячных» измерять спичкой или линейкой с делениями на миллиметры, ее надо удалять от глаз на 500 мм (50 см), тогда деление в 1 мм будет равно
, т.е. двум «тысячным» (0-02).
6. Определение расстояний по измеренным углам.Каждый предмет, видимый под углом 1°, удален на расстояние, в 57 раз больше своего размера в поперечнике (точнее в 57,3 раза). Палка длиной 1 м на расстоянии 57 м или длиной 1 см на расстоянии 57 см видна под углом 1°.
Для измерения углов можно воспользоваться следующим правилом. Каждый предмет, который покрывается ногтем указательного пальца (1 см), виден под углом 1° и отстоит на расстоянии, в 57 раз большем своего поперечника. Если ноготь покрывает половину предмета, значит, угловая его величина равна 2°, а расстояние — 28 поперечникам.
При угле в 1° расстояние в 3438 раз больше размера предмета, в 0,5° — в 114 раз, в 5° — в 11 раз, в 7° — в 8 раз.
Угловое расстояние между концами большого и указательного пальцев, максимально раздвинутых, соответствует углу в 15°. Ширина четырех пальцев у ладони равна 7° (рис. 6).

Пример. Вдали виден пассажирский вагон, который закрывается примерно половиной сустава большого пальца, т.е. виден под углом 2°. Длина вагона известна и равна 24,5 м, следовательно, он находится на расстоянии
. Если он покрывается указательным пальцем, то расстояние равно величине предмета, умноженной на 30.
Если предмет закрывается граненым карандашом, то расстояние до него равно величине предмета, умноженной на 100.
7. Измерение расстояний до недоступных предметов. На противоположном берегу реки человек идет параллельно берегу слева направо. Вытянув руку по направлению движения пешехода, смотрите одним правым глазом на конец пальца, ожидая, когда человек заслонится им. В тот же момент закройте правый глаз и откройте левый — человек словно отскочит назад. Сейчас же считайте, сколько шагов сделает пешеход, прежде чем снова поравняется с вашим пальцем (рис. 7).

Расстояние от вас до человека на другом берегу реки определяется из пропорции
Пример. Расстояние между зрачками глаз Г=6 см, от конца вытянутой руки до глаза Л=60 см. Пешеход прошел расстояние П, равное 18 шагам; в среднем шаг равен 75 см.
Подставляя эти величины в формулу, получаем
шагам, или
Измерив расстояния между зрачками и от глаз до конца вытянутой руки, надо получить и запомнить их отношение, которое у большинства людей достигает 10.
Затруднение может возникнуть лишь в определении пройденного расстояния, так как не всегда можно воспользоваться шагами человека. В этом случае нужно запомнить длину наиболее распространенных предметов. Таким образом, можно оценить пройденное человеком расстояние, сравнив его с длиной дома, вагона, шириной окна и других предметов, до которых надо определить расстояние. Остается только умножить их длину на полученное отношение
8. Измерение расстояний путем мысленного последовательного отложения известного отрезка. Вы видите опору линии электропередачи и, не доходя до нее, столбик. Становитесь с ним в створ. Оценивайте расстояние от себя до столбика. Допустим, оно равно 100 м. Эту длину мысленно переносите на участок между столбиком и опорой, учитывая, что расстояние кажется тем меньшим, чем далее от наблюдателя оно откладывается. В данном случае первый отрезок оказался равным второму. Таким образом, расстояние от вас до опоры равно 200 м (рис. 8).

Ошибки бывают очень грубые при резкой перемене обстановки, например при переходе с заросшей кустарником поляны на пашню, ночью при лунном свете на городских улицах, при определении расстояния до предмета, основание которого заслонено какой-нибудь возвышенностью (холм, дом и т.п.).
9. Измерение ширины реки при помощи травинки. Выбираем на противоположном берегу, в непосредственной близости от него, два заметных предмета и, стоя по другую сторону реки с вытянутыми руками, в которых зажата травинка, закрываем промежуток между выбранными предметами. Один глаз должен быть закрыт.
После этого, сложив травинку пополам, отходим от берега реки до тех пор, пока расстояние между выбранными предметами не закроется сложенной травинкой. Затем измеряем промежуток между двумя точками своего стояния. Расстояние между ними будет равно ширине реки (рис. 9).

10. Определение ширины реки шагами. Выбираем на противоположном берегу какой-нибудь заметный предмет, например лодку. Становимся против нее и под прямым углом к этому направлению, вдоль берега, отсчитываем определенное число шагов, например 50. Ставим палку, затем в том же направлении снова отсчитываем уже половинное число шагов (в нашем примере 25) и от этого места идем под прямым углом от берега до тех пор, пока не окажемся на одной прямой с палкой и лодкой. Удвоенное количество шагов от берега до нашей остановки в створе, т.е.
шагов, и есть ширина реки (рис. 10).

Если после установки палки, как и до ее установки, мы отсчитали 50 шагов, то расстояние от берега до створа равно ширине реки.
Определение высоты
1. Измерение по тени предмета. Ставим отвесно палку в тени дерева недалеко от ее верхушки и измеряем длину части палки, покрытой тенью (рис. 11).

Тогда
, откуда
, т.е., разделив длину покрытой тенью части палки на расстояние от нее до верхушки тени дерева и помножив это число на длину тени от дерева, получим высоту дерева или любого другого предмета.
Пример. Длина палки 2 м, а ее тень 1,5 м, следовательно, высота предмета пропорционально больше длины его тени (рис. 12).

Когда тень от палки равна ее длине, то высота предмета также равна длине своей тени.
Измерение по росту человека. Отойдя от дерева на известное расстояние АД (рис. 13), ложимся головой к точке А и ногами, между которыми зажата палка, к дереву в точке Б так, чтобы наш луч зрения проходил через верх палки на вершину дерева. Тогда

| Прикрепленный файл | Размер |
|---|---|
| Тема 4.8. Топография и ориентирование на местности.pdf | 1.65 Мб |