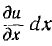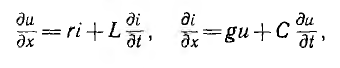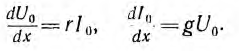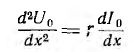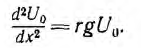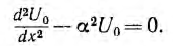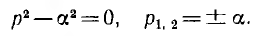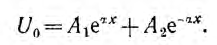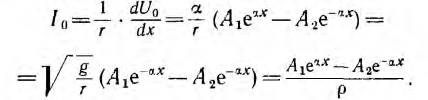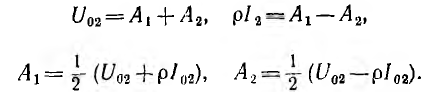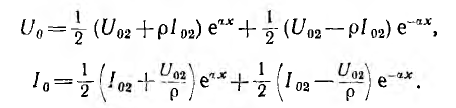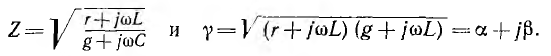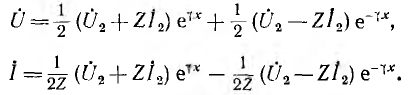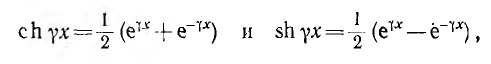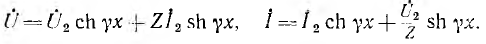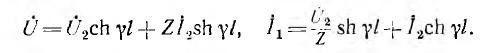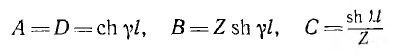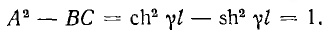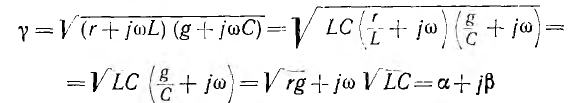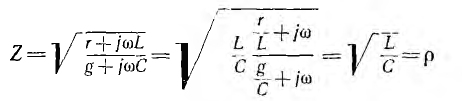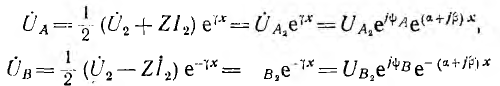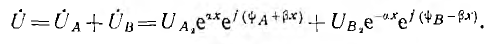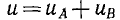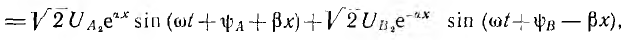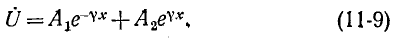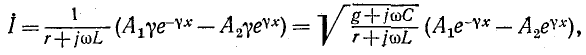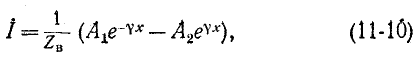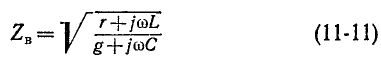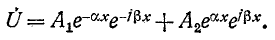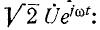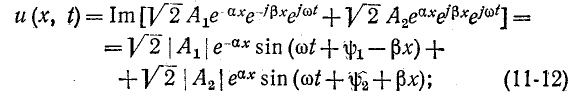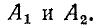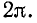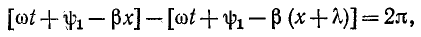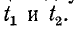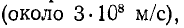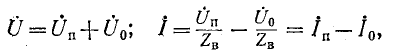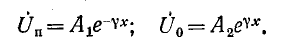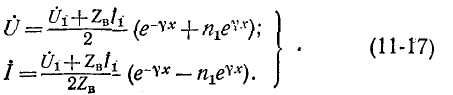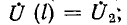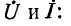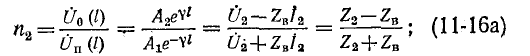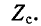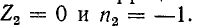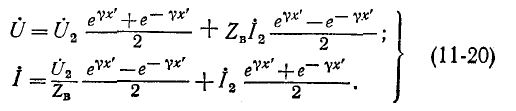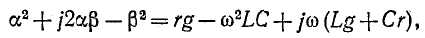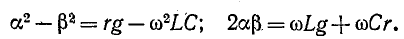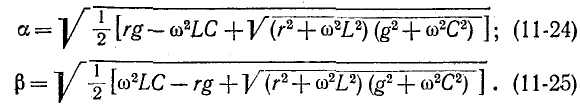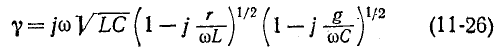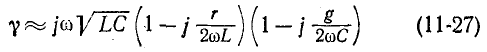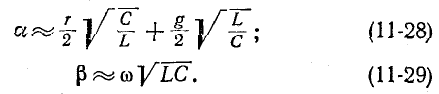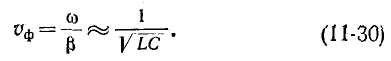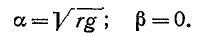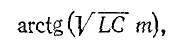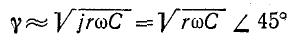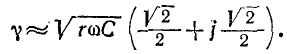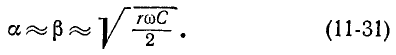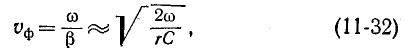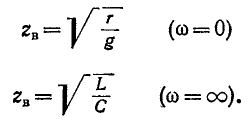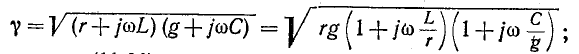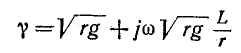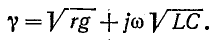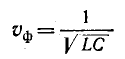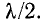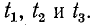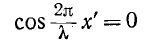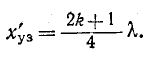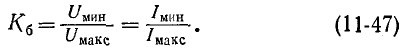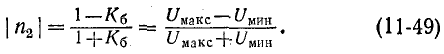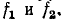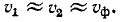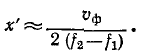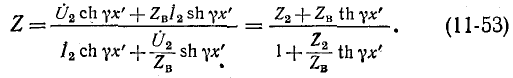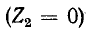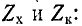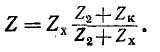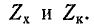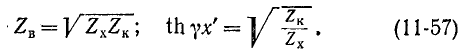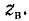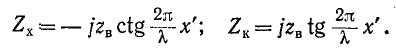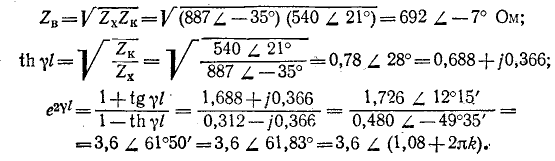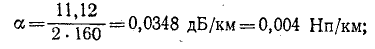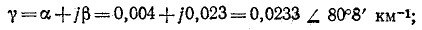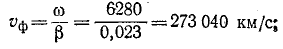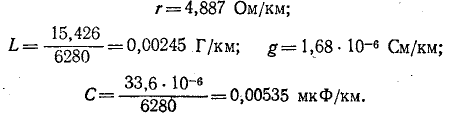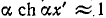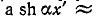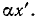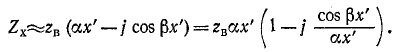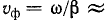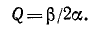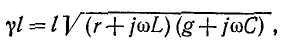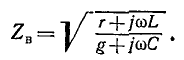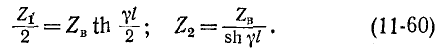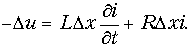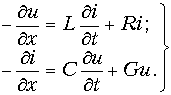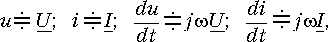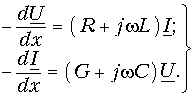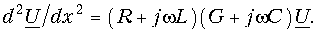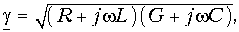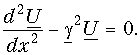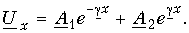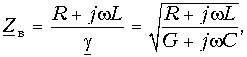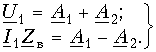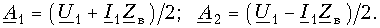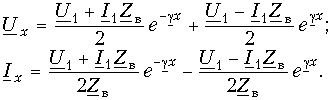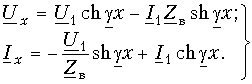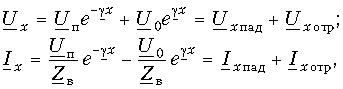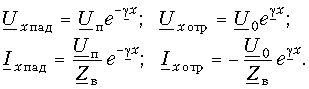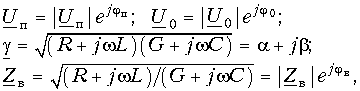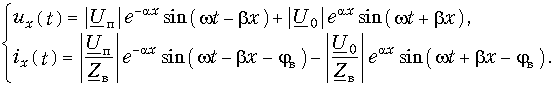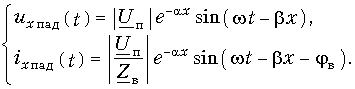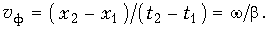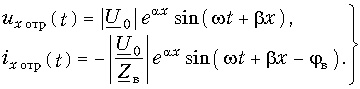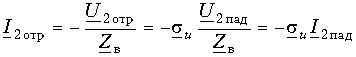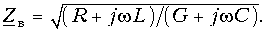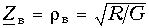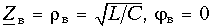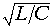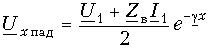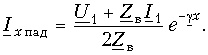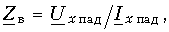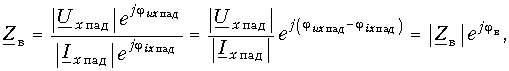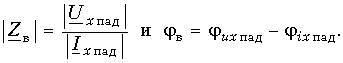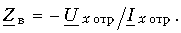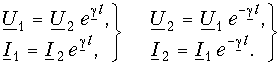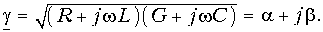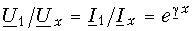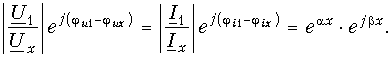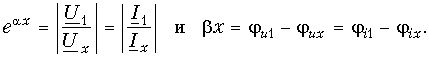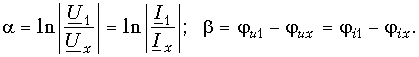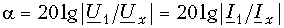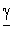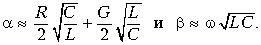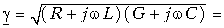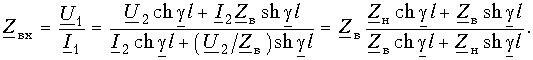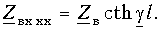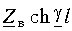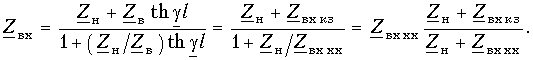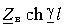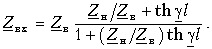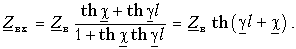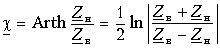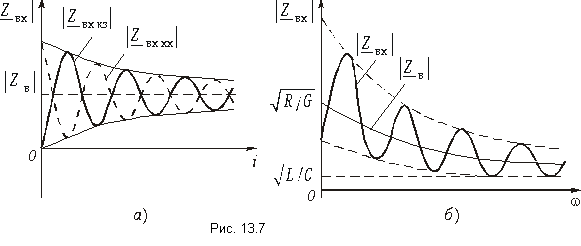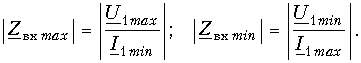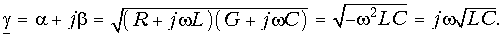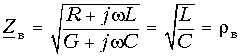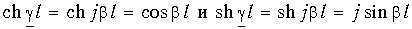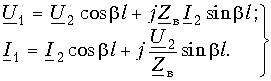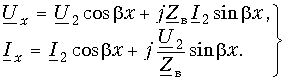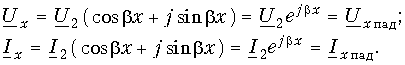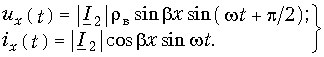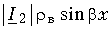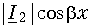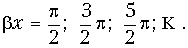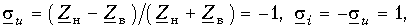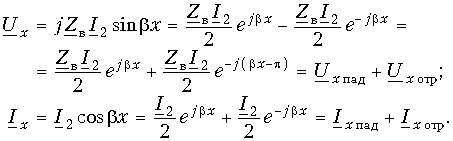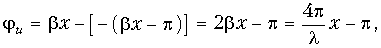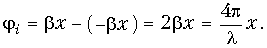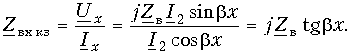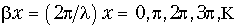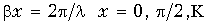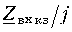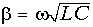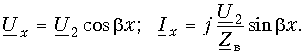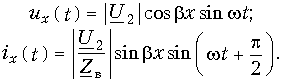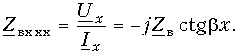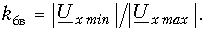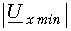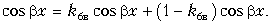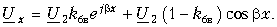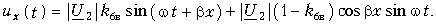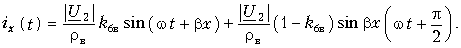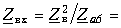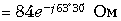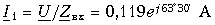Алгоритм решения
задач по физике для расчета характеристик электрической цепи.
Малкова Анастасия Викторовна, ГБОУ школа №
258 Колпинского района Санкт-Петербурга
Цель: систематизация знаний учащихся по теме «Электрический
ток», применение полученных знаний для решения задач на расчет характеристик
электрической цепи в случае смешанного соединения проводников
Характеристиками электрической цепи являются значения
сопротивления элементов ее составляющих, сила тока и напряжение на них, а также
работа и мощность.
Основополагающим для школьников среднего звена при
изучении электрического тока является закон Ома для участка цепи:
I = U / R
Также необходимо не забывать о правилах при вычислении
тех или иных характеристик цепи при разных типах соединения проводников. Для
удобства восприятия все необходимые для вычисления формулы можно
систематизировать в таблице:
|
Сила тока I (А) |
Сопротивление R (Ом) |
Напряжение U (В) |
Работа А (Дж) |
Мощность Р (Вт) |
|
|
Определение |
I = q/t |
R = U / I |
U = A / q |
A = UIt |
P = UI |
|
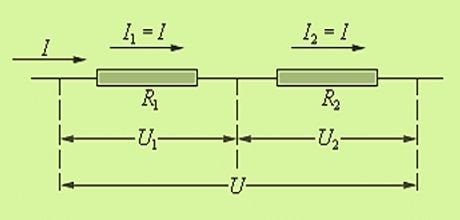
Последовательное соединение |
I = I1 = I2 |
R= R1 + R2 |
U = U1 + U2 |
A = I2Rt |
P = I2R |
|
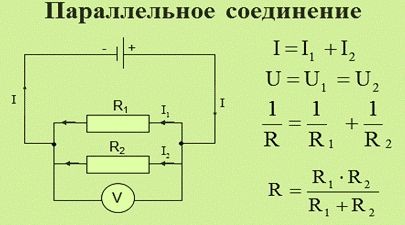
Параллельное соединение |
I = I1 + I2 |
1/R = 1/R1 + 1/R2 |
U = U1 = U2 |
A = U2t / R |
P = U2 / R |
При
рассмотрении задач на смешанное соединение проводников необходимо делить их на
небольшие задачки, в каждой из которых рассматривать уже только один тип
соединения.
Рассмотрим
задачу:
Найдите
распределение сил токов и напряжений в цепи, общее сопротивление элементов
цепи, если амперметр показывает 3 А, а R1=2 Ом, R2=4 Ом, R3=3 Ом, R4=1 Ом, R5=12Ом.
|
Дано: Ia= R1=2Ом R2=4Ом R3=3Ом R4=1Ом R5=12Ом |
Решение: Задача представляет из себя пример смешанного соединение проводников. I этап. Нахождение общего сопротивления цепи. Рассмотрим 1 и 2 резисторы, они между собой связаны последовательным R12 = R1 + R2
|
|
Найти: Rобщ — ? I1 , I2 ,I3 ,I4 ,I5 — ? U1 , U2 ,U3 ,U4 ,U5 — ? |

Резисторы
R12 и R5 соединены в цепь последовательно.
Преобразовываем схему и применяем формулу
=
+
Приводим
формулу и рассчитываем R125

R125 = = 4 Ом
Элементы
R3, R4, R125 последовательно соединены. Делаем последнее преобразование цепи и
применяя формулы для расчеты сопротивления проводников при последовательном
соединении , находим значение R общ
Rобщ = R3 + R4 + R125
Rобщ = 3 Ом + 4 Ом + 1 Ом
= 8 Ом
II этап. Нахождение распределения сил токов и
напряжений на элементах электрической цепи.
Для
наиболее наглядного представления результатов вычислений рекомендуется
использовать таблицу. По данным задачи мы можем внести в нее значение
сопротивлений всех элементов цепи и общее значение силы тока (поскольку именно
это значение измеряется при данном подключении амперметра). Также мы можем
заполнить ячейку с ранее вычисленным общим значением сопротивления цепи.
|
1 |
2 |
3 |
4 |
5 |
общее |
|
|
Сила тока I (А) |
3 |
|||||
|
Напряжение U (В) |
||||||
|
Сопротивление R (Ом) |
2 |
4 |
3 |
1 |
12 |
8 |
Исходя
из данных таблицы найдем значение напряжения по закону Ома для участка цепи:
Uобщ = Iобщ * Rобщ
Uобщ = 3А * 8 Ом = 24 В
По
правилу распределения тока в цепи Iа = I3 = I3 = I125 = 3А
Можем
воспользовавшись законом Ома для участка цепи определить напряжения на 3-ем и
4-ом проводниках:
U3 = I3 * R3
U3 = 3А * 3Ом = 9 В
U4 = I4 * R4
U4
= 3А * 1 Ом = 3
В
Рассмотрим
элемент, состоящий из 1го, 2го и 5го проводников. Поскольку между 5м и 1-2м
параллельное соединение, то воcпользуемся формулой:
U125 = U12 = U5 = 12 В
Зная
значение напряжения на 5м проводнике и его сопротивление, найдем значение силы
тока на нем:
I5 =
U5 / R5
I5 = 12 / 12 = 1 А
Для
нахождения тока на 1-2 резисторах воспользуемся правилом (т к 1-2 и 5
проводники соединены параллельно) :
I125
= I12 + I5
Следовательно,
I12 = I125 — I5 = 3А – 1А = 2А
Т
к проводники между собой соединены последовательно , то и значение сил токов на
них совпадают, а значит
I1 =I2 = I12 = 2А
Осталось
по закону Ома для участка цепи вычислить значение напряжений на этих резисторах
U1 =
I1 * R1
U1 = 2А * 2Ом = 4 В
U2 = I2 * R2
U2 = 2А * 4 Ом = 8 В
Все
полученные результаты вычислений были занесены в таблицу.
|
1 |
2 |
3 |
4 |
5 |
общее |
|
|
Сила тока I (А) |
2 |
2 |
3 |
3 |
1 |
3 |
|
Напряжение U (В) |
4 |
8 |
9 |
3 |
12 |
24 |
|
Сопротивление R (Ом) |
2 |
4 |
3 |
1 |
12 |
8 |
Таким
образом сложную задачу удалось решить методом последовательного упрощения
электрической схемы или рассмотрения отдельных элементов этой цепи.
Задача для самостоятельной работы:
Найдите
распределение сил токов и напряжений в цепи, общее сопротивление элементов
цепи, если вольтметр показывает 68 В, а R1=2 Ом, R2=8 Ом, R3=3 Ом, R4=6 Ом, R5=3,4 Ом.
Ответы
к задаче:
|
1 |
2 |
3 |
4 |
5 |
общее |
|
|
Сила тока I (А) |
16 |
4 |
13,3 |
6,6 |
20 |
20 |
|
Напряжение U (В) |
32 |
32 |
40 |
40 |
68 |
140 |
|
Сопротивление R (Ом) |
2 |
8 |
3 |
6 |
3,4 |
7 |
to continue to Google Sites
Not your computer? Use Guest mode to sign in privately. Learn more
Во всех электрических схемах используются резисторы, представляющие собой элементы, с точно установленным значением сопротивления. Благодаря специфическим качествам этих устройств, становится возможной регулировка напряжения и силы тока на любых участках схемы. Данные свойства лежат в основе работы практически всех электронных приборов и оборудования. Так, напряжение при параллельном и последовательном соединении резисторов будет отличаться. Поэтому каждый вид соединения может применяться только в определенных условиях, чтобы та или иная электрическая схема могла в полном объеме выполнять свои функции.
Напряжение при последовательном соединении
При последовательном соединении два резистора и более соединяются в общую цепь таким образом, что каждый из них имеет контакт с другим устройством только в одной точке. Иначе говоря, конец первого резистора соединяется с началом второго, а конец второго – с началом третьего и т.д.
Особенностью данной схемы является прохождение через все подключенные резисторы одного и того же значения электрического тока. С возрастанием количества элементов на рассматриваемом участке цепи, течение электрического тока становится все более затрудненным. Это происходит из-за увеличения общего сопротивления резисторов при их последовательном соединении. Данное свойство отражается формулой: Rобщ = R1 + R2.
Распределение напряжения, в соответствии с законом Ома, осуществляется на каждый резистор по формуле: VRn = IRn x Rn. Таким образом, при увеличении сопротивления резистора, возрастает и падающее на него напряжение.
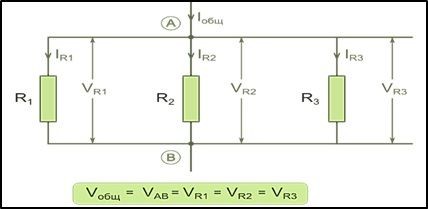
Напряжение при параллельном соединении
При параллельном соединении, включение резисторов в электрическую цепь выполняется таким образом, что все элементы сопротивлений подключаются друг к другу сразу обоими контактами. Одна точка, представляющая собой электрический узел, может соединять одновременно несколько резисторов.
Такое соединение предполагает течение отдельного тока в каждом резисторе. Сила этого тока находится в обратно пропорциональной зависимости с сопротивлением резистора. В результате, происходит увеличение общей проводимости данного участка цепи, при общем уменьшении сопротивления. В случае параллельного соединения резисторов с различным сопротивлением, значение общего сопротивления на этом участке всегда будет ниже самого маленького сопротивления отдельно взятого резистора.
На представленной схеме, напряжение между точками А и В представляет собой не только общее напряжение для всего участка, но и напряжение, поступающее к каждому отдельно взятому резистору. Таким образом, в случае параллельного соединения, напряжение, подаваемое ко всем резисторам, будет одинаковым.
В результате, напряжение при параллельном и последовательном соединении будет отличаться в каждом случае. Благодаря этому свойству, имеется реальная возможность отрегулировать данную величину на любом участке цепи.
Цепи с распределенными параметрами
Содержание:
Цепи с распределенными параметрами:
Как было показано в гл. I, электрическое и магнитное поле, а также превращение электромагнитной энергии в тепло, имеют место в каждом элементарном участке любых электрических устройств — индуктивных катушках, обмотках электрических машин и трансформаторов, линиях передачи электрической энергии и т. п. Следовательно, все устройства являются цепями с распределенными индуктивностью, емкостью и сопротивлением.
Однако, когда эти устройства рассматриваются в целом, они обычно заменяются эквивалентными двухполюсниками или четырехполюсниками с сосредоточенными параметрами г, L и С. Если устройство работает при одной частоте, эквивалентные схемы приводятся к простейшим — последовательному или параллельному соединению активного и реактивного сопротивлений для двухполюсника и к Т-образной или П-образной схеме с теми же элементами для четырехполюсника.
Если необходимо провести анализ для некоторого диапазона частот, эквивалентная схема становится тем сложней, чем шире этот диапазон. В общем случае приходится рассматривать цепь такой, какая она есть в действительности, т. е. как цепь с распределенными параметрами.
Необходимость рассмотрения устройств как цепей с распределенными параметрами возникает также в тех случаях, когда анализ должен выявить соотношения внутри устройства, например требуется определить напряжение и ток в разных точках линии передачи.
Далее методы расчета цепей с распределенными параметрами изучаются на примере однородных линий передач, широко применяемых в электроэнергетике и технике электрической связи.
Уравнения однородной линии
В двухпроводных однородных линиях индуктивность и сопротивление линии, а также емкость и проводимость через несовершенную изоляцию между проводами можно считать распределенными равномерно. Эти параметры на единицу длины двухпроводной линии, подсчитанные для линий различной конфигурации, в дальнейшем обозначены, соответственно, L, г, с, g.
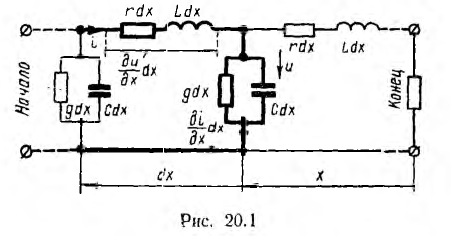
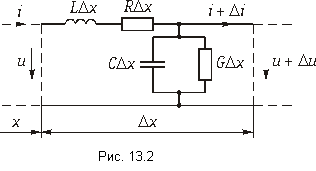
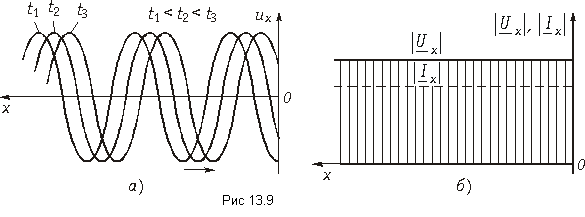
Бесконечно малый элемент двухпроводной линии длиной dx может быть заменен эквивалентной схемой с параметрами Ldx, rdx, Cdx и rdx. На рис. 20.1 эта схема изображена жирными линиями и выбраны управления напряжений и токов. При этом индуктивность и сопротивление являются продольными параметрами линии, а емкость и проводимость — ее поперечными параметрами.
В каждом элементе dx линии происходит падение напряжения
В общем случае переменных напряжений и токов для элемента, расположенного на расстоянии х от конца линии и отмеченного на рис. 20.1 жирными линиями,
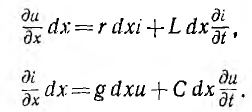
После сокращения на dx получается система уравнений в частных производных для мгновенных значений напряжений и токов:
решение которой при заданных начальных и граничных условиях определит u и i в функции х и t.
При анализе процессов в трехфазной линии каждая ее фаза может рассматриваться, как однофазная двухпроводная линия. Не приводя вывода, можно, например, указать, что для симметричной трехфазной воздушной линии, провода которой расположены в вершинах равностороннего треугольника и удалены от земли, эквивалентная каждой фазе двухпроводная линия имеет индуктивность I, вдвое меньшую, а емкость С, вдвое большую, чем двухпроводная линия с таким же расстоянием между проводами, как и трехфазная линия. Сопротивление г эквивалентной двухпроводной линии равно сопротивлению провода одной фазы, а проводимость g — проводимости одной фазы по отношению к земле.
Решение уравнений однородной линии для установившихся режимов
Режим постоянного напряжения:
Если к началу линии приложено постоянное напряжение U01, npи установившемся режиме напряжения и токи в линии будут также постоянными. При подстановке в уравнения линии вместо переменных мгновенных значений u и i постоянных во времени U0 и I0 в каждой точке линии производные по t будут равны нулю и уравнения станут обыкновенными дифференциальными уравнениями, в которых независимой переменной является x — расстояние от конца линии:
Для получения из приведенной выше системы одного уравнения с одним неизвестным U0 надо взять производную по х от первого уравнения:
и подставить сюда значение 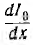
Если положить, что 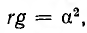
Характеристическое уравнение и его корни имеют вид:
Общее решение для напряжения на расстоянии х от конца линии получает вид:
Следовательно, ток в этой точке
Отсюда видно, что однородную линию характеризуют две величины: 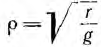
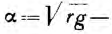
Постоянные интегрирования определяются из граничных условий, которыми могут быть две из четырех величин, например напряжение U01 ток I01 в начале линии или U02, I02 в конце линии. Пусть заданы напряжение U02 и сопротивление r2 нагрузки и тем самым ток 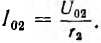
Откуда
Следовательно, напряжение и ток на расстоянии х от конца линии будут:
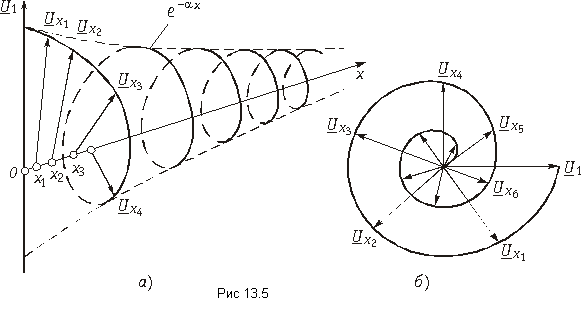
Таким образом, напряжение и ток в любой точке линии определяются алгебраическими суммами ординат двух экспоненциальных кривых. Ординаты кривой с 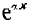
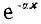
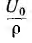
Следовательно, в однородной линии постоянного тока происходит затухание напряжения и тока вдоль линии, определяемое коэффициентом распространения 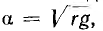
Режим синусоидального напряжения
Если к началу линии приложено синусоидальное напряжение постоянной угловой частоты ω, при установившемся режиме напряжение и ток в каждой точке линии будут также синусоидальными функциями времени той же частоты. Так как синусоидальные напряжение и ток являются частным случаем переменных и и i, в расчетах надо учесть все параметры линии рис. 20.1, т. е. r, L, g и С.
Применяя символический метод, можно использовать результаты расчета для линии постоянного тока (п. 1), заменив продольное сопротивление r комплексным сопротивлением 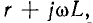
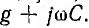
Вещественная часть а коэффициента распространения является коэффициентом затухания, а мнимая 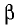
При указанном переходе от постоянного тока к синусоидальному комплексные напряжения и ток на расстоянии х от конца линии получают вид:
Если ввести гиперболические функции
выражения для 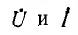
Эти уравнения аналогичны уравнениям для однородных симметричных цепных схем, что и следовало ожидать, так как однородная линия рассматривалась как однородная цепная схема с бесконечно большим числом элементарных звеньев.
Однородная линия в целом является симметричным пассивным четырехполюсником. Его уравнения получают из последних выражений при х =1, где 1 — длина линии:
Параметры этого четырехполюсника
Из уравнений линии видно, что напряжение и ток в любой точке линии являются также функцией частоты ω, так как от нее зависят волновое сопротивление Z, коэффициент распространения у и его составляющие 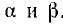
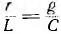
и, следовательно, коэффициент затухания а = 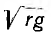
является вещественным числом, т. е. активным сопротивлением, также независящим от частоты. В результате передача будет осуществляться без искажения. Такая линия называемся неискажающей.
Бегущие и стоячие волны
Уравнения линии для режима синусоидального напряжения могут быть преобразованы. После введения значения 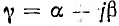
комплекс напряжения в линии получает вид:
Переходя к мгновенному значению напряжения
его можно рассматривать как сумму двух составляющих 
В любой фиксированный момент времени первая составляющая иА распределена вдоль линии по закону синуса с амплитудой, которая и соответствии с множителем е» возрастает от конца линии к ее началу, т. е. затухает от начала линии к ее концу. Если в данный момент времени I’ в точке х’
то в точке х» 2 , прив р, тогда коэффициент отражения n от конца линии равен отношению отраженной волны к падающей, вычисленному в п. 2:
и. волна напряжения U0 отразится от конца линии без перемены знака, а волна тока I0 с переменой знака. На рис. 20.11, а показан напряжение и ток линии после отражения для г2 = 4р, т.е. для = 0,6. Отраженные волны 0,6 U0 и — 0,6 I0 увеличивают напряжение до 1,6 U0 и уменьшают ток до 0,4 I0. После отражения от начала инии волна — 0,6 U0 снизит напряжение линии до U0, а волна — 6 I0 снизит ток до — 0,2 I0 (рис. 20.11, б). В результате второго отра-ения от конца линии напряжение на ней будет 0,64 U0, а ток 0,16 I0 же. 20.11, в) и т. д.
При включении короткозамкнутой линии ее конец, как. и начало, удут отражать волну напряжения с переменой знака, а волну тока — без перемены. При включении такой линии волны напряжения U0 I тока I0 при t 1 Обоснованием высказанного положения является линейность уравнений (11-2) и (11-3), так как только в таких уравнениях сохраняется синусоидальность всех функций.
Применяя комплексную форму записи, перепишем уравнения в комплексном виде: 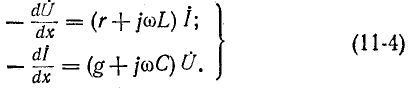
Ввиду того что комплексные значения
Исключая из системы (11-4) ток 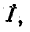
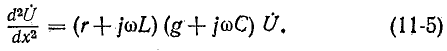
Аналогично, исключая из (11-4) напряжение 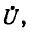
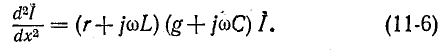
Обозначим квадратный корень из комплексного множителя при 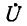
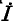
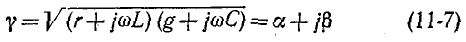
и назовем эту величину коэффициентом распространения
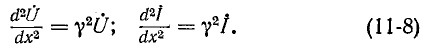
Получились одинаковые однородные линейные дифференциальные уравнения второго порядка. Решение первого из них имеет вид:
Ток 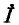
или
где
называется волновым сопротивлением линии
Смысл такого названия объяснен дальше. Подставив (11-7) в (11-9), получим:
Мгновенное значение напряжения в точке х равно мнимой части выражения
здесь 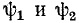
Таким образом, мгновенное значение напряжения в любой точке линии слагается из двух функций.
Рассмотрим вначале первую из этих слагающих функций.
Если считать точку х фиксированной и рассматривать изменение напряжения в данной точке в зависимости от времени, то первая слагающая выражения (11-12) представит собой синусоидальную функцию с постоянной амплитудой.
Если же считать момент времени t фиксированным и рассматривать изменение мгновенного напряжения вдоль линии (т. е. в зависимости от х), то получим затухающую синусоидальную волну напряжения, амплитуда которой 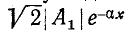
Величина а, характеризующая изменение амплитуды волны на единицу длины линии, называется коэффициентом ослабления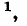
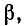
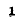
Убывание амплитуды волны вдоль линии обусловливается потерями в линии, а изменение фазы — конечной скоростью распространения электромагнитных колебаний.
Оба эти коэффициента а и 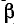
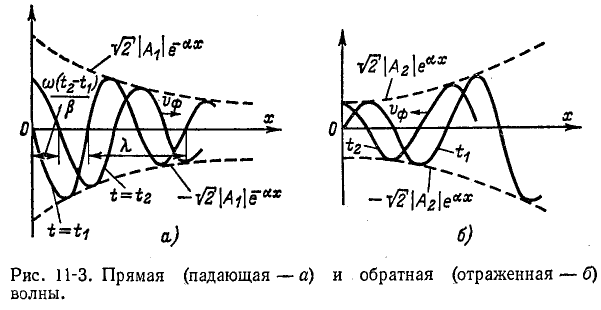
На рис. 11-3, а буквой 
Полученная формула выражает зависимость, существующую между длиной волны и коэффициентом фазы линии.
На рис. 11-3, а изображены волны напряжения, соответствующие двум следующим друг за другом моментам времени:
С течением времени волна перемещается от начала линии к ее концу; она носит название прямой, или п а-дающей, волны.
Скорость перемещения падающей волны вдоль линии, называемая фазовой скоростью волны 
Эго условие записывается для прямой волны в виде
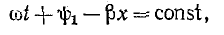
откуда
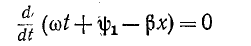
и, следовательно, 
Аналогичное исследование второго слагаемого выражения (11-12) показывает, что для произвольного момента времени оно представляет синусоидальную волну, амплитуда которой 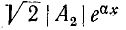
Фазовая скорость обратной волны получается равной
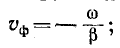
движется в направлении, противоположном направлению прямой волны.
Итак, мгновенное напряжение можно рассматривать как сумму двух волн, движущихся в противоположных направлениях, причем каждая из этих волн затухает в направлении движения.
На основании (11-13) и (11-14) 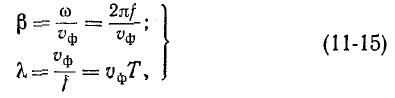
т. е. за время, равное одному периоду, как падающая, так и отраженная волны перемещаются на расстояние, равное длине волны.
Линии, физическая длина которых соизмерима с длиной волны, считаются длинными линиями. При достаточно высоких частотах практически любая протяженная электрическая цепь становится «длинной» по отношению к длине волны.
Как будет показано ниже, фазовая скорость в воздушной линии близка к скорости света
и поэтому частоте 50 Гц будет соответствовать длина волны 6000 км, а частоте 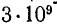
Возвращаясь к уравнениям (11-9) и (11-10) и записывая прямую и обратную волны в комплексной форме, имеем:
Напряжение и ток прямой и соответственно обратной волн связаны законом Ома: 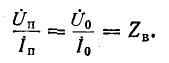
Это соотношение объясняет смысл названия 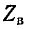
Постоянные интегрирования 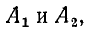
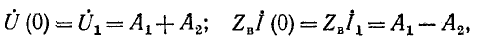
откуда
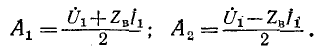
Введем понятие коэффициента отражения волны в начале линии:
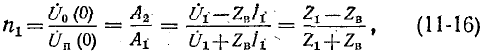
где 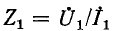
Подстановка выражений для 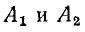
Если заданы граничные условия на конце линии, то удобнее отсчитывать расстояние от конца, приняв координату х’.
Заменяя в уравнениях (11-9) и (11-10) х на (l — х’) и используя заданные граничные условия 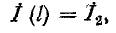
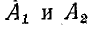
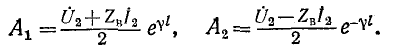
Подставив их в (11-9) и (11-10), получим окончательные выражения для
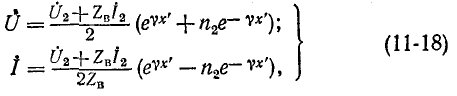
где аналогично предыдущему 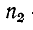
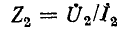
Если сопротивление приемника равно волновому сопротивлению линии 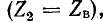
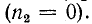
Это важное свойство реализуется в линиях связи, отражения в которых нежелательны по ряду причин.
Во-первых, если затухание в линии невелико, то отраженная волна создает эффект эха в начале линии.
Во-вторых, отражения связаны с потерей энергии. Часть энергии, достигшая приемного конца, не поступает в приемник, а возвращается по линии в виде энергии отраженной волны. При этом возникают дополнительные потери энергии в сопротивлении r и проводимости g линии. Если сопротивление источника, питающего линию, не равно волновому сопротивлению линии, то отраженная волна, достигнув начала линии, претерпевает повторное отражение и т. д. Происходящая вследствие этого потеря энергии в линии понижает общий к. п. д. передачи.
В-третьих, в случае отражений может иметь место нежелательное увеличение напряжения или тока в линии.
Вследствие указанных причин на практике стремятся согласовать сопротивление приемника с волновым сопротивлением линии. При согласовании нагрузки с линией выражения (11-18) упрощаются: с учетом того, что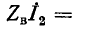
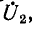
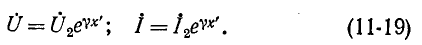
Эти выражения показывают, что при перемещении точки наблюдения вдоль линии, нагруженной согласованно-на конце, в направлении от конца к началу линии, модуль напряжения возрастает в 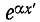
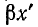
Уравнения (11-19) аналогичны уравнениям симметричного четырехполюсника при согласованной нагрузке. Поэтому показатель распространения на всю длину линии 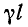
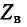
Выражения (11-19) показывают, что при согласованной нагрузке 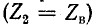
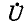
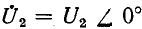
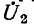
Большой интерес представляет также рассмотрение двух частных случаев нагрузки линии, а именно случаев, когда линия на конце разомкнута (режим холостого хода)
или замкнута (режим короткого замыкания). В первом случае 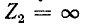

К рассмотрению этих двух случаев мы вернемся несколько позже.
Система уравнений (11-18) может быть переписана в следующем виде:
Уравнения (11-18) и (11-20) представляют собой уравнения линии в показательной (или волновой) форме при отсчете расстояния от конца линии. Они преобразуются с помощью гиперболических функций:
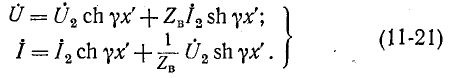
Положив в этих уравнениях х’ = l, получим уравнения линии в гиперболической форме, выражающие напряжение и ток в начале через напряжение и ток в конце линии:
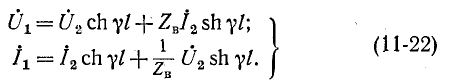
Обращает на себя внимание сходство полученных уравнений с уравнениями симметричного четырехполюсника. Эти уравнения показывают, что однородная линия представляет собой симметричный четырехполюсник с характеристическими параметрами 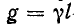
Применяя параметры 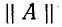
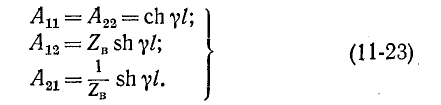
Показательная и гиперболическая формы записи уравнений линии (11-18) и (11-21) дополняют друг друга и применяются в зависимости от условий задачи.
Преимущество показательной формы записи уравнений заключается в большей наглядности рассмотрения физических процессов в линии с помощью прямых и обратных волн и удобстве построения геометрических мест на комплексной плоскости. Поэтому уравнения (11-18) широко использованы в последующих параграфах данной главы.
Гиперболическая форма записи уравнений также представляет в ряде случаев известные удобства с точки зрения исследования и расчета электрических величин в линии и их фазовых соотношений.
Рассмотрение линии как четырехполюсника базируется обычно на гиперболической форме записи уравнений.
Вторичные параметры однородной линии
Вторичными, или характеристическими, параметрами линии являются коэффициент ослабления, коэффициент фазы 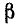
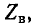
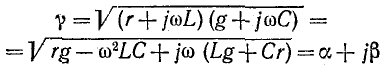
Совместное решение этих уравнений дает:
Из полученных выражений следует, что 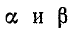
Формула (11-25) позволяет выразить фазовую скорость распространения электромагнитной волны через первичные параметры линии и частоту по формуле (11-14).
Выражения (11-24) и (11-25) неудобны для практического использования ввиду их громоздкости. Существует ряд приближенных расчетных формул для вычисления вторичных параметров линии, учитывающих, что в области высоких частот (порядка 1 МГц и выше) сопротивление r весьма мало по сравнению 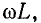
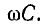
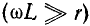
Используя для выражения
бином Ньютона, ограничиваясь первыми двумя членами разложения
и пренебрегая ввиду малости слагаемым — 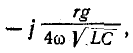
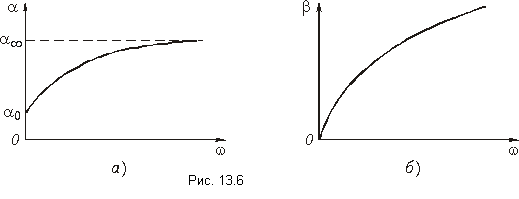
Эти формулы представляют собой пределы, к которым стремятся коэффициент ослабления и коэффициент фазы с ростом частоты.
Выражение (11-28) не следует понимать в том смысле, что а не зависит от частоты; входящие в него параметры r и g сами являются функциями частоты.
Первое слагаемое в правой части выражения (11-28) определяет ту долю ослабления, которая обусловливается продольным активным сопротивлением линии. Второе слагаемое определяет долю ослабления, которая вносится в передачу вследствие наличия поперечной активной проводимости линии.
Для уменьшения потерь при передаче электромагнитной энергии по линии стремятся к тому, чтобы сопротивление линии r и проводимость изоляции g были по возможности малы.
Фазовая скорость согласно (11-14) и (11-29) равна:
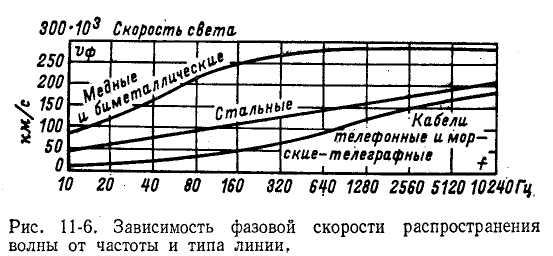
Это предельная фазовая скорость распространения волны вдоль линии при бесконечно большой частоте. При постоянном токе 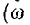
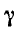
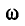
На рис. 11-5 показан характер изменений а и 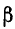
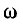
где m — масштабный коэффициент.
Для кабельных линий характерна резко выраженная емкостная проводимость 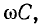
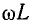
или
Соответственно фазовая скорость распространения волны в кабельной линии равна
т. е. прямо пропорциональна корню квадратному из частоты.
В теории электромагнитного поля доказывается, что произведение удельных значений индуктивности и емкости в линии
где с — скорость света в пустоте (около 3* 108 м/с); 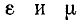
Предел, к которому с ростом частоты стремится фазовая скорость волны, равен на основании (11-30) и (11-33): 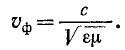
В случае воздушной линии 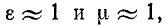
В случае кабельной линии 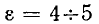
Рисунок 11-6 иллюстрирует зависимость фазовой скорости волны от частоты и типа линии.
Волновое сопротивление линии
при постоянном токе 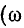
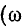
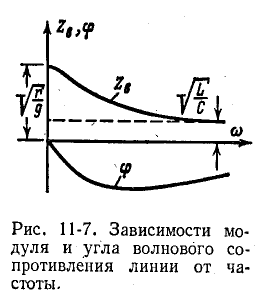
В остальной части диапазона частот волновое сопротивление линии имеет емкостный характер, так как обычно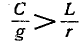
правой части (11-34) больше аргумента числителя].
На рис. 11-7 показаны кривые изменения модуля 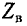
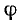
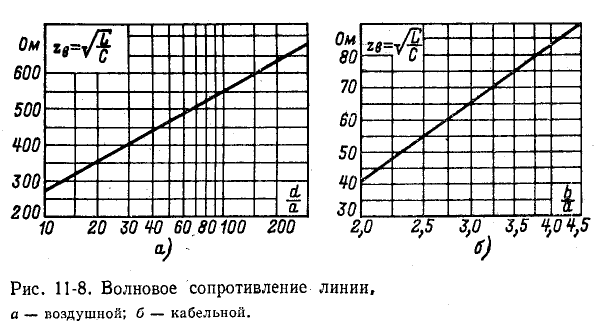
Подставив выражения для L и С в формулу 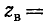
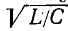
Средние значения 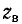
Рисунок 11-8 иллюстрирует графические зависимости 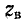
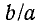
Линия без искажений
Сигналы, передаваемые по линии связи, представляют собой совокупность множества различных частот: дискретных — в случае периодических несинусоидальных сигналов и образующих непрерывный спектр — в случае непериодических сигналов.
Неискаженной передачей сигнала называется такая передача, при которой форма сигнала в начале и конце линии одинакова, т. е. все ординаты кривой напряжения или тока в конце линии прямо пропорциональны соответствующим ординатам кривой в начале линии. Такое явление имеет место в том случае, когда коэффициент ослабления линии, а также фазовая скорость на всех частотах одинаковы.
Неодинаковое затухание на разных частотах создает так называемые амплитудные искажения, а неодинаковая скорость волн на разных частотах — фазовые искажения.
Согласно (П-31) и (11-32) коэффициент ослабления и фазовая скорость в случае кабельных линий пропорциональны квадратному корню из частоты. В случае воздушных линий также существует зависимость а и 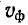
Итак, для неискаженной передачи требуется, чтобы коэффициент ослабления а не зависел от частоты, а коэффициент фазы 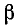
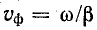
Такое положение имеет место при условии, что
В этом случае коэффициент распространения равен:
Если считать, что первичные параметры линии не зависят от частоты, то коэффициент ослабления в данном случае будет постоянен: 
а коэффициент фазы — прямо пропорционален частоте: 
Линия, параметры которой удовлетворяют условию (11-36), называется линией без искажений, поскольку любые сигналы распространяются по ней с сохранением их формы. Линия без искажений является одновременно и линией с минимальным затуханием, которое только и возможно при заданных параметрах r и g.
Волновое сопротивление линии без искажений — действительное число, что равносильно активному сопротивлению, не зависящему от частоты; в соответствии с (11-34) оно выражается простой формулой 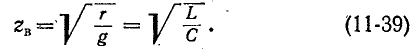
Фазовая скорость в линии без искажений постоянна и совпадает с полученным ранее выражением (11-30) для предельной скорости распространения волны вдоль линии при бесконечно большой частоте: 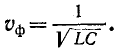
Для устранения искажений, вызываемых несогласованностью сопротивления приемника с сопротивлением линии, т. е. во избежание возникновения отражений на приемном конце, сопротивление приемника должно быть равно 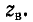
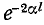
Ввиду того что волновое сопротивление линии без искажений является активным, при согласованной нагрузке напряжение и ток в любой точке линии совпадают по фазе. Отношение мгновенных значений напряжения и тока в любой точке такой линии равно: 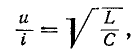
откуда
Следовательно, на любом отрезке линии без искажений, нагруженной согласованно, энергия магнитного поля в каждый момент времени равна энергии электрического поля.
Следует заметить, что на практике условие (11-36), как правило, не выполняется; отношение 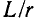
Чтобы линия наиболее соответствовала условию (11-36), следовало бы изменить какой-либо первичный параметр, например уменьшить r или С либо увеличить g или L.
Уменьшение активного сопротивления r возможно за счет применения проводов большего диаметра, что, однако, значительно удорожало бы линию. Увеличение проводимости изоляции g невыгодно, так как при этом возросло бы затухание линии.
Наилучшим средством для приближения первичных электрических параметров к оптимальному соотношению (11-36) является искусственное увеличение индуктивности включением в линию через определенное расстояние индуктивных катушек или применением кабеля, проводящие жилы которого обмотаны тонкой лентой из материала с высокой магнитной проницаемостью.
Линия без потерь
Независимо от того, соблюдается ли оптимальное соотношение первичных параметров (11-36) или не соблюдается, во всех случаях желательно, чтобы активное сопротивление r и проводимость изоляции g были по возможности малы (для уменьшения потерь энергии).
В воздушных линиях обычно индуктивное сопротивление линии 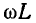
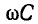
В ряде случаев оказывается полезным в первом приближении рассматривать линию, не имеющую потерь, т. е. пренебрегать активными сопротивлением и проводимостью по сравнению с соответствующими реактивными составляющими. Такая идеализация допускается для приближенной качественной и количественной оценки исследуемых явлений. При этом весьма упрощаются расчетные выражения и гиперболические уравнения линии переходят в тригонометрические.
Итак, основным исходным предложением, которое делают при рассмотрении линии без потерь, .является приближенное условие, что 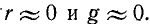
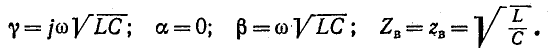
Саедовательно, в линии без потерь ослабление отсутствует. Ввиду постоянства фазовой скорости
отсутствуют также фазовые искажения.
Выражения для коэффициента фазы, фазовой скорости и волнового сопротивления линии без потерь совпадают с выражениями, полученными для линии без искажений. Следовательно, все сказанное о линии без искажений полностью относится и к линии без потерь.
Ввиду того, что гиперболические функции с мнимым аргументом преобразуются в тригонометрические функции, гиперболические уравнения линии (11-21) принимают тригонометрическую форму: 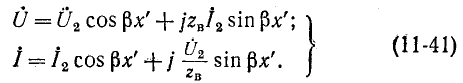
Эти уравнения используются ниже при рассмотрении стоячих волн в линии без потерь.
Энергия, передаваемая по линии, складывается из энергии электрического и магнитного полей.
В том случае, когда к концу линии без потерь присоединено сопротивление, равное волновому, на любом отрезке линии соблюдается условие (11-40), полученное для линии без искажении. При этом вся энергия, доставляемая падающей волной, поглощается в сопротивлении нагрузки.
Если сопротивление нагрузки отлично от волнового, то в месте присоединения нагрузки энергия перераспределяется между полями, в результате чего возникают отражения.
В предельном случае, когда линия на конце разомкнута, падающая волна встречает бесконечно большое сопротивление; ток в конце линии обращается в нуль, и соответственно энергия магнитного поля переходит в энергию электрического поля. Напряжение на разомкнутом конце линии удваивается, и возникает отраженная волна того же знака, что и падающая 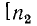
В другом предельном случае, когда линия на конце замкнута накоротко,, падающая волна встречает сопротивление, равное нулю, напряжение в конце линии обращается в нуль и соответственно энергия электрического поля переходит в энергию магнитного поля. Ток на короткозамкнутом конце линии удваивается, и возникает отраженная волна, знак которой противоположен знаку падающей волны 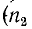
При активной нагрузке 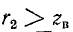
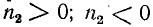
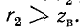
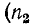
Режимы работы линии без потерь. Стоячие волны
Исследуем закон распределения действующих напряжения и тока вдоль линии без потерь. С этой целью воспользуемся уравнениями линии (11-18) и (11-41) в комплексной и гиперболической формах.
Приняв в (11-18) мнимый коэффициент распространения 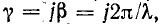
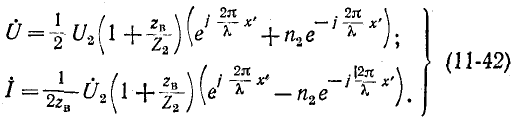
Входящий в эти уравнения коэффициент отражения
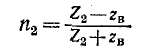
представляет собой в общем случае комплексную величину.
Выражения (11-42) наглядно свидетельствуют о том, что комплексное напряжение в любой точке х’ слагается
из падающей и отраженной волн напряжения, амплитуды которых находятся в соотношении 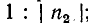
Точкам 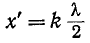
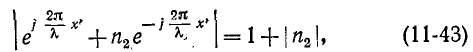
соответствует максимальное действующее значение U, так как при этом фазы падающей и отраженной волн напряжения совпадают. На расстоянии 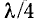
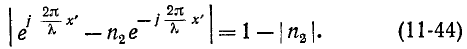
Координаты максимумов и минимумов U, являющиеся многозначными функциями 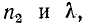
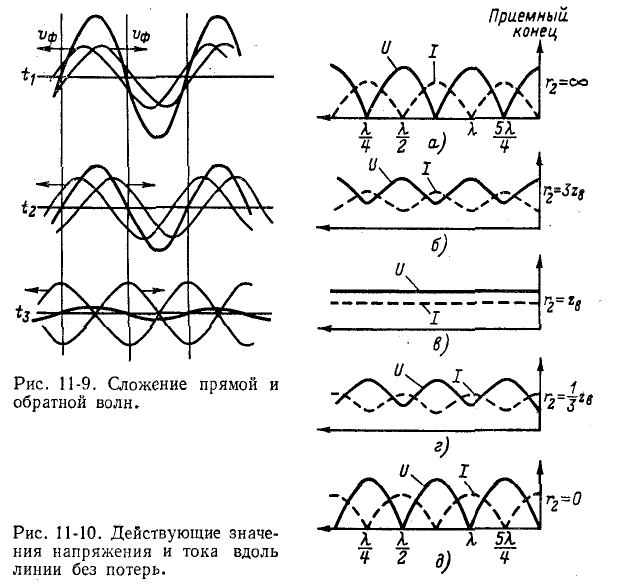
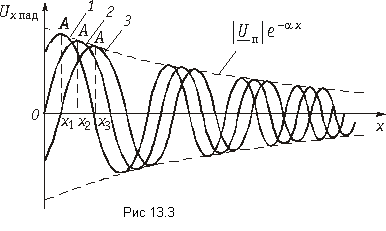
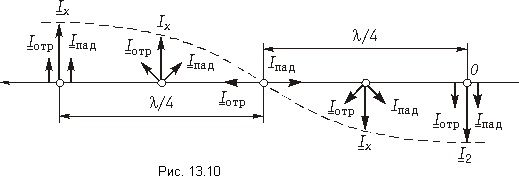
Таким образом, кривая действующих значений напряжения вдоль линии без потерь представляет собой волнообразную кривую, максимумы и минимумы которой чередуются (см. дальше рис. 11-10, б и г).
Аналогичные рассуждения приводят к выводу, что и кривая действующих значений тока вдоль линии без потерь представляет собой волнообразную кривую, смещенную относительно кривой действующих значений напряжения на четверть длины волны. Места максимумов напряжения совпадают с местами минимумов тока и, наоборот, минимумы U совпадают с максимумами I.
При отсутствии отраженной волны 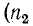
Чем больше приближается коэффициент отражения 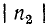
При 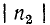
Из сказанного выше следует, что узлы напряжения совпадают с пучностями тока и, наоборот, узлы тока сов-
падают с пучностями напряжения. Соответственно узлы (или пучности) напряжения и тока сдвинуты на четверть длины волны друг относительно друга.
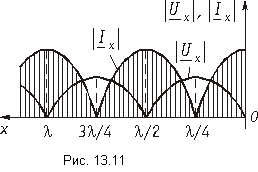
На рис. 11-9 в виде примера показано сложение прямой и обратной волн напряжения, имеющих одинаковые амплитуды, для трех моментов времени: 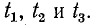
Из этого рисунка видно, что на протяжении всего участка между двумя соседними узлами стоячей волны синусоидальное изменение напряжения во времени происходит с одинаковой начальной фазой: при прохождении узла начальная фаза синусоидальных колебаний изменяется скачкообразно на величину 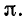
На основании приведенного выше выражения для коэффициента отражения 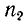
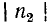
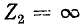
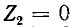
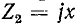
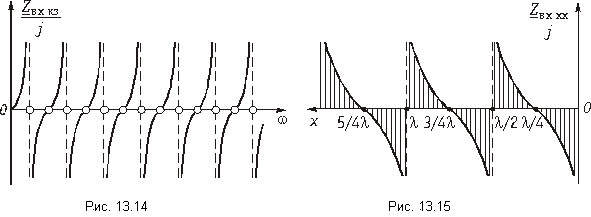
Распределение действующих значений напряжения и тока вдоль линии для холостого хода и короткого замыкания иллюстрируется на рис. 11-10, а и д.
Для сравнения на рис. 11-10 показано распределение напряжения и тока для других режимов работы линии.
При активной нагрузке 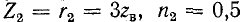
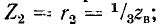
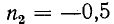
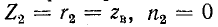
Стоячие волны легко исследуются с помощью уравнений (11-41).линии без потерь.
При холостом ходе 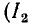
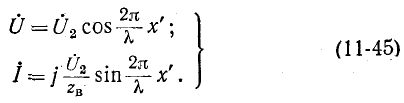
Узлы напряжения находятся в точках, для которых
или 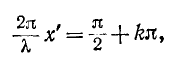
откуда
Пучности напряжения находятся в точках, для которых
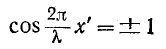
или 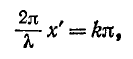
откуда
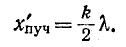
Разомкнутый конец линии совпадает с узлом тока и пучностью напряжения (рис. 11-10, а).
Как видно из (11-45), ток опережает по фазе напряжение на 90°, когда 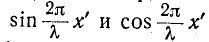
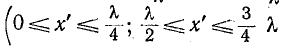
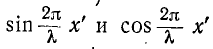
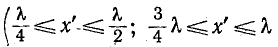
При коротком замыкании, положив в (11-41) 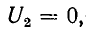
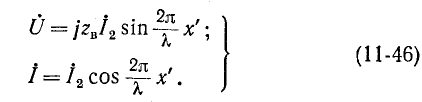
На замкнутом конце линии х’ = 0 и в точках, удаленных от него на целое число полуволн х’ 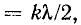
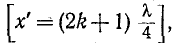
Как видно из (11-46), ток отстает по фазе от напряжения на 90°, когда 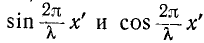
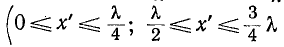
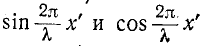
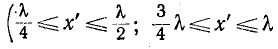
Следует заметить, что наличие хотя бы самых малых потерь в реальных линиях приводит к тому, что действующие значения U и I не снижаются до нуля, а достигают некоторых минимальных значений в точках, соответствующих узлам.
В случае стоячих волн мощность в узлах напряжения и тока равна нулю. В остальных точках линии имеет место только реактивная мощность, так как напряжение и ток сдвинуты по фазе на 90°. В этом случае энергия не передается вдоль линии, а происходит лишь обмен энергией между электрическим и магнитным нолями на участках линии, ограниченных узлами напряжения и тока.
Если в линии имеются потери или приемник потребляет активную мощность, то узлы исчезают; амплитуда падающей волны превышает амплитуду отраженной волны, н за счет разности амплитуд происходит процесс передачи энергии вдоль линии.
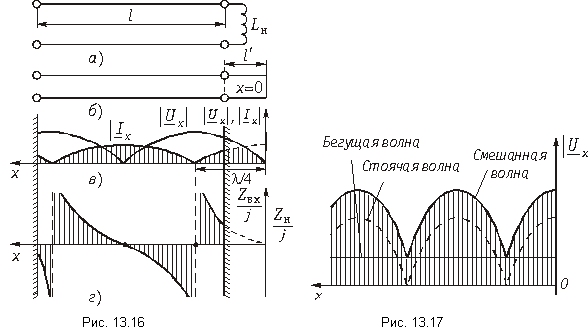
Для количественной оценки степени согласования линии с нагрузкой в радиотехнике используется коэффициент бегущей волны, под которым понимается отношение минимума кривой распределения U или I к максимуму той же величины:
С учетом (11-43) и (11-44) имеем:
откуда
В случае активной нагрузки выражение (Н-48) упрощается. При 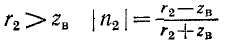
при 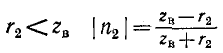
В реальных условиях коэффициент бегущей волны обычно не ниже 0,5—0,6.
Кривую распределения действующих значений напря* жения вдоль линии используют на практике для измерения длины волны или частоты. Длина волны определяется удвоенным расстоянием между соседними максимумами или минимумами кривой распределения, а частота вычисляется по длине волны на основании (11-15).
Входное сопротивление линии
Входное сопротивление линии, измеренное в произвольной точке на _ расстоянии х’ от конца, определяется отношением 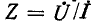
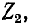
Комплексная форма выражения для входного сопротивления линии получается на основании (11-18): 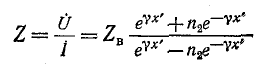
или 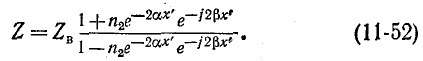
Данное выражение показывает, что с изменением координаты х’ модуль входного сопротивления линии колеблется между некоторыми максимумами и минимумами (которые в общем случае отличаются друг от друга).
Допустим, что модуль Z достигает некоторого максимума в точке 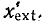
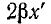
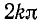
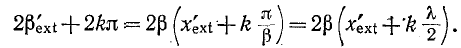
Следовательно, максимумы чередуются через каждые полволны. Посредине между максимумами будут минимумы, которые также чередуются через каждые полволны.
Если вместо координаты 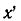

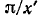
В этом случае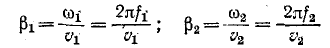
и, следовательно,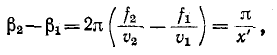
откуда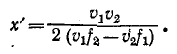
При малом расхождении частот 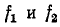
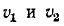
Данная формула позволяет определить расстояние от точки наблюдения до ближайшей точки линии, в которой имеет место отражение (например, при коротком замыкании на линии), производя измерение только в одной точке.
Волнообразный характер кривой z подчиняется в общем случае закону изменения модуля гиперболического тангенса с комплексным аргументом, что видно из следующего вывода.
Непосредственно из (11-21) следует:
Обозначив 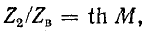
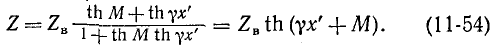
При холостом ходе 

а при коротком замыкании
С учетом (11-55) и (11-56) входное сопротивление Z легко выразить через
Этой формулой пользуются в том случае, когда из опытов холостого хода и короткого замыкания известны
Данные опытов холостого хода и короткого замыкания используются также для вычисления характеристических параметров линии.
На основании (11-55) и (11-56)
Эти формулы совпадают с (9-35). Ввиду того что коэффициент фазы р определяется по (11-57) неоднозначно, при вычислении производится проверка на основании (11-14), причем первоначально фазовая скорость 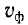
Вычисление характеристических параметров по формулам (11-57) иллюстрировано ниже примером 11-1.
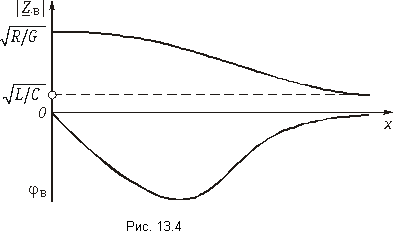
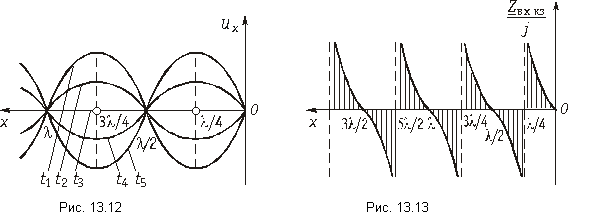
На рис. 11-11 показаны кривые изменения модулей 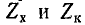
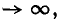
Входные сопротивления линии без потерь при холостом ходе и коротком замыкании могут быть получены из (11-55) и (11-56) заменой
Эти реактивные входные сопротивления с учетом их знака изображаются котангенсоидами и тангенсоидами (рис. 11-12). Аргументом может служить также величина 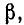
Сопоставляя эти графики с частотными характеристиками сопротивлений реактивных двухполюсников, легко убедиться в их сходстве: резонансы напряжений и токов чередуются, однако в отличие от двухполюсников, имеющих ограниченное число резонансов, линия без потерь имеет бесконечное число резонансных точек, что соответствует представлению линии как цепочки из бесконечного числа индуктивностей и емкостей.
Входное сопротивление линии без потерь при 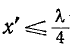
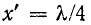
Следует отметить, что в реальных условиях вследствие наличия потерь входное сопротивление линии никогда не снижается до нуля и никогда не достигает бесконечного значения.
При этом короткозамкнутая линия при 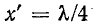
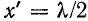
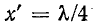
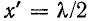
Пример 11-1.
Даны результаты измерения входных сопротивлений линии длиной 160 км на частоте 1000 Гц при холостом ходе и коротком замыкании: 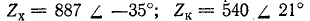
Расчет начинается с вычисления волнового сопротивления и коэффициента распространения:
Целое число к находится на основании ориентировочного расчета величины 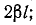
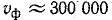
Следовательно, надо принять
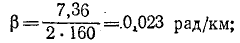
коэффициент распространения
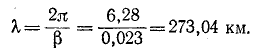
Первичные параметры линии находятся на основании выражений:
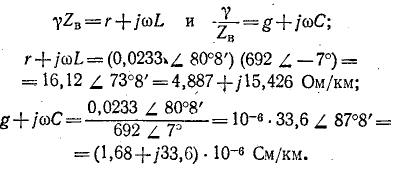
Таким образом,
Линия как элемент резонансной цепи
Четвертьволновая линия с малыми потерями, разомкнутая на конце, обладает свойствами резонансной цепи, состоящей из последовательно соединенных r, L и С. При частоте, при которой на линии укладывается четверть волны (такую частоту условимся называть резонансной), входное сопротивление линии будет активным и притом минимальным.
При малом отклонении частоты от резонансной модуль входного сопротивления линии резко возрастает: входное сопротивление приобретает емкостный характер при понижении частоты и индуктивный характер — при повышении.
Входное сопротивление линии с малыми потерями, разомкнутой на конце, можно получить из (11-21), разлагая 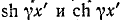
Выражение примет вид: 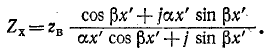
Вблизи резонансной частоты 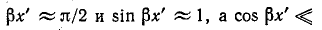
Если через 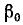
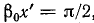
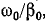
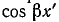
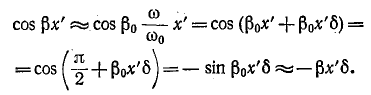
Здесь, так же как и 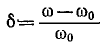
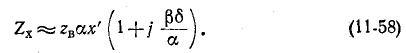
Было показано, что при частоте, близкой к резонансной, когда 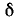

Рассматривая четвертьволновую линию как резонансную цепь, можно в силу одинаковой структуры выражений (11-58) и (11-59) считать, что добротность линии равна:
При этом резонансные характеристики, приведенные, применимы и к рассматриваемой линии.
Соответственно полоса пропускания, представляющая собой величину, обратную добротности, равна: 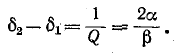
Здесь под полосой пропускания, подразумевается отнесенная к резонансной частоте ширина резонансной кривой между точками, соответствующими половине максимальной мощности (когда
При малых значениях коэффициента а добротность получается высокой, достигая примерно 1000—4000, что намного превышает добротность контуров r, L и С, В связи с этим возрастает и острота настройки.
Искусственные линии
Искусственной линией называется цепь с сосредоточенными параметрами, приближающаяся по своим частотным характеристикам (в заданном диапазоне частот) к цепи с распределенными параметрами.
Искусственные линии находят широкое применение в лабораторных условиях и в особенности в современной импульсной радиотехнике для получения требуемого запаздывания сигналов.
Отмечалось, что всякая однородная линия представляет собой симметричный четырехполюсник с. мерой передачи, равной
и характеристическим сопротивлением, равным волновому:
Заменяя линию эквивалентным Т-образным четырехполюсником, согласно рис. 9-17, а получаем на основании формул (11-23) расчетные выражения:
Для какой-либо фиксированной частоты такой Т-образный четырехполюсник может быть осуществлен. Однако при передаче сигналов в некоторой заданной полосе частот величины 
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Электрическая энергия, ее свойства и применение
- Электрическая цепь
- Электрический ток
- Электрические цепи постоянного тока
- Анализ переходных и установившихся процессов методом интеграла свертки
- Операторный метод расчета переходных процессов
- Метод пространства состояний электрических цепей
- Синтез электрических цепей
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Установившиеся процессы в линиях электропередачи
1. Установившиеся процессы в линиях электропередачи
Расчеты установившихся режимов в дальних электропередачах находят применение в таких задачах, как проектирование защиты от перенапряжений, выбор мероприятий по повышению пропускной способности ЛЭП, определение токов короткого замыкания и уставок устройств релейной защиты, определение места повреждения в линиях.
Строгое решение уравнений реальной многопроводной линии являет собой комплексную инженерную задачу, решение которой в общем случае можно получить только численным путем. Для понимания физического смысла явлений в многопроводных линиях полезно использовать представления о процессах в двухпроводных линиях передачи.
1.1. Установившиеся процессы в однородной двухпроводной линии
Распределение напряжения и тока вдоль однородных двухпроводных линий на установившейся частоте описывается системой двух обыкновенных дифференциальных уравнений с постоянными коэффициентами, называемых «телеграфными уравнениями»:


где 









Дифференцируя уравнение (1.1) по x и подставляя в него уравнение (1.2), получим линейное дифференциальное уравнение второго порядка относительно напряжения:

где 


Решение уравнения (1.3) в каждой точке линии имеет вид суммы комплексов напряжений прямой 


где 

Ток в линии 

где 


Постоянные интегрирования 







Подставив 




Эти формулы позволяют определить напряжение и ток в любой точке линии по их заданным значениям в начале линии.
Если заданы значения напряжения 



При исследовании процессов в линии важно знать входное сопротивление линии. Под входным сопротивлением линии 

где 
Если известен режим нагрузки, расчет распределения напряжений и токов в линии проводят следующим образом. Определяют входное сопротивление линии по формуле (1.9), что позволяет рассчитать режим в начале линии (

Рис. 1. Схема двухпроводной линии передачи с нагрузкой и система координат
Определим входные сопротивления линии в режимах короткого замыкания и холостого хода.
В режиме короткого замыкания 

В режиме холостого хода 

Если в конце линии включено сопротивление нагрузки, равное волновому сопротивлению линии 

Обратившись к формулам (1.6) с учетом (1.12), находим, что

т. е. обратная волна в линии не возникает. Такую нагрузку называют согласованной нагрузкой. Из уравнений (1.7) видно, что для линии в режиме согласованной нагрузки выполняется соотношение 
При рассмотрении процессов в линиях бывает весьма полезно пренебречь потерями. Такая идеализация действительной линии позволяет упростить расчетные выражения и качественно проанализировать результаты. Рассмотрим на примере линии без потерь распределения напряжения и тока для различных случаев комплексной нагрузки.
1.2. Распределение напряжения и тока вдоль линии без потерь
При отсутствии потерь в линии параметры 


Уравнения (1.8) преобразуются с учетом (1.14) к виду:

Входное сопротивление линии без потерь равно:

В режимах короткого замыкания и холостого хода линии входное сопротивление имеет реактивный характер:


Режим произвольной нагрузки линии характеризуется комплексной нагрузкой 




Выражения (1.20) описывают распределение действующего значения 


Распределение комплекса тока вдоль линии в соответствии с (1.15) имеет вид:


Рассмотрим частные случаи комплексной нагрузки линии без потерь. Распределения действующих значений напряжения и тока в этих случаях приведены на рис. 2.
1) Режим согласованной нагрузки 

Распределение действующего значения напряжения не зависит от 
Рис. 2. Распределение действующих значений напряжения и тока
вдоль линии без потерь
2) Режим активной нагрузки 


3) Режим поглощения чисто реактивной мощности.
Такой режим реализуется при холостом ходе, коротком замыкании и чисто реактивной нагрузке. В линиях без потерь, передающих чисто реактивную мощность, распределение напряжения и тока имеет вид стоячих волн. Стоячей волной называется процесс, получающийся от наложения прямой и обратной волн с одинаковыми амплитудами.
Обозначим комплексы прямой и обратной волн напряжения:

В произвольной точке линии отношение напряжений обратной и прямой волн в соответствии с (1.4) составляет:

где учтено, что координата 
В точках линии 



где 

В формуле (1.29) 
В точках линии с координатами 


Таким образом для распределения напряжения и тока вдоль линии в режиме передачи чисто реактивной мощности характерно чередование максимумов и минимумов через расстояния, равные четверти длины волны.
В режиме короткого замыкания линии 


где 

В режиме холостого хода 


Распределение действующего значения напряжения косинусоидально (рис. 2в).
В режиме индуктивной нагрузки линии (рис. 2г) 


Распределение действующего значения 

В режиме емкостной нагрузки линии (рис. 2д) 

Ближайший к нагрузке узел напряжения имеет координату:

В двух последних режимах распределение фазы имеет аналогично режимам КЗ и ХХ скачкообразный характер с учетом смещения кривой распределения относительно конца линии.
1.3. «Телеграфные уравнения» многопроводной линии
Установившиеся процессы в n — проводной линии электропередачи при синусоидальных токах и напряжениях описываются системой из 2n обыкновенных дифференциальных уравнений первого порядка:


где 





В формулах (1.41) и (1.42) матрица N характеризует внешние собственные и взаимные индуктивные сопротивления проводов при идеальной проводимости земли, матрица 

Рис. 3. Геометрические размеры многопроводной линии
На рис. 3 условно показаны провода линии и их зеркальные изображения в поверхности земли. В соответствии с обозначениями, приведенными на рисунке, элементы матрицы N выражаются следующим образом



где 
Выражения для элементов матриц 

Линии электропередачи с номинальным напряжением 330 кВ и выше для снижения потерь на корону имеют расщепленные фазы, в которых составляющие провода каждой фазы одинаковы и электрически связаны между собой проводящими распорками. Для определения параметров таких линий пренебрегаем эффектом близости в проводах расщепленной фазы и полагаем, что токи в проводах расщепленной фазы одинаковы. Эти допущения не приводят к существенным погрешностям, так как расстояния между проводами в фазе много больше их диаметра и много меньше расстояний от проводов до земли и между фазами. Для линий с расщепленными фазами выражения для 



где 







При определении параметров воздушных линий необходимо учитывать провисание проводов. Для этого в инженерных расчетах 

где 
1.4. Решение матричных «телеграфных уравнений».
Метод волновых каналов.
Преобразуем уравнение (1.39), исключая из него матрицу токов. Дифференцируя (1.39) по x и подставляя в него уравнение (1.40), получим систему дифференциальных уравнений для напряжений в фазах линии

Применяя аналогичное преобразование к уравнению (1.40), получим

Заметим, что ввиду симметричности матриц 

Решение уравнений (1.47) и (1.48) можно выполнить двумя способами: фазным методом и методом волновых каналов. Последний, обладая физической наглядностью, получил наиболее широкое распространение в инженерных расчетах.
Математически метод волновых каналов представляет собой матричное преобразование систем уравнений (1.47) и (1.48) с целью получить систему независимых уравнений, решение которых по отдельности существенно проще, чем решение системы взаимосвязанных уравнений. В результате такого преобразования матрицы 

Из курса линейной алгебры известно, что для некоторой квадратной матрицы А в результате преобразования

матрица 

Обозначим преобразующие матрицы для уравнений (1.47) и (1.48) как 






Известно, что транспонированная матрица имеет такие же собственные значения, как и исходная матрица. В связи с этим имеем:


где 


при этом очевидно, что


Подставляя (1.53) и (1.54) в (1.51) и (1.52), получаем:

Уравнения (1.56) являются искомой системой независимых уравнений. Каждому s соответствует своя пара скалярных уравнений относительно напряжения и тока, которая представляет собой волновые («телеграфные») уравнения двухпроводной линии. Таким образом, в n-проводной линии можно выделить в общем случае n независимых каналов распространения электромагнитных волн, каждый из которых характеризуется своим коэффициентом распространения 
С физической точки зрения волновой канал представляет собой форму распространения электромагнитной волны вдоль многопроводной линии, т. е. определенную форму электромагнитного поля и связанную с ней систему токов и напряжений, распространяющуюся по линии с одним коэффициентом распространения независимо от возбуждения в линии других форм волн. Токи и напряжения в фазных проводах при этом являются линейной комбинацией токов и напряжений независимых волновых каналов. Коэффициенты линейной комбинации представляют собой строки матриц преобразования 

Следует отметить, что существование в ЛЭП независимых каналов распространения электромагнитных волн напрямую следует из решения системы уравнений Максвелла для многопроводной линии. С этим решением подробно можно ознакомиться в [1].
Определим параметры двухпроводных линий, соответствующих волновым каналам. Умножим слева уравнение (1.39) на 


– диагональная матрица продольных сопротивлений волновых каналов.
Применяя схожие преобразования к уравнению (1.40), получим выражение, определяющее погонные проводимости волновых каналов:

Метод волновых каналов при известных фазных напряжениях и токах в начале линии* позволяет найти распределение напряжений и токов в проводах по длине линии и их значения в конце. В общем виде решение проводится в три этапа.
На первом этапе методами линейной алгебры находят матрицы преобразования «по напряжению» 

На практике фазные напряжения и токи в начале линии неизвестны. В этом случае метод волновых каналов позволяет определить параметры симметричного многополюсника, эквивалентирующего отрезок однородной многопроводной линии. Уравнения этого многополюсника связывают фазные напряжения и токи в начале и в конце линии.
Расчет режимов многопроводных линий и применение метода волновых каналов существенно упрощается при принятии допущения об отсутствии потерь в линии.
1.5. Многопроводные линии без потерь
В линиях без потерь элементы матриц погонных сопротивлений 








В выражениях (1.61) 




Из (1.41) и (1.42) следует, что при отсутствии потерь в линии

где 

Из уравнения (1.62) следует, что для линии без потерь матрицы преобразования «по напряжению» 


и, следовательно, диагонализация матриц 


Трехфазные воздушные линии электропередачи выполняют транспонированными, в результате чего собственные и взаимные параметры линии для всех фаз в среднем по длине линии становятся одинаковыми, и матрицы индуктивностей и емкостных коэффициентов линии можно записать в следующем виде:


Равенство диагональных и внедиагональных элементов между собой в (1.64) приводит к тому, что матрицы 

Одним из удобных выборов матрицы преобразования 

где 
При этом для симметричных трехфазных напряжений прямой и обратной последовательности токи в проводах также образуют симметричные системы прямой и обратной последовательности. Для напряжений и токов нулевой последовательности обратным проводом служит земля.
В технике высоких напряжений для формирования параметров волновых каналов получило распространение следующее преобразование:

1.6. Ограничение повышения напряжения
промышленной частоты в дальних электропередачах.
На конце разомкнутой линии при промышленной частоте f = 50 Гц начиная с 300 – 500 км длины возможны повышения напряжения. Для линий без потерь справедливо соотношение

где U(l) – напряжение в конце линии; U(0) – напряжение в начале линии.
Например, при длине линии в 1000 км напряжение в конце линии почти в 2 раза превосходит напряжение в начале (b » 6°/100 км, bl » 60°).
Абсолютному возрастанию напряжения в конце линии способствует внутреннее индуктивное сопротивление Xи источника синусоидальной ЭДС e(t) = Eм sin(w t + j). Дело в том, что при длине линии, меньшей 1500 км, входное сопротивление разомкнутой линии имеет емкостный характер:

где Zc – волновое сопротивление линии.
Напряжение в начале линии возрастает по сравнению с амплитудой ЭДС

т. е. 
По условиям надежной и длительной работы изоляции линии напряжение в любых режимах линии не должно превосходить 1,05Uном, где Uном – номинальное напряжение линии электропередачи. Для ограничения повышения напряжения в разомкнутой с одного конца линии в различных точках линии (обычно в начале, середине или конце линии) включают между проводом и землей индуктивности, получившие название реакторов поперечной компенсации.
Рассмотрим включение реактора в произвольной точке разомкнутой линии (рис. 1.4).
Напряжение на реакторе

Ток в начале участка l2


где 
Рис. 1.4. Схема линии с реактором в промежуточной точке
Ток в конце участка l1

Соответствующие напряжение и ток в начале линии


Реактор в начале линии снижает напряжение, т. к. частично компенсирует емкостный ток линии, проходящий через индуктивное сопротивление источника ЭДС. Для полной компенсации емкостного тока линии необходимая мощность реактора q = tg bl. При этом входное сопротивление линии совместно с компенсирующим реактором становится бесконечно большим, а ток от источника ЭДС становится равным нулю. Отметим, что на характер распределения напряжения вдоль линии реактор в начале линии влияния не оказывает.
Реактор в конце линии не только ограничивает повышение напряжения, но и меняет характер распределения напряжения в линии. Напряжение в конце линии подсчитывается по формуле



Последнее выражение можно трактовать следующим образом. Известно, что входное сопротивление короткозамкнутой линии с волновой длиной j э равно jZctgjэ. Таким образом, компенсирующий реактор можно представить как короткозамкнутую линию с входным сопротивлением Xр и волновой длиной jэ. Тогда всю линию можно рассматривать как короткозамкнутую с волновой длиной bl + jэ. Это позволяет рассчитать распределение напряжения U(x) вдоль линии по формуле

В частности, максимум напряжения соответствует точке, для которой

Учитывая (1.78), (1.79) и (1.80), можно последнее выражение в (1.80) представить в виде

На рис. 1.5 приведена кривая распределения тока, проходящего вдоль линии. На начальном участке происходит повышение напряжения, т. к. по нему протекает емкостный ток, значение которого становится равным нулю в точке, в которой напряжение проходит через максимум. Далее ток становится индуктивным, что вызывает падение напряжения вдоль линии.
Рис. 1.5. Распределение напряжения и тока в линии с реактором на ее конце
По (1.79) можно найти мощность реактора, при которой напряжения в начале и конце линии равны между собой:

т. е. 

Пользуясь приведенными формулами и приемами, можно рассчитать напряжение на линии с реакторами в нескольких точках.
Задание на выполнение первой части курсовой работы.
Трехфазная транспонированная линия электропередачи длиной l подключена к источнику ЭДС с внутренним сопротивлением 
1. Рассчитать с учетом транспозиции фазных проводов емкостные коэффициенты и индуктивности линии в приближении отсутствия в линии потерь. Рассчитать первичные и вторичные параметры прямого и нулевого волновых каналов.
2. Рассчитать на промышленной частоте емкостные коэффициенты, собственные и взаимные индуктивности и активные сопротивления линии с учетом проникновения электромагнитного поля в землю и в фазные провода. Для расчета параметров линии с учетом потерь воспользоваться m-файлом tlp_driver.m (прилагается к заданию). Учесть транспозицию. Сопоставить результаты с результатами п.1 и письменно объяснить причины различия.
3. Построить графики распределения действующих значений и фазы напряжения 

а) холостого хода;
б) трехфазного короткого замыкания в конце линии;
в) симметричной согласованной нагрузки;
г) симметричной емкостной (
д) симметричной индуктивной (
Сопротивления нагрузок принять равными 
4. Построить график распределения напряжения вдоль ненагруженной транспонированной линии на промышленной частоте при питании ее от симметричного источника. Выбрать мощность реакторов поперечной компенсации, обеспечивающих напряжение во всех точках электропередачи в интервале (0,95 . 1,05) Uном.
Распределение токов в электрических цепях
РАСПРЕДЕЛЕНИЕ ПОТЕНЦИАЛОВ И ТОКА В ЭЛЕКТРИЧЕСКОЙ ЦЕПИ
Для того чтобы разобраться в прохождении тока по электрическим цепям, надо представить, как распределяются в ней электрические потенциалы. Электрический ток проходит всегда от точек цепи, находящихся под большим потенциалом, к точкам, находящимся под меньшим потенциалом. Если какая-либо точка цепи соединена с землей, то потенциал ее принимается равным нулю; в этом случае потенциалы других точек цепи будут равны напряжениям, действующим между этими точками и землей.
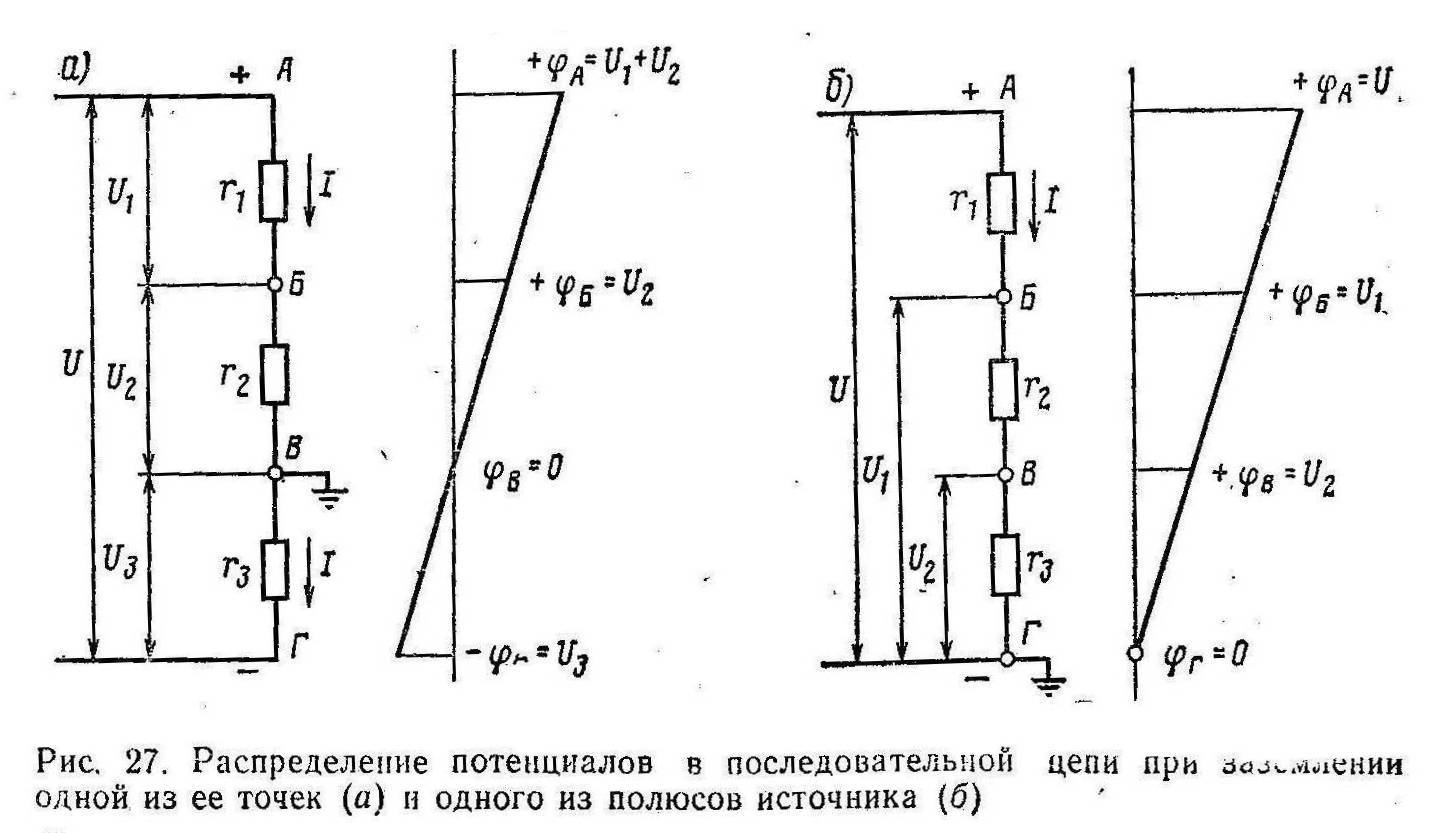
На рис. 27, б показано распределение потенциалов вдоль последовательной цепи при заземлении точки Г у одного из полюсов источника питания. Как видно из графика, потенциал различных точек цепи по мере приближения к заземленной точке падает, т. е. уменьшается напряжение, действующее между этими точками и землей. По этой причине обмотки возбуждения тяговых двигателей и вспомогательных машин, в которых при резких изменениях тока могут возникать большие перенапряжения, стараются включать в силовую цепь электроподвижного состава ближе к «земле» (за обмоткой якоря). В этом случае на изоляцию этих обмоток будет действовать меньшее напряжение, чем если бы они были включены под более высоким потенциалом (ближе к контактной сети в электровозах постоянного тока или к незаземленному полюсу выпрямительной установки в электровозах переменного тока). Точно так же точки электрической цепи, находящиеся под более высоким потенциалом, являются более опасными для человека, соприкасающегося с токоведущими частями электрических установок. При этом он попадает под более высокое напряжение по отношению к «земле».
На рис. 28, а показано распределение потенциалов в последовательной цепи при ее обрыве у точки В. Все точки цепи от точки А до места обрыва будут иметь потенциал точки А (по цепи не идет ток и на резисторах r1, r2 и r3 нет падения напряжения), а от места обрыва до точки Г — нулевой потенциал. Следовательно, соприкосновение человека с точкой В будет в этом случае также опасно, как и с точкой А; точка же Д не будет находиться под напряжением. Рассмотренный пример наглядно показывает, что некоторые точки электрических цепей, которые при нормальных условиях заземлены, могут при обрыве цепи оказаться под высоким напряжением.
На рис. 28, б показано распределение токов в последовательной цепи с двумя источниками, имеющими э. д. с. Е1 и E2 параллельно которым включены резисторы с одинаковыми сопротивлениями r1 = r2. При равенстве э. д. с. Е1 и Е2 разности потенциалов между точками Б—В и В—Г (т. е. напряжения UБВ и UВГ) будут равны, поэтому по резисторам будут, протекать одинаковые токи: I1 = I2. Однако, если э. д. с. Е1 по какой-либо причине увеличится, то увеличится потенциал φБ точки Б и напряжение UБB станет больше напряжения UBГ. Ток I1 возрастет и станет больше, чем I2. Если увеличится э. д. с. Е2, то возрастет разность потенциалов между точками В и Г, при этом напряжение UВГ станет больше UБВ, а ток I2 больше I1.

Таким способом по распределению потенциалов между отдельными точками электрической цепи определяют прохождение тока по сложным электрическим цепям.
Методы расчета электрических цепей
Чтобы верно рассчитать электроцепь, ее параметры на разных частях, применяют специальные методы, такие как:
- метод преобразования цепи;
- метод наложения;
- метод контурных токов;
- метод эквивалентного генератора;
- метод узловых потенциалов;
- метод применения законов Кирхгофа.
Метод контурных токов базируется на использовании дополнительных значений контурных токов, соответствующих закону Кирхгофа.
Метод эквивалентного генератора применяют для вычисления токов одного или нескольких разветвлений. Данный метод также называется теоремой об активном двухполюснике.
Метод узловых потенциалов дает возможность уменьшить порядок системы уравнений. Он заключается в определении потенциалов всех узлов цепи по заданным потенциалам токов всех разветвлений. В основе данного метода лежит первый закон Кирхгофа.
Самые часто применяемые методы для вычисления параметров цепи – это метод применения законов Кирхгофа и метод преобразования цепи. Рассмотрим их подробнее.
Метод применения законов Кирхгофа
Законы Кирхгофа являются базовыми законами, которым подчиняются все процессы в электроцепях, не зависимо от параметров ее элементов.
Первый закон Кирхгофа описывает силу тока и гласит о том, что суммарная величина всех значений силы тока, сходящихся в одном узле, равняется нулю:
Сила тока в разных разветвлениях электрической цепи может иметь различное направление. Принято считать, что токи, которые направляются к узлу, имеют знак минус, а противоположные – знак плюс.
Такой метод применяют для сложных цепей. В цепи есть разветвления ((NB)) , что соединены в узлы ((NY)) , и разветвления с источниками ((NJ)) . В цепи также есть все основные компоненты: сопротивления, источники ЭДС и тока.
Не нашли что искали?
Просто напиши и мы поможем
Для вычисления параметров электрической цепи с использованием первого закона Кирхгофа сначала устанавливают число неизвестных токов, указывают их знаки, предварительно выбрав направление тока в разветвлениях, после чего формируют уравнения.
Конфигурация уравнений, нужных для полного расчета цепи, зависит от ее типа и вида соединений ее разветвлений. Для этого рассматривают каждое разветвление и узлы их соединения, используя топологический граф схемы электрической цепи. Изображая граф разветвления, определяют каким типом разветвления его можно заменить. Первый тип обычно наносят с помощью сплошной линии. Разветвления второго типа, где величина силы тока устанавливается источником тока, наносят пунктирной линией.
Разветвления графа (NB) , как и узлы (NY) , нумеруются как разветвления схемы и узлы исследуемой электроцепи. Напряжения и токи в разветвлениях графа направлены, как в исследуемой цепи. Напряжения и токи в каноническом разветвлении первого типа направлены всегда в одну сторону, потому они ориентируются на разветвление графа. Разветвление, содержащее исключительно источник напряжения, считается вырожденным. Направление тока в графе такого разветвления выбирается по источнику и направлено в сторону, противоположную направлению ЭДС.
Топологический граф начинают анализировать с разветвлений дерева графа ((N_Д)) и разветвлений связи ((NC)) . Связный подграф формируется всеми разветвлениями дерева. Это точка, которая соединяет все узлы, где нет замкнутого контура. Разветвления дерева выбираются произвольно. Исключение составляют разветвления графа, замещающие источники тока.
Разветвления связи дополняют разветвления дерева. При включении нового разветвления связи к разветвлениям дерева, которые уже существуют, формируется замкнутый контур. Данный контур именуется главным.
Сложно разобраться самому?
Попробуй обратиться за помощью к преподавателям
Число независимых уравнений (N_1) , что составляются по первому закону Кирхгофа, равняется числу разветвлений дерева (N_Д) . То есть, соответствует числу, равному на один меньше количества узлов:
После чего составляют уравнения второго закона Кирхгофа. Их количество (N_2) рассчитывается по следующему выражению:
Здесь (N_Н-N_Д=(NB-NJ)) – это число разветвлений с неизвестными токами,
(NJ) – число разветвлений с известными источниками тока.
К уравнениям (N_Н=N_1+N_2) дописывают уравнения по закону Ома для каждого разветвления, которые связывают силу тока и напряжение, и именуются компонентными уравнениями.
Метод преобразования электрической цепи
Этот метод состоит в том, чтобы верно рассчитать распределение токов в цепи. Подключенные последовательно или параллельно сопротивления заменяют на одно сопротивление, в результате чего распределение тока не изменяется.
В случае последовательного соединения сопротивлений они будут подключены так, что конец предыдущего будет соединяться с началом последующего. При таком соединении сила тока будет иметь одинаковую величину в каждом резисторе.
В любой электроцепи есть источники и приемники электроэнергии, что соединены проводами. Такое соединение делает возможным движение тока по проводам от одного элемента к другому. Источники бывают источниками напряжения и тока.
Идеальным источником напряжения считается такой, напряжение на клеммах которого не меняется во времени, не зависимо от силы тока, который он выдает в нагрузку, а его внутреннее сопротивление приравнивается к нулю.
Идеальным источником тока считается такой, который выдает постоянное во времени значение силы тока, не зависящее от напряжения на клеммах, а его внутреннее сопротивление приравнивается к бесконечно большой величине.
Тема 1.2. Электрические цепи постоянного тока
Электрические цепи и ее элементы
Электрической цепью постоянного тока называют совокупность устройств и объектов: источников электрической энергии, преобразователей, потребителей, коммутационной, защитной и измерительной аппаратуры, соединительных проводов или линии электропередачи.
Электрические и электромагнитные процессы в этих объектах описываются с помощью понятий об электродвижущей силе (ЭДС — E ), токе ( I ) и напряжении ( U ).
Элементы цепи можно разделить на три группы:
1) элементы, предназначенные для генерирования электроэнергии (источники энергии, источники ЭДС);
2) элементы, преобразующие электроэнергию в другие виды энергии: механическую, тепловую, световую, химическую и т.д. (эти элементы называются приемниками электрической энергии или потребителями);
3) элементы, предназначенные для передачи электрической энергии от источника к приемникам (линии электропередачи, соединительные провода); элементы, обеспечивающие уровень и качество напряжения и т.д.
Источники питания цепи постоянного тока – это гальванические элементы, электрические аккумуляторы, электромеханические генераторы, термо- и фотоэлементы и др.
Электрическими приемниками или потребителями постоянного тока являются электродвигатели, преобразующие электрическую энергию в механическую, нагревательные и осветительные приборы, электролизные установки и др. Все электоприемники характеризуются электрическими параметрами, среди которых основные – напряжение и мощность. Для нормальной работы электроприемника на его зажимах необходимо поддерживать номинальное напряжение. По ГОСТ 721-77 напряжение равно 27, 110, 220, 440 В, так же 6, 12, 24, 36 В.
Коммутационная аппаратура служит для подключения потребителей к источникам, то есть для замыкания и размыкания источников электроцепи.
Защитная аппаратура предназначена для размыкания цепи в аварийных ситуациях.
Измерительная аппаратура предназначена для замера тока, напряжения и других электрических величин.
Линии электропередачи используются, когда источники и потребители удалены друг от друга на большие расстояния. Соединительные провода предназначены для соединения между собой зажимов или электродов элементов электрической цепи.
Активные и пассивные элементы
Элемент называется пассивным , если он не может вызывать протекание тока, то есть если он не создает тока или ЭДС. Если собрать несколько пассивных элементов (резисторы, конденсаторы, катушки индуктивности) в электрическую цепь, то ток в цепи не потечет.
Элемент, который создает ЭДС и вызывает протекание тока, называется активным (источники электроэнергии).
Линейные и нелинейные цепи
Электрическая цепь называется линейной , если электрическое сопротивление или другие параметры участков, не зависят от значений и направлений токов и напряжений. Электрические процессы линейной цепи описываются линейными алгебраическими и дифференциальными уравнениями.
Если электрическая цепь содержит хотя бы один нелинейный элемент , то она является нелинейной.
Топологические элементы электрической цепи.
Графическое изображение электрической цепи называется электрической схемой. Электрическая схема включает: узлы, ветви, контуры.
Ветвь – совокупность элементов, соединенных последовательно. По ветви протекает один и тот же ток.
Узел – точка соединения трех или более ветвей.
Контур – совокупность ветвей, при обходе которых осуществляется замкнутый путь.
Простейшая электроцепь имеет один контур с одной ветвью и не имеет узлов. Сложные электроцепи имеют несколько контуров.
Положительные направления тока, напряжения и ЭДС.
Чтобы правильно записать уравнения, описывающие процессы в электрических цепях, и произвести анализ этих процессов, необходимо задать условные положительные направления ЭДС источников питания, тока в элементах или ветвях цепи и напряжения на зажимах элементов цепи или между узлами цепи.
Внутри источника ЭДС постоянного тока положительным является направление ЭДС от отрицательного полюса к положительному полюсу. Это соответствует определению ЭДС как величины, характеризующей способность сторонних сил вызывать электрический ток.
По отношению к источнику ЭДС все элементы цепи составляют внешний участок цепи.
За положительное направление тока в цепи принимают направление, совпадающее с направлением ЭДС. Во внешней цепи положительным является направление от положительного полюса источника к отрицательному полюсу. В электронной теории – направление совпадает с направлением положительно заряженных частиц.
Условным положительным направлением падения напряжения (или просто напряжения) на элементах цепи или между двумя узлами цепи принимают направление, совпадающее с условно положительным направлением тока в этом элементе или в этой ветви. Положительное направление напряжения на зажимах источника ЭДС всегда противоположно положительному направлению ЭДС.
Действительные направления электрических величин, определяемые расчетом, могут совпадать или не совпадать с условными направлениями. При расчетах если определено, что ток, ЭДС и напряжения положительны, то их действительные направления совпадают с условно принятыми положительными направлениями, если отрицательны, то не совпадают.
Основные законы электрической цепи
Условное обозначение параметров в цепях постоянного и переменного тока.
i – переменный ток; I – постоянный ток;
u – переменное напряжение; U – постоянное напряжение;
e – переменная ЭДС; E – постоянная ЭДС;
Схемы Электрических Цепей Постоянного Тока
При расчете электрических цепей в большинстве случаев известны параметры источников ЭДС или напряжения, сопротивления элементов электрической цепи, и задача сводится к определению токов в ветвях цепи. Таким образом, электрическая цепь на рис.
Точка Н определяет номинальный режим, если напряжение и ток соответствуют их номинальным значениям Uном и Iном, приведенным в паспорте источника электрической энергии.
Элемент электрической цепи, параметры которого сопротивление и др.
Электрические цепи (часть 1)
Электрическая цепь постоянного тока
Алгебраическая сумма падений напряжений на резистивных элементах в любом замкнутом контуре равно алгебраической сумме ЭДС. Нелинейный элемент, например лампа накаливания, имеет сопротивление, величина которого увеличивается при повышении напряжения, а следовательно и тока, подводимого к лампочке.
Источник электрической энергии характеризуется понятием ЭДС Е , под которой понимают величину, численно равную энергии, получаемой внутри источника единицей электрического заряда.
При расчете в схеме электрической цепи выделяют несколько основных элементов. Этот метод основан на составлении уравнений по первому закону Кирхгофа: Схема сложной электрической цепи с двумя узлами.
Для разных электротехнических устройств указывают свои номинальные параметры.
Электрическая цепь в режиме короткого замыкания имеет сопротивление, которое равно нулю. В этой схеме реальные элементы цепи изображаются условными обозначениями, причем вспомогательные элементы цепи обычно не изображаются, а если сопротивление соединительных проводов намного меньше сопротивления других элементов цепи, его не учитывают.
Как видно, при параллельном соединении источников ток и мощность внешней цепи равны соответственно сумме токов и мощностей источников.
В случае последовательного соединения сопротивлений в ветви В общем виде уравнения узловых потенциалов имеют вид: Если в схеме имеются источники тока, то слагаемое в правой части будет равно сумме источников тока: Метод узловых потенциалов имеет преимущество, если число независимых узлов меньше числа контуров. Желательно во всех контурах положительные направления обхода выбирать одинаковыми, например, по часовой стрелке, как показано на рис.
Устройство и принцип работы двигателя постоянного тока. Схема двигателя постоянного тока.
Похожие статьи
Такая система известна, как электрическая цепь. Схема электрической цепи.
Ознакомившись с основными характеристиками и видами такой системы, как электрическая цепь, становится возможным понять принцип функционирования любого электрооборудования.
Отключение цепи от источника постоянной ЭДС 5. В противном случае это слагаемое отрицательно. При анализе электрической цепи рассматривают следующие режимы работы: холостого хода, номинальный, короткого замыкания и согласованный.
Электрическая цепь и электрический ток, протекающий по ней, характеризуют электромагнитные процессы при помощи напряжения и силы тока. Для электрической цепи на рис.
Для контура. Это произойдет, если к зажимам аb двухполюсника присоединена внешняя цепь с источниками питания. Точка К характеризует режим короткого замыкания к. Первый закон Кирхгофа: сумма токов в узле равна нулю 1.
Elektrotechnik fuer Grundlagen der Elektronik
Эта вольт-амперная характеристика строится по двум точкам 1 и 2 рис. Активный двухполюсник содержит источники электрической энергии, а пассивный двухполюсник их не содержит.
Мощность цепи несинусоидального тока 4. Для расчета цепей с двухполюсниками реальные активные и пассивные элементы цепи представляются схемами замещения. По этой причине для расчета сложных электрических цепей разработаны более рациональные методы расчета, основные из них рассмотрены ниже. За направление электрического тока в электротехнике принято направление, противоположное направлению движения электронов. Сложной электрической цепью называется цепь, содержащая несколько источников и которую нельзя свернуть до простой цепи последовательного или параллельного соединения.
Зная токи, можно найти напряжения на элементах цепи, мощность отдельных элементов и электрической цепи в целом, мощность источников и др. Контур — любой замкнутый путь, проходящий по нескольким ветвям.
как решать задачи со сложными схемами
Элементы цепи
При сравнении внешних характеристик источника ЭДС рис. Мощность трёхфазной цепи 3.
Классический метод расчёта переходных процессов 5. В зависимости от электропроводности все вещества подразделяют на: 1.
Последовательное соединение в цепи Большое количество электрических цепей состоят из нескольких приемников тока.
Согласованный режим Согласованный режим электрической цепи обеспечивает максимальную передачу активной мощности от источника питания к потребителю. На схеме этот элемент выглядит следующим образом. В этой схеме реальные элементы цепи изображаются условными обозначениями, причем вспомогательные элементы цепи обычно не изображаются, а если сопротивление соединительных проводов намного меньше сопротивления других элементов цепи, его не учитывают.
Метод узловых потенциалов
Идеальному источнику тока приписывают внутреннее сопротивление, стремящееся к бесконечно большому значению, и неизменный ток Iк не зависящий от напряжения на его зажимах, равный току коротного замыкания, вследствие чего неограниченное увеличение присоединенной к источнику нагрузки сопровождается теоретически неограниченным возрастанием напряжения и мощности. Электрическая цепь и электрический ток, протекающий по ней, характеризуют электромагнитные процессы при помощи напряжения и силы тока.
Различают два рода тока: 1. Ветвь электрической цепи схемы — участок цепи с одним и тем же током. Последовательное включение источников питания источников ЭДС применяется тогда, когда требуется создать напряжение требуемой величины, а рабочий ток в цепи меньше или равен номинальному току одного источника ЭДС рис. Между узлами 1 и 3 имеются две параллельные ветви с источниками ЭДС Е1 и Е2 , между узлами 2 и 3 также имеются две параллельные ветви с резисторами R1 и R2. Данное устройство работы системы применяется к любому электрическому бытовому прибору.
По этой причине для расчета сложных электрических цепей разработаны более рациональные методы расчета, основные из них рассмотрены ниже. Сопротивление в этой электрической цепи приравнивается к сумме сопротивлений всех проводников системы. При сравнении внешних характеристик источника ЭДС рис. В случае когда у одного приемника энергии сопротивление меньше, через него может пройти больше тока, чем через другие элементы системы.
Классический метод расчёта переходных процессов 5. Стрелка в кружке указывает направление возрастания потенциала внутри источника ЭДС. Электрический ток в такой электрической системе имеет несколько вариантов пути прохождения. Это уравнение является линейным. В состав цепи входят: 1.
Законы Кирхгофа — Теория и задача
http://pandia.ru/text/78/296/64257.php
http://lemzspb.ru/raspredeleniye-tokov-v-elektricheskikh-tsepyakh/
13.1. Общие положения
13.2. Уравнения передачи однородной линии
13.3. Падающие и отраженные волны
13.4. Вторичные параметры однородной линии
13.5. Входное сопротивление линии
13.6. Линия без потерь
13.7. Применение отрезков линий с пренебрежимо малыми потерями
13.8. Вопросы и задания для самопроверки
13.1. Общие положения
До сих пор рассматривались R L С электрические цепи в предположении, что параметры сосредоточены в определенных элементах цепи: индуктивность сосредоточена в катушке (энергия магнитного поля катушки локализована в ее магнитопроводе), емкость сосредоточена в конденсаторе (энергия электрического поля локализована между обкладками конденсатора); резистивное сопротивление сосредоточено в резисторе (преобразование электрической энергии в резисторе в тепловую осуществляется в токопроводящем слое резистора). Такие цепи получили название цепей с сосредоточенными параметрами
Однако представление электрических цепей в виде цепей с сосредоточенными параметрами не всегда возможно. Например, рассматривая передачу электромагнитной энергии в линии связи, фидере, антенне, волноводе и т. д., следует учитывать, что магнитное и электрическое поля распределены по всей длине этих устройств и превращение электромагнитной энергии в тепло также происходит по всей длине устройств. В таких цепях приходится сталкиваться с распределенными по длине индуктивностями, емкостями, резистивными сопротивлениями, поэтому они называются цепями с распределенными параметрами
Ток и напряжение на выходе сколь угодно малого участка (отрезка) цепи с распределенными параметрами не равны соответственно току и напряжению на его входе и отличаются как по величине, так и по фазе. Таким образом, ток и напряжение в любой точке цепи являются функциями не только времени t, но и пространственных координат (например, расстояния от одного из концов цепи).
Заметим, что деление цепей на два класса – с сосредоточенными и распределенными параметрами, достаточно условно. Одну и ту же цепь следует рассматривать как систему с сосредоточенными или распределенными параметрами в зависимости от частоты, на которой она работает. Действительно, если на входе цепи действует гармонический сигнал, то в силу конечной скорости распространения электромагнитных колебаний (близкой к скорости света) возмущение от источника за время, равное периоду колебания T, пройдет расстояние, равное длине волны электромагнитного колебания: l = cT= c/f, где с – скорость света; f – частота колебания.
При длине цепи, совпадающей с длиной волны колебания, изменение мгновенного значения напряжения в конце цепи запаздывает на целый период по сравнению с изменением мгновенного значения напряжения источника. В цепях, длина которых l > l, запаздывание может составлять большое число периодов. Следовательно, если длина цепи соизмерима или значительно превышает длину волны распространяющегося в ней электромагнитного колебания, то напряжение (ток) является функцией времени и расстояния от начала цепи. Цепь является системой с распределенными параметрами.
Если длина цепи намного меньше длины волны, то изменения напряжения в любой точке и в конце цепи происходят одновременно с изменением мгновенного значения напряжения источника. Никакого запаздывания в такой цепи нет: напряжение (ток) является только функцией времени. Эту цепь можно считать системой с сосредоточенными параметрами. Например, отрезок коаксиального кабеля длиной 30 см при передаче по нему телевизионных сигналов (с наивысшей частотой 8,5 мГц) может считаться цепью с сосредоточенными параметрами, поскольку l = c/fmax = 3×108/(8,5×106) = 35 м >> 0,3 м. Наоборот, в области дециметровых волн (l — десятки сантиметров) этот же отрезок кабеля должен рассматриваться как цепь с распределенными параметрами. Отрезок же коаксиального кабеля длиной, например, в 1 км является цепью с распределенными параметрами и для телевизионного сигнала.
В дальнейшем из обширного класса цепей с распределенными параметрами будем изучать так называемые длинные линии, предназначенные для передачи электромагнитной энергии на расстояние и имеющие длину, превышающую длину волны электромагнитных колебаний. К ним относятся двухпроводные воздушные линии связи, симметричные и коаксиальные кабельные линии проводных систем связи, фидеры, связывающие радиопередатчики с антеннами и т. д. При этом будем полагать, что конструктивные данные длинной линии (материал и диаметр ее проводов, их взаимное расположение) и ее параметры сохраняются неизменными по длине линии. Такие длинные линии называются однородными
Целью изучения однородных длинных линий является анализ распределений напряжений и токов вдоль линии. В основе анализа лежит представление о длинной линии как о цепи с бесконечно большим числом бесконечно малых по величине пассивных элементов, распределенных равномерно по ее длине.
13.2. Уравнения передачи однородной линии
Первичные параметры. Длинные линии могут иметь самую различную конструкцию. Так, двухпроводная воздушная линия (рис. 13.1, а) состоит из параллельных неизолированных проводов, укрепленных с помощью изоляторов на специальных опорах. Симметричная кабельная цепь представляет собой два изолированных скрученных друг с другом провода, образующих так называемую пару (рис. 13.1, б). Скрученные между собой пары (или четверки), заключенные в металлическую или пластмассовую защитную оболочку, образуют симметричный кабель.
Коаксиальная пара является основой коаксиального кабеля и состоит из внутреннего цилиндра – провода сплошного сечения, помещенного в полый цилиндр (рис. 13.1, в).
Сопротивление R – это сопротивление проводов линии единичной длины. Например, для двухпроводной линии сопротивление (Ом/км)
где r – удельное сопротивление материала проводов при температуре 20° С, Ом×мм2/м; l – длина линии, м; S – площадь поперечного сечения провода, мм2; r – радиус провода, мм.
При температурах, отличных от 20° С, сопротивление проводов вычисляется по формуле
где sT – температурный коэффициент, 1/град; Т – температура, ° С. Так, сопротивление двухпроводной медной линии длиной 1 км (километрическое сопротивление) из проводов диаметром 4 мм при температуре Т= 20° С для частоты f = 0 составляет 2,84 Ом/км.
Наличие поверхностного эффекта (вытеснение тока из внутренних слоев проводника на его поверхность при увеличении частоты) приводит к увеличению сопротивления R с ростом частоты.
Индуктивность L определяется отношением магнитного потока, сцепляющегося с контуром единичной длины, к току, вызывающему этот поток. Индуктивность линии складывается из внешней и внутренней индуктивностей. Первая определяется геометрическими размерами линии и не зависит от частоты; вторая зависит от материала проводов, их диаметра и частоты.
Поверхностный эффект уменьшает внутреннюю индуктивность при возрастании частоты. Например, километрическая индуктивность двухпроводной медной цепи (Гн/км)
с диаметром проводов 2r = 4 мм и расстоянием между проводами lпр = 200 мм составляет на частоте f = 10 кГц (с учетом магнитной проводимости m = 1 и коэффициента действия поверхностного эффекта kпэ = 1,8) 1,89 мГн/км.
Емкость С определяется отношением заряда, приходящегося на единицу длины линии, к напряжению между проводами линии.
Для двухпроводной линии емкость (Ф/км)
где e – диэлектрическая проницаемость вещества в пространстве между проводами. Например, километрическая емкость воздушной двухпроводной медной цепи (для воздуха e= 1) из проводов диаметром 2r = 4 мм и расстоянием между проводами lпр= 200мм составляет 7,4 нФ/км.
Проводимость G обусловлена несовершенством изоляции и представляет собой активную составляющую проводимости изоляции между проводами, отнесенную к единице длины линии. Для воздушной линии проводимость изоляции зависит от климатических условий (влажности, температуры и др.), чистоты поверхностей изоляторов и т. д.
Проводимость изоляции возрастает с ростом частоты (особенно для кабельных цепей) за счет увеличения потерь в диэлектрике. Для воздушных цепей проводимость (См/км) G = G0 +kпf, где G0 – проводимость изоляции на постоянном токе; kп – коэффициент, учитывающий потери в диэлектрике при переменном токе; f –частота.
Для кабельных цепей G =G0 +wCtgd, где tgd – тангенс угла диэлектрических потерь
После введения первичных параметров можно уточнить понятие однородной длинной линии. Однородной называется такая линия, первичные параметры которой неизменны на всей ее длине.
Уравнения передачи однородной линии. Найдем распределения напряжения и тока в линии по ее длине и во времени.
Выделим элементарный участок линии длиной Dx, находящийся на расстоянии х от начала линии (рис. 13.2). Его эквивалентную схему можно приближенно представить в виде последовательно включенных сопротивления RDx и индуктивности LDx и параллельно включенных активной проводимости GDx и емкости СDх
Таким образом, линия рассматривается как цепь с бесконечно большим числом звеньев, электрические параметры которых бесконечно малы. При стремлении Dх к нулю точность такого представления возрастает.
Здесь и далее используются частные производные, так как напряжение и ток являются функциями переменных t и х
Уменьшение тока на участке Dх происходит за счет ответвления тока через емкость СDх и проводимость изоляции GDx. Пренебрегая изменением напряжения как величиной второго порядка малости, можно написать
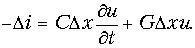
Разделив обе части уравнений (13.1 а и б) на Dх и перейдя к пределу при Dх ® 0, получим дифференциальные уравнения линии:
Эти уравнения называются телеграфными так как впервые были получены для линии телеграфной связи.
Будем считать, что в линии имеет место режим установившихся гармонических колебаний. Поскольку закон изменения напряжений и токов во времени известен, то из дифференциальных уравнений (13.2) остается найти лишь законы изменения амплитуд и фаз напряжений и токов с расстоянием х
Используя символический метод анализа гармонических колебаний, в котором
преобразуем уравнения (13.2) к виду
Так как комплексные действующие значения U и I являются функциями только х, уравнения записываются не в частных, а в полных производных.
Продифференцировав первое уравнение из (13.3) по х и подставив в него второе уравнение,получим
Введя обозначение
перепишем это уравнение в виде
Корни характеристического уравнения p2– 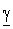
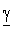
Из первого уравнения системы (13.3) имеем
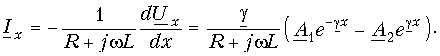
Введя еще одно обозначение
запишем решение для тока в точке х в форме
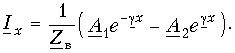
Постоянные интегрирования A1 и A2 можно найти из начальных условий: при х = 0 Ux = U1 и Ix = I1, где U1 и I1 – напряжение и ток в начале линии. Тогда из (13.6 а и б) для х = 0:
Откуда
Подстановка полученных значений постоянных интегрирования в (13.6) дает следующие уравнения для определения напряжения Ux и тока Ix в произвольной точке х длинной линии
Это есть уравнения передачи однородной длинной линии. Параметры 
Если учесть, что
то уравнения передачи (13.8) можно переписать в более компактной форме:
В конце линии x = l и Ux = U2 Ix = I2. Уравнения (13.9 а) примут вид
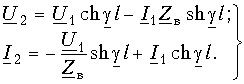
Разрешая эту систему уравнений относительно напряжения U1 и тока I1 в начале линии, получаем
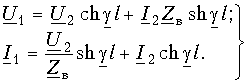
Эти уравнения совпадают с известными нам уравнениями передачи (12.35) для симметричного четырехполюсника при 
13.3. Падающие и отраженные волны
Обозначим в уравнениях передачи (13.8) Uп = (U1 + I1Zв)/2 и U0 = (U1 – I1Zв)/2. С учетом этих обозначений запись уравнений передачи однородной длинной линии упростится и будет иметь вид
где
Напряжение и ток состоят из сумм двух слагаемых. Первые слагаемые уменьшаются с увеличением расстояния от начала линии х, вторые – возрастают. Создается впечатление о существовании в линии двух типов волн: падающей и отраженной. Чтобы убедиться в этом, рассмотрим мгновенные значения напряжения и тока.
Помня, что в (13.10) все величины в общем случае комплексные
можно по известным правилам перейти от (13.10) для комплексных значений к уравнениям передачи для мгновенных значений напряжений и токов. Для простоты положим jп = j0 = 0. Тогда
Проанализируем сначала первые слагаемые этих уравнений, которые обозначим
В каждом сечении линии (т. е. в каждой точке х) колебания напряжения и тока являются гармоническими. Амплитуда этих колебаний уменьшается по мере удаления от начала линии по закону е–aх. В каждой последующей точке линии колебания отстают по фазе от колебаний в предыдущей точке (на это указывает знак «минус» перед bх).
Если в момент времени t1 сделать фотографию распределения, например, напряжения uxпад вдоль линии, то она будет иметь вид кривой 1 (рис. 13.3). В следующий момент t2 фаза напряжения в каждой точке линии изменится на величину w(t2 – t1), и вся картина как бы сместится вдоль оси х вправо (кривая 2 на рис. 13.3). Аналогичная ситуация будет наблюдаться и в момент времени t3 > t2 (кривая 3 на рис. 13.3).
Если сделать последовательно ряд мгновенных фотографий и затем их проецировать на экран, то создается впечатление движущейся волны напряжения вдоль цепи. Фактически же вдоль цепи распространяется состояние равной фазы. Например, можно взять точку цепи х1, соответствующую максимуму напряжения в момент времени t1 (точка А на рис. 13.3) и определить скорость ее перемещения. Скорость распространения вдоль цепи состояния равной фазы называется фазовой скоростью распространения
В момент времени t1 в точке х1 имеется определенное фазовое состояние wt1 – bх1. Это же фазовое состояние будет наблюдаться в точке х2, но уже в момент времени t2 wt2 – bх2. Приравнивая их получаем wt1– bх1= wt2– bх2
Фазовую скорость распространения (км/с) найдем как отношение расстояния х2– х1, пройденного точкой A, ко времени t2 – t1
Таким образом, уравнения (13.12) описывают волны напряжения и тока, распространяющиеся от начала к концу линии. Такие волны называются падающими
Обратимся ко вторым слагаемым выражений (13.11), которые обозначим
Эти слагаемые описывают волны точно такого же характера, как и падающие, но распространяющиеся в обратном направлении, т. е. от конца линии к началу. Эти волны называются отраженными волнами напряжения и тока. Амплитуды отраженных волн убывают от конца линии к началу, наибольшая амплитуда наблюдается в конце линии.
В соответствии с рассмотренной картиной можно сказать, что в установившемся режиме гармонических колебаний напряжение и ток в любой точке линии складываются из падающих и отраженных волн напряжения и тока, т. е. ux = uxпад + uxотр; ix = ixпад + + ixотр. Отраженные волны возникают в конце линии.
Складывая эти равенства и вычитая из первого второе, имеем:
Отношение комплексной амплитуды отраженной волны к комплексной амплитуде падающей волны называется коэффициентом отражения по напряжению
Отсюда
Коэффициент отражения по напряжению показывает, какую часть амплитуды падающей волны в конце линии составляет амплитуда отраженной волны. Амплитуда отраженной волны тока
В то же время I2отр = siI2пад, где si – коэффициент отражения по току. Отсюда видно, что si = —su, т. е. коэффициент отражения по току равен по значению и противоположен по знаку коэффициенту отражения по напряжению.
Рассмотрим некоторые частные режимы работы линии. Если линия замкнута накоротко на конце (короткое замыкание (КЗ)), т. е. Zн = 0, то коэффициент su= —1, а коэффициент si= 1. Падающая и отраженная волны напряжения в конце линии имеют равные амплитуды и сдвинуты по отношению друг к другу на 180°. Амплитуда результирующей волны напряжения в конце линии будет равна нулю. В то же время падающая и отраженная волны тока будут иметь равные амплитуды, что приведет к увеличению тока в конце короткозамкнутой линии.
При холостом ходе (XX) в конце линии Zн = ¥ коэффициент su = 1 и si=—1, т. е. картина изменится на противоположную: ток в нагрузке будет равен нулю, а напряжение увеличится вдвое. Случай, когда Zн = Zв, рассмотрен ниже.
13.4. Вторичные параметры однородной линии
Волновое сопротивление. Одним из вторичных параметров однородной линии является волновое сопротивление линии, определяемое через первичные параметры формулой (13.7)
При w= 0
и jв = 0, т. е. волновое сопротивление чисто активное. Точно такой же характер имеет Zв при w=бесконечность;
Для всех реально существующих цепей R/G > L/C, поэтому модуль волнового сопротивления с увеличением частоты уменьшается, стремясь к величине
Угол jв изменяется от нулевого значения при w = 0 до нулевого значения при w=бесконечность;. Следовательно, на какой-то частоте он будет иметь максимум. Можно показать, что угол jв на всех частотах является отрицательным. На рис. 13.4 показаны графики частотных зависимостей модуля и угла волнового сопротивления однородной линии.
Чтобы выяснить физический смысл волнового сопротивления, воспользуемся выражениями для комплексных амплитуд падающих волн напряжения и тока из (13.10):
и
откуда
Аналогичным образом можно сказать, что
Волновое сопротивление не зависит от длины линии – оно постоянно в любой точке линии.
Пример. Определим волновое сопротивление воздушной медной линии из проводов диаметром 2r = 4 мм и расстоянием между проводами lпр = 20 см и кабельной линии с бумажной изоляцией жил диаметром 2r = 0,5 мм на частотах f = 0; 0,8 и 10 кГц для воздушной цепи и f = 0 и 0,8 кГц для кабельной цепи.
Для воздушной линии первичные параметры, взятые из справочника: R = = 2,84 Ом/км; С = 6,3 нФ/км; L = l,93 мГн/км; G = 0,57×10 См/км.
При f = 0 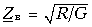
На частоте f = 10кГц wL R и wC G, поэтому
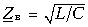
Для кабельной линии: R = 190 Ом/км, С = 50 нФ/км, L = 0,7 мГн/км, G = 5×10–4 мкСм/км. На частоте f = 0 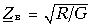
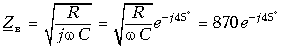
Согласованное включение линии. Рассмотрим режим работы линии, когда Zн = Zв. В этом случае коэффициенты отражения su = si = 0 и отраженные волны напряжения и тока будут отсутствовать (Uxотр = 0 и Ixотр = 0).
Напряжение и ток в любой точке линии, в том числе и на входе (x = 0), будут определяться только падающими волнами. Согласно (13.14)
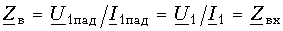
т. е. входное сопротивление такой линии равно ее волновому сопротивлению. Таким образом, волновое сопротивление линии является аналогом характеристического сопротивления симметричного четырехполюсника
Указанный режим работы линии является режимом согласованного включения. При этом вся энергия поглощается в конце линии нагрузочным сопротивлением. Этот режим работы наиболее выгоден для передачи сигналов связи, так как отражение энергии от нагрузки приводит помимо увеличения рабочего ослабления линии к появлению так называемых эхо-сигналов, накладывающихся на основной сигнал и искажающих его.
Уравнения передачи однородной линии в режиме согласованного включения могут быть легко получены из (13.9 б и в), если учесть, что при согласованном включении
а также что
Для любой точки линии
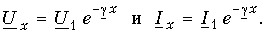
Коэффициент распространения. Ко вторичным параметрам линии относится также коэффициент распространения, введенный в рассмотрение формулой (13.4):
В режиме согласованного включения линии из (13.15) имеем:
или
Отсюда
Для отрезка линии единичной длины (1 км, 1 м и т. д.) можно записать:
Вещественная часть коэффициента распространения a характеризует изменение напряжения и тока по абсолютной величине при распространении энергии на расстояние, равное единице длины линии. Она называется коэффициентом ослабления линии и измеряется в неперах, отнесенных к единице длины линии (в проводной связи – Нп/км, в радиосвязи – Нп/м). При использовании десятичного логарифма вместо натурального
измеряется в дБ/км или дБ/м.
Мнимая часть коэффициента распространения b характеризуется изменением напряжения и тока по фазе. Она называется коэффициентом фазы линии и измеряется в рад/км или рад/м. Вместо радиан могут использоваться градусы.
Процесс изменения напряжения (тока) вдоль согласованно нагруженной линии можно проиллюстрировать векторной диаграммой, показанной на рис. 13.5, а или так называемой спиральной диаграммой, приведенной на рис. 13.5, б
Численные значения коэффициентов a и b можно найти по первичным параметрам из общей формулы (13.4). Однако в ряде случаев можно получить более простые выражения. Так, на высоких частотах (для электрической цепи из меди, например, это частоты 10 кГц), где выполняются условия wL > R и wC > G пользуются упрощенными формулами:
Вывод этих формул дан в специальной литературе и здесь не приводится. Для кабельных цепей в области низких частот (например, от 0 до 800 Гц) выполняются соотношения R wL и wC G. В этом случае можно показать, что a = b =
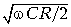
Вторичные параметры a и b зависят от частоты сложным образом. На рис. 13.6, а и б даны графики, качественно отражающие эту зависимость.
Пример. Определим коэффициент распространения воздушной медной линии c параметрами 2r = 4 мм и lпр = 20 см на частоте f = 800 Гц.
Значение коэффициента 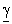
Отсюда коэффициент ослабления a = 2,86×10–3 Нп/км = 2,86 мНп/км. Перевод непер в децибелы дает a (дБ) = a (Нп)´8,7 = 24,9×10–3 дБ/км. Коэффициент фазы b = 17,6×10–3 рад/км.
Постоянная передачи длинной линии. При распространении энергии по линии на расстояние l напряжение и ток уменьшаются в e^(al) раз, а фазы напряжения и тока изменятся на величину bl
Величина al описывает ослабление напряжения и тока при распространении энергии по всей длине линии и называется характеристической (собственной) постоянной ослабления линии: Ас = al
Из формул (13.15 а) следует, что
где S1 и S2 – полные мощности на входе и выходе линии. Поэтому
Величина Bс = al = ju1 – ju2 = ji1 – ji2 называется характеристической (собственной) постоянной фазы линии
По аналогии с теорией четырехполюсников величина Гс = Ас + jВс является характеристической (собственной) постоянной передачи линии
Заметим, что при отсутствии согласования, т. е. при Zн ¹ Zв условия передачи энергии по линии следует оценивать величиной рабочей постоянной передачи Гp = Аp + jВp по формулам, полученным в общей теории четырехполюсников.
13.5. Входное сопротивление линии
Входное сопротивление линии определяется отношением напряжения и тока в начале линии. Найдем выражение для Zвх, используя уравнения передачи линии в форме (13.9 в):
Рассмотрим некоторые частные режимы работы линии.
При согласованном включении линии (Zн = Zв) из (13.16) получим, что Zвх = Zв как и было установлено ранее.
Если выходные зажимы линии замкнуты накоротко (Zн = 0), формула (13.16) упрощается и принимает вид
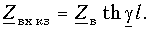
В случае разомкнутых выходных зажимов (Zн = бесконечность)
Когда линия нагружена на произвольное сопротивление, не равное волновому (Zн <> Zв), можно пользоваться для расчетов общей формулой (13.16). Однако иногда удобно выразить Zвх через параметры XX и КЗ. Для этого разделим числитель и знаменатель (13.16) на
Данная формула позволяет по измеренным значениям сопротивлений XX и КЗ рассчитать входное сопротивление линии.
Существует еще одна форма представления входного сопротивления. Для получения ее перепишем выражение (13.16) после деления на
в другом виде:
Обозначим
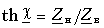
Тогда
Эта формула дает возможность по заданным параметрам Zв и Zн определить
и затем найти входное сопротивление линии.
Во всех случаях, когда нагрузка на конце линии не равна ее волновому сопротивлению, входное сопротивление определяется гиперболическим тангенсом комплексного аргумента. Чтобы дать представление о характере изменения входного сопротивления линии, на рис. 13.7, а показаны зависимости модулей сопротивлений XX и КЗ от длины линии, построенные в соответствии с формулами (13.17), а на рис. 13.7, б изображена зависимость модуля Zвх от частоты из (13.18) при несогласованной нагрузке линии.
13.6. Линия без потерь
Вторичные параметры и уравнения передачи. Реальная линия всегда обладает потерями. Однако в ряде случаев удобно считать линию идеальной, т. е. не имеющей потерь. Линия без потерь – это линия, у которой рассеяние энергии отсутствует, что имеет место при значениях первичных параметров R = 0 и G =0.
Такая идеализация оправдана для коротких по длине линий, работающих на сверхвысоких частотах (фидеров, элементов радиотехнических устройств, полосковых линий, измерительных линий, согласующих СВЧ устройств и др.), где выполняются условия R 
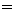
Коэффициент распространения линии без потерь
Отсюда коэффициент ослабления a = 0, а коэффициент фазы b = w 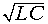
Волновое сопротивление линии без потерь
является чисто активным (резистивным).
Коэффициент фазы b связан с длиной волны электромагнитного колебания. Длиной волны l называется расстояние между двумя точками, взятыми в направлении распространения волны, фазы в которых отличаются на 2p. Следовательно, bl = 2p и l = 2p/b
Уравнения передачи линии без потерь получаются из (13.9 в), если учесть, что
При анализе процессов, происходящих в линии без потерь, общепринято расположение той или иной точки на линии характеризовать ее удалением не от начала линии, как это делали прежде, а от конца линии (рис. 13.8). В этом случае уравнения передачи линии без потерь, выражающие комплексные действующие значения напряжения и тока в произвольной точке линии х, отсчитанной от ее конца, записываются в виде:
Рассмотрим различные режимы работы линии без потерь.
Заменяя комплексные амплитуды их модулями и фазами, т. е.
и
и полагая для упрощения ju2 = = ji2 = 0, перейдем к уравнениям передачи для мгновенных значений напряжений и токов. Тогда
Эти уравнения описывают падающие волны, распространяющиеся в линии слева направо, т. е. от начала к концу линии (рис. 13.9, а). На направление распространения волн указывает знак «плюс» перед bx (напомним, что расстояние х отсчитывается от конца линии).
Таким образом, при согласованном включении линии без потерь в ней существуют только падающие, или бегущие, волны напряжения и тока. При этом амплитуды колебаний постоянны по всей длине линии (рис. 13.9, б). Данный режим работы линии называют также режимом бегущей волны. Сдвиг фаз между напряжением их и током ix равен нулю, поэтому энергия бегущей волны носит активный характер.
Короткое замыкание линии. При Zн = 0 напряжение в конце линии U2 = 0. Уравнения передачи (13.19) для данного режима работы линии принимают вид:
Если положить для простоты начальную фазу ji2 тока в конце линии равной нулю, то мгновенные значения напряжения и тока в любой точке линии описываются выражениями:
Амплитуды напряжения
и тока
являются функциями координаты х. В линии есть точки, в которых амплитуда напряжения (тока) в любой момент времени равна нулю. Это так называемые узлы напряжения (тока). Имеются также точки, в которых амплитуда напряжения (тока) приобретает максимальное значение – пучности напряжения (тока).
Узлы напряжения и пучности тока образуются в точках, в которых bx = 0, p, 2p, …, так как при этом sin bx = 0 и ux = 0, a cos bx = ±1 и ток ix имеет максимальную амплитуду. Пучности напряжения и узлы тока возникают в тех точках линии, где
При этих значениях bх sin bх = ±1, в этом случае амплитуда напряжения ux оказывается максимальной, a cos bх = 0 и амплитуда тока ix равной нулю. Рассмотрим причины появления узлов и пуч-ностей напряжения и тока.
При КЗ линии коэффициенты отражения имеют значения
т. е. происходит полное отражение энергии, в результате чего в любой точке цепи результирующее напряжение (ток) оказывается равным сумме падающих и отраженных волн. Действительно, из уравнений в комплексной форме (13.20) следует:
Поскольку потерь в линии нет, амплитуды падающих и отраженных волн во всех точках линии одинаковы.
Сдвиг фаз между падающей и отраженной волнами напряжения в точке х
а между падающей и отраженной волнами тока
Удобно рассматривать в линии без потерь точки х, отстоящие от конца линии на расстояния, кратные четверти длины волны, т. е. кратные l/4. В конце линии (х = 0) ju = —p и ji = 0. Следовательно, падающая и отраженная волны напряжения находятся в противофазе, а падающая и отраженная волны тока – в фазе. Поэтому в конце линии наблюдается узел напряжения и пучность тока.
В промежуточных точках между узлами и пучностями фазовые соотношения отличны от 0, p 2p и т. д. В них амплитуды напряжения и тока принимают промежуточные значения между нулем и максимальным значением.
Векторная диаграмма, приведенная на рис. 13.10, иллюстрирует соотношение фаз между падающей и отраженной волнами тока в различных точках КЗ линии.
Распределение модулей комплексных амплитуд напряжения |Ux| и тока |Ix| по длине линии представлено на рис. 13.11. Расстояние между соседними узлами (пучностями) равно l/2.
Таким образом, в КЗ линии возникают волны напряжения и тока, которые не распространяются вдоль линии, находятся на одном месте. Такие волны называются стоячими а уравнения передачи (13.20) и (13.21) – уравнениями стоячих волн. Описываемый режим работы линии получил также название режима стоячих волн
Определим входное сопротивление КЗ линии в произвольной точке х. Из (13.20) следует, что
При x = 0, l/2, l, 3l/2, … величина
и входное сопротивление 
и входное сопротивление 
На рис. 13.13 приведена зависимость
от длины линии (расстояния х от конца линии).
Меняя длину КЗ линии без потерь, можем получить входное сопротивление, имеющее индуктивный характер (в диапазоне x = = 0 … l/4), емкостный характер (х = l/4 … l/2), затем опять индуктивный (х = l/2 … 3l/4) и т. д.
При длинах, кратных l/4, входное сопротивление короткозамкнутой линии без потерь эквивалентно входному сопротивлению параллельного колебательного контура, а при длинах, кратных l/2 – входному сопротивлению последовательного колебательного контура.
Учитывая, что в линиях, без потерь
и, следовательно, частота w и длина линии l (или расстояние от конца линии х) входят в выражение 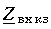
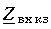
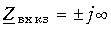
а где bl кратно p, 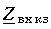
Размыкание линии. В режиме XX Zн = ¥ и I2 = 0. Уравнения передачи получим из (13.19):
Для мгновенных значений имеем (при начальной фазе напряжения ju2 = 0):
Сравнивая уравнения передачи (13.22) и (13.23) с уравнениями КЗ линии (13.20) и (13.21), видим, что полученные уравнения также являются уравнениями стоячих волн. Разница состоит в том, что узлы и пучности напряжения при XX совпадают с узлами и пучностями тока при коротком замыкании, а узлы и пучности тока разомкнутой линии – с узлами и пучностями напряжения КЗ линии. В конце разомкнутой линии образуется пучность напряжения и узел тока.
Данный режим работы линии по аналогии с предыдущим называется режимом стоячих волн. Входное сопротивление разомкнутой линии без потерь определяется из (13.22):
Его график, отражающий зависимость от х, дан на рис. 13.15.
Включение линии на реактивное сопротивление. Пусть линия нагружена на индуктивность Lн (рис. 13.16, а). При заданной частоте w сопротивление нагрузки Zн = jwLн
Из рис. 13.13 видно, что отрезок закороченной линии длиной меньше l/4 имеет входное сопротивление индуктивного характера. Поэтому всегда можно подобрать такую длину отрезка l¢, при которой его входное сопротивление равнялось бы заданному сопротивлению Zн. Заменим индуктивность Lн отрезком КЗ линии (рис. 13,16, б). Эта замена позволяет применить теорию КЗ линии и сразу же построить кривые распределения напряжения и тока в линии, нагруженной на индуктивность (рис. 13.16, в). В рассматриваемой линии возникают стоячие волны. Этот режим отличается от режима КЗ замыкания тем, что ближайший узел и пучность сдвинуты от конца линии на некоторое расстояние.
В случае, когда линия нагружена на емкость Cн с сопротивлением Zн = = 1/(jwCн), можно заменить эту емкость отрезком разомкнутой линии длиной l < l/4 (см. рис. 13.15), входное сопротивление которого равняется заданному 1/(jwCн). Очевидно, и в этом случае в линии возникают стоячие волны. Предоставляем читателю возможность проанализировать данный режим работы линии самостоятельно.
Включение линии на резистивное сопротивление, не равное волновому. Положим для определенности, что сопротивление нагрузки Rн > Zв = rв, и рассмотрим распространение по линии волны напряжения.
Падающая волна не вся поглощается нагрузкой, часть ее отражается обратно в линию. Амплитуда отраженной волны меньше амплитуды падающей волны, поэтому падающую волну можно представить в виде суммы двух волн. Одна из них, равная по амплитуде отраженной волне, взаимодействуя с ней, образует стоячую волну. Отставшаяся падающая волна является бегущей. Таким образом, в линии возникает смешанная волна, состоящая из бегущей и падающей волн. Данный режим работы называется режимом смешанных волн
На рис. 13.17 показано распределение по длине линии модуля комплексной амплитуды напряжения. В линии будут отсутствовать узлы и пучности, а будут наблюдаться минимумы и максимумы амплитуды волн.
Чтобы оценить близость данного режима к режиму бегущей волны, вводят коэффициент бегущей волны
Величина kбв изменяется в пределах от 0 <= kбв <= 1. При kбв = 0 в линии имеет место стоячая волна, при kбв = 1 – бегущая волна.
Коэффициент бегущей волны можно выразить через отношение волнового сопротивления и сопротивления нагрузки. Действительно, минимальное значение амплитуды смешанной волны
представляет собой амплитуду бегущей волны
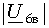
т. е. той волны, которая поглощается частью сопротивления нагрузки, равной волновому сопротивлению. Поэтому
Максимальное значение амплитуды смешанной волны
где |Ucв| – максимальная амплитуда стоячей волны. Отсюда находим
Часто используют обратную величину kcв = 1/kбв которую называют коэффициентом стоячей волны
Из общих уравнений передачи линии без потерь (13.19) рассмотрим сначала уравнение для напряжения:
Воспользуемся подстановкой в виде тождества
Тогда после несложных преобразований получим
Уравнение передачи для мгновенных значений напряжения находим как обычно (полагая при этом ju2 = 0):
Первое слагаемое этого уравнения является бегущей волной, второе слагаемое – стоячей волной. При kбв = 0 первое слагаемое обращается в нуль и в уравнении присутствует только стоячая волна. При kбв = 1 обращается в нуль второе слагаемое и уравнение содержит только бегущую волну.
Рассматривая аналогичным образом уравнение для тока ix(t), имеем:
Можно сделать некоторые выводы:
- если переносимая вдоль линии энергия полностью рассеивается на ее конце (линия нагружена на резистивное сопротивление, равное волновому), то отражение энергии отсутствует и в линии существуют только бегущие волны;
- если энергия в конце линии не рассеивается (короткое замыкание, холостой ход, реактивная нагрузка), то происходит полное отражение волн, и, как следствие этого, в линии образуются только стоячие волны;
- когда переносимая вдоль линии энергия лишь частично рассеивается на ее конце (линия замкнута на резистивное сопротивление, не равное волновому), в линии одновременно присутствуют как бегущие, так и стоячие волны.
13.7. Применение отрезков линий с пренебрежимо малыми потерями
Колебательный контур. В технике сверхвысоких частот вместо колебательных контуров на сосредоточенных реактивных элементах используют отрезки короткозамкнутых или разомкнутых линий с малыми потерями. Частотные характеристики входных сопротивлений таких отрезков (см. рис. 13.14) в области частот, прилегающих к резонансной, достаточно хорошо воспроизводят характеристики колебательных контуров. Значения добротностей отрезков линий достаточно велики и могут достигать, например, для короткозамкнутых четвертьволновых отрезков нескольких тысяч единиц. Это позволяет успешно использовать их для селекции колебаний весьма высоких частот.
Линейный вольтметр. Непосредственное включение в цепь обычного измерительного прибора при очень высокой частоте нарушает режим работы цепи, так как вносит в нее добавочное реактивное и резистивное сопротивления. Измерительный прибор с малым входным сопротивлением, включенный через четвертьволновый отрезок линии, называют линейным вольтметром (рис. 13.19). Подключение измерительного прибора к отрезку линии практически создает КЗ. Входное сопротивление линейного вольтметра оказывается очень большим, и он не оказывает заметного влияния на цепь, в которой измеряется напряжение. Измеряемое действующее значение напряжения связано с действующим значением тока, протекающего через измерительный прибор, зависимостью U = rвI, что следует из уравнения (13.20) при х = l/4.
Полосовой фильтр. На сверхвысоких частотах, где потери в линии пренебрежимо малы, КЗ отрезки линии могут быть использованы для построения фильтров. В качестве примера на рис. 13.20, а показана схема полосового фильтра, построенного на двух КЗ отрезках линии. В продольное плечо схемы включен полуволновый отрезок, в поперечное плечо – четвертьволновый. Первый отрезок имеет входное сопротивление, аналогичное входному сопротивлению последовательного колебательного контура. Второй, четвертьволновый, отрезок играет роль параллельного колебательного контура. Эквивалентная электрическая схема фильтра дана на рис. 13.20, б
Четвертьволновой трансформатор сопротивлений. При длине отрезка х = l/4 уравнения передачи (13.19) упрощаются и принимают вид:
Такой отрезок можно использовать в качестве согласующего трансформатора сопротивлений. Если включаемые каскадно линии имеют разные волновые сопротивления Zв1 и Zв2, то у четвертьволнового согласующего трансформатора в качестве сопротивления нагрузки выступает волновое сопротивление Zв2. Входное сопротивление согласующего трансформатора должно быть равно Zв1. Для выполнения этого условия достаточно выбрать Zв трансформатора равным
Тогда
Такой согласующий трансформатор приведен на рис. 13.21.
Пример. На входе отрезка линии без потерь длиной l/2, нагруженного на резистивное сопротивление Rн = 37,5 Ом, включен источник с Uг = 10 В. Волновое сопротивление отрезка Zв = rв = 75 Ом. На расстоянии l/4 от конца отрезка к нему подключен короткозамкнутый шлейф длиной lш = l/8 и волновым сопротивлением Zв = rв = 75 Ом. Определим входное сопротивление отрезка и ток на его входе.
Отрезок линии с короткозамкнутым шлейфом изображен на рис. 13.22. Найдем сначала входное сопротивление части отрезка длиной l/4 от сопротивления Rн до точек а—б, рассматривая эту часть как трансформатор сопротивления:
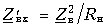
Входное сопротивление КЗ шлейфа длиной l/8, определяется по формуле
где
Таким образом, левая часть отрезка длиной l/4 оказалась нагруженной на параллельное соединение сопротивлений
и
т. е. на сопротивление
Входное сопротивление всего отрезка определим, рассматривая первую половину отрезка как трансформатор сопротивления. Поэтому
Ток на входе отрезка линии
13.8. Вопросы и задания для самопроверки
1. Привести примеры применения длинных линий.
2. Как рассчитывается длина волны, излучаемой радиовещательной станцией?
3. Рассчитать и построить графики первичных параметров коаксиального кабеля 2,6/9,4 мм в диапазоне частот 812 … 17569 кГц. При расчетах принять e = 1,1; tg d = 0,6×10–4, длина кабеля l = 1 км.
Ответ: L = 2,57×10–4 Гн/км, С = 47,5 нФ/км,
R = 4,1×10–2 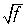
4. Используя данные задачи 3, рассчитать волновое сопротивление кабеля 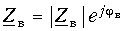
Ответ: Zв = 73,5 Ом, l = 0,286×109/f
5. Первичные параметры линии на частоте w = 104 с–1 имеют значения: R = 10 Ом/км, L = 0,5 мГн/км, С = 4×10–8 Ф/км, G = = 10–6 См/км. Рассчитать волновое сопротивление, коэффициент распространения и длину волны.
Ответ: Zв = 167,2 Ом, jв = –0,552 рад, a = 0,0157, b = –0,065 (для l = 1 км).
6. Почему кабельные линии связи работают в режиме согласованной нагрузки? Что произойдет, если волновое сопротивление антенного фидера не будет согласовано с входным сопротивлением телевизионного приемника?
7. Запишите уравнения передачи линии без потерь. Чем они отличаются от уравнений передачи линии с потерями?
8. Чем отличаются напряжения и токи в различных сечениях согласованно нагруженной линии без потерь?
9. Укажите различия между следующими понятиями: падающие и отраженные волны; бегущие, стоячие и смешанные волны.
10. Линия без потерь с волновым сопротивлением r = 90 Ом нагружена на сопротивление Rн. Коэффициент бегущей волны равен 0,6. Определить сопротивление нагрузки Rн
Ответ: 5,4 Ом.
11. Какой минимальной длины необходимо взять отрезок линии без потерь с параметрами L = 0,49 мкГн, С = 25 мФ/м, чтобы на частоте f = 108 Гц получить из него индуктивность 0,223 мкГн.
Ответ: короткозамкнутый отрезок длиной 0,347 м.
*При анализе работы длинной линии под U и I в дальнейшем будем понимать их комплексные амплитуды (без введения индекса: Um и Im).


 R
R