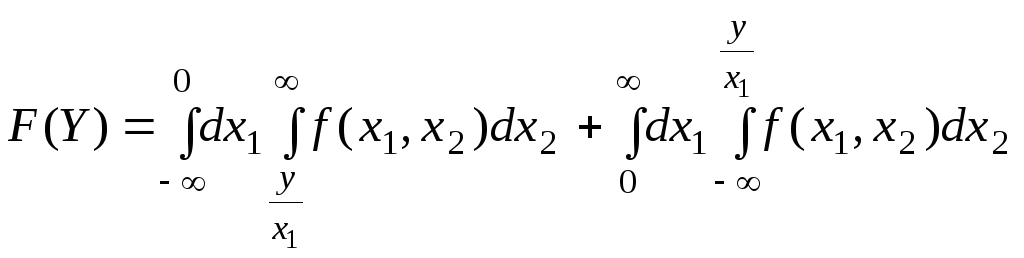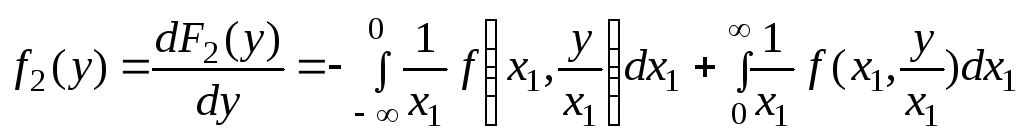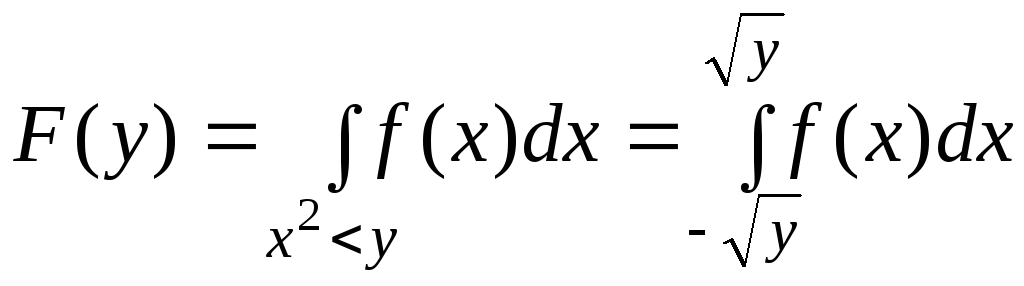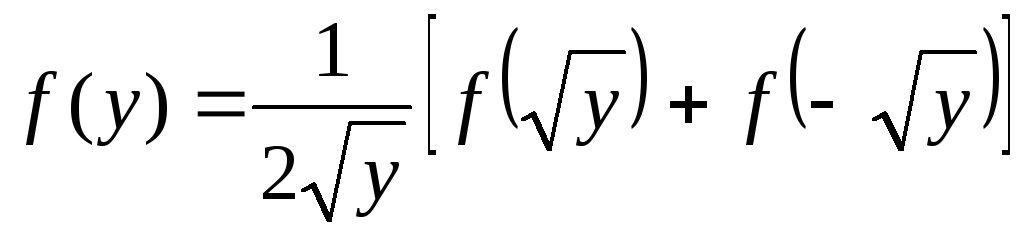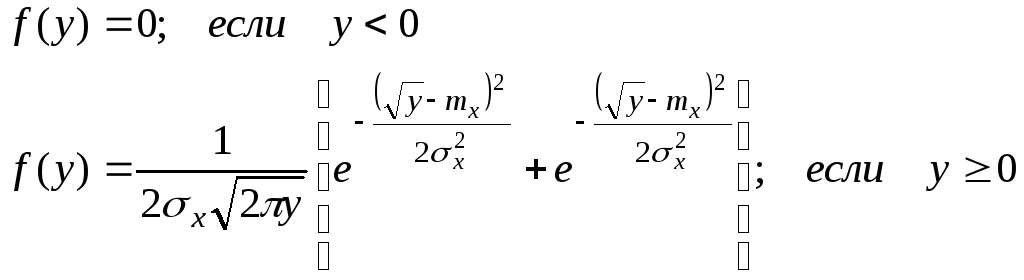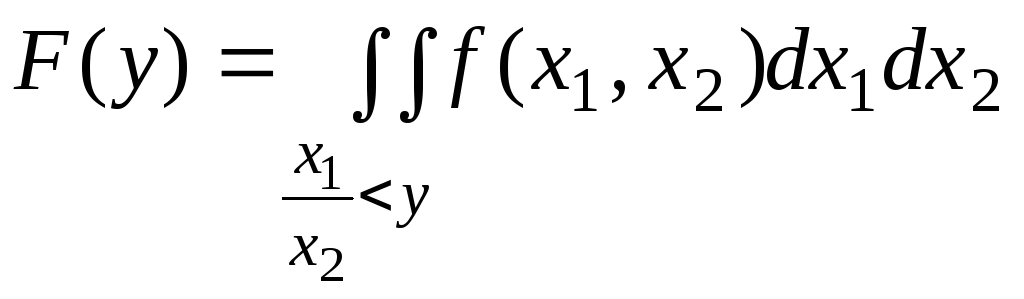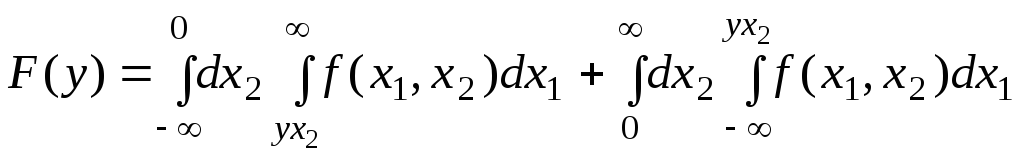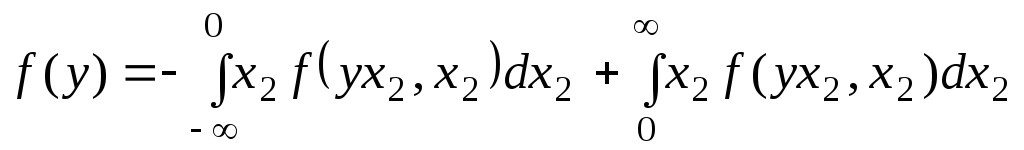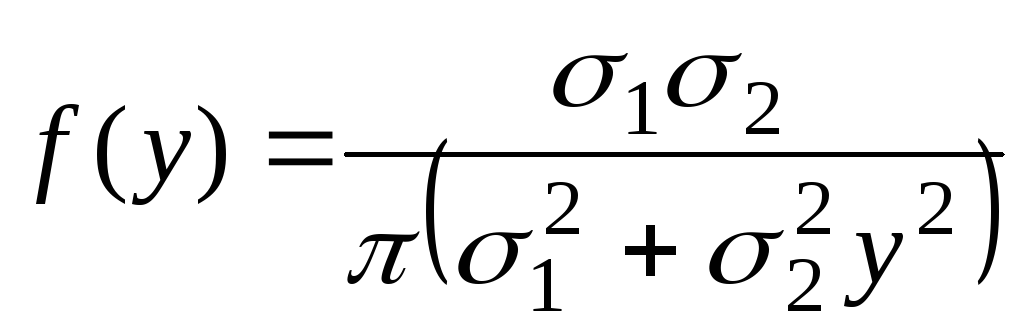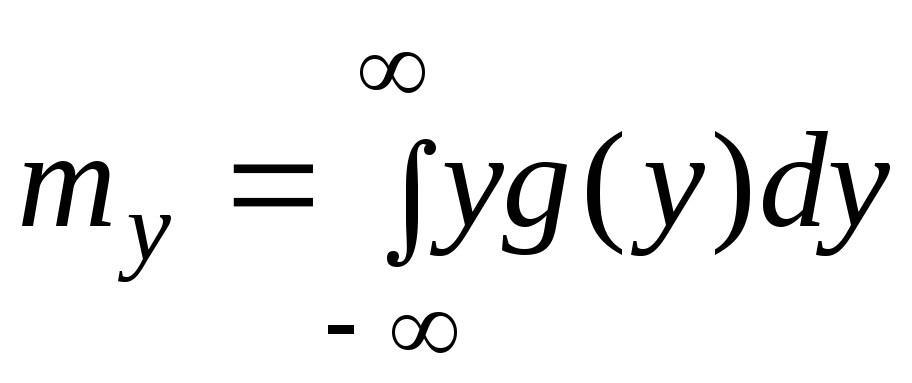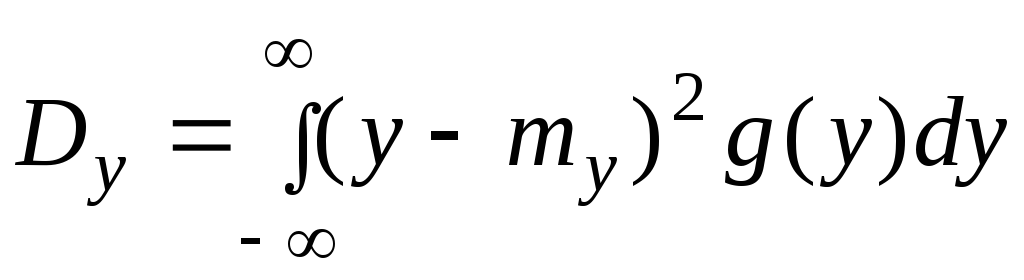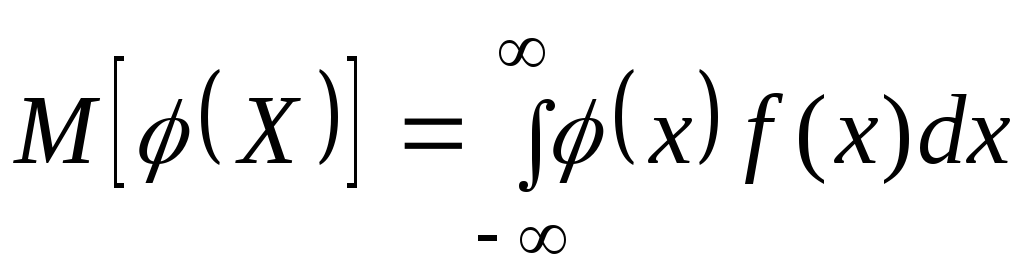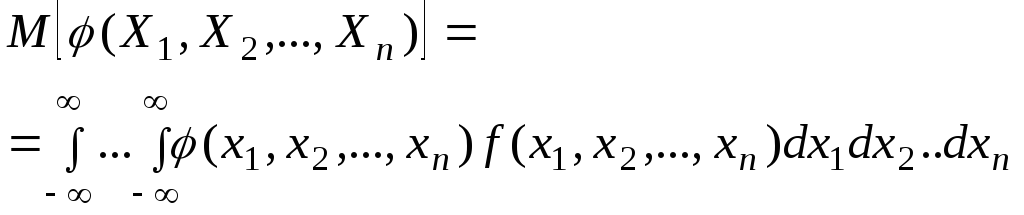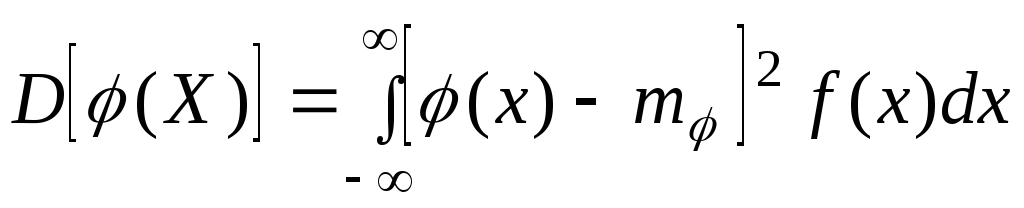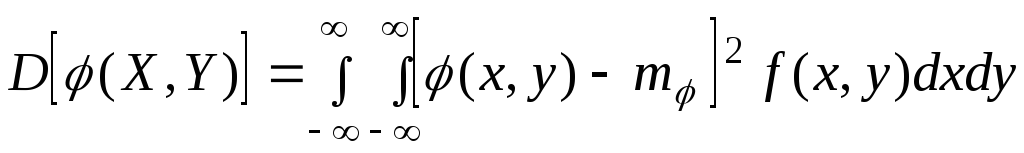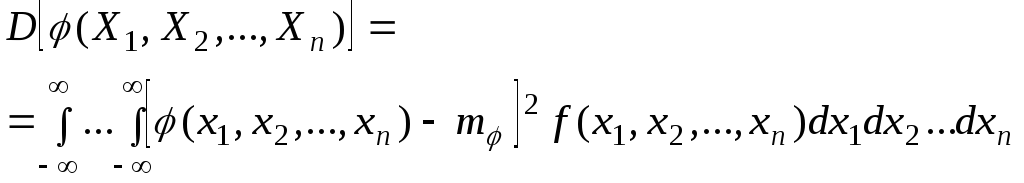Как найти распределение квадрата случайной величины - Avtoru.top

Пусть
,
гдеи— скалярные случайные величины с
совместной плотностью распределения.
Найдем распределениеY.

(6.4.1)

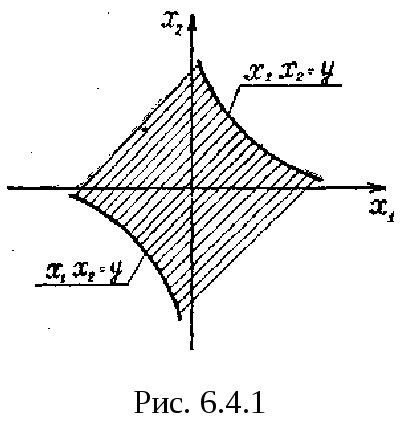
На
рис. событие
показано штриховкой. Теперь очевидно,
что

	(6.4.2)
	(6.4.3)

6.5. Распределение квадрата случайной величины.

Пусть

;
X
— непрерыная случайная величина с
плотностью
.
Найдем.
Если,
тои.
В том случае, когдаполучаем:

	(6.5.1)
	(6.5.2)

В
частном случае, когда
,
имеем:

(6.5.3)

Если
при этом
,
,
то

(6.5.4)

6.6. Распределение частного.

Пусть

;
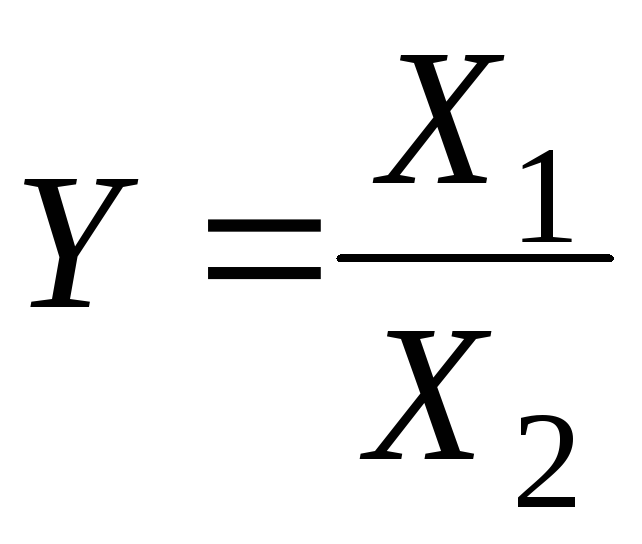
X
— непрерывная случайная величина с
плотностью
.
Найдем.

(6.6.1)

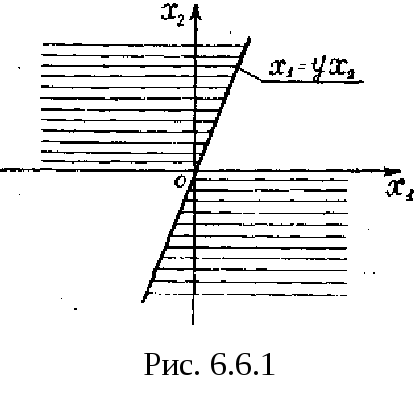
На
рис. 6.6.1 видно, что событие —
изображают
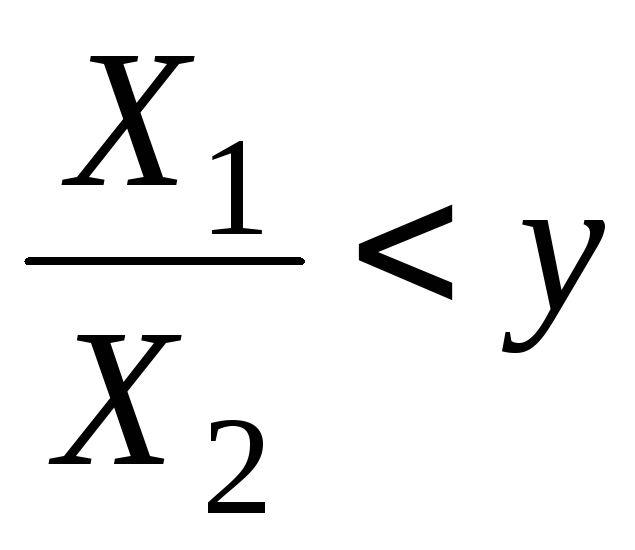
заштрихованные области. Поэтому

	(6.6.2)
	(6.6.3)

Если

;

независимы, то легко получить:

(6.6.4)

Распределение
(6.6.4) носит имя Коши. Оказывается, это
распределение не имеет математического
ожидания и дисперсии.

6.7. Числовые характеристики функций случайных величин.

Рассмотрим
следующую задачу: случайная величина
Y
есть
функция нескольких случайных величин
;

(6.7.1)

Пусть
нам известен закон распределения системы
аргументов
;
требуется
найти числовые характеристики величины
Y,
в первую очередь—математическое
ожидание и дисперсию.

Представим
себе, что нам удалось найти закон
распределения g(у)
величины Y.
Тогда
задача об определении числовых
характеристик становится простой; они
находятся по формулам:

	(6.7.2)
	(6.7.3)

Однако
задача нахождения закона распределения
g(y)
величины
Y
часто
оказывается довольно сложной. Для
решения поставленной задачи нахождение
закона распределения величины Y
не
нужно: чтобы найти только числовые
характеристики величины Y,
нет
надобности знать ее закон распределения;
достаточно знать закон распределения
аргументов
.

Таким образом,
возникает задача определения числовых
характеристик функций случайных
величин, не определяя законов распределения
этих функций.

Рассмотрим задачу
об определении числовых характеристик
функции при заданном законе
распределения аргументов. Начнем с
самого простого случая — функции одного
аргумента.

Имеется
случайная величина X
с
заданным законом распределения;
другая случайная величина Y
связана
с X
функциональной
зависимостью: Y=
(Х).

Требуется,
не находя закона распределения величины
Y,
определить ее математическое ожидание:

(6.7.4)

Рассмотрим
сначала случай, когда X
есть
дискретная случайная величина с рядом
распределения:

Табл. 6.7.1

x_i	X₁	x₂	…	x_n
p_i	P₁	p₂	…	p_n

Запишем
в виде таблицы возможные значения
величины Y
и вероятности этих значений:

Табл. 6.7.2

( x_i)	( x₁)	( x₂)	…	( x_n)
p_i	P₁	P₂	…	p_n

Таблица
6.7.2 не является рядом распределения
величины Y,
так как в общем случае некоторые из
значений

(6.7.5)

могут
совпадать между собой. Для того чтобы
от таблицы (6.7.1) перейти к подлинному
ряду распределения величины Y,
нужно
было бы расположить значения (6.7.5)
в порядке возрастания, объединить
столбцы, соответствующие равным
между собой значениям Y,
и
сложить соответствующие вероятности.
Математическое ожидание величины Y
можно
определить по формуле

(6.7.6)

Очевидно,
величина т_у
— М((Х)),определяемая
по формуле (6.7.6),
не может измениться от того, что под
знаком суммы некоторые члены будут
объединены заранее, а порядок членов
изменен.

В
формуле (6.7.6)
для математического ожидания функции
не содержится в явном виде закона
распределения самой функции, а содержится
только закон распределения аргумента.
Таким образом, для
определения математического ожидания
функции вовсе не требуется знать закон
распределения этой функции, а достаточно
знать закон распределения аргумента.

Заменяя
в формуле (6.7.6)
сумму интегралом, а вероятность р_i—
элементом вероятности, получим аналогичную
формулу для непрерывной случайной
величины:

(6.7.7)

где
f(x)
—
плотность распределения величины X.

Аналогично
может быть определено математическое
ожидание функции у(Х,Y)
от
двух случайных аргументов X
и
Y.
Для
дискретных величин

(6.7.8)

где

—
вероятность
того, что система (X,Y)
примет
значения (x_i
y_j).
Для непрерывных величин

(6.7.9)

где
f(x,
у)
—
плотность распределения системы (X,
Y).

Аналогично
определяется математическое ожидание
функции от произвольного числа случайных
аргументов. Приведем соответствующую
формулу только для непрерывных величин:

(6.7.10)

где

— плотность
распределения системы
.

Формулы
типа (6.7.10)
весьма часто встречаются в практическом
применении теории вероятностей, когда
речь идет об осреднении каких-либо
величин, зависящих от ряда случайных
аргументов.

Таким образом,
математическое ожидание функции любого
числа случайных аргументов может быть
найдено помимо закона распределения
функции. Аналогично могут быть найдены
и другие числовые характеристики функции
— моменты различных порядков. Так как
каждый момент представляет собой
математическое ожидание некоторой
функции исследуемой случайной величины,
то вычисление любого момента может быть
осуществлено приемами, совершенно
аналогичными вышеизложенным. Здесь
мы приведем расчетные формулы только
для дисперсии, причем лишь для случая
непрерывных случайных аргументов.

Дисперсия функции
одного случайного аргумента выражается
формулой

(6.7.11)

где
т=М[(x)]
— математическое ожидание функции
(X);
f(х)
—
плотность распределения величины X.

Аналогично
выражается дисперсия функции двух
случайных аргументов:

(6.7.12)

где
— математическое ожидание функции(Х,Y);
f(x,у)
— плотность распределения системы
(X,Y).
Наконец, в случае произвольного числа
случайных аргументов, в аналогичных
обозначениях:

(6.7.13)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Distributions of Sampling Statistics

Sheldon M. Ross, in Introductory Statistics (Third Edition), 2010

Definition

If Z₁, …, Z_n are independent standard normal random variables, then the random variable

∑i=1nZi2

is said to be a chi-squared random variable with n degrees of freedom.

Figure 7.5 presents the chi-squared density functions for three different values of the degree of freedom parameter n.

FIGURE 7.5. Chi—squared density function with n degrees of freedom, n = 1, 3, 10.

To determine the expected value of a chi-squared random variable, note first that for a standard normal random variable Z,

1=Var (Z)=E[Z2]−(E[Z])2=E[Z2] since E[Z]=0

Hence, E[Z²] = 1 and so

E[∑i=1nZi2]=∑i=1nE[Zi2]=n

The expected value of a chi-squared random variable is equal to its number of degrees of freedom.

Suppose now that we have a sample X₁, …, X_n from a normal population having mean μ and variance σ². Consider the sample variance S² defined by

S2=∑i=1n(Xi−X¯)2n−1

The following result can be proved:

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780123743886000077

Chi-Squared Goodness-of-Fit Tests

Sheldon M. Ross, in Introductory Statistics (Fourth Edition), 2017

13.5 Use of R

Chi-squared probabilities can be obtained from R. If you want the probability that a chi-squared random variable with n degrees of freedom is less than x, just type pchisq(x,n) and the probability will be given upon hitting return. If you want the probability that it is greater than x, type 1−pchisq(x,n). For instance, the probability that a chi-squared with 10 degrees of freedom is greater than 15 is obtained from

>1−pchisq(15,10)[1]0.1320619

If you want the value χn,α2 such that P(X>χn,α2)=α, when X is a chi-squared random variable with n degrees of freedom, just type qchisq(1−α,n). For instance, we obtain χ12,.042 as follows:

>qchisq(1−.04,12)[1]21.78511

By the way, the reason we type qchisq(1−α,n) rather than qchisq(α,n) is that qchisq(β,n) yields the 100β percentile; that is, the probability that the chi-square will be less than qchisq(β,n) is β, and so the probability that it will be greater than qchisq(β,n) is 1−β.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780128043172000138

Nonparametric Hypotheses Tests

Sheldon M. Ross, in Introductory Statistics (Third Edition), 2010

Solution

We see by the preceding that R_A = 18, R_B = 18, R_C = 24. Hence,

TS =(18−20)2+(18−20)2+(24−20)2=24

Because 1210⋅3⋅4 TS = TS10 is, when H₀ is true, approximately a chi-squared random variable with 2 degrees of freedom, and because the data give that TS10 = 2.4, the

p value of the test of H₀ is

pvalue≈P(χ22≥2.4)=.3012

showing that the data are not inconsistent with the hypothesis that the wines are of identical quality.

The preceding test for the equality of multiple population distributions when the data consists of a set of comparison rankings is known as the Freedman test.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780123743886000144

Advanced Math and Statistics

Robert Kissell, Jim Poserina, in Optimal Sports Math, Statistics, and Fantasy, 2017

Chi-Square Distribution

A chi-square distribution is a continuous distribution with k degrees of freedom. It is used to describe the distribution of a sum of squared random variables. It is also used to test the goodness of fit of a distribution of data, whether data series are independent, and for estimating confidences surrounding variance and standard deviation for a random variable from a normal distribution. Additionally, chi-square distribution is a special case of the gamma distribution.

Chi-Square Distribution Statistics¹

Notation	χ(k)
Parameter	k=1,2,…
Distribution	x≥0
Pdf	(xk2−1e−x2)/(2k2Γ(k2))
Cdf	γ(k2,x2)/Γ(k2)
Mean	k
Variance	2k
Skewness	8/k
Kurtosis	12/k

where γ(k2,x2) is known as the incomplete Gamma function (www.mathworld.wolfram.com).

Chi-Square Distribution Graph

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780128051634000049

Random Variables

Sheldon M. Ross, in Introduction to Probability Models (Tenth Edition), 2010

2.2 Definition

IfZ₁,…,Z_n are independent standard normal random variables, then the random variable∑i=1nZi2 is said to be a chi-squared random variable with n degrees of freedom.

We shall now compute the moment generating function of∑i=1nZi2. To begin, note that

E[exp{tZi2}]=12∫−∞∞etx2e−x2/2 dx =12∫−∞∞e−x2/2σ2 dx where σ2=(1−2t)−1 =σ =(1−2t)−1/2

Hence,

E[exp{t∑i=1nzi2}]=∏i=1nE[exp{tZi2}]=(1−2t)−n/2

Now, let X₁,…,X_n be independent normal random variables, each with mean μ and variance σ², and letX¯=∑i=1nXi/n and S² denote their sample mean and sample variance. Since the sum of independent normal random variables is also a normal random variable, it follows thatX¯ is a normal random variable with expected value μ and variance σ²/n. In addition, from Proposition 2.4,

(2.22)Cov(X¯,Xi−X¯)=0, i=1,⋯,n

Also, sinceX¯,X1−X¯,X2−X¯,⋯Xn−X¯ are all linear combinations of the independent standard normal random variables(Xi−μ)σ,i=1,⋯n, it follows that the random variablesX¯,X1−X¯,X2−X¯,⋯Xn−X¯ have a joint distribution that is multivariate normal. However, if we let Y be a normal random variable with mean μ and variance σ²/n that is independent of X₁,…X_n, then the random variables Y,Y,X1−X¯,X2−X¯,⋯Xn−X¯ also have a multivariate normal distribution, and by Equation (2.22), they have the same expected values and covariances as the random variablesX¯,Xi−X¯,i,=1,⋯n. Thus, since a multivariate normal distribution is completely determined by its expected values and covariances, we can conclude that the random vectors Y,Y,X1−X¯,X2−X¯,⋯Xn−X¯ andX¯,X1−X¯,X2−X¯,⋯Xn−X¯ have the same joint distribution; thus showing thatX¯is independent of the sequence of deviations,Xi−X¯,i,=1,⋯n

SinceX¯ is independent of the sequence of deviations,Xi−X¯,i,=1,⋯n it follows that it is also independent of the sample variance

S2≡∑i=1n(Xi−X¯)2n−1

To determine the distribution of S², use Indentity (2.21) to Obtain

(n−1)S2=∑i=1n(Xi−μ)2−n(X¯−μ)2

Dividing both sides of this equation by σ²yields

(2.23)(n−1)S2σ2+(X¯−μσ/n)2=∑i=1n(Xi−μ)2σ2

Now,∑i=1n(Xi−μ)2/σ2 is the sum of the squares of n independent standard normal random variables, and so is a chi-squared random variable with n degrees of freedom; it thus has moment generating function(1−2t)−n/2. Also[(X¯−μ)/(σ/n)]2 is the square of a standard normal random variable and so is a chi-squared random variable with one degree of freedom; it thus has moment generating function(1−2t)−1/2. In addition, we have previously seen that the two random variables on the left side of Equation (2.23) are independent. Therefore, because the moment generating function of the sum of independent random variables is equal to the product of their individual moment generating functions, we obtain that

E[et(n−1)S2/σ2](1−2t)−1/2=(1−2t)−n/2

E[et(n−1)S2/σ2]=(1−2t)−(n−1)/2

But because(1−2t)−(n−1)/2 is the moment generating function of a chi-squared random variable with n−1 degrees of freedom, we can conclude, since the moment generating function uniquely determines the distribution of the random variable, that this is the distribution of(n−1)S2/σ2.

Summing up, we have shown the following.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780123756862000108

Random Variables

Sheldon M. Ross, in Introduction to Probability Models (Twelfth Edition), 2019

2.6.1 The Joint Distribution of the Sample Mean and Sample Variance from a Normal Population

Let X1,…,Xn be independent and identically distributed random variables, each with mean μ and variance σ2. The random variable S2 defined by

S2=∑i=1n(Xi−X¯)2n−1

is called the sample variance of these data. To compute E[S2] we use the identity

(2.21)∑i=1n(Xi−X¯)2=∑i=1n(Xi−μ)2−n(X¯−μ)2

which is proven as follows:

∑i=1n(Xi−X¯)=∑i=1n(Xi−μ+μ−X¯)2=∑i=1n(Xi−μ)2+n(μ−X¯)2+2(μ−X¯)∑i=1n(Xi−μ)=∑i=1n(Xi−μ)2+n(μ−X¯)2+2(μ−X¯)(nX¯−nμ)=∑i=1n(Xi−μ)2+n(μ−X¯)2−2n(μ−X¯)2

and Identity (2.21) follows.

Using Identity (2.21) gives

E[(n−1)S2]=∑i=1nE[(Xi−μ)2]−nE[(X¯−μ)2]=nσ2−nVar(X¯)=(n−1)σ2fromProposition2.4(b)

Thus, we obtain from the preceding that

E[S2]=σ2

We will now determine the joint distribution of the sample mean X¯=∑i=1nXi/n and the sample variance S2 when the Xi have a normal distribution. To begin we need the concept of a chi-squared random variable.

Definition 2.2

If Z1,…,Zn are independent standard normal random variables, then the random variable ∑i=1nZi2 is said to be a chi-squared random variable with n degrees of freedom.

We shall now compute the moment generating function of ∑i=1nZi2. To begin, note that

E[exp⁡{tZi2}]=12π∫−∞∞etx2e−x2/2dx=12π∫−∞∞e−x2/2σ2dxwhereσ2=(1−2t)−1=σ=(1−2t)−1/2

Hence,

E[exp⁡{t∑i=1nZi2}]=∏i=1nE[exp⁡{tZi2}]=(1−2t)−n/2

Now, let X1,…,Xn be independent normal random variables, each with mean μ and variance σ2, and let X¯=∑i=1nXi/n and S2 denote their sample mean and sample variance. Since the sum of independent normal random variables is also a normal random variable, it follows that X¯ is a normal random variable with expected value μ and variance σ2/n. In addition, from Proposition 2.4,

(2.22)Cov(X¯,Xi−X¯)=0,i=1,…,n

Also, since X¯,X1−X¯,X2−X¯,…,Xn−X¯ are all linear combinations of the independent standard normal random variables (Xi−μ)/σ,i=1,…,n, it follows that the random variables X¯,X1−X¯,X2−X¯,…,Xn−X¯ have a joint distribution that is multivariate normal. However, if we let Y be a normal random variable with mean μ and variance σ2/n that is independent of X1,…,Xn, then the random variables Y,X1−X¯,X2−X¯,…,Xn−X¯ also have a multivariate normal distribution, and by Eq. (2.22), they have the same expected values and covariances as the random variables X¯,Xi−X¯,i=1,…,n. Thus, since a multivariate normal distribution is completely determined by its expected values and covariances, we can conclude that the random vectors Y,X1−X¯,X2−X¯,…,Xn−X¯ and X¯,X1−X¯,X2−X¯,…,Xn−X¯ have the same joint distribution; thus showing that X¯ is independent of the sequence of deviations Xi−X¯, i=1,…,n.

Since X¯ is independent of the sequence of deviations Xi−X¯,i=1,…,n, it follows that it is also independent of the sample variance

S2≡∑i=1n(Xi−X¯)2n−1

To determine the distribution of S2, use Identity (2.21) to obtain

(n−1)S2=∑i=1n(Xi−μ)2−n(X¯−μ)2

Dividing both sides of this equation by σ2 yields

(2.23)(n−1)S2σ2+(X¯−μσ/n)2=∑i=1n(Xi−μ)2σ2

Now, ∑i=1n(Xi−μ)2/σ2 is the sum of the squares of n independent standard normal random variables, and so is a chi-squared random variable with n degrees of freedom; it thus has moment generating function (1−2t)−n/2. Also [(X¯−μ)/(σ/n)]2 is the square of a standard normal random variable and so is a chi-squared random variable with one degree of freedom; it thus has moment generating function (1−2t)−1/2. In addition, we have previously seen that the two random variables on the left side of Eq. (2.23) are independent. Therefore, because the moment generating function of the sum of independent random variables is equal to the product of their individual moment generating functions, we obtain that

E[et(n−1)S2/σ2](1−2t)−1/2=(1−2t)−n/2

E[et(n−1)S2/σ2]=(1−2t)−(n−1)/2

But because (1−2t)−(n−1)/2 is the moment generating function of a chi-squared random variable with n−1 degrees of freedom, we can conclude, since the moment generating function uniquely determines the distribution of the random variable, that this is the distribution of (n−1)S2/σ2.

Summing up, we have shown the following.

Proposition 2.5

If X1,…,Xn are independent and identically distributed normal random variables with mean μ and variance σ2, then the sample mean X¯ and the sample variance S2 are independent. X¯ is a normal random variable with mean μ and variance σ2/n;(n−1)S2/σ2 is a chi-squared random variable with n−1 degrees of freedom.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B978012814346900007X

Linear Regression

Sheldon M. Ross, in Introductory Statistics (Third Edition), 2010

12.4 ERROR RANDOM VARIABLE

We have defined the linear regression model by the relationship

Y=α+βx+e

where α and β are unknown parameters that will have to be estimated and e is an error random variable having mean 0. To be able to make statistical inferences about the regression parameters α and β, it is necessary to make some additional assumptions concerning the error random variable e. The usual assumption, which we will be making, is that e is a normal random variable with mean 0 and variance σ². Thus we are assuming that the variance of the error random variable remains the same no matter what input value x is used.

Put another way, this assumption is equivalent to assuming that for any input value x, the response variable Y is a random variable that is normally distributed with mean

E[Y]=α+βx

and variance

Var (Y)=σ2

An additional assumption we will make is that all response variables are independent. That is, for instance, the response from input value x₁ will be assumed to be independent of the response from input value x₂.

The quantity σ² is an unknown that will have to be estimated from the data. To see how this can be accomplished, suppose that we will be observing the response values Y_i corresponding to the input values x_i, i = 1, …, n. Now, for each value of i, the standardized variable

Yi−E[Yi]Var(Yi)=Yi−(α+βxi)σ

will have a standard normal distribution. Thus, since a chi-squared random variable with n degrees of freedom is defined to be the sum of the squares of n independent standard normals, we see that

∑i=1n(Yi−αˆ−βˆxi)2σ2

is chi squared with n degrees of freedom.

If we now substitute the estimators αˆ and βˆ for α and β in the preceding expression, then the resulting variable will remain chi squared but will now have n – 2 degrees of freedom (since 1 degree of freedom will be lost for each parameter that is estimated). That is,

∑i=1n(Yi−αˆ−βˆxi)2σ2

is chi squared with n – 2 degrees of freedom.

The quantities

Yi−αˆ−βˆxi i=1, …, n

are called residuals. They represent the differences between the actual and the predicted responses. We will let SS_R denote the sum of the squares of these residuals. That is,

SSR=∑i=1n(Yi−αˆ−βˆxi)2

From the preceding result, we thus have

SSRσ2

is chi squared with n – 2 degrees of freedom.

Since the expected value of a chi-squared random variable is equal to its number of degrees of freedom, we obtain

E[SSR]σ2=n−2

E[SSRn−2]=σ2

In other words, SS_R/(n – 2) can be used to estimate σ².

SSRn−2

is the estimator of σ².

Program 12-1 can be utilized to compute the value of SS_R.

Example 12.3

Consider Example 12.2 and suppose that we are interested in estimating the value of σ². To do so, we could again run Program 12-1, this time asking for the additional statistics. This would result in the following additional output:

S(x, Y) = –125.3499

S(x, x) = 281.875

S(Y, Y) = 61.08057

SS_R = 5.337465

THE SQUARE ROOT OF (n – 2)S(x, x)/SS_R is 17.80067

The estimate of σ² is 5.3375/6 = 0.8896.

The following formula for SS_R is useful when you are using a calculator or computing by hand.

Computational formula for SS_R:

SSR=SχχSYY−SxY2Sχχ

The easiest way to compute SS_R by hand is first to determine S_xx, S_xY, and S_YY and then to apply the preceding formula.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780123743886000120

Special random variables

Sheldon M. Ross, in Introduction to Probability and Statistics for Engineers and Scientists (Sixth Edition), 2021

5.8.1 The chi-square distribution

Definition

If Z1,Z2,…,Zn are independent standard normal random variables, then X, defined by

(5.8.1)X=Z12+Z22+⋯+Zn2

is said to have a chi-square distribution with n degrees of freedom. We will use the notation

X∼χn2

to signify that X has a chi-square distribution with n degrees of freedom.

The chi-square distribution has the additive property that if X1 and X2 are independent chi-square random variables with n1 and n2 degrees of freedom, respectively, then X1+X2 is chi-square with n1+n2 degrees of freedom. This can be formally shown either by the use of moment generating functions or, most easily, by noting that X1+X2 is the sum of squares of n1+n2 independent standard normals and thus has a chi-square distribution with n1+n2 degrees of freedom.

If X is a chi-square random variable with n degrees of freedom, then for any α∈(0,1), the quantity χα,n2 is defined to be such that

P{X≥χα,n2}=α

This is illustrated in Figure 5.11.

Figure 5.11. The chi-square density function with 8 degrees of freedom.

Chi-square probabilities, as well as the values χα,n2 can be obtained using R. To obtain P(X⩽x), when X is a chi-squared random variable with n degrees of freedom, just use the R command pchisq(x,n). To obtain χα,n2 , type qchisq(1−α,n).

Example 5.8.a

Determine P{χ262≤30} when χ262 is a chi-square random variable with 26 degrees of freedom.

Solution

R yields the solution

>pchisq(30,26)[1]0.732389■

Example 5.8.b

Find χ.05,152.

Solution

R yields the result

>qchisq(.95,15)[1]24.99579■

Example 5.8.c

Suppose that we are attempting to locate a target in three-dimensional space, and that the three coordinate errors (in meters) of the point chosen are independent normal random variables with mean 0 and standard deviation 2. Find the probability that the distance between the point chosen and the target exceeds 3 meters.

Solution

If D is the distance, then

D2=X12+X22+X32

where Xi is the error in the ith coordinate. Since Zi=Xi/2, i=1,2,3, are all standard normal random variables, it follows that

P{D2>9}=P{Z12+Z22+Z32>9/4}=P{χ32>9/4}

R now gives

>1−pchisq(9/4,3)[1]0.5221672■

We can plot chi-square densities using R. To plot the density of a chi-square with 5 degrees of freedom, say going from 0 to 12 in increments of size .001, do the following:

>x=seq(0,12,.001)>f=dchisq(x,5)>plot(x,f)

5.8.1.1 The relation between chi-square and gamma random variables⁷

Let us compute the moment generating function of a chi-square random variable with n degrees of freedom. To begin, we have, when n=1, that

(5.8.2)E[etX]=E[etZ2]whereZ∼N(0,1)=∫−∞∞etx2fZ(x)dx=12π∫−∞∞etx2e−x2/2dx=12π∫−∞∞e−x2(1−2t)/2dx=12π∫−∞∞e−x2/2σ¯2dxwhereσ¯2=(1−2t)−1=(1−2t)−1/212πσ¯∫−∞∞e−x2/2σ¯2dx=(1−2t)−1/2

where the last equality follows since the integral of the normal (0, σ¯2) density equals 1. Hence, in the general case of n degrees of freedom

E[etX]=E[et∑i=1nZi2]=E[∏i=1netZi2]=∏i=1nE[etZi2]by independence of the Zi=(1−2t)−n/2from Equation (5.8.2)

which we recognize as being the moment generating function of a gamma random variable with parameters (n/2,1/2). Hence, by the uniqueness of moment generating functions, it follows that these two distributions — chi-square with n degrees of freedom and gamma with parameters n/2 and 1/2 — are identical, and thus we can conclude that the density of X is given by

f(x)=12e−x/2(x2)(n/2)−1Γ(n2),x>0

The chi-square density functions having 1, 3, and 10 degrees of freedom, respectively, are plotted in Figure 5.12.

Figure 5.12. The chi-square density function with n degrees of freedom.

Let us reconsider Example 5.8.c, this time supposing that the target is located in the two-dimensional plane.

Example 5.8.d

When we attempt to locate a target in two-dimensional space, suppose that the coordinate errors are independent normal random variables with mean 0 and standard deviation 2. Find the probability that the distance between the point chosen and the target exceeds 3.

Solution

If D is the distance and Xi,i=1,2, are the coordinate errors, then

D2=X12+X22

Since Zi=Xi/2, i=1,2, are standard normal random variables, we obtain

P{D2>9}=P{Z12+Z22>9/4}=P{χ22>9/4}=e−9/8≈.3247

where the preceding calculation used the fact that the chi-square distribution with 2 degrees of freedom is the same as the exponential distribution with parameter 1/2. ■

Since the chi-square distribution with n degrees of freedom is identical to the gamma distribution with parameters α=n/2 and λ=1/2, it follows from Equations (5.7.3) and (5.7.4) that the mean and variance of a random variable X having this distribution is

E[X]=n,Var(X)=2n

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780128243466000144

Proficiency Testing in Analytical Chemistry

M. Thompson, in Comprehensive Chemometrics, 2009

1.03.3 Validation of Test Materials

1.03.3.1 Introduction

Test materials distributed by the scheme should be of a matrix typically encountered in the relevant analytical sector and, in the long term, should contain analyte concentrations representing both acceptable and unacceptable levels. Materials must be sufficiently stable and homogeneous, so that differences in composition among the units received by the participants are insignificantly small in comparison with the uncertainty of the measurement process. Such a requirement calls for regular (or at least occasional) testing by the scheme provider. Because of this restriction, it is usually impossible to distribute materials in their native state. For example, rock samples have to be distributed as a fine powder to ensure a sufficient degree of homogeneity, and vegetable samples as a puree.

1.03.3.2 Testing for Homogeneity

To ensure that participants receive portions of test material with only inconsequential differences in composition (a condition known as ‘sufficient homogeneity’), it is necessary to test the material after it has been divided into containers for distribution. As it is universally recognized that it is the analyst’s responsibility to take a representative test portion from the laboratory sample, there is no need to test for heterogeneity within individual containers, only between containers.

The test comprises the selection of 10 or more distribution units at random from the complete set and the analysis of each in duplicate, in a random sequence, under repeatability conditions, by a method with appropriate precision (i.e., with a standard deviation σ_an < 0.3σ_p; the results must be recorded with sufficient digit resolution to support the statistical analysis). The between-unit variance σ_sam is then found by analysis of variance and compared with a maximum-allowable variance σ_all to test whether it is significantly greater. Two precautions, however, are needed to make this test meaningful.

First, the randomization has to be strictly conducted, so that the data contain no systematic features that could falsely enhance or reduce the appearance of heterogeneity. It is worthwhile to give the analysts explicit instructions on how to do that: experience has shown that implicit instructions are often misunderstood or ignored. It is also necessary to check every data set for systematic effects by inspection of a simple display of result versus sample number. Undesirable features that may invalidate the test are a trend or discontinuity (Figure 13), bias between the first and second results (Figure 14), or insufficient digit resolution of data (Figure 15).

Figure 13. Data from a homogeneity test showing the first (red) and second (green) results from each distribution unit. The data show a trend, probably because the data were analyzed in the order of their code numbers rather than in a random order. This feature would tend to suggest falsely that the material was significantly heterogeneous.

Figure 14. Data from a homogeneity test showing the first (red) and second (green) results from each distribution unit. The data show a bias between the first and second results, indicating that the analysis was conducted in two sequences, with each unit analyzed once in each sequence. This feature would tend to disguise significant heterogeneity.

Figure 15. Data from a homogeneity test showing a single outlying result, normally attributable to an analytical mistake.

Second, a statistical approach more sophisticated than the simple F-test of the hypothesis

(8)H0:σsam=0versusHA:σsam>0

is required to avoid an undue probability of rejection of good test material or rejection of the whole data set as incapable of supporting the required decision.²⁹ The problem here is that, given an analytical method of sufficiently high precision, almost any material can be shown to be significantly heterogeneous. This does not necessarily mean, however, that the material is unsuitable for use in the proficiency test. In addition, as homogeneity testing is expensive (often requiring as much as one-third of the whole cost of the proficiency test), it is desirable to minimize the false rejection rate. For example, if σ_sam is acceptable but only slightly less than σ_all, about one-half of all sufficiently homogeneous materials would be rejected. To deal with these problems, it is necessary to test a different hypothesis, namely

(9)H0:σsam≤σallversusHA:σsam>σall

where σ_all is the maximum-allowable value, determined independently by the practical requirements of the proficiency test (i.e., not derived from the data).

To carry out this test, we calculate σˆan and σˆsam in the normal way from the mean squares in the analysis of variance, and reject the material when

(10)σˆsam2>σall2χn−12n−1+σˆan2(Fn−1,n−1)2

1.: χ_n−1² is the value exceeded with a probability of 0.05 by a chi-squared random variable with n − 1 degrees of freedom.
2.: F_n−1, n is the value exceeded with a probability of 0.05 by a random variable with the F-distribution with n − 1 and n degrees of freedom.
3.: n is the number of units analyzed in duplicate. (Duplicate analysis is assumed in Equation (10).)
4.: A suitable value for the allowable variance is σall2≤σp2/9 (i.e., σ_all ≤ σ_p/3 where σ_p is the target value), which ensures that any heterogeneity between distribution units has a negligible effect on the z-scores.

As each homogeneity test requires at least 20 replicate analyses, the occurrence of an analytical outlier in a data set is not rare. The first edition¹ of the Harmonized Protocol stated that no outlying data should be excluded from the analysis of variance, because outliers comprised valid evidence of heterogeneity. However, a single analytical outlier (Figure 15) has the (perhaps) unexpected effect of making rejection of the null hypothesis less probable, because it has a bigger effect on the within-sample mean square than the between-sample mean square. Moreover, a single outlier must have occurred because of an analytical lapse, as the analyst should have ensured that both test portions were representative of the distribution unit. More recent opinion, therefore, is that a single outlier should be rejected before the calculation of the mean squares. Cochran’s test for unequal variances at 95% confidence is suitable for this purpose. (There is a potential exception to this rule. Some trace analytes occur only as rare discrete particles containing a high concentration of the analyte, even in ‘homogenized’ material. This could give rise to a valid solitary outlier. An example would be the determination of platinum in an ore.) However, a pair of apparently outlying results from the same distribution unit (Figure 16) must never be rejected: it is a true indication of heterogeneity. The occurrence of two outlying results from different distribution units suggests that the analysis was unreliable and that the whole data set should be discarded.

Figure 16. Data from a homogeneity test showing a pair of outlying results from a single unit. This is a strong indication of heterogeneity.

It should be noted that homogeneity tests have a low statistical power unless an unrealistically large number of distribution units are tested. The test should therefore be regarded as a screen to ensure that serious problems are avoided.

1.03.3.3 Testing for Stability

Materials distributed in proficiency tests should be sufficiently stable over the period during which the assigned value is designed to be definitive. The term ‘sufficiently stable’ implies that any changes that occur during the relevant period have an inconsequential effect on the interpretation of the results of a round. Normally, the period in question is the interval between preparation of the material and the deadline for return of the results, although the period may be longer if the provider intends subsequently to offer unused distribution units for sale. Before the stability test, the material should be packed in containers in which it is to be distributed. It is not usually necessary or even feasible that the material for every round in a series should be tested. However, each newly considered material/analyte combination should be tested once before it is used in a proficiency test and occasionally thereafter.

Stability tests comprise a comparison of the material before and after the ‘appropriate’ treatment. This usually requires a batch of the distribution units to be randomly divided into two equal subsets. The ‘experimental’ subset is subjected to the appropriate treatment, whereas the ‘control’ subset is kept under conditions of maximum stability, for example, low temperatures and low oxygen tension. Ideally, the stability test should involve exposing the experimental subset to the most extreme conditions likely to be encountered during the distribution and storage. More realistically, because of the low power of the statistical test, the experimental subset should be kept under conditions of accelerated decomposition, for example, higher temperatures than normal. After the treatment, the two subsets are analyzed by a method of high precision.

Although simple in principle, stability tests must be carefully designed to avoid confounding any change in the material with variation in the efficacy of the analytical method used. Analysis of the control material at the beginning of the test period and experimental material at the end automatically includes any run-to-run analytical difference in the results and may well lead to an incorrect conclusion. The recommended approach is, if at all possible, to analyze the experimental and control subsets together in a random order, within a single run of analysis, that is, under repeatability conditions. Any highly significant difference between the mean results of the two subsets can then safely be regarded as evidence of instability. However, it must be emphasized that such tests are of low statistical power unless inordinately large numbers of test units are involved or high-precision analytical methods are employed.

Although, in principle, a distinction must be drawn between statistically significant instability and consequential instability, because of the low statistical power of the test given practicable conditions of testing, a significant result is unlikely. For instance, given an analytical method with repeatability standard deviation σ_an and two subsets of 10 distribution units each, an instability change of a magnitude of σ_an would be found significant in only 56% of the experiments by using the two-sample t-test at 95% confidence. Thus, if it were deemed that a change in the z-score of ±0.05 would be inconsequential, then an instability amounting to a change in analyte concentration of 0.05σ_p could be tolerated. However, an analytical method with σ_an≈0.05σ_p is unlikely to be available.

Read full chapter

URL:

https://www.sciencedirect.com/science/article/pii/B9780444527011000922

Источник

Статистика приходит к нам на помощь при решении многих задач, например: когда нет возможности построить детерминированную модель, когда слишком много факторов или когда нам необходимо оценить правдоподобие построенной модели с учётом имеющихся данных. Отношение к статистике неоднозначное. Есть мнение, что существует три вида лжи: ложь, наглая ложь и статистика. С другой стороны, многие «пользователи» статистики слишком ей верят, не понимая до конца, как она работает: применяя, например, тест Стьюдента к любым данным без проверки их нормальности. Такая небрежность способна порождать серьёзные ошибки и превращать «поклонников» теста Стьюдента в ненавистников статистики. Попробуем поставить точки над i и разобраться, какие модели случайных величин должны использоваться для описания тех или иных явлений и какая между ними существует генетическая связь.

В первую очередь, данный материал будет интересен студентам, изучающим теорию вероятностей и статистику, хотя и «зрелые» специалисты смогут его использовать в качестве справочника. В одной из следующих работ я покажу пример использования статистики для построения теста оценки значимости показателей биржевых торговых стратегий.

В работе будут рассмотрены дискретные распределения:

Бернулли;
биномиальное;
геометрическое;
Паскаля (отрицательное биномиальное);
гипергеометрическое;
Пуассона,

а также непрерывные распределения:

Гаусса (нормальное);
хи-квадрат;
Стьюдента;
Фишера;
Коши;
экспоненциальное (показательное) и Лапласа (двойное экспоненциальное, двойное показательное);
Вейбулла;
гамма (Эрланга);
бета.

В конце статьи будет задан вопрос для размышлений. Свои размышления по этому поводу я изложу в следующей статье.

Некоторые из приведённых непрерывных распределений являются частными случаями распределения Пирсона.

Дискретные распределения

Дискретные распределения используются для описания событий с недифференцируемыми характеристиками, определёнными в изолированных точках. Проще говоря, для событий, исход которых может быть отнесён к некоторой дискретной категории: успех или неудача, целое число (например, игра в рулетку, в кости), орёл или решка и т.д.

Описывается дискретное распределение вероятностью наступления каждого из возможных исходов события. Как и для любого распределения ( в том числе непрерывного) для дискретных событий определены понятия матожидания и дисперсии. Однако, следует понимать, что матожидание для дискретного случайного события — величина в общем случае нереализуемая как исход одиночного случайного события, а скорее как величина, к которой будет стремиться среднее арифметическое исходов событий при увеличении их количества.

В моделировании дискретных случайных событий важную роль играет комбинаторика, так как вероятность исхода события можно определить как отношение количества комбинаций, дающих требуемый исход к общему количеству комбинаций. Например: в корзине лежат 3 белых мяча и 7 чёрных. Когда мы выбираем из корзины 1 мяч, мы можем сделать это 10-ю разными способами (общее количество комбинаций), но только 3 варианта, при которых будет выбран белый мяч (3 комбинации, дающие требуемый исход). Таким образом, вероятность выбрать белый мяч: (распределение Бернулли).

Следует также отличать выборки с возвращением и без возвращения. Например, для описания вероятности выбора двух белых мячей важно определить, будет ли первый мяч возвращён в корзину. Если нет, то мы имеем дело с выборкой без возвращения (гипергеометрическое распределение) и вероятность будет такова: — вероятность выбрать белый мяч из начальной выборки умноженная на вероятность снова выбрать белый мяч из оставшихся в корзине. Если же первый мяч возвращается в корзину, то это выборка с возвращением (Биномиальное распределение). В этом случае вероятность выбора двух белых мячей составит .

наверх

Распределение Бернулли

(взято отсюда)

Если несколько формализовать пример с корзиной следующим образом: пусть исход события может принимать одно из двух значений 0 или 1 с вероятностями и соответственно, тогда распределение вероятности получения каждого из предложенных исходов будет называться распределение Бернулли:

$Bin_{p,q}left(xright)=begin{cases}q,x=0\ p, x=1end{cases}$

По сложившейся традиции, исход со значением 1 называется «успех», а исход со значением 0 — «неудача». Очевидно, что получение исхода «успех или неудача» наступает с вероятностью .

Матожидание и дисперсия распределения Бернулли:

$E{Bin_{p,q}}=p left(1.1.2right)$

$D{Bin_{p,q}}=pq=pleft(1-pright) left(1.1.3right)$

наверх

Биномиальное распределение

(взято отсюда)

Количество успехов в испытаниях, исход которых распределен по Бернулли с вероятностью успеха (пример с возвращением мячей в корзину), описывается биномиальным распределением:

$B_{n,p}(k)=C^k_np^kq^{n-k} (1.2.1)$

где $C^k_n={n!over{k!(n-k)!}}$ — число сочетаний из по .

По другому можно сказать, что биномиальное распределение описывает сумму из независимых случайных величин, умеющих распределение Бернулли с вероятностью успеха .
Матожидание и дисперсия:

$E{B_{n,p}}=np (1.2.2)$

$D{B_{n,p}}=npq (1.2.3)$

Биномиальное распределение справедливо только для выборки с возвращением, то есть, когда вероятность успеха остаётся постоянной для всей серии испытаний.

Если величины и имеют биномиальные распределения с параметрами и соответственно, то их сумма также будет распределена биномиально с параметрами .

наверх

Геометрическое распределение

(взято отсюда)

Представим ситуацию, что мы вытягиваем мячи из корзины и возвращаем обратно до тех пор, пока не будет вытянут белый шар. Количество таких операций описывается геометрическим распределением. Иными словами: геометрическое распределение описывает количество испытаний до первого успеха при вероятности наступления успеха в каждом испытании . Если подразумевается номер испытания, в котором наступил успех, то геометрическое распределение будет описываться следующей формулой:

$Geom_p(n)=q^{n-1}p (1.3.1)$

Матожидание и дисперсия геометрического распределения:

$E{Geom_p}={1over{p}} (1.3.2)$

$D{Geom_p}={qover{p^2}} (1.3.3)$

Геометрическое распределение генетически связано с экспоненциальным распределением, которое описывает непрерывную случайную величину: время до наступления события, при постоянной интенсивности событий. Геометрическое распределение также является частным случаем отрицательного биномиального распределения.

наверх

Распределение Паскаля (отрицательное биномиальное рспределение)

(взято отсюда)

Распределение Паскаля является обобщением геометрического распределения: описывает распределение количества неудач в независимых испытаниях, исход которых распределен по Бернулли с вероятностью успеха до наступления успехов в сумме. При , мы получим геометрическое распределение для величины .

$NB_{r,p}(k)=C^k_{k+r-1}p^rq^k (1.4.1)$

где $C^k_n={n!over{k!(n-k)!}}$ — число сочетаний из по .

Матожидание и дисперсия отрицательного биномиального распределения:

$E{NB_{r,p}}={rqover{p}} (1.4.2)$

$D{NB_{r,p}}={rqover{p^2}} (1.4.3)$

Сумма независимых случайных величин, распределённых по Паскалю, также распределена по Паскалю: пусть имеет распределение , а — . Пусть также и независимы, тогда их сумма будет иметь распределение

наверх

Гипергеометрическое распределение

(взято отсюда)

До сих пор мы рассматривали примеры выборок с возвращением, то есть, вероятность исхода не менялась от испытания к испытанию.

Теперь рассмотрим ситуацию без возвращения и опишем вероятность количества успешных выборок из совокупности с заранее известным количеством успехов и и неудач (заранее известное количество белых и чёрных мячей в корзине, козырных карт в колоде, бракованных деталей в партии и т.д.).

Пусть общая совокупность содержит объектов, из них помечены как «1», а как «0». Будем считать выбор объекта с меткой «1», как успех, а с меткой «0» как неудачу. Проведём n испытаний, причём выбранные объектв больше не будут участвовать в дальнейших испытаниях. Вероятность наступления успехов будет подчиняться гипергеометрическому распределению:

$HG_{N,D,n}(k)={C^k_DC^{n-k}_{N-D}over{C^n_N}} (1.5.1)$

где $C^k_n={n!over{k!(n-k)!}}$ — число сочетаний из по .

Матожидание и дисперсия:

$E{HG_{N,D,n}}={nDover{N}} (1.5.2)$

$D{HG_{N,D,n}}=n{Dover{N}}{N-Dover{N}}{N-nover{N-1}} (1.5.3)$

наверх

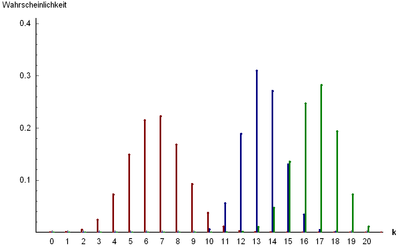
Распределение Пуассона

(взято отсюда)

Распределение Пуассона значительно отличается от рассмотренных выше распределений своей «предметной» областью: теперь рассматривается не вероятность наступления того или иного исхода испытания, а интенсивность событий, то есть среднее количество событий в единицу времени.

Распределение Пуассона описывает вероятность наступления независимых событий за время при средней интенсивности событий :

$P_{lambda,t}(k)={left(lambda tright)^kover{k!}}e^{-lambda t} (1.6.1)$

Матожидание и дисперсия распределения Пуассона:

$E{P_{lambda,t}}=lambda t (1.6.2)$

$D{P_{lambda,t}}=lambda t (1.6.3)$

Дисперсия и матожидание распределения Пуассона тождественно равны.

Распределение Пуассона в сочетании с экспоненциальным распределением, описывающим интервалы времени между наступлениями независимых событий, составляют математическую основу теории надёжности.

наверх

Непрерывные распределения

Непрерывные распределения, в отличие от дискретных, описываются функциями плотности (распределения) вероятности , определёнными, в общем случае, на некоторых интервалах.

Если известна плотность вероятности для величины : и определено преобразование , то плотность вероятности для y может быть получена автоматически:

$f_y(y)=fleft(g^{-1}(y)right)left|{dg^{-1}over{dy}}(y)right| (2.0.1)$

при условии однозначности и дифференцируемости .

Плотность вероятности суммы случайных величин и () с распределениями и описывается свёрткой и :

Если распределение суммы случайных величин принадлежит к тому же распределению, что и слагаемые, такое распределение называется бесконечно делимым. Примеры бесконечно делимых распределений: нормальное, хи-квадрат, гамма, распределение Коши.

Плотность вероятности произведения случайных величин x и y () с распределениями и может быть вычислена следующим образом:

Некоторые из приведённых ниже распределений являются частными случаями распределения Пирсона, которое, в свою очередь, является решением уравнения:

${dfover{dx}}(x)={a_0+a_1xover{b_0+2b_1x+b_2x^2}}f(x) (2.0.4)$

где и — параметры распределения. Известны 12 типов распределения Пирсона, в зависимости от значений параметров.

Распределения, которые будут рассмотрены в этом разделе, имеют тесные взаимосвязи друг с другом. Эти связи выражаются в том, что некоторые распределения являются частными случаями других распределений, либо описывают преобразования случайных величин, имеющих другие распределения.

На приведённой ниже схеме отражены взаимосвязи между некоторыми из непрерывных распределений, которые будут рассмотрены в настоящей работе. На схеме сплошными стрелками показано преобразование случайных величин (начало стрелки указывает на изначальное распределение, конец стрелки — на результирующее), а пунктирными — отношение обобщения (начало стрелки указывает на распределение, являющееся частным случаем того, на которое указывает конец стрелки). Для частных случаев распределения Пирсона над пунктирными стрелками указан соответствующий тип распределения Пирсона.

Предложенный ниже обзор распределений охватывает многие случаи, которые встречаются в анализе данных и моделировании процессов, хотя, конечно, и не содержит абсолютно все известные науке распределения.

наверх

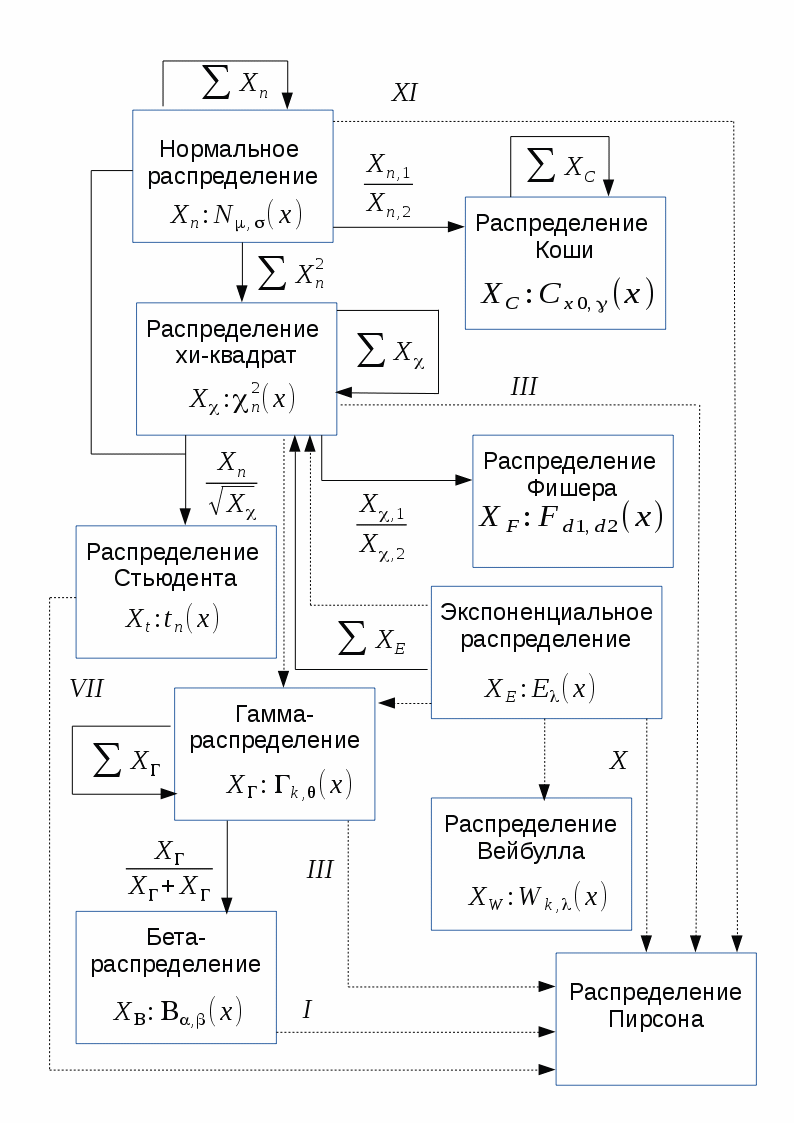
Нормальное распределение (распределение Гаусса)

(взято отсюда)

Плотность вероятности нормального распределения с параметрами и описывается функцией Гаусса:

$f(x)={1over{sigma sqrt{2 pi}}}e^{(x-mu)^2over{2sigma^2}} (2.1.1)$

Если и , то такое распределение называется стандартным.

Матожидание и дисперсия нормального распределения:

$E{N_{mu,sigma}}=mu (2.1.2)$

$D{N_{mu,sigma}}=sigma^2 (2.1.3)$

Область определения нормального распределения — множество дествительных чисел.

Нормальное распределение является распределение Пирсона типа XI.

Сумма квадратов независимых нормальных величин имеет распределение хи-квадрат, а отношение независимых Гауссовых величин распределено по Коши.

Нормальное распределение является бесконечно делимым: сумма нормально распределенных величин и с параметрами и соответственно также имеет нормальное распределение с параметрами , где и .

Нормальное распределение хорошо моделирует величины, описывающие природные явления, шумы термодинамической природы и погрешности измерений.

Кроме того, согласно центральной предельной теореме, сумма большого количества независимых слагаемых одного порядка сходится к нормальному распределению, независимо от распределений слагаемых. Благодаря этому свойству, нормальное распределение популярно в статистическом анализе, многие статистические тесты рассчитаны на нормально распределенные данные.

На бесконечной делимости нормального распределении основан z-тест. Этот тест используется для проверки равенства матожидания выборки нормально распределённых величин некоторому значению. Значение дисперсии должно быть известно. Если значение дисперсии неизвестно и рассчитывается на основании анализируемой выборки, то применяется t-тест, основанный на распределении Стьюдента.

Пусть у нас имеется выборка объёмом n независимых нормально распределенных величин из генеральной совокупности со стандартным отклонением выдвинем гипотезу, что . Тогда величина будет иметь стандартное нормальное распределение. Сравнивая полученное значение z с квантилями стандартного распределения можно принимать или отклонять гипотезу с требуемым уровнем значимости.

Благодаря широкой распространённости распределения Гаусса, многие, не очень хорошо знающие статистику исследователи забывают проверять данные на нормальность, либо оценивают график плотности распределения «на глазок», слепо полагая, что имеют дело с Гауссовыми данными. Соответственно, смело применяя тесты, предназначенные для нормального распределения и получая совершенно некорректные результаты. Наверное, отсюда и пошла молва про статистику как самый страшный вид лжи.

Рассмотрим пример: нам надо измерить сопротивления набора резистров некоторого номинала. Сопротивление имеет физическую природу, логично предположить, что распределение отклонений сопротивления от номинала будет нормальным. Меряем, получаем колоколообразную функцию плотности вероятности для измеренных значений с модой в окрестности номинала резистров. Это нормальное распределение? Если да, то будем искать бракованные резистры используя тест Стьюдента, либо z-тест, если нам заранее известна дисперсия распределения. Думаю, что многие именно так и поступят.

Но давайте внимательнее посмотрим на технологию измерения сопротивления: сопротивление определяется как отношение приложенного напряжения к протекающему току. Ток и напряжение мы измеряли приборами, которые, в свою очередь, имеют нормально распределенные погрешности. То есть, измеренные значения тока и напряжения — это нормально распределенные случайные величины с матожиданиями, соответствующими истинным значениям измеряемых величин. А это значит, что полученные значения сопротивления распределены по Коши, а не по Гауссу.

Распределение Коши лишь напоминает внешне нормальное распределение, но имеет более тяжёлые хвосты. А значит предложенные тесты неуместны. Надо строить тест на основании распределения Коши или вычислить квадрат сопротивления, который в данном случае будет иметь распределение Фишера с параметрами (1, 1).

к схеме
наверх

Распределение хи-квадрат

(взято отсюда)

Распределение описывает сумму квадратов случайных величин , каждая из которых распределена по стандартному нормальному закону :

$chi^2_k(x)={{left(1over 2 right)}^{kover 2}over{Gammaleft({kover{2}}right)}}x^{{kover 2}-1}e^{-{xover 2}} (2.2.1)$

где — число степеней свободы, $x=sumlimits_{i=1}^n {X^2_i}$ .

Матожидание и дисперсия распределения :

$E{chi^2_n}=n (2.2.2)$

$D{chi^2_n}=2n (2.2.3)$

Область определения — множество неотрицательных натуральных чисел. является бесконечно делимым распределением. Если и — распределены по и имеют и степеней свободы соответственно, то их сумма также будет распределена по и иметь степеней свободы.

является частным случаем гамма-распределения (а следовательно, распределением Пирсона типа III) и обобщением экспоненциального распределения. Отношение величин, распределенных по распределено по Фишеру.

На распределении основан критерий согласия Пирсона. с помощью этого критерия можно проверять достоверность принадлежности выборки случайной величины некоторому теоретическому распределению.

Предположим, что у нас имеется выборка некоторой случайной величины . На основании этой выборки рассчитаем вероятности попадания значений в интервалов (). Пусть также есть предположение об аналитическом выражении распределения, в соответствие с которым, вероятности попадания в выбранные интервалы должны составлять . Тогда величины будут распределены по нормальному закону.

Приведем к стандартному нормальному распределению: ,
где $m={1over n}sum limits_{i=1}^n {D_i}$ и $S=sqrt {{1over {n-1}}sum limits_{i=1}^n {D_i^2}}$ .

Полученные величины имеют нормальное распределение с параметрами (0, 1), а следовательно, сумма их квадратов распределена по с степенью свободы. Снижение степени свободы связано с дополнительным ограничением на сумму вероятностей попадания значений в интервалы: она должна быть равна 1.

Сравнивая значение с квантилями распределения можно принять или отклонить гипотезу о теоретическом распределении данных с требуемым уровнем значимости.

к схеме
наверх

Распределение Стьюдента (t-распределение)

(взято отсюда)

Распределение Стьюдента используется для проведения t-теста: теста на равенство матожидания выборки стандартно нормально распределённых случайных величин некоторому значению, либо равенства матожиданий двух нормальных выборок с одинаковой дисперсией (равенство дисперсий необходимо проверять f-тестом). Распределение Стьюдента описывает отношение нормально распределённой случайной величины к величине, распределённой по хи-квадрат.

T-тест является аналогом z-теста для случая, когда дисперсия или стандартное отклонение выборки неизвестно и должно быть оценено на основании самой выборки.

Рассмотрим пример проверки равенства матожидания нормальной выборки некоторому значению: пусть нам дана выборка нормальных величин объёмом n из некоторой генеральной совокупности, выдвинем и проверим гипотезу о том, что матожидание этой совокупности равно .

Рассчитаем величину . Эта величина будет иметь распределение хи-квадрат. Тогда величина будет иметь распределение Стьюдента c степенью свободы, где:

$T_{n}(x)={Gamma left({n+1 over 2}right) over {sqrt{n pi}Gamma left({n over 2}right)left(1+{x^2 over n}right)^{n+1 over 2}}} (2.3.1)$

где — гамма-функция Эйлера.

Полученное значение можно сравнивать с квантилями распределения Стьюдента и принимать либо отклонять гипотезу о равенстве маотожидания значению с требуемым уровнем значимости.

Матожидание и дисперсия распределения Стьюдента:

$E{T_{n}}=0 (2.3.2)$

$D{T_{n}}={n over {n-2}} (2.3.3)$

при .

к схеме
наверх

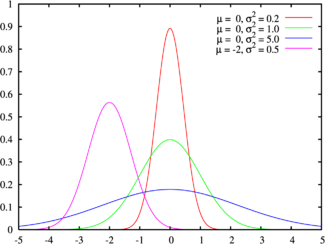
Распределение Фишера

(взято отсюда)

Пусть и независимые случайные величины, имеющие распределение хи-квадрат со степенями свободы и соответственно. Тогда величина будет иметь распределение Фишера со степенями свободы , а величина — распределение Фишера со степенями свободы .
Распределение Фишера определено для действительных неотрицательных аргументов и имеет плотность вероятности:

$F_{n_1,n_2}(x)={sqrt{ (n_1x)^{n_1}n_2^{n_2}over {(n_1x+n_2)^{n_1+n_2}}} over {xBleft({n_1 over 2},{n_2 over 2} right)}} (2.4.1)$

Матожидание и дисперсия распределения Фишера:

$E{F_{n_1,n_2}}={n_2 over {n_2-2}} (2.4.2)$

$D{F_{n_1,n_2}}={2n_2^2(n_1+n_2-2) over {n_1(n_2-2)^2(n_2-4)}} (2.4.3)$

Матожидание определено для , а диспересия — для .

На распределении Фишера основан ряд статистических тестов, таких как оценка значимости параметров регрессии, тест на гетероскедастичность и тест на равенство дисперсий нормальных выборок (f-тест, следует отличать от точного теста Фишера).

F-тест: пусть имеются две независимые выборки и нормально распределенных данных объёмами и соответственно. Выдвинем гипотезу о равенстве дисперсий выборок и проверим её статистически.

Рассчитаем величину . Она будет иметь распределение Фишера со степенями свободы .

Сравнивая значение с квантилями соответствующего распределения Фишера, мы можем принять или отклонить гипотезу о равенстве дисперсий выборок с требуемым уровнем значимости.

к схеме
наверх

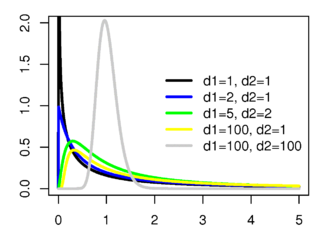
Распределение Коши

(взято отсюда)
Распределение Коши описывает отношение двух нормально распределенных случайных величин. В отличие от других распределений, для распределения Коши не определены матожидание и дисперсия. Для описания распределения используются коэффициенты сдвига и масштаба .

$C_{x_0,gamma}(x)={1over{pi gamma left(1+left({x-x_0over {gamma}} right)^2 right)}} (2.5.1)$

Распределение Коши является бесконечно делимым: сумма независимых случайных величин, распределённых по Коши, также распределена по Коши.

к схеме
наверх

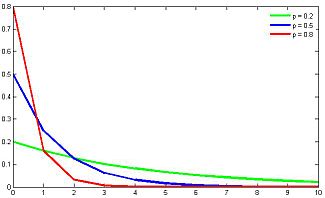
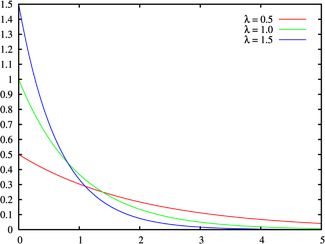
Экспоненциальное (показательное) распределение и распределение Лапласа (двойное экспоненциальное, двойное показательное)

(взято отсюда)

Экспоненциальное распределение описывает интервалы времени между независимыми событиями, происходящими со средней интенсивностью . Количество наступлений такого события за некоторый отрезок времени описывается дискретным распределением Пуассона. Экспоненциальное распределение вместе с распределением Пуассона составляют математическую основу теории надёжности.

Кроме теории надёжности, экспоненциальное распределение применяется в описании социальных явлений, в экономике, в теории массового обслуживания, в транспортной логистике — везде, где необходимо моделировать поток событий.

Экспоненциальное распределение является частным случаем распределения хи-квадрат (для n=2), а следовательно, и гамма-распределения. Так-как экспоненциально распределённая величина является величиной хи-квадрат с 2-мя степенями свободы, то она может быть интерпретирована как сумма квадратов двух независимых нормально распределенных величин.

Кроме того, экспоненциальное распределение является честным случаем распределения Вейбулла.

Дискретный вариант экспоненциального распределения — это геометрическое распределение.

Плотность вероятности экспоненциально распределения:

$E_lambda(x)=lambda e^{-lambda x} (2.6.1)$

определена для неотрицательных действительных значений .

Матожидание и дисперсия экспоненциального распределения:

$E{E_lambda}={1 over lambda} (2.6.2)$

$E{E_lambda}={1 over lambda^2} (2.6.3)$

Если функцию плотности вероятностей экспоненциального распределения отразить зеркально в область отрицательных значений, то есть, заменить на , то получится распределение Лапласа, также называемое двойным экспоненциальным или двойным показательным.

(взято отсюда)

Для большего обобщения, вводится параметр сдвига, смещающий центр «соединения» левой и правой частей распределения вдоль оси абсцисс. В отличие от экспоненциального, распределение Лапласа, определено на всей действительной числовой оси.

$L_{alpha,beta}(x)={alpha over 2}e^{-alpha left|x-betaright|} (2.6.4)$

где — параметр масштаба, а — параметр сдвига.

Матожидание и дисперсия:

$E{L_{alpha, beta}}=beta (2.6.5)$

$D{L_{alpha, beta}}={2 over {alpha^2}} (2.6.6)$

Благодаря более тяжёлым хвостам, чем у нормального распределения, распределение Лапласа используется для моделирования некоторых видов погрешностей измерения в энергетике, а также находит применение в физике, экономике, финансовой статистике, телекоммуникации и т.д.

к схеме
наверх

Распределение Вейбулла

(взято отсюда)

Распределение Вейбулла описывается функцией плотности вероятности следующего вида:

$W_{k, lambda}(x)={k over {lambda}}left({x over {lambda}}right)^{k-1}e^{-left({x over {lambda}}right)^k} (2.7.1)$

где ( > 0)- интенсивность событий (аналогично параметру экспоненциального распределения), а — показатель нестационарности (). При , распределение Вейбулла вырождается в экспоненциальное распределение, а в остальных случаях описывает поток независимых событий с нестационарной интенсивностью. При моделируется поток событий с растущей со временем интенсивностью, а при — со снижающейся. Область определения функции распределения плотности вероятностей: неотрицательные действительные числа.

Таким образом, распределение Вейбулла — обобщение экспоненциального распределения на случай нестационарной интенсивности событий. Используется в теории надёжности, моделировании процессов в технике, в прогнозировании погоды, в описании процесса измельчения и т.д.

Матожидание и дисперсия распределения Вейбулла:

$E{W_{k, lambda}}=lambda Gammaleft(1 + {1 over k} right) (2.7.2)$

$D{W_{k, lambda}}=lambda^2 left(Gammaleft(1 + {2 over k} right ) - Gammaleft(1 + {1 over k} right )^2right) (2.7.3)$

где — гамма-функция Эйлера.

к схеме
наверх

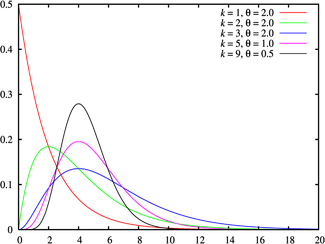
Гамма-распределение (распределение Эрланга)

(взято отсюда)

Гамма-распределение является обобщением рапсределения хи-квадрат и, соответственно, экспоненциального распределения. Суммы квадратов нормально распределённых величин, а также суммы величин распределённых по хи-квадрат и по экспоненциальному распределению будут иметь гамма-распределение.

Гамма-распределение является распределением Пирсона III рода. Область определения гамма-распределения — натуральные неотрицательные числа.

Гамма-распределение определяется двумя неотрицательными параметрами — число степеней свободы (при целом значении степеней свободы, гамма-распределение называется распределением Эрланга) и коэффициент масштаба .

Гамма-распределение является бесконечно делимым: если величины и имеют распределения и соответсвенно, то величина будет иметь распределение

$G_{k,theta}(x)=x^{k-1}{e^{-{x over theta}}over Gamma(k) theta^k} (2.8.1)$

где — гамма-функция Эйлера.

Матожидание и дисперсия:

$E{G_{k,theta}}=ktheta (2.8.2)$

$D{G_{k,theta}}=ktheta^2 (2.8.3)$

Гамма распределение широко применяется для моделирования сложных потоков событий, сумм временных интервалов между событиями, в экономике, теории массового обслуживания, в логистике, описывает продолжительность жизни в медицине. Является своеобразным аналогом дискретного отрицательного биномиального распределения.

к схеме
наверх

Бета-распределение

(взято отсюда)

Бета-распределение описывает долю суммы двух слагаемых, приходящуюся на каждое из них, если слагаемые являются случайными величинами, имеющими гамма-распределение. То есть, если величины и имеют гамма-распределение, величины и будут иметь бета-распределение.

Очевидно, что область определения бета-распределения . Бета-распределение является распределение Пирсона I типа.

$B_{alpha,beta}={x^{alpha -1}(1-x)^{beta - 1}over{B(alpha, beta)}} (2.9.1)$

где параметры и — положительные натуральные числа, — бета-функция Эйлера.

Матожидание и дисперсия:

$E{B_{alpha, beta}}={alpha over{alpha+beta}} (2.9.2)$

$D{B_{alpha, beta}}={alpha beta over{(alpha+beta)^2(alpha+beta+1)}} (2.9.3)$

к схеме
наверх

Вместо заключения

Мы рассмотрели 15 распределений вероятности, которые, на мой взгляд, охватывают большинство наиболее популярных приложений статистики.

Напоследок, небольшое домашнее задание: для оценки надёжности биржевых торговых систем используется такой показатель как профит-фактор. Профит-фактор рассчитывается как отношение суммарного дохода к суммарному убытку. Очевидно, что для системы, приносящей доход, профит-фактор больше единицы, и чем его значение выше, тем система надёжнее.

Вопрос: какое распределение имеет значение профит-фактора?

Свои размышления по этому поводу я изложу в следующей статье.

P.S. Если Вы захотите сослатья на нумерованные формулы из этой статьи, то можете использовать такую сслыку: ссылка_на_статью#x_y_z, где (x.y.z)- номер формулы, на которую Вы ссылаетесь.

Источник

6.5. Распределение квадрата случайной величины.

6.6. Распределение частного.

6.7. Числовые характеристики функций случайных величин.

Distributions of Sampling Statistics

Definition

Chi-Squared Goodness-of-Fit Tests

13.5 Use of R

Nonparametric Hypotheses Tests

Solution

Advanced Math and Statistics

Chi-Square Distribution

Random Variables

2.2 Definition

Random Variables

2.6.1 The Joint Distribution of the Sample Mean and Sample Variance from a Normal Population

Linear Regression

12.4 ERROR RANDOM VARIABLE

Example 12.3

Special random variables

5.8.1 The chi-square distribution

5.8.1.1 The relation between chi-square and gamma random variables7

Proficiency Testing in Analytical Chemistry

1.03.3 Validation of Test Materials

1.03.3.1 Introduction

1.03.3.2 Testing for Homogeneity

1.03.3.3 Testing for Stability

Дискретные распределения

Распределение Бернулли

Биномиальное распределение

Геометрическое распределение

Распределение Паскаля (отрицательное биномиальное рспределение)

Гипергеометрическое распределение

Распределение Пуассона

Непрерывные распределения

Нормальное распределение (распределение Гаусса)

Распределение хи-квадрат

Распределение Стьюдента (t-распределение)

Распределение Фишера

Распределение Коши

Экспоненциальное (показательное) распределение и распределение Лапласа (двойное экспоненциальное, двойное показательное)

Распределение Вейбулла

Гамма-распределение (распределение Эрланга)

Бета-распределение

Вместо заключения

Не пропустите также:

5.8.1.1 The relation between chi-square and gamma random variables⁷