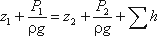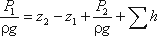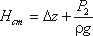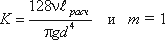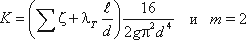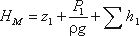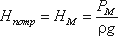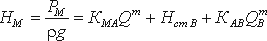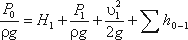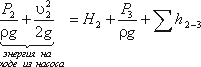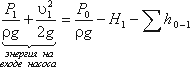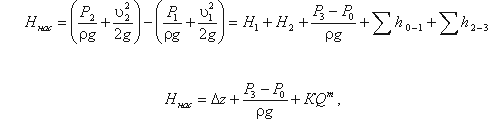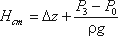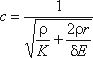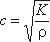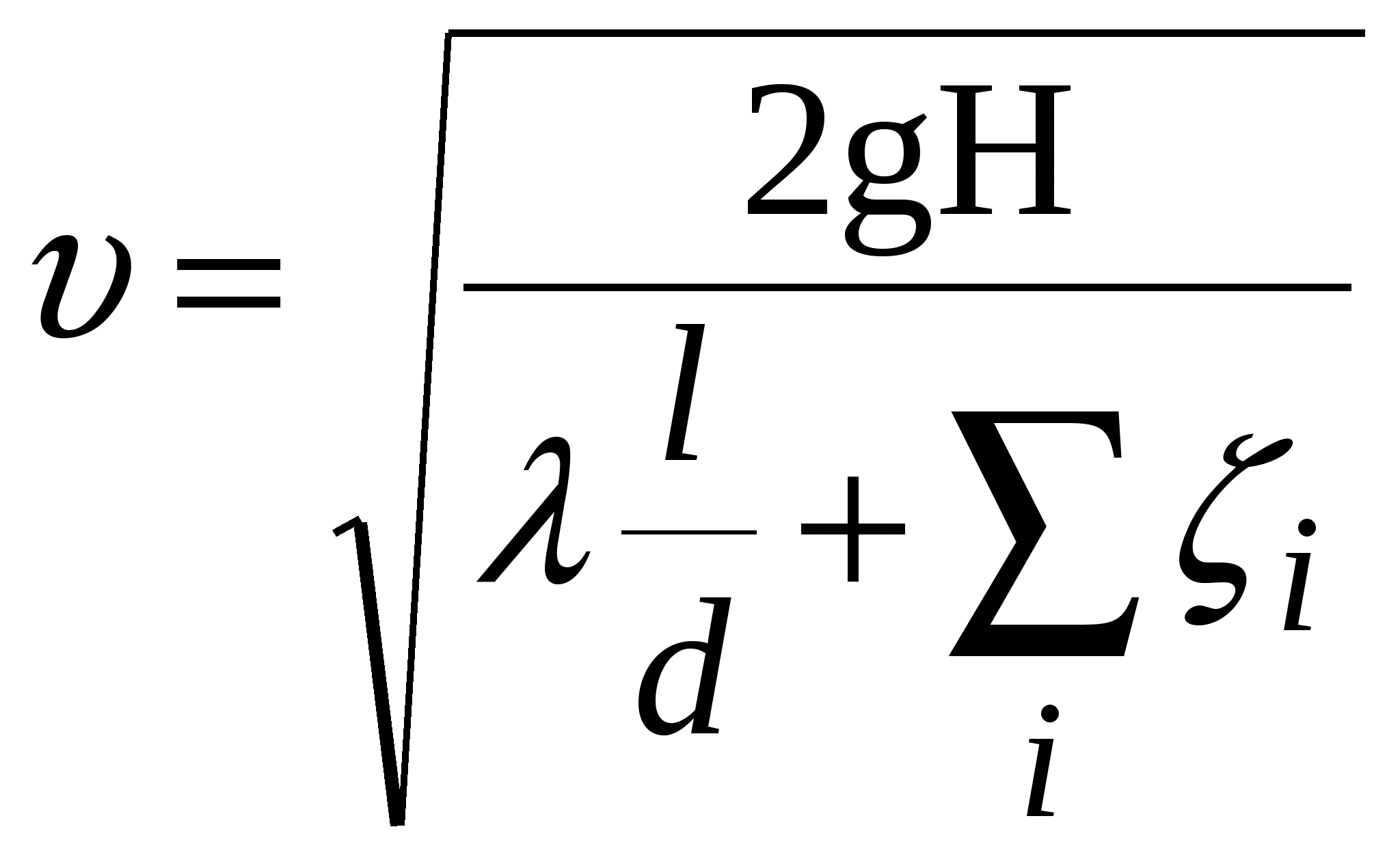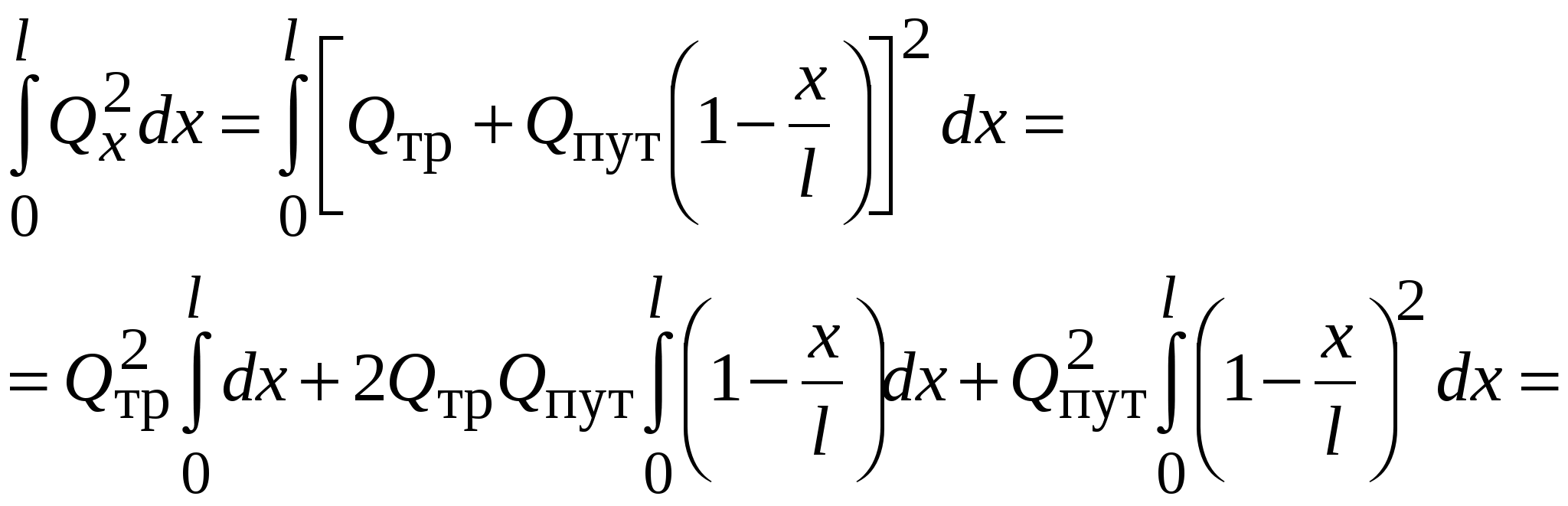«Как рассчитать объемный расход жидкости?» является одним из наиболее часто задаваемых вопросов в химической промышленности относительно бесперебойного, безопасного и экономичного выполнения процесса.
Движение жидкостей по трубе на машиностроительной установке имеет большое значение, особенно для обеспечения правильной пропорции различных химических веществ для реакции. Расчет объемного расхода от различных объектов играет важную роль.
Объемный расход – это объем жидкости, протекающей по трубе, воздуховоду, каналу или другой конструкции подобного типа в единицу времени.
Объемный расход, Q или V=Av
Где A = площадь поперечного сечения секции в м2
А v=средняя скорость жидкости по сечению в м/с.
Единица Объемный расход м3/с(куб.м/сек), м3/ч (кубический метр/час), л/с (литр/секунда), л/мин. (литр/минута), мл/с (миллилитр/секунда) и т. д.
В случае очень малого расхода (например, жидкости внутри шприца) предпочтительнее мл/с, а для очень большого объемного расхода (например, расход воды в реке) он выражается в м3/ H.
Как рассчитать объемный расход по объему и времени?
Объемный расход — это общий термин, связанный с измерением расхода, особенно в случае жидкостей и газов.
Чтобы рассчитать объемный расход жидкости, используя количество жидкости, проходящей через проход (в кубических метрах) в течение определенного периода времени (в секундах), мы можем использовать следующую формулу:
Объемный расход, Q=V/t
Объемный расход жидкости (газа и жидкости) — это объем жидкости, проходящий через данную точку за заданный период времени. Единицы измерения: литр в минуту, кубический сантиметр в минуту и т. д. Обозначается Q или
Здесь объем жидкости = Ad
А — площадь поперечного сечения трубы в м.2 d — расстояние, пройденное жидкостью в м.
Q= Объемный расход м3/с или л/с.
V=Объем жидкости в литрах или кубических метрах
= Средняя скорость потока в м/с
Здесь мы рассматриваем среднее значение скорости, так как из-за силы трения скорость у стенки трубы меньше, чем на среднем участке.
A = площадь поперечного сечения, занимаемая движущейся жидкостью, м2
Следовательно,
Как найти объемный расход с давлением?
Для движения жидкости по воздуховоду между двумя концами воздуховода должна быть разница давлений, которая называется градиентом давления.
Уравнение Хагена-Пуазейля дает связь между падение давления и скорость потока жидкости через длинную цилиндрическую трубу. Уравнение применяется для ламинарного течения несжимаемой жидкости, протекающей по трубе постоянного сечения.
Если мы рассмотрим две точки на пути потока и посмотрим на давление, огромная разница давление приводит к более высокому массовому расходу и наоборот.
Перемещение жидкости по трубе происходит за счет разности давлений, жидкость перемещается из точки высокого давления в точку низкого давления.
Формула закона Пуазейля определяется выражением
Где Delta p — разница давлений между двумя концами трубы.
L – длина трубы,
μ — динамика вязкость,
объемный скорость потока,
R — радиус трубы,
А — поперечное сечение трубы.
Из уравнения (1)
Используя уравнение (2), мы можем определить объемный расход по градиенту давления.
Одно из распространенных приложений Уравнение Хагена-Пуазейля (или закон Хагена-Пуазейля) наблюдается при течении жидкости через соломинку для питья. Здесь считается падение давления из-за вязкости жидкости.
В случае несжимаемых жидкостей, таких как вода, мы можем применить уравнение Бернулли, чтобы узнать взаимосвязь между потоком жидкости и давлением. Здесь скорость потока несжимаемой невязкой жидкости определяется по измерениям давления.
Математически принцип Бернулли можно представить как
Р = давление
v = скорость
ρ = плотность жидкости
г = гравитация
h = высота
Как найти объемный расход без скорости?
Объемный расход — это общий термин, связанный с измерением расхода, особенно в случае жидкостей и газов.
Уравнение для определения объемного расхода жидкости без знания ее скорости выглядит следующим образом.:
Q=В/т
Где Q = объемный расход м3/s
V = объем жидкости, проходящей через определенную площадь поперечного сечения в м3
t = время, затрачиваемое жидкостью в секунду
На приведенном выше рисунке жидкость проходит через воздуховод, если V — это объем жидкости, пересекающий единицу площади поперечного сечения трубы A в течение периода времени «t», тогда объемный расход Q определяется выражением
Q=В/т
Как рассчитать объемный расход воздуха?
Другой Типы устройств используются для измерения объемного расхода Скорость жидкости в зависимости от ее точности в измерении и ее цене на рынке.
Для расчета объемного расхода воздуха мы можем использовать следующую формулу:
Q=площадь поперечного сечения x средняя скорость
Как правило, скорость воздуха, т. е. расстояние, проходимое воздухом в единицу времени, выражается в футах в минуту и неодинакова в каждой части воздуховода.
Скорость воздуха наименьшая у стенок воздуховода из-за трения, учитывая это, мы можем использовать усредняющую трубку Пито, имеющую несколько точек измерения, для более точного определения средней скорости.
Если размер воздуховода нам известен, мы можем легко рассчитать площадь поперечного сечения воздуховода, а затем, умножив ее на среднюю скорость, мы можем определить объемный расход, как правило, в кубических футах в минуту.
Следующие устройства измеряют объемный расход:
- Положительное смещение метры
- Турбинные расходомеры
- Диафрагмы
- Вентури
- Вихревые расходомеры
- Трубы Пито
- Ротометры
Как рассчитать объемный расход воды?
Количество воды, протекающей через воздуховод или трубу за определенный период времени, известное как объемный расход, можно рассчитать с помощью следующего уравнения:
Q=площадь поперечного сечения x средняя скорость
Здесь мы рассматриваем среднюю скорость воды, так как скорость воды неодинакова по всей трубе, скорость максимальна в центре трубы и минимальна у бокового участка.
Различные типы Используются расходомеры, большинство из которых следует теореме Бернулли для определения скорости потока в зависимости от давления. градиент между двумя точками прохождения жидкости.
Чтобы узнать больше об объемном расходе(кликните сюда)
Проблема 1: Вода течет по трубе с внутренним радиусом 10 см с объемным расходом 0.50. m3/с. Вычислите скорость воды в трубе.
Решение: Приведены данные:
Радиус трубы, r=10 см=0.1м
Объемный расход, Q=0.50 м3/s
Теперь площадь трубы,A= πr2=3.14 х 0.01=0.0314 м2
Мы знаем, что Q=vA
Здесь v — скорость или скорость воды в м/с.
Скорость воды, v=Q/A=0.50/0.0314=15.92 м/с
Problem2: Насадка радиусом 0.150 см присоединена к садовому шлангу радиусом 0.700 см. Скорость потока через шланг и сопло составляет 0.500 л/с. Определить скорость воды (а) в шланге и (б) в насадке.
Решение:
а) скорость воды в шланге
Мы знаем, что Q=vA
Радиус шланга,r1=0.700см=0.007м
Площадь шланга A1=πr2=3.14 х 0.000049=00015 м2
Расход, Q=0.500 л/с=0.0005 м3/s
Следовательно, скорость воды в шланге v1=Q/A1=0005/00015=3.33 м/с.
б) скорость воды в сопле.
Радиус сопла, r2 = 150 см = 0015 м
Мы знаем из уравнения непрерывности, A1v1=A2v2
Следовательно,
Теперь,
Цель работы – выполнить аппроксимацию зависимости расходов от уровней в гидрометрическом створе р. Ия – г. Тулун в виде аналитического выражения в форме параболы В. Г. Глушкова. Известно, что для подсчета стока и определения ежедневных расходов воды используются кривые расходов, которые служат графическим представлением зависимости наблюденных расходов и уровней воды в конкретном гидростворе. Указанная выше связь расходов и уровней определяется в результате совокупности многократных дискретных измеренных уровней и расходов воды в конкретном гидрометрическом створе [2].
Для автоматизации процесса подсчета стока и производства расчетов ежедневных расходов воды необходимо представить кривую расходов в виде аналитического выражения. Как правило, для аппроксимации кривой расходов используют или параболу Глушкова, или полиномиальную зависимость. Парабола Глушкова в целом показывает хорошее натурным данным и была выбрана в качестве аналитического выражения в рамках данной работы.
Русло р. Ии в створе гидропоста г. Тулуна, расположенного в Иркутской области, соответствует условиям наличия однозначной зависимости между расходом и уровнем воды, при которой одному конкретному уровню соответствует одно конкретное значение расхода воды. Кривая расхода, устанавливающая в графическом виде связь между расходами и уровнями воды, в гидрометрическом створе поста р. Ия – г. Тулун представлена на рис. а. Данная кривая получена по измеренным расходам в заданном гидростворе и экстраполирована вверх с применением способа «по элементам расхода». Способ состоит в том, что до требуемого уровня достраивается кривая площадей, которая в данной работе построена с применением данных радиолокационной топографической съемки SRTM (Shuttle radar topographic mission) [1] и показана на рис. б. Кривая средних скоростей в рамках исследования экстраполирована до требуемых значений по линейному уравнению, определенному средствами MS Excel (см. рис. в). Расход воды определяется как произведение площади поперечного сечения и средней скорости при конкретном уровне.
Рис. Кривые расхода (а), площадей (б), средних скоростей (в) в створе гидропоста р. Ия – г. Тулун
В ходе работы для аппроксимации кривой расходов использована парабола Глушкова, выражающая зависимость расходы от уровня в следующеи виде [2]:

где Q – расход воды, м³/с; H – наблюденный уровень воды, см; H0 – уровень нулевого расхода, при котором расход воды в данном створе равен нулю, см; и n – параметры уравнения, определяемые в рамках работы по опорной кривой расходов (см. рис. а).
Как правило, отметка нуля графика гидропоста не соответствует уровню нулевого расхода. Отметка нулевого расхода может быть определена по результатам промерных работ, но ее определение на практике бывает затруднено и требует привлечения дополнительных морфометрических материалов, которые часто оказываются недоступными без выполнения дополнительных полевых работ. В этом случае уровень нулевого расхода находится аналитически путем решения системы уравнений, написанных для трёх точек: одной, расположенной в нижней части кривой расходов (Q1; H1), второй — в верхней части (Q2; H2). Абсциссу третьей точки находят как 

В таблице (табл. 1) приведены координаты точек 1-3 и по формуле (1) получено значение нулевого расхода, равное 9 см.
Таблица 1
Координаты точек 1-3 для определения уровня нулевого расхода
|
№ точки |
Расход воды Q, м3/с |
Уровень воды H, см |
|---|---|---|
|
1 |
841 |
629 |
|
2 |
23060 |
1929 |
|
3 |
4404 |
1100 |
После этого методом наименьших квадратов ведётся определение параметров параболы Глушкова a и n. Для этого вычисляются следующие определители матриц:



По методу Крамера находим a и n:


Проведем оценку средней вероятной ошибки построения кривой расходов в форме таблицы (табл. 2) путем сопоставления с координатами опорной кривой расходов (см. рис. а).
Таблица 2
Проверка ошибки аппроксимации кривой расходов аналитической зависимостью по формуле Глушкова
|
№ расхода |
H, см |
Q1, м3/с по опорной кривой расходов |
Q2, м3/с по формуле Глушкова |
ΔQ, м3/с |
Δσ, % |
Δσ2, (%)2 |
|---|---|---|---|---|---|---|
|
1 |
629 |
841 |
817 |
-23 |
-2,9 |
8,2 |
|
2 |
729 |
1272 |
1270 |
-2 |
-0,2 |
0,0 |
|
3 |
829 |
1846 |
1863 |
17 |
0,9 |
0,9 |
|
4 |
929 |
2589 |
2616 |
27 |
1,0 |
1,0 |
|
5 |
1029 |
3518 |
3546 |
29 |
0,8 |
0,6 |
|
6 |
1129 |
4647 |
4672 |
25 |
0,5 |
0,3 |
|
7 |
1229 |
5996 |
6012 |
16 |
0,3 |
0,1 |
|
8 |
1329 |
7575 |
7584 |
9 |
0,1 |
0,0 |
|
9 |
1429 |
9405 |
9415 |
10 |
0,1 |
0,0 |
|
10 |
1529 |
11512 |
11506 |
-6 |
-0,1 |
0,0 |
|
11 |
1629 |
13914 |
13882 |
-32 |
-0,2 |
0,1 |
|
12 |
1729 |
16634 |
16562 |
-72 |
-0,4 |
0,2 |
|
13 |
1829 |
19687 |
19563 |
-124 |
-0,6 |
0,4 |
|
14 |
1929 |
23060 |
22903 |
-157 |
-0,7 |
0,5 |
|
σ, % |
0,6 |
Аппроксимация кривой формулой Глушкова отклоняется от опорной кривой расхода на 0,6 %. Также полученная аппроксимация проверена путем сопоставления с эталонной кривой, за которую в рамках работы принята кривя расходов по многолетним данным, составленная в Иркутском управлении по гидрометеорологии и мониторингу окружающей среды, на участке, освященный данными натурных измерений расходов. Среднее вероятное отклонение от эталонной кривой, составляет 4,0 %, как и у опорной кривой, экстраполированной способом «по элементам расхода». Результаты работы демонстрируют возможность использования полученного аналитического выражения в практическом приложении.
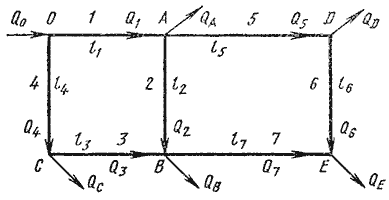
Лекция 6. ГИДРАВЛИЧЕСКИЙ РАСЧЕТ ПРОСТЫХ ТРУБОПРОВОДОВ
При расчетах напорных трубопроводов основной задачей является либо определение пропускной способности
(расхода), либо потери напора на том или ином участке, равно как и на всей длине, либо диаметра трубопровода
на заданных расходе и потерях напора.
В практике трубопроводы делятся на короткие и длинные. К первым относятся все трубопроводы,
в которых местные потери напора превышают 5…10% потерь напора по длине. При расчетах таких трубопроводов
обязательно учитывают потери напора в местных сопротивлениях. К ним относят, к примеру, маслопроводы объемных
передач.
Ко вторым относятся трубопроводы, в которых местные потери меньше 5…10% потерь напора по длине. Их расчет
ведется без учета местных потерь. К таким трубопроводам относятся, например, магистральные водоводы,
нефтепроводы.
Учитывая гидравлическую схему работы длинных трубопроводов, их можно разделить также на простые
и сложные. Простыми называются последовательно соединенные трубопроводы одного или различных сечений,
не имеющих никаких ответвлений. К сложным трубопроводам относятся системы труб с одним или несколькими
ответвлениями, параллельными ветвями и т.д. К сложным относятся и так называемые кольцевые трубопроводы.
Жидкость по трубопроводу движется благодаря тому, что ее энергия в начале трубопровода больше, чем в
конце. Этот перепад уровней энергии может создаваться несколькими способами: работой насоса, разностью уровней
жидкости, давлением газа.
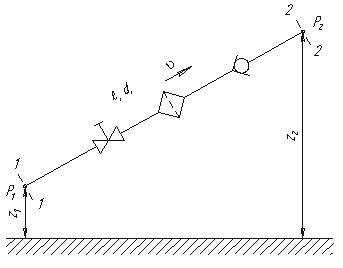
Рассмотрим простой трубопровод постоянного сечения, который расположен произвольно в пространстве
(рис. 6.1), имеет общую длину l и диаметр d, а также содержит ряд местных сопротивлений
(вентиль, фильтр и обратный клапан). В начальном сечении трубопровода 1-1 геометрическая высота равна
z1 и избыточное давление Р1, а в конечном сечении 2-2 —
соответственно z2 и Р2. Скорость потока в этих сечениях вследствие
постоянства диаметра трубы одинакова и равна ν.
Рис. 6.1. Схема простого трубопровода
Запишем уравнение Бернулли для сечений 1-1 и 2-2. Поскольку скорость в обоих сечениях
одинакова и α1 = α2, то скоростной напор можно не
учитывать. При этом получим
или
Пьезометрическую высоту, стоящую в левой части уравнения, назовем потребным напором
Нпотр. Если же эта пьезометрическая высота задана, то ее называют располагаемым напором
Нрасп. Такой напор складывается из геометрической высоты Hпотр, на которую
поднимается жидкость, пьезометрической высоты в конце трубопровода и суммы всех потерь напора в трубопроводе.
Назовем сумму первых двух слагаемых статическим напором, который представим как некоторую
эквивалентную геометрическую высоту
а последнее слагаемое Σh — как степенную функцию расхода
Σh = KQm
тогда
Hпотр = Hст + KQm
где K — величина, называемая сопротивлением трубопровода;
Q — расход жидкости;
m — показатель степени, который имеет разные значения в зависимости от режима течения.
Для ламинарного течения при замене местных сопротивлений эквивалентными длинами сопротивление
трубопровода равно
где lрасч = l + lэкв.
Численные значения эквивалентных длин lэкв для различных местных сопротивлений обычно
находят опытным путем.
Для турбулентного течения, используя формулу Вейсбаха-Дарси, и выражая в ней скорость через расход,
получаем
По этим формулам можно построить кривую потребного напора в зависимости от расхода. Чем больше расход
Q, который необходимо обеспечить в трубопроводе, тем больше требуется потребный напор
Нпотр. При ламинарном течении эта кривая изображается прямой линией (рис.6.2, а), при
турбулентном — параболой с показателем степени равном двум (рис.6.2, б).
Рис.6.2. Зависимости потребных напоров от расхода жидкости в трубопроводе
Крутизна кривых потребного напора зависит от сопротивления трубопровода K и возрастает с увеличением
длины трубопровода и уменьшением диаметра, а также с увеличением местных гидравлических сопротивлений.
Величина статического напора Нст положительна в том случае, когда жидкость движется вверх
или в полость с повышенным давлением, и отрицательна при опускании жидкости или движении в полость с
пониженным давлением. Точка пересечения кривой потребного напора с осью абсцисс (точка А) определяет
расход при движении жидкости самотеком. Потребный напор в этом случае равен нулю.
Иногда вместо кривых потребного напора удобнее пользоваться характеристиками трубопровода. Характеристикой
трубопровода называется зависимость суммарной потери напора (или давления) в трубопроводе от расхода:
Σh = f(q)
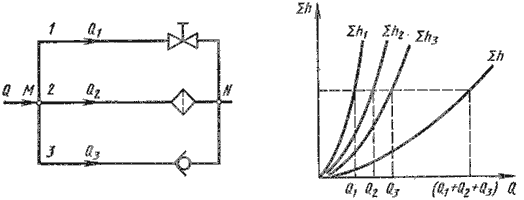
Простые трубопроводы могут соединяться между собой, при этом их соединение может быть последовательным
или параллельным.
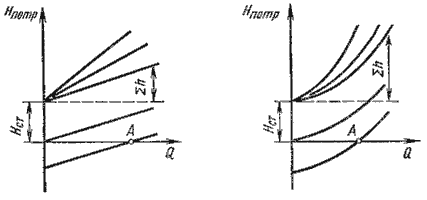
Последовательное соединение. Возьмем несколько труб различной длины, разного диаметра и
содержащих разные местные сопротивления, и соединим их последовательно (рис. 6.3, а).
Рис. 6.3. Последовательное соединение трубопроводов
При подаче жидкости по такому составному трубопроводу от точки М к точке N расход жидкости
Q во всех последовательно соединенных трубах 1, 2 и 3 будет одинаков, а полная
потеря напора между точками М и N равна сумме потерь напора во всех последовательно
соединенных трубах. Таким образом, для последовательного соединения имеем следующие основные уравнения:
Q1 = Q2 = Q3 = Q
ΣhM-N = Σh1 + Σh2 + Σh3
Эти уравнения определяют правила построения характеристик последовательного соединения труб (рис. 6.3, б).
Если известны характеристики каждого трубопровода, то по ним можно построить характеристику всего
последовательного соединения M-N. Для этого нужно сложить ординаты всех трех кривых.
Параллельное соединение. Такое соединение показано на рис. 6.4, а. Трубопроводы 1,
2 и 3 расположены горизонтально.
Рис. 6.4. Параллельное соединение трубопроводов
Обозначим полные напоры в точках М и N соответственно HM и
HN , расход в основной магистрали (т.е. до разветвления и после слияния) — через Q,
а в параллельных трубопроводах через Q1, Q2 и Q3;
суммарные потери в этих трубопроводах через Σ1 , Σ2 и Σ3.
Очевидно, что расход жидкости в основной магистрали
Q = Q1 = Q2 = Q3
Выразим потери напора в каждом из трубопроводов через полные напоры в точках М и N :
Σh1 = HM — HN; Σh2 = HM — HN; Σh3 = HM — HN
Отсюда делаем вывод, что
Σh1 = Σh2 = Σh3
т.е. потери напора в параллельных трубопроводах равны между собой. Их можно выразить в общем виде через
соответствующие расходы следующим образом
Σh1 = K1Q1m; Σh2 = K2Q2m; Σh3 = K3Q3m
где K и m — определяются в зависимости от режима течения.
Из двух последних уравнений вытекает следующее правило: для построения характеристики параллельного
соединения нескольких трубопроводов следует сложить абсциссы (расходы) характеристик этих трубопроводов при
одинаковых ординатах ( Σ h). Пример такого построения дан на рис. 6.3, б.
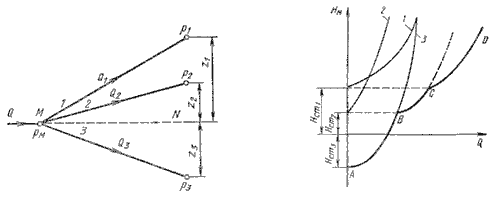
Разветвленное соединение. Разветвленным соединением называется совокупность нескольких
простых трубопроводов, имеющих одно общее сечение — место разветвления (или смыкания) труб.
Рис. 6.5. Разветвленный трубопровод
Пусть основной трубопровод имеет разветвление в сечении М-М, от которого отходят, например, три
трубы 1, 2 и 3 разных диаметров, содержащие различные местные сопротивления (рис. 6.5, а).
Геометрические высоты z1, z2 и z3 конечных сечений и
давления P1, P2 и P3 в них будут также различны.
Так же как и для параллельных трубопроводов, общий расход в основном трубопроводе будет равен сумме
расходов в каждом трубопроводе:
Q = Q1 = Q2 = Q3
Записав уравнение Бернулли для сечения М-М и конечного сечения, например первого трубопровода,
получим (пренебрегая разностью скоростных высот)
Обозначив сумму первых двух членов через Hст и выражая третий член через расход (как
это делалось в п.6.1), получаем
HM = Hст 1 + KQ1m
Аналогично для двух других трубопроводов можно записать
HM = Hст 2 + KQ2m
HM = Hст 3 + KQ3m
Таким образом, получаем систему четырех уравнений с четырьмя неизвестными: Q1,
Q2 и Q3 и HM.
Построение кривой потребного напора для разветвленного трубопровода выполняется сложением кривых
потребных напоров для ветвей по правилу сложения характеристик параллельных трубопроводов (рис. 6.5, б) —
сложением абсцисс (Q) при одинаковых ординатах (HM). Кривые потребных напоров для
ветвей отмечены цифрами 1, 2 и 3 , а суммарная кривая потребного напора для всего разветвления обозначена
буквами ABCD. Из графика видно, что условием подачи жидкости во все ветви является неравенство
HM > Hст1.
Сложный трубопровод в общем случае составлен из простых трубопроводов с последовательным и параллельным их
соединением (рис. 6.6, а) или с разветвлениями (рис. 6.6, б).
Рис. 6.6. Схемы сложных трубопроводов
Рассмотрим разомкнутый сложный трубопровод (рис. 6.6, б). магистральный трубопровод разветвляется в точках
А и С. Жидкость подается к точкам (сечениям) B, D и E с расходами Q
B и QD и QE .
Пусть известны размеры магистралей и всех ветвей (простых трубопроводов), заданы все местные сопротивления,
а также геометрические высоты конечных точек, отсчитываемые от плоскости M — N и избыточные давления
в конечных точках PB и PD и PE.
Для этого случая возможны два вида задач:
Задача 1. Дан расход Q в основной магистрали MA. Необходимо
определить расходы QB и QD и QE, а также потребный
напор в точке М.
Задача 2. Дан напор в точке М. Определить расход в магистрали Q и расходы в
каждой ветви.
Обе задачи решают на основе одной и той же системы уравнений, число которых на единицу больше числа
конечных ветвей, а именно:
уравнение расходов:
Q = QB = QD = QE
уравнение равенства потребных напоров для ветвей CD и CE
Hст D + KCDQDт = Hст E + KCEQEт
уравнение равенства потребных напоров для ветви АВ и сложного трубопровода АСЕD
Hст B + KABQBт = Hст D + KCDQDт + KAC(QD + QE)т
выражение для потребного напора в точке М
Расчет сложных трубопроводов часто выполняют графоаналитическим способом, т.е. с применением кривых
потребного напора и характеристик трубопроводов. Кривую потребного напора для сложного трубопровода следует
строить следующим образом:
1) сложный трубопровод разбивают на ряд простых;
2) строят кривые потребных напоров для каждого из простых трубопроводов;
3) складывают кривые потребных напоров для ветвей (и параллельных линий, если они имеются) по правилу
сложения характеристик параллельных трубопроводов;
4) полученную кривую складывают с характеристикой последовательно присоединенного трубопровода по
соответствующему правилу (см. п.6.2).
Таким образом, при расчете идут от конечных точек трубопровода к начальной точке, т.е. против течения
жидкости.
Сложный кольцевой трубопровод. Представляет собой систему смежных замкнутых контуров, с
отбором жидкости в узловых точках или с непрерывной раздачей жидкости на отдельных участках (рис. 6.7).
Рис. 6.7. Схема сложного кольцевого трубопровода
Задачи для таких трубопроводов решают аналогичным методом с применением электроаналогий (закон Кирхгофа).
При этом основываются на двух обязательных условиях. Первое условие — баланс расходов, т.е. равенство
притока и оттока жидкости для каждой узловой точки. Второе условие — баланс напоров, т.е. равенство нулю
алгебраической суммы потерь напора для каждого кольца (контура) при подсчете по направлению движения часовой
стрелки или против нее.
Для расчета таких трубопроводов типичной является следующая задача. Дан максимальный напор в начальной
точке, т.е. в точке 0, минимальный напор в наиболее удаленной точке Е, расходы во всех шести узлах и
длины семи участков. Требуется определить диаметры трубопроводов на всех участках.
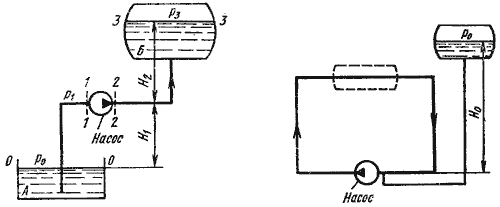
Как уже отмечалось выше, перепад уровней энергии, за счет которого жидкость течет по трубопроводу, может
создаваться работой насоса, что широко применяется в машиностроении. Рассмотрим совместную работу трубопровода
с насосом и принцип расчета трубопровода с насосной подачей жидкости.
Трубопровод с насосной подачей жидкости может быть разомкнутым, т.е. по которому жидкость
перекачивается из одной емкости в другую (рис. 6.8, а), или замкнутым (кольцевым), в котором
циркулирует одно и то же количество жидкости (рис. 6.8, б).
Рис. 6.8. Трубопроводы с насосной подачей
Рассмотрим трубопровод, по которому перекачивают жидкость из нижнего резервуара с давлением P
0 в другой резервуар с давлением P3 (рис. 6.8, а). Высота расположения оси
насоса H1 называется геометрической высотой всасывания, а трубопровод, по которому
жидкость поступает к насосу, всасывающим трубопроводом или линией всасывания. Высота
расположения конечного сечения трубопровода H2 называется геометрической высотой
нагнетания, а трубопровод, по которому жидкость движется от насоса, напорным или линией
нагнетания.
Составим уравнением Бернулли для потока рабочей жидкости во всасывающем трубопроводе, т.е. для сечений
0-0 и 1-1 (принимая α = 1):
Это уравнение является основным для расчета всасывающих трубопроводов.
Теперь рассмотрим напорный трубопровод, для которого запишем уравнение Бернулли, т.е. для сечений
2-2 и 3-3:
Левая часть этого уравнения представляет собой энергию жидкости на выходе из насоса. А на входе насоса
энергию жидкости можно будет аналогично выразить из уравнения:
Таким образом, можно подсчитать приращение энергии жидкости, проходящей через насос. Эта энергия сообщается
жидкости насосом и поэтому обозначается обычно Hнас.
Для нахождения напора Hнас вычислим уравнение :
где Δz — полная геометрическая высота подъема жидкости, Δz = H
1 + H2;
КQm — сумма гидравлических потерь,
P3 и Р0 — давление в верхней и нижней емкости соответственно.
Если к действительной разности уровней Δz добавить разность пьезометрических высот
( P3 — Р0 ) ( ρg ), то можно рассматривать увеличенную
разность уровней
и формулу можно переписать так:
Hнас = Hст + KQm
Из этой формулы делаем вывод, что
Hнас = Hпотр
Отсюда вытекает следующее правило устойчивой работы насоса: при установившемся течении жидкости в
трубопроводе насос развивает напор, равный потребному.
На этом равенстве основывается метод расчета трубопроводов с насосной подачей, который заключается в
совместном построении в одном и том же масштабе и на одном графике двух кривых: напора Hпотр =
f1(Q) и характеристики насоса Hнас = f2(Q) и в
нахождении их точки пересечения (рис. 6.9).
Рис. 6.9. Графическое нахождение рабочей точки
Характеристикой насоса называется зависимость напора, создаваемого насосом, от его подачи (расхода
жидкости) при постоянной частоте вращения вала насоса. На рис. 6.9 дано два варианта графика: а —
для турбулентного режима; б — для ламинарного режима. Точка пересечения кривой потребного напора с
характеристикой насоса называется рабочей точкой. Чтобы получить другую рабочую точку, необходимо
изменить открытие регулировочного крана (изменить характеристику трубопровода) или изменить частоту вращения
вала насоса.
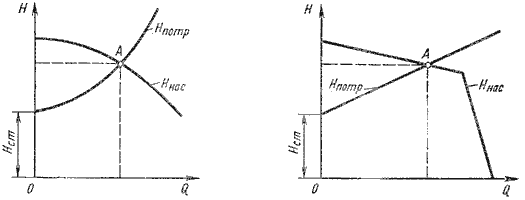
Гидравлическим ударом называется резкое повышение давления, возникающее в напорном трубопроводе при
внезапном торможении потока рабочей жидкости. Этот процесс является очень быстротечным и характеризуется
чередованием резких повышений и понижений давления, которое связано с упругими деформациями жидкости и
стенок трубопровода. Гидравлический удар чаще всего возникает при резком открытии или закрытии крана или
другого устройства, управляемого потоком.
Пусть в конце трубы, по которой движется жидкость со скоростью υ0, произведено
мгновенное закрытие крана (рис. 6.10, а).
Рис. 6.10. Стадии гидравлического удара
При этом скорость частиц, натолкнувшихся на кран, будет погашена, а их кинетическая энергия перейдет в
работу деформации стенок трубы и жидкости. При этом стенки трубы растягиваются, а жидкость сжимается в
соответствии с увеличением давления на величину ΔPуд, которое называется
ударным. Область (сечение n — n), в которой происходит увеличение давления, называется ударной волной.
Ударная волна распространяется вправо со скоростью c, называемой скоростью ударной волны.
Когда ударная волна переместится до резервуара, жидкость окажется остановленной и сжатой во всей трубе,
а стенки трубы — растянутыми. Ударное повышение давления распространится на всю длину трубы (рис. 6.10, б).
Далее под действием перепада давления ΔPуд частицы жидкости устремятся
из трубы в резервуар, причем это течение начнется с сечения, непосредственно прилегающего к резервуару. Теперь
сечение n-n перемещается обратно к крану с той же скоростью c, оставляя за собой выровненное
давление P0 (рис. 6.10, в).
Жидкость и стенки трубы предполагаются упругими, поэтому они возвращаются к прежнему состоянию,
соответствующему давлению P0. Работа деформации полностью переходит в кинетическую энергию,
и жидкость в трубе приобретает первоначальную скорость υ0, но направленную теперь
в противоположную теперь сторону.
С этой скоростью весь объем жидкости стремится оторваться от крана, в результате возникает отрицательная
ударная волна под давлением P0 — ΔPуд, которая
направляется от крана к резервуару со скоростью c, оставляя за собой сжавшиеся стенки трубы и
расширившуюся жидкость, что обусловлено снижением давления (рис. 6.10, д). Кинетическая энергия жидкости
вновь переходит в работу деформаций, но противоположного знака.
Состояние трубы в момент прихода отрицательной ударной волны к резервуару показано на рис. 6.10, е. Так же
как и для случая, изображенного на рис. 6.10, б, оно не является равновесным. На рис. 6.10, ж, показан процесс
выравнивания давления в трубе и резервуаре, сопровождающийся возникновением движения жидкости со
скоростью υ0.
Очевидно, что как только отраженная от резервуара ударная волна под давлением ΔP
уд достигнет крана, возникнет ситуация, уже имевшая место в момент закрытия крана. Весь цикл
гидравлического удара повторится.
Протекание гидравлического удара во времени иллюстрируется диаграммой, представленной на рис. 6.11, а и б.
Штриховыми линиями показано теоретическое изменение давления у крана в точке А, а сплошной
действительный вид картины изменения давления по времени (рис. 6.11, а). При этом затухание колебаний
давления происходит за счет потерь энергии жидкости на преодоление сил трения и ухода энергии в резервуар.
Если давление P0 невелико (P0 < ΔP
уд), то картина изменения амплитуды давления получается несколько иная, примерно такая, как
показано на рис. 6.11, б.
Рис. 6.11. Изменение давления по времени у крана
Повышение давления при гидравлическом ударе можно определить по формуле
ΔPуд = ρυ0c
Данное выражение носит название формулы Жуковского. В нем скорость распространения ударной волны c
определится по формуле:
где r — радиус трубопровода;
E — модуль упругости материала трубы;
δ — толщина стенки трубопровода;
K — объемный модуль упругости (см. п.1.3)
Если предположить, что труба имеет абсолютно жесткие стенки, т.е. E = 
ударной волны определится из выражения
Для воды эта скорость равна 1435 м/с, для бензина 1116 м/с, для масла 1200 — 1400 м/с.
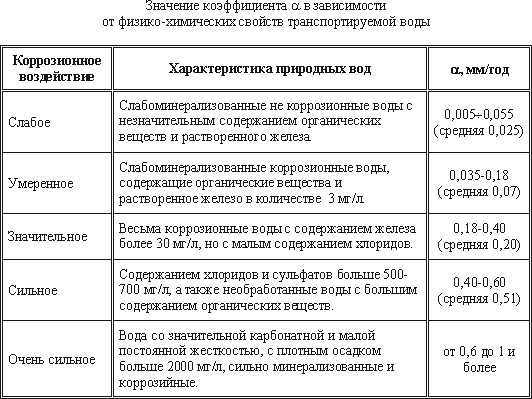
При проектировании напорных трубопроводов следует учитывать, что их пропускная способность в период
эксплуатации снижается (например, для водопроводных труб до 50% и даже ниже). Вследствие коррозии и
образования отложений в трубах (инкрустации), шероховатость труб увеличивается. Это можно оценить по
формуле:
kt = k0 + αt
где k0 — абсолютная шероховатость для новых труб, (мм),
kt — шероховатость через t лет эксплуатации,
α — коэффициент характеризующий быстроту возрастания шероховатости (мм/год).
Таблица 6.1
Проверить себя ( Тест )
Наверх страницы
Подборка по базе: Проектная деят.3 Основы экономических расчётов для оценки эффект, апарат расчет.docx, Проектный расчет коксовой батареи.docx, Автоматизация расчета заработной платы .doc, Уроки маскировки от расчёта Раk.docx, ОБОЛОЧКА (ПЕРЕПРОВЕРКА РАСЧЁТОВ).docx, 5 Расчёт предохранительных клапанов.docx, ППВТ расчет.docx, Реферат — Методика расчета параметров тушения пожаров ЛВЖ и ГЖ в, 1. Расчет изменений энтропии (теория и решение задач).doc
Гидравлический расчет трубопроводов
Различные способы расчета потерь
Рассматривается равномерное напорное движение жидкости в круглой трубе. При равномерном движении форма и площадь живого сечения, средняя скорость потока и эпюра скоростей по длине не изменяются. В этих условиях живое сечение характеризуется одним линейным размером – диаметром. Напомним: .
Общая формула для потерь напора по длине имеет вид .
Для круглых труб .
Это установленная экспериментально формула Дарси-Вейсбаха. Безразмерный коэффициент называют коэффициентом гидравлического трения или коэффициентом Дарси. Коэффициент гидравлического трения зависит от относительной шероховатости трубопровода и числа Re.
. Для нахождения
существуют эмпирические формулы (режимы ламинарный – переходный –турбулентный; область гидравлически гладких труб, доквадратичная область, квадратичная область).
При равномерном движении жидкости средняя скорость потока, не изменяющаяся по длине из формулы равна
. Обозначим
.
Коэффициент называют коэффициентом Шези. Вспомним, что гидравлический уклон
и получим формулу Шези для средней скорости при равномерном движении
, где
.
Потери напора по длине с учетом коэффициента Шези .
Коэффициент Шези в отличие от безразмерного коэффициента Дарси имеет размерность
. В справочниках приводятся таблицы значений коэффициента Шези для трубопроводов различного диаметра и различной шероховатости. Существует много эмпирических формул для расчета коэффициента Шези.
Зная формулу для средней скорости потока получим формулу Шези для расхода при равномерном движении .
При расчете трубопровода обычно составляют уравнение Бернулли для потока вязкой жидкости. Пренебрегая местными потерями и скоростными напорами, получаем .
Вспомним, что гидравлический уклон , откуда
. Подставим найденное значение гидравлического уклона в формулу Шези для скорости потока
. Решаем уравнение относительно напора
. Заметим на будущее, что напор пропорционален квадрату скорости.
Запишем формулу Шези для расхода при равномерном движении .
Объединим параметры, зависящие от диаметра трубопровода, представим их виде так называемой расходной характеристики трубопровода (модуля расхода) .
Расходная характеристика представляет собой расход в данной трубе при гидравлическом уклоне, равном единице.
Тогда расход , напор
.
При этом расход и расходная характеристика
должны быть выражены в одних и тех же единицах. В таблицах для гидравлических расчетов приводятся значения расходной характеристики
для трубопроводов различного диаметра с различной относительной шероховатостью. На этой основе производится расчет трубопроводов «с использованием таблиц».
Получим значение расчетным путем. Гидравлический уклон равен 1, значит потери равны длине
. Потери по длине
. Отсюда
.
;
.
В квадратичной области турбулентного режима
Замечание. При равномерном движении гидравлический и пьезометрический уклоны равны. Пренебрегая скоростным напором, получим, что линия полного напора и пьезометрическая лини совпадают.
Классификация трубопроводов
Простой трубопровод – трубопровод, не имеющий ответвлений и состоящий из труб одинакового диаметра, выполненных из одного материала.
Приведем два примера простых трубопроводов.
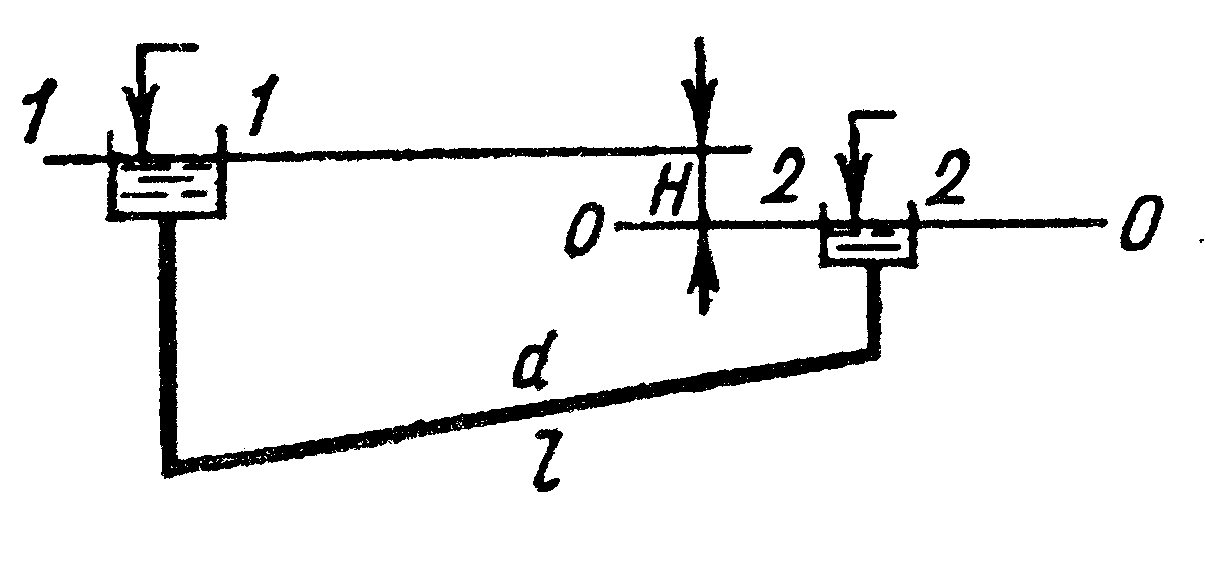 |
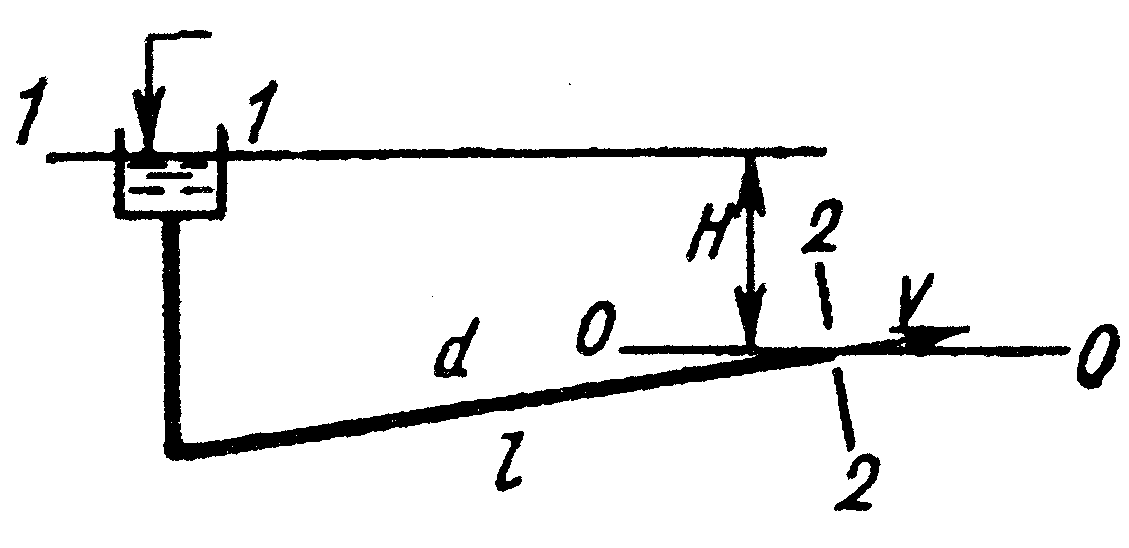 |
Движение жидкости в трубе обусловлено напором , равным разности напоров в резурвуаре-питателе и приемнике или разности напоров в резервуаре питателе и в струе на выходе из трубы, если резервуар-приемник отсутствует. Если указанная разность напоров не изменяется во времени, то движение установившееся. Мы рассматриваем расчет только трубопроводов с установившимся движением.
Потери напора в трубопроводе можно рассматривать как сумму потерь на трение по длине трубопровода и потерь в местных сопротивлениях .
По соотношению потерь по длине и в местных сопротивлениях в общей величине потерь трубопроводы делятся на гидравлически короткие и гидравлически длинные.
В гидравлически длинном (или просто длинном) трубопроводе потери напора по длине настолько превышают местные потери (и скоростной напор), что местные потери не вычисляют, а принимают как некоторую часть потерь по длине.
Практически при расчете длинных трубопроводов находят потери напора по длине , а затем суммарные местные потери напора учитывают, увеличивая найденное значение
на
%.
.
В гидравлически коротком трубопроводе потери напора по длине и местные потери сопоставимы по значению. При гидравлическом расчете коротких трубопроводов учитывают как местные потери напора, так и потери по длине, а в балансе напоров учитывают скоростные напоры в сечениях потока.
Классификация задач расчета трубопроводов
При расчете простого трубопровода необходимо установить связь следующих характеристик
Задачи по расчету трубопроводов подразделяются на задачи проектирования и задачи эксплуатации. Полагается, что длина трубопровода во всех случаях известна.
Задачи проектирования : определение диаметра трубопровода, напора или давления на одном из его концов при заданной скорости жидкости в трубе или ее расходе.
Задачи эксплуатации : определение эксплуатационных характеристик (расход, скорость жидкости) готового (существующего в натуре или в проекте) трубопровода с известным диаметром и шероховатостью, а также с определенными напорами (давлениями) на концах трубы.
По методу расчета подразделяют задачи прямые и обратные.
При решении прямых задач искомые величины находятся по расчетным формулам в явном виде. В обратных задачах искомую величину в явном виде выразить не удается, решение находят с помощью итерационных процедур.
Расчетные формулы
Располагаемый напор равен потерям. Потери складываются из потерь по длине и потерь в местных сопротивлениях. Потери по длине определяются по формуле Дарси-Вейсбаха (первая водопроводная формула). Потери в местных сопротивлениях суммируются по всем местным сопротивлениям и зависят от коэффициента потерь в каждом из них . Получаем формулу, которая связывает среднюю скорость и располагаемый напор.
;
;
;
;
При расчете трубопровода «с использованием таблиц» , где расходная характеристика
берется из таблиц.
По определению средняя скорость потока . Очевидно
Число Рейнольдса или
. Значения динамической вязкости и плотности или кинематической вязкости жидкости при данной температуре известны.
Коэффициент сопротивления трения ( коэффициент Дарси ) определяется по эмпирическим формулам и зависит от Re и абсолютной эквивалентной шероховатости , которая для данного вида труб (материала, исполнения) известна (задается в справочниках, для новых стальных труб
=0,2 мм, для старых водопроводных
=1,5 мм).
Применение тех или иных эмпирических формул определяется режимом движения жидкости (числом Re ), а при турбулентном режиме областью сопротивления.
I – ламинарный режим движения
Границы Формула
II – переходный режим движения
Границы Формула
III – область гладких труб
Границы:. Формула Блазиуса
IV – область доквадратичного сопротивления (или переходная)
Границы : . Формула Альтшуля
V- область квадратичного сопротивления (или шероховатых труб)
Границы: . Формула Шифринсона
Расчет простого трубопровода
Задачи, чаще всего встречающиеся в практике, приведены ниже
( четыре параметра, два заданы, два оставшиеся определяются расчетом; число различных сочетаний из 4 по 2 равно 6)
| Известны (заданы) | Требуется определить | Вид задачи | Характеристика | |
| 1 | прямая | проектная | ||
| 2 | прямая | проектная | ||
| 3 | прямая | проектная | ||
| 4 | обратная | эксплуатационная | ||
| 5 | обратная | проектная | ||
| 6 | обратная | учебная |
Решение прямых задач начинается с нахождения числа Re.
1. и
=> Re
2. и
=>
=> Re
3. и
=>
=> Re
Дальнейший алгоритм расчета одинаков Re => =>
.
При решении обратных задач «без использования таблиц» не удается получить аналитического решения. Следует применить итерационную процедуру, т.е. задаться искомым значением, а затем уточнять его.
Выражение для располагаемого напора следует решить относительно скорости
Задача 4 (подбираем скорость) :
,
=> задаемся
=> Re =>
=>
(больше/меньше заданного) =>новое
.
Задача 5 (подбираем диаметр):
,
=> задаемся
=>
=> Re =>
=>
(больше/меньше заданного) => новое
.
Задача 6 (подбираем диаметр):
,
=> задаемся
=> Re =>
=>
(больше/меньше заданного) => новое
.
В учебных целях рекомендуется сопровождать решение графической иллюстрацией процесса последовательных приближений. Для этого по имеющимся расчетным данным следует изобразить следующие зависимости:
Задача 4. . Задачи 5 и 6.
Графоаналитический метод решения задач обратного типа состоит в следующем ( на примере задачи 4). Задаемся значением скорости , находим напор
, который, разумеется, отличается от заданного в условии. Если полученное значение меньше заданного, то увеличиваем скорость, если больше, то уменьшаем. Повторяем расчет. Строим в масштабе зависимость
. Для построения зависимости необходимо не менее 3-х точек. Из полученной графической зависимости находим значение
, которому соответствует заданный напор
. Производим проверку найденного значения.
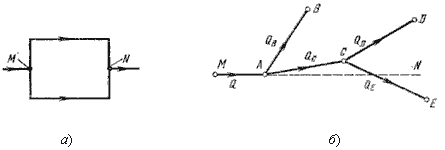
Последовательное соединение трубопроводов
Рассмотрим систему из последовательно соединенных длинных труб различных диаметров и длин. В общем случае материал труб может быть различным (различная шероховатость).
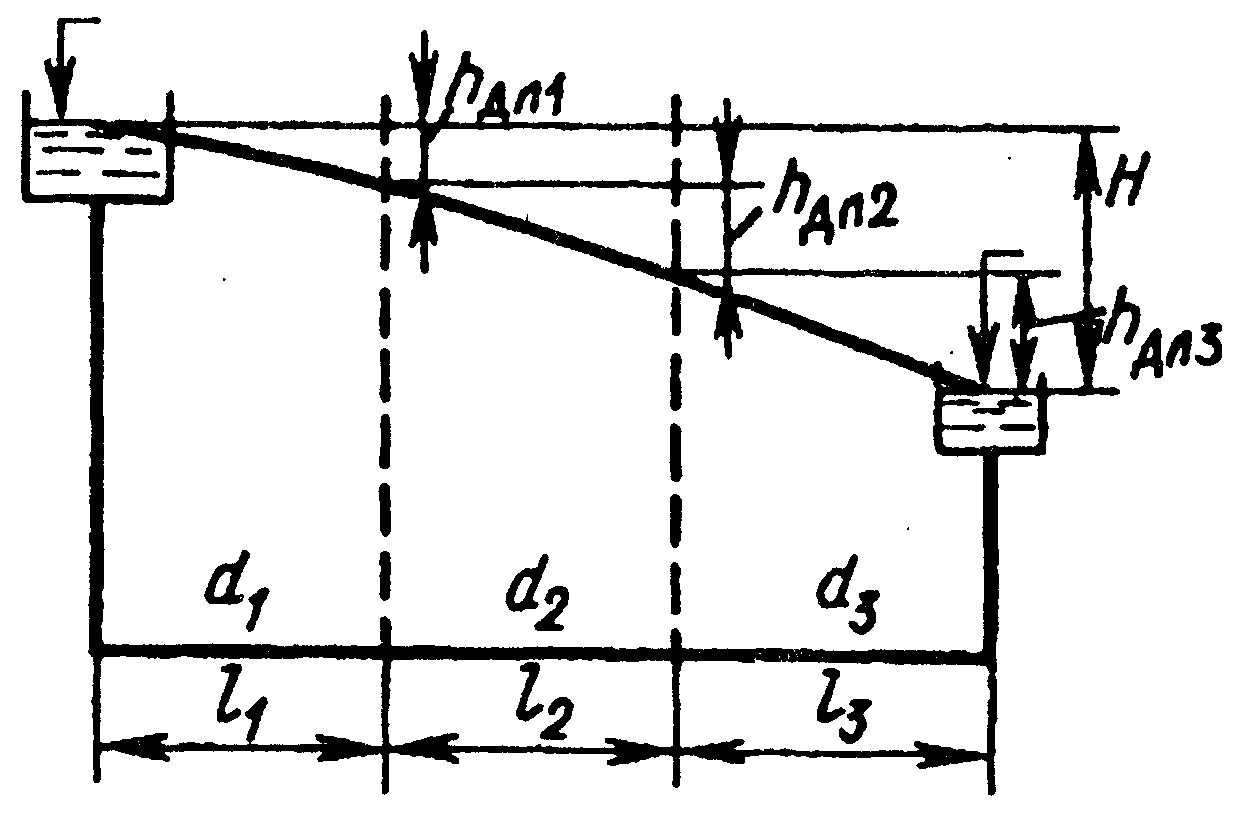 |
Заданы расход |
, где i= 1, 2 … n – номер участка.
Поскольку местными потерями пренебрегаем, напор затрачивается на преодоление потерь напора по длине и будет равен сумме потерь напора на отдельных участках
Вывод.
Для последовательного соединения расход одинаков, а напор равен сумме напоров.
Аналогия – последовательное соединение сопротивлений, ток одинаков а напряжения суммируются.
Параллельное соединение трубопроводов
Рассмотрим систему из параллельно соединенных длинных труб.
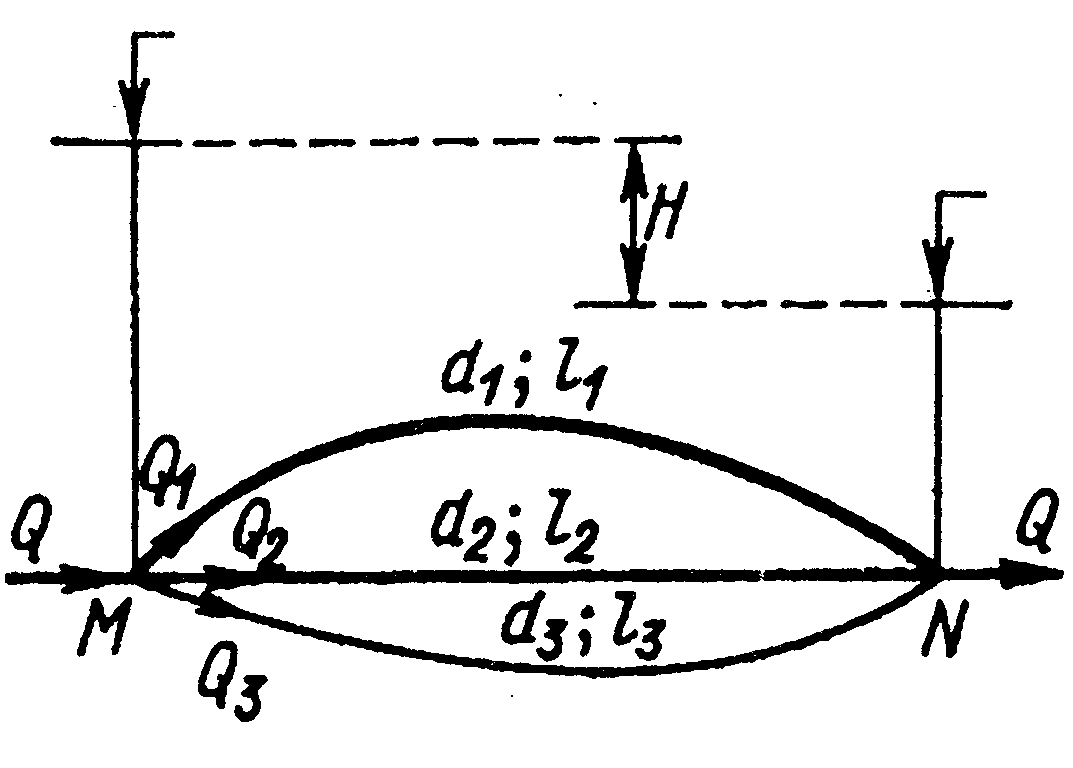 |
Между точками M и Nпроходит несколько труб.
Заданы общий расход Разность пьезометрических напоров в начале и в конце труб составляет напор |
Расход, проходящий по любому участку . Для всех участков имеем n уравнений для
. Сумма расходов на отдельных участках должна быть равна общему расходу, поступающему в систему параллельно соединенных трубопроводов в точке M и выходящему из системы в точке N.
.
Таким образом, имеем n+1уравнение, из которых может быть найден необходимый напор и расход в каждом из параллельных участков. Распределение расходов между участками заранее не известно. Поэтому все расходы выражают через какой-нибудь один, например через . Имеем
, откуда
.
Суммарный расход 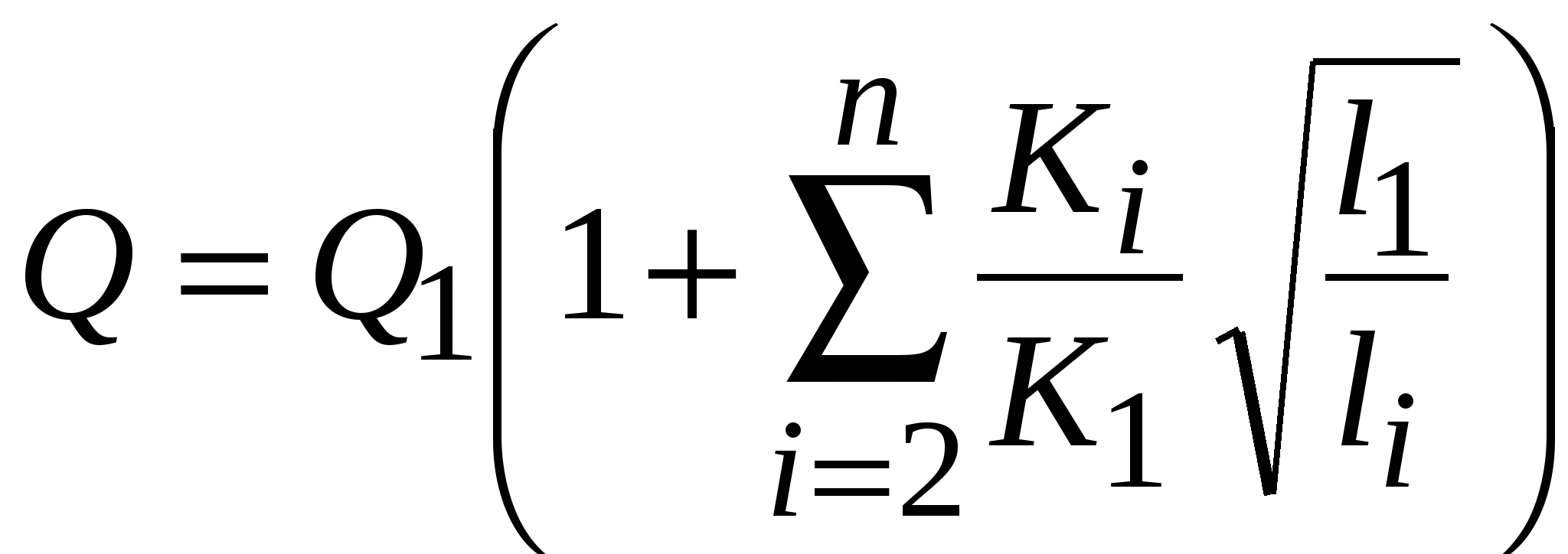
и все остальные.
Вывод.
Для параллельного соединения напор одинаков, а расход равен сумме расходов.
Аналогия – параллельное соединение сопротивлений, напряжение одинаково, а токи суммируются.
Расходная характеристика участка трубопровода
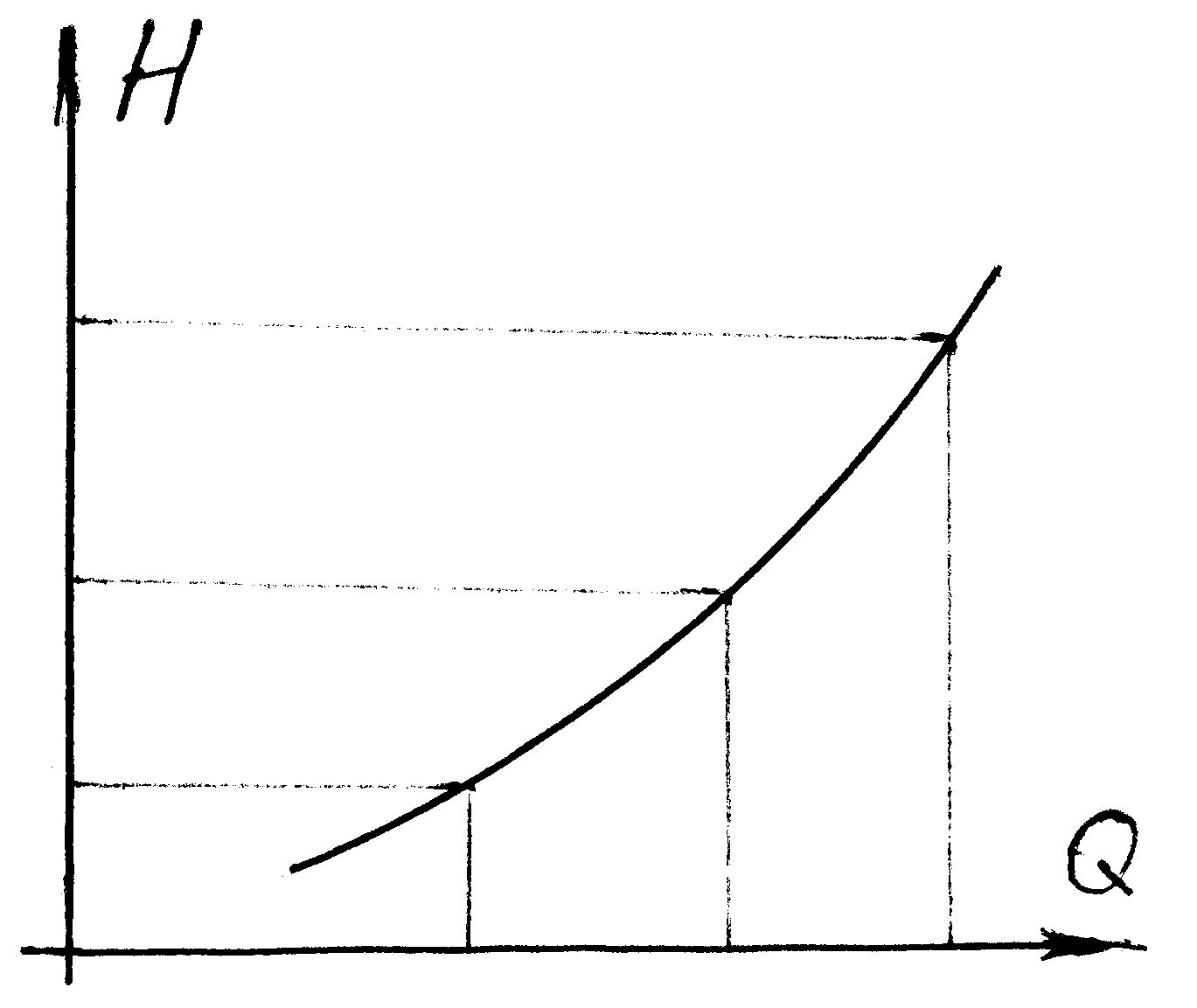 |
Зависимость напора от расхода |
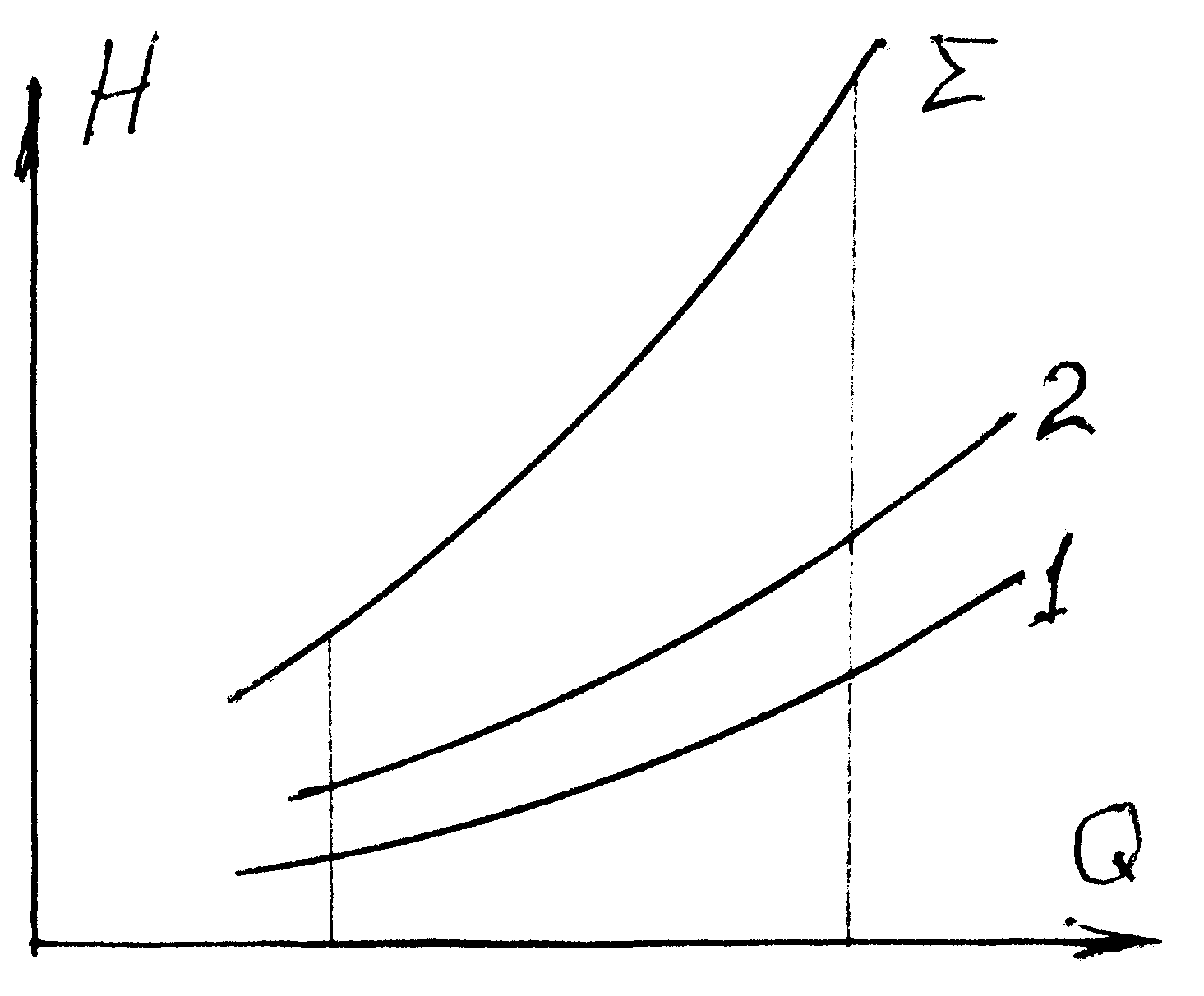 |
Для последовательного соединения трубопроводов расходная характеристика может быть получена как сумма напоров характеристик отдельных участков. По ней для заданного напора можно найти расход и напоры на участках трубопровода. |
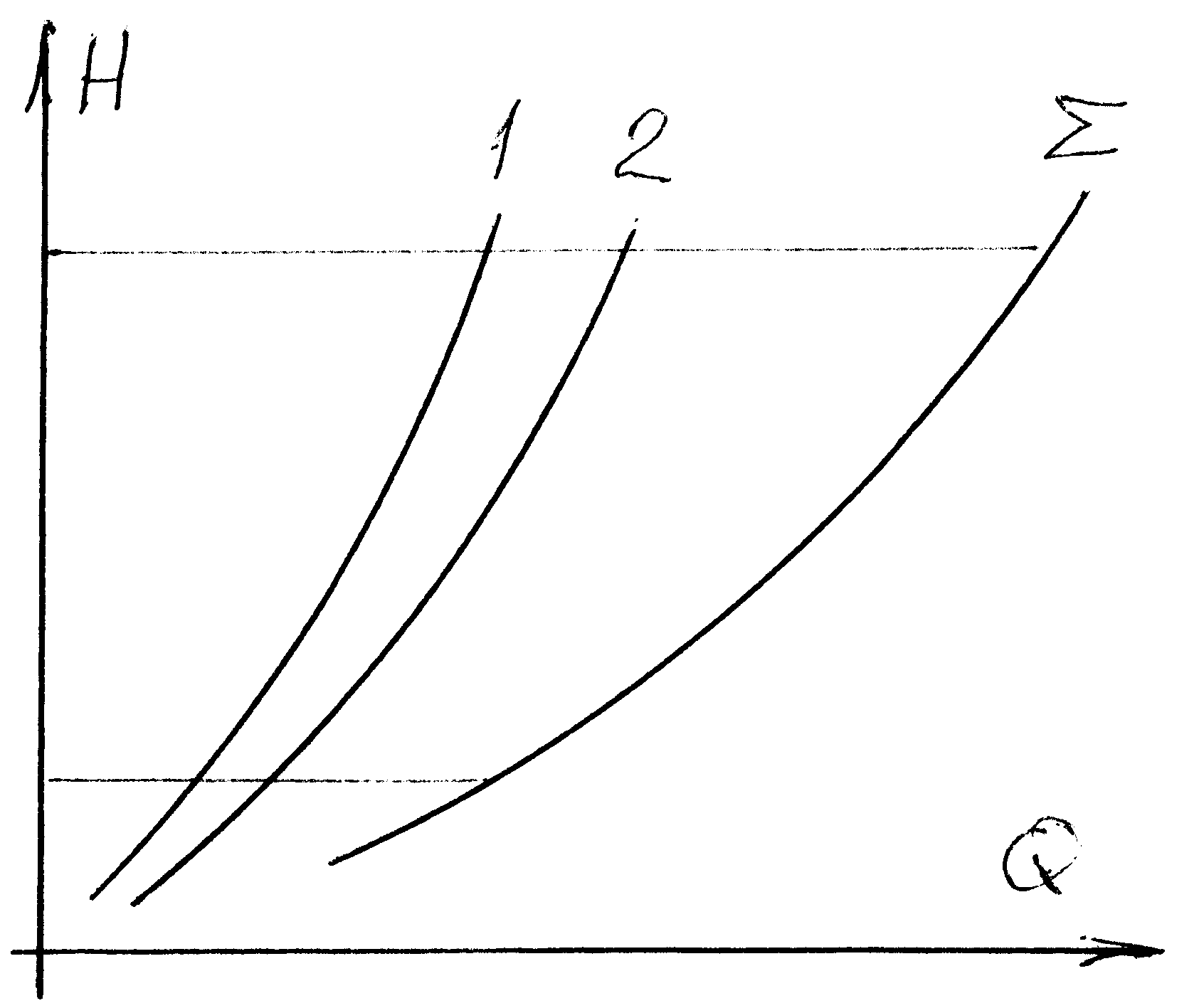 |
Для параллельного соединения трубопроводов расходная характеристика может быть получена как сумма расходов отдельных участков. По ней для заданного напора можно найти расходы в ветвях и суммарный расход. |
Расчет трубопровода с непрерывным изменением расхода по длине
Часто встречаются случаи, когда по длине трубопровода происходит раздача некоторой части или всего расхода, причем отбор жидкости (воды) потребителями происходит в нескольких сечениях по длине трубопровода. К таким трубопроводам относятся городские и сельские водопроводы, поливные трубопроводы, подающие воду в каждую борозду через отверстия, трубопроводы различных технических систем, в том числе внутрипочвенного и капельного орошения. Собирающие трубопроводы (дренажные коллекторы) работают с увеличением расхода по длине.
Трубопроводы с непрерывной равномерной раздачей воды вдоль пути характеризуются тем, что точки разбора находятся на одинаковом расстоянии друг от друга, а расходы разбора в этих точках одинаковы. При этом удельный путевой расход на единицу длины составляет .
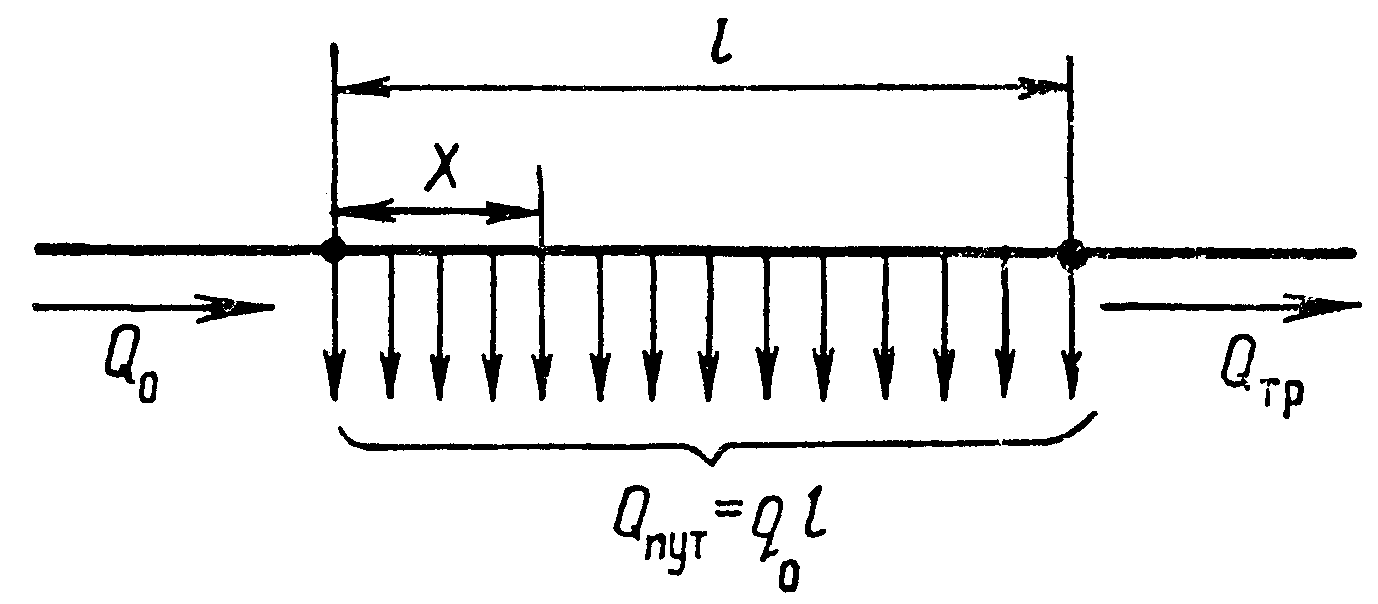 |
Общий (полный) расход путевого |
Определим потери напора на таком участке.
В любом сечении на расстоянии от начала разбора расход
.
Гидравлический уклон , откуда
. Для нахождения потерь напора на длине
интегрируем полученное выражение в пределах от 0 до
:
Раскроем подынтегральное выражение1
.
Подставляем значение интеграла в формулу для потерь напора
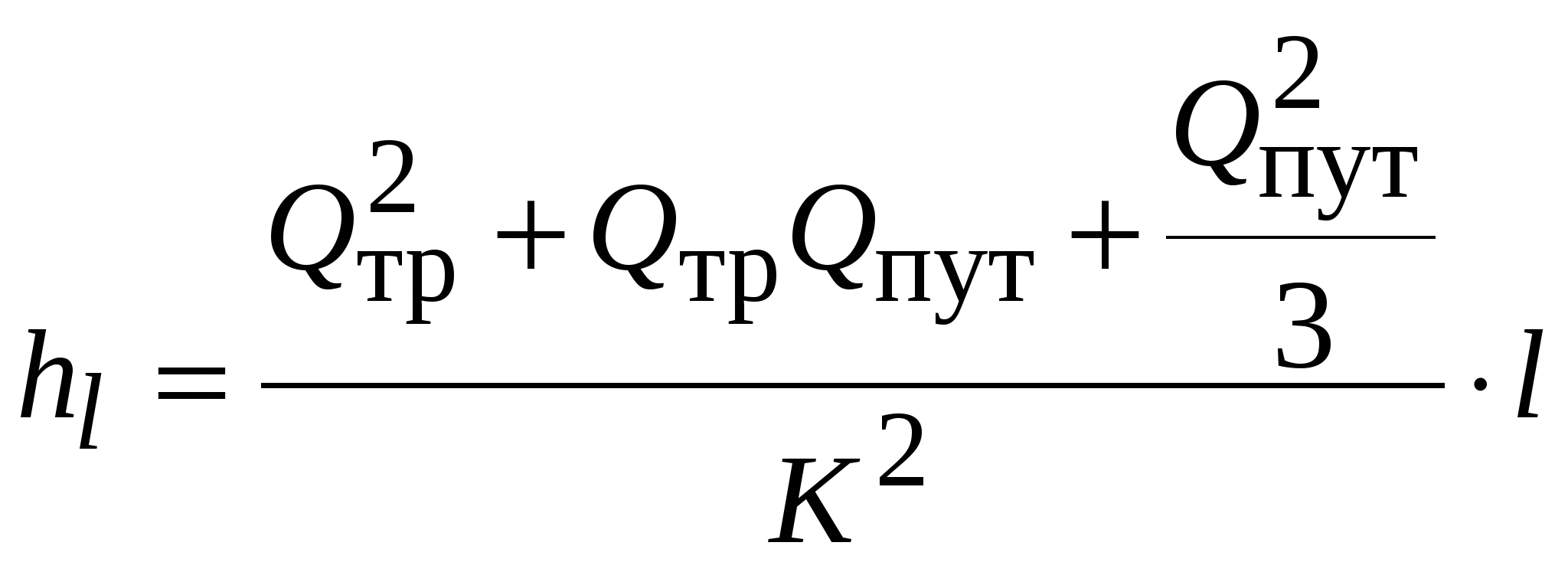
Введем понятие расчетного расхода
Окончательно расчетная зависимость имеет вид .
Расчетный расход больше транзитного, но меньше полного расхода в начале трубопровода.
В практических расчетах для упрощения принимают .
Оптимальные диаметр трубопровода и средняя скорость
Необходимость определения диаметра трубопровода возникает в задачах проектирования. Один и тот же расход может быть подан через трубопровод большего диаметра с меньшими потерями напора или наоборот. Оптимальный диаметр трубопровода определяется по сопоставлению капитальных и эксплуатационных затрат.
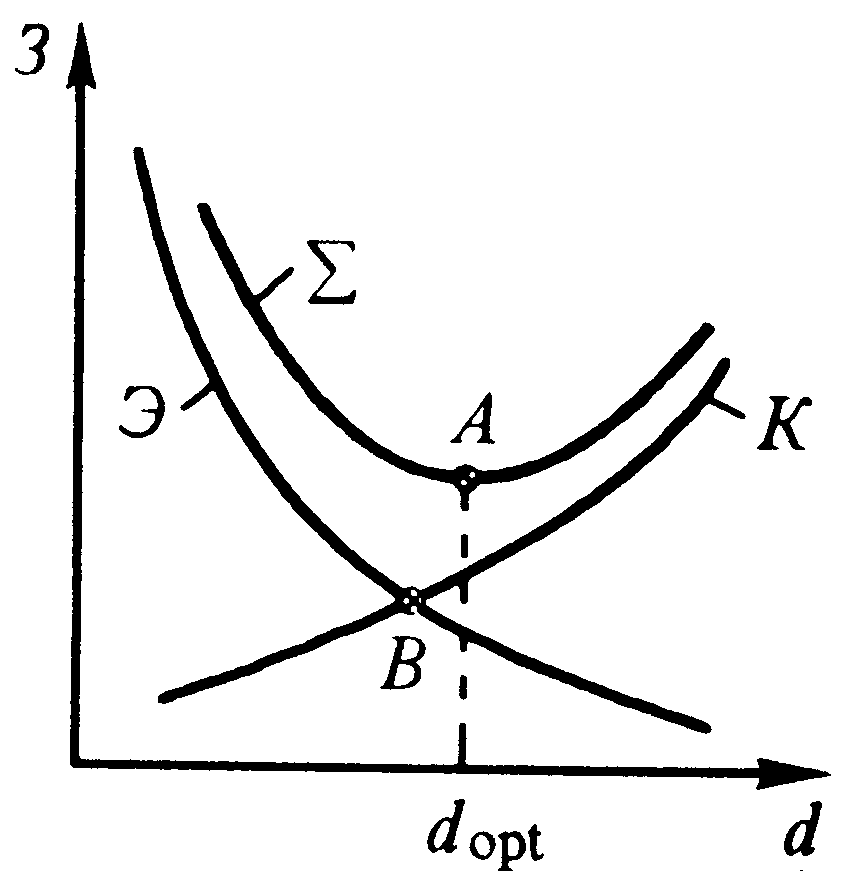 |
С увеличением диаметра возрастают капитальные затраты (точнее – амортизационные). Кривая К.
С увеличением диаметра при заданном расходе снижается средняя скорость потока, а с ней и энергия, затрачиваемая на преодоление гидравлического сопротивления. Эксплутационным (прежде всего энергетическим) затратам отвечает кривая Э. Оптимальным является диаметр трубопровода, при котором суммарные затраты (кривая ) минимальны. |
На рисунке минимуму кривой отвечает точка ; значит следует подбирать трубопровод, близкий по диаметру к оптимальному:
.
Заметим, что в учебниках иногда ошибочно определяют как абсциссу точки
; несмотря на возможную близость в каких-то случаях к
, диаметр
, отвечающий равенству капитальных и эксплуатационных затрат, вообще говоря никакого интереса не представляет.
Сравнение капитальных и эксплуатационных затрат не всегда возможно из-за отсутствия необходимой информации. На практике используют таблицу рекомендуемых предельных скоростей и предельных расходов (таблица приводится выборочно)
| Диаметр трубопровода, мм | Рекомендуемая предельная скорость, м/с | Рекомендуемый предельный расход, л/с |
| 50 | 0,96 | 1,88 |
| 100 | 1,15 | 9,03 |
| 200 | 1,34 | 42,1 |
| 500 | 1,45 | 284 |
| 1000 | 1,68 | 1280 |
Таблица применима для стальных труб, прокладываемых в центральных и западных районах России. Для районов Сибири и Урала приведенные в таблице расходы и скорости увеличивают на 1015%. Для Южных районов СНГ уменьшают на 10%. Причины: в Сибири и на Урале более дешевая электроэнергия, но большие капиталовложения в строительство трубопроводов в связи с большой глубиной прокладки труб; в южных районах СНГ более дорогая электроэнергия, но меньше затраты на строительство.
Кольцевые и тупиковые водопроводные сети
Водопроводные сети, по которым вода из водонапорной башни поступает к потребителям, делят на разветвленные (тупиковые) и кольцевые.
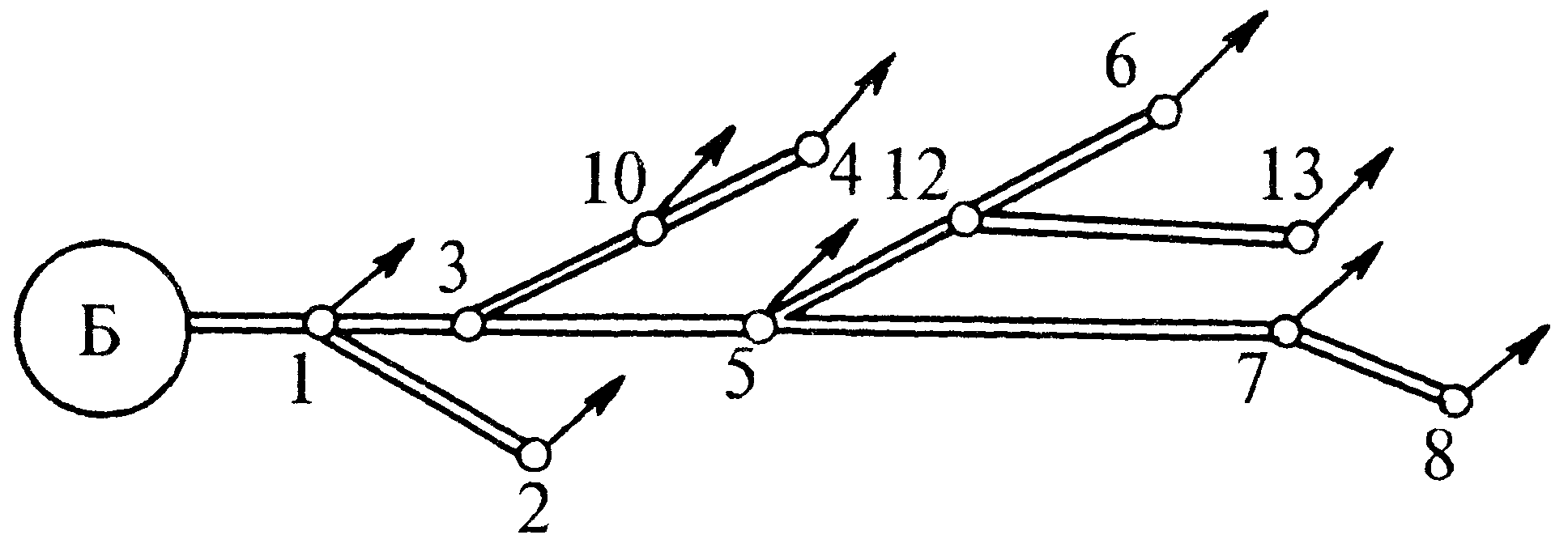 |
Разветвленные трубопроводы состоят из основной магистрали и отходящих от узлов сети ответвлений, которые могут состоять из одной линии (простые ответвления) или нескольких участков трубопроводов (сложные ответвления). |
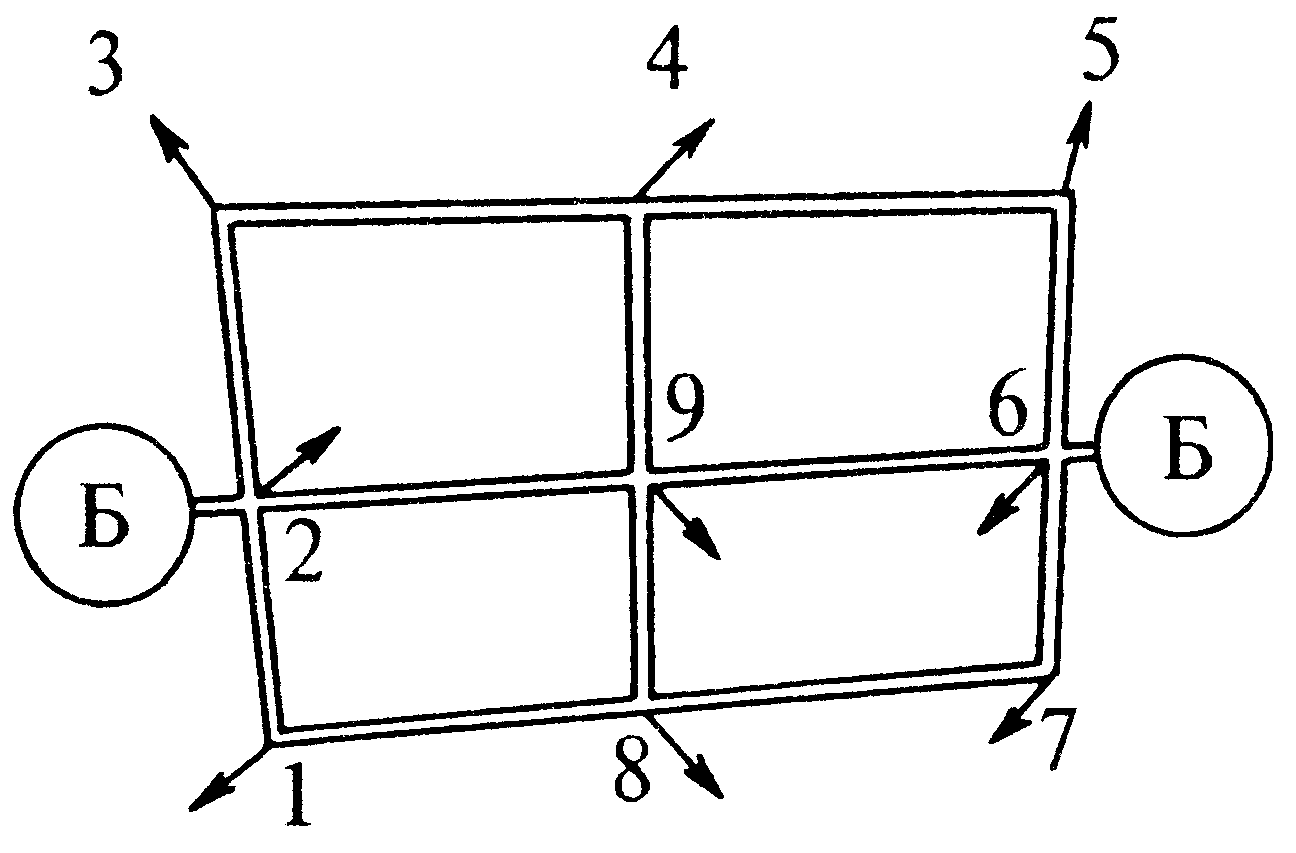 |
Городские водопроводы обычно выполняются в виде кольцевых сетей обеспечиваются водой от двух и более водонапорных башен Б. В узлах 1-9 находятся потребители (например жилые массивы, предприятия и т.п.) |
Кольцевая сеть позволяет осуществлять водоснабжение всех потребителей в случае аварии или ремонта отдельных участков водопроводной сети. При этом, конечно, потребности в воде будут удовлетворяться не полностью, а , например, на несколько часов в сутки, причем иногда обеспечиваются лишь нижние этажи зданий и т.п., но все же водоснабжение не буден отключено полностью на все время ремонта, что может произойти, если сеть тупиковая.
Строительными нормами и правилами рекомендуется обеспечить пьезометрический напор не менее 10 м при одноэтажной застройке, добавляя 4 м на каждый этаж.
Расчет разветвленного трубопровода.
Определить расход жидкости, протекающей по разветвленному трубопроводу в пункты 1 и 2 (истечение в атмосферу). Напор в резервуаре постоянен и известен. Длины и диаметры отдельных участков трубопровода известны. Кинематическая вязкость жидкости и абсолютная эквивалентная шероховатость известны. Местными потерями напора и скоростным напором пренебречь.
 |
Примечание.
- Как правило задается не кинематическая вязкость, а вид жидкости и рабочая температура. Кинематическую вязкость берут по таблицам в справочниках.
- При истечении в атмосферу не потерь на вход в бак, однако в точных расчетах необходимо учитывать скоростной напор выходящей из трубы жидкости. Если им пренебречь и не учитывать местные потери, то весь располагаемый напор равен сумме потерь напора по длине в общем трубопроводе и в разветвленной части (в двух трубопроводах разветвления напор одинаков, однако длины и/или диаметры различны, а значит различны средние скорости и расходы).
Решение.
В разветвленном трубопроводе сохраняется баланс расходов .
Неизвестны два расхода, третий находится по балансу. Потери в ветвях разветвляющейся части одинаковы, т.е. . Располагаемый напор
. Потери в каждом трубопроводе рассчитываются по формуле Дарси-Вейсбаха
.
Расход по участку . Площади
известны. Тогда

В первом приближении примем, что режим движения жидкости в трубопроводе турбулентный, квадратичная область сопротивления (в дальнейшем это утверждение будет уточнено). Коэффициент Дарси для каждого диаметра может быть определен по формуле Шифринсона . Потери в каждом участке трубопровода могут найдены через его расходную характеристику, при чем последняя не берется из таблиц, а определяется аналитически.
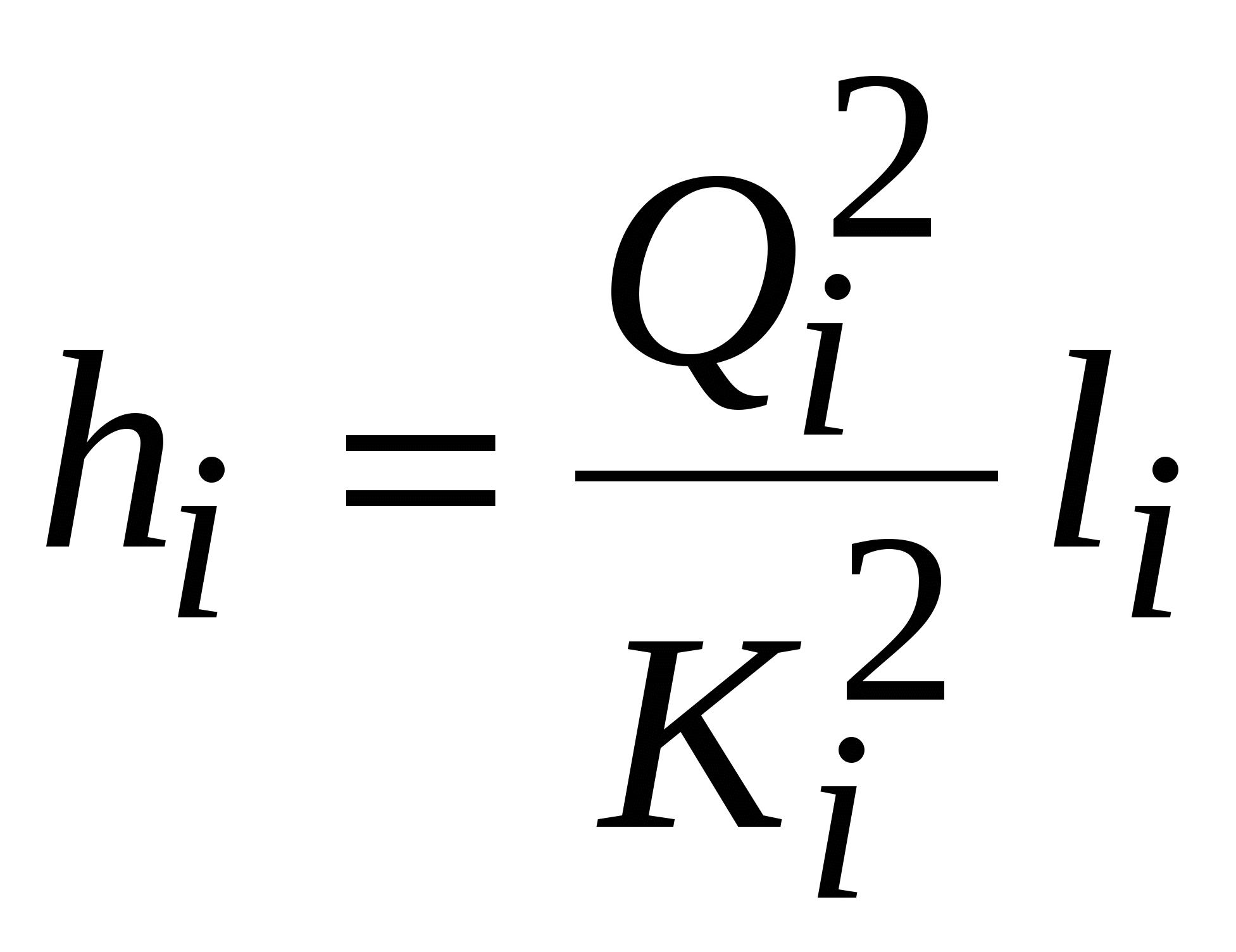
.
Получим шесть уравнений с шестью неизвестными (расходы и потери напора в участках)
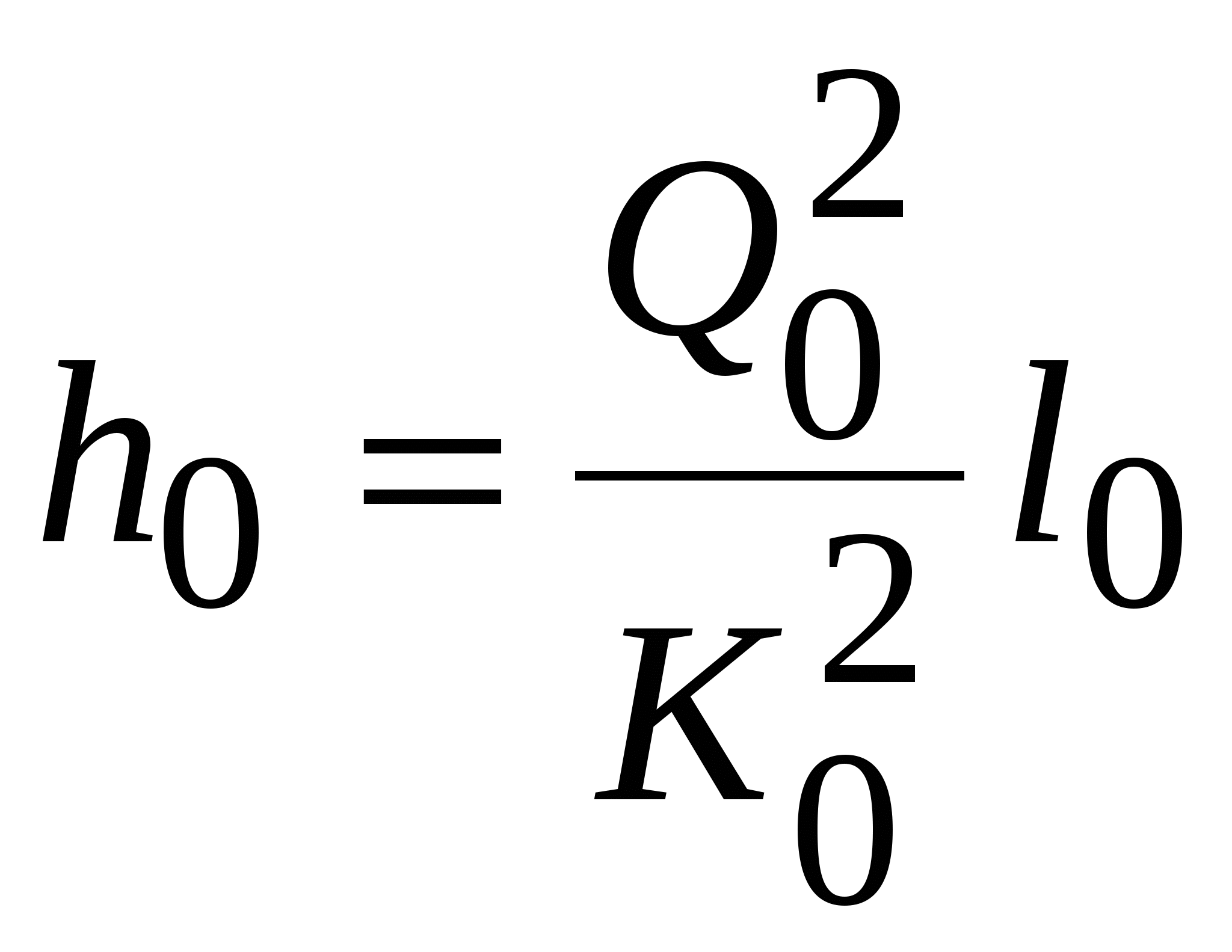

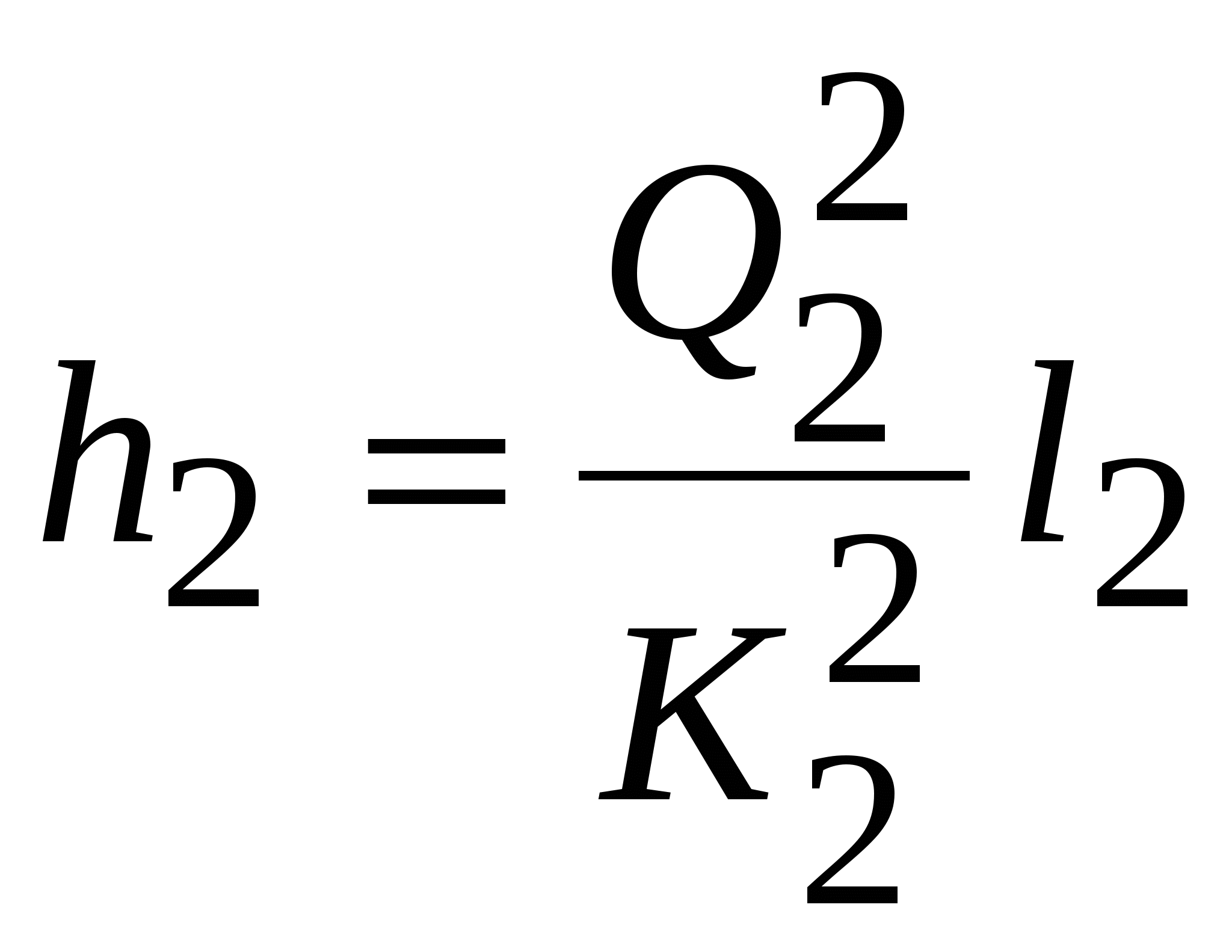
,
,
.
Несложные алгебраические преобразования приводят к следующим результатам:
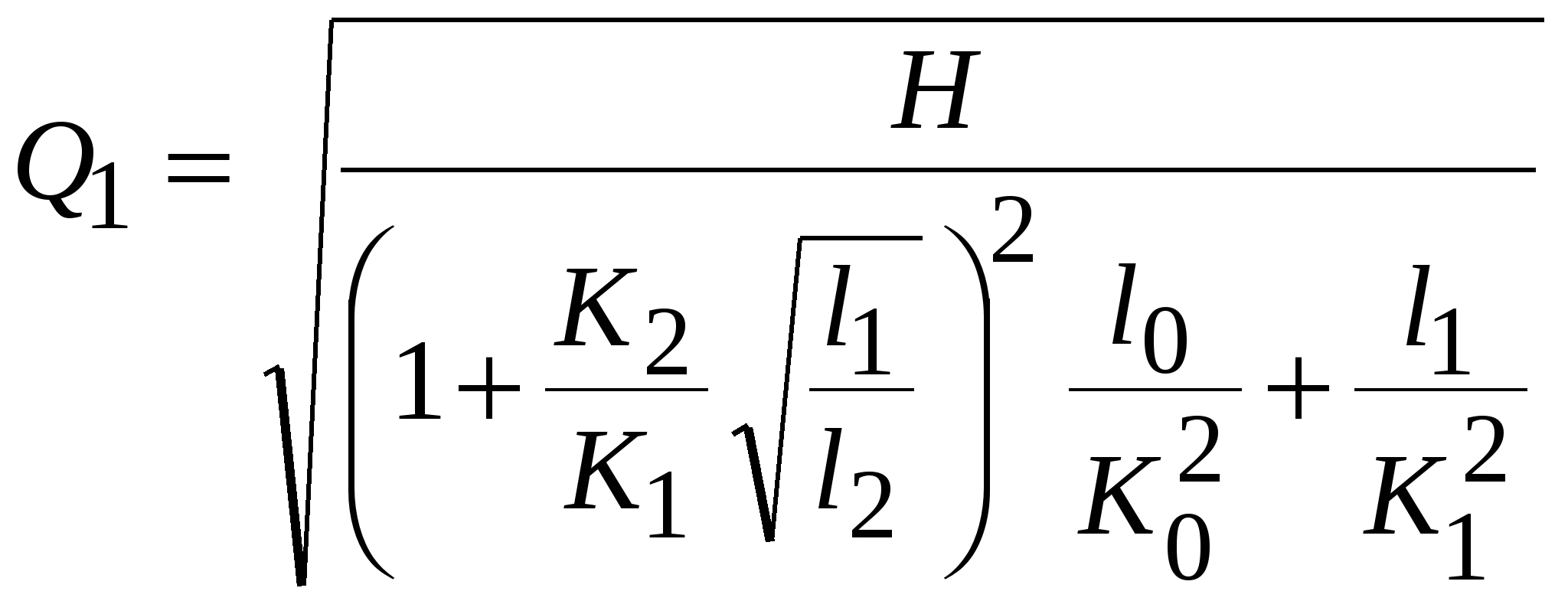
Уточнение полученных результатов производится в следующей последовательности. Находят средние скорости во всех участках трубопровода, числа Re. Определяют область гидравлического сопротивления, в которой работает каждый участок, и по соответствующим эмпирическим формулам (Блазиуса, Альтшуля, Шифринсона и др.) вычисляют значение коэффициента Дарси. Уточняют значения расходных характеристик участков и вновь вычисляют расходы по участкам.
Такой способ позволяет получить решение с любой требуемой точностью.
Графоаналитический способ решения задачи.
Задаются начальным приближением по скорости. Пусть, например 2 м/с по участку 1.
Скорость по участку 2 определяют из простой пропорции (равенство потерь по длине при одинаковом коэффициенте Дарси.
.
Находим расход по участкам и общий расход а также скорость на участке 0.
На каждом участке находим число Re, определяем область сопротивления и по соответствующей формуле находим коэффициент Дарси. Вычисляем потери по длине на каждом участке.
 |
На одном графике строим расходные характеристики участков 1 и 2. Эти участки соединены параллельно, суммарная характеристика строится путем суммирования расходов при одинаковом напоре (кривая 1+2). На этом же графике строим характеристику участка 0. Этот участок соединен с участком 1+2 последовательно, суммарная характеристика всего трубопровода строится суммированием напоров при одинаковом расходе (кривая ). По заданному суммарному напору
по кривой
находим расход через весь трубопровод и через участок 0. (Линия
—a—b—c—
.) Точке b соответствует напор на участках 1 и 2, точке с напор на участке 0. Пересечение горизонтали через точку b с характеристиками трубопроводов 1 и 2 определяет расходы в них. (Линии b—d—
иb—e—
.)
Рассмотренный графоаналитический способ расчета не дает точного решения, однако позволяет разработать алгоритм его нахождения с использованием средств вычислительной техники.
1 Напомним использованные сведения из математики.
Квадрат суммы . Квадрат разности
.
Постоянные выносятся за знак интеграла. Интеграл суммы (разности) есть сумма (разность) интегралов.
Табличные интегралы
Открывая новое дело, бизнесмен должен понимать, что первое время он будет работать на то, чтобы покрыть расходы. И лишь с определенного момента доходы станут выше понесенных затрат. Именно тогда бизнес проходит то, что принято называть «точка безубыточности» (ТБУ). Что это такое и как она определяется, расскажем в этой статье.
Содержание статьи
- 1 Что такое точка безубыточности
- 2 Зачем нужен расчет точки безубыточности
- 3 На каких этапах рассчитывается показатель
- 4 Кому важно знать значение ТБУ
- 5 Как рассчитать точку безубыточности: формулы и примеры
- 5.1 Какие показатели нужны для расчета
- 5.2 Формула точки безубыточности в денежном выражении
- 5.3 Формула расчета ТБУ в натуральном выражении
- 5.4 Пример расчета
- 5.5 Расчет с построением графика точки безубыточности
- 5.6 Расчет точки безубыточности в Excel
- 5.7 Расчет ТБУ по Шеремету
- 6 Интерпретация результатов расчета
- 7 Возможные проблемы при подсчете ТБУ
- 8 Какие еще показатели можно рассчитать
- 8.1 Запас финансовой прочности
- 8.2 Реальная точка безубыточности
- 8.3 Долговая точка безубыточности
- 9 Анализ и планирование ведения бизнеса на основе ТБУ
- 10 Как достичь точки безубыточности
- 11 Плюсы и минусы использования точки безубыточности
- 12 Часто задаваемые вопросы
Что такое точка безубыточности
Точка безубыточности – это точка, после которой бизнес начинает получать прибыль от производства продукции или оказания услуг. Как правило, измеряется она объемом производимой продукции, но это может быть и денежное выражение (выручка).
Любая предпринимательская деятельность сопряжена с риском, потому что сначала в дело нужно вложить определенный объем денег. Это может быть строительство мощностей с нуля, переоборудование помещений, покупка оборудования, авансирование в оборотные средства и другие траты. Но траты есть не только на старте – в течение всей деятельности компания закупает сырье, платит зарплаты, содержит помещения и несет иные виды расходов.
А из-за того, что некоторые издержки постоянные и не зависят от объема производства, есть определенное количество продукта, произвести которое просто необходимо, чтобы хотя бы не получать убытки.
То есть, по мере роста объемов производства выручка растет быстрее, чем суммарные расходы. А если у предприятия нет постоянных затрат (что едва возможно и лишь в теории), точки безубыточности у него нет – и даже с первой произведенной единицы продукции оно получает прибыль (если, конечно, цена выше средних переменных затрат).
По-другому точку безубыточности называют «нулевой точкой», «нулем бизнеса». По-английски это звучит как «break-even point». А вообще слово «точка» в данном случае имеет отношение к графику, где показана зависимость выручки и себестоимости от объема производства. То есть, это буквально точка пересечения двух прямых:
Пример графика безубыточности
Простыми словами, точка безубыточности – это то количество произведенной продукции, после которого каждая новая единица начинает приносить прибыль. В компании появляются собственные средства, полученные в результате производственной деятельности. До этого организация пользуется средствами, которые у нее были до старта производства – это деньги учредителей, заемные или прочие привлеченные средства.
Зачем нужен расчет точки безубыточности
Этот показатель позволяет определить, сколько продукции нужно выпустить и реализовать, чтобы покрыть произведенные расходы. Его анализ помогает понять, что можно сделать, чтобы выйти на прибыль: увеличить продажи, сократить издержки, отказаться от производства данной продукции и т. п.
Основная цель расчета ТБУ – видение перспектив развития бизнеса. Показатель дает возможность сориентироваться, сколько времени нужно предприятию, чтобы рассчитаться с долгами, которые образуются в момент запуска производства, а также когда можно рассчитывать на получение собственной прибыли.
С помощью ТБУ можно сориентироваться, сколько должно поступать средств от заказчиков, покупателей, чтобы предприятие «держалось на плаву», то есть работало без убытков.
Расчет точки дает важную информацию для руководства предприятия:
- минимальную цену продукции, товара, стоимость услуги, ниже которой продажи становятся нецелесообразными;
- насколько безубыточный объем продукции вообще можно произвести и позволяют ли это производственные мощности;
- точный расчет постоянных затрат покажет, на чем можно сэкономить и сместить точку безубыточности в меньшую сторону.
Соответственно, метод анализа точки безубыточности используется для определения минимального объема производства, однако необходимые для ее расчета данные важны в различных ситуациях.
На каких этапах рассчитывается показатель
Первоначально ТБУ рассчитывается при запуске нового проекта, чтобы собственники могли понять, когда появится первый рубль прибыли, сколько средств и времени на это понадобится. Расчет производится также в течение всего периода деятельности предприятия, чтобы планировать текущие расходы.
Вообще же расчет точки безубыточности нужен в следующих ситуациях:
- при запуске нового проекта, чтобы понять, когда он перейдет на самоокупаемость;
- для определения цен на производимую продукцию, покупные товары, оказываемые услуги;
- для анализа финансового состояния фирмы (есть ли у нее запас финансовой прочности);
- для анализа влияния цены на финансовый результат.
Расчет ТБУ должен быть организован на предприятии постоянно. Если не проводится анализ, то есть вероятность, что продажи приносят убыток, а излишнее количество произведенной продукции залеживается на складах. Поэтому важно учитывать в расчете не просто произведенную, а еще и реализованную продукцию.
Точка безубыточности также рассчитывается, когда планируется продать компанию, при разработке франшизы, когда предприятие попадает в кризисную ситуацию, из которой нужно найти выход.
Кому важно знать значение ТБУ
На предприятиях точку безубыточности в своих подсчетах могут использовать разные подразделения:
- коммерческий директор – при планировании продаж;
- производственный отдел – для составления производственного плана;
- отдел продаж – для оценки конкурентоспособности бизнеса с учетом актуальных цен;
- финансовый отдел – для проведения анализа финансовой устойчивости;
- высшее руководство и собственник – чтобы понять, насколько целесообразно продолжать производственную деятельность.
Но, вместе с тем, ТБУ важна и для внешних участников. Так, банк должен ее знать, определяя платежеспособность предприятия при выдаче кредита, а инвесторы – перед принятием решения об инвестировании в проект.
Например, компания имеет обособленное подразделение, занимающееся общепитом. Есть дополнительное помещение, в котором можно поставить столики для обслуживания клиентов. В этом случае придется нанимать дополнительный персонал и закупать больше продуктов. Задача экономиста – рассчитать, сколько компания может выделить для этого денег, чтобы затраты не стали прямыми убытками.
Как рассчитать точку безубыточности: формулы и примеры
ТБУ определяется исходя из постоянных и переменных затрат. Задача – найти, сколько нужно получить дохода, чтобы их покрыть. Чтобы посчитать точку безубыточности, можно использовать несколько формул, а для самого расчета берутся планируемые или фактические показатели.
Какие показатели нужны для расчета
Прежде всего потребуются данные о предстоящих расходах и предполагаемой выручке, а также в расчет берутся запланированные цены (или фактические). Какие показатели нужно иметь до расчета:
| Показатель | Что в него входит |
|---|---|
| Постоянные расходы | Затраты, не зависящие от объема производства и количества продаж. Сюда относятся: заработная плата управленческого персонала, содержание офиса, канцелярские принадлежности, затраты на оргтехнику |
| Переменные расходы | Расходы на товары для продажи, сырье, материалы, упаковку, сдельная зарплата тех, кто участвует в производстве, содержание основных средств, участвующих в производстве |
| Переменные издержки из расчета на единицу продукции | Это – расходы, указанные в предыдущем пункте, разделенные на количество произведенной продукции |
| Выручка | Деньги, полученные от покупателей и заказчиков |
| Цена единицы продукции | Стоимость единицы изделия, по которой ее приобретает потребитель |
| Количество произведенной продукции | Это – общий объем производства за определенный период |
| Маржа | Выручка без учета переменных расходов |
Формула точки безубыточности в денежном выражении
ТБУ может рассчитываться в денежном выражении и в натуральном. В денежном выражении формула точки безубыточности покажет минимальную сумму выручки, достаточную для того, чтобы предприятие работало не в убыток:
- ТБУ = (Выручка * Постоянные расходы) / (Выручка – Переменные расходы)
В знаменателе представлен маржинальный доход – то есть, рассчитывать ТБУ можно как для предприятия в целом, так и по одному виду продукции.
Но когда в расчет включено несколько видов продукции, то проще применять понятие «коэффициент маржинального дохода»:
- Коэффициент маржинального дохода = Маржинальный доход / Выручка
Отсюда формула точки безубыточности будет выглядеть так:
- ТБУ = Постоянные расходы / Коэффициент маржинального дохода
Полученная цифра даст понимание – до какого уровня нужно нарастить выручку, чтобы предприятие вышло в прибыль. Справедливо и обратное – до какого размера допустимо снизить выручку, чтобы не начать получать убыток.
Формула расчета ТБУ в натуральном выражении
Гораздо более наглядным будет расчет точки безубыточности в единицах продукции. Если требуется рассчитать, сколько нужно выпустить товара для того, чтобы предприятие вышло «в ноль» и перестало приносить убытки, применяется формула расчета точки безубыточности в натуральном выражении:
- ТБУ = Постоянные расходы / Маржинальный доход
Если значение маржинального дохода неизвестно, то найти точку безубыточности в натуральном выражении можно по формуле:
- ТБУ = Постоянные расходы / (Цена единицы продукции – Переменные затраты на единицу продукции)
Другими словами, это объем производства, при котором доходы за минусом переменных расходов полностью покрывают постоянные расходы.
Пример расчета
Разберем расчет ТБУ на конкретном примере. Компания оказывает образовательные услуги, основные данные для расчета такие:
- постоянные расходы – 1 048 000 рублей;
- переменные расходы (на одного учащегося) – 1 100 рублей;
- цена обучения одного человека – 9 000 рублей.
Точка безубыточности в натуральном выражении составит:
- ТБУ = 1 048 000 / (9 000 – 1 100) = 133 учащихся
То есть, чтобы выйти в ноль и покрыть постоянные расходы, нужно за период (год) обучать не менее 133-х человек. А если принять на обучение, например, 134-го ученика, он принесет компании прибыль в размере маржинального дохода – это 7 900 рублей.
В денежном выражении это будет равно:
- ТБУ = (9 000 * 1 048 000) / (9 000 – 1 100) = 1 193 924 рубля
Но так как нельзя принять на обучение меньше одного ученика, то стоит округлить расчет:
- ТБУ = 133 ученика * 9 000 рублей = 1 197 000 рублей.
Это – минимальный размер выручки, которую необходимо получать, чтобы компания работала безубыточно.
Если предположить, что в группу было набрано 150 учеников, то, исходя из стоимости обучения, выручка составит 1 350 000 рублей. Это больше ТБУ, что позволяет компании получить прибыль.
Расчет с построением графика точки безубыточности
Так как изначально понятие точки безубыточности имеет отношение к графику, то это будет самый наглядный вариант расчета. Для построения нужно:
- на горизонтальной оси отложить объем продаж от нуля до максимально возможного;
- на вертикальной оси отложить понесенные затраты и выручку от продажи.
Затем по нескольким точкам нужно провести линии кривых выручки и суммарных затрат. В точке пересечения и будет точка безубыточности – в натуральном измерении по горизонтальной оси и в денежном – по вертикальной.
Выглядит это так (по примеру из прошлого раздела):
Построить график безубыточности проще всего в Excel – для этого достаточно рассчитать данные по нескольким вариантам объема производства, главное – чтобы в диапазон попала и точка безубыточности. Выглядит это примерно так:
Затем по этим данным легко можно построить график. Но также в Excel или в Google-таблицах можно рассчитать ТБУ и математически.
Расчет точки безубыточности в Excel
Хотя графический расчет с подбором данных по разным объемам производства интуитивно понятный, однако более точно и просто посчитать ТБУ можно и другими способами.
Ввод формул
Для начала нужно на лист с расчетом ввести первоначальные данные – цену единицы продукции, переменные и постоянные затраты. Используем данные из прошлого примера.
Дальше нужно создать базу для последующего расчета, подготовив таблицу с нужными формулами. В нее нужно забить данные для расчета валовых затрат, выручки, маржинального дохода и чистой прибыли:
Затем – проставить ссылки и формулы в нужных местах:
Важно: чтобы «зафиксировать» ссылку на ячейку при протягивании, нужно перед буквой и цифрой поставить знак «$». И проще всего сделать это, нажав F4 при наведении на ссылку.
Построение графика
Дальше нужно просчитать показатели по разным вариантам объема производства. Достаточно ввести только объемы и протянуть все формулы – расчет будет произведен автоматически:
Как видно, точка безубыточности – где-то между 130 и 140. Заменим объемы производства на этот диапазон и повторим расчет:
Таким образом, в натуральном выражении точка безубыточности – 133 человека, как и показал более ранний расчет.
Шаблон для своего расчета можно взять здесь:
 |
«Шаблон для расчета точки безубыточности и построения графика безубыточности» Нужно подставить собственные значения в выделенные желтым ячейки |
Чтобы повторить расчет, достаточно ввести свои данные по цене, постоянным и переменным расходам, а также примерно предположить свои объемы производства. Изменяемые ячейки выделены желтым цветом. График строится на второй вкладке в файле.
Расчет ТБУ по Шеремету
В расчете точки безубыточности есть разные теории и концепции, но самую полную схему предложил российский автор А. Д. Шеремет.
Он предлагает использовать такой алгоритм:
- сначала собрать необходимые для анализа данные – плановый и фактический объем производства и продаж, фактическую прибыль или убыток;
- рассчитать постоянные и переменные расходы, а из них – определить зону финансовой безопасности и точку безубыточности;
- с учетом всего этого – определить объем производства, который обеспечит устойчивое состояние предприятию.
То есть, суть этой схемы – в том, чтобы увязать расчет ТБУ с показателями финансовой устойчивости. Ведь, по сути, точка – это нижняя граница финансовой устойчивости, при которой может существовать предприятие. И с учетом этих данных нужно дальше использовать возможности по расширению зоны финансовой безопасности.
Интерпретация результатов расчета
Главное, что показывает точка безубыточности, – это при каком объеме продаж появляется прибыль. Соответственно:
- если фактический объем продаж оказывается ниже показателя ТБУ, то это означает, что компания работает в убыток;
- важно, чтобы безубыточного объема предприятие достигало в середине периода, а не в конце – иначе при малейшем сбое оно уйдет в убыток.
Когда предприятие выпускает на рынок новый продукт, не следует увеличивать постоянные затраты до тех пор, пока не будет определен уровень спроса на него. Иначе продукция будет залеживаться на складах, при этом издержки возрастут, а выручка нет.
Возможные проблемы при подсчете ТБУ
Существуют ситуации, когда возникают сложности при расчете показателя:
- когда снижаются цены на продукцию, предоставляются бонусы и скидки – это означает, что график выручки не будет прямой, что затрудняет расчет;
- когда нет стабильных цен на сырье и материалы – не получится рассчитать точные суммы расходов;
- иногда сложно разграничить состав затрат, какие следует отнести к постоянным, а какие – к переменным (особенно, если есть условно-постоянные расходы);
- новым компаниям бывает сложно установить эффективную систему оплаты труда (выбрать повременную или сдельную).
Кроме того, при проведении экономических расчетов сложно учесть все возможные непредвиденные расходы.
Какие еще показатели можно рассчитать
Для стабильной работы компании нужно учитывать не только настоящее состояние дел, но и возможные внешние перемены, которые негативно скажутся на результатах деятельности предприятия. Например, повысятся ставки налогов или стоимость энергоносителей, и все прошлые расчеты будут неактуальными. Поэтому дополнительно рассчитываются иные показатели.
Запас финансовой прочности
Это величина, которая показывает, насколько фактический объем производства и продаж превосходит тот, который соответствует точке безубыточности. Она рассчитывается по формуле:
- ЗФП = (Выручка – ТБУ в денежном выражении) / Выручка
То есть, результат – это коэффициент, показывающий долю «свободных» средств от общей выручки.
Запас финансовой прочности на графике
Рассчитаем запас финансовой прочности по прошлому примеру:
- ЗФП = (1 350 000 – 1 197 000) / 1 350 000 = 0,11, или 11%
Такое значение считается низким, а нормальный ЗФП начинается от 0,5 (50%).
Реальная точка безубыточности
В расчет берутся затраты текущего периода, не учитывая те, что накопились в виде долгов с момента существования предприятия. В расчет берутся показатели не только тех расходов, которые заложены в себестоимость, но и те, которые оплачиваются из прибыли.
Формула имеет вид:
- Реальная точка безубыточности = (Постоянные затраты + Расходы, оплачиваемые из прибыли) / (1 – Доля переменных затрат)
При расчете ТБУ экономисты зачастую забывают учитывать, к примеру, налог на прибыль. В этом же случае в числителе суммируются постоянные расходы и этот налог. В знаменателе из единицы вычитается доля переменных расходов, равная сумме переменных расходов, разделенной на сумму выручки.
Долговая точка безубыточности
Компания может накапливать долги в процессе деятельности. Для того чтобы реально посчитать ТБУ, недостаточно ориентироваться на текущие расходы, но следует учесть и имеющиеся долговые обязательства. Для этого рассчитывается долговая точка безубыточности:
- Долговая точка безубыточности = Постоянные платежи / (1 – Доля переменных затрат),
- где постоянные платежи – это сумма постоянных расходов, платежей из прибыли и расходов в счет погашения долгов.
Долговая точка безубыточности рассчитывается по аналогии с предыдущим показателем – только в числителе добавляется сумма долга, накопившаяся за предыдущие периоды.
Анализ и планирование ведения бизнеса на основе ТБУ
Основной показатель, который рассчитывается на основе ТБУ, – это величина выручки, которая должна быть получена для безубыточной работы. Если эта величина не достигается, то проводится анализ отдельных показателей:
- объема продаж – возможно, стоит изучить варианты с его наращиванием;
- цены товара – если она неконкурентоспособна, ее стоит снизить, а если она занижена – увеличить;
- постоянных и переменных издержек – найти резервы для их снижения.
Если на издержки, связанные с производством единицы продукции, повлиять сложно, то постоянные издержки можно пересмотреть и уменьшить.
Также анализу подвергается цена продукции. Иногда целесообразно ее снизить, чтобы увеличить объемы продаж. В этом случае ТБУ достигается со сдвигом по времени, то есть прибыль меньше благодаря снижению цены, но объемы продаж увеличатся за счет привлечения большего количества покупателей.
Как достичь точки безубыточности
Чтобы предприятие начало работать безубыточно, важно составить план производства и продаж таким образом, чтобы направление бизнеса не оказалось заранее убыточным.
Делается это поэтапно:
- проводится анализ с целью выявления возможности снизить себестоимость и повысить уровень продаж;
- составляется прогноз цен, по которым будет продаваться продукция, оказываться услуги;
- составляется план продаж;
- рассчитывается ТБУ исходя из рассчитанных плановых показателей.
Если взять пример по набору учеников на курсы, который был приведен ранее, то нужно оценить возможность набрать на обучение определенное количество студентов.
Если заранее понятно, что сделать это не получится, то следует задуматься о перенаправлении деятельности компании.
Плюсы и минусы использования точки безубыточности
Расчет ТБУ применяется в экономическом анализе достаточно широко, однако у него есть не только сильные, но и слабые стороны:
Так что использовать показатель ТБУ можно, но только в комплексе с другими экономическими индикаторами.
Часто задаваемые вопросы
Что делать, если не удается достичь рассчитанного по ТБУ объема продаж?
Этот вопрос проще решается в небольших компаниях, занимающихся торговлей или оказанием услуг. Например, некоторые торговые точки проводят распродажу, увеличивая сумму выручки, но теряя при этом показатель маржинальности.
Чтобы нужно сделать, чтобы быстрее достичь ТБУ?
Для этого существуют два способа: снижение издержек и повышение цены. Первый вариант может привести к ухудшению качества, например, если сократить количество работников или уменьшить зарплату. Второй вариант сработает в том случае, если в данном сегменте слабая конкуренция.
Что делать, если постоянные расходы – на самом деле условно-постоянные?
В этом случае нужно рассчитывать сумму переменных и постоянных расходов при каждом возможном объеме производства.