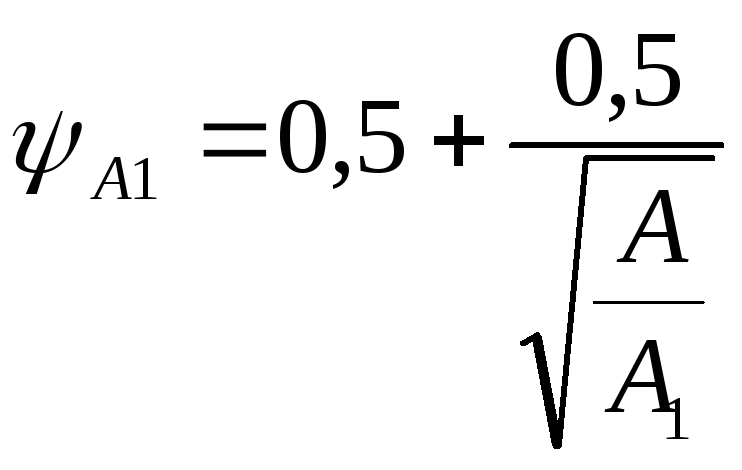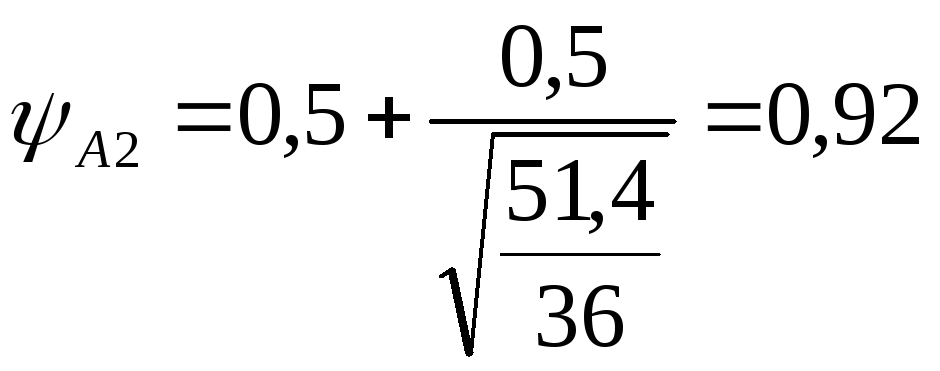Как определить расчетный пролет балки (плиты, перемычки)

При расчете любого изгибаемого элемента, будь то плита, балка или перемычка, прежде всего, следует определить расчетный пролет. При переводе объемных конструкций в плоскую расчетную схему очень важно задаться правильными размерами элементов. Ведь в расчетной схеме все просто: балка – это стержень, а опора – точка. На самом же деле опора имеет свой размер – глубину опирания, и балка не зависает на краях стены (от точки до точки), часть ее работает в пролете, но часть – «отдыхает» на опорах.
Создавая расчетную схему, мы сталкиваемся с двумя величинами: реальной длиной балки и расстоянием в свету между опорами. Какую из этих величин следует принять за расчетную? Если брать полную длину балки, это будет неверно, т.к. все-таки та ее часть, которая лежит на опоре, не подвержена таким напряжениям, как в пролете. Но брать за расчетную длину расстояние между опорами можно только в отдельных случаях, ниже мы рассмотрим, что да как.
Далеко не всегда расчетная длина балки совпадает с пролетом в свету между опорами.
Есть два варианта размера расчетного пролета.
1) Если опирание жесткое, т.е. балка защемлена на опоре (либо является частью монолитной конструкции), то расчетный пролет L0 равен расстоянию в свету между опорами.
2) Если же опирание шарнирное, то расчетный пролет всегда больше этого расстояния.
Рассмотрим глубже определение расчетного пролета при шарнирном опирании элемента. Во-первых, следует четко определиться с требованиями глубины опирания шарнирных элементов (поможет статья «В чем разница между шарнирным опиранием и жестким защемлением»). Если вы делаете расчет шарнирно опираемой железобетонной балки (плиты и т.п.), глубина ее опирания должна быть не более высоты сечения – иначе, это будет уже защемление или переходное состояние между шарниром и защемлением, а там и расчет другой, и длина расчетного пролета – согласно пункту 1. Т.е. если вы плиту толщиной 200 мм опираете на 450 мм с каждой стороны, то пользоваться нижеприведенным расчетом не следует.
Для ленивых во многих учебниках есть правило: L0 = 1.05L, т.е. берем расстояние между опорами в свету и умножаем на 1,05.
Но сейчас мы постараемся понять, в чем же суть увеличения расчетного пролета, и как поточнее его определить.
При расчете балки мы привыкли получать реакции на опоре в виде сосредоточенных сил.
Но если рассмотреть точнее, нагрузка от балки на опору передается в виде распределенной нагрузки, причем даже не равномерно распределенной: максимальная ее величина расположена у края опоры, а к концу балки она сходит на нет.
По общепринятым правилам перевода распределенной нагрузки в сосредоточенную, положение сосредоточенной нагрузки будет в центре тяжести треугольника, т.е. на расстоянии 1/3 от края опоры. В этом же месте будет расположена искомая реакция. А расстояние между этими реакциями будет равно расчетному пролету.
Таким образом, если глубина опирания балки с одной стороны равна А, а с другой стороны В, то расчетный пролет мы найдем по формуле:
L0 = L + A/3 + B/3.
Если же глубина опирания с двух сторон одинаковая и равна А, то
L0 = L + 2A/3.
Такое увеличение расчетного пролета по отношению к реальному (в районе 5%) дает определенный запас прочности и приближает нас к реальному положению вещей – ведь длина балки может быть разной, а глубина опирания обычно одинаковая. И пять процентов при трехметровом пролете значительно отличается от пяти процентов при восьмиметровом.
Надеюсь, статья оказалась вам полезной.
Номинальная
длина второстепенных балок 9,4 м. Расстояние
между осями второстепенных балок 1850
мм. Предварительные размеры второстепенной
балки hxb
= 65×30 см. Размеры главной балки принимаем
h∙b
=80×40 см.
Расчетной
схемой второстепенной балки является
неразрезная многопролетная балка
таврового сечения с высотой равной h
= 65 см. Изгибающие моменты от расчетных
и нормативных нагрузок вычисляются в
соответствии с расчетной схемой и
заданными нагрузками. Усилия определяются
с учетом их перераспределения вследствие
возникновения и развития пластических
деформаций.
Расчетный пролет
второстепенной балки в крайних пролетах
равен расстоянию между боковой
поверхностью главной балки и серединой
площадки опирания балки на стены, в
средних пролетах — расстоянию в свету
между главными балками. Приняв глубину
заделки балки 200 мм, получим расчетную
длину первого пролета:
l01
= 9400 — 200/2 — 400/2 = 9100 мм
(9,1
м).
Расчетная длина
средних пролетов:
l0
= 9400 – 2∙400/2 = 9000 мм
(9,00 м).
Нагрузка
на плиты, ригели, колонны, стены и
фундаменты может снижаться в зависимости
от отношения грузовой площади к общей
площади.
Поскольку
балка воспринимает нагрузку от одного
перекрытия, коэффициент ψА
вычисляется по формуле (при А > А1=
36 м2)
Общая
длина расчетной грузовой полосы балки
равна расстоянию между внутренними
гранями поперечных стен, 28200 – 2∙200 = 27
800 мм. Ширина грузовой полосы равна 1,85
м.
Грузовая площадь
балки средних рядов равна
А
= 1,85×27,8 = 51,4 м2
> А2
= 36 м2,
следовательно, коэффициент сочетаний
ψА
необходимо учитывать:
Расчетная погонная
нагрузка от собственного веса балки
(без учета плиты)
gб
=h∙b1∙p∙γf∙γn∙ψA=
0,59∙0,3∙1,0∙25∙1,1∙0,95∙0,92 = 4,3 кН/м.
Полная
расчетная нагрузка на один погонный
метр балки с учетом коэффициента по
назначению здания γf
= 0,95 и коэффициента сочетаний ψА
= 0,92.
q=1,85∙16,54∙0,95∙0,92+4,3=
31,04 кН/м.
Расчетная временная
эквивалентная нагрузка
v
= 1,85∙13,8∙0,95∙0,92 = 22,3 кН/м.
Расчетная постоянная
нагрузка
G
= 1,85∙2,737∙0,95∙0,92+4,3 = 8,7 кН/м.
2.3.2. Определение усилий в балке
Изгибающие
моменты в средних пролетах и на средних
опорах от полной расчетной нагрузки
q
= 31,04 кН/м:
Изгибающие
моменты на крайней опоре от полной
расчетной нагрузки q
= 31,04 кН/м:
Изгибающие
моменты в крайнем пролете от полной
расчетной нагрузки q
= 31,04 кН/м:
Расчетные
поперечные силы от полной расчетной
нагрузки q
= 31,04 кН/м.
На
крайней опоре Q01=
0,4qlo1
= 0,4∙31,04∙9,1=113,0 кН.
На
первой промежуточной опоре слева Qв,л=
0,6ql0l=
0,6∙31,04∙9,1 =169,5 кН.
На
первой промежуточной опоре справа Qв,np
= 0,5ql0
= 0,5∙31,04∙9,1 = 141,23 кН.
На
остальных опорах справа и слева Q=0,5ql0=
0,5∙31,04∙9,0 = 139,7 кН.
2.3.3. Прочность нормальных сечений (расчет рабочей продольной арматуры)
Необходимо вычислить
расчетную ширину полки второстепенной
балки:
• с≤l/6
= 7,4/6=1,23м,
• так
как h’f=
6 см > 0,1∙h=
0,1∙65 = 6,5 см, с<0,5l0
= а/2 = 155/2 =77,5 см,
а — расстояние в
свету между второстепенными балками.
Таким образом,
ширина полки, вводимая в расчет, составит
b’f=b+
2с = 30 + 2∙77,5 =185 см = 1,85 м.
Продольная
арматура подбирается на действие
пролетных и опорных моментов как для
балки таврового сечения с полкой в
сжатой зоне и размерами h
x
b’f
= 65 см х185 см. Арматура класса А400, Rs=
355 МПа (355∙103
кН/м2),
а = 30 мм.
Соседние файлы в папке Курсовой проект
- #
- #
22.05.2017724.45 Кб66ЖБК СВЕТА(4курс 2 семестр).dwg
Как определить расчетный пролет балки
При расчете любого изгибаемого элемента, будь то плита, балка или перемычка, прежде всего, следует определить расчетный пролет. При переводе объемных конструкций в плоскую расчетную схему очень важно задаться правильными размерами элементов. Ведь в расчетной схеме все просто: балка – это стержень, а опора – точка. На самом же деле опора имеет свой размер – глубину опирания, и балка не зависает на краях стены (от точки до точки), часть ее работает в пролете, но часть – «отдыхает» на опорах.
Создавая расчетную схему, мы сталкиваемся с двумя величинами: реальной длиной балки и расстоянием в свету между опорами. Какую из этих величин следует принять за расчетную? Если брать полную длину балки, это будет неверно, т.к. все-таки та ее часть, которая лежит на опоре, не подвержена таким напряжениям, как в пролете. Но брать за расчетную длину расстояние между опорами можно только в отдельных случаях, ниже мы рассмотрим, что да как, так же смотрите расчет элементов строительных конструкций.
Далеко не всегда расчетная длина балки совпадает с пролетом в свету между опорами.
Есть два варианта размера расчетного пролета. Если опирание жесткое, т.е. балка защемлена на опоре (либо является частью монолитной конструкции), то расчетный пролет L0 равен расстоянию в свету между опорами. Если же опирание шарнирное, то расчетный пролет всегда больше этого расстояния.
Рассмотрим глубже определение расчетного пролета при шарнирном опирании элемента. Во-первых, следует четко определиться с требованиями глубины опирания шарнирных элементов (поможет статья «В чем разница между шарнирным опиранием и жестким защемлением»). Если вы делаете расчет шарнирно опираемой железобетонной балки (плиты и т.п.), глубина ее опирания должна быть не более высоты сечения – иначе, это будет уже защемление или переходное состояние между шарниром и защемлением, а там и расчет другой, и длина расчетного пролета – согласно пункту 1. Т.е. если вы плиту толщиной 200 мм опираете на 450 мм с каждой стороны, то пользоваться нижеприведенным расчетом не следует.
Но сейчас мы постараемся понять, в чем же суть увеличения расчетного пролета, и как поточнее его определить.
При расчете балки мы привыкли получать реакции на опоре в виде сосредоточенных сил.