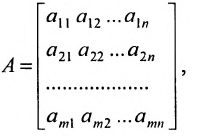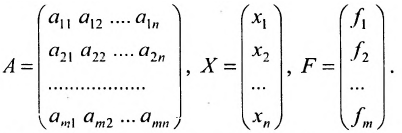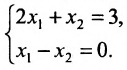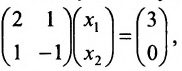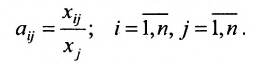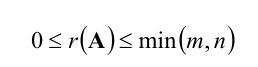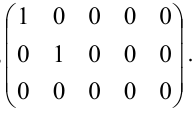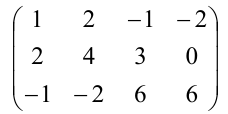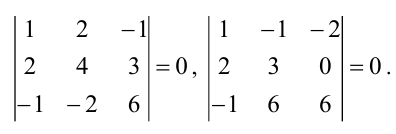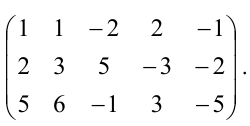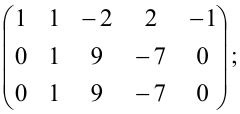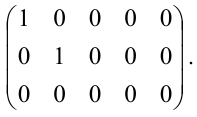Ранг матрицы
4 раздела
от теории до практики
примеров
Примеры решения задач
видео
Примеры решения задач
-
Определение ранга матрицы.
Начать изучение
-
Основные теоремы.
Начать изучение
-
Ранг произведения матриц.
Начать изучение
-
Нахождение ранга матрицы.
Начать изучение
Определение ранга матрицы.
Определение
Пусть в матрице A существует линейно независимая система из r строк, и нет линейно независимой системы из большего числа строк. Тогда мы будем говорить, что строчный ранг матрицы A равен r. Нулевая матрица не содержит никакой линейно независимой системы строк, и ее строчный ранг по определению равен нулю.
Аналогично определяется столбцовый ранг матрицы. Он равен r_{1}, если есть линейно независимая система из r_{1} столбцов, и нет линейно независимой системы из большего числа столбцов. Столбцовый ранг нулевой матрицы по определению равен нулю.
Утверждение 1.
Система из r строк линейно независима тогда и только тогда, когда в этих строках найдется невырожденная подматрица порядка r.
Доказательство.
1^{circ}. Пусть r строк линейно зависимы. Рассмотрим произвольную подматрицу порядка r, расположенную в этих строках. Если строки линейно зависимы, то также линейно зависимы (с теми же коэффициентами) и отрезки этих строк, составляющие подматрицу, и подматрица является вырожденной.
2^{circ}. Обратное утверждение докажем по индукции. Одна строка линейно независима, если она не нулевая. В этом случае она содержит ненулевой элемент, составляющий невырожденную подматрицу порядка 1.
Пусть теперь даны r линейно независимых строк. Первые r-1 из них также линейно независимы, и по предположению индукции содержат невырожденную подматрицу порядка r-1. Пусть j_{1},…, j_{r-1} — номера столбцов этой подматрицы. Рассмотрим отрезок r-й строки, расположенный под подматрицей, то есть составленный из элементов с номерами j_{1},…, j_{r-1}. По следствию из ранее доказанной теоремы этот отрезок раскладывается в линейную комбинацию строк подматрицы. Коэффициенты этой линейной комбинации обозначим alpha_{1},…, alpha_{r-1}.
Теперь будем рассматривать полные строки. Вычтем из последней строки линейную комбинацию предыдущих с теми же коэффициентами alpha_{1},…, alpha_{r-1}. Это обратит в нуль j_{1},…, j_{r-1}-й элементы r-й строки, но не всю строку, так как строки линейно независимы. Таким образом, в преобразованной r-й строке есть ненулевой элемент a_{j}^{r}, и его номер j отличен от номеров j_{1},…, j_{r-1}.
В преобразованной матрице рассмотрим столбцы, имеющие номера j_{1},…, j_{r-1}, j. (Мы для удобства пишем j на последнем месте, хотя в действительности столбцы располагаются в порядке возрастания номеров.) Легко видеть, что эти столбцы линейно независимы. Действительно, пусть tag{1} alpha_{1}boldsymbol{a}_{j_{1}}+…+alpha_{r-1}boldsymbol{a}_{j_{r-1}}+alpha boldsymbol{a}_{j}=boldsymbol{o} их нулевая линейная комбинация. Тогда для последних элементов столбцов alpha_{1}0+…+alpha_{r-1}0+alpha a_{j}^{r}=0. Так как a_{j}^{r} neq 0, отсюда следует alpha=0, и мы получаем alpha_{1}boldsymbol{a}_{j_{1}}+…+alpha_{r-1}boldsymbol{a}_{j_{r-1}}=boldsymbol{o}. Если бы среди коэффициентов этой линейной комбинации были отличные от нуля, то столбцы с номерами j_{1},…, j_{r-1} были бы линейно зависимы. Это противоречило бы тому, что исходная подматрица порядка n-1 невырождена. Таким образом, все коэффициенты в (1) равны нулю, и столбцы с номерами j_{1},…, j_{r-1}, j линейно независимы. Отсюда следует, что составленная ими подматрица порядка r невырождена.
Невырождена соответствующая подматрица и в непреобразованной матрице, так как элементарными преобразованиями мы превратили ее в невырожденную матрицу. Это заканчивает доказательство.
Определение
В матрице A размеров m times n подматрица порядка r называется базисной, если она невырождена, а все квадратные подматрицы большего порядка, если они существуют, вырождены.
Столбцы и строки матрицы A, на пересечении которых стоит базисная подматрица, называются базисными столбцами и строками A.
В силу утверждения 1 базисные столбцы и строки линейно независимы.
Определение
Рангом матрицы называется порядок базисной подматрицы или, иначе, самый большой порядок, для которого существуют невырожденные подматрицы. Ранг нулевой матрицы по определению считают нулем.
Отметим два очевидных свойства ранга.
Свойство 1
bullet Ранг матрицы не меняется при транспонировании, так как при транспонировании матрицы все ее подматрицы транспонируются, и при этом невырожденные подматрицы остаются невырожденными, а вырожденные — вырожденными.
Свойство 2
bullet Если A’ — подматрица матрицы A, то ранг A’ не превосходит ранга A, так как любая невырожденная подматрица, входящая в A’, входит и в A.
Основные теоремы.
Из утверждения 1 прямо следует теорема о ранге матрицы:
Теорема 1.
Ранг любой матрицы равен ее строчному рангу и ее столбцовому рангу.
Доказательство.
Действительно, если строчный ранг A равен r, то в A найдется линейно независимая система из r строк, а значит, и невырожденная подматрица порядка r. Если при этом есть p > r различных строк A, то они линейно зависимы, и любая подматрица порядка p в них вырождена. Столбцовый ранг равен строчному рангу A^{T}, значит, и рангу A^{T}, а потому — рангу A.
Таким образом, мы видим, что все три определения на самом деле определяют одно и то же число, и впредь не будем их различать. Будем говорить ранг матрицы и обозначать его mathbf{Rg},A.
Из теоремы о ранге матрицы мы получаем теорему о базисном миноре, на которую существенно опирается все дальнейшее изложение. Слово “минор” означает “детерминант подматрицы”. В частности, базисный минор — это детерминант базисной подматрицы. О детерминантах будет речь в следующем параграфе, а здесь это слово можно воспринимать просто как составную часть названия теоремы.
Теорема 2.
Каждый столбец матрицы раскладывается в линейную комбинацию ее базисных столбцов.
Доказательство.
Каждый из базисных столбцов, разумеется, раскладывается по базисным: для этого достаточно взять его самого с коэффициентом 1, а остальные с нулевыми коэффициентами.
Пусть теперь boldsymbol{a}_{j} — не базисный столбец. Базисные столбцы обозначим через boldsymbol{a}_{i_{1}},…, boldsymbol{a}_{i_{r}}. По теореме о ранге матрицы любые r+1 столбцов линейно зависимы, и найдутся такие коэффициенты, что alpha_{1}boldsymbol{a}_{i_{1}}+…+alpha_{r}boldsymbol{a}_{i_{r}}+alpha boldsymbol{a}_{j}=boldsymbol{o}. При этом мы можем быть уверены, что alpha neq 0, так как иначе это равенство означало бы линейную зависимость базисных столбцов. Деля на alpha, мы получаем нужное нам разложение boldsymbol{a}_{j}=-alpha^{-1}alpha_{1}boldsymbol{a}_{i_{1}}-…-alpha^{-1}alpha_{r}boldsymbol{a}_{i_{r}}.
Следствие.
Каждая строка матрицы раскладывается по ее базисным строкам.
Ранг произведения матриц.
Согласно ранее доказанным утверждениям элементарные преобразования не меняют столбцового ранга. Таким образом, справедливо
Утверждение 2.
Ранг матрицы не меняется при элементарных преобразованиях.
Отсюда и из ранее доказанного утверждения прямо следует
Утверждение 3.
Если матрица A невырождена и определены произведения AB и CA, то mathbf{Rg},AB=mathbf{Rg},B и mathbf{Rg},CA=mathbf{Rg},C.
В общем случае имеет место
Утверждение 4.
Ранг произведения двух матриц не превосходит рангов сомножителей.
Доказательство.
Пусть определено произведение AB. Рассмотрим матрицу D, составленную из всех столбцов матриц A и AB. Так как AB — подматрица, mathbf{Rg},AB leq mathbf{Rg},D.
По утверждению о том, что столбцы AB — линейные комбинации столбцов A. Легко видеть, что приписывание к матрице линейной комбинации ее столбцов не меняет ранга матрицы. Действительно, не меняя ранга, элементарными преобразованиями столбцов мы можем обратить приписанный столбец в нулевой, а добавление нулевого столбца не создает новых невырожденных подматриц. Отсюда следует, что mathbf{Rg},D=mathbf{Rg},A. Итак, mathbf{Rg},AB leqmathbf{Rg},A.
Аналогично доказывается, что mathbf{Rg},AB leqmathbf{Rg},B. Для этого надо составить матрицу D’ из всех строк матриц B и AB.
Нахождение ранга матрицы.
Определение
Матрица размеров m times n называется упрощенной (или имеет упрощенный вид), если некоторые r ее столбцов являются первыми r столбцами единичной матрицы порядка m и, в случае m > r, ее последние (m-r) строк — нулевые.
Утверждение 5.
Каждую матрицу с помощью элементарных преобразований строк можно превратить в упрощенную матрицу.
Доказательство.
Если матрица нулевая, то она уже упрощенная (r=0). В общем случае применим метод Гаусса. В ранее доказанном утверждении мы превратили квадратную невырожденную матрицу элементарными преобразованиями строк в единичную матрицу. Это — частный случай доказываемого утверждения. То обстоятельство, что матрица невырождена, использовалось, когда мы в очередной строке преобразованной матрицы находили ненулевой элемент.
В общем случае ненулевой элемент может не найтись, то есть очередная строка окажется нулевой. Все встречающиеся нулевые строки будем переставлять на последние места и будем продолжать преобразования так, как при доказательстве утверждения, на которое ссылались выше.
Преобразования закончатся, когда либо будут исчерпаны все строки, либо останутся только нулевые строки. При этом не существенно, квадратная матрица или нет. Конечно, может случиться, что некоторые столбцы не будут превращены в столбцы единичной матрицы, но это нам и не требуется. Пусть всего в столбцы единичной матрицы преобразовано r столбцов. Если остались строки ниже r-й, они нулевые, иначе преобразования можно продолжить. Предложение доказано.
Пусть мы привели матрицу A к упрощенному виду, и в упрощенной матрице A’, столбцы boldsymbol{a}_{j_{1}},…, boldsymbol{a}_{j_{r}} (j_{1} <…< j_{r}) превращены в столбцы единичной матрицы boldsymbol{e}_{1},…, boldsymbol{e}_{r}. Можно считать, что boldsymbol{a}_{j_{k}} rightarrow boldsymbol{e}_{k} для всех k=1,…, r. Это достигается перестановкой строк.
Рассмотрим упрощенную матрицу A’. В ней есть невырожденная подматрица порядка r, а невырожденных подматриц большего порядка, очевидно, нет. Следовательно, ранг матрицы равен r, а подматрица базисная.
Из этого следует, что mathbf{Rg},A=r, так как ранг не изменился при элементарных преобразованиях. За базисную подматрицу в A можно принять подматрицу, расположенную в столбцах с номерами j_{1},…, j_{r} и строках, которые после перестановок попали на места 1,…, r в упрощенной матрице. Это видно из того, что, преобразуя матрицу, мы не прибавляли к пересекающим ее строкам никаких строк, которые ее не пересекают.
Таким образом, если мы не знали ранга матрицы и ее базисной подматрицы, то приведя ее к упрощенному виду, мы их определим. С другой стороны, имеет место
Утверждение 6.
Какова бы ни была базисная подматрица матрицы A, элементарными преобразованиями строк можно привести A к такому упрощенному виду, в котором базисные столбцы будут первыми столбцами единичной матрицы.
Доказательство.
Действительно, небазисные строки можно обратить в нулевые, вычитая из них подходящие линейные комбинации базисных. После этого можно превратить базисную подматрицу в единичную так, как это было сделано здесь. (Элементарные преобразования производятся, конечно, над полными строками.)
Ранг матрицы и базисный минор матрицы
Пусть — матрица размеров
, а
— натуральное число, не превосходящее
и
:
. Минором k-го порядка матрицы
называется определитель матрицы k-го порядка, образованной элементами, стоящими на пересечении произвольно выбранных
строк и
столбцов матрицы
. Обозначая миноры, номера выбранных строк будем указывать верхними индексами, а выбранных столбцов — нижними, располагая их по возрастанию.
Пример 3.4. Записать миноры разных порядков матрицы
Решение. Матрица имеет размеры
. Она имеет: 12 миноров 1-го порядка, например, минор
; 18 миноров 2-го порядка, например,
; 4 минора 3-го порядка, например,
В матрице размеров
минор r-го порядка называется базисным, если он отличен от нуля, а все миноры (r+1)-ro порядка равны нулю или их вообще не существует.
Рангом матрицы называется порядок базисного минора. В нулевой матрице базисного минора нет. Поэтому ранг нулевой матрицы, по определению полагают равным нулю. Ранг матрицы обозначается
.
Пример 3.5. Найти все базисные миноры и ранг матрицы
Решение. Все миноры третьего порядка данной матрицы равны нулю, так как у этих определителей третья строка нулевая. Поэтому базисным может быть только минор второго порядка, расположенный в первых двух строках матрицы. Перебирая 6 возможных миноров, отбираем отличные от нуля
Каждый из этих пяти миноров является базисным. Следовательно, ранг матрицы равен 2.
Замечания 3.2
1. Если в матрице все миноры k-го порядка равны нулю, то равны нулю и миноры более высокого порядка. Действительно, раскладывая минор (k+1)-ro порядка по любой строке, получаем сумму произведений элементов этой строки на миноры k-го порядка, а они равны нулю.
2. Ранг матрицы равен наибольшему порядку отличного от нуля минора этой матрицы.
3. Если квадратная матрица невырожденная, то ее ранг равен ее порядку. Если квадратная матрица вырожденная, то ее ранг меньше ее порядка.
4. Для ранга применяются также обозначения .
5. Ранг блочной матрицы определяется как ранг обычной (числовой) матрицы, т.е. не обращая внимания на ее блочную структуру. При этом ранг блочной матрицы не меньше рангов ее блоков: и
, поскольку все миноры матрицы
(или
) являются также минорами блочной матрицы
.
Теоремы о базисном миноре и о ранге матрицы
Рассмотрим основные теоремы, выражающие свойства линейной зависимости и линейной независимости столбцов (строк) матрицы.
Теорема 3.1 о базисном миноре. В произвольной матрице каждый столбец {строка) является линейной комбинацией столбцов (строк), в которых расположен базисный минор.
Действительно, без ограничения общности предполагаем, что в матрице размеров
базисный минор расположен в первых
строках и первых
столбцах. Рассмотрим определитель
который получен приписыванием к базисному минору матрицы соответствующих элементов s-й строки и k-го столбца. Отметим, что при любых
и
этот определитель равен нулю. Если
или
, то определитель
содержит две одинаковых строки или два одинаковых столбца. Если же
и
, то определитель
равен нулю, так как является минором (r+l)-ro порядка. Раскладывая определитель по последней строке, получаем
где — алгебраические дополнения элементов последней строки. Заметим, что
, так как это базисный минор. Поэтому
, где
Записывая последнее равенство для , получаем
т.е. -й столбец (при любом
) есть линейная комбинация столбцов базисного минора, что и требовалось доказать.
Теорема о базисном миноре служит для доказательства следующих важных теорем.
Условие равенства нулю определителя
Теорема 3.2 (необходимое и достаточное условие равенства нулю определителя). Для того чтобы определитель был равен нулю необходимо и достаточно, чтобы один из его столбцов {одна из его строк) был линейной комбинацией остальных столбцов (строк).
В самом деле, необходимость следует из теоремы о базисном миноре. Если определитель квадратной матрицы n-го порядка равен нулю, то ее ранг меньше , т.е. хотя бы один столбец не входит в базисный минор. Тогда этот выбранный столбец по теореме 3.1 является линейной комбинацией столбцов, в которых расположен базисный минор. Добавляя, при необходимости, к этой комбинации другие столбцы с нулевыми коэффициентами, получаем, что выбранный столбец есть линейная комбинация остальных столбцов матрицы. Достаточность следует из свойств определителя. Если, например, последний столбец
определителя
линейно выражается через остальные
то прибавляя к столбец
, умноженный на
, затем столбец
, умноженный на
, и т.д. столбец
, умноженный на
, получим определитель
с нулевым столбцом, который равен нулю (свойство 2 определителя).
Инвариантность ранга матрицы при элементарных преобразованиях
Теорема 3.3 (об инвариантности ранга при элементарных преобразованиях). При элементарных преобразованиях столбцов (строк) матрицы ее ранг не меняется.
Действительно, пусть . Предположим, что в результате одного элементарного преобразования столбцов матрицы
получили матрицу
. Если было выполнено преобразование I типа (перестановка двух столбцов), то любой минор (r+l)-ro порядка матрицы
либо равен соответствующему минору (r+l)-ro порядка матрицы
, либо отличается от него знаком (свойство 3 определителя). Если было выполнено преобразование II типа (умножение столбца на число
), то любой минор (г+l)-ro порядка матрицы
либо равен соответствующему минору (r+l)-ro порядка матрицы
, либо отличается от него множителем
(свойство 6 определителя). Если было выполнено преобразование III типа (прибавление к одному столбцу другого столбца, умноженного на число
), то любой минор (г+1)-го порядка матрицы
либо равен соответствующему минору (г+1) -го порядка матрицы
(свойство 9 определителя), либо равен сумме двух миноров (r+l)-ro порядка матрицы
(свойство 8 определителя). Поэтому при элементарном преобразовании любого типа все миноры (r+l)-ro порядка матрицы
равны нулю, так как равны нулю все миноры (г+l)-ro порядка матрицы
. Таким образом, доказано, что при элементарных преобразованиях столбцов ранг матрицы не может увеличиться. Так как преобразования, обратные к элементарным, являются элементарными, то ранг матрицы при элементарных преобразованиях столбцов не может и уменьшиться, т.е. не изменяется. Аналогично доказывается, что ранг матрицы не изменяется при элементарных преобразованиях строк.
Следствие 1. Если одна строка (столбец) матрицы является линейной комбинацией других ее строк (столбцов), то эту строку (столбец) можно вычеркнуть из матрицы, не изменив при этом ее ранга.
Действительно, такую строку при помощи элементарных преобразований можно сделать нулевой, а нулевая строка не может входить в базисный минор.
Следствие 2. Если матрица приведена к простейшему виду (1.7), то
Действительно, матрица простейшего вида (1.7) имеет базисный минор r-го порядка.
Следствие 3. Любая невырожденная квадратная матрица является элементарной, другими словами, любая невырожденная квадратная матрица эквивалентна единичной матрице того же порядка.
Действительно, если — невырожденная квадратная матрица n-го порядка, то
(см. п.З замечаний 3.2). Поэтому, приводя элементарными преобразованиями матрицу
к простейшему виду (1.7), получим единичную матрицу
, так как
(см. следствие 2). Следовательно, матрица
эквивалентна единичной матрице
и может быть получена из нее в результате конечного числа элементарных преобразований. Это означает, что матрица
элементарная.
Теорема 3.4 (о ранге матрицы). Ранг матрицы равен максимальному числу линейно независимых строк этой матрицы.
В самом деле, пусть . Тогда в матрице
имеется
линейно независимых строк. Это строки, в которых расположен базисный минор. Если бы они были линейно зависимы, то этот минор был бы равен нулю по теореме 3.2, а ранг матрицы
не равнялся бы
. Покажем, что
— максимальное число линейно независимых строк, т.е. любые
строк линейно зависимы при
. Действительно, образуем из этих
строк матрицу
. Поскольку матрица
— это часть матрицы
, то
. Значит, хотя бы одна строка матрицы
не входит в базисный минор этой матрицы. Тогда по теореме о базисном миноре она равна линейной комбинации строк, в которых расположен базисный минор. Следовательно, строки матрицы
линейно зависимы. Таким образом, в матрице
не более, чем
линейно независимых строк.
Следствие 1. Максимальное число линейно независимых строк в матрице равно максимальному числу линейно независимых столбцов:
Это утверждение вытекает из теоремы 3.4, если ее применить к строкам транспонированной матрицы и учесть, что при транспонировании миноры не изменяются (свойство 1 определителя).
Следствие 2. При элементарных преобразованиях строк матрицы линейная зависимость (или линейная независимость) любой системы столбцов этой матрицы сохраняется.
В самом деле, выберем любые столбцов данной матрицы
и составим из них матрицу
. Пусть в результате элементарных преобразований строк матрицы
была получена матрица
, а в результате тех же преобразований строк матрицы
была получена матрица
. По теореме 3.3
. Следовательно, если столбцы матрицы
были линейно независимы, т.е.
(см. следствие 1), то и столбцы матрицы
также линейно независимы, так как
. Если столбцы матрицы
были линейно зависимы
, то и столбцы матрицы
также линейно зависимы
. Следовательно, для любых столбцов матрицы
линейная зависимость или линейная независимость сохраняется при элементарных преобразованиях строк.
Замечания 3.3
1. В силу следствия 1 теоремы 3.4 свойство столбцов, указанное в следствии 2, справедливо и для любой системы строк матрицы, если элементарные преобразования выполняются только над ее столбцами.
2. Следствие 3 теоремы 3.3 можно уточнить следующим образом: любую невырожденную квадратную матрицу, используя элементарные преобразования только ее строк (либо только ее столбцов), можно привести к единичной матрице того же порядка.
В самом деле, используя только элементарные преобразования строк, любую матрицу можно привести к упрощенному виду
(рис. 1.5) (см. теорему 1.1). Поскольку матрица
невырожденная
, то ее столбцы линейно независимы. Значит, столбцы матрицы
также линейно независимы (следствие 2 теоремы 3.4). Поэтому упрощенный вид
невырожденной матрицы
совпадает с ее простейшим видом (рис. 1.6) и представляет собой единичную матрицу
(см. следствие 3 теоремы 3.3). Таким образом, преобразовывая только строки невырожденной матрицы, ее можно привести к единичной. Аналогичные рассуждения справедливы и для элементарных преобразований столбцов невырожденной матрицы.
Ранге произведения и суммы матриц
Теорема 3.5 (о ранге произведения матриц). Ранг произведения матриц не превышает ранга множителей:
В самом деле, пусть матрицы и
имеют размеры
и
. Припишем к матрице
матрицу
. Разумеется, что
, так как
— это часть матрицы
(см. п.5 замечаний 3.2). Заметим, что каждый столбец
, согласно операции умножения матриц, является линейной комбинацией столбцов
матрицы
Такой столбец можно вычеркнуть из матрицы , при этом ее ранг не изменится (следствие 1 теоремы 3.3). Вычеркивая все столбцы матрицы
, получаем:
. Отсюда,
. Аналогично можно доказать, что одновременно выполняется условие
, и сделать вывод о справедливости теоремы.
Следствие. Если невырожденная квадратная матрица, то
и
, т.е. ранг матрицы не изменяется приумножении ее слева или справа на невырожденную квадратную матрицу.
Теорема 3.6 о ранге суммы матриц. Ранг суммы матриц не превышает суммы рангов слагаемых:
Действительно, составим матрицу . Заметим, что каждый столбец матрицы
есть линейная комбинация столбцов матриц
и
. Поэтому
. Учитывая, что количество линейно независимых столбцов в матрице
не превосходит
, а
(см. п.5 замечаний 3.2), получаем доказываемое неравенство.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
-
Ранг произведения двух матриц не выше ранга каждого из сомножителей.
Пусть
имеются две матрицы А
и В,
которые можно перемножать и пусть
АВ = С.
В
i—й
строке, и j—м
столбце матрицы-произведения С
стоит элемент
,
определяемый формулами:
при
i = 1
при
i = 2
при
произвольном i
(9)
Здесь видно, что j—й
столбец матрицы С представляет
собой линейную комбинацию столбцов
матрицы А, взятых с коэффициентами
.
Отсюда следует, что система столбцов
матрицы С линейно выражается через
систему столбцов матрицы А, и ранг
системы столбцов С не превышает
ранга системы столбцов А.
Если
теперь использовать формулу (9) для
элементов произвольной строки матрицы
С,
то получится:
при
j = 1
при
j = 2
и так далее.
Отсюда
видно, что система строк матрицы С
является линейной комбинацией системы
строк матрицы В,
следовательно,
ранг системы строк
матрицы
С
не может превышать ранга
системы строк матрицы В,
и теорема доказана.
2. Ранг произведения произвольной матрицы а справа или слева на невырожденную квадратную матрицу q равен рангу матрицы а.
Доказательство.
Пусть
AQ = C (**)
Из первой теоремы о ранге матрицы
следует, что ранг матрицы С не выше
ранга матрицы А. Если умножить обе
части равенства (**) на Q–1
справа, получится равенство
A = CQ–1
Из той же теоремы о ранге матрицы следует,
что ранг А не выше ранга С. Отсюда
следует, что ранги матриц А и С
совпадают.
Теорема Кронекера-Капелли.
Рассмотрим систему
уравнений
(3)
Обозначим
через
А матрицу
её коэффициентов и через А*
её расширенную матрицу.
Теорема. Для того, чтобы система линейных
уравнений была совместной, необходимо
и достаточно, чтобы ранг матрицы её
коэффициентов равнялся рангу расширенной
матрицы.
Доказательство. Пусть система (3)
совместна. Тогда существует набор чисел
,
который будет решением системы. Если
подставить этот набор чисел в систему,
то получится выражение столбца свободных
членов в виде линейной комбинации
столбцов коэффициентов. Всякий другой
столбец расширенной матрицы системы
очевидно тоже можно представить в виде
линейной комбинации столбцов матрицы
коэффициентов. Очевидно, что и любой
столбец матрицы коэффициентов системы
можно представить в виде линейной
комбинации столбцов расширенной матрицы.
Таким образом, системы столбцов матрицы
коэффициентов и столбцов расширенной
матрицы эквивалентны. Это означает, что
их ранги равны.
Пусть теперь ранги
матрицы коэффициентов системы и
расширенной матрицы системы (3) равны.
Тогда некоторая максимальная линейно
независимая система столбцов матрицы
коэффициентов будет также максимальной
линейно независимой системой столбцов
расширенной матрицы. Отсюда следует,
что столбец свободных членов может быть
представлен в виде линейной комбинации
столбцов матрицы коэффициентов. Набор
коэффициентов этой линейной комбинации
и будет решением рассматриваемой системы
уравнений.
Системы линейных однородных уравнений.
Рассмотрим
однородную систему т
уравнений
с п
неизвестными
(4)
Эта
система всегда совместна. Если матрица
коэффициентов системы (4) имеет ранг r,
равный п,
то система имеет единственное решение,
которое является нулевым. Если r < п,
то система имеет решения, отличные от
нулевого. Однородная система п
линейных уравнений с
п
неизвестными имеет только нулевое
решение, если определитель матрицы
коэффициентов системы отличен от нуля.
Если этот определитель равен нулю, то
такая система имеет бесконечное множество
решений.
Если
некоторый вектор zT
= (z1
z2,,zn)
является решением системы (4), то при
любом числе k
вектор
kzT
= (kz1,
kz2,,
kzn)
также
будет решением этой системы. Если
несколько различных векторов являются
решениями системы (4), то любая их линейная
комбинация также будет решением этой
системы. Очевидно, что система векторов,
являющихся решениями системы (4), должна
содержать максимальную линейно
независимую систему, содержащую не
более п
векторов. Всякое решение системы
уравнений (4) будет представлять собой
линейную комбинацию векторов выбранной
максимальной линейно независимой
системы. Всякую максимальную линейно
независимую систему решений однородной
системы уравнений будем называть
фундаментальной
системой решений.
п-мерный
вектор тогда и только тогда является
решением системы (4), если он является
линейной комбинацией векторов данной
фундаментальной системы.
Система (4) может
обладать многими различными фундаментальными
системами решений. Все эти системы
эквивалентны между собой, и поэтому
состоят из одного и того же числа решений.
Теорема.
Если ранг r
матрицы
коэффициентов системы (4) меньше числа
уравнений п,
то всякая фундаментальная система
решений системы уравнений (4) состоит
из п – r
решений.
Доказательство.
Рассмотрим произвольный, отличный от
нуля определитель порядка п – r:
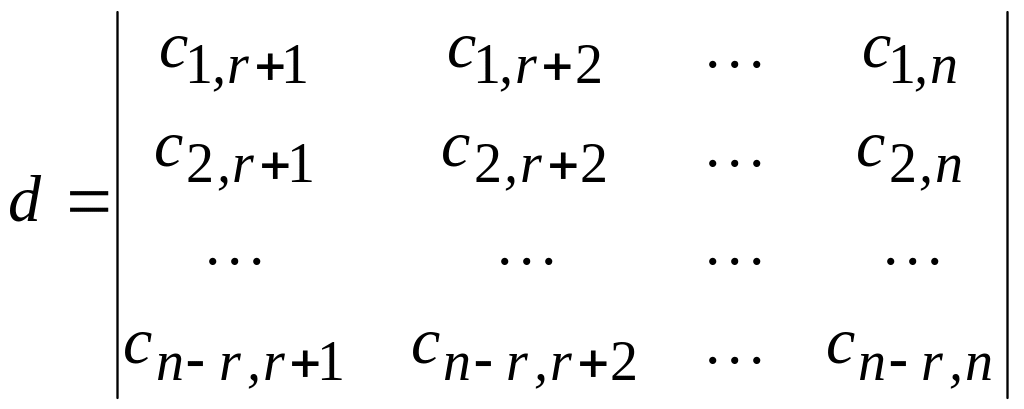
Придадим свободным неизвестным системы
значения из i—й
строки определителя: xr+1 = ci,r+1,
xr+2 = ci,r+2,,
xп = ci,п.
Тогда однозначно определятся значения
базисных переменных х1,
х2,
, хr.
Таким образом, можно получить определённое
решение системы (4)
Перебрав все строки определителя d,
получим систему векторов
, (5)
которая является фундаментальной
системой решений системы (4). Чтобы это
доказать, нужно, во-первых, доказать,
что система (5) линейно независима, и
во-вторых, что любое решение системы
(4) можно представить в виде линейной
комбинации системы векторов (5). Первое
очевидно, так как матрица, составленная
из векторов системы (5), имеет отличный
от нуля минор порядка n r,
равный d.
Чтобы доказать
второе, предположим, что вектор
(6)
является некоторым решением системы
(4). Обозначим
i—ю строку
определителя d и
.
Система векторов
очевидно, линейно зависима (число
векторов превышает размерность векторов),
и существует набор чисел
,
что
(7)
Теперь рассмотрим п-мерный вектор
Вектор является
решением системы (4). Из (7) следует, что
в решении все
свободные переменные равны нулю. Однако,
при всех свободных неизвестных, равных
нулю, система (4) может иметь только
нулевое решение, то есть = 0,
откуда следует, что
,
и теорема доказана.
Рассмотрим систему
(8)
Очевидна справедливость
двух выводов:
-
Сумма любого решения
системы (4) с любым решением системы (8)
будет решением системы (8). -
Разность двух любых
решений системы (8) является решением
системы (4).
Отсюда следует
теорема: любое решение системы (8) можно
получить в виде суммы любого другого
решения этой системы и линейной комбинации
решений системы (4).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Элементарные преобразования матриц:
Рассмотрим прямоугольную матрицу:
состоящую из m строк и n столбцов. В п.3.2 отмсчалось, что каждую строку матрицы можно рассматривать как n-мсрный вектор, а каждый столбец — как m-мерный вектор. Тогда матрицу А можно записать в виде:
и, следовательно, данную матрицу можно рассматривать как систему вектор строк или вектор столбцов. Б указанных системах вектор-строк и вектор-столбцов можно выделять линейно независимые (зависимые) векторы. Тогда будем говорить, что строки (столбцы) матрицы линейно независимы (зависимы), если соответствующие им векторы независимы (зависимы).
Определения
Определение: Рангом системы строк (соответственно столбцов) матрицы А называется наибольшее число линейно независимых среди них.
Поскольку легко доказать, что ранг системы строк матрицы равен рангу системы её столбцов, то справедливо следующее
Определение: Рангом матрицы, обозначаемым r(А), называется максимальное число линейно независимых строк (столбцов) матрицы.
При транспонировании матрицы ранг её не изменяется.
Другой метод определения ранга матрицы связан с понятием определителя.
Выделим в матрице А любые k строк и k столбцов. Элементы, стоящие на их пересечении, образуют квадратную матрицу, определитель которой называется минором k-го порядка матрицы А. Ясно, что величина к должна удовлетворять двум условиям: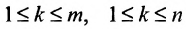
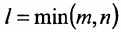
Определение: Рангом матрицы, обозначаемым r(А), называется порядок самого старшего минора этой матрицы, не равного нулю.
Из определения следует, что если ранг матрицы А равен l, то среди всех её миноров существует хотя бы один минор l-го порядка, отличный от нуля, но все миноры (l+1)-го порядков либо равны нулю, либо не могут быть составлены.
Вычисление ранга матрицы путём перебора всех её миноров весьма трудоёмко. Существует, однако, более простой способ вычисления ранга матрицы, основанный на упрощении структуры матрицы с помощью элементарных преобразований. Элементариыми преобразованиями матрицы называют следующие преобразования:
- обмен местами двух строк или двух столбцов матрицы;
- умножение всех элементов строки или столбца матрицы на произвольное число
, не равное нулю;
- прибавление ко всем элементам строки (столбца) матрицы соответствующих элементов другой строки (столбца), предварительно умноженных на одно и то же число;
- исключение из матрицы строки или столбца, состоящего из нулей.
Матрицы называются эквивалентными, если от одной из них к другой можно перейти путём конечного числа элементарных преобразований.
Ступенчатой матрицей называется матрица, удовлетворяющая тому свойству, что если в какой-либо из сё строк первый отличный от нуля элемент стоит на l-м месте, то во всех следующих строках на первых l местах стоят нули:
где элементы 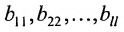
Для вычисления ранга матрицы приводят её с помощью цепочки элементарных преобразований к ступенчатому виду. Тогда ранг матрицы совпадает с числом её ненулевых диагональных элементов.
Теоремы о ранге матриц. Свойства ранга матриц
Относительно ранга матриц можно сформулировать следующие теоремы:
Теорема: Если матрица имеет минор порядка r, отличный от нуля, для которого все содержащие его миноры порядка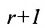
Вычисление ранга матрицы при помощи метода окаймления нужно вести от низших порядков к высшим. Сначала ищем минор первого порядка (т.е. элемент матрицы) или сразу второго порядка, отличный от нуля. Затем вычисляем окаймляющие его миноры следующего порядка, пока не найдём среди них отличного от нуля и т.д., пока не найдем минор порядка l, отличный от нуля, для которого либо все окаймляющие его миноры порядка l+1 равны нулю, либо такие миноры не могут быть составлены.
Теорема: Элементарные преобразования не меняют ранга матрицы.
Доказательство теоремы следует из определения ранга матрицы и свойств определителей.
Пример:
Найти ранг матрицы:
Решение:
Минор первого порядка в левом верхнем углу равен 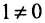
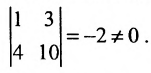
Значит ранг матрицы равен 2.
Пример:
Найти ранг матрицы:
Решение:
При помощи элементарных преобразований приведём данную матрицу к ступенчатому виду. На первом шаге умножим последовательно первую строку на 3, 3, 2 и вычтем из второй, третьей, четвёртой строк соответственно:
В эквивалентной матрице прибавим к третьей строке вторую и вычтем вторую из четвёртой строки:
(поменяем местами третью и четвертую строки)
(поменяем местами третий, четвёртый и пятый столбцы со вторым и опустим строки, состоящие из нулей) 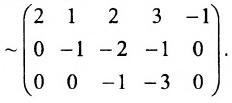
Отмстим некоторые свойства ранга матриц.
- Ранг суммы двух (или нескольких) матриц не больше суммы их рангов.
- Любую матрицу ранга r можно представить в виде суммы r матриц ранга 1, но нельзя представить в виде суммы менее чем r таких матриц.
- Любую матрицу С ранга r можно представить в виде произведения
, где А состоит из r линейно независимых столбцов, г B -из r линейно независимых строк.
- Ранг произведения матриц порядка n удовлетворяет неравенству
.
Определение системы m линейных уравнений с n неизвестными
Системой m линейных уравнений с n неизвестными 
Числа 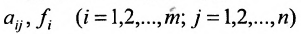
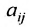
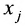
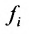
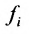
С помощью знака суммирования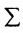
Матрица
составленная из коэффициентов системы 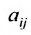
системы. Если к этой матрице добавить столбец свободных членов, то получим расширенную матрицу системы: 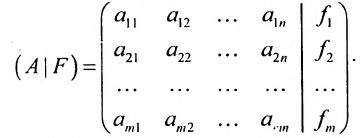
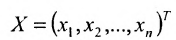
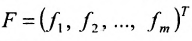

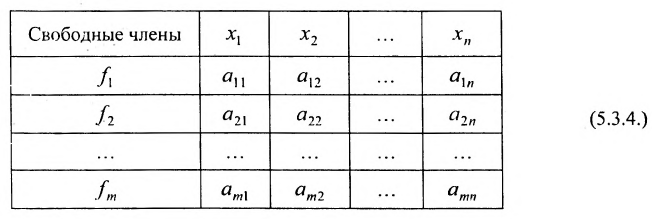
Используется также табличная форма записи системы (5.3.1):
Отметим, что (5.3.1), (5.3.2), (5.3.3), (5.3.4)- различные виды записи одной и той же системы линейных уравнений.
Решением системы (5.3.1) называется любой упорядоченный набор действительных чисел 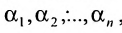
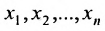
Система уравнений (5.3.1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений. Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
Две системы уравнений с одинаковыми наборами неизвестных 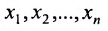
Отмстим, что для любой системы (5.3.1) возможны только три случая:
- система (5.3.1) имеет единственное решение;
- система (5.3.1) имеет бесчисленное множество решений;
- система (5.3.1) несовместна.
Множество всех решений системы (5.3.1) называется ее общим решением.
Решить систему (5.3.1) — значит найти ее общее решение.
Пример:
Пусть задана система
Тогда эту систему можно записать в матричном виде:
или в виде таблицы:
Система определенная, так как она имеет единственное решение 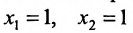
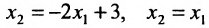
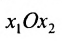
Экономические задачи, приводящие к системе линейных уравнений
Предположим, что производственные мощности для изготовления n различных видов продукции установлены в т цехах. Пусть 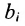
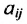
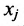
Широкий круг задач экономики приводит к составлению системы уравнений. Так в примере 4.3.2 составлялась система линейных уравнений (4.3.1) балансовой модели для трёх отраслей. В общем случае под балансовой моделью понимается система уравнений, каэ/сдое из которых выражает требование баланса между производимым количеством продукции и совокупной потребностью в этой продукции.
При построении балансовых моделей используется понятие чистой (или технологической) отрасли, т.е. условной отрасли, объединяющей всё производство данного продукта независимо от ведомственной (административной) подчинённости и форм собственности предприятий и фирм. Всё народное хозяйство представляется в виде совокупности п отраслей, каждая из которых рассматривается как производящая и как потребляющая.
Если обозначить через:
то систему уравнений баланса можно записать в виде:
или в матричной форме:
где Х- вектор-столбец валовой продукции; Y- вектор-столбец конечной продукции; А — матрица коэффициентов прямых затрат.
Основу экономико-математической модели межотраслевого баланса составляет технологическая матрица А, содержащая коэффициенты прямых затрат на производство единицы продукции:
Коэффициент!,! прямых затрат являются довольно стабильной величиной во времени.
Переписав матричное уравнение (5.4.2) в виде EX-AX = Y или (E-A)X = Y, (5.4.3) получим стандартную форму записи системы уравнений.
Определение ранга матрицы
Рассмотрим прямоугольную матрицу (4.1). Если в этой матрице выделить произвольно 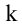
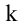
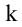
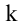
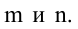
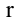
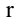
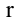
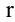
Очевидно, что выполняется соотношение
Ранг матрицы находится либо методом окаймления миноров, либо методом элементарных преобразований. При вычислении ранга матрицы первым способом следует переходить от миноров низших порядков к минорам более высокого порядка. Если уже найден минор D 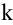
Элементарными называются следующие преобразования матрицы:
- перестановка двух любых строк (или столбцов),
- умножение строки (или столбца) на отличное от нуля число,
- прибавление к одной строке (или столбцу) другой строки (или столбца), умноженной на некоторое число.
Две матрицы называются эквивалентными, если одна из них получается из другой с помощью конечного множества элементарных преобразований.
Эквивалентные матрицы не являются, вообще говоря, равными, но их ранги равны. Если матрицы А и В эквивалентны, то это записывается так: А ~ В.
Канонической матрицей называется матрица, у которой в начале главной диагонали стоят подряд несколько единиц (число которых может равняться нулю), а все остальные элементы
равны нулю, например,
При помощи элементарных преобразований строк и столбцов любую матрицу можно привести к канонической. Ранг канонической матрицы равен числу единиц на ее главной диагонали.
- Заказать решение задач по высшей математике
Пример:
Найти методом окаймления миноров ранг матрицы
Решение:
Начинаем с миноров 1-го порядка, т.е. с элементов матрицы А. Выберем, например, минор (элемент) 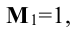
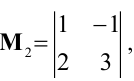
Переходим теперь к минорам 3-го порядка, окаймляющим 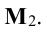
Таким образом, асе окаймляющие миноры третьего порядка оказались равными нулю. Ранг матрицы А равен двум.
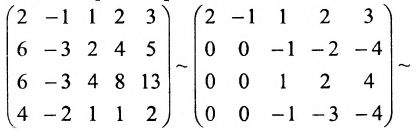
Пример:
Найти ранг матрицы 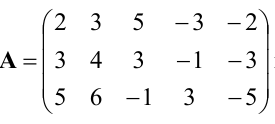
Решение:
Из второй строки вычтем первую и переставим эти строки:
Теперь из второй и третьей строк вычтем первую, умноженную соответственно на 2 и 5:
из третьей строки вычтем первую; получим матрицу 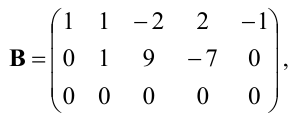
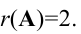
Вычисление ранга матрицы
Для исследования разрешимости систем линейных уравнений важную роль играет понятие ранга матрицы. Рассмотрим прямоугольную матрицу А
Выделим k произвольных строк и k произвольных столбцов этой матрицы. Определитель k-го порядка, составленный из элементов матрицы А, расположенных на пересечении выделенных строк и столбцов, называется минором k-го порядка матрицы А.
Рангом матрицы А называется наибольший порядок ее миноров, отличных от нуля. Обозначение: rank А,
Базисным минором матрицы называется всякий отличный от нуля ее минор, порядок которого равен рангу матрицы.
Рассмотрим некоторые методы вычисления ранга матрицы.
Метод окаймляющих миноров
Минор порядка k+1, содержащий в себе минор порядка k, называется окаймляющим минором.
Вычисляя ранг матрицы, удобнее переходить от миноров меньших порядков к минорам больших порядков. Если найден минор k-го порядка, отличный от нуля, а все окаймляющие его миноры порядка k+1 равны нулю, то ранг матрицы равен k.
- Определители второго и третьего порядков и их свойства
- Метод Гаусса — определение и вычисление
- Прямая линия на плоскости и в пространстве
- Плоскость в трехмерном пространстве
- Кратный интеграл
- Ряды в математике
- Дифференциальные уравнения с примерами
- Обратная матрица — определение и нахождение
§ 10. Теорема о ранге произведения линейных операторов
Пусть — линейный оператор,
— (1)
Базис пространства , а
— (2)
Базис пространства . Аналогично тому, как определялась матрица линейного оператора пространства
в себя в заданном базисе, определяется и матрица оператора
в паре базисов (1) и (2). Найдем образы векторов базиса (1):
, (3)
Каждый из них разложим по базису (2), обозначим координатный столбец вектора
в базисе (2),
, и составим систему
(4)
Из этих координатных столбцов.
Матрицей линейного оператора в паре базисов (1) и (2) называется матрица
, составленная из координатных столбцов образов векторов базиса (1) в базисе (2). Очевидно, эта матрица имеет размеры
.
Нетрудно показать, что при умножении линейных операторов их матрицы в соответствующих парах базисов перемножаются, как это было доказано для случая линейных операторов пространства в себя.
Теорема 1. Пусть — линейный оператор, A его матрица в паре базисов (1) и (2). Тогда
.
►В § 3 третьей главы мы показали, что векторы линейно независимы тогда и только тогда, когда линейно независимы их координатные столбцы. Поэтому максимальное число линейно независимых элементов в системах (3) и (4) будет одинаковым. Обозначим это число .
Так как каждый из векторов можно разложить по базису (1), то
. Следовательно,
. Тогда:
[теорема 1 § 7 главы 3] =
=
= [теорема 2 § 7 главы 3] = .◄
Следствие. Если — изоморфизм, то матрица A — Невырождена.
Теорема 2. Пусть и
— линейные операторы. Тогда
, причем, если один из операторов — изоморфизм, то ранг произведения равен рангу второго оператора.
►Обозначим . Нетрудно убедиться, что
— подпространство пространства
, и поэтому,
. Тогда:
=
;
=
.
Кроме того, если — изоморфизм, то
.
Если же — изоморфизм, то
.◄
Следствие. Ранг произведения матриц не превосходит ранга каждого из сомножителей. Причем, если один из сомножителей — матрица невырожденная, то ранг произведения равен рангу второго сомножителя.
§ 11. Линейные формы
Определение. Линейной формой на линейном пространстве над полем
называется линейный оператор
.
Мы уже знаем, что множество всех линейных форм на линейном пространстве
также является линейным пространством над тем же полем, что и
, относительно операций сложения линейных форм и умножения линейной формы на число. Пространство
будем называть сопряженным пространству
, и обозначать
, его элементы будем называть ковекторами и тоже для удобства отмечать стрелками, но снизу (например,
).
Рассмотрим — мерное линейное пространство
и выберем в нем какой-либо базис
. (1)
Пусть — произвольный вектор пространства
,
— линейная форма. Тогда
. (2)
Мы видим, что значение линейной формы для вектора зависит от его координат и некоторых чисел
, вовсе с вектором
не связанных. Обозначим
и назовем эти числа Компонентами формы
в базисе (1). Теперь (2) можно переписать и так:
.
Выберем в ещё один базис
(3)
И обозначим компоненты линейной формы
в базисе (3).Тогда
=
= [определение матрицы перехода] =
=
= [линейность ] =
.
Мы получили закон изменения компонент линейной формы при изменении базиса.
В пространстве линейных форм выберем
линейных форм
(4)
По следующему принципу:
, (5)
Т. е. форма принимает значение, равное 0, для всех базисных векторов, за исключением одного,
, для которого она принимает значение, равное 1. Существование таких форм вытекает из теоремы § 2. Докажем линейную независимость (4). Как обычно, составим линейную комбинацию и приравняем её нейтральному элементу.
{(4) линейно независима}.
Пусть теперь — произвольная линейная форма,
— её компоненты в базисе (1). Обозначим
. Тогда
Таким образом, =
, следовательно, система (4) в пространстве
является системой образующих, а значит, и базисом. Итак, пространство, сопряженное к конечномерному линейному пространству, имеет ту же размерность. Базисы (1) и (4) пространств
и
Называются сопряженными или взаимными. Следовательно, компоненты линейной формы
в базисе (1) пространства
– это её координаты во взаимном базисе пространства
.
§ 12. Собственные векторы линейного оператора
Определение. Ненулевой вектор линейного пространства V над полем P называется Собственным вектором линейного оператора
, если существует такое число
P, что
=
. (1)
Число из равенства (1) называется Собственным значением оператора F, соответствующим собственному вектору
.
Очевидно, все векторы линейного пространства являются собственными векторами нулевого оператора с собственным значением, равным 0, они же являются собственными векторами тождественного оператора с собственным значением, равным 1. Оператор проектирования трехмерного пространства на ось ОX имеет следующие собственные векторы: векторы, параллельные оси ОX – собственные с собственным значением, равным 1, а векторы, перпендикулярные оси ОX – собственные с собственным значением, равным 0. При любом функция
является собственным вектором (или собственной функцией) оператора дифференцирования
, причем собственное значение равно
.
Свойства собственных векторов
1º. Каждому собственному вектору соответствует единственное собственное значение.
► Предположим, что некоторому собственному вектору соответствуют два разных собственных значения
и
(
). Тогда
. (2)
По шестому следствию § 1 гл. 3, из (2) следует, что , что противоречит определению собственного вектора.◄
2º. Собственные векторы с различными собственными значениями линейно независимы.
►Пусть ,
,…,
— собственные векторы линейного оператора
с собственными значениями
соответственно, причем
при
. Доказательство проведем методом математической индукции по количеству векторов.
A) . Предположим, что векторы линейно зависимы. Тогда один из них можно выразить через другой, например,
. Имеем:
,
Откуда получаем, что (т. к.
,
), а значит,
, что противоречит определению собственного вектора.
Б) Предположим, что утверждение справедливо для (N-1)-го вектора и докажем его справедливость для N векторов. Пусть векторы ,
,…,
с различными собственными значениями
линейно зависимы. Значит, один из них можно представить в виде линейной комбинации остальных, например,
. (3)
Так как , получаем:
. (4)
По предположению индукции, векторы ,
,…,
линейно независимы. Поэтому из (4) вытекает, что
,
Так как
, то
при
. Но тогда из (3) видно, что
, что противоречит определению собственного вектора.◄
3º. Множество всех собственных векторов линейного оператора
с одним и тем же собственным значением
вместе с нулевым вектором является подпространством линейного пространства V.
►Заметим, что состоит из всех векторов, удовлетворяющих условию (1),
т. к.
при любом
. Докажем замкнутость
относительно операций, заданных в V. Действительно,
{
;
}
{
}
{
};
{
}
{
}
{
}.
На основании теоремы §6 главы 3, — подпространство линейного пространства V.◄
4º. Пусть — линейный оператор,
— его различные собственные значения. Обозначим


Тогда в существует
линейно независимых собственных векторов оператора
.
►В каждом из подпространств выберем
линейно независимых векторов
и покажем, что система
— (5)
Линейно независима. Для этого составим её линейную комбинацию и приравняем :

Обозначим 
,
Откуда вытекает, что система линейно зависима. Поэтому, на основании свойства 2º, не все из векторов
являются собственными, т. е. среди них есть нулевые. Пусть, например,
. Это означает, что
(объясните, почему), и что
. Теперь видим, что система
линейно зависима. Значит, и среди этих векторов есть нулевые. Пусть, например,
со всеми вытекающими отсюда последствиями. После конечного числа шагов получаем, что в (6) все коэффициенты
, откуда и следует линейная независимость системы (5).◄
§ 13. Правило нахождения собственных векторов
Пусть — линейный оператор. Выберем в
какой-либо базис и обозначим А матрицу оператора
в этом базисе. Если Х – координатный столбец собственного вектора
в заданном базисе, а
– соответствующее ему собственное значение, то (1) § 5 Равносильно равенству
, которое, в свою очередь, равносильно следующему:
. (1)
Равенство (1) можно рассматривать как матричную запись однородной системы линейных уравнений, причем нас интересуют только ее нетривиальные решения. Как следует из §5 главы 2, для существования таковых необходимо и достаточно, чтобы выполнялось условие
. (2)
Определение. Характеристическим многочленом матрицы А называется многочлен , уравнение (2) называется Характеристическим уравнением Матрицы А, а корни этого уравнения – ее Характеристическими числами.
Лемма 1. Подобные матрицы имеют одинаковые характеристические многочлены.
►Пусть матрицы А и подобны, значит существует невырожденная матрица
такая, что
. Тогда
Таким образом, матрицы и (
) тоже подобны, а значит, они имеют одинаковые определители.◄
Эта лемма позволяет сформулировать следующее
Определение. Характеристическим многочленом (характеристическим уравнением, характеристическими числами) линейного оператора называется характеристический многочлен (характеристическое уравнение, характеристические числа) его матрицы в некотором, а значит, и в любом базисе.
Из изложенного выше мы видим, что каждое собственное значение линейного оператора является корнем его характеристического уравнения, т. е. характеристическим числом. Обратно, если
– корень уравнения (2) и
, то система (1) имеет нетривиальное решение Х0, значит, АХ0=
Х0 и тогда, если
— вектор, координатный столбец которого в выбранном базисе совпадает с
, то
, т. е.
— собственное значение оператора
. Если же
, то оно не может быть собственным значением согласно определению.
Итак, собственные значения линейного оператора – это те его характеристические числа, которые принадлежат полю P.
Теперь можно сформулировать следующее правило. Пусть А – матрица линейного оператора в некотором базисе. Чтобы найти собственные векторы оператора
поступаем следующим образом:
1) составляем характеристическое уравнение (2) матрицы А и находим его корни . Те из них, которые принадлежат основному полю, являются собственными значениями (т. е., если Р=С, то все, если Р=R – Только действительные);
2) для каждого из полученных собственных значений находим соответствующие ему собственные векторы., решая однородную систему (1) при
.
Лемма 2. Если определитель квадратной системы линейных уравнений
AX=О, (3)
Равен нулю, то при любом набор
(,
,…,
), (4)
Где -алгебраическое дополнение к элементу
матрицы А, – решение системы (3).
►Действительно, подставив (4) в каждое из уравнений (3), получаем:
. (5)
Равенство (5) верно, т. к. при его левая часть представляет собой разложение
по
-ой строке, а при
оно верно на основании теоремы аннулирования. ◄
Пример. Найдем собственные векторы линейного оператора , матрица которого в некотором базисе пространства V3 имеет вид

▼1. Составляем характеристический многочлен:
.
Характеристическое уравнение оператора выглядит так:
,
А его характеристическими числами будут λ1=2; λ2=3-I; λ3=3+I.
Если P = R, то собственное значение только одно – λ1=2; если же P=C, то все значения будут собственными. Мы рассмотрим случай, когда P=C.
2. λ1=2:

Однородная система с матрицей (6) решается устно: . Значит, собственные векторы с этим собственным значением выглядят так:
=α(1;0;1),
.
λ2=3-I:

Так как , то
. Поэтому достаточно найти один собственный вектор, а все остальные будут ему коллинеарными. Для нахождения же этого вектора воспользуемся леммой 2 и найдем упорядоченный набор из алгебраических дополнений к элементам, например, первой строки матрицы (7):
Тогда все собственные векторы с собственным значением
– это
.
λ3=3+I:

Заметим, что матрицы (7) и (8)- комплексно-сопряженные. Значит, и решения систем с этими матрицами – тоже комплексно-сопряженные, и поэтому, .▲
§14. Приведение квадратной матрицы к диагональному виду
Лемма 1. Для того чтобы матрица А линейного оператора в некотором базисе пространства
имела диагональный вид необходимо и достаточно, чтобы этот базис состоял из собственных векторов оператора F, причем диагональными элементами матрицы А Являются собственные значения этого оператора.
►Пусть
— (1)
Базис пространства , A – матрица оператора F в этом базисе. Тогда
{А — диагональная}
{(1) состоит из собственных векторов оператора
а
— его собственные значения}.◄
Определение. Говорят, что квадратная матрица А с элементами из поля P приводится к диагональному виду над P, если существует невырожденная квадратная матрица Т с элементами из P такая, что матрица — диагональная.
Теорема 1. Пусть А – квадратная матрица с элементами из поля P, — линейное пространство над Р,
— тот линейный оператор, матрица которого в некотором базисе (1) пространства
Совпадает с А. Тогда для приводимости матрицы А к диагональному виду над полем Р необходимо и достаточно, чтобы в
существовал базис, состоящий из собственных векторов оператора F.
►Выберем в еще один базис
(2)
И обозначим Т матрицу перехода от исходного базиса (1) к базису (2). Матрица оператора F В этом базисе имеет вид . Тогда:
{в
Базис (2), состоящий из собственных векторов оператора F }
{матрица
оператора
в базисе (2) диагональная}
{А приводится к диагональному виду}.◄
Следствие. Если все характеристические числа матрицы А различны и принадлежат полю Р, то А приводится к диагональному виду над Р.
Замечание. Если матрица А приводится к диагональному виду — матрице , то диагональными элементами последней являются собственные значения матрицы А, а матрица Т, приводящая А к диагональному виду, есть ни что иное, как матрица перехода от исходного базиса к базису из собственных векторов.
Лемма 2. Пусть — собственное значение кратности
линейного оператора
. Тогда
.
►Предположим, что . Выберем в
какой-либо базис
и дополним его до базиса
(3)
Пространства . В базисе (3) матрица А оператора F выглядит так:

А ее характеристический многочлен (значит, и характеристический многочлен оператора F ) имеет вид:, где
-некоторый многочлен степени
. Очевидно,
— корень характеристического многочлена. Если
— кратность
, то
, что противоречит условию.◄
Теорема 2. Для того чтобы квадратная матрица А N–го порядка приводилась к диагональному виду над полем Р необходимо и достаточно, чтобы все ее характеристические числа принадлежали этому полю, и чтобы для каждого из них выполнялось бы условие
, (4)
Где — кратность корня
характеристического уравнения матрицы А.
►Пусть — линейный оператор, построенный в теореме 1. На основании свойства 4º §5 количество всех линейно независимых собственных векторов линейного оператора
совпадает с суммой размерностей подпространств
по всем собственным значениям
. Если это количество линейно независимых собственных векторов обозначать через M, то

Тогда
{А приводится к диагональному виду}{в
существует базис из собственных векторов оператора F}
{любое характеристическое число
является собственным значением и
}
и
и
.◄
Правило приведения квадратной матрицы к диагональному виду над полем Р
1. Составляем характеристический многочлен матрицы А и находим его корни. Если какой-либо из них не принадлежит полю Р, то А к диагональному виду не приводится.
2. Если все характеристические числа принадлежат полю Р, то для кратных корней проверяем условие (4) (для однократных оно выполняется всегда). Если для какого-то из корней условие (4) не выполняется, то А К диагональному виду не приводится.
3. Если для каждого из собственных значений условие (4) выполняется, то А к диагональному виду приводится. Записываем этот диагональный вид – матрицу , располагая на ее главной диагонали собственные значения
в произвольном порядке, причем каждое из них повторяем столько раз, какова его кратность.
4. Записываем матрицу Т, приводящую А к диагональному виду – матрицу перехода от исходного базиса к базису из собственных векторов, сохраняя порядок, установленный матрицей .
Пример. Найдем диагональный вид матрицы А и невырожденную матрицу Т, приводящую к этому диагональному виду, если

▼1.
2.

Следовательно, А к диагональному виду приводится.
3.
4. Находим собственные векторы:


Для искомого базиса находим два линейно независимых собственных вектора (фундаментальную систему решений): и
.

;
( находим с помощью алгебраических дополнений).
4. Записываем T — матрицу перехода от исходного базиса к построенному базису из собственных векторов:

§ 15. Присоединенные векторы линейного оператора
Определение. Если — собственное значение линейного оператора
, а система векторов
пространства
удовлетворяет условиям:

То вектор называется I-ым Присоединенным Вектором к собственному вектору
линейного оператора
.
Теорема. Пусть – линейное пространство над полем Р. Если все характеристические числа линейного оператора
принадлежат полю Р, то в
существует базис, состоящий из собственных и присоединенных векторов оператора F, причем каждому собственному значению в этом базисе соответствует столько собственных векторов и присоединенных к ним, какова кратность этого собственного значения (без доказательства).
Правило нахождения присоединенных векторов
Обозначим А матрицу линейного оператора в некотором базисе,
— координатный столбец вектора
в том же базисе. Тогда в матричном виде уравнение для нахождения
будет выглядеть так:
Что равносильно уравнению
. (2)
Таким образом, видим, что для отыскания I-ого присоединенного вектора к собственному вектору с собственным значением
следует решить систему линейных уравнений с той же матрицей, что и для отыскания собственного вектора
, но неоднородную, причем в качестве столбца свободных членов берется координатный столбец предыдущего присоединенного вектора.
Пример. Найдем базис из собственных и присоединенных векторов линейного оператора , матрица которого в некотором базисе совпадает с матрицей
▼ Находим собственные значения.
.
Таким образом, мы имеем единственное собственное значение, кратность которого равна 3. Сначала определим количество собственных и присоединенных векторов.

, значит, в искомом базисе будет один собственный вектор и два присоединенных. Находим собственный вектор, решая однородную систему с матрицей
.


Получаем систему:
В качестве собственного вектора можно взять, например, частное решение . Теперь находим первый присоединенный вектор, дописывая в цепочке (3) к матрице
в качестве столбца свободных членов координатный столбец найденного собственного вектора и пересчитывая столбец свободных членов по намеченным стрелкам:

Получаем систему

Первый присоединенный вектор находим как частное решение системы (4):
, а второй — как решение системы с той же матрицей, но в качестве столбца свободных членов уже дописываем координатный столбец вектора
, и опять пересчитываем его по намеченным стрелкам:


Частное решение системы (5) и будет вторым присоединенным вектором: .
Итак, искомый базис: — собственный;
— 1-ый присоединенный;
— 2-ой присоединенный векторы.▲
Замечание. На практике все три цепочки объединяются в одну, новый столбец свободных членов просто дописывается к матрице предыдущей системы и пересчитывается по намеченным стрелкам.
§ 16. Жорданова нормальная форма матрицы
Определение. Жордановой клеткой — го порядка называется матрица
— го порядка вида

У Жордановой клетки все диагональные элементы одинаковые, диагональ, параллельная главной и расположенная над ней, состоит из единиц, а все остальные элементы равны нулю.
Характеристический многочлен жордановой клетки (1) выглядит так:
.
Таким образом, жорданова клетка имеет единственное характеристическое число
, причем его кратность равна порядку этой клетки.
Пусть матрица линейного оператора в некотором базисе
(2)
Пространства Совпадает с жордановой клеткой (1). Тогда:
.
Отсюда видно, что первый вектор этого базиса — собственный с собственным значением , а остальные – присоединенные к нему.
Определение. Жордановой матрицей называется блочно диагональная матрица, диагональными блоками которой являются жордановы клетки: .
Теорема. Для любой комплексной квадратной матрицы А Существует невырожденная матрица Т такая, что матрица – жорданова (без доказательства).
Матрица называется Жордановой нормальной формой матрицы А. Жорданова нормальная форма матрицы определяется однозначно с точностью до порядка следования клеток.
Замечание. Жорданова нормальная форма действительной матрицы А может оказаться матрицей комплексной. Она тоже будет действительной в том и только в том случае, когда все характеристические числа этой матрицы — действительные.
Некоторые свойства жордановой матрицы
1. Характеристический многочлен жордановой матрицы равен произведению характеристических многочленов составляющих её жордановых клеток.
2. Диагональными элементами жордановой матрицы являются её характеристические числа или собственные значения, что для комплексной матрицы одно и тоже.
3. Сумма размерностей всех клеток, соответствующих одному и тому же собственному значению, равна кратности этого собственного значения.
4. Число клеток, соответствующих одному и тому же собственному значению, равно количеству линейно независимых собственных векторов с этим собственным значением.
5. Число клеток порядка не ниже , соответствующих данному собственному значению, равно количеству линейно независимых собственных векторов с этим собственным значением, имеющих
— е присоединенные векторы.
Пример 1. Найдем жорданову нормальную форму матрицы

▼1. Составляем характеристический многочлен матрицы А:

Таким образом, А имеет единственное собственное значение , причем кратность его равна 4.
2. Находим собственные векторы:

Общее решение системы:
. (3)
Число линейно независимых собственных векторов равно двум, значит, жорданова форма имеет две клетки.
3. Находим присоединенные векторы:


Система (4) имеет решения при любых значениях свободных неизвестных, поэтому любой собственный вектор имеет присоединенный. Общее решение этой системы:
Таким образом, обе клетки имеют второй порядок, и жорданова форма выглядит так:

4. Матрица Т, приводящая А к виду — это матрица перехода от исходного базиса к базису, в котором матрица оператора совпадает с
. Из (5) видно, что
, т. е.
и
— векторы собственные, а
и
— присоединенные к ним. Чтобы найти
и
, записываем фундаментальную систему по решению (3):
. Векторы
и
— частные решения системы (4) при соответствующих значениях
и
, т. е.
— решение системы

А — системы
Например, . Таким образом,

Пример 2.

▼ Проведём вычисления по тому же плану, что и в первом примере.

.
Таким образом, .
2.

. (6)
, следовательно, два линейно независимых собственных вектора, значит, в матрице
будет две клетки.
3.

Система (7) имеет решение только в том случае, когда . Поэтому только один из собственных векторов имеет присоединенные. Значит, одна из клеток будет иметь первый порядок, а вторая – третий.

4). ;
.
Находим и
:

;


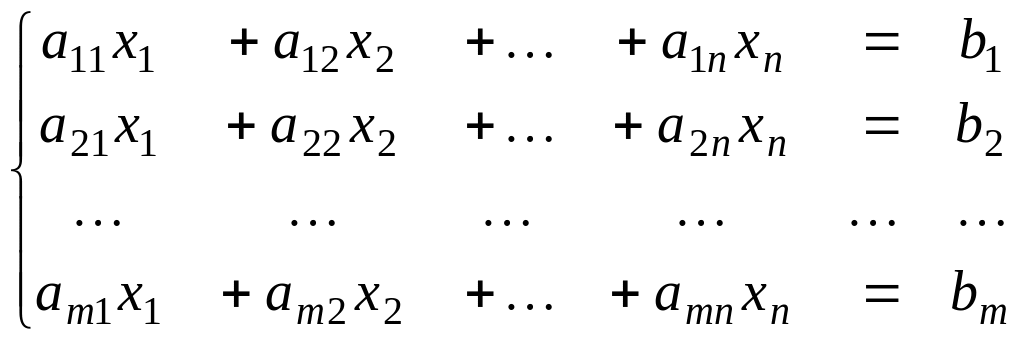
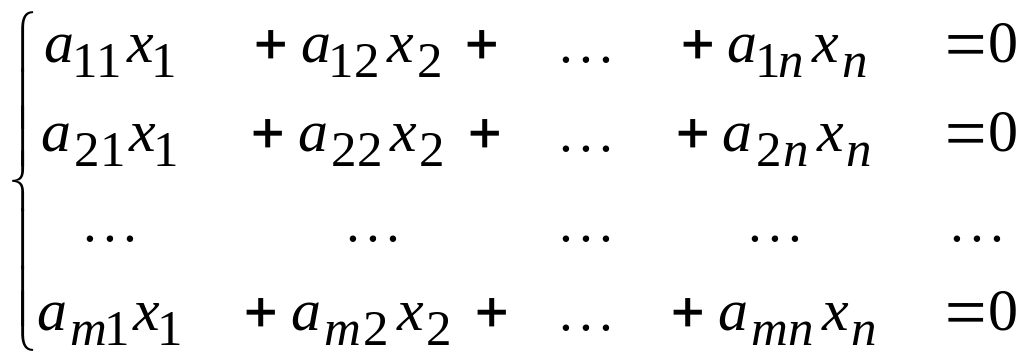
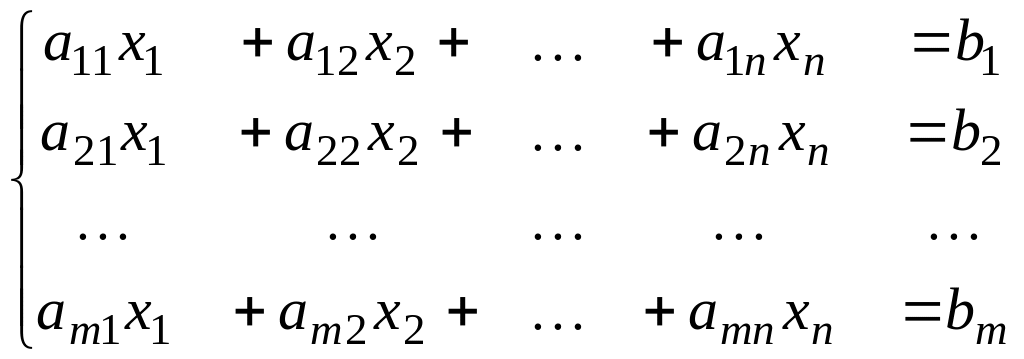

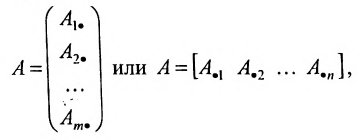
 , не равное нулю;
, не равное нулю;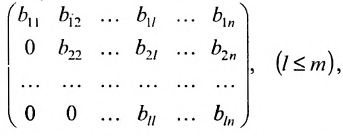
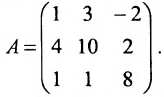
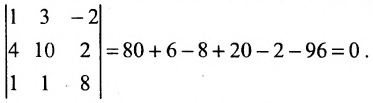



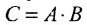 , где А состоит из r линейно независимых столбцов, г B -из r линейно независимых строк.
, где А состоит из r линейно независимых столбцов, г B -из r линейно независимых строк.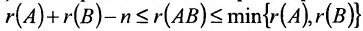 .
.