Радиус и высота сегмента круга
Свойства
Зная радиус и высоту сегмента, можно найти центральный угол α, через который становится возможным рассчитать все остальные измерения сегмента, такие как длина дуги, длина хорды и площадь сегмента круга. Из формулы высоты следует, что косинус половинного угла равен разности единицы и отношения высоты к радиусу. cos〖α/2〗=1-h/r
Вычислив таким образом центральный угол сегмента круга, подставляем его в следующие формулы для длины дуги и длины хорды. Длина дуги вычисляется как произведение угла на радиус, а длина хорды находится из прямоугольного треугольника как удвоенное произведение радиуса на синус половинного угла (рис.141). P=αr c=2r sin〖α/2〗
Площадь сегмента круга наряду с площадью равнобедренного треугольника, образованного двумя радиусами и хордой, является составляющей площади сектора круга. Поэтому, чтобы найти площадь сегмента необходимо вычесть из последней площадь треугольника. Упростив такое выражение, получаем половину квадрата радиуса, умноженную на разность угла α и его синуса. S=S_сек-S_тр=(r^2 α)/2-r^2 sinα=1/2 r^2 (α-sinα )
Сегмент круга
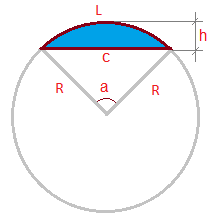
Данный калькулятор считает параметры сегмента круга, а именно:
- длину дуги (L),
- длину хорды (C),
- площадь (S),
- высоту (h),
Перед вами 2 калькулятора, чтобы рассчитать параметры сегмента:
1) сегмент круга решается с помощью радиуса (R) и угла (A).
2) сегмент круга находим с помощью высоты и длины хорды.
Как найти радиус окружности
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Основные понятия
Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.
Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.
Возможно тебе интересно узнать — как найти длину окружности?
Формула радиуса окружности
Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.
Если известна площадь круга
R = √ S : π, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.
Если известна длина
R = P : 2 * π, где P — длина (периметр круга).
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).
Если известен диаметр окружности
R = D : 2, где D — диаметр.
Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.
Если известна диагональ вписанного прямоугольника
R = d : 2, где d — диагональ.
Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:
d = √ a 2 + b 2 , где a, b — стороны вписанного прямоугольника.
Если известна сторона описанного квадрата
R = a : 2, где a — сторона.
Сторона описанного квадрата равна диаметру окружности.
Если известны стороны и площадь вписанного треугольника
R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.
Если известна площадь и полупериметр описанного треугольника
R = S : p, где S — площадь треугольника, p — полупериметр треугольника.
Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.
Если известна площадь сектора и его центральный угол
R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.
Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.
Если известна сторона вписанного правильного многоугольника
R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.
В правильном многоугольнике все стороны равны.
Скачать онлайн таблицу
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.
http://hostciti.net/calc/matematika/segment-of-the-circle.html
http://skysmart.ru/articles/mathematic/radius-okruzhnosti
Выберите подписку для получения дополнительных возможностей Kalk.Pro
Любая активная подписка отключает
рекламу на сайте
-
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
-
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Доступ к скрытым чертежам -
Безлимитные сохранения расчетов
-
Более 10 000 пользователей уже воспользовались расширенным доступом для успешного создания своего проекта. Подробные чертежи и смета проекта экономят до 70% времени на подготовку элементов конструкции, а также предотвращают лишний расход материалов.
Подробнее с подписками можно ознакомиться здесь.
По сегменту определить радиус окружности
Небольшой калькулятор, который позволит нам тремя измерениями заданного сегмента круга определить его радиус
Вам нужно всего три измерения и два/один инструмент: линейка +уголок(что бы отмерить прямой угол)
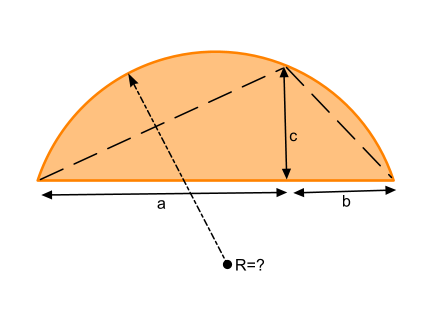
Итак, у вас есть неизвестный сегмент круга и вы измерили три значения (a,b,c)
Соединим точки на окружности между собой (пунктирная линия). Мы получили треугольник, с высотой (c) и общим основанием (a+b)
Этот треугольник оказывается вписанным в окружность, а мы знаем связь между площадью треугольника, его сторонами (p, q, m) и описанной окружностью радиусом (R)
(S=cfrac{pqm}{4R})
Тогда (R=cfrac{pqm}{4S})
Одна сторона нам известна (a+b)
две другие мы найдем по теореме Пифагора (sqrt{a^2+c^2}) и (sqrt{b^2+c^2})
Осталось решить что же делать с площадью
Вспомним, что площадь треугольника равна половине произведения основания треугольника на его высоту
(S=cfrac{(a+b)c}{2})
подставим все найденные выражения и получим
(R=cfrac{sqrt{a^2+c^2}sqrt{b^2+c^2}}{2c})
Если бы мы выбрали (a) и (b) равными то получили бы
(R=cfrac{{a^2+c^2}}{2c})
где (с) — уже являлась бы высотой сегмента.
Сегмент круга
Данный калькулятор считает параметры сегмента круга, а именно:
Перед вами 2 калькулятора, чтобы рассчитать параметры сегмента:
1) сегмент круга решается с помощью радиуса (R) и угла (A).
2) сегмент круга находим с помощью высоты и длины хорды.
Однако, как справедливо заметил наш пользователь:«на практике hourто случается, что как радиус дуги, так и угол неизвестны» (см. длина дуги ). Для этого случая для расчета площади сегмента и длины дуги можно использовать следующий калькулятор:
Калькулятор вычисляет радиус круга по длине хорды и высоте сегмента по следующей формуле:
Далее зная радиус и длину хорды, легко найти угол сегмента по формуле:
Остальные параметры сегмента, вычисляются аналогично первому калькулятору, по формулам, приведенным в начале статьи.
Следующий калькулятор вычисляет площадь сегмента по высоте и радиусу:
Информация по назначению калькулятора
Сегмент круга — это область, ограниченная дугой и хордой этого круга. Когда что-то делится на части, каждая часть называется сегментом. Точно так же сегмент является частью окружности. Но сегмент — это не какая-то случайная часть окружности, это определенная часть окружности, которая разрезана ее хордой.
Дуга — это часть окружности круга. Хорда — это отрезок прямой, соединяющий любые две точки на окружности круга.
Существует два типа сегментов: один — второстепенный сегмент, а другой — основной сегмент. Второстепенный сегмент образован малой дугой, а основной сегмент образован большой дугой окружности.
Далее представлены свойства сегмента круга:
⇒ Это область, которая окружена хордой и дугой.
⇒ Угол, уменьшенный на отрезок в центре окружности, совпадает с углом, уменьшенным на соответствующую дугу. Этот угол обычно известен как центральный угол.
⇒ Меньший сегмент получается путем удаления соответствующего большого сегмента из общей площади круга.
⇒ Большой сегмент получается путем удаления соответствующего меньшего сегмента из общей площади окружности.
⇒ Полукруг — это самый большой сегмент в любом круге, образованном диаметром и соответствующей дугой.
Онлайн калькулятор предназначен для нахождения параметров сегмента круга, таких как:
- Площадь
- Длина хорды
- Высота
- Длина дуги
- Периметр сегмента
- Центральный угол сегмента в градусах и радианах
— дуга и два радиуса окружности образуют сектор. Эти два радиуса и хорда сегмента вместе образуют треугольник. Таким образом, площадь сегмента окружности получается путем вычитания площади треугольника из площади сектора.
— находится через радиус и угол между радиусами (c = 2r * sin(α / 2))
— можно найти зная радиус и длину хорды (h = r — √(r2 — c2 / 4))
— находится путем умножения радиуса на центральный угол сектора в радианах (L = r * α)
— равен сумме длины дуги и длины хорды (Ps = L + c)