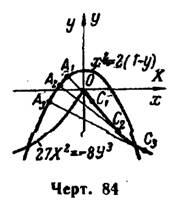Как найти радиус кривизны параболы в вершине - Avtoru.top

‹— Назад

Радиус кривизны

Определение 8.3 Радиусом кривизны кривой в точке называется число , где — кривизна линии в точке . Если кривизна в точке равна 0, то радиус кривизны формально полагаем равным .

Заметим, что для окружности это определение даёт значение радиуса кривизны, совпадающее с радиусом окружности (постоянное во всех точках окружности).

Без доказательства сообщим, что из всех окружностей, касающихся линии в фиксированной точке , наиболее плотно прилегает²⁴ к линии та окружность, которая имеет радиус, равный радиусу кривизны кривой в точке , и выпуклость в ту же сторону, что кривая . Эта окружность называется окружностью кривизны линии в точке .

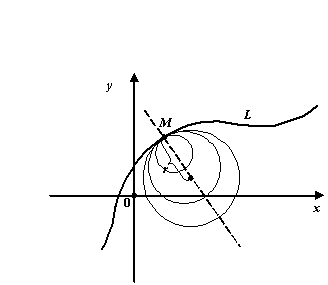
Рис.8.6.Окружности, касающиеся линии , и окружность кривизны

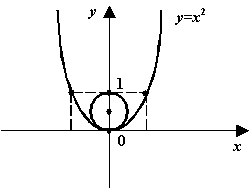
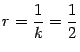
Пример 8.7 Радиус кривизны параболы в её вершине равен . Значит, окружность радиуса с центром в точке наилучшим образом приближает параболу в окрестности её вершины, то есть является для параболы окружностью кривизны в вершине параболы.

Рис.8.7.Окружность кривизны для параболы в вершине

Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции

Источник

(На
рисунке) В двух точках кривой M и M′
проведем единичные векторы касательных

.
Угол между этими касательными, называемый
углом
смежности,
обозначим через Δθ , а длину соответствующей
дуги MM′ траектории точки M – через
Δs . Отношение Κ_*
= Δθ/Δs
называется средней
кривизной кривой
на дуге MM′ , а предел этого отношения
при sΔ →0, если он существует,

называется кривизной
кривой в данной точке,
и она равна отношению величины

элементарного угла смежности к величине
элемента дуги

в этой точке. Очевидно, что кривизна
окружности радиуса R равна:

и постоянна во всех ее точках. Кривизна
произвольной кривой вообще не
постоянна и изменяется от точки к точке.
Если через три точки M₁,M,M₂
любой кривой провести окружность, то
в пределе (при приближении точек M₁
и M₂
к точке M ), она будет лежать в
соприкасающейся плоскости. Эта
предельная окружность называется
соприкасающимся
кругом или
кругом
кривизны.
Кривизна
кривой в точке M равна кривизне
соприкасающегося круга.
Центр круга
кривизны называется центром
кривизны, а
радиус этого круга –
радиусом кривизны кривой
в точке M . Обозначая радиус кривизны
через ρ , получим выражение кривизны
кривой в точке M :

.

Радиус
кривизны.Радиусом
кривизны кривой L
в точке

называется число

, где k
—
кривизна линии L
в точке M
. Если кривизна в точке
M
равна 0, то радиус кривизны формально
полагаем равным
+∞
. Заметим, что для окружности это
определение даёт значение радиуса
кривизны, совпадающее с радиусом
окружности (постоянное во всех точках
окружности). Без доказательства сообщим,
что из всех окружностей, касающихся
линии L
в фиксированной точке

, наиболее плотно прилегает к линии
L
та окружность, которая имеет радиус,
равный радиусу кривизны кривой в точке
M
, и выпуклость в ту же сторону, что кривая
L.
Эта окружность называется окружностью
кривизны
линии L
в точке M
.

Рис.1.Окружности,
касающиеся линии , и окружность кривизны.

Радиус кривизны параболы

в её вершине равен

. Значит, окружность радиуса

с центром в точке

наилучшим образом приближает параболу
в окрестности её вершины, то есть
является для параболы окружностью
кривизны в вершине параболы
окружностью
кривизны в вершине параболы.

Рис.2Окружность
кривизны для параболы в вершине

19.Проекции скоростей в ортогональной криволинейной системе координат.

Ортогональными
называются координаты в которых
метрический тензор имеет диагональный
вид.

где
d

В
ортогональных системах координат q =
(q¹,
q², …, q^d)
координатные поверхности ортогональны
друг другу. В частности, в декартовой
системе координат ортогональны друг
другу координатные оси Ox, Oy и Oz.
Ортогональные координаты представляют
собой частный случай криволинейных
координат. Наиболее часто в качестве
ортогональных координат используются
декартовы координаты, так как именно
в этих координатах большинство уравнений
имеют наиболее простой вид. Прочие
системы ортогональных координат
используются реже, в частности, для
решения краевых задач, таких как задача
о теплопроводности, диффузии и т. д.
Выбор той или иной системы ортогональных
координат определяется симметрией
системы. Например, при решении задачи
о распространении электромагнитной
волны от точечного источника выгодно
пользоваться сферической системой
координат; при решении задачи о колебании
мембраны предпочтительней цилиндрическая
система координат.

Изображения
по методу прямоугольных (ортогональных)
проекций основаны на следующем приеме:
проектируемый предмет представляют
себе помещенным внутри трехгранного
угла из взаимно перпендикулярных
плоскостей, причем так, чтобы каждое
из трех основных измерений предмета
(его длина, ширина и высота) располагалось
параллельно одной из трех плоскостей
проекций, как называют плоскости
трехгранного угла (рис. 2 и 3). Затем из
каждой точки, характеризующей размеры
и форму проектируемого предмета,
например призмы, проводят лучи,
направленные к каждой плоскости проекций
под прямым углом (перпендикулярно), и
точки пересечения лучей с плоскостью
проекций соединяют линиями подобно
тому, как они связаны между собой на
самом предмете. При ортогональном
проектировании намечают три плоскости
проекций для изображения видов спереди,
сверху и сбоку (справа или слева); оси
проекций — OX, OY, OZ, по направлениям
которых расположены длина, ширина и
высота призмы, помещенной внутри
трехгранного угла плоскостей проекций.Из
каждой вершины призмы ко всем трем
плоскостям проекций направлены
проектирующие лучи перпендикулярно к
одной из плоскостей для получения
проекций (изображений) данной вершины,
например А. Так получены: горизонтальная
проекция а1, вертикальная проекция a2,
профильная проекция а3, точно
воспроизводящие положение в пространстве
вершины А призмы. В результате подобного
проектирования всех других вершин
призмы получаются три изображения
призмы, называемые в архитектурной
практике планом, фасадом и боковым
фасадом архитектурных сооружений.
Следует отметить, что изображение ребер
призмы на этой плоскости проекций, к
которой они перпендикулярны, превращается
в точку (например, ребра АВ на профильной
плоскости в3 — а3), а изображение граней
призмы, перпендикулярных к двум из трех
плоскостей проекций, превращается в
прямую линию. О длине ребер, величине
и форме граней призмы можно судить лишь
по их изображениям на той плоскости
проекций, к которой параллельны данные
ребра или грань. Так, например, грань
призмы А — В — С — Е — F изображена в
истинную величину лишь на вертикальной
плоскости V. Однако на этом изображении
призмы нет размера ее толщины; два
других изображения призмы превратились
в прямоугольники и не дают представления
о форме передней и задней граней. Таким
образом, при ортогональном проектирований
представить себе форму и величину
предмета, изображенного в трех проекциях,
можно лишь путем сопоставления всех
трех его изображений. В практической
работе по ортогональному проектированию
описанный прием осуществляют не в
трехгранном углу, а на листе бумаги,
представляя себе, что плоскости угла
развернуты и расположены рядом; вид
призмы спереди — точно над видом сверху,
а вид сбоку — рядом с видом спереди и
справа или слева от него, в зависимости
от направления проектирующих лучей
(рис. 2, II). Рассматривая изображения
призмы, убеждаешься, что три ее вида
дают точное представление о размерах,
да и о форме призмы. Однако очевидным
недостатком таких изображений является
их малая наглядность — только в
результате опыта развивается умение
„читать» чертежи в ортогональных
проекциях, в данном примере — представить
себе форму призмы по трем ее изображениям
с разных сторон.

(рисуно
2)
Ортогональные
проекции геометрических тел

(рисунок
1)
процесс ортогонального проектирования

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Пример 3. Найти координаты центра кривизны и построить кривую и круг кривизны кривой:
1) $y=4x-x^{2}$ в ее вершине;
2) x=t-sin t,: y=1-cos t в точке, где $displaystyle t=frac{pi }{2}$ .
Решение. 1) Данное уравнение определяет параболу, ось которой параллельна оси . Найдем ее вершину как точку, где касательная параллельна оси , т. е. где y'=0 :

y'=4-2x;: y'=0 при x=2;: y(2)=4.

Далее по формулам

$displaystyle X=x-frac{dot{x}^{2}+dot{y}^{2}}{dot{x}ddot{y}-dot{y}ddot{x}}dot{y}=x-frac{1+(y')^{2}}{y''}y',$

$displaystyle Y=y+frac{dot{x}^{2}+dot{y}^{2}}{dot{x}ddot{y}-dot{y}ddot{x}}dot{x}=y+frac{1+(y')^{2}}{y''}.; ; (2)$

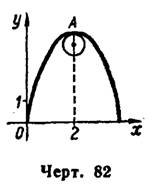
находим координаты центра кривизны данной параболы в ее вершине (2; 4)

$displaystyle X=x-frac{1+(y')^{2}}{y''}y'=2;: Y=y+frac{1+(y')^{2}}{y''}=frac{7}{2}$

и строим параболу и круг кривизны в ее вершине (рис. 82).
2) Находим производные dot{x}=1-cos t,: ddot{x}=sin t,: dot{y}=sin t,: ddot{y}=cos t , их значения при $displaystyle t=frac{pi }{2}$ :

$displaystyle dot{x}left ( frac{pi }{2} right )=1,: ddot{x}left ( frac{pi }{2} right )=1,: dot{y}left ( frac{pi }{2} right )=1,: ddot{y}left ( frac{pi }{2} right )=0,$

и по формулам (2) координаты центра кривизны

$displaystyle X=x-frac{dot{x}^{2}+dot{y}^{2}}{dot{x}ddot{y}-dot{y}ddot{x}}dot{y}=frac{pi }{2}+1;: Y=y+frac{dot{x}^{2}+dot{y}^{2}}{dot{x}ddot{y}-dot{y}ddot{x}}dot{x}=-1.$

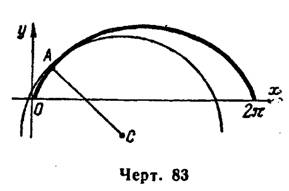
Затем строим данную циклоиду, ее точку $displaystyle Aleft ( frac{pi }{2}-1;1 right )$ , где
$displaystyle t=frac{pi }{2}$ , найденный центр кривизны $displaystyle Cleft ( frac{pi }{2}+1;-1 right )$ и круг кривизны (рис. 83).

Пример 4. В каких точках параболы $displaystyle y=sqrt{2}x^{2}$ радиус кривизны равен единице?
Решение. Находим производные displaystyle y'=2sqrt{2}x,: y''=2sqrt{2} и по формуле (1)

$displaystyle K=frac{left | y'' right |}{left [ 1+(y')^{2}right ]^{frac{3}{2}}}=frac{left | dot{x}ddot{y}-dot{y}ddot{x} right |}{(dot{x}^{2}+dot{y}^{2})^{frac{3}{2}}}, ; ; ; ; (1)$

радиус кривизны параболы в любой ее точке с абсциссой :

$displaystyle R(x)=frac{(1+8x^{2})^{frac{3}{2}}}{2sqrt{2}}.$

Полагая R(x)=1 , получим абсциссы искомых точек

$displaystyle 2sqrt{2}=(1+8x^{2})^{frac{3}{2}};: (2sqrt{2})^{frac{2}{3}}=1+8x^{2};: 8x^{2}=1;: x=pm frac{1}{2sqrt{2}}.$

$
Пример 5. В какой точке кривая $displaystyle y=e^{x}$ имеет наибольшую кривизну?
Решение. Находим производные $displaystyle y'=y''=e^{x}$ и кривизну данной кривой в любой точке:

$displaystyle K(x)=frac{e^{x}}{(1+e^{2x})^{frac{3}{2}}}.$

Далее ищем наибольшее значение функции K(x) , которая определена и непрерывна на всей числовой оси:

$displaystyle K'(x)=frac{e^{x}(1-2e^{2x})}{(1+e^{2x})^{frac{5}{2}}};: K'(x)=0$ при $displaystyle 1-2e^{2x}=0,$

т.е. в единственной точке $displaystyle x_{0}=-frac{ln 2}{2}$ . Определяя знаки K'(x) слева и справа от этой критической точки:

$displaystyle left{begin{matrix} X=x-frac{1+(y')^{2}}{y''}=x-frac{1+x^{2}}{-1}(-x);\ Y=y+frac{1+(y')^{2}}{y''}=1-frac{x^{2}}{2}+frac{1+x^{2}}{-1}; end{matrix}right.$

$displaystyle left{begin{matrix} X=-x^{3};\ Y=-frac{3}{2}x^{2}. end{matrix}right.$

Это параметрические уравнения эволюты. Исключая из них параметр , получим $displaystyle 27X^{2}=-8Y^{3}$ — уравнение полукубической параболы. Данная парабола и найденная ее эволюта изображены на рис. 84.

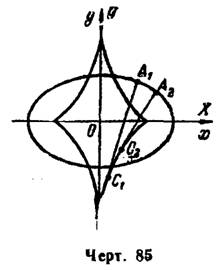
2) Из уравнений эллипса найдем производные dot{x}=-asin t,: ddot{x}=-acos t,: dot{y}=bcos t,: ddot{y}=-bsin t и по формулам (2) получим, после упрощений, параметрические уравнения эволюты эллипса

$displaystyle X=frac{c^{2}}{a}cos ^{3}t,: Y=-frac{c^{2}}{b}sin ^{3}t,$ где $displaystyle c^{2}=a^{2}-b^{2}$

Эллипс и его эволюта построены на рис. 85.

Источник

По этой ссылке вы найдёте полный курс лекций по математике:

Пусть 7 — регулярная кривая и Af0 — точка этой кривой. Определение. Кривизной к кривой 7 в точке М0 называется предел отношения при — наименьший угол между касательными к кривой 7 в точках — длина дуги ^М0М (рис. 16). Кривизна кривой характеризует скорость ее откл онения от касательной. Кривизна прямой равна нулю в каждой ее точке.

Кривизна окружности постоянна и равна j, где о — радиус окружности. 2-регулярная кривая имеет в каждой своей точке определенную кривизну. Если — естественная параметризация кривой 7, то ее кривизна может быть найдена по формуле 6 случае произвольной параметризации Кривизна плоской кривой. Радиус кривизны. Эволюта и эвольвента плоской кривой Наглядный способ образования эвольвенты Пространственные кривые. Способы задания При явном способе задания Пример 1.

Кривизна параболы у = г1 в ее вершине 0(0,0) равна 2. Кривизна плоской кривой по определению неотрицательна. Однако во многих ^y4a#v кривизне плоской кривой полезно отнести знак. Обычно выбор знака связы-ваютс папра °нием вращения касательной к кривой при перемещении вдоль кривой при возрастании параметра: «4-»: кривизна кривой положительна, если касательная вращается против часовой стрелки (в положительном направлении); «-»: кривизна кривой отрицательна, если касательная вращается по часовой стрелке (в отрицательном направлении) (рис. 17). шсдосрмвиэ на явно задан ной кривой ВЫЧИСЛЯЕТСЯ ПО’ Прмир 2.

Кривизна синусоиАы у = sin г положи тельнв (равна 1)вточ*е J, -l) и отрицательна (равна -1) в точив l) (рис. 18). В точке о ириеиэна синуахд* рвана нулю. Если кривизна кривой в точке Мо(*о) отлична от нуля, то определен родное кривизны кривой в этой точке О Окружность радиуса R(to), проходящая через точку Afb(fo), имеющая в этой точке с кривой 7 об- рнс.18 шую касательную и лежащ ая поту же сторону от этой касательной, что и кривая 7, называете я соприкасающейся окружностью кривой 7 в точке Afo, или окружностью кривизны (рис. 19).

Ясно, что кривизны кривой и ее окружности кривизны в их общей точке совпадают. Центр соприкасаю-щейсяокружности называ ется центром кривизны кривой в точке Af0. Его координаты а и b вычисляются по формулам • Пример 3. Для параболы у = х2 в ее вершина 0(0,0) имеем Я» j, в =0. Поэтом у окружность кривизны параболы в точев О может быть задана уратежем (рис.20).

Эволютой регулярной плоской кривой называете я множество ее центро в крив нзны (рис. 21). Уравнения эволюты кривой 7, заданной параметрически, имеют следующий вид: Найти эволюту параболы Пример 5. Эволюта окружности состоит из одной точки — ее центра 0(0,0). Если кривизна регулярной кривой 7 отлична от нуля и производная к (s) сохрани ет знак вдоль кривой 7, то эволюта этой кривой состоит только из регулярных точек.

Если кривизна k(s) регулярной кривой 7 равна нулю в некоторой точке кривой, k(so) = 0, а ее производная сохраняет знак вдоль кривой 7, то эволюта этой кривой распадается на две регулярные кривые, являющиеся эволютами частей кривой 7 при s Каждая из этих ветвей уходит в бесконечность при s -> sq.

Пример в. Кривизна параболы у = х2 в ее вершине 0(0,0) отлична от нуля, а производная кривизны 2 не сохраняет знака вдоль параболы. Поэтому эволюта параболы и имеет особенность — точку возврата первого рода (см. рис. 22). Пример 7. Кривизна кубичной параболы у = х3 Кривизна плоской кривой. Радиус кривизны. Эволюта и эвольвента плоской кривой Наглядный способ образования эвольвенты Пространственные кривые.

Способы задания при х = Q обращается в нуль, а ее производная в окрестности точки 0(0,0) сохраняет знак. Поэтому эволюта кубической параболы распадается на две регулярные ветви (рис. 23). / Эвольвентой кривой 7 называется кривая, для которой данная кривая 7 является эволютой. Эвольвента кривой 7 совпадает с множеством концов отрезков касательных к кривой 7, отложенных от точек касания, длины которых убывают на величину, равную приращению дуги кривой 7. Наглядный способ образования эвольвенты Отложим на кривой 7 от ироизвольной точки Мо этой кривой дугу длины с.

Обозначим второй конец дуги через Af. Представим теперь, что на дугу ^mqm наложена гибкая нерастяжимая нить, один из концов которой закреплен в точке mq . При сматывании натянутой нити с кривой 7 (как с шаблона) второй ее конец М опишет эвольвенту кривой 7 (рис. 24). где с — произвольная постоянная. Тем самым, у любой регулярной кривой существует бесконечное число эвольвент. Пример 8. Эвольвенты окружности описываются уравнениями вида где с — параметр семейства эвольвент (рис. 25). § 3.

Пространственные кривые. Способы задания Onptделение. Параметрически заданной пространственной кривой называется множество 7 точек М, координаты х, у и г которых определяются соотношениями где — функции,непрерывные на отрезке [а, Ь), или в векторной форме г, где Наглядно параметрически заданную кривую можно представлять какслед движущейся точки М с координатами , Пример 1. ‘ уравнение дау» «итко*винтовой лимии (рис.27). : ТЪчки А и Л кривой 7, Отвечающие значениям t = а и t = 6 параметра соответственно, называются начальной и конечной точками кривой у. Кривая 7 называется зо-мкнутой, если эти точки совпадают.

Возможно вам будут полезны данные страницы:

Понятия гладкой и регулярной пространственной кривой вводятся в полном соответствии с плоским случаем: кривая 7, заданная параметрическим векторным уравнением s называется п-регулярной, если 1) векторная функция г(() имеет на отрезке [а, Ь) непрерывные производные порядка п и 2) скорость кривой пайЬжительна в каж^бй^очке. Другим распространенным способом задания пространственной кривой является неявный способ задания кривой как множества точек М, координаты х,у и z которых являются решением системы уравнений где функции ) подчиняются определенным условиям. Укажем важный частный случай, наиболее часто встречающийся на практике:

z) являются гладкими функциями своих аргументов и в некоторой точке выполнены условия: Неявно заданная пространственная кривая, в каждой точке которо й выполняется условие (3), будет регулярной. Пример 2. Кримя, мдамша* уронвниями будет регулярной (рис.28). Эта кримя предсташлиет собой большую окружность — о>ч*нй» сферы плоскостью, препод*-щей *вр*э ее центр. Пусть 7 — регулярная кривая, заданная параметрически. Обозначим через Мо точку кривой 7, отвечающую значению to параметра, а через М — точку кривой, отвечающую значению t из некоторой окрестности *о»

Прямая MqT называется касательной к кривой 7 в точке Мо, если при М —» Мо наименьший из углов АО между этой прямой и переменной прямой М0М Рис. 2s стремится к нул ю. Регулярная кривая имееткасател ьиую в каждой своей точке. Вектор скорости кривой в точке М0 коллинеарен ее касательн ой в этой точке. Уравнения касательной к кривой 7 в точке Мо(®е» Уо, «о) имеют следующий вид Любая прямая, проходящая через точку Щ перпендикулярно касательной к кривой 7 в точке М0, называется нормалью кривой 7 в точке Мо.

Плоскость/ Проходящая через точку М0

кривой 7 перпендикулярно ее касательной MoT в этой точке, называется нормальной плоскостью кривой в точке Мо (рис. 29). Уравнение нормальной плоскости кривой, заданной параметрически, имеет следующий вид: Ясно, что все нормали кривой в точке Мо лежат в ее нормальной плоскости в этой точке. Пример 3. Касательная и нормальная плоскость винтовой линии в точке ^, (при t = j) описываются уравнениями соответственно. Регулярная пространственная кривая спрямляема.

Длина кривой, заданной векторным уравнением вычисляется по формуле В случае координатного задания кривой Кривизна плоской кривой. Радиус кривизны. Эволюта и эвольвента плоской кривой Наглядный способ образования эвольвенты Пространственные кривые. Способы задания имеем Значение функции равно длине дуги кривой 7, заключенной между точками А(а) и M(t) (рис. 30). Эта функция строго возрастает на отрезке [о, Ь), причем Тем самым, длину дуги можно взять за новый параметр на кривой.

Параметризация кривой, где в качестве параметра взята длина дуги з, называется естественной параметризацией. Кривая с естественной параметризацией имеет единичную скорость (Ьтносительно этой параметризации). Для того, чтобы параметризация кривой была естественной, необходимо и достаточно выполнение условия или, что то же самое, Пример 4. Для винтовой линии имеем Поэтому естественная параметризация винтовой линии может быть записана так

Источник

Радиус кривизны

19.Проекции скоростей в ортогональной криволинейной системе координат.

Не пропустите также: