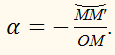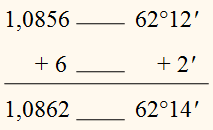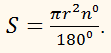Как найти радианной мере величины углов

Угол может измеряться следующими величинами:

1. Градусами (и соответствующими ему величинами: угловыми минутами и секундами);
2. Радианами.

Градусная мера угла

Если взять развернутый угол (это два прямых угла) и поделить его на 180 частей, то одна такая часть будет называться одним градусом. Для того, чтобы измерить градусную меру угла, необходимо посчитать, сколько раз 1 градус входит в данный угол. Полученное число и будет ответом.

Если угол таков, что его нельзя измерить целым числом, либо же он меньше единичного угла, то используют такие меры измерения как угловые минуты и секунды.

Если градус поделить на 60 частей, то одной такой частью будет минута. В свою же очередь, если минуту разделить на те же 60 частей, то полученным числом будет 1 секунда.

Радианная мера угла

Радианом называют угол, образованный дугой окружности длинной равной радиусу этой окружности.

Длина окружности равна:

где rr — радиус этой окружности.

Тогда, разделив на радиус, получаем, что полный угол в радианах равен:

lr=2⋅π⋅rr=2⋅π радианfrac{l}{r}=frac{2cdotpicdot r}{r}=2cdotpitext{ радиан}

В градусах этот же угол равен, как известно, 360∘360^{circ}.

Отсюда находим связь между радианами и градусами:

Это та главная формула, которая нужна, чтобы переводить градусы в радианы и наоборот.

Перевод градусов в радианы

Если по условию известна градусная мера угла, то чтобы перевести ее в радианную, нужно сделать следующие действия: умножить ее на πpi и разделить на 180.

Перевод радиан в градусы

Чтобы перевести радианы в градусы, нужно умножить угол в радианах на 180 и разделить на πpi.

Ищете, где можно заказать задачу по математике недорого? Обратитесь к нашим экспертам в данной области!

Тест по теме «Перевод градусов в радианы и наоборот»

ВИДЕО УРОК

Помимо градусной меры
углов существует так называемая радианная мера. Эта мера широко используется в
тригонометрии, в математическом анализе и в его приложениях.

Рассмотрим
произвольный положительный угол  α. Возьмём на
стороне  ОА  этого угла

 произвольную точку  М,
не совпадающую с вершиной  О  угла. Пусть 

– путь, который
пройдёт точка  М, если произвести указанный поворот  α  от  ОА  к  ОВ.

Радианной мерой
угла  α  называется отношение этого пути к
радиусу  ОМ.
Радианную меру угла условимся обозначать той же буквой, что и сам угол:

Если  α –
отрицательный угол,

то радианной мерой
назовём отрицательное число:

Радианная мера угла определяется только
углом.

Единицей при радианном
измерении углов служит радиан.

Радианом называется
центральный угол, опирающийся на дугу окружности, длина которой равна длине
радиуса той же окружности.

В основе определения радиана – всё равно окружность.
Угол в  1  радиан, это
угол, который вырезает из окружности дугу, длина которой (L) равна длине радиуса
(R).

Соотношение между радианом и градусом.

На рисунке этот малюсенький
угол имеет величину  1 градус:

Один радиан много больше одного градуса. А во сколько раз ?

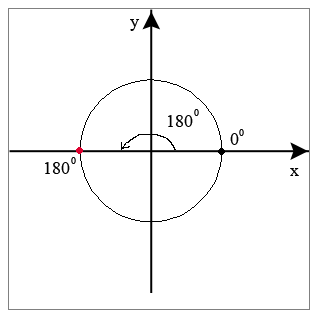
 Смотрим следующую картинку. Развёрнутый угол размером в  180°.

А теперь нарежем этот полукруг радианами.

 Видим, что в  180°  укладывается  3  с хвостиком
радиана. Этот хвостик – 0,1415926 … .

Действительно, в 
180°  укладывается  3,1415926… радиан. Всё время
писать 3,1415926… неудобно. Поэтому
вместо этого бесконечного числа всегда пишут просто:

π

Вот теперь можно записать приближённое равенство:

180° ≈ 3,14 радиан

Или точное равенство:

180° = π радиан

Определим, сколько градусов в
одном радиане. Если в  3,14  радианах  180°  градусов, то в  1  радиане в  3,14  раз меньше! То есть, мы делим
первое уравнение (формула – это тоже уравнение!) на 3,14:

В одном радиане примерно  60°.

Человек видит «Пи» и считает, что это  180°. Но «Пи» – это число! Число  3,14, а никакие не градусы! Это «Пи» радиан = 180°!

Ещё раз: «Пи» – это число! 3,14. Иррациональное, но
число. Такое же, как  5  или  8. Можно, к примеру,
сделать примерно «Пи» шагов. Три шага и ещё немножко. Или купить
«Пи» килограммов конфет. Если продавец образованный попадётся…

Перевод градусов в радианы и
обратно.

Если угол задан в радианах с числом «Пи»,
всё очень просто. Мы знаем, что

«Пи» радиан
= 180°.

Вот и подставляем вместо «Пи» радиан – 180°. Получаем угол в
градусах. Сокращаем, что сокращается, и ответ готов.

ПРИМЕР:

Нужно выяснить, сколько градусов в угле «Пи»/2 радиан.

Или:

Обратный перевод чуть сложнее. Если угол дан в градусах,
мы должны знать, чему равен один градус в радианах, и умножить это число на
количество градусов.

ПРИМЕР:

Чему
равен  1°  в радианах ?

Смотрим на формулу и видим, что если  180° = «Пи» радиан,
то  1°  в  180  раз меньше. Или, другими словами, делим
уравнение (формула – это тоже уравнение!) на  180:

Умножаем
число градусов на это значение и получаем угол в радианах.

ПРИМЕР:

 Или, аналогично:

Чтобы найти радианную
меру любого угла по его данной градусной мере, надо умножить число градусов на

число минут – на

число секунд – на

и сложить найденные произведения.

ПРИМЕР:

Выразить в радианах угол,
равный  22°30‘.

РЕШЕНИЕ:

Искомое число радианов получим, умножив

ПРИМЕР:

Найти радианную меру угла  12°30‘  с точностью до четвёртого
десятичного знака.

РЕШЕНИЕ:

Умножим  12  на  0,017453 

получим  ≈ 0,2094.

Умножим  30  на  0,000291 

получим  ≈ 0,00873.

12°30‘ ≈ 0,2094 + 0,00873 ≈ 0,2181
рад.

Чтобы
найти градусную меру любого угла по его данной радианной  мере, надо умножить число радиан на

(относительная
погрешность результата составит 0,0004%,
что составляет абсолютной погрешности  5»  для полного оборота  360°).

ПРИМЕР:

Выразить в градусах угол,
равный  ^𝜋/₁₂ радианов.

РЕШЕНИЕ:

Имеем:

ПРИМЕР:

Найти градусную меру угла  1,4
рад  с точностью
до  1‘.

РЕШЕНИЕ:

Последовательно найдём

1 рад ≈ 57°17‘45»,

0,4
рад ≈ 0,4×57°.296
= 22°.9184,

0°.9184×60 ≈ 55‘.104,

0‘.104×60 ≈ 6».

Таким
образом

0,4
рад ≈
22°55‘6».

И тогда:

1 рад ≈ 57°17‘45»  +  0,4 рад ≈
22°55‘6»

 = 1,4 рад ≈ 80°12‘51».

После
округления этого результата до требуемой точности в  1‘  окончательно
получим

1,4
рад ≈
80°13‘.

В обозначении меры угла в радианах почти всегда опускают
слово <<радиан>>. Таким образом, записи

α =
2, α = ¹/₂, α = ⁷/₉

надо понимать как

α =
2 радиана,

α =
¹/₂ радиана,

α = ⁷/₉ радиана.

ПРИМЕР:

Выразить в градусах угол  α, равный  2.

РЕШЕНИЕ:

Имеем:

α ≈ 57°3 ∙ 2 ≈ 114°6.

Широко распространено соглашение, по которому под словом <<угол>>
подразумевают не угол как геометрический образ, а число, измеряющее его в
радианах или градусах.

ПРИМЕР:

Угол  ^π/₂, угол  36°,
угол  1.

 В частности, в
выражениях типа  <<угол
поворота>> под словом <<угол>>  понимается обычно мера угла.

Таблица соотношений между градусным и радианным
выражениями некоторых углов.

Для облегчения вычислительной работы при переходе от
градусной меры угла к радианной и обратно пользуются специальными таблицами.

Отметим, что радианная мера одного полного
оборота

 равна:

Если углы измерены в градусах, то один полный
положительный оборот будет равен  360°. Отсюда вытекают следующие соотношения:

360° = 2π (≈
6,2832) радианов,

270° = ^3𝜋/₂ (≈ 4,7124) радианов,

180° = π (≈ 3,1416)
радианов,

 90° = ^𝜋/₂ (≈ 1,5708) радианов,

 60° = ^𝜋/₃ (≈ 1,0472) радианов,

 45° = ^𝜋/₄ (≈ 0,7854) радианов,

 30° = ^𝜋/₆ (≈ 0,5236) радианов.

Как пользоваться таблицами Брадиса ?

В книге В. Брадиса <<Четырёхзначные математические таблицы>>
под номером  XVI  помещена таблица, которая озаглавлена
<<Радианная мера>>.

Пометка в скобках
расшифровывается так: дуга, содержащая  A°, равна

радианов.

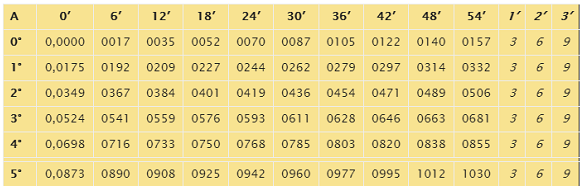
В левом столбце таблицы
под буквой  А  даны
числа градусов, содержащихся в угле, а в верхней и самой нижней строках – числа
минут, кратных  6.

Покажем на примерах как пользоваться этой таблицей.

ПРИМЕР:

Угол  71°24‘  перевести в радианы.

РЕШЕНИЕ:

На пересечении строки,
начинающейся с  71°, и столбца, помещённого
вверху  24‘,
читаем:

1,2462

(число целых указывается в таблице в начале строки и дальше даются
только десятичные знаки).

При переводе в радианы угла с любым числом минут, не кратным  6, пользуются соответствующими поправками, которые помещены
в последних трёх столбцах под числами минут:

1‘, 2‘,
3‘.

ПРИМЕР:

Угол  23°20‘  перевести в радианы.

РЕШЕНИЕ:

Имеем:

Данный угол  23°20‘  равен  0,4073  радиана.

 ПРИМЕР:

Найти градусное выражение угла,
содержащего  1,0862 радиана.

РЕШЕНИЕ:

Имеем из таблицы:

Данный угол равен  62°14‘.

Когда то в Древнем Египте мучились следующим вопросом. Во
сколько раз длина окружности больше длины её диаметра? И так измеряли, и
этак… Всё получалось немного больше трёх. Пока окончательно не доказали, что
как бы мелко не нарезать окружность на равные кусочки, из таких кусочков
составить ровно длину диаметра нельзя… В принципе нельзя.
Ну, во сколько раз окружность больше диаметра установили. Примерно. В  3,1415926… раз.

Это и есть число
«Пи». После запятой – бесконечное число цифр без всякого порядка…
Такие числа называются иррациональными. Это и означает, что из равных кусочков
окружности диаметр ровно не сложить. Никогда.

Для практического применения принято запоминать всего
две цифры после запятой:

π = 3,14.

Так как длина окружности больше диаметра в
«Пи» раз, имеет смысл запомнить формулу длины окружности:

L = π d

где  L – длина окружности,
а  d – её диаметр. 

При радианном измерении углов заметно упрощается ряд формул. Так, для окружности
радиуса  r  длина  l  его дуги  α  радиан можно
найти по формуле

l
= αr,

площадь S  сектора круга радиусом  r, в дуге которого находится  α  радиан, вычислим по формуле

Эти формулы проще, чем аналогичные формулы

и

Для вычисления дуги окружности и площади
сектора, дуги которых (величиной  n°) измеряются с помощью
градусной меры. Эти особенности радианной меры привели к тому, что в
тригонометрии отдают преимущество радианному, а не градусному измерении.

Для того, чтобы дать ответ на поставленный вопрос необходимо выяснить соотношение между градусами и радианами.

Мы чаще сталкивается с тем, что в геометрии углы измеряются градусами. Но есть еще и радианная мера угла.

Чтобы понять, что это такое, возьмем развернутый угол ( 180 градусов ), стороны которого одновременно являются диаметром окружности. Для вычисления радианной меры данного угла нужно длину окружности между сторонами угла разделить на длину радиуса:

(π х r)/r = π ( радиан ), а в градусах этот угол составляет 180.

π радиан = 180 градусов, отсюда 1 градус = π/180 радиан.

Чтобы перевести градусную меру угла в радианную необходимо заданное количество градусов умножить на π и разделить на 180.

Если провести вычисления, то мы узнаем, что 1 градус = 0,0175 радиана. Теперь можно действовать еще проще: заданное количество градусов умножить на 0,0175.

****************­*****************­*****************­******

Рассмотрим пример:

Найдем радианную меру угла 30 градусов.

Для этого 30 х 0,0175 = 0,525 (радиана).

Радианная мера угла 30 градусов составляет 0,525 радиана.

Перевод градусов в радианы и обратно

Чтобы перевести градусы в радианы и обратно, воспользуйтесь нашим удобным онлайн конвертером:

Перевод градусов в радианы

Просто введите значение угла в градусах и получите результат в радианах с подробным решением.

Перевод радиан в градусы

Просто введите значение угла в радианах и получите результат в градусах с подробным решением.

Теория

Градусы в радианы

Радианы в градусы

§ 11. Радианная мера углов

1. Понятие угла

В геометрии 
Угол — геометрическая фигура, образованная двумя лучами, которые выходят из одной точки.

В тригонометрии*
Угол — фигура, образованная при повороте луча на плоскости около начальной точки.

2. Измерение углов
Градусная мера углачасть развернутого угла)

Каждому углу ставится в соответствие градусная мера α ∈ [0°; 180°].

Каждому углу как фигуре ставится в соответствие угол поворота, с помощью которого образован этот угол. Угол поворота

α ∈ (–×; +×).

Объяснение и обоснование

1. Понятие угла. В курсе геометрии угол определяется как геометрическая фигура, образованная двумя лучами, которые выходят из одной точки. Например, угол AOB, изображенный в первом пункте таблицы 16, — это угол, образованный лучами OA и OB.

Угол можно рассматривать также как результат поворота луча на плоскости около начальной точки. Например, поворачивая луч OA около точки O от начального положения OA до конечного положения OB, также получим угол AOB. Заметим, что достичь конечного положения ОВ можно при повороте луча OA как по часовой стрелке, так и против нее.

2. Измерение углов. Данные выше различные определения угла приводят к различному пониманию измерения углов.

В курсе геометрии каждому углу соответствует его градусная мера, которая может находиться только в пределах от 0° до 180°, и поэтому, например, для прямого угла AOB  его мера записывается однозначно: ∠ AOB = 90° (1° — это 1/180 часть развернутого угла).

При измерении углов поворота договорились, что направление поворота против часовой стрелки считается положительным, а по часовой стрелке — отрицательным.

Поэтому при измерении углов, образованных при повороте луча около начальной точки, мы можем получить как положительные, так и отрицательные значения углов поворота. Например, если угол AOB, в котором лучи ОА и ОВ являются взаимно перпендикулярными, получен при повороте луча OA на угол 90° против часовой стрелки, то значение угла поворота β (см. соответствующий рисунок в пункте 2 табл. 16) равно +90° (или просто 90°). Если тот же угол AOB получен при повороте луча OA на угол 270° по часовой стрелке (понятно, что полный оборот — это 360°), то значение угла поворота γ равно (–270°). Этот же угол AOB можно получить также при повороте луча OA против часовой стрелки на 90° и еще на полный оборот; в этом случае значение угла поворота ϕ равно 90° + 360°, то есть 450° и т. д.
 Выбрав как значение угла поворота произвольное отрицательное или положительное число (градусов), мы всегда можем повернуть луч OA (по часовой стрелке или против нее) и получить соответствующий угол AOB. Таким образом, величина угла поворота (в градусах) может принимать все действительные значения от.

Для измерения углов принимают определенный угол за единицу измерения и с ее помощью измеряют другие углы.

За единицу измерения можно принять любой угол, например один градус (1°) — 1/180 часть развернутого угла.

В технике за единицу измерения углов принимают полный оборот (заметим, что 1 градус — это 1/360 часть полного оборота).

В мореходстве за единицу измерения углов принимают румб, равный 1/32 час ти полного оборота.

В математике и физике, кроме градусной меры углов, используется также радианная мера углов.

Если рассмотреть некоторую окружность,

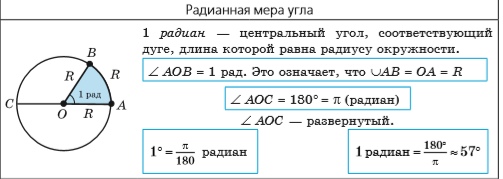
то 1 радиан — это центральный угол, соответствующий дуге, длина которой равна радиусу окружности.

Таким образом, если угол AOB равен одному радиану (рис. 59), то это означает, что ∪AB = OA = R.

Установим связь между радианной и градусной мерами углов. Центральному развернутому углу AOC, с градусной мерой 180°, соответствует полуокружность, то есть дуга, длина которой равна πR, а углу в один радиан — дуга длиной R. Итак, радианная мера развернутого угла AOC равна радиан. Таким образом, одному и тому же развернутому углу АОС соответствует градусная мера 180° и радианная мера π радиан. Это соответствие часто записывают так: 

Задача 1 Выразите в радианах величины углов, градусная мера которых равна: 30°; 45°; 60°; 90°; 270°; 360°.
 Поскольку 30° — это 1/6часть угла 180°, то из соответствия 180° = π (рад)
получаем, что 30°=6/π (рад).

Аналогично можно вычислить и величины других углов.

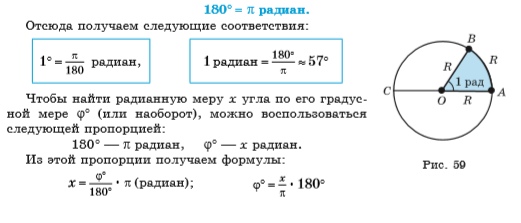
В общем случае учитываем, что 1°=π/180 радиан, тогда:

Поскольку радианными мерами рассмотренных углов приходится пользоваться достаточно часто, запишем полученные результаты в виде справочной таблицы:

Замечание. Чаще всего при записи радианной меры углов наименование единицы измерения «радиан» (или сокращенно рад) не пишут, но подразумевают его. Например, вместо равенства 90 2 °=π радиан пишут иногда 90 °=π/2 .

Задача 2 Выразите в градусах величины углов, радианнная мера которых равна: π/10 ; 2π/3 ; 3π/4 ; 5.

 Поскольку π/10 — это 1/10 часть угла π, то из соответствия π = 180° получаем, что π/10=18° . Аналогично можно вычислить и величины углов 2π /3  и 3π/4 .

В общем случае учитываем, что 1 радиан=180°/π , тогда:

Отметим, что далее в этом разделе будет рассматриваться в основном радианная мера угла и утверждения будут доказаны для радианной меры угла. Однако их можно переформулировать и для градусной меры угла, пользуясь приведенными выше соотношениями.

Условимся далее вместо слов «угол, радианная мера которого равна α радиан» говорить коротко «угол α».

Вопросы для контроля

1. Объясните, как можно определить угол с помощью поворота луча. Как при таком определении измеряются углы?

2. Как вы понимаете такие утверждения: «Величина угла равна 450°», «Величина угла равна (–225°)»? Изобразите эти углы.

3. Как можно определить угол в 1°?

4. Дайте определение угла в 1 радиан.

5. Чему равна градусная мера угла в π радиан?

6. Объясните на примерах, как по радианной мере угла найти его градусную меру и наоборот — по градусной мере угла найти его радианную меру.
Упражнения

1°. Изобразите угол, образованный поворотом луча OA около точки O на: 1) 270°; 2) –270°; 3) 720°;

4) –90°; 5) 225°; 6) –45°;

7) 540°; –180°; 9) 360°; 10) –60°.

2°. Чему равны градусные и радианные меры углов поворота, показанных на рисунке 60?

3. Выразите в радианной мере величины углов, градусная мера которых равна:

1 °) 225°; 2°) 36°; 3) 100°; 4) –240°; 5) –22,5°; 6) –150°.

4. Выразите в градусной мере величины углов, радианная мера которых равна:

1) 3π; 2) 3 4 π; 3) −2 5 π;

4) 7 6 π; 5) − π 18 ;

6) 11 6 π;7) −π 8 ; 3.
 5. С помощью калькулятора (или таблиц) найдите радианные меры углов, градусная мера которых равна:

1) 27°; 2) 132°; 3) 43°; 4) 114°.

6. С помощью калькулятора (или таблиц) найдите градусные меры углов, радианная мера которых равна:

1) 0,5585; 2) 0,8098; 3) 3,1416; 4) 4,4454.