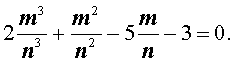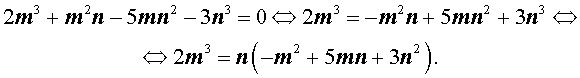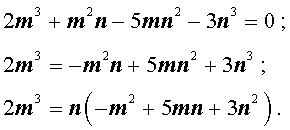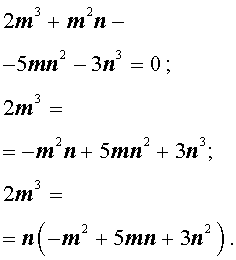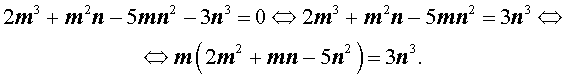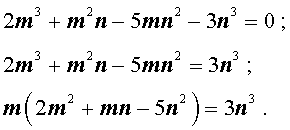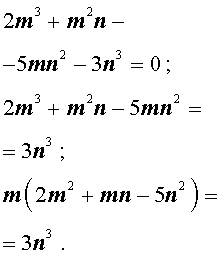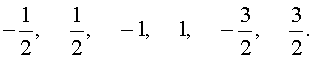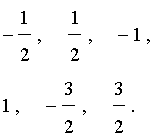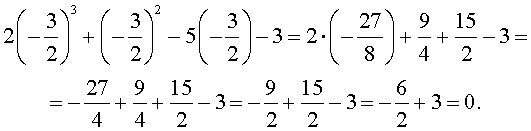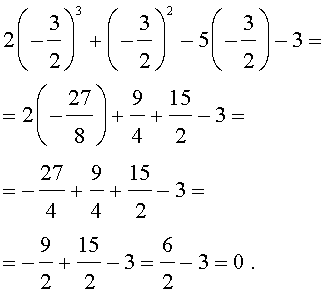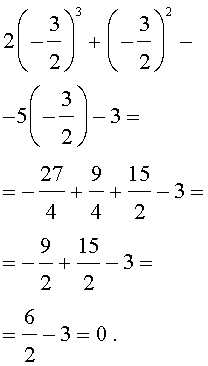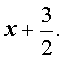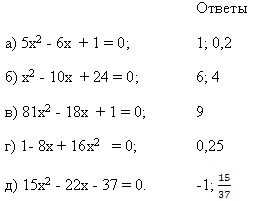Как найти рациональный корень квадратного уравнения

10.5. НАХОЖДЕНИЕ РАЦИОНАЛЬНЫХ КОРНЕЙ МНОГОЧЛЕНА С ЦЕЛЫМИ КОЭФФИЦИЕНТАМИ

Умножим обе части равенства (1) на (q ≠ 0). Получаем

В равенстве (2) все слагаемые, кроме последнего, делятся на р. Поэтому

Но когда мы записываем рациональное число в виде p/q, то эта дробь счи­тается несократимой, то есть р и q не имеют общих делителей. Произве­дение a0q n может делиться на р (если р и q — взаимно простые числа) только тогда, когда a0 делится на р. Таким образом, р — делитель свобод­ного члена a0.

Аналогично все слагаемые равенства (2), кроме первого, делятся на q. Тогда

Отметим два следствия из этой теоремы. Если взять q = 1, то корнем многочлена будет целое число р — делитель a0. Таким образом, имеет место:

Следствие 1. Любой целый корень многочлена с целыми коэффи­циентами является делителем его свободного члена.

Если в заданном многочлене f (х) коэффициент аn = 1, то делителями аn могут быть только числа ±1, то есть q =±1, и имеет место:

Следствие 2. Если коэффициент при старшем члене уравнения с целыми коэффициентами равен 1, то все рациональные корни этого уравнения (если они существуют) — целые числа.

Задача 1 Найдите рациональные корни многочлена 2х 3 – х 2 + 12х – 6.

Пусть несократимая дробь p/q является корнем многочлена. Тогда р не­обходимо искать среди делителей свободного члена, то есть среди чисел ±1, ±2, ±3, ±6, а q — среди делителей старшего коэффициента: ±1, ±2.

Таким образом, рациональные корни многочлена необходимо искать сре­ди чисел ±1/2, ±1, +±3/2, ±2, ±3, ±6. Проверять, является ли данное число корнем многочлена, целесообразно с помощью схемы Горнера. При x = 1/2 имеем следующую таблицу.

Кроме того, по схеме Горнера мож­но записать, что

Многочлен 2х 2 + 12 не имеет действительных корней (а тем более рацио­нальных), поэтому заданный многочлен имеет единственный рациональ­ный корень x =1/2.

Задача 2 Разложите многочлен Р (х) = 2х 4 + 3х 3 – 2х 2 – х – 2 на множители.

Ищем целые корни многочлена среди делителей свободного члена: ±1, ±2. Подходит 1. Делим Р (х) на х – 1 с помощью схемы Горнера.

Тогда Р (х) = (х – 1)(2х3 + 5х 2 + 3х + 2). Ищем целые корни кубического многочлена 2х 3 + 5х 2 + 3х + 2 среди делителей его свободного члена: ±1, ±2. Подходит (–2). Делим на х + 2

Квадратный трехчлен 2х 2 + х +1 не имеет действительных корней и на линейные множители не расклады­вается.

Ответ: Р (х) = (х – 1)(х + 2)(2х 2 + х +1).

Отметим, что во множестве действительных чисел не всегда можно найти все корни многочлена (например, квадратный трехчлен х 2 + х + 1 не имеет действительных корней). Таким образом, многочлен n-й степени не всегда можно разложить на линейные множители. В курсах высшей алгебры дока­зывается, что многочлен нечетной степени всегда можно разложить на ли­нейные и квадратные множители, а многочлен четной степени представить в виде произведения квадратных трехчленов.

Например, многочлен четвертой степени раскладывается в произведение двух квадратных трехчленов. Для нахождения коэффициентов этого раз­ложения иногда можно применить метод неопределенных коэффициентов.

Задача 3 Разложите на множители многочлен х 4 + х 3 + 3х 2 + х + 6.

Попытка найти рациональные корни ничего не дает: многочлен не имеет рациональных (целых) корней.

Попытаемся разложить этот многочлен в произведение двух квадратных трехчленов. Поскольку старший коэффициент многочлена равен 1, то и у квадратных трехчленов возьмем старшие коэффициенты равными 1. То есть будем искать разложение нашего многочлена в виде:

где а, b, с и d — неопределенные (пока что) коэффициенты. Многочлены, стоящие в левой и правой частях этого равенства, тождественно равны, поэтому и коэффициенты при одинаковых степенях х у них равны. Рас­кроем скобки в правой части равенства и приравняем соответствующие коэффициенты. Это удобно записать так:

Попытка решить эту систему методом подстановки приводит к уравне­нию 4-й степени, поэтому попробуем решить систему (4) в целых числах. Из последнего равенства системы (4) получаем, что b и d могут быть толь­ко делителями числа 6. Все возможные варианты запишем в таблицу.

Коэффициенты b и d в равенстве (3) равноправны, поэтому мы не рас­сматриваем случаи b = 6 и d = 1 или b = –6 и d = –1 и т. д.

Для каждой пары значений b и d из третьего равенства системы (4) най­дем ас = 3 – (b + d), а из второго равенства имеем а + с = 1.

Зная а + с и ас, по теореме, обратной теореме Виета, находим а и с как корни квадратного уравнения. Найденные таким образом значения а, b, с, d подставим в четвертое равенство системы (4) bс + ad = 1, чтобы выбрать те числа, которые являются решениями системы (4). Удобно эти рассуждения оформить в виде таблицы:

Как видим, системе (4) удовлетворяет набор целых чисел а = –1, b = 2, с = 2, d = 3. Тогда равенство (3) имеет вид

Поскольку квадратные трехчлены х 2 – х + 2 и х 2 + 2х + 3 не имеют не только рациональных, но и действительных корней, то равенство (5) дает окончательный ответ.

Упражнения

  1. Найдите целые корни многочлена:
  1. Найдите рациональные корни уравнения:
  1. Разложите многочлен на множители:
  1. Найдите действительные корни уравнения:

5*. Разложите многочлен на множители методом неопределенных коэффи­циентов:

6*. Разложите многочлен на множители, заранее записав его с помощью ме­тода неопределенных коэффициентов в виде (х 2 + bх + с) 2 – (mх + n) 2 : :

Нахождение рациональных корней

Содержание:

Теорема о рациональных корнях

Если для многочлена с целыми коэффициентами существует рациональный корень, то этот корень имеет вид

Доказательство:

Пусть несократимая дробь является корнем многочлена с целыми коэффициентами:

Умножим обе части равенства на :

Так как в последнем равенстве каждый член, кроме члена , содержит множитель и каждый член, кроме члена , содержит множитель , то коэффициент должен делится на , а коэффициент должен делится на .

Задача пример №8

Найдите рациональные корни многочлена .

Решение:

свободный член 6, старший коэффициент 2.

Для , запишем все возможные числа вида

, т.е. одним из множителей является двучлен . Другие множители найдем, используя синтетическое деление:

Так как, , получим, что являются корнями многочлена.

Следствие 1. Если старший коэффициент ±1 и многочлен имеет рациональный корень, то он является целым числом.

Следствие 2. Целые корни многочлена с целыми коэффициентами (если они имеются) являются делителями свободного члена.

Задача пример №9

Найдите корни многочлена .

Решение:

по теореме о рациональных корнях многочлена, целый корень данного многочлена (если он существует) надо искать среди делителей числа 5. Это числа ±5; ±1.

Запишем это короче при помощи синтетического деления и проверим, являются ли эти числа корнями многочлена.

Так как , то, решив квадратное уравнение , получим другие корни: . Значит данный многочлен третьей степени имеет три корня: —.

Внимание! Если коэффициенты многочлена являются рациональными числами, то для нахождения рациональных корней уравнения сначала обе части уравнения надо умножить на такое число (отличное от нуля), чтобы коэффициенты стали целыми.

Например, для нахождения корней многочлена надо умножить все члены уравнения на 12, а затем решить полученное уравнение .

Для нахождения рациональных корней выполните следующие действия:

1. Записывается множество всех возможных дробей, числителями которых являются делители свободного члена, а знаменателями являются делители старшего коэффициента.

2. Из этих чисел выбирается число (обращающее значение многочлена в нуль), которое является корнем многочлена, т.е. определяется двучлен , на который многочлен делится без остатка.

3. Для данного многочлена при помощи синтетического деления на двучлен определяется другой множитель.

4. Если другой множитель является квадратным трехчленом или его можно разложить при помощи формул сокращенного умножения, находятся другие корни. Иначе все линейные множители находятся синтетическим делением.

5. Возможно, что ни одно число из списка не будет нулем многочлена. В этом случае многочлен не имеет рациональных корней. Например, рациональными корнями многочлена могут являться числа ±1.

Проверим: ; . Значит, многочленах не имеет рациональных корней.

Исследование:

1) Перепишите примеры в тетрадь и проведите обсуждение.

a) Многочлен первой степени имеет один корень:

b) Многочлен второй степени имеет два корня: , ;

c) Многочлен третьей степени имеет три корня:

d) Многочлен четвертой степени имеет четыре корня:

e) Принимая во внимание, что уравнение имеет кратные корни, получим 5 корней:

2) Укажите степень и найдите корни многочленов, разложение на множители которых имеет вид .

3) Равна ли степень произвольного многочлена количеству его корней?

Покажем на примере, что многочлен n-ой степени имеет n корней.

Задача пример №10

Найдите все корни многочлена .

Решение:

рациональными корнями данного многочлена (если они существуют), согласно правилу, могут являться числа ±1, ±5. Проверим:

.

Значит, является корнем данного многочлена . Другие корни найдем синтетическим делением.

В выражении для множителя вновь применим теорему о рациональных корнях и синтетическое деление. Тогда ; . Решим уравнение ; ; (корень кратности 2); ;

Корни:

Во всех рассмотренных нами примерах уравнение n-ой степени всегда имеет n корней, включая кратные корни (действительных или комплексных).

Эта лекция взята из раздела решения задач по математике, там вы найдёте другие лекци по всем темам математики:

Математика: полный курс решений задач в виде лекций

Другие темы которые вам помогут понять математику:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Рациональные корни многочленов с целыми коэффициентами. Алгебраические и трансцендентные числа

Рациональные корни многочленов с целыми коэффициентами

Прежде, чем дать общую формулировку теоремы о рациональных корнях многочленов с целыми коэффициентами , решим следующую задачу.

Задача . Найти все корни уравнения

Решение . Предположим, что рассматриваемое уравнение имеет корень, являющийся рациональным числом. Тогда, поскольку каждое рациональное число можно представить в виде несократимой дроби

,

где m – число целое, а n – число натуральное, то выполняется равенство:

Умножая это равенство на n 3 , получаем равенство:

2m 3 + m 2 n – 5 m n 2 –
– 3n 3 = 0.		 (1)

Теперь преобразуем равенство (1):

Отсюда вытекает, что число 2m 3 нацело делится на число n . А из этого, в свою очередь, следует, что, поскольку числа m и n не имеют общих простых делителей, то число n является делителем числа 2 . Таким образом, число n равно 1 или 2 .

Теперь преобразуем равенство (1) по-другому:

Значит, число 3n 3 нацело делится на число m . А из этого, в свою очередь, следует, что, так как числа m и n не имеют общих простых делителей, то число m является делителем числа 3. Таким образом, число m может быть равно: – 1, 1, – 3 или 3 .

Далее, рассматривая все возможные комбинации чисел m и n , получаем, что дробь

может принимать только следующие значения:

Таким образом, если у исходного уравнения и есть рациональный корень, то искать его нужно среди полученных шести чисел. Других рациональных корней у исходного уравнения быть не может.

Подставляя поочередно каждое из этих чисел в исходное уравнение, получаем, что корнем уравнения является лишь число .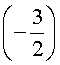

Оставляя читателю проверку того, что другие числа корнями исходного уравнения не являются, покажем, что число 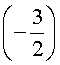действительно является его корнем:

Ответ . Число 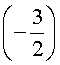является единственным рациональным корнем исходного уравнения.

Замечание . Для того, чтобы найти все остальные корни исходного уравнения, нужно, воспользовавшись теоремой Безу, разделить многочлен

В результате деления получится квадратный трехчлен

Теорема . Если рациональное число (несократимая дробь)

,

где m – число целое, а n – число натуральное, является корнем многочлена k -ой степени

которого являются целыми числами, то числитель дроби m является делителем коэффициента ak , а знаменатель дроби n является делителем коэффициента a0 .

Коэффициент a0 называют старшим коэффициентом многочлена, а коэффициент ak – свободным членом многочлена.

Алгебраические и трансцендентные числа

Определение . Действительное число называют действительным алгебраическим числом , если существует многочлен с целочисленными коэффициентами, корнем которого это число является. Если же такой многочлен не существует, то указанное число называют действительным трансцендентным числом .

Замечание . Числа π и e – наиболее известные примеры действительных трансцендентных чисел.

Утверждение . Каждое рациональное число является алгебраическим числом.

Доказательство . Каждое рациональное число представимо в виде несократимой дроби

,

где m – число целое, а n – число натуральное. Но указанная дробь является корнем уравнения первой степени

что и требовалось доказать.

Следствие . Каждое действительное трансцендентное число является иррациональным числом.

источники:

http://natalibrilenova.ru/nahozhdenie-ratsionalnyih-kornej/

http://www.resolventa.ru/spr/algebra/ratroot.htm

Источник

Содержание:

  1. Теорема о рациональных корнях
  2. Задача пример №8
  3. Задача пример №9
  4. Задача пример №10

Теорема о рациональных корнях

Если для многочлена Нахождение рациональных корней с целыми коэффициентами существует рациональный корень, то этот корень имеет вид

Нахождение рациональных корней

Доказательство:

Пусть несократимая дробь Нахождение рациональных корней является корнем многочлена Нахождение рациональных корней с целыми коэффициентами:

Нахождение рациональных корней

Умножим обе части равенства на Нахождение рациональных корней:

Нахождение рациональных корней

Так как в последнем равенстве каждый член, кроме члена Нахождение рациональных корней, содержит множитель Нахождение рациональных корней и каждый член, кроме члена Нахождение рациональных корней, содержит множитель Нахождение рациональных корней, то коэффициент Нахождение рациональных корней должен делится на Нахождение рациональных корней, а коэффициент Нахождение рациональных корней должен делится на Нахождение рациональных корней.

Задача пример №8

Найдите рациональные корни многочлена Нахождение рациональных корней.

Решение:

свободный член 6, старший коэффициент 2.

Для Нахождение рациональных корней, Нахождение рациональных корней запишем все возможные числа вида

Нахождение рациональных корней

Нахождение рациональных корней, т.е. одним из множителей является двучлен Нахождение рациональных корней. Другие множители найдем, используя синтетическое деление:

Нахождение рациональных корней

Нахождение рациональных корней

Так как, Нахождение рациональных корней Нахождение рациональных корней, получим, что Нахождение рациональных корней являются корнями многочлена.

Следствие 1. Если старший коэффициент ±1 и многочлен имеет рациональный корень, то он является целым числом.

Следствие 2. Целые корни многочлена с целыми коэффициентами (если они имеются) являются делителями свободного члена.

Задача пример №9

Найдите корни многочлена Нахождение рациональных корней.

Решение:

по теореме о рациональных корнях многочлена, целый корень данного многочлена (если он существует) надо искать среди делителей числа 5. Это числа ±5; ±1.

Нахождение рациональных корней

Запишем это короче при помощи синтетического деления и проверим, являются ли эти числа корнями многочлена.

Так как Нахождение рациональных корней, то, решив квадратное уравнение Нахождение рациональных корней, получим другие корни: Нахождение рациональных корней. Значит данный многочлен третьей степени имеет три корня: —Нахождение рациональных корней.

Внимание! Если коэффициенты многочлена являются рациональными числами, то для нахождения рациональных корней уравнения Нахождение рациональных корней сначала обе части уравнения надо умножить на такое число (отличное от нуля), чтобы коэффициенты стали целыми.

Например, для нахождения корней многочлена Нахождение рациональных корней надо умножить все члены уравнения Нахождение рациональных корней на 12, а затем решить полученное уравнение Нахождение рациональных корней.

Для нахождения рациональных корней выполните следующие действия:

1. Записывается множество всех возможных дробей, числителями которых являются делители свободного члена, а знаменателями являются делители старшего коэффициента.

2. Из этих чисел выбирается число Нахождение рациональных корней (обращающее значение многочлена в нуль), которое является корнем многочлена, т.е. определяется двучлен Нахождение рациональных корней, на который многочлен делится без остатка.

3. Для данного многочлена при помощи синтетического деления на двучлен Нахождение рациональных корней определяется другой множитель.

4. Если другой множитель является квадратным трехчленом или его можно разложить при помощи формул сокращенного умножения, находятся другие корни. Иначе все линейные множители находятся синтетическим делением.

5. Возможно, что ни одно число из списка не будет нулем многочлена. В этом случае многочлен не имеет рациональных корней. Например, рациональными корнями многочлена Нахождение рациональных корней могут являться числа ±1.

Проверим: Нахождение рациональных корней; Нахождение рациональных корней. Значит, многочленах Нахождение рациональных корней не имеет рациональных корней.

Исследование:

1) Перепишите примеры в тетрадь и проведите обсуждение.

a) Многочлен первой степени Нахождение рациональных корней имеет один корень: Нахождение рациональных корней

b) Многочлен второй степени Нахождение рациональных корней имеет два корня: Нахождение рациональных корней, Нахождение рациональных корней; Нахождение рациональных корней

c) Многочлен третьей степени Нахождение рациональных корней имеет три корня: Нахождение рациональных корней

d) Многочлен четвертой степени Нахождение рациональных корней имеет четыре корня: Нахождение рациональных корней

e) Принимая во внимание, что уравнение Нахождение рациональных корней имеет кратные корни, получим 5 корней: Нахождение рациональных корней

2) Укажите степень и найдите корни многочленов, разложение на множители которых имеет вид Нахождение рациональных корней.

3) Равна ли степень произвольного многочлена количеству его корней?

Покажем на примере, что многочлен n-ой степени имеет n корней.

Задача пример №10

Найдите все корни многочлена Нахождение рациональных корней.

Решение:

рациональными корнями данного многочлена (если они существуют), согласно правилу, могут являться числа ±1, ±5. Проверим:

Нахождение рациональных корней.

Значит, Нахождение рациональных корней является корнем данного многочлена Нахождение рациональных корней. Другие корни найдем синтетическим делением.

Нахождение рациональных корней

В выражении Нахождение рациональных корней для множителя Нахождение рациональных корней вновь применим теорему о рациональных корнях и синтетическое деление. Тогда Нахождение рациональных корней Нахождение рациональных корней; Нахождение рациональных корней. Решим уравнение Нахождение рациональных корней; Нахождение рациональных корней; Нахождение рациональных корней (корень кратности 2); Нахождение рациональных корней; Нахождение рациональных корней

Корни: Нахождение рациональных корней

Во всех рассмотренных нами примерах уравнение n-ой степени всегда имеет n корней, включая кратные корни (действительных или комплексных).

Эта лекция взята из раздела решения задач по математике, там вы найдёте другие лекци по всем темам математики:

Другие темы которые вам помогут понять математику:

  • Теорема об остатке
  • Теорема о разложении на множители
  • Основная теорема алгебры
  • Функция-многочлен

Лекции:

  • Свойства прямоугольного треугольника
  • Частное решение дифференциального уравнения
  • Интегрирование иррациональных функций
  • Площадь поверхности. Интеграл по площади поверхности
  • Формула Пуассона
  • Найти производную функции
  • Исследовать функцию на непрерывность: пример решения
  • Преобразование графиков функций
  • Полный дифференциал функции: пример решения
  • Прямые и плоскости в пространстве
Источник

Теорема Виета

Теорема Виета звучит так:

Теорема Виета широко используется при решении задач, в которых

  • не требуется найти корни квадратного уравнения, а лишь некоторое их соотношение;
  • нужно найти значение параметра, при котором значение корней удовлетворяет заданному соотношению.

С помощью теоремы Виета можно устно находить корни квадратного уравнения, а также проверять, являются ли заданные числа корнями уравнения.

Чтобы грамотно использовать теорему Виета, ее нужно хорошо понимать.

Остановимся подробнее на каждом слове этой теоремы. Сначала о коэффициентах квадратного уравнения:

Квадратное уравнение называется приведенным, если старший коэффициент равен 1, то есть если

В общем случае не каждое квадратное уравнение является приведенным, например, уравнение не является приведенным. В этом уравнении .

Но каждое квадратное уравнение можно сделать приведенным, для этого достаточно обе части уравнения вида разделить на :

В полученном уравнении старший коэффициент равен 1, второй коэффициент равен , свободный член равен .

То есть корни произвольного квадратного уравнения , согласно теоремы Виета, удовлетворяют системе:

Например корни уравнения

Обратная теорема Виета позволяет составить квадратное уравнение по значениям его корней:

Например, числа -7 и -2 являются корнями уравнения , или

Решим несколько задач с использованием теоремы Виета.

Задача 1. Составьте квадратное уравнение с рациональными коэффициентами, если известно, что один из корней равен

Так как произведение корней должно быть числом рациональным, второй корень может представлять выражение, сопряженное выражению , то есть дополняющее его до формулы разности квадратов. Это выражение :

Тогда ;

Отсюда получаем уравнение:

Задача 2. Найдите значения выражения , где и — корни уравнения .

Если в задаче не требуется найти значения корней квадратного уравнения, а только их соотношение, следовательно, нужно воспользоваться теоремой Виета.

Запишем теорему Виета для этого уравнения:

Теперь мы знаем, чему равны сумма и произведение корней. Представим выражение в виде комбинации суммы и произведения. Приведем дроби к общему знаменателю.

Задача 3. Найдите значение выражения , где и — корни уравнения .

Эта задача аналогична предыдущей, только в ней чуть сложнее преобразование выражения в комбинацию выражений и .

Вспомним формулу квадрата суммы: . Перенесем влево и получим соотношение (1)

Запишем теорему Виета для уравнения :

(по формуле 1)

Задача 4. Решите устно уравнение:

Теорем Виета позволяет в некоторых случаях легко находить корни квадратного уравнения.

Для этого удобно придерживаться такой последовательности шагов:

  1. Выписываем теорему Виета для данного уравнения.
  2. Определяем знаки корней.
  3. Раскладываем на два множителя свободный член, и определяем, какая пара множителей в сумме дает второй коэффициент, взятый с противоположным знаком.

Для данного уравнения

1

2 Определим знаки корней.

Для определения знаков удобно пользоваться такой таблицей:

Так как в уравнении произведение корней отрицательно, корни имеют разные знаки. Сумма корней также отрицательна, следовательно, корень с большим модулем отрицателен.

3. Будем раскладывать на множители число 24, имея в виду, что множитель с большим модулем отрицателен, и выбираем пару чисел, сумма которых равна -2.

Очевидно, что это числа -6 и 4.

Задача 5. Решите устно уравнение:

1

2 Определим знаки корней.

Так как в уравнении

произведение корней отрицательно, корни имеют разные знаки. Сумма корней отрицательна, следовательно, корень с большим модулем отрицателен.

В данном случае корни проще подобрать, зная их сумму: . Можно предположить, что . Проверим, чему равно произведение этих выражений:

Ответ:

Следствием из теоремы Виета являются такие полезные факты:

Задача 6. Найти корни уравнения:

Заметим, что , следовательно, .

Найти корни уравнения:

Заметим, что , следовательно,

Как решать задачи с параметром с помощью теоремы Виета читайте здесь.

Тема урока: «Рациональные решения квадратных уравнений». 8-й класс

Разделы: Математика

Класс: 8

Цели:

  • образовательная: обобщить и систематизировать знания и умения решения квадратных уравнений;
  • развивающая: формировать умения определять тип квадратного уравнения и выбирать рациональное решение по его коэффициентам;
  • воспитательная: воспитывать внимательность и краткость изложения решений.

Тип урока: обобщение знаний и умений решения квадратных уравнений.

Оборудование: компьютер, интерактивная доска, карточки с заданиями, доска.

Эпиграф

Метод решения хорош, если с самого начала мы можем предвидеть — и далее подтвердить это, — что, следуя этому методу, мы достигнем цели.
(Г.Лейбниц)

ХОД УРОКА

1. Организационный момент.

Учитель настраивает учащихся на урок и даёт установку на внимательность в подходе к решению квадратных уравнений.

2. Проверка домашнего задания.

Учащиеся сдают тетради на проверку. Учитель отвечает на возникшие вопросы у учащихся.

3. Формулирование цели и задачи урока.

Рассмотрим несколько вариантов решения квадратных уравнений, сравним их и научимся выбирать рациональное решение.

4. Классификация квадратных уравнений.

На интерактивной доске учащимся представляется таблица классификации квадратных уравнений и предлагается её прокомментировать.

Полное квадратное уравнение Частные случаи полного квадратного уравнения
ax 2 + bx + c = 0, где х – переменная,

a, b, c – некоторые числа, причем a 0.

D = b 2 – 4ac (дискриминант);

если D > 0, то уравнение имеет два корня

х1 ; х2 ;

если D = 0, то уравнение имеет один корень (или ещё говорят, имеет два равных корня)

х (х1 х2 = );

если D 2 +2kx + c =0,

D = 4(k 2 –ac) = 4D1 (дискриминант), где D1 = k 2 –ac;

если D1 >0, то D >0, уравнение имеет два корня

х1 ; х2;

если D1 = 0, то D = 0, уравнение имеет один корень х ;

б) D > 0, если a+b+c=0, то

х1 = 1; х2 = ;

D = 0, если a+b+c=0, то

в) D > 0, если a-b+c=0, то

х1 = -1; х2 = ;

D = 0, если a-b+c=0, то

х = -1.Приведенное квадратное уравнениеЧастный случай приведенного квадратного уравненияx 2 + px + q = 0, если D > 0, уравнение имеет два корня и решается по теореме, обратной теореме Виета х1+х2 = -p, х1·х2 = q.Если p – четное, D = 4(– q)= 4D2 (дискриминант),

где D2 = (– q);

D2 > 0, то D > 0, уравнение имеет два корня

х1 + , х2 — .

Неполное квадратное уравнениеа) ax 2 + c = 0, где с0;

если — > 0, то

х1 — , х2 = ;

если — 2 + bx = 0, где b0; уравнение имеет два корня

х1 = 0, х2 = — .в) ax 2 = 0; уравнение имеет один корень

х = 0.Метод “переброски”

ax 2 + bx + c = 0, для решения данного квадратного уравнения составим и решим вспомогательное квадратное уравнение путём умножения свободного члена на первый коэффициент и запишем это произведение в новом уравнении свободным членом, т.е. получим квадратное уравнение вида

у 2 + by + ac = 0. Полученное квадратное уравнение можно решать любым рациональным способом (как правило, по теореме, обратной теореме Виета). Его корни — у1 и у2. Корни исходного квадратного уравнения:

х1 = и х2 = .

5. Ознакомившись с таблицей классификации, трём учащимся предлагается составить свои уравнения для каждого случая и решить их на доске с последующими комментариями.

1. 5х 2 – 11х + 2 = 0;

D = b 2 – 4ac = (-11) 2 — 45·2 = 81; D > 0, уравнение имеет два корня;

х1 = = = 0,2;

х2 = = = 2.

2. 3х 2 – 14х + 16 = 0;

D1 = k 2 –ac = (-7) 2 — 316 = 1; D > 0, уравнение имеет два корня;

х1 = = = 2;

х2 = = = 2.

Ответ: 2; 2.

3. 15х 2 +22х — 37 = 0;

D > 0, уравнение имеет два корня;

Так как 15 + 22 – 37 = 0, то х1 = 1, х2 = = — 2 .

Ответ: 1; — 2 .

Следующим трём учащимся предлагается аналогичное задание, но для других случаев.

4. -15х 2 + 22х + 37 = 0;

D > 0, уравнение имеет два корня;

Так как -15– 22 + 37 = 0, то х1 = -1 , х2 = = 2 .

Ответ: -1; 2 .

5. х 2 – 5х + 6 = 0;

D > 0, уравнение имеет два корня;

по теореме, обратной теореме Виета х1+х2 = 5, х1·х2 = 6.

6. х 2 – 6х + 7 = 0;

D > 0, уравнение имеет два корня;

по формуле корней приведенного квадратного уравнения с чётным вторым коэффициентом имеем

х1 + , х2 — .

Ответ: — , + .

Следующему учащемуся предлагается решить квадратное уравнение методом “переброски”.

7. 5х 2 + 37х — 24 = 0;

D > 0, уравнение имеет два корня;

составим вспомогательное уравнение

у 2 + 37y – 120 = 0; по теореме, обратной теореме Виета у1+ у2 = -37, у1·у2 = -120.

Значит, у1 = -40, у2 = 3, тогда корни исходного уравнения

х1 = — 8, х2 = .

Ответ: — 8, .

6. Устные упражнения:

(учащимся предлагается прокомментировать возможные способы рационального решения квадратного уравнения).

1. 2х 2 + 3х + 1 = 0; (D > 0, a – b + c = 0);

2. х 2 + 5х — 6 = 0; (D > 0, a + b + c = 0);

3. 3х 2 — 7х + 4 = 0; (D > 0, a + b + c = 0);

4. 5х 2 + 8х + 3 = 0; (D1 > 0, значит, D > 0, a – b + c = 0);

5. у 2 — 10y – 24 = 0; (D2 > 0, значит, D > 0, по формуле корней приведенного квадратного уравнения с чётным вторым коэффициентом);

6. у 2 + y – 90 = 0; (D > 0, по теореме, обратной теореме Виета);

7. у 2 — 8y – 84 = 0; (D2 > 0, значит, D > 0, по формуле корней приведенного квадратного уравнения с чётным вторым коэффициентом);

8. 3х 2 — 8х + 5 = 0; (D1 > 0, значит, D > 0, a + b + c = 0);

9. 3х 2 + 6х = 0; (неполное квадратное уравнение; случай б));

10. 4х 2 — 16 = 0; (неполное квадратное уравнение; случай а));

11. 3у 2 — 3y + 1 = 0; (D 2 — 5х — 1 = 0; (D > 0, метод “переброски”).

7. Творческая самостоятельная работа

(по карточкам; в двух вариантах; с последующей устной проверкой).

8. Домашнее задание.

1. Повторите таблицу классификации квадратных уравнений.

2. Решите квадратные уравнения наиболее рациональным способом:

3. Составить пять квадратных уравнений с недостающими коэффициентами.

Составьте квадратное уравнение с рациональными коэффициентами, если известно, что один из корней уравнения равен :а) — √6 ;б)√7 ;в)2 — √5Покажите как это делается плиз(очень надо), сделайте хотя бы пе?

Алгебра | 5 — 9 классы

Составьте квадратное уравнение с рациональными коэффициентами, если известно, что один из корней уравнения равен :

Покажите как это делается плиз(очень надо), сделайте хотя бы первые 2!

Если х1 и х2 — корни квадратного уравнения, то это уравнение можно записать в виде а(х — х1)(х — х2) = 0.

А) х1 = — √6 пусть у нас а = 1, тогда х2 = √6 и получим (х — √6)(х + √6) = 0, т.

б) аналогично для х1 = √7 пусть у нас а = 1, тогда х2 = — √7 и получим (х — √7)(х + √7) = 0, т.

в) сложнее для х1 = 2 — √5.

Чтобы при умножении избавиться от символа «корень», берем х2 = 2 + √5, тогда

$(x-(2-sqrt5))(x-(2+sqrt5))=0\ x^2-(2-sqrt5)x-(2+sqrt5)x+(2-sqrt5)(2+sqrt5)=0\ x^2-2x+xsqrt5-2x-xsqrt5+4-5=0\ x^2-4x-1=0$.

Составьте квадратное уравнение с целыми коэффициентами, если : сумма корней равна — 1дробь6, а произведение равно 11дробь12?

Составьте квадратное уравнение с целыми коэффициентами, если : сумма корней равна — 1дробь6, а произведение равно 11дробь12.

Существует ли квадратное уравнение с целыми коэффициентами один из корней которого равен?

Существует ли квадратное уравнение с целыми коэффициентами один из корней которого равен.

Составьте квадратное уравнение с целыми коэффициентами, у которого один из корней равен ?

Составьте квадратное уравнение с целыми коэффициентами, у которого один из корней равен .

Составьте квадратное уравнение с рациональными коэффициентами, один из корней которого равен 1 / (6 + корень из 2)?

Составьте квадратное уравнение с рациональными коэффициентами, один из корней которого равен 1 / (6 + корень из 2).

1. СОСТАВЬТЕ КВАДРАТНОЕ УРАВНЕНИЯ В КОТОРОМ КОЭФФИЦИЕНТ ПРИ НЕИЗВЕСТНОМ В ПЕРВОЙ СТЕПЕНИ РАВНЯЛСЯ БЫ — 15 И ОДИН КОРЕНЬ БЫЛ БЫ ВДВОЕ БОЛЬШЕ ДРУГОГО 2?

1. СОСТАВЬТЕ КВАДРАТНОЕ УРАВНЕНИЯ В КОТОРОМ КОЭФФИЦИЕНТ ПРИ НЕИЗВЕСТНОМ В ПЕРВОЙ СТЕПЕНИ РАВНЯЛСЯ БЫ — 15 И ОДИН КОРЕНЬ БЫЛ БЫ ВДВОЕ БОЛЬШЕ ДРУГОГО 2.

Составьте квадратное уравнение, корнями которого являются x1 — 2 и x2 — 2 где x1и x2 — корни квадратного уравнения 3×2 — 2x — 5 = 0.

Составьте квадратное уравнение с целыми коэффициентами корнями которого являются числа, — 1 / 2и 3?

Составьте квадратное уравнение с целыми коэффициентами корнями которого являются числа, — 1 / 2и 3.

Составьте квадратное уравнение с рациональными коэффицентами один из корней которого равен 1 разделить на 6 + корень из 2?

Составьте квадратное уравнение с рациональными коэффицентами один из корней которого равен 1 разделить на 6 + корень из 2.

Составьте квадратное уравнение у которого старший коэффициент равен 8 коэффициент при Х равен 5 свободный член равен 1?

Составьте квадратное уравнение у которого старший коэффициент равен 8 коэффициент при Х равен 5 свободный член равен 1.

Составьте приведённое квадратное уравнение если известны его корни 1 и 5?

Составьте приведённое квадратное уравнение если известны его корни 1 и 5.

Составьте квадратное уравнение, если известны корни х 1 = — 1, 8 и х2 = 5?

Составьте квадратное уравнение, если известны корни х 1 = — 1, 8 и х2 = 5.

На этой странице вы найдете ответ на вопрос Составьте квадратное уравнение с рациональными коэффициентами, если известно, что один из корней уравнения равен :а) — √6 ;б)√7 ;в)2 — √5Покажите как это делается плиз(очень надо), сделайте хотя бы пе?. Вопрос соответствует категории Алгебра и уровню подготовки учащихся 5 — 9 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно ознакомиться с вариантами ответов других посетителей страницы или обсудить с ними интересующую тему. Здесь также можно воспользоваться «умным поиском», который покажет аналогичные вопросы в этой категории. Если ни один из предложенных ответов не подходит, попробуйте самостоятельно сформулировать вопрос иначе, нажав кнопку вверху страницы.

источники:

http://urok.1sept.ru/articles/648424

http://algebra.my-dict.ru/q/2932729_sostavte-kvadratnoe-uravnenie-s-racionalnymi-koefficientami/

Источник

Способы решения квадратных уравнений

Квадратные уравнения — это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств. Все мы умеем решать квадратные уравнения со школьной скамьи (8 класс), до окончания вуза.

В школьном курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Однако имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать многие уравнения. Имеется десять способов решения квадратных уравнений. Подробно в своей работе я разобрала каждый из них.

1. СПОСОБ: Разложение левой части уравнения на множители.

х 2 + 10х — 24 = 0.

Разложим левую часть на множители:

х 2 + 10х — 24 = х 2 + 12х — 2х — 24 = х(х + 12) — 2(х + 12) = (х + 12)(х — 2).

Следовательно, уравнение можно переписать так:

(х + 12)(х — 2) = 0

Так как произведение равно нулю, то, по крайней мере, один из его множителей равен нулю. Поэтому левая часть уравнения обращается нуль при х = 2, а также при х = — 12. Это означает, что число 2 и — 12 являются корнями уравнения х 2 + 10х — 24 = 0.

2. СПОСОБ: Метод выделения полного квадрата.

Решим уравнение х 2 + 6х — 7 = 0.

Выделим в левой части полный квадрат.

Для этого запишем выражение х 2 + 6х в следующем виде:

х 2 + 6х = х 2 + 2* х * 3.

В полученном выражении первое слагаемое — квадрат числа х, а второе — удвоенное произведение х на 3. По этому чтобы получить полный квадрат, нужно прибавить 3 2 , так как

х 2 + 2* х * 3 + 3 2 = (х + 3) 2 .

Преобразуем теперь левую часть уравнения

х 2 + 6х — 7 = 0,

прибавляя к ней и вычитая 3 2 . Имеем:

х 2 + 6х — 7 = х 2 + 2* х * 3 + 3 2 — 3 2 — 7 = (х + 3) 2 — 9 — 7 = (х + 3) 2 — 16.

Таким образом, данное уравнение можно записать так:

(х + 3) 2 — 16 =0, (х + 3) 2 = 16.

Следовательно, х + 3 — 4 = 0, х1= 1, или х + 3 = -4, х2 = -7.

3. СПОСОБ: Решение квадратных уравнений по формуле.

Умножим обе части уравнения

ах 2 + bх + с = 0, а ? 0

на 4а и последовательно имеем:

4а 2 х 2 + 4аbх + 4ас = 0,

((2ах) 2 + 2ах * b + b 2 ) — b 2 + 4ac = 0,

(2ax + b) 2 = b 2 — 4ac,

2ax + b = ± v b 2 — 4ac,

2ax = — b ± v b 2 — 4ac,

Примеры.

а) Решим уравнение: 4х 2 + 7х + 3 = 0.

а = 4, b = 7, с = 3, D = b 2 — 4ac = 7 2 — 4 * 4 * 3 = 49 — 48 = 1,

D > 0, два разных корня;

Таким образом, в случае положительного дискриминанта, т.е. при

b 2 — 4ac >0 , уравнение ах 2 + bх + с = 0 имеет два различных корня.

б) Решим уравнение: 4х 2 — 4х + 1 = 0,

а = 4, b = — 4, с = 1, D = b 2 — 4ac = (-4) 2 — 4 * 4 * 1= 16 — 16 = 0,

D = 0, один корень;

Итак, если дискриминант равен нулю, т.е. b2 — 4ac = 0, то уравнение

ах 2 + bх + с = 0 имеет единственный корень,

в) Решим уравнение: 2х 2 + 3х + 4 = 0,

а = 2, b = 3, с = 4, D = b 2 — 4ac = 3 2 — 4 * 2 * 4 = 9 — 32 = — 13 , D < 0.

Данное уравнение корней не имеет.

Итак, если дискриминант отрицателен, т.е. b 2 — 4ac < 0,

уравнение ах 2 + bх + с = 0 не имеет корней.

Формула (1) корней квадратного уравнения ах 2 + bх + с = 0 позволяет найти корни любого квадратного уравнения (если они есть), в том числе приведенного и неполного. Словесно формула (1) выражается так: корни квадратного уравнения равны дроби, числитель которой равен второму коэффициенту, взятому с противоположным знаком, плюс минус корень квадратный из квадрата этого коэффициента без учетверенного произведения первого коэффициента на свободный член, а знаменатель есть удвоенный первый коэффициент.

4. СПОСОБ: Решение уравнений с использованием теоремы Виета.

Как известно, приведенное квадратное уравнение имеет вид

х 2 + px + c = 0. (1)

Его корни удовлетворяют теореме Виета, которая при а =1 имеет вид

x1 x2= q,

x1 + x2= — p

Отсюда можно сделать следующие выводы (по коэффициентам p и q можно предсказать знаки корней).

а) Если сводный член q приведенного уравнения (1) положителен (q > 0), то уравнение имеет два одинаковых по знаку корня и это зависти от второго коэффициента p. Если р < 0, то оба корня отрицательны, если р < 0, то оба корня положительны.

x 2 — 3x + 2 = 0; x1= 2 и x2= 1, так как q = 2 > 0 и p = — 3 < 0;

x 2 + 8x + 7 = 0; x1 = — 7 и x2= — 1, так как q = 7 > 0 и p= 8 > 0.

б) Если свободный член q приведенного уравнения (1) отрицателен (q < 0), то уравнение имеет два различных по знаку корня, причем больший по модулю корень будет положителен, если p < 0 , или отрицателен, если p > 0 .

x 2 + 4x — 5 = 0; x1= — 5 и x2= 1, так как q= — 5 < 0 и p = 4 > 0;

x 2 — 8x — 9 = 0; x1 = 9 и x2= — 1, так как q = — 9 < 0 и p = — 8 < 0.

5. СПОСОБ: Решение уравнений способом «переброски».

Рассмотрим квадратное уравнение

ах 2 + bх + с = 0, где а ? 0.

Умножая обе его части на а, получаем уравнение

а 2 х 2 + аbх + ас = 0.

Пусть ах = у, откуда х = у/а; тогда приходим к уравнению

у 2 + by + ас = 0,

равносильно данному. Его корни у1 и у2 найдем с помощью теоремы Виета.

х1= у1/а и х1= у2/а.

При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.

Решим уравнение 2х 2 — 11х + 15 = 0.

Решение. «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение

у 2 — 11у + 30 = 0.

Согласно теореме Виета

у1 = 5 х1= 5/2 x1= 2,5

у2= 6 x2= 6/2 x2= 3.

6. СПОСОБ: Свойства коэффициентов квадратного уравнения.

А. Пусть дано квадратное уравнение

ах 2 + bх + с = 0, где а ? 0.

1) Если, а+ b + с = 0 (т.е. сумма коэффициентов равна нулю), то х1 = 1,

Доказательство. Разделим обе части уравнения на а ? 0, получим приведенное квадратное уравнение

x 2 + b/a * x + c/a = 0.

Согласно теореме Виета

x1+ x2= — b/a,

x1x2= 1* c/a.

По условию а — b + с = 0, откуда b = а + с. Таким образом,

x1+ x2= — а + b/a= -1 — c/a,

x1x2= — 1* ( — c/a),

т.е. х1= -1 и х2= c/a, что м требовалось доказать.

1) Решим уравнение 345х 2 — 137х — 208 = 0.

Решение. Так как а + b + с = 0 (345 — 137 — 208 = 0), то

х1= 1, х2= c/a = -208/345.

Ответ: 1; -208/345.

2)Решим уравнение 132х 2 — 247х + 115 = 0.

Решение. Так как а + b + с = 0 (132 — 247 + 115 = 0), то

х1= 1, х2= c/a = 115/132.

Ответ: 1; 115/132.

Б. Если второй коэффициент b = 2k — четное число, то формулу корней

Пример.

Решим уравнение 3х2 — 14х + 16 = 0.

Решение. Имеем: а = 3, b = — 14, с = 16, k = — 7;

D = k 2 — ac = (- 7) 2 — 3 * 16 = 49 — 48 = 1, D > 0, два различных корня;

В. Приведенное уравнение

х 2 + рх + q= 0

совпадает с уравнением общего вида, в котором а = 1, b = р и с = q. Поэтому для приведенного квадратного уравнения формула корней

Формулу (3) особенно удобно использовать, когда р — четное число.

Пример. Решим уравнение х 2 — 14х — 15 = 0.

Решение. Имеем: х1,2=7±

Ответ: х1= 15; х2= -1.

7. СПОСОБ: Графическое решение квадратного уравнения.

Если в уравнении

х 2 + px + q = 0

перенести второй и третий члены в правую часть, то получим

х 2 = — px — q.

Построим графики зависимости у = х 2 и у = — px — q.

График первой зависимости — парабола, проходящая через начало координат. График второй зависимости —

прямая (рис.1). Возможны следующие случаи:

— прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квад- ратного уравнения;

— прямая и парабола могут касаться ( только одна общая точка), т.е. уравнение имеет одно решение;

— прямая и парабола не имеют общих точек, т.е. квадратное уравнение не имеет корней.

1) Решим графически уравнение х 2 — 3х — 4 = 0 (рис. 2).

Решение. Запишем уравнение в виде х 2 = 3х + 4.

Построим параболу у = х 2 и прямую у = 3х + 4. Прямую

у = 3х + 4 можно построить по двум точкам М (0; 4) и

N (3; 13). Прямая и парабола пересекаются в двух точках

А и В с абсциссами х1= — 1 и х2 = 4. Ответ: х1= — 1;

2) Решим графически уравнение (рис. 3) х 2 — 2х + 1 = 0.

Решение. Запишем уравнение в виде х 2 = 2х — 1.

Построим параболу у = х 2 и прямую у = 2х — 1.

Прямую у = 2х — 1 построим по двум точкам М (0; — 1)

и N(1/2; 0). Прямая и парабола пересекаются в точке А с

абсциссой х = 1. Ответ: х = 1.

3) Решим графически уравнение х 2 — 2х + 5 = 0 (рис. 4).

Решение. Запишем уравнение в виде х 2 = 5х — 5. Построим параболу у = х 2 и прямую у = 2х — 5. Прямую у = 2х — 5 построим по двум точкам М(0; — 5) и N(2,5; 0). Прямая и парабола не имеют точек пересечения, т.е. данное уравнение корней не имеет.

Ответ. Уравнение х 2 — 2х + 5 = 0 корней не имеет.

8. СПОСОБ: Решение квадратных уравнений с помощью циркуля и линейки.

Графический способ решения квадратных уравнений с помощью параболы неудобен. Если строить параболу по точкам, то требуется много времени, и при этом степень точности получаемых результатов невелика.

Предлагаю следующий способ нахождения корней квадратного уравнения ах 2 + bх + с = 0 с помощью циркуля и линейки (рис. 5).

Допустим, что искомая окружность пересекает ось

абсцисс в точках В(х1; 0 ) и D (х2; 0), где х1 и х2 — корни уравнения ах 2 + bх + с = 0, и проходит через точки

А(0; 1) и С(0; c/a) на оси ординат. Тогда по теореме о секущих имеем OB * OD = OA * OC, откуда OC = OB * OD/ OA= х1х2/ 1 = c/a.

Центр окружности находится в точке пересечения перпендикуляров SF и SK, восстановленных в серединах хорд AC и BD, поэтому

1) построим точки (центр окружности) и A(0; 1);

2) проведем окружность с радиусом SA;

3) абсциссы точек пересечения этой окружности с осью Ох являются корнями исходного квадратного уравнения.

При этом возможны три случая.

1) Радиус окружности больше ординаты центра (AS > SK, или R > a + c/2a), окружность пересекает ось Ох в двух точках (рис. 6,а) В(х1; 0) и D(х2; 0), где х1 и х2 — корни квадратного уравнения ах 2 + bх + с = 0.

2) Радиус окружности равен ординате центра (AS = SB, или R = a + c/2a), окружность касается оси Ох (рис. 6,б) в точке В(х1; 0), где х1 — корень квадратного уравнения.

3) Радиус окружности меньше ординаты центра окружность не имеет общих точек с осью абсцисс (рис.6,в), в этом случае уравнение не имеет решения.

Решим уравнение х 2 — 2х — 3 = 0 (рис. 7).

Решение. Определим координаты точки центра окружности по формулам:

Проведем окружность радиуса SA, где А (0; 1).

Ответ: х1= — 1; х2= 3.

9. СПОСОБ: Решение квадратных уравнений с помощью номограммы.

Это старый и незаслуженно забыты способ решения квадратных уравнений, помещенный на с.83 (см. Брадис В.М. Четырехзначные математические таблицы. — М., Просвещение, 1990).

Таблица XXII. Номограмма для решения уравнения z 2 + pz + q = 0. Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициен там определить корни уравнения.

Криволинейная шкала номограммы построена по формулам (рис.11):

Полагая ОС = р, ED = q, ОЕ = а (все в см.), из подобия треугольников САН и CDF получим пропорцию

откуда после подстановок и упрощений вытекает уравнение

z 2 + pz + q = 0,

причем буква z означает метку любой точки криволинейной шкалы.

1) Для уравнения z 2 — 9z + 8 = 0 номограмма дает корни

z1= 8,0 и z2= 1,0 (рис.12).

2) Решим с помощью номограммы уравнение

2z 2 — 9z + 2 = 0.

Разделим коэффициенты этого уравнения на 2, получим уравнение

z 2 — 4,5z + 1 = 0.

Номограмма дает корни z1= 4 и z2= 0,5.

3) Для уравнения

z 2 — 25z + 66 = 0

коэффициенты p и q выходят за пределы шкалы, выполним подстановку z = 5t, получим уравнение

t 2 — 5t + 2,64 = 0,

которое решаем посредством номограммы и получим t1= 0,6 и t2= 4,4, откуда z1= 5t1= 3,0 и z2= 5t2= 22,0.

10. СПОСОБ: Геометрический способ решения квадратных уравнений.

В древности, когда геометрия была более развита, чем алгебра, квадратные уравнения решали не алгебраически, а геометрически. Приведу ставший знаменитым пример из «Алгебры» ал — Хорезми.

1) Решим уравнение х 2 + 10х = 39.

В оригинале эта задача формулируется следующим образом : «Квадрат и десять корней равны 39» (рис.15).

Решение. Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники так, что другая сторона каждого из них равна 2,5, следовательно, площадь каждого равна 2,5х. Полученную фигуру дополняют затем до нового квадрата ABCD, достраивая в углах четыре равных квадрата , сторона каждого их них 2,5, а площадь 6,25.

Площадь S квадрата ABCD можно представить как сумму площадей: первоначального квадрата х 2 , четырех прямоугольников (4* 2,5х = 10х ) и четырех пристроенных квадратов (6,25* 4 = 25), т.е. S = х 2 + 10х + 25. Заменяя

х 2 + 10х числом 39, получим, что S = 39 + 25 = 64, откуда следует, что сторона квадрата ABCD, т.е. отрезок АВ = 8. Для искомой стороны х первоначального квадрата получим

2) А вот, например, как древние греки решали уравнение у 2 + 6у — 16 = 0.

Решение представлено на рис. 16, где

у 2 + 6у = 16, или у 2 + 6у + 9 = 16 + 9.

Решение. Выражения у 2 + 6у + 9 и 16 + 9 геометрически представляют собой один и тот же квадрат, а исходное уравнение у 2 + 6у — 16 + 9 — 9 = 0 — одно и то же уравнение. Откуда и получаем, что у + 3 = ± 5, или у1= 2, у2= — 8 (рис.16).

3) Решить геометрически уравнение у 2 — 6у — 16 = 0.

Преобразуя уравнение, получаем

у 2 — 6у = 16.

На рис. 17 находим «изображения» выражения у 2 — 6у, т.е. из площади квадрата со стороной у два раза вычитается площадь квадрата со стороной, равной 3. Значит, если к выражению у 2 — 6у прибавить 9, то получим площадь квадрата со стороной у — 3. Заменяя выражение у 2 — 6у равным ему числом 16,

получаем: (у — 3) 2 = 16 + 9, т.е. у — 3 = ± v25, или у — 3 = ± 5, где у1= 8 и у2= — 2.

Квадратное уравнение

Квадратное уравнение — важное уравнение не только в школьном курсе алгебры. Квадратное уравнение часто используется в геометрии при расчете. Поэтому знать формулы корней квадратного уравнения, чтобы решать его быстрее, нужно всем.

Определение квадратного уравнения

Квадратное уравнение — это уравнение вида ax^2+bx+c=0, где x— переменная, a, b, c— некоторые числа, причем a neq 0. В квадратном уравнении ax^2+bx+c=0коэффициент aназывают первым коэффициентом, b— вторым коэффициентом, c— свободным членом.

Формула корней

Формула корней квадратного уравнения имеет вид:

displaystyle x_{1,2}=frac{-b pm sqrt{b^2-4ac}}{2a}

Выражение b^2-4acназывается дискриминантом квадратного уравнения и обозначается буквой D.

Влияние дискриминанта на корни квадратного уравнения

Максимальное количество корней квадратного уравнения равно степени уравнения. Квадратное уравнение имеет вторую степень переменной, поэтому и должно иметь два корня. Однако возможны случаи совпадения корней, тогда формально говорят, что «уравнение имеет один корень», хотя правильнее говорить — «уравнение имеет одно значение переменной», или «корни уравнения совпадают и равны…» Есть еще вариант, что уравнение не имеет действительных корней или не имеет действительных решений. Узнать о том — решается квадратное уравнение и сколько имеет корней можно вычислив дискриминант.

  1. Если D=0, то существует только одно значение переменной, удовлетворяющее уравнению ax^2+bx+c=0. Однако условились говорить, что в этом случае квадратное уравнение имеет два равных действительных корня, а само число displaystyle - frac{b}{2a}называют корнем кратности два.
  2. Если D<0, то квадратное уравнение не имеет действительных корней.
  3. Если D>0, то квадратное уравнение имеет два различных действительных корня.

Приведенное квадратное уравнение

Пусть дано квадратное уравнение ax^2+bx+c=0. Так как a neq 0, то, разделив обе части уравнения на a, получим уравнение displaystyle x^2+ frac{b}{a} x + frac{c}{a} = 0. Считая, что displaystyle frac{b}{a}=pи displaystyle frac{c}{a}=q, получим уравнение displaystyle x^2+px+q=0, в котором первый коэффициент равен 1. Это уравнение называется приведенным.

Формула корней приведенного квадратного уравнения имеет вид:

displaystyle x_{1,2}=- frac{p}{2} pm sqrt{frac{p^2}{4}-q}

Неполные квадратные уравнения

Уравнения вида ax^2+bx=0(c=0), ax^2+c=0(b=0)и ax^2=0(b=0, c=0)называются квадратными уравнениями.

Биквадратное уравнение

Уравнение вида ax^4+bx^2+c=0называется биквадратным уравнением. Оно решается с помощью замены переменной по формуле x^2=tи приводится к квадратному уравнению at^2+bt+c=0.

Примеры решения квадратного уравнения

Уравнение 1

Решите уравнение x^2+5x-6=0

Решение:Найдем дискриминант D=25+24=49, D>0.

Найдем корни уравнения по формуле корней квадратного уравнения: displaystyle x_{1,2}=frac{-5 pm sqrt{49}}{2}.

displaystyle x_{1}= frac{-5-7}{2}=-6, displaystyle x_{2}=frac{-5+7}{2}=1.

Ответ: x_{1}=-6, x_{2}=1.

Уравнение 2

Решите уравнение 2x^2-3x+1=0.

Решение: находим дискриминант D=3^2-4 cdot 2 cdot 1=1, D>0. Применим формулу корней квадратного уравнения: displaystyle x_{1,2}=frac{3 pm sqrt{1}}{4}. Тогда

displaystyle x_{1}=frac{1}{2}, displaystyle x_{2}=1.

Ответ: x_{1}=0,5, x_{2}=1.

Уравнение 3

Решите уравнение 2x^2-3x+4=0.

Решение: найдем дискриминант D=3^2-4 cdot 2 cdot 4=9-32, D<0. Так как дискриминант отрицателен, то уравнение не имеет корней.

Ответ: нет корней.

Уравнение 4

Решите уравнение 9x^2+6x+1=0

Решение: находим дискриминант D=6^2-4 cdot 9 cdot 1=36-36=0, D=0. Применим формулу корней квадратного уравнения

displaystyle x_{1,2}=frac{-6 pm sqrt{0}}{18}.

displaystyle x_{1}=frac{-6+0}{18}=-frac{1}{3},

displaystyle x_{2}=frac{-6-0}{18}=-frac{1}{3}

Таким образом, уравнение имеет единственный корень displaystyle x_{1,2}=- frac{1}{3}.

Ответ: displaystyle x_{1,2}=- frac{1}{3}

Уравнение 5

Решите квадратное уравнение x^2-10x+24=0

Решение: Применим формулу корней для приведенного квадратного уравнения: x_{1,2}=5 pm 1. Отсюда x_1=5-1=4, x_2=5+1=6.

Ответ: x_1=4, x_2=6.

Квадратные уравнения

где a, b и c – произвольные вещественные числа, отличные от нуля.

Неполными квадратными уравнениями называют квадратные уравнения следующих типов:

Решение неполных квадратных уравнений

Покажем, как решаются неполные квадратные уравнения на примерах.

Пример 1 . Решить уравнение

Пример 2 . Решить уравнение

Решение . Вынося в левой части уравнения (3) переменную x за скобки, перепишем уравнение в виде

Поскольку произведение двух сомножителей равно нулю тогда и только тогда, когда, или первый сомножитель равен нулю, или второй сомножитель равен нулю, то из уравнения (4) получаем:

Пример 3 . Решить уравнение

Пример 4 . Решить уравнение

Решение . Поскольку левая часть уравнения (5) положительна при всех значениях переменной x , а правая часть равна 0, то уравнение решений не имеет.

Выделение полного квадрата

Выделением полного квадрата называют представление квадратного трёхчлена (1) в виде:

Для того, чтобы получить формулу (6), совершим следующие преобразования:

Формула (6) получена.

Дискриминант

Дискриминантом квадратного трёхчлена (1) называют число, которое обозначается буквой D и вычисляется по формуле:

Дискриминант квадратного трёхчлена играет важную роль, и от того, какой знак он имеет, зависят различные свойства квадратного трёхчлена.

Используя дискриминант, формулу (6) можно переписать в виде

Разложение квадратного трёхчлена на множители

Утверждение . В случае, когда , квадратный трёхчлен (1) разлагается на линейные множители. В случае, когда D < 0 , квадратный трехчлен нельзя разложить на линейные множители.

Доказательство . В случае, когда D = 0 , формула (8) и является разложением квадратного трехчлена на линейные множители:

В случае, когда D > 0 , выражение, стоящее в квадратных скобках в формуле (8), можно разложить на множители, воспользовавшись формулой сокращенного умножения «Разность квадратов»:

Таким образом, в случае, когда D > 0 , разложение квадратного трехчлена (1) на линейные множители имеет вид

В случае, когда D < 0 , выражение, стоящее в квадратных скобках в формуле (8), является суммой квадратов и квадратный трёхчлен на множители не раскладывается.

Замечание . В случае, когда D < 0 , квадратный трехчлен всё-таки можно разложить на линейные множители, но только в области комплексных чисел, однако этот материал выходит за рамки школьного курса.

Формула для корней квадратного уравнения

Из формул (9) и (10) вытекает формула для корней квадратного уравнения .

Действительно, в случае, когда D = 0 , из формулы (9) получаем:

Следовательно, в случае, когда D = 0 , уравнение (1) обладает единственным корнем, который вычисляется по формуле

В случае, когда D > 0 , из формулы (10) получаем:

Таким образом, в случае, когда D > 0 , уравнение (1) имеет два различных корня , которые вычисляются по формулам

Замечание 1 . Формулы (12) и (13) часто объединяют в одну формулу и записывают так:

Замечание 2 . В случае, когда D = 0 , обе формулы (12) и (13) превращаются в формулу (11). Поэтому часто говорят, что в случае, когда D = 0 , квадратное уравнение (1) имеет два совпавших корня , вычисляемых по формуле (11), а саму формулу (11) переписывают в виде:

Замечание 3 . В соответствии с материалом, изложенным в разделе «Кратные корни многочленов», корень (11) является корнем уравнения (1) кратности 2.

В случае, когда D = 0 , разложение квадратного трехчлена на линейные множители (9) можно переписать по-другому, воспользовавшись формулой (15):

ax 2 + bx + c =
= a (x – x1) 2 .		 (16)

В случае, когда D > 0 , разложение квадратного трехчлена на линейные множители (10) с помощью формул (12) и (13) переписывается так:

ax 2 + bx + c =
= a (x – x1) (x – x2) .		 (17)

Замечание 4 . В случае, когда D = 0 , корни x1 и x2 совпадают, и формула (17) принимает вид (16).

Прямая и обратная теоремы Виета

Раскрывая скобки и приводя подобные члены в правой части формулы (17), получаем равенство

Отсюда, поскольку формула (17) является тождеством, вытекает, что коэффициенты многочлена

равны соответствующим коэффициентам многочлена

Таким образом, справедливы равенства

следствием которых являются формулы

Формулы (18) и составляют содержание теоремы Виета (прямой теоремы Виета) .

Словами прямая теорема Виета формулируется так: — «Если числа x1 и x2 являются корнями квадратного уравнения (1), то они удовлетворяют равенствам (18)».

Обратная теорема Виета формулируется так: — «Если числа x1 и x2 являются решениями системы уравнений (18), то они являются корнями квадратного уравнения (1)».

Для желающих ознакомиться с примерами решений различных задач по теме «Квадратные уравнения» мы рекомендуем наше учебное пособие «Квадратный трехчлен».

Графики парабол и решение с их помощью квадратных неравенств представлены в разделе «Парабола на координатной плоскости. Решение квадратных неравенств» нашего справочника.

Источник

Цели:

  • образовательная: обобщить и систематизировать
    знания и умения решения квадратных уравнений;
  • развивающая: формировать умения определять тип
    квадратного уравнения и выбирать рациональное
    решение по его коэффициентам;
  • воспитательная: воспитывать внимательность и
    краткость изложения решений.

Тип урока: обобщение знаний и умений
решения квадратных уравнений.

Оборудование: компьютер,
интерактивная доска, карточки с заданиями, доска.

Эпиграф

Метод решения хорош, если с самого начала
мы можем предвидеть — и далее подтвердить это, —
что, следуя этому методу, мы достигнем цели.
(Г.Лейбниц) 

ХОД УРОКА

1. Организационный момент.

Учитель настраивает учащихся на урок и даёт
установку на внимательность в подходе к решению
квадратных уравнений.

2. Проверка домашнего задания.

Учащиеся сдают тетради на проверку. Учитель
отвечает на возникшие вопросы у учащихся.

3. Формулирование цели и задачи урока.

Рассмотрим несколько вариантов решения
квадратных уравнений, сравним их и научимся
выбирать рациональное решение.

4. Классификация квадратных уравнений.

На интерактивной доске учащимся
представляется таблица классификации
квадратных уравнений и предлагается её
прокомментировать.

Полное квадратное
уравнение		 Частные случаи полного
квадратного уравнения
ax2 + bx + c = 0, где х –
переменная,

a, b, c – некоторые числа, причем a 0.

D = b2 – 4ac (дискриминант);

если D > 0, то уравнение имеет два корня

х1 ;
х2 ;

если D = 0, то уравнение имеет один корень (или
ещё говорят, имеет два равных корня)

х (х1 х2
= );

если D < 0, то уравнение не имеет корней.

(D не всегда обязательно вычислять, иногда
достаточно сравнить с нулём).

 а) если b=2k, то ax2 +2kx + c =0,

D = 4(k2
–ac) = 4D1 (дискриминант), где D1 = k2
–ac;

если D1 >0, то D >0, уравнение имеет два
корня

х1 ;
х2;

если D1 = 0, то D = 0, уравнение имеет один
корень х ;

б) D > 0, если a+b+c=0, то

х1 = 1; х2 = ;

D = 0, если a+b+c=0, то

х=1;

в) D > 0, если a-b+c=0, то

х1 = -1; х2 = ;

D = 0, если a-b+c=0, то

х = -1.
Приведенное квадратное
уравнение		 Частный случай
приведенного квадратного уравнения
x2 + px + q = 0, если D > 0,
уравнение имеет два корня и решается по теореме,
обратной теореме Виета  х1+х2 = -p, х1·х2
= q.		 Если p – четное, D = 4(– q)= 4D2
(дискриминант),

где D2 = (– q);

D2 > 0, то D > 0, уравнение имеет два корня

х1 + , х2 — .

Неполное квадратное
уравнение
а) ax2 + c = 0, где с0;

если — > 0, то

х1 — , х2 =
  ;

если —
< 0, то уравнение не имеет корней.

 б) ax2 + bx = 0, где b0; уравнение имеет
два корня

х1 = 0, х2 = — .

 в) ax2 = 0; уравнение имеет один
корень

х = 0.
Метод “переброски”

ax2 + bx +
c = 0, для решения данного квадратного уравнения
составим и решим вспомогательное квадратное
уравнение путём умножения свободного члена на
первый коэффициент и запишем это произведение в
новом уравнении свободным членом, т.е. получим
квадратное уравнение вида

у2 + by + ac = 0. Полученное квадратное
уравнение можно решать любым рациональным
способом (как правило, по теореме, обратной
теореме Виета). Его корни — у1 и у2.
Корни исходного квадратного уравнения:

х1 = и х2 = .

5. Ознакомившись с таблицей
классификации, трём учащимся предлагается
составить свои уравнения для каждого случая и
решить их на доске с последующими комментариями.

Например:

1. 5х2 – 11х + 2 = 0;

D = b2 – 4ac = (-11)2 — 45·2 = 81; D > 0, уравнение имеет два
корня;

х1 = = = 0,2;

х2 = = = 2.

Ответ: 0,2; 2.

2. 3х2 – 14х + 16 = 0;

D1 = k2 –ac = (-7)2 — 316 = 1; D > 0, уравнение
имеет два корня;

х1 = = = 2;

х2 = = = 2.

Ответ: 2; 2.

3. 15х2 +22х — 37 = 0;

D > 0, уравнение имеет два корня;

Так как 15 + 22 – 37 = 0, то х1 = 1, х2 = = — 2 .

Ответ: 1; — 2 .

Следующим трём учащимся предлагается
аналогичное задание, но для других случаев.

4. -15х2 + 22х + 37 = 0;

D > 0, уравнение имеет два корня;

Так как -15– 22 + 37 = 0, то х1 = -1 , х2 = = 2 .

Ответ: -1; 2 .

5. х2 – 5х + 6 = 0;

D > 0, уравнение имеет два корня;

по теореме, обратной теореме Виета х1+х2
= 5, х1·х2 = 6.

Значит, х1 = 2, х2 = 3.

Ответ: 2; 3.

6. х2 – 6х + 7 = 0;

D > 0, уравнение имеет два корня;

по формуле корней приведенного квадратного
уравнения с чётным вторым коэффициентом имеем

х1
+ , х2 — .

Ответ:
— , + .

Следующему учащемуся предлагается решить
квадратное уравнение методом “переброски”.

7. 5х2 + 37х — 24 = 0;

D > 0, уравнение имеет два корня;

составим вспомогательное уравнение

у2 + 37y – 120 = 0; по теореме, обратной теореме
Виета у1+ у2 = -37, у1·у2 = -120.

Значит, у1 = -40, у2 = 3, тогда корни
исходного уравнения

х1 = — 8, х2 = .

Ответ: — 8, .

6. Устные упражнения:

(учащимся предлагается прокомментировать
возможные способы рационального решения
квадратного уравнения).

1. 2х2 + 3х + 1 = 0; (D > 0, a – b + c = 0);

2. х2 + 5х — 6 = 0; (D > 0, a + b + c = 0);

3. 3х2 — 7х + 4 = 0; (D > 0, a + b + c = 0);

4. 5х2 + 8х + 3 = 0; (D1 > 0, значит, D > 0, a –
b + c = 0);

5. у2 — 10y – 24 = 0;  (D2 > 0, значит, D >
0, по формуле корней приведенного квадратного
уравнения с чётным вторым коэффициентом);

6. у2 + y – 90 = 0; (D > 0, по теореме, обратной
теореме Виета);

7. у2 — 8y – 84 = 0; (D2 > 0, значит, D > 0, по
формуле корней приведенного квадратного
уравнения с чётным вторым коэффициентом);

8. 3х2 — 8х + 5 = 0; (D1 > 0, значит, D > 0, a + b
+ c = 0);

9. 3х2 + 6х = 0;  (неполное квадратное
уравнение; случай б));

10. 4х2 — 16 = 0;  (неполное квадратное
уравнение; случай а));

11. 3у2 — 3y + 1 = 0;  (D < 0, уравнение не имеет
корней);

12. 14х2 — 5х — 1 = 0;  (D > 0, метод
“переброски”).

7. Творческая самостоятельная работа

(по карточкам; в двух вариантах; с последующей
устной проверкой).

8. Домашнее задание.

1. Повторите таблицу классификации квадратных
уравнений.

2. Решите квадратные уравнения наиболее
рациональным способом:

3. Составить пять квадратных уравнений с
недостающими коэффициентами.

Источник

Понравилась статья? Поделить с друзьями:

Не пропустите также:

  • Как найти аналитическое решение уравнения
  • Как найти квоту экономика
  • Как ватсап найти человека без номера телефона
  • Как найти кольцо в домашних условиях
  • Как найти основы прямоугольной трапеции

    • 0 0 голоса
    Рейтинг статьи
    Подписаться
    Уведомить о
    guest

    0 комментариев
    Старые
    Новые Популярные
    Межтекстовые Отзывы
    Посмотреть все комментарии