Работа расширения или сжатия газа
Одним
из основных термодинамических процессов,
совершающихся в большинстве тепловых
машин, является процесс расширения газа
с совершением работы. Легко определить
работу, совершаемую при изобарном
расширении газа.
Если
при изобарном расширении газа от объема
V1
до объема V2
происходит перемещение поршня в цилиндре
на расстояние l
(рис. 7.3), то работа A’,
совершенная газом, равна
,
(7.27)
где
p
— давление газа,
—
изменение его объема.
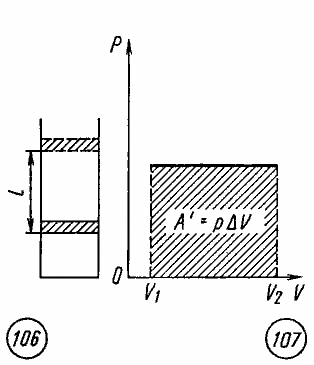
Рис
7.3 Рис 7.4
Как
видно из рисунка 7.4, при изображении
изобарного процесса расширения газа в
координатных осях p
, V
площадь фигуры, ограниченной графиком
процесса, координатами V1
и V2,
осью абсцисс, пропорциональна работе
газа A’.
Работа
при произвольном процессе расширения
газа.
Произвольный процесс расширения газа
от объема V1
до объема V2
можно представить как совокупность
чередующихся изобарных и изохорных
процессов.
При
изохорных процессах работа равна нулю,
так как поршень в цилиндре не перемещается.
Работа при изобарных процессах
пропорциональна площади фигуры на
диаграмме p,
V
под соответствующим участком изобары
(рис. 7.5).
Рис.
7.5
Рис. 7.6
Следовательно,
работа при произвольном процессе
расширения газа прямо пропорциональна
площади фигуры под соответствующим
участком графика процесса на диаграмме
p,
V.
Работа
при изотермическом расширении газа.
Сравнивая площади фигур под участками
изотермы и изобары (рис. 7.6), можно сделать
вывод, что расширение газа от объема V1
до объема V2
при одинаковом начальном значении
давления газа сопровождается в случае
изобарного расширения совершением
большей работы.
Работа
при сжатии газа.
При расширении газа направление вектора
силы давления газа совпадает с направлением
вектора перемещения, поэтому работа
A’,
совершенная газом, положительна (A’
> 0), а работа А
внешних сил отрицательна: A
= —A’
< 0.
При
сжатии газа направление вектора внешней
силы совпадает с направлением перемещения,
поэтому работа А
внешних сил положительна (A
> 0), а работа A’,
совершенная газом, отрицательна (A’
< 0).
Адиабатный
процесс.
Кроме изобарного, изохорного и
изотермического процессов, в термодинамике
часто рассматриваются адиабатные
процессы.
Адиабатным
процессом
называется процесс, происходящий в
термодинамической системе при отсутствии
теплообмена с окружающими телами, т. е.
при условии Q
= 0.
Отсутствие
теплообмена с окружающей средой может
быть обеспечено хорошей теплоизоляцией
газа. Быстрые процессы расширения или
сжатия газа могут быть близкими к
адиабатному и при отсутствии теплоизоляции,
если время, за которое происходит
изменение объема газа, значительно
меньше времени, необходимого для
установления теплового равновесия газа
с окружающими телами.
Примерами
адиабатных процессов могут служить
процессы сжатия воздуха в цилиндре
воздушного огнива, в цилиндре двигателя
внутреннего сгорания. В соответствии
с первым законом термодинамики, при
адиабатном сжатии изменение внутренней
энергии газа
равно
работе внешних сил А:
(7.28)
Так
как работа внешних сил при сжатии
положительна, внутренняя энергия газа
при адиабатном сжатии увеличивается,
его температура повышается.
При
адиабатном расширении газ совершает
работу A’
за счет уменьшения своей внутренней
энергии:
,
(7.29)
поэтому
температура газа при адиабатном
расширении понижается. Это можно
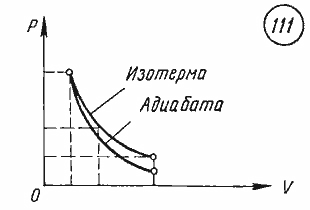
обнаружить в следующем опыте. Если в
бутылку, содержащую насыщенный водяной
пар, накачивать с помощью насоса воздух,
то пробка вылетает (рис. 7.7).
Рис.
7.7
Работа
A’
по выталкиванию пробки совершается
воздухом за счет уменьшения его внутренней
энергии, так как расширение воздуха
происходит за очень короткое время и
теплообмен с окружающей средой не
успевает произойти. Образование капель
тумана доказывает, что при адиабатном
расширении воздуха его температура
понизилась и опустилась ниже точки
росы.
График
адиабатного процесса.
Поскольку при адиабатном сжатии
температура газа повышается, то давление
газа с уменьшением объема растет быстрее,
чем при изотермическом процессе.
Понижение температуры газа при адиабатном
расширении приводит к тому, что давление
газа убывает быстрее, чем при изотермическом
расширении.
График
адиабатного процесса в координатных
осях p,
V
представлен на рисунке 1.8. На том же
рисунке для сравнения приведен график
изотермического процесса.
Рис.
7.8
Вну́тренняя
эне́ргия
тела (обозначается как E
или U) —
полная энергия этого тела за вычетом
кинетической
энергии
тела как целого и потенциальной
энергии
тела во внешнем поле сил. Следовательно,
внутренняя энергия складывается из
кинетической энергии хаотического
движения молекул,
потенциальной энергии взаимодействия
между ними и внутримолекулярной энергии.
Внутренняя
энергия является однозначной функцией
состояния системы. Это означает, что
всякий раз, когда система оказывается
в данном состоянии, её внутренняя энергия
принимает присущее этому состоянию
значение, независимо от предыстории
системы. Следовательно, изменение
внутренней энергии при переходе из
одного состояния в другое будет всегда
равно разности между ее значениями в
конечном и начальном состояниях,
независимо от пути, по которому совершался
переход.
Внутреннюю
энергию тела нельзя измерить напрямую.
Можно определить только изменение
внутренней энергии:
где
—подведённая
к телу теплота,
измеренная в джоулях
—работа,
совершаемая телом против внешних сил,
измеренная в джоулях
Эта
формула является математическим
выражением первого
начала термодинамики
Для
квазистатических
процессов
выполняется следующее соотношение:
где
—температура,
измеренная в кельвинах
—энтропия,
измеренная в джоулях/кельвин
—давление,
измеренное в паскалях
—химический
потенциал
—количество
частиц в системе
Идеальные
газы
Согласно
закону Джоуля, выведенному эмпирически,
внутренняя энергия идеального
газа
не зависит от давления или объёма. Исходя
из этого факта, можно получить выражение
для изменения внутренней энергии
идеального газа. По определению молярной
теплоёмкости
при постоянном объёме,
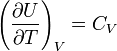
Так как внутренняя энергия идеального
газа является функцией только от
температуры, то

(7.30)
Эта
же формула верна и для вычисления
изменения внутренней энергии любого
тела, но только в процессах при постоянном
объёме (изохорных
процессах);
в общем случае CV
(T,V)
является функцией и температуры, и
объёма.
Если
пренебречь изменением молярной
теплоёмкости при изменении температуры,
получим:
ΔU
= νCVΔT,
(7.31)
где
ν — количеств о вещества, ΔT —
изменение температуры.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Работа в термодинамике
В термодинамике, в отличие от механики, рассматривается не движение тела как целого, а лишь относительное изменение частей термодинамической системы, в результате которого меняется ее объем.
Рассмотрим работу газа при изобарическом расширении.
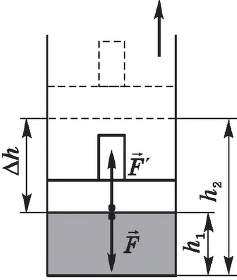
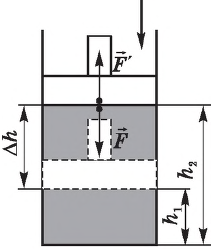
Вычислим работу, совершаемую газом при его действии на поршень с силой ${F’}↖{→}$, равной по величине и противоположной по направлению силе ${F’}↖{→}$, действующей на газ со стороны поршня: ${F’}↖{→}=-{F’}↖{→}$ (согласно третьему закону Ньютона), $F’=pS$, где $p$ — давление газа, а $S$ — площадь поверхности поршня. Если перемещение поршня $∆h$ в результате расширения мало, то давление газа можно считать постоянным и работа газа равна:
$A’=F’∆h=pS∆h=p∆V$
Если газ расширяется, он совершает положительную работу, та к как перемещение поршня совпадает по направлению с силой ${F’}↖{→}$. Если газ сжимается, то работа газа отрицательна, поскольку перемещение поршня противоположно силе ${F’}↖{→}$. В формуле $A’=F’∆h=pS∆h=p∆V$ появится знак «минус»: $∆V < 0$, поскольку $∆h < 0$.
Работа внешних сил $А$, наоборот, положительна при сжатии газа и отрицательна при расширении:
$A=-A’=-p∆V$
Совершая над газом положительную работу, внешние тела передают ему часть своей энергии. При расширении газа внешние тела отбирают у газа часть его энергии — работа внешних сил отрицательна.
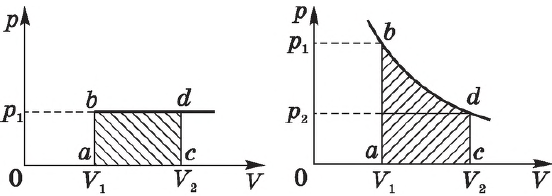
На графике зависимости давления от объема $р(V)$ работа определяется как площадь, ограниченная кривой $р(V)$, осью $V$ и отрезками $ab$ и $cd$, равными давлениям $р_1$ в начальном ($V_1$) и $р_2$ в конечном ($V_2$) состояниях, как для изобарного, так и для изотермического процессов.
Первый закон термодинамики
Первое начало (первый закон) термодинамики — это закон сохранения и превращения энергии для термодинамической системы.
Согласно первому началу термодинамики, работа может совершаться только за счет теплоты или какой-либо другой формы энергии. Следовательно, работу и количество теплоты измеряют в одних единицах — джоулях (как и энергию).
Первое начало термодинамики было сформулировано немецким ученым Ю. Л. Майером в 1842 г. и подтверждено экспериментально английским ученым Дж. Джоулем в 1843 г.
Первый закон термодинамики формулируется так:
Изменение внутренней энергии системы при переходе ее из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе:
$∆U=A+Q$
где $∆U$ — изменение внутренней энергии, $А$ — работа внешних сил, $Q$ — количество теплоты, переданной системе.
Из $∆U=A+Q$ следует закон сохранения внутренней энергии. Если систему изолировать от внешних воздействий, $A=0$ и $Q=0$,а следовательно, $∆U=0$.
При любых процессах, происходящих в изолированной системе, ее внутренняя энергия остается постоянной.
Если работу совершает система, а не внешние силы, то уравнение ($∆U=A+Q$) записывается в виде:
$Q=∆U+A’$
где $А’$ — работа, совершаемая системой ($А’=-А$).
Количество теплоты, переданное системе, идет на изменение ее внутренней энергии и на совершение системой работы над внешними телами.
Первое начало термодинамики может быть сформулировано как невозможность существования вечного двигателя первого рода, который совершал бы работу, не черпая энергию из какого-либо источника, т. е. только за счет внутренней энергии.
Действительно, если к телу не поступает теплота ($Q=0$), то работа $А’$, согласно уравнению $Q=∆U+A’$, совершается только за счет убыли внутренней энергии $A’=-∆U$. После того, как запас энергии окажется исчерпанным, двигатель перестает работать.
Следует помнить, что как работа, так и количество теплоты являются характеристиками процесса изменения внутренней энергии, поэтому нельзя говорить, что в системе содержится определенное количество теплоты или работы. Система в любом состоянии обладает лишь определенной внутренней энергией.
Применение первого закона термодинамики к различным процессам
Рассмотрим применение первого закона термодинамики к различным термодинамическим процессам.
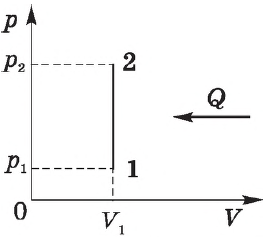
Изохорный процесс. Зависимость $р(Т)$ на термодинамической диаграмме изображается изохорой.
Изохорный (изохорический) процесс — термодинмический процесс, происходящий в системе при постоянном объеме.
Изохорный процесс можно осуществить в газах и жидкостях, заключенных в сосуд с постоянным объемом.
При изохорном процессе объем газа не меняется ($∆V=0$), и, согласно первому началу термодинамики $Q=∆U+A’$,
$∆U=Q$
т. е. изменение внутренней энергии равно количеству переданного тепла, т. к. работа ($A=p∆V=0$) газом не совершается.
Если газ нагревается, то $Q > 0$ и $∆U > 0$, его внутренняя энергия увеличивается. При охлаждении газа $Q < 0$ и $∆U < 0$, внутренняя энергия уменьшается.
Изотермический процесс графически изображается изотермой.
Изотермический процесс — это термодинамический процесс, происходящий в системе при постоянной температуре.
Поскольку при изотермическом процессе внутренняя энергия газа не меняется ($T=const$), то все переданное газу количество теплоты идет на совершение работы:
$Q=A’$
При получении газом теплоты ($Q > 0$) он совершает положительную работу ($А’ > 0$). Если газ отдает тепло окружающей среде, $Q < 0$ и $А’ < 0$. В этом случае над газом совершается работа внешними силами. Для внешних сил работа положительна. Геометрически работа при изотермическом процессе определяется площадью под кривой $р(V)$.
Изобарный процесс на термодинамической диаграмме изображается изобарой.
Изобарный (изобарический) процесс — термодинамический процесс, происходящий в системе с постоянным давлением $p$.
Примером изобарного процесса является расширение газа в цилиндре со свободно ходящим нагруженным поршнем.
При изобарном процессе согласно формуле $Q=∆U+A’$ передаваемое газу количество теплоты идет на изменение его внутренней энергии $∆U$ и на совершение им работы $A’$ при постоянном давлении:
$Q=∆U+A’$
Работа идеального газа определяется по графику зависимости $p(V)$ для изобарного процесса ($A’=p∆V$).
Для идеального газа при изобарном процессе объем пропорционален температуре, в реальных газах часть теплоты расходуется на изменение средней энергии взаимодействия частиц.
Адиабатический процесс
Адиабатический процесс (адиабатный процесс) — это термодинамический процесс, происходящий в системе без теплообмена с окружающей средой ($Q=0$).
Адиабатическая изоляция системы приближенно достигается в сосудах Дьюара, в так называемых адиабатных оболочках. На адиабатически изолированную систему не оказывает влияния изменение температуры окружающих тел. Ее внутренняя энергия и может меняться только за счет работы, совершаемой внешними телами над системой, или самой системой.
Согласно первому началу термодинамики ($∆U=A+Q$), в адиабатной системе
$∆U=A$
где $А$ — работа внешних сил.
При адиабатном расширении газа $А < 0$.
Следовательно,
$∆U={i}/{2}·{m}/{M}R∆T < 0,$
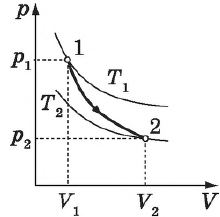
что означает уменьшение температуры при адиабатном расширении. Оно приводит к тому, что давление газа уменьшается более резко, чем при изотермическом процессе.
На рисунке адиабата $1—2$, проходящая между двумя изотермами, наглядно иллюстрирует сказанное. Площадь под адиабатой численно равна работе, совершаемой газом при его адиабатическом расширении от объема $V_1$ до $V_2$.
Адиабатное сжатие приводит к повышению температуры газа, т. к. в результате упругих соударений молекул газа с поршнем их средняя кинетическая энергия возрастает, в отличие от расширения, когда она уменьшается (в первом случае скорости молекул газа увеличиваются, во втором — уменьшаются).
Резкое нагревание воздуха при адиабатическом сжатии используется в двигателях Дизеля.
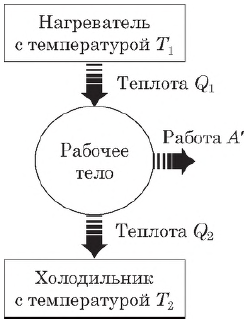
Принцип действия тепловых двигателей
Тепловой двигатель — это устройство, преобразующее внутреннюю энергию топлива в механическую энергию.
Согласно второму началу термодинамики, тепловой двигатель может непрерывно совершать периодически повторяющуюся механическую работу за счет охлаждения окружающих тел, если он не только получает теплоту от более горячего тела (нагревателя), но при этом отдает теплоту менее нагретому телу (холодильнику). Следовательно, на совершение работы идет не все количество теплоты, полученное от нагревателя, а только часть ее.
Таким образом, основными элементами любого теплового двигателя являются:
- рабочее тело (газ или пар), совершающее работу;
- нагреватель, сообщающий энергию рабочему телу;
- холодильник, поглощающий часть энергии от рабочего тела.
Коэффициент полезного действия теплового двигателя
Согласно закону сохранения энергии, работа, совершаемая двигателем, равна:
$A’=|Q_1|-|Q_2|$
где $Q_1$ — количество теплоты, полученное от нагревателя, $Q_2$ — количество теплоты, отданное холодильнику.
Коэффициентом полезного действия (КПД) теплового двигателя называется отношение работы $А’$, совершаемой двигателем, к количеству теплоты, полученному от нагревателя:
$η={A’}/{|Q_1|}={|Q_1|-|Q_2|}/{|Q_1|}=1-{|Q_2|}/{|Q_1|}$
Так как у всех двигателей некоторое количество теплоты передается холодильнику, то $η < 1$.
КПД теплового двигателя пропорционален разности температур нагревателя и холодильника. При $T_1 — T_2=0$ двигатель не может работать.
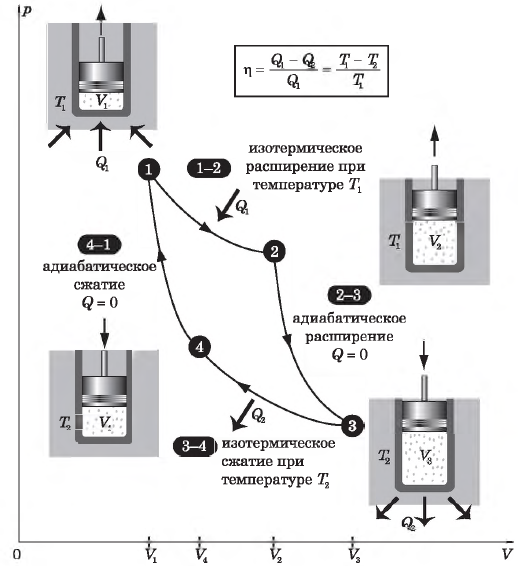
Цикл Карно
Цикл Карно — это круговой обратимый процесс, состоящий из двух изотермических и двух адиабатических процессов.
Впервые этот процесс был рассмотрен французским инженером и ученым Н. Л. С. Карно в 1824 г. в книге «Размышления о движущей силе огня и о машинах, способных развивать эту силу».
Целью исследований Карно было выяснение причин несовершенства тепловых машин того времени (они имели КПД $< 5%$)и поиски путей их усовершенствования.
Выбор двух изотермических и двух адиабатических процессов был обусловлен тем, что работа газа при изотермическом расширении совершается за счет внутренней энергии нагревателя, а при адиабатном процессе — за счет внутренней энергии расширяющегося газа. В этом цикле исключен контакт тел с разной температурой, следовательно, исключена теплопередача без совершения работы.
Цикл Карно — самый эффективный из всех возможных. Его КПД максимален.
На рисунке изображены термодинамические процессы цикла. В процессе изотермического расширения ($1-2$) при температуре $Т_1$ работа совершается за счет изменения внутренней энергии нагревателя, т. е. за счет подведения к газу количества теплоты $Q_1$:
$A_{12}=Q_1.$ Охлаждение газа перед сжатием ($3-4$) происходит при адиабатном расширении ($2-3$). Изменение внутренней энергии $∆U_{23}$ при адиабатном процессе ($Q=0$) полностью преобразуется в механическую работу:
$A_{23}=-∆U_{23}$
Температура газа в результате адиабатического расширения ($2-3$) понижается до температуры холодильника $Т_2 < Т_1$. В процессе ($3-4$) газ изотермически сжимается, передавая холодильнику количество теплоты $Q_2$:
$A_{34}=Q_2,$
Цикл завершается процессом адиабатического сжатия ($4—1$), при котором газ нагревается до температуры $Т_1$.
Максимальное значение КПД тепловых двигателей, работающих на идеальном газе, по циклу Карно:
$η={T_1-T_2}/{T_1}=1-{T_2}/{T_1}$
Суть формулы $η={T_1-T_2}/{T_1}=1-{T_2}/{T_1}$ выражена в доказанной С. Карно теореме о том, что КПД любого теплового двигателя не может превышать КПД цикла Карно, осуществляемого при той же температуре нагревателя и холодильника.
Работа в термодинамике.
В термодинамике работа — это взаимодействие системы с внешними объектами, в результате чего изменяются параметры системы
Рассмотрим цилиндр с идеальным газом, который находится под подвижным поршнем. Пусть внешняя сила, действующая на поршень, перемещает его из состояния 1 в состояние 2
Работа силы равна . Со стороны газа на поршень действуют сила, равная произведению давлению газа на поршень и площадь сечения поршня
. Подставив вторую формулу в первую, получим
.
Знак «-» в формуле означает, что при уменьшении объема (как в нашем примере, ) работа внешних сил положительная. И наоборот, когда газ расширяется, работа внешней силы, удерживающей поршень, отрицательная.
Графическое определение работы
Строим график процесса p(V). Определяем на графике точки, которые соответствуют состоянию системы в 1 и 2 состояниях. Площадь фигуры под графиком — есть термодинамическая работа самой системы. Внешняя работа над системой равна работе системы, но с противоположным знаком
Работа термодинамической системы при изобарном процессе
Работа термодинамической системы при изотермическом процессе
При изохорном процессе объем не изменяется, работа равна нулю A=0.
| Работа (A) |
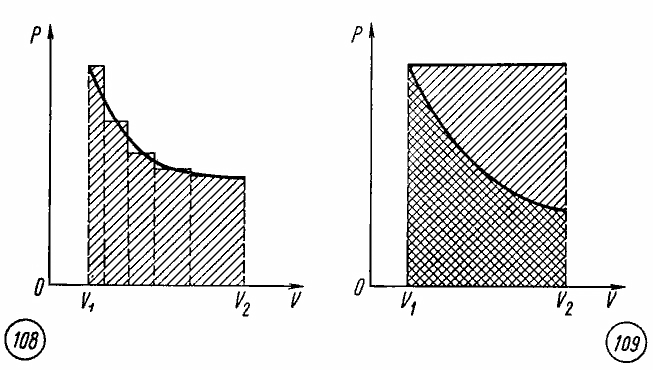
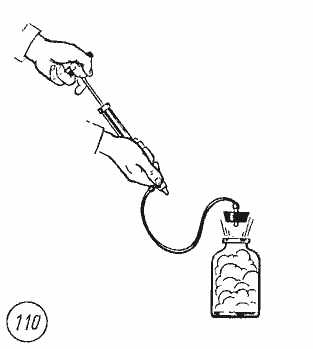
Работа — физическая величина, характеризующая способ передачи энергии термодинамической системе (газу), при котором изменяются внешние параметры (например, объём (V)). Работа газа (A) над внешними телами при малом изменении объёма (V) и/или при изобарном процессе вычисляется по формуле: (boxed{A = pDelta V > 0}). ((1)) Работа внешних сил над газом (A’) вычисляется по формуле: (boxed{A’ = -A = -pDelta V < 0}). ((2)) В общем случае работа газа (или работа внешних сил) вычисляется как площадь заштрихованной фигуры в координатах ((p), (V)): для изобарного процесса — площадь прямоугольника (рис. (1)), для любого другого процесса — площадь криволинейной фигуры (рис. (2)).
|
||
| Количество теплоты (Q) |
Количество теплоты — физическая величина, характеризующая способ передачи энергии термодинамической системе (газу), при котором не изменяются внешние параметры (например, объём (V)). Количество теплоты (Q > 0), если энергия сообщается термодинамической системе (газу) без изменения внешних параметров (например, объёма (V)). Если термодинамическая система не обменивается с внешними телами энергией в форме теплоты, то она называется адиабатной: (Q = 0). Работа (A) [Дж] и количество теплоты (Q) [Дж] — физические величины, которые характеризуют процесс изменения энергии термодинамической системы |
||
| Теплоёмкость |
Теплоёмкость — физическая величина, определяющая количество теплоты (Q), которое изменяет температуру термодинамической системы на (1) К: (boxed{C = frac{Q}{Delta T}}), (C = [frac{Дж}{К}]). ((3)) Удельная теплоёмкость: (boxed{c = frac{Q}{mDelta T}}), (c = [frac{Дж}{кг · К}]). ((4)) Молярная теплоёмкость: (boxed{C_M = frac{Q}{nu Delta T}}), (C_M = [frac{Дж}{моль · К}]). ((5)) Уравнение Майера: (boxed{C_p — C_V = R}) ((nu = 1)), ((6)) где (R) — универсальная газовая постоянная; (boxed{C_p = frac{Q_p}{nu Delta T}}) — молярная теплоёмкость при изобарном процессе, (boxed{C_V = frac{Q_V}{nu Delta T}}) — молярная теплоёмкость при изохорном процессе |
При изучении физики в восьмом классе мы говорили о том, что
изменить состояние термодинамической системы, то есть её внутреннюю энергию, можно
двумя способами: используя теплопередачу или совершая механическую работу.
Поговорим о последней более подробно.
Итак, когда мы изучали механику, мы с вами говорили о том,
что работа силы (то есть механическая работа) связана с превращением одного
вида энергии в другой, например, механической энергии во внутреннюю. При этом работу
силы мы рассматривали как меру изменения энергии физической системы.
А вот как определить работу в термодинамике, ведь при
рассмотрении термодинамических процессов механическое перемещение макротел в
целом не рассматривается?
Забавно, но работа в термодинамике определяется так же, как и
в механике, но она равна изменению не механической энергии тела, а изменению
его внутренней энергии.
Итак, давайте рассмотрим газ, находящийся в цилиндрическом
сосуде с площадью основания S, и закрытый
подвижным поршнем. Взаимодействие газа с поршнем, а также со стенками сосуда
можно характеризовать давлением, которое газ оказывает на них.
Начнём медленно нагревать газ так, чтобы его давление не
изменялось. Очевидно, что в этом случае газ будет изобарически расширяться, а
поршень начнёт перемещаться за счёт работы силы давления газа над внешними
телами.
Предположим, что поршень переместился на расстояние ∆l.
Так как в процессе расширения давление газа не изменялось, то и сила давления
газа на поршень оставалась неизменной:
F
= pS.
Поэтому работу этой силы мы можем найти как произведение
модуля силы на модуль перемещения и на косинус угла между направлением вектора
силы и вектора перемещения (в нашем примере правда, этот угол равен нулю):
Подставим в записанное уравнение выражение для силы давления:
А теперь давайте подумаем, что определяет произведение площади
основания сосуда (она же площадь основания поршня) и модуля перемещения поршня?..
Да, оно определяет приращение объёма:
Тогда работа газа при его изобарном расширении будет
определяться произведением давления газа на изменение его объёма:
Из этой формулы следует, что сила давления газа совершает
работу только в процессе изменения объёма газа.
А так как давление газа всегда величина положительная, то из
формулы также следует, что при расширении газ совершает положительную работу. При
сжатии же газа сила давления будет совершать отрицательную работу.
Процесс медленного изобарного сжатия газа можно
характеризовать и работой внешних сил над газом, которая отличается от работы
самого газа только знаком:
А теперь давайте запишем уравнение Клайперона — Менделеева
для двух состояний газа в цилиндре:
И вычтем из второго уравнение первое:
В левой части полученного равенства у нас стоит произведение
давления газа на изменение его объёма. А это, как мы с вами нашли ранее, есть не
что иное, как работа газа при изобарном процессе:
Теперь предположим, что в сосуде под поршнем находится один
моль идеального газа и в результате изобарного расширения его температура
изменилась на один кельвин. Тогда получим, что «А равно Эр»:
Отсюда вытекает физический смысл универсальной газовой
постоянной: она численно равна работе, совершаемой одним молем идеального
газа при его изобарном нагревании на один кельвин.
Работе газа при его изобарном расширении или сжатии можно
дать простое геометрическое токование. Для этого давайте построим график
зависимости давления газа от занимаемого им объёма. Очевидно, что графиком
является прямая линия, параллельная оси абсцисс.
А площадь прямоугольника, ограниченного графиком процесса,
осью V и прямыми, соответствующими значениям объёмов в начальном и
конечном состояниях газа, — это есть ничто иное, как работа газа.
Если процесс перехода газа из начального состояния в конечное
не является изобарным, то кривую зависимости давления газа от занимаемого им
объёма можно представить как ломаную, состоящую из большого числа изохор и
изобар. Работа на изохорных участках равна нулю, а суммарная работа на всех
изобарных участках будет равна площади заштрихованной фигуры.
А теперь для закрепления материала решим с вами несколько
классических задач. В первой задаче нам необходимо будет определить работу, совершаемую
силой давления идеального газа определённой массы при его изобарном нагревании от
290 К до 355 К, если давление газа и его начальный объём соответственно 200 кПа
и 0,1 м3.
Задача 2. Идеальный газ в количестве 3 молей находится
при температуре 350 К. После изохорного охлаждения, в результате которого
давление уменьшилось в два раза, газ испытывает изобарное расширение, причём в
конечном состоянии температура равна первоначальной. Изобразите графически эти
процессы в осях p, V и вычислите совершённую газом работу.