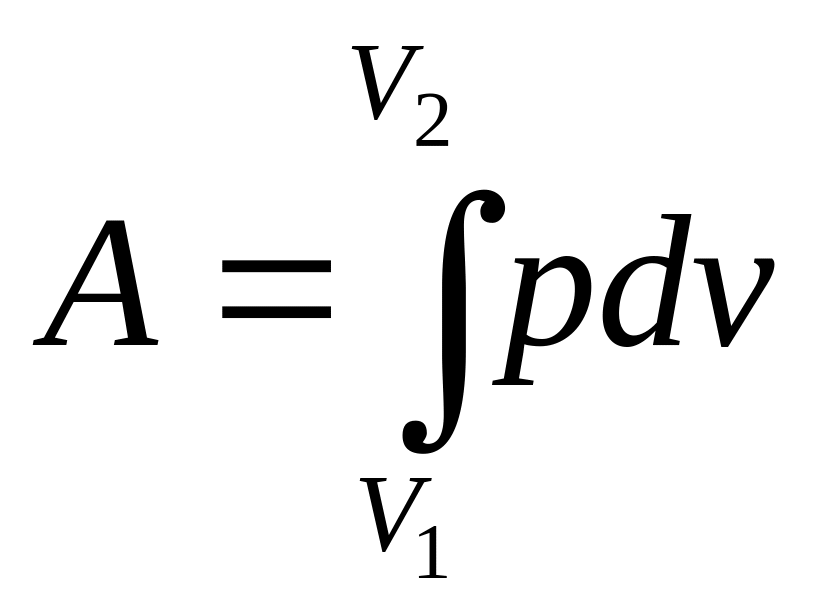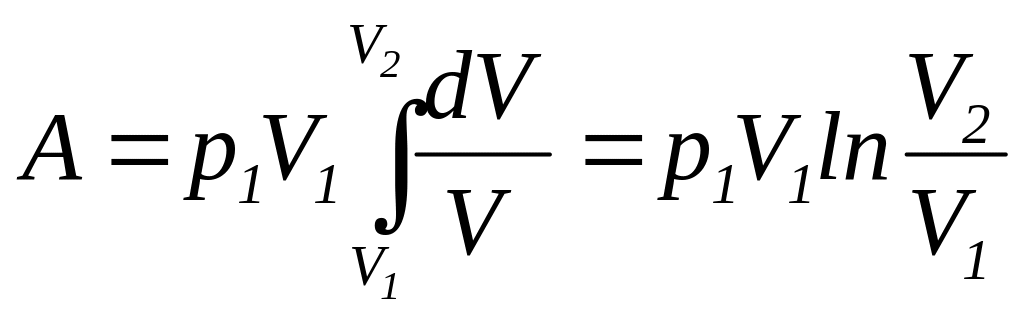Изменение
объема газа, т.е. его расширение или
сжатие, можно произвести так, чтобы
температура газа оставалась постоянной.
Такой процесс изменения состояния газа
или другой системы, который проходит
при постоянной температуре, называется
изотермическим. Для того чтобы процесс
в системе мог протекать изотермически,
она должна быть помещена в среду с
постоянной температурой, к примеру, в
термостат — аппарат, в котором специальное
устройство — терморегулятор —
автоматически поддерживает температуру
постоянной. Расширяясь в термостате,
т.е. при T=const,
система производит некоторую работу,
которая по первому началу термодинамики
равна:
|
(109) |
где
― количество теплоты, поглощенной
системой от термостата, а
― изменение ее внутренней энергии.
В
случае идеального газа внутренняя
энергия зависит только от температуры
и не зависит от занимаемого им объема.
Поэтому при изотермическом расширении
или сжатии идеального газа его внутренняя
энергия остается неизменной при
и
.
Первое начало термодинамики (109) в этом
случае принимает вид:
|
(110) |
|
(111) |
A=Q
Это
равенство показывает, что при изотермическом
расширении объема идеального газа
работа
может производится только за счет
поглощаемого им тепла
.
Если газ изотермически расширяется
(
),
то он совершает положительную работу
(
)
и согласно равенству (110) получает извне
(от среды термостата) такое же количество
тепла (
).
Если же внешние силы совершают над газом
работу при его изотермическом сжатии
(
,
),
то он отдает такое же количество тепла
(
).
Таким образом, в случае изотермического
расширения газ полностью преобразует
подводимое к нему тепло в совершаемую
работу. Наоборот, при изотермическом
сжатии работа, затраченная на сжатие,
полностью преобразуется в отдаваемое
газом внешней среде (среде термостата)
тепло. Именно по этой причине внутренняя
энергия и температура газа остаются
неизменными. Газ при изотермическом
процессе ведет себя как тело с бесконечно
большой теплоемкостью. Математически
это следует из общего определения
теплоемкости; обозначив изотермическую
теплоемкость через СТ,
получаем
,
т. к.
,
Из
сказанного выше ясно, что для того, чтобы
расширение газа могло происходить
изотермически, ему необходимо непрерывно
передавать тепло извне. Наоборот, чтобы
сжатие газа протекало изотермически,
от него необходимо непрерывно отбирать
тепло. Изотермический процесс,
следовательно, возможен лишь при идеально
хорошем обмене теплом между газом и
внешней средой (средой термостата).
Практически приблизиться к изотермическому
процессу можно, заставляя протекать
его настолько медленно, чтобы температура
газа все время успевала выравниваться
с температурой окружающей среды.
Вычислим
работу, совершаемую идеальным газом
при изотермическом изменении его объема
от V1
до V2.
Работа, производимая любой системой
при изменении ее объема, как мы видели,
определяется интегралом
|
(112) |
Чтобы
произвести интегрирование, нужно знать,
как при рассматриваемом процессе
давление p
связано с объемом V,
т.е. необходимо знать уравнение процесса
в переменных p,
V.
Уравнение изотермического процесса
для идеального газа получается
непосредственно из его уравнения
состояния
|
(113) |
Так
как при изотермическом процессе T=const,
то для данной массы газа
и, следовательно,
|
(114) |
где
p1
и V1
― значения давления и объема газа в
начальном состоянии. Таким образом, при
изотермическом процессе давление и
объем идеального газа связаны между
собой законом Бойля-Мариотта. Выражая
из (114) давление газа через объем и
значение параметров в начальном состоянии
|
(115) |
и
подставляя полученное выражение в
(112), находим
|
(116) |
Так
как
,
то формулу для работы идеального газа
при изотермическом изменении его объема
можно представить в виде
|
(117) |
Из
(116) и (117) видно, что работа идеального
газа при изотермическом процессе
изменения объема зависит не от разности
объемов как для изобарического процесса,
между которыми происходит расширение
или сжатие, а от их отношения (т. е. степени
расширения или сжатия газа).
Так
как при изотермическом процессе работа
A
производится идеальным газом за счет
передаваемого ему извне тепла, то
полученные выше формулы могут в равной
мере служить как для определения
совершаемой газом изотермической
работы, так и для расчета количества
теплоты Q,
необходимой для его изотермического
расширения или сжатия
|
(118) |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Термодинамические основы сжатия газов
Уравнение состояния газа
В теории компрессорных машин, работающих в условиях, когда можно пренебречь межмолекулярными силами и размерами молекул, используется уравнение состояния идеального газа.
При сжатии воздуха и его составляющих (азот, кислород, аргон, водород, гелий и др.) в области давлений до 10 МПа и температур более 273 К применение уравнения дает погрешность не более 2%.
При более высоких давлениях сжатия сказывается объем молекул газа и влияние силы межмолекулярного притяжения. Многоатомные газы и пары при давлениях и температурах, близких к критическим, не следуют уравнению состояния идеального газа. В этом случае газ рассматривается как реальный.
Объем реального газа при низких давлениях и температурах из-за. взаимного притяжения молекул меньше, чем у идеального газа, а при высоких давлениях больше, чем у идеального при влиянии собственного объема молекул. Избыточный объем газа, учитывающий объем молекул и влияние сил межмолекулярного притяжения, равен разности при одинаковых условиях.
Значения коэффициента и показателя отклонения сжимаемости Р в зависимости от давления и температуры для ряда газов приведены на рис 2.1 и в приложении П.З.
Для газовой смеси, если ее компоненты в процессе сжатия не конденсируются и не вступают друг с другом в химическую реакцию, справедливы уравнения состояния идеального и реального газов, приведенные выше. Использование этих уравнений возможно, если известны значения газовой постоянной смеси Rcm и коэффициента сжимаемости смеси 5см.
Использование правила аддитивности для определения коэффициента ξсм дает надежные результаты только в тех случаях, когда значения коэффициентов сжимаемости отдельных газов, составляющих смесь, близки друг к другу. Если же они существенно отличаются друг от друга, сумма парциальных объемов отдельных газов, составляющих газовую смесь, будет отличаться от объема смеси и поэтому значение, найденное по (2.10), будет неточным.
Для более точного определения может быть рекомендован метод, основанный на использовании закона соответственных состояний.
Процессы сжатия в компрессорных машинах
Процессы сжатия газа в компрессорных машинах обычно рассматриваются в системах Т, s- и р, υ-координат.
Термодинамический рабочий процесс компрессора протекает по политропе и описывается уравнением р/рη — const.
Для начальных и конечных параметров сжимаемого газа в изо-энтропном процессе (рис. 2.2) повышение температуры пропорционально увеличению давления и зависит от показателя k:
В теории компрессорных машин рассматриваются так называемые эталонные процессы: для машин без внутреннего охлаждения (лопастной компрессор)—адиабатный процесс; для машин с внутренним охлаждением (поршневой компрессор, многоступенчатый компрессор) — изотермический процесс.
Действительные рабочие процессы характеризуются наличием теплообмена с окружающей средой, а также наличием внутреннего теплопритока в результате работы сил трения в процессе сжатия газа.
Пренебрегая теплообменом с окружающей средой и работой сил трения в ступени центробежного компрессора, получаем эталонный процесс сжатия — изоэнтропное сжатие (n = k) (адиабатное сжатие без учета работы сил трения). Рабочим процессом ступени центробежного компрессора считается по-литропное сжатие с учетом работы сил трения (n>k)y если пренебречь теплообменом с окружающей средой. Эталонным процессом охлаждаемых машин считается изотермический, а рабочим процессом — политропный, проходящий с охлаждением (рис. 2.3).
Изотермический процесс сжатия газа в компрессоре изображен на рис. 2.3 горизонтальной линией при Т = const pv — const.
Уравнения сохранения энергии в компрессорных машинах
Энергия, сообщенная сжимаемому газу в компрессоре, расходуется на изменение энтальпии газа, кинетической и потенциальной энергии его и на покрытие тепловых потерь в окружающую среду. Пренебрегая изменением потенциальной энергии положения, дифференциальное уравнение энергии потока газа, отнесенное к 1 Кг массы газа, Дж/кг, можно записать, где dLi — элементарная энергия, сообщенная газу; dh — изменение энтальпии газа; d(c2/2) — изменение кинетической энергии газа; dqo — отведенное от газа количество теплоты. Интегрируя от входа до выхода компрессора получаем, что
Для неохлаждаемой ступени лопастного компрессора, если пренебречь теплообменом с окружающей средой,
где Li — внутренняя удельная работа лопастного компрессора. Энергия газового потока характеризуется единым параметром, называемым полная энтальпия:
Полная энтальпия h* и полная температура T* соответствуют так называемому полному давлению р*, которое имел бы газ при преобразованной без потерь кинетической энергии (адиабатный поток).
Движение реального (вязкого) газа сопровождается внутренними потерями энергии на трение и вихреобразование в рабочих органах компрессора. Энергия, израсходованная на трение и вихреобразование, Lr полностью превращается в тепловую энергию qr и передается потоку газа.
Уравнение сохранения энергии (первый закон термодинамики) имеет вид
dq = du + pdv,
где dq — элементарное количество теплоты, сообщенное газу; du — элементарное изменение внутренней энергии газа; pdv — элементарная внешняя работа газового процесса.
Известно, что для идеального газа
dh = du + d(pv) = du + pdv + vdp или
du = dq — pdv — vdp.
Подставим значение du в уравнение:
dq = dh — vdp,
где vdp — элементарная работа сжатия и перемещения газа.
В общем случае величина dq в компрессоре равна
dq = dqr — dq0
где dqr = dLr — элементарное количество теплоты, сообщенной газу вследствие потерь на трение и вихреобразование; dq0 — элементарное количество теплоты, отведенной от. газа. Из уравнений следует
vdp + dLr = dh + dq0.
Рассмотренные уравнения энергии используются в теории и расчетах компрессорных машин.
Охлаждение газа в компрессоре
Охлаждение газа в компрессоре уменьшает работу сжатия. При этом температура сжимаемого газа уменьшается до допустимых значений. Охлаждение в процессе сжатия обычно применяется при относительно высокой степени сжатия на ступень (поршневые компрессоры) или при большом значении показателя адиабаты (газы с большой молекулярной массой).
В компрессоростроении применяются следующие способы охлаждения сжимаемого газа: внутреннее, внешнее, комбинированное и предварительное, а также охлаждение путем впрыска охлаждающей среды в проточную часть машины.
Внутреннее охлаждение осуществляется непосредственно в процессе сжатия газа путем охлаждения стенок рабочих органов компрессора и обычно применяется в объемных машинах (поршневые, винтовые, ротационные и др. компрессоры) . Охлаждаемая среда — обычно вода или окружающий воздух.
В лопастных компрессорах внутреннее охлаждение применяется редко по ряду причин: увеличиваются размеры компрессора и компрессорной установки, увеличиваются гидравлические потери в неподвижных элементах рабочих органов из-за увеличения поверхности охлаждения, возможна конденсация влаги, имеющейся в сжимаемом газе и др.
Внешнее охлаждение газа осуществляется в межступенных холодильниках, расположенных вне проточной части компрессора. Сжатый газ охлаждается во внешнем холодильнике при некотором снижении давления из-за гидравлических потерь в холодильнике почти до первоначальной температуры.
На рис. 1.10 показана схема трехступенчатого поршневого компрессора с двумя промежуточными (межступенчатыми холодильниками). На рис. 2.5 показана Т, s-диаграмма рабочего процесса сжатия вышеуказанного компрессора при условии, что газ сжимается в отдельных ступенях по политропе п > k и охлаждается почти до первоначальной температуры в каждой ступени без потерь давления в холодильниках, т. е. при р = const. Заштрихованная площадь диаграмм соответствует уменьшению подводимой энергии на сжатие газа при межступенном охлаждении. Имеющаяся в сжимаемом газе влага конденсируется в межступенных холодильниках и удаляется.
Рис. 2.5. Т, s-диаграмма трехсекционного лопастного компрессора с промежуточным охлаждением
Комбинированное охлаждение предусматривает применение одновременно внутреннего и внешнего охлаждения (поршневые, винтовые и другие компрессоры объемного типа). На рис. 2.6 показана Т, s-диаграмма различных процессов сжатия в компрессоре.
Предварительное охлаждение целесообразно применять, когда имеется существенная разница между температурой всасываемого газа и охлаждающей водой. Установленный перед компрессором холодильник, снижая температуру поступающего газа, увеличивает плотность, массовый расход и потребляемую мощность. С энергетической точки зрения предварительное охлаждение нерационально, так как экономия работы сжатия за счет охлаждения невелика из-за повышения потребляемой мощности при увеличении плотности газа.
Применение промежуточных холодильников увеличивает металлоемкость и усложняет конструкцию машины, повышает ее себестоимость на 20—30 % по сравнению с неох-лаждаемыми компрессорами. Использование охлаждающей воды увеличивает эксплуатационные затраты. Применение охлаждения газа должно основываться на результатах технико-экономических расчетов. Считается возможным изготовлять неохлаждаемые компрессоры стационарного типа с 8 2, а при сжатии пропана или фреона-12 (k = 1,14) при е > 10. При дефиците воды используется воздушное охлаждение.
Теплоту, отводимую от компрессоров, можно иногда использовать в качестве вторичных энергетических ресурсов для обогрева теплиц, зданий и др.
Охлаждение впрыском жидкости в поток перекачиваемого газа можно применять, если впрыскиваемая жидкость существенно не влияет на свойства перекачиваемых газов (вода — воздух; жидкий аммиак — аммиак; слабый раствор азотной кислоты — нитрозный газ). Охлаждение газа происходит за счет теплоты испарения жидкости. Жидкость от постороннего источника через распыливающие форсунки впрыскивается непосредственно в проточную часть компрессора. Например, при впрыскивании 1% по массе воды температура сжимаемого воздуха снижается примерно на 25°С.
При применении предварительного охлаждения газа обычно приходится использовать специальную холодильную установку. Так, например, на компрессорных станциях магистральных северных газопроводов газ предварительно охлаждается во избежание подтаивания грунта в зоне трубопровода.
Влияние начального давления на работу сжатия компрессора
Давление всасывания воздушного компрессора зависит от барометрического давления, определяемого высотой установки компрессора над уровнем моря. Для дожимающих и циркуляционных компрессоров давление всасывания может изменяться в широких пределах в соответствии с требованиями
технологических процессов. Поэтому необходимо определить, как зависит работа, затрачиваемая на сжатие газа в ступени компрессора, от давления всасывания.
Для определения отношения давления, соответствующего максимуму работы, продифференцируем зависимость.
Применение тепловых диаграмм при расчете поршневого компрессора
Выполнение теплового расчета поршневого компрессора с использованием тепловых s, Т- и s, ft-диаграмм позволяет существенно упростить расчет. На s, 7-диаграмму (рис. 2.8) наносятся изобары (р = — const), а также линии постоянной энтальпии (h — const).
Удельная энтальпия идеального газа зависит только от температуры. Удельная энтальпия реального газа зависит от температуры и давления, поэтому линии постоянной энтальпии представляют собой кривые, которые с уменьшением энтропии в области относительно низких давлений.
Линия, разграничивающая эти области и проходящая через точку К, соответствующую состоянию газа, при котором ε == 1, называется кривой инверсии.
Параметры реального газа на этой кривой подчиняются уравнению состояния идеального газа. Область диаграмм, расположенная справа от кривой инверсии, соответствует состояниям, при которых дросселирование газа от давления Pi до давления р2 приводит к снижению температуры на A7 = 7i — Т2. Для состояний газа, охватываемых областью диаграмм слева от кривой инверсии, характерно повышение температуры при дросселировании.
На диаграмме имеется граничная кривая, проходящая через точку К. и соответствующая критическим параметрам состояния газа; она разграничивает диаграмму на две области. Над кривой находится область сухого пара или газа; под кривой — область влажного пара или газа.
Ha s, Т-диаграмме q изображается площадью под линией процесса, ограниченной двумя ординатами. Энтропия газа возрастает, если процесс изменения его состояния осуществляется с подводом теплоты, и убывает, если этот процесс происходит с отводом теплоты. В случае же, еслц процесс изменения состояния газа идет без теплообмена (и без потерь), энтропия газа не изменяется.
На диаграмме показаны изотермический (7 = const линия 1-2) у изоэнтропный (n-const линия 1-2′) и политропный (линия 1-2″ и 1-2″) процессы сжатия идеального газа от давления р1 до давления р2. Количество теплоты, отводимой от газа в изотермическом процессе, выражается площадью диаграммы под линией 1-2.
Изоэнтропический процесс характеризуется отсутствием теплообмена и потерь, вследствие чего для этого процесса s = const. Что касается политропного процесса, то в случае, если показатель политропы п меньше показателя изоэнтро-пы, процесс происходит с отводом теплоты и кривая процесса 1-2″ располагается левее линии изоэнтропического процесса 1-2′.
Количество подводимой к 1 кг газа теплоты изображается площадью под кривой 1-2″ (+q), а от-водимой — площадью под кривой 1-2″ (—q). s, Г-диаграмма позволяет найти и количество теплоты, отводимой от 1 кг газа в холодильнике.
При условии охлаждения газа от температуры нагнетания Т2 до температуры всасывания Т1 количество теплоты равно площади диаграммы под отрезком изобары р2» соответствующим изменению температуры газа от Т2 до Т1.
Суммарное удельное количество теплоты qc, отводимое от идеального газа в цилиндре и холодильнике при охлаждении газа до температуры Ти равно удельной работе цикла
qс = l = q1 + q2,
где q2 — удельное количество теплоты, подводимое к газу (или отводимое от него) в цилиндре; q1 — удельное количество теплоты, отводимое от газа в холодильнике.
В изотермическом цикле q1 = О и l = q2. В изоэнтропическом цикле q2 = 0 и l = q1. В политропном цикле l = q2 + q1 причем q2 может быть положительным в зависимости от» того, подводится теплота к газу в цилиндре в процессе сжатия или отводится от него.
При сжатии реального газа связь между количеством теплоты, отведенной от газа в цилиндре и холодильнике, и работой 1, затраченной на осуществление цикла в ступени, выражается зависимостью
qc = l — (h» — h1),
где h1 — энтальпия всасываемого в ступень газа; h» — энтальпия газа, выходящего из холодильника.
Для реального газа даже если температура газа, выходящего из холодильника T», равна температуре всасываемого в ступень газа Т1. Работа и теплота в s, T-диаграмме при изотермическом и изоэнтропном сжатии реального газа показаны на рис. 2.9.
Из рисунка видно, что в зависимости от того, какой знак имеет разность h» — h1 работа, затрачиваемая в изотермическом и изоэнтропном сжатии реального газа, может превышать количество отводимой теплоты или быть меньше. Аналогично и при политропном сжатии реального газа.
В общем случае если сжатие осуществляется при состояниях газа, соответствующих области, расположенной на s, Г-диаграмме левее и выше кривой инверсии (высокие давления и температуры газа), затраченная работа превышаем количество теплоты qc, отводимое от газа в цилиндре и холодильнике. Если сжатие осуществляется при состояниях газа, соответствующих области, расположенной на s, Г-диаграмме правее кривой инверсии (низкие давления и температуры газа), затраченная работа меньше количества теплоты — qc.
В s, T-диаграмме (рис. 2.10) по горизонтальной оси откладывается удельная энтропия s и по вертикальной оси — удельная энтальпия Л. На диаграмму нанесены изобары р = const и изотермы Т = const, s, h-диаграмма применяется для определения удельной работы в изо энт р опическом. реального газа ta и удельного количества теплоты q1 отводимого от реального газа в холодильнике.
Электронная библиотека
Основная цель термодинамического расчета компрессора – это определение работы (мощности), которую следует затратить, чтобы получить некоторое количество газа при заданных параметрах начала и конца сжатия. Работу определяют по уравнению (9.1).
Когда процесс сжатия идет по изотерме pv = const, работа идеального «изотермического» компрессора, отнесенная к 1 кг газа, с учетом того, что
При адиабатном сжатии работа сжатия равна:
Работу «адиабатного» компрессора находят из выражения:
Пользуясь выражением (9.4), работу компрессора удобно рассчитывать с помощью hS-диаграммы.
Как адиабатный, так и изотермический процессы сжатия газа могут рассматриваться только как теоретические. В действительности процессы сжатия идут по политропе, имеющей переменный показатель. Показатель политропы зависит от интенсивности теплообмена в процессе сжатия газа в компрессоре:
· для охлаждаемого компрессора k > n > 1;
· для неохлаждаемого компрессора (центробежного, осевого) n > k.
Для политропного процесса работа сжатия равна:
Следовательно, работу «политропного» компрессора можно найти по формуле:
Среднее значение показателя политропы, как правило, определяется по параметрам газа в начале и конце процесса сжатия.
В случае охлаждаемого компрессора (рис.
lиз Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00
Блог об энергетике
энергетика простыми словами
Основные термодинамические процессы
Основными процессами в термодинамике являются:
- изохорный, протекающий при постоянном объеме;
- изобарный, протекающий при постоянном давлении;
- изотермический, происходящий при постоянной температуре;
- адиабатный, при котором теплообмен с окружающей средой отсутствует;
- политропный, удовлетворяющий уравнению pv n = const.
Изохорный, изобарный, изотермический и адиабатный процессы являются частными случаями политропного процесса.
При исследовании термодинамических процессов определяют:
- уравнение процесса в p—v иT—s координатах;
- связь между параметрами состояния газа;
- изменение внутренней энергии;
- величину внешней работы;
- количество подведенной теплоты на осуществление процесса или количество отведенной теплоты.
Изохорный процесс

При изохорном процессе выполняется условие v = const.
Из уравнения состояния идеального газа (pv = RT) следует:
т. е. давление газа прямо пропорционально его абсолютной температуре:
Работа расширения в изохорном процессе равна нулю (l = 0), так как объем рабочего тела не меняется (Δv = const).
Количество теплоты, подведенной к рабочему телу в процессе 1-2 при cv = const определяется по формуле:
Т. к.l = 0, то на основании первого закона термодинамики Δu = q, а значит изменение внутренней энергии можно определить по формуле:
Изменение энтропии в изохорном процессе определяется по формуле:
Изобарный процесс
Изобарным называется процесс, протекающий при постоянном давлении p = const. Из уравнения состояния идеального газа слуедует:
т. е. в изобарном процессе объем газа пропорционален его абсолютной температуре.
Работа будет равна:
Количество теплоты при cp = const определяется по формуле:
Изменение энтропии будет равно:
Изотермический процесс
При изотермическом процессе температура рабочего тела остается постоянной T = const, следовательно:
т. е. давление и объем обратно пропорциональны друг другу, так что при изотермическом сжатии давление газа возрастает, а при расширении – снижается.
Работа процесса будет равна:
Так как температура остается неизменной, то и внутренняя энергия идеального газа в изотермическом процессе остается постоянной (Δu = 0) и вся подводимая к рабочему телу теплота полностью превращается в работу расширения:
При изотермическом сжатии от рабочего тела отводится теплота в количестве, равном затраченной на сжатие работе.
Изменение энтропии равно:
Адиабатный процесс
Адиабатным называется процесс изменения состояния газа, который происзодит без теплообмена с окружающей средой. Так как dq = 0, то уравнение первого закона термодинамики для адиабатного процесса будет иметь вид:
В адиабатном процессе работа расширения совершается только за счет расходования внутренней энергии газа, а при сжатии, происходящем за счет действия внешних сил, вся совершаемая ими работа идет на увеличение внутренней энергии газа.
Обозначим теплоемкость в адиабатном процессе через cад, и условие dq = 0 выразим следующим образом:
Это условие говорит о том, что теплоемкость в адиабатном процессе равна нулю (cад = 0).
и уравнение кривой адиабатного процесса (адиабаты) в p, v-диаграмме имеет вид:
В этом выражении k носит название показателя адиабаты (так же ее называют коэффициентом Пуассона).
kвыхлопных газов ДВС = 1,33
Из предыдущих формул следует:
Техническая работа адиабатного процесса (lтехн) равна разности энтальпий начала и конца процесса (i1 – i2).
Адиабатный процесс, происходящий без внутреннего трения в рабочем теле, называется изоэнтропийным. В T, s-диаграмме он изображается вертикальной линией.
Обычно реальные адиабатные процессы протекают при наличии внутреннего трения в рабочем теле, в результате чего всегда выделяется теплота, которая сообщается самому рабочему телу. В таком случае ds > 0, и процесс называется реальным адиабатным процессом.
Политропный процесс
Политропным называется процесс, который описывается уравнением:
Показатель политропы n может принимать любые значения в пределах от -∞ до +∞, но для данного процесса он является постоянной величиной.
Из уравнения политропного процесса и уравнения Клайперона можно получить выражение, устанавливающее связь между p, vи Tв любых двух точках на политропе:
Работа расширения газа в политропном процессе равна:
В случае идеального газа эту формулу можно преобразовать:
Количество подведенной или отведенной в процессе теплоты определяется с помощью первого закона термодинамики:
представляет собой теплоемкость идеального газа в политропном процессе.
При cv, k и n = const cn = const, поэтому политропный процесс иногда определят как процесс с постоянной теплоемкостью.
Политропный процесс имеет обобщающее значение, ибо охватывает всю совокупность основных термодинамических процессов.
Графическое представление политропа в p, v координатах в зависимости от показателя политропа n.
pv 0 = const (n = 0) – изобара;
pv = const (n = 1) – изотерма;
p 0 v = const, p 1/∞ v = const, pv ∞ = const – изохора;
n > 0 – гиперболические кривые,
n По материалам моего конспекта лекций по термодинамике и учебника «Основы энергетики». Автор Г. Ф. Быстрицкий. 2-е изд., испр. и доп. — М. :КНОРУС, 2011. — 352 с.
http://libraryno.ru/9-5-rabota-i-moschnost-na-privod-kompressora-teplotexnikavinogradov/
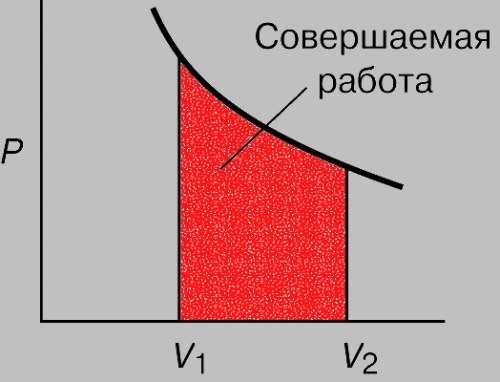
Как определить работу при изотермическом процессе
При изотермическом процессе, который протекает при постоянной температуре, газ выполняет работу за счет расширения. Расширение газа характеризуется его объемом, который изменяется в зависимости от изменения давления газа, обусловленного внешними воздействиями.
Вам понадобится
- — герметичный сосуд с поршнем;
- — весы;
- — термометр;
- — линейка.
Инструкция
Рассчитайте работу газа при постоянной температуре. Для этого определите, какой газ выполняет работу, и рассчитайте его молярную массу. С помощью периодической таблицы найдите молекулярную массу, которая численно равна молярной массе, измеренной в г/моль.
Найдите массу газа. Для этого откачайте воздух из герметичного сосуда и взвесьте его на весах. После этого закачайте газ, работа которого определяется, и снова взвесьте сосуд. Разность масс пустого и заполненного сосудов и будет равна массе газа. Измеряйте ее в граммах.
Измерьте при помощи термометра температуру газа. При изотермическом процессе она будет постоянна. Если измерение производится при комнатной температуре, достаточно измерить температуру окружающего воздуха. Измерения произведите в Кельвинах. Для этого к температуре, измеренной в градусах Цельсия, прибавьте число 273.
Определите начальный и конечный объем газа при выполнении работы. Для этого сосуд берите с подвижным поршнем, и, вычисляя уровень его подъема, рассчитайте первичный и вторичный объем геометрическими методами. Для этого используйте формулу для объема цилиндра V=π•R²•h, где π≈3,14, R – радиус цилиндра, h его высота.
Рассчитайте работу газа при изотермическом процессе. Для этого поделите массу газа m на его молярную массу M. Полеченный результат умножьте на универсальную газовую постоянную R=8,31 и значение температуры Т в Кельвинах. Полученный результат умножьте на натуральный логарифм из отношения конечного и начального объемов V2 и V1, A = m/M•R•T•ln(V2/V1).
В том случае, когда известно количество теплоты Q, которое получило тело при изотермическом процессе, используйте второе начало термодинамики Q = ∆U + A. Где A – работа газа, а ΔU – изменение его внутренней энергии. Поскольку изменение внутренней энергии зависит от температуры, а при изотермическом процессе она остается постоянной, то ΔU=0. В этом случае работа газа равна теплоте, переданной ему Q = A.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.